Effects of nuclear deformation and surface polarization on proton-emission half-lives

Proton radioactivity is a process in which one proton is spontaneously emitted from the parent nucleus. This rare decay phenomenon was first observed in $ ^{53}\text{Co}^m $ in 1970 [1]. Subsequently, the ground-state proton emissions were reported in $ ^{151}\text{Lu} $ [2] and $ ^{147}\text{Tm} $ [3]. To date, over 40 proton emitters, ranging from $ ^{53}\text{Co}^m $ to $ ^{185}\text{Bi} $, have been experimentally identified, including both ground-state and isomeric transitions. These proton emitters, characterized by their negative proton separation energy, are usually the neutron-deficient nuclei closed to the proton drip line, which represents the fundamental limit of nuclear existence [4]. Thus, researches on proton radioactivity would provide valuable insights into the nuclear structure of proton-rich nuclei and the properties of exotic nuclei beyond the stability limit.

To investigate the mechanism of proton emission, various theoretical models have been developed, such as Gamow-like model [5], coupled channels description [6, 7], unified fission model (UFM) [8, 9], effective liquid-drop model (ELDM) [10], generalized [11, 12] liquid-drop model (GLDM), covariant density functional theory (CDFT) [13, 14], etc. Among these theoretical models, the key point of proton emission is determining daughter-proton interactions, the well established approaches main include Woods-Saxon potential [15], $ \cosh $ potential [16], Jeukenne, Lejeune and Mahaux (JLM) interaction [17], density-dependent M3Y interaction (DDM3Y) [17−19], Skyrme interaction [20, 21], Yukawa effective interaction [22], etc. Within the well constructed interactions, the penetration probability could then be determined using the Wentzel–Kramers–Brillouin (WKB) approximation [17, 18, 23], distorted wave Born approximation (DWBA) [15] and other methods. All of these theoretical methods could give satisfactory descriptions of proton emission from different perspectives.

However, the nuclear surface polarization, an exotic phenomenon linked to the geometry of nuclei and the anisotropic diffuseness of nuclear density distribution, has not been included in previous research on proton emission. In Ref. [24], researchers successfully developed a parametrization of surface polarization for deformed nuclei, calculating the corresponding parameters of various nuclides using energy density functional (EDF) theory based on the Skyrme effective interaction. In Refs. [25−27], the authors proposed an improved density dependent cluster model, which incorporated the anisotropic nuclear surface diffuseness of deformed nucleus into the study of α-decay and cluster radioactivity, as well as explored the effects of nuclear diffuseness anisotropy and polarization on their half-lives. Within this correction, the improved model known as DDCM+ significantly enhanced its accuracy compared with the original model. Inspired by these works [25−27], we tend to investigate the effect of polarization on proton radioactivity in this work.

Recently, two branches of proton emission from the high angular momentum excited state $ 19/2^- $ of $ ^{53}\text{Co}^m $ have been successfully identified in experiment [28]. As the first observed proton emitter, research on $ ^{53}\text{Co}^m $ is crucial for understanding high spin neutron-deficient nuclei, and its daughter nucleus, $ ^{52}\text{Fe} $, holds significant value in astrophysics research as the endpoint of $ rp $-process at specific temperature and density conditions [29−31]. Additionally, it also provides an opportunity to study the exchange symmetry between neutrons and protons in $ fp $-shell [32]. In this work, the newly observed proton emission branches are also included, which is expected to deepen our understanding of $ ^{53}\text{Co}^m $.

The remaining parts of this article are organized as follows. The details of theoretical framework are presented in Sec. II. In Sec. III, we firstly discuss the effect of deformation and polarization on the proton decay width and spectroscopic factors. Then we continue to present the theoretical half-lives, in which a new deformation and diffuseness dependent spectroscopic factor form is proposed. Noticeably, the new observed proton-emission branches of $ ^{53}\text{Co}^m $ are also discussed. Finally, a summary is given in Sec. IV.

Most proton emitters are far from magic nuclei, so the deformation of daughter nuclei is usually not negligible. Meanwhile, the deformation of proton is extremely small, so the system is constructed by a proton and a deformed nucleus. The total interaction between the proton and daughter nucleus is

where r is the distance between the centers of emitted proton and daughter nucleus, and θ is the polar angle while the axis of deformation serves as the polar axis. Proton to be emitted in parent nucleus is in the quasi-bound state denoted by $ n\ell_j $, and emits by tunneling phenomenon through the Coulomb potential barrier. The reduced mass of this binary system is $ m_\mu=m_pm_D/(m_p+m_D) $, where $ m_p $ and $ m_D $ are respectively the mass of proton and daughter nucleus.

In this work, the nuclear potential $ V_N(r,\theta) $ is chosen as Woods-Saxon potential to facilitate the consideration of deformation and polarization

For spherical nucleus, radius parameter $ R_N $ and diffuseness parameter $ a_N $ are both constants. But for axially deformed nucleus, the radius of the potential is changed in each θ, which can be expanded by spherical harmonics

where $ \beta_2 $ and $ \beta_4 $ are respectively quadrupole and hexadecapole deformation parameters, $ Y_{\ell m} $ is spherical harmonics. Additionally, nuclear surface polarization makes $ a_N $ lose the anisotropy and be a function of θ. Considering the difference between the normal and radial directions of the deformed surface, the final diffuseness parameter with axial deformation and polarization is given by [24]

where $ \tilde{\beta}_2 $ and $ \tilde{\beta}_4 $ are polarization parameters, representing the mode and degree of the nuclear surface polarization.

The next part of interaction potential is Coulomb potential. On the condition of spherical daughter nucleus with uniformly distributed charge, the Coulomb potential created by the charge of nucleus can be easily calculated by classical electrodynamics, which is independent with the orientation angle θ

where $ Z_De $ and $ Z_pe $ are the charge of daughter nucleus and single proton, and $ R_{C0} $ is the radius of charge distribution. However, the deformed Coulomb potential cannot be determined by changing the radius straightforwardly. Deformation of Coulomb potential is usually considered by density dependent model, but this cannot give an analytical result. In this work, we consider this deformed Coulomb potential by multipole expansion. In spherical coordinates, the anisotropy Coulomb potential is expanded as [33]

where $ K_\lambda(r,\theta,\phi) $ is a function of Coulomb radius $ R_C(\theta,\phi)=R_{C0}\left[1+\beta_2Y_{20}(\theta)+\beta_4Y_{40}(\theta)\right] $

In our work, considering the axial deformation, the radius $ R_C $ and $ K_\lambda $ is independent with ϕ, and those terms including $ e^{in\phi^\prime} $ in $ Y^*_{\lambda\mu}(\theta^\prime,\phi^\prime) $ will be $ 0 $ after integrated, so only $ \mu=0 $ terms survives when $ \lambda\neq0 $. Finally, we conclude that the final expression of axially deformed Coulomb potential is

which is the multipole expansion for Coulomb potential of axially deformed nuclei, where λ can only be taken as even numbers. The diffuseness of charge distribution is neglected in this result, justified by the limited impact at large distances of the charge diffuseness within a confined area on the Coulomb potential, so expanded deformed Coulomb potential Eq. (8) with neglected charge diffuseness is used in this work.

The third component of potential is spin-orbit potential. Different from α particle, emitted proton has spin angular momentum, so the spin-orbit interaction potential should be considered. The state of proton $ j^\pi $ is determined by the selection rule of angular momentum and parity in proton emission process [34, 35]

where $ I_{P,D} $ and $ \pi_{P,D} $ are spins and parities of respectively parent and daughter nucleus, and j is the total angular momentum of emitted proton. The minimum value among all possible j is adopted in our calculations [27], except for some certain proton emitter determined in previous research [4, 11, 36]. Based on the quantum number $ \ell $ and j obtained above, the spin-orbit interaction is expressed as Thomas form [15]

where $ V_{so0} $, $ R_{so} $ and $ a_{so} $ are respectively the depth, radius and diffuseness. For a more concise presentation, the values of parameters adopted in the interactions are listed in Table 1. Deformation and nuclear surface polarization, Eqs. (3) and (4), are also applied in this potential, which is similar to Woods-Saxon potential.

Parameters	Values	Parameters	Values
$ R_{C0} $	$ 1.21A_D^{1/3} $	$ V_{so0} $	$ 6.2 $
$ R_{N0} $	$ 1.27A_D^{1/3}-0.1 $ [41, 42]	$ a_{N0} $	$ 0.75 $ [41, 42]
$ R_{so0} $	$ 1.01A_D^{1/3} $	$ a_{so0} $	$ 0.75 $
$ \lambda_\pi^2 $	$ 2.0 $

Table 1.  Parameters of the daughter-proton interaction potential [15, 41, 42]. Values with energy and length dimensions have units of $ \text{MeV} $ and $ \text{fm} $, respectively.

To modify the depth of the nuclear potential, the renormalization factor η is introduced in Eq. (1). In this work, the quasibound state energy is adjusted by η to be equal to the kinetic energy of emitted proton in experiment $ E_0=QA_D/(A_D+1) $, where Q is decay energy and $ A_D $ is the number of nucleons in daughter nuclei. Hence, the approximated depth of Woods-Saxon nuclear potential is determined for each θ by the quasibound condition [34, 37]

where $ r_{1,2,3}(\theta) $ are three classical turning points at θ, i.e., the roots of $ V(r,\theta)=E_0 $. G is the global quantum number determined by the Wildermuth condition [4], which has been used in some previous research on proton radioactivity [4, 9, 11, 37]

From the viewpoint of the shell model, except for highly excited proton emitters, G is usually taken as $ 4 $ or $ 5 $ [4, 11]. Quantum number n denotes the nodes of radial wave function of proton except for the origin.

To calculate the decay width, WKB approximation was employed as a semiclassical method. However, to improve the accuracy of calculation, in this work we choose to use a quantum method, in which the energy and wave function of the quasibound proton should be calculated. Two-potential approach is a method to obtain them [15], but aimed to avoid approximations and decrease possible errors, we choose to directly solve the quasibound wave function. Because Coulomb potential plays a major role at the large distance, the boundary condition of wave function is spherical outgoing Coulomb wave function [38]

where $ F_\ell(kr) $ and $ G_\ell(kr) $ are regular and irregular Coulomb wave functions, and $ N_\ell $ represents a normalization constant. With this boundary condition, the solution of time-independent Schrödinger equation gives the quasibound wave function and a more accurate depth of $ \eta V_{N0} $.

Based on the interaction potential and the wave function, the decay width, as a function of θ, can be calculated using the distorted wave Born approximation (DWBA) approach [15]

with $ \delta V_C^\theta(r)=V_C^\theta(r)-Z_pZ_De^2/(4\pi\varepsilon_0r) $. Therefore, the total decay width can be expressed as the average by integration along all orientation angle

The relationship of decay width and half-life is $ T_{1/2}=\hbar\ln{2}/(S_p\Gamma) $, where $ S_p $ is the spectroscopic factor. The value of $ S_p $ is closely related to the structure properties of proton emitters. In spherical cases it can be calculated using the relativistic mean field (RMF) models combined with BCS pairing methods [4], accounting for the probability that the orbital of the emitted proton is unoccupied in the assumed spherical daughter nucleus [34, 39, 40]. However, the deformation would give an important correction to the value of $ S_p $ in deformed cases. It could be calculated as the the internal component multiplied by the amplitude to find the final proton Nilsson state in the initial quasi-particle state more accurately [34].

In this section, we intend to explore the effects of deformation and polarization on half-lives and reproduce the available experimental data on proton emission. The parameters involved in the interaction potential are listed in Table 1, and most of them are taken from Ref. [15]. Recent researches [41, 42] on the radius and diffuseness of the Woods-Saxon potential yield different values from those in Ref. [15]. So we adopt the new values instead, which are determined based on Skyrme energy-density functional approaches. In our calculations, the masses of parent and daughter nuclei are taken from Ref. [43], the spin-parities of parent and daughter nuclei are mainly from Refs. [43, 44], the deformation parameters of daughter nuclei are obtained from Ref. [45], and the kinetic energies $ E_0 $ with uncertainties of emitted protons are taken from experimental decay energies [36]. The experimental half-lives on proton emission are taken from Ref. [43, 44] for comparison. The spectroscopic factors $ S_p^{\text{RMF}} $ calculated using RMF are mainly from Ref. [11].

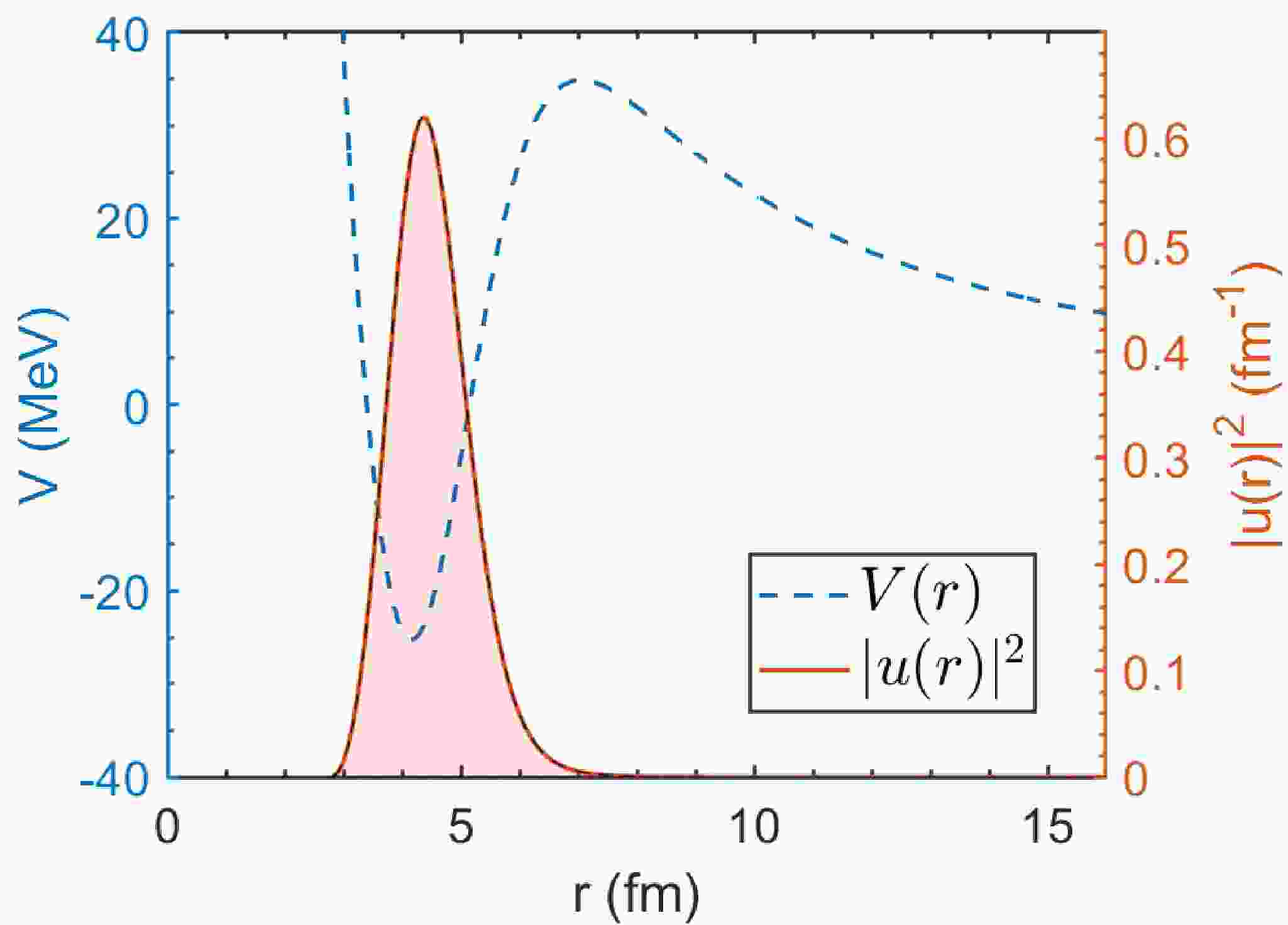
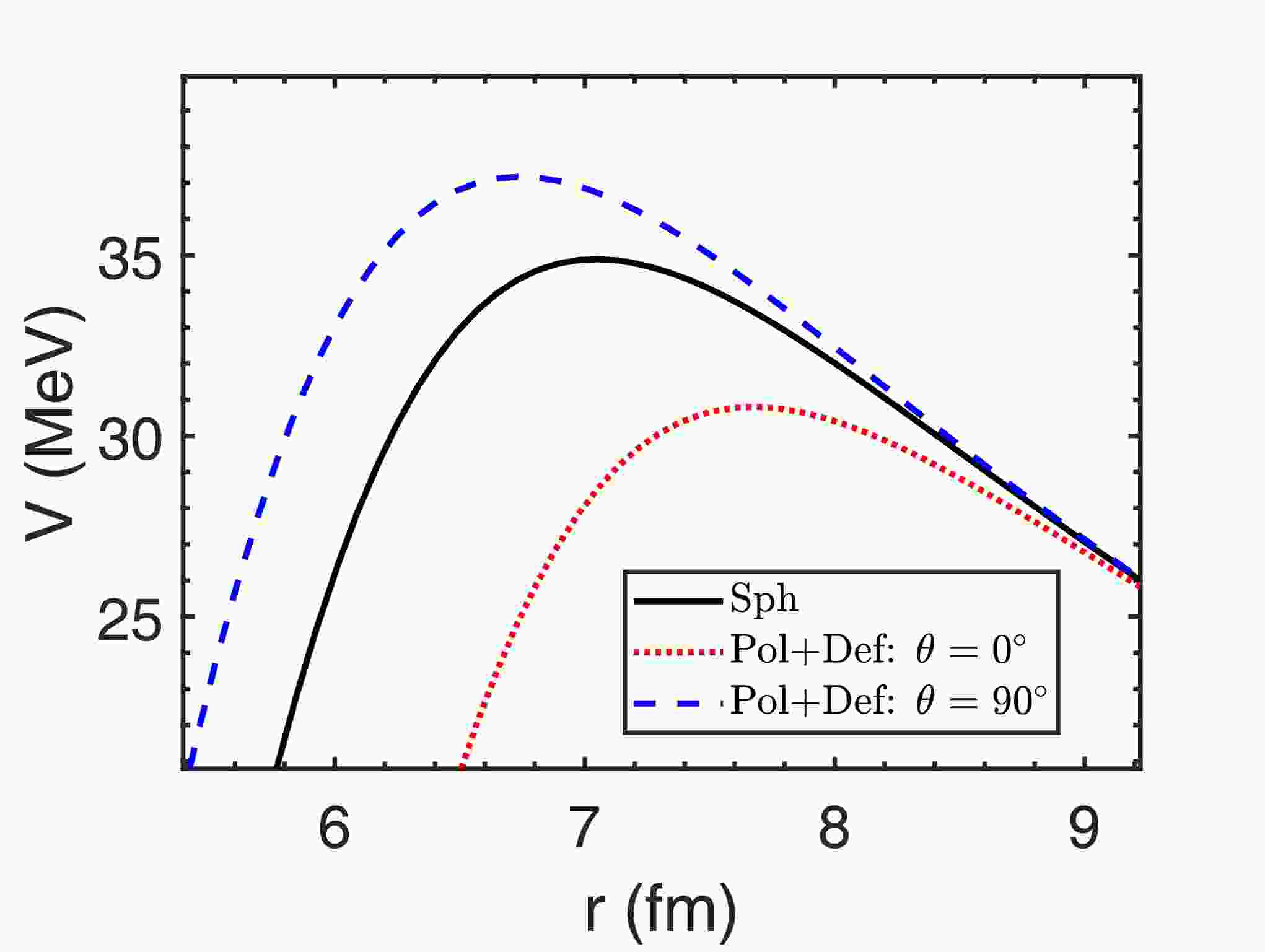
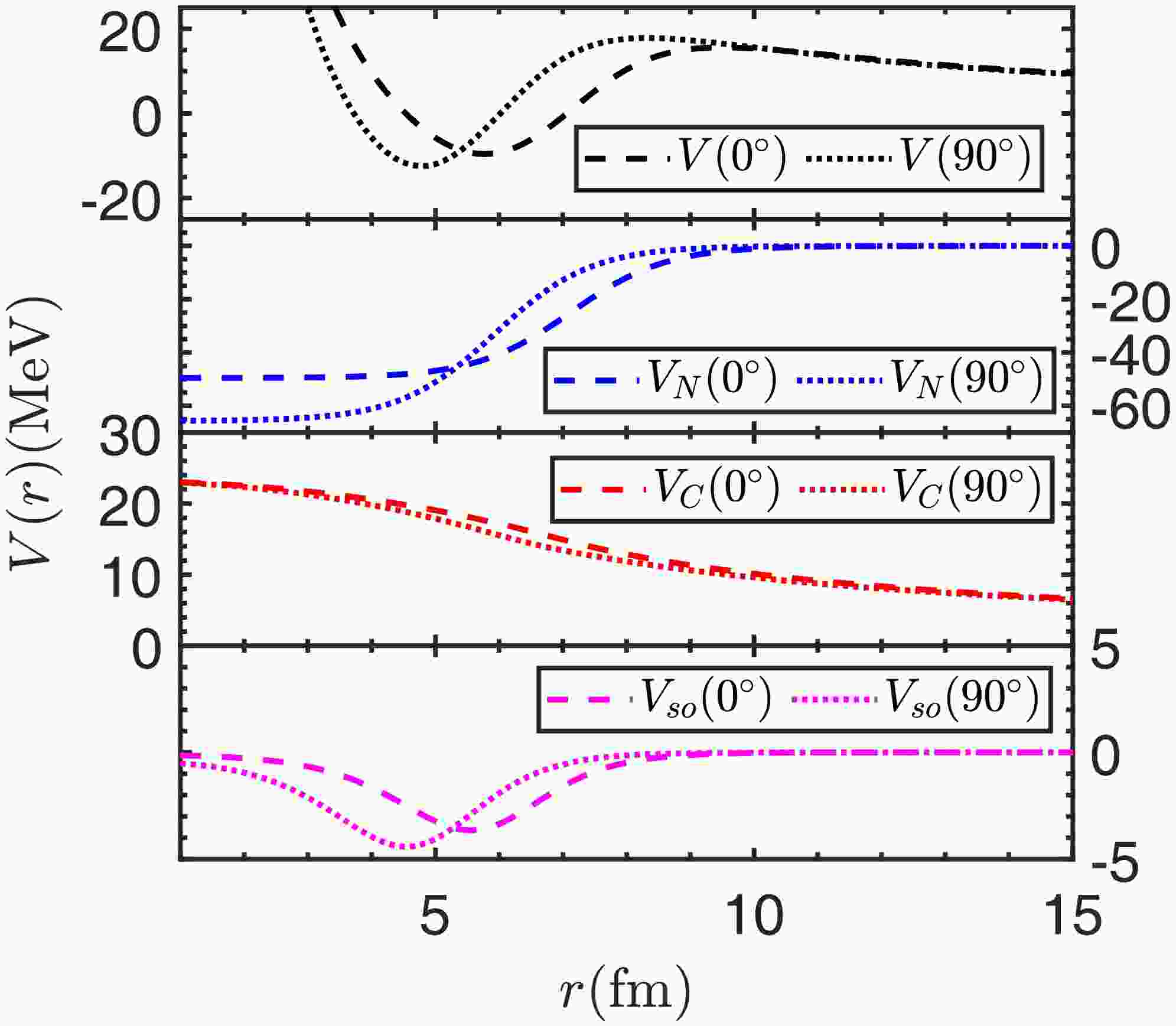
In this subsection, we focus on the deformation of daughter nuclei, which has influence on the daughter-proton interaction and spectroscopic factor. Note that the nuclear surface polarization is not taken into account at this stage. In order to examine the reliability of our calculation, we selected a highly deformed proton emitter $ ^{145}\text{Tm} $ for instance, allowing a more detailed analysis of deformation effect.

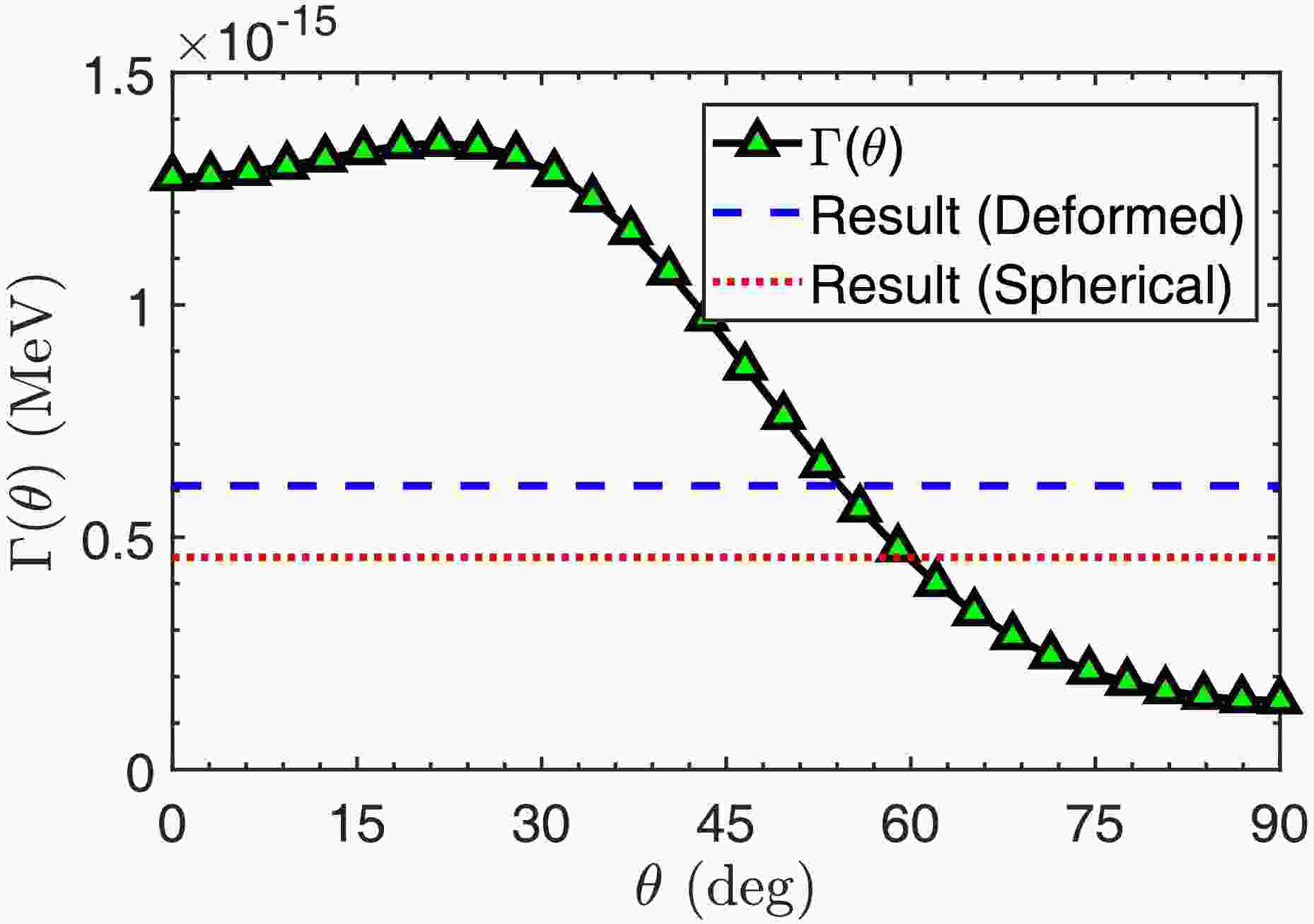
Fig. 1 illustrates the total potential $ V_N(r,\theta) $ for the proton emitter $ ^{145}\text{Tm} $ in two directions $ \theta=0^\circ $ and $ \theta=90^\circ $, together with the three components: the Woods-Saxon nuclear potential $ V_N(r,\theta) $, Coulomb potential $ V_C(r,\theta) $, and spin-orbit interaction potential $ V_{so}(r,\theta) $. The centrifugal potential is not shown in the figure as it has no dependence on the direction θ. As for the total potential, it is evident that the proton to be emitted is bound on a quasibound state by the potential barrier. Although the main contribution to the barrier comes from the Coulomb potential $ V_C(r,\theta) $, the barrier variation with directions results from the nuclear plus spin-orbit interaction potentials. As one can see, the barrier shape between $ r=6-10 $ fm is a direct outcome of the nuclear plus spin-orbit interaction potentials. The barrier height at $ \theta=90^\circ $ is larger than that at $ \theta=0^\circ $ owing to the positive quadrupole deformation $ \beta_2 $. This would bring in more intense quantum tunneling at $ \theta=0^\circ $ compared with $ \theta=90^\circ $. We calculated the decay widths at a discretized grid of direction θ using the DWBA method. Fig. 2 shows the decay width of $ ^{145}\text{Tm} $ as a function of direction θ. In view of the symmetry associated with quadrupole and hexadecapole deformations, the angular distribution is shown only for the angles ranging from $ 0^\circ $ to $ 90^\circ $. As one would expect, the decay width at $ \theta=0^\circ $ is much larger than at $ \theta=90^\circ $, showing an active response to the total potential shown in Fig. 1. Besides, the results calculated respectively with and without deformation are also shown for comparison. It is found that the $ ^{144} $Er deformation overall decreases the half-life of the proton emitter $ ^{145}\text{Tm} $.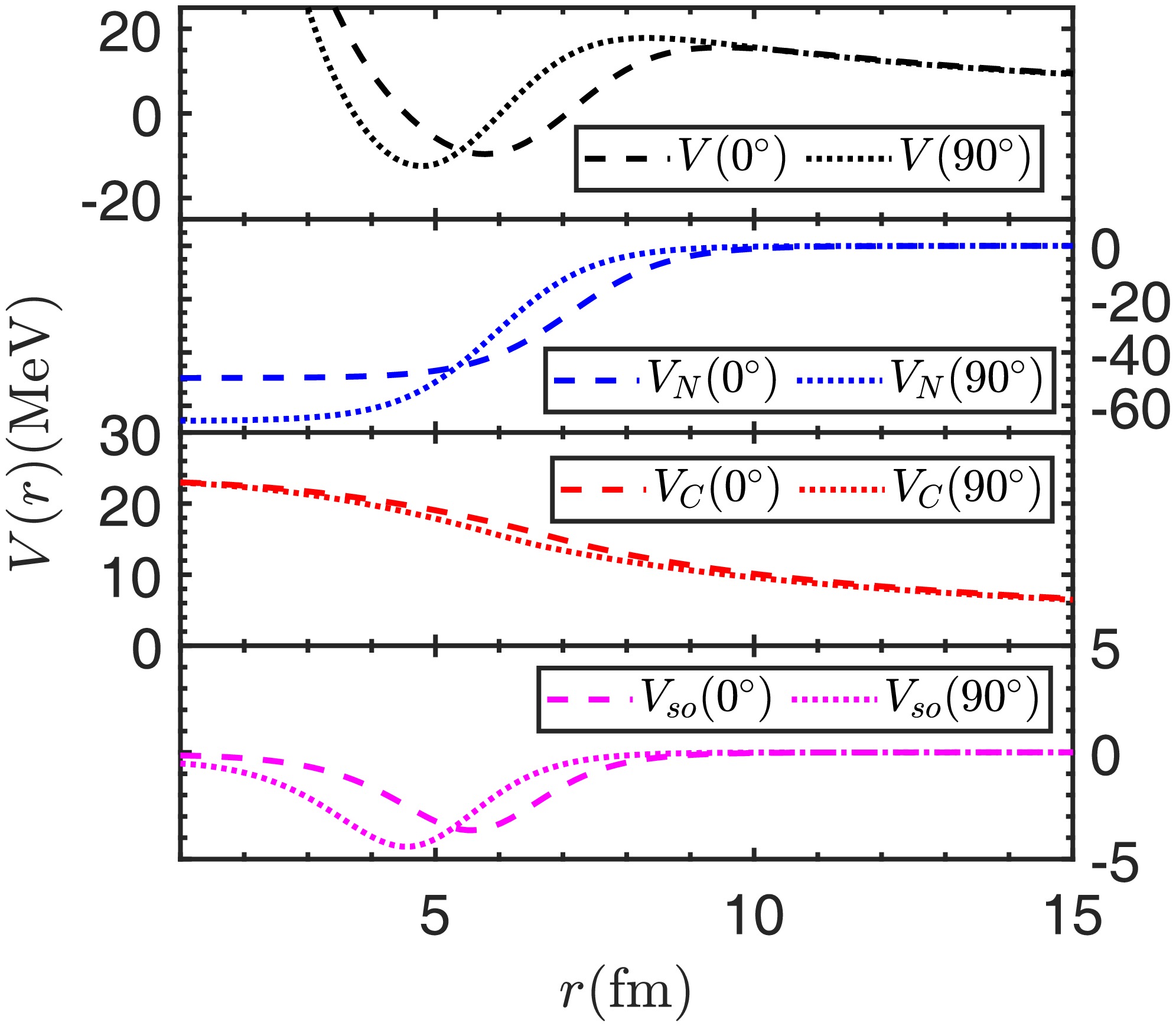

Figure 1.  (color online) Daughter-proton interactions for the proton emission of $ ^{145}\text{Tm} $. The total potential and three components including nuclear potential $ V_N $, Coulomb potential $ V_C $, and spin-orbit potential $ V_{so} $ are shown in two directions $ \theta=0^\circ $ (dashed lines) and $ \theta=90^\circ $ (dotted lines).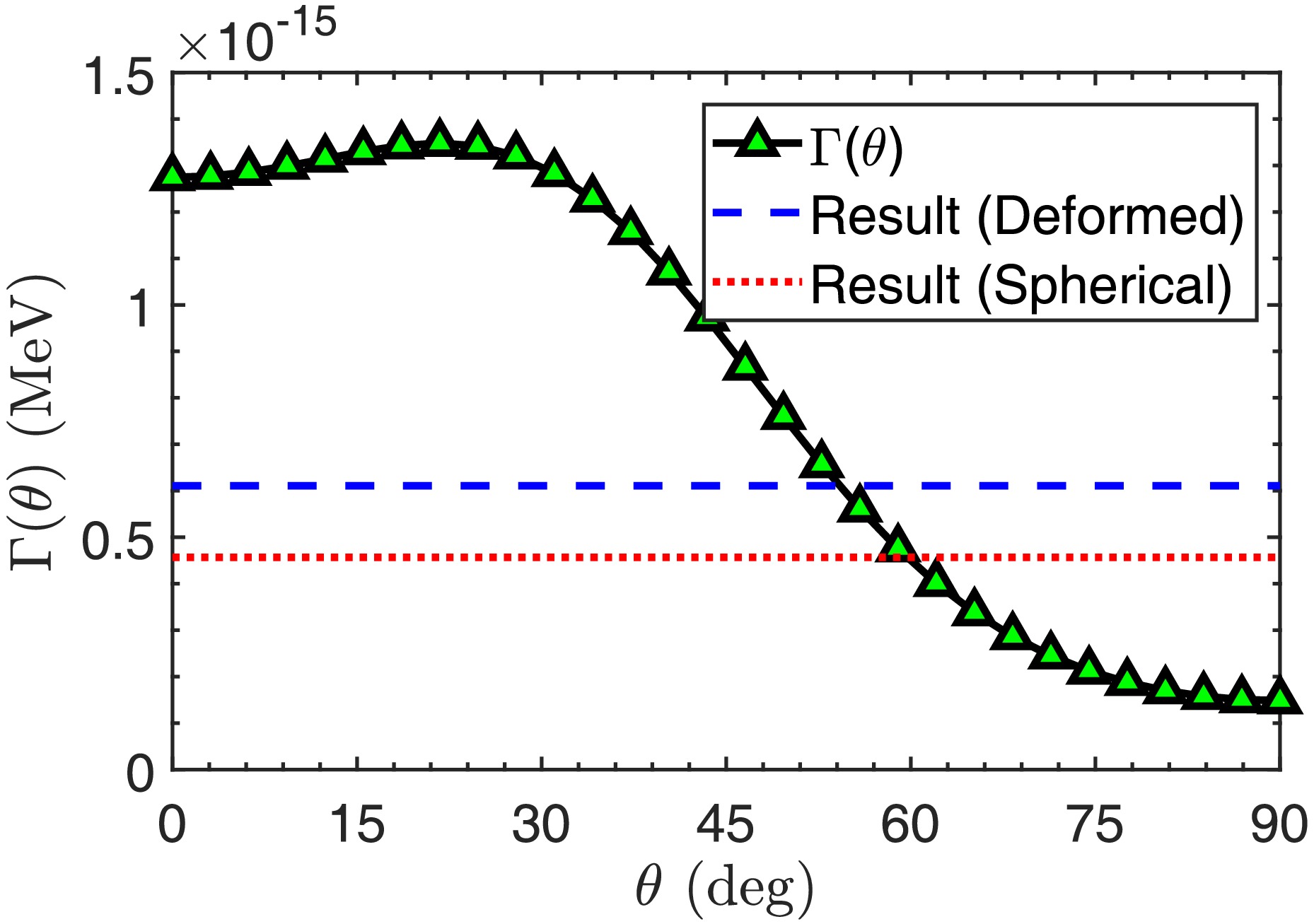

Figure 2.  (color online) Decay widths as a function of direction θ for the proton emission from $ ^{145}\text{Tm} $ into $ ^{144}\text{Er} $. The black curve with green triangle represents $ \Gamma(\theta) $. The red line corresponds to the calculated decay width without deformation, and the blue line represents the overall decay width calculated using Eq. (15).

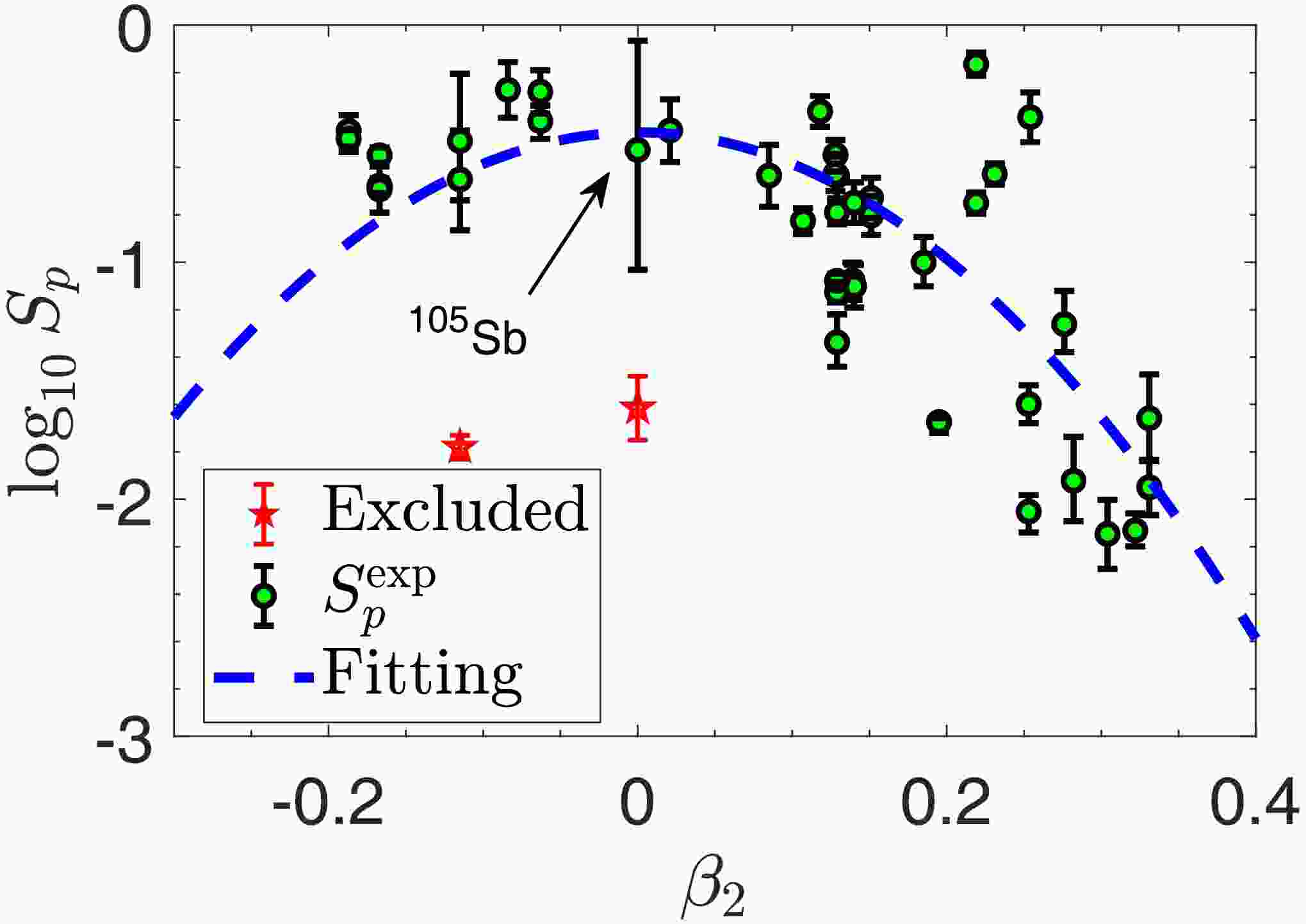
Deformation also affects the spectroscopic factor. Recent researches [16, 36] have detected the logarithmic relationship between $ \log_{10}S_p $ and $ \beta_2 $. In this work, we would like to propose an analytic formula to calculate the spectroscopic factor $ S_p^{\text{def,fit}} $ of various proton emitters. The experimental spectroscopic factors are defined as $ S_p^{\text{exp}}=\hbar\ln2/(T_{1/2}^{\text{exp}}\Gamma) $, where Γ is the decay width calculated using the DWBA method. Fig. 3 shows the experimental spectroscopic factors as a function of the quadrupole deformation of daughter nuclei for $ 43 $ proton emitters with the uncertainty of experimental decay energy. Except for $ ^{105} $Sb, for most emitters, the consequent uncertainties of $ S_p $ is not considerable. Therefore, a strong correlation between $ S_p^{\text{exp}} $ and $ \beta_{2} $ is in evidence: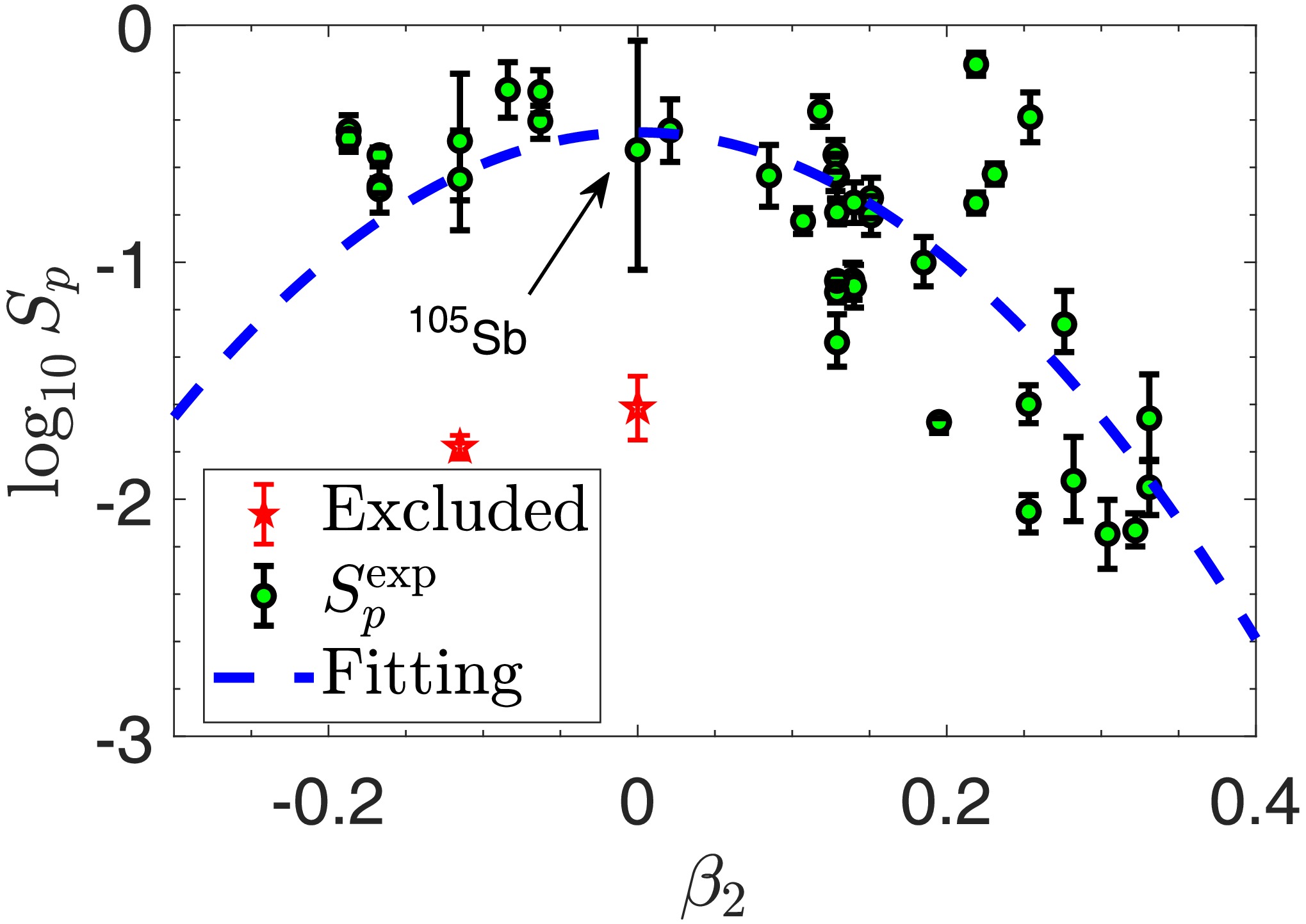

Figure 3.  (color online) Experimental spectroscopic factors $ S_p^{\text{exp}} $ as a function of the quadrupole deformation of daughter nuclei for $ 43 $ proton emitters along with the uncertainties arising from the experimental decay energies. Except for $ ^{105}\text{Sb} $, most emitters have small uncertainties. $ ^{185}\text{Bi} $ and $ ^{177}\text{Tl}^m $ are labeled by red pentagrams due to their strong shell effect. Blue lines are the fitting to the experimental spectroscopic factors $ S_p^{\text{def,fit}} $ except $ ^{185}\text{Bi} $ and $ ^{177}\text{Tl}^m $.

After the fitting to the experimental spectroscopic factors, the parameters in Eq. (16) are determined as $ b_1=-13.352 $, $ b_2=-0.452 $. Note that some nuclei near the proton magic number, such as $ ^{185}\text{Bi} $ and $ ^{177}\text{Tl}^m $, are excluded because their strong shell effect doninates over the deformation effect. The results of half-lives related to $ S_p^{\text{def,fit}} $ will be discussed in subsequent subsections.

To summarize this subsection, the deformation of daughter nuclei mainly affects the Woods-Saxon nuclear potential plus spin-orbit coupling potential, resulting in anisotropy in the probability of proton emission along the different directions from proton emitters. On the whole, it has influence on the half-life of proton emission. Besides, a analytic approximate relationship between spectroscopic factors and deformation is explored in detail.

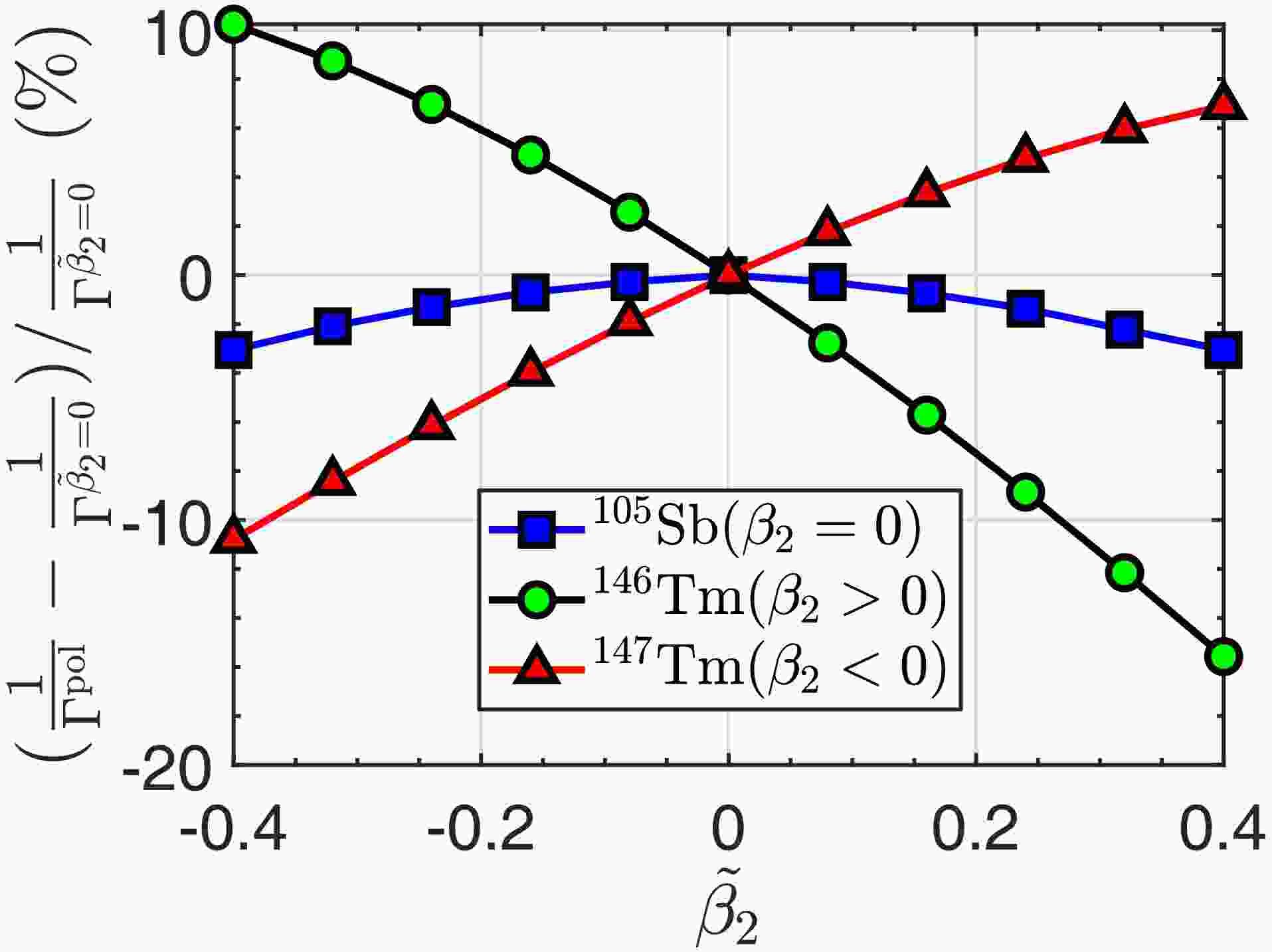
Next, we focus on the proton emitters with polarized daughter nuclei and discuss the effect of nuclear surface polarization. Polarization is parameterized in Ref. [24], where the polarization parameters are given using two functionals SkM* and Sly4 for the nuclei ranging from $ ^{16}\text{O} $ to $ ^{276}\text{Hs} $. Considering the parameters of the two functionals are similar, we only use the result of SkM* functional to give an instance to analyse the polarization effect. In order to distinguish the polarization effect from the deformation effect, we firstly choose three proton emitters, $ ^{105}\text{Sb} $, $ ^{146}\text{Tm} $ and $ ^{147}\text{Tm} $, with different deformation modes for example. Here, we changed the polarization parameter $ \tilde{\beta}_2 $ from negative to positive values within a certain interval and neglected the effect of $ \tilde{\beta}_4 $. The calculated decay widths are illustrated in Fig. 4. As can be seen, the three cases with different deformations exhibit various behavior with the changing polarization parameter $ \tilde{\beta}_2 $. More specifically, the case with positive quadrupole deformation $ \beta_2>0 $ decreases the half-life of $ ^{146} $Tm with increasing the polarization parameter $ \tilde{\beta}_2 $, while the case with negative deformation parameters $ \beta_2<0 $ shows the opposite variation with increasing $ \tilde{\beta}_2 $. The case with $ \beta_2=0 $ shows the relatively smooth variation, where both positive and negative quadrupole polarization lead to a small reduction in the half-life of $ ^{105} $Sb. It is obvious that the polarization effect is closely correlated with nuclear deformation.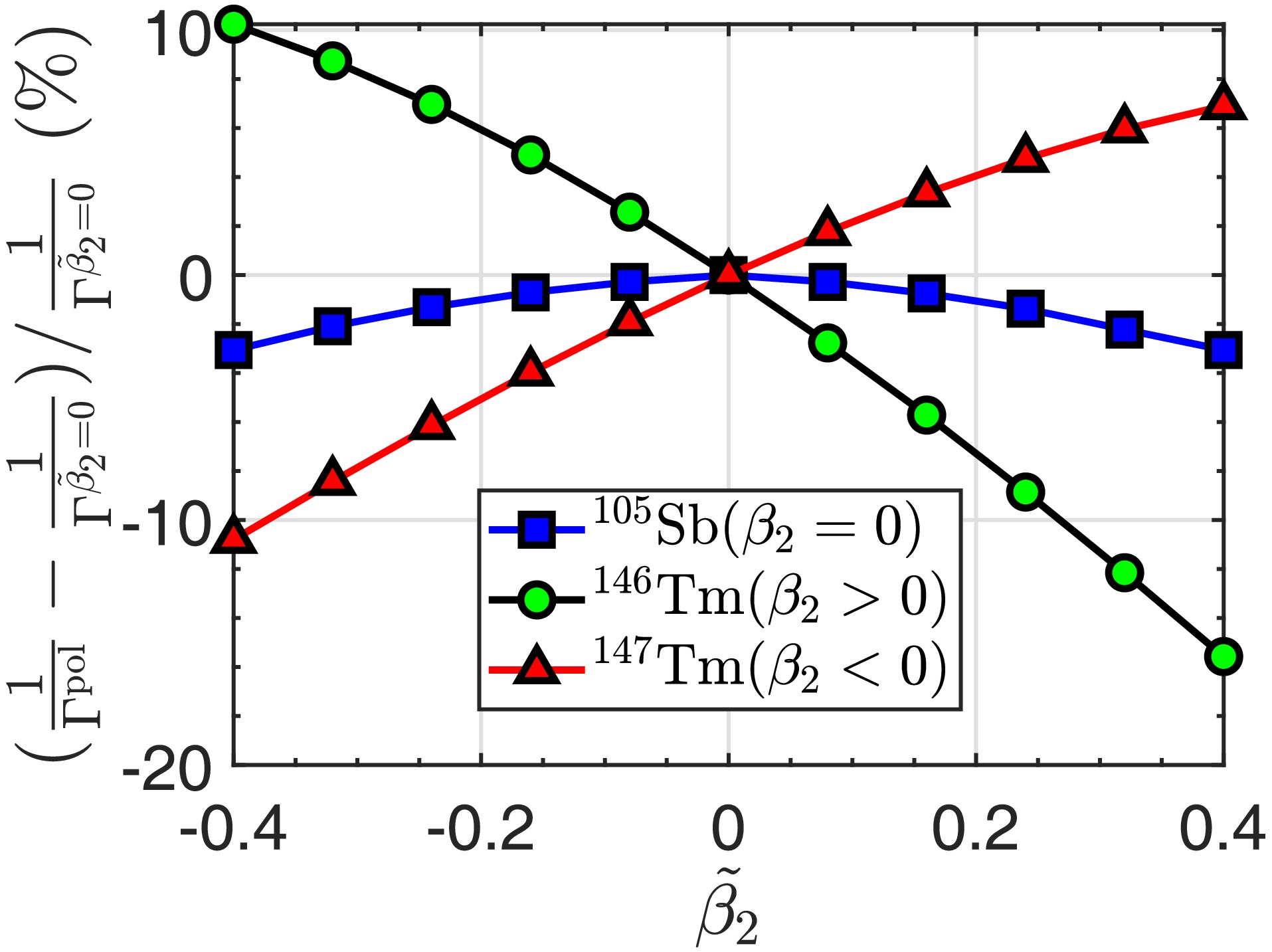

Figure 4.  (color online) Variations in the inverse of calculated decay widths $ 1/\Gamma $ as a function of the polarization parameter $ \tilde{\beta}_2 $ for three different deformed nuclei: (a) $ ^{146}\text{Tm} $ with prolate deformation ($ \beta_2>0 $), (b) $ ^{105}\text{Sb} $ without deformation ($ \beta_2=0 $), and (c) $ ^{147}\text{Tm} $ with oblate deformation ($ \beta_2<0 $).

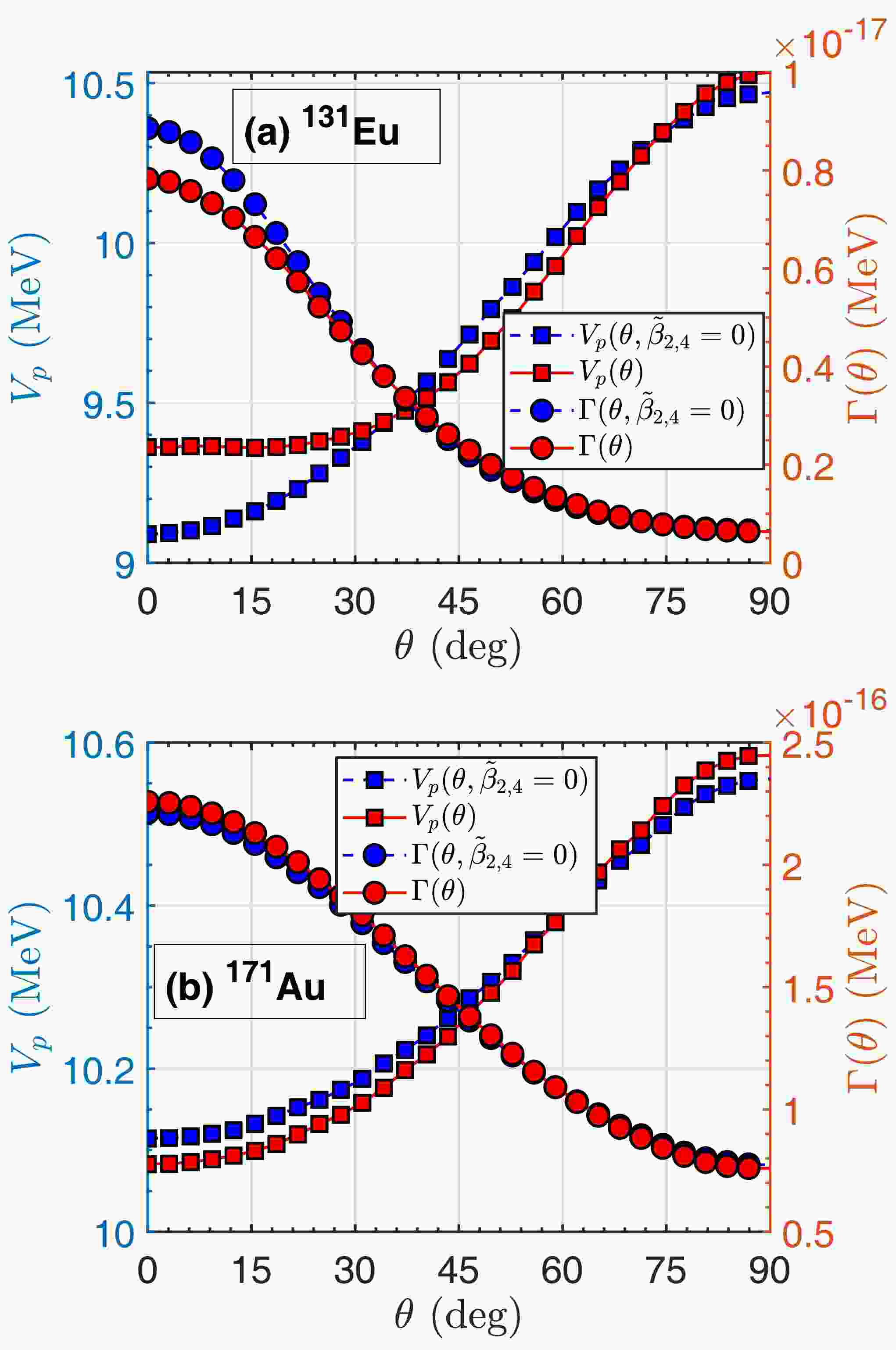
To gain a deeper insight into the surface polarization, we also consider the polarization parameters in reality from Ref. [24]. Two proton emitters $ ^{131}\text{Eu} $ and $ ^{171}\text{Au} $ are chosen due to the strong deformation and different polarization modes of their daughter nuclei. The barrier height $ V_p(\theta) $ along each orientation angle is displayed in Fig. 5 for both of them. Also, the decay widths for each orientation angle are calculated and shown in the figure as well. They are compared with the results calculated without polarization $ \tilde{\beta}_{2,4}=0 $. First of all, nuclear surface polarization has influence on the daughter-proton interaction potential and hence the decay half-life. Second, different polarization lead to various changes in the potential and decay width. It can be seen that the polarization effect is more considerable for $ ^{131} $Eu in particular for small orientation angles θ. In terms of the tendency as shown in Fig. 4, the half-life of $ ^{131} $Eu should be enhanced by the polarization effect due to its prolate daughter nucleus and a negative polarization parameter $ \tilde{\beta}_2 $. Actually, its half-life is still decreased after including the polarization effect. Such an unexpected discrepancy is attributed to the large polarization parameter $ \tilde{\beta}_4>\tilde{\beta}_2 $ in its daughter nucleus $ ^{130}\text{Sm} $. For the proton emitter $ ^{171}\text{Au} $ with the prolate daughter nucleus, the positive $ \tilde{\beta}_2 $ and small $ \tilde{\beta}_4 $ bring in a reduction in its half-life. This is quite consistent with the tendency depicted in Fig. 4.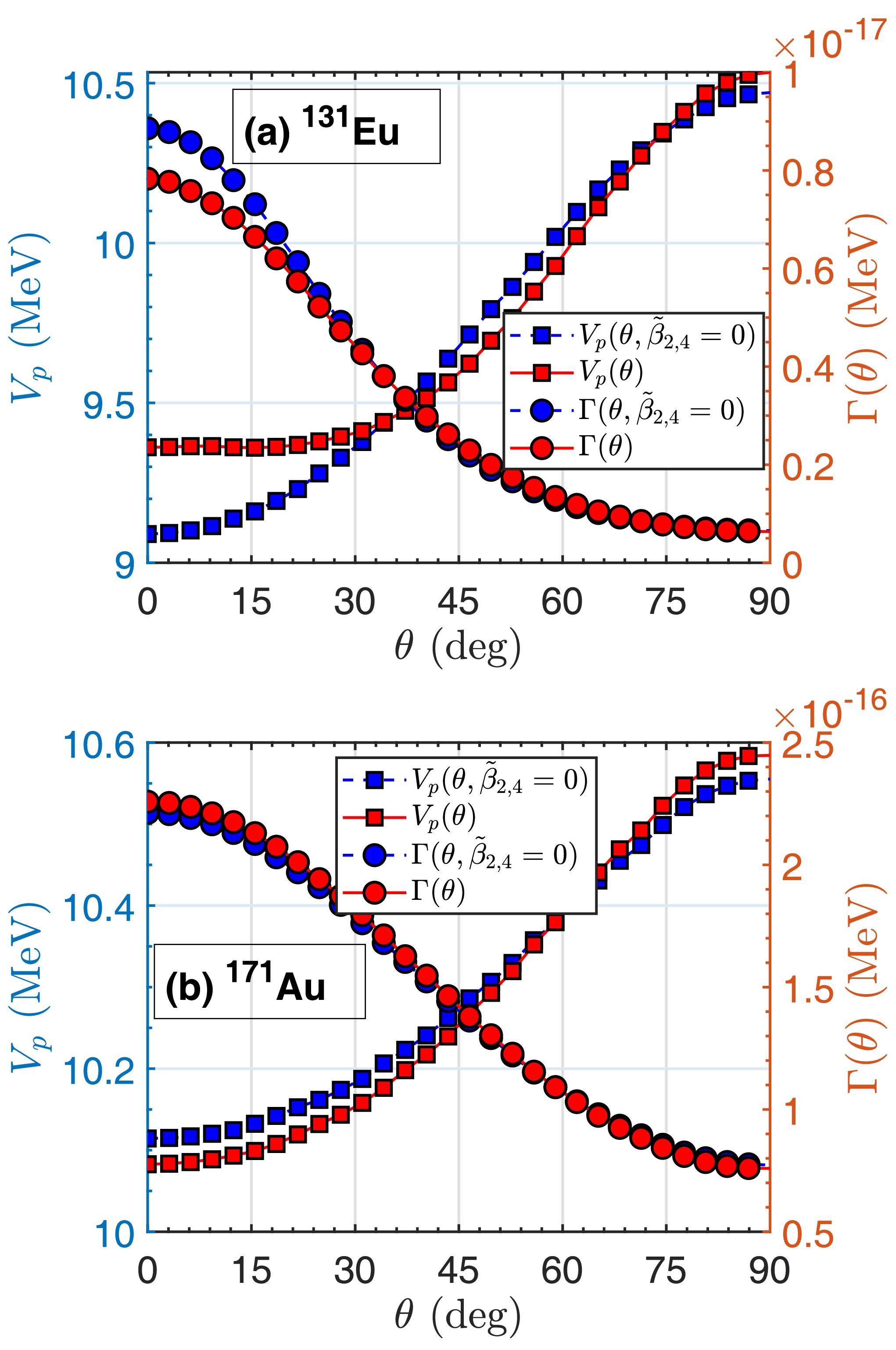

Figure 5.  (color online) The potential barrier height $ V_p(\theta) $ (circles) and decay width $ \Gamma(\theta) $ (squares) as a function of θ in two proton emitters within polarization (a) $ ^{131}\text{Eu} $ and (b) $ ^{171}\text{Au} $, which have opposite signs of quadrupole polarization parameters. Blue lines are calculated on the condition of $ \tilde{\beta}_{2,4}=0 $ for comparison.

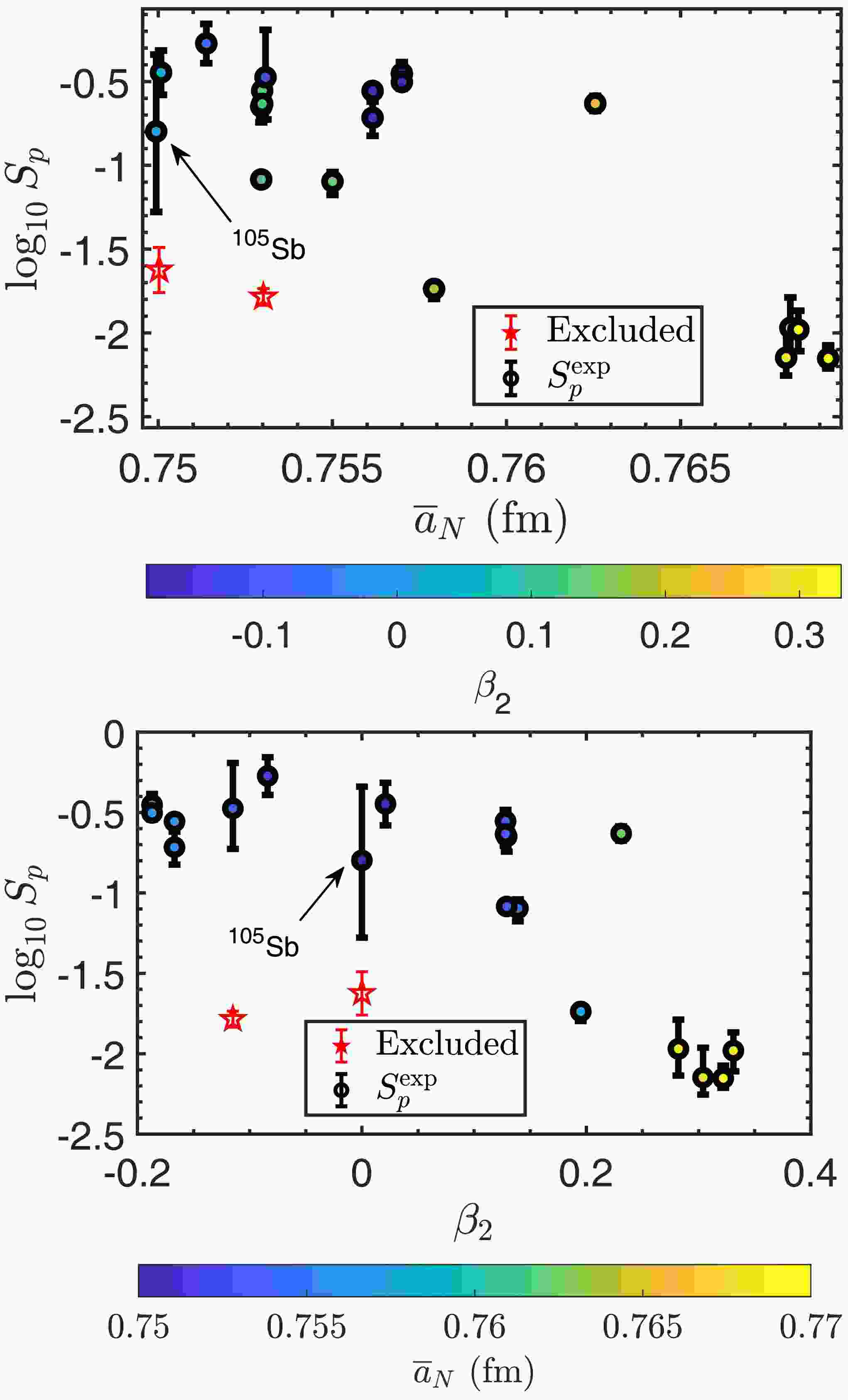
In addition to nuclear deformation, nuclear surface polarization affects the spectroscopic factor $ S_p $ as well. In this work we propose an average quantity to describe the intensity of polarization,

The experimental spectroscopic factors are shown in Fig. 6 for all proton emitters with even-even daughter nuclei. It should be noted that Γ and $ S_p^{\text{exp}}=\hbar\ln2/(T_{1/2}^{\text{exp}}\Gamma) $ are recalculated in this subsection considering the nuclear surface polarization. One can see that there is an obvious relationship between $ S_p $ and $ \overline{a}_N $ except for those special proton emitters with the strong shell effect. For a given $ \beta_2 $, the proton emitter with larger $ \overline{a}_N $ generally exhibits smaller $ S_p $. The underlying physics of this negative correlation requires further research in the future. Moreover, the experimental spectroscopic factors are also shown in Fig. 6 versus the quadrupole deformation $ \beta_{2} $. The correlation between $ S_p $ and $ \beta_{2} $ remains, as illustrated in Fig. 3. Combining the effects of deformation and polarization, we propose a quadratic form for the spectroscopic factor based on the distribution of $ S_p $ in Figs. 3 and 6,

Figure 6.  (color online) Relationship between quadrupole deformation $ \beta_2 $ and average polarization $ \overline{a}_N $ of daughter nuclei and experimental spectroscopic factors $ S_p^{\text{exp}} $ with the uncertainties introduced by the experimental decay energies. Except for two nuclei with strong shell effect $ ^{185}\text{Bi} $ and $ ^{177}\text{Tl}^m $ marked out, larger polarization generally exhibits smaller spectroscopic factor. The uncertainties for some emitters are quite small, making those error bars not obvious.

where the diffuseness parameter $ \overline{a}_N $ is in unit of fm, and the parameters are determined as $ c_1=-9.812 $, $ c_2=-1.901 $, $ c_3=-8.649 $, $ c_4=6.056 $, and the corresponding half-lives will be discussed in the next subsection. Similar to the analysis in previous subsection, considering the experimental uncertainty of Q, most emitters do not have considerable uncertainties of $ S_p $, so the uncertainties are temporarily neglected in fitting.

In subsections above we discussed the effects of deformation and polarization on decay width and spectroscopic factor, so the discussion of half-lives $ T_{1/2}=\hbar\ln{2}/(S_p\Gamma) $ of various proton emitters can be explored. First, based on our theoretical model, we calculated the half-lives of $ 43 $ proton emitters that have been measured by experiments over the past many decades, via the DWBA method considering deformation. Table 2 shows the result considering deformation without polarization. Based on the nuclear parameters in the table, using spectroscopic factor $ S_p^{\text{RMF}} $ calculated using RMF theory [11], our results are calculated respectively considering the daughter nuclei as spherical and deformed nuclei, as $ \log_{10}T_{1/2}^{\text{sph}} $ and $ \log_{10}T_{1/2}^{\text{def}} $. For comparison, except for the theoretical result of $ \beta_2 $, we also utilize the experimental deformation parameters [46, 47] in calculation, which is shown in the table with the superscript ex. However due to the lack of experiments near the proton drip line, only $ \beta_2 $ of the daughter nuclei of $ ^{105} $Sb and $ ^{109} $I are available. The results show that the differences between theoretical and experimental $ \beta_2 $ do not lead to considerable effects. Therefore, to ensure the consistency of the data used for the calculations, only theoretical deformation values were employed in the previous fitting process for $ S_p^{\text{def,exp}} $.

Emitter	$ j^\pi $	$ E_0(\text{MeV}) $	$ \beta_2 $	$ \beta_4 $	$ \log_{10}T_{1/2}^{\text{exp}}(\text{s}) $	$ S_p^{\text{RMF}} $	$ \log_{10}T_{1/2}^{\text{sph}}(\text{s}) $	$ \log_{10}T_{1/2}^{\text{def}}(\text{s}) $	$ S_p^{\text{def,fit}} $	$ \log_{10}T_{1/2}^{\text{def,fit}}(\text{s}) $
$ ^{105}\text{Sb} $	$ 5/2^+ $	0.478$ _{-0.015}^{+0.015} $[50]	0.000	0.000	2.049 [43, 44]	0.999	1.561$ _{-0.459}^{+0.507} $	1.561$ _{-0.459}^{+0.507} $	0.353	2.012$ _{-0.459}^{+0.507} $
			$ 0.110^{\text{ex}} $					$ 1.558^{+0.473}_{-0.468} $	0.224	$ 2.174^{+0.473}_{-0.468} $
$ ^{109}\text{I} $	$ 3/2^+ $	0.819$ _{-0.005}^{+0.005} $	0.139	0.056	−4.029 [36]	0.726	−4.945$ _{-0.092}^{+0.056} $	−4.966$ _{-0.074}^{+0.082} $	0.195	−4.396$ _{-0.074}^{+0.082} $
			$ 0.153^{\text{ex}} $					−$ 4.965^{+0.553}_{-0.884} $	0.172	−$ 4.341^{+0.553}_{-0.884} $
$ ^{112}\text{Cs} $	$ 3/2^+ $	0.816$ _{-0.007}^{+0.007} $	0.185	0.052	−3.310	0.369	−3.850$ _{-0.108}^{+0.110} $	−3.878$ _{-0.108}^{+0.100} $	0.123	−3.403$ _{-0.108}^{+0.100} $
$ ^{113}\text{Cs} $	$ 3/2^+ $	0.967$ _{-0.003}^{+0.003} $	0.195	0.054	−4.752	0.373	−5.950$ _{-0.036}^{+0.036} $	−5.998$ _{-0.016}^{+0.046} $	0.110	−5.467$ _{-0.016}^{+0.046} $
$ ^{117}\text{La} $	$ 3/2^+ $	0.807$ _{-0.011}^{+0.011} $ [51]	0.282	0.106	−1.602	0.311	−2.923$ _{-0.178}^{+0.182} $	−3.016$ _{-0.185}^{+0.171} $	0.031	−2.010$ _{-0.185}^{+0.171} $
$ ^{121}\text{Pr} $	$ 3/2^+ $	0.893$ _{-0.010}^{+0.010} $ [51]	0.304	0.087	−2.000	0.122	−3.104$ _{-0.145}^{+0.147} $	−3.233$ _{-0.144}^{+0.147} $	0.021	−2.461$ _{-0.144}^{+0.147} $
$ ^{130}\text{Eu} $	$ 3/2^+ $ [36]	1.031$ _{-0.015}^{+0.015} $	0.331	0.018	−3.046	0.816	−4.478$ _{-0.186}^{+0.190} $	−4.616$ _{-0.186}^{+0.175} $	0.012	−2.790$ _{-0.186}^{+0.175} $
$ ^{131}\text{Eu} $	$ 3/2^+ $	0.952$ _{-0.009}^{+0.009} $	0.331	0.018	−1.699	0.029	−1.972$ _{-0.127}^{+0.128} $	−2.111$ _{-0.110}^{+0.117} $	0.012	−1.734$ _{-0.110}^{+0.117} $
$ ^{135}\text{Tb} $	$ 7/2^- $	1.191$ _{-0.007}^{+0.007} $	0.322	−0.037	−3.027	0.028	−3.475$ _{-0.073}^{+0.074} $	−3.606$ _{-0.072}^{+0.067} $	0.015	−3.322$ _{-0.072}^{+0.067} $
$ ^{140}\text{Ho} $	$ 7/2^- $ [36]	1.098$ _{-0.010}^{+0.010} $	0.276	−0.047	−2.222	0.952	−3.363$ _{-0.121}^{+0.123} $	−3.462$ _{-0.140}^{+0.117} $	0.034	−2.015$ _{-0.140}^{+0.117} $
$ ^{141}\text{Ho} $	$ 7/2^- $	1.182$ _{-0.008}^{+0.008} $	0.253	−0.039	−2.387	0.008	−2.268$ _{-0.087}^{+0.088} $	−2.342$ _{-0.070}^{+0.088} $	0.049	−3.133$ _{-0.070}^{+0.088} $
$ ^{144}\text{Tm} $	$ 11/2^- $	1.713$ _{-0.016}^{+0.016} $	0.254	−0.064	−5.569 [36]	0.558 [40]	−5.554$ _{-0.105}^{+0.106} $	−5.703$ _{-0.104}^{+0.106} $	0.049	−4.644$ _{-0.104}^{+0.106} $
$ ^{145}\text{Tm} $	$ 11/2^- $	1.741$ _{-0.007}^{+0.007} $	0.231	−0.068	−5.499	0.580	−5.764$ _{-0.045}^{+0.045} $	−5.890$ _{-0.045}^{+0.045} $	0.069	−4.962$ _{-0.045}^{+0.045} $
$ ^{146}\text{Tm} $	$ 11/2^- $	1.202$ _{-0.004}^{+0.004} $	0.219	−0.057	−0.810 [43]	0.962	−1.427$ _{-0.044}^{+0.045} $	−1.543$ _{-0.044}^{+0.045} $	0.081	−0.468$ _{-0.044}^{+0.045} $
$ ^{147}\text{Tm} $	$ 11/2^- $	1.066$ _{-0.005}^{+0.005} $	−0.187	−0.022	0.587	0.581	0.448$ _{-0.066}^{+0.067} $	0.378$ _{-0.066}^{+0.067} $	0.121	1.060$ _{-0.066}^{+0.067} $
$ ^{150}\text{Lu} $	$ 11/2^- $	1.274$ _{-0.003}^{+0.003} $	−0.167	−0.035	−1.197	0.497	−1.514$ _{-0.031}^{+0.032} $	−1.571$ _{-0.031}^{+0.031} $	0.150	−1.050$ _{-0.031}^{+0.031} $
$ ^{151}\text{Lu} $	$ 11/2^- $	1.245$ _{-0.003}^{+0.003} $	−0.167	−0.035	−0.896	0.490	−1.077$ _{-0.033}^{+0.033} $	−1.134$ _{-0.033}^{+0.033} $	0.150	−0.620$ _{-0.033}^{+0.033} $
$ ^{155}\text{Ta} $	$ 11/2^- $	1.459$ _{-0.015}^{+0.015} $	0.021	0.000	−2.538	0.422	−2.606$ _{-0.131}^{+0.133} $	−2.607$ _{-0.131}^{+0.133} $	0.349	−2.524$ _{-0.131}^{+0.133} $
$ ^{156}\text{Ta} $	$ 3/2^+ $	1.023$ _{-0.005}^{+0.005} $	−0.063	0.001	−0.842	0.761	−1.122$ _{-0.074}^{+0.074} $	−1.128$ _{-0.065}^{+0.074} $	0.313	−0.742$ _{-0.065}^{+0.074} $
$ ^{157}\text{Ta} $	$ 1/2^+ $	0.941$ _{-0.007}^{+0.007} $	−0.084	0.014	−0.527	0.797	−0.693$ _{-0.117}^{+0.112} $	−0.701$ _{-0.117}^{+0.118} $	0.284	−0.254$ _{-0.117}^{+0.118} $
$ ^{160}\text{Re} $	$ 3/2^+ $ [4]	1.277$ _{-0.005}^{+0.005} $	0.107	0.004	−3.045	0.507	−3.558$ _{-0.054}^{+0.055} $	−3.576$ _{-0.054}^{+0.055} $	0.249	−3.266$ _{-0.054}^{+0.055} $
$ ^{161}\text{Re} $	$ 1/2^+ $	1.206$ _{-0.006}^{+0.006} $	0.128	0.018	−3.357	0.892	−3.833$ _{-0.071}^{+0.071} $	−3.854$ _{-0.063}^{+0.071} $	0.214	−3.233$ _{-0.063}^{+0.071} $
$ ^{166}\text{Ir} $	$ 3/2^+ $	1.161$ _{-0.007}^{+0.007} $	0.140	−0.005	−0.824	0.415	−1.511$ _{-0.090}^{+0.091} $	−1.543$ _{-0.090}^{+0.091} $	0.193	−1.211$ _{-0.090}^{+0.091} $
$ ^{167}\text{Ir} $	$ 1/2^+ $	1.089$ _{-0.006}^{+0.006} $	0.151	−0.004	−1.028	0.912	−1.706$ _{-0.085}^{+0.085} $	−1.717$ _{-0.085}^{+0.085} $	0.175	−1.001$ _{-0.085}^{+0.085} $
$ ^{170}\text{Au} $	$ 3/2^+ $	1.479$ _{-0.012}^{+0.012} $	0.129	0.007	−3.493	0.511	−4.511$ _{-0.111}^{+0.109} $	−4.539$ _{-0.118}^{+0.102} $	0.212	−4.157$ _{-0.118}^{+0.102} $
$ ^{171}\text{Au} $	$ 1/2^+ $	1.455$ _{-0.010}^{+0.010} $	0.129	−0.006	−4.770 [11]	0.848	−5.312$ _{-0.093}^{+0.094} $	−5.334$ _{-0.093}^{+0.094} $	0.212	−4.732$ _{-0.093}^{+0.094} $
$ ^{176}\text{Tl} $	$ 1/2^+ $	1.275$ _{-0.018}^{+0.018} $	−0.115	−0.030	−2.284	0.926	−2.885$ _{-0.210}^{+0.214} $	−2.901$ _{-0.206}^{+0.214} $	0.235	−2.306$ _{-0.206}^{+0.214} $
$ ^{177}\text{Tl} $	$ 1/2^+ $	1.173$ _{-0.020}^{+0.020} $	−0.115	−0.030	−1.176	0.733	−1.513$ _{-0.264}^{+0.271} $	−1.530$ _{-0.284}^{+0.251} $	0.235	−1.036$ _{-0.284}^{+0.251} $
$ ^{185}\text{Bi} $	$ 1/2^+ $	1.615$ _{-0.016}^{+0.016} $	0.000	0.012	−4.191	0.011	−3.847$ _{-0.134}^{+0.136} $	−3.847$ _{-0.134}^{+0.135} $
$ ^{141}\text{Ho}^m $	$ 1/2^+ $	1.246$ _{-0.008}^{+0.008} $	0.253	−0.039	−5.137	0.048	−5.353$ _{-0.080}^{+0.080} $	−5.417$ _{-0.080}^{+0.080} $	0.049	−5.429$ _{-0.080}^{+0.080} $
$ ^{146}\text{Tm}^m $	$ 9/2^- $	1.132$ _{-0.004}^{+0.004} $	0.219	−0.057	−0.703	0.962	−0.735$ _{-0.049}^{+0.049} $	−0.851$ _{-0.049}^{+0.049} $	0.081	0.224$ _{-0.049}^{+0.049} $
$ ^{147}\text{Tm}^m $	$ 3/2^+ $	1.125$ _{-0.003}^{+0.003} $	−0.187	−0.022	−3.444	0.953	−3.862$ _{-0.036}^{+0.036} $	−3.902$ _{-0.036}^{+0.055} $	0.121	−3.004$ _{-0.036}^{+0.055} $
$ ^{151}\text{Lu}^m $	$ 3/2^+ $	1.323$ _{-0.010}^{+0.010} $	−0.167	−0.035	−4.796	0.858	−5.388$ _{-0.097}^{+0.098} $	−5.422$ _{-0.097}^{+0.098} $	0.150	−4.664$ _{-0.097}^{+0.098} $
$ ^{156}\text{Ta}^m $	$ 11/2^- $	1.120$ _{-0.007}^{+0.007} $	−0.063	0.001	0.933	0.493	0.969$ _{-0.091}^{+0.092} $	0.960$ _{-0.091}^{+0.092} $	0.313	1.157$ _{-0.091}^{+0.092} $
Continued on next page

Table 2.  Comparison of the results of proton emitters with spherical and deformed daughter nuclei using $ S_p^{\text{RMF}} $ and $ S_p^{\text{def,fit}} $. The first two columns denote the emitters and the spin-parity of emitted proton from Refs. [43, 44] using Eq. (9) except for those marked out in the table. Kinetic energy $ E_0 $ of proton is taken from Ref. [36] with uncertainties. Spectroscopic factor $ S_p $ are respectively taken from Ref. [11] $ S_p^{\text{RMF}} $ and our fitting $ S_p^{\text{def,fit}} $ in Eq. (16). Deformation parameters of the daughter nucleus are taken from Ref. [45]. The experimental half-lives of proton emitters mainly taken from [43, 44]. $ \log_{10}T_{1/2}^{\text{sph}} $ and $ \log_{10}T_{1/2}^{\text{def}} $ are results of respectively spherical and deformed daughter nuclei with $ S_p^{\text{RMF}} $, and $ \log_{10}T_{1/2}^{\text{def,fit}} $ is the result with $ S_p^{\text{def,fit}} $ for $ S_p^{\text{def,fit}} $. Besides, the experimental data and $ S_p $ of $ ^{54}\text{Ni}^m $ are taken from Ref. [48].

Except for 43 proton emitters from $ ^{105} $Sb to $ ^{177} $Tl$ ^m $, we also calculate a newly measured emitter $ ^{54} $Ni$ ^m $ with two branches in Table 2 experimental data and theoretical GFPX1A spectroscopic factors [48]. The emission on $ 11/2^- $ orbital has an excited final state, which lacks experimental or theoretical deformation parameters, so only the spherical case is calculated. Due to the extremely small $ S_p $, the fitting result of Eq. (16) is not used. However, the results for this branch differ significantly from the experimental value, and even when the deformation of daughter nucleus is considered, the discrepancy remains, and previous theoretical calculations on half-lives also gave similar discrepancy [48]. We attribute this discrepancy to the difficulty in accurately calculating extremely small $ S_p $, because in previous studies [48], $ S_p $ respectively predicted by the GFPX1A and KB3G Hamiltonians differ by more than an order of magnitude, showing a strong model-dependence. Therefore, $ ^{54} $Ni$ ^m $ is excluded in subsequent calculations in this work. It is expected that future theoretical improvements in $ S_p $ calculations will reduce this discrepancy.

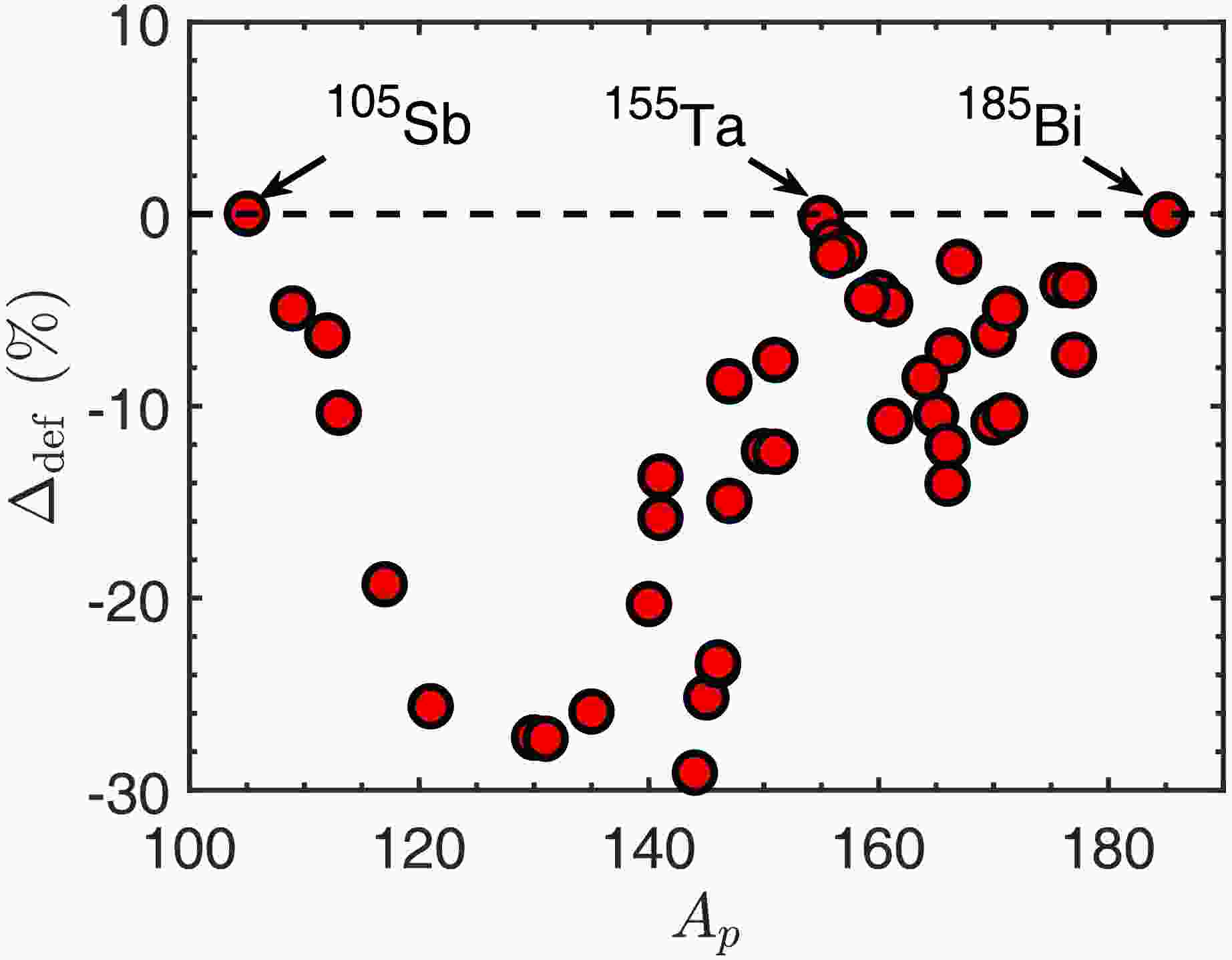
Besides, the result of $ S_p^{\text{def,fit}} $ and corresponding half-lives $ \log_{10}T_{1/2}^{\text{def,fit}} $ are also listed in Table 2. According to the numerical results, the dimensionless impact of deformation on half-lives independent to $ S_p $ is defined as

where $ T^{\text{def}}_{1/2} $ and $ T^{\text{sph}}_{1/2} $ are the results respectively considering and neglecting nuclear deformation. As shown in Fig. 7, $ \Delta_{\text{def}} $ is different in various proton emitters, but for almost every proton emitter, the deformation effect decreases the half-lives, except for three nuclei $ ^{105}\text{Sb} $, $ ^{155}\text{Ta} $ and $ ^{185}\text{Bi} $, whose daughter nuclei have protons or neutrons of magic number, leading to an extremely slight deformation related to the shell model. This result is consistent with previous theoretical analysis on α decay [49], implying the similarity of mechanism between proton emission and α decay.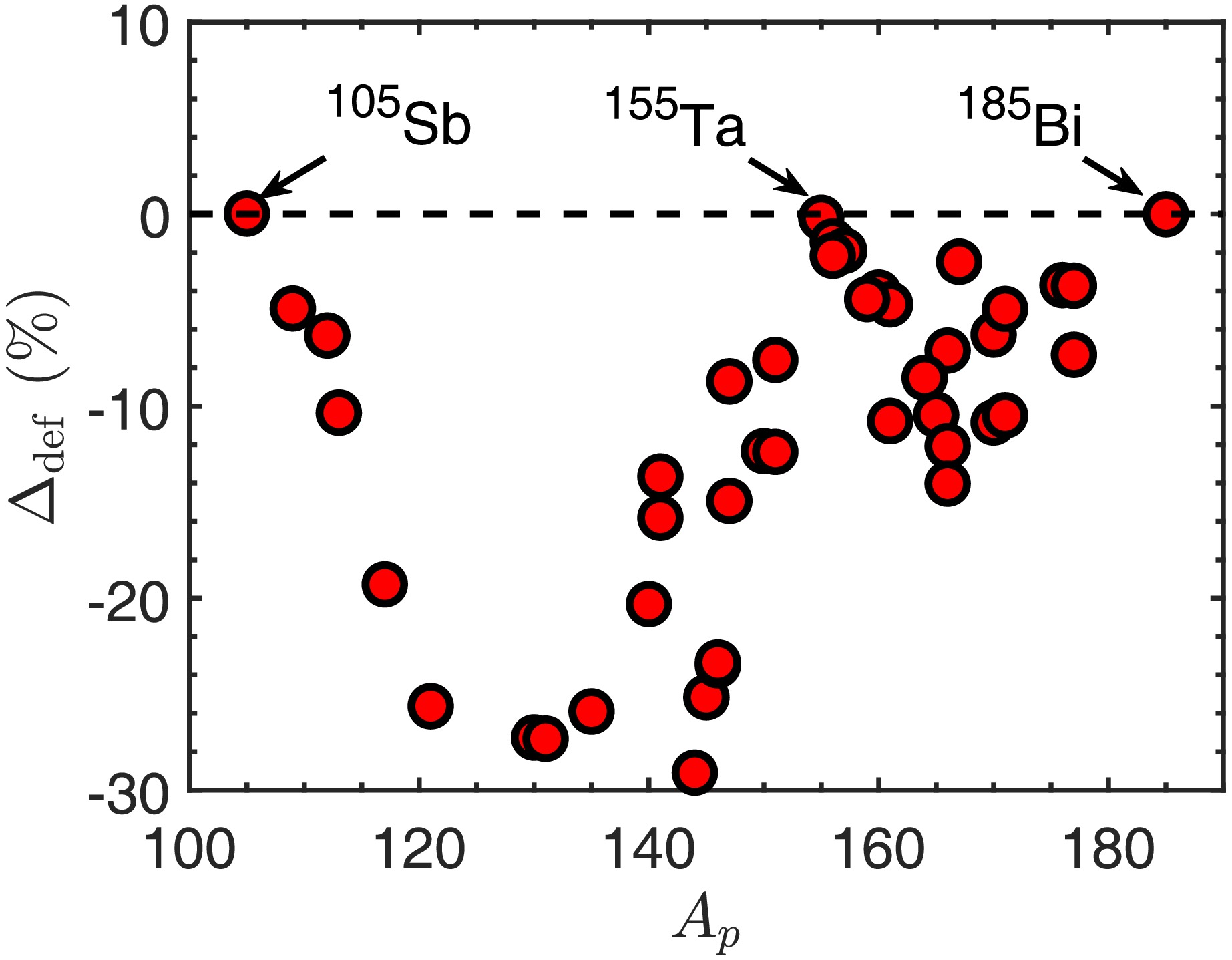

Figure 7.  (color online) Deformation effect on various proton emitters using Eq. (19). For all proton emitters, the negative $ \Delta_{\text{def}} $ implies that both prolate and oblate deformation reduces the half-lives.

Subsequently, considering nuclear surface polarization, the parameters $ \tilde{\beta}_2 $, $ \tilde{\beta}_4 $ and results considering polarization are shown in Table 3 for those emitters whose polarization parameters are given in Ref. [24], where we use $ S_p^{\text{def,fit}} $ to calculate the half-lives $ \log_{10}T_{1/2}^{\text{pol}} $ considering polarization, and compared with the results when $ \tilde{\beta}_{2,4}=0 $ to analyse the effect of polarization. The calculations in the previous subsection demonstrate that the difference between the experimental and theoretical deformation parameters has a minimal impact on the half-life, so only the theoretical deformation parameters are used in Table 3. The relative variation of half-life independent to spectroscopic factor is defined as

Emitter	$ \tilde{\beta}_2 $	$ \tilde{\beta}_4 $	$ \log_{10}T^{\tilde{\beta}_{2,4}=0}_{1/2}\ (\text{s}) $	$ \Delta^{\text{pol}}_{\tilde{\beta}_{2,4}=0}({\text{%}}) $	$ \log_{10}T^{\text{pol}}_{1/2}\ (\text{s}) $	$ \Delta^{\text{pol}} $(%)	$ \overline{a}_N $ (fm)	$ S_p^{\text{pol,fit}} $	$ \log_{10}T_{1/2}^{\text{pol,fit}}\ (\text{s}) $
$ ^{105}\text{Sb} $	0.00089	−0.00154	2.029$ _{-0.459}^{+0.480} $	3.95	2.013$ _{-0.459}^{+0.480} $	0.30	0.74994	0.371	1.992$ _{-0.459}^{+0.480} $
$ ^{109}\text{I} $	0.09182	0.07041	−4.390$ _{-0.053}^{+0.079} $	1.38	−4.370$ _{-0.077}^{+0.059} $	6.05	0.75500	0.137	−4.217$ _{-0.077}^{+0.059} $
$ ^{113}\text{Cs} $	0.10746	0.01397	−5.475$ _{-0.036}^{+0.058} $	−1.90	−5.488$ _{-0.042}^{+0.023} $	−4.86	0.75792	0.070	−5.294$ _{-0.042}^{+0.023} $
$ ^{117}\text{La} $	0.10284	−0.02272	−2.032$ _{-0.161}^{+0.182} $	−4.89	−2.041$ _{-0.183}^{+0.164} $	−6.92	0.76815	0.017	−1.775$ _{-0.183}^{+0.164} $
$ ^{121}\text{Pr} $	0.00738	−0.05577	−2.446$ _{-0.110}^{+0.132} $	3.42	−2.485$ _{-0.156}^{+0.135} $	−5.37	0.76803	0.012	−2.233$ _{-0.156}^{+0.135} $
$ ^{131}\text{Eu} $	−0.02801	−0.07369	−1.733$ _{-0.128}^{+0.114} $	0.04	−1.747$ _{-0.120}^{+0.121} $	−3.04	0.76838	0.007	−1.513$ _{-0.120}^{+0.121} $
$ ^{135}\text{Tb} $	−0.04780	−0.07435	−3.356$ _{-0.073}^{+0.073} $	−7.60	−3.347$ _{-0.055}^{+0.083} $	−5.58	0.76924	0.008	−3.098$ _{-0.055}^{+0.083} $
$ ^{145}\text{Tm} $	−0.08100	−0.00213	−4.974$ _{-0.034}^{+0.045} $	−2.68	−4.963$ _{-0.034}^{+0.056} $	−0.14	0.76255	0.040	−4.729$ _{-0.034}^{+0.056} $
$ ^{147}\text{Tm} $	0.01349	−0.01452	1.055$ _{-0.066}^{+0.067} $	−1.28	1.056$ _{-0.066}^{+0.068} $	−0.96	0.75700	0.272	0.703$ _{-0.066}^{+0.068} $
$ ^{151}\text{Lu} $	0.00070	−0.00119	−0.625$ _{-0.033}^{+0.033} $	−1.08	−0.625$ _{-0.032}^{+0.033} $	−1.06	0.75615	0.304	−0.931$ _{-0.032}^{+0.033} $
$ ^{155}\text{Ta} $	0.00108	−0.00184	−2.524$ _{-0.131}^{+0.133} $	−0.07	−2.524 $ _{-0.131}^{+0.133} $	−0.07	0.75008	0.342	−2.516 $ _{-0.131}^{+0.133} $
$ ^{157}\text{Ta} $	0.00094	−0.00158	−0.261$ _{-0.117}^{+0.118} $	−1.60	−0.261$ _{-0.116}^{+0.118} $	−1.59	0.75138	0.405	−0.414$ _{-0.116}^{+0.118} $
$ ^{161}\text{Re} $	0.00068	−0.00144	−3.243$ _{-0.071}^{+0.071} $	−2.35	−3.231$ _{-0.071}^{+0.071} $	0.40	0.75298	0.158	−3.101$ _{-0.071}^{+0.071} $
$ ^{171}\text{Au} $	0.02322	−0.00585	−4.723$ _{-0.095}^{+0.092} $	2.00	−4.745$ _{-0.095}^{+0.092} $	−2.95	0.75296	0.157	−4.614$ _{-0.095}^{+0.092} $
$ ^{177}\text{Tl} $	0.00800	−0.00863	−1.048$ _{-0.264}^{+0.271} $	−2.66	−1.033$ _{-0.264}^{+0.271} $	0.71	0.75308	0.378	−1.239$ _{-0.264}^{+0.271} $
$ ^{147}\text{Tm}^m $	0.01349	−0.01452	−3.010$ _{-0.055}^{+0.018} $	−1.36	−3.009$ _{-0.054}^{+0.024} $	−1.13	0.75700	0.272	−3.362$ _{-0.054}^{+0.024} $
$ ^{151}\text{Lu}^m $	0.00070	−0.00119	−4.669$ _{-0.097}^{+0.098} $	−1.15	−4.669$ _{-0.097}^{+0.108} $	−1.15	0.75615	0.304	−4.976$ _{-0.097}^{+0.108} $
$ ^{161}\text{Re}^m $	0.00068	−0.00144	−0.640$ _{-0.072}^{+0.073} $	−1.01	−0.640$ _{-0.073}^{+0.073} $	−1.01	0.75298	0.158	−0.510$ _{-0.073}^{+0.073} $
$ ^{171}\text{Au}^m $	0.02322	−0.00585	−3.062$ _{-0.030}^{+0.030} $	−0.81	−3.065$ _{-0.032}^{+0.028} $	−1.35	0.75296	0.157	−2.934$ _{-0.032}^{+0.028} $

Table 3.  Comparison of nuclear surface polarization effect of proton emitters with even-even daughter nuclei. Half-lives $ \log_{10}T^{\text{pol}}_{1/2} $ are calculated with uncertainties arising from decay energies in Ref. [36] based on the parameterized polarization using $ \tilde{\beta}_2 $ and $ \tilde{\beta}_4 $ taken from Ref. [24]. Result $ \log_{10}T^{\tilde{\beta}_{2,4}=0}_{1/2} $ is calculated when $ \tilde{\beta}_{2,4}=0 $. The spectroscopic factors are calculated by our fitting results Eq. (16), except for the last column, which is based on the fitting considering polarization Eq. (18).

which are listed in Table 3. Result shows that the average effect of surface polarization defined by Eq. (20) is $ \sum{|{\Delta_i^{\text{pol}}}|}/N=2.35 $%, which means that this effect is smaller than the counterpart of deformation. However, when the deformation and polarization are large in the daughter nuclei, $ \Delta_i^{\text{pol}} $ can even reach more than 6%, such as $ ^{109}\text{I} $ and $ ^{117}\text{La} $ in Table 3. Compared with polarization in α decay [25, 26], the proton emitters are relatively less impacted by the polarization, because the nuclear interaction of proton decay is significantly weaker than α decay. Hence, it is difficult to directly observe the polarization effect on the half-life of spontaneous proton emission in experiments. To detect polarization, it is promising to extract the polar angular distributions of the nuclear surface by comparing the yield ratios of free spectator neutrons to protons in the central tip-tip and body-body collisions in the relativistic heavy-ion collisions [52, 53]. Another approach is to measure the inverse process of proton emission via proton scattering, and directly observe its angular dependence. Particularly, we also show the spectroscopic factor $ S_p^{\text{pol,fit}} $ by fitting with polarization Eq. (18) and the corresponding half-lives in the last two columns.

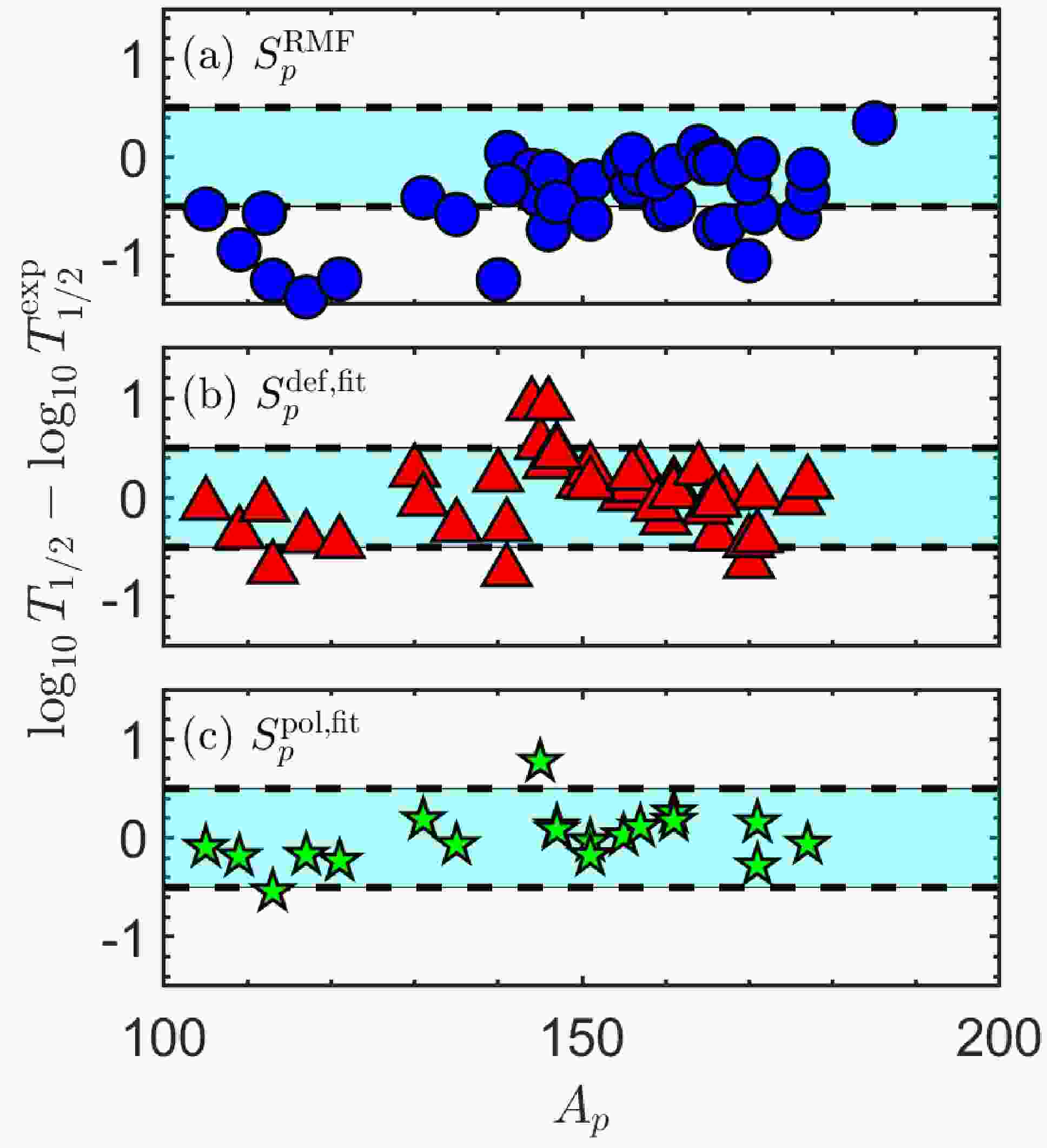
To measure the error of results of differrent $ S_p $, compared with experimental data, the standard deviation is defined as

As shown in Fig. 8 (a) and (b), considering the half-lives respectively using $ S_p^{\text{RMF}} $ and $ S_p^{\text{def,fit}} $, the standard deviation is reduced from $ \sigma^{\text{RMF}}=0.620 $ to $ \sigma^{\text{def,fit}}=0.348 $, which proves the feasibility of the relationship Eq. (16). Furthermore, considering the correlation between spectroscopic factors and deformation and polarization in Eq. (18), compared with experimental data, the standard deviation of calculated half-lives was further reduced from $ \sigma^{\text{def,fit}}=0.345 $ (for only emitters in Table 3) to $ \sigma^{\text{pol,fit}}=0.264 $ as illustrated in Fig. 8(c), implying the correctness of the relationship of $ S_p $ and polarization.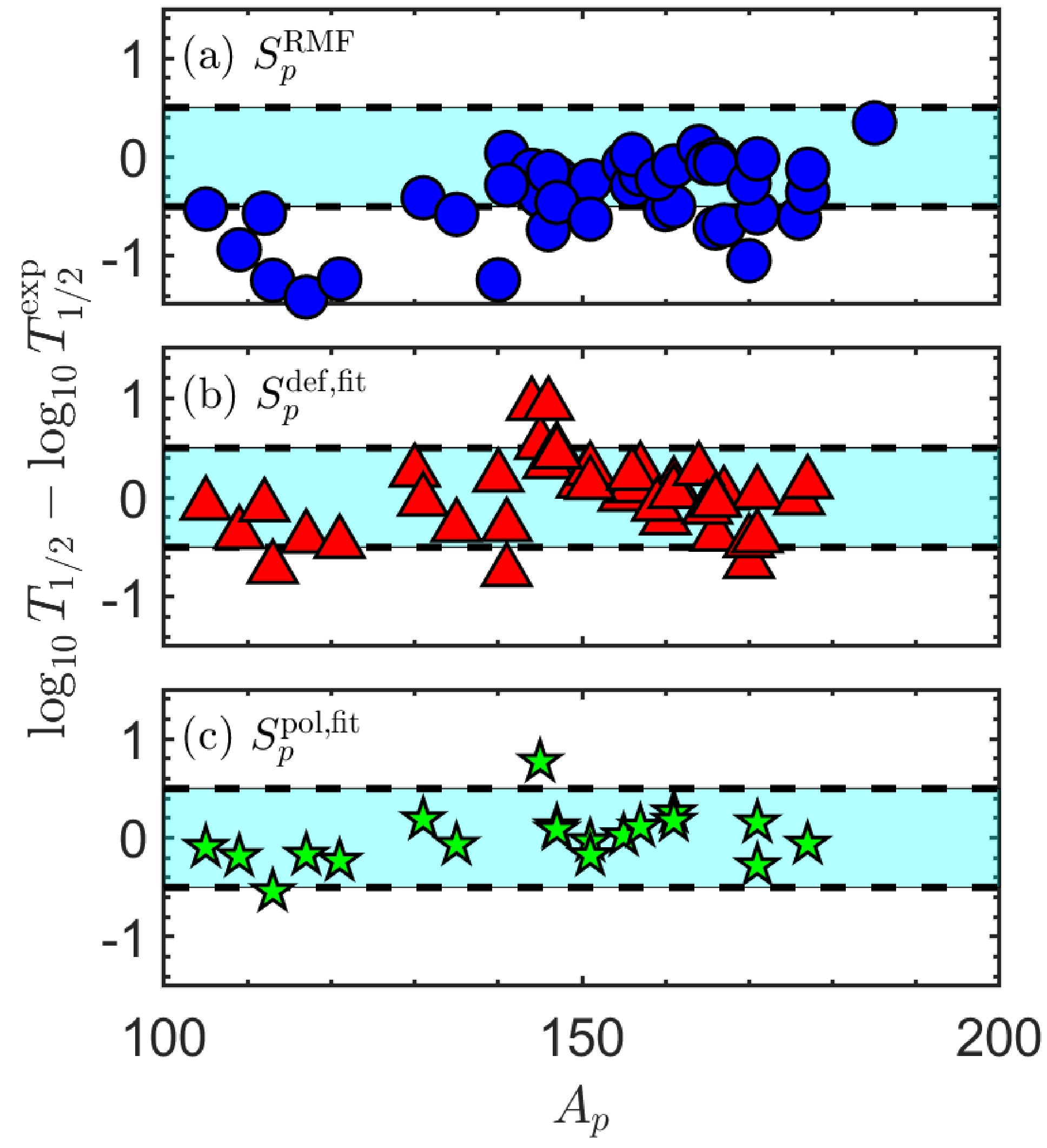

Figure 8.  (color online) Error of calculation compared with experimental results. Spectroscopic factors are respectively taken from (a) RMF theory $ S_p^{\text{RMF}} $ [11], (b) fitting of $ S_p^{\text{def,fit}} $ in Eq. (16) with only deformation and (c) fitting considering polarization $ S_p^{\text{pol,fit}} $ in Eq. (18). The cyan regions represent the difference less than $ 0.5 $. The abscissa $ A_P $ represents the number of nucleons in parent nuclei.

To conclude, the approximate relationship between $ S_p $ and deformation plus polarization provides a more convenient and accurate method to estimate the spectroscopic factor for proton emitters with deformed and polarized daughter nuclei.

In subsections above we calculated various proton emitters, and these emitters are usually chosen as instances for calculation to verify different kinds of theoretical models in previous research. However, theoretical calculations and discussions related to $ ^{53}\text{Co}^m $, the first proton emitter identified, are not more sufficient than other nuclei. Recently L. G. Sarmiento, et al. measured the half-life and decay energy of its proton emission into $ ^{52}\text{Fe} $ by experiment [28], and meanwhile gave a theoretical calculation via barrier-penetration model and R-matrix theory of nuclear reaction, obtaining a successful result. But their calculation only gave the result of spherical daughter nuclei, neglecting the deformation and surface polarization in the theoretical system, so we intend to give a further calculation on this special proton emitter.

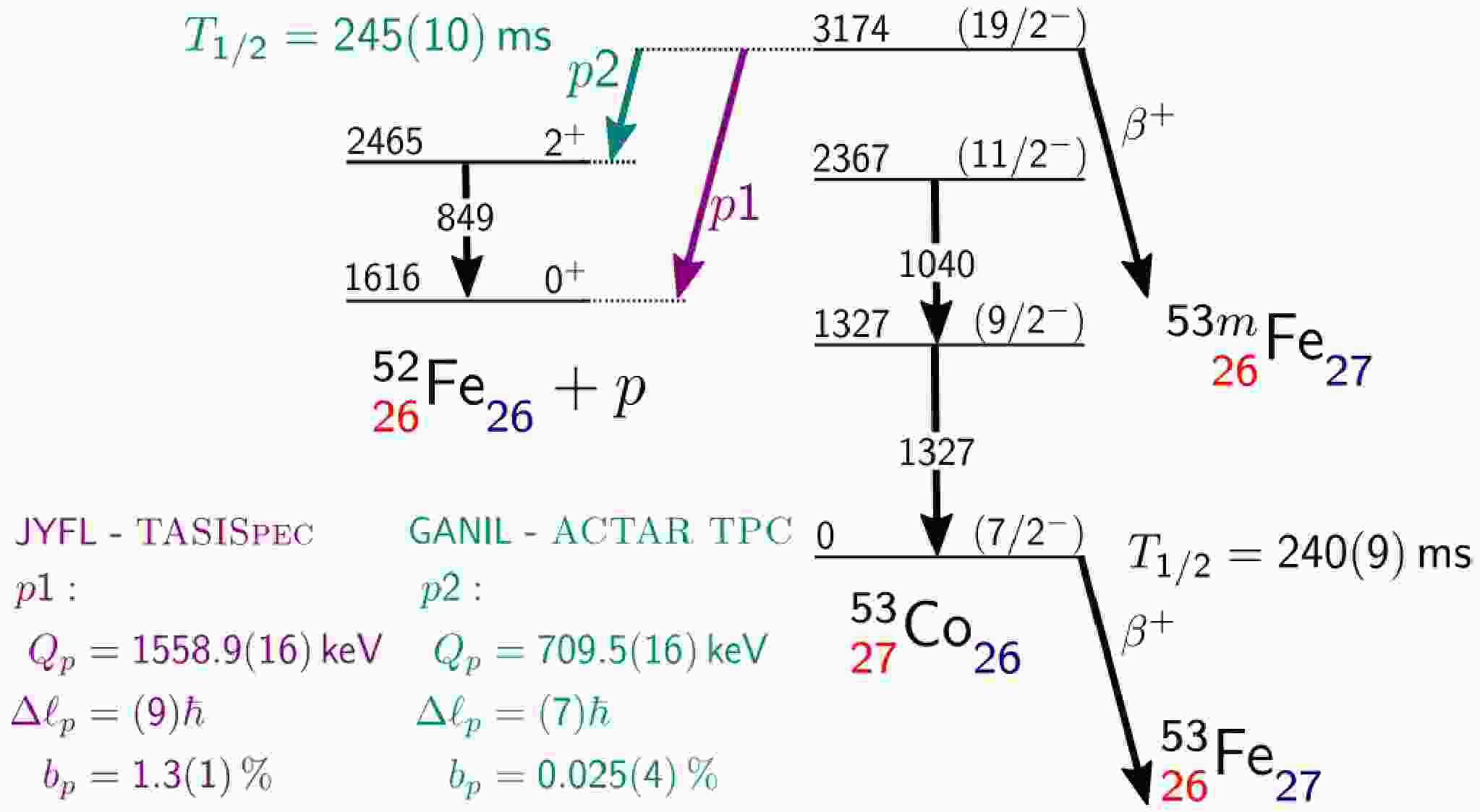
On the basis of previous experiments on $ ^{53}\text{Co}^m $ to date, there are two decay branches of proton emission in $ 19/2^+ $ state, which are shown in the decay scheme Fig. 9. In the first branch, the daughter nucleus is in the ground state $ 0^+ $, so according to Eq. (9) and Ref. [28], the state of emitted proton is $ n=1,\ell=9, j=19/2 $; similarly, the other state of proton in the other decay channel is $ n=1,\ell=7,j=15/2 $. Other parameters including branching ratio, decay energy and half-life are noted in the scheme.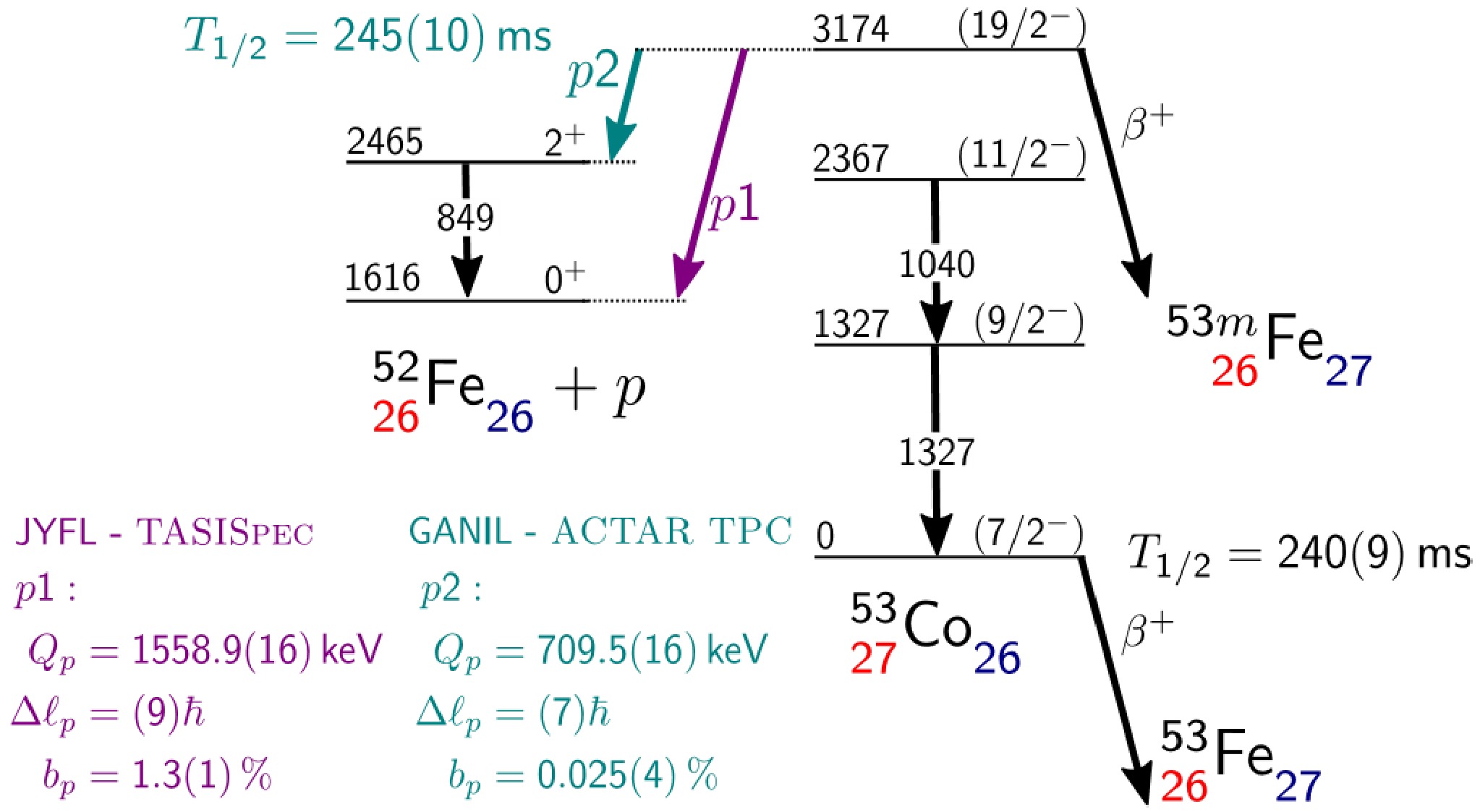

Figure 9.  (color online) Decay scheme of $ ^{53}\text{Co}^m $ from Ref. [28]. Two proton emission branches are denoted by arrows p1 and p2 with corresponding half-lives, branching ratios and decay energies.

Based on the experimental data, the two proton emission branches are calculated using our theoretical model. The recently observed excited state $ 2^+ $ of daughter nucleus $ ^{52}\text{Fe} $ is not included in Ref. [43, 45], so in our present work the mass of it is determined by the mass of $ ^{53}\text{Co}^m $ and the decay energy $ Q_2 $, and its deformation parameters are considered to be same to its ground state due to the absence of theoretical and experimental research. In the future, it is expected that the deformation parameters can be obtained through experiments, such as laser nuclear spectroscopy. To improve the accuracy of our calculation, we use the result of deformation given in a newer research [54], in which Skyrme interaction with various parameters was used to calculate the deformation. We employ the results of SKP parameters for its improvement for pairing matrix elements [54] and its consistency to other research [44]. In our calculation, in order to compare the result with the previous theoretical calculation results, we modified the radius of the Coulomb potential and spin-orbit potential in Table 1 to the same parameters equal to the theoretical calculation program wspot used in Ref. [28]. Other parameters are listed in Table 4, by which we gives the result of potential and corresponding quasibound state wave function. It should be noted that compared with other proton emitters, $ ^{53}\text{Co}^m $ has abnormal small spectroscopic factors, which is the reason that we choose to use $ S_p $ calculated by reduced matrix element theoretical calculation in Ref. [28] rather than using our analytic formula Eq. (16) or Eq. (18). Considering the decay branch $ 19/2^-\to0^+ $, Fig. 10 illustrates the quasibound state wave function for spherical daughter nuclei, in which the density distribution is concentrated between the Coulomb barrier and strong centrifugal potential. More details of deformed Coulomb potential are depicted in Fig. 11 as a function of r and θ respectively considering and neglecting the deformation and polarization, indicating the effect of deformed and polarized Woods-Saxon potential and spin-orbit coupling potential similar to Fig. 1. The final results of half-lives in two branches using our model are shown in Table 5. The high centrifugal barrier reduces the sensitivity of the half-life to the decay energy, and combined with the relatively lower experimental uncertainty, it leads to a smaller uncertainty in the half-life compared with most nuclei listed in Tables 2 and 3. Additionally, compared with the previous theoretical results [28], our results are more consistent with the recent experimental data.

Parameters	Values	Parameters	Values
$ \beta_2 $	$ 0.237 $ [54]	ME($ ^{52}\text{Fe}^m $)	$ -47483.6 (16)\ \text{keV} $
$ \tilde{\beta}_2 $	$ -0.05746 $	$ \tilde{\beta}_4 $	$ -0.00089 $
$ Q_1 $	$ 1558.9(16)\ \text{keV} $	$ Q_2 $	$ 709.5(16)\ \text{keV} $
$ S_p^{p1} $	$ 6.2\times10^{-8} $	$ S_p^{p2} $	$ 1.3\times10^{-7} $

Table 4.  Parameters used in our calculation of $ ^{53}\text{Co}^m $ proton emission. Deformation and polarization parameters are related to the ground state of $ ^{52}\text{Fe} $ in branch p1. Polarization parameters are taken from Ref. [24] of neutron and proton distribution by SkM* functional. ME denotes the mass excess of $ ^{52}\text{Fe}^m $ calculated by the nuclear mass and decay energy in Ref. [28]. Spectroscopic factors of two branches are taken from the results of reduced matrix element [28].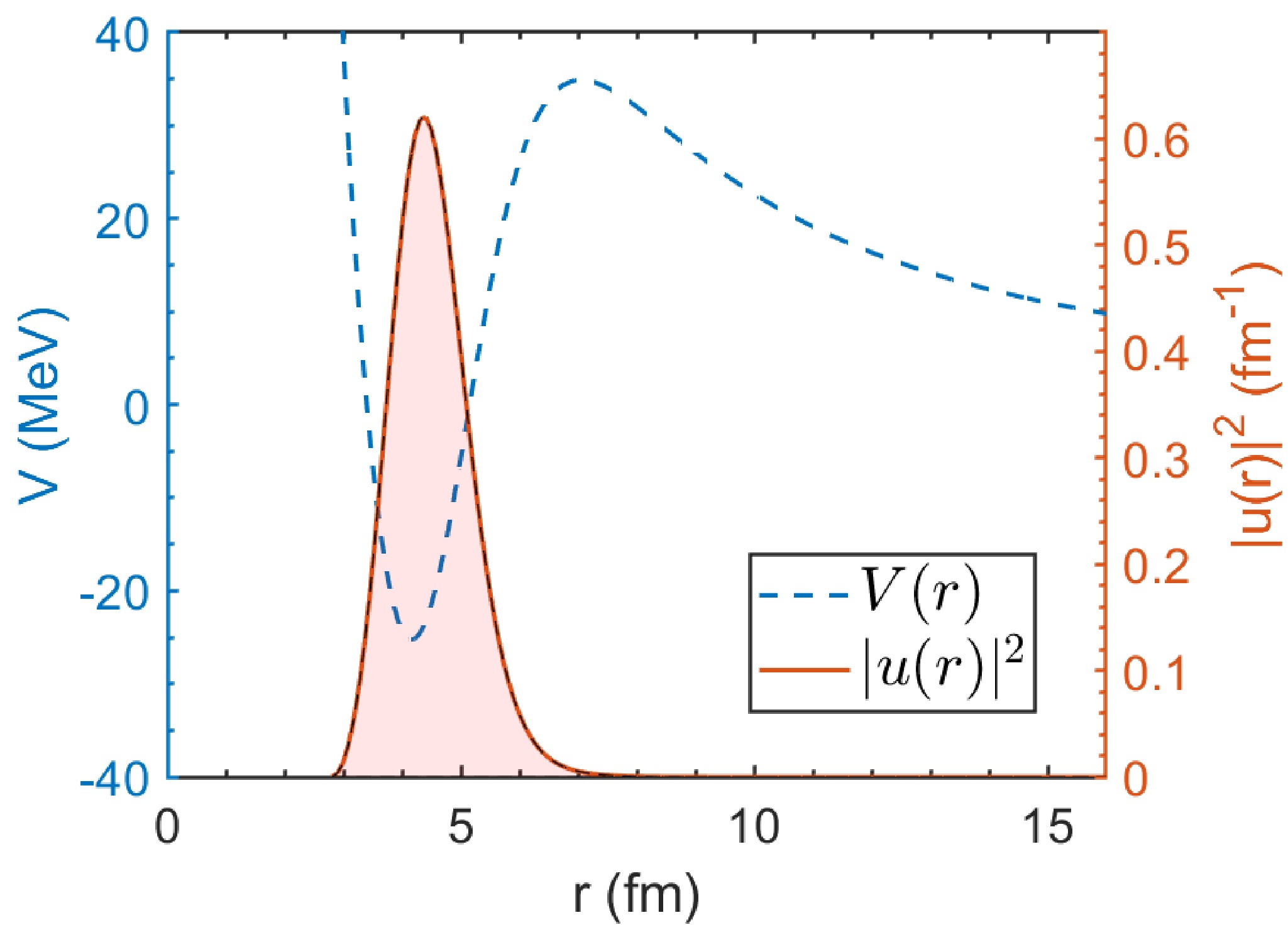

Figure 10.  (color online) Quasibound state of emitted proton in $ ^{53}\text{Co}^m $ [28] of the branch $ 19/2^-\to0^+ $. In order to make the figure more concise, deformation and polarization are not considered in this figure.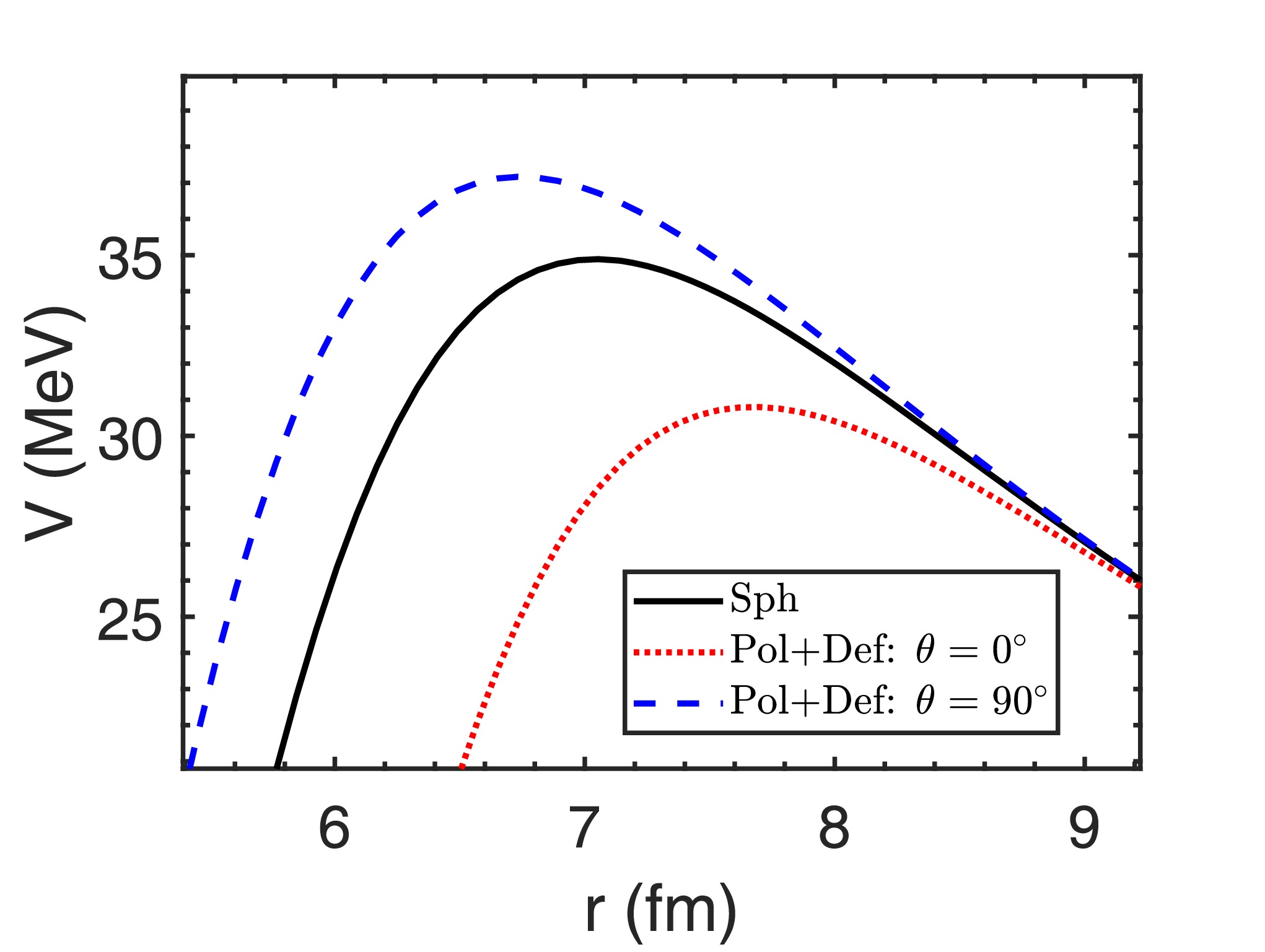

Figure 11.  (color online) Coulomb barrier in $ ^{53}\text{Co}^m $ of the branch $ 19/2^-\to0^+ $ combining the deformation and surface polarization of daughter nucleus. The red dotted line represents the potential at $ \theta=90^\circ $, and the blue dashed line represents the potential at $ \theta=0^\circ $.

Results	Reference [28]			This Work
	Exp	Cal		Sph	Def + Pol
$ T_{1/2}^{p1} $ (s)	$ 18.8 $$ ^{+1.6}_{-1.6} $	$ 55 $		$ 59.4^{+1.0}_{-1.0} $	$ 43.4^{+0.7}_{-0.7} $
$ T_{1/2}^{p2} $ (s)	$ 980 $$ ^{+162}_{-162} $	$ 450 $		713$ ^{+29}_{-28} $	$ 587^{+22}_{-20} $

Table 5.  Theoretical results of our calculation and comparison with experiment. Superscript p1 and p2 respectively denote the two branches of proton emission in $ ^{53}\text{Co}^m $ in Fig. 9. Results of calculation and experiment in Ref. [28] are shown in the second and third columns. The fourth to fifth columns represent the results of our theoretical model for the spherical daughter nucleus and deformed and polarized daughter nucleus respectively with uncertainties introduced by experimental decay energies.

Overall, our calculations show the conspicuously special characteristics of the first discovered proton emitter $ ^{53}\text{Co}^m $, which is a lighter proton emitter and has extremely high angular momentum and small spectroscopic factor. In comparison to previous studies, our theoretical model considering deformation and nuclear surface polarization gives more accurate results.

In this work, in conclusion, we reviewed the quantum tunneling model of proton emission through deformed and polarized interaction potential, by which we calculate the half-lives of various proton emitters via distorted wave Born approximation. Based on this theoretical model, we further calculate the effect of deformation and nuclear surface polarization. Polarization destroys the isotropy of diffuseness, changing the geometry of daughter-proton interaction. Results show that polarization will reduce or increase the half-life of various proton emitters, and the intensity is relatively small and dependent on the value of parameters. In more detail, compared with $ \tilde{\beta}_{2,4}=0 $ case, it can be concluded that for prolate daughter nuclei, positive quadrupole polarization relatively decreases the half-life, and negative quadrupole polarization increases the half-life. On the contrary, for oblate daughter nuclei, positive quadrupole polarization increase the half-life.

Sequentially, we also investigate the correlation between spectroscopic factor and deformation and polarization parameters. The quadratic relationship between spectroscopic factor and quadrupole deformation and average polarization is proposed as an analytic formula by fitting and validated by comparison with the experimental data. Compared with RMF theory, our fitting considering deformation and nuclear surface polarization gives the more accurate spectroscopic factor and reduces the standard deviation of our theoretical results of half-lives, suggesting the necessity to consider the surface polarization in calculation.

In addition, based on the recent experiment of $ ^{53}\text{Co}^m $, the first observed proton emitter, we calculated the two branches of proton emission, obtaining a result more consistent with the experiment. Our calculations verifies that this proton emitter has an extremely small spectroscopic factor and a relatively long half-life. Results shows that our theoretical model considering deformation and polarization gives more consistent results with the new experimental data. In the future, more explorations of nuclear surface polarization are anticipated. We hope that these calculation in neutron-deficient nuclei within deformation and polarization can be useful for future research, and our calculation on $ ^{53}\text{Co}^m $ is also anticipated to expand the insight of special proton emitters.