-
Observations from astrophysics and cosmology have provided overwhelming evidence for the existence of DM [1]. However, the microscopic properties of DM are still poorly known as all of such observations are based on its gravitational effects. Weakly Interacting Massive Particles (WIMPs) are canonical DM candidates. Such a scenario can easily fulfill the relic abundance through the thermal freeze-out mechanism (the “WIMP miracle”) [2] and can be naturally embedded in many popular theoretical frameworks [3, 4]. Moreover, owing to their weak interaction with SM particles, WIMPs can be probed through three experimental prongs, i.e., collider, direct, and indirect detections.
Typically, the interactions between DM and SM particles are model-dependent, and exploring the complete model landscape is signifcantly challenging. Instead of exhausting all possible theoretical model parameter spaces, the Effective Field Theory (EFT) framework is extensively used, which enables us to capture some key features of the high-scale physics effects on the electroweak scale while significantly simplifying the analysis procedures. For EFT collider searches, various signal channels based on different SM portal effective operators have been extensively studied at the hadron and electron colliders [5−34].
Among them, the parameter space of DM-quark interaction that fulfills the correct relic density has a conflict with the exclusion limits from direct detection, indirect detection, and collider searches. In this work, we consider dimension-6 (7) DM-diboson effective operators for scalar (Dirac fermion) DM and examine their sensitivity at the current LHC and future electron and electron-proton colliders. The current limits of DM-diboson operators at the LHC are primarily constrained by mono-j and mono-γ signal channels, and the mono-γ signature is a sensitive channel at the CEPC. The two most currently promising proposals for electron-proton colliders are the LHeC and FCC-ep. The LHeC is based on an economic LHC upgrade, and a 60−140 GeV electron beam is planned for collision with a 7 TeV proton beam in the LHC ring during the High Luminosity LHC (HL-LHC) run. The FCC-ep is designed to collide a 60 GeV electron with the 50 TeV proton beam. DM pairs can be produced through the VBF process with a cleaner background, which corresponds to a
$ {\not E}_T+e^-j $ signal.The remainder of this paper is organized as follows. In Sec.II, we briefly describe the DM-diboson effective operators. Subsequently, the relevant collider phenomenology of the
$ {\not E}_T+e^-j $ signal channel at the LHeC and FCC-ep is discussed in Sec. III, including event simulations, kinematical distributions of final states, and cut selections related to signals and backgrounds. In Sec. IV, we present the sensitivity at the CEPC with a mono-γ signature. The limits from the LHC with current mono-j and mono-γ searches are updated in Sec. V. The constraints from current direct and indirect DM search experiments are discussed in Sec. VI. The results are presented in Sec. VII. Finally, we provide a summary and conclusion in Sec. VIII. -
We consider the DM particle as a Dirac fermion (χ) or scalar (ϕ) that connects with a SM sector through high-dimensional DM-gauge boson effective operators. At the lowest order, such operators enable DM to couple with a single gauge boson, which induces electromagnetic dipole and anapole interactions [35, 36]. However, these interactions lead to monochromatic gamma-rays when the unsuppressed cross-section of DM annihilates into the
$ \gamma\gamma $ and$ \gamma Z $ modes, which are severely constrained by current indirect detection experiments [37]. Thus, we start from DM-diboson operators:$ \begin{array}{*{20}{l}} {\cal O}_B^\phi = \phi^*\phi B^{\mu\nu}B_{\mu\nu}, \qquad {\cal O}_W^\phi = \phi^*\phi W^{a,\mu\nu}W^a_{\mu\nu}, \end{array} $

(1) $ \begin{array}{*{20}{l}} {\cal O}_B^\chi = \overline{\chi}\chi B^{\mu\nu}B_{\mu\nu}, \qquad {\cal O}_W^\chi = \overline{\chi}\chi W^{a,\mu\nu}W^a_{\mu\nu}. \end{array} $

(2) These operators are assumed to be generated at the energy scale Λ, with other high energy resonances much heavier than Λ being all decoupled. Note that in this scenario, the coupling between DM and the SM quarks can also be induced through the RGE from the Λ scale down to the electroweak scale
$ \mu_{\rm EW} $ . Consequently, two extra dimension-6 (7) operators$ \begin{array}{*{20}{l}} {\cal O}_y^\phi = y_q\phi^*\phi \bar q H q, \qquad {\cal O}_H^\phi = \phi^*\phi(H^\dagger H)^2, \end{array} $

(3) $ \begin{array}{*{20}{l}} {\cal O}_y^\chi = y_q\bar \chi \chi \bar q H q, \qquad {\cal O}_H^\phi = \bar \chi \chi (H^\dagger H)^2, \end{array} $

(4) must be considered. In the above equations,
$ y_q=\sqrt{2}m_q/v $ denotes the Yukawa couplings of SM quarks, and v is the vacuum expectation value (VEV) of the SM Higgs doublet H. Subsequently, the total effective Lagrangian at scale μ ($ \mu_{\rm EW} < \mu < \Lambda $ ) is given by$ \mathcal{L}_{\rm eff}^{\phi,\chi} = \sum\limits_{k=B,W,y,H} \frac{C^{\phi,\chi}_k(\mu)}{\Lambda^2} {\cal O}_k\,. $

(5) At the leading logarithmic (LL) order, the Wilson coefficients of the effective operators
$ {\cal O}_y $ and$ {\cal O}_H $ at the scale$ \mu_{\rm EW} $ are [38]$ C_y(\mu_{\rm EW}) \simeq \frac{6Y_{qL}Y_{qR}\alpha_1}{\pi}\ln\left(\frac{\mu_{\rm EW}}{\Lambda}\right), $

(6) $ C_H(\mu_{\rm EW}) \simeq -9 \alpha^2_2\ln\left(\frac{\mu_{\rm EW}}{\Lambda}\right) C_W(\Lambda), $

(7) where
$ Y_{qL}\,(Y_{qR}) $ denotes the hypercharges of the left-handed (right-handed) quarks with$Y_{uL}=Y_{dL}= 1/6 $ ,$ Y_{uR}=2/3$ , and$ Y_{dR}=1/3 $ , and$ \alpha_1 $ and$ \alpha_2 $ are the gauge coupling constants of the$ U(1)_Y $ and$S U(2)_Y$ gauge groups, respectively. In our calculation, we set$ \mu_{\rm EW}\equiv m_Z $ with$ \alpha_1\simeq 1/98 $ and$ \alpha_2\simeq 1/29 $ . After electroweak symmetry breaking (EWSB), the gauge eigenstate fields$ B_\mu $ and$ W_\mu^3 $ mix into the physical massless photon field$ A_\mu $ and massive gauge field$ Z_\mu $ . Subsequently, the effective DM-diboson and DM-quark operators are recast as$ \begin{aligned}[b]& {\cal O}_{FF}^\phi = \phi^*\phi F^{\mu\nu}F_{\mu\nu}, \quad {\cal O}_{FF}^\chi = \overline{\chi}\chi F^{\mu\nu}F_{\mu\nu}, \\& {\cal O}_{q}^\phi = m_q \phi^*\phi\bar{q}q, \quad {\cal O}_{q}^\chi = m_q \overline{\chi}\chi\bar{q} q, \end{aligned} $

(8) where
$FF=AA,\;AZ,\;ZZ,\;WW$ . The relevant matching conditions are$ \begin{aligned}[b] {C_{AA}(\mu_{\rm EW})}=&C_B(\mu_{\rm EW}) \cos ^{2} \theta_{W}+C_W(\mu_{\rm EW}) \sin ^{2} \theta_{W}, \\ {C_{Z Z}(\mu_{\rm EW})} =&C_W(\mu_{\rm EW}) \cos ^{2} \theta_{W}+C_B(\mu_{\rm EW}) \sin ^{2} \theta_{W}, \\ {C_{A Z}(\mu_{\rm EW})} =&\left(C_W(\mu_{\rm EW})-C_B(\mu_{\rm EW})\right) \sin 2 \theta_{W}, \\ {C_{W W}(\mu_{\rm EW})}=&C_W(\mu_{\rm EW}), \\ {C_{q}(\mu_{\rm EW})}=&C_y(\mu_{\rm EW})-\frac{v^2}{m_h^2}C_H(\mu_{\rm EW}), \end{aligned} $

(9) with
$ \theta_{W} $ is the Weinberg angle.Integrating out the heavy top quarks, the effective DM-gluon operators
$ \begin{array}{*{20}{l}} {\cal O}_{q}^\phi = \alpha_s \phi^*\phi G^{a,\mu\nu}G_{\mu\nu}^a, \quad {\cal O}_{q}^\chi = \alpha_s \overline{\chi}\chi G^{a,\mu\nu}G_{\mu\nu}^a \end{array} $

(10) can be generated, where
$ G_{\mu\nu}^a $ denotes the gluon field strength. The matching condition at leading order is given by [39]$ C_{G}(m_t)=-\frac{1}{12\pi}C_t(m_t). $

(11) When RGEs are evolved from the EW scale down to the hadronic scale
$ \mu_{\rm had}\simeq 1 $ GeV,$ {\cal O}_{AA} $ will contribute to$ {\cal O}_{q} $ through the exchanging of virtual photons. For scale μ with$ m_q<\mu<\mu_{\rm EW} $ , we obtain [40]$ {C_{q}(\mu)}\simeq C_{q}(\mu_{\rm EW})+ \frac{6 Q_q^2\alpha_{\rm em}}{\pi} \ln\left(\frac{\mu}{\mu_{\rm EW}}\right) C_{AA}(\mu_{\rm EW}) $

(12) at the LL order, where
$ Q_q $ is the electric charge of a quark, and the electromagnetic coupling constant$ \alpha_{\rm em} \simeq 1/137 $ .At the
$ m_b $ and$ m_c $ threshold, we must integrate out the corresponding heavy bottom and charm quarks by considering Eq. (11) again. At the scale$ \mu_{\rm had}\simeq 1 $ GeV, we obtain$ \begin{aligned}[b] C_{q}\left(\mu_{\rm had}\right) \simeq& \left(\frac{6 Y_{q_{L}} Y_{q_{R}} \alpha_{1}}{\pi} C_{B}(\Lambda)+ 9 \alpha_2^2 \frac{v^{2}}{m_{h}^{2}} C_{W}(\Lambda)\right) \ln \left(\frac{\mu_{\rm EW}}{\Lambda}\right) \\ &+\frac{6 Q_{q}^{2} \alpha_{\rm em}}{\pi} C_{AA}(\mu_{\rm EW}) \ln \left(\frac{\mu_{\rm had}}{\mu_{\rm EW}}\right), \end{aligned} $

(13) $ \begin{aligned}[b] C_{G}\left(\mu_{\rm had}\right) \simeq& -\frac{1}{12 \pi}\Bigg\{\left(\frac{\alpha_{1}}{\pi} C_{B}(\Lambda)+ 27 \alpha_2^2 \frac{v^{2}}{m_{h}^{2}} C_{W}(\Lambda)\right) \ln \left(\frac{\mu_{\rm EW}}{\Lambda}\right) \\ &+\frac{2 \alpha_{\rm em}}{3 \pi} C_{AA}(\mu_{\rm EW})\left[\ln \left(\frac{m_b}{\mu_{\rm EW}}\right)+4 \ln \left(\frac{m_c}{\mu_{\rm EW}}\right)\right]\Bigg\}, \end{aligned} $

(14) where the Wilson coefficient
$ C_{AA}(\mu_{\rm EW}) $ is determined by the first matching condition in Eq. (9). -
In this section, we investigate the sensitivity of the DM-gauge boson effective operators at future electron-proton colliders.
-
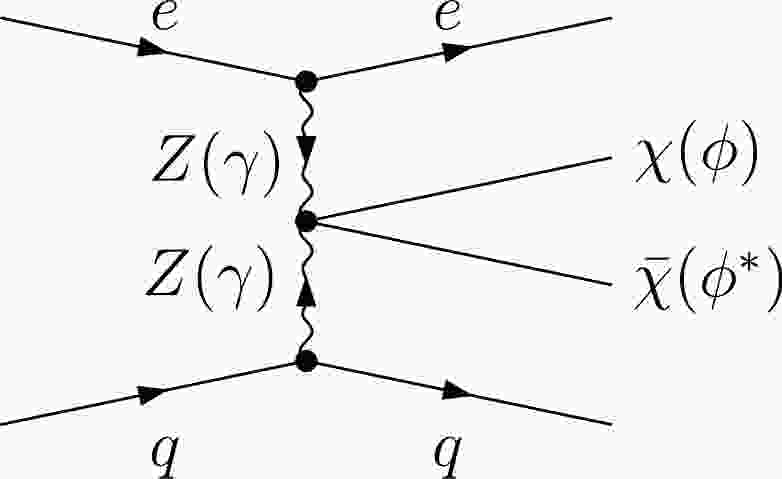
From the effective interactions in Eqs. (1) and (2), DM pairs can be produced at the electron-proton collider through both the Charged Current (CC) and Neutral Current (NC), which respectively correspond to the W boson and
$ \gamma/Z $ modes of VBF processes. In CC production, DM can be generated through the process of$ e^- p \to \nu_e j \chi\bar\chi(\phi\phi^*) $ via$ WW $ fusion, resulting in a mono-jet plus missing energy signature. Note that the mono-jet signature coincidentally aligns with the background of CC deeply inelastic scattering. Owing to the absence of kinematic handles in the final state, distinguishing this signal channel from its primary background poses a significant challenge. Consequently, our study is primarily focused on NC production – specifically the process$ e^- p \to e^-j \chi\bar\chi\; (\phi\phi^*) $ , as depicted in Fig. 1. Thus, the corresponding signature is characterized as the$ {\not E}_T+e^-j $ channel.For SM background estimation, we consider both the reducible background (RB) and irreducible background (IB). The IB is primarily due to the processes
$e^-p\to e^-j\nu_\ell\bar\nu_\ell\; (\ell=e,\; \mu,\; \tau)$ . Among them, both$ W/Z $ -boson bremsstrahlung processes$e^-p\to e^-jZ/\nu_ejW^-\; (Z\to\nu_e\bar\nu_e/ W^-\to e^-\bar\nu_e)$ contribute to$ \nu_e $ final state, whereas for$ \nu_{\mu,\tau} $ , only the bremsstrahlung process$ e^-p\to e^-jZ\; (Z\to\nu_{\mu,\tau}\bar\nu_{\mu,\tau}) $ is relevant. For the RB, a major contribution is from$ e^- p \to e^- j W^\pm $ with a W leptonic decay$ W^\pm\to\ell^\pm \nu_\ell $ . Therefore, two possibilities must be considered. One is that electron and muon final states exceed the detector acceptance, and the τ final state mimics a hard jet in the detector. Another possibility is that the products of hadronic τ decays are too soft to be tagged [41, 42]. Consequently, the SM background can be summarized as follows:● IB:
$ e^-p\to e^-j\nu_\ell\bar\nu_\ell $ ,● RB:
$ e^- p \to e^- j \ell^\pm \nu_\ell\; (\bar\nu_\ell) $ ,where
$ \ell=e,\mu,\tau $ . -
For an event simulation, we generate a Universal FeynRules Output (UFO) [43] model file using the FeynRules package [44], which is fed into MadGraph@NLO [45] to generate parton-level events. For both signal and backgrounds at the parton level, we apply the following pre-selection cuts:
$ \begin{aligned}[b] &p^{j,\ell}_T > 5\,{\rm GeV}, \quad \ |\eta_{j,\ell}|\ < 5, \\ &\Delta R_{j\ell} > 0.4, \quad \Delta R_{\ell\ell} > 0.4, \end{aligned} $

(15) where
$ p_T $ and η are the transverse momentum and pseudorapidity of the corresponding particles, respectively, and$ \Delta R =\sqrt{\Delta \phi^2+\Delta y^2} $ is the separation in the azimuthal angle-rapidity ($ \phi-y $ ) plane. Note that all of the cuts in Eq. (15) are defined in the laboratory frame. We then use Pythia6.4 [46] to implement parton shower and hadronization and Delphes3.4 [47] for rapid detector simulation according to the LHeC designed parameters [48].To suppress the RB, we apply the following veto criteria [42] as basic cuts:
● events must contain exactly one hard electron, one hard jet, and
$ {\not E}_T $ ,● events containing any extra jets with
$ p_T^j>3 $ GeV and$ |\eta_j|<2 $ or leptons with$ p_T^{e,\mu}>5 $ GeV or tagged τ jets are vetoed.Fig. 2 and Fig. 3depict the normalized distributions of the missing transverse energy
$ {\not E}_T $ , invariant mass of tagged electron and jet system$ M(e^-,j) $ , and inelasticity variable y for both signal and backgrounds after the basic cuts, at the 140 GeV$ \otimes $ 7 TeV LHeC and 60 GeV$ \otimes $ 50 TeV FCC-ep, respectively. For the signal, we assume benchmark values of$ m_{\chi,\; \phi}=1 $ GeV,$ C_{B,\; W}=1 $ , and$ \Lambda= $ 500 GeV. For the inelasticity variable y, we follow the definition in Ref. [41], which is given as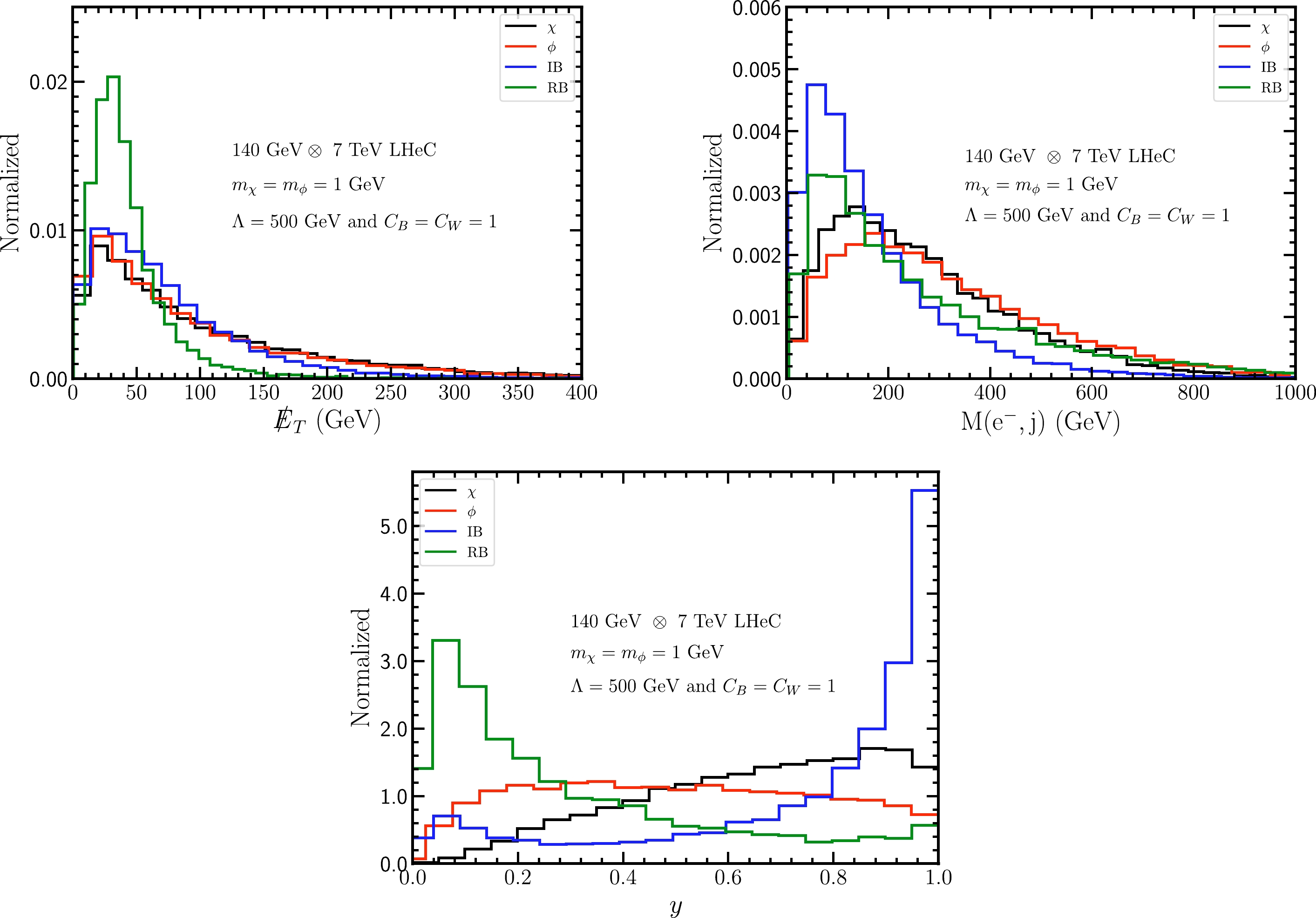
Figure 2. (color online) Normalized distributions of the missing transverse energy
${\not E}_T$ (left), invariant mass of electron-jet system$ M(e^-,j) $ (middle), and inelasticity variable y (right) with$ m_\chi=m_\phi=1 $ GeV,$ \Lambda=500 $ GeV, and$ C_B=C_W=1 $ at the 140 GeV$ \otimes $ 7 TeV LHeC. The red and black curves correspond to scalar and fermion DM signals, respectively, and the green and blue lines show the SM RB and IB, respectively.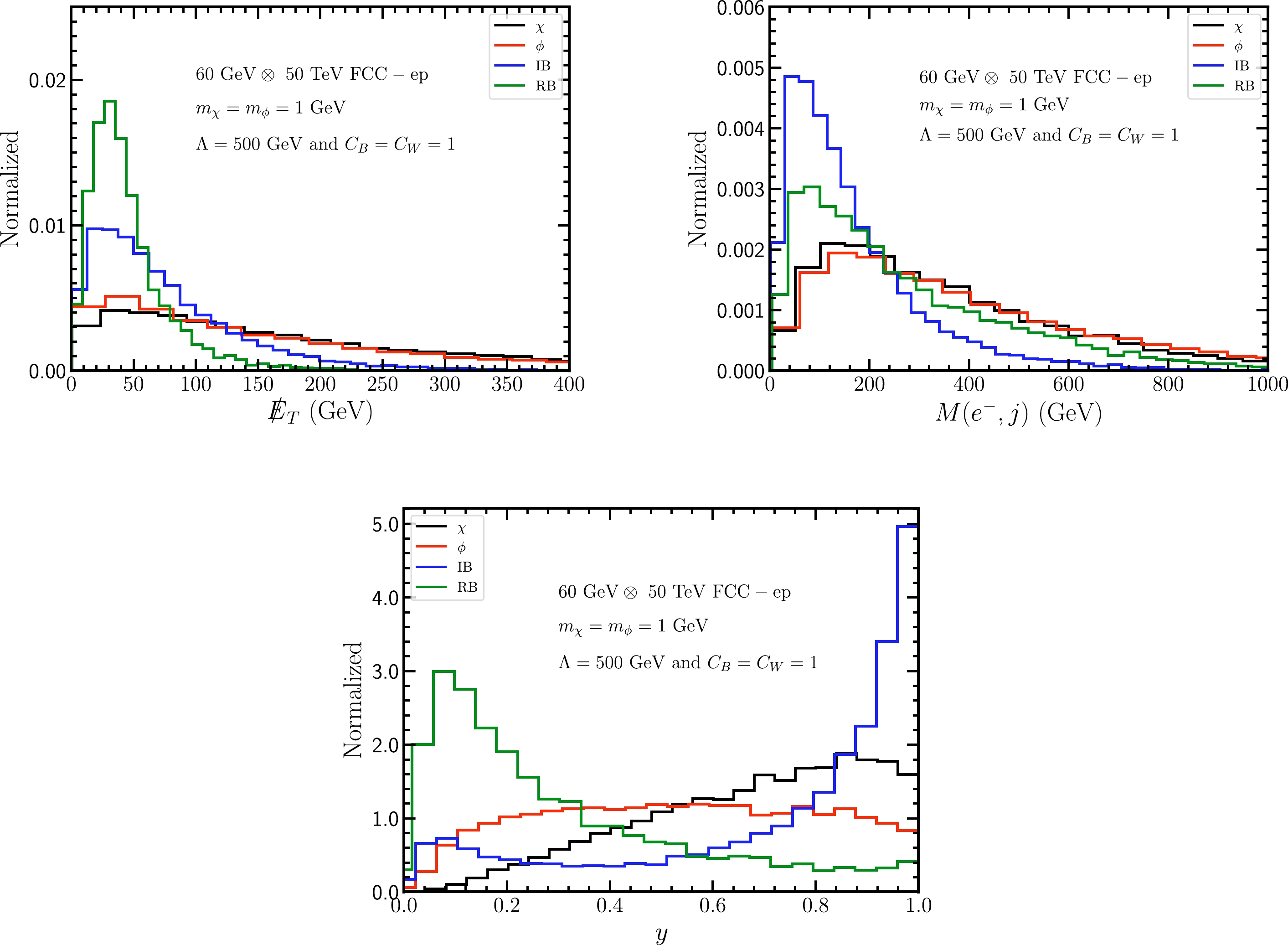
Figure 3. (color online) Same as Fig. 2 but at the 60 GeV
$ \otimes $ 50 TeV FCC-ep.$ y\equiv\frac{k_P\cdot(k_e-p_e)}{k_P\cdot k_e}, $

(16) where
$ k_{P,\; e} $ are the 4-momenta of the initial proton and electron, and$ p_e $ is the 4-momenta of the final electron. We can observe the following characteristics:● for
$ {\not E}_T $ distribution, the SM RB tends to have a smaller value,$ {\not E}_T <100 $ GeV, compared with signals, whereas the SM IB has values similar to those of signals,● for y distribution, the SM RB and IB tend to distribute at small and large y values, respectively, whereas signals exhibit a relatively flat distribution.
Such distinct behaviors of signals and SM backgrounds indicate that we can impose the following kinematical cuts for the LHeC (FCC-ep) to further extract signals:
$ \begin{aligned}[b] &{\not E}_T > 100\quad(220)\,{\rm GeV}, \\ &M(e^-,j) > 100 \quad (200)\,{\rm GeV}, \\ &0.3 < y < 0.8 \quad (0.1 < y < 0.9). \end{aligned} $

(17) Table 1 and Table 2 show the cut-flows for the fermion and scalar DM signals and backgrounds at the LHeC and FCC-ep, respectively. The corresponding significance
$ {\cal S}=N_S/\sqrt{N_B} $ and signal-to-background ratio${\cal R}= N_S/N_B$ with the total integrated luminosity$ L = 2\; {\rm ab}^{-1} $ are also shown, where$ N_{S,\; B}=\sigma_{S,\; B}\cdot L $ are the surviving event numbers of signals and backgrounds, respectively. Both$ {\cal S} $ and$ {\cal R} $ increase when each cut is imposed. After the pre-selection cuts, RB contribution is still large, whereas the basic cuts suppress the RB by a factor of 4.5 (5.0) at the LHeC (FCC-ep). Moreover, the RB is dramatically reduced by the$ {\not E}_T $ cut, which only survives about$ 1.26 $ % (0.07%) at the LHeC (FCC-ep).Process Signal (ϕ) Signal (χ) RB IB $ {\cal S}_\phi $ 

$ {\cal S}_\chi $ 

$ {\cal R}_\phi $ 

$ {\cal R}_\chi $ 

pre-selection cuts 7.57 10.28 1421.87 260.39 8.26 11.20 0.0045 0.0061 basic cuts 4.91 6.84 316.83 155.21 10.11 14.08 0.010 0.014 ${\not E}_T > 100$ GeV

1.71 2.62 18.28 38.33 10.16 15.58 0.030 0.046 $ M(e^-,j)> 100 $ GeV

1.56 2.33 15.46 29.28 10.46 15.56 0.035 0.052 $ 0.3< y< 0.8 $ 

1.01 1.54 5.40 9.16 11.80 18.05 0.070 0.106 Table 1. Remaining cross-section (in units of fb) of the signal and background after corresponding cuts with
$ m_{\chi, \phi}=1 $ GeV,$ C_{B, W}=1 $ , and$ \Lambda=500 $ GeV at the 140 GeV$ \otimes $ 7 TeV LHeC. The corresponding significance$ {\cal S}=N_S/\sqrt{N_B} $ and signal-to-background ratio$ {\cal R}=N_S/N_B $ were obtained for$L=2 ~{\rm ab}^{-1}$ , where$ N_S $ and$ N_B $ are the numbers of signal and background events, respectively.Process Signal (ϕ) Signal (χ) RB IB $ {\cal S}_\phi $ 

$ {\cal S}_\chi $ 

$ {\cal R}_\phi $ 

$ {\cal R}_\chi $ 

pre-selection cuts 18.17 64.85 1232.28 222.80 21.31 76.03 0.012 0.045 basic cuts 11.56 42.58 244.95 125.09 26.87 98.98 0.031 0.12 ${\not E}_T > 220$ GeV

3.10 13.44 0.86 4.32 60.88 264.17 0.060 2.60 $ M(e^-,j)> 200 $ GeV

2.59 10.71 0.61 2.13 70.21 289.95 0.95 3.92 $ 0.1< y< 0.9 $ 

2.41 9.48 0.57 1.44 75.94 298.87 1.19 4.71 Table 2. Same as Table 1 but at the 60 GeV
$ \otimes $ 50 TeV FCC-ep.At the LHeC, after all cuts, the fermion (scalar) DM signal can survive
$ 13.2 $ % ($ 14.9 $ %), whereas the RB (IB) only survives$ 0.37 $ % ($ 3.5 $ %). At the FCC-ep, the signal for fermion (scalar) DM survived$ 13.3 $ % ($ 14.6 $ %), and the RB (IB) ultimately survives$ 0.047 $ % ($ 0.65 $ %). Note that the remaining cross-section of the background at the FCC-ep is only$ 14 $ % of ones that at the LHeC, whereas the signal for fermion (scalar) DM production at the FCC-ep can reach$ 6 $ ($ 1.5 $ ) times that at the LHeC, which implies that the FCC-ep exhibits a considerable improvement in significance compared with the LHeC. -
Owing to the effective DM-diboson operators in Eqs. (1) and (2), a WIMP can be produced at
$ e^+e^- $ colliders via the process$ e^+ e^- \to V^{\prime*} \to \phi\phi^*(\bar \chi \chi) + V\ (V=\gamma,Z) $ , which results in mono-photon or mono-Z signatures. The corresponding Feynman diagrams are shown in Fig. 4. In this section, we focus on the mono-photon signature at the future projected CEPC [49, 50] with three different running modes: the Higgs factory mode for a seven year run at$ \sqrt{s}=240\ \mathrm{GeV} $ with a total luminosity of$ \sim 5.6\ \mathrm{ab}^{-1} $ , the Z factory mode for a two year run at$ \sqrt{s}=91.2\ \mathrm{GeV} $ with a total luminosity of$ \sim 16\ \mathrm{ab}^{-1} $ , and the$ W^+W^- $ threshold scan mode for a one year run at$ \sqrt{s} \sim 158-172\ \mathrm{GeV} $ with a total luminosity of$ \sim 2.6\ \mathrm{ab}^{-1} $ .1 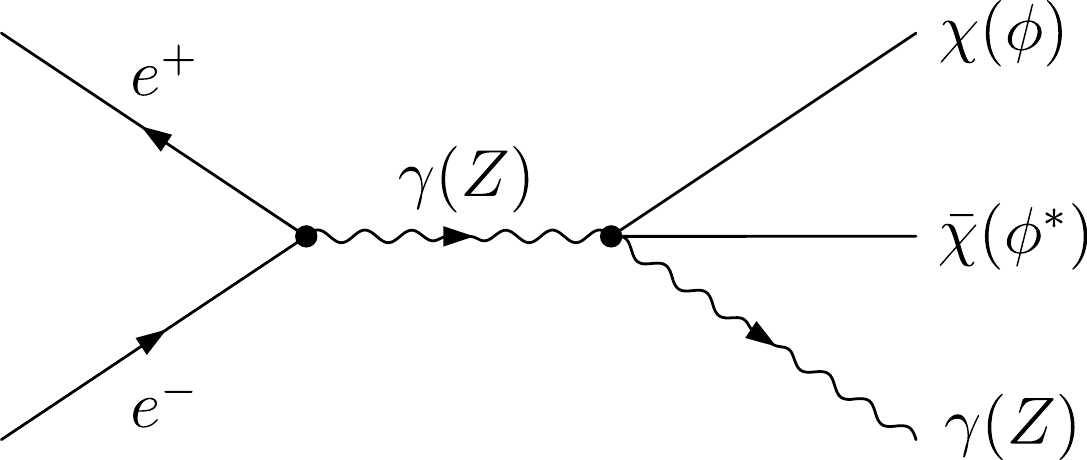
Figure 4. Feynman diagrams for the process
$e^+ e^- \to $ $ \phi\phi^*(\bar \chi \chi) + Z$ or$ e^+ e^- \to \phi\phi^*(\bar \chi \chi) + \gamma $ .For the monophoton signature at the CEPC, an irreducible background results from the neutrino production
$ e^+e^-\to\nu_l\bar\nu_l\gamma $ processes, where$ \nu_l=\nu_e,\nu_\mu,\nu_\tau $ . Owing to the Breit-Wigner distribution of the Z boson in the irreducible BG, a resonance occurs in the final photon energy spectrum, which is located at$ E_\gamma^Z=\frac{s-M_Z^2}{2\sqrt{s}} $

(18) with a full-width-at-half-maximum of
$ \Gamma_\gamma^Z=M_Z\Gamma_Z/\sqrt{s} $ . To suppress the irreducible background contribution, we veto the events within$ 5\Gamma_\gamma^Z $ at the Z resonance in the monophoton energy spectrum [27]. The vetoing cut can be expressed as$ \begin{array}{*{20}{l}} |E_\gamma-E_\gamma^Z|<5\Gamma_\gamma^Z. \end{array} $

(19) The main reducible SM backgrounds result from the
$ e^+e^-\to\gamma+{\not X} $ processes, where only one photon is visible in the final state, and$ {\not X} $ denotes the other undetectable particle(s) owing to the limited detection capability of the detectors. In our analysis, the parameters for the EMC coverage,$ |\cos\theta| <0.99 $ and$ E>0.1 $ GeV, are adopted based on CEPC CDR [50]. The processes$ e^+e^-\to f\bar f \gamma $ and$ e^+e^-\to\gamma\gamma\gamma $ provide dominant contributions to the reducible background when the final$ f\bar f $ and$ \gamma\gamma $ are emitted with$ |\cos\theta| >0.99 $ . Owing to the momentum conservation in the transverse direction and energy conservation, the maximum photon energy as a function of its polar angle can be obtained as [27]$ E_\gamma^m(\theta_\gamma) = \sqrt{s}\left(\frac{\sin\theta_\gamma}{\sin\theta_b}\right)^{-1}, $

(20) where the polar angle
$ \theta_b $ corresponds to the boundary of the EMC with$ |\cos\theta| <0.99 $ . To suppress the monophoton events resulting from the reducible background, we adopt the detector cut$ E_\gamma>E_\gamma^m(\theta_\gamma) $ on the final state photon in our analysis. -
Through the DM-diboson operators, a WIMP can be produced via the processes
$ q q^\prime \to V^{\prime*} \to \phi\phi^*(\bar \chi \chi) + V (V=\gamma,Z,W) $ , which can exhibit a mono-photon ($ {{\not E}_T+\gamma)} $ or mono-jet ($ {{\not E}_T+W/Z\ (\to {\rm hardons})} $ ) signature, respectively. The representative Feynman diagrams are shown in Fig. 5. Moreover, the loop-induced effective DM-quarks ($ {\cal O}_q $ ) and DM-gluons ($ {\cal O}_G $ ) operators can result in the mono-jet signature via the$ q \bar q \to \bar\chi \chi +g $ ,$ gg \to \bar\chi \chi +g $ , and$ q g \to \bar\chi \chi +q $ processes. The representative Feynman diagrams are shown in Fig. 6.
Figure 5. Representative Feynman diagrams for mono-photon (left) and mono-jet (right) signatures resulting from DM-diboson operators.
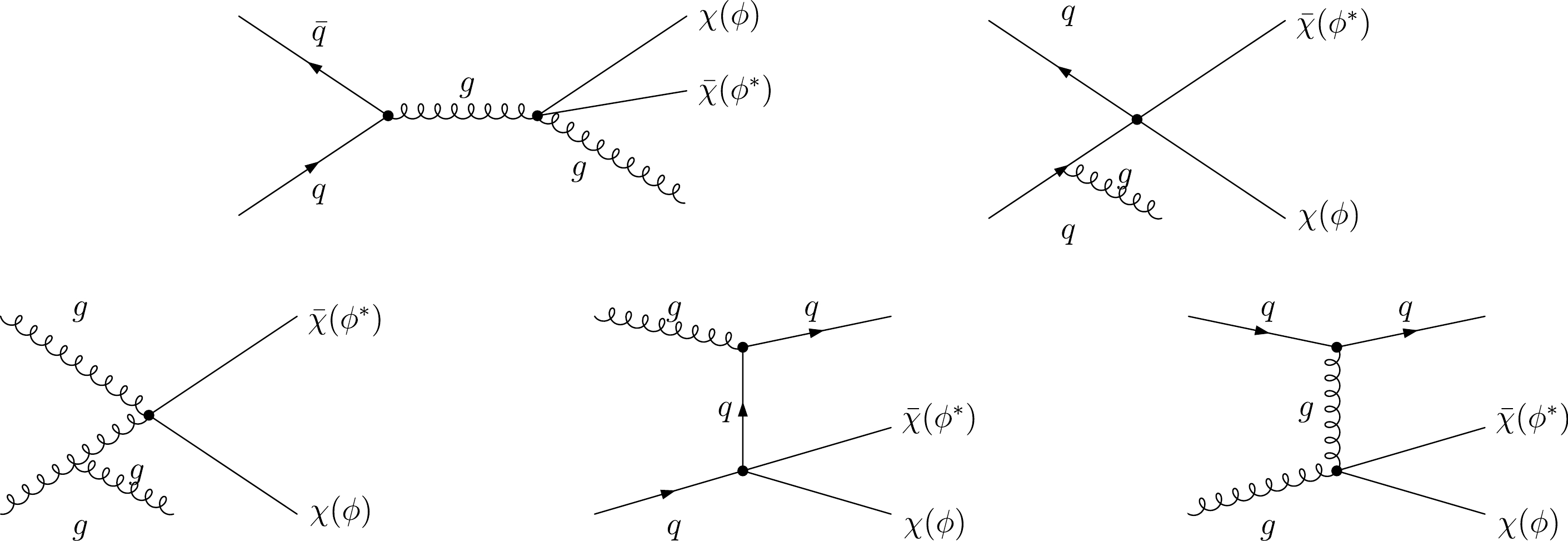
Figure 6. Representative Feynman diagrams for a mono-jet signature resulting from loop-induced effective DM-quarks and DM-gluons operators.
In this section, we consider the sensitivities from LHC mono-j and mono-γ searches. To simulate the signal from dark matter, we genrate the parton-level events using MadGraph@NLO [45], and the subsequent parton shower and hadronization are generated using Pythia6.4 [46]. We use Delphes3.4 [47] to conduct a rapid detector simulation for the ATLAS or CMS detector with the corresponding parameter setup. We follow the procedure of the latest mono-photon [51] and mono-jet [52] analysis by the ATLAS Collaboration with an integrated luminosity of 139 fb
$ ^{-1} $ at a center-of-mass energy of 13 TeV.For the
$ {{\not E}_T+\gamma} $ search channel, events in our analysis are required to have a leading γ with$ E_{{T}}^{\gamma}>150 \mathrm{GeV}, \ |\eta^\gamma|<1.37 \text { or } 1.52<|\eta^\gamma|<2.37,\ \Delta \phi\left(\gamma,\ \boldsymbol{E}_{{T}}^{\text {miss }}\right)>0.4, $ 0 or 1 jet with$ p_{{T}}>30 \mathrm{GeV},\ |\eta|<4.5 \text { and } \Delta \phi\left(\mathrm{jet},\ \boldsymbol{E}_{{T}}^{\mathrm{miss}}\right)>0.4 $ , and no leptons. Moreover, the ATLAS Collaboration performs the measurement in seven different signal regions with a varying cut on the missing transverse momentum$ {E}_{{T}}^{\mathrm{miss}} $ . We observe that the strongest bounds on the parameter space in our case are given with the most severe cut of$ {E}_{{T}}^{\mathrm{miss}}> 375 $ GeV. The corresponding 95% C.L. limit on the fiducial cross-section is$ \sigma_{\rm fid}< $ 0.53 fb.For mono-jet search, events with identified muons, electrons, photons, or τ-leptons in the final state are vetoed. Selected events have a leading jet with
$ p_T>150 $ GeV and$ |\eta|<2.4 $ , and up to three additional jets with$ p_T>30 $ GeV and$ |\eta|<2.8 $ . Separation in the azimuthal angle between the missing transverse momentum direction and each selected jet$ \Delta \phi\left(\mathrm{jet},\ \boldsymbol{E}_{{T}}^{\mathrm{miss}}\right)>0.4 (0.6) $ is required for events with$ {E}_{\mathrm{T}}^{\mathrm{miss}}>250 $ GeV ($200\; \mathrm{GeV} < {E}_{{T}}^{\mathrm{miss}} < 250$ GeV). We observe that the stronger restriction of$ {E}_{{T}}^{\mathrm{miss}} > 1200 $ GeV provides the best limits. At 95% C.L., the bound on the corresponding fiducial cross section is given by$ \sigma_{\rm fid}< $ 0.3 fb.Table 3 presents the ratio of the number of events for mono-jet signature at LHC from the process
${pp\to \chi\bar\chi+W/Z\ (\to {\rm hardons})}$ via dimension-7 DM-diboson operators with the Feynman diagrams shown in Fig. 5 to one from the process${pp\to \chi\bar\chi+ q/g}$ via loop-induced DM-quarks and DM-gluons operators with the Feynman diagrams shown in Fig. 6 with Λ=1000 GeV. Here, we consider three cases, i.e.,$ C_{B}=C_{W}=500 $ ,$C_{B}=0, \; C_{W}=500$ , and$ C_{B}=500,\; C_{W}=0 $ . We observe that all the ratios in the three cases increase with an increment in the DM mass. Furthermore, the contributions from tree-level DM-diboson operators to the mono-jet signature at the LHC are about two orders of magnitude above those from loop-induced DM-quarks and DM-gluons operators, especially for$C_{B}=1, C_{W}=0$ , with the contributions being about three orders higher; thus, we ignore the contributions from DM-quarks and DM-gluons operators in the following analysis.$ m_\chi $ 

1 300 800 2000 3000 $ C_B=500,C_W=0 $ 

638.22 699.35 752.11 1435.32 2733.95 $ C_B=0,C_W=500 $ 

95.00 99.55 104.29 181.55 302.49 $ C_B=500,C_W=500 $ 

79.20 80.33 91.64 158.94 271.41 Table 3. Ratio of the number of events for the mono-jet signature at the LHC from the process
$ {pp\to \chi\bar\chi+W/Z\ (\to {\rm hardons})} $ via DM-diboson operators with the Feynman diagrams shown in Fig. 5 to$ {pp\to \chi\bar\chi+ q/g} $ via loop-induced DM-quarks and DM-gluons operators with the Feynman diagrams shown in Fig. 6 at Λ=1000 GeV. -
In this section, we discuss the bounds on Λ from current direct and indirect search experiments. The effective operators
$ {\cal O}_B $ and$ {\cal O}_W $ lead to the non-relativistic cross-sections of DM annihilation$ \chi\bar\chi,\ \phi\phi^*\to\gamma\gamma/\gamma Z/ZZ/WW $ as follows:$ \begin{array}{*{20}{l}} \langle\sigma_k v\rangle = a_k + b_k v^2+ {\cal O}(v^4) \end{array} $

(21) with
$ k=B,W $ annihilation channels. The coefficients of a and b are [37]$ \begin{array}{*{20}{l}} \chi\left\{\begin{aligned} a_B =&a_W=0,\\ b_B =&\frac{\left|C_{B}(\Lambda)\right|^{2}}{\pi} \frac{m_{\chi}^{4}}{\Lambda^{6}}\Big[c_{w}^{4}+\frac{c_{w}^{2} s_{w}^{2}}{8} \beta_{\gamma Z}^{2}\left(x_{Z}-4\right)^{2}\Theta(M_Z<2m_\chi) +\frac{s_{w}^{4}}{8} \beta_{Z Z}\left(3 x_{Z}^{2}-8 x_{Z}+8\right)\Theta(M_Z<m_\chi)\Big], \\ b_W =&\frac{\left|C_{W}(\Lambda)\right|^{2}}{\pi} \frac{m_{\chi}^{4}}{\Lambda^{6}}\Big[s_{w}^{4}+\frac{c_{w}^{2} s_{w}^{2}}{8} \beta_{\gamma Z}^{2}\left(x_{Z}-4\right)^{2}\Theta(M_Z<2m_\chi) +\frac{c_{w}^{4}}{8} \beta_{Z Z}\left(3 x_{Z}^{2}-8 x_{Z}+8\right)\Theta(M_Z<m_\chi)\\ &+\frac{1}{4} \beta_{W W}\left(3 x_{W}^{2}-8 x_{W}+8\right)\Theta(M_W<m_\chi)\Big], \end{aligned}\right. \end{array} $

(22) $ \begin{array}{*{20}{l}} \phi\left\{\begin{aligned} a_B =& \frac{\left|C_{B}(\Lambda)\right|^{2}}{\pi} \frac{2m_{\phi}^{2}}{\Lambda^{4}}\Big[c_{w}^{4} +\frac{c_{w}^{2} s_{w}^{2}}{8} \beta_{\gamma Z}^{2}\left(x_{Z}-4\right)^{2}\Theta(M_Z<2m_\phi)+\frac{s_{w}^{4}}{8} \beta_{Z Z}\left(3 x_{Z}^{2}-8 x_{Z}+8\right)\Theta(M_Z<m_\phi)\Big],\\ a_W =& \frac{\left|C_{W}(\Lambda)\right|^{2}}{\pi} \frac{2m_{\phi}^{2}}{\Lambda^{4}}\Big[s_{w}^{4} +\frac{c_{w}^{2} s_{w}^{2}}{8} \beta_{\gamma Z}^{2}\left(x_{Z}-4\right)^{2}\Theta(M_Z<2m_\phi)+\frac{c_{w}^{4}}{8} \beta_{Z Z}\left(3 x_{Z}^{2}-8 x_{Z}+8\right)\Theta(M_Z<m_\phi) \\ &+\frac{1}{4} \beta_{W W}\left(3 x_{W}^{2}-8 x_{W}+8\right)\Theta(M_W<m_\phi)\Big], \\ b_{B} =&\frac{\left|C_{B}(\Lambda)\right|^{2}}{\pi} \frac{2m_{\phi}^{2}}{\Lambda^{4}}\Big[c_{w}^{4}/2 +\frac{c_{w}^{2} s_{w}^{2}}{4} \beta_{\gamma Z}^{2}\left(x_{Z}-4\right)\Theta(M_Z<2m_\phi)+s_{w}^{4} \beta_{Z Z}\left(1/2-x_Z\right)\Theta(M_Z<m_\phi)\Big], \\ b_{W} =&\frac{\left|C_{W}(\Lambda)\right|^{2}}{\pi} \frac{2m_{\phi}^{2}}{\Lambda^{4}}\Big[s_{w}^{4}/2 +\frac{c_{w}^{2} s_{w}^{2}}{4} \beta_{\gamma Z}^{2}\left(x_{Z}-4\right)\Theta(M_Z<2m_\phi)+c_{w}^{4} \beta_{Z Z}\left(1/2-x_Z\right)\Theta(M_Z<m_\phi)\\ &+\beta_{W W}\left(1-2x_Z\right)\Theta(M_W<m_\phi)\Big]. \end{aligned}\right. \end{array} $

(23) In above equations, we have defined the phase space factor
$ \beta_{i j}=\sqrt{1-\left(m_{i}+m_{j}\right)^2/\left(4 m_{\rm DM}^2\right)} $ and$ x_i=m_i^2/m_{\rm DM}^2 $ with$ {\rm DM}=\chi,\phi $ . Using the results for$ a_{B,W} $ and$ b_{B,W} $ , the relic density can then be calculated using$ \Omega_{\rm DM} h^{2}=\frac{1.09 \times 10^{9} x_{F} \mathrm{GeV}^{-1}}{M_{P l} \sqrt{g_{*}\left(x_{F}\right)}\left(a+3 b / x_{F}\right)}, $

(24) where
$ a=a_B+a_W $ and$ b=b_B+b_W $ .$ x_F=m_{\rm DM}/T_F $ is the ratio of the mass of DM$ m_{\rm DM} $ and the early-universe freeze-out temperature$ T_F $ , which can be obtained by solving$ x_F=\ln\left[c(c+2)\sqrt{\frac{45}{8}}\frac{m_{\rm DM}M_{Pl}(a+6b/x_F)}{2\pi^3\sqrt{g_*(x_F)}}\right]. $

(25) The loop-induced effective DM-quarks (
$ {\cal O}_q $ ) and DM-gluons ($ {\cal O}_G $ ) operators can result in the interaction between DM and nucleons. The spin-independent (SI) cross section for elastic scalar and Dirac WIMP scattering on a nucleon has the form$ \begin{aligned}[b] \sigma_{\rm SI}^{\mathrm{\phi}} \simeq& \frac{\mu_N^{2} m_{N}^{2}}{\pi m_\phi^2 \Lambda^{4}}\Bigg|\frac{\alpha Z^{2}}{A} f_{A}^{N} C_{AA}\left(\mu_{\rm had}\right)\\&+\frac{Z}{A} f_{p}\left(\mu_{\rm had}\right)+\frac{A-Z}{A} f_{n}\left(\mu_{\rm had}\right)\Bigg|^{2}\,, \end{aligned} $

(26) $ \begin{aligned}[b] \sigma_{\rm SI}^{\mathrm{\chi}} \simeq& \frac{\mu_N^{2} m_{N}^{2}}{\pi \Lambda^{6}}\Bigg|\frac{\alpha Z^{2}}{A} f_{A}^{N} C_{AA}\left(\mu_{\rm had}\right)\\&+\frac{Z}{A} f_{p}\left(\mu_{\rm had}\right)+\frac{A-Z}{A} f_{n}\left(\mu_{\rm had}\right)\Bigg|^{2}\,. \end{aligned} $

(27) In above equations,
$ m_N\simeq 0.939 $ GeV is the average nucleon mass, and$ \mu_N=m_{\phi,\chi}m_N/(m_{\phi,\chi}+m_N) $ is the reduced mass of the DM-nucleon system. The form factor$ f_{A}^{N} $ describes the Rayleigh scattering of two photons on the entire nucleus. At a zero-momentum transfer limit,$ f_{A}^{N}\simeq0.08 $ for a xenon target. The form factor$ f_{N=p,n} $ describing the couplings between the DM and nucleon is expressed as [40, 53]$ f_{N}\left(\mu_{\rm had}\right)=\sum\limits_{q=u, d, s} f_{q}^{N} C_{q}\left(\mu_{\rm had}\right)-\frac{8 \pi}{9} f_{G}^{N} C_{G}\left(\mu_{\rm had}\right), $

(28) where the form factors
$ f_{q}^{N} $ describing the scalar couplings between quarks and nucleon are given by [54]$ \begin{aligned}[b]& f_{d}^{p}=0.0191, \;\;\ f_{u}^{p}=0.0153, \;\;\ f_{d}^{n}=0.0273,\\& f_{u}^{n}=0.0110,\ \;\; f_{s}^{p}=f_{s}^{n}=0.0447, \end{aligned} $

(29) and
$ f_{G}^{N}=1-\sum\limits_{q=u, d, s} f_{q}^{N}. $

(30) -
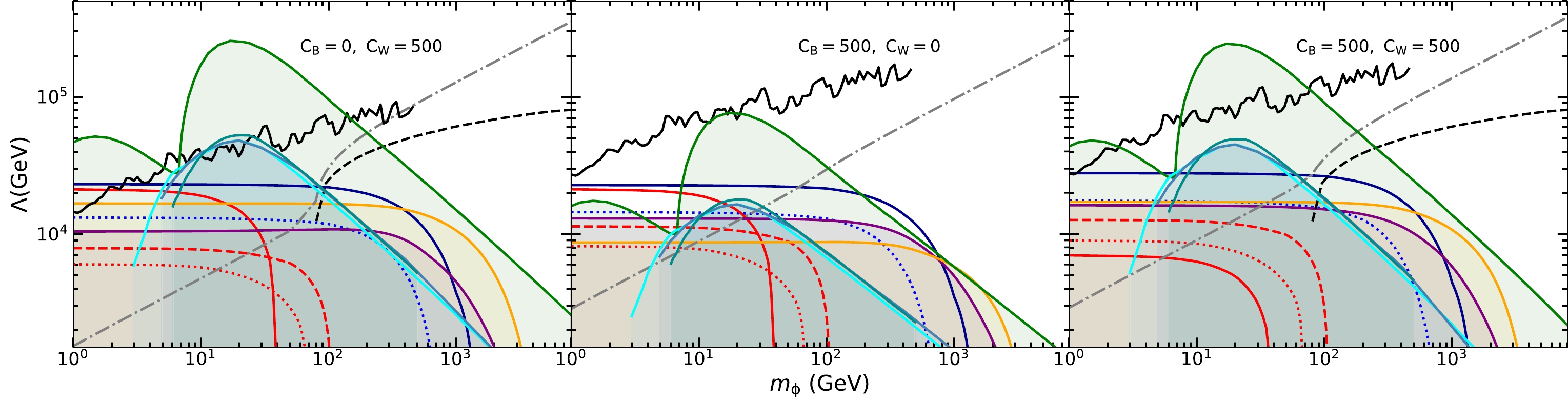
We apply simple
$ \chi^2 $ analysis to derive the lower bounds on Λ for effective operators in Eq. (5) at the future LHeC, FCC-ep, and CEPC at$ 95 $ % C.L. by requiring$ \chi^2=N_S^2/N_B=3.84 $ [55] with the specified luminosities. For LHeC and FCC-ep, the total integrated luminosities are assumed as$ L = 2\; {\rm ab}^{-1} $ . The limits of Λ as a function of the mass of Dirac fermion and scalar DM are shown in Figs. 7 and 8, respectively. We also present the exclusion limits derived from the mono-photon [51] search and mono-jet [52] search at the LHC and from the direct DM experiments XENON1T [56, 57], XENONnT [58], and PandaX-4T [59]. For illustration, we plot the contours of the relic abundance$ \Omega_{\rm DM} h^{2}=0.1186\pm0.0020 $ . The neutrino floor is also shown, which represents the WIMP-discovery limit obtained using an assumed exposure of 1000$ ^8B $ neutrinos detected on a xenon target [60]. For the scalar DM, we also show the constraints from the DM indirect searches through the gamma-ray and$ WW $ observations by the Fermi-LAT Collaboration [61]. Here, we consider three typical cases, i.e.,$C_{B}=0 $ ,$C_{W}=500$ ,$ C_{B}=500,\; C_{W}=0 $ , and$ C_{B}=C_{W}=500 $ .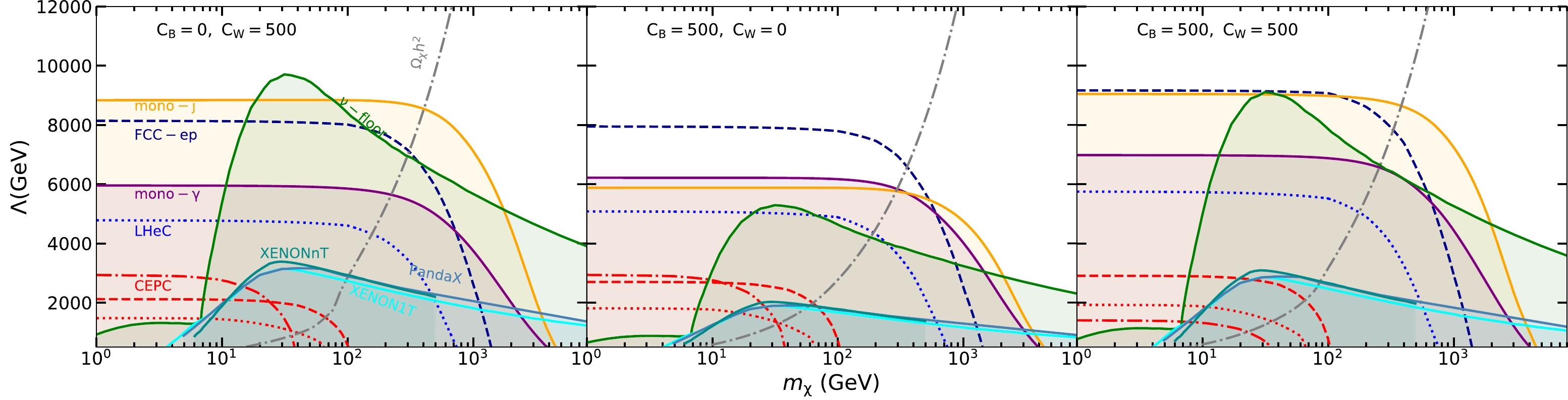
Figure 7. (color online) Constraints in the
$ m_\chi-\Lambda $ plane for the fermion DM with$ C_B^{6(7)}=0,C_W^{6(7)}=500 $ (left panel),$ C_B^{6(7)}=500,C_W^{6(7)}=0 $ (middle panel), and$ C_B^{6(7)}=500,C_W^{6(7)}=500 $ (right panel). The purple and orange solid lines denote the exclusion limits from the mono-photon [51] and mono-jet [52] searches at the 95% C.L. at the 13 TeV LHC, respectively. For the direct searches, recent bounds from XENON1T [56, 57], XENONnT [58], and PandaX-4T [59] are shown as cyan, dark cyan, and steel blue solid lines, respectively. For illustration, the contours of the relic abundance$ \Omega_{\rm DM} h^{2}=0.1186 $ are also plotted as gray dash-dotted curves. The neutrino floor is shown as green-shaded regions. The expected 95% C.L. bounds at the future LHeC (blue dotted lines), FCC-ep (dark blue dashed lines), and CEPC (red dotted lines for Z factory mode, red dash-dotted lines for$ W^+W^- $ threshold scan mode, red dashed lines for Higgs factory mode) are shown.For fermion DM, the bounds from the CEPC with all the three running modes can touch the neutrino floor with the DM mass less than a few GeV, whereas the
$ e^+e^- $ collider CEPC is not competitive with other$ ep $ and$ pp $ colliders. At the LHC, the sensitivity from mono-jet search is better with$ C_{B}=0, C_{W}=500 $ , and$ C_{B}=C_{W}=500 $ but is slightly worse with$ C_{B}=500,\; C_{W}=0 $ than the mono-photon search. Moreover, the LHC mono-jet search can provide the best constraint with$C_{B}=0,\; C_{W}=500$ compared with other collider experiments. The figures further validate that the FCC-ep has significant advantages to constrain DM-gauge boson effective interactions compared with the LHeC, as mentioned earlier. For$ C_{B}=500,\; C_{W}=0 $ , and$ C_{B}=C_{W}=500 $ , the FCC-ep can incorporate the region unconstrained by other experiments when the DM mass in less than several hundred GeV and extend the limits up to about 8000 and 9000 GeV, respectively.For scalar DM, in the case of
$ C_{B}=0, C_{W}=500 $ , all the collider searches cannot escape the neutrino floor, whereas the indirect searches of DM by the Fermi-LAT Collaboration provide the leading constraints and can include the neutrino floor in the mass regions of$ 5\ {\rm GeV} \lesssim m_\phi \lesssim 7 $ GeV and$ m_\phi \gtrsim 130 $ GeV with gamma-ray observation and$ m_\phi\gtrsim280 $ GeV with$ WW $ observation. For$C_{B}=500, C_{W}=500$ , the FCC-ep can reach the neutrino floor in the mass region of$ 5\ {\rm GeV} \lesssim m_\phi \lesssim 6 $ GeV, whereas other collider searches cannot escape the neutrino floor. Similar to the case of$ C_{B}=0, C_{W}=500 $ , DM searches by the Fermi-LAT Collaboration can reach the neutrino floor for$ 3\ {\rm GeV} \lesssim m_\phi \lesssim 7 $ GeV and$ m_\phi \gtrsim 80 $ GeV with cosmic gamma-ray observation and$ m_\phi > 250 $ GeV with$ WW $ observation. For$ C_{B}=500,\; C_{W}=0 $ , the cosmic gamma-ray observation by the Fermi-LAT Collaboration almost lies above the neutrino floor in the plotted region, and$ WW $ observation cannot provide any constraint because$ \phi\bar\phi W^+W^- $ coupling vanishes. For the collider searches, the future FCC-ep provides the most stringent restrictions relative to the other colliders for all the considered three cases with$ m_\phi $ less than a few hundred GeV. Moreover, for$ C_{B}=500,\; C_{W}=0 $ , the FCC-ep and CEPC in the Z factory mode can probe a light DM ($ m_\phi \lesssim 7 $ GeV) reaching the neutrino floor. -
In this study, we focus on the constraints on dimension-6 (7) effective operators between scalar (Dirac fermion) DM and SM gauge bosons at future
$ ep $ colliders LHeC and FCC-ep via the$ {\not E}_T+e^-j $ signature for the first time. We observe that SM irreducible and reducible backgrounds can be effectively suppressed by imposing appropriate kinematic cuts. We also consider the sensitivity at the future$ e^+e^- $ collider CEPC under three different modes with a mono-photon signature and update the limits from the LHC with current mono-j and mono-γ searches. In addition to the contribution from$ {{\not E}_T+W/Z (\to {\rm hardons})} $ channel due to the DM-diboson operators for mono-j at LHC, we investigate the contribution from the loop induced effective DM-quarks and DM-glouns operators. We observe that the contribution from DM-quarks and DM-gluons operators can be ignored. We present the constraints on the effective energy scale Λ as a function of DM mass with three typical cases of Wilson coefficients:$ C_{B}^{6(7)}=C_{W}^{6(7)}=500 $ ,$ C_{B}^{6(7)}=0, C_{W}^{6(7)}=500 $ , and$ C_{B}^{6(7)}=500, C_{W}^{6(7)}=0 $ . The FCC-ep exhibits better sensitivity than the LHeC in all cases for scalar and Dirac fermion DM. We observe that the collider searches can probe light DM reaching the neutrino floor.
Exploring dark matter-gauge boson effective interactions at current and future colliders
- Received Date: 2023-09-07
- Available Online: 2024-06-15
Abstract: In this study, we systematically investigate collider constraints on effective interactions between Dark Matter (DM) particles and electroweak gauge bosons. We consider the simplified models in which scalar or Dirac fermion DM candidates couple only to electroweak gauge bosons through high dimensional effective operators. Considering the induced DM-quarks and DM-gluons operators from the Renormalization Group Evolution (RGE) running effect, we present comprehensive constraints on the effective energy scale Λ and Wilson coefficients






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: