HTML
-
On the basis of numerous observations, there is no doubt that the expansion of the Universe is accelerating. The accelerated expansion of the Universe was first discovered in 1998 by two independent observations: the Supernovae Cosmology Project and the High-Z Supernovae Search Team [1]. The most promising physically relevant candidate to describe the acceleration of the expansion of the Universe is dark energy. However, the nature of dark energy is still unclear except for its consequence: it is generating repulsive gravity. Several models elaborating on the nature of this substance have been proposed: the Chaplygian gas, cosmological constant, K-essence, quintessence, etc.
Among other proposals, the quintessence is attracting special interest, and it can be considered as the fifth interaction in Nature [2]. The equation of the state parameter of quintessence is restricted to
$ -1<\omega_q<-1/3 $ . Particularly, depending on the value of the$ \omega_q $ , one may distinguish the type of matter:$ \omega_q=-1 $ corresponds to the standard cosmological constant,$ \omega_q=-2/3 $ represents the pure quintessence field, and$ \omega_q=-1/3 $ refers to cosmic strings [3]. The quintessence of astrophysical processes may affect the dynamics of the particles around a compact object through gravitational interaction. Thus, one needs to take into account the effect caused by this substance through the analysis of the particle dynamics. In particular, the effect of quintessence on the photon trajectory around a compact object has been explored in Ref. [4]. To investigate the particle dynamics, it is necessary to consider the exact solution describing the spacetime around a compact object surrounded by quintessence. It was Kiselev who first obtained the spherically symmetric black hole (BH) solution with the non-vanishing quintessence parameter [5]. Several authors explored various aspects of the Kiselev solution, including the optical properties of spacetime [6−10]. Later, the Kiselev solution was extended to the case of the presence of a string cloud [11]. The string cloud may be considered a structure formation that occurred in the early Universe during the symmetry break [12]. It is also worth noting that the thermodynamics of spacetime, timeline, and null geodesics around quintessential BHs with string clouds were analyzed in [13, 14].The chaos of motion of a relativistic particle orbiting around a BH has been extensively studied. The unstable circular geodesics of neutral particles are related to their Lyapunov exponents. In this study of the dynamics of particles, we relate the stability of the orbits and the Lyapunov exponent, and the chaotic behavior is studied graphically. A relativistic particle moving near a BH horizon is considered. External forces (such as electromagnetic or scalar forces) pull the particles outward while orbiting around the BH. The repulsion force is so strong that it can prevent the particle from falling, even if it comes very close to the horizon.
Further, to probe the gravity models, one may use several independent observations/experiments. One of the directions of testing the gravity models is using the quasiperiodic oscillations (QPOs) generated by microquasars. The microquasar is referred to as a binary system containing a BH and an ordinary star. The matter accretes to the BH from the donor star and forms the accretion disc. Due to the friction of the matter in the disc, one may observe the generation of electromagnetic radiation in the X-ray band. The QPOs are detected in the power density of X-ray data received from these objects. The QPO frequencies may provide a useful tool to test the accretion disc properties together with the gravity models describing the BH. It is also worth noting that one may distinguish the high-frequency (HF) and low-frequency (LF) QPOs according to the range of observed frequencies, which are up to 0.5 kHz and 30 Hz, respectively. Most HF QPOs are observed with a twin peak ratio of 3:2. Numerous studies have been dedicated to the analysis of the different models of QPOs based on the dynamics of the test particles around compact objects [15−29].
In this study, we analyze the dynamics of test particles around a quintessential BH surrounded by a cloud of strings with the aim of applying the results to study the QPOs. The rest of this paper is organized as follows. In Sec. II, we describe the solution of the quintessential BH surrounded by a string cloud. Section III is devoted to studying the dynamics of test particles around a BH with non-vanishing quintessence and string cloud parameters. We analyze the fundamental frequencies in Sec. V and then apply them to the modeling of QPOs in Sec. VI. We provide a summary of the research in Sec. VIII. Throughout this paper, we use a system of units where
$ c=1=G $ and the spacetime signature is (–, +, +, +). -
In this study, we investigate a BH in the quintessential field (
$ T_{\mu \nu} $ ) and cloud of strings ($ {\cal T}_{\mu \nu} $ ) with the effective energy-momentum tensor$ T_{\mu \nu}^{\rm eff}=T_{\mu \nu}+{\cal T}_{\mu \nu} $ . The cloud of strings is described by the following nonzero components of the field energy-momentum tensor [30]$ {\cal T}^t_t={\cal T}^r_r=\rho_c=-\frac{\alpha}{r^2}, $

(1) $ \begin{array}{*{20}{l}} {\cal T}_\theta^\theta={\cal T}^\phi_\phi=0, \end{array} $

(2) where the dimensionless parameter α represents the strength of the cloud of strings (
$ 0<\alpha <1 $ ). The non-zero components of the energy-momentum tensor of the quintessential field suggested by Kiselev are defined as$ \begin{array}{*{20}{l}} T^t_t=T^r_r=-\rho_q, \end{array} $

(3) $ T_\theta^\theta=T^\phi_\phi=\frac{1}{2}\rho_q(3\omega_q+1)\ , $

(4) where
$ \omega_q $ is the parameter of quintessence responsible for the EoS as$ p_q=\omega_q\rho_q \ , \quad \rho_q=-\frac{\gamma}{2} \frac{3\omega_q}{r^{3(\omega_q+1)}}, $

and
$ \gamma>0 $ is a normalization factor. The non-zero components of the energy-momentum tensor corresponding to the quintessence and cloud of strings are defined as [31]$ T^t_t=T^r_r=-\rho_q-\frac{\alpha}{r^2}, $

(5) $ T_\theta^\theta=T^\phi_\phi=\frac{1}{2}\rho_q(3\omega_q+1)\ , $

(6) where
$ \rho_q $ is the density of the quintessence field. The static and spherically symmetric BH solution associated with the quintessence and cloud of strings is described by the following line element within the spherical coordinates$ x^\mu =\left(t,r,\theta,\varphi\right) $ [31]:$ {\rm d}s^2=-f\left(r\right){\rm d}t^2+\frac{{\rm d}r^2}{f\left(r\right)}+r^2{\rm d}\theta^2+r^2\sin^2\theta\,{\rm d}\varphi^2, $

(7) with the lapse function
$ f\left(r\right)=1-\alpha -\frac{2M}{r}-\frac{\gamma}{r^{3\omega_{q}+1}}, $

(8) where M is the BH's total mass.
For the perfect fluid distribution of matter/energy, the EoS parameter takes a value in the range of
$ -1<\omega_{q}< -\dfrac{1}{3} $ , and when$ \omega_{q}=-1 $ , it recovers the cosmological constant. Therefore, in this paper, as test values, we work with the cases$ \omega_{q}=-\dfrac{1}{2} $ and$ \omega_q=-\dfrac{2}{3} $ :$ f(r)=1-\alpha-\frac{2M}{r}- \begin{cases} \gamma r^{\frac{1}{2}} \ , \ \ \omega_q=-{1}/{2}\\ \gamma r \ \ , \ \ \omega_q=-{2}/{3} \end{cases} $

(9) In general, the radius of the event horizon of a spherically symmetric BH can be defined by
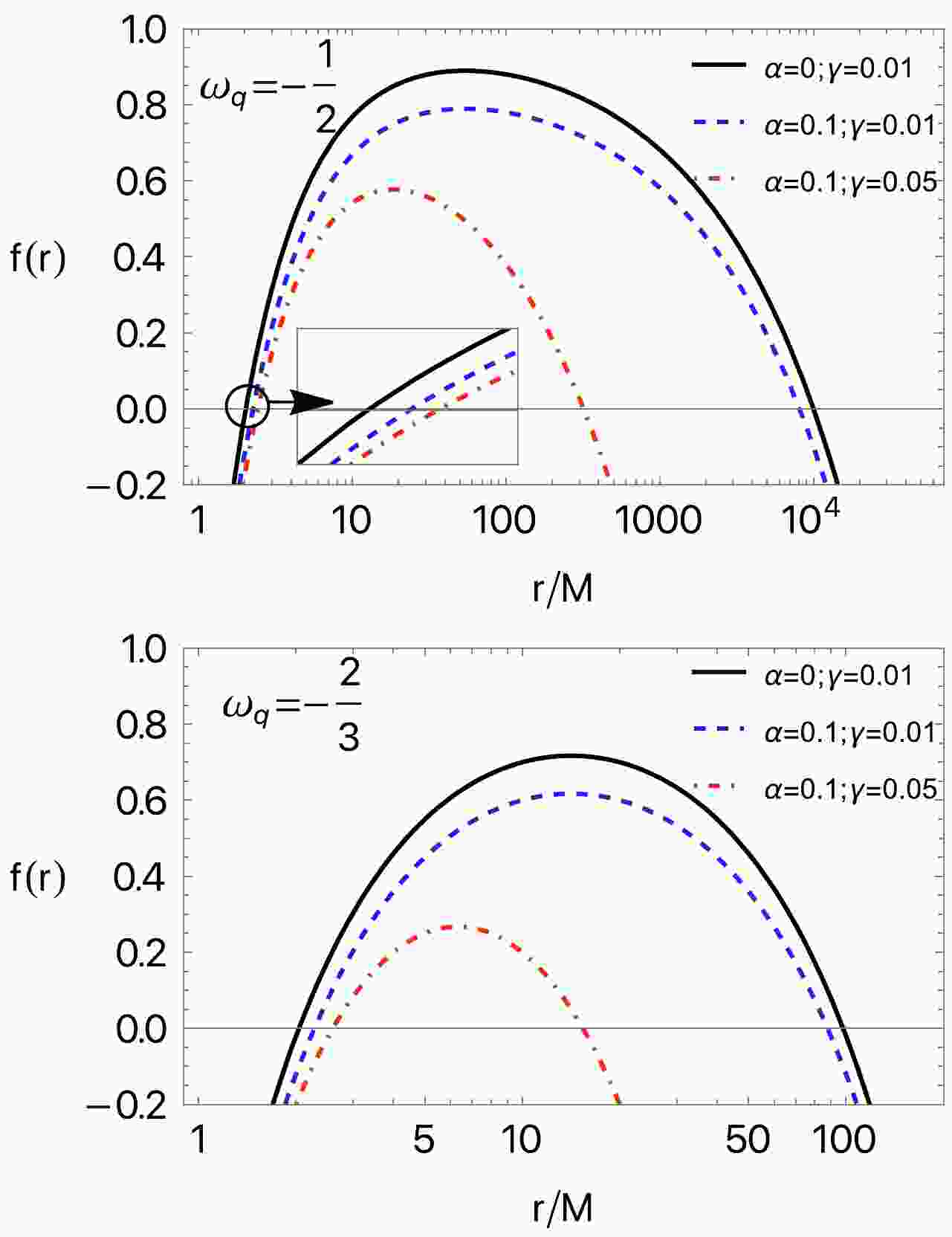
$ g^{rr}=0 $ .Figure 1 shows the radial dependence of the metric function
$ f(r) $ for the different values of α and γ in the cases$ \omega_q=-\dfrac{1}{2} $ and$ -\dfrac{2}{3} $ . One can see from both panels that the lines cross zero (the metric function takes zero) values at two different distances, representing the event and cosmological-like horizons (due to the quintessential field). In the presence of both the string cloud and quintessential field, the horizons come close to each other. Moreover, it can be observed that the radius of a cosmological-like horizon is very sensitive.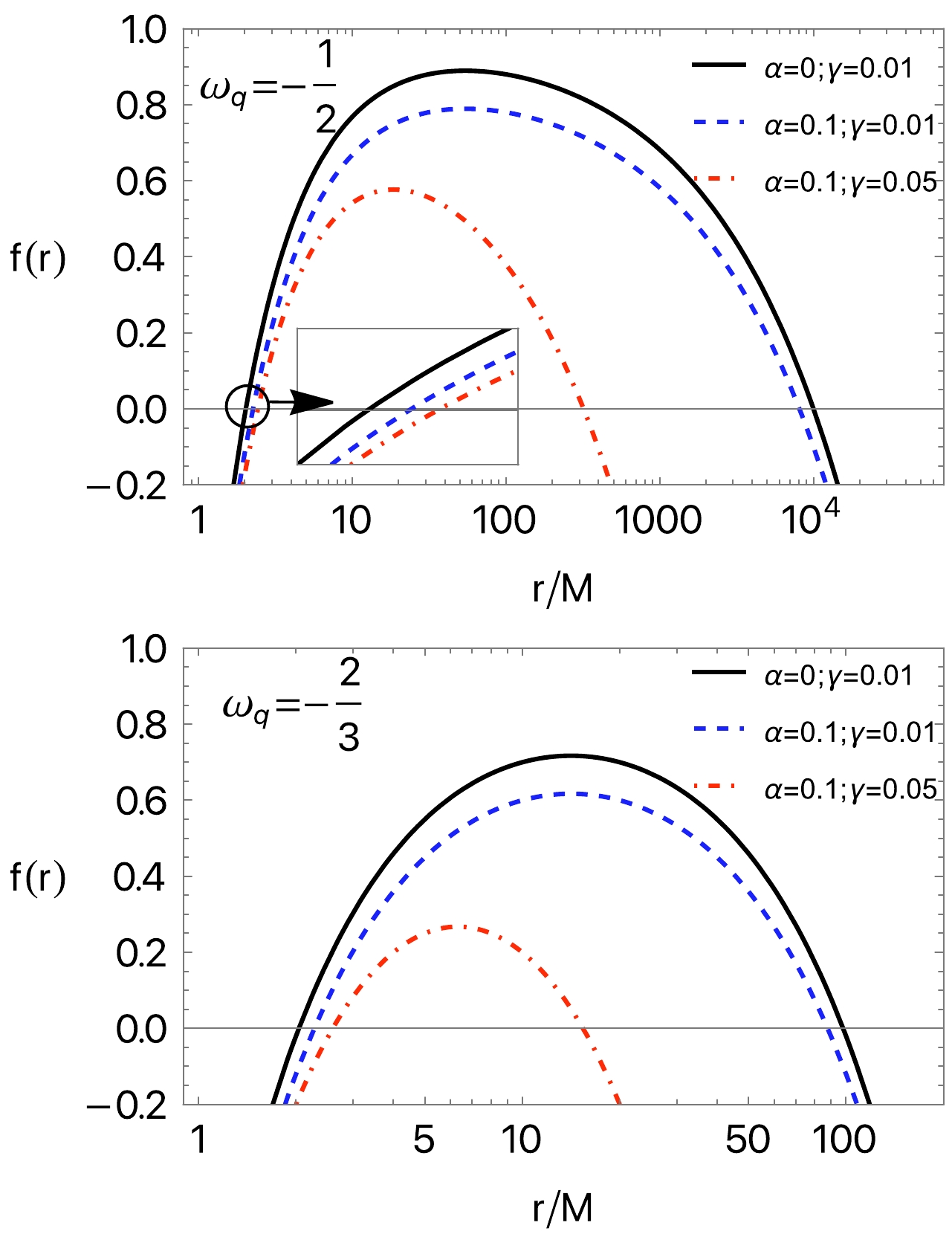
Figure 1. (color online) Dependence of event horizon radius on the string cloud α for different values of γ and
$ \omega_q $ .The analytic expression for the radius of the event horizon becomes large and is complicated to see the effects of the parameters γ and α. For this reason, below, we will simply show the analyses graphically.
The dependence of the radius of the event horizon on the string cloud parameter for different values of the parameters γ and
$ \omega_q $ is shown in Fig. 2. As can be observed from the figure, the increase in the string cloud and quintessential parameters causes a sufficient increase in the event horizon radius. However, the maximum value of the radius of the event horizon at the extreme value of the field parameter of the string cloud decreases with increasing$ \omega_q $ . Now, one may obtain the values of the quintessential and string cloud parameters, allowing the metric (8) to describe the BH. To obtain the ranges for the possible values of α and γ, one may set the equations$ f(r)=0 $ and$ f'(r)=0 $ and solve the system of equations with respect to the spacetime parameters. Owing to the complicated form of the solutions, we provide a graphical analysis. Figure 3 demonstrates the relationships between the quintessential and string cloud field parameters for the values of$ \omega_q=-\dfrac{1}{2} $ and$ -\dfrac{2}{3} $ . We divide the plots in this figure into two areas, shaded and unshaded areas, which correspond to the BH and no BH solutions, respectively. One can see from the figure that the value of γ decreases, the corresponding values of the parameter are approximately two times larger at$ \omega_q=-\dfrac{1}{2} $ than they are at$ \omega_q=-\dfrac{2}{3} $ , and the shaded area shrinks. The blue line corresponds to the parameter's extreme values.
Figure 2. (color online) Dependence of event horizon radius on the string cloud α for different values of γ and
$ \omega_q $ , with$ M=1 $ .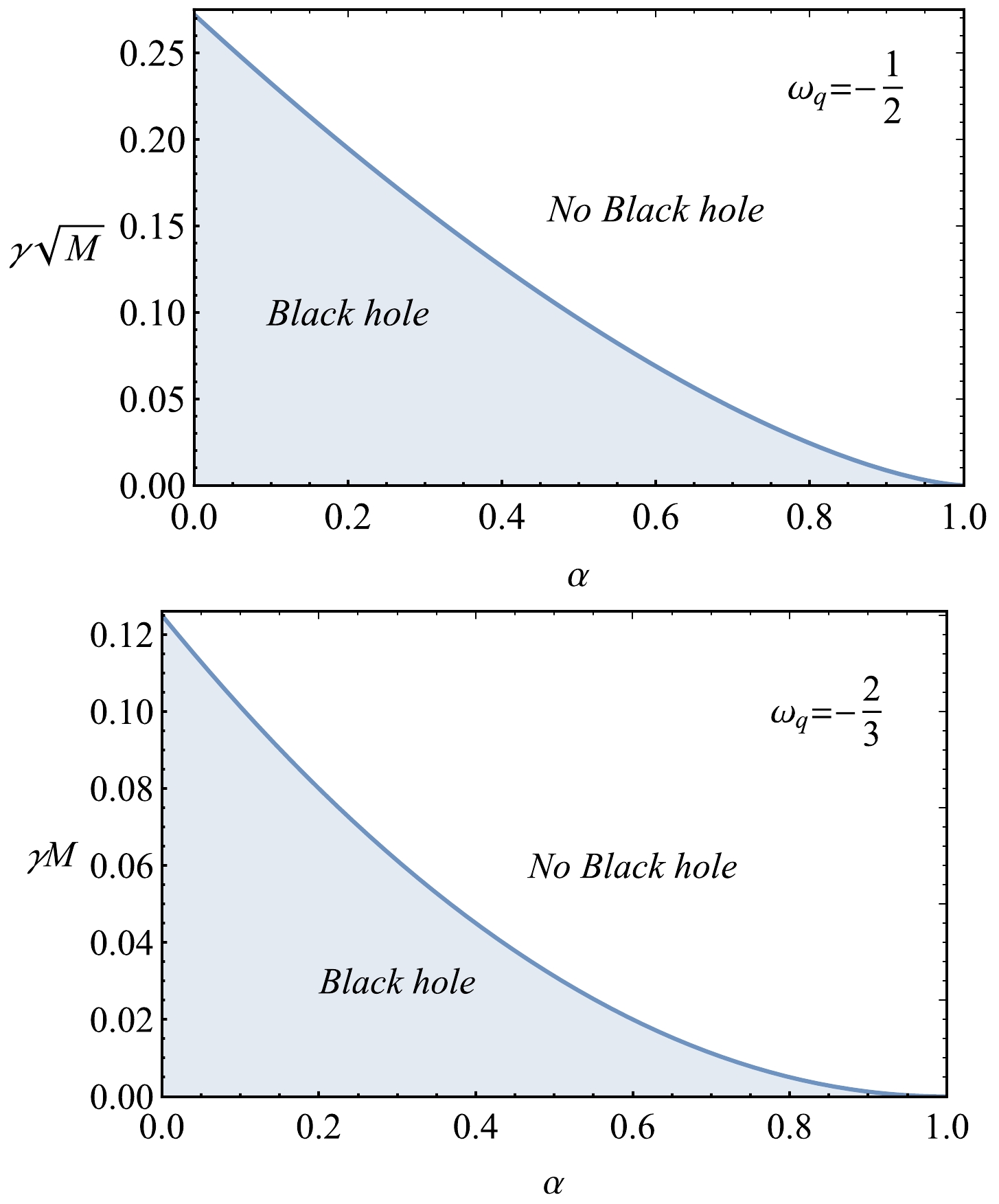
Figure 3. (color online) Possible relationships between extreme values of parameters γ and α for fixed values of parameter
$ \omega_q=-\dfrac{1}{2} $ (left panel) and$ -\dfrac{2}{3} $ (middle panel). The shaded area, under the lines, corresponds to the values of the parameters that may allow the spacetime to be a BH spacetime. -
We consider the dynamics of test particles around the quintessential BH in a string cloud. We will also study the energy of test particles in stable circular orbits.
-
First, we derive the equation of motion using the following Lagrangian:
$ L_{\rm p}=\frac{1}{2}m g_{\mu\nu} \dot{x}^{\mu} \dot{x}^{\nu} \ , $

(10) where m is the mass of the particle. Now, one may easily obtain the integrals of motion, the particle's specific energy
$ {\cal E}=E/m $ and angular momentum$ {\cal L}=L/m $ , in the following form:$ \begin{array}{*{20}{l}} g_{tt}\dot{t}=-{\cal E}\ , \qquad g_{\phi \phi}\dot{\phi} = {\cal L}. \end{array} $

(11) To govern the equations of motion for test particles with nonzero rest mass, we use the normalization condition
$ g_{\mu \nu}u^{\mu}u^{\nu}=-1 $ .The time-like geodesics of particles can be easily obtained by using the normalization condition and integrals of the motion (11) in the following form [32, 33, 34]:
$ \dot{r}^2={{\cal E}^2+g_{tt}\left(1+\frac{\cal K}{r^2}\right)}\ , $

(12) $ \dot{\theta}^2=\frac{1}{g_{\theta \theta}^2} \left({\cal K}-\frac{{\cal L}^2}{\sin^2\theta}\right)\ , $

(13) where
$ {\cal K} $ is the Carter constant corresponding to the total angular momentum of the particle.Hereafter, we consider the motion of particles at the equatorial plane (
$ \theta=\pi/2 $ and$ \dot{\theta}=0 $ ) in which the Carter constant$ {\cal K}={\cal L}^2 $ . Consequently, the equation for the radial motion of a particle takes the following form:$ \begin{array}{*{20}{l}} \dot{r}^2={\cal E}^2-V_{\rm eff}(r,\theta)\ , \end{array} $

(14) where the effective potential has the form
$ V_{\rm eff}(r) = f(r) \left(1 + \frac{{\cal L}^2}{r^2}\right) \ . $

(15) We now perform a graphical analysis of the effects of the quintessential field and string cloud as well as their combined effects on the effective potential. In Fig. 4, we show the radial dependence of the effective potential for the different values of the parameters α, γ, and
$ \omega_q $ . We also conduct a comparison with the Schwarzschild case, where all parameters are equal to zero. One can see from the figure that the presence of the string-cloud field causes a decrease in the potential, which means that a particle that does not interact with the string cloud can come closer to the central BH. Similarly, the quintessential field also decreases the effective potential, and its maximum shifts out of the central object. -
In this subsection, we explore the stable circular orbits. The following conditions determine such orbits of a test particle around a spherically symmetric BH:
$ \begin{array}{*{20}{l}} V_{\rm eff}={\cal E}, \qquad V_{\rm eff}'=0 \ . \end{array} $

(16) The expressions for the angular momentum and energy of test particles corresponding to circular orbits take the form
$ {\cal L}^2=-\frac{r^2 \left(\gamma +2 M r^{3 \omega _q}+3 \gamma \omega _q\right)}{2 (3 M+(\alpha -1) r) r^{3 \omega _q}+3 \gamma \left(\omega _q+1\right)}, $

(17) $ {\cal E}^2=-\frac{2 r^{-3 \omega _q-1} \left(\gamma +(2 M+(\alpha -1) r) r^{3 \omega _q}\right){}^2}{2 (3 M+(\alpha -1) r) r^{3 \omega _q}+3 \gamma \left(\omega _q+1\right)} . $

(18) Figure 5 demonstrates the radial dependence of the angular momentum of test particles corresponding to circular orbits around Schwarzschild BHs in string clouds and the quintessential field for the different values of spacetime parameters. It is observed from the figure that, in the presence of the string cloud, the value of the angular momentum increases, whereas the presence of the quintessential field causes it to decrease. One can note that the effect of γ is dominant at larger distances, affecting dark matter. At larger distances, there is a maximum in the angular momentum, and the maximum decreases and shifts toward the central BH due to the increase in both quintessential field parameters. Figure 6 shows the radial dependence of the energy of the test particles corresponding to circular orbits around a quintessence BH in a string cloud for different values of the parameters α, γ, and
$ \omega_q $ . The innermost stable circular orbit (ISCO) should satisfy the condition$ \partial_{rr}V_{\rm eff}(r_{\rm ISCO})=0 $ and/or$ \partial_r{\cal L}=0 $ together with the conditions expressed in (16). For the effective potential defined as (15), the corresponding equation for the ISCO radius takes the following form:
Figure 5. (color online) Angular momentum of test particles in circular orbits as a function of radial coordinates for different values of the parameters α, γ, and
$ \omega_q $ .
Figure 6. (color online) Energy of test particles at circular orbits around the black hole as a function of the radial coordinate for the different values of α, γ, and
$ \omega_q $ .$ \begin{aligned}[b] & \gamma \bigg\{6 M \left[\omega _q \left(3 \omega _q-4\right)-2\right]+(\alpha -1) r_{\rm ISCO} \left(9 \omega _q^2-1\right)\bigg\}\\ &\quad -\frac{2 M}{r_{\rm ISCO}^{-3 \omega_q}} \bigg[6 M+(\alpha -1) r_{\rm ISCO}\bigg]\\ &\quad -\frac{3 \gamma ^2}{r_{\rm ISCO}^{3 \omega_q}} \left(\omega _q+1\right) \left(3 \omega _q+1\right)=0\ . \end{aligned} $

(19) One can easily see from Eq. (19) that, in the Schwarzschild case, when
$ \alpha=\gamma =0 $ , the ISCO radius$ r_{\rm ISCO}=6M $ . However, Eq. (19) is quite complicated to be solved analytically. Therefore, we present graphical analyses of the behavior of the ISCO radius with respect to the variation of the quintessential and string cloud parameters. The ISCO radius as a function of the parameter α is shown inFig. 7 for different values of quintessence parameters. It can be observed that the ISCO is enlarged in the presence of both the string cloud and quintessential field.
Figure 7. (color online) ISCO radius as a function of the parameter α for different cases of γ and
$ \omega_q $ .In Fig. 8 we present the dependence of the energy and angular momentum of test particles at the ISCO on the radius of the ISCO for different values of quintessence parameters. Here, the parametric plot is used for the range of string clouds from 0 to 1. It is observed from the figure that, as the ISCO radius increases, the angular momentum also increases, whereas the energy corresponding to the radius decreases. The presence of γ causes a decrease in the angular momentum and a slight increase in the energy. It can also be observed that, at
$ \gamma=0.005 $ and$\omega_q=-{2}/{3}$ , the values of both energy and angular momentum are small due to the behavior of the ISCO radius at the same values of the parameter (see also Fig. 7). -
Another interesting issue in relation to the dynamics of test particles is their energy release while falling to the central object. While the test particle accrets to the BH, one may observe the energy extraction by converting it to either electromagnetic or gravitational radiation energy. The energy of the radiation is determined by the difference between the particle's rest energy and the energy of the particle at the ISCO measured by a local observer. The total bolometric luminosity of the accretion disk is proportional to the energy efficiency of the central BH through the relation
$ \eta=L_{\rm bol}/ (\dot{M}c^2) $ , where$ \dot{M} $ is the accretion rate [35]. Thus, the expression of the energy efficiency of the accretion disk has the following form [36]:$ \begin{array}{*{20}{l}} \eta=1-{\cal E}|_{\,r=r_{\rm ISCO}}, \end{array} $

(20) where
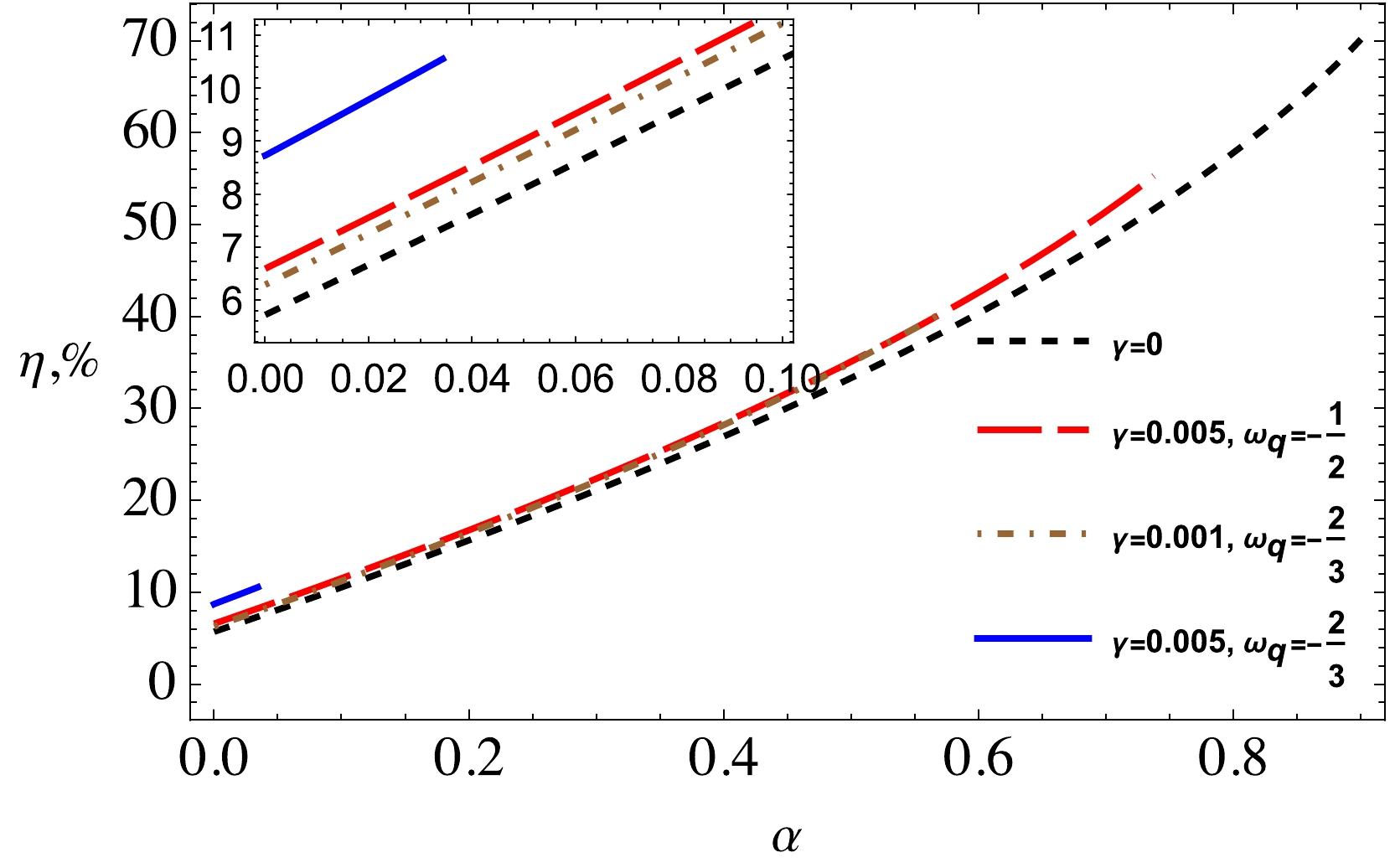
$ {\cal E}|_{\,r=r_{\rm ISCO}}={\cal E}_{\rm ISCO} $ is the energy of the particle at the ISCO that is characterized by the ratio of the binding energy (BH and particle system) and the rest energy of test particle.Figure 9 represents the dependence of the energy efficiency of the string cloud parameter for different values of γ and
$ \omega_q $ . It can be observed from this figure that, in the absence of the quintessential field, the efficiency reaches approximately 70%; however, it decreases with the increase in both the γ and$ \omega_q $ parameters. -
The stability of bounded orbits could be analyzed using the effective potential, which helps to find the possibility of stable circular orbits of particles moving in the equatorial plane. The regular trajectories of neutral particles moving in the geometry of a Kiselev BH with a cloud of strings near the equatorial plane are studied graphically. The effects of the quintessence parameter
$ \omega_q $ and string parameters γ and α are observed in this study.The radiation exerts a reaction force on the dynamics of the particles, especially on the chaotic nature of the motion and oscillatory frequencies, influencing these dynamics in the vicinity of BHs.
The observations are made at a given angular momentum of the particles and different values of quintessential parameters,
$ \omega_q=-1/2 $ and$ \omega_q=-2/3 $ . The strengths of the clouds of strings α affect the trajectories, acting as the source of attraction. It is observed in the trajectories of a neutral test particle that the average orbit radius of a test particle is larger, which means that an increase in these parameters makes the resultant interaction between the particle and BH weaker.In Fig. 2 and 3, the trajectories of the neutral particle in the geometry of a BH (in the Kiselev string cloud) are presented for
$ \omega_q=-1/2 $ and$ \omega_q=-2/3 $ . A comparison with the Schwarzschild BH (first row, top panel) shows that the bound orbits are at a larger (smaller) distance from the BH in the absence (presence) of stringy BH parameters. The second row of Fig. 2 shows that the gravitational potential of the BH increases with an increasing value of γ. No oscillating trajectories are observed when γ is nonzero and the value of α is zero (see the second row). Meanwhile, it is clear from the third and the fourth rows of Fig. 2 that oscillating trajectories are observed in the presence of α and γ, and a combined effect of both parameters results in stable circular orbits. This occurs because α contributes as the source of gravitation and traps the surrounding particles, whereas the role of γ is the opposite.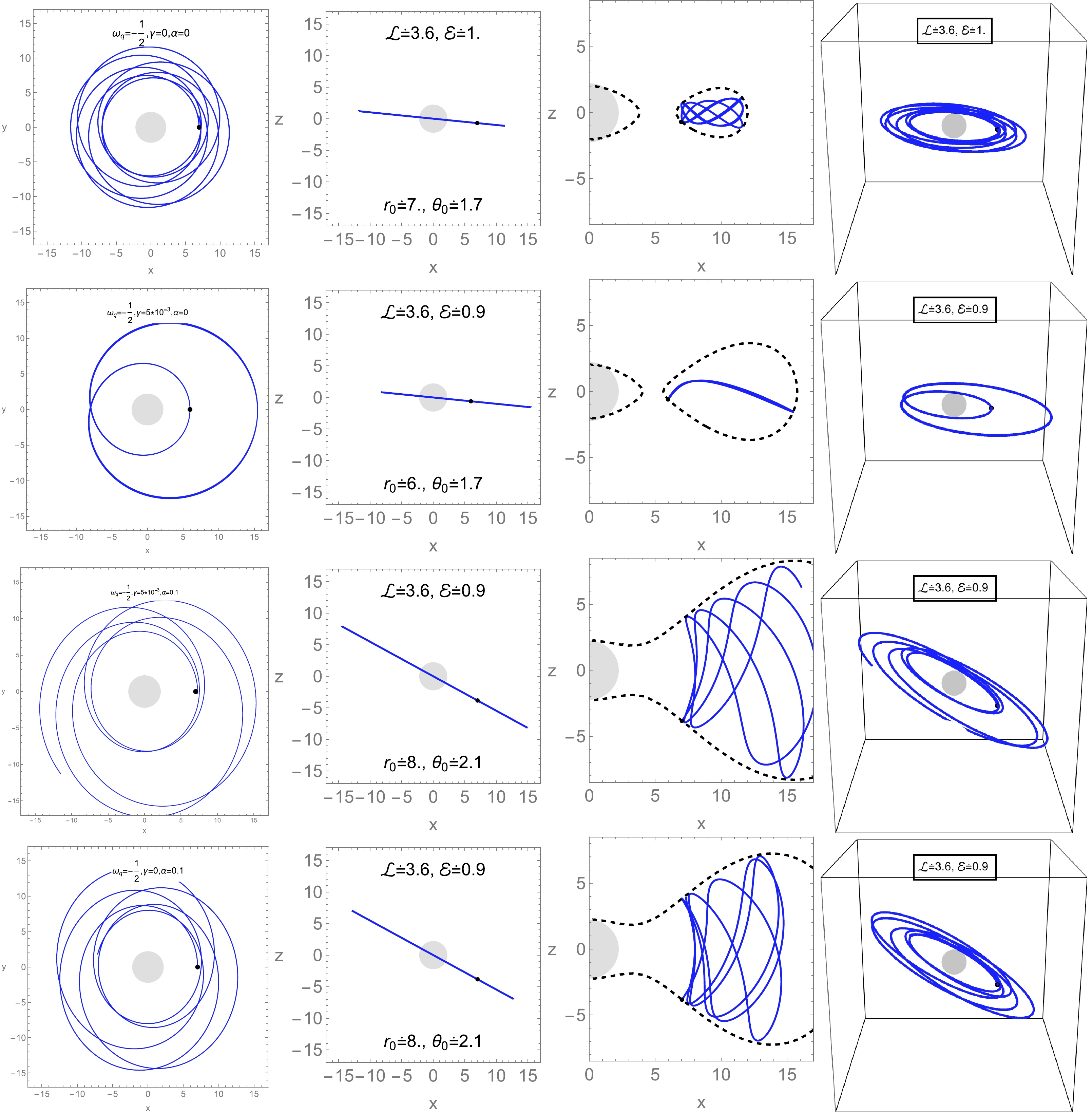
Figure 10. (color online) Trajectories of test neutral particles for different values of black hole parameters α, γ, and
$ \omega_q=-1/2 $ . The first row (top panel) presents the trajectories in the Schwarzschild geometry; the second row presents those for$\omega_q=-1/2,\alpha=0,\gamma=5\times10^{-3}$ ; the third line presents those for$\omega_q=-1/2,\alpha=0.1,\gamma=5\times10^{-3}$ ; and the fourth line presents those for$ \alpha=0.1, \gamma=0 $ .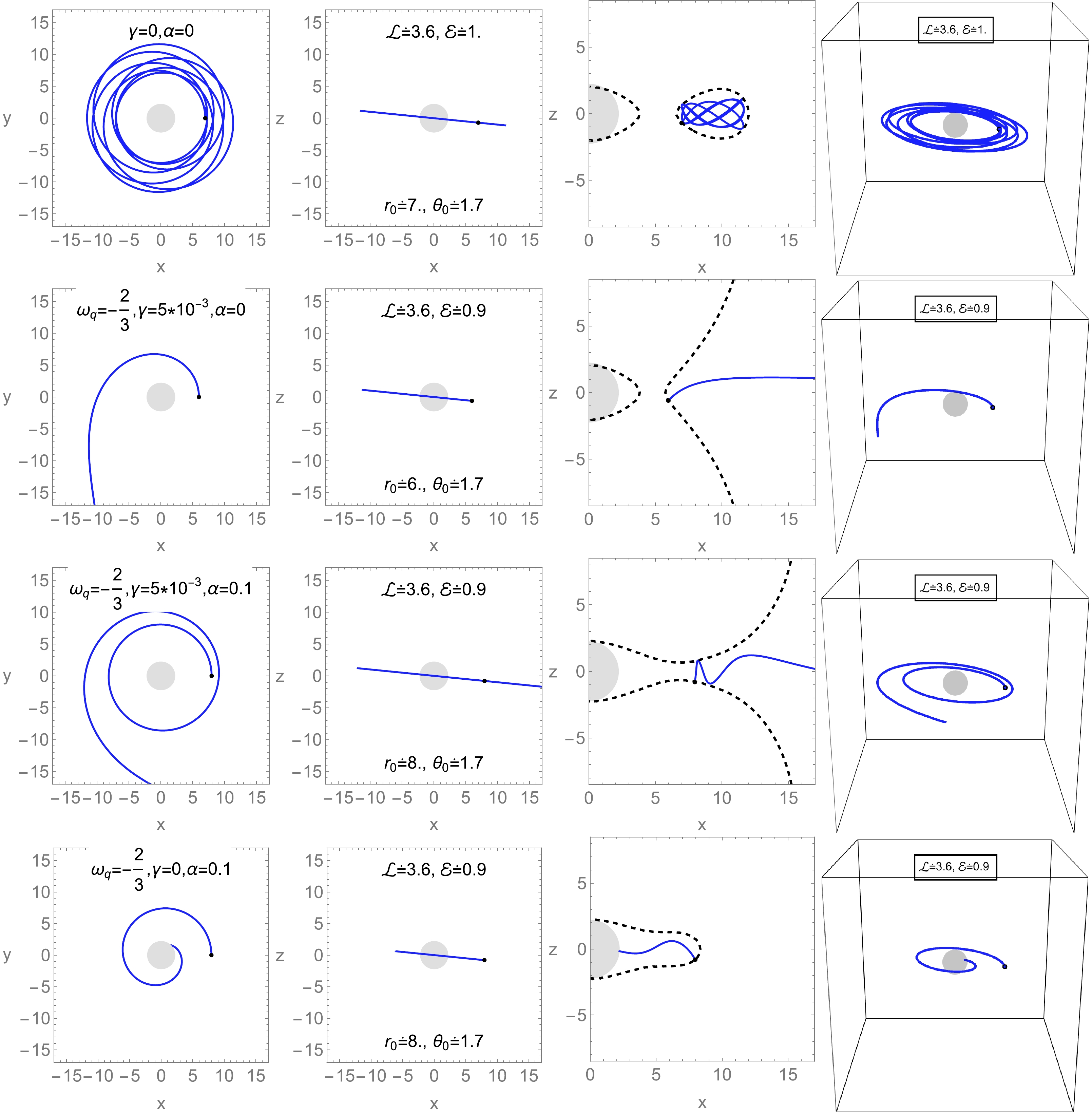
Figure 11. (color online) Trajectories of test neutral particles for different values of black hole parameters α, γ, and
$ \omega_q=-2/3 $ . The first row (top panel) presents the trajectories in the Schwarzschild geometry; the second row presents those for$\omega_q=-2/3,\,\alpha=0,\,\gamma=5\times10^{-3}$ ; the third line presents those for$\omega_q=-2/3,\,\alpha=0.1,\,\gamma=5\times 10^{-3}$ ; and the fourth line presents those for$ \alpha=0.1, \gamma=0 $ .In Fig. 3, the quintessential parameter is
$ \omega_q=-2/3 $ . A comparison with Fig. 2 shows that, for lower values of$ \omega_q $ , the gravitational potential of the BH increases with an increasing value of γ, and the trajectories are not in bounded orbits for the nonzero value of γ. The chances for an unstable motion of the particle become high in the presence of γ and zero value of α. No oscillating trajectories are observed for nonzero values of γ.In the third row of Fig. 3, note that oscillating trajectories are observed in the presence of α and γ, but their combined effect results in stable circular orbits. The analysis of trajectory for non-zero α and zero value of γ results in unstable circular orbits, shown in the last row of Fig. 3. Here, α has a contribution toward the source of attraction, and the particles cannot escape from the surroundings of the BH. In conclusion, for nonzero values of α and γ, the trajectories become stable and bounded.
-
The stability or instability of the circular orbits of the test particles is very important in the analysis of the dynamics of the particles around a BH. We calculate a local maximum of the effective potential of the particle, at which the Lyapunov exponent λ can be calculated for the particle trajectories. The Lyapunov exponent
$ \lambda_L $ determines the convergence (divergence) of the trajectories in phase space. It helps to measure the stability of geodesics:$ \lambda=\pm \sqrt{\frac{ -V^{\prime \prime}_{\rm eff}(r_0)}{2 \dot{t}^2(r_0)}}, $

(21) with
$V^{\prime \prime}_{\rm eff}(r_0)$ as the effective potential of the particle moving in the circular orbits. We consider the positive values of λ, ignoring the sign$ \pm $ ; λ is a real-valued function for unstable orbits, and imaginary for stable circular orbits. The orbit is said to be marginally stable when$ \lambda=0 $ . The asymptomatic behavior of the particle dynamics is observed by$ \lambda_L $ in Fig. 12, and it is a tool to analyze the behavior of trajectories (in the orbital motion). Note that, as the values of γ increase, λ decreases. At a long distance from the BH, λ is positive, showing instability in the dynamics of the particles. Then, it starts decreasing and eventually ends up with negative values. The negative values show the stability in the dynamics of the particle as it becomes closer to the ISCO. The behavior of λ is the same for different values of α when the particle is away from the BH, but as it gets closer, the increasing value of α results in a decrease in λ.
Figure 12. (color online) Lyapunov exponent of a particle moving in circular orbits around the LQGBH, plotted against
$ r/M $ for different values of parameters α and γ.It is observed that, for
$ \omega_q=-2/3 $ , λ is negative throughout, which means that the stability of orbits increases for decreasing values of$ \omega_q $ .The Kolmogorov-Sinai (KS) entropy reveals the loss or gain of information from the chaotic behavior of orbits [37, 38]. Zero KS entropy,
$ h_{ks}=0 $ , corresponds to the ordered or non-chaotic system, and$ h_{ks}>0 $ represents the chaotic or disordered system. Evolving with time, it plays an important role in studying dynamical systems. The KS entropy ($ h_{ks} $ ) is defined with the help of the Lyapunov exponents [39]:$ \begin{array}{*{20}{l}} h_{ks}=\Sigma {\lambda_j}, \; \; \; \lambda_j>0, \end{array} $

(22) and, in terms of the effective potential, it becomes
$ h_{ks}=\sqrt{\frac{ (\dot{r}^2)^{\prime \prime}}{2}}, $

(23) or
$ \begin{aligned}[b] h_{ks}=&\frac{1}{2C^3}\Big\{-4 r (f'(r))^3 (4r f'(r)+C)\\ &- 16f^3(r)(4f''(r)+ f^{(3)}(r))-4f^2(r)\\&\times(4f'(r)^2+ 4 C f''(r) +4r^2 (f''(r))^2+r C f^{(3)}(r) \\ &-2rf'(r)(4f''(r)+ f f^{(3)}(r)))+f(r)\Big(32 r (f'(r))^3 \\ &-3r^2 C (f''(r))^2+ f'(r)^2(5C +16 r^2 f''(r)) \\ &+2C r f'(r) \Big[7 f''(r) + r f^{(3)}(r)\Big]\Big)\Big\}^{1/2} , \end{aligned} $

(24) where
$ \begin{array}{*{20}{l}} C=\sqrt{4 f(r)-2rf'(r)}, \end{array} $

(25) whereas
$ f'(r), f''(r), f^{(3)}(r) $ represent the first, second, and third order derivatives of$ f(r) $ w.r.t. r, respectively.The behavior of λ is studied graphically in Fig. 12. It is observed that, as the value of α increases, the value of the Lyapunov exponent decreases (Fig. 12, top panel). This indicates that the instability of the orbits decreases in the presence of α. A comparison is conducted with the Schwarzschild BH when
$ \alpha=0=\gamma $ . The behavior of the Lyapunov exponent for non-zero values of parameter γ is observed in Fig. 12, bottom panel. It can be observed that the instability of the circular orbits increases again as the value of γ increases. -
Now we study the fundamental frequencies of test particles around a quintessential BH with string clouds. We start by calculating the angular velocity of the test particles in Keplerian orbits and the frequencies of the radial and vertical oscillations of the particles around the stable circular orbits.
-
For the angular velocity of test particles in bounded circular orbits, the so-called Keplerian orbits,
$ \Omega_K=\dot{\phi}/\dot{t} $ in the spacetime around the BH in the quintessential field and string clouds is given as$ \Omega_K=\frac{\sqrt{2 M r^{3 \omega _q}+\gamma \left(3 \omega _q+1\right)}}{\sqrt{2} r^{\frac{3}{2} \left(\omega _q+1\right)}}\ . $

It is worth noting that we express all the frequencies in the unit of Hz,
$ \nu = \frac{1}{2\pi}\frac{c^3}{GM} \Omega\ , [{\rm Hz}]\ , $

(26) where
$c=3 \times 10^8 \rm m/sec$ is the vacuum speed of light, and$G=6.67 \times 10^{-11}\rm m^3/(kg^2\cdot sec)$ is the gravitational constant.Figure 13 shows the angular momentum of test particles orbiting a BH in the quintessential field and string clouds. One can easily see from the figure that an increase of γ at a given
$ \omega_q $ Keplerian frequency turns to zero at a distance far from the object, and an increase in the parameter γ causes a decrease in the distance where the Keplerian frequency is zero. -
Let us assume that a test particle orbiting a spherically symmetric BH along stable circular orbits oscillates along radial, angular, and vertical directions. We consider the oscillation with small displacement concerning stable orbits as
$ r_0+\delta r $ and$ \pi/2+\delta \theta $ . The frequencies of radial and vertical oscillations can be evaluated by the following equations [40]:$ \frac{{\rm d}^2\delta r}{{\rm d}t^2}+\Omega_r^2 \delta r=0\ , $

(27) $ \frac{{\rm d}^2\delta\theta}{{\rm d}t^2}+\Omega_\theta^2 \delta\theta=0\ , $

(28) where
$ \Omega_r^2=-\frac{1}{2g_{rr}(u^t)^2}\partial_r^2V_{\rm eff}(r,\theta)\Big |_{\theta=\pi/2}\ , $

(29) $ \Omega_\theta^2=-\frac{1}{2g_{\theta\theta}(u^t)^2}\partial_\theta^2V_{\rm eff}(r,\theta)\Big |_{\theta=\pi/2}\ , $

(30) are the radial and vertical frequencies, respectively.
After some mathematical calculations, one may easily obtain the expressions for the frequencies,
$ \begin{aligned}[b] \frac{\Omega_r^2}{\Omega_K^2} = &\frac{3 \gamma \omega _q \left(3 \omega _q (2 M+(\alpha -1) r)+(\alpha -1) r\right)}{r \left(\gamma +2 M r^{3 \omega _q}+3 \gamma \omega _q\right)}\\ &-\alpha -\frac{3 \gamma \left(\omega _q+1\right)}{r^{3 \omega _q+1}}, \end{aligned} $

(31) $ \Omega_\theta = \Omega_K= \Omega_\phi\ , $

(32) where
$ \Omega_\phi $ is the angular velocity of the particle measured by an observer at infinity.The radial dependence of the frequencies of the radial oscillations of particles along stable circular orbits around the Schwarzschild BH in a quintessential field and string cloud is shown in Fig. 14. One can see from the figure that the presence of both the cloud of strings and the quintessential field causes a decrease in the maximum frequency. Moreover, the frequency equals zero at a distance in the given value of the non-zero quintessential field parameter, and the distance shifts toward the central BH with the decrease in
$ \omega_q $ .
Figure 14. (color online) Radial profiles of the frequencies of radial oscillations for different values of the quintessential field and string cloud parameters.
Now, we show the effects of the quintessential field and clouds of strings on the maximum differences in the oscillation frequencies in the radial direction of the test particles.
Figure 15 shows the color mapping of the values of the maximum differences in the frequencies of radial oscillations between the Schwarzschild BH and Kiselev BH cases
$ \gamma-\alpha $ . Near, the difference increases as the string clouds become strong and the quintessential field becomes denser. -
As a BH cannot radiate, it is not possible to obtain electromagnetic information coming from the BH directly. Meanwhile, a BH is the source of the curvature of spacetime around it, which derives all the radiation processes in the accretion disk. QPOs are astrophysical phenomena observed in the electromagnetic spectrum in the accretion disk using Fourier analyses of the noisy continuous X-ray data from the disk. One may distinguish high-frequency (HF) QPOs corresponding to the frequency range of 0.1 to 1 kHz and low-frequency (LF) QPOs corresponding to the frequency range
$ < $ 0.1 kHz. At present, a number of QPOs have been detected in the electromagnetic band (radio to X-ray) of radiation from the accretion disk around astrophysical compact gravitating objects, not only BHs but also neutron stars, white dwarfs, and their binary systems including companion stars [41]. QPOs observed from low-mass X-ray binaries (LMXBs) have no similar behaviors that suggest that there are individual original mechanisms that are connected with the surface magnetic field of magnetized neutron stars and their rotation [42]. The source mechanism of the electromagnetic emission in the accretion disk around the central BH is connected with particle oscillations. Charged particles radiate with the same frequency as their oscillation frequency around the BH. The dynamics of the charged test particles around BHs explain the existence of QPOs based on quasi-harmonic oscillations of the particles in the radial and angular directions. In this section, we consider the upper and lower frequencies of twin-peaked QPOs in the relativistic precession (RP) model. The RP model defines the upper and lower frequencies by the frequencies of the radial, vertical, and orbital oscillations as$ \nu_U=\nu_\phi $ and$ \nu_L=\nu_\phi-\nu_r $ .In Fig. 16, we present a diagram of the upper and lower frequencies of twin peak QPOs around a BH in the presence of the quintessential field and string clouds in the relativistic precession model. The curves in the diagram for
$ \nu_U-\nu_L $ are compared with the Schwarzschild case in both the$ \omega_q=-{1}/{2} $ and$ -{2}/{3} $ cases, and it is obtained that when$ \omega_q=-{1}/{2} $ , the presence of a quintessential field with$ \gamma=10^{-3} $ causes a slight decrease in the frequencies at HF QPOs. It is also observed that LF QPOs below approximately 5 Hz are not observed, whereas in the presence of a cloud of strings with$ \alpha=0.01 $ , the frequency shifts up to approximately 20 Hz. However, at$\omega=-{2}/{3}$ , the effect of γ on the minimum upper and lower frequencies can be observed more strongly than that of α. It can also be observed that, with the increase in α, the upper and lower frequencies of HF QPOs sufficiently decrease for both values of$ \omega_q $ . -
In this section, we focus on obtaining the constraints on the values of the parameters of the cloud of strings and quintessential field surrounding the Schwarzschild BH, along with its mass, using frequencies of the QPOs from the microquasars GRO J1655-40 and GRS 1915+105. In the frame of the RP model, the frequencies of the periastron precession
$ \nu_{\rm per} $ and the nodal precession$ \nu_{\rm nod} $ are defined by the$ \nu_{\rm per }=\nu_{\phi}-\nu_{r} $ and$ \nu_{ \rm nod }=\nu_{\phi}-\nu_{\theta} $ relations, respectively [43, 44].To obtain the estimation of the five parameters as the peak frequencies of the QPOs observed in the microquasars, we perform
$ \chi^2 $ analysis with [45]$ \begin{aligned}[b] \chi^{2}(M,B,r_{1},r_{2})=&\frac{(\nu_{1\phi}-\nu_{1\rm U})^{2} }{\sigma_{1\rm U}^2}+\frac{(\nu_{1\rm per}-\nu_{1\rm L})^{2} }{\sigma_{1 \rm L}^2}\\ &+\frac{(\nu_{1\rm nod}-\nu_{1\rm C})^{2} }{\sigma_{1\rm C}^2}+\frac{(\nu_{2\phi}-\nu_{2\rm U})^{2}} {\sigma_{2\rm U}^2}\\ &+\frac{(\nu_{2\rm nod}-\nu_{2\rm C})^{2}} {\sigma_{2\rm C}^2}\; . \end{aligned} $

(33) In fact, the best estimates for the values of the parameters M, γ, α,
$ r_{1} $ , and$ r_{2} $ should be at the minimum of$ \chi_{\rm min}^{2} $ , and the range of the parameters at the confidence level (C.L.) can be determined in the interval$ \chi_{\rm min}^{2}+\Delta\chi^{2} $ .It is clear that at the best-fit values of the unknown parameters M, γ, α,
$ r_{1} $ , and$ r_{2} $ ,$ \chi^2 $ takes its minimum. Thus, first, we find the minimum and the best-fit values of these parameters. Then, we plot the contours of the$ \alpha-M $ space for different values of C.L. In the case of five degrees of freedom, the intervals with$ \Delta \chi^2 $ = 5.89, 11.29, and 17.96 correspond to 68.3%, 95.4%, and 99.7% C.L., respectively, which are the probability intervals designated as$ 1\sigma $ , 2σ, and 3σ. -
Here, we obtain the constraints on the mass of the BH and surrounding magnetic fields in the microquasar GRO J1655-40 using the two sets of QPO frequencies in the astrophysical observations [18],
$ \begin{aligned}[b] \nu_{1\mathrm{U}}=441\mathrm{\; Hz},\quad & \sigma_{1\mathrm{U}}=2\mathrm{\; Hz} ,\\ \nu_{1\mathrm{L}}=298\mathrm{\; Hz},\quad & \sigma_{1\mathrm{L}}=4\mathrm{\; Hz} ,\\ \nu_{1\mathrm{C}}=17.3\mathrm{\; Hz},\quad & \sigma_{1\mathrm{C}} =0.1\mathrm{\; Hz} \end{aligned} $

(34) and
$ \begin{array}{*{20}{l}} \nu_{2\mathrm{U}}=451\mathrm{\; Hz},\quad & \sigma_{2\mathrm{U}}=5\mathrm{\; Hz} ,\\ \nu_{2\mathrm{C}}=18.3\mathrm{\; Hz},\quad & \sigma_{2\mathrm{C}} =0.1\mathrm{\; Hz}\; . \end{array} $

(35) It is obtained that
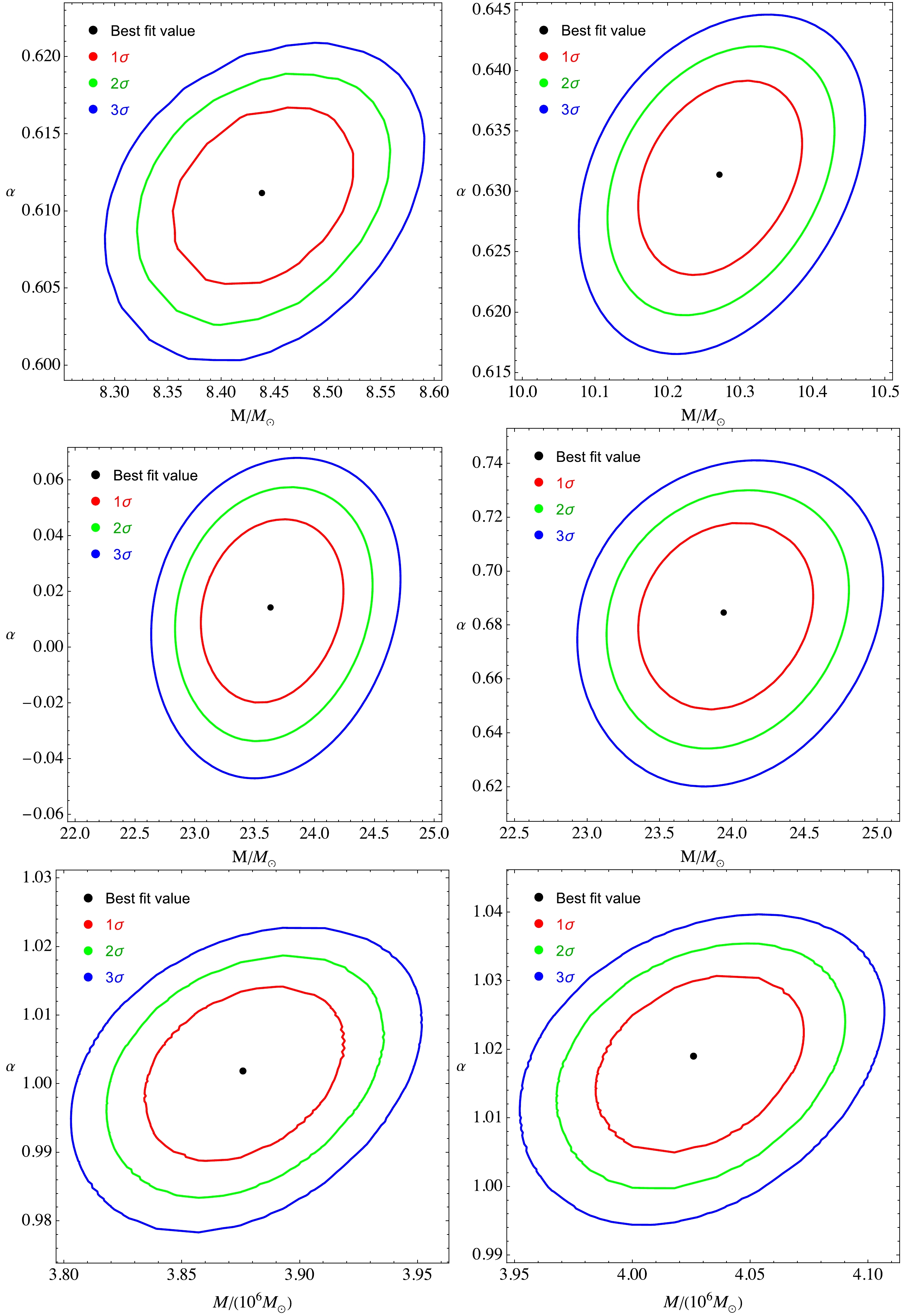
$ \chi^2 $ takes a minimum at$ M= 8.43816M_\odot $ ,$ \gamma = 0.135198 $ ,$\alpha =0.61116,\; r_1=6.75063M$ , and$ r_2=6.55197M $ when$ \omega_q=-2/3 $ and at$M= 18.4921M_\odot$ ,$ \gamma = 0.0432701 $ ,$\alpha =0.6346, \;\; r_1=2.50143 M$ , and$r_2=3.45285 M$ when$ \omega_q=-1/2 $ -
We perform a similar analysis on the GRS 1915 + 105 microquasar with QPO frequencies [46],
$ \begin{aligned}[b] \nu_{1 {\rm U}}=184.10 {\rm \; Hz},\quad & \sigma_{1{\rm U}}=1.84{\rm\; Hz} ,\\ \nu_{2{\rm U}}=142.98{\rm\; Hz},\quad & \sigma_{2{\rm U}}=3.48{\rm\; Hz}, \end{aligned} $

(36) and
$ \begin{aligned}[b] \nu_{1{\rm L}}=67.40 {\rm\; Hz},\quad & \sigma_{1{\rm L}}=0.60{\rm\; Hz} ,\\ \nu_{2{\rm L}}=65.89{\rm\; Hz},\quad & \sigma_{2{\rm L}} =0.52{\rm\; Hz}\; ,\\ \nu_{3{\rm L}}=69.58{\rm\; Hz},\quad & \sigma_{3{\rm L}} =0.49{\rm\; Hz}. \end{aligned} $

(37) Our analyses show that
$ \chi^2 $ is minimum at$M= 23.6308M_\odot$ ,$ \gamma = 0.0942358 $ ,$ \alpha =0.0142575, r_1=4.89813M $ , and$ r_2=6.48403M $ when$ \omega_q=-2/3 M=23.9409M_\odot $ ,$\gamma = 0.579733$ ,$\alpha =0.684607, \;\; r_1=4.89813M$ , and$r_2=6.84089 M$ when$ \omega_q=-1/2 $ -
A twin peak QPO has been detected around the supermassive BH SgrA* located in the center of the Milky Way galaxy, with upper and lower frequencies of 1.445
$ \pm $ 0.16 and 0.866$ \pm $ 0.04 mHz, respectively. In this case, we have only two frequency data: upper and lower frequencies. Therefore, in our$ \chi^2 $ analyses, we use only the first two terms in Eq. (33). Consequently, we find from the$ \chi^2 $ analyses that its minimum is approximately$ 0.0014 $ at$ M=4.0259\times10^6M_\odot $ ,$ \alpha=1.001939765 $ ,$\gamma = 0.00008378$ , and$ r=6.7860193M $ when$ \omega_q=-2/3 $ . Meanwhile, when$ \omega_q=-1/2 $ ,$ \chi^2 $ takes its minimum at$ M=3.8759679\times10^6M_\odot $ ,$ \alpha=1.0182913 $ ,$ \gamma =0.00037665 $ , and$ r=6.214789M $ .In Fig. 17, we present the constraint values for α and the mass of the central BH candidates at the center of GRO J1655-40 (top row), GRS 1915+105 (middle row), and Sgr A* at
$ \omega_q=-2/3 $ (left column) and$\omega_q= -1/2$ (right column) and the contour levels 1σ, 2σ, and 3σ of α and$ M/M_\odot $ . -
In the present study, we investigated the motion of test particles around a Schwarzschild BH in a cloud of strings and the quintessential field between the event horizon and the cosmological one due to the presence of the quintessential field. In our analysis, we studied two different values of the parameter
$ \omega_q $ ,$ -{1}/{2} $ and$ -{2}/{3} $ . We found that the presence of the cloud of strings causes a slight increase (decrease) in the event (cosmological) horizon and the quintessential field causes a slight increase in the event horizon, whereas the cosmological one decreases sufficiently. We also analyzed the corresponding values of the parameters of the two fields in relation to the presence/absence of the event horizon, together with the effects of the fields' effects on the event horizon radius. It was found that the event horizon increases in the presence of string clouds, whereas it decreases with the increase in the parameter γ. We also analyzed the effective potential for different values of α and γ and showed that an increase in both parameters causes a decrease in the effective potential. Studies of the particle energy and angular momentum corresponding to circular orbits have shown that the angular momentum increases for values of α, whereas in the presence of a quintessential field (γ), the momentum decreases. Moreover, the energy decreases with the increase in both α and β. We provide analyses of the radius of the ISCO as a function of α for different values of α and$ \omega_q $ and show that the energy (angular momentum) of particles decreases (increases) as the ISCO radius increases. The energy efficiency increases with α and reaches 70% in the absence of a quintessential field. However, it decreases with increasing parameters γ and α. Figs. 2 and 3 show that in the presence of α and γ, oscillating trajectories are observed. The combined effect of both parameters results in stable circular orbits, and the trajectories become stable and bounded. The effects of the fields on the fundamental oscillation frequencies of test particles around stable circular orbits were examined. It was found that the Keplerian frequency goes to a distance in the presence of the quintessential field, and the distance decreases with the increase in γ. As an application of these studies, we considered twin peak QPOs in the RP model and showed that LF QPOs ($ < $ 20 Hz) are not observed in the presence of the quintessential field. However, the frequencies in HF regimes decrease as a result of the presence of the quintessential field.Finally, we obtained the constraint values of the mass of the BH in the microquasars GRS 1915+105, GRO J1655-40, and Sgr A*, along with the string cloud parameters, using observed QPO data for the EoS parameter
$ \omega_q=-2/3 $ and$ -1/2 $ . The results of the analyses performed using the$ \chi^2 $ method showed that the mass of the BH in GRO J1655-40 is approximately$ (8.4-18.4)M_\odot $ , whereas it is approximately$ (23.6-23.9)M_\odot $ for GRS 1905+105 and$ (3.8-4.02)M_\odot $ for SgrA*. In our future studies, we plan to obtain constraints on the parameters of the BHs and gravity theories in the rotating spacetime, developing on the QPO studies. -
JR acknowledges Silesian University in Opava for its hospitality during his visit.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: