The outer crust of neutron stars based on the Brueckner-Hartree-Fock method

A neutron star (NS) provides a natural laboratory for studying extreme conditions such as high densities, strong gravitational fields, and strong electromagnetic fields [1−4]. Since Baade and Zwicky first devised the concept of NSs in 1934 [5], experimental observations and theoretical studies of NSs have developed rapidly over the past century, connecting nuclear physics, particle physics, and astrophysics. Recently, LIGO and Virgo first detected gravitational waves from the binary NS merger event GW170817 [6, 7] in 2017 and GW190814 [8] in 2019, providing an important basis for better understanding the properties of NSs, opening the era of multi-messenger research.

As the densest form of matter in the universe, NSs have a very large density span from the core to the atmosphere, involving different forms of physics and related equations of state (EOSs) [9]. It is common to assume that thermodynamic and β equilibrium have been reached in NSs at $ T = 0 $, which means the NS has had enough time to cool down and equilibrate since the supernova explosion. Another important assumption is the absence of accretion [10]. The outermost layer is the atmosphere, which is composed of a gaseous plasma and is very thin, usually between a few millimeters and a few centimeters, but has an important influence on the NS's thermal radiation spectrum. Beneath it lies the outer crust, where electronic degeneracy pressure plays the main supporting role. The surface of the outer crust ($ \rho \sim 10\; {\text{kg cm}} ^{-3} \sim 10^{-12}\;\text{fm}^{-3} $) consists of $ ^{56} {\rm{Fe}}$ atoms. With increasing density, the free electrons will be captured by nuclei to stay energetically favorable. Therefore, the atoms gradually become neutron-rich until the neutron drip density ($ \rho \sim 4\times10^{11}\; {\text{g cm}} ^{-3} \sim 2.5\times10^{-4}\;\text{fm}^{-3} $) is reached, which is the boundary between the outer and inner crust [11, 12].

In the inner crust of the NS, neutrons begin to drip out of the nuclei and neutron degeneracy pressure comes into play. At this point, the neutron-rich nuclei may no longer be spherical, but might appear in bubbles, rods, sheets, tubes, and other shapes [13, 14]. The inner and outer crust are only a few hundred meters thick. As the density continues to increase, the outer core of the NS, which is about a few kilometers thick, becomes a fluid of neutrons, protons, and electrons in β equilibrium. The composition of the inner-core region of a NS, where the density and pressure are extremely high, is uncertain and may involve hyperons, mesons, or quark matter [4, 15−18]. It may also be in a superfluid and superconducting state [4, 19−22].

In this paper we are interested in the outer crust of NSs, where the nuclei and the electron Fermi gas prefer to crystallize into a body-centered-cubic lattice to lower the total energy. The masses of neutron-rich nuclei are therefore an important input to calculate the crustal composition and EOS. But nuclear physics experiments cannot determine the properties of very neutron-rich nuclei close to the neutron drip line, appearing in the outer crust with increasing density. Therefore, theoretical approaches need to be devised to extrapolate to very neutron-rich matter.

In 1971, Baym, Pethick, and Sutherland [11] developed the BPS model to determine the composition and EOS of the outer crust by using the 1966 nuclear mass table [23]. After that, a large number of papers followed the BPS model to calculate the sequence of nuclei by using different nuclear models. For example, [24] studied the outer-crust composition using the experimental nuclear data mass table of 1993 [25] and the theoretical nuclear data by the liquid-drop models [26] and [27]. More recently [28] studied the composition and neutron drip point by using the updated mass table of 2003 [29] and various theoretical nuclear data, such as the Skyrme models BSk2 and BSk8 [30−35], the relativistic model TMA [36], the finite-range drop model (FRDM) [27, 37], and others. [10] calculated the properties of the outer crust based on the Hartree-Fock-Bogoliubov (HFB) method using four interactions: three Skyrme forces HFB-19,20,21 and the Gogny force D1M [38]. This work was later extended to a unified EOS for the entire NS using Skyrme forces HFB-22,24,25,26 [39, 40]. Similarly, [41] used the AME2012 [42] table together with deformed HFB calculations performed with the Barcelona-Catania-Paris-Madrid (BCPM) energy-density functional. [43] used the AME2016 [44] and the theoretical values within the quark-meson coupling (QMC) model.

According to this previous work, the main uncertainty is associated with the theoretical computation of very neutron-rich nuclei. The sequence and onset densities of nuclei in the outer crust, and the neutron drip point, are all sensitive to the nuclear binding energies, although the final crustal EOS is not. More accurate experimental data on neutron-rich nuclei are expected to improve the accuracy of the theoretical models.

As a quantum many-body system, it has long been a difficult problem to explain and predict the properties of nuclear matter based on nucleon-nucleon interactions. Among the various approaches proposed to address this complexity [4], the Brueckner-Hartree-Fock (BHF) method stands out for its microscopic foundation. The BHF method is rooted in realistic nucleon-nucleon interactions and explicitly incorporates three-body forces (TBFs), ensuring a microscopically consistent description of nuclear forces. This contrasts with Skyrme-Hartree-Fock (SHF) or relativistic mean-field (RMF) models, which rely on phenomenological parametrization of effective interactions fitted to properties of stable nuclei. BHF self-consistently accounts for short-range correlations, medium polarization, and isospin-dependent effects critical for neutron-rich systems, which ensures robust extrapolations towards the neutron drip line.

However, it should be noted that the computation of the NS crust requires the modeling of several finite-size effects beyond the bulk calculation, and this effectively compensates the differences between the nuclear-matter calculations to some extend, as will be seen.

In this work, we use the state-of-the-art experimental binding energies from AME2020 [45], and beyond that extend the nuclear mass table by using a liquid-drop model based on a microscopic BHF energy-density functional. We obtain the composition and EOS of the outer crust and determine the neutron drip point. Solving the Tolman-Oppenheimer-Volkov (TOV) equations [46, 47], we obtain the mass, the thickness, and other properties of the outer crust. Several other theoretical models for the outer crust are compared. We use natural units $ \hbar = c = G = 1 $.

We briefly review the BHF approach [41, 48, 49], which is based on the Bethe-Goldstone equation for the in-medium scattering matrix G,

where Q is the Pauli operator, E is the starting energy, $ k_F $ is the Fermi momentum, and V is the nucleon-nucleon interaction, which is the bare two-nucleon potential (Argonne $ V_{18} $ [50] in our case) plus an averaged TBF, reduced to an effective, density-dependent two-body force [51, 52]. The single-particle energy is given by

where the continuous-choice single-particle potential is determined by

where $ {\left|kk'\right\rangle_a} \equiv \left|kk'\right\rangle - \left|k'k\right\rangle $. Eqs. (1-3) are coupled to each other. When they are solved self-consistently and reach convergence, the BHF energy per nucleon is obtained as

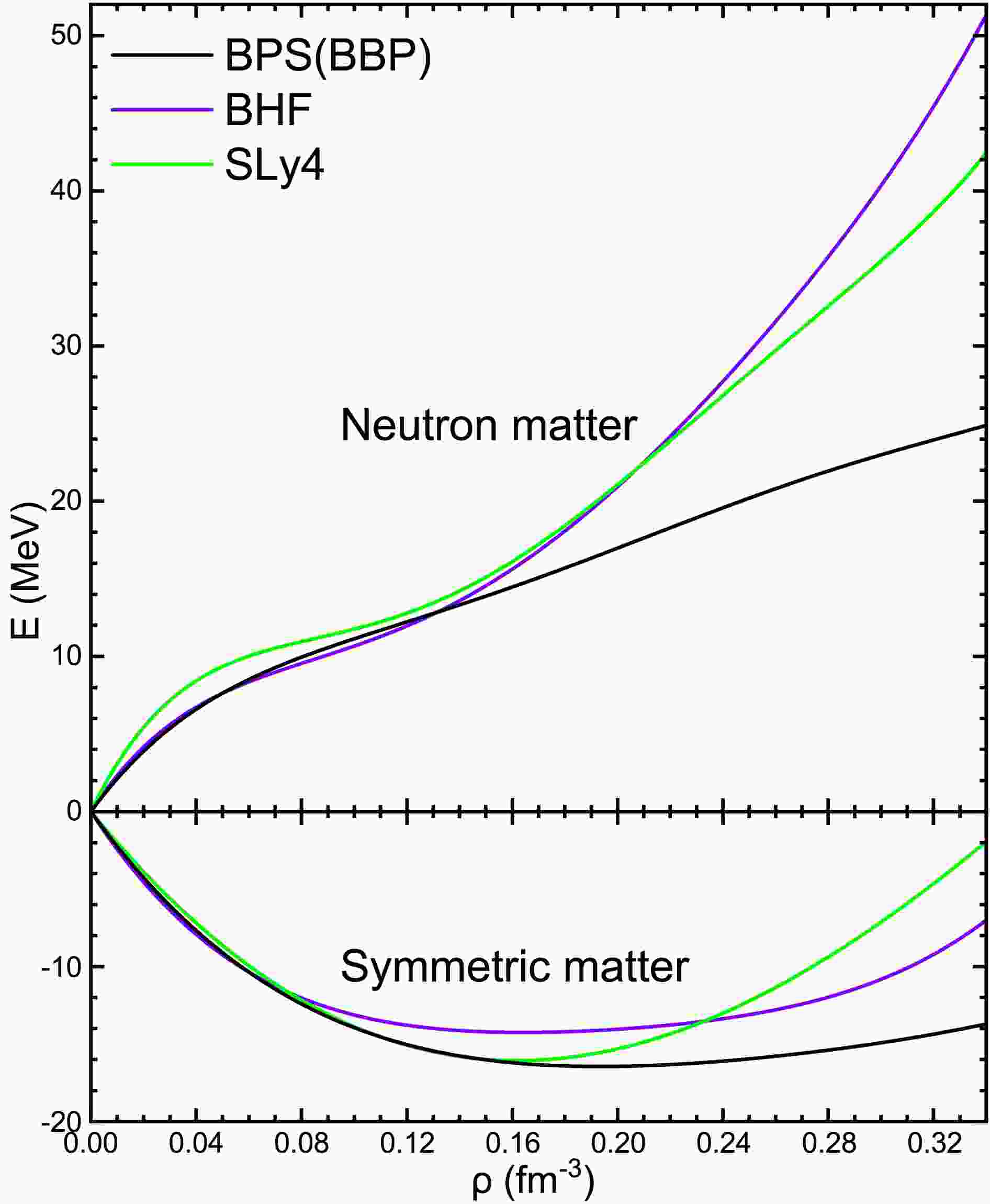
In Fig. 1 we show the energies per nucleon for symmetric nuclear matter (SNM) and pure neutron matter (PNM) obtained in this way as a function of total baryon number density ρ. The BHF EOS reproduces the saturation properties of nuclear matter, with the saturation density $ \rho_0\approx0.18\;\text{fm}^{-3} $, the binding energy per particle $ E_0\approx-14.6\;\text{MeV} $ of SNM, the incompressibility $ K_0\equiv 9\rho_0^2 {d^2 E_\text{SNM}}/{d\rho^2}(\rho_0) \approx 207\;\text{MeV} $, and the symmetry energy $ E_\text{sym}\approx E_\text{PNM}(\rho_0)-E_\text{SNM}(\rho_0) \approx 33\;\text{MeV} $. It also satisfies all current observational constraints for NSs, like maximum mass, radii, tidal deformability, etc., see [53].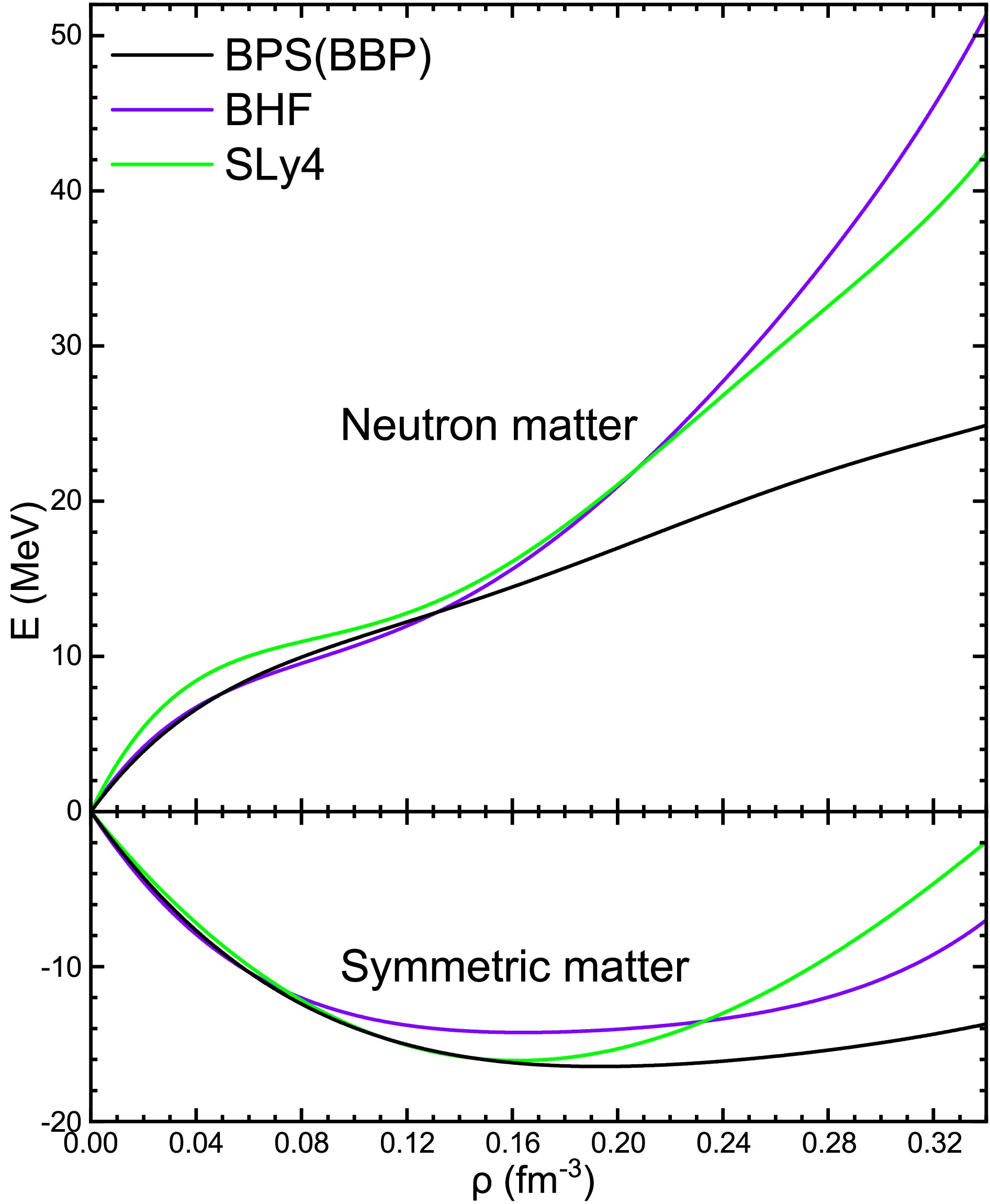

Figure 1.  (color online) The energy per nucleon for symmetric nuclear matter and pure neutron matter of the BPS, BHF, and SLy4 models versus the baryon number density.

For comparison, we show in the plot also the results for the BBP parameterized EOS [54], used in BPS [11], and the SLy4 SHF EOS [55, 56], with respective saturation parameters $ \rho_0\approx0.20\;\text{fm}^{-3} $, $ E_0\approx-16.5\;\text{MeV} $, $ K_0\approx143\;\text{MeV} $, $ E_\text{sym}\approx33\;\text{MeV} $ (BBP) and $ \rho_0\approx0.16\;\text{fm}^{-3} $, $ E_0\approx-16.0\;\text{MeV} $, $ K_0\approx230\;\text{MeV} $, $ E_\text{sym}\approx32\;\text{MeV} $ (SLy4). It is evident that the EOSs are mainly distinguished by their compressibilities, even unrealistically low for the BBP EOS. Nevertheless it turns out that the predicted crustal properties of all three models are very similar, due to compensation by the various finite-size effects introduced later.

Furthermore, the energy per nucleon at any asymmetry parameter $ \beta = (\rho_n-\rho_p)/(\rho_n+\rho_p) $ is obtained through the well-tested parabolic relation [49, 52, 57−60]

where $ x = \rho_p/\rho $ is the proton fraction, $ E_\text{sym}(\rho) = E(\rho,0)-E(\rho,0.5) $, the latter two terms being the energy of PNM and SNM, respectively. Therefore, only parametrizations of the energy per nucleon for SNM and PNM are required.

Next, we use a simple liquid-drop model [61−64] to link the BHF energy density $ \varepsilon_\text{BHF} = \rho E(\rho,x) $ with the energy of a finite nucleus,

composed of the volume-, surface-, and Coulomb-energy terms. For simplicity, we ignore the pairing energy and other refinements. The surface-energy parameter $ f_0 $ will be used as a fit parameter for the experimental binding energies.

The proton and neutron densities are written as standard two-parameter Fermi distributions

with radius $ R_i $ and diffuseness $ d_i $, and the normalization $ a_i $ fixed by

For each nucleus, the four parameters $ R_i $ and $ d_i $ are determined by minimizing the total energy Eq. (6).

We follow the BPS model [11] to describe the composition and EOS of the outer crust of a NS. See more references in [10, 28, 41, 43, 65]. Considering a nonaccreting cold NS, it is convenient and reasonable to assume that thermodynamic and chemical equilibrium have been reached in the outer crust, and that the nuclei and the electron gas crystallize into a body-centered-cubic lattice [66, 67]. Then the total energy per nucleus can be written as

in terms of nuclear, electron, and lattice energy. The equilibrium nucleus is determined by the competition between surface energy (which tends to favor large-A nuclei) and Coulomb energy (which tends to favor small-A nuclei). The latter consists of positive nuclear Coulomb self-energy and negative lattice energy. To find the equilibrium nucleus, $ E(Z,N,\rho) $ is minimized by varying Z and N at fixed ρ.

The nuclear contribution, corresponding to the total mass of the nucleus, is given by

where $ m_{n/p} $ is the mass of neutron or proton, and $ B(Z,N) $ is the binding energy per nucleus Eq. (6).

The electron contribution $ E_e = \varepsilon_e V_\text{WS} = \varepsilon_e A/\rho $ is the one of a relativistic Fermi gas,

where $ x = k_e/m_e $ is the dimensionless kinetic parameter with the electron mass $ m_e $ and Fermi momentum $ k_e = (3\pi^2 n_e)^{1/3} $, related to the electron number density $ n_e = (Z/A)\rho $.

The lattice energy is [68]

where a is the lattice constant, $ C_L = 3.407 \times10^{-3} $, and $ k_B \equiv (3{\pi^2}{\rho})^{1/3} $.

The pressure obtained from the equilibrium energy is

where

and $ \mu_e = \sqrt{k_e^2 + m_e^2} $.

The baryon (neutron) chemical potential is

Since the pressure p and chemical potentials $ \mu,\mu_e $ change continuously with increasing depth of the crust, there is a density discontinuity at each change of the equilibrium nucleus,

It is therefore more convenient to use the pressure as independent variable and minimize the chemical potential at fixed pressure by using tabulated nuclear masses $ E_N(Z,N) $.

The main uncertainty in the composition of the outer crust is due to the unknown binding energies of the neutron-rich heavy nuclei close to the transition to the inner crust, defined by $ \mu = m_n $, which determines the onset density of the inner crust and the terminal nucleus of the outer crust. Many works followed the same theoretical procedure using different nuclear mass tables and their extensions. We use the nuclear energies from the most recent AME2020 mass table and our nuclear model as described before for this purpose.

From the EOS $ p(\varepsilon) $, we can obtain the internal structure of a static and spherically-symmetric NS by solving the well-known TOV equations [46, 47]

where $ m(r) $ is the enclosed mass. The integration is performed from the center, $ p(r = 0) = p_c $, to the surface, $ p(R) = 0 $ [10, 69]. Since only the EOS of the outer crust is obtained in our calculation, we adopt the compatible BHF V18 EOS [70] in the core, and the Shen20 EOS [71] in the inner crust. The transition density between the inner crust and core is optimized to ensure continuous pressure and energy density across the β-stable EOS phases. From the composition of the outer crust calculated before, we then obtain the total extension and mass of the outer crust, among other quantities.

The space-time metric of slowly and uniformly rotating axisymmetric NSs can be expressed as

where γ, ρ, β, ω are the metric potentials, which are functions of r and θ only. The moment of inertia (MI) of the NS can be written as [72−74]

With the EOS $ p(\varepsilon) $ as input, these equations can be solved numerically together with the TOV equations, to obtain the mass, the thickness, and the MI of the NS and its outer crust [40].

We present now our numerical results for the binding energies of finite nuclei based on the BHF method, and properties of the outer crust of NSs, like composition, EOS, drip line, crust mass, thickness, moment of inertia, adiabatic index, and speed of sound.

Based on the BHF energy-density functional and the liquid-drop model, the nuclear binding energies can be calculated as outlined before: For each known nucleus we fit the experimental binding energy by adjusting the surface-energy parameter $ f_0 $. Then for either fixed proton number Z or fixed neutron number N, the results are extrapolated into the unknown neutron-rich region up to the predicted neutron dripline, see, e.g., the curves in Fig. 2(c) for the first method. Results of both ways are carefully compared. This procedure works well within the shell limits, i.e., $ Z = 28-50 $ and $ N = 50-82 $, which turns out to be sufficient for our purpose.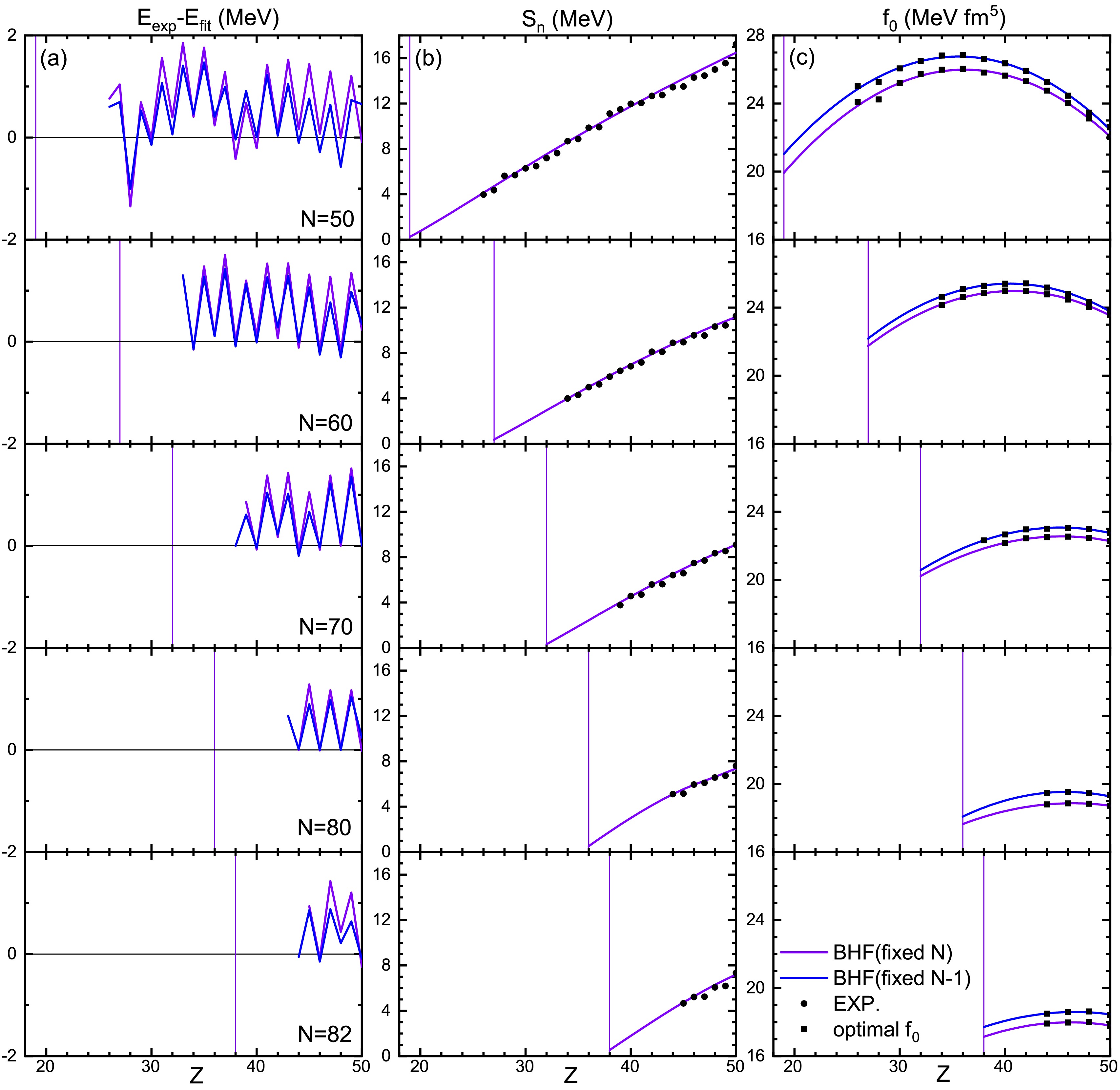

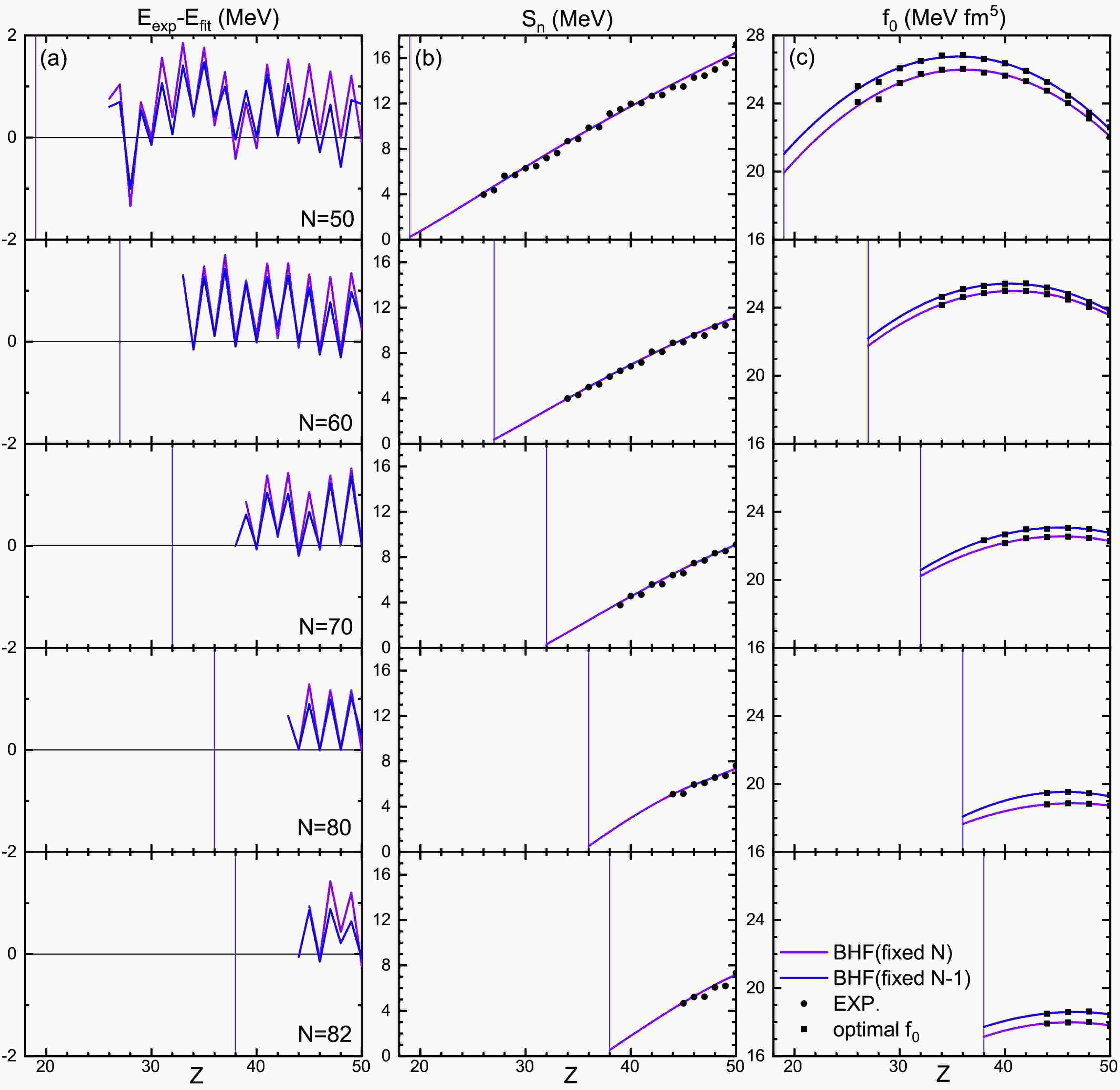
Figure 2.  (color online) The fitting results for the neutron number $ N = 50,60,70,80,82 $ isotones as a function of the proton number Z: (a) difference between fit and experimental energies, $ E_\text{exp}-E_\text{fit} $, (b) neutron separation energy $ S_n $, (c) optimal surface energy parameter $ f_0 $. Results for BHF (violet and blue curves fitting square markers), and experimental AME2020 data [45] (black round markers) are compared. Vertical lines indicate the neutron drip point.

For illustration, Fig. 2 shows results for fixed $ N = 50,60,70,80,82 $, which are important isotones in the later calculation, especially $ N = 50 $ and 82. Since the computation of the neutron separation energy $ S_n $ requires the knowledge of the $ (Z,N) $ and $ (Z,N-1) $ energies, we need to fit the surface-energy parameter $ f_0 $ of even-Z nuclei for both fixed N and fixed $ N-1 $, see Fig. 2(c). It can be seen that the fit quality is very good: The difference between fit and experimental AME2020 [45] total energies, $ E_\text{exp}-E_\text{fit} $, is accurate within $ 2\;\text{MeV} $ (because pairing energies are not taken into account in our liquid-drop model) and nearly perfect for even nuclei. The (predicted) neutron separation energy $ S_n $ of each nucleus before the neutron drip point is shown in panels (b). For example, for $ N = 82 $ this method predicts the energies of the $ Z = 44-38 $ nuclei down to the dripline, as required for the crust calculation. From the above it is clear that inclusion of pairing into the formalism could only affect the dripline by one unit, and is therefore a small effect, see also [28].

Table 1 contains the results in terms of the sequence of nuclei in the outer crust, following the formalism of Sec. 2 and using the AME2020 [45] nuclear energies when available, extrapolating towards the neutron dripline as just described. The table contains threshold densities $ \rho_\text{min}, \rho_\text{max} $, energy density ε, pressure p, ratio of electron and lattice pressures $ p_e/|p_L| $, neutron chemical potential $ \mu_n $, and electron chemical potential $ \mu_e $ for the different stages. Experimental nuclei appear up to $ \rho = 1.00\times10^{-4}\;\text{fm}^{-3} $, which is the magic nucleus $ ^{80} $Ni. At higher density the theoretically calculated neutron-rich nuclei emerge. For our calculation these are the $ N = 82 $ nuclei $ ^{124} {\rm{Mo}}$, $ ^{122} {\rm{Zr}}$, and $ ^{120}{\rm{Sr}} $, which is the final nucleus at the outer-inner crust boundary, with $ \rho_\text{max} = 2.44\times10^{-4}\;\text{fm}^{-3} $, $ \varepsilon_\text{max} = 0.229\;\text{MeV}\,\text{fm}^{-3} $.

Element	Z	N	$\rho_\text{min}\;( \;\text{fm}^{-3})$	$\rho_\text{max}\;( \;\text{fm}^{-3})$	$\varepsilon_\text{max}\;(\text{MeV}\,\text{fm}^{-3})$	$p_\text{max}\;(\text{MeV}\,\text{fm}^{-3})$	$ p_e/|p_L| $	$ -\mu_n $ (MeV)	$ \mu_e $ (MeV)
Common
$ ^{56} {\rm{Fe}}$	26	30	0	5.04 × 10−9	4.69 × 10−6	3.46 × 10−10	19.3	8.93	0.96
$ ^{62} {\rm{Ni}}$	28	34	5.20 × 10−9	1.66 × 10−7	1.54 × 10−4	4.43 × 10−8	23.0	8.22	2.62
$ ^{64} {\rm{Ni}}$	28	36	1.71 × 10−7	8.10 × 10−7	7.55 × 10−4	3.61 × 10−7	23.6	7.50	4.34
$ ^{66} {\rm{Ni}}$	28	38	8.37 × 10−7	9.10 × 10−7	8.48 × 10−4	4.05 × 10−7	23.6	7.44	4.47
$ ^{86} {\rm{Kr}}$	36	50	9.30 × 10−7	1.88 × 10−6	1.75 × 10−3	1.04 × 10−6	20.0	6.98	5.65
$ ^{84} {\rm{Se}}$	34	50	1.95 × 10−6	6.85 × 10−6	6.39 × 10−3	5.63 × 10−6	20.9	5.85	8.58
$ ^{82} {\rm{Ge}}$	32	50	7.10 × 10−6	1.68 × 10−5	1.57 × 10−2	1.78 × 10−5	21.8	4.79	11.42
$ ^{80} {\rm{Zn}}$	30	50	1.75 × 10−5	3.19 × 10−5	2.98 × 10−2	3.98 × 10−5	22.8	3.88	13.95
BHF
$ ^{78} {\rm{Ni}}$	28	50	3.33 × 10−5	8.13 × 10−5	7.60 × 10−2	1.31 × 10−4	23.9	2.22	18.77
$ ^{80} {\rm{Ni}}$	28	52	8.38 × 10−5	1.00 × 10−4	9.36 × 10−2	1.67 × 10−4	23.9	1.83	19.94
$ ^{124} {\rm{Mo}}$	42	82	1.05 × 10−4	1.35 × 10−4	1.27 × 10−1	2.36 × 10−4	18.2	1.25	21.82
$ ^{122} {\rm{Zr}}$	40	82	1.40 × 10−4	1.89 × 10−4	1.77 × 10−1	3.54 × 10−4	18.8	0.53	24.13
$ ^{120} {\rm{Sr}}$	38	82	1.96 × 10−4	2.44 × 10−4	2.29 × 10−1	4.76 × 10−4	19.5	$ \approx0 $	25.97
SLy4
$ ^{78} {\rm{Ni}}$	28	50	3.33 × 10−5	8.13 × 10−5	7.60 × 10−2	1.31 × 10−4	23.9	2.22	18.77
$ ^{80} {\rm{Ni}}$	28	52	8.38 × 10−5	9.27 × 10−5	8.68 × 10−2	1.51 × 10−4	23.9	1.99	19.45
$ ^{124} {\rm{Mo}}$	42	82	9.73 × 10−5	1.17 × 10−4	1.10 × 10−1	1.95 × 10−4	18.2	1.58	20.80
$ ^{122} {\rm{Zr}}$	40	82	1.21 × 10−4	1.79 × 10−4	1.67 × 10−1	3.28 × 10−4	18.8	0.68	23.67
$ ^{120} {\rm{Sr}}$	38	82	1.85 × 10−4	2.46 × 10−4	2.31 × 10−1	4.81 × 10−4	19.5	$ \approx0 $	26.04
FRDM
$ ^{78} {\rm{Ni}}$	28	50	3.33 × 10−5	6.69 × 10−5	6.26 × 10−2	1.01 × 10−4	23.9	2.63	17.59
$ ^{126} $Ru	44	82	7.01 × 10−5	7.77 × 10−5	7.27 × 10−2	1.17 × 10−4	17.7	2.41	18.32
$ ^{124} {\rm{Mo}}$	42	82	8.05 × 10−5	1.12 × 10−4	1.05 × 10−1	1.84 × 10−4	18.2	1.71	20.50
$ ^{122} {\rm{Zr}}$	40	82	1.16 × 10−4	1.60 × 10−4	1.50 × 10−1	2.83 × 10−4	18.8	0.98	22.82
$ ^{120} {\rm{Sr}}$	38	82	1.66 × 10−4	2.27 × 10−4	2.12 × 10−1	4.31 × 10−4	19.5	0.22	25.33
$ ^{118} {\rm{Kr}}$	36	82	2.35 × 10−4	2.60 × 10−4	2.44 × 10−1	4.93 × 10−4	20.2	$ \approx0 $	26.19
BPS
$ ^{56} {\rm{Fe}}$	26	30		4.88 × 10−9	4.54 × 10−6	3.30 × 10−10	19.3	8.97	0.95
$ ^{62} {\rm{Ni}}$	28	34		1.62 × 10−7	1.51 × 10−4	4.31 × 10−8	23.0	8.26	2.60
$ ^{64} {\rm{Ni}}$	28	36		7.48 × 10−7	6.97 × 10−4	3.25 × 10−7	23.5	7.57	4.24
$ ^{84} {\rm{Se}}$	34	50		4.90 × 10−6	4.58 × 10−3	3.61 × 10−6	20.9	6.24	7.69
$ ^{82} {\rm{Ge}}$	32	50		1.34 × 10−5	1.25 × 10−2	1.32 × 10−5	21.8	5.15	10.61
$ ^{80} {\rm{Zn}}$	30	50		2.93 × 10−5	2.74 × 10−2	3.56 × 10−5	22.8	4.09	13.58
$ ^{78} {\rm{Ni}}$	28	50		9.74 × 10−5	9.16 × 10−2	1.67 × 10−4	23.9	1.89	19.97
$ ^{76} {\rm{Fe}}$	26	50		1.07 × 10−4	1.00 × 10−1	1.77 × 10−4	25.1	1.79	20.25
$ ^{124} {\rm{Mo}}$	42	82		1.12 × 10−4	1.04 × 10−1	1.83 × 10−4	18.2	1.74	20.50
$ ^{122} {\rm{Zr}}$	40	82		1.60 × 10−4	1.50 × 10−1	2.84 × 10−4	18.8	1.00	22.86
$ ^{120} {\rm{Sr}}$	38	82		2.23 × 10−4	2.10 × 10−1	4.24 × 10−4	19.5	0.28	25.25
$ ^{118} {\rm{Kr}}$	36	82		2.59 × 10−4	2.43 × 10−1	4.91 × 10−4	20.2	$ \approx0 $	26.19

Table 1.  Composition and EOS of the outer crust for the BHF, SLy4, FRDM, and BPS models. The first nine common nuclei and $ ^{80} {\rm{Ni}}$ are calculated by experimental data AME2020 [45]. The BPS results are from [28].

For comparison, we also list the BPS results recalculated in [28] using the AME2003 table [29] and the theoretical nuclear-mass table from Myers and Swiatecki [23], the finite-range-droplet model (FRDM) [75], and the HFB results with SLy4 Skyrme energy-density functional [56]. Because of the sensitivity to the nuclear binding energies, different models predict different nuclear sequences at high density. In fact, even a small variation in total binding energy of about $ 1\;\text{MeV} $ can lead to a change in the composition prediction. It is remarkable that our results indicate the same nuclei as the SLy4 model, albeit with slightly different density domains.

The results are also visualized in Fig. 3(e) as a function of density. One can see that as the density increases from the outermost $ ^{56} {\rm{Fe}}$ nucleus, the composition follows a sequence of plateaus at the magic numbers, first $ Z = 28 $, then also $ N = 50 $, and finally $ N = 82 $. Above $ \rho\approx10^{-4}\;\text{fm}^{-3} $ all models follow the $ N = 82 $ shell. During this evolution, the proton fraction $ Z/A $ (d), the neutron separation energy $ S_n $ (c), and the binding energy per nucleon $ E(Z,N) $ of the equilibrium nuclei (b) decrease steadily in magnitude, until the dripline is reached at about $ \rho\approx2.5\times10^{-4}\;\text{fm}^{-3} $. The top panel (a) shows the relation between pressure and density, i.e., the EOS. The pressure increases continuously with increasing depth, apart from small jumps in density as one nucleus transits to another, which our formalism is unable to model accurately. The pressures are very similar across various models, with only small differences at the end of the outer crust. This suggests that the nuclear binding energy has little effect on the EOS. This is not surprising, as the pressure at the densities of interest is dominated by relativistic electrons, which account for approximately 95% of the total pressure within the outer crust, as indicated by the relevant ratio $ p_e/|p_L| $ in Table 1.

Figure 3.  (Color online) Properties of the NS outer crust as a function of baryon density: (a) pressure p, (b) binding energy per nucleon $E(Z,N)$, (c) neutron separation energy $S_n$, (d) $Z/A$, and (e) $Z,N,A$ of the equilibrium nuclei. Results for BHF (violet curves), BPS [28] (black), FRDM [75] (orange), and SLy4 [56] (green) are compared. Vertical lines indicate the neutron drip point.

Fig. 4 shows the sequence of crust nuclei in the $ (Z,N) $ plane, and the corresponding projections on N and Z with their density dependence. In the experimental-nuclei region, the results are very similar because all models used experimental mass tables. At higher density, all models predict the magic number $ N = 82 $ with $ Z = 36-44 $, but different density intervals for given Z.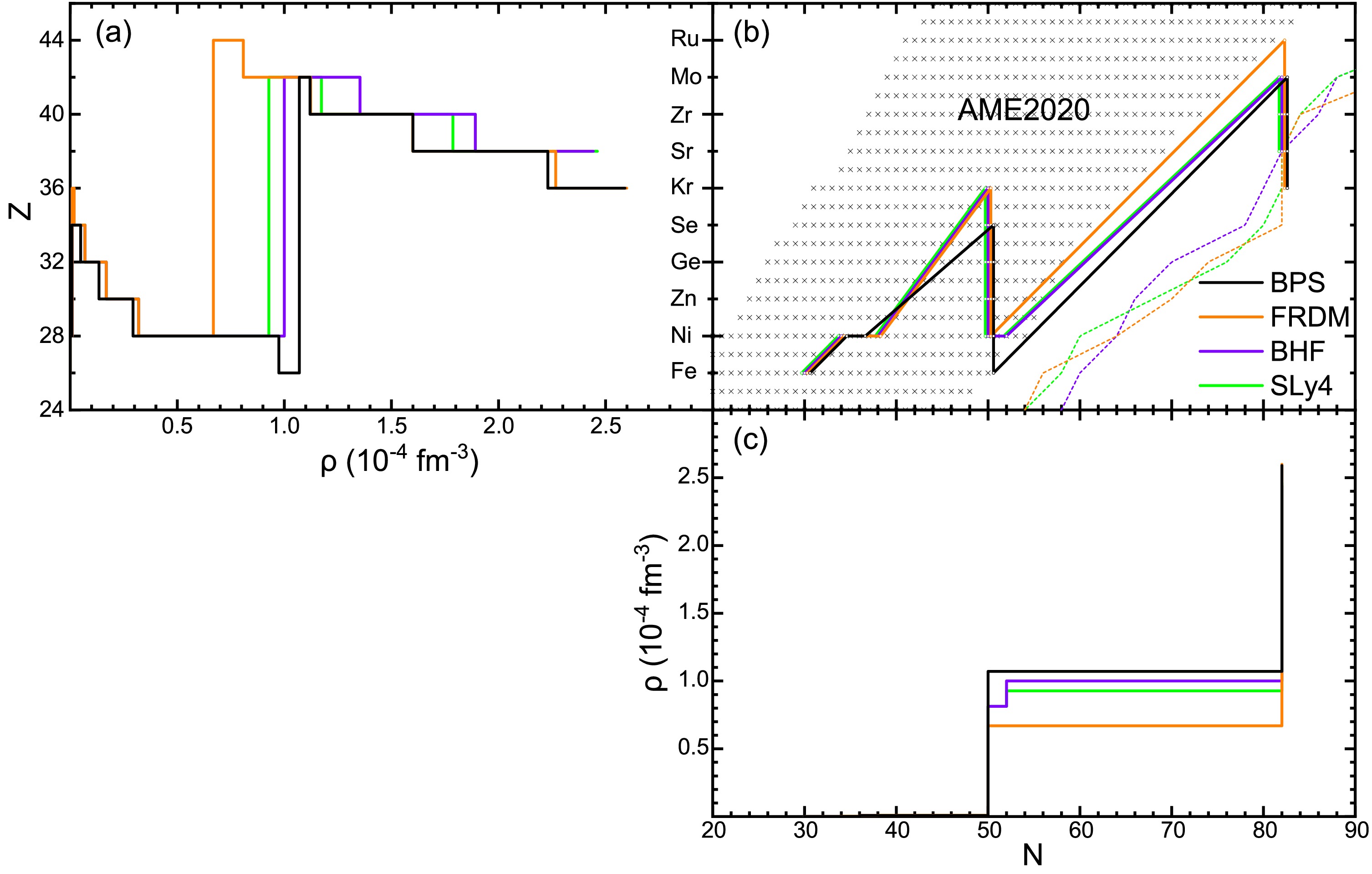

Figure 4.  (Color online) (b) Sequence of outer-crust nuclei in the nuclear $ (Z,N) $ chart for various models (thick solid lines and markers), and their neutron drip lines (thin dotted lines). The crosses represent nuclei in the AME2020 database [45]. (a,c) The corresponding Z and N dependence on baryon number density.

The neutron drip lines of the different models are also shown. It can be seen that each model predicts a slightly different drip line. This is however only relevant at the limit of the crust, when the nuclear sequences of all models meet their respective drip line. The prediction of the neutron drip line is thus crucial for determining the last nucleon in the outer crust and the density and pressure at the boundary between the inner and outer crust. At $ N = 82,Z = 38 $ the theoretical driplines of all four considered EOSs meet, and the predicted final nuclei of the BHF, BPS, SLy4, FRDM models are all $ N = 82 $, namely $ ^{118} {\rm{Kr}}$ for BPS and FRDM, and $ ^{120} {\rm{Sr}}$ for BHF and SLy4. Also the corresponding inner-outer crust transition densities are similar for these models.

The observation of the NS merger event GW170817 [6, 7], particularly its associated kilonova AT2017gfo, revealed that r-process nucleosynthesis in the ejected material occurs under extreme physical conditions near the NS's outer crust. These observations indicate that the r-process pathway predominantly follows trajectories close to the neutron drip line, providing additional validation for nuclear mass models [73, 76, 77]. Future combination of precise radioactive beam measurements and advanced gravitational wave detector observations will critically refine the neutron drip line predictions and thereby also the NS crustal properties.

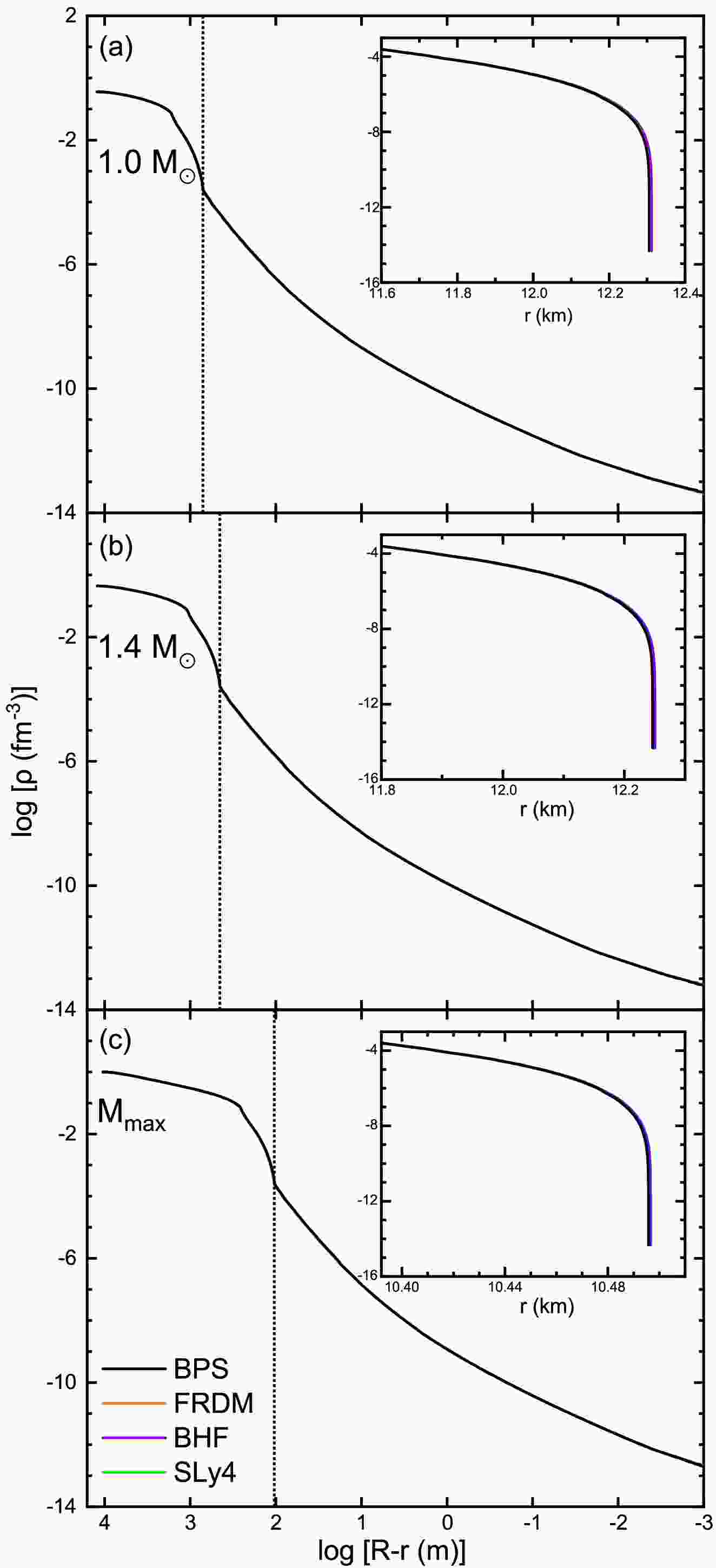
Fig. 5 represents the baryon density profiles for NSs with $ M_G = 1.0M_\odot $ (a), $ 1.4M_\odot $ (b), and $ M_\text{max}\approx2.34M_\odot $ (c) with different EOSs. All EOSs have a similar maximum mass $ \sim2.34M_\odot $, with a radius of $ 10.50\; $km, because of the same core and inner-crust EOS. The inner-outer crust boundary is indicated. The density drops dramatically in the outer crust, by about 11 orders of magnitude, but occupies only a small part of the stellar radius, in particular for massive NSs.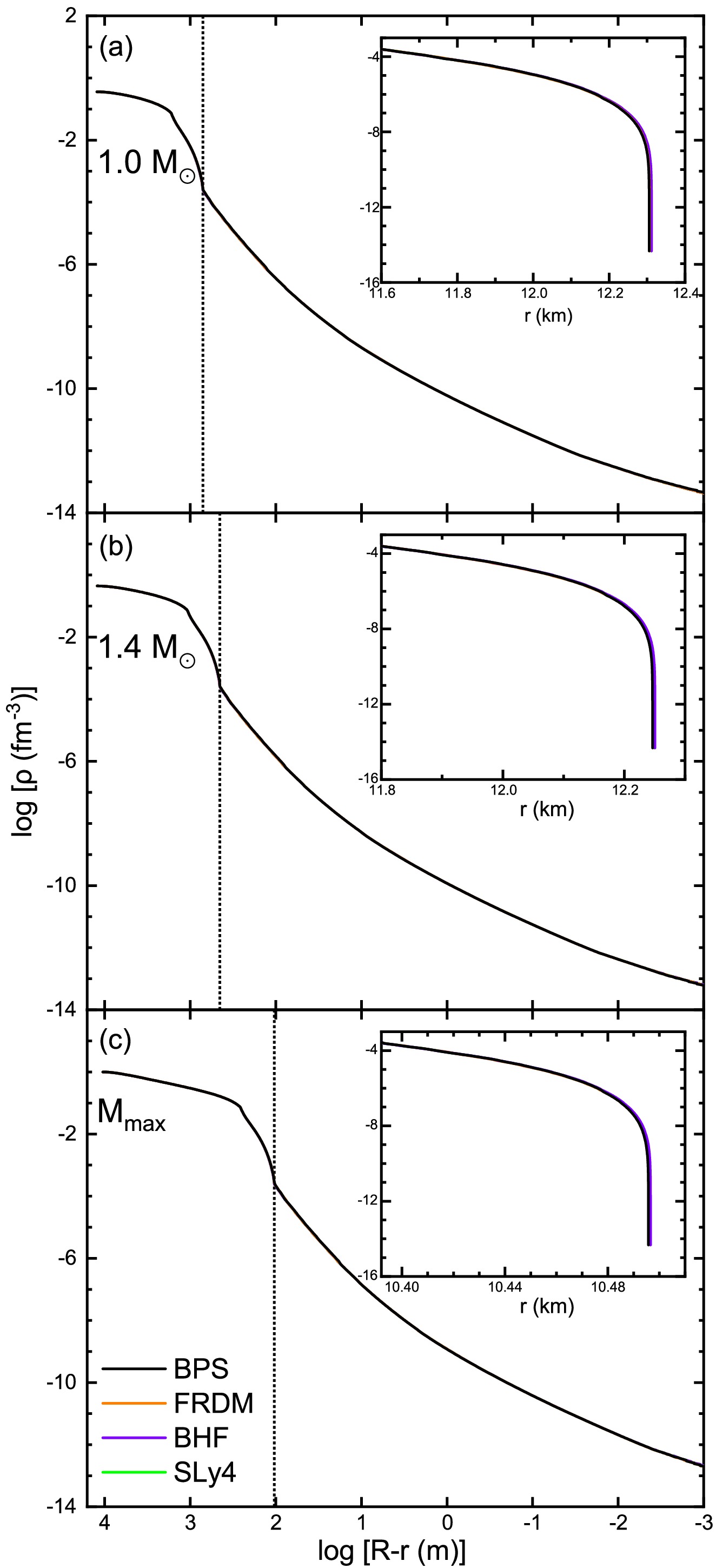

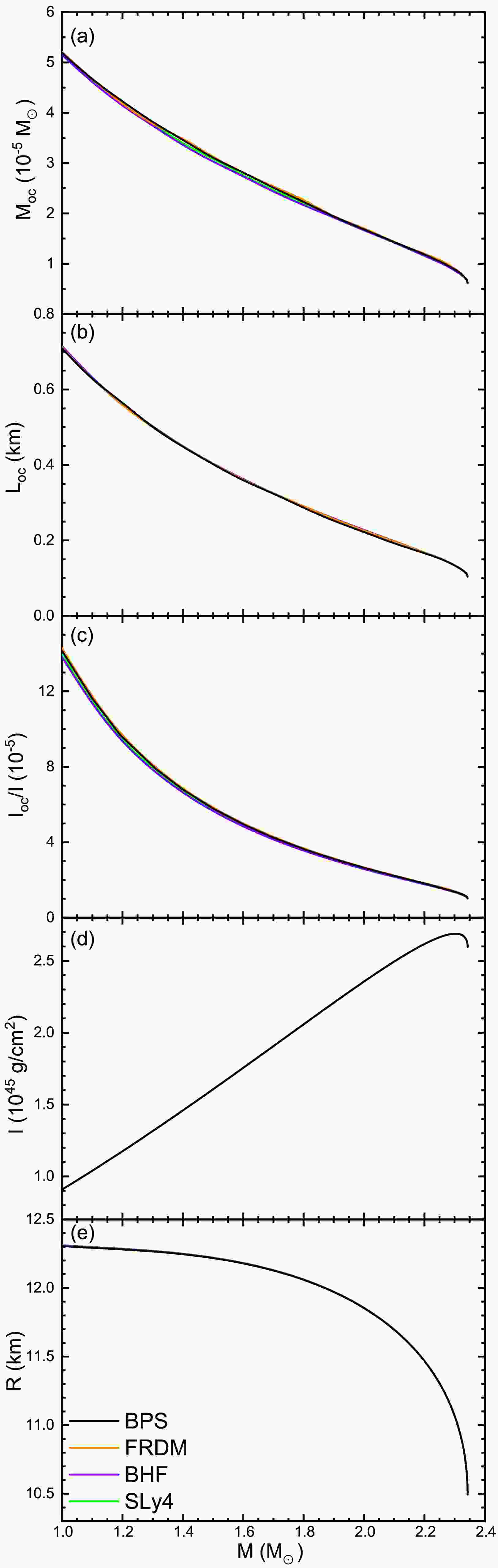
Figure 5.  (Color online) Density profiles for $M_G=1.0M_\odot , $$ 1.4M_\odot ,M_\text{max}$ NSs with different EOSs. Vertical dotted lines indicate the inner-outer crust boundary. The insets show only the outer crust.

Fig. 6(a,b,c) shows the mass, the radial extension, and the static MI of the outer crust as a function of the total NS mass. The crustal mass accounts for only a small portion $ \sim 10^{-5}M_\odot $ of the whole NS (Therefore also the relative crustal contribution to the total MI is of order $ 10^{-5} $), whereas the extension of a few hundred meters for medium-mass NSs is more notable. All quantities decrease continuously with the increase of the NS mass. The total MI (d) increases nearly linearly with the mass of the NS, since the NS radius (e) varies very little apart from the highest masses. The results obtained by the four EOSs are nearly identical. A slight variation is seen for the crustal mass, and consequently the same relative variation for the crustal MI, since the NS radii (e) are nearly identical for the four EOSs. Certain theoretical models indeed postulate universal relations between I, M, and R [73, 74, 78, 79], suggesting that the intrinsic properties of I may be inferred from observational determinations of stellar mass and radius, and vice versa. Thus, future precise measurements of I could also provide tighter constraints on NS radii through the universal relations.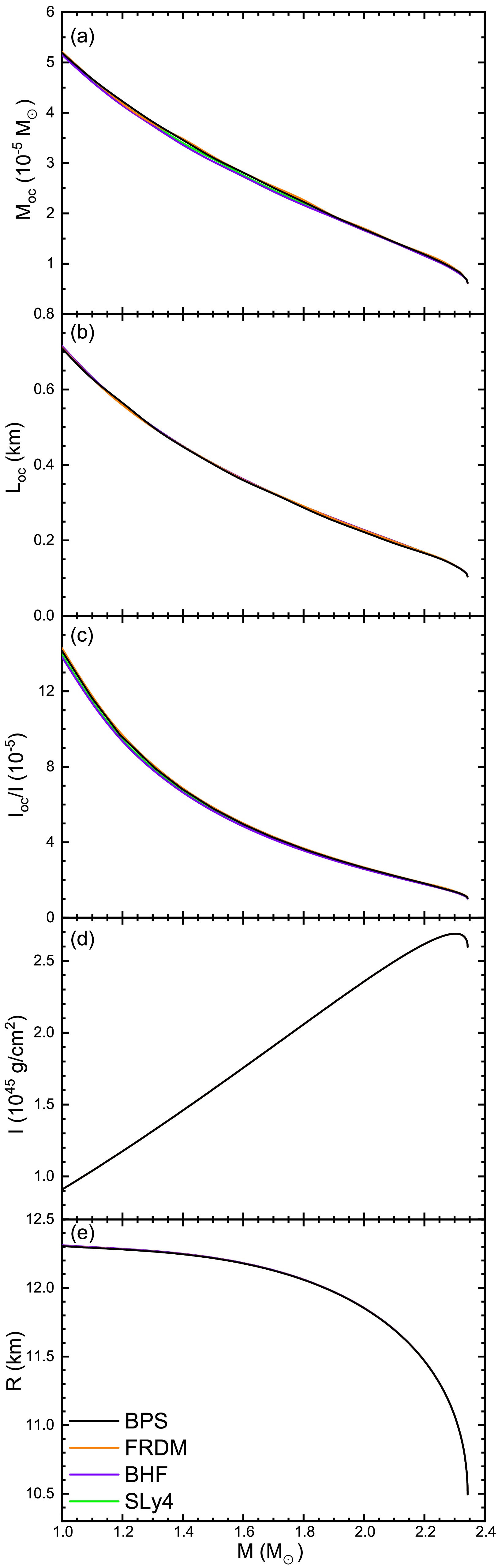

Figure 6.  (Color online) The outer-crust mass (a), radial thickness (b), relative contribution to the MI (c), and the total MI (d) and radius (e) of the star as a function of NS mass for different EOSs.

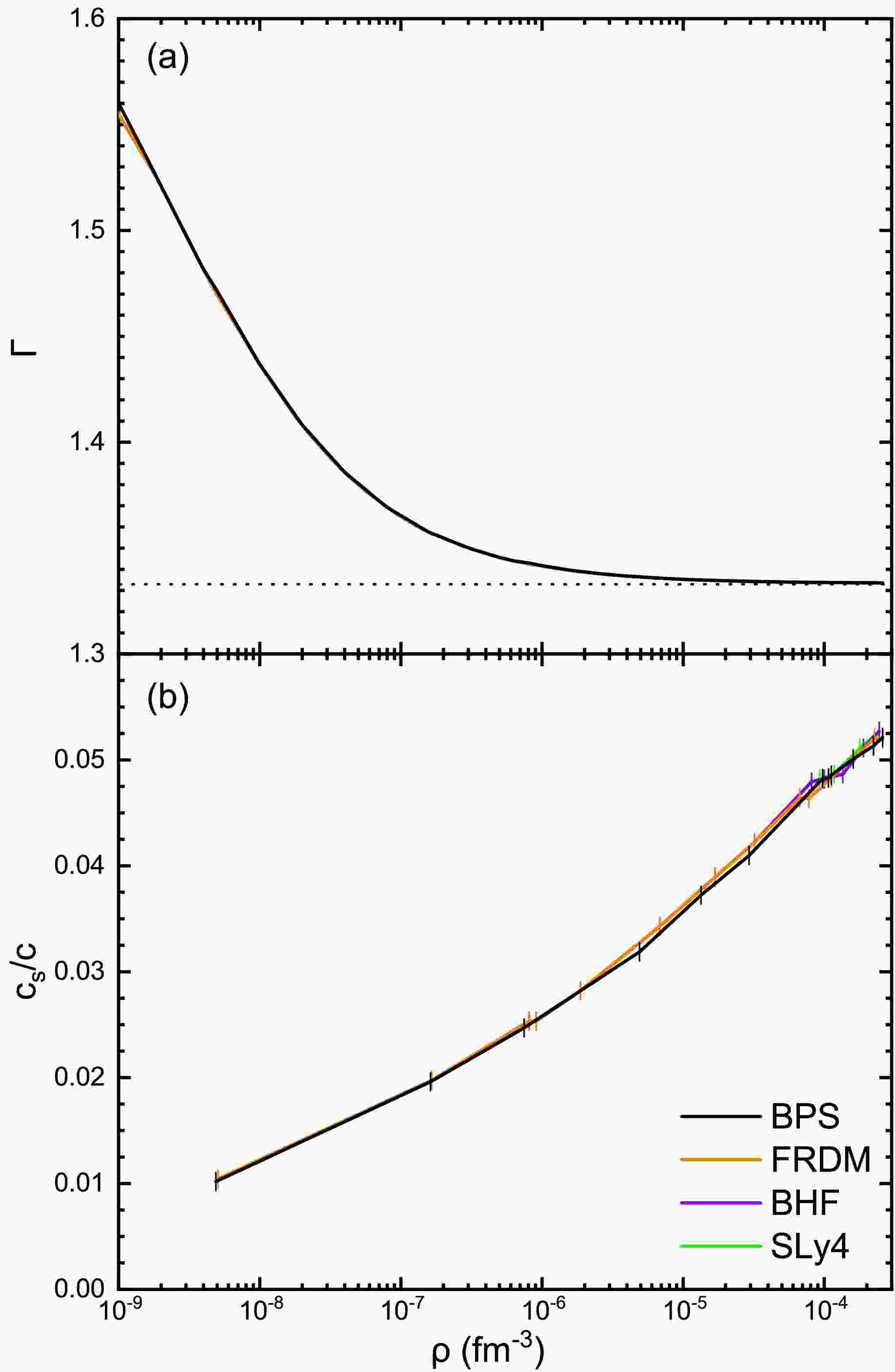
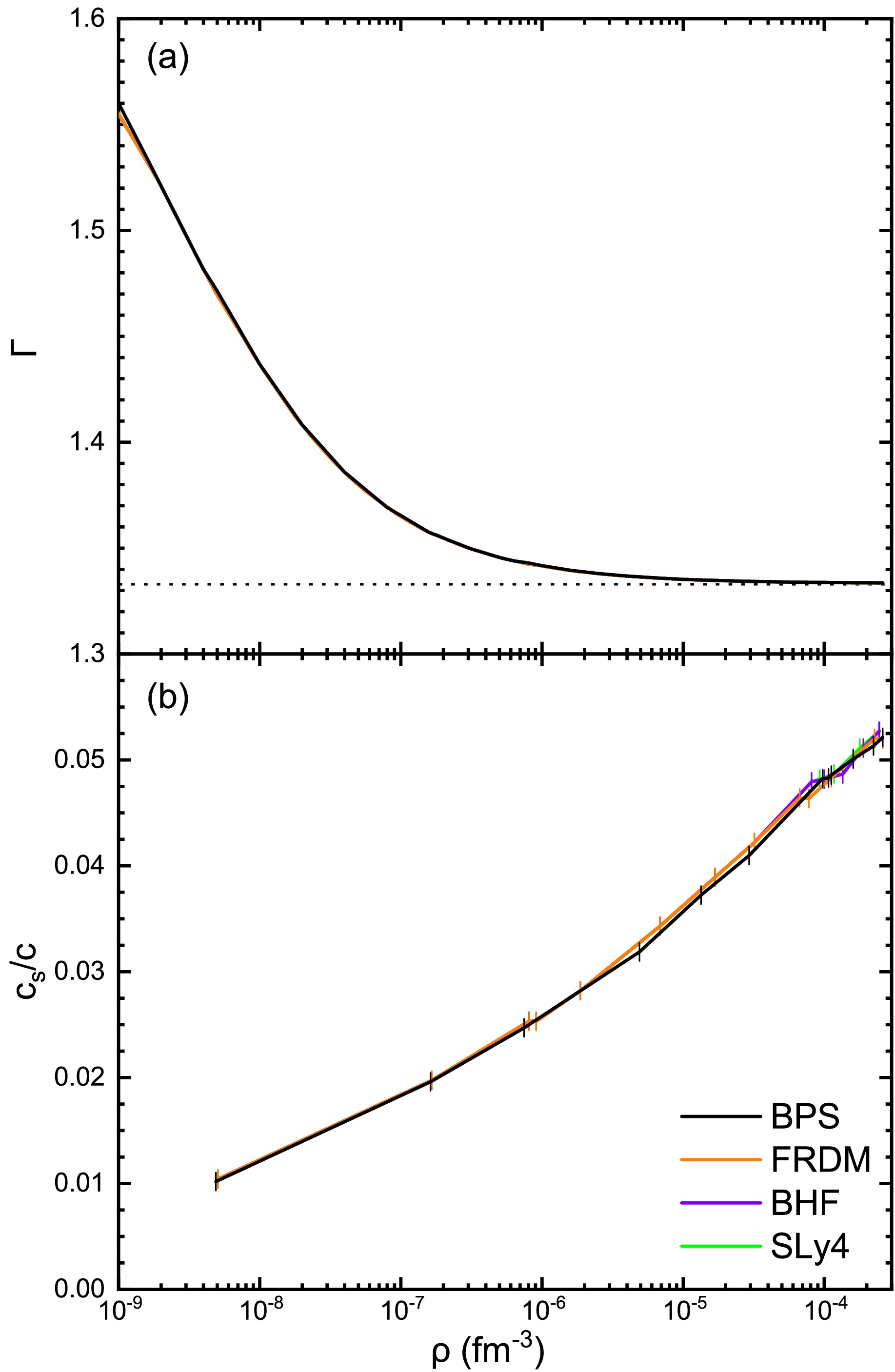
The adiabatic index defined as

which represents the stiffness of the EOS [28, 41, 43], is shown in Fig. 7(a) for the different models, and also turns out nearly model independent, as the pressure itself, Fig. 3(a). With increasing density, Γ approaches the limit of 4/3, since the electron and lattice pressures $ \sim\rho^{4/3} $ become dominant in the outer crust. When one nucleus transits to another, the adiabatic index drops to zero, which is not shown for simplicity [28]. Also the speed of sound $ c_s^2 = dp/d\varepsilon $ [43], shown in Fig. 7(b), is practically EOS independent.

Figure 7.  (Color online) The adiabatic index (a) and speed of sound (b) versus the baryon number density for four models. The horizontal dotted line indicates 4/3. The markers indicate transitions between different equilibrium nuclei.

We calculated the properties of the outer crust of nonaccreting cold NSs. Based on a BHF energy-density functional, we fitted the experimental nuclear binding energies within a liquid-drop model by adjusting the surface-energy parameter, and extrapolated into the unknown neutron-rich region up to the predicted neutron dripline. We then used the BPS formalism to obtain the outer-crust composition and EOS using the state-of-the-art AME2020 nuclear energies when available, and the extrapolated nuclear data towards the neutron dripline based on BHF theory.

The composition follows a sequence of plateaus along the magic numbers $ Z = 28 $, $ N = 50 $, $ N = 82 $. The results are very similar to those obtained by using the SLy4 Skyrme force and also very close to the original BPS results. In particular the predicted neutron drip (onset of the inner crust) occurs at $ ^{120} {\rm{Sr}}$ for BHF at $ \rho = 2.44\times 10^{-4}\;\text{fm}^{-3} $, $ ^{120} {\rm{Sr}}$ for SLy4 at $ \rho = 2.46\times10^{-4}\;\text{fm}^{-3} $, $ ^{118} {\rm{Kr}}$ for BPS at $ \rho = 2.59\times10^{-4}\;\text{fm}^{-3} $. Consequently the EOSs for the different models are basically the same. Combining the outer-crust EOS with the BHF V18 EOS for the core and the Shen20 EOS for the inner crust, we analyzed the mass, the thickness, and the MI of the outer crust and confirmed that there are only slight differences between the various EOSs, as is the case for adiabatic index and the speed of sound in the outer crust.

Our work thus confirms the validity and accuracy of the original BPS EOS, as already found in other previous investigations with updated nuclear data and different theoretical frameworks [28].