The nucleon-Δ elastic cross section in isospin-asymmetric nuclear medium with the inclusion of scalar-isovector δ meson field

The investigation of the properties of isospin-asymmetric nuclear matter under extreme conditions is a topical issue in both nuclear physics and nuclear astrophysics [1−4]. It plays a crucial role in understanding the sophisticated dynamic processes of heavy-ion collisions (HICs), the structure of nuclei, and the production and evolution of dense stars, such as neutron star [5−7]. Especially, in the past two decades, significant progress has been made in constraining the isospin-symmetric nuclear equation of state (EoS) at subnormal and normal densities through theoretical calculations and comparisons with nuclear experimental data. However, its density-dependent behaviour, especially in high-density regions, remains largely ambiguous, and the uncertainty promptly increases with the increase in density [8−10]. Furthermore, the construction of advanced radioactive beam facilities and new HICs experiments on them, including the High Intensity heavy ion Accelerator Facility (HIAF) in China [11], the Facility for Antiproton and Ion Research (FAIR) in Germany [12], the Beam Energy Scan (BES) program and fixed target (FXT) program at Relativistic Heavy Ion Collider (RHIC) in the United States [13], the Nuclotron-based Ion Collider fAcility (NICA) in Russia [14], is expected to open up new opportunities for experimental and theoretical investigations into the higher energy and higher density EoS of isospin-asymmetric nuclear matter.

The charged-pion related observables are commonly employed as sensitive probes for investigating the high-density asymmetric nuclear EoS in HICs at intermediate energies, and have attracted considerable attention in recent years [15−22]. However, there are differences between the predictions from different hadronic transport models for charged-pion related observables, especially at high densities. For instance, the pion yields and ratios, the rapidity and transverse momentum distributions predicted by the transport models cannot get consistent results and describe experimental data well [23−25]. It is known that, in HICs at intermediate energies, the pions are dominantly produced from the decay of $ \Delta $(1232) particles, therefore, the production, evolution, and decay of $ \Delta $ particles in the isospin-asymmetric nuclear medium are critical for precisely understanding and constraining the asymmetric nuclear EoS with experimental measurement and dynamic simulations [19, 26−30].

As for the cross sections of particle production, evolution and decay used in the simulation of HICs, usually one can derive them based on Brueckner theory [31, 32], Dirac-Brueckner theory [33, 34], variational approach [35], as well one-boson-exchange model [36−39]. And they also can be parameterised from the comparison of theoretical calculations with experimental data [40−42]. With the help of self-consistent relativistic BUU (RBUU) transport theory, the isospin-dependent in-medium nucleon-nucleon (NN) elastic cross section ($ \sigma^{*}_{NN\rightarrow NN} $) has been systematically studied [43, 44]. For the $ \Delta $-related cross sections, such as the NN inelastic cross section $ \sigma^{*}_{NN \rightarrow N\Delta} $ (hard-$ \Delta $ production), the soft-$ \Delta $ production channel $ \sigma^{*}_{N\pi \rightarrow \Delta} $, and the $ \Delta $ absorption channel $ \sigma^{*}_{N\Delta \rightarrow NN} $, have been calculated within the framework of the RBUU approach in which the $ \sigma $, $ \omega $, $ \rho $ and $ \delta $ meson fields are considered [19, 26, 27]. The calculated results not only confirm that these cross sections are energy-, density-, and isospin-dependent, but also indicate that the $ \delta $ meson field will cause a splitting effect on the effective masses of nucleons and $ \Delta $ particles, leading to splitting in the cross section of individual channels.

Recently, the charged-pion yields from Au+Au collisions at several GeV energies have been measured by the STAR and HADES Collaborations [20, 24]. Although these beam energies are too high to accurately investigate the nuclear symmetry energy using pion-related observables so far, they provide more precise experimental data to improve the theoretical description of pion production in HICs, thereby accurately constraining the EoS of high-density nuclear matter. However, there is a major mismatch between the charged-pion yields calculated by various transport models and the experimental measured values from the HADES collaboration [24], and by considering an isospin-dependent reduction factor on the $ \Delta $ production, the charged-pion yields can be described rather well [19, 45]. To obtain a more accurate understanding of the dense nuclear EoS by comparing the measured pion-related observables with transport model simulation results, not only the channels of single-$ \Delta $ production and absorption should be considered, but also other channels (e.g., the $ N\Delta $ elastic channels) should be self-consistently treated in the same transport model.

In the previous work [46], the $ N\Delta $ elastic cross section $ \sigma^{*}_{N\Delta\rightarrow N\Delta} $ was calculated within the RBUU approach, and only the isoscalar $ \sigma $ and $ \omega $ meson exchanges were involved. Then, the isovector $ \rho $ meson exchange was further considered to investigate the contribution of the isovector field on the $ \sigma^{*}_{N\Delta\rightarrow N\Delta} $[47]. In the relativistic mean field theory, the bulk properties of nuclei, such as binding energy and charge radius, can be precisely predicted by introducing the isovector $ \rho $ meson field [48, 49]. In addition, it has been pointed out that the $ \delta $ meson field will make a crucial contribution to a proper description of the strong isospin asymmetric matter at high densities in neutron stars, directly affecting the density dependence of the symmetry energy, and giving rise to the splitting of the Dirac mass for protons and neutrons in asymmetric matter. [26, 50−52]. For instance, Ref. [53] demonstrated that the inclusion of $\delta$ meson field not only improves the accuracy of mass and radius predictions for finite nuclei but also influences the EoS at higher densities, leading to much better agreement with heavy-ion collision data. Furthermore, the $\sigma^2\delta^2$ mixing terms in the nonlinear coupling of the effective Lagrangian significantly affect astrophysical observables, such as the radius and tidal deformability of neutron stars [54].

In this work, based on the effective Lagrangian within the same framework of the RBUU microscopic transport theory, in which the scalar-isovector $ \delta $ meson exchange is further considered, accordingly the energy-, density-, and isospin-dependent $ N\Delta \rightarrow N\Delta $ cross section can be more systematically studied.

The paper is arranged as follows, a brief review of the RBUU equation and the analytic expressions of in-medium $ N\Delta \rightarrow N\Delta $ cross sections are given in Sec.II, the numerical results of total and individual $ \sigma^{*}_{N\Delta} $, as well as the effective mass splitting effects on the cross section are presented in Sec.III, and the conclusion and outlook are given in Sec.IV.

The same theoretical framework as that established in Refs. [27, 43, 44, 46] is employed in this work. By using the closed time-path Green's function technique, which is extensively used to process issues related to non-equilibrium systems [55], and incorporating the semi-classical and quasi-particle approximations, the RBUU equation for the $ \Delta $ distribution function can be derived as [46]:

Here, $ m_{\Delta}^{*} $ and $ f_{\Delta}({\bf{x}}, {\bf{p}}, \tau) $ represent the effective mass and the distribution function of $ \Delta(1232) $, respectively. $ \Sigma_{\Delta}^{S} $ and $ \Sigma_{\Delta}^{\mu,\nu} $ on the left side characterize the Hartree terms of the $ \Delta $ self-energies. The $ C^{\Delta}(x, p) $ on the right side represents the collision term, which is determined by the collisional self-energy and is closely related to the in-medium elastic and inelastic cross sections.

In the present work, we exploratorily introduce the scalar-isovector $ \delta $ meson field in the effective Lagrangian, alongside the scalar-isoscalar $ \sigma $ meson field, the vector-isoscalar $ \omega $ meson field, and the vector-isovector $ \rho $ meson field, with the aim of understanding the impact of including the $ \delta $ meson field on the description of $ N \Delta \rightarrow N \Delta $ scattering. It should be noted that the $ N\Delta $ elastic cross section in free space can be understood primarily with the help of $ \pi $ meson exchange, owing to the long-range nuclear exchange characteristics of $ \pi $ meson, which effectively provide the cross section within free space, and shows good agreement with Cugnon’s parametrization in the higher energy region. However, in the nuclear medium, other meson exchanges, such as $ \sigma $, $ \omega $, $ \rho $, and $ \delta $, become increasingly significant and dominant at higher densities.

Thus, the effective Lagrangian can be written as

the $ L_{F} $ is the free Lagrangian density, and the $ L_{I} $ is for the interaction part,

where $ F_{\mu \nu} \equiv \partial_{\mu} \omega_{v}-\partial_{v} \omega_{\mu} , L_{\mu \nu} \equiv \partial_{\mu} \vec{\rho}_{v}-\partial_{v} \vec{\rho}_{\mu} $, $ \psi $ is the Dirac spinor, $ \psi_{\triangle} $ is the Rarita-Schwinger spinor.

In this study, we adopt density-dependent coupling constants, which have been extensively applied in the calculation of both elastic and inelastic reaction channels, and provide a more accurate description of cross sections for $ NN\rightarrow NN $, $ NN\rightarrow N\Delta $, and $ N\pi \rightarrow \Delta $[26, 27, 44, 56]. Thus, it can be quantitatively parameterized as

where $ u=\rho_{b}/\rho_{0} $, $ \rho_{b} $ and $ \rho_{0} $ are the baryon density and the normal nuclear density, respectively, $ f_{q}(u) $ reads as

For the $ \Delta $-$ \Delta $-meson vertex, the coupling constant ratio is defined as $ \chi_{q} = g^{q}_{\Delta \Delta}/g^{q}_{NN} $, and $ \chi_{\sigma}=1.0 $, $ \chi_{\omega}=0.8 $ are adopted in this work, these parameters lie within the parameter space, which is drawn by comparing theoretical investigations and experimental data [57−61]. As for $ \chi_\rho $ and $ \chi_\delta $, they have not been strictly constrained by comparing theoretical predictions and experimental data. In Ref.[62], $ 0.7 \leq \chi_\rho \leq 1.3 $ was adopted to investigate the $ \Delta- $admixed neutron stars, and it was shown that for a large domain of the parameter space, nucleation of $ \Delta $s opens-up the nucleonic dUrca process which is otherwise forbidden. Here, a fixed value of $ \chi_\delta $ = $ \chi_\rho=0.7 $ is adopted for simplicity. It is noticed that the variation in $ \chi_\rho $ and $ \chi_\delta $ within 0.7~1.3 introduces to some extent uncertainties in the calculated cross sections but the main conclusions drawn in this investigation are not influenced by the choice of this parameter.

According to the relativistic mean field theory, the effective masses of the nucleons and $ \Delta $ particles are related to the average value of the meson fields, and have the following forms[18]:

Here, the nucleon mass $m_{N}$ in free space is taken as 0.938 GeV, and $ m^{*}_{p} $, $ m^{*}_{n} $, $ m^{*}_{\Delta^{++}} $, $ m^{*}_{\Delta^{+}} $, $ m^{*}_{\Delta^{0}} $, and $ m^{*}_{\Delta^{-}} $ represent the effective masses of the proton, neutron, $ \Delta^{++} $, $ \Delta^{+} $, $ \Delta^{0} $, and $ \Delta^{-} $ in the nuclear medium, respectively. The coupling constants $ g_{\sigma} $, $ g_{\omega} $, $ g_{\rho} $, $ g_{\delta} $ are derived from Eq. 5. And the values of the $ \sigma $ and $ \delta $ meson fields are determined by solving the corresponding Klein-Gordon equation. In neutron-rich matter, the isospin asymmetry parameter is defined as $ \alpha=(\rho_{n}-\rho_{p})/(\rho_{n}+\rho_{p})\neq0 $, the effective masses of nucleons and $ \Delta $ particles obey $m^{*}_{p} > m^{*}_{n}$ and $m^{*}_{\Delta^{++}} > m^{*}_{\Delta^{+}} > m^{*}_{\Delta^{0}} > m^{*}_{\Delta^{-}}$ [27].

The collision term in Eq. 1 can be divided into the $ \Delta $-related elastic, inelastic, and decay interaction parts [46, 63, 64],

and the elastic part can be further distinguished into $ N\Delta $ and $ \Delta\Delta $ elastic interaction parts,

Here, we focus exclusively on the $ N\Delta $ elastic scattering, and it can be expressed as

the $ \sigma^{N\Delta}_{\rm{el}}(s,t) $ is $ N \Delta \rightarrow N \Delta $ cross section, $ F_{2} $ and $ F_{1} $ are Uehling-Uhlenbeck Pauli-blocking factors of the loss and gain terms. The transition probability in $ N\Delta\rightarrow N\Delta $ can be written as

and

where $ T_{e} $ and $ \Phi_{e} $ are the isospin matrix and the spin matrix, the terms $ g^{A, B}_{\Delta \Delta}, g^{A, B}_{N N} $ are the coupling constants for $ \Delta $-$ \Delta $-meson and nucleon-nucleon-meson interactions, respectively, and (A, B) denotes the type of meson exchanges involved.

The individual differential cross sections read as

The indices r=1 to 10 correspond respectively to the meson exchange terms: $ \sigma-\sigma $, $ \omega-\omega $, $ \sigma-\omega $, $ \rho-\rho $, $ \delta-\delta $, $ \delta-\rho $, $ \sigma-\delta $, $ \sigma-\rho $, $ \omega-\delta $, and $ \omega-\rho $. The detailed information of the parameters $ d_{i} $ and $ D_{i} $ can be found in Table 1 and App. A. For the $ d_{i} $ component of the total cross section, it is necessary to average the isospin matrix for each individual channel, as shown in the last row of Table 1.

	$ \sigma-\sigma $, $ \omega-\omega $	$ \delta-\delta $, $ \rho-\rho $,	$ \omega-\rho $, $ \sigma-\delta $,
	$ \sigma-\omega $	$ \delta-\rho $	$ \sigma-\rho $, $ \omega-\delta $
$ p\Delta^{++}(n\Delta^{-}) $	1	9/4	3/2
$ n\Delta^{++}(p\Delta^{-}) $	1	9/4	-3/2
$ p\Delta^{+}(n\Delta^{0}) $	1	1/4	1/2
$ n\Delta^{+}(p\Delta^{0}) $	1	1/4	-1/2
$ N\Delta\rightarrow N\Delta $	1	5/4	0

Table 1.  The isospin matrix parameter sets $ T_{e} $ for individual $ N\Delta \rightarrow N\Delta $ reaction channels.

In addition, the following phenomenological effective form factor for the nucleon-nucleon-meson vertex is used, due to the finite size and short-range correlation properties of baryons:

The cutoff masses for different meson, denoted by $ \Lambda_{q} $, are taken as $ \Lambda_{\sigma}=1.1 $ GeV, $ \Lambda_{\omega}=0.783 $ GeV, $ \Lambda_{\rho}=0.770 $ GeV, $ \Lambda_{\delta}=0.983 $ GeV [43, 44], and $ \Lambda_{\Delta}=0.4\Lambda $, consistent with the value chosen in Ref. [47].

Moreover, other factors, which might affect the $ N\Delta $ scattering, should be noticed here, such as the canonical momenta correction and the threshold effect. Here, we primarily focus on the isospin dependence of the $ N\Delta $ elastic cross section at densities $ u \leq 3\rho_{0} $. Above such density, the quasi-particle approximation adopted for this transport theory might become unreliable, as it should not properly describe the strong modifications to baryon properties in extreme conditions, as well, the possible phase transition from hadronic gas to quark-gluon-plasma (QGP) might occur[65, 66]. Although the above factors have some degree of influence on the production and absorption of $ \Delta $ and pion, as well as the charged-pion ratio [18, 67] and should be considered carefully, their integrated effects will complicate the conclusions of this work, and will be uniformly considered in numerical microscopic transport model simulations.

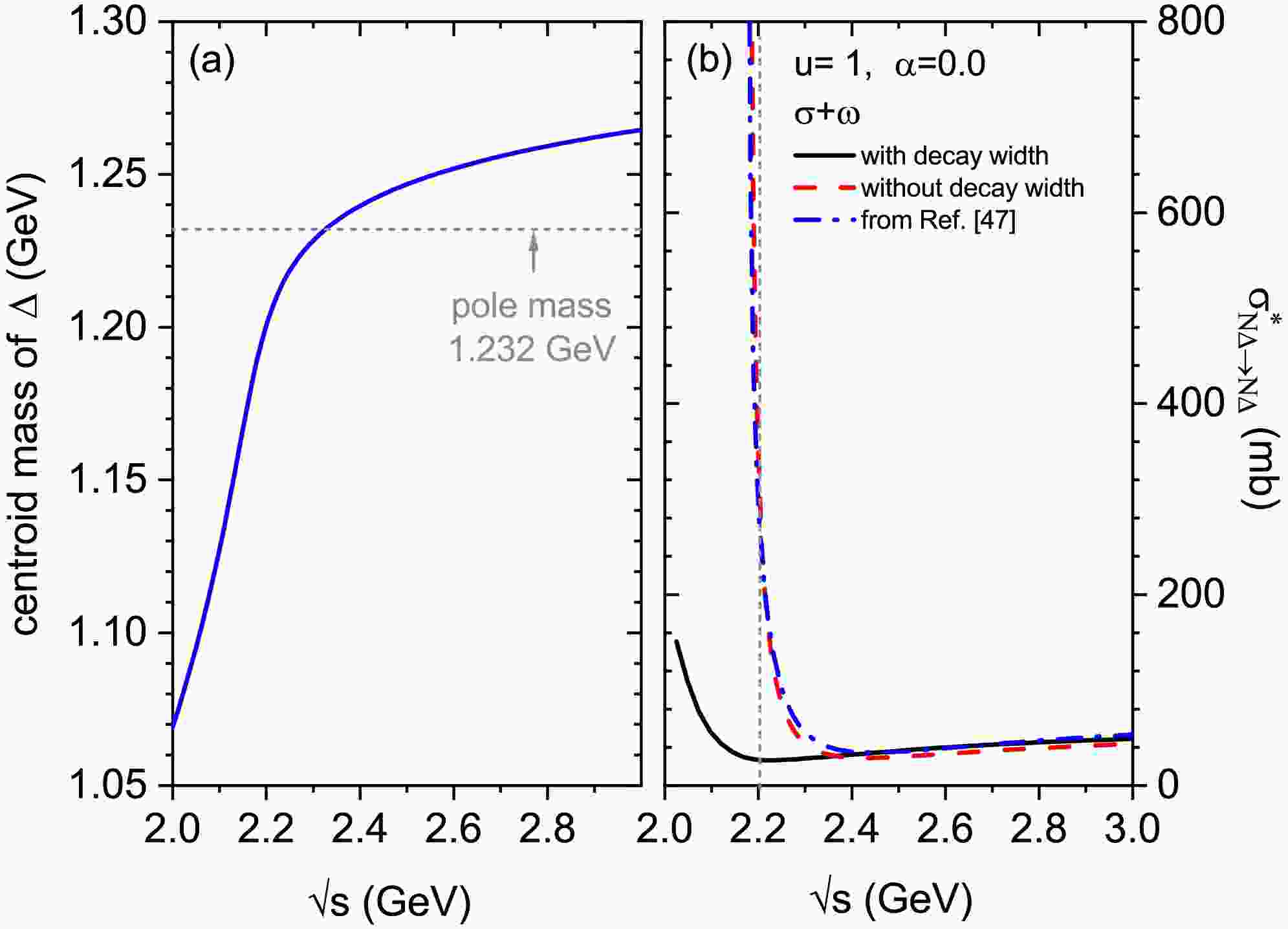
Firstly, since the $ \Delta $ particle is an unstable resonance state in nature, it is important to investigate the influence of its decay width on the $ N \Delta \rightarrow N \Delta $ cross section. Commonly, the decay width of $ \Delta $-isobar can be calculated by using quantum field theory or decided by the widely used momentum-dependent phenomenological formula [21, 67, 68]. In the calculations of $ NN\rightarrow N \Delta $ and $ N\pi \rightarrow \Delta $ cross sections, the dependence of cross sections on the decay width of $ \Delta $ is accounted for by introducing the Breit-Wigner distribution function integral [18, 27, 69]. To estimate the effect of the decay width of $ \Delta $ on the $ N \Delta \rightarrow N \Delta $ cross section, the centroid mass of $ \Delta $ proposed by Refs. [46, 68] is used here. The energy dependence of the centroid mass of $ \Delta $ is shown in Fig. 1(a) with the blue solid line, while the grey dashed line represents the value of the $ \Delta(1232) $ pole mass. The centroid mass of $ \Delta $ increases rapidly with increasing center of mass (c.m.) energy at the energy below about 2.2 GeV and then slows down noticeably.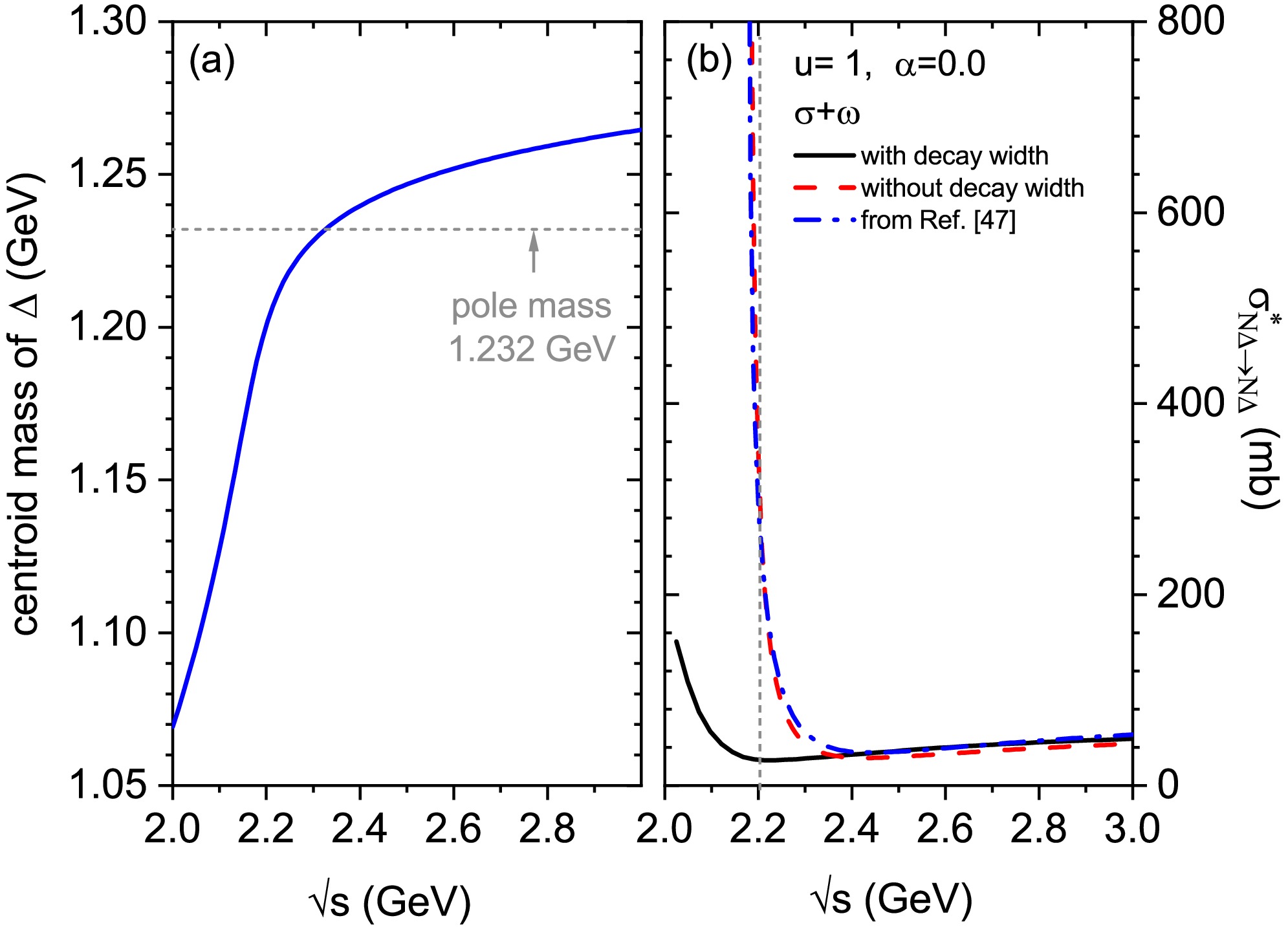

Figure 1.  (Color online) Panel (a): the blue solid line represents the centroid mass of $ \Delta(1232) $ as a function of center of mass (c.m.) energy, and the grey dashed line represents the pole mass of $ \Delta $. Panel (b): the isospin-independent $ N\Delta \rightarrow N\Delta $ cross sections with (black solid line) and without (red dash line) considering the $ \Delta $ resonance decay width for $ \alpha $=0 at u=1, the blue dashed-dot line represents the result from Ref. [47] without considering the $ \Delta $ resonance decay width.

Figure 1(b) shows the $ N\Delta \rightarrow N\Delta $ cross section, which only includes the contributions of $ \sigma $ and $ \omega $ meson related exchanges, with (black solid line) and without (red dashed line) considering the $ \Delta $ resonance decay width for $ \alpha $=0 at the reduced density u=1. In addition, the result shown in Fig. 2(a) of Ref. [47] is depicted with the blue dashed-dot line for comparison. Although the coupling constants used in the effective Lagrangian density are different, the calculation result in this work is close to it, because both coupling constant sets are obtained by fitting the properties of the finite nuclei. Furthermore, when the $ \Delta $ resonance decay width is considered, a significant suppression effect on the $ \sigma^{*}_{N\Delta} $ at lower energies ($ \sqrt{s}\lesssim $ 2.2 GeV, left of the vertical grey dashed line) can be observed, while at higher energies ($ \sqrt{s}\gtrsim $ 2.2 GeV), the cross section becomes rather weakly dependent of the $ \Delta $ resonance decay width. Therefore, in the following, the pole mass of $ \Delta $ particle will be adopted for simplicity, and the $ N\Delta \rightarrow N\Delta $ cross section at energies above 2.2 GeV will be mainly focused on, and the isospin and density dependence of the $ N\Delta \rightarrow N\Delta $ cross sections at $ \sqrt{s}= $2.5 GeV will be analyzed systematically.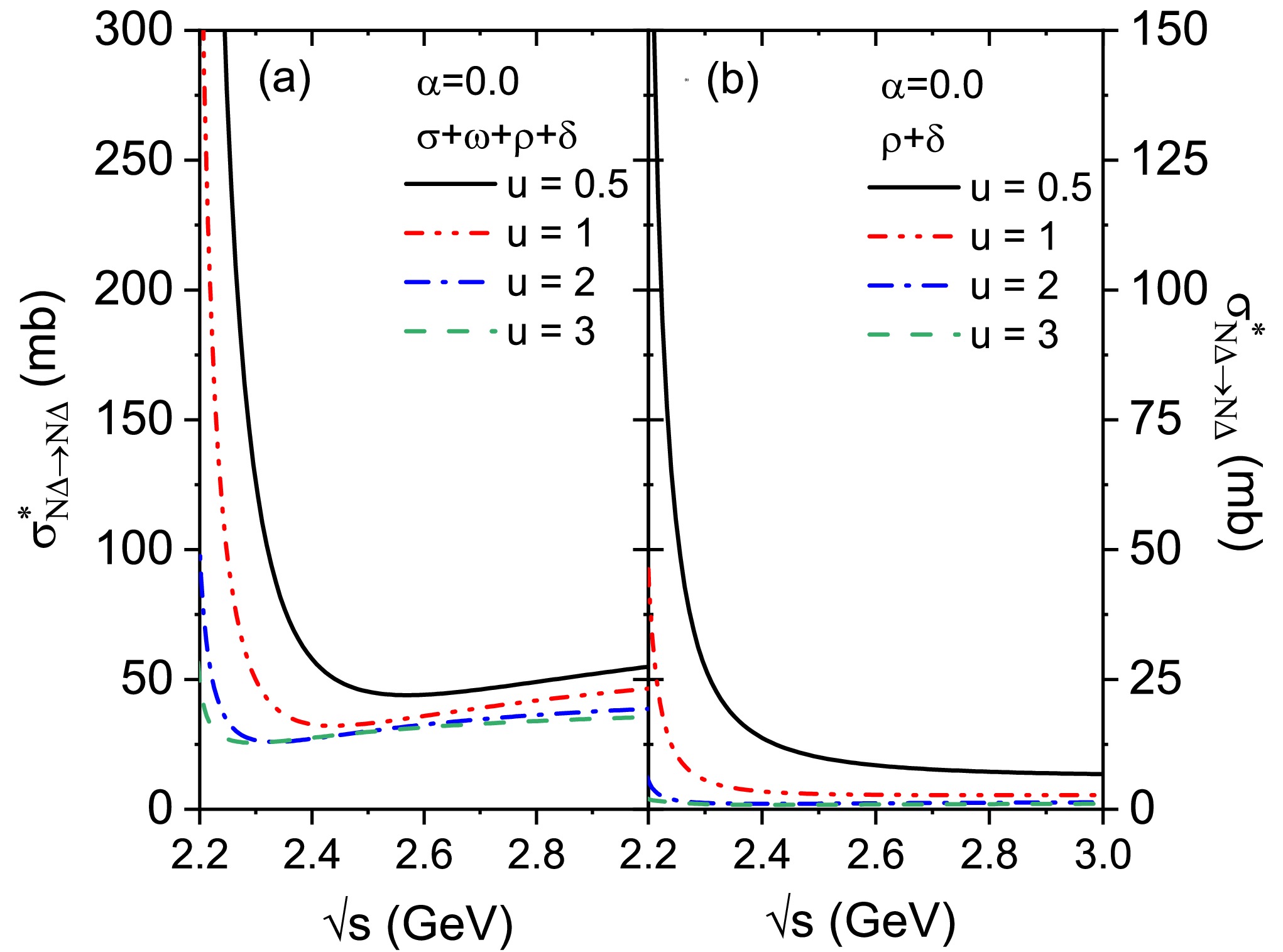

Figure 2.  (Color online) The $ N\Delta\rightarrow N\Delta $ cross section as a function of c.m. energy for symmetric nuclear matter ($ \alpha=0 $) at u=0.5, 1, 2, and 3. Panel (a) and (b) are calculated with the inclusion of the $ \sigma+\omega+\rho+\delta $ and $ \rho+\delta $ meson exchanges, respectively.

Then, Fig. 2(a) shows the total contributions of $ \sigma $, $ \omega $, $ \rho $, and $ \delta $ meson exchanges to the energy- and density-dependent $ \sigma^{*}_{N\Delta}(\sqrt{s},u) $ at various densities (u=0.5, 1, 2, and 3) when $ \alpha=0 $. Similar to the $ \sigma^{*}_{NN\rightarrow N\Delta} $ shown in Refs. [18, 26], and to the $ \sigma^{*}_{N\Delta} $ (only include $ \sigma $, $ \omega $ and $ \rho $ meson exchanges) shown in Ref. [47], the $ \sigma^{*}_{N\Delta} $ shown in Fig. 2(a) decreases with increasing reduced density, indicating a visible density dependent suppression of nuclear medium on this cross section, especially at energies below about 2.4 GeV, due mainly to the decrease of the baryon effective mass with increasing density [26]. When the energies exceed 2.4 GeV, the density dependence of the cross section weakens, and the cross section is slightly enhanced with increasing energy. Since based on the Walecka model, the scalar $ \sigma $ and vector $ \omega $ meson fields contribute to an attractive and a repulsive potential, respectively. Further, the relative momentum between the ingoing nucleon and $ \Delta $ increases with the increase of $ \sqrt{s} $, and the momentum-dependent repulsion might be dominant and has a more obvious effect, resulting in a possible increase of $ \sigma^{*}_{N\Delta} $.

To clearly see the total effects of the isovector meson fields on the $ \sigma^{*}_{N\Delta}(\sqrt{s},u) $, Fig. 2(b) shows the contributions of $ \rho $ and $ \delta $ meson involved terms (include the crossing terms with $ \sigma $, $ \omega $) to the $ \sigma^{*}_{N\Delta \rightarrow N \Delta} $ at u=0.5, 1, 2, and 3 when $ \alpha $=0. By comparing with Fig. 2(a), it can be found that the proportion of the contributions of $ \rho $ and $ \delta $ meson involved terms in total $ \sigma^{*}_{N \Delta \rightarrow N \Delta} $ is more pronounced at lower densities, and then suppressed as increasing density. When further comparing with the $ \sigma^{*}_{N \Delta \rightarrow N \Delta} $ in which only the $ \rho $ meson involved terms are contributed as shown in Fig. 2(c) of Ref. [47], one can see clearly that the $ \rho $ and $ \delta $ meson related-terms have a larger contribution than that of $ \rho $ meson field merely.

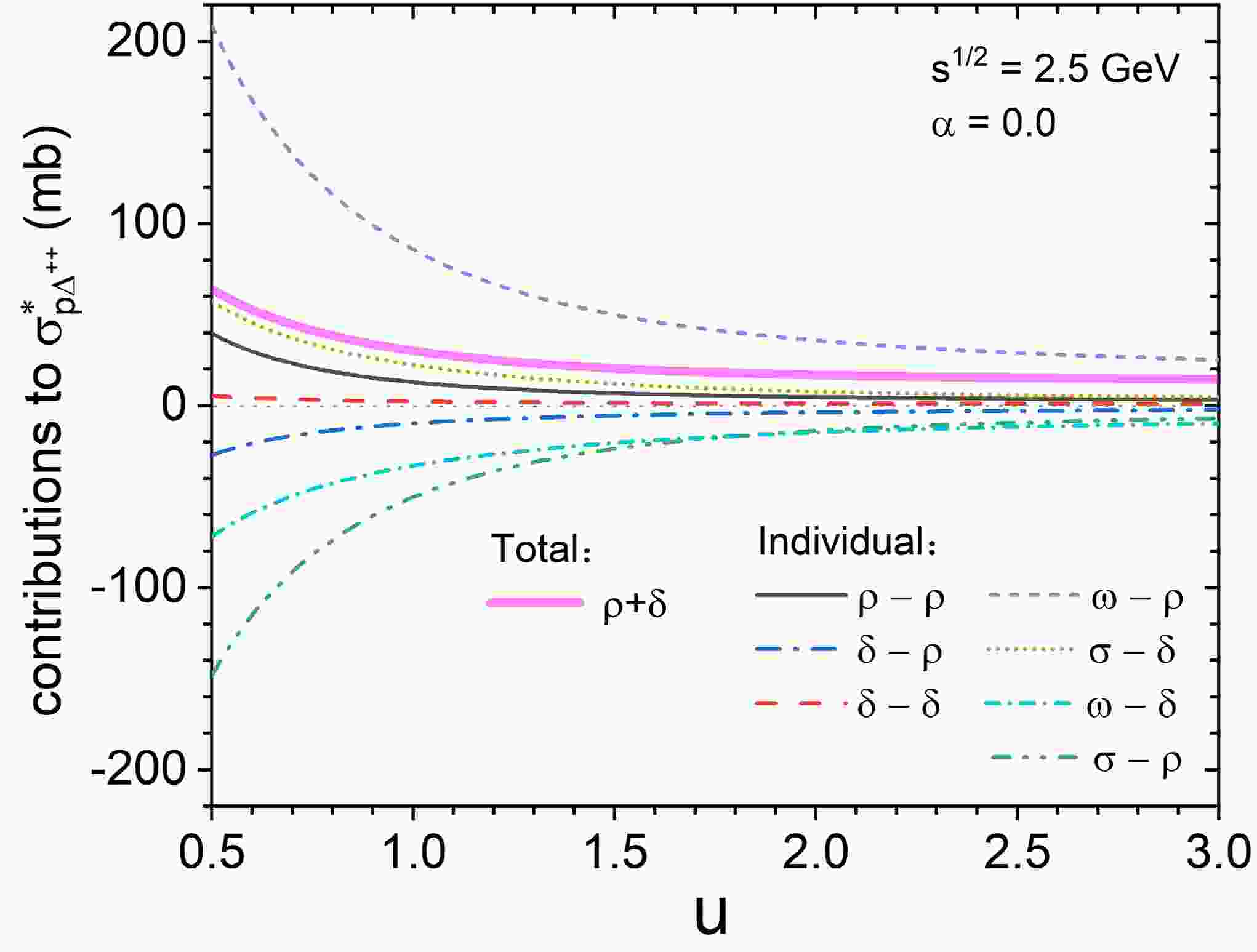
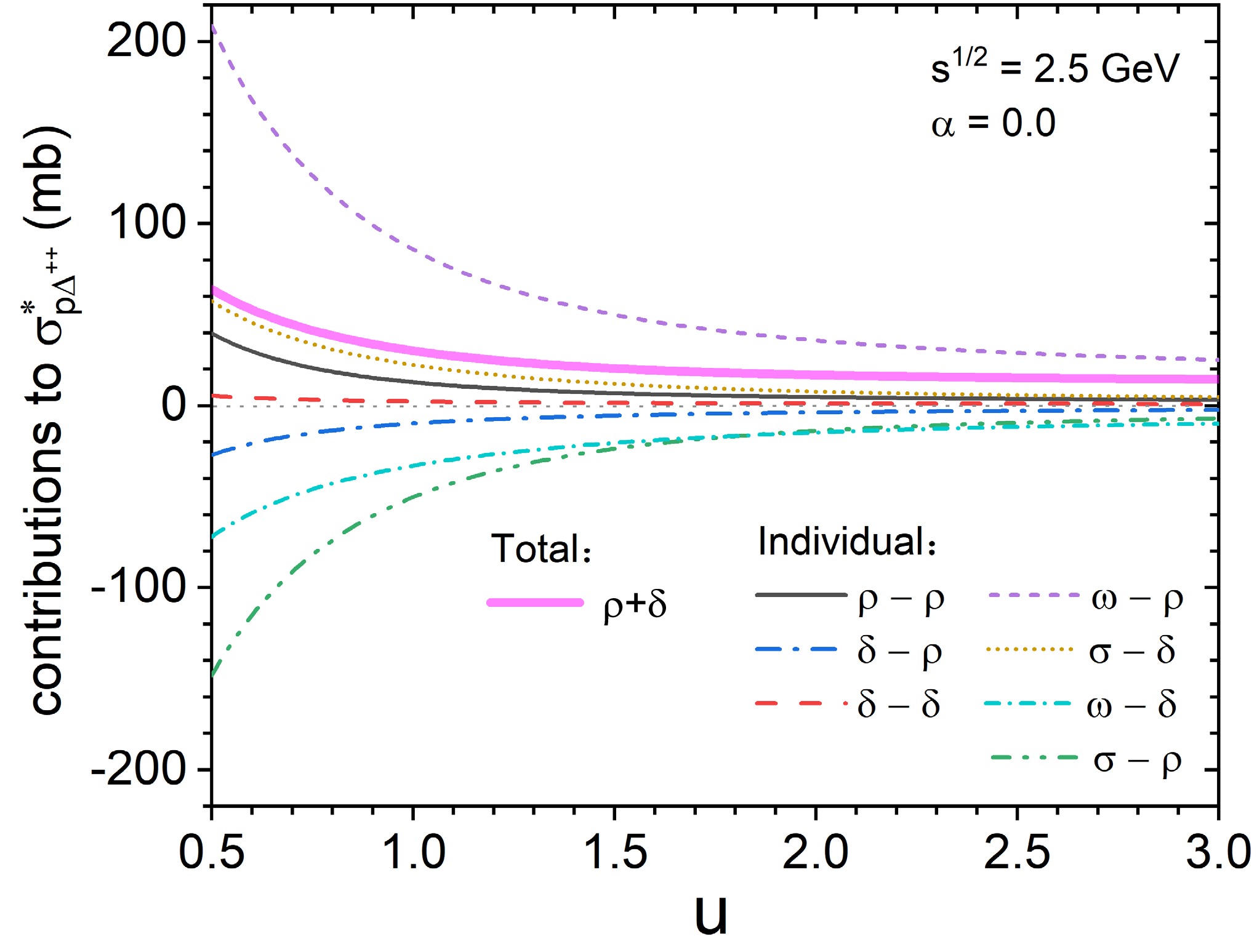
It is interesting to further explore the individual contribution of each isovector meson related exchange to the $ \sigma^{*}_{N \Delta}(\sqrt{s},u) $. As shown in Table 1, the isospin matrix in Eq. 12 of isospin vector-vector meson exchanges is 5/4, while that of isospin scalar-vector meson exchanges is 0 for the total $ N \Delta \rightarrow N \Delta $ channel. Therefore, for the contributions of $ \rho $ and $ \delta $ related exchanges to the total $ \sigma^{*}_{N \Delta} $, only the isospin vector-vector meson exchanges are taken into account. However, for individual channels, the isospin matrixes of isospin scalar-vector and vector-vector meson exchanges are different, thus the total contribution of $ \rho $ and $ \delta $ related exchange terms to the $ \sigma^{*}_{p\Delta^{++}} $, which is shown by the thick solid magenta line in Fig. 3, is larger than that to the $ \sigma^{*}_{N\Delta} $ which is shown in Fig. 2(b). In addition, the individual contributions of $ \rho $ and $ \delta $ related exchanges to each channel deserve to be further studied. Here, taking the $ \sigma^{*}_{p \Delta^{++}} $ with $ \alpha $=0 at $ \sqrt{s} $=2.5 GeV as an example, the individual contribution of $ \rho $ and $ \delta $ meson related exchange is shown in Fig. 3. It can be found that the contribution of each meson exchange term to the $ \sigma^{*}_{p \Delta^{++}} $ decreases with increasing reduced density, this density dependence originates from the baryon-baryon-meson coupling constants and the effective masses of nucleons and $ \Delta $ particles. This density-dependent characteristic of the cross section suggests that, in addition to the liner term, an exponential term should be introduced in the parameterized formula, as shown in Eq. 15 and will be discussed in Sec. IIIC. In addition, there exists an obvious cancellation effect between $ \omega-\rho $ and $ \sigma-\rho $, $ \sigma-\delta $ and $ \omega-\delta $, $ \rho-\rho $ and $ \delta-\rho $, $ \delta-\delta $ and $ \delta-\rho $, respectively. However, the absolute values of the contributions of $ \omega-\rho $, $ \sigma-\delta $, $ \rho-\rho $, and $ \delta-\delta $ meson exchange terms to the $ \sigma^{*}_{p \Delta^{++}} $ are larger than those of the corresponding terms, thus the net contribution of $ \rho $ and $ \delta $ related exchange terms to the $ \sigma^{*}_{p\Delta^{++}} $ is larger than zero (grey dotted line).

Figure 3.  (Color online) The total (thick solid magenta line) and individual contributions of the $ \rho $ and $ \delta $ related exchange terms to $ \sigma^{*}_{p\Delta^{++}} $ with $ \alpha=0 $ at $ \sqrt{s}= $2.5 GeV. The horizontal grey dotted line represents zero.

Further, the energy, density, and isospin asymmetry dependence of the individual $ \sigma_{N \Delta}^{*} $ have been calculated and shown in Fig. 4. The individual $ \sigma^{*}_{p\Delta} $ are shown in the top panels (a-d), while the individual $ \sigma^{*}_{n\Delta} $ are shown in the bottom panels (e-h). The results for $ \alpha $=0.3 with u = 1.0, 2.0, and 3.0 are shown by blue solid, black dash-dot, and green dash-dot-dot lines, respectively. Similar to the results shown in Figs. 2 and 3, some individual cross sections are suppressed with increasing reduced densities and/or energies, especially at lower energies, while some other elastic cross sections exhibit a slight enhancement with increasing densities at higher energies, a more detailed discussion of this energy dependence will be given in the following and shown in Fig. 6. In addition, the density dependence of the $ \sigma_{p \Delta^{++}}^{*} $ and $ \sigma_{n \Delta^{-}}^{*} $ is stronger than other individual cross sections, since the isospin matrices of these two channels are 3/2 for isospin scalar-vector terms and 9/4 for isospin vector-vector terms, which are larger than the values for other channels, as shown in Table 1.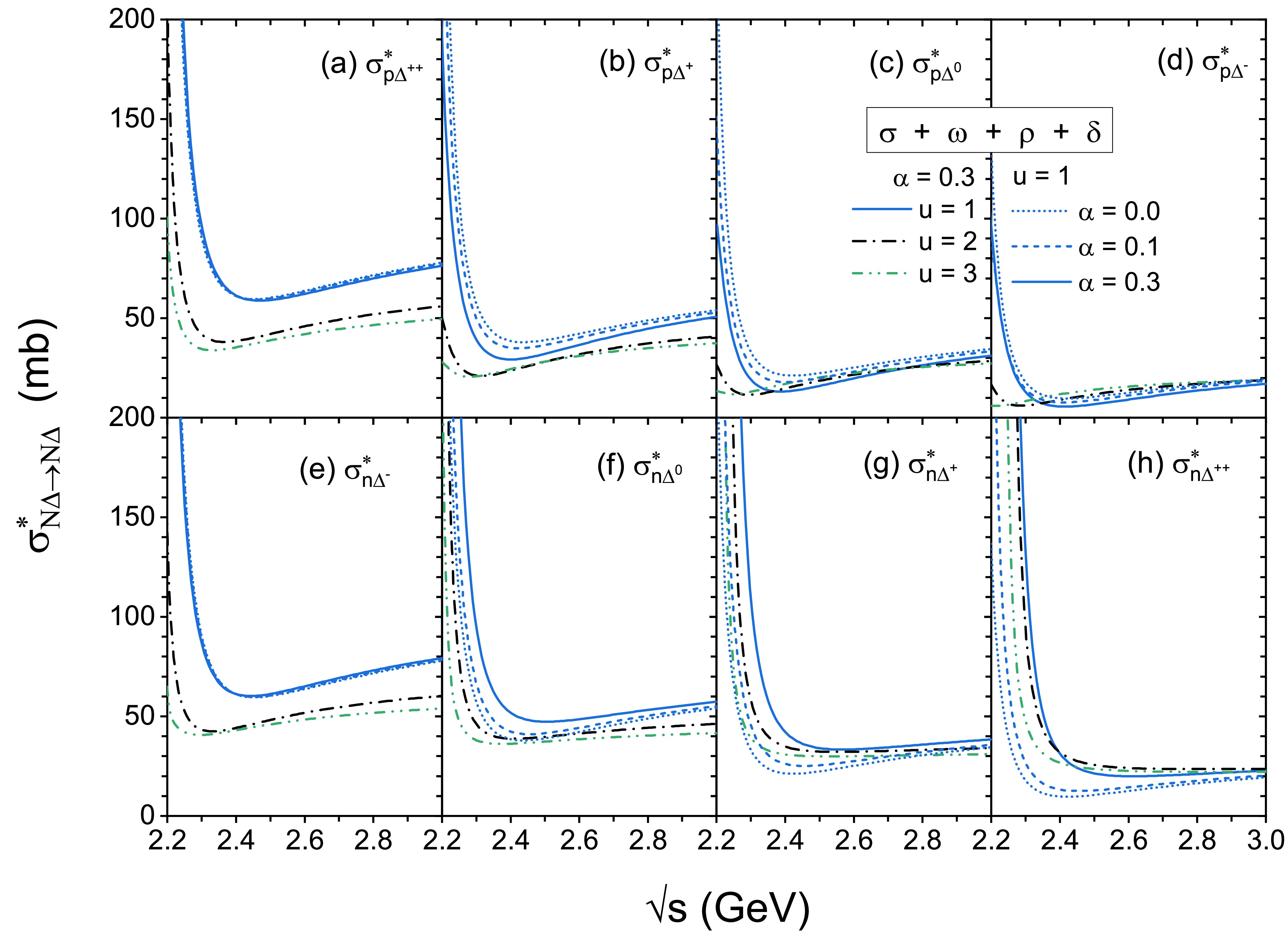

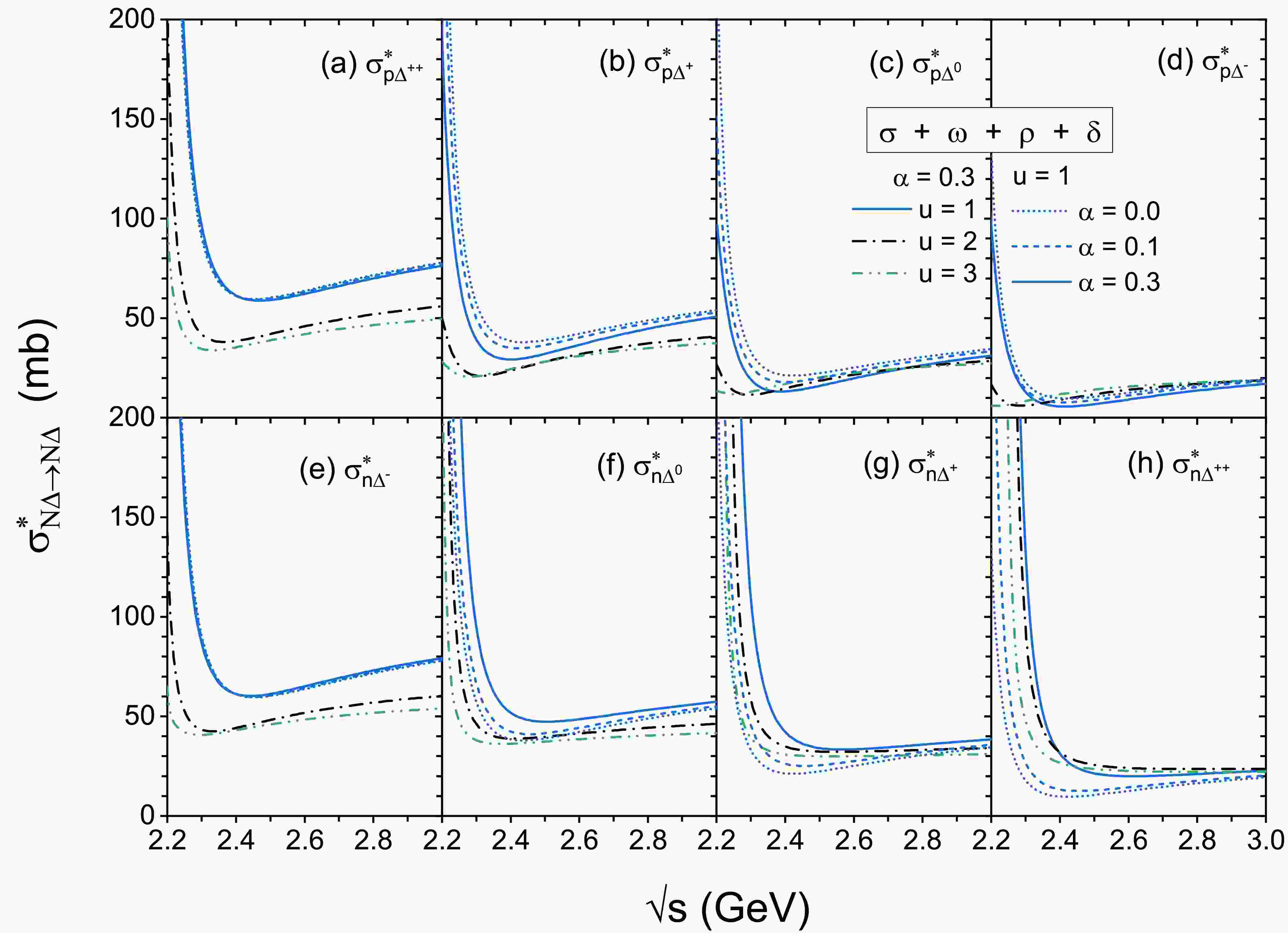
Figure 4.  (Color online) The $ \sigma^{*}_{N\Delta\rightarrow N \Delta} $ as a function of c.m. energy at various densities (u=1, 2, 3) with isospin asymmetry degree ($ \alpha $=0.0, 0.1, 0.3). The top and bottom panels correspond to the individual $ p\Delta $ and $ n\Delta $ elastic cross sections, respectively.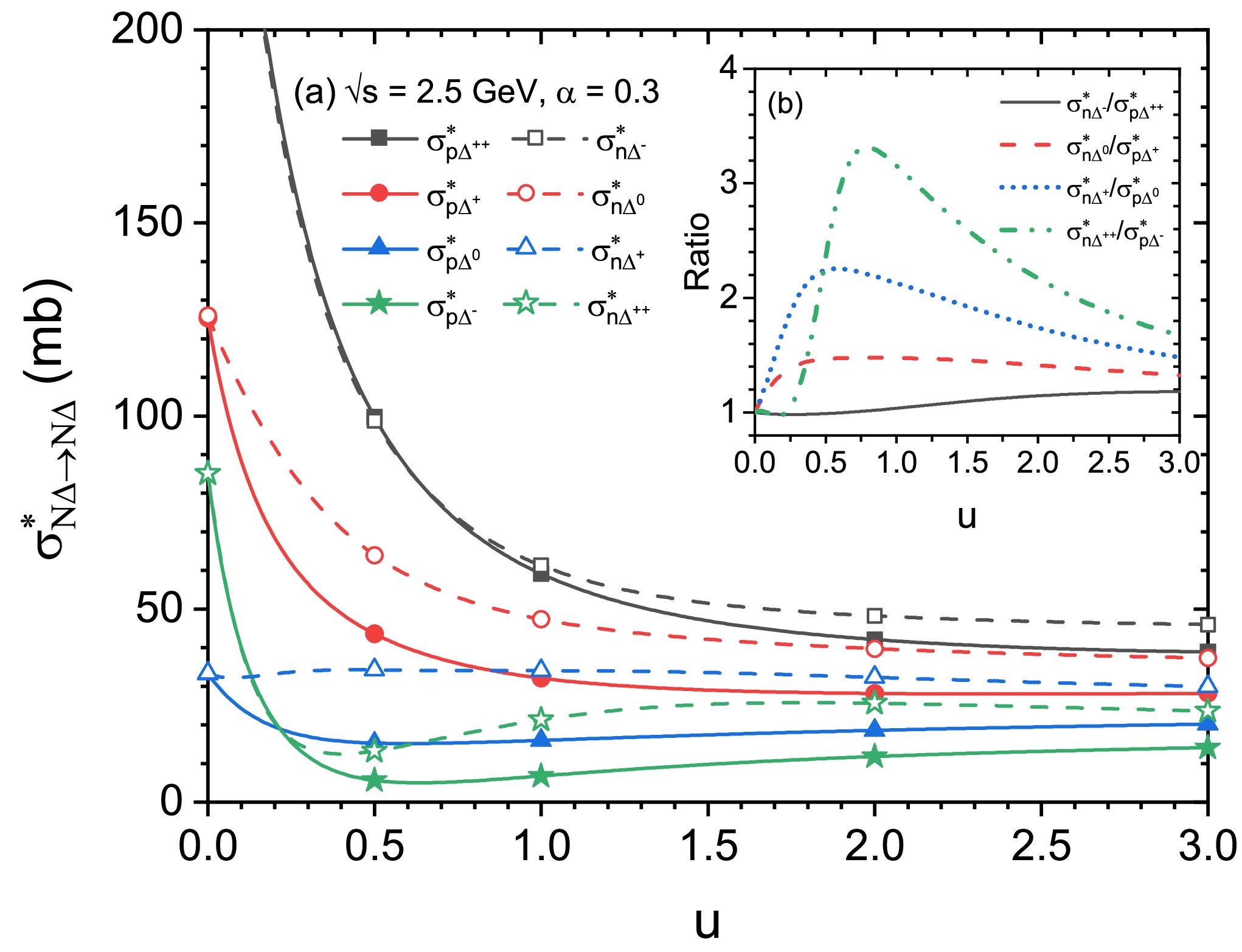

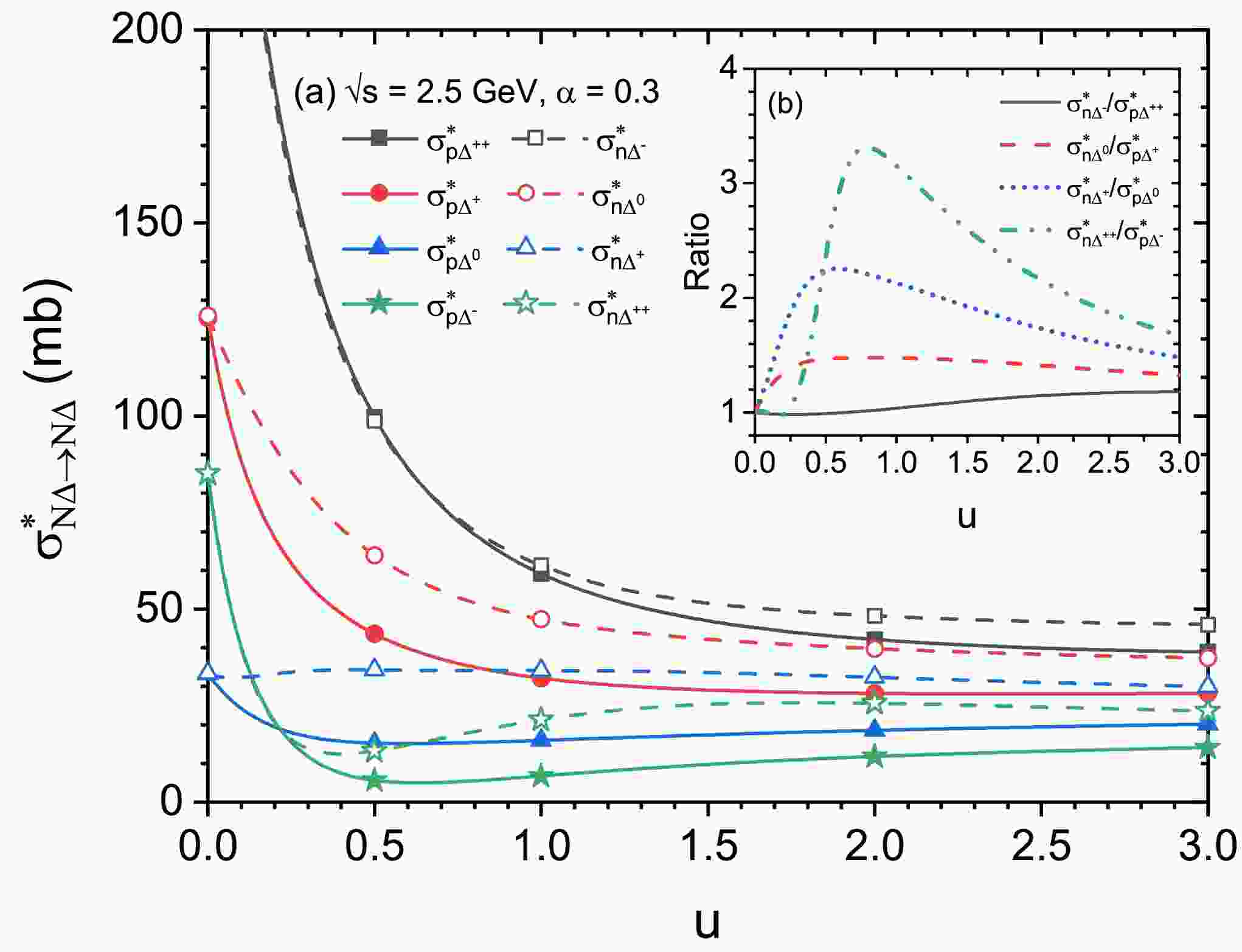
Figure 6.  (Color online) Panel (a): the individual $ N\Delta $ elastic cross sections at $ \sqrt{s} $= 2.5 GeV as a function of reduced density for asymmetric nuclear matter ($ \alpha $=0.3). The insert panel (b) shows the $ \sigma^{*}_{n\Delta^{-}} $/$ \sigma^{*}_{p\Delta^{++}} $, $ \sigma^{*}_{n\Delta^{0}} $/$ \sigma^{*}_{p\Delta^{+}} $, $ \sigma^{*}_{n\Delta^{+}} $/$ \sigma^{*}_{p\Delta^{0}} $, $ \sigma^{*}_{n\Delta^{++}} $/$ \sigma^{*}_{p\Delta^{-}} $ ratios.

In Fig. 4, the calculated cross sections as a function of $ \sqrt{s} $ for $ \alpha=0.0 $, 0.1, and 0.3 at u=1 are also shown by blue short dot, blue short dashed and blue solid lines, respectively. As the isospin asymmetry $ \alpha $ increases from 0.0 to 0.3, the individual cross sections of $ p\Delta $ channels are suppressed, while the individual cross sections of $ n\Delta $ channels are enhanced. A clear splitting between individual $ p\Delta $ and $ n\Delta $ channels can be found, due to the different effective mass splitting effect, on neutrons and protons, as well as differently charged $ \Delta $ particles. This splitting effect is also observed in the $ NN\rightarrow NN $, $ NN\rightarrow N\Delta $, and $ N\pi \rightarrow \Delta $ cross sections when $ \delta $ meson exchange is taken into account [26, 27, 44]. In addition, the variation in the isospin-dependent elastic cross section of $ n\Delta $ is relatively larger than that of $ p\Delta $, while the $ \sigma^{*}_{p\Delta^{++}} $ (panel (a)) and $ \sigma^{*}_{n\Delta^{-}} $ (panel (e)) show the weakest $ \alpha $ dependence among these eight channels.

To further see clearly the isospin dependence of $ \sigma^{*}_{N\Delta\rightarrow N\Delta} $ as shown above. The isospin-dependent ratio $ R(\alpha)=\sigma^*(\alpha)/\sigma^*(\alpha=0) $ of all channels for $ u = 1 $ at $ \sqrt{s} $=2.5 GeV is depicted in Fig. 5. It can be found that the $ R(\alpha) $ ratio deviates from unity (grey dotted line) and the ratio of $ p\Delta $ channels (solid symbols) is decreased while that for $ n\Delta $ channels (open symbols) is increased as $ \alpha $ increases from 0.0 to 0.3, since the contribution of $ \delta $ meson exchange to the effective masses of proton, neutron and $ \Delta $-isobars have opposite signs, and have a further influence on the individual cross sections [26]. And, the ratio follows that $ R(\alpha)_{n\Delta^{++}}>R(\alpha)_{n\Delta^{+}} > R(\alpha)_{n\Delta^{0}} > R(\alpha)_{n\Delta^{-}} > 1 > R(\alpha)_{p\Delta^{++}} > R(\alpha)_{p\Delta^{+}} > R(\alpha)_{p\Delta^{0}} > R(\alpha)_{p\Delta^{-}} $. At a higher isospin asymmetry parameter $ \alpha = 0.3 $, $ R(\alpha) $=2.02, 1.02, 0.98, and 0.64 for $ n\Delta^{++} $, $ n\Delta^{-} $, $ p\Delta^{++} $, and $ p\Delta^{-} $ respectively. Comparing these ratios with those of $ NN \rightarrow N\Delta $ and $ N\pi \rightarrow \Delta $ discussed in Refs. [26, 27], one can find that the isospin effect in $ N\Delta\rightarrow N\Delta $ channel should also not be negligible even at such a high $ \sqrt{s} $. Thus, the yields of $ \Delta $-isobars and its daughter pions, the charged-pion ratio in intermediate-energy HICs should be influenced by the isospin-dependent in-medium correction on the $ N\Delta $ elastic cross section, which comes from the isovector $ \rho $ and $ \delta $ meson fields [19, 26].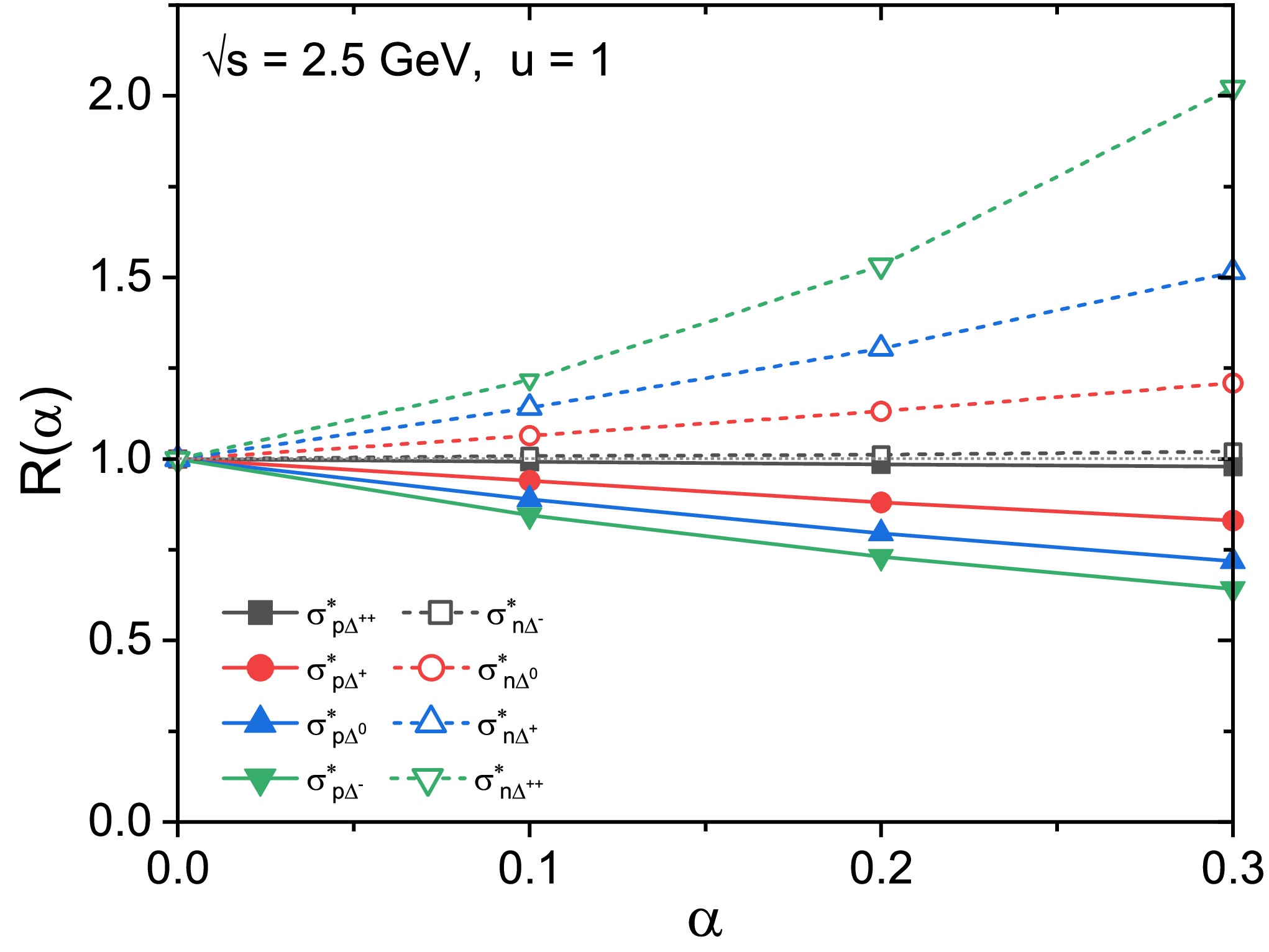

Figure 5.  (Color online) The $ R(\alpha)=\sigma^*(\alpha)/\sigma^*(\alpha=0) $ ratios of all channels as a function of the isospin asymmetry $ \alpha $ for u = 1 at $ \sqrt{s} $ = 2.5 GeV, the horizontal grey dotted line represents unity

Furthermore, as an extension to Fig. 4, the individual $ N\Delta $ cross sections for asymmetric nuclear matter ($ \alpha=0.3 $) at $ \sqrt{s} $ = 2.5 GeV as a function of reduced density is shown in Fig. 6(a). It is firstly seen that, the reduced density below about 0.5, the $ \sigma_{p\Delta^{++}(n\Delta^{-})}^{*} $ (black squares), $ \sigma_{p\Delta^{+}(n\Delta^{0})}^{*} $ (red circles) and $ \sigma_{p\Delta^{-}(n\Delta^{++})}^{*} $ (green stars) decrease rapidly with increasing density, while the $ \sigma_{p\Delta^{0}(n\Delta^{+})}^{*} $ (blue triangles) shows a much weaker dependence on the density. At the density above about 1.0, the density dependence of all individual cross sections gradually weakened, and finally leveled off. These irregular density-dependent behaviours of the individual $ N\Delta $ elastic cross sections can be explained by the integrated contributions of the spin and isospin matrices, the density-dependent coupling constants, and the density-dependent effective masses of nucleons and charged $ \Delta $s. Also, one can see that even within the range of 2-3 times normal density, there still exists obvious differences between the channels which have the same isospin matrix parameter sets but different effective masses, such as an obvious splitting in $ \sigma^{*}_{p\Delta^{++}} $ and $ \sigma^{*}_{n\Delta^{-}} $. This indicates that the influence of isovector $ \rho $ and $ \delta $ meson fields on the cross section is still visible at such a high density and can not be ignored. In addition, the related $ \sigma^{*}_{n\Delta^{-}} $/$ \sigma^{*}_{p\Delta^{++}} $, $ \sigma^{*}_{n\Delta^{0}} $/$ \sigma^{*}_{p\Delta^{+}} $, $ \sigma^{*}_{n\Delta^{+}} $/$ \sigma^{*}_{p\Delta^{0}} $, $ \sigma^{*}_{n\Delta^{++}} $/$ \sigma^{*}_{p\Delta^{-}} $ ratios are shown in the subgraph Fig. 6(b). For each ratio, both the numerator and denominator share the same isospin matrix set, as shown in Table 1. And the behaviours of these ratios vs density indicate that the influence of the splitting in the effective masses of nucleons and charged $ \Delta $s on the $ \sigma_{n\Delta^{++}}^{*}/\sigma_{p\Delta^{-}}^{*} $ (green dashed dot-dot line) is more pronounced than that of $ \sigma_{n\Delta^{+}}^{*}/\sigma_{p\Delta^{0}}^{*} $, then is the $ \sigma_{n\Delta^{0}}^{*}/\sigma_{p\Delta^{+}}^{*} $ and $ \sigma_{n\Delta^{-}}^{*}/\sigma_{p\Delta^{++}}^{*} $. It is understandable that the different coefficients of the contributions of the $ \delta $ meson field in Eq. 7 to the effective mass of proton, neutron, $ \Delta^{++} $, $ \Delta^{+} $, $ \Delta^{0} $, and $ \Delta^{-} $ result in different effects on the splitting in the effective masses of ingoing nucleon and $ \Delta $, and further influence the individual cross sections as well as their ratios.

Last, to accurately and conveniently describe the dynamics process of HICs and understand the properties of dense nuclear matter, the two-body cross section should be treated carefully in microscopic transport models. However, due to the complex nature of cross sections, the parameterized formulas based on some theoretical calculations are commonly adopted in relevant models, such as the density- and energy-dependent formula for the NN cross section proposed by Ref.[70] and used in Isospin-dependent quantum molecular dynamics model [71], the parameterized NN elastic and inelastic cross sections used in the Giessen Boltzmann–Uehling–Uhlenbeck model [55] and the relativistic Vlasov-Uehling-Uhlenbeck model [19]. Here, based on the above calculations within the RBUU theoretical framework, a parametrization for the energy ($ \sqrt{s} $)-, density (u)-, and isospin ($ \alpha $)-dependent $ N\Delta $ elastic cross section is proposed, which reads as

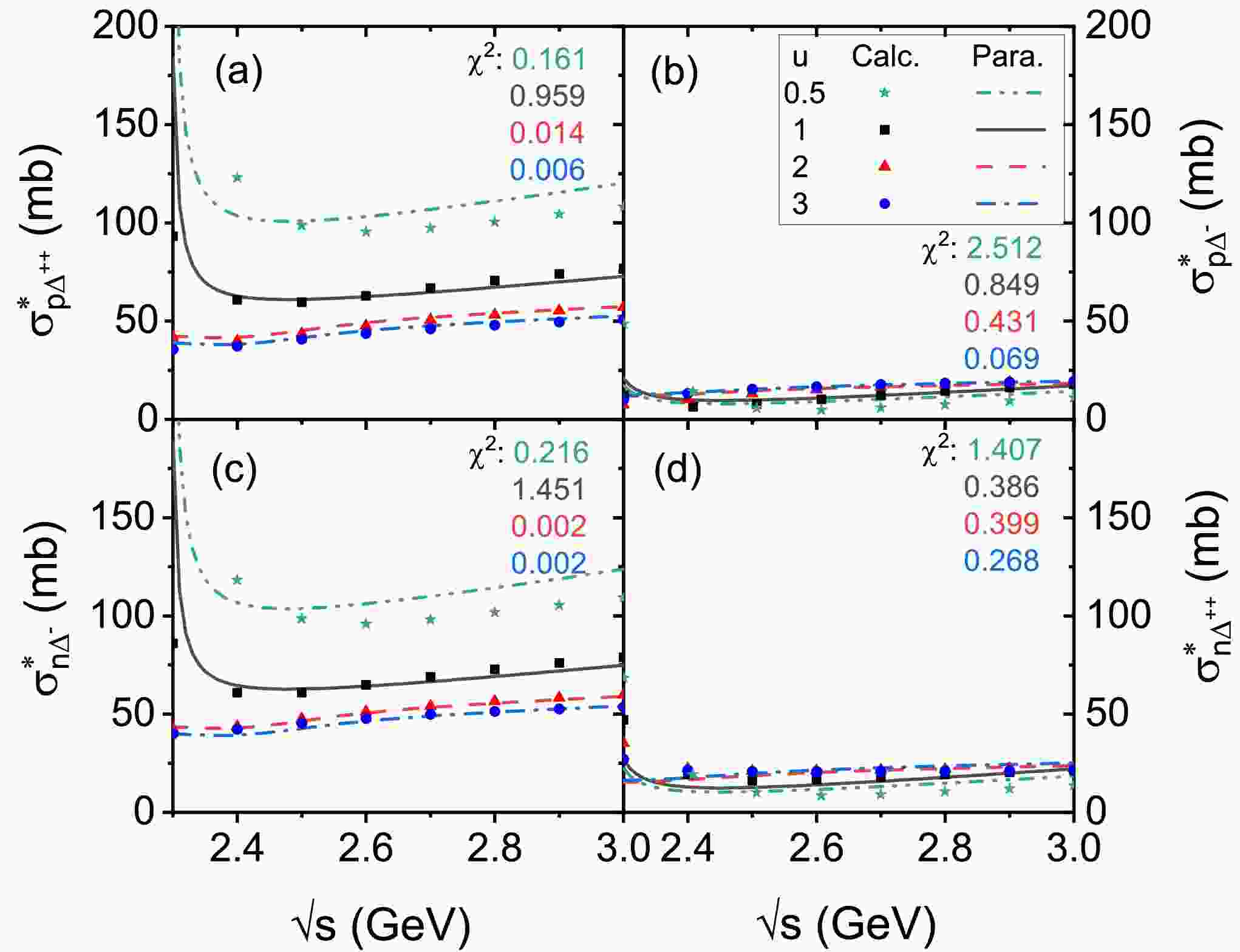
where the a to l are the adjustable parameters for each individual channel, and $ \sqrt{s} $ is in the unit of GeV. The energy, density, and isospin dependence of the $ \sigma^{*}_{N\Delta} $ can be given by the three parts of the parametrization in the brackets in sequence, respectively. Figure 7 gives the comparison of the theoretically calculated results (symbols) to the parametrization results (lines) of $ \sigma^{*}_{p\Delta^{++}} $, $ \sigma^{*}_{p\Delta^{-}} $, $ \sigma^{*}_{n\Delta^{-}} $, and $ \sigma^{*}_{n\Delta^{++}} $ at u=0.5, 1, 2, and 3 with $ \alpha $=0.2, respectively, the $ \chi^2 $ values are shown in each panel with corresponding colours, and the adjustable parameter sets of Eq. 15 for these four channels are shown in the App. B. It is seen that the parametrization can well reproduce the microscopic calculation results within the c.m. energy region of $ 2.3 \leq \sqrt{s} \leq 3 $ GeV and the density range $ 0.5 \leq u \leq 3 $ at $ \alpha $=0.2, which indicates that the proposed formula provides a reliable description of cross section within a wide range of energy, density, as well isospin asymmetry, and can serve as a trustworthy input for transport model simulations of HICs.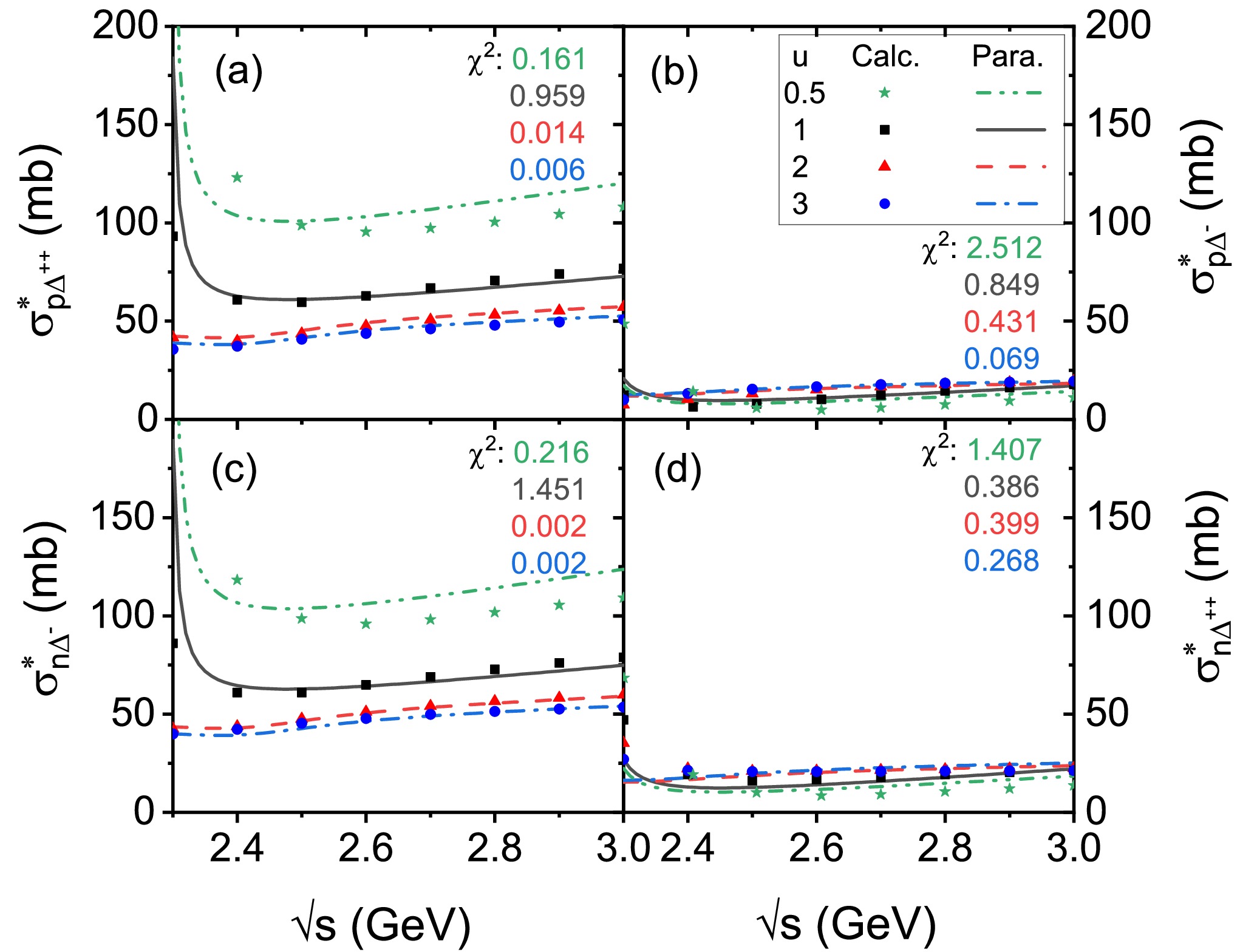

Figure 7.  (Color online) The $ \sigma^{*}_{p\Delta^{++}} $ (a), $ \sigma^{*}_{p\Delta^{-}} $ (b), $ \sigma^{*}_{n\Delta^{-}} $ (c), and $ \sigma^{*}_{n\Delta^{++}} $ (d) as functions of the c.m. energy at u = 0.5 (stars), 1 (squares), 2 (triangles) and 3 (circles) with $ \alpha=0.2 $, respectively. The calculation results based on the RBUU approach are represented by the symbols, while the parametrization results of Eq.15 are represented by lines.

In this work, the energy-, density- and isospin-dependent $ N\Delta \rightarrow N\Delta $ elastic cross section $ \sigma^{*}_{N\Delta} $ is calculated based on the density-dependent relativistic hadron field theory within the RBUU theoretical framework, in which the isovector $ \delta $ meson field is further considered. The calculation results show that the decay width of $ \Delta $ has a significant influence on the $ \sigma^{*}_{N\Delta} $ at lower energies ($ \sqrt{s}\lesssim $ 2.2 GeV), while at higher energies ($ \sqrt{s}\gtrsim $ 2.2 GeV), the cross section becomes rather weakly dependent of the $ \Delta $ resonance decay width. The total $ \sigma^{*}_{N\Delta} $ is suppressed with increasing reduced density, and both $ \rho $ and $ \delta $ meson related exchange terms have non-negligible contributions to $ \sigma^{*}_{N\Delta} $. By further analysing the contribution of each $ \rho $ and $ \delta $ meson related exchange terms to the $ \sigma^{*}_{p\Delta^{++}} $, it is found that there exists a significant cancellation effect among these meson exchange terms, due to the delicate balance of isovector $ \rho $ and $ \delta $ meson related terms. Importantly, by including the $ \delta $ meson field, the individual $ \sigma^{*}_{N\Delta} $ exhibit an obvious isospin asymmetry dependence, mainly due to the splitting in the effective masses of nucleons and $ \Delta $ particles. And, as $ \alpha $ increases, the $ p\Delta $ related cross sections are suppressed, while the $ n\Delta $ related cross sections are enhanced. Furthermore, the isospin effect introduced by the isovector $ \rho $ and $ \delta $ meson fields still has an unignorable effect on the individual $ N\Delta $ elastic cross section even at 2-3 $ \rho_{0} $. In addition, a reliable parameterized formula of the energy-, density-, and isospin-dependent $ N\Delta $ cross section is proposed.

In the near future, the effects of the canonical momenta correction and the threshold effect will be further uniformly considered, and the parameterized formula for the $ N\Delta \rightarrow N\Delta $ cross section will be improved and introduced into the UrQMD model to get a more comprehensive understanding of the production, evolution, and decay of the $ \Delta $ particles in heavy-ion collisions at intermediate energies, since they are critical to making more reliable constraints on the high-density nuclear equation of state by pion related observables from HICs.

The authors are grateful to the C3S2 computing center in Huzhou University for calculation support.

In this appendix, the analytical expressions of the collision terms of $ \Delta $'s RBUU equation are presented. For the spin matrices of $ N_{2}\Delta \rightarrow N_{4}\Delta_{3} $ scattering, the scalar-scalar $ D_{11} $, vector-vector $ D_{12} $, scalar-vector $ D_{13} $ meson exchange components in differential cross section are represented as:

Correspondingly, the $ D_{1-10} $ can be expressed as follows:

where s, t, and u are Mandelstam variables, are defined as:

The scattering angle in the c.m. system is $ \theta $, and