Double-folding analysis of elastic and inelastic ³He-nucleus scattering at 60 MeV

Understanding nucleus-nucleus interactions remains a fundamental challenge in nuclear physics. All observable scattering quantities can be computed once the optical potential is defined—and, consequently, the scattering matrix is determined. For heavy-ion collisions, microscopic models, particularly the double-folding method, have been among the most successful approaches for calculating optical potentials [1-6]. This method relies on two key inputs: (1) the nuclear densities of the colliding nuclei and (2) an effective nucleon-nucleon (NN) interaction between projectile and target nucleons. While nuclear densities can be accurately derived from models or electron scattering experiments, developing a realistic, effective NN interaction remains an open problem [7, 8].

Despite extensive theoretical and experimental efforts, the nature of effective NN interactions remains incompletely understood. Recent progress has been made through relativistic mean-field (RMF) theory, which has yielded new microscopic NN interactions (e.g., R3Y(HS), R3Y(L1), R3Y(W), and Z). The NN interaction obtained in this theory was remarkably related to the inbuilt fundamental parameters of RMF where the HS, L1, W and Z parameters have been extensively validated in the literature for reproducing nuclear ground-state properties, such as binding energies, charge radii, and deformation parameters [9, 10]. These interactions have been successfully applied to cluster radioactive decays [11, 12] and were used to investigate the elastic scattering cross-sections of proton and neutron halo nuclei [7] and the analysis of ⁶Li(3He,d)⁷Be transfer reaction [13]. However, further validation is needed, particularly in intermediate-energy scattering, where nuclear and Coulomb forces play significant roles.

One of the primary sources of knowledge about the characteristics of the ground and low-lying excited states of atomic nuclei is the study of the elastic and inelastic processes of helium isotope ³He interaction with nuclei [14]. Over the past few decades, researchers have extensively investigated ³He scattering on light nuclei at energies reaching 150 MeV [15-23]. The energy range of the incident particles can be classified into three major categories. The first includes energies below 15-20 MeV. In this range, the Coulomb interaction is the dominant scattering determinant, and the nucleus's inner region does not affect differential cross-sections. In the second category, nuclear forces become relevant with incident particle energies of 20-40 MeV. As a result, the scattering takes on a different character and a diffraction pattern appears in the angular distributions, similar to that of an absorbing sphere. Lastly, the ³He scattering properties change at energies greater than 40 MeV. Recently, elastic-scattering data of ³He on ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si at 60 MeV have been used to experimentally determine the parameters of the optical potentials [19, 22, 24, 25].

This work investigates ³He elastic and inelastic scattering from ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si at 60 MeV using a double-folding model with RMF-derived NN interactions. Specifically, we aim to evaluate the performance of R3Y(HS), R3Y(L1), R3Y(W), and R3Y(Z) interactions in reproducing elastic scattering data; examine the impact of NN interaction regularization and exchange potentials on cross-section predictions; determine the optimal NN interaction and associated parameters for describing ³He scattering; compare the deformed potential (DP) and double-folding (DF) models for inelastic scattering to excited states; and investigate the sensitivity of inelastic scattering descriptions to the choice of transition potential model and the relevance of the Bohr-Mottelson and Tassie models for describing collective nuclear excitations. The theoretical framework is presented in Section 2. The results of the calculations are given in Section 3, analyzing scattering observables obtained from the double-folding model for the various target nuclei and discussing the sensitivity of the results to model parameters and associated uncertainties. Finally, Section 4 summarizes the key findings, discusses their implications for our understanding of ³He-nucleus scattering, and outlines potential avenues for future research.

In the double-folding approach, the real part of the optical potential is generated by folding the matter density of the projectile and the target with an effective NN interaction [26]. The folded potential could be expressed as follows:

where $ {V}^{D} $ and $ {V}^{EX} $ are the direct and exchange potentials, respectively. The direct part of the folded potential, representing the nuclear interaction independent of nuclear spins and isospins, takes the following form:

where $ {\rho }_{p,t} $ are the nuclear matter densities of the projectile and target, respectively. $ {v}_{NN}^{D} $ is a direct part of the NN effective interaction. The exchange part $ {V}^{EX} $, which considers the effect of a single knock-on exchange, has two forms; the first has the form [1]:

where, $ {\widehat{J}}_{00}\left(E\right) $ represents the strength of the exchange term, which exhibits a weak linear dependence on energy. The Dirac delta function $ \delta \left(s\right) $ ensures the interaction is local, effectively transforming it into a zero-range pseudo-potential. This form is widely used in heavy-ion scattering studies. The knock-on interaction $ {J}_{00}\left(E\right)\delta \left(s\right) $ is a semi-phenomenological formula that requires calibration for both nucleon-nucleus and nucleus-nucleus scattering.

A more rigorous and theoretically grounded approach to approximating the exchange potential has been proposed as an alternative to the simpler, semi-phenomenological approach of the first form [1]. This approach explicitly accounts for the finite range of the interaction. Although this form is non-local, it has been demonstrated [27, 28] that an accurate local approximation could be obtained by treating the relative motion locally as a plane wave, yielding the following expression:

with,

and

where $ K\left(r\right) $ is the local momentum of relative motion. This exchange form involves a self-consistency problem, which could be readily solved using a realistic approximation for the density. The potential is then evaluated using an iterative method [26], yielding a local self-consistent potential.

There are several types of effective NN interactions. These interactions were phenomenological, derived by fitting experimental scattering data and phase shifts. New microscopic NN interactions were derived from RMF theory. A relativistic mean-field Lagrangian density of a nucleon-meson many-body system was assumed [29-31], which was constructed from the Lagrangian density of Dirac spinor fields for the nucleons, four different meson fields (σ, ω, ρ, δ) and the electromagnetic field due to the interaction of the charged particles. Assuming a heavy and static baryonic medium with a one-meson exchange, the solution of single NN potential for scalar (σ, δ) and vector (ω, ρ) fields was determined. The resultant effective NN interactions were obtained from the summation of the scalar and vector parts of the single meson fields and were defined as [11]

where $ {g}_{\sigma } $, $ {g}_{\omega } $ ,$ {g}_{\rho } $ and $ {g}_{\delta } $ are the coupling constants for σ, ω, ρ and δ mesons, respectively. $ {m}_{\sigma } $, $ {m}_{\omega } $ ,$ {m}_{\rho } $ and $ {m}_{\delta } $ are the masses of σ, ω, ρ and δ mesons, respectively. For a standard nuclear medium, the contribution $ {V}_{\delta } $ of δ meson could be neglected, compared to the magnitudes of both $ {V}_{\omega } $ and $ {V}_{\sigma } $, then Eq. 10 took the form:

The derived NN interaction from RMF theory was inserted into Eq. 4 to obtain a real direct folded potential based on RMF. Using the R3Y(HS) parameters from Table 1 in Eq. 11 as illustrative examples, one could obtain the following:

Set	$ {m}_{\sigma } $ (MeV)	$ {m}_{\omega } $ (MeV)	$ {m}_{\rho } $ (MeV)	$ {g}_{\sigma } $	$ {g}_{\omega } $	$ {g}_{\rho } $	$ {{g}_{\omega }}^{2}/\pi $ (MeV)	$ {{g}_{\rho }}^{2}/\pi $ (MeV)	$ {{g}_{\sigma }}^{2}/\pi $ (MeV)
R3Y(HS)	520	783	770	10.47	13.80	08.08	11956.94	4099.06	6882.64
L1	550	783	−	10.30	12.60	−	9967.88	−	6660.95
W	550	783	−	09.57	11.67	−	8550.74	−	5750.24
Z	551.31	780	763	11.19	13.83	10.89	12008.98	7445.91	7861.80

Table 1.  The parameters of effective NN interactions are based on Eq. 11 for different RMF models [11].

An essential aspect of using the effective NN potentials in the form of Yukawa potential was related to their regularization due to singularities. This regularization aimed to eliminate the singularities at $ \left|s\right|=0 $, which lacked physical significance. While the singularity could have impacted the analysis of nucleon-nucleon scattering, it did not pose any challenges when calculating the folding integral for generating the nucleon-nucleus or nucleus-nucleus potential. However, certain studies (e.g., [32, 33]) utilized "regularized" M3Y potentials of the NN interaction that did not include the singularity mentioned. In this study, we explored this issue further. Such problems could be attributed to the breakdown of the meson theory at extremely short distances, which was caused by the extended structure of nucleons [34]. The one-boson-exchange potentials are commonly regularized by incorporating several cut-off factors, such as monopole, dipole, and exponential cut-off form factors [35]. In this work, the approach of [33] was followed. The regularized Yukawa function $ {\phi }_{c} $ was derived from the Fourier transform to configuration space through the incorporation of a momentum cut-off form factor $ F\left(\overrightarrow{p}\right) $,

The cut-off form factor was defined as the nucleon form factor $ {\rho }_{N}\left(p\right) $,

After some transformations, we obtain for the regularized Yukawa function $ {\phi }_{C}\left(r\right) $ the expression [36]

Then, the regularized effective NN potential, which consist of three Yukawa function, could be written in the regularized form as [33],

where $ {\rho }_{N}(\vec{r}) $ is the nucleon density distribution, which was parameterized based on experimental data in [37] using a sum of Gaussian functions:

In addition to the effective NN interaction, the folding calculation required nuclear density distributions for the colliding nuclei. The nuclear matter density distribution of the projectile nucleus ³He was assumed to follow a Gaussian distribution (GD),

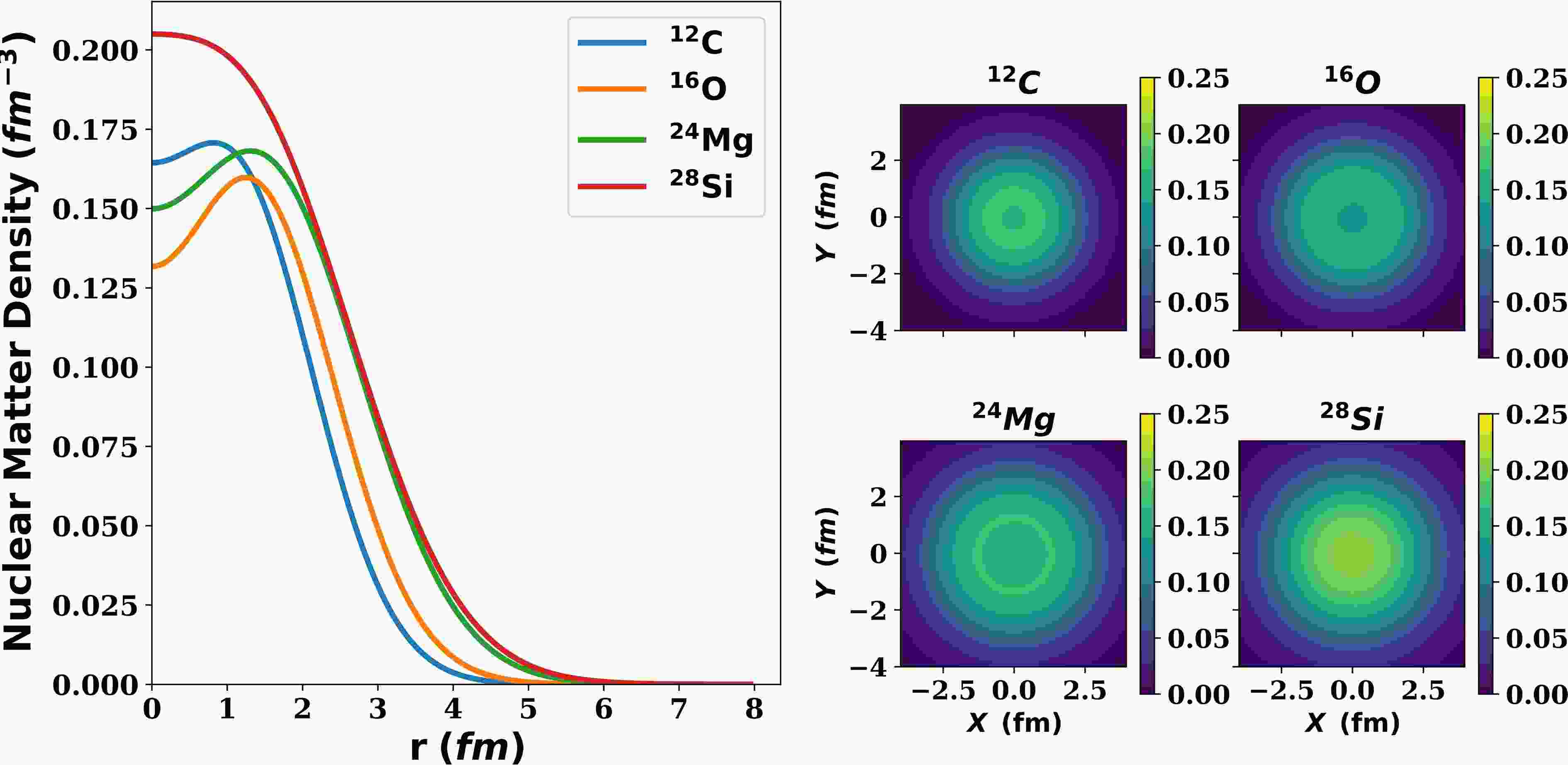
For the target nuclei, the densities were assumed to follow modified Gaussian distributions (MGD), which exhibited a nuclear bubble structure [43], see Figure 2,

Figure 2.  (color online) The right panel shows the radial nuclear matter densities of ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si nuclei. The left panel shows 2D nuclear matter distributions.

where $ {\rho }_{M}\left(0\right) $ values were obtained from the normalization condition:

the parameters for $ {\rho }_{M}\left(0\right) $ , ω and β used in Eq. 17 and 18 are given in Table 2.

An imaginary potential (W) was introduced into the optical potential to accommodate absorption into alternative reaction channels. Since surface absorption was determined to predominate within this energy range, the imaginary potential was modelled as a surface potential. Two forms of the imaginary potential were used. The first form consisted of a phenomenological potential obtained from the first derivative of a Woods-Saxon (WS) potential,

The second form was formulated based on the first derivative of the obtained folded potential itself and is expressed as follows:

where $ a $ is the diffuseness parameter of the folded potential, obtained by fitting the folded potential to a WS form. $ {N}_{I} $ is a normalization constant introduced for scaling purposes. The second form was employed to reduce the number of free parameters and provide a less ambiguous method for examining the different effective interactions.

Finally, the local optical potential took the form,

here, the real component of the optical potential, denoted as $ {V}^{DF} $, was scaled by a normalization factor $ {N}_{R} $. This normalization factor was incorporated to accommodate minor adjustments required to address dynamic polarization contributions, higher-order effects omitted in the methodology employed to derive the folded potential, and slight uncertainties inherent in the folding inputs. It was anticipated that this factor would remain proximate to unity, affirming the folded potential's physical significance. The Coulomb potential, $ {V}_{C} $, describing the interaction between the projectile and the target, was assumed to correspond to the interaction between a point particle and a uniformly charged sphere with radius $ {R}_{C} $. Accordingly, the Coulomb potential is expressed as follows:

The optical potentials can be characterized by real $ {J}_{V} $ and imaginary $ {J}_{W} $ volume integrals per nucleon defined as,

For inelastic scattering, the 2^λ -pole component of the transition potential $ {U}_{\lambda } $ is

In the DF model, the real part of the transition potential of the inelastic scattering is taken to be:

where $ {\left({V}_{C}\right)}_{\lambda } $ is Coulomb's transition potential. $ {V}_{\lambda }^{D} $ and $ {V}_{\lambda }^{EX} $ are direct and exchange transition potentials, respectively. The transition potential was obtained by folding the transition density $ {\rho }_{t}^{\left(\lambda \right)} $, which describes the inelastic excitation of the target nucleus, with the ground-state density of the projectile and the effective interaction as [2],

A simple "collective" model is usually used when the excitation is "isoscalar" and strong [44]. In this work, the Bohr–Mottelson (BM) model [45] was adopted, in which the radial transition density (with $ \lambda \ge 2) $was assumed to be proportional to the radial derivative of the ground-state density,

where $ {\beta }_{\lambda }^{m} $ is the matter deformation parameter, and R is the nucleus radius, which is taken to be $ R=1.2{A}^{1/3}fm $ [2].

In the deformed potential (DP) model, the radial transition potential was taken to be proportional to the radial first derivative of the normalized folded potential,

where $ {\beta }_{\lambda }^{V} $ is the deformation parameter of the folded potential $ {V}_{\lambda }\left(r\right) $. To compare the DP model with the DF approach for the inelastic form factor, it was assumed that,

The deformed imaginary part $ {W}_{\lambda } $ was taken as the deformed surface WS of the phenomenological imaginary elastic scattering potential [46],

then $ {W}_{\lambda } $ had the form [47],

The deformation parameter of the imaginary potential served as a measure of absorption in the considered channel. In this approach, the Coulomb deformation was not included; only the nuclear part of the transition potential was considered. The deformation parameter was typically adjustable and was determined by comparing the computed inelastic cross-section with the observed data. In both models, it was assumed that the real and imaginary deformations were equal,

Since all deformation parameters were derived by modifying the potentials, they should be denoted as $ {\beta }^{\left(pot\right)} $. However, for simplicity, they will be referred to as β. All the DF calculations were performed using a modified version of BiFold code [48]. The code originally calculates the density-dependent or independent DF potentials between two colliding spherical nuclei. The modifications extend the code's capability to calculate the transition potentials based on Eq. 29 and Eq. 30.

In this work, a double-folding analysis of ³He elastic and inelastic scattering off ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si at 60 MeV was performed. The experimental data for elastic and inelastic differential cross-sections were taken from [19, 22, 24, 25].

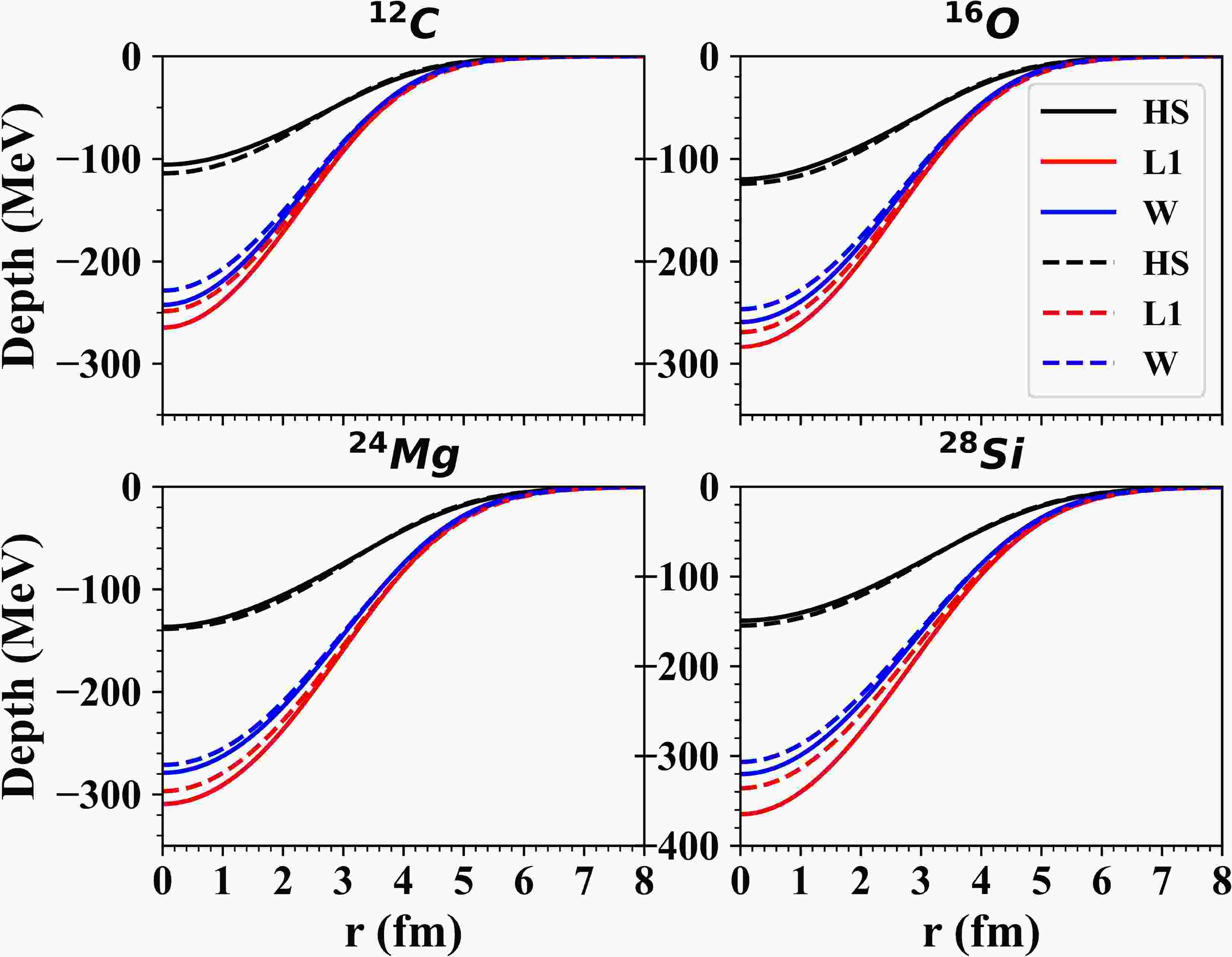
The angular distributions of the elastic and inelastic scattering were calculated using the DF approach. The real part of the optical potential was calculated using new effective NN interactions, and the imaginary part of the optical potential was assumed to have two forms: a surface WS and the first derivative of the folded potential. First, the effective NN interactions were regularized to consider the effect of regularization on the nucleus-nucleus potential. The present work used four effective NN interactions obtained from the RMF model (R3Y(HS), R3Y(L1), R3Y(W), and Z) to examine their validity in describing the elastic and inelastic scattering of light projectiles and to investigate their effects on the nucleus-nucleus scattering. Figure 1 illustrates the effective NN interactions before and after the regularization. The cut-off form factor's impact on the effective NN interactions removed the singularity. It preserved the potential behavior, which was repulsive at the core and attractive as the separation increased. The depth of the regularized interactions was observed to be reduced (about 30% of their original value). At the core, the R3Y(Z) interaction had the largest repulsive strength, followed by the R3Y(HS) interaction and then the R3Y(L1) and R3Y(W) interactions.

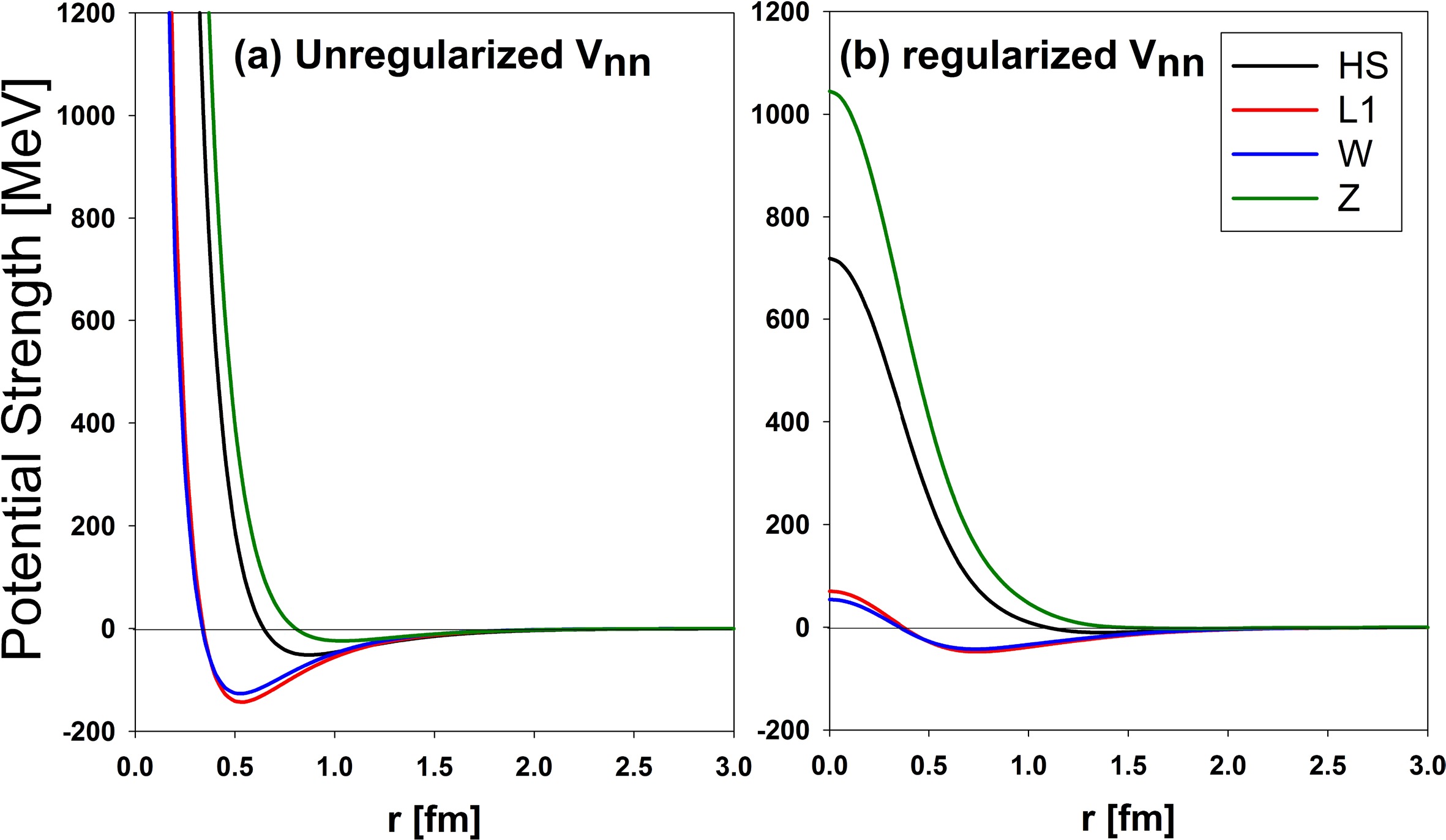
Figure 1.  (color online) Comparison of (a) unregularized effective NN potentials and (b) regularized effective NN potentials. The impact of regularization on the shape and strength of the potentials is illustrated.

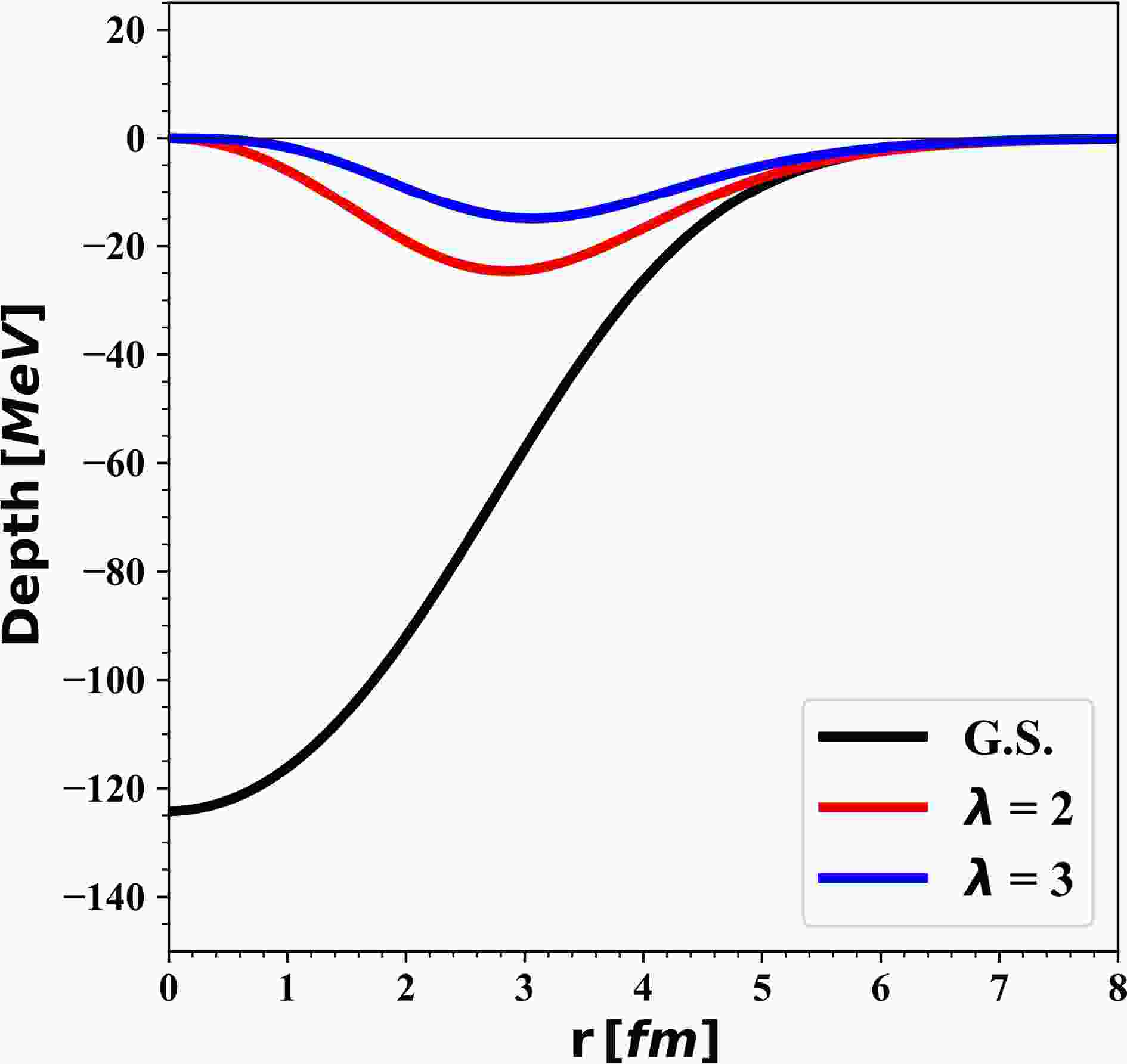
Second, the regularized effective interactions were folded with the nuclear matter densities for ³He and target nuclei. The direct component of folded potentials exhibited a repulsive nature for R3Y(HS) and R3Y(Z) interactions, similar to the DF potentials derived from the M3Y Paris interaction [1]. For R3Y(L1) and R3Y(W) interactions, the direct component of folded potentials was attractive, similar to the DF potentials derived from the M3Y Reid interaction [1]. The exchange part of the folded potential was added to the direct part. The study explored the effects of employing both zero-range and finite-range exchange interactions within the potential model. Zero-range exchange interactions produced a deeper total folded potential than finite-range exchange interactions, requiring a small normalization constant to fit the differential cross-section data. Therefore, considering the finite-range exchange interactions, the direct potentials were combined with the exchange potential, resulting in a combination denoted as R3Y+EX(FR). An additional examination of the exchange potential was conducted with both Reid and Paris finite exchange interactions. For the R3Y(HS) interaction, the direct part R3Y(HS) was combined with both EX(FR/Reid) and EX(FR/Paris) to obtain R3Y(HS)+EX(FR/Reid) and R3Y(HS)+EX(FR/Paris), respectively. The generated total folded potential based on the Reid interaction was very shallow, making it unsuitable. The obtained shallow potential was similar to [7]; the author used the Reid EX(ZR), and one can see in Figure 2 in [7] that the folded potential R3Y(HS)+EX(ZR/Reid) had the smallest depth. Conversely, combining the exchange potential based on the Paris interaction with the direct part of R3Y(HS) produced a more suitable potential than the Reid exchange. For R3Y(L1) and R3Y(W) interactions, It was found that using the Reid finite exchange potential to generate the total folded potential R3Y(L1)+EX(ZR/Reid) and R3Y(W)+EX(ZR/Reid) was the best choice. The analysis revealed that the folded potential generated by R3Y(Z)+EX(FR) exhibited a repulsive characteristic, with the majority of the contribution arising from the direct component of the potential (see Fig. 3). Therefore, The R3Y(Z) interaction was excluded from this analysis because a purely repulsive potential for the ³He-nucleus scattering is considered physically meaningless within this energy range. The direct, exchange and total potentials for ¹²C were plotted in Figure 3.

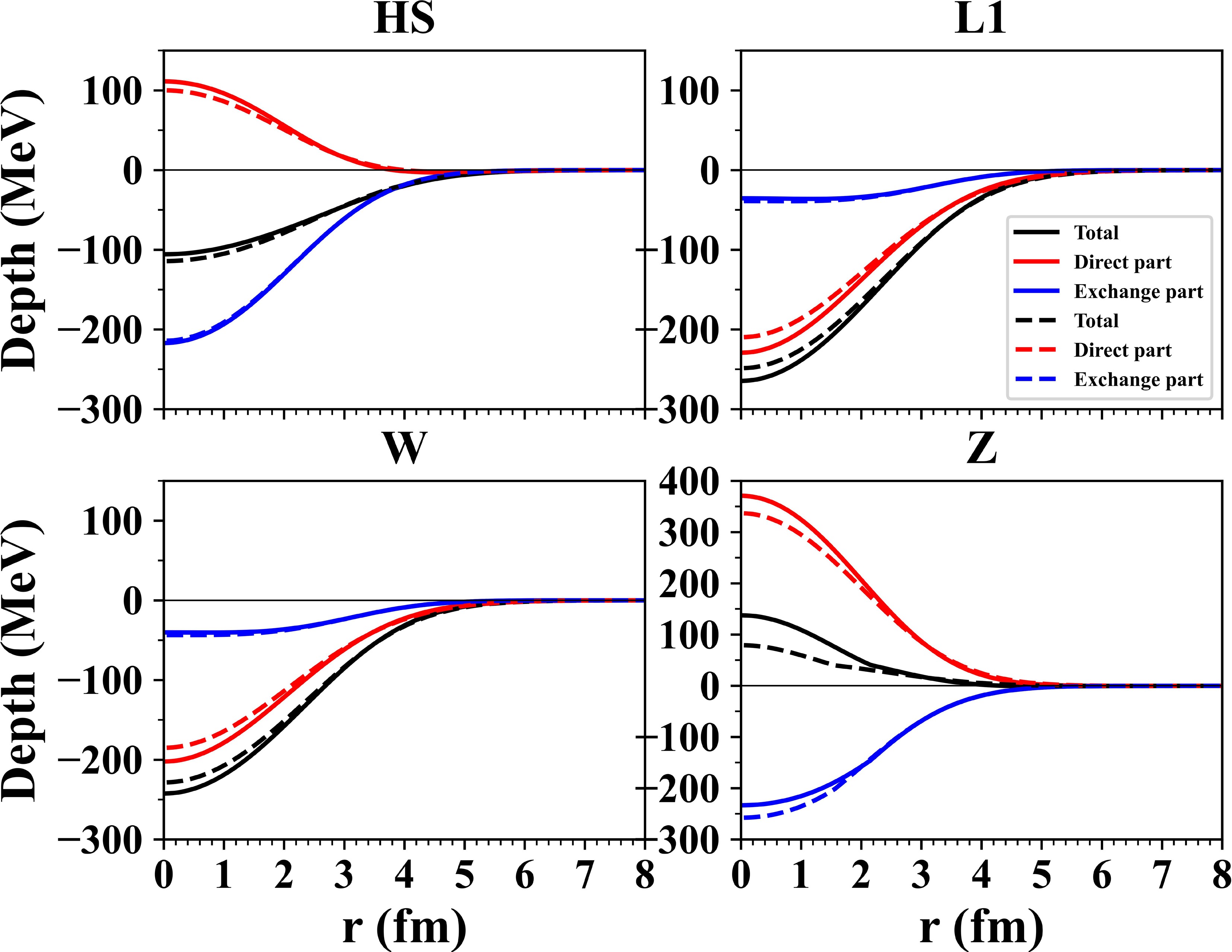
Figure 3.  (color online) The Folded potential for ³He+¹²C at 60 MeV based on unregularized (Solid line) and regularized NN effective interactions (Dashed line). Paris exchange interaction is used for R3Y(HS) and R3Y(Z), whereas Reid exchange potential is used for R3Y(L1) and W. The colored lines represent the total, direct, and exchange potentials for R3Y+EX(FR).

Folded potentials, obtained from regularized effective NN interactions, were examined to investigate how regularization affects nucleus-nucleus scattering. The regularization decreased the direct portion of the folded potential while marginally boosting the exchange portion, resulting in an overall rise in the R3Y(HS) folded potential and decreases in the R3Y(L1) and R3Y(W) folded potentials. The repulsive nature of the folded potential based on the R3Y(Z) interaction remained unchanged by regularization, reinforcing our choice to exclude R3Y(Z) from this analysis. The total folded potentials for ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si are illustrated in Figure 4.

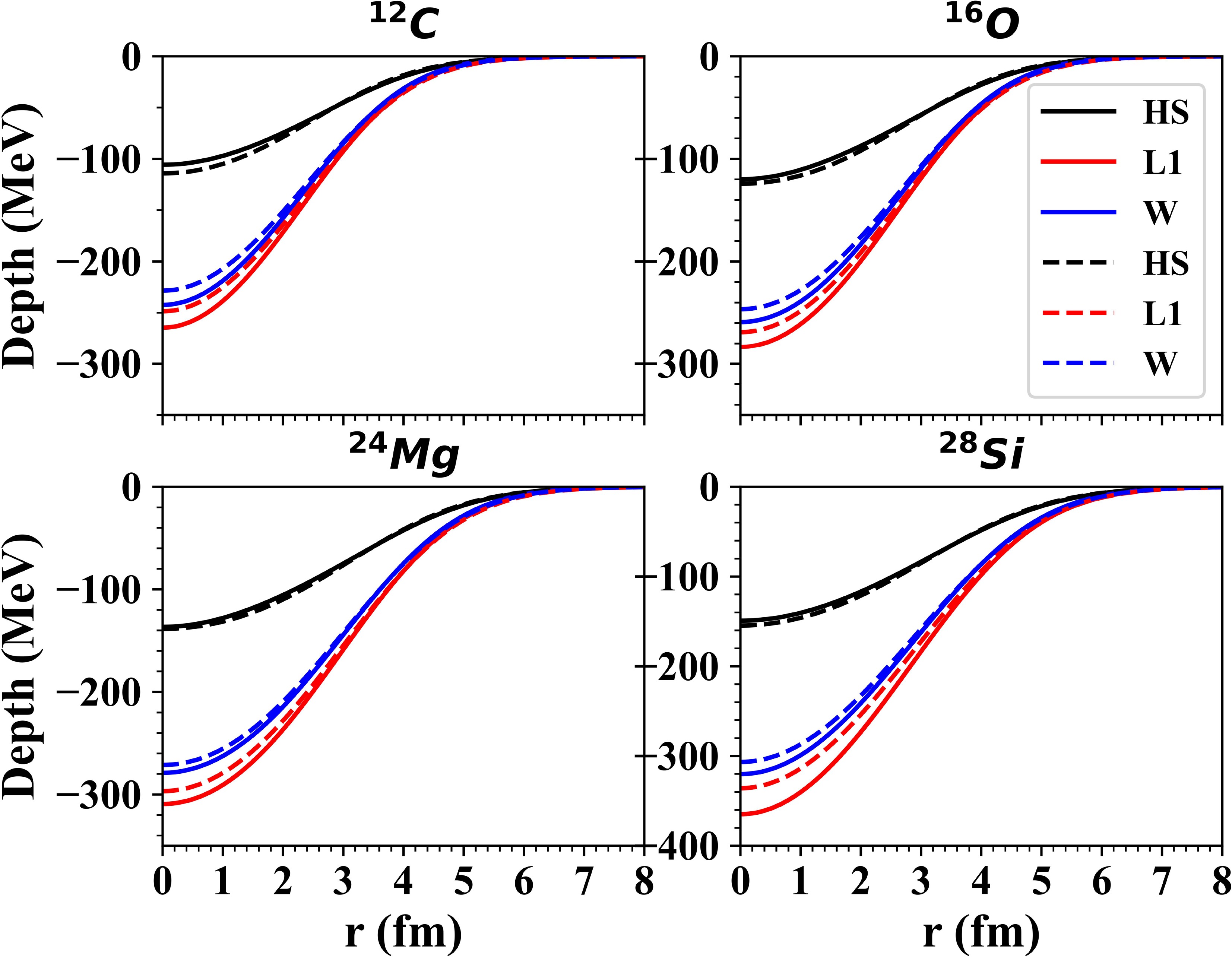
Figure 4.  (color online) The unnormalized folded potentials R3Y(HS)+EX(ZR/Paris) and R3Y(HS)+EX(ZR/Reid) for ³He+¹²C, ³He+¹⁶O, ³He+²⁴Mg, and ³He+²⁸Si at 60 MeV based on unregularized (solid lines) and regularized (dashed lines) effective NN interactions obtained from the RMF model.

Next, Calculations were carried out to obtain the elastic scattering cross-sections of the ³He+¹²C, ³He+¹⁶O, ³He+²⁴Mg, and ³He+²⁸Si systems at 60 MeV. The folded potentials served as the real component of the optical potentials, while surface WS or the derivative of the folded potential were used as the imaginary components. The a's values used to derive the imaginary potentials from the folded potentials based on Eq. 21 and its equivalent Woods-Saxon (WS) parameters are listed in Table 3.

Reaction	$ {V}_{NN} $	$ V $ (MeV)	$ R $ (fm)	$ a\pm \mathrm{\Delta }a $ (fm)
3He+12C	HS	−121.10	2.5412	0.8404±0.0022
	L1	−264.84	2.4338	0.8364±0.0030
	W	−242.97	2.4393	0.8303±0.0029
3He+16O	HS	−130.51	2.7806	0.8694±0.0023
	L1	−283.92	2.6631	0.8701±0.0032
	W	−259.70	2.6732	0.8632±0.0032
3He+24Mg	HS	−144.81	3.1105	0.9453±0.0028
	L1	−311.68	2.9864	0.9464±0.0036
	W	−284.34	3.0010	0.9393±0.0035
3He+28Si	HS	−162.70	3.0941	0.9885±0.0032
	L1	−356.57	2.9348	0.9926±0.0039
	W	−324.94	2.9497	0.9866±0.0038

Table 3.  Parameters of Woods-Saxon potentials equivalent to folded potentials based on the regularized NN interactions R3Y(HS)+EX(FR/Paris), R3Y(L1)+EX(FR/Reid) and R3Y(W)+EX(FR/Reid).

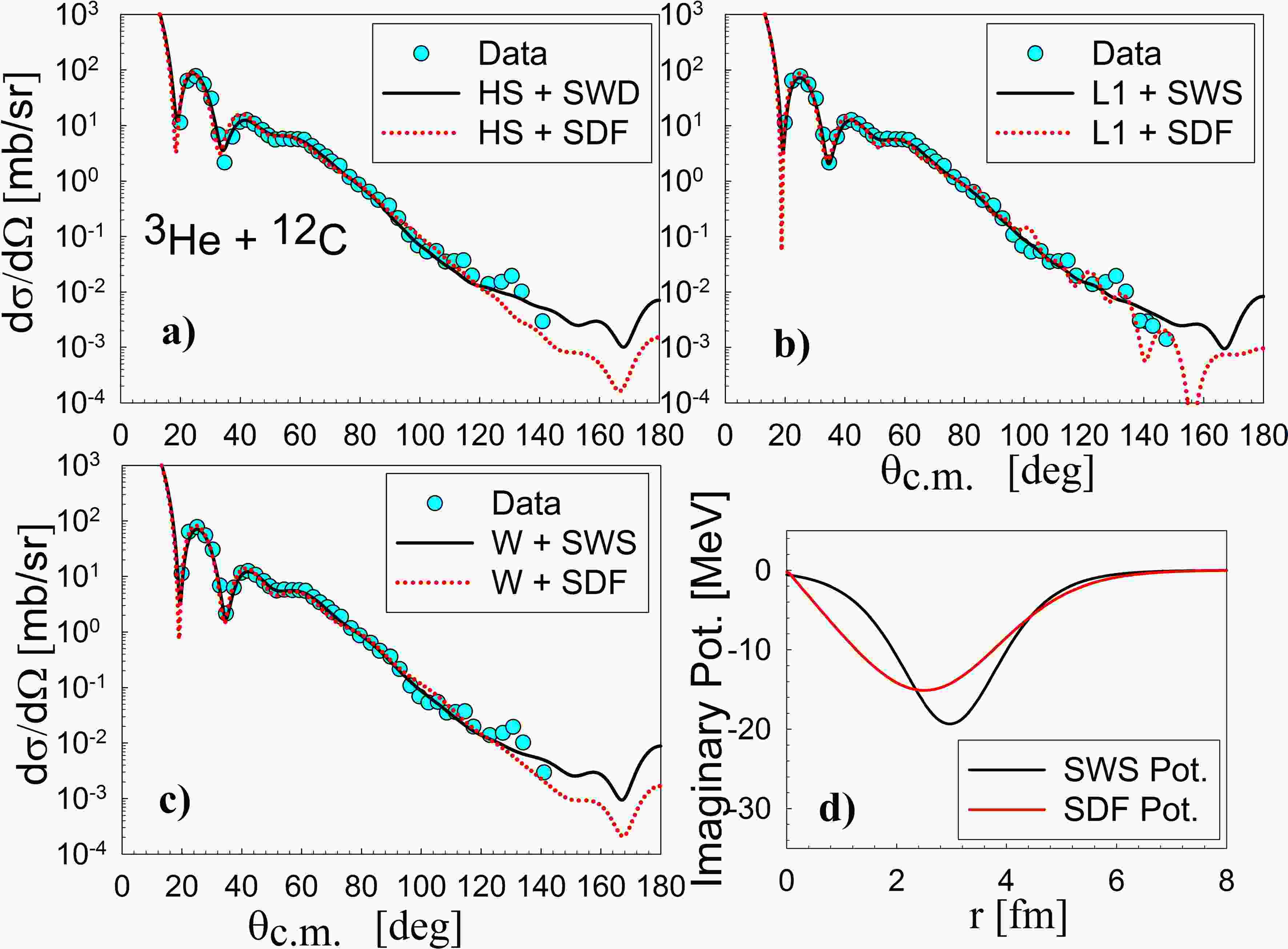
Table 4 identifies the optimal parameter set (including normalization and imaginary potential parameters) for describing elastic scattering. The folded potentials, derived from regularized interactions, effectively fit the experimental data, as shown in Figure 6. For the ³He+¹²C system, Figure 5 illustrates how the imaginary component influences the differential cross sections, with the SWS outperforming the SDF. This outcome is expected because the SWS incorporates more adjustable parameters—such as depth, radius, and diffuseness of the potential - while the SDF is restricted to a single parameter $ {N}_{I} $ that only adjusts the potential's depth. Additionally, a limitation of the SDF is its lack of a microscopic foundation and the use of a fixed geometry that may not adequately reflect the absorption process. The assumption that the imaginary part is proportional to the real folded potential part is somewhat arbitrary, employed here merely to simplify the parameter count and facilitate comparisons between different effective interactions. The results in Table 4 show that both the SWS and SDF provide equivalent normalization constant values across diverse R3Y interactions. This shows that, despite its many parameters, the SWS may be useful for testing and evaluating R3Y interactions. The choice of imaginary potentials appears to affect the normalization constant, with SDF potentials obtaining slightly higher $ {N}_{R} $ values than SWS potentials, but with less fitting (a large χ² value). The diffraction pattern at forward angles formed by SDF potentials has a deep first minimum that does not match experimental data, suggesting that SDF may not be the best option. It is also worth noting that the performance of SDF is very dependent on the folded potential and its shape; in this situation, folded potentials obtained from R3Y do not appear to be adequate for generating the imaginary potential at this energy. Moving forward in this study, the SWS will be used to simulate the imaginary component of the optical potential in further investigations.

Reaction	$ {V}^{DF} $ + Img.	$ {N}_{R} $	$ {J}_{R} $ (MeV fm3)	$ {W}_{D}{/N}_{I} $ (MeV)	$ {r}_{D} $ (fm)	$ {a}_{D} $ (fm)	$ {J}_{I} $ (MeV.fm3)	$ {\sigma }_{R} $ (mb)	$ {\chi }^{2} $
3He+12C	R3Y(HS)+SWS	0.98	449.8	19.342	1.298	0.608	164.0	869.3	8.5
	R3Y(HS)+SDF	0.96	441.7	0.13	−	−	157.3	953.9	20.4
	R3Y(L1)+SWS	0.46	414.9	18.480	1.223	0.658	146.2	859.2	4.5
	R3Y(L1)+SDF	0.46	414.9	0.064	−	−	156.4	600.6	14.4
	R3Y(W)+SWS	0.50	413.0	18.378	1.237	0.645	144.6	851.0	5.4
	R3Y(W)+SDF	0.49	411.7	0.070	−	−	155.8	877.4	9.2
3He+16O	R3Y(HS)+SWS	0.90	413.6	12.746	1.549	0.686	152.8	1141.3	8.4
	R3Y(HS)+SDF	0.95	436.3	0.14	−	−	165.0	1082.5	22.1
	R3Y(L1)+SWS	0.43	390.8	11.662	1.505	0.769	152.4	1183.0	10.9
	R3Y(L1)+SDF	0.51	460.3	0.079	−	−	188.3	1058.4	31.4
	R3Y(W)+SWS	0.47	386.7	11.488	1.491	0.783	151.1	1185.6	11.4
	R3Y(W)+SDF	0.57	470.6	0.089	−	−	193.0	1059.8	31.5
3He+24Mg	R3Y(HS)+SWS	0.79	364.8	14.295	1.169	1.067	159.0	1601.1	42.3
	R3Y(HS)+SDF	0.80	367.9	0.14	−	−	163.5	1292.3	53.4
	R3Y(L1)+SWS	0.40	362.6	16.410	1.171	0.980	162.0	1496.2	32.5
	R3Y(L1)+SDF	0.43	387.8	0.075	−	−	176.3	1263.2	71.9
	R3Y(W)+SWS	0.39	318.3	13.513	1.008	1.313	169.2	1848.2	43.1
	R3Y(W)+SDF	0.47	387.8	0.084	−	−	179.6	1262.1	75.15
3He+28Si	R3Y(HS)+SWS	0.79	357.8	18.243	1.030	1.047	150.9	1571.2	23.8
	R3Y(HS)+SDF	0.82	373.7	0.12	−	−	142.6	1355.0	37.8
	R3Y(L1)+SWS	0.39	349.7	19.723	1.018	0.989	147.3	1473.7	8.6
	R3Y(L1)+SDF	0.40	358.0	0.062	−	−	149.2	1297.6	15.3
	R3Y(W)+SWS	0.43	349.0	19.839	1.021	0.982	147.3	1465.7	9.0
	R3Y(W)+SDF	0.45	368.4	0.070	−	−	153.3	1298.2	16.2

Table 4.  The normalization constants (N_R, N_I), the depth ($ {W}_{D} $), the radius and diffuseness parameters ($ {r}_{D} $ and $ {a}_{D} $), the total cross-sections (σ), $ {\chi }^{2} $ values and volume integrals ($ {J}_{R} $ and $ {J}_{I} $) for the theoretical analysis with the regularized NN interactions R3Y(HS)+EX(FR/Paris), R3Y(L1)+EX(FR/Reid) and R3Y(W)+EX(FR/Reid).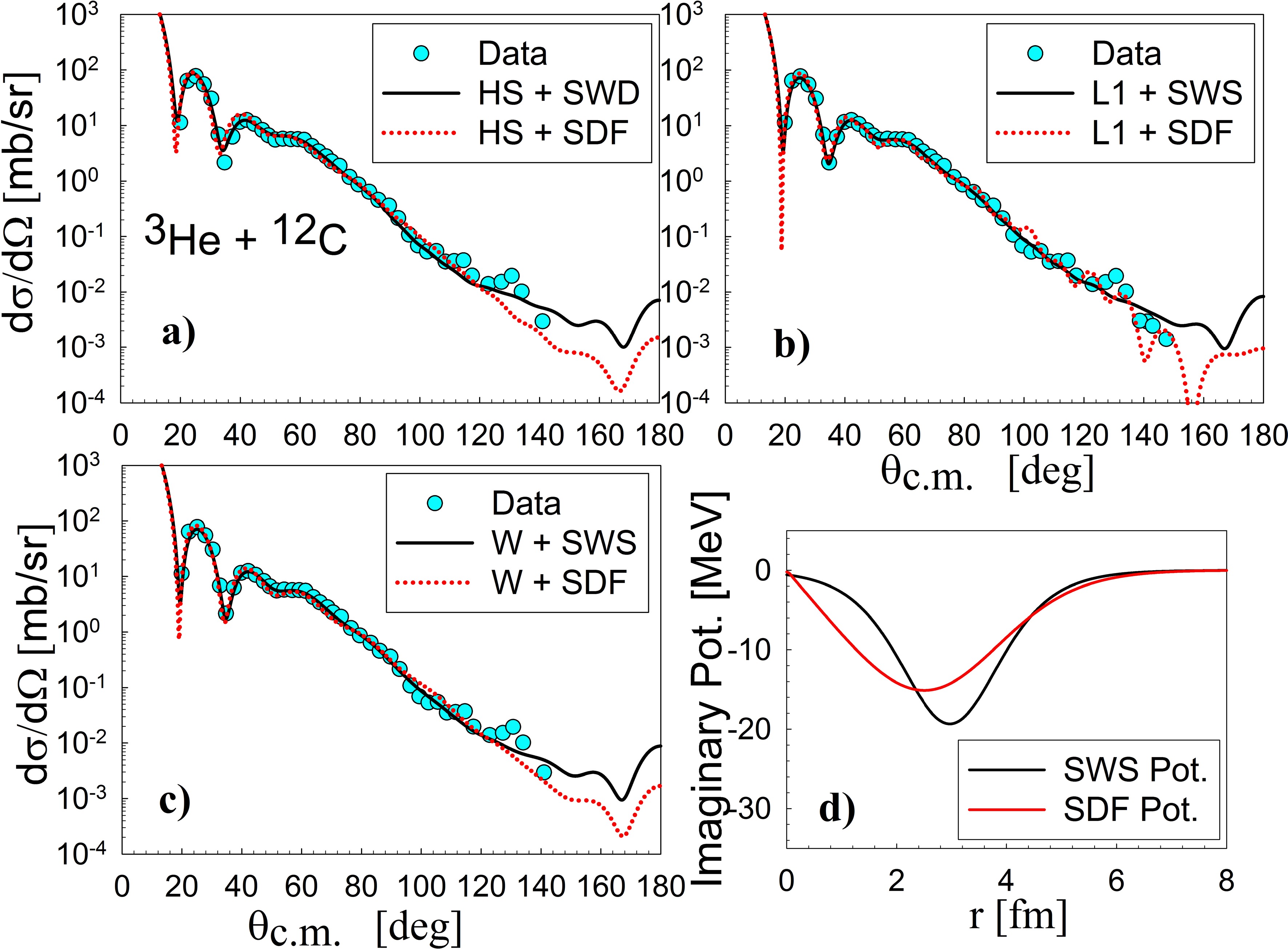

Figure 5.  (color online) Elastic differential cross-sections for ³He + ¹²C scattering at 60 MeV, calculated with folded potentials using a) R3Y(HS), b) R3Y(L1), and c) R3Y(W) real parts, and surface Woods-Saxon (SWS) or folded derivative (SDF) imaginary parts. (d) Compares SWS and SDF within R3Y(HS) model.

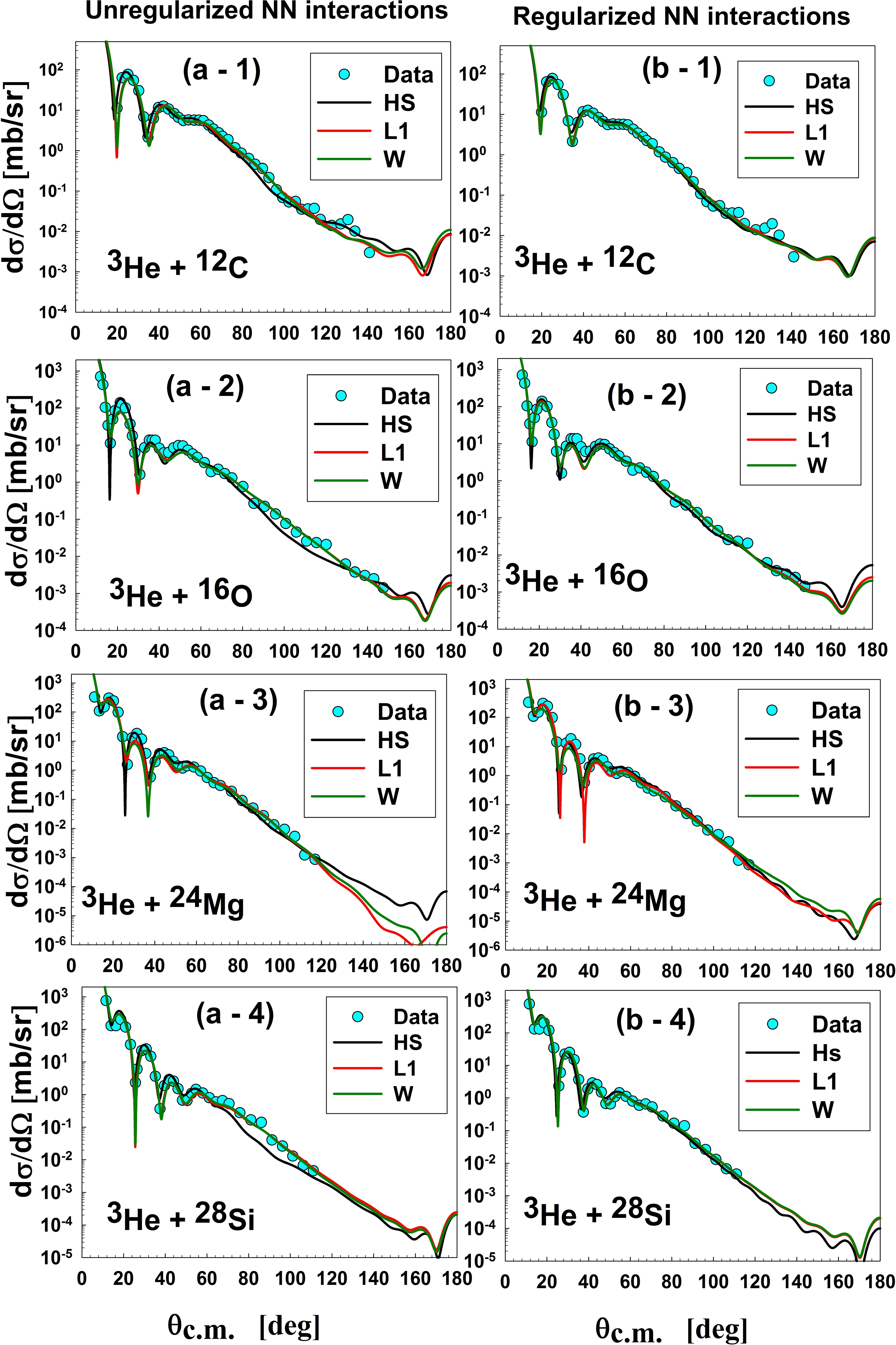
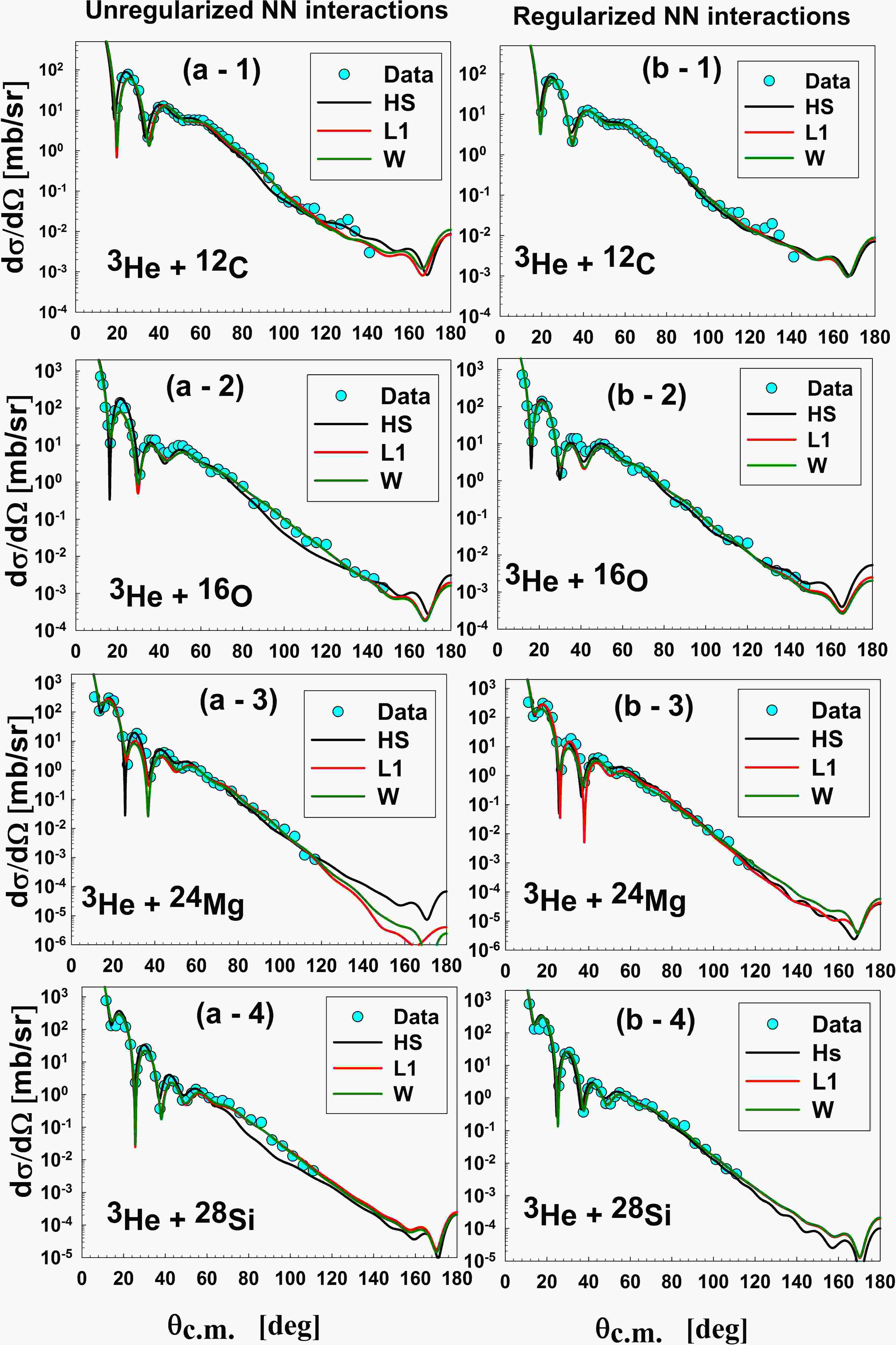
Figure 6.  Elastic differential cross-sections of for ³He on ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si at 60 MeV. The graphs compare differential cross-sections calculated using a folded potential with different nucleon-nucleon (NN) interactions: a) unregularized (left) and b)regularized (right). The specific interactions used are R3Y(HS)+EX(FR/Paris), R3Y(L1)+EX(FR/Reid), and R3Y(W)+EX(FR/Reid), all with a SWS imaginary potential.

The effect of regularization on elastic differential cross-sections was investigated by comparing calculations using unregularized and regularized NN interactions. Figure 6 demonstrates that regularization consistently enhances the differential cross-sections within the diffraction region for all interactions considered. Specifically, the regularized HS interaction yielded a substantially better fit to the data than the unregularized HS interaction. This improvement suggests that the shape of the folded potentials derived from regularized NN interactions more accurately represents the physical system. The $ {N}_{R} $ constant associated with the regularized HS interaction was found to be lower than that of the unregularized HS interaction but higher than those obtained with the unregularized L1 and W interactions. Finally, the impact of regularization was negligible for scattering angles less than 25 degrees.

The N_R for the R3Y(HS) interaction with SWS imaginary potentials are 0.98, 0.90, 0.79, and 0.79 for ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si, respectively, with real volume integrals of about 350–450 MeV·fm³. The R3Y(L1) and R3Y(W) interactions were able to reproduce the experimental data with a normalization constant of less than half (see Table 4), which indicates that R3Y(L1) and R3Y(W) interactions produce deeper potentials than required, meaning that both are not good candidates for nuclear potentials for the description of ³He scattering at this energy. The N_R decreases as the mass number increases, indicating that the R3Y interactions are suitable for light nuclei.

The inelastic scattering of ³He has been analyzed using the DWBA and CC methods based on the Schrödinger equation for the low-lying 2⁺ state for ¹²C, 3^- state for ¹⁶O, 2⁺ state for ²⁴Mg, and 2⁺ state for ²⁸Si at 60 MeV. Two real form factors of the transition potentials were considered: the simple deformed optical potential (DP) and double folded potentials (DF). In the deformed optical potential approach, the transition potentials were calculated using Eq. 31. In the folded transition potential approach, the real part of the form factor was calculated by folding the R3Y(HS)+EX(FR/Paris) regularized NN interaction with the ground state of ³He and the target transition density using Eq. 28 and Eq. 29. The R3Y(L1) and R3Y(W) interactions were excluded due to their low normalization constants. The target transition density was assumed to follow the Bohr-Mottelson model (BM) as in Eq. 30. The imaginary part of the transition potentials was taken as the deformed surface WS potential derived from the semi-microscopic elastic potential as in Eq. 35.

The DWBA calculations were carried out using the ECIS06 code by inserting the real part of the obtained transition potentials and setting the imaginary part parameters. It was assumed that $ {\beta }_{R}={\beta }_{I} $ and searched for the deformation parameters that best fit the inelastic experimental data. The obtained values are listed in Table 5 (see DWBA (DP) and DWBA (DF) columns).

Target	$ {\lambda }^{\pi } $	$ {E}_{ex} $ (MeV)	Previous Studies	Semi-Microscopic
				DWBA (DP)	DWBA (DF)	CC (DP)	CC (DF)
12C	2+	4.44	+0.51 (3He, 3He`)[49] $ +0.6 $ (p, p`)[49]a $ -0.45 $ (e, e`)[49]	+0.618	+0.810 (BM) +0.336 (T)	+0.54	+0.719 (BM) +0.313 (T)
16O	3−	6.13	+0.331 (3He, 3He`) [19]	+0.329	+0.507 (BM) +0.245 (T)	+0.314	+0.511 (BM) +0.249 (T)
24Mg	2+	1.37	$ +0.67 $ (3He, 3He`) [24] $ +0.47 $ (p, p`) [50] $ +0.45 $ (e, e`) [50]	+0.520	+0.655 (BM)	+0.436	+0.562 (BM)
28Si	2+	1.78	+0.49 (3He, 3He`) [25] −0.37 (p, p`) [50] −0.39 (e, e`) [50]	+0.386	+0.495 (BM)	+0.322	+0.407 (BM)
a The reference did not determine the sign of the parameter.

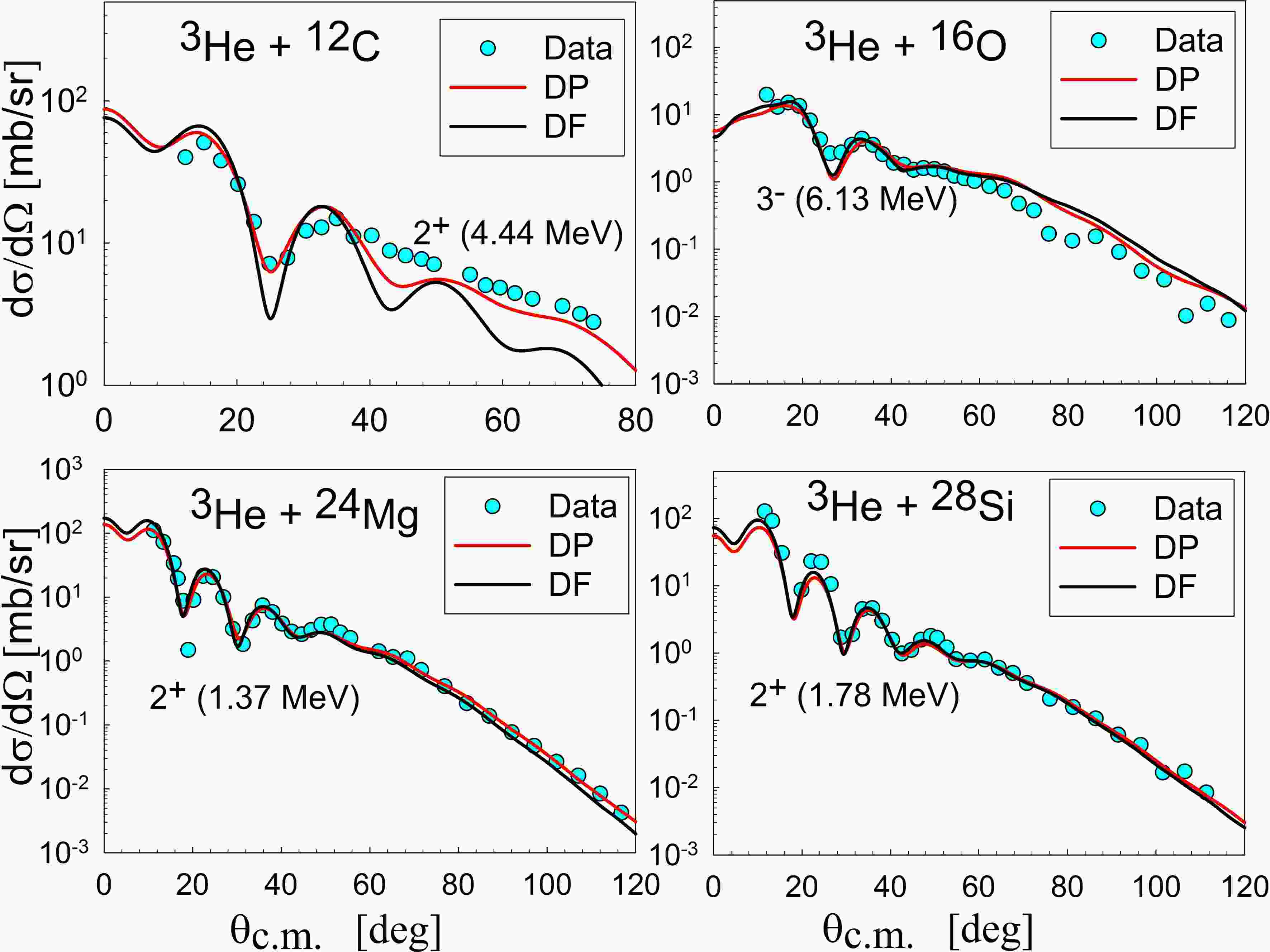
Table 5.  The target nuclei, excited state ($ {\lambda }^{\pi } $), excitation energy ($ {E}_{ex} $ in MeV), and deformation parameters.

For the low-lying 2⁺ state of ¹²C, the transition potentials based on the DP and DF models, with the R3Y(HS) regularized NN interaction based on the Bohr-Mottelson (BM) model for transition density, were obtained (see Fig. 7 (c)). The DP potential was significantly deeper and possessed a distinct form factor compared to the DF potential. DP and DF potentials described the inelastic scattering well at small angles but failed at large ones (see Figure 10). This failure confirms the strong coupling between states and supports the application of the CC method. The DP model gave a better result than the DF model. The deformation parameter obtained from the DP model is consistent with the parameter obtained from proton scattering. It is larger than the results obtained from electron and ³He scattering (see Table 5). The deformation parameter obtained from the DF approach had a large value (β = 0.81). Although this result could indicate that the DF approach struggled to yield realistic transition potentials, we should not conclude that until we examine the DF approach in the CC framework.

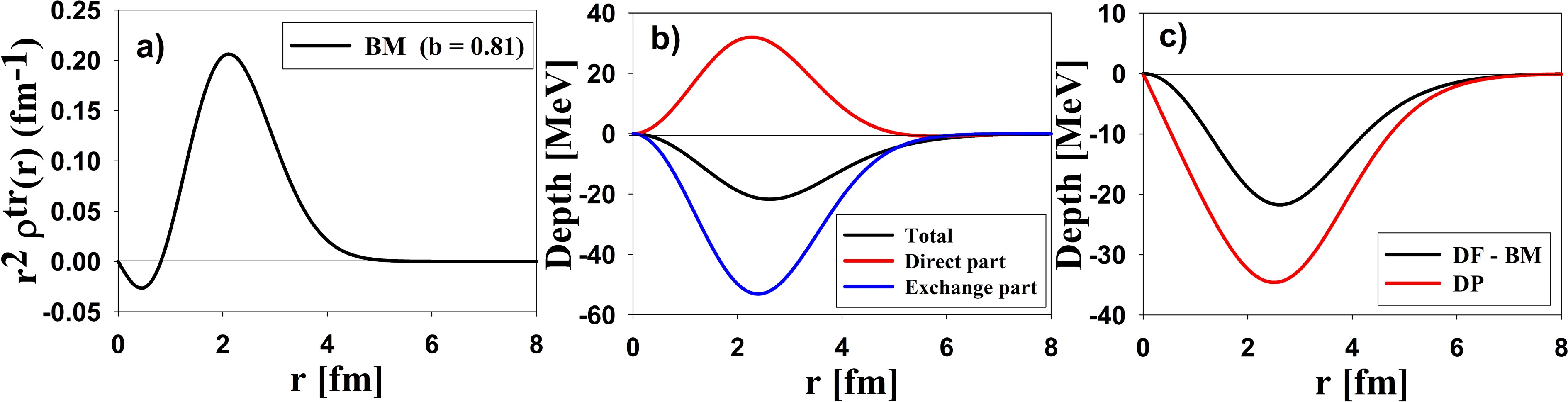
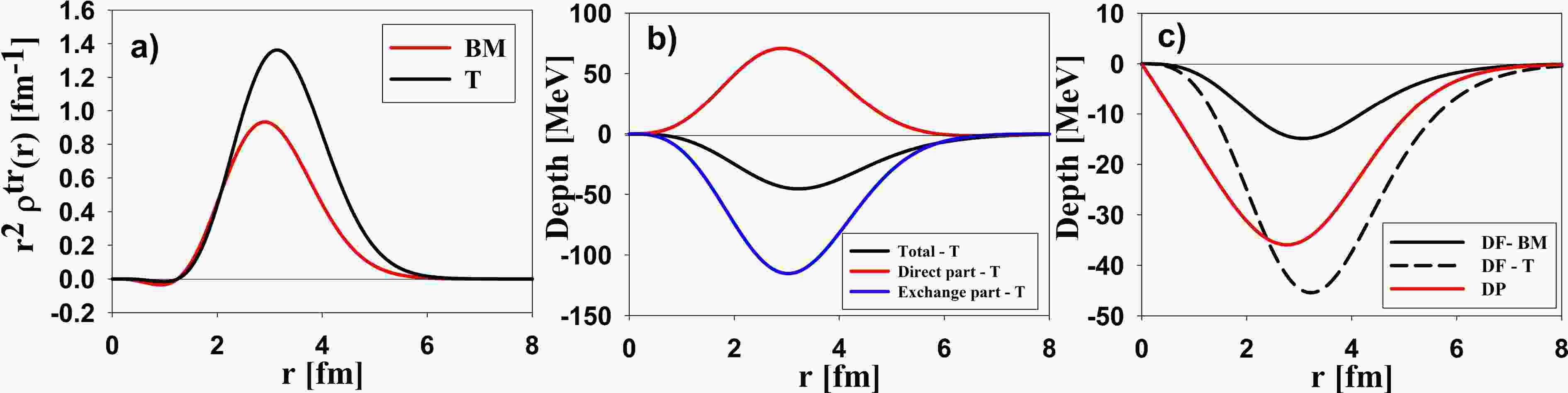
Figure 7.  (color online) a) The transition density for ¹²C based on the Bohr-Mottelson (BM) model ($ \beta =0.81 $). b) The unnormalized direct and exchange parts of the transition potential based on the DF approach with regularized R3Y(HS)+EX(FR/Paris). c) Transition potentials based on the DP and DF models (setting $ \beta R=1 $ for comparison).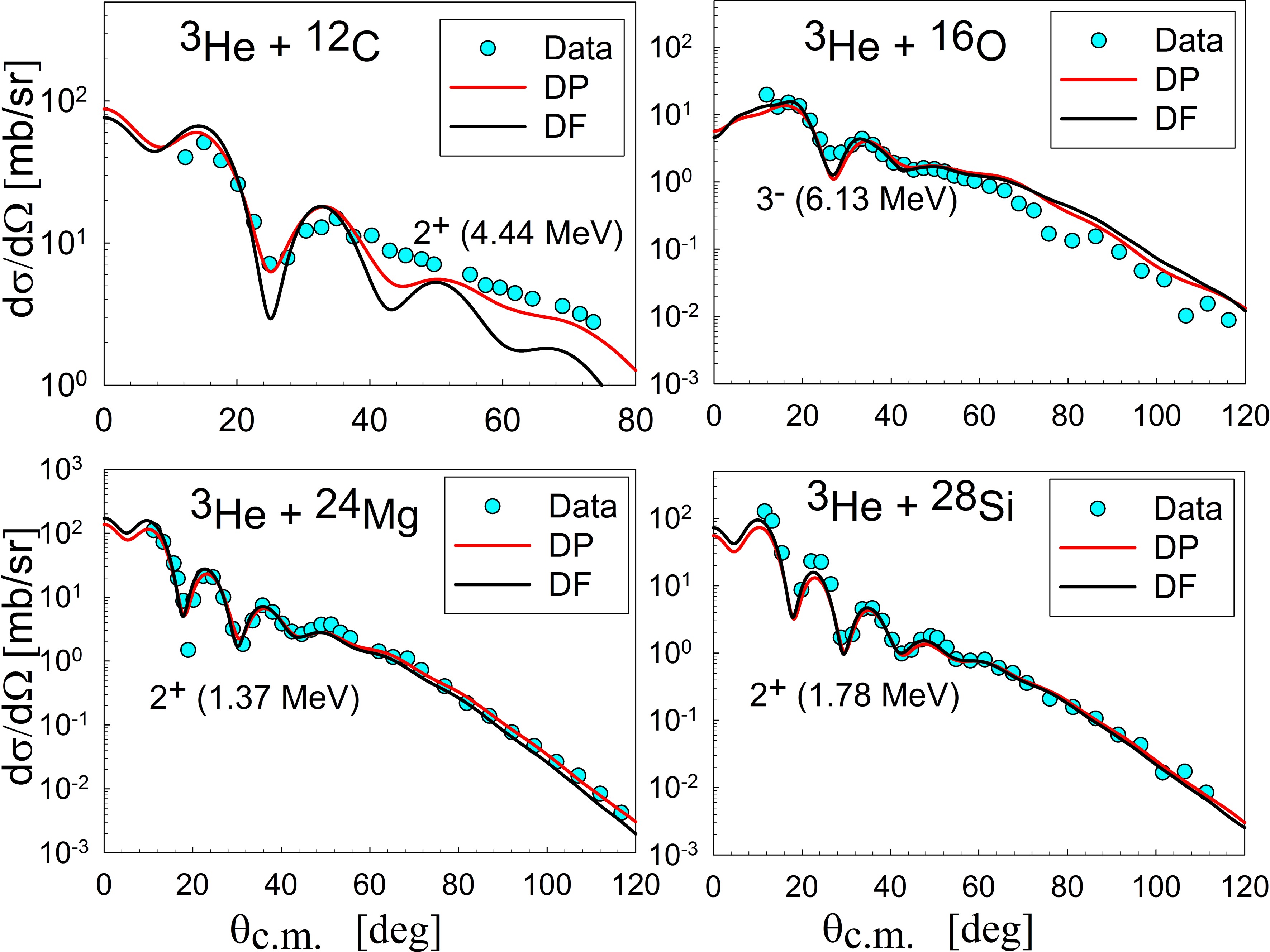

Figure 10.  (color online) DWBA calculations for elastic scattering of ³He on ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si at 60 MeV.

For the low-lying 3^- state of ¹⁶O, the DF transition potential did not provide a good fit and required a large deformation parameter. In Figure 8, the folded potential of the ground state and the transition potentials obtained via the microscopic method for multipole λ = 2 and λ = 3 were plotted. As the multipolarity increases, the depth of the transition potentials decreases; that is why the transition potential for the inelastic 3^- state of ¹⁶O requires a large deformation parameter. The ¹⁶O nucleus may exhibit collective excitations in the form of vibrational modes. While the deep core retains the ground state's shape in such modes, a few nucleons beyond this core participate in surface oscillations, leading to vibrational spectra [51]. Therefore, it may not be appropriate to treat the transition density of the 3- state in the same way as that of the 2⁺ state. Consequently, it was speculated that the transition density might be the source of the problem. It is known that the Bohr-Mottelson (BM) transition density is not suitable for weaker transitions or larger multipolarities [44]. An appropriate deformation parameter could be obtained when a Tassie-like (T) transition density [52] is used, in which the radial transition density was taken to be,

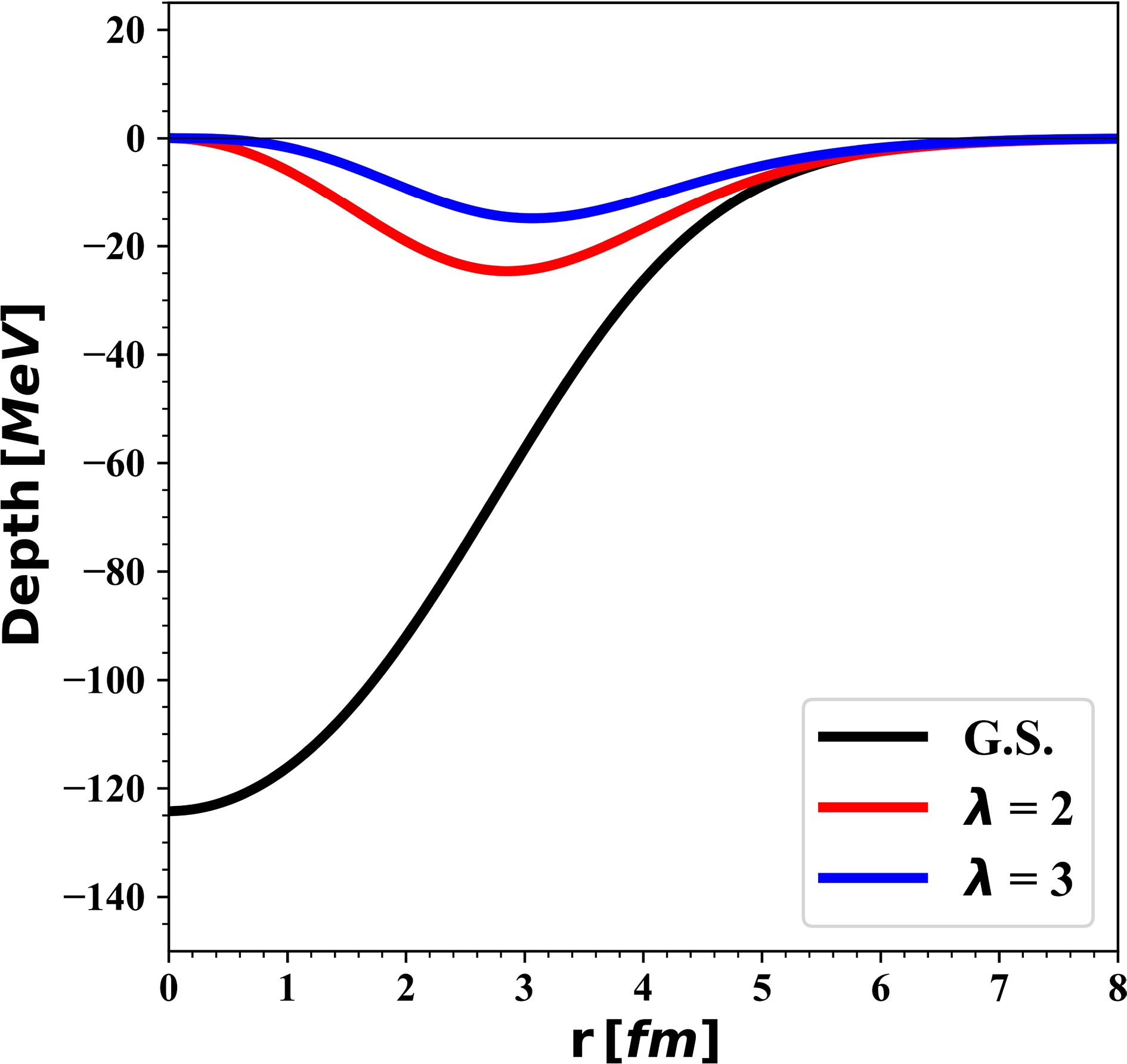
Figure 8.  (color online) The unnormalized ground state folded potential (black line) and the transition potentials of ¹⁶O for different multipolarities based on the DF approach with R3Y(HS)+EX(FR/Paris) interaction (colored lines) and the Bohr-Mottelson (BM) model for transition density (Setting $ {\beta }_{\lambda }^{m}R=1 $ for comparison).

where $ {\tau }_{\lambda }^{m} $ is the matter deformation , with dimensionality (fm⁻¹), used to construct the nuclear transition density for multipole λ.

The transition potential obtained by the Tassie-like transition density, denoted as DF-T, reproduced the inelastic data better than the transition potential obtained by the Bohr-Mottelson (BM) model, denoted as DF-BM (see Figure 9). The deformation parameter obtained from fitting the data has a reasonable value (τ = 0.245 fm⁻¹). In Figure 9, a comparison was made between the transition potentials obtained from the BM and T models and the transition potential of the DP model for the ³He+¹⁶O system. The BM model generated a shallow transition potential, whereas the T model generated the deepest one. Similar to the ¹²C case, both DP and DF models gave satisfactory results at small angles but failed at large angles. An attempt was made to extend the T model to ¹²C inelastic scattering, but no satisfactory result was obtained; the deformation parameters had a very small value (β = 0.336) compared to the BM model value (β = 0.81). The analysis revealed that the BM model yielded larger deformation parameter values than the T model, particularly when considering the transition potential estimated for ¹²C and ¹⁶O. A possible explanation for the failure of the Tassie model in describing the 2⁺ state of ¹²C is that this state exhibits rotational rather than vibrational characteristics. The Bohr-Mottelson collective model, which successfully describes rotational bands, would therefore be more appropriate for ¹²C, in contrast to the Tassie model usually employed for vibrational excitations [53]. This discrepancy elucidates why the Tassie model effectively represents the vibrational excitations of ¹⁶O, but the rotating characteristics of ¹²C require the Bohr-Mottelson model.

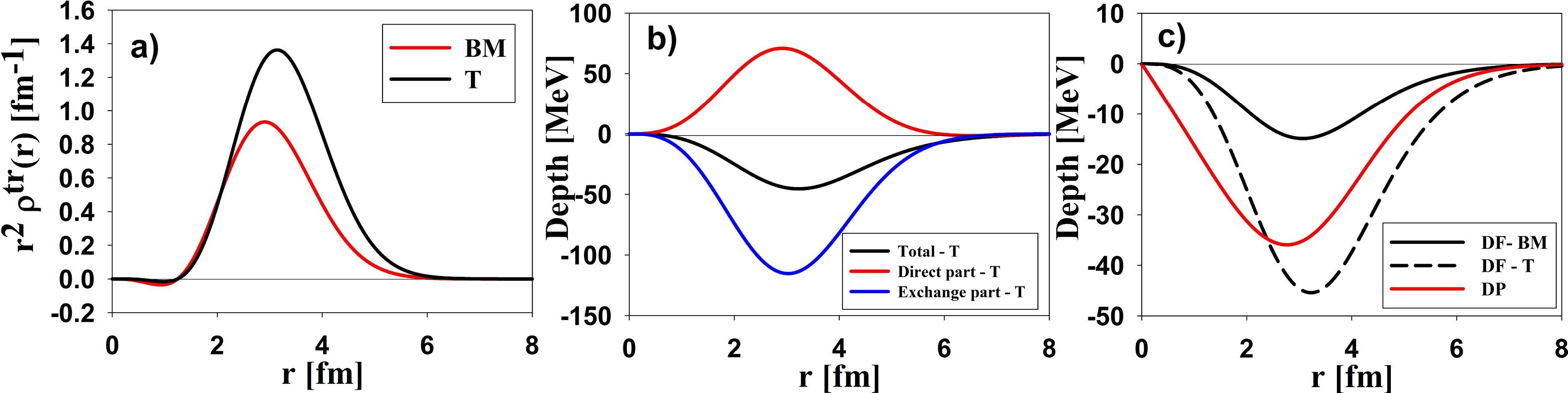
Figure 9.  (color online) a) The transition density of ¹⁶O based on the Bohr-Mottelson (BM) and Tassie-like (T) models (setting $ \beta R=\tau R=1 $ for comparison). b) The unnormalized direct and exchange parts of the transition potential are based on the DF calculation for the T model. c) The transition potentials are based on the DP and DF models.

The transition potentials of the inelastic 2⁺ state for ²⁴Mg and ²⁸Si were determined for the DP model and for the DF approach using the BM transition density. Both models yielded satisfactory results for small and large angles. The DP model exhibited a slightly enhanced result, particularly at large angles. The deformation parameters based on the DF approach are consistent with previous ³He scattering studies (β = 0.655 and 0.495 for ²⁴Mg and ²⁸Si, respectively). DP and DF models yield deformation parameters that exceed those derived from electron and proton scattering. The real and imaginary parts of the transition potentials after fitting with the inelastic data were plotted in Figure 11. The maximum depth for the transition potential of ¹²C, ²⁴Mg, and ²⁸Si ranged between 11 and 14 MeV, while for ¹⁶O, the maximum depth was around 9 MeV. The rms radii for the real part of the transition potential were 3.872, 3.865, 4.636, and 4.720 fm for ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si, respectively. The rms radii of the transition potential for the 2⁺ state were factors of 1.134, 1.177, and 1.177 larger than the rms radius for the ground state DF potential of ¹²C, ²⁴Mg, and ²⁸Si, respectively. For the ¹⁶O nucleus, the rms radius of the transition potential for the 3^- state was 1.075 times larger than the ground-state DF potential. The calculated rms radii did not represent the radii of the excited states; rather, they should be interpreted as the rms radii of the interaction range between the ³He particle and the target nuclei. Changes in these radii relative to the ground state could provide insights into nuclear deformation. These Changes for ¹²C, ²⁴Mg, and ²⁸Si exceeded that of ¹⁶O, likely due to their significant static nuclear deformation.

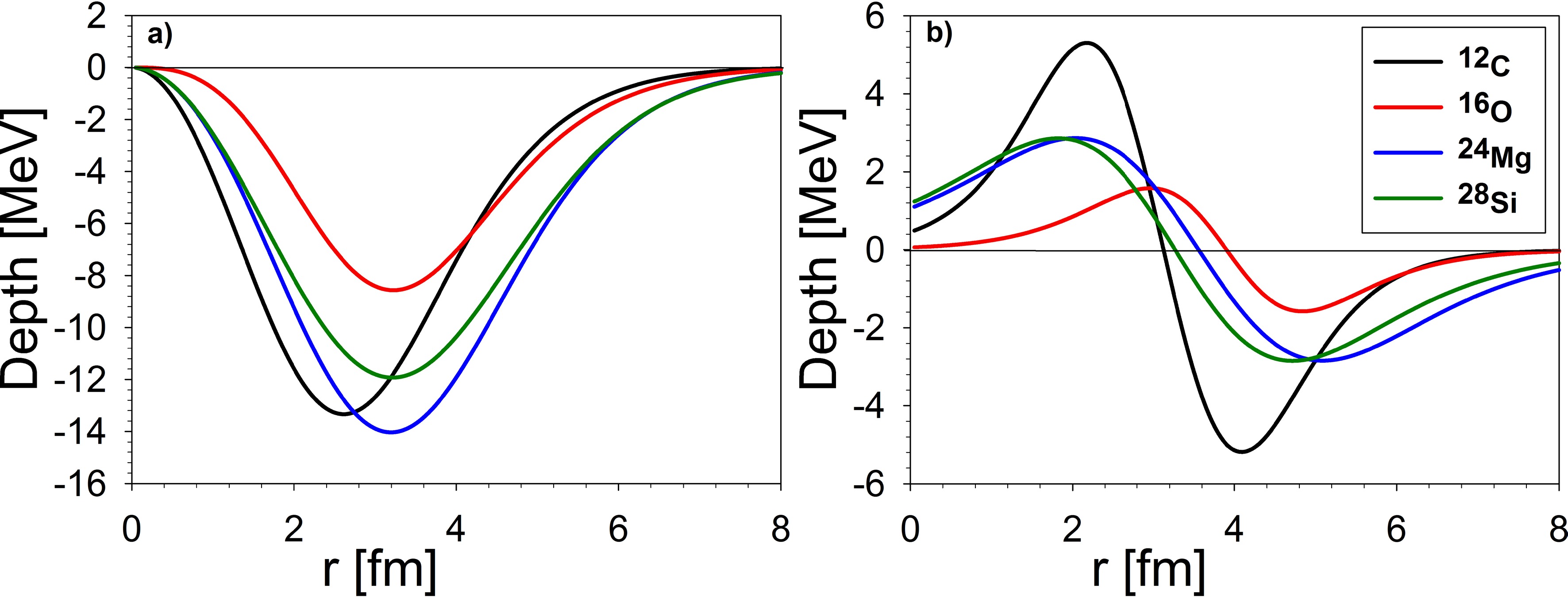
Figure 11.  (color online) a) The real part of the DF transition potentials for the scattering of ³He on ¹²C (⁺2 state – BM model), ¹⁶O (^-3 state – T model), ²⁴Mg (⁺2 state – BM model) and ²⁸Si (⁺2 state – BM model) at 60 MeV based on the regularized HS+EX (FR/Paris) interaction. b) The imaginary part of the transition potentials.

Next, the CC method was applied to measure the strength of coupling between states based on the semi-microscopic optical potentials. In the CC calculations, the (0⁺, 2⁺) coupling schemes were studied using the collective rotational model for ¹²C, ²⁴Mg, and ²⁸Si, while the (0⁺, 3^-) coupling schemes were used for ¹⁶O. The CC calculations involved the variation of the normalization constant, surface WS potential parameters, and deformation parameters permitted to simultaneously optimize the fit for elastic and inelastic data. The results are listed in Table 6. The deformation parameters are listed in Table 5 (see CC (DP) and CC (DF) columns). The potentials derived from elastic scattering were utilized as the initial potentials for the CC calculations, with inelastic data incorporated into the process. Channel coupling was found to influence the ground-state scattering behavior [54, 55], requiring a comparison of CC calculations for both elastic and inelastic cross-sections.

Reaction	Model	$ N $	$ {W}_{D} $ (MeV)	$ {r}_{D} $ (fm)	$ {a}_{D} $ (fm)	$ {\sigma }_{R} $ (mb)	β/τ	$ {\chi }_{elastic}^{2} $	$ {\chi }_{inelastic}^{2} $
3He+12C	DP	0.863	10.431	1.569	0.596	915.5	+0.54	18.37	2.66
	DF – BM	0.892	10.843	1.569	0.611	915.5	+0.719	30.70	11.2
3He+16O	DP	0.892	10.969	1.594	0.701	1159.7	+0.314	7.89	151.22
	DF – T	0.861	13.593	0.858	1.126	1249.5	+0.249	9.98	769.91
3He+24Mg	DP	0.722	9.882	1.230	1.146	1639.3	+0.436	37.3	9.26
	DF – BM	0.739	10.095	1.243	1.126	1624.8	+0.562	37.5	6.52
3He+28Si	DP	0.761	13.576	1.126	1.037	1546.9	+0.322	12.4	13.1
	DF – BM	0.777	14.055	1.123	1.022	1529.7	+0.407	11.2	11.2

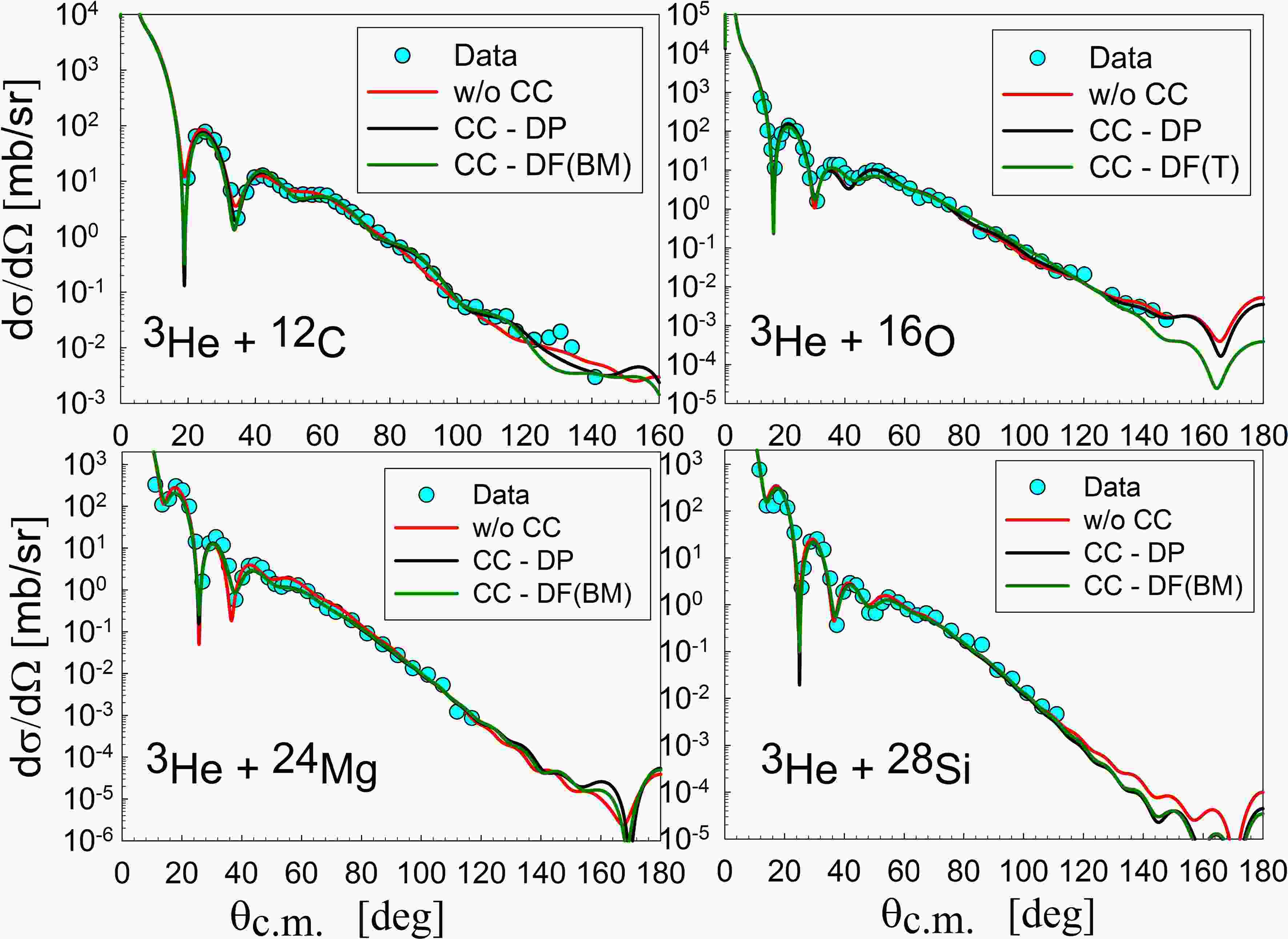
Table 6.  The normalization constant (N_R), the depth ($ {W}_{D} $) in MeV, the radius and diffuseness parameters ($ {r}_{D} $ and $ {a}_{D} $), the total cross-sections (σ_R) and $ {\chi }^{2} $ values of elastic and inelastic scattering for the CC calculations based on the folding model with regularized R3Y(HS) interaction.

First, the coupling effect on the elastic scattering was analyzed. The sensitivity of the coupling to the inelastic form factor was explored by examining both the DP and DF models. The elastic scattering with and without coupling was depicted in Figure 12 for both models. The CC method accurately described elastic scattering within the angular range of 10 to 100 degrees. For the ¹²C nucleus, the CC approach produced an oscillation within the angular range of 80 to 120 degrees, consistent with the data and not observed in the DWBA method. The CC calculation based on the DP potential, referred to as CC-DP, had a better result than the calculation based on the DF potential, denoted CC-DF, with BM densities. The oscillation was out of phase at angles over 120 degrees in the DF calculation. For the ¹⁶O nucleus, the CC method agreed with the DWBA method up to an angle of 120 degrees. The CC-DF disagreed with both DWBA and CC-DP from a large angle. The effect of coupling is not evident in the ¹⁶O case. No significant difference was observed for the ²⁴Mg and ²⁸Si nuclei compared to the DWBA calculations. The DP results are slightly better than the DF results, except for the ¹⁶O nucleus. The coupling effect consistently decreased the normalization constant across all cases. Additionally, the explicit inclusion of inelastic states reduced the imaginary potentials' depth and required larger values for the radius parameter. In all cases, $ {r}_{D} > {a}_{D} $ is satisfied, except for the DF calculation of ¹⁶O. The CC method yields larger total reaction cross-sections than the DWBA method.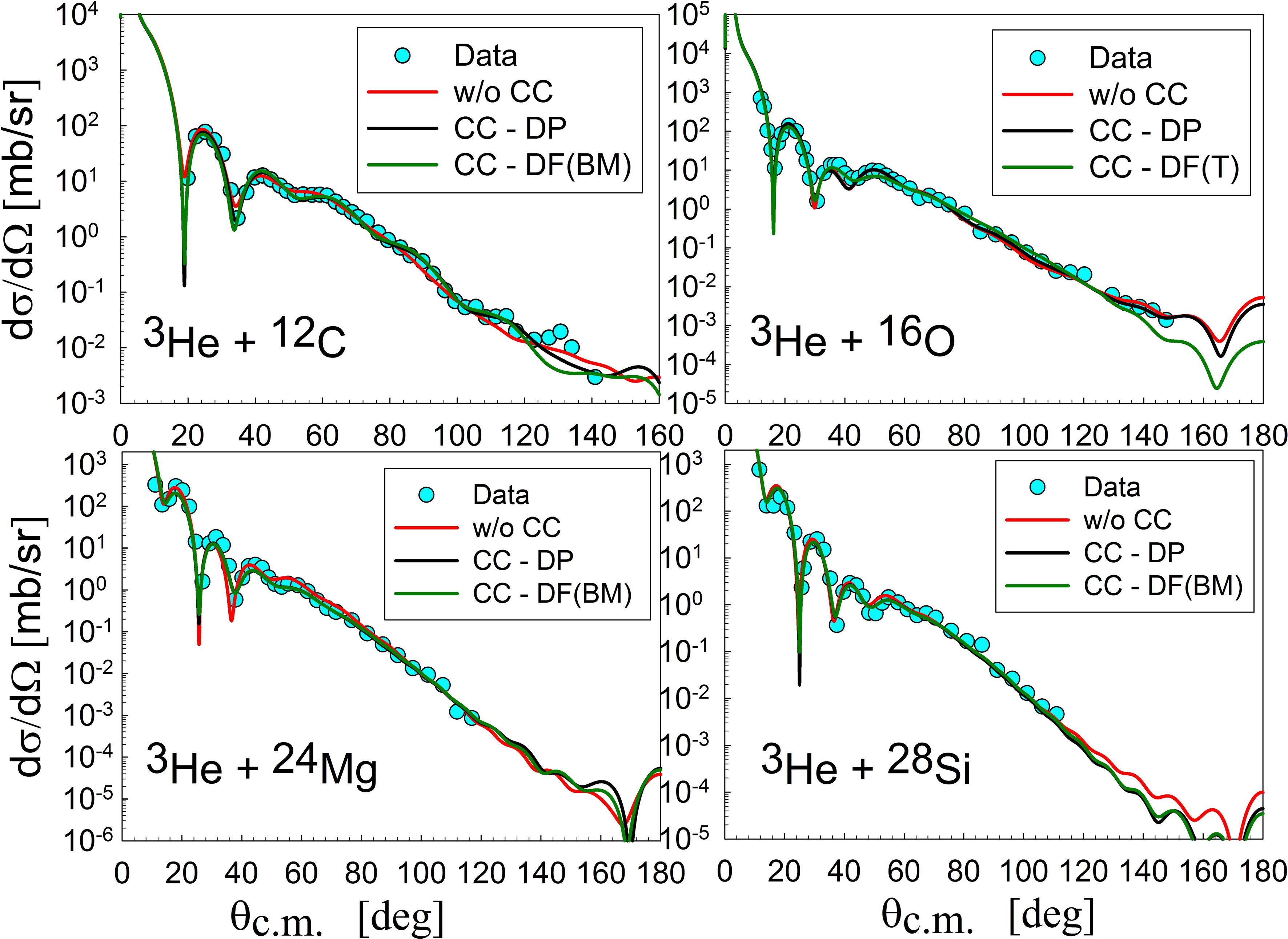

Figure 12.  (color online) Coupled channels calculations for elastic scattering of ³He on ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si at 60 MeV.

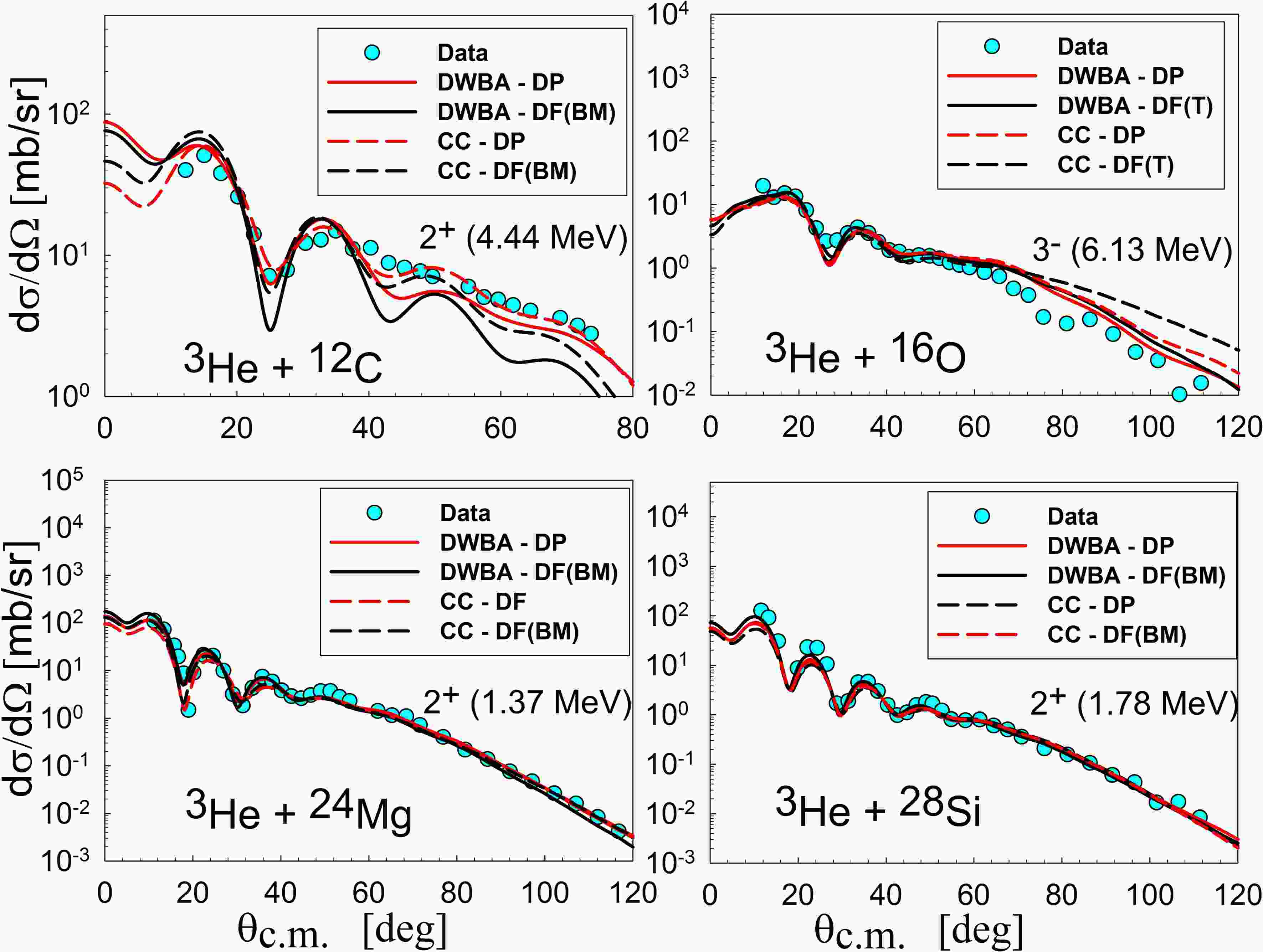
Secondly, the inelastic cross sections calculated using the CC method were analyzed and were presented in Figure 13. The solid lines depict the results obtained using the DWBA method, whereas the dashed lines represent those from the CC method. The CC calculations were initiated with the most suitable DF transition potentials identified within the DWBA analysis. Regarding the DF model, the transition potentials based on the BM model were applied to ¹²C, ²⁴Mg, and ²⁸Si, while the T model was utilized for ¹⁶O. For ¹²C, the CC method enhanced the accuracy of results at both small and large angles for both DP and DF potentials (see Fig. 13). This improvement suggests strong coupling between nuclear states. The DP potential provided a better fit for the experimental data than the DF potential. Coupling reduced the deformation parameter by 12.6% for the DP potential and 11.2% for the DF potential. An evaluation of the DF potential based on the T model showed unsatisfactory results; the small value obtained for the deformation parameters supported the conclusion that the BM transition density is the optimal choice for the 2⁺ state ¹²C.

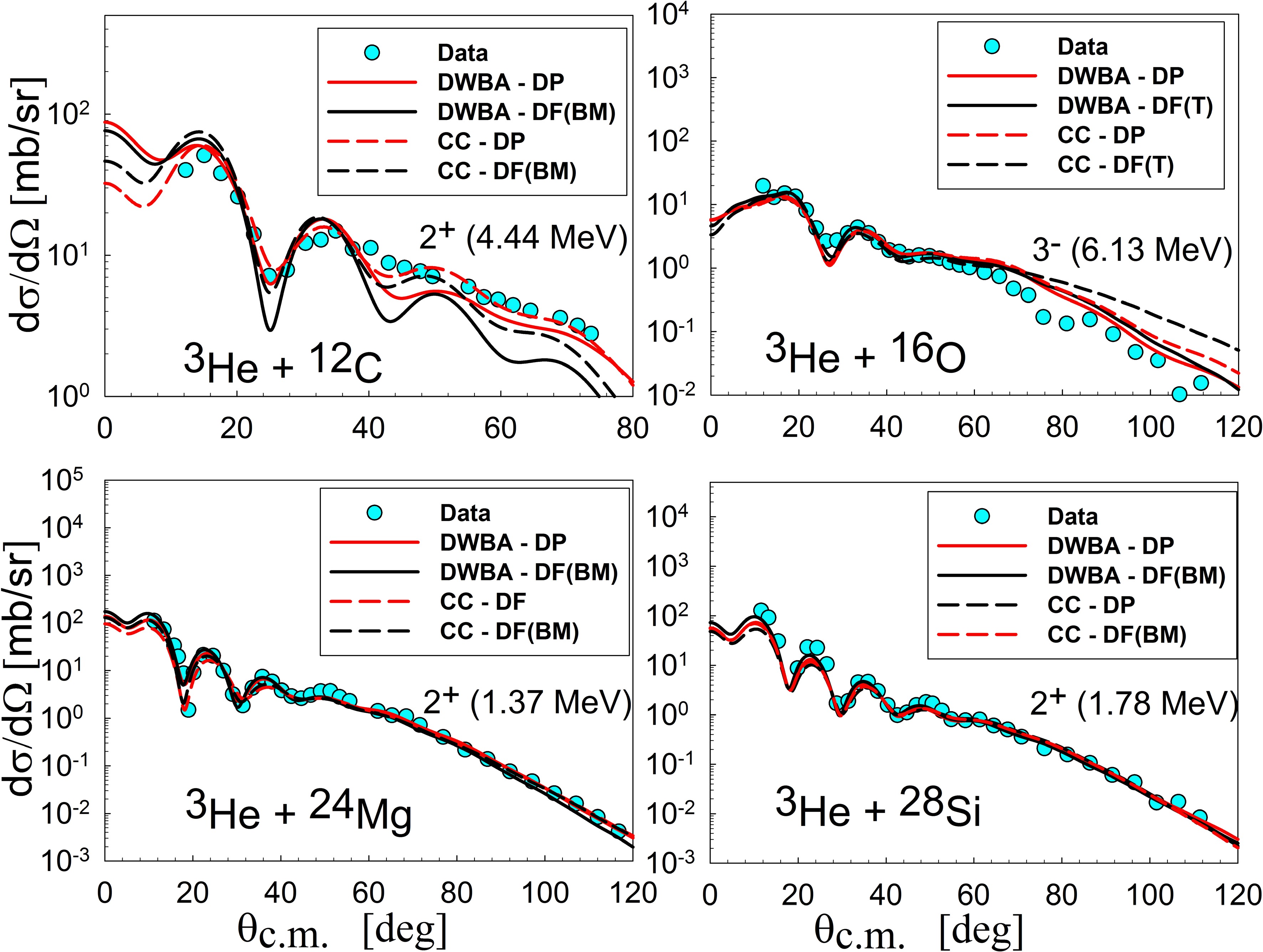
Figure 13.  (color online) Coupled channels Schrödinger-based calculations for inelastic scattering of ³He on ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si at 60 MeV.

For the 3^- state of ¹⁶O, the CC method provided accurate descriptions within an angular range of 10 to 50 degrees. However, for larger angles, neither CC-DP nor CC-DF showed significant improvement. The calculated cross-sections at angles greater than 80° are significantly higher than the experimental ones. The DWBA results outperformed those of the CC method. This finding aligns with the results of a previous study [19]. Burtebayev et al. have taken into account the coupling of the elastic and inelastic scattering in both the forward and reverse directions in the framework of the collective and microscopic models, respectively. Still, the results were unsatisfactory (See Fig. 4 in [19]). The deformation decreased by 4.56% for the DP potential and increased by 1.63% for the DF potential. The DP potential produced a very consistent value of β.

For the 2⁺ state of ²⁴Mg, applying coupled channel calculations improved the results in the diffraction region for both DP and DF potentials. At large angles, the DWBA and CC calculations exhibited no significant difference. The present result exceeded the results obtained by Sadykov et al. (See Fig. 7 [24]) in the comparison. The authors utilized only the deformed real potential, a common approach in light particle scattering studies, allowing them to compare their results with existing data. The present study provides evidence for the crucial role of imaginary part deformation in describing inelastic scattering. The coupling decreased the value of β. The DP potential produced β = 0.436, consistent with proton and electron scattering results. In contrast, the DF potential yielded β = 0.562, aligning with findings from ³He scattering (see Table 5). Compared to the CC-DP results, the CC-DF results showed a marginal improvement.

For the 2⁺ state of ²⁸Si, the implementation of coupled channel calculations demonstrated minimal enhancement in the accuracy of inelastic cross-section determinations. Consequently, coupled channel calculations had virtually no effect on the accuracy of inelastic cross-section predictions. CC-DF calculations produced a β value of 0.322, consistent with proton and electron scattering experiment results. The CC-DP calculations yielded the lowest value of the deformation parameter. Similar to the case of ²⁴Mg, the CC-DF results showed only a marginal improvement over the CC-DP results, suggesting that the DF approach is not particularly advantageous for light targets.

The deformation parameters extracted from ³He scattering systematically exceed those obtained from electron scattering, consistent with previous observations of projectile-dependent results [56]. This discrepancy arises because electron scattering interacts with protons solely via the Coulomb force, exclusively probing their charge distribution. In contrast, ³He scattering interacts with protons via both Coulomb and nuclear forces and with neutrons via the nuclear force, thus exhibiting sensitivity to both neutron and proton distributions. The extracted deformation values may reflect dynamic deformation effects, where nuclear distortions emerge from the interplay between the target nucleus's internal structure and the incident projectile. Such dynamic deformation should fundamentally depend on both the nuclear structure and the effective NN interactions during the scattering process. A comparison between the extracted deformation parameters and proton scattering results offers additional support for dynamical deformation effects, with the expectation that this effect will be more pronounced in ³He scattering due to its greater deformation magnitude.

This study investigated ³He elastic and inelastic scattering off ¹²C, ¹⁶O, ²⁴Mg, and ²⁸Si at 60 MeV using a double-folding approach. Optical potentials were calculated based on RMF-derived NN interactions R3Y(HS), R3Y(L1), R3Y(W), and R3Y(Z) for the real part. The results of the present study can be summarized as follows:

I. The regularization procedure maintained the characteristic behavior of NN interactions while reducing the potential well depth. The R3Y(Z) interaction was excluded from our analysis as a purely repulsive potential was deemed unphysical for ³He-nucleus scattering in this energy regime. The regularized potentials demonstrated improved agreement with experimental data. Comparative analysis revealed that a surface Woods-Saxon (WS) imaginary potential provided superior results to those derived from folded potentials. Furthermore, the selection of imaginary potential influenced the required normalization constant significantly.

II. The R3Y(HS) interaction successfully reproduced experimental scattering data with an optimal normalization constant N ≈ 1 for ¹²C and 0.9, 0.79 and 0.79 for ¹⁶O, ²⁴Mg and ²⁸Si, respectively. In contrast, both R3Y(L1) and R3Y(W) interactions required significantly smaller normalization constants (N < 0.5), producing unrealistically deep potentials that rendered them unsuitable for describing ³He-nucleus scattering. Notably, we observed an inverse relationship between the normalization constant and target mass number, suggesting that the RMF-derived R3Y(HS) interaction demonstrate better performance for lighter nuclear systems.

III. Analysis of inelastic scattering was conducted within the Distorted Wave Born Approximation (DWBA) framework, employing two distinct approaches for transition potentials: a phenomenological deformed potential (DP) and a microscopic double-folded potential (DF). The DP approach yielded larger potential depth for the 2⁺ excited state of ¹²C than the DF method. While both models successfully reproduced small-angle scattering cross-sections, their accuracy diminished at larger angles, with the DP model demonstrating a better performance in this regime. In the case of ¹⁶O's 3⁻ state, the DF approach based on Bohr-Mottelson collective models required an anomalously large deformation parameter (β₃ > 0.5). A better agreement with experimental data was achieved using a Tassie-type transition density, which provided more realistic nuclear deformation characteristics. For the 2⁺ states of ²⁴Mg and ²⁸Si, both DP and DF approaches incorporating Bohr-Mottelson transition densities produced comparable and satisfactory results across the measured angular range.

IV. The coupled channels (CC) method was also applied to analyze both elastic and inelastic scattering processes, demonstrating varying degrees of success across different nuclear systems. For elastic scattering, the CC calculations showed excellent agreement with experimental data in the angular range of 10°-100°, particularly for the ¹²C nucleus, which accurately reproduced the characteristic oscillatory pattern observed between 80°-120. An analysis of the effects of coupling various transition potentials on elastic scattering revealed that the deformed potential implementation (CC-DP) consistently outperformed the double-folded potential approach with Bohr-Mottelson densities (CC-DF), with the latter exhibiting phase discrepancies beyond 120° that limited its effectiveness for backward-angle scattering. In the analysis of inelastic scattering, the CC method proved particularly effective for the ¹²C nucleus, significantly improving the agreement with experimental data across both forward and backward angles for both transition potential formulations, suggesting strong coupling between nuclear states in this system. The method also provided accurate descriptions of the 3⁻ state in ¹⁶O for scattering angles up to 50°, though its effectiveness diminished at larger angles regardless of the potential used. The results were more varied for the 2⁺ states of heavier nuclei: the ²⁴Mg case showed noticeable improvement in the diffraction region. At the same time, the ²⁸Si system exhibited only minimal enhancement in cross-section determination, indicating weaker coupling effects in these heavier nuclei.