Search for doubly charged scalars in type-II seesaw mechanism through photon fusion at the LHC

Neutrino oscillation experiments strongly motivate small yet non-zero neutrino masses, providing clear evidence for new physics beyond the Standard Model (SM) of particle physics. One of the most well-known and widely-studied schemes to this problem is the Weinberg dimension-5 operator $ {\cal{L}}\propto\ell_{L}HH\ell_{L}/\Lambda $ [1], where $ \ell_{L} $ and H refer to the $ SU(2)_{L} $ doublet lepton and the SM Higgs doublet, respectively. With a relatively high-scale cutoff Λ, tiny neutrino masses of Majorana nature can then be generated naturally after the electroweak symmetry breaking (EWSB). Ultraviolet completion of the Weinberg operator at tree level exists in only three ways, generally known as the three types of seesaw mechanisms [2−11], introducing to the SM right-handed neutrinos (type-I), $ SU(2)_{L} $ triplet scalars (type-II) or $ SU(2)_{L} $ triplet fermions (type-III). Different from type-I/III seesaw which mixes Dirac- and Majorana-type masses, the type-II scenario generates neutrino masses via Yukawa couplings of the triplet scalar Δ with the SM lepton doublets $ m_{\nu}\sim Y_{\nu}v_{\Delta} $, where $ Y_{\nu} $ is the neutrino Yukawa coupling and $ v_{\Delta} $ the vacuum expectation value (VEV) of the neutral component of Δ. A seesaw style thus appears after the EWSB considering the mixing between the SM Higgs and the triplet $ v_{\Delta}\sim\mu v^{2}_{0}/m^{2}_{\Delta} $, with the triplet mass $ m_{\Delta} $ being orders larger than the electroweak scale $ v_{0}\sim246 $ GeV. The dimensional mixing parameter μ in type-II seesaw is allowed to be naturally small enough according to 't Hooft naturalness argument [12, 13] so that in such a scenario, the Yukawa coupling $ Y_{\nu} $ not only relates neutrino oscillation experiments data to collider searches through dileptonic decay of the new scalar, its mass $ m_{\Delta} $ can also be low enough to be accessible at current collider experiments including the Large Hadron Collider (LHC).

Searches for the triplet scalar at colliders and studies on the relevant features have been extensively conducted [14−20], as its charged components, especially the doubly charged ones are predicted not only in the type-II seesaw, but also in a variety of other beyond SM models such as the left-right symmetric models [21−23], Zee-Babu model [24, 25], Georgi-Machacek model [26, 27], etc. The most commonly considered production channels at hadron colliders are the Drell-Yan processes, where the doubly charged scalars are produced in pairs or in association with a singly charged one through a neutral or charged current, respectively. Since these exotic scalars couple to the electroweak bosons via gauge interaction, their production cross sections through Drell-Yan processes can be predicted as a function of their masses. As an example, for $ m_{\Delta^{\pm\pm}}\sim1 $ TeV, the pair production cross section can reach $ \sim0.1 $ fb at the leading order (LO) with colliding energy of 14 TeV and the next-to-leading order (NLO) QCD corrections can give a k-factor $ k=\sigma^{NLO}/\sigma^{LO} $ in the range of $ 1.1\sim1.3 $ [28, 29].

As for the decays, there are three modes of the doubly charged scalars: dileptonic, dibosonic and cascade decay channels, among which the dileptonic and dibosonic ones are mostly studied for collider searches. It is the value of $ v_{\Delta} $ that largely determines the dominance of these two modes. Assuming $ v_{\Delta} $ far less than $ 10^{-4} $ GeV, the dileptonic decay channels $ \Delta^{\pm\pm}\to\ell^{\pm}\ell^{'\pm} $ dominate. With this assumption of dileptonic dominance and equal branching ratios into different possible final states, that is, Br($ \Delta^{\pm\pm}\to\ell^{\pm}\ell^{'\pm})=1/6\; (\ell,\ell^{'}=e,\mu,\tau) $, the ATLAS collaboration derived a stringent lower limit for the doubly charged scalar mass at 95% C.L. $ m_{\Delta}>1080 $ GeV at the 13 TeV LHC using integrated luminosity of 139 fb^-1 [30]. With a larger $ v_{\Delta}>10^{-4} $ GeV, the dileptonic decay channels are highly suppressed due to the increasing $ v_{\Delta} $ and only diboson channels $ \Delta^{\pm\pm}\to W^{\pm}W^{\pm} $ are relevant, the ATLAS collaboration obtained relatively weaker bounds at $ 200\sim220 $ GeV for a degenerate spectrum at the 13 TeV LHC with 36 fb^-1 collected events [31]. In the parametric region of a moderate mass separation $ \Delta m\gtrsim5 $ GeV or even larger splitting, the third channel cascade decay $ \Delta^{\pm\pm}\to\Delta^{\pm}W^{\pm*}\to\Delta^{0}W^{\pm*}W^{\pm*} $ becomes dominant over the dileptonic and dibosonic ones if $ v_{\Delta} $ is not very far from $ 10^{-4} $ GeV by orders (either larger or smaller) [32]. For a non-degenerate spectrum with a mass difference of up to 100 GeV, lower limits of 350 and 230 GeV are obtained for pair and associated production, respectively, at $ \sqrt{s}=13 $ TeV with luminosity of 139 fb^-1 [33]. Although most current experimental searches assumed degeneracy or a tiny mass splitting, it is allowed to be as large as $ \Delta m\sim40 $ GeV for hundreds-GeV triplet Higgs bosons if considering the electroweak precision data, since heavy scalars' contribution to the oblique parameter T is compensated by the mass difference among the triplet components [32, 34]. Hence, the experimental bounds for the doubly charged Higgs bosons are generally sensitive to different parametric regions of the model, mainly concerned with the triplet scalar VEV $ v_{\Delta} $ and the mass spectrum of the charged and neutral components. And due to the large hadronic background at the LHC, a tiny $ v_{\Delta} $ is typically assumed for a dominant dileptonic mode in experimental searches as well as phenomenological studies.

While the above-mentioned conclusions on experimental bounds are mostly drawn by taking into consideration of Drell-Yan production of the triplet scalars, initial photon fusion from elastic collisions of protons, although receiving less attention, becomes increasingly attractive recently as the forward detectors have been launched at the LHC, including the CMS-TOTEM Precision Proton Spectrometer (CT-PPS) [35] and the ATLAS Forward Proton detector (AFP) [36]. These forward physics facilities (FPF) are located close to the colliding beams and around 220 meters from the collision point. With the FPFs installed successfully, new windows are opened to the elastic events at the LHC since the forward detectors are designed mainly to identify the unsuccessfully colliding protons. Those protons go through what are generally known as the ultraperipheral collisions (UPC) and remain intact when reaching the forward detectors. Along with the UPC processes, initial photon fusion can occur since the electromagnetic field around the fast-moving protons can be approximated to on-shell photons (equivalent photon approximation, EPA). Accompanying the elastic collisions between protons, the photon fusion can lead to pair production of charged particles, such as the doubly charged scalars. Although it has been shown that the contribution from photon-fusion is less than that of neutral current Drell-Yan production [37, 38], the elastic nature of collisions will leave unique signatures of two unharmed protons reaching the forward detectors, forming a special topology with rapidity gaps between those forward protons and the central particles. These features make the photon fusion in UPC processes a new, promising way to search for new physics in the forward regions, which was not even possible before the launch of forward facilities. Utilizing forward proton-tagging, an increasing number of phenomenological studies have been conducted for probing new particles beyond the SM at the LHC, including the supersymmetric dark matter candidates [39, 40], quasistable or nearly-degenerate charginos in specific SUSY scenarios [41−43] and multiple charged scalars in seesaw and left-right symmetric models [44−46].

In this paper, we will propose a search strategy for probing degenerate doubly-charged scalars in the type-II seesaw model via tagging forward protons at the LHC, within the context of both normal and inverted hierarchies of neutrino mass spectra. In the next section, we concisely introduce the multiple scalars of the type-II seesaw and their production and decay at the hadron collider, as well as the connection to neutrino physics. In Section III, details on the signals and simulation will be presented. Section IV is about our proposed search strategies and results. Finally, we draw the conclusion in Section V.

The seesaw mechanism of type-II for neutrino mass generation can be realized in a simple way by extending the SM with a complex scalar triplet lying in the adjoint representation of the weak group $ SU(2)_{L} $,

with hypercharge $ Y_{\Delta}=1 $ as in the convention for the formula $ Q=T_{3}+Y $. A gauge-invariant and most general renormalizable Lagrangian for the type-II seesaw scalar sector can be expressed as [47, 48]

where H is the SM Higgs doublet $ H=\left(\phi^{+},\,\phi^{0}\right)^{{\rm{T}}} $ and $ V(H,\Delta) $ stands for the scalar potential, including contributions from the SM Higgs and the triplet scalar [47, 48]

in which $ m^{2}_{H,\Delta} $ are mass parameters for the SM Higgs and the triplet scalar. λ and $ \lambda_{1\sim4} $ are quartic couplings that can be taken as real numbers without loss of generality. μ is the coupling for trilinear terms, which may violate lepton number conservation.

Besides the kinetic terms and scalar potential, type-II seesaw introduces an additional Yukawa interaction between the triplet scalar and the SM lepton doublets $ L=(\nu_{\ell}\,,\ell)^{T} $ for neutrino mass generation,

where $ y_{\Delta} $ is the Yukawa coupling and C the charge conjugation operator. Once the doublet and triplet scalars develop non-vanishing vacuum expectation values after the spontaneous electroweak symmetry breaking as $ v_{0} $ and $ v_{\Delta} $, respectively, the seesaw mechanism works to generate Majorana masses of neutrinos

where the complex symmetric matrix $ {\cal{M}}_{\nu} $ can be diagonalized using the PMNS mixing matrix U as $ {\cal{M}}_{\nu}=U^{*}m_{\nu}U^{\dagger} $. The parameterization of PMNS matrix can generally be expressed in the following way [49]

in which $ c_{ij}=\cos\theta_{ij} $ and $ s_{ij}=\sin\theta_{ij} $ with $ \theta_{ij} $ being the mixing angles lying in the range of [0,$ \pi/2 $] without loss of generality. δ and $ \eta_{1,2} $ refer to Dirac and Majorana phases, respectively. Diagonal $ m_{\nu} $ incorporates three physical neutrino masses mixed by three flavors through the mixing matrix, entries of which can be largely determined by various neutrino oscillation experiments except for the minimal neutrino mass $ \nu_{1/3} $, corresponding to normal hierarchy (NH)/inverted hierarchy (IH), and two Majorana phases. As the minimalization of the scalar potential Eq (3) leads to $ v_{\Delta}\approx\mu v^{2}_{0}/m^{2}_{\Delta} $ with the electroweak vacuum $ v^{2}=v^{2}_{0}+v^{2}_{\Delta}\approx246^{2}\,{\rm{GeV}}^{2} $, one can infer that a large $ m_{\Delta} $ or a small μ can both induce a small $ v_{\Delta} $, giving tiny neutrino masses in a seesaw way. Besides, triplet scalar VEV contributes to radiative corrections for ρ parameter in electroweak precision observables as a result of modifications to W and Z masses, leading to the prediction $ \rho\approx1-2v^{2}_{\Delta}/v^{2} $. Given the current results for global fit $ \rho=1.00031\pm0.00019 $ [49], an upper limit for $ v_{\Delta} $ can be obtained around 2.8 GeV at $ 3\sigma $ C.L., far less than the doublet VEV $ v_{0} $. Since the non-diagonal Yukawa matrix $ y_{\Delta} $ gives rise to lepton flavor violating processes including $ \mu^{-}\to e^{+}e^{-}e^{-} $ and $ \mu^{-}\to e^{-}\gamma $, upper bounds for the branching ratios of these rare decays [50, 51] can then be translated into a bound from below for $ v_{\Delta} $ depending on $ m_{\Delta^{\pm\pm}} $:

exhibiting the order of magnitude of $ v_{\Delta} $ for TeV-scale $ \Delta^{\pm\pm} $ [52, 53].

As stated briefly above in Section. 1, decay modes of the doubly charged scalars depend on the triplet VEV $ v_{\Delta} $ and their mass spectrum. Decay width for the leptonic decay modes can be given as [32, 47, 48, 54]:

which, if $ v_{\Delta}<10^{-4} $ GeV, dominate over the gauge bosonic ones:

where i, j stand for lepton flavors, $ \delta_{ij} $ the Kronecker delta symbol and g the weak gauge coupling. Cascade decay channels $ \Delta^{\pm\pm}\to\Delta^{\pm}W^{\pm} $ are possible kinematically only if the mass difference $ \Delta m= m_{\Delta^{\pm\pm}}-m_{\Delta^{\pm}}>0 $ and are dominant for a sufficiently large value of $ \Delta m $ to a few or tens of GeV [48], which is beyond the scope of the present work focusing on the case of a degenerate mass spectrum. For the case of non-degeneracy, relevant studies [48] and references therein can be referred to, where cascade decays are taken into consideration. In the present paper, considering the constraints from electroweak precision measurements and lepton flavor violating decays discussed above in Section. 1, we can safely assume a triplet VEV much smaller than $ 10^{-4} $ GeV so that only leptonic decay modes will be relevant in our following analysis of the collider search for the doubly charged Higgs bosons.

Different from the well-studied Drell-Yan production for the doubly charged scalars introduced in Section. 1, we study in the present paper a search strategy through photon fusion pair production $ \gamma\gamma\to\Delta^{\pm\pm}\Delta^{\mp\mp} $, where the initial photons come from equivalent photon approximation (EPA) alongside the ultraperipheral collision of protons at the LHC. Two colliding protons remain intact in the final states to be tagged by the forward detectors. This way of production arises from the fully elastic channel whose total cross section can be written as

where $ \gamma^{el}_{1/2}(z_{1/2}) $ are γ-PDFs, distribution functions of the elastic equivalent photon in a proton with $ z_{1/2} $ being momentum fractions. Elastic γ-PDFs indicate the probabilities a proton radiates a photon elastically while itself remains undamaged, analytic expressions of which can be found in [55, 56]. The convolution integral over the momenta should not be taken over the whole range of parametric space, as the forward detectors measure final protons with various efficiencies depending on the proton energy loss $ \xi\equiv1-E_{{\rm{out}}}/E_{{\rm{in}}} $, with $ E_{{\rm{in}}/{\rm{out}}} $ referring to energies of the ingoing/outgoing protons. These effects are taken into account by translating the tagging efficiencies for protons to the ones for the elastic photons, which we will discuss below.

To realize a better sensitivity in the hadronic environment at the LHC, we assume $ v_{\Delta}<10^{-4} $ GeV as discussed in the previous section and decay the doubly charged Higgs bosons into pairs of leptons ($ e^{\pm} $ or $ \mu^{\pm} $). Such a process through elastic photon fusion can then be expressed as

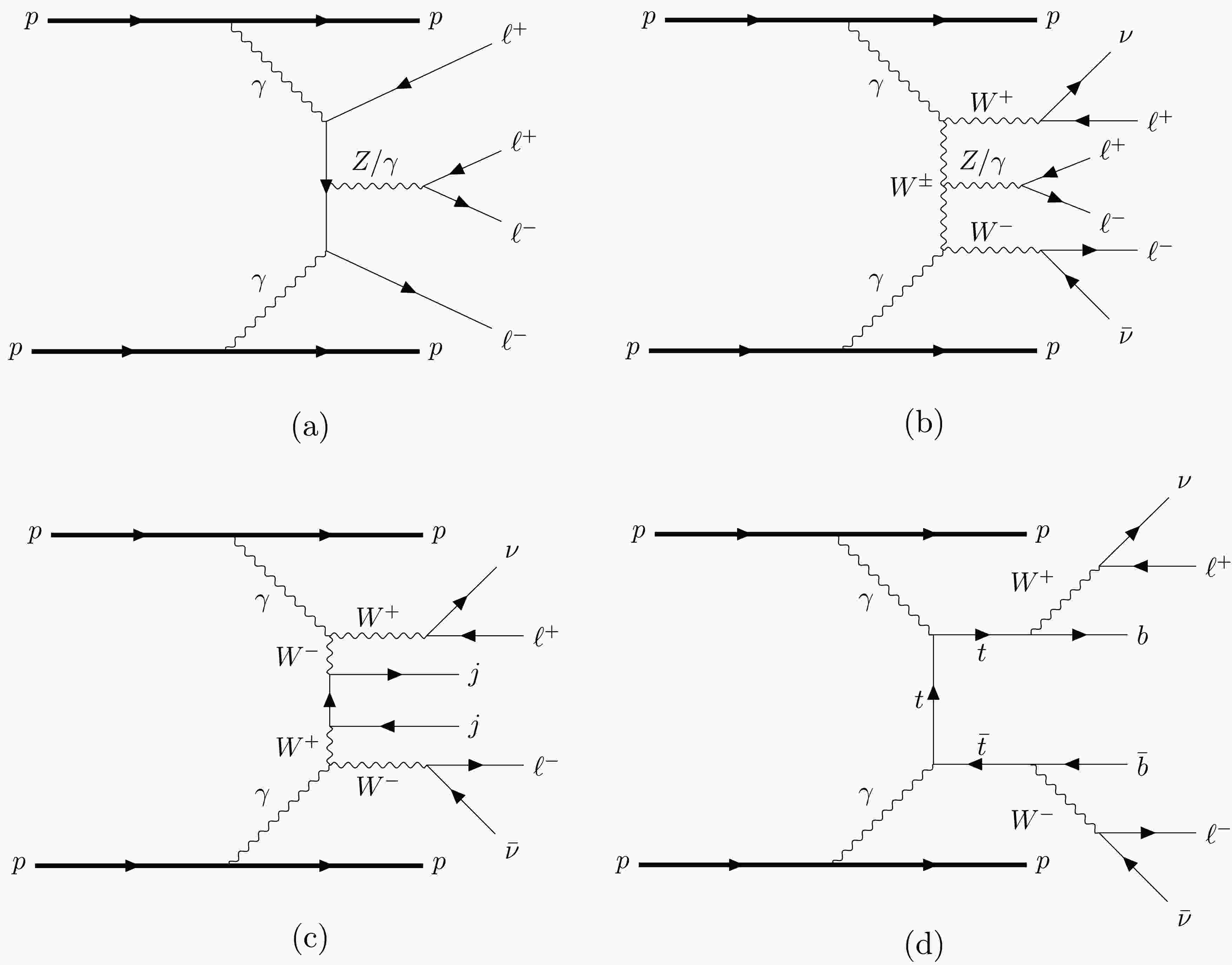
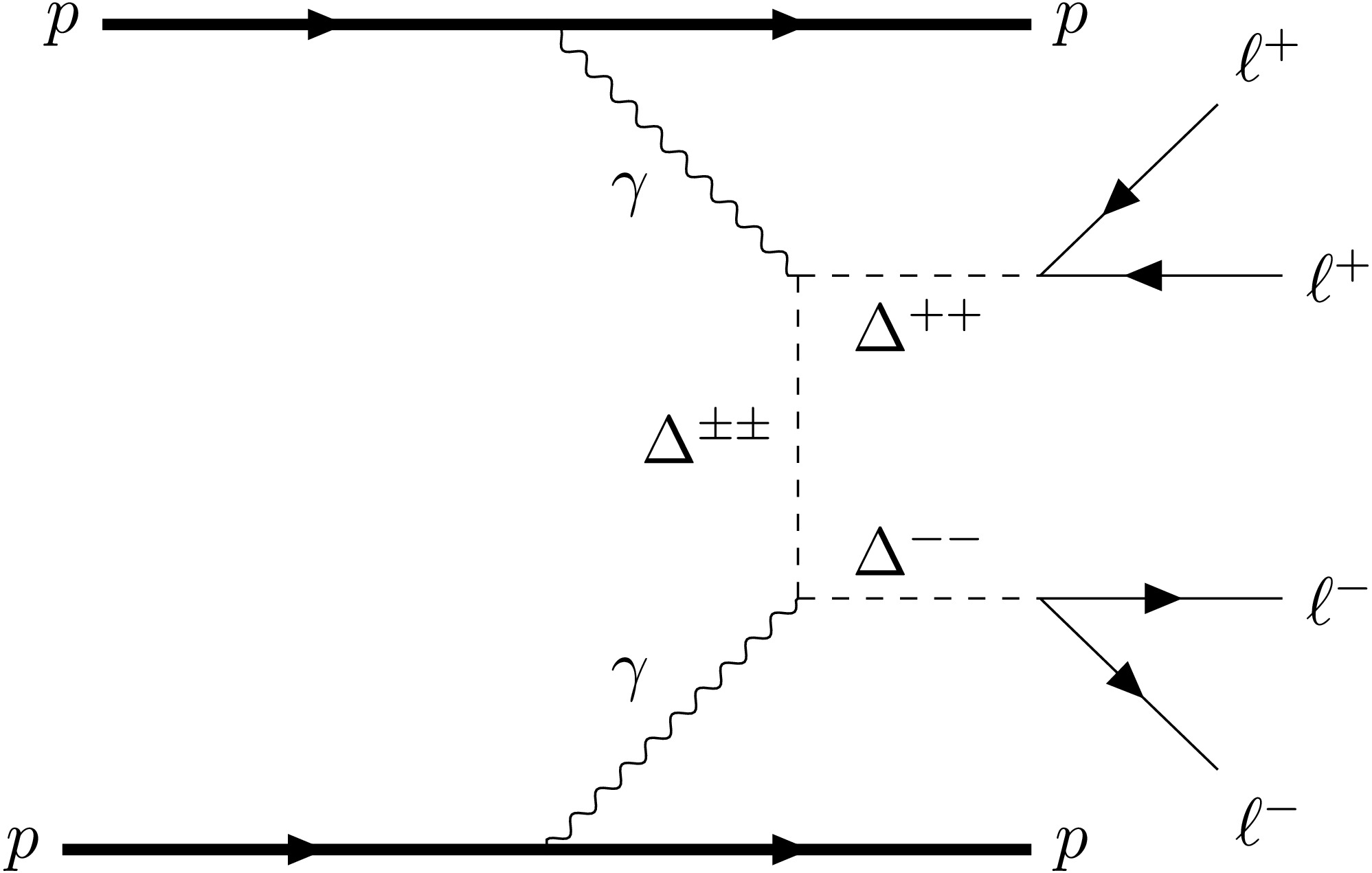
where $ \ell_{1,2,3,4} $ can be different combinations of lepton flavors. Corresponding Feynman diagrams are displayed in Figure. 1, drawn using the TikZ-Feynman package [57]. According to the expression of decay width Eq.(8), although the nature of neutrino mass is still unknown which is sensitive to the neutrinoless double beta decay experiment, the oscillation data can, to a large extent, fix some elements of the neutrino mass matrix $ {\cal{M}}_{\nu} $ and then the branching ratios of certain leptonic decay channels. In our following simulation, we adopt the best-fit values for neutrino mixing parameters for the NH and IH cases [58, 59]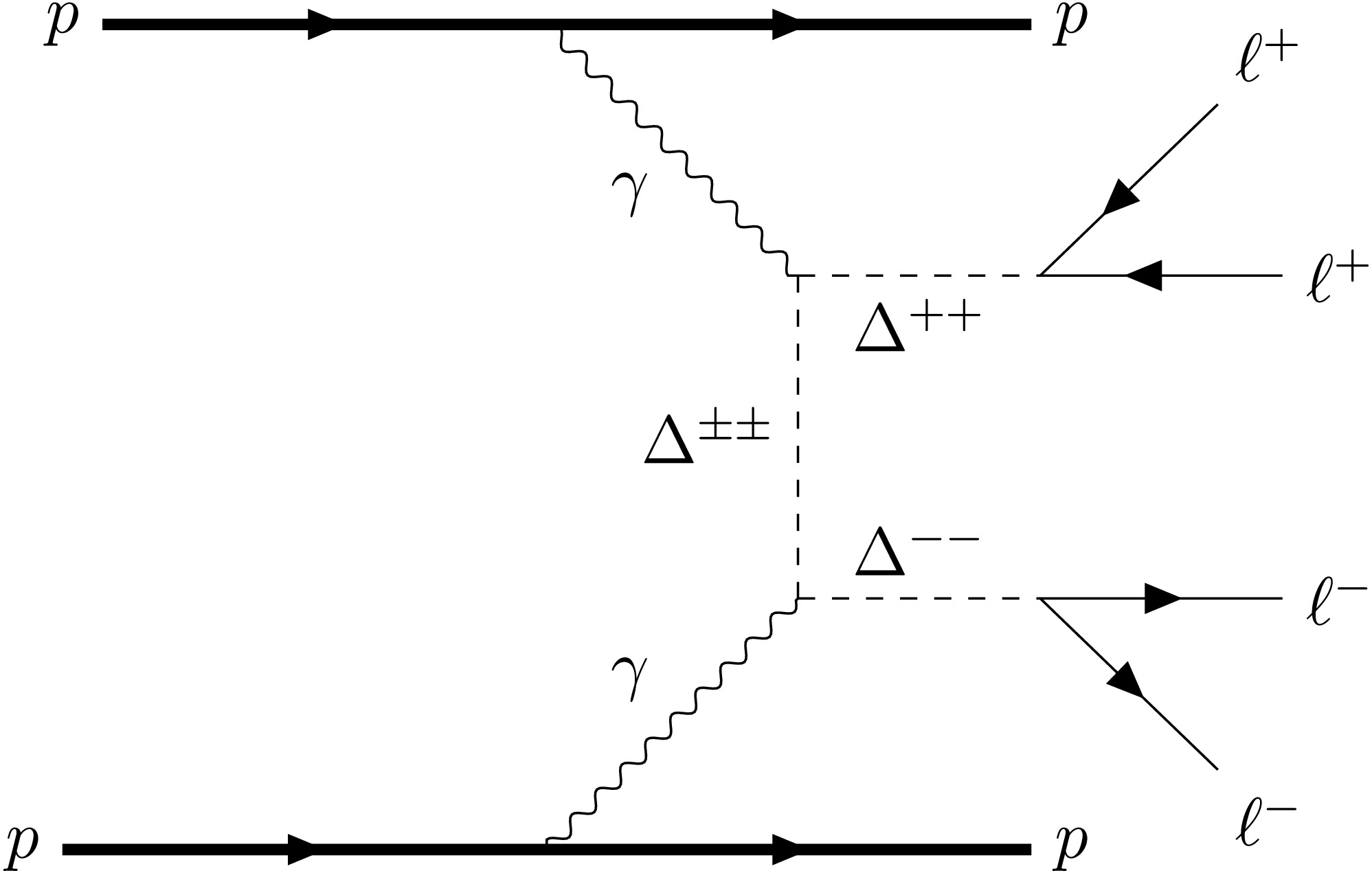

Figure 1.  Feynman diagram for the signal process of fully leptonic channel from doubly charged scalars pair production through elastic photon fusion at the LHC.

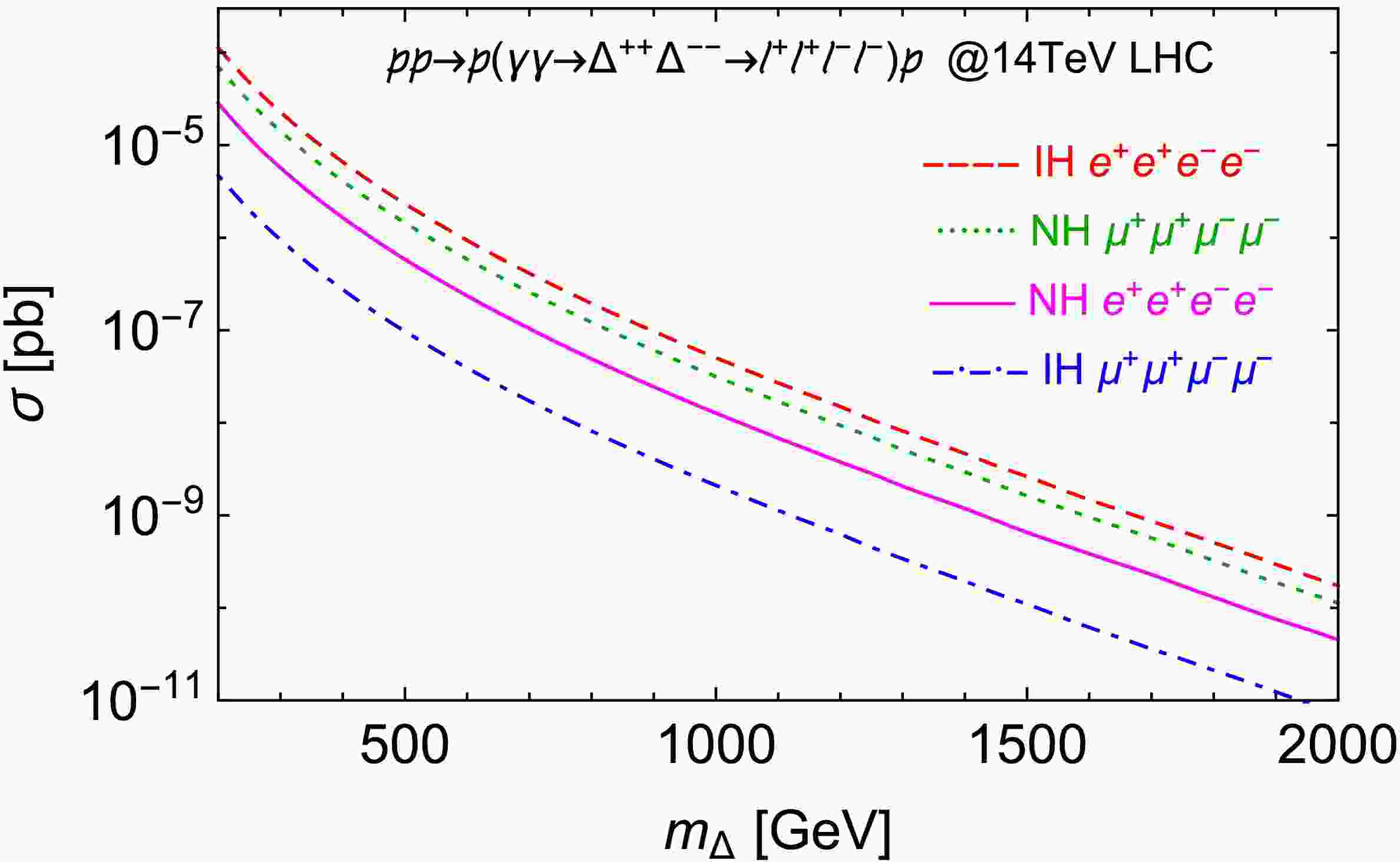
Note that two Majorana phases are assumed to vanish and the lightest neutrino mass is adopted as $ 10^{-4} $ eV. With these best-fit values input, the leading decay channel is $ \Delta^{\pm\pm}\to\mu^{\pm}\tau^{\pm} $ (BR~ 35%) for NH case and $ \Delta^{\pm\pm}\to e^{\pm}e^{\pm} $ (BR~ 47%) for IH case [60]. In consideration of better detection efficiencies at the LHC experiments for electrons and muons, we choose only electrons and muons in the final states as our signals where both scalars decay into $ \ell_{1\sim4}=\mu $ (BR~ 25% for $ \Delta^{\pm\pm}\to\mu^{\pm}\mu^{\pm} $ under the above assumptions for neutrino mixing [60]) for NH and $ \ell_{1\sim4}=e $ for IH. Figure. 3 displays cross sections for these processes versus the triplet scalar mass ranging from 200 GeV to 2 TeV, in which the difference of branching ratios of Δ decaying into different lepton flavors also manifests itself as discussed above: for NH, the muon channel surpasses the electron one and vice versa for IH.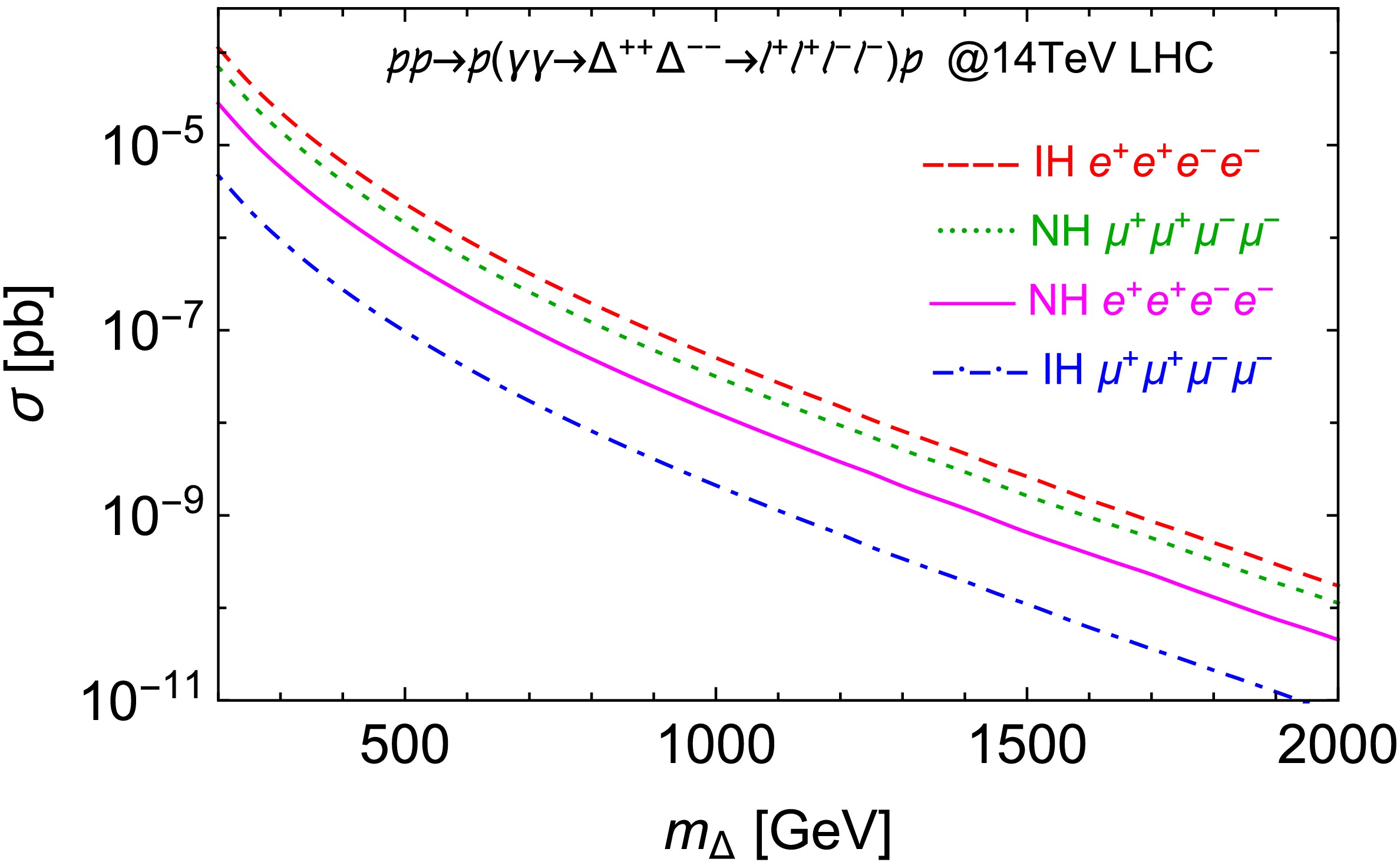

Figure 3.  (color online) Total cross sections of $ pp\to p(\gamma\gamma\to $$ \ell^{+}\ell^{+}\ell^{-}\ell^{-})p $ with 4-electron and 4-muon final states for both normal and inverted hierarchies of neutrino mass spectra.

Standard Model background corresponding to the above signals includes direct production of charged leptons through elastic photon fusion associated with a $ Z/\gamma $ decaying into a lepton pair (Figure. 2(a)), as well as a W pair production through the photon fusion associated with a $ Z/\gamma $ (Figure. 2(b)), with two intact protons in the final state,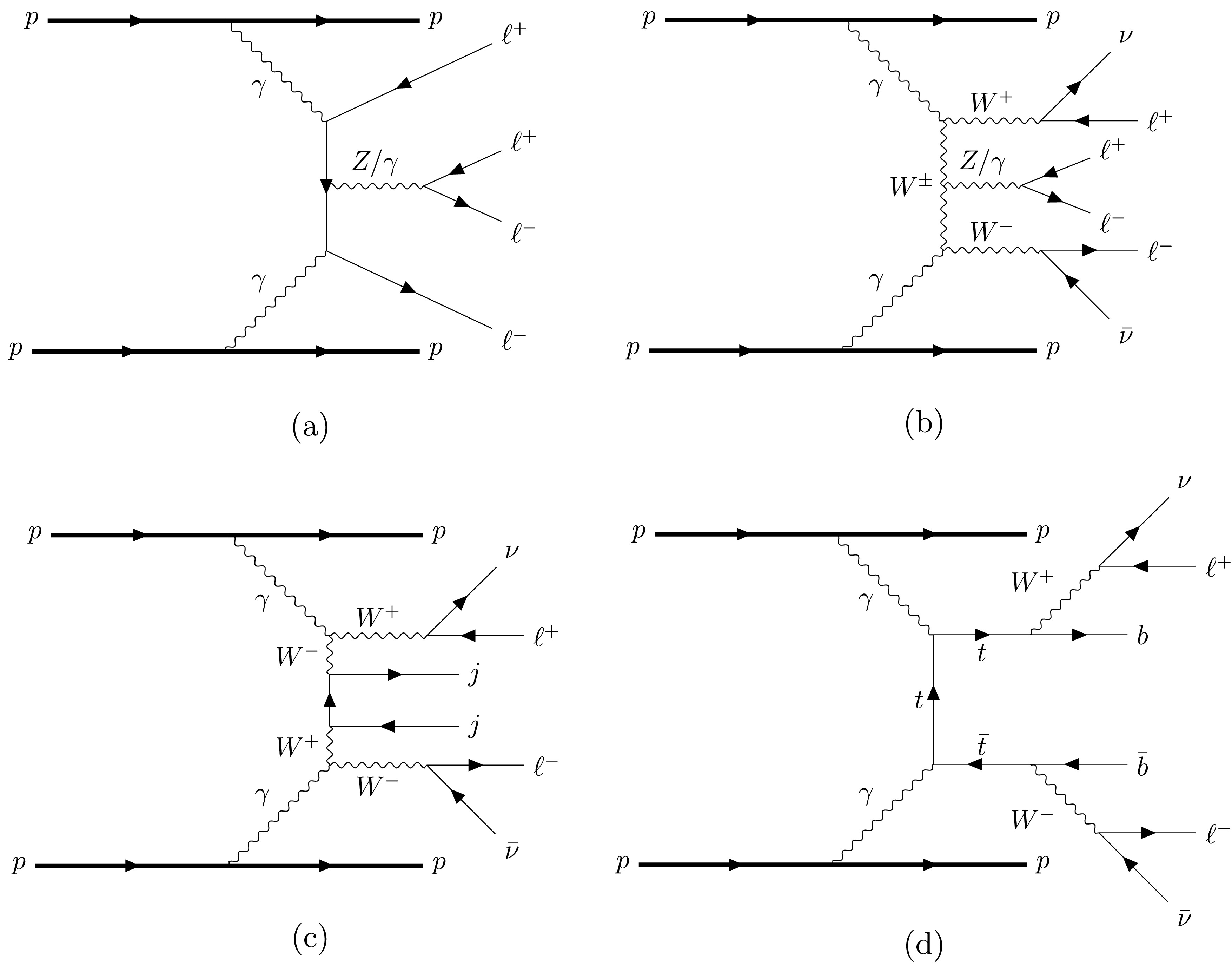

Figure 2.  Feynman diagrams of the Standard Model background for fully leptonic channels through elastic photon fusion at the LHC. t-channel $ Z/\gamma $-mediating diagrams in (a) and (b) are not shown but taken into consideration in our analysis.

Note that in the above diagrams, the mediating gauge boson $ Z/\gamma $ is shown going through s-channel, while a t-channel contribution is also considered but not shown in the figures for simplicity. Similar to the process in Figure. 2(b), associated production of two light jets along with the photon fusion into two W bosons can also mimic the signal when the jets are misidentified as leptons, so the following process is also considered as one of our background (Figure. 2(c))

Another background is top quark pair production through EPA photon fusion, followed by the top leptonic decay (Figure. 2(d)),

which also contaminates the signal if b-jets are misidentified as leptons.

To arrive at an effective search strategy for the fully leptonic channel from the doubly charged scalar at the LHC, we perform simulations using MᴀᴅGʀᴀᴘʜ5_ᴀMC@NLO (v3.5.6) [61] for parton-level events generation and calculations for cross sections. Parton showering and detector simulation are realized by Pʏᴛʜɪᴀ-8.2 [62] and Dᴇʟᴘʜᴇs-3.5.0 [63] embedded in ChᴇᴄᴋMATE2 [64] for further analysis and event selection. For model files, we use the Tʏᴘᴇɪɪsᴇᴇsᴀᴡ Universal Fᴇʏɴʀᴜʟᴇs Output (UFO) libraries that are developed in [38]. γ-UPC packages [66] are used as γ-PDF for event generation of elastic photon fusion in ultra-peripheral collision of protons.

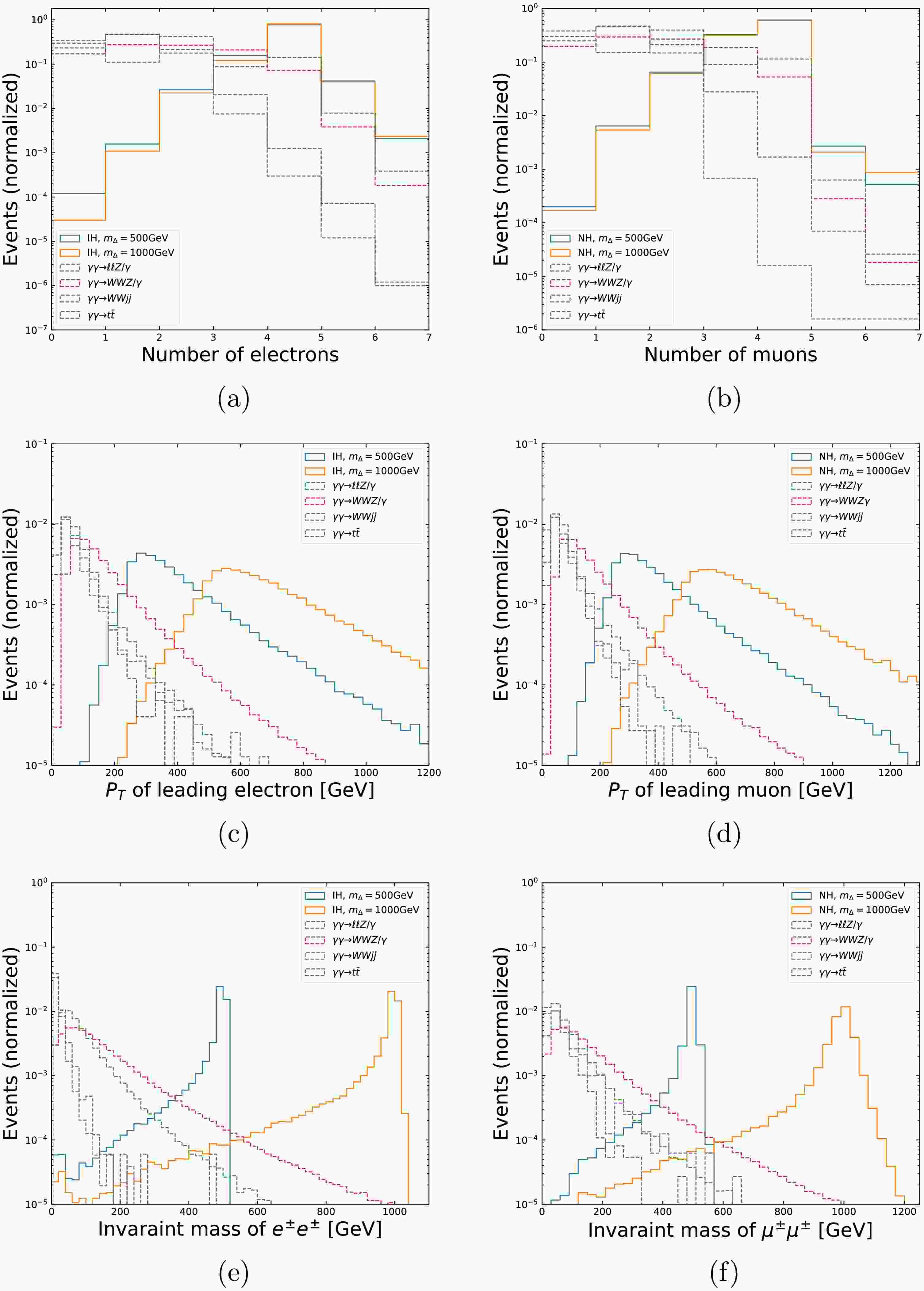
One of the most characteristic features of the signal is the final two intact protons, and, as discussed in Section. 3, they are not 100% detectable by the forward detectors at the LHC, but rather measured at some rates depending on their energy losses. In view of the elastic nature of the ultraperipheral collision, the energies of elastic photons $ E_{\gamma} $ emitted from the protons can be considered equal to the energy losses. For $ E_{\gamma} $ from 100 GeV to 1 TeV, the detection rate for final protons approximates 100% at the 13 TeV LHC, which can be translated to the energy loss ξ of (0.015, 0.15) defined in Section. 3 [35, 36]. In our simulation, we adopt more conservative detection rates (Table 1) since lower efficiencies around 90% are generally indicated by phenomenological studies [40]. These values of proton tagging rates are then applied to the generated events, leaving only part of the events for further selection. This procedure can be viewed as a pre-selection in which the four-momenta of final protons are smeared with a 5%-width Gaussian function prior to the tagging rates application to realize the forward detector simulation. We use PYLHE [65] package to process the MG5-generated events and to do the smearing.

Events surviving the pre-selection then go through further cuts based on different features of kinematic distributions for the signal and background. We present for illustration the histograms of three typical kinematic variables for signal and background events in Figure. 4, including the number of electrons (muons), transverse momentum of the leading electron (muon) and the invariant mass of same-sign electrons (muons) for inverted (normal) hierarchy. As examples, the benchmarks are chosen as $ m_{\Delta}=500 $ and 1000 GeV and the final states correspond to Eq. (11) with $ \ell=e $ (for IH) and $ \ell=\mu $ (for NH), while the histograms for background correspond to Eq. (14) to (17). For simplicity, we show only one of the neutrino mass hierarchies in each figure of kinematic distributions. The histograms corresponding to the other hierarchy are not shown here, as they behave similarly to the displayed one. One can tell from Figure. 4(a) and (b) that the number of electrons or muons for either IH or NH centers around 4, while for the SM backgrounds, the distributions peak around a much smaller electron or muon number. Since each pair of the final same-sign leptons in the signal events comes from the decay of a heavy scalar, their momenta tend to be much larger than those in the background events. And as the mass of Δ increases, the peak values grow larger as well, which can be seen clearly from the distributions of leading lepton $ p_{T} $ in Figure. 4(c) and (d). Hence, one of the key features to distinguish the signal from backgrounds is multiple leptons with high $ p_{T} $. Another distinctive feature of the signal also comes from Δ decay, which is displayed in Figure. 4(e) and (f), showing distributions of the invariant mass reconstructed from same-sign electrons or muons. For signal events, the histograms exhibit clear endpoints centering around the values of $ m_{\Delta} $, while the background ones peak at a smaller range with relatively longer tails.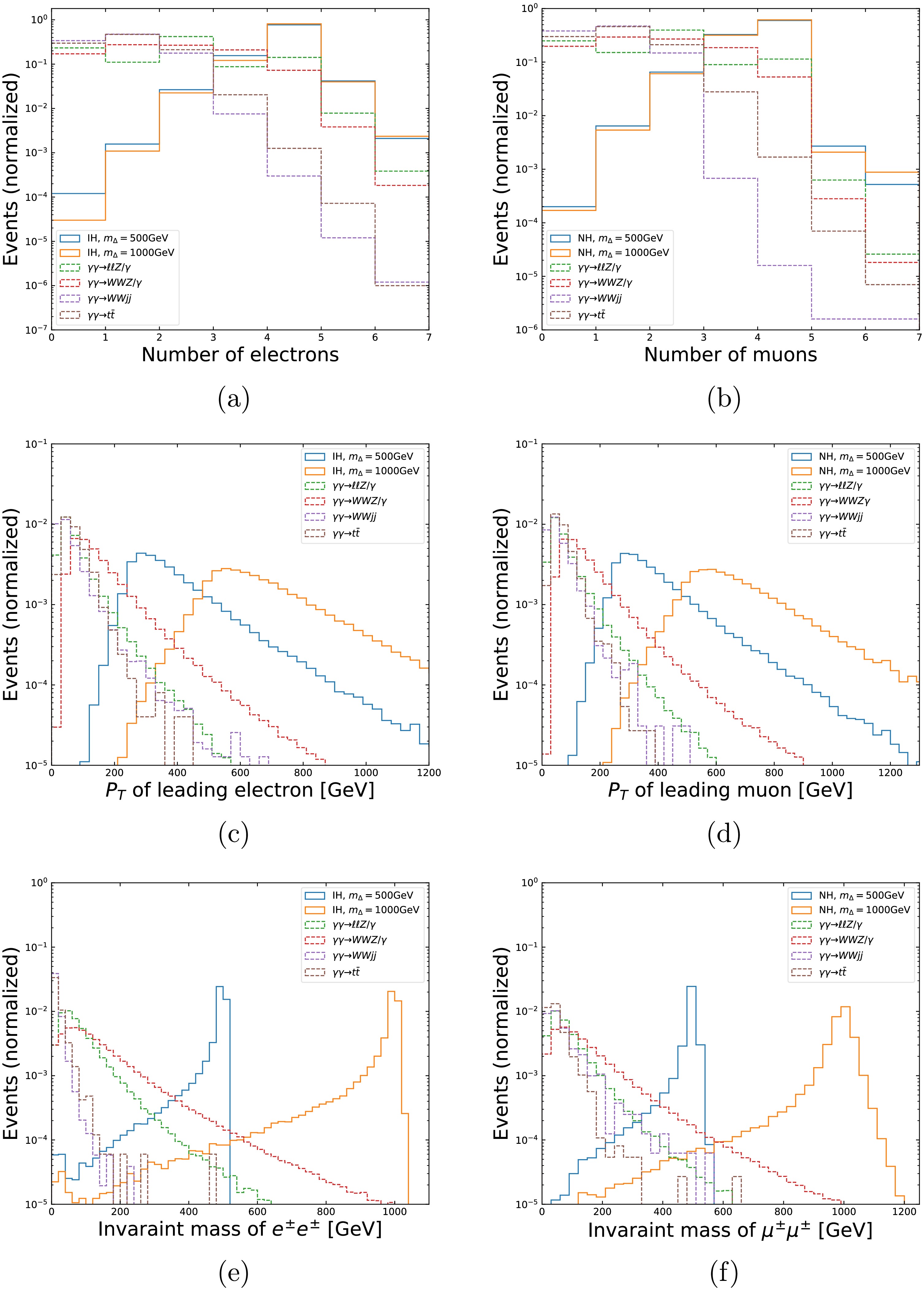

Figure 4.  (color online) Kinematic distributions of electron (muon) number, transverse momentum of the leading electron (muon) and invariant mass of same-sign electrons (muons) from elastic photon fusion at the LHC: $ pp\to p(\gamma\gamma\to\Delta^{++}\Delta^{--}\to\ell^{+}\ell^{+}\ell^{-}\ell^{-})p $, for inverted (normal) hierarchy spectrum as signal, as well as for four SM background processes at the LHC. Histograms for the signals are shown in solid lines and those for backgrounds are shown in dashed lines.

Based on the above kinematic distributions for $ 4e $ events of the IH case and $ 4\mu $ events of the NH case, we perform event selections (Table 2) to achieve a better signal significance for each case. As discussed, the final two intact protons are detected with certain efficiencies (Table 1), we can regard this procedure as a step of pre-selection of the events. Then two pairs of opposite same-sign electrons ($ e^{+}e^{+}e^{-}e^{-} $) and muons ($ \mu^{+}\mu^{+}\mu^{-}\mu^{-} $) are required as cut-1 for IH and NH, respectively. Cut-2 is $ p_{T}>50 $ GeV for the leading lepton and cut-3 on the invariant mass of the pair of same-sign leptons $ m({\ell^{\pm}\ell^{\pm}}) $. To realize a relatively optimal selection strategy and signal significance, we apply specific selection criteria on $ m({\ell^{\pm}\ell^{\pm}}) $ to each benchmark point of $ m_{\Delta} $. For the final states of $ e^{+}e^{+}e^{-}e^{-} $ in signal region of IH, cut-3 is adopted as $ m(e^{\pm}e^{\pm})\in[m_{\Delta}-25,m_{\Delta}+15] $ GeV, while for $ \mu^{+}\mu^{+}\mu^{-}\mu^{-} $ final states in signal region of NH, cut-3 is $ m(\mu^{\pm}\mu^{\pm})\in[m_{\Delta}-20,m_{\Delta}+20] $ GeV. As examples, Table 3 and 4 display cutflows of effective cross sections for the signal and background through these cuts for $ m_{\Delta}=500 $ and 850 GeV under NH and IH, respectively. For both cases, we can see from the tables that cut-1 on leptonic multiplicities can largely suppress the backgrounds of $ W^{+}W^{-}jj $ and $ t\bar{t} $ events, while cut-3 on invariant mass of same-sign lepton pair can basically filter out the other two: $ \ell^{+}\ell^{-}Z/\gamma $ and $ W^{+}W^{-}Z/\gamma $.

Masses of the doubly charged scalar are scanned with a step of 50 GeV from 200 to 1500 GeV under both IH and NH spectra of neutrino mass. Event selections are then applied according to Table. 2 with regard to two different final states of $ e^{+}e^{+}e^{-}e^{-} $ and $ \mu^{+}\mu^{+}\mu^{-}\mu^{-} $, under neutrino mass spectra of IH and NH, respectively. The expected significance is finally calculated for each scanned point of $ m_{\Delta} $ using the formula

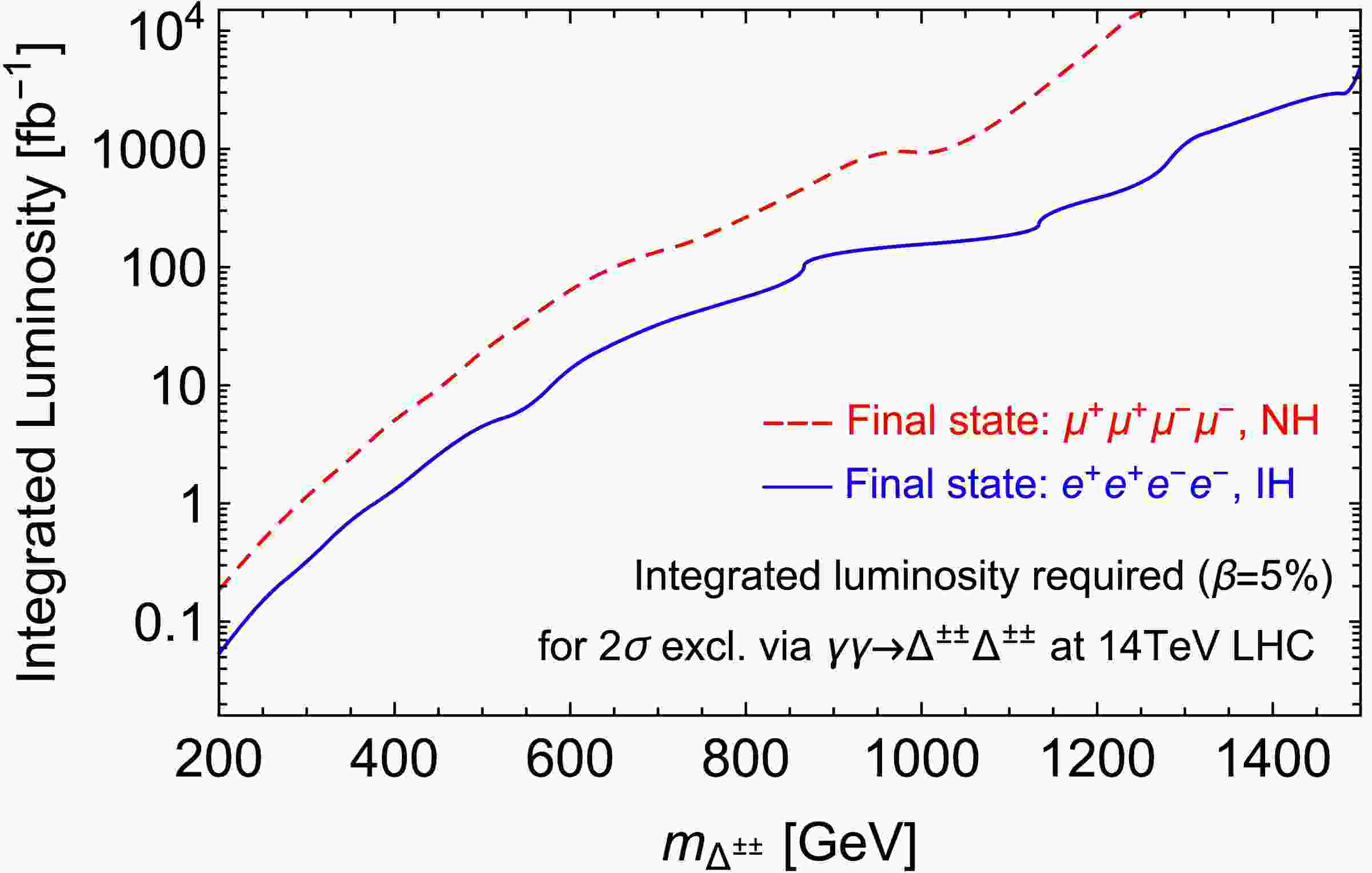
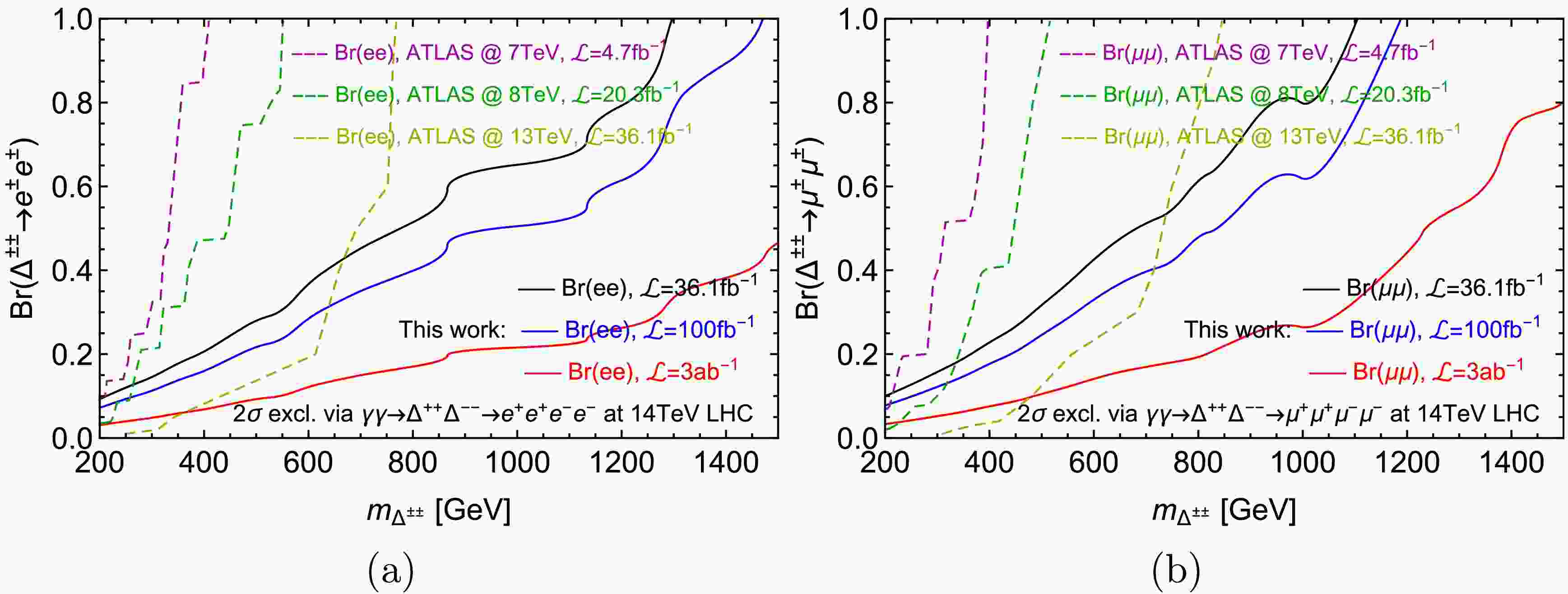
where $ S(B) $ refers to signal (background) events after the event selections in Table. 2 and β the systematic uncertainty. Given the parameters input for the neutrino mixing matrix in the cases of IH and NH (Eq. 13 and 12), we obtain the luminosities needed to arrive at $ 2\sigma $ exclusion limits for every scanned $ m_{\Delta} $, the fitted curves of which are shown in Figure. 5. For luminosities of 36.1 fb^-1, 100 fb^-1 and 3 ab^-1, $ 2\sigma $ exclusion limits are also obtained for the branching ratios of $ \Delta\to\mu\mu $ for NH and the ones of $ \Delta\to ee $ for IH at each point of $ m_{\Delta} $. We present in Figure. 6 showing contours in the parametric space of the diagonal branching ratios versus $ m_{\Delta} $. As a comparison, exclusion bounds are also presented from searching for prompt same-sign lepton pairs by the ATLAS experiment [67−69] at 7, 8 and 13 TeV with 4.7, 20.3 and 36.1 fb^-1 of integrated luminosities, respectively.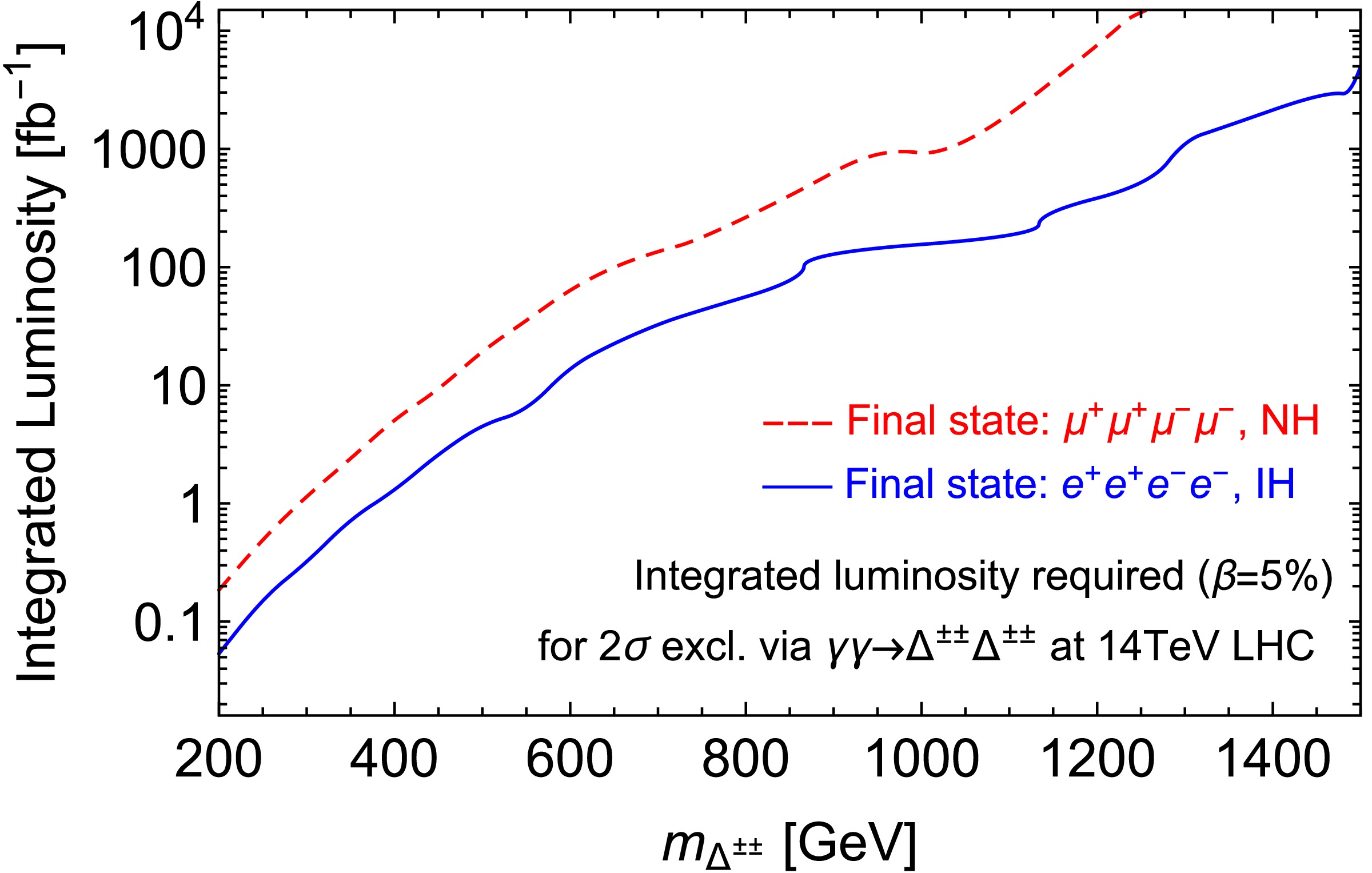

Figure 5.  (color online) Integrated luminosities required to reach $ 2\sigma $ exclusion searching for fully elastic photon fusion $ pp\to p(\gamma\gamma\to\Delta^{++}\Delta^{--}\to\ell^{+}\ell^{+}\ell^{-}\ell^{-})p $ at the 14 TeV LHC. Systematic uncertainty β is assumed as 5%. Red dashed lines correspond to $ \mu^{+}\mu^{+}\mu^{-}\mu^{-} $ state in case of NH, while blue solid lines correspond to $ e^{+}e^{+}e^{-}e^{-} $ state in case of IH.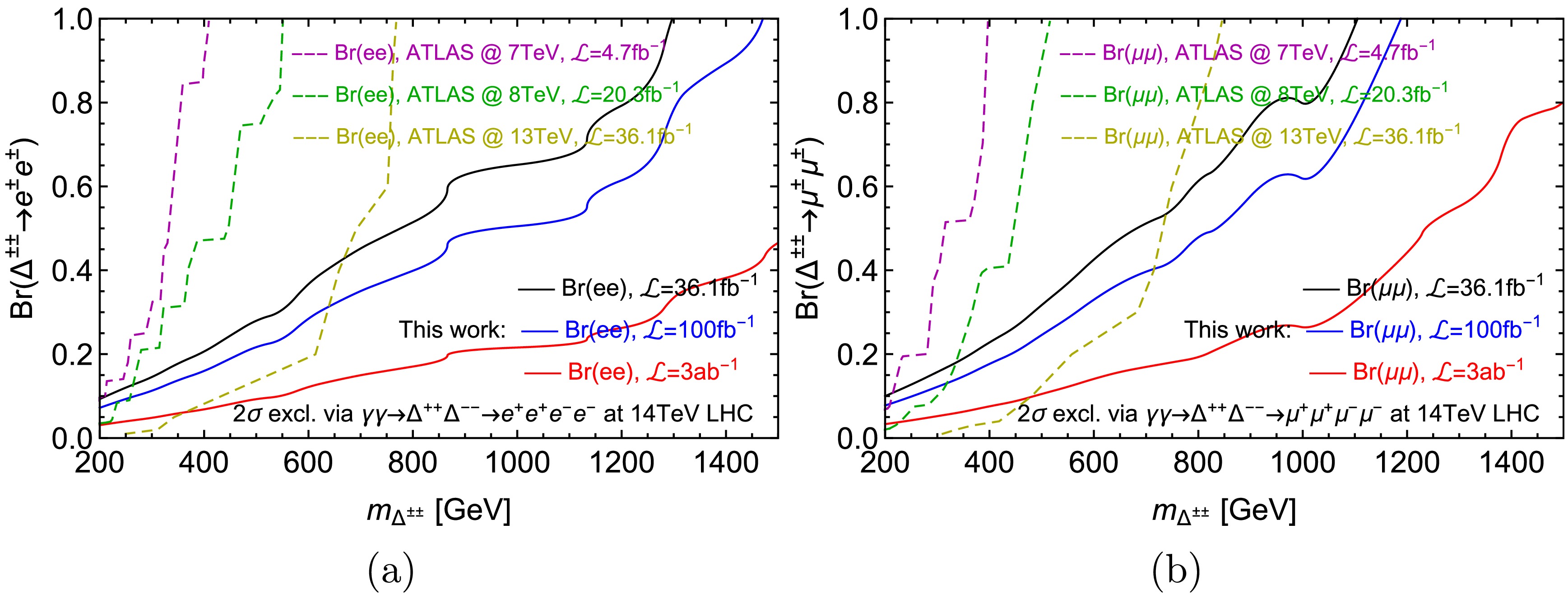

Figure 6.  (color online) Branching ratios that can be excluded at 95% C.L. via searching for fully elastic photon fusion $ pp\to p(\gamma\gamma\to\Delta^{++}\Delta^{--}\to\ell^{+}\ell^{+}\ell^{-}\ell^{-})p $ at the 14 TeV LHC, shown in black ($ {\cal{L}}=36.1{\rm{fb}}^{-1} $), blue ($ {\cal{L}}=100{\rm{fb}}^{-1} $) and red ($ {\cal{L}}=3{\rm{ab}}^{-1} $) solid lines. Systematic uncertainty β is assumed as 5%. Figure (a) and (b) are respectively for branching ratios of $ \Delta^{\pm\pm}\to e^{\pm}e^{\pm} $ and $ \mu^{\pm}\mu^{\pm} $. Dashed lines are bounds from the ATLAS experiment [67−69].

From Figure. 5 and 6, one can infer that sensitivities for $ e^{+}e^{+}e^{-}e^{-} $ final states are better than that for $ \mu^{+}\mu^{+}\mu^{-}\mu^{-} $. This performance results partly from our assumptions for NH and IH neutrino mass spectra under which the Δ decay branching ratio into electrons (~ 47%) is larger than that into muons (~ 25%). As $ m_{\Delta} $ increases, the cross sections of elastic photon fusion production of $ \Delta^{++}\Delta^{--} $ decrease rapidly, leading to lower sensitivities for branching ratios in the range of larger masses as expected (see solid lines in Figure. 3). Similar behavior of exclusion curves can be seen in the searches through Drell-Yan production followed by multileptonic final states (see dashed lines in Figure. 3 [69]). However, comparing these results, it can be seen that for both $ e^{+}e^{+}e^{-}e^{-} $ and $ \mu^{+}\mu^{+}\mu^{-}\mu^{-} $ states, the sensitivity for branching ratios via elastic photon fusion decreases more slowly and smoothly as $ m_{\Delta} $ grows than that of the Drell-Yan production searches. For example, in the mass range below 650 GeV, the Drell-Yan production search can probe smaller branching ratios Br$ (\Delta^{\pm\pm}\to e^{+}e^{+})<40 $% with $ {\cal{L}}=36.1 $ fb^-1. While for a relatively larger mass range beyond 650 GeV, the photon fusion search of the present work displays better sensitivity and can extend the $ 2\sigma $ exclusion limit until TeV region for similar branching ratios (see black solid lines in Figure. 6). As for the probing sensitivity for branching ratio Br$ (\Delta^{\pm\pm}\to \mu^{+}\mu^{+}) $, photon fusion search exceeds the Drell-Yan search in the mass range larger than 750 GeV with $ {\cal{L}}=36.1 $ fb^-1. Similar advantages of the photon fusion search across larger mass range can also be seen in other luminositiy scenarios (see blue and red solid lines in Figure. 6 for $ {\cal{L}}=100 $ fb^-1 and 3 ab^-1).

Specifically, with a collision energy of 14 TeV and integrated luminosity of 36.1 fb^-1, a $ 2\sigma $ exclusion limit for $ m_{\Delta} $ can reach 730 GeV for Br$ (\Delta\to ee)$~47% under IH spectrum and surpasses the limits given by the ATLAS experiment at $ m_{\Delta}\sim685 $ GeV [69]. With higher luminosities of 100 fb^-1 and 3 ab^-1, this bound can be extended to $ m_{\Delta}\sim880 $ GeV and 1.5 TeV, respectively. However, considering the angular limitation of forward detectors for outgoing protons, there exists an upper limit for forward detectors on the invariant mass of final states around 2.6 TeV [45]. For the case of pair production of the doubly charged scalars $ \Delta^{\pm\pm} $, each one has an upper mass limit around 1.3 TeV that the forward detectors can reach. Hence, the exclusion limit of 1.5 TeV obtained in the case of IH spectrum with $ {\cal{L}}=3 $ ab^-1, exceeding the 1.3 TeV upper bound set by the detector itself, should be lowered to 1.3 TeV. On the other hand, with luminosities of 36.1 fb^-1 and 100 fb^-1 the results through $ \mu^{+}\mu^{+}\mu^{-}\mu^{-} $ search are less promising, excluding at 95% C.L. around $ m_{\Delta}\sim430 $ and 520 GeV, respectively, for Br$ (\Delta\to\mu\mu)\sim25 $% under the NH spectrum. But with a higher luminosity of 3 ab^-1, the mass exclusion bound can be improved up to $ m_{\Delta}\sim1 $ TeV, surpassing the limit set by the ATLAS experiment at $ m_{\Delta}\sim620 $ GeV [69].

It should be noted that the enhancement in the sensitivity to $ e^{+}e^{+}e^{-}e^{-} $ final states in the IH case than that of $ \mu^{+}\mu^{+}\mu^{-}\mu^{-} $ states in the NH case largely relies on the enhanced branching ratio of the exotic scalar decaying into electrons. This enhancement is sensitive to the assumed lightest neutrino mass of $ 10^{-4} $ eV, the increase of which will reduce the distinction between branching ratios into leptons of different flavors. Hence, the conclusions for mass exclusion hold for our chosen parameters, especially in the neutrino sector. Note also that the contours shown in Figure. 6 from the ATLAS experiment and the present work both assume a tiny $ v_{\Delta}<10^{-4} $ GeV, so that only dileptonic decay modes are relevant. While under the assumption of $ v_{\Delta}>10^{-4} $ GeV and dominant dibosonic decay, the decay channels $ \Delta^{\pm\pm}\to W^{\pm}W^{\pm} $ have also been thoroughly searched for at the 13 TeV LHC as discussed in Section 2. But due to a larger hadronic background at the hadron collider, weaker bounds on $ m_{\Delta} $ were obtained around $ 200\sim350 $ GeV for degenerate or non-degenerate mass spectra using 36.1~139 fb^-1 collected events [31, 33].

We study the sensitivities for pair production of doubly charged scalars within the type-II seesaw mechanism (with a degenerate mass spectrum of the scalar components) through elastic photon fusion at the 14 TeV LHC: $ pp\to p(\gamma\gamma\to\Delta^{++}\Delta^{--})p $. Two kinds of neutrino mass spectra, normal and inverted hierarchies, are considered. In the case of normal hierarchy, final states of $ \mu^{+}\mu^{+}\mu^{-}\mu^{-} $ are studied as the signal process with integrated luminosities of 36.1 fb^-1, 100 fb^-1 and 3 ab^-1, the $ 2\sigma $ exclusion limits on $ m_{\Delta} $ can reach around 430,520 and 1000 GeV respectively, for branching ratio of $ \Delta^{\pm\pm}\to\mu^{\pm}\mu^{\pm}\sim $ 25%, which is set by adopting the best-fit values of PMNS matrix under NH spectrum. And for the case of inverted hierarchy and a largely fixed branching ratio $ \Delta^{\pm\pm}\to e^{\pm}e^{\pm}\sim $ 47%, final states of $ e^{+}e^{+}e^{-}e^{-} $ are studied as signal under the same luminosities with the exclusion bounds on $ m_{\Delta} $ reaching about 730,880 and 1300 GeV, corresponding to the above luminosities.