-
To date, several pentaquark candidates
$ P_c $ and$ P_{cs} $ have been observed through LHCb collaboration. In 2015, the LHCb collaboration observed$ P_c(4380) $ and$ P_c(4450) $ by analyzing the$ \Lambda_b^0\rightarrow J/\psi K^-p $ decay [1]. In 2019, through the LHCb collaboration, the experimental data were re-investigated at one order of magnitude higher than the previously analyzed data, and observed a narrow pentaquark candidate$ P_c(4312) $ in the$ J/\psi p $ mass spectrum. Its measured Breit-Wigner mass and width were$4311.9\pm0.7^{+6.8}_{-0.6}\,\;{\rm{MeV}}$ and$9.8\pm2.7^{+3.7}_{-4.5}\,\;{\rm{MeV}}$ , respectively [2]. The investigation also showed that$ P_c(4450) $ actually comprised two narrow overlapping peaks$ P_c(4440) $ and$ P_c(4457) $ [2].In 2020, through the LHCb collaboration, evidence of a new structure
$ P_{cs}(4459) $ was observed in the$ J/\psi \Lambda $ mass spectrum with a significance of$ 3.1\sigma $ in the$ \Xi_b^- \to J/\psi K^- \Lambda $ decays [3]. In 2021, the LHCb collaboration observed evidence of a new structure$ P_c(4337) $ in the$ J/\psi p $ and$ J/\psi \bar{p} $ systems in the$ B_s^0 \to J/\psi p \bar{p} $ decays with a significance of$ 3.1\sim3.7\, \sigma $ [4]. In 2022, the LHCb collaboration observed evidence of a new structure$ P_{cs}(4338) $ in the$ J/\psi \Lambda $ mass spectrum in the$ B^- \to J/\psi \Lambda \bar{p} $ decays with Breit-Wigner masses and widths of$ 4338.2\pm 0.7\pm 0.4~{\rm{MeV}} $ and$7.0\pm1.2\pm1.3~{\rm{MeV}}$ , respectively, and the preferred spin-parity$J^P={ \frac{1}{2}}^-$ [5].The spins and parities of those
$ P_c $ and$ P_{cs} $ states have not been fully determined experimentally, and their physical natures are still highly contested. Besides$ P_c(4337) $ , the masses of those$ P_c $ and$ P_{cs} $ states are near the thresholds of the$ \Sigma_c^{(*)}\bar{D}^{(*)} $ and$ \Xi_c\bar{D}^{(*)} $ pairs, respectively. Thus, a typical interpretation is that they are the S-wave hidden-charm meson-baryon molecules with definite isospin I, spin J, and parity P [6−15]. Mass and width are two basic parameters to determine the physical nature of a hadronic state. Recently, many theoretical groups applied different methods to study their masses [6−21] and strong decays [22−28] under the physical picture of meson-baryon hadronic molecules. Different interpretations, such as the diquark-diquark-antiquark type pentaquark states and baryon-meson molecular states, lead to different branching fractions in the strong decays. Moreover, even under the same physical assignments, different theoretic groups obtain very different branching fractions. For example, in the picture of the$ \bar{D}\Sigma_c $ molecular state, the calculations based on the effective Lagrangian (quasipotential Bethe-Salpeter equation) approach indicate that the$ J/\psi p $ and$ \eta_c p $ decay channels play a small role [22, 23] ([24]). The calculations based on the Weinberg-Salam compositeness condition indicate that the ratio$ \Gamma(P_c(4312)\rightarrow \eta_cp):\Gamma(P_c(4312)\rightarrow J/\psi p) =3 $ [25], and the calculations based on the QCD sum rules indicate that the ratio$ \Gamma(P_c(4312)\rightarrow \eta_cp):\Gamma(P_c(4312)\rightarrow J/\psi p) =0.24 $ ($ 3.3 $ ) [26] ([27]).The
$ P_c(4312) $ was observed in the$ J/\psi p $ invariant mass spectrum. Thus, it should have the isospin$I= \frac{1}{2}$ . However, the isospin of the$ \bar{D}\Sigma_c $ state was not specified when it was explored with the QCD sum rules [8−10, 14, 15, 26, 27]. In Refs. [16−18], we comprehensively investigated the color-singlet-color-singlet (or meson-baryon) type hidden-charm pentaquark molecular states without strange, with strange, and with double-strange by distinguishing the isospin. We made possible the reasonable assignments of the$ P_c(4312) $ ,$ P_c(4380) $ ,$ P_c(4440) $ ,$ P_c(4457) $ ,$ P_{cs}(4338) $ , and$ P_{cs}(4459) $ , with many predictions on the masses for the molecular states that future experimental data would confirm.The QCD sum rules approach is a powerful non-perturbative theoretical tool proposed by Shifman, Vainshtein, and Zakharov in 1979 [29, 30]. It has been widely applied to study hadron masses, decay constants, form-factors, and coupling constants [31, 32]. We usually use the three-point or two-point light-cone correlation functions to study the three-hadron coupling constants. On the QCD side, we perform operator product expansion in the large space-like region and at the light cone. Then, we obtain the QCD spectral densities in the spectral representation and match them with the hadron side below the continuum thresholds. Finally, we perform the double Borel transform to obtain the QCD sum rules.
In Ref. [33], we suggested a novel approach to calculating the three-hadron coupling constants with the three-point QCD sum rules based on rigorous duality for the first time. Afterward, rigorous duality was successfully applied to study the strong decays of the exotic tetraquark and pentaquark (molecular) states [26, 34−38]. In this work, we take the
$ P_c(4312) $ as the$ \bar{D}\Sigma_c $ molecular state with the isospin$I= \frac{1}{2}$ and extend our previous work to explore its two-body strong decays with the QCD sum rules based on rigorous duality. Furthermore, we investigate the decays of its higher isospin cousin$ P_c(4330) $ to cross-check the molecule assignment. Observing$ P_c(4330) $ in the$ J/\psi \Delta $ and$ \eta_c \Delta $ decay modes would shed light on the nature of the$ P_c $ states.In our previous work, we observed that a resonant molecular state
$ P_c(4330) $ possibly exists with the isospin$(I,I_3)=( \frac{3}{2}, \frac{1}{2})$ as the cousin of the$ P_c(4312) $ based on the QCD sum rules [16]. We cannot assign a hadron by mass alone; we should at least explore the decays. Herein, we explore its two-body strong decays to select the best channel to search for it experimentally and try to provide a guide for high energy physics experiments. If the predictions can be testified, it would in return prove our interpretations for the nature of the$ P_c(4312) $ . In Refs. [16−18], we distinguish the isospins and comprehensively investigate the hidden-charm molecular states without strange, with strange, and with double-strange. Exploring all the two-body strong decays with the QCD sum rules (also including the mixing effects) and making predictions on the partial decay widths to provide a valuable guide for international high energy physics experiments is very interesting. However, we can only accomplish the tedious calculations one by one.The remainder of the paper is organized as follows: We obtain the QCD sum rules for the strong decays of
$ P_c(4312) $ and$ P_c(4330) $ in Sec. II; we obtain the QCD sum rules for the Δ baryon with isospin$ (I,I_3)=(\frac{3}{2},\frac{1}{2}) $ in Sec. III; we present the numerical results and discussions in Sec. IV; and Sec. V is reserved for our conclusions. -
Following Ref. [16], the quantum numbers
$ (I,J^P) $ of the$ P_c(4312) $ and$ P_c(4330) $ are$ (\frac{1}{2},\frac{1}{2}^-) $ and$ (\frac{3}{2},\frac{1}{2}^-) $ , respectively. Considering the conservation of the isospin I in the strong decays, we study the following processes,$ \begin{aligned}[b] P_c(4312)&\;\rightarrow \eta_c+N\, , \\ P_c(4312)&\;\rightarrow J/\psi+N\, , \\ P_c(4330)&\;\rightarrow \eta_c+\Delta\, , \\ P_c(4330)&\;\rightarrow J/\psi+\Delta\, , \end{aligned} $

(1) where N represents the proton to avoid confusion owing to the four momentum
$ p_\mu $ , and the Δ baryon has the$ (I,J^P)=(\frac{3}{2},\frac{3}{2}^+) $ . We apply the currents$ J_{\eta_c}(x) $ ,$ J_{J/\psi,\mu}(x) $ ,$ J_{N}(x) $ ,$ J_{\Delta,\mu}(x) $ ,$ J_{P}(x) $ , and$ J_{P'}(x) $ to interpolate the$ \eta_c $ ,$ J/\psi $ , N, Δ,$ P_c(4312) $ , and$ P_c(4330) $ , respectively, and list them out explicitly,$ \begin{aligned}[b]& J_{\eta_c}(x) = \overline{c}(x) {\rm i}\gamma_5c(x)\, , \\& J_{J/\psi,\mu}(x) = \overline{c}(x)\gamma_\mu c(x)\, , \\& J_{N}(x) = \varepsilon^{ijk}u^{iT}(x)C\gamma_{\alpha}u^{j}(x)\gamma^{\alpha}\gamma_5d^{k}(x)\, , \\& J_{\Delta,\mu}(x) = \frac{1}{\sqrt{3}} \varepsilon^{ijk}u^{iT}(x)C\gamma_{\mu}u^{j}(x)d^{k}(x)\\&\quad\quad\quad\quad+\sqrt{\frac{2}{3}} \varepsilon^{ijk}u^{iT}(x)C\gamma_{\mu}d^{j}(x)u^{k}(x)\, , \end{aligned} $

(2) $ \begin{aligned}[b] J_{P}(x) =\;& \frac{1}{\sqrt{3}}\varepsilon^{ijk}\overline{c}(x){\rm i}\gamma_5u(x)u^{iT}(x)C\gamma_{\alpha}d^{j}(x)\gamma^{\alpha}\gamma_5c^{k}(x)\\ & -\sqrt{\frac{2}{3}}\varepsilon^{ijk}\overline{c}(x) {\rm i}\gamma_5{\rm d}(x)u^{iT}(x)C\gamma_{\alpha}u^{j}(x)\gamma^{\alpha}\gamma_5c^{k}(x)\, , \\ J_{P'}(x) =\;& \sqrt{\frac{2}{3}}\varepsilon^{ijk}\overline{c}(x) {\rm i}\gamma_5u(x)u^{iT}(x)C\gamma_{\alpha}d^{j}(x)\gamma^{\alpha}\gamma_5c^{k}(x)\\ &+\frac{1}{\sqrt{3}}\varepsilon^{ijk}\overline{c}(x){\rm i}\gamma_5d(x)u^{iT}(x)C\gamma_{\alpha}u^{j}(x)\gamma^{\alpha}\gamma_5c^{k}(x)\, , \end{aligned} $

(3) where the C is the charge conjugation matrix, and i, j, and k are the color indexes. We can observe that the interpolating currents (see Eq. (3)) for the lower and higher isospins of the
$ P_c $ states are different from those constructed in Ref. [26], where we do not consider the clear definition of the isospin. Thus, the calculations of all the related hadronic coupling constants differ significantly at the QCD sides.Generally, we can construct several currents to interpolate one hadron or one current to interpolate several hadrons, as a hadron may have several Fock components. As the currents with the same quantum numbers could mix with each other under renormalization, we should introduce the mixing matrixes U to obtain the diagonal currents,
$ J^{\prime }=UJ $ , which couple potentially to (more) physical states. The matrixes U can be determined by directly calculating the anomalous dimensions of the current operators. However, to date, even for the conventional baryons, we cannot obtain a diagonal current that is a special superposition of several non-trial currents to match with all the considerable Fock states. In this study, we only consider the$ \bar{D}\Sigma_c $ components of the$ P_c(4312) $ and$ P_c(4330) $ with definite spins and isospins. In fact, the$ P_c(4312) $ and$ P_c(4330) $ may have other important Fock components, such as the$ \eta_c N $ ,$ \bar{D}^*\Sigma_c $ ,$ \bar{D}^*\Sigma_c^* $ , and$ \eta_c \Delta $ , where the$ \bar{D} $ ,$ \bar{D}^* $ ,$ \cdots $ ,$ \Sigma_c $ ,$ \Sigma_c^* $ ,$ \cdots $ denote the color-singlet clusters having the same quantum numbers as the conventional mesons and baryons, not the physical mesons and baryons, as we choose the local five-quark currents. We prefer to explore this possibility and accomplish the tedious tasks in our next work, as it will take several months at least. In this study, we calculate the correlation functions with the full QCD, while in Ref. [28], only the heavy quark symmetry and phenomenological contact four-hadron interactions are retained. We should not be surprised if different conclusions are obtained; all the predictions should be compared with future experimental data.Now, we write down the three-point correlation functions in the QCD sum rules,
$ \Pi(p,q) = {\rm i}^2 \int {\rm d}^4x{\rm d}^4y {\rm e}^{{\rm i}p\cdot x}{\rm e}^{{\rm i}q\cdot y} \langle 0|T \left\{ J_{\eta_c}(x)J_N(y) \bar{J}_{P}(0) \right\}|0\rangle\, , $ 
(4) $ \Pi_{1,\mu}(p,q) = {\rm i}^2 \int {\rm d}^4x{\rm d}^4y {\rm e}^{{\rm i}p\cdot x}{\rm e}^{{\rm i}q\cdot y} \langle 0|T \left\{ J_{J/\psi,\mu}(x)J_N(y) \bar{J}_{P}(0) \right\}|0\rangle\, , $

(5) $ \Pi_{2,\mu}(p,q) = {\rm i}^2 \int {\rm d}^4x{\rm d}^4y {\rm e}^{{\rm i}p\cdot x}{\rm e}^{{\rm i}q\cdot y} \langle 0|T \left\{ J_{\eta_c}(x)J_{\Delta,\mu}(y) \bar{J}_{P'}(0) \right\}|0\rangle\, , $

(6) $ \Pi_{\mu\nu}(p,q) = {\rm i}^2 \int {\rm d}^4x{\rm d}^4y {\rm e}^{{\rm i}p\cdot x}{\rm e}^{{\rm i}q\cdot y} \langle 0|T \left\{ J_{J/\psi,\mu}(x)J_{\Delta,\nu}(y) \bar{J}_{P'}(0) \right\}|0\rangle\, . $

(7) At the hadron side, we insert the complete sets of intermediate hadron states with the same quantum numbers as the currents
$ J_{\eta_c}(x) $ ,$ J_{J/\psi,\mu}(x) $ ,$ J_{N}(x) $ ,$ J_{\Delta,\mu}(x) $ ,$ J_{P}(x) $ , and$ J_{P'}(x) $ into those three-point correlation functions and isolate the contributions of the ground states,$ \Pi(p,q) = \frac{f_{\eta_c}m_{\eta_c}^2}{2m_c}\lambda_N\lambda_{P} g_{P} \frac{\left( \not {q}+m_N\right)\left(\not {p}'+m_{P}\right)} {\left(m^2_{P}-p'^2\right)\left(m^2_{\eta_c}-p^2\right)\left(m^2_{N}-q^2\right)}+\cdots\, , $

(8) $ \begin{aligned}[b] \Pi_{1,\mu}(p,q)=\;&f_{J/\psi}m_{J/\psi}\lambda_N\lambda_{P}\frac{-{\rm i}}{\left(m^2_{P}-p'^2\right)\left(m^2_{J/\psi}-p^2\right)\left(m^2_{N}-q^2\right)}\left( -g_{\mu\alpha}+\frac{p_{\alpha}p_{\mu}}{p^2}\right)\\ &\left( \not {q}+m_N\right)\left(g_V\gamma^{\alpha}-\frac{{\rm i}g_T}{m_{P}+m_N}\sigma^{\alpha\beta}p_{\beta}\right) \gamma_5\left(\not {p}'+m_{P}\right)+\cdots\, , \end{aligned} $

(9) $ \Pi_{2,\mu}(p,q) = \frac{f_{\eta_c}m_{\eta_c}^2}{2m_c}\frac{g_{P'}\lambda_\Delta\lambda_{P'}p^{\alpha}} {\left(m^2_{P'}-p'^2\right)\left(m^2_{\eta_c}-p^2\right)\left(m^2_{\Delta}-q^2\right)} \left( \not {q}+m_{\Delta}\right)\left( g_{\mu\alpha}-\frac{1}{3}\gamma_\mu\gamma_\alpha-\frac{2}{3}\frac{q_\mu q_\alpha}{m_{\Delta}^2}+\frac{q_\mu\gamma_\alpha-q_{\alpha}\gamma_\mu}{3m_\Delta} \right)\gamma_5\left(\not {p}'+m_{P'}\right)+\cdots\,, $

(10) $\begin{aligned}[b] \Pi_{\mu\nu}(p,q)=\;& f_{J/\psi}m_{J/\psi}\lambda_{\Delta}\lambda_{P'}\frac{-1}{\left(m^2_{P'}-p'^2\right)\left(m^2_{J/\psi}-p^2\right)\left(m^2_{\Delta}-q^2\right)} \left({\not {q}}+m_{\Delta}\right)\left( g_{\nu\alpha}-\frac{1}{3}\gamma_\nu\gamma_\alpha-\frac{2}{3}\frac{q_\nu q_\alpha}{m_{\Delta}^2}+\frac{q_\nu\gamma_\alpha-q_{\alpha}\gamma_\nu}{3m_\Delta} \right)\varepsilon_{\mu} \\ & \left[ g_A(p_{\alpha}{\not {\varepsilon}}-\varepsilon_{\alpha}{\not {p}})-g_B({\rm P}\cdot\varepsilon p_{\alpha}-{\rm P}\cdot p\varepsilon_{\alpha})+g_C(-p^2\varepsilon_{\alpha}) \right]\left({\not {p}'}+m_{P'}\right)+\cdots\,, \end{aligned} $

(11) where the
$ g_{P} $ ,$ g_{P'} $ ,$ g_V $ ,$ g_T $ ,$ g_A $ ,$ g_B $ , and$ g_C $ are the hadronic coupling constants, the$ \lambda_{P} $ ,$ \lambda_{P'} $ ,$ \lambda_{N} $ , and$ \lambda_{\Delta} $ are the pole residues, the$ f_{\eta_c} $ and$ f_{J/\psi} $ are the decay constants,$ \verb"P"=\dfrac{q+p'}{2} $ , and we have applied the definitions,$ \begin{aligned}[b]& \langle 0| J_{P}(0)|\mathcal{P}_{P}(p')\rangle = \lambda_{P}U_{P}(p')\,, \\& \langle 0| J_{P'}(0)|\mathcal{P}_{P'}(p')\rangle = \lambda_{P'}U_{P'}(p')\,, \\& \langle 0| J_{N}(0)|N(q)\rangle = \lambda_NU(q)\,, \\& \langle 0| J_{\Delta,\mu}(0)|\Delta(q)\rangle = \lambda_{\Delta}U_{\mu}(q)\,, \\& \langle 0| J_{J/\psi,\mu}(0)|J/\psi(p)\rangle = f_{J/\psi}m_{J/\psi}\varepsilon_{\mu}\,, \\& \langle 0| J_{\eta_c}(0)|\eta_{c}(p)\rangle = \frac{f_{\eta_c}m_{\eta_c}^2}{2m_c}\,, \end{aligned} $

(12) $\begin{aligned}[b]& \langle \eta_c(p)N(q)|\mathcal{P}_{P}(p')\rangle = {\rm i}g_{P}\overline{U}(q)U_{P}(p')\,, \\& \langle J/\psi(p)N(q)|\mathcal{P}_{P}(p')\rangle = \overline{U}(q)\varepsilon_{\alpha}^*\left(g_V\gamma^{\alpha}-{\rm i}\frac{g_T}{m_{P}+m_N} \sigma^{\alpha\beta}p_{\beta}\right)\\&\quad\quad\quad\quad\quad\quad\quad\quad\quad\times\gamma_5U_{P}(p')\,, \\& \langle \eta_c(p)\Delta(q)|\mathcal{P}_{P'}(p')\rangle = -{\rm i}g_{P'}\overline{U}_{\alpha}(q)\gamma_5U_{P'}(p')p^{\alpha}\,,\\& \langle J/\psi(p)\Delta(q)|\mathcal{P}_{P'}(p')\rangle = {\rm i}\overline{U}_{\alpha}(q)[g_A(p_{\alpha}\not {\varepsilon}-\varepsilon_{\alpha}\not {p}) \\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad-g_B({\rm P}\cdot \varepsilon p_{\alpha}-{\rm P}\cdot p\varepsilon_{\alpha})\\&\quad\quad\quad\quad\quad\quad\quad\quad\quad+g_{C}(p\cdot\varepsilon p_{\alpha}-p^2\varepsilon_{\alpha})]U_{P'}(p')\,, \end{aligned} $

(13) where the
$ U(q) $ ,$ U_{P}(p') $ , and$ U_{P'}(p') $ are the Dirac spinors, the$ U_{\mu}(q) $ is the Rarita-Schwinger spinor, and the$ \varepsilon_\mu $ represents the polarization vector of the$ J/\psi $ ,$ p\cdot \varepsilon=0 $ . The$ |\eta_c\rangle $ ,$ |J/\psi\rangle $ ,$ |N\rangle $ ,$ |\Delta\rangle $ ,$ |\mathcal{P}_{P}\rangle $ , and$ |\mathcal{P}_{P'}\rangle $ denote the ground states of the$ \eta_c $ ,$ J/\psi $ , N, Δ,$ P_{c}(4312) $ , and$ P_{c}(4330) $ , respectively. For the definition of the vertex$ \langle J/\psi(p)\Delta(q)|\mathcal{P}_{P'}(p')\rangle $ , one can consult Ref. [39].It is natural to consider that the correlation functions at the hadronic side should match those of the QCD side; that is,
$\Pi_{H}(p,q)=\Pi_{\rm QCD}(p,q)$ , where Π represents the correlation functions in Eqs. (4)−(7), and the subscripts H and$ QCD $ denote the hadron and QCD sides, respectively. It is then reasonable to have the relation$Tr[\Pi_{H}(p,q)\cdot\Gamma]= Tr[\Pi_{\rm QCD}(p,q)\cdot\Gamma]$ , where the Γ is the same chosen$ \gamma- $ matrix in the Dirac spinor space. For the$ \Pi(p,q) $ in Eq. (4), we choose$ \Gamma=\sigma_{\mu\nu} $ and$ \gamma_\mu $ , and select the corresponding tensor structures$ p_{\mu}q_{\nu}-q_{\mu}p_{\nu} $ and$ q_\mu $ , respectively. For the$ \Pi_{1,\mu}(p,q) $ and$ \Pi_{2,\mu}(p,q) $ in Eq. (5) and Eq. (6), we set$ \Gamma=\gamma_5 \not {z} $ and$ \gamma_5 $ , and choose the tensor structures$ q_\mu p\cdot z $ and$ q_\mu $ , respectively [26, 38], where z is a four vector. For the$ \Pi_{\mu\nu}(p,q) $ in Eq. (7), we pick out its tensor structures$ \not {p} \not {q}g_{\mu\nu} $ and$ \not {p}(\gamma_{\mu}p_\nu+\gamma_{\nu}p_{\mu}+\gamma_{\mu}q_\nu+\gamma_{\nu}q_{\mu}) $ , simplify$ \Pi_{\mu\nu}\cdot \not {z} $ , and choose the structure$ \not {p} \not {q} (\gamma_{\mu}p_\nu+\gamma_{\nu}p_{\mu}+\gamma_{\mu}q_\nu+\gamma_{\nu}q_{\mu})p\cdot z $ . The selected structures are expressed as,$ \begin{aligned}[b]& \frac{1}{4}Tr[\Pi(p,q)\sigma_{\mu\nu}] = \Pi_a(p'^2,p^2,q^2)i(p_\mu q_\nu-q_\mu p_\nu)+\cdots\,, \\& \frac{1}{4}Tr[\Pi(p,q)i\gamma_{\mu}] = \Pi_b(p'^2,p^2,q^2)iq_\mu+\cdots\,, \\& \frac{1}{4}Tr[\Pi_{1,\mu}(p,q)\gamma_{5} \not {z}] = \Pi_c(p'^2,p^2,q^2)iq_\mu p\cdot z+\cdots\,, \\& \frac{1}{4}Tr[\Pi_{1,\mu}(p,q)\gamma_{5}] = \Pi_d(p'^2,p^2,q^2)iq_\mu +\cdots\,, \\& \frac{1}{4}Tr[\Pi_{2,\mu}(p,q)\gamma_{5} \not {z}] = \Pi_e(p'^2,p^2,q^2)iq_\mu p\cdot z+\cdots\,, \\& \frac{1}{4}Tr[\Pi_{2,\mu}(p,q)\gamma_{5}] =\Pi_f(p'^2,p^2,q^2)iq_\mu +\cdots\,, \end{aligned} $

(14) $ \begin{aligned}[b]& \Pi_{\mu\nu}(p,q) = \Pi_A(p'^2,p^2,q^2)\not {p} \not {q}g_{\mu\nu}+ \Pi_C(p'^2,p^2,q^2)\not {p}\\&\quad\quad\quad\quad\quad\times (\gamma_{\mu}p_\nu+\gamma_{\nu}p_{\mu}+\gamma_{\mu}q_\nu+\gamma_{\nu}q_{\mu})+\cdots\,, \\& \Pi_{\mu\nu}(p,q)\cdot \not {z} = \Pi_B(p'^2,p^2,q^2)\not {p}\not {q} (\gamma_{\mu}p_\nu\\&\quad\quad\quad\quad\quad+\gamma_{\nu}p_{\mu}+\gamma_{\mu}q_\nu+\gamma_{\nu}q_{\mu})p\cdot z+\cdots\, . \end{aligned} $

(15) We apply the same analysis for the components of the correlation functions
$ \Pi_Z(p'^2,p^2,q^2) $ , as discussed in Refs. [26, 38], where Z represents a, b,$ \cdots $ , f, A, B, and C.At the QCD side, after accomplishing the operator product expansion, we perform the trace and choose the selected tensor structures. For the relation between
$ p' $ , p, and q, they satisfy$ p'=p+q $ for all the decays. We set$ p'^2=\xi p^2 $ , where the ξ is a parameter. For example, in the decay$ P_c(4312)\rightarrow \eta_c+N $ ,$ 0\leq \xi\leq \dfrac{2m_N^2}{m_{\eta_c^2}}+2 $ , we can set$ \xi= \dfrac{m_N^2}{m_{\eta_c^2}}+1 $ . Just like in our previous works [26, 33−38], we take the rigorous quark-hadron duality below the continuum thresholds and perform double Borel transformation to obtain the QCD sum rules for the hadronic coupling constants,$ \begin{aligned}[b] & \frac{f_{\eta_c}m_{\eta_c}^2\lambda_N\lambda_{P} g_{P}^a}{2m_c \xi}\frac{1}{\frac{m_{P}^2}{\xi}-m_{\eta_c}^2}\left\{ {\rm exp} \left( -\frac{m_{\eta_c}^2}{T_1^2} \right)-{\rm exp} \left( -\frac{m_{P}^2}{\xi T_1^2} \right) \right\}{\rm exp} \left( -\frac{m_N^2}{T_2^2} \right) \\ & +C_a {\rm exp} \left( -\frac{m_{\eta_c}^2}{T_1^2}-\frac{m_N^2}{T_2^2} \right)=\int_{4m_c^2}^{s_{\eta_c}^0}{\rm d}s\int_0^{s_N^0}{\rm d}u\, \rho_a(s,u){\rm exp}\left( -\frac{s}{T_1^2}-\frac{u}{T_2^2} \right)\,, \end{aligned} $

(16) $ \begin{aligned}[b] & \frac{f_{\eta_c}m_{\eta_c}^2\lambda_N\lambda_{P} g_{P}^b}{2m_c \xi}\frac{m_{P}+m_N}{\frac{m_{P}^2}{\xi}-m_{\eta_c}^2}\left\{ {\rm exp} \left( -\frac{m_{\eta_c}^2}{T_1^2} \right)-{\rm exp} \left( -\frac{m_{P}^2}{\xi T_1^2} \right) \right\}{\rm exp} \left( -\frac{m_N^2}{T_2^2} \right) \\ & +C_b {\rm exp} \left( -\frac{m_{\eta_c}^2}{T_1^2}-\frac{m_N^2}{T_2^2} \right)=\int_{4m_c^2}^{s_{\eta_c}^0}{\rm d}s\int_0^{s_N^0}{\rm d}u\, \rho_b(s,u){\rm exp}\left( -\frac{s}{T_1^2}-\frac{u}{T_2^2} \right)\,, \end{aligned} $

(17) $ \begin{aligned}[b] & \frac{f_{J/\psi}m_{J/\psi}\lambda_N\lambda_{P} }{\xi}\frac{g_{T/V}}{\frac{m_{P}^2}{\xi}-m_{J/\psi}^2}\left\{ {\rm exp} \left( -\frac{m_{J/\psi}^2}{T_1^2} \right)-{\rm exp} \left( -\frac{m_{P}^2}{\xi T_1^2} \right) \right\}{\rm exp} \left( -\frac{m_N^2}{T_2^2} \right) \\ & +C_{T/V} {\rm exp} \left( -\frac{m_{J/\psi}^2}{T_1^2}-\frac{m_N^2}{T_2^2} \right)=\int_{4m_c^2}^{s_{J/\psi}^0}{\rm d}s\int_0^{s_N^0}{\rm d}u\, \rho_{T/V}(s,u){\rm exp}\left( -\frac{s}{T_1^2}-\frac{u}{T_2^2} \right)\,, \end{aligned} $

(18) $ \begin{aligned}[b] & \frac{f_{\eta_c}m_{\eta_c}^2\lambda_{\Delta}\lambda_{P'} g_{P'}^e}{4m_cm_{\Delta}\xi}\frac{M_X^2}{\frac{m_{P'}^2}{\xi}-m_{\eta_c}^2}\left\{ {\rm exp} \left( -\frac{m_{\eta_c}^2}{T_1^2} \right)-{\rm exp} \left( -\frac{m_{P'}^2}{\xi T_1^2} \right) \right\}{\rm exp} \left( -\frac{m_{\Delta}^2}{T_2^2} \right) \\ & +C_{e} {\rm exp} \left( -\frac{m_{\eta_c}^2}{T_1^2}-\frac{m_{\Delta}^2}{T_2^2} \right)=\int_{4m_c^2}^{s_{\eta_c}^0}{\rm d}s\int_0^{s_{\Delta}^0}{\rm d}u\, \rho_{e}(s,u){\rm exp}\left( -\frac{s}{T_1^2}-\frac{u}{T_2^2} \right)\,, \end{aligned} $

(19) $ \begin{aligned}[b] & \frac{f_{\eta_c}m_{\eta_c}^2\lambda_{\Delta}\lambda_{P'} g_{P'}^f }{12m_cm_{\Delta}^2\xi}\frac{M_X^2\left( 2m_{\Delta}m_{P'}-M_X^2-2m_{\Delta}^2 \right)}{\frac{m_{P'}^2}{\xi}-m_{\eta_c}^2}\left\{ {\rm exp} \left( -\frac{m_{\eta_c}^2}{T_1^2} \right)-{\rm exp} \left( -\frac{m_{P'}^2}{\xi T_1^2} \right) \right\}{\rm exp} \left( -\frac{m_{\Delta}^2}{T_2^2} \right) \\ & +C_{f} {\rm exp} \left( -\frac{m_{\eta_c}^2}{T_1^2}-\frac{m_{\Delta}^2}{T_2^2} \right)=\int_{4m_c^2}^{s_{\eta_c}^0}{\rm d}s\int_0^{s_{\Delta}^0}{\rm d}u\, \rho_{f}(s,u){\rm exp}\left( -\frac{s}{T_1^2}-\frac{u}{T_2^2} \right)\,, \end{aligned} $

(20) $ \begin{aligned}[b] & \frac{f_{J/\psi}m_{J/\psi}\lambda_{\Delta}\lambda_{P'} }{\xi}\frac{1}{\frac{m_{P'}^2}{\xi}-m_{J/\psi}^2}\left\{ {\rm exp} \left( -\frac{m_{J/\psi}^2}{T_1^2} \right)-{\rm exp} \left( -\frac{m_{P'}^2}{\xi T_1^2} \right) \right\}{\rm exp} \left( -\frac{m_{\Delta}^2}{T_2^2} \right) \\ & K\cdot\begin{bmatrix}g_A\\g_B\\g_C\end{bmatrix}+\begin{bmatrix}C_A\\C_B\\C_C\end{bmatrix} {\rm exp} \left( -\frac{m_{J/\psi}^2}{T_1^2}-\frac{m_{\Delta}^2}{T_2^2} \right) =\int_{4m_c^2}^{s_{J/\psi}^0}{\rm d}s\int_0^{s_{\Delta}^0}{\rm d}u \begin{bmatrix} \rho_{A}(s,u)\\ \rho_{B}(s,u)\\ \rho_{C}(s,u) \end{bmatrix}{\rm exp}\left( -\frac{s}{T_1^2}-\frac{u}{T_2^2} \right)\,, \end{aligned} $

(21) where
$ \begin{aligned}[b]& M_X^2 = m_{P'}^2-m_{\Delta}^2-m_{\eta_c}^2 \,, \\& M_Y^2 = m_{\Delta}^2+2m_{\Delta}m_{P'}+m_{P'}^2-m_{J/\psi}^2 \,,\\& C_T = \left[ (m_{P}-m_N)C_c+C_d \right]\frac{m_{P}+m_N}{m_{P}^2-m_N^2-m_{J/\psi}^2}\,,\\& \rho_T(s,u) = \left[ (m_{P}-m_N)\rho_c(s,u)+\rho_d(s,u) \right]\frac{m_{P}+m_N}{m_{P}^2-m_N^2-m_{J/\psi}^2}\,,\end{aligned} $

$ \begin{aligned}[b]& C_V = \left( \frac{m_{J/\psi}^2}{m_{P}+m_N}C_c+C_d \right)\frac{m_{P}+m_N}{m_{P}^2-m_N^2-m_{J/\psi}^2}\,,\\& \rho_V(s,u) = \left( \frac{m_{J/\psi}^2}{m_P+m_N}\rho_c(s,u)+\rho_d(s,u) \right)\frac{m_{P}+m_N}{m_{P}^2-m_N^2-m_{J/\psi}^2}\,,\\& K = \begin{bmatrix} \dfrac{M_Y^2}{3m_{\Delta}}\left(4m_{\Delta}^2 -M_Y^2\right)&\dfrac{2}{3}M_Y^2(m_{P'}^2-m_{\Delta}^2)&-\dfrac{4}{3}m_{J/\psi}^2M_Y^2 \\ \dfrac{4(m_{\Delta}m_{P'}-m_{P'}^2+m_{J/\psi}^2)}{3m_{\Delta}^2}& -\dfrac{2(m_{\Delta}^2-m_{P'}^2+3m_{J/\psi}^2)}{3m_{\Delta}}&\dfrac{8m_{J/\psi}^2}{3m_{\Delta}}\\ \dfrac{4}{3}m_{\Delta}&-\dfrac{2}{3}M_Y^2&\dfrac{4}{3}M_Y^2\nonumber \end{bmatrix}\,, \end{aligned} $

and
$ \rho_{Z}(s,u)= {\lim\limits_{\epsilon_2\to 0}} \,\,{\lim\limits_{\epsilon_1\to 0}}\,\,\frac{ {\rm Im}_{s}\,{\rm Im}_{u}\,\Pi_{Z}(p^{\prime 2},s+{\rm i}\epsilon_2,u+{\rm i}\epsilon_1) }{\pi^2} \, , $

(22) are the spectral densities at the QCD side. We add the superscripts a and b to denote the hadronic coupling constant
$ g_{P} $ from the components$ \Pi_a(p'^2,p^2,q^2) $ and$ \Pi_b(p'^2,p^2,q^2) $ , respectively, and add the superscripts e and f to denote the hadronic coupling constant$ g_{P'} $ from the components$ \Pi_e(p'^2,p^2,q^2) $ and$ \Pi_f(p'^2,p^2,q^2) $ , respectively.$ C_Z $ denotes the unknown parameters, which are determined in the numerical calculations to obtain flat platforms [26, 33−38]. -
In Eq. (2), the current
$ J_{\Delta,\mu}(x) $ is the isospin eigenstate$ |II_3\rangle=|\frac{3}{2}\frac{1}{2}\rangle $ . We write down the two-point correlation function,$ \Pi_{\Delta,\mu\nu}(q)={\rm i}\int {\rm d}^4y {\rm e}^{{\rm i}q\cdot y} \langle 0|T\left\{ J_{\Delta,\mu}(y)\bar{J}_{\Delta,\nu}(0)\right\}|0\rangle\, . $

(23) At the hadron side, we insert a complete set of baryon states with the same quantum number as the current into the correlation function
$ \Pi_{\Delta,\mu\nu} $ and isolate the contribution of the ground state,$ \Pi_{\Delta,\mu\nu}(q) =\lambda_\Delta^2 \frac{ \not {q}+m_\Delta}{m_\Delta^2-q^2}\left(-g_{\mu\nu}+\cdots\right)+\cdots\, . $

(24) We choose tensor structures
$ \not {q}g_{\mu\nu} $ and$ g_{\mu\nu} $ for analysis. After accomplishing the operator product expansion, we obtain the corresponding spectral densities$\rho^1_{\rm QCD}(u)$ and$\rho^0_{\rm QCD}(u)$ , respectively, then adopt quark-hadron duality, and obtain two QCD sum rules,$ \begin{aligned}[b] &\lambda_{\Delta}^2 {\exp}\left(-\frac{m_{\Delta}^2}{T^2}\right)=\int_0^{s_{\Delta}^0}\rho^1_{\rm QCD}(u)\,{\rm exp} \left(-\frac{u}{T^2}\right){\rm d}u\,,\\& m_{\Delta}\lambda_{\Delta}^2 {\exp}\left(-\frac{m_{\Delta}^2}{T^2}\right)= \int_0^{s_{\Delta}^0}\rho^0_{\rm QCD}(u)\,{\rm exp} \left(-\frac{u}{T^2}\right){\rm d}u\, , \end{aligned} $

(25) where
$ \begin{aligned}[b] \rho^1_{\rm QCD}(u) =\;& \left(\frac{\sqrt{2}}{2560} + \frac{7}{3072}\right) \frac{u^2}{\pi^{4}} - \left(\frac{17}{13824 \sqrt{2}} + \frac{49}{55296}\right)\\&\times \langle g_s^2GG\rangle \frac{1}{ \pi^{4}}\\ &+ \left(\frac{1}{3 \sqrt{2}} + \frac{11}{36}\right) \langle\bar{q}q\rangle^2 \delta\left(u\right) + \frac{ g_s^2 \langle\bar{q}q\rangle^2}{324} \frac{\delta(u) }{\pi^{2}}\\ & - \left(\frac{23}{108 \sqrt{2}} + \frac{13}{54}\right) \langle\bar{q}q\rangle \langle\bar{q}g_s\sigma Gq\rangle \frac{\delta(u)}{T^2}\,, \end{aligned} $

(26) $ \begin{aligned}[b] \rho^0_{\rm QCD}(u) =\;& \left(\frac{ \sqrt{2}}{72}-\frac{1}{8 \sqrt{2}} - \frac{23}{288}\right) \langle\bar{q}q\rangle \frac{u}{\pi^{2}} + \left(\frac{1}{16 \sqrt{2}} + \frac{7}{192}\right)\\&\times \langle\bar{q}g_s\sigma Gq\rangle \frac{1}{\pi^{2}}\\ &+ \left(\frac{1}{288 \sqrt{2}} + \frac{11}{3456}\right) \langle g_s^2GG\rangle \langle\bar{q}q\rangle \frac{\delta(u)}{\pi^{2}}\\ &+ \left(\frac{4}{729 \sqrt{2}} + \frac{5}{729}\right) g_s^2\langle\bar{q}q\rangle^3 \frac{\delta(u)}{T^2}\,. \end{aligned} $

(27) We differentiate Eq. (25) with respect to
$ \tau=\dfrac{1}{T^2} $ , then obtain the mass$ m_\Delta $ through a fraction,$ m^{2}_{\Delta} = \frac{-\dfrac{\partial}{\partial \tau}\int_0^{s_{\Delta}^0}\rho^{1/0}_{\rm QCD}(u){\rm exp}\left(-\dfrac{u}{T^2}\right){\rm d}u}{\int_0^{s_{\Delta}^0}\rho^{1/0}_{\rm QCD}(u){\rm exp}\left(-\dfrac{u}{T^2}\right){\rm d}u}\,. $

(28) -
The standard values of the vacuum condensates are listed as
$ \langle\overline{q}q\rangle=-(0.24\pm0.01\,{\rm GeV})^3 $ ,$ \langle\overline{q}g_s\sigma Gq\rangle=m_0^2\langle\overline{q}q\rangle $ ,$ m_0^2=(0.8\pm0.1)\,{\rm GeV}^2 $ , and$ \langle\frac{\alpha_s}{\pi}GG\rangle=(0.33\,{\rm GeV})^4 $ at the energy scale$ \mu=1\,{\rm GeV} $ [29, 30, 31, 32], and we apply the value of the$ \overline{MS} $ mass$ m_c(m_c)=1.275\pm0.025\,{\rm GeV} $ from the Particle Data Group [40]. The energy-scale dependence of those parameters are written as,$ \begin{aligned}[b]& \langle\overline{q}q\rangle(\mu)=\langle\overline{q}q\rangle(1{\rm GeV})\left[\frac{\alpha_s(1{\rm GeV})}{\alpha_s(\mu)}\right]^{\frac{12}{33-2n_f}}\, ,\\& \langle\overline{q}g_s\sigma Gq\rangle(\mu) =\langle\overline{q}g_s\sigma Gq\rangle(1{\rm GeV})\left[\frac{\alpha_s(1{\rm GeV})}{\alpha_s(\mu)}\right]^{\frac{2}{33-2n_f}}\, ,\\& m_c(\mu)=m_c(m_c)\left[\frac{\alpha_s(\mu)}{\alpha_s(m_c)}\right]^{\frac{12}{33-2n_f}}\, ,\\& \alpha_s(\mu)=\frac{1}{b_0t}\left[1 - \frac{b_1}{b_0^2}\frac{{\rm{log}} {t}}{t} + \frac{b_1^2({\rm{log}}^2 {t} - {\rm{log}} {t} - 1)+ {b}_0 {b}_2}{b_0^4t^2}\right] , \end{aligned} $

where
$t={\rm log}\dfrac{\mu^2}{\Lambda_{\rm QCD}^2}$ ,$ b_0=\dfrac{33-2n_f}{12\pi} $ ,$ b_1=\dfrac{153-19n_f}{24\pi^2} $ ,$ b_2=\dfrac{2857-\dfrac{5033}{9}n_f+\dfrac{325}{27}n_f^2}{128\pi^3} $ , and$\Lambda_{\rm QCD}=213$ MeV, 296 MeV,$ 339 $ MeV for flavor numbers$ n_f=5,4,3 $ , respectively [40, 41]. The flavor numbers$ n_f $ for the$ P_c $ decays and Δ state are$ n_f=4 $ and$ n_f=3 $ , respectively. We set the energy scales for the decays$ P_c(4312)\rightarrow \eta_c N $ ,$ P_c(4330)\rightarrow \eta_c \Delta $ as$ \mu=\dfrac{1}{2}m_{\eta_c} $ , and for the decays$ P_c(4312)\rightarrow J/\psi N $ ,$ P_c(4330)\rightarrow J/\psi \Delta $ as$ \mu=\dfrac{1}{2}m_{J/\psi} $ [26, 42]. For the Δ baryon state, we set the energy scale$ \mu=1 $ . We obey the experimental data and set$ m_P=4.312\,{\rm GeV} $ [2], and we set$ m_{P'}=4.330\,{\rm GeV} $ , considering the calculation/conclusion in Ref. [16]. From the Particle Data Group [40], we take$ m_{\eta_c}=2.984\,{\rm GeV} $ ,$ m_N=0.938\,{\rm GeV} $ ,$ m_{J/\psi}=3.097\,{\rm GeV} $ , and$ m_{\Delta}=1.232\,{\rm GeV} $ . For the decay constants, we choose$ f_{J/\psi}=0.418\,{\rm GeV} $ ,$ f_{\eta_c}=0.387\,{\rm GeV} $ [43]. For the pole residues, we set$ \lambda_N=3.20\times 10^{-2}\,{\rm GeV^3} $ [44],$ \lambda_P=3.25\times 10^{-3}\,{\rm GeV^6} $ , and$ \lambda_{P'}=1.97\times10^{-3}\,{\rm GeV^6} $ [16]. For the threshold parameters, we apply$ \sqrt{s_{\eta_c}^0}=3.50\,{\rm GeV} $ ,$ \sqrt{s_{N}^0}=1.30\,{\rm GeV} $ , and$ \sqrt{s_{J/\psi}^0}=3.60\,{\rm GeV} $ [26].For the Δ baryon state, we find that the numerical values of the masses in the
$ m_{\Delta}^0-T^2 $ curve (due to$\rho_{\rm QCD}^0(u)$ ) are slightly larger that in the$ m_{\Delta}^1-T^2 $ (due to$\rho_{\rm QCD}^1(u)$ ) if the same input parameters are considered. However, it is difficult to judge which tensor structure is better. Thus, we phenomenologically solve the mass and pole residue of the baryon states via$ m_\Delta=\dfrac{1}{2}(m_{\Delta}^1+m_{\Delta}^0) $ and$ \lambda_\Delta=\dfrac{1}{2}(\lambda_{\Delta}^1+\lambda_{\Delta}^0) $ , where we add the superscripts$ 1 $ and$ 0 $ to denote the spectral densities. The$ m_{\Delta}-T^2 $ and$ \lambda_{\Delta}-T^2 $ curves are shown in the Fig. 1, and the related parameters extracted from the Borel platforms are listed as$ \sqrt{s_{\Delta}^0}=1.61\,{\rm GeV} $ ,$ m_{\Delta}=1.230\,{\rm GeV} $ ,$ \lambda_{\Delta}=7.63\times 10^{-3}\,{\rm GeV^3} $ , and the Borel windows$ T^2=1.1-1.5\,{\rm GeV^2} $ . Further, the pole contribution in the QCD sum rules is$ (41-59)\% $ and the convergency of the operator product expansion is satisfied very well.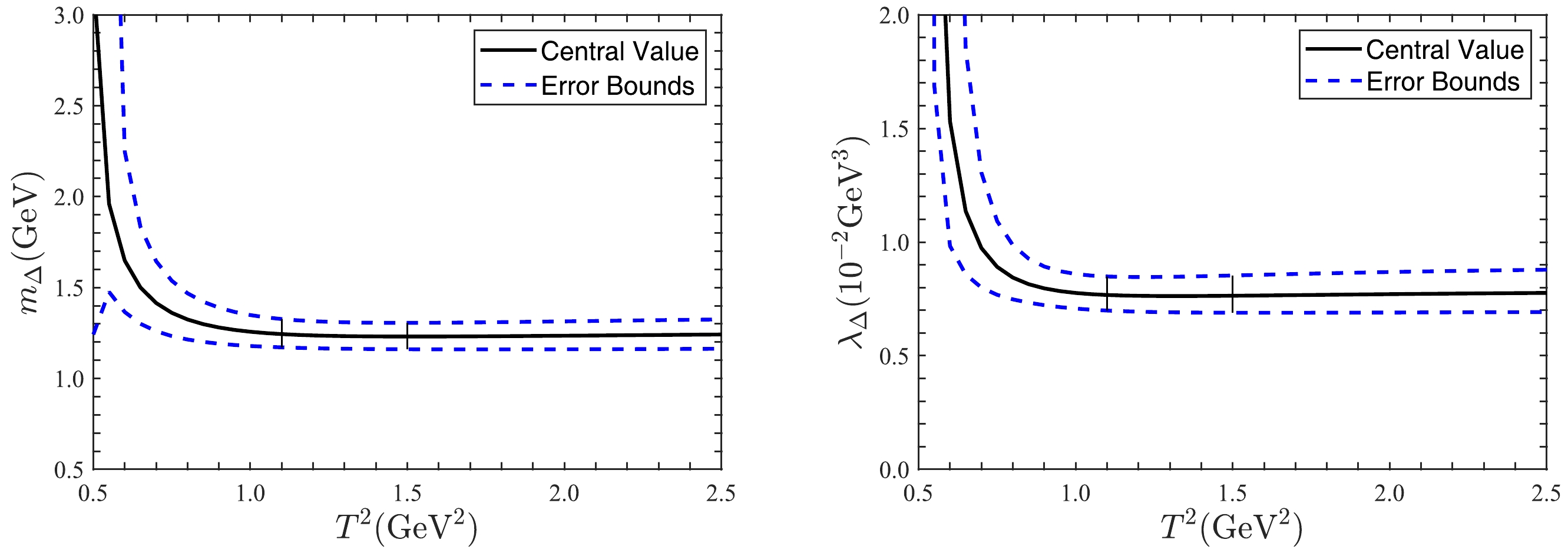
Figure 1. (color online) The
$ m_\Delta-T^2 $ (left) and$ \lambda_\Delta-T^2 $ (right) curves of the Δ baryon.In the present study, the
$ 3D $ surfaces of$ g_Z=g_Z(T_1^2,T_2^2) $ are solved for the first time, where$ g_Z $ represents the hadronic coupling constants. The Borel platforms of each coupling constant are determined under the same intervals of the Borel parameters$ T_1^2 $ and$ T_2^2 $ . They are$\left(T_1^2\right)_{\rm max}-\left(T_1^2\right)_{\rm min}=1\,{\rm GeV^2}$ and$\left(T_2^2\right)_{\rm max}-\left(T_2^2\right)_{\rm min}= 1\,{\rm GeV^2}$ . One important requirement of the QCD sum rules is that the Borel platform should be "flat enough," which means that the error bounds originating from the Borel parameters could be neglected. For the hadronic decay constants, we argue that one can quantify the "flat surface" via the average relative error bound$ \chi_Z $ , which is defined as,$ \chi_Z = \sum\limits_{i=1}^n\frac{|g_Z(T_{1,c}^2,T_{2,c}^2)-g_Z(T_{1,i}^2,T_{2,i}^2)|}{n g_Z(T_{1,c}^2,T_{2,c}^2)}\,, $

(29) where the
$ T_{1,c}^2 $ and$ T_{2,c}^2 $ denote the central points in the Borel platforms, the$ T_{1,i}^2 $ and$ T_{2,i}^2 $ are the selected points inside the Borel platforms, and the n is the number of points on the grids in the Borel platforms. In the QCD sum rules (see Eqs. (16)−(21)), there is a free (or unknown) parameter$ C_Z $ accompanying each hadronic coupling constant$ g_Z $ , we determine the optimal values of$ C_Z $ by minimizing$ \chi_{Z} $ . Taking$ g_{P}^a $ for example, the Borel platforms chosen via trial and error are$\left(T_{1}^2\right)_{\rm min} = 4\,{\rm GeV^2}$ ,$\left(T_{2}^2\right)_{\rm min}=4\,{\rm GeV^2}$ ,$\left(T_{1}^2\right)_{\rm max} =5\,{\rm GeV^2}$ , and$\left(T_{2}^2\right)_{\rm max}= 5\,{\rm GeV^2}$ . The$ \chi_a-C_a $ curve is shown in Fig. 2,$ C_a $ is determined by the minimum value of$ \chi_a $ , i.e.,$C_a= 4.299 \times 10^{-6}\,{\rm GeV^9}$ . Similarly, we find
Figure 2. (color online) The free parameter
$ C_a $ is determined by the minimum value of$ \chi_a $ , where the dash-dotted line represents the chosen value of the$ C_a $ .$ \begin{aligned}[b]&C_b=8.855 \times 10^{-5} {\rm GeV^{10}} \\& C_T= (-6.960 {\rm GeV^2}+0.049 T_1^2-0.083T_2^2)\times 10^{-5} {\rm GeV^9}\\& C_V= (-7.407\;{\rm GeV^2} +\;0.053\; T_1^2-0.088\;T_2^2)\times 10^{-5} \; {\rm GeV^9}\\& C_e= -9.864 \times 10^{-7}\; {\rm GeV^9}\\& C_f=(1.214\;{\rm GeV^2}-0.109T^2_1+ 0.170T^2_2)\times 10^{-6}\;{\rm GeV^{10}}\\& C_A^{\prime}=(-6.341\;{\rm GeV^2}+0.064T^2_1- 0.075T_2^2)\times 10^{-5}\,{\rm GeV^{10}}\\& C_B^{\prime}=(-4.903\;{\rm GeV^2}+0.039\,T_1^2- 0.054\,T_2^2)\times 10^{-5}\,\;{\rm GeV^8}\\& C_C^{\prime}= (-2.830{\rm GeV^2}+0.023T_1^2- 0.031T_2^2)\times 10^{-5}\,{\rm GeV^8} \end{aligned} $

and
$(C_A, C_B\,,C_C)=(C_A^{\prime}\,,C_B^{\prime}\,,C_C^{\prime})\cdot K^T$ . The$ 3D $ graphs of the$ g_{P}^a $ are shown in Fig. 3. For the graphs of the other hadronic coupling constants, please consult the preprint version of this paper [45]. One can clearly see that "flat surfaces" are obtained for all the hadronic coupling constants, which also presents a reference that it is reasonable to set$ T_1^2=T_2^2 $ for simplicity [26, 37, 38, 46].
Figure 3. (color online) The
$ g_{P}^a(T_1^2,T_2^2) $ surface (left) and error bounds of the diagonal of the Borel platform (right), where$ T^2=\sqrt{T_1^2+T_2^2} $ and$ T_1^2=T_2^2 $ .For the error bounds of the hadronic coupling constants, we follow the approximations
$\dfrac{\delta \lambda_P}{\lambda_P} = \dfrac{\delta \lambda_{P^\prime}}{\lambda_{P^\prime}}= \dfrac{\delta \lambda_\Delta}{\lambda_\Delta}=\dfrac{\delta \lambda_N}{\lambda_N}=\dfrac{\delta f_{J/\psi}}{f_{J/\psi}}=\dfrac{\delta f_{\eta_c}}{f_{\eta_c}}$ to estimate the uncertainties [38, 46]. Notably, the uncertainties of the masses of$ P_c(4312) $ and$ P_c(4330) $ are due to the input parameters$ \langle\overline{q}q\rangle $ ,$ \langle\overline{q}g_s\sigma Gq\rangle $ , and$ m_0^2 $ [16]. Therefore, we do not consider their contributions to the uncertainties for the strong coupling constants to avoid over evaluating the uncertainties. Additionally, we abandon the error bounds due to the uncertainties of the free parameters$ \delta C_Z $ [26, 37, 38, 46]. Since the error bounds shown on the$ 3D $ graphs are unclear, we draw the curves of the uncertainties of the diagonals of the Borel platforms in Fig. 3 for$ g_{P}^a $ (the other graphs can be found in the preprint version [45]) and extract the numerical results in Table 1. We find that the strict constraint condition$ \chi_Z<6\% $ holds for all the Borel platforms. Accordingly, we obtain the partial decay widths,$ g_Z $ 

$T_1^2 \;\; {\rm /GeV^2}$ 

$T_2^2 \;\; {\rm /GeV^2}$ 

$ \chi_Z $ 

Values $ g_{P}^a $ 

$ 3.5-4.5 $ 

$ 3.5-4.5 $ 

0.75% $ 0.06^{+0.01}_{-0.01} $ 

$ g_{P}^b $ 

$ 3.5-4.5 $ 

$ 3.5-4.5 $ 

5.46% $ 0.06^{+0.01}_{-0.01} $ 

$ g_{T} $ 

$ 5.0-6.0 $ 

$ 5.0-6.0 $ 

0.83% $ 0.36^{+0.10}_{-0.10} $ 

$ g_{V} $ 

$ 5.0-6.0 $ 

$ 5.0-6.0 $ 

0.56% $ 0.58^{+0.14}_{-0.12} $ 

$ g_{P'}^e $ 

$ 4.5-5.5 $ 

$ 4.5-5.5 $ 

0.79% $ 0.30^{+0.02}_{-0.02}\,{\rm GeV}^{-1} $ 

$ g_{P'}^f $ 

$ 4.5-5.5 $ 

$ 4.5-5.5 $ 

1.59% $ 0.30^{+0.09}_{-0.09}\,{\rm GeV}^{-1} $ 

$ g_{A} $ 

$ 5.5-6.5 $ 

$ 5.5-6.5 $ 

2.78% $ 0.58^{+0.08}_{-0.08}\,{\rm GeV}^{-1} $ 

$ g_{B} $ 

$ 6.0-7.0 $ 

$ 6.0-7.0 $ 

1.74% $ 0.43^{+0.08}_{-0.08}\,{\rm GeV}^{-2} $ 

$ g_{C} $ 

$ 6.0-7.0 $ 

$ 6.0-7.0 $ 

2.98% $ 0.59^{+0.08}_{-0.08}\,{\rm GeV}^{-2} $ 

Table 1. The parameters and numerical results for the hadronic coupling constants
$ \begin{aligned}[b] \Gamma^{a} (P_c(4312)\rightarrow \eta_c N) =\;& 0.11^{+0.03}_{-0.03} \,{\rm MeV}\,, \\ \Gamma^{b} (P_c(4312)\rightarrow \eta_c N) =\;& 0.11^{+0.02}_{-0.02} \,{\rm MeV}\,, \\ \Gamma (P_c(4312)\rightarrow J/\psi N) =\;& 10.78^{+8.97}_{-8.09} \,{\rm MeV}\,, \\ \Gamma^{e} (P_c(4330)\rightarrow \eta_c \Delta) =\;& 0.10^{+0.01}_{-0.01} \,{\rm MeV}\,, \\ \Gamma^{f} (P_c(4330)\rightarrow \eta_c \Delta) =\;& 0.10^{+0.06}_{-0.06} \,{\rm MeV}\,, \\ \Gamma (P_c(4330)\rightarrow J/\psi \Delta) =\;& 57.86^{+33.00}_{-32.90} \,{\rm MeV}\,, \end{aligned} $

(30) where the superscripts a, b, e, and f denote the hadronic coupling constants
$ g_{P}^a $ ,$ g_{P}^b $ ,$ g_{P'}^e $ , and$ g_{P^\prime}^f $ have been chosen, respectively. From Eq. (31), we can see explicitly that the partial decay widths using the hadronic coupling constants$ g_P $ and$ g_{P'} $ from different QCD sum rules are consistent with each other, which indicates that the calculations are reliable. The partial decays$ P_c(4312)\rightarrow J/\psi N $ and$ P_c(4330)\rightarrow J/\psi \Delta $ almost satisfy the total decay widths, and the total decay width$ \Gamma_{P_c(4312)}=10.89^{+8.97}_{-8.09} \,{\rm MeV} $ is in very good agreement with the experimental data$ 9.8\pm2.7^{+3.7}_{-4.5}\,{\rm{MeV}} $ from the LHCb collaboration [2], and supports assigning the$ P_c(4312) $ as the$ \bar{D}\Sigma_c $ molecular state having the isospin$ |I,I_3\rangle=|\frac{1}{2},\frac{1}{2}\rangle $ . The observation of its isospin cousin$ P_c(4330) $ with the$ |I,I_3\rangle=|\frac{3}{2},\frac{1}{2}\rangle $ in the$ J/\psi \Delta $ mass spectrum could shed light on the nature of the$ P_c $ states.As the decay mode
$ \Delta \to N\pi $ accounts for$ 99.4\% $ of the total width of the Δ from the Particle Data Group [40], we expect that the partial decay widths have the relations$ \Gamma(P^\prime\to J/\psi \Delta)=\Gamma(P^\prime\to J/\psi N\pi) $ and$ \Gamma(P^\prime\to \eta_c \Delta)= \Gamma(P^\prime\to \eta_c N\pi) $ . Then, we consider the finite width effects of the Δ and obtain the partial decay widths,$ \begin{aligned}[b] \Gamma(P^\prime\to \eta_c N\pi)=\;&\frac{1 }{16\pi^2 m_{P^\prime}^2 } \int_{(m_N+m_\pi)^2}^{(m_{P^\prime}-m_{\eta_c})^2}{\rm d}s\,|T_{\eta_c}|^2\\&\times\frac{\sqrt{s}\,\Gamma_{\Delta}(s)\, p(m_{P^\prime},m_{\eta_c},\sqrt{s})}{(s-m_{\Delta}^2)^2+s\Gamma_{\Delta}^2(s)}\ , \\ =\;& 0.057^{+0.008}_{-0.007} \,{\rm{MeV}}\, ,\\ \Gamma(P^\prime\to J/\psi N\pi)=\;&\frac{1 }{16\pi^2 m_{P^\prime}^2 } \int_{(m_N+m_\pi)^2}^{(m_{P^\prime}-m_{J/\psi})^2}{\rm d}s\,|T_{J/\psi}|^2\\&\times \frac{\sqrt{s}\,\Gamma_{\Delta}(s)\,p(m_{P^\prime},m_{J/\psi},\sqrt{s})}{(s-m_{\Delta}^2)^2+s\Gamma_{\Delta}^2(s)}\ , \\ =\;&93.87^{+52.91}_{-51.12} \,{\rm{MeV}}\, , \end{aligned} $

(31) where
$ \begin{aligned}[b] |T_{J/\psi}|^2=\;&\Sigma \, |\langle J/\psi(p)\Delta(q)|\mathcal{P}_{P^\prime}(p^\prime)\rangle|^2\, , \\ |T_{\eta_c}|^2=\;&\Sigma\, |\langle \eta_c(p)\Delta(q)|\mathcal{P}_{P^\prime}(p^\prime)\rangle|^2\, , \\ \Gamma_{\Delta}(s)=\;& \Gamma_{\Delta}(m_{\Delta}^2)\frac{p(\sqrt{s},m_N,m_\pi)^3}{p(m_\Delta,m_N,m_\pi)^3}\, , \end{aligned} $

(32) $ p^\prime=q+p $ ,$ p(A,B,C)=\frac{\sqrt{\left[A^2-(B+C)^2\right]\left[A^2-(B-C)^2\right]}}{2A} $ ,$ p^{\prime2}=m_{P^\prime}^2 $ ,$ p^2=m^2_{J/\psi} $ or$ m^2_{\eta_c} $ ,$ q^2=s $ , and$ \Gamma_{\Delta}(m_{\Delta}^2)=117\,{\rm{MeV}} $ [40]. The partial decay width$ \Gamma(P^\prime\to J/\psi N\pi) $ ($ \Gamma(P^\prime\to \eta_c N\pi) $ ) is greatly amplified (diminished) when the finite width of the Δ is included. We can estimate the total width via the dominant decay mode,$ \Gamma_{P_c(4330)}=93.87^{+52.91}_{-51.12} \,{\rm{MeV}} $ , which is compatible with our naive expectation that the resonant states have widths of the order of 100 MeV.The masses of the
$ \bar{D}\Sigma_c $ molecular states with the isospins$ I=\frac{1}{2} $ and$ \frac{3}{2} $ are$ 4.31^{+0.07}_{-0.07}\,{\rm{MeV}} $ and$ 4.33^{+0.09}_{-0.08}\,{\rm{GeV}} $ , respectively [16]. The$ P_c(4312) $ can be assigned as the$ \bar{D}\Sigma_c $ molecular state with the isospin$ I=\frac{1}{2} $ , while the molecular state with the$ I=\frac{3}{2} $ (or$ P_c(4330) $ ) has not been observed yet. For example, the uncertainty of the mass$ \delta={}^{+0.09}_{-0.08}\,{\rm{GeV}} $ leads to the uncertainties$ {}^{+196.04}_{-90.37}\,{\rm{MeV}} $ and$ {}^{+0.232}_{-0.056}\,{\rm{MeV}} $ for the partial decay widths$ \Gamma(P^\prime \to J/\psi \Delta) $ and$ \Gamma(P^\prime \to \eta_c \Delta) $ , respectively, which are too large. We discard them, as the central value of the mass of the$ P_c(4330) $ corresponds to that of the$ P_c(4312) $ , and we take the central values in calculating the decay widths. According to the calculations of the QCD sum rules, the uncertainties of the masses and pole residues also come from the uncertainties of the input parameters at the QCD side, including both the uncertainties of the hadron masses and the hadronic coupling constants suffering from doubling counting.In Ref. [26], we choose the current which does not have a definite isospin. Contributions from both the
$I={1}/{2}$ and${3}/{2}$ molecular states exist with$ J^P={\frac{1}{2}}^- $ , as the mass-gap between the$I={1}/{2}$ and${3}/{2}$ molecular states are very small, and they have almost degenerated pole residues, so it cannot make much difference in assuming that they are the same particle, if only numerical values are concerned. For the partial decay widths of the$ P_c(4312)\to \eta_c N $ and$ J/\psi N $ , the predictions in Ref. [26] and in the present work are almost degenerated. However, we should bear in mind that the$ P_c(4312) $ and$ P_c(4330) $ are two different particles and have different isospins. Even if they have degenerated masses and pole residues, we still want to distinguish them and obtain flawless predictions.In Ref. [38], we take the
$ P_c(4312) $ as the diquark-diquark-antiquark type hidden-charm pentaquark state with the$ J^P={\frac{1}{2}}^- $ . We investigate the partial decay widths with the QCD sum rules, and observe that the partial decay widths of the$ P_c(4312)\to \eta_c N $ and$ J/\psi N $ are comparable, which differ significantly from the predictions in Ref. [26]. We can search for the decay mode$ P_c(4312)\to \eta_c N $ and precisely measure the branching fractions to distinguish the pentaquark and molecule assignment. -
In the present study, we investigate the strong decays of the
$ P_c(4312) $ and its possible higher isospin cousin$ P_c(4330) $ considering the conservation of the isospin. The hadronic coupling constants in the four decay channels$ P_c(4312) \rightarrow \eta_c+N $ ,$ J/\psi+N $ ,$ P_c(4330)\rightarrow \eta_c+\Delta $ , and$ J/\psi+\Delta $ are calculated in detail via the QCD sum rules. Then, we obtain the partial decay widths, among which, the partial decays$ P_c(4312)\rightarrow J/\psi N $ and$ P_c(4330)\rightarrow J/\psi \Delta $ almost saturate the total decay widths, and the width$ \Gamma_{P_c(4312)}=10.89^{+8.97}_{-8.09} \,{\rm MeV} $ is in very good agreement with the experimental data$ 9.8\pm2.7^{+3.7}_{-4.5}\,{\rm{MeV}} $ from the LHCb collaboration, and supports assigning the$ P_c(4312) $ as the$ \bar{D}\Sigma_c $ molecular state with the isospin$ |I,I_3\rangle=|\frac{1}{2},\frac{1}{2}\rangle $ . The observation of its isospin cousin$ P_c(4330) $ with the$ |I,I_3\rangle=|\frac{3}{2},\frac{1}{2}\rangle $ in the$ J/\psi \Delta $ mass spectrum could shed light on the nature of the$ P_c $ states.
Strong decays of the Pc(4312) and its isospin cousin via the QCD sum rules
- Received Date: 2024-01-07
- Available Online: 2024-05-15
Abstract: In this study, considering the conservation of isospin in the strong decays, we investigate the strong decays of the pentaquark molecule candidate






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: