-
For compatibility to general relativity, the accepted idea that the expansion of the universe is accelerating requires the introduction of some unusual forms of matter. However, several authors have proposed that instead of creating strange hypothesis on some yet unobservable species of matter, one should follow the original concept of Einstein’s first paper on cosmology and consider modifying the equations that control the gravitational metric in the cosmic scene. This possibility prompted us to re-examine the evolution of the topological invariant containing two duals in a dynamical universe, the so called Gauss-Bonnet (GB) topological invariant. The particular interest on this invariant emerges from the fact that, in a homogeneous and isotropic universe, it drives the cosmic acceleration. In a decelerating scenario and as a necessary previous condition of an ulterior acceleration, this invariant must have an extremum identified to its maximum value. We will examine the conditions for this to occur and a description of the universe with epochs of accelerated and decelerated expansion.
Modified theories of gravity have been proposed to account for astronomical data, such as the cosmic late acceleration. Two of such propositions that have have become popular are the f(R) theory and GB topological invariant modified gravity [1−4]. GB modified gravity utilizes the topological invariant of the same name, which is only an invariant in 4D space-time, commonly expressed as
$ {\cal{G}} $ .This topological invariant,
$ {\cal{G}} $ , by itself does not affect the dynamics of general relativity in 4D when added to the Einstein-Hilbert action. Instead, it can be inplemented in three basic ways: first, by coupling$ {\cal{G}} $ to a scalar field ϕ [5−7]; second, by considering a nontrivial function of the topological invariant,$ f({\cal{G}}) $ modified gravity; third, by implementing the topological invariant to a Einstein-Hilbert action of higher dimension D, in which$ {\cal{G}} $ is no longer a topological invariant, and taking the limit$ D\rightarrow4 $ , yielding nontrivial modified dynamics [8]. Some researchers have used observational data to determine constraints to different approaches to GB modified gravity [9−13]. Comprehensive reviews of modified theories of gravity are available in Refs. [14−18].Studies on
$ f({\cal{G}}) $ gravity have shown its capabily to mimick λCDM cosmology and describe radiation/matter epochs followed by cosmic acceleration [19]. The main critique for$ f({\cal{G}}) $ is on the appearance of higher order derivative terms in the equations, which may lead to instabilities in the theory in first order perturbation models [20, 21]. This requires the establishment of criteria and conditions to exclude possible unphysical solutions (see Ref. [5] for example).In this paper, we use the
$ f({\cal{G}}) $ GB modified gravity approach by applying the simplest non-trivial function of$ {\cal{G}} $ . We examine its consequences on a homogeneous and isotropic Friedmann's geometry, first in an empty space-time and then in a case with source matter as cosmic dust. Section II provides a brief definition of topological invariants in 4D. Section III presents the standard$ f({\cal{G}}) $ gravity; subsection III.A presents a relationship between$ f({\cal{G}}) $ and the Fierz representation of a spin-2 particle. Section IV applies the theory to Friedmann's universe; subsection IV.A presents a case for${\cal{G}} = {\rm{constant}}$ , which yields several important constraints to filter out non-physical solutions; subsection IV.B considers the simplest non-trivial function of$ {\cal{G}} $ , that is$ f({\cal{G}}) = \sigma {\cal{G}}^2 $ ; first, we assume an empty space-time, which produces a 2D dynamical system, and a complete qualitative description of numerical solutions near and around the critical points is presented; second, we assume cosmic dust as a source, producing a 3D dynamical system, and present a set of qualitative behavior of numerical solutions. Section V presents the conclusion. -
4D Riemannian geometry has two topological invariants, that is
$ I = \int \sqrt{- g} \, A \, \mathrm{d}^{4}x, $

(1) $ II = \int \sqrt{- g} \, {\cal{G}} \, \mathrm{d}^{4}x, $

(2) where
$ A = R_{\alpha\beta\mu\nu}^{*} \, R^{\alpha\beta\mu\nu} $

(3) and
$ {\cal{G}} $ is the GB topological invariant:$ {\cal{G}} = R_{\alpha\beta}^{*}{}_{\mu\nu}^{*} \, R^{\alpha\beta\mu\nu}. $

(4) The dual is defined for any anti-symmetric tensor
$ F_{\mu\nu} $ as$ F_{\mu\nu}^{*} = \frac{1}{2} \, \eta_{\mu\nu\alpha\beta} \, F^{\alpha\beta}, $

(5) $ \eta_{\mu\nu\alpha\beta} = \sqrt{-g} \, \epsilon_{\mu\nu\alpha\beta}, $

(6) where
$ \epsilon_{\mu\nu\alpha\beta} $ is the completely anti-symmetric Levi-Cività symbol.We note that invariant
$ {\cal{G}} $ can be expressed in terms of the curvature tensor (without the dual operation) using the identity$ {\cal{G}} = - R_{\alpha\beta\mu\nu} \, R^{\alpha\beta\mu\nu} + 4 \, R_{\mu\nu} \, R^{\mu\nu} - R^{2}. $

(7) This
$ {\cal{G}} $ satisfies the identity$ {R}{^{\overset{\ast}{\mu\nu} {\overset{\ast}{\alpha\beta}}}} {R}{^\epsilon_{\nu\alpha\beta}} = \frac{1}{4} {\cal{G}} {g}{^{\mu\epsilon}}. $

(8) -
For an arbitrary function,
$ f({\cal{G}}) $ , the variation in action$ S = \int \sqrt{-g}\left(R+f({\cal{G}})+L_m\right), $

(9) where
$ L_m $ is the matter Lagrangian, leads to the following set of dynamic equations:$ R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}+Z_{\mu\nu} = -T_{\mu\nu}, $

(10) where
$ Z_{\mu\nu} $ is defined as$ Z_{\mu\nu}\equiv \frac{1}{2}\left(f'{\cal{G}}-f\right)g_{\mu\nu}+2{H}{^\alpha_{\;(\mu\nu);\alpha}}, $

(11) $ {H}^{\mu\nu\beta}\equiv f''{\cal{G}}_{,\sigma} {R}{^{\overset{\ast}{\mu\nu} {\overset{\ast}{\beta\sigma}}}}, $

(12) where
$f' = \dfrac{\mathrm{d}f}{\mathrm{d}{\cal{G}}}$ .Note that contraction of the last two indices of
$ {H}^{\mu\nu\alpha} $ implies the following identity:$ {H^{\mu\nu}}{_\nu} = -f''{\cal{G}}_{,\nu} \left({R}^{\mu\nu}-\frac{1}{2}R{g}^{\mu\nu}\right). $

(13) -
Let us show that quantity
$ {H}^{\mu\nu\beta} $ defined by Eq. (12) may be associated with a spin-2 field. We begin by remembering that two basic representations can be used to solve a spin-2 field, which we call the Einstein and Fierz representations (both were introduced by Fierz):● Einstein representation:
$ \varphi_{\mu\nu}, $ ● Fierz representation:
$ F_{\alpha\beta\mu}. $ Tensor
$ \varphi_{\mu\nu} $ is symmetric and has 10 independent components. Tensor$ F_{\alpha\beta\mu} $ has symmetries$ {F}^{\mu\nu\beta} = -{F}^{\nu\mu\beta}, $

(14) which states that this tensor has 24 independent components. The second property states that the dual has no trace, that is,
$ {F}_{\mu\nu\beta}+{F}_{\beta\mu\nu}+{F}_{\nu\beta\mu} = 0, $

(15) or, equivalently,
$ {{F}{^{\overset{\ast}{\mu\alpha}}}_\alpha} = 0, $

(16) which reduces this number to 20. Identity
$ {{F}{^{\mu\nu\beta}}_{;\beta}} = 0 $

(17) makes this number 14, and finally, the property of vanishing trace,
$ {F^{\alpha\mu}}{_\mu} = 0, $

(18) reduces the number of independent components to 10.
We can directly to show that tensor
$ {H}^{\mu\nu\alpha} $ , defined in Eq. (12),$ f''{\cal{G}}_{,\sigma} {R}{^{\overset{\ast}{\mu\nu} {\overset{\ast}{\beta\sigma}}}}, $

(19) satisfies all the conditions above, showing that a spin-2 tensor is hidden in the above dynamics, constructed with invariant
$ {\cal{G}} $ .Tensor
$ {H}^{\mu\nu\beta} $ has four properties:● Anti-symmetry in the first two indices:
${H}^{\mu\nu\beta} = -{H}^{\nu\mu\beta};$ ● Cyclic identity:
${H}_{\mu\nu\beta}+{H}_{\beta\mu\nu}+{H}_{\nu\beta\mu} = 0 \Leftrightarrow {H^{\overset{\ast}{\mu\alpha}}}{_\alpha} = 0;$ ● Null divergence in the last indice:
${H^{\mu\nu\beta}}{_{;\beta}} = 0;$ ● Contraction of the last two indices:
${H^{\mu\nu}}{_\nu} = -X_{\nu} \left({R}^{\mu\nu}-\frac{1}{2}R{g}^{\mu\nu}\right).$ Therefore, quantity
$ {H}^{\mu\nu\beta} $ satisfies all these conditions, showing that it can be associated with a spin-2 tensor hidden in the above dynamics. This is only a formal property of quantity$ H^{\mu\nu\alpha} $ related to derivatives of second order of the metric tensor. -
Let us consider the homogeneous and isotropic Friedmann's metric,
$ \mathrm{d}s^2 = \mathrm{d}t^2-a(t)^2(\mathrm{d}x^2+\mathrm{d}y^2+\mathrm{d}z^2), $

(20) where
$ a(t) $ is the scale factor. With the definition of the Hubble parameter,$ H\equiv \dot{a}/a $ , the GB topological invariant yields$ {\cal{G}} = -24\frac{\ddot{a}\dot{a}^2}{a^3} = -24(\dot{H}+H^2)H^2, $

(21) note that the sign of
$ {\cal{G}} $ indicates the sign of the acceleration of the scale factor.From (10), the new term,
$ Z_{\mu\nu} $ , can be considered a geometric source, and for metric (20), when$ {\cal{G}} $ is only a function of time, it can be associated with a perfect fluid [22], that is,$ R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu} = -Z_{\mu\nu}-T_{\mu\nu}, $

(22) where
$ Z_{\mu\nu} $ can be expressed as$ Z_{\mu\nu} = (\rho_z+p_z)v_\mu v_\nu -p_z g_{\mu\nu}, $

(23) Thus, the corresponding geometric density
$ \rho_z $ and geometric pressure$ p_z $ are given by$ \rho_z = \frac{1}{2}\left(f'{\cal{G}}-f\right)+12f'' \dot{{\cal{G}}} H^3 $

(24) and
$ p_z = -\frac{1}{2}\left(f'{\cal{G}}-f\right)-4\left[\left(f'''\dot{{\cal{G}}}^2+f''\ddot{{\cal{G}}}\right)H^2+2f''\dot{{\cal{G}}} H(\dot{H}+H^2)\right]. $

(25) The modified dynamical equations from (22) are straightforward:
$ 3H^2 = \rho_z+\rho_m, $

(26) $ 2\dot{H}+3H^2 = -p_z-p_m, $

(27) where the energy-matter source satisfies the conservation law,
$ 0 = \dot{\rho_m}+3(\rho_m+p_m)H. $

(28) We observe that differentiating (26) with respect to time and applying Eqs. (21) and (28) result in Eq. (27), that is, Eq. (27) is not an independent equation and can be interpreted as a cinematic relation with respect to the expansion parameter of the model.
To observe qualitative and quantitative properties of the model, we utilize the theory of dynamical systems. With variables
$ {\cal{G}} $ , H, and$ \rho_m $ and through Eqs. (21), (24), (26), and (28), the problem can be enunciated in a general dynamical system form:$ \dot{{\cal{G}}} = \frac{1}{12f''H^3}\left[3H^2 -\frac{1}{2}(f'{\cal{G}}-f) -\rho_m\right] , $

(29) $ \dot{H} = -\frac{{\cal{G}}}{24H^2}-H^2, $

(30) $ \dot{\rho_m} = -3(\rho_m +p_m)H, $

(31) where Eq. (31) refers to one class of matter-energy source; when other independent sources of matter-energy are added to the system, the corresponding source density dynamical variables and equations can be identified. In addition, the equation of state relating
$ \rho_m $ and$ p_m $ , frequently of form$ p = \omega \rho $ , must be identified for a given value of ω.One class of functions for
$ {\cal{G}} $ to consider is of the type$ f({\cal{G}}) = \sigma{\cal{G}}^n $ , where σ is a constant parameter and$n = 2, 3, \cdots$ to produce nontrivial effects. The choice of a particular$ f({\cal{G}}) $ only affects Eq. (29):$ \dot{{\cal{G}}} = \frac{1}{12\sigma n(n-1){\cal{G}}^{n-2}H^3}\left[3H^2-\frac{n-1}{2}\sigma{\cal{G}}^n -\rho_m \right]. $

(32) For
$ n>2 $ , the dynamical system presents a singularity when$ {\cal{G}} = 0 $ in the phase space, which may provide a barrier for the system to transition between the positive and negative values of$ {\cal{G}} $ . Subsequently,$ n = 2 $ provides the simplest case for$ {\cal{G}} $ to have the ability to change the sign, and consequently, give rise to a model with epochs of accelerated and decelerated rates of expansion. We will see later that this system can have solutions where Gauss-Bonnet topological invariant$ {\cal{G}} $ is cyclically dampened, changing its sign periodically. This can be used to describe a universe with stages of acceleration and deceleration. However, we must first consider a case in which$ {\cal{G}} $ is constant for an interval or indefinitely. -
The most simple behavior we could get from
$ {\cal{G}} $ is constant α, let$ {\cal{G}}\equiv \alpha, $

(33) therefore,
$ \dot{{\cal{G}}} = 0 $ and$ \ddot{{\cal{G}}} = 0 $ . Thus, the geometric density and pressure Eqs. (24) and (25) are also constants, respectively given by$ \rho_z = \frac{1}{2}\left(f'(\alpha)\alpha-f(\alpha)\right), $

(34) $ p_z = -\frac{1}{2}\left(f'(\alpha)\alpha-f(\alpha)\right). $

(35) From the definition of
$ {\cal{G}} $ in (21), the problem involves solving the following integral:$ \int \frac{-H^2}{H^4+\frac{\alpha}{24}}\mathrm{d} H = t+k. $

(36) The solutions for Eq. (36) have three classes, depending on if α is positive, negative, or zero. A fourth class of solutions can be obtained by assuming H as a constant.
-
The implicit solution of Eq. (36) for
$ \alpha>0 $ is$ \begin{aligned}[b]& -\left(\frac{3}{8\alpha}\right)^{{1}/{4}} \Bigg[ \frac{1}{2}\ln \left( \frac{H^2-\left(\dfrac{\alpha}{6}\right)^{1/4}H+\left(\dfrac{\alpha}{24}\right)^{1/2}}{H^2+\left(\dfrac{\alpha}{6}\right)^{1/4}H+\left(\dfrac{\alpha}{24}\right)^{1/2}} \right)\\& +\arctan \left( 2\left(\frac{6}{\alpha}\right)^{{1}/{4}}H+1 \right) +\arctan \left( 2\left(\frac{6}{\alpha}\right)^{{1}/{4}}H-1 \right) \Bigg] \\ & =\; t+k, \end{aligned} $

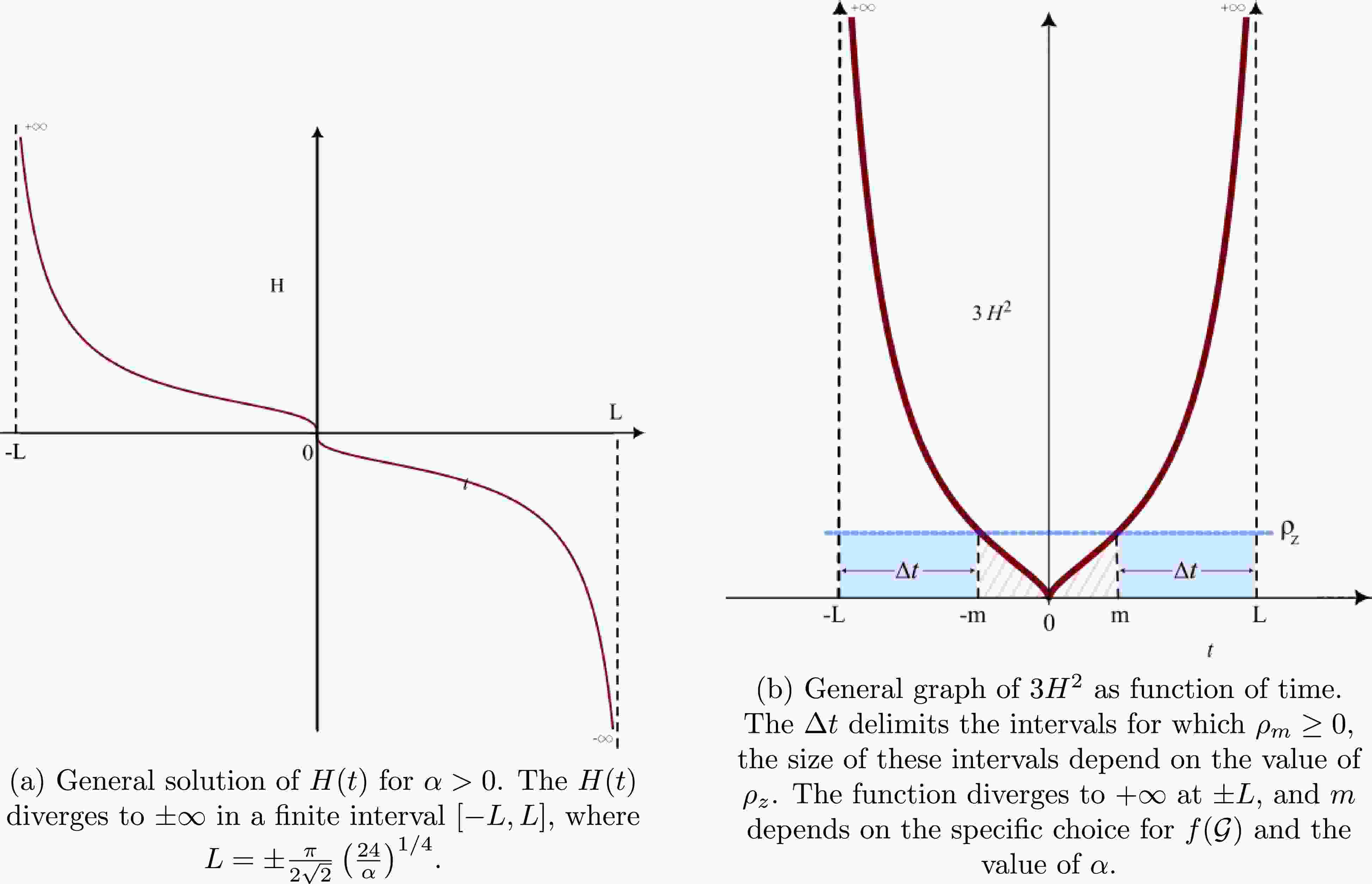
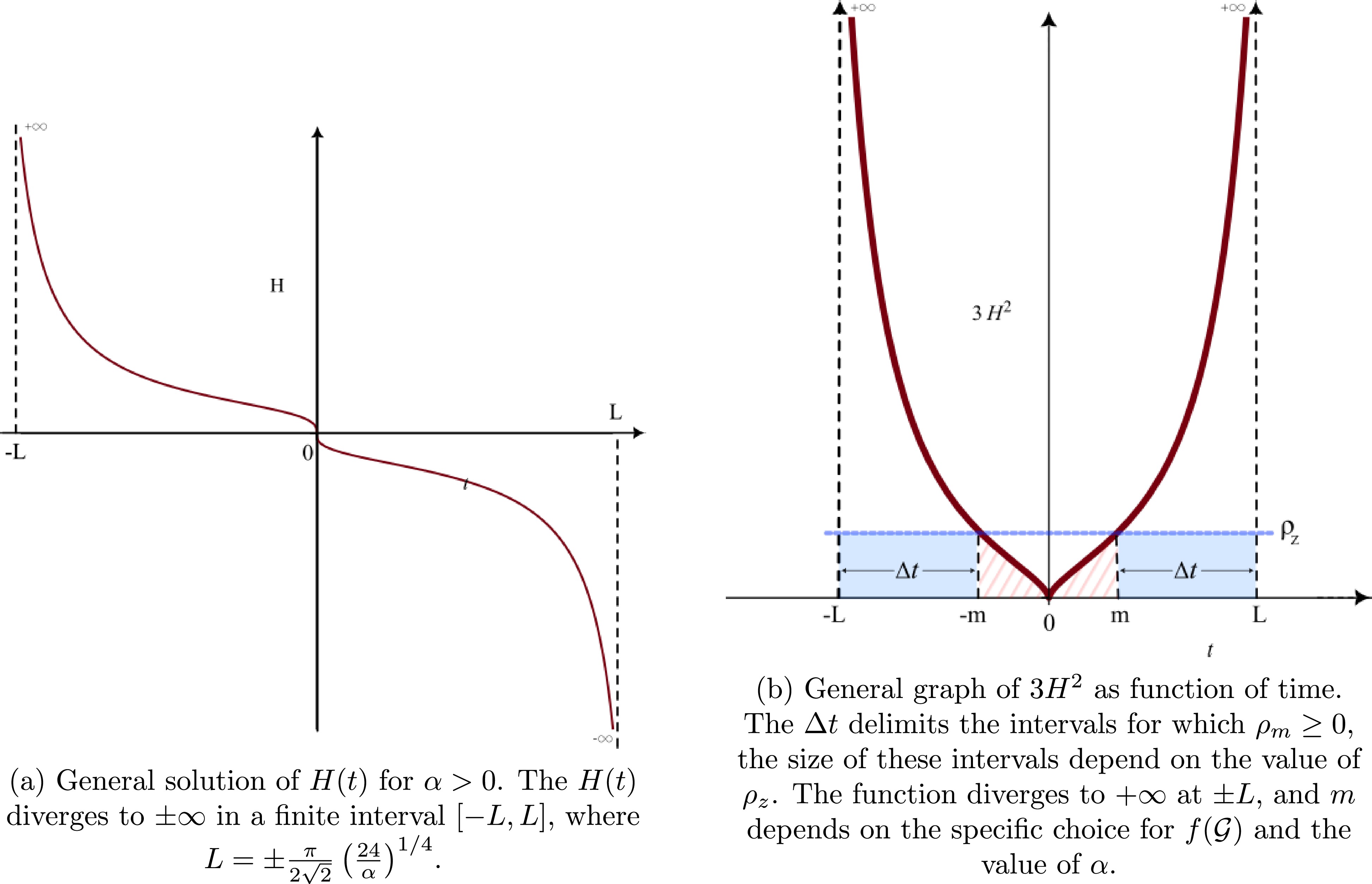
(37) where k is a constant of integration that simply shifts the solution in time. Assuming
$ k = 0 $ and taking the limit for$ H\rightarrow \pm\infty $ on the left side of Eq. (37), we obtain$ L = \pm\frac{\pi}{2\sqrt{2}}\left(\frac{24}{\alpha}\right)^{{1}/{4}}. $

(38) This implies that the Hubble parameter diverges to
$ \pm\infty $ in a finite interval. The general solution is expressed in Fig. 1(a).From Eq. (26), the source density can be expressed as
$ \rho_m = 3H^2 -\rho_z, $

(39) this means that if
$ \rho_z $ is positive, condition$ \rho_m\geq 0 $ is only satisfied in intervals$ -L<t\leq -m $ and$ m\leq t<L $ , where$ \pm m $ is time t for which relation$ 3H^2 -\rho_z = 0 $ is satisfied. The value of m depends on the choice of function$ f({\cal{G}}) $ and α. The conclusion is that, for$ {\cal{G}} $ as a constant and α and$ \rho_z $ being positive, the evolution of H is confined in one of the intervals$ [-L,-m] $ or$ [L,m] $ for source density$ \rho_m $ to be greater than or equal to zero; therefore, H can be either positive or negative in this configuration. Fig. 1(b) shows the graph of$ 3H^2 $ and its corresponding allowed intervals. -
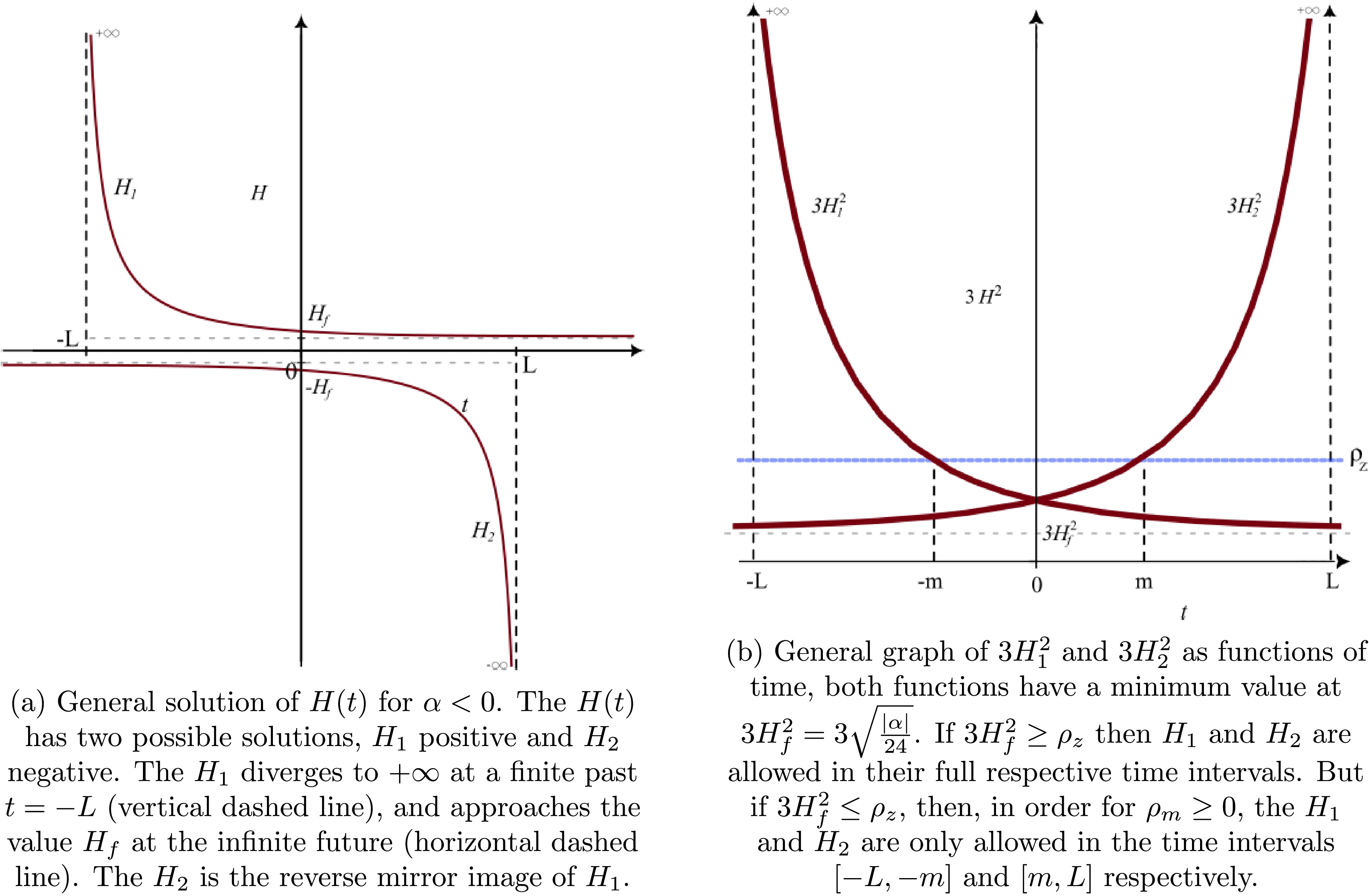
The implicit solution of (36) for
$ \alpha<0 $ is${\begin{aligned}[b]& \left(\frac{3}{2|\alpha|}\right)^{{1}/{4}} \left[{1}/{2}\ln\left(\frac{H+\left(\dfrac{|\alpha|}{24}\right)^{{1}/{4}}}{H-\left(\dfrac{|\alpha|}{24}\right)^{{1}/{4}}}\right) -\arctan\left(\left(\frac{24}{|\alpha|}\right)^{{1}/{4}}H\right) \right] \\& =\; t+k.\end{aligned}} $

(40) Here, k is a constant of integration. For
$ k = 0 $ , the implicit solution above implies two possible solutions for$ H(t) $ : one is$ H_1 (t) $ , which is always positive and diverges to$ +\infty $ at a finite past time$ t = -L $ ; for infinite future ($ t\rightarrow\infty $ ), it stabilizes at the value of$H_f = \left({|\alpha|}/{24}\right)^{1/4}$ . The other solution is$ H_2 (t) $ , which is always negative and diverges to$ -\infty $ in finite future$ t = L $ ; for infinite past ($ t\rightarrow -\infty $ ), it approaches the value of$ -H_f $ . Solutions$ H_1 $ and$ H_2 $ are inverse mirror images of each other, obtained using transformation$ H_2(t) = -H_1 (-t) $ (Fig. 2(a)). The values of$ \pm L $ are obtained using limits$ H_1\rightarrow +\infty $ and$ H_2\rightarrow -\infty $ , given by$ |L| = \sqrt{\frac{3}{2}}\frac{\pi}{(24|\alpha|)^{1/4}}. $

(41) Functions
$ 3H_1^2 $ and$ 3H_2^2 $ have the same minimum value at$ 3H_f^2 $ . Using the condition for the positivity of matter source ($ \rho_m \geq 0 $ ) given by (26), that is,$ 3H^2\geq \rho_z $ , we obtain two possibilities. (a) If$ 3H_f^2 \geq\rho_z $ , then solutions$ H_1 $ and$ H_2 $ are valid over their respective time intervals ($ [-L,+\infty] $ and$ [-\infty,L] $ ). (b) If$ 3H_f^2 \leq\rho_z $ , then$ H_1 $ is only valid in interval$ [-L,-m] $ , and the same for$ H_2 $ in interval$ [m,L] $ , where$ \mp m $ is the time for which$ 3H_1^2 = \rho_z $ and$ 3H_2^2 = \rho_z $ , respectively (Fig. 2(b)). The value of$ \pm m $ depends on the specific choice of function$ f({\cal{G}}) $ and the value of α. -
For
$ {\cal{G}} $ as a constant with a value of zero, we can obtain an explicit solution for the Hubble parameter. Solving Eq. (36) for$ \alpha = 0 $ provides the solution for H:$ H = \frac{1}{t+K_1}, $

(42) where
$ K_1 $ is a constant of integration. For scale factor$ a(t) $ $ a(t) = K_2(t+K_1), $

(43) where
$ K_2 $ is a constant of integration.Therefore, if
$ {\cal{G}} $ is constant and zero, then the scale factor increases or decreases linearly over time, and the Hubble parameter presents a singularity at$ t = -K_1 $ . The condition for the positivity of the matter source ($ \rho_m\geq 0 $ ) can be obtained explicitly from Eq. (26):$ \rho_m = \frac{3}{(t+K_1)^2}-\rho_{z}. $

(44) Eq. (44) shows that if geometric density
$ \rho_{z} $ is less or equal to zero, then$ \rho_m $ is always positive; but if$ \rho_{z} $ is positive, then$ \rho_m $ will be positive only in the following interval:$ -\sqrt{\frac{3}{\rho_{z}}}-K_1\leq t\leq \sqrt{\frac{3}{\rho_{z}}}-K_1, $

(45) which depends on the initial condition for
$ H(t) $ . -
Finally, one more class of solutions can be obtained by assuming the Hubble parameter as constant
$ H_c $ . For$ H_c\neq 0 $ and using the equation of state,$ p_m = \omega \rho_m $ , the dynamical equation (26) and conservation equation (28), that is,$ \rho_m = 3H_c^2-\rho_z $

(46) $ \dot{\rho_m} = -3\rho_m(1+\omega)H_c, $

(47) can only be satisfied if
$ \rho_m = 0 $ , because Eq. (46) implies$ \rho_m $ as a constant, but Eq. (47) makes$ \dot{\rho_m}\neq 0 $ if$ \rho_m\neq 0 $ . From Eqs. (46) and (21), we obtain the relationships among$ H_c $ , α, and$ \rho_z $ :$ H_c^2 = \frac{\rho_z}{3} = \sqrt{\frac{-\alpha}{24}}, $

(48) where α must be negative for the quantities to be real numbers. Therefore, a constant Hubble parameter can only describe an empty space-time.
Note that for
$ H_c = 0 $ , Eq. (21) implies$ \alpha = 0 $ , and Eqs. (46) and (47) are both satisfied, with the matter source assuming the following condition:$ \rho_m = -\rho_z = \frac{1}{2}f(0), $

(49) where Eq. (34) is used. Here, we have a description of a static universe with homogeneous matter density
$ \rho_m $ as a constant directly controlled by function$ f(0) $ . Because the Hubble parameter is zero, the scale factor is a constant$ a_c $ in the metric. The positivity of the matter source imposes the condition$ \rho_m \geq 0 \Rightarrow f(0) \geq 0. $

(50) In summary, when
$ {\cal{G}} $ is assumed to be constant, specific conditions emerge for the matter source$ \rho_m $ to be strictly positive; even in some cases,$ {\cal{G}} $ cannot be constant indefinitely but must vary over time. These specific conditions are highly dependent on the choice of function$ f({\cal{G}}) $ . This may be useful in the future to filter only solutions with$ \rho_m \geq 0 $ . The separation of solutions through the sign of$ {\cal{G}} $ is useful because it indicates if the system is under accelerated, decelerated, or null accelerated expansion, according to Eq. (21). When the Hubble parameter is assumed constant, the direct influence of function$ f({\cal{G}}) $ over the system is clear, either dictating the expansion rate in an empty universe or controlling the value of homogeneous source matter density$ \rho_m $ in a static universe. -
We now consider the first non-trivial term in the Taylor expansion of
$ f({\cal{G}}) $ , that is, function$ f({\cal{G}}) = \sigma {\cal{G}}^2 $ , with σ as a constant. Here, the geometric density and pressure assume the following forms:$ \frac{\rho_z}{\sigma} = \frac{{\cal{G}}^2}{2}+24\dot{{\cal{G}}}H^3, $

(51) $ \frac{p_z}{\sigma} = -\frac{{\cal{G}}^2}{2}-8\left[\ddot{{\cal{G}}}H^2+2\dot{{\cal{G}}}H\left(\dot{H}+H^2\right)\right], $

(52) and we must solve the set of differential equations
$ 3H^2 = \rho_z+\rho_m, $

(53) $ 0 = \dot{\rho_m}+3(\rho_m+p_m)H, $

(54) $ {\cal{G}} = -24(\dot{H}+H^2)H^2. $

(55) -
Let us consider a case with an empty space-time. Under this condition, Eq. (54) is identically zero. Applying the dynamical system expression of the problem, given by Eqs. (29) and (30), we obtain
$ \dot{{\cal{G}}} = \frac{1}{24H^3}\left[\frac{3H^2}{\sigma}- \frac{{\cal{G}}^2}{2}\right], $

(56) $ \dot{H} = -\frac{{\cal{G}}}{24H^2}-H^2. $

(57) This 2D dynamical system represents the entire problem in an empty space-time. Its numerical solutions will prove useful in providing a map to search for certain types of structures and behaviors in the complete problem with energy-matter sources, which is a dynamical system of higher dimension.
For
$ \dot{{\cal{G}}} = 0 $ and$ \dot{H} = 0 $ , the equilibrium points in phase space$ ({\cal{G}}(t) \times H(t)) $ are${\cal{G}}_0 = {\sigma^{-2/3}}\left(\frac{3}{2}\right)^{{1}/{3}}$ and$H_0 = \pm{\left({\sigma 96}\right)^{-1/6}}$ , respectively; these imply that constant σ must be positive for the equilibrium points to be real. We have observed in subsection IV.A.4 that solutions for the Hubble parameter as a constant$ H_0 $ are viable in an empty space-time, which means that in these equilibrium points, the scale factor behaves as an exponential manner, given by$ a(t)\sim \exp{(H_0 t)} $ . We observe that line$ H = 0 $ in the phase space is a singularity region, and for the origin$ H = {\cal{G}} = 0 $ of the phase space, the dynamical system is undefined. However, from Eqs. (53) and (55), we observe that the equations are identically satisfied. Subsequently, to determine the behavior of solutions near the origin, we must apply specific methods of analyses.The next step is to determine the behavior of solutions near the equilibrium points. For this, we analyze the Jacobian matrix of the system in the equilibrium points,
$ a = \left(\dfrac{\partial\dot{{\cal{G}}}}{\partial {\cal{G}}}\right)_{({\cal{G}}_0,H_0)} $ ,$ b = \left(\dfrac{\partial\dot{{\cal{G}}}}{\partial H}\right)_{({\cal{G}}_0,H_0)} $ ,$ c = \left(\dfrac{\partial\dot{H}}{\partial {\cal{G}}}\right)_{({\cal{G}}_0,H_0)} $ , and$ d = \left(\dfrac{\partial\dot{H}}{\partial H}\right)_{({\cal{G}}_0,H_0)} $ , and compute the eigenvalues of the matrix$ \begin{vmatrix} a-\lambda & b\\ c & d-\lambda \end{vmatrix} = 0. $

(58) We observe that the two eigenvalues are real and of opposite signs for both equilibrium points; therefore, these equilibrium points are saddle points, that is, trajectories near the equilibrium points are attracted or repelled depending on the direction they approach these points [23].
Now, to obtain more information on the solutions for this problem, we can numerically integrate the solutions for given initial conditions. To numerically integrate the solutions, we assume
$ \sigma\equiv 1 $ , and using the Runge–Kutta method [24], we integrate for different initial conditions inside interval$[{\cal{G}} = -2,\cdots,1, H = -1,\cdots,1]$ , which contains the two equilibrium saddle points and produces the behavior map in Fig. 3.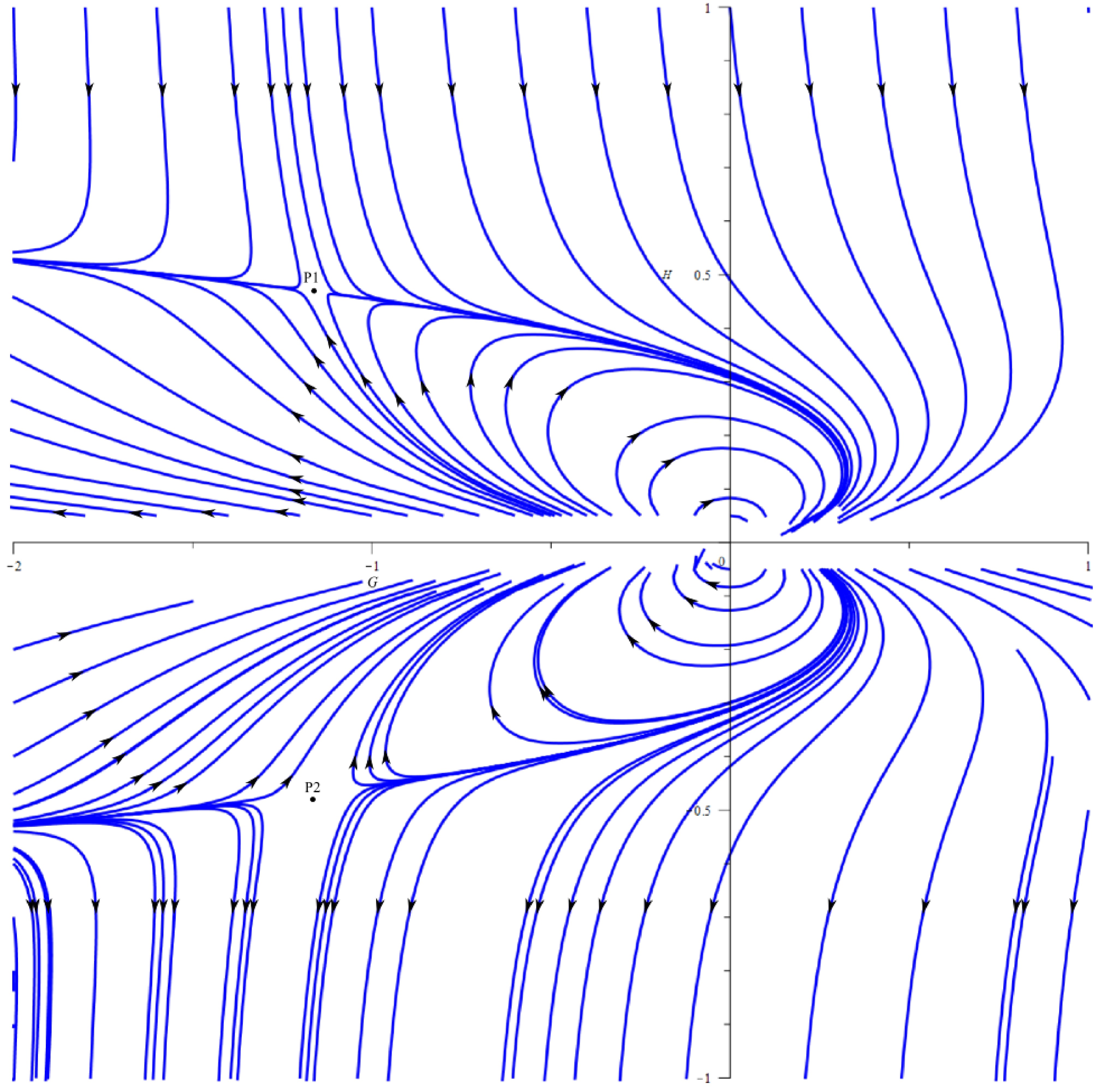
Figure 3. (color online) Integral solutions for the 2D dynamical system in phase space
$ [{\cal{G}}(t)\times H(t)] $ . Points$ P1 $ and$ P2 $ are the corresponding equilibrium points of the system. The$ {\cal{G}} $ axis is a singularity for the system and we cannot infer its behavior numerically.Numerical solutions are only possible far from the region of singularity of the system, but through approximation, we can determine the behavior of solutions near the singularity region (for
$ H \approx 0 $ ). From Eqs. (56) and (57), we obtain$ \frac{\dot{H}}{\dot{{\cal{G}}}} = \frac{\mathrm{d}H}{\mathrm{d}{\cal{G}}} = -H\frac{\left({\cal{G}}+24H^4\right)}{3H^2-{{\cal{G}}^2}/{2}}. $

(59) For
$ |H|<<1 $ and$ |{\cal{G}}|>>1 $ , Eq. (59) simplifies to$\dfrac{\mathrm{d}H}{\mathrm{d}{\cal{G}}}\approx 0$ , with solution$ H(t)\approx cte $ , that is, in the phase space,$ H(t) $ is constant near the$ {\cal{G}} $ axis when not close to the origin. Let us now focus on the behavior of solutions near the origin of the phase space; because$ {\cal{G}}\approx 0 $ and$ H\approx 0 $ , the$ H^4 $ term can be dropped compared with$ {\cal{G}} $ in Eq. (59), yielding$ \frac{\mathrm{d}H}{\mathrm{d}{\cal{G}}}\approx -\frac{H{\cal{G}}}{3H^2-{{\cal{G}}^2}/{2}}, $

(60) and the solutions to this system are given by
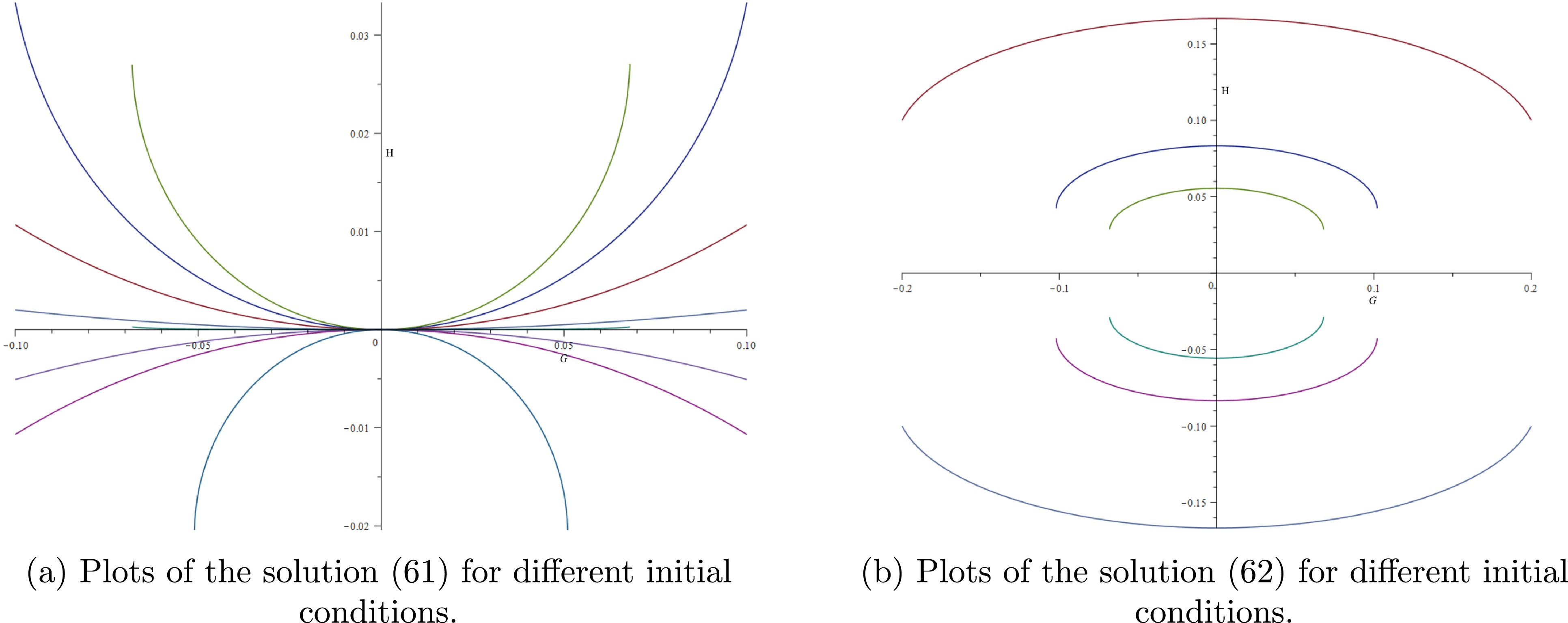
$ H({\cal{G}}) = \frac{1}{12a}\left(1-\sqrt{1-24a^2{\cal{G}}^2}\right), $

(61) and
$ H({\cal{G}}) = \frac{1}{12b}\left(1+\sqrt{1-24b^2{\cal{G}}^2}\right), $

(62) where a and b are the constants that depend on the initial conditions. We note that the value of
$ H(t) $ is bounded. The plots of Eqs. (61) and (62), for different values for a and b, are given in Figs. 4(a) and 4(b). Although the dynamical system is undefined at the origin of the phase space, we observe that its solutions near it are well defined, and the origin acts as a convergence and divergence of solutions, depending on the region it is approached.The final step to understanding the whole qualitative picture for the behavior of this simplified problem is to determine the interactions of the numerical solutions given in Fig. 3 with solutions near the origin of the phase space (61) and (62). We can take a direct approach: first, considering solution (61) with an arbitrary value for a, because of its square root, both
$ {\cal{G}} $ and H have two extreme values in this solution. Therefore, selecting one of the extreme values and considering them as initial conditions for the 2D dynamical system (56) and (57), we can numerically integrate it to obtain an integral solution. Two things can occur to this integral solution: it can grow away from the origin of the phase space (Fig. 3) or it can return to the origin in two forms: to the original solution (61), where the integral solution is cyclic closed, or with a different value for constant a in (61), where the integral solution is cyclic open or has a vortex-like behavior. Depending on the initial conditions selected, the integral solution grows away from the origin or cycles back in a vortex-like behavior nearing the origin of the phase space. Figure. 5 shows some examples of the first result, and Fig. 6 shows an example of the second result.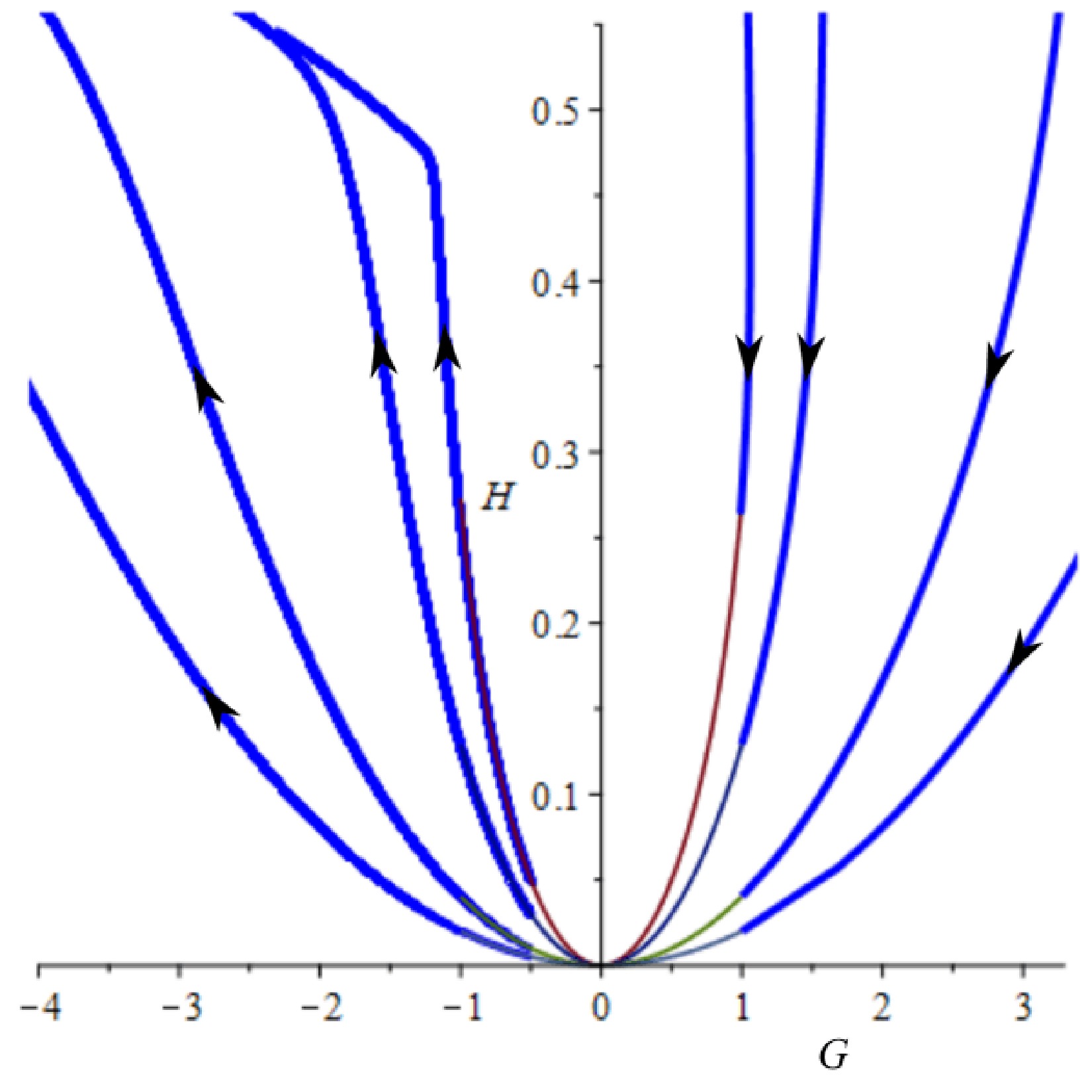
Figure 5. (color online) Examples of integral solutions that pass one time through the origin of phase space
$ {\cal{G}} \times H $ .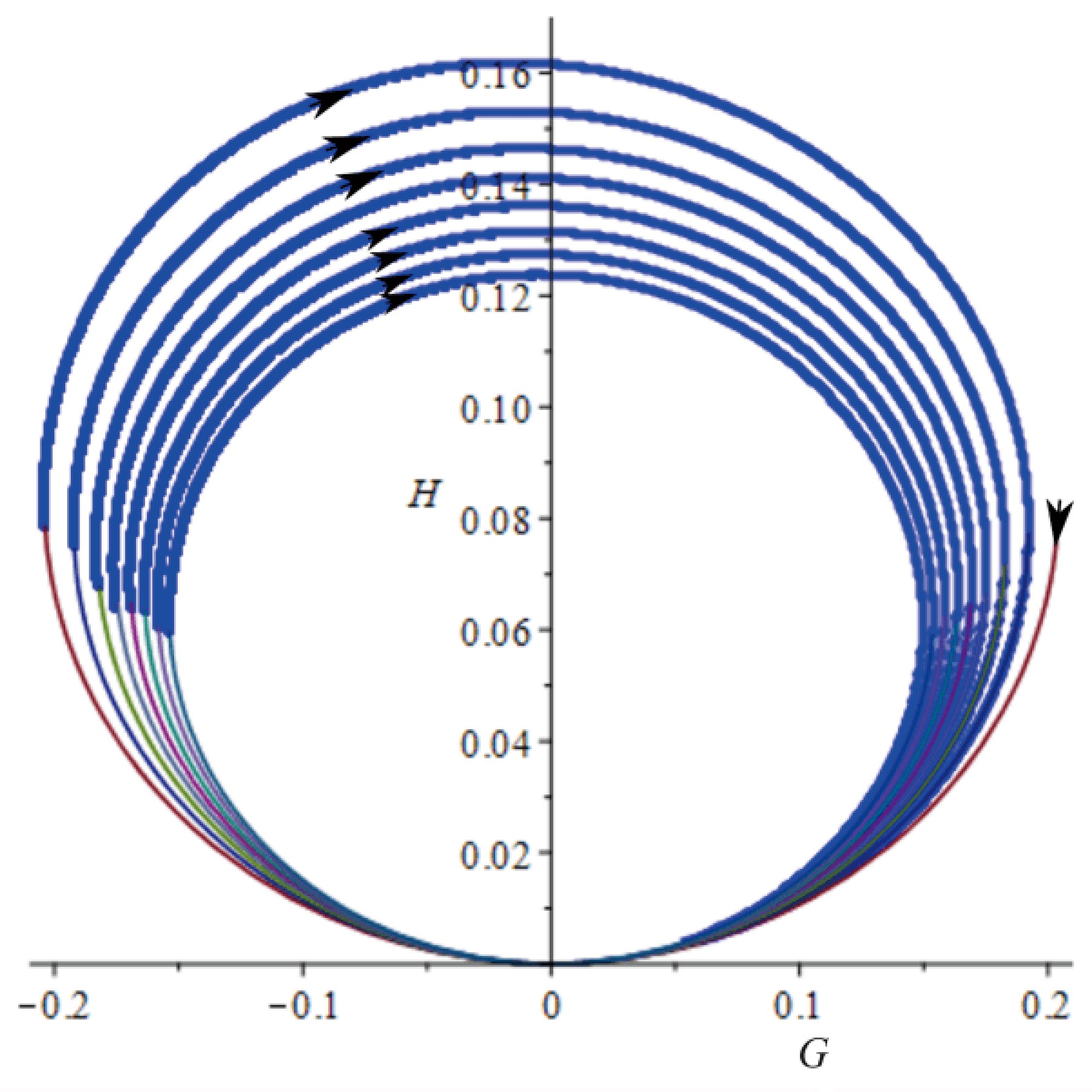
Figure 6. (color online) One example of an integral solution presenting an open cyclic behavior (vortex-like) near the origin, each time passing through the origin with an smaller arch of travel, that is, the origin acts as an attraction pole.
Figures. 3, 5, and 6 summarize the global behavior for the 2D dynamical system (56) and (57). Focusing on positive H, we can divide the phase space into four quadrants, as shown in Fig. 7. The first quadrant (I) produces initial conditions under which H decreases to a minimum positive value and increases afterward. The second quadrant (II) has initial conditions with integral solutions that converge to the origin of the phase space and are connected to the fourth quadrant (IV). Subsequently, for initial conditions in II, H decreases to zero and increases afterward in region IV. In region III, the initial conditions result in integral solutions that are open cyclic around the origin of the phase space, where the origin acts as an attraction pole.
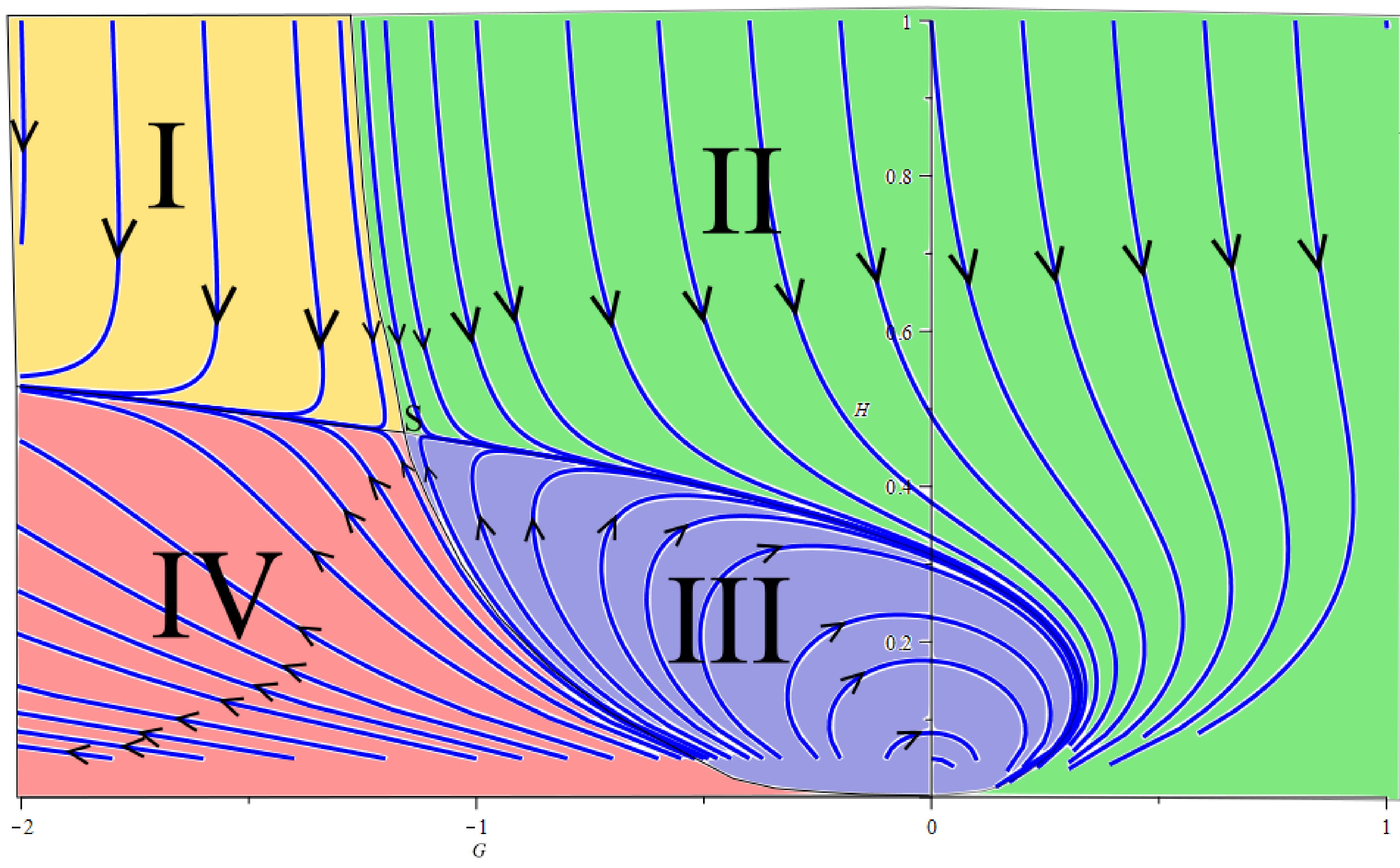
Figure 7. (color online) Global behavior of the 2D dynamical system (56) and (57) for positive H. Quadrants II and IV are connected through the origin, and quadrant (III) has open cyclic solutions attracted to the origin.
Therefore, having a global qualitative behavior for the empty space-time problem, we have a map of the behavior to look for in the real case with energy-matter sources. The complete problem is given by the set of Eqs. (53) to (55); for an empty space-time, this set yields a 2D dynamical system, and adding matter-energy source yields a higher dimension dynamical system. Figures 3 and 7 provide an approximation of the behavior of the integral solutions in these higher dimensional cases.
The behavior of the Hubble parameter, and consequently of the scale factor, is highly dependent on the initial conditions, as we observe in Fig. 7. On quadrant II, it can describe a universe initially in an epoch of accelerated expansion, followed by a period of deceleration, and finally a last epoch of steady increase in acceleration and rate of expansion in region IV. Region I offers only the behavior of an ever increasing rate of expansion and acceleration of the system. Solutions on quadrants I and II/IV tend to converge to a single path in the phase space. While region III describes an empty Friedmann's universe in which
$ {\cal{G}} $ changes sign periodically, Eq. (21) implies that acceleration of the scale factor$ a(t) $ changes sign periodically, but H is always positive or negative. In other words, it can describe an empty universe that is always expanding but periodically accelerating and decelerating. Moreover, the intensity of this acceleration and deceleration decreases over time. Points of equilibrium$ {\cal{G}}_0 $ and$ H_0 $ are saddle points, which implies that perturbations in these points may lead to two outcomes: the system is attracted to either the convergence of solutions of quadrants I and II/IV or the periodical solutions of quadrant III. Points$ {\cal{G}} = 0 $ and$ H = 0 $ is a special point of convergence and divergence of solutions. This means that small perturbations to the system near this origin may lead to radical differences in the evolution of the system, hinting to a possibly chaotic nature of behavior. In future work, we will present a study on when perturbations are applied to the system.Eqs. (26), (27), and (30) imply that
$ \rho_z = 3H^2 $ , and the geometrical equation of state relating the geometrical density and geometrical pressure is given by$ p_z = \frac{{\cal{G}}}{4\rho_z}-\frac{\rho_z}{3}. $

(63) Because geometrical density
$ \rho_z $ is always positive,$ {\cal{G}} $ is the factor responsible for the sign of the effective pressure in the model. Geometrical density$ \rho_z $ will be associated with a positive effective pressure when$ {\cal{G}} $ satisfies the following condition:$ {\cal{G}}>\frac{4}{3}\rho^2_z, $

(64) and the negative pressure occurs under the following condition:
$ {\cal{G}}<\frac{4}{3}\rho^2_z. $

(65) In particular, if
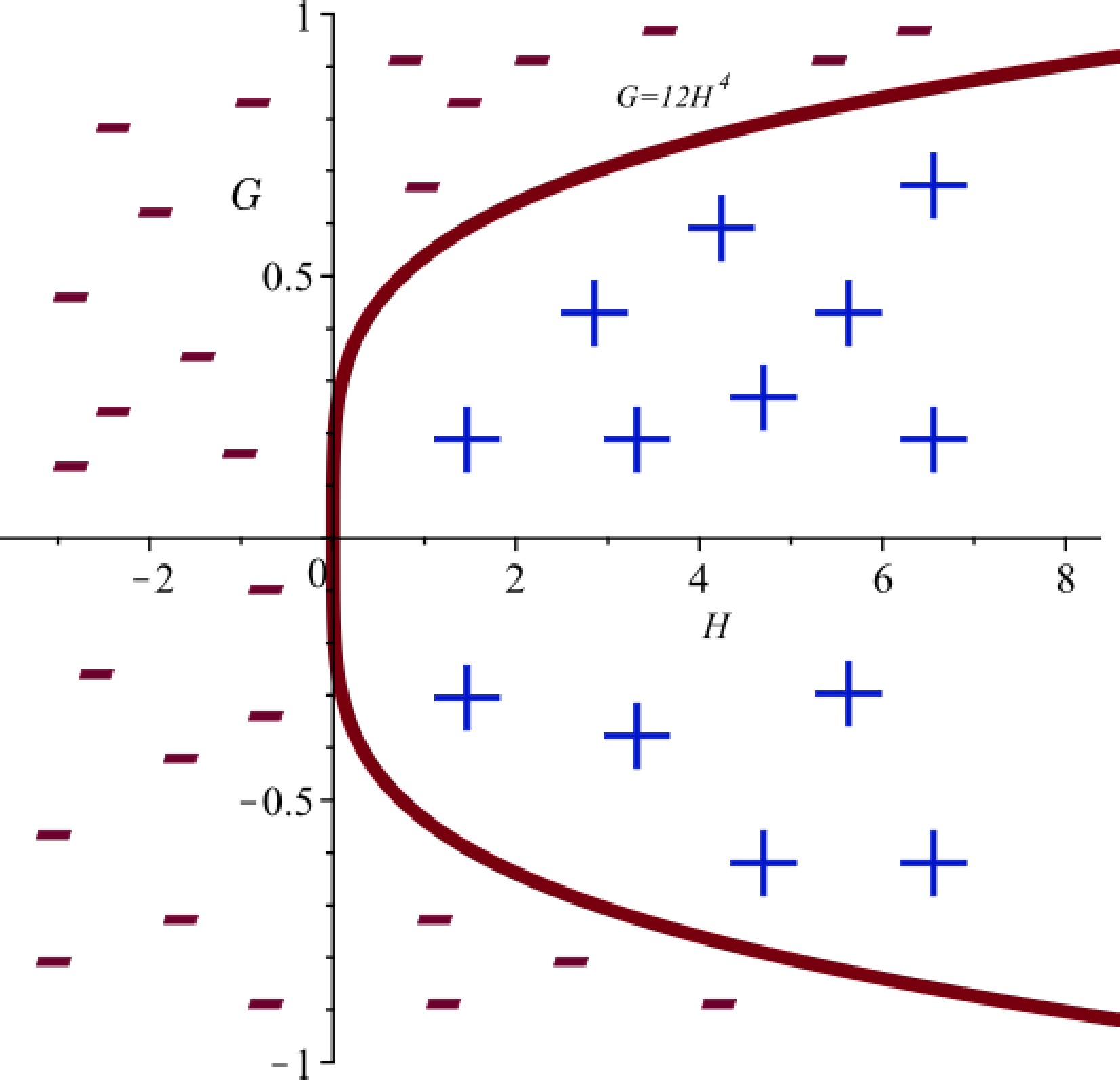
$ {\cal{G}}<0 $ , then$ p_z<0 $ is satisfied automatically.In phase space
$ {\cal{G}} \times H $ , the positive and negative signs of the effective pressure are divided by curve$ {\cal{G}} = 12H^4 $ (Fig. 8). If we compare with the global behavior map given in Fig. 7, then, if$ {\cal{G}} $ is in the cyclic region III, the effective pressure changes sign periodically, whereas, in region II, the pressure may change sign from negative to positive. In region IV, it becomes negative again, and finally, in region I, it is always negative. -
Let us consider a Friedmann's universe with cosmic dust. Here,
$ p_m = 0 $ . The differential equations are$ 3H^2 = \rho_z+\rho_m, $

(66) $ 0 = \dot{\rho_m}+3\rho_m H, $

(67) $ {\cal{G}} = -24(\dot{H}+H^2)H^2. $

(68) This set of equations may be expressed as an autonomous 3D dynamical system in terms of independent variables
$ {\cal{G}} $ , H, and$ \rho_m $ given by Eqs. (29), (30), and (31), that is,$ \dot{{\cal{G}}} = \frac{1}{24\sigma H^3}\left[3H^2-\sigma \frac{{\cal{G}}^2}{2}-\rho_m\right], $

(69) $ \dot{H} = -\frac{{\cal{G}}}{24H^2}-H^2, $

(70) $ \dot{\rho_m} = -3\rho_m H. $

(71) The equilibrium points of the system obtained by setting
$ \dot{{\cal{G}}} = 0 $ ,$ \dot{H} = 0 $ , and$ \dot{\rho_m} = 0 $ are$ {\cal{G}}_o = -\left(\frac{3}{2\sigma^2}\right)^{\frac{1}{3}}, $

(72) $ H_o = \pm\left(\frac{1}{96\sigma}\right)^{\frac{1}{6}}, $

(73) $ \rho_{m_o} = 0, $

(74) which are the same equilibrium points as in the case of an empty universe. The eigenvalues of the Jacobian matrix of the system, applied at the equilibrium points, have mixed signs. This implies that they behave as saddle points for the integral solutions, similar to the empty space case. In addition to these two equilibrium points, solution
$ H = 0 $ satisfies Eqs. (66) to (68), under conditions$ {\cal{G}} = 0 $ and$ \rho_m = 0 $ , as shown in subsection IV.A.4, with$ \rho_m = -\rho_z = \dfrac{1}{2}f(0) = 0 $ .Numerical solutions to this system present behaviors similar to those observed in the empty space case, that is, for positive
$ H(t) $ and σ, solutions in which the Hubble parameter decreases to a minimum positive or zero value and increases afterward or exhibits open cyclic behavior in the phase space. Because we are now involving a 3D dynamical system, a compilation of integral solutions in one 3D graph on the phase space becomes convoluted. A sample of two integral solutions, representing the two described behaviors, with given initial conditions, are given below:In Figs. 9(a), 9(b), 10(a), and 10(b), we have a case of integral solution with cyclic behavior. This shows that cosmic dust has a dampening effect on the evolution of the system; the integral solution need not necessarily pass through the origin in the
$ {\cal{G}} \times H $ phase plane (as shown in Fig. 9(a)); H begins with an initial value and then decreases periodically over time, similar to a ball bouncing from a surface a few times, approaching a stable value (as observed in Fig. 9(b));$ {\cal{G}} $ changes its sign a few times until a point in time when it approaches a stable value (as observed in Fig. 10(a)), that is, it describes a Friedmann's universe that goes through epochs of accelerated and decelerated expansion, approaching a stable value with zero acceleration; finally, the matter density decreases as expected.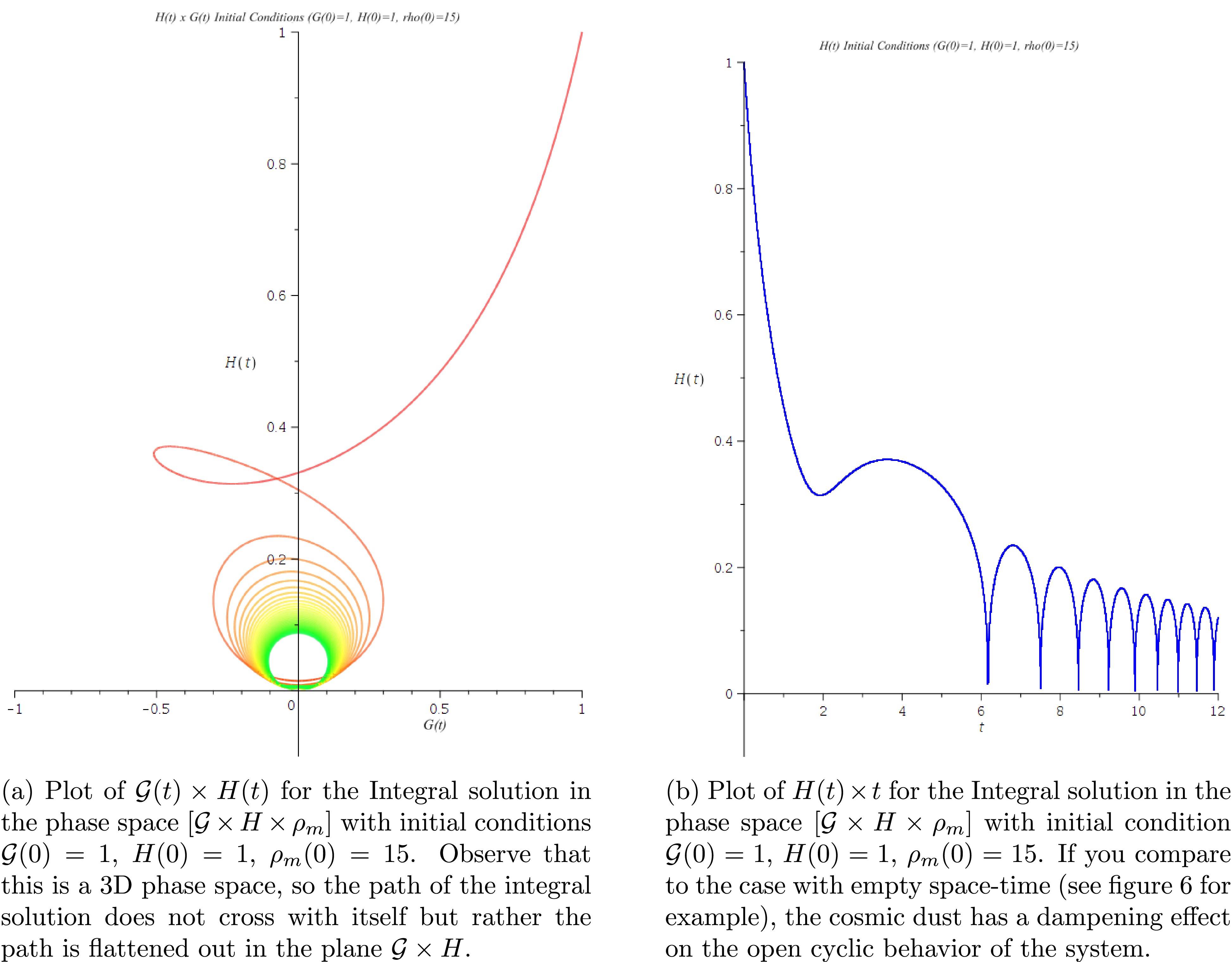
Figure 9. (color online) Numerical solution of the dynamical system in phase space
$ {\cal{G}} \times H \times \rho_m $ . Initial conditions$ {\cal{G}}(0) = 1 $ ,$ H(0) = 1 $ ,$ \rho_m (0) = 15 $ .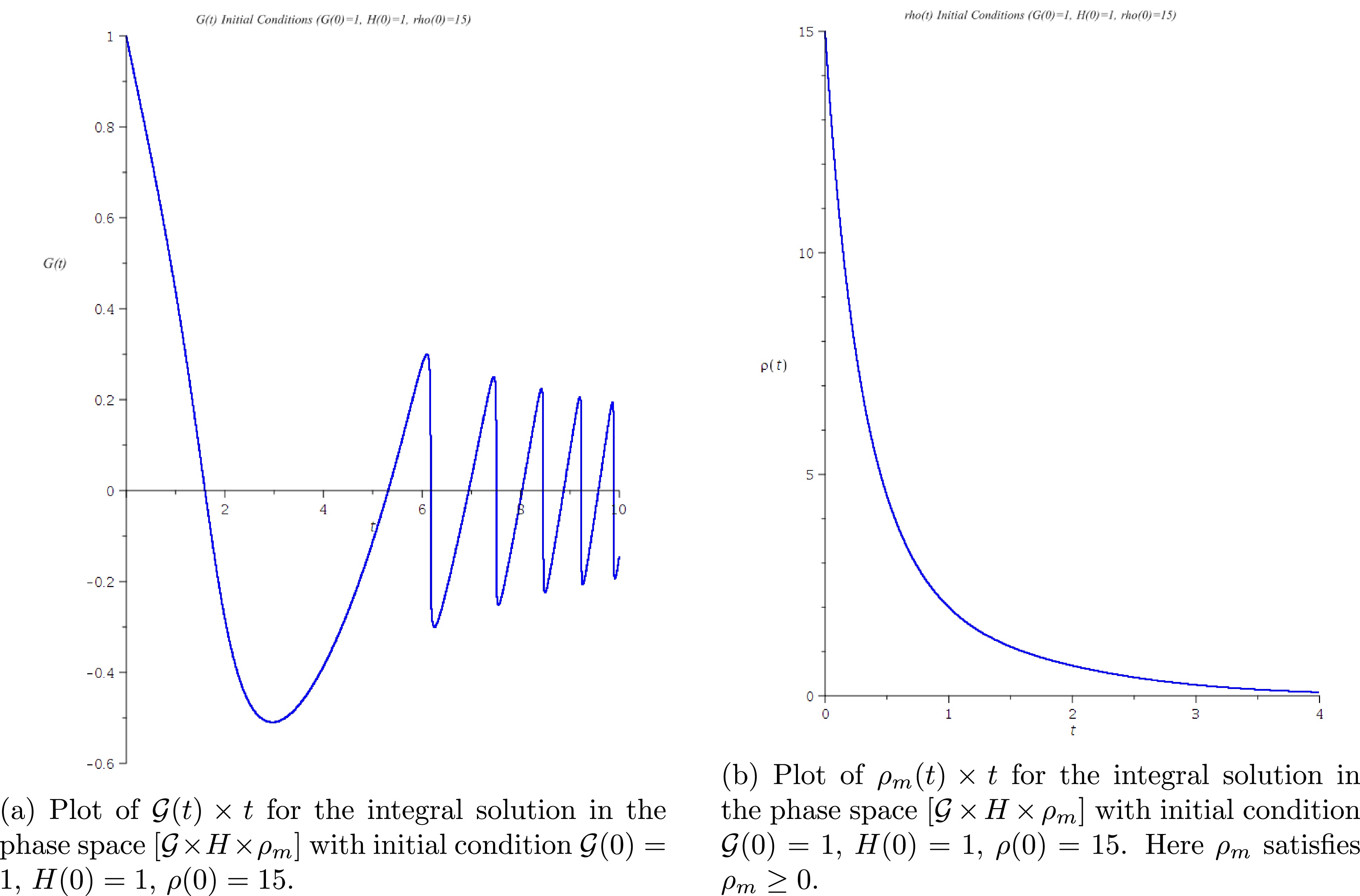
Figure 10. (color online) Numerical solution of the dynamical system in phase space
$ {\cal{G}} \times H \times \rho_m $ . Initial conditions$ {\cal{G}}(0) = 1 $ ,$ H(0) = 1 $ ,$ \rho_m (0) = 15 $ .Figures. 11(a), 11(b), 12(a), and 12(b) show a case where the Hubble parameter has only one minimum positive value, and the topological invariant changes sign only one time.
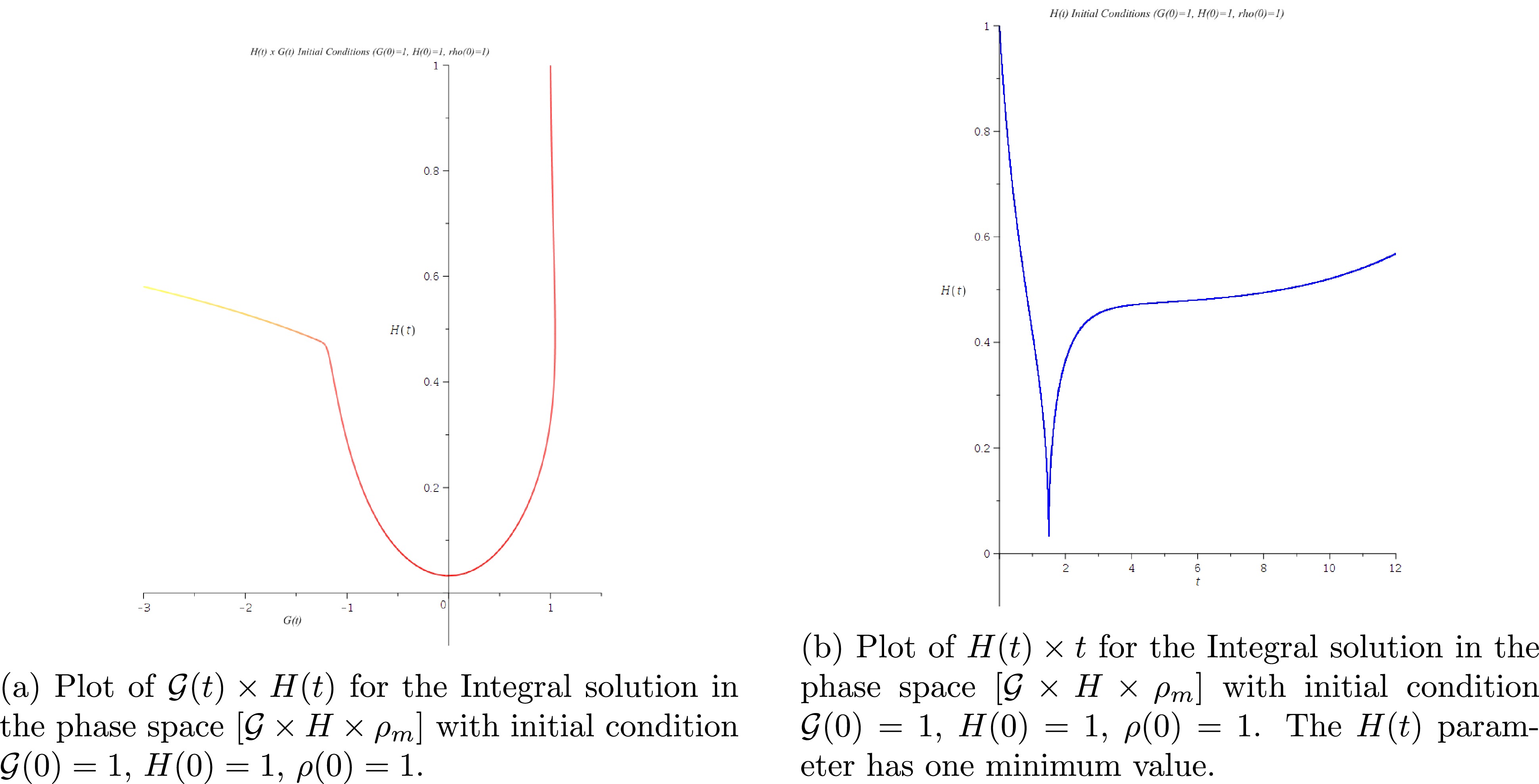
Figure 11. (color online) Numerical solution of the dynamical system in phase space
$ {\cal{G}} \times H \times \rho_m $ . Initial conditions$ {\cal{G}}(0) = 1 $ ,$ H(0) = 1 $ ,$ \rho(0) = 1 $ .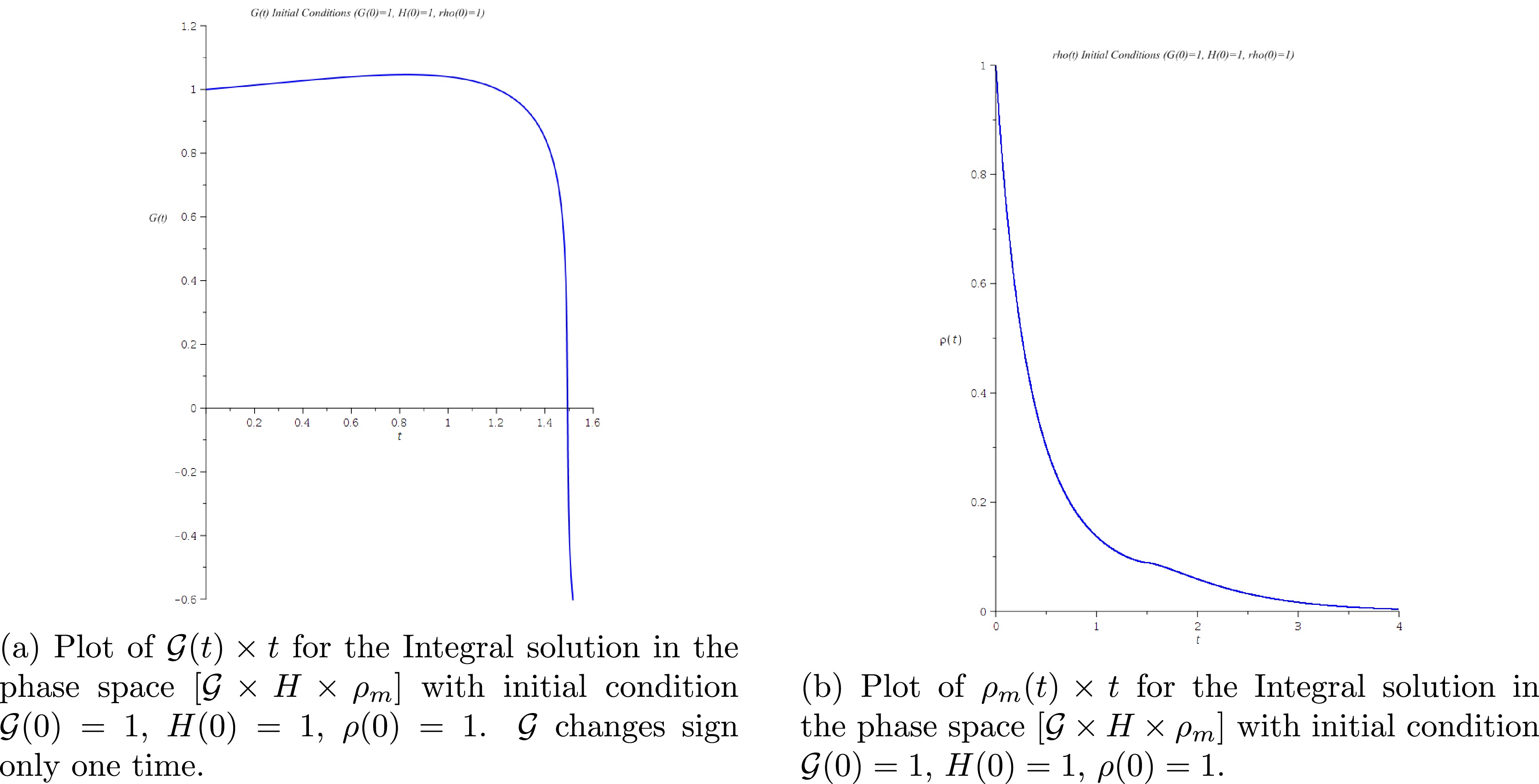
Figure 12. (color online) Numerical solution of the dynamical system in phase space
$ {\cal{G}} \times H \times \rho_m$ . Initial conditions$ {\cal{G}}(0)=1$ ,$ H(0)=1$ ,$\rho(0)=1$ .One important qualitative result here is that, given a positive value for σ, and fixed initial conditions for
$ {\cal{G}}(0) $ and$ H(0) = 0 $ , the initial value of cosmic dust density$ \rho_m(0) $ will dictate which type of behavior the system will develop, that is, if the Hubble parameter will have only one minimum value, or have a cyclic behavior with epochs of acceleration and deceleration. Then,$ \rho_m $ plays an important role in the evolution of the system.The dampening effect due to the cosmic dust in the system is a consequence of its direct action on
$ \dot{{\cal{G}}} $ , as shown in Eq. (69). When the system is about to change from a positive to negative$ {\cal{G}} $ , this implies$ \dot{{\cal{G}}} < 0 $ , and Eqs. (69) and (70) show that the presence of the cosmic dust increases the negative value of$ \dot{{\cal{G}}} $ but does not directly affect$ \dot{H} $ . The consequence of this modification to the dynamical system is that the cosmic dust accelerates the change in sign of the topological invariant from positive to negative before the Hubble parameter can reach zero. For example, consider the cyclic solution in Fig. 9(a): when it is approaching the change in sign of$ {\cal{G}} $ from positive to negative, the condition over the Hubble parameter is$ \dot{{\cal{G}}}<0 \rightarrow 3H^2 < \frac{{\cal{G}}^2}{2} + \rho_m, $

(75) and when the topological invariant is exactly zero, we have the following specific condition:
$ \dot{{\cal{G}}}<0 \; and \; {\cal{G}} = 0 \rightarrow 3H^2 < \rho_m. $

(76) The above condition shows a mechanism for which cosmic dust
$ \rho_m $ limits the maximum value that H can have when$ {\cal{G}} $ changes sign from positive to negative, that is, when the model changes from an epoch of decelerated expansion to an epoch of accelerated expansion. As$ \rho_m $ tends to zero (Fig. 10(b)), condition (78) implies that$ H\rightarrow 0 $ , which is the behavior of the empty space-time solution observed, for example, in Fig. 6. -
The rank-3 tensor representation of a spin-2 field appears directly in the modified equations of
$ f({\cal{G}}) $ gravity as a covariant divergent. In a homogeneous and isotropic Friedmann's universe, the trivial case for topological invariant$ {\cal{G}} $ as a constant results in specific conditions for$ \rho_m\geq 0 $ to be true: depending on the sign of$ {\cal{G}} $ , geometric density$ \rho_z $ must satisfy certain conditions and Hubble parameter$ H(t) $ may only vary over delimited time intervals. In other words, in some cases,$ {\cal{G}} $ can only be constant over a finite interval of time for density mass$ \rho_m $ to be strictly positive. This results in one necessary but insufficient tool for filtering non-physical solutions.The first non-trivial case we can consider,
$ f({\cal{G}}) = \sigma G^2 $ , yields different behaviors for the Friedmann's universe. In the empty space-time case, it can describe a universe that is always in accelerated expansion or that decelerates and accelerates at a later phase; or it describes a universe that is expanding in phases of decreasing acceleration and deceleration. When cosmic dust is added to the system, its initial value will dictate the evolution of this universe: if it will expand with increasing dampened phases of acceleration and deceleration or expand with ever increasing acceleration. Hubble parameter H as a non-zero constant is a viable solution for an empty space-time, whereas$ H = 0 $ is a possible solution when constant source matter$ \rho_m $ is added.The next step would be to add a gas of photons to the system, study its influence, and compare the numerical solutions with real observational data to constrain the value of σ and verify if it is reasonable. In our dynamical systems,
$ {\cal{G}} $ is unbounded. An interesting aspect to investigate would be to bound$ {\cal{G}} $ to a finite interval using a Born-Infeld type function, sum or multiply the original function, and verify the effects of this boundary for$ {\cal{G}} $ and its variation on the evolution of the system. Another point of interest would be to study perturbations to determine how stable and unstable the equilibrium points are and, in particular, to study the origin of the phase space that may present chaotic behavior in the evolution of the system. -
M. Novello thanks Fundação de Amparo e Pesquisa do Estado do Rio de Janeiro (FAPERJ) for a fellowship.
Fábio H. M. dos Anjos thanks Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) fot the support.
Friedmann’s universe controlled by Gauss-Bonnet modified gravity
- Received Date: 2024-08-06
- Available Online: 2025-04-15
Abstract: We consider a Lagrangian to describe gravity using a nonlinear term depending on the Gauss-Bonnet topological invariant. We examine the conditions for a bouncing and the existence of an ulterior accelerated phase of the universe. The original concept of Einstein's first paper on cosmology was to modify the equations that control the gravitational metric. Based on this, several authors have proposed different formalisms to modify general relativity. Herein, a function of the topological invariant is used in a homogeneous and isotropic cosmological model. First, a case with the topological invariant as a constant is thoroughly examined, yielding specific constraints on the evolution of the Hubble parameter. Subsequently, we study a function of the topological invariant squared. In an empty space-time scenario, the term that modifies Einstein’s equations functions as an effective geometrical density, and we map regions in the phase space in which the effective pressure is positive or negative. This results in non-trivial integral solutions such as cyclic stages of acceleration and deceleration of the scale factor in the model, among other behaviors. We add cosmic dust to the system, and for certain classes of solutions, we observe that the minimum positive value of the Hubble parameter is limited by the cosmic dust matter density. If this matter density reaches zero, the minimum value of the Hubble parameter also reaches zero.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: