Nanohertz gravitational waves and primordial quark nuggets from dense QCD matter in the early Universe

After the big bang, the Universe experiences cosmic phase transitions, e.g., the electroweak phase transition at $ t=10^{-10} $ s around $ T=100 $ GeV and the quantum chromodynamics (QCD) phase transition at $ t=10^{-5} $ s around $ T=150 $ MeV. The cosmic QCD phase transition sets the initial condition for big bang nucleosynthesis (BBN) and is essential to understand the property of compact stars at high baryon density.

Though the peak structure of the sound velocity describing the neutron stars and GWs emitted the from binary neutron stars may favor a crossover at high baryon density and low temperature [1] and for physical quark mass, lattice QCD calculations indicate a crossover at high temperature [2] at zero or small chemical potential in 2-flavor as well as 3-flavor systems [3, 4], a first-order phase transition is of our interest due to intriguing and unique imprints in the early Universe. The first-order QCD phase transition at high temperatures can be found in a massless 3-flavor system [5] as a chiral phase transition, the confinement-deconfinement phase transition in the pure gluon system [5] and Friedberg-Lee model [6−8], as well as in the chirality imbalanced system [9, 10].

The QCD phase transition is also possibly a first-order phase transition at high chemical potential. The high baryon density can be generated through the elegant and well established Affleck-Dine baryogenesis [11−13] which tends to generate dense baryon clumps instead of homogeneous ones in the early Universe and the high density can be subsequently diluted to the level observed today through the little inflation [14−18]. The high baryon density clumps can be inhomogeneously distributed in the early Universe through first-order electroweak/QCD phase transitions or fluctuations [19−25]. High baryon density clumps known as the primordial quark nuggets (PQNs) through cosmic QCD phase transitions were proposed by Witten in 1984 [20] and have been investigated in many aspects [21, 26−28], especially the strangelet, which is more stable than the ordinary nuclear matter, has attracted a lot of interest. The PQNs proposed by Witten are generated by the remaining and shrinking false vacuum squeezed by the propagation of the true vacuum bubbles. The PQNs only occupy a minute fraction of the Universe but contain 80%-99% of the baryon excess with a density of $ 10^{15} $ $ \mathrm{g/cm^3} $ and a mass of $ 10^9-10^{18} $ g approximately [20], which corresponds to a size of $ 10^{-2}-10^1 $ cm.

A first-order phase transition is also required to produce the stochastic background gravitational waves (SBGWs) in the early Universe. Recent observation results from several pulsar timing array (PTA) collaborations, including the Parkes Pulsar Timing Array (PPTA), the North American Nanohertz Observatory for Gravitational Waves (NANOGrav) [29, 30], the European Pulsar Timing Array (EPTA) and the Chinese Pulsar Timing Array (CPTA) [31−35], have independently detected the evidence of stochastic GW signals in the nanohertz band. The nanohertz GWs may come from the orbiting or mergers of supermassive ($ 10^{35}-10^{40} $ kg) black hole binaries [36], or from cosmic phase transitions in the electroweak [37] or the QCD epoch [38, 39].

The transition rate $ \beta/H $, also known as the inverse duration time of the phase transition, describes the frequency of the bubble collisions and is a crucial parameter to decide the peak frequency and the peak energy density of the GW spectra. Ref. [39] gives a bound $ \beta/H<15 $ for QCD phase transitions to generate the nanohertz GWs. It is noticed that in some references, $ \beta/H $ is treated as a free parameter. For example, $ \beta/H $ is taken in the order of $ 1-10 $ for the pure gluon system to produce the nanohertz GWs [40, 41]. However, for typical first-order chiral and confinement phase transitions at high temperature, the bona fide calculations in the low-energy effective QCD-like theories and holographic QCD models give $ \beta/H\sim 10^{4-5} $ [42−46]. The corresponding peak frequency of GWs typically lies in the region of $ 10^{-4}-10^{-2} $ Hz with the power spectrum in the range of $ 10^{-8}-10^{-7} $, which lies in the ranges of LISA and Taiji.

In this work, we investigate the possibility of producing the nanohertz GWs from first-order QCD phase transitions, particularly if high baryon density QCD matter can be generated in the early Universe. We will show that the baryon chemical potential can significantly reduce the transition rate, and there exists a narrow window of high baryon chemical potential with the transition rate in the order of $ \beta/H \sim 10^1 $ to produce the nanohertz GWs. There exists a critical nucleation point (CNP), where the bubble nucleation can barely happen and the transition rate is zero $ \beta/H=0 $. Zero $ \beta/H $ implies that the phase transition from the quark matter to the hadronic matter cannot be completed, thus it is possible that primordial ``quarklet" or PQNs exist in the early Universe. In this short letter, we offer an explanation on the appearance of the CNP, and analyze the property of the PQNs formed by the long-lived false vacuum.

First-order phase transitions complete via the bubble nucleation. Once the phase transition starts, parts of the Universe jump to the true vacuum from the false vacuum, forming bubbles with lower vacuum energy density, then the latent heat released is converted into the energy of the bubble walls. These bubbles expand and collide and pass kinetic energy to the surrounding media, generating GWs from the collisions of the bubbles, the sound waves and the magnetohydrodynamic (MHD) turbulence [47].

The bubble nucleation rate per volume per time has the exponential form $ \Gamma(t)=Ae^{-S_4(t)} $ [48−50], where $ S_4 $ is the Euclidean action of an $ O(4) $-symmetric solution and reduces to $ S_3/T $ at high temperature T, and the coefficient A has the form of $ A(T)=T^4(S_3/(2{\pi}T))^{3/2} $ [51]. Here $ S_3 $ is the bounce action of the field configuration between the false and the true vacuum of an $ O(3) $-symmetric bubble, which can be determined by the equation of motion.

Bubbles of the true vacuum start to occur at the nucleation temperature $ T_n $, at which the nucleation rate catches the expansion rate of the Universe. In the QCD epoch, $ T_n $ can be quickly estimated by $ S_3/T\sim 180 $ [42, 52, 53]. More precisely, one bubble per Hubble volume per Hubble time $ {\Gamma}(t)/H^4\sim1 $ is expected at $ T_n $ [48, 50], where H is the Hubble parameter given by the Friedmann equation.

Approximately $ T_n $ is also the temperature of the thermal bath with weak reheating, thus the transition rate β is defined as

Another parameter to which the GW spectra are sensitive is α, which quantifies the transition strength, i.e., the relative magnitude of the latent heat released in the phase transition compared to the background radiation energy density $ \rho_r $ [50, 51]. α can be calculated with finite μ as

where Δ means the difference between the true and false vacuum. $ T_p $ is the percolation temperature and $ T_p{\approx}T_n $ is used when $ \beta/H \gg 1 $, i.e., the false vacuum decays rapidly and hence the temperature is nearly constant during the phase transition. In specific models, the thermal background is not the perfect ideal gas and thus the background radiation energy density $ \rho_r=\dfrac{{\pi}^2gT^4}{30} $ (g is the number of relativistic degrees of freedom) is not accurate, especially when the chemical potential μ cannot be neglected compared with temperature $ \mu\gtrapprox T $. Instead, the thermal energy density is given by the effective grand potential $ \Omega=-p $

here $ p_{vac} $ is the vacuum pressure at $ T=\mu=0 $ and must be deducted.

The energy from bubble collisions is negligibly small for relativistic bubbles [54], only two dominant sources, i.e., the sound waves and the MHD turbulence contribute to the total GW spectra, i.e.,

In terms of the parameters above, the numerical results of GWs from the sound waves and the MHD turbulence take the forms of [51, 54]

and

respectively. Parameters $ \kappa_v $ and $ \kappa_{tb} $ are respectively the fraction of the vacuum energy converted into the kinetic energy of the plasma and the MHD turbulence which can be analytically fitted [54−56]. The GW spectra are not sensitive to a relativistic bubble velocity $ v_w $ and thus in our following calculations we take a good approximation $ v_w=\dfrac{\sqrt{1/3}+\sqrt{\alpha^2+2\alpha/3}}{1+\alpha} $ for strong phase transitions. $ S_{sw}(f) $ and $ S_{tb}(f) $ have the power-law forms

The peak frequencies are $ f_{tb} = 1.42f_{sw}=\dfrac{16.36}{v_w}\frac{\beta}{H}h $, where $ h=1.65\times10^{-8}\dfrac{T_n}{1{\rm{GeV}}}(\dfrac{g}{100})^{\frac{1}{6}} $ Hz is the Hubble rate.

In the following, we investigate the GW spectra induced by the first-order deconfinement phase transition and chiral phase transition at high baryon chemical potentials by using two simple but representative models, i.e., the Friedberg-Lee (FL) model and the quark-meson (QM) model, which can reveal the main features of the GW spectra induced by QCD phase transitions.

The FL model provides a dynamical mechanism to confine quarks inside the nucleon by a complicated nonperturbative vacuum. It is described by the interaction of a phenomenological scalar field ϕ and the quark field Ψ [6−8], and the Lagrangian takes the form of

Here the potential $ U_{FL}(\phi) $ takes a Ginzburg-Landau type with a quartic form $ U_{FL}(\phi)=\dfrac{1}{2!}a\phi^2+\dfrac{1}{3!}b\phi^3+\dfrac{1}{4!}c\phi^4 $.

In the following numerical calculations, we fix four parameters $ a=0.68921 $ GeV$ ^2 $, $ b=-287.59 $ GeV, $ c=20000 $ and $ g=12.16 $ as in Ref. [57] to successfully reproduce the static properties of the nucleon.

Including the one-loop contribution, the effective grand potential at finite temperature and quark chemical potential is [58, 59]

with $ \nu=2N_fN_c=12 $ and $ E_i=\sqrt{p^2+m_i^2} $ $ (i=\phi,\Psi) $. The effective mass of the quark is $ m_{\Psi}=g\phi $ and that of the scalar field is $ m^2_{\phi}=a+b\phi+\frac{c}{2}\phi^2 $, respectively. The order parameter ϕ can be determined by solving the gap equation $ {\partial\Omega}_{FL}/{\partial\phi}=0 $.

The FL model can be used to describe a deconfinement phase transition. At $ T<T_c $, there exists a soliton solution serving as a ``bag" to confine the quarks, while there is only a damping oscillation solution at $ T>T_c $ where the quarks are set free.

The chiral phase transition can be described by the QM model, and the Lagrangian of the two-flavor QM model has the form of [60, 61]

The potential is $ U_{QM}(\sigma,\vec\pi)=\dfrac{\lambda}{4}(\sigma^2+\vec\pi^2-v^2)^2-H\sigma $, with $ \Psi=(u,d) $ and $ \vec\tau $ the Pauli matrices. The interaction between the quarks and the scalar mesons contains three terms of the pions $ \vec\pi $ and one of the σ meson.

The effective grand potential in the QM model is

with $ E=\sqrt{\vec{p}^2+m_q^2} $.

The chiral symmetry is spontaneously broken in the vacuum and σ obtains a nonzero vacuum expectation value $ \sigma=f_{\pi}=93 $ MeV. The effective quark mass is $ m_q=gf_{\pi} $ with $ g=3.3 $, where we have assumed that $ m_q $ contributes to one-third of the mass of the nucleon. The partial conservation of the axial current gives the parameter $ H=f_{\pi}m^2_{\pi} $ with the pion mass $ m_{\pi}=138 $ MeV in the case of nonzero current quark mass. The order parameter can be solved from the gap equation $ {\partial\Omega}_{QM}/{\partial\sigma}=0 $.

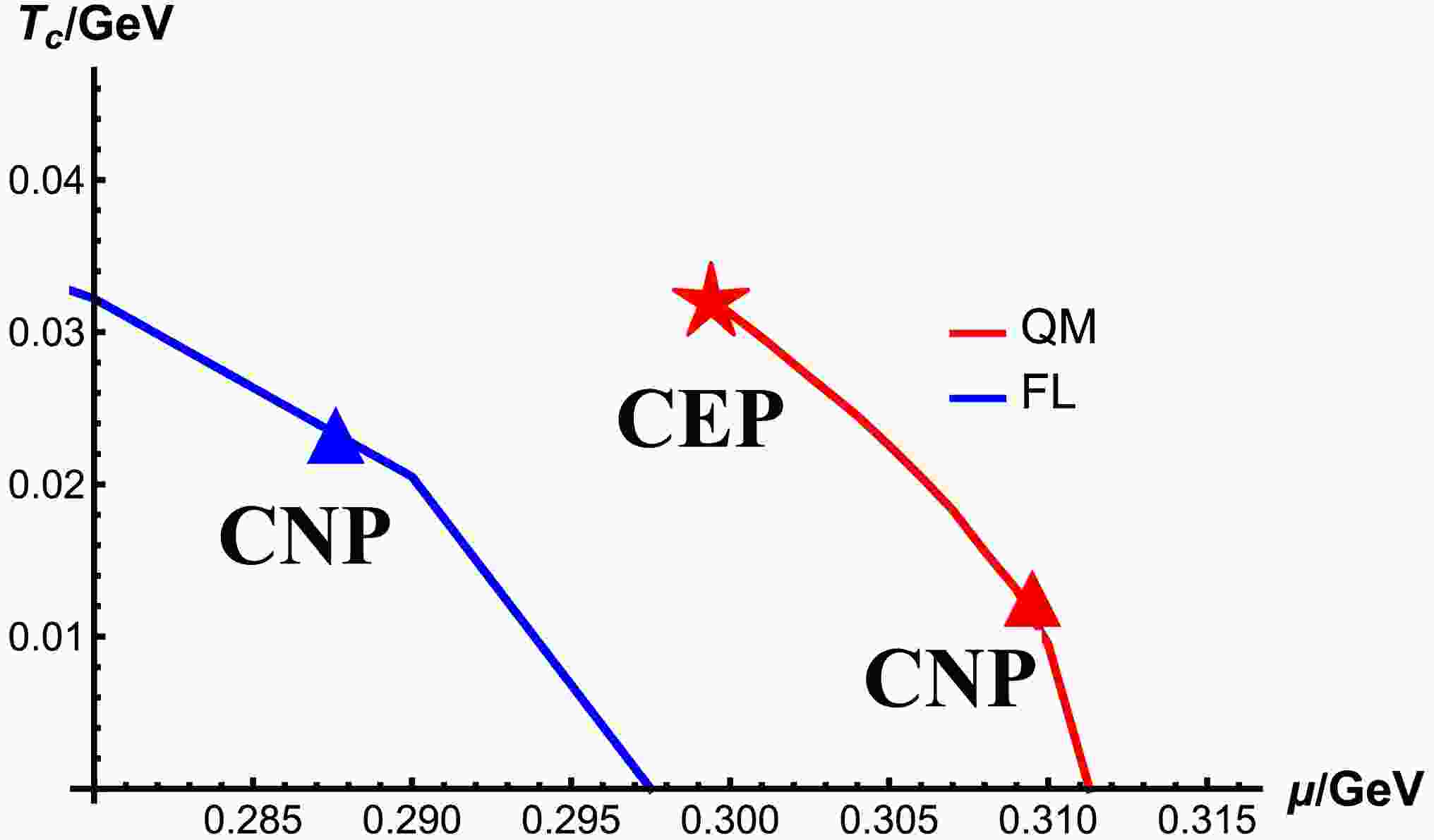
The phase diagrams of the FL model and the QM model are shown in Fig. 1. The phase transition of the FL model is always of first-order from zero chemical potential to the critical chemical potential $ \mu_c=297.5 $ MeV and no CEP exists ($ \mu_E=0 $), while the chiral transition in the QM model is a crossover in the low chemical potential region and of first-order in the high chemical potential region until $ \mu_c=311.3 $ MeV, thus there exists a CEP located at $ T_E=32.17 $ MeV, $ \mu_E=299.4 $ MeV in the QM model as indicated by the red star. The triangles indicate the CNPs where the nucleation of bubbles can barely happen. The blue one at $ \mu=287.55 $ MeV is for the FL model and the red one at $ \mu=309.6 $ MeV for the QM model.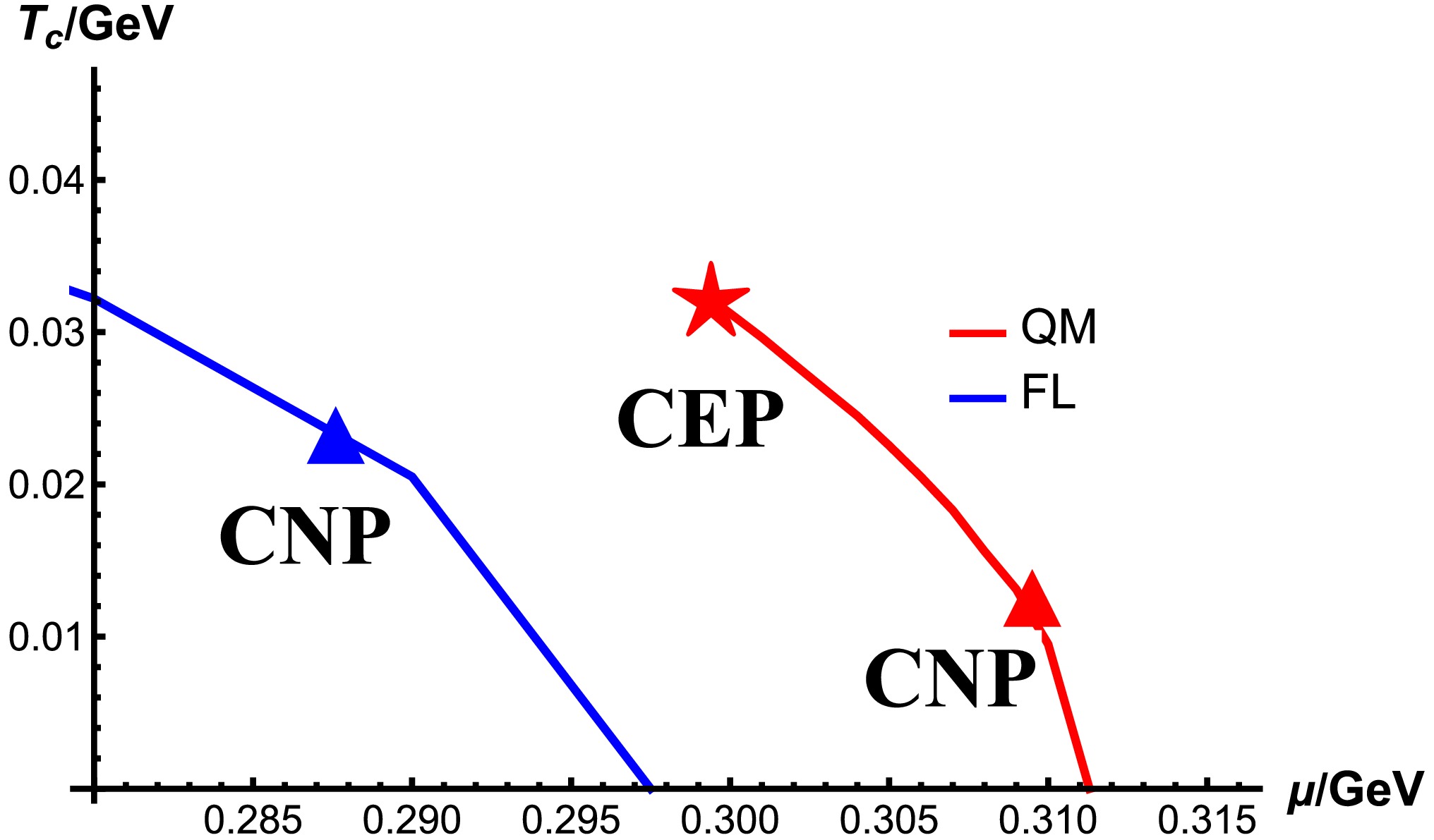

Figure 1.  (color online) The $ T-\mu $ phase diagrams of the FL model and the QM model. The red star is for the CEP at $ \mu=299.4 $ MeV in the QM model, and triangles for the CNPs at $ \mu=309.6 $ MeV in the QM model and $ \mu= 287.55 $ MeV in the FL model, respectively. $ T_c $ approaches $ 0 $ at $ \mu=311.3 $ MeV in the QM model and $ \mu=297.5 $ MeV in the FL model.

The transition rates in the FL model and the QM model are shown in Fig. 2 with the rescaled chemical potential

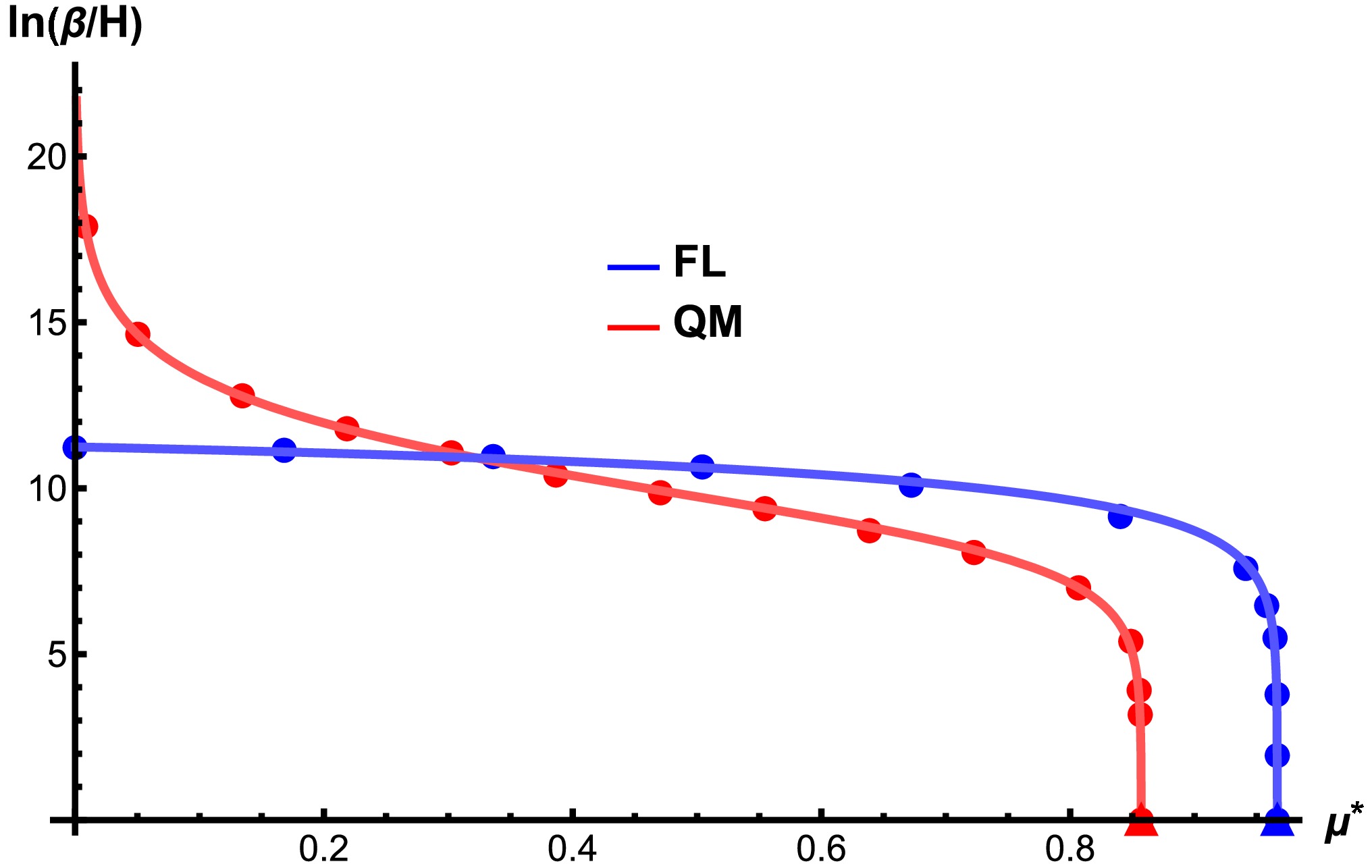
Figure 2.  (color online) $ \beta/H $ with different rescaled chemical potential $ \mu^*=(\mu-\mu_E)/(\mu_c-\mu_E) $ in the FL (blue) and QM (red) model.

In the FL model, values of $ \beta/H $ decrease from $ 10^5 $ to $ 10^3 $ when μ increases from $ 0 $ to $ 280 $MeV and sharply fall from $ 10^3 $ to $ 0 $ in a very narrow window of the chemical potential. The transition rate drops to $ 0 $ before $ \mu_c $, corresponding to the CNP where $ \mu_{CNP}=287.55 $ MeV as marked by the blue triangles in Fig. 1 and 2.

In the QM model, it is found that the transition rate is almost infinity close to the CEP. A straightforward reason is that the potential barrier barely appears near the CEP and thus the transition is ephemeral like a crossover. $ \beta/H $ starts to fall from infinity from the CEP when the chemical potential μ increases and soon reaches a plateau during which $ \beta/H $ varies from $ 10^4 $ to $ 10^3 $ in the region of $ 309 $ MeV $ >\mu>306 $ MeV and sharply falls from $ 10^3 $ to $ 0 $ in a very narrow interval near the CNP $ \mu_{CNP}=309.6 $ MeV as marked by the red triangles in Fig. 1 and 2.

For the GW spectra, we select some specific values of chemical potential $ \mu=306 $, $ 309 $, $ 309.5 $, $ 309.59 $ MeV in the QM model and $ \mu=250 $, $ 280 $, $ 287 $, $ 287.5 $ MeV in the FL model, which corresponds to the magnitude of $ \beta/H $ in the order of $ 10^4 $, $ 10^3 $, $ 10^2 $, $ 10 $, and the values of the phase transition strength α are also calculated. These parameters are shown in the table inserted in Fig. 3 as well as the GW spectra, and the pure gluon system at zero chemical potential [62] is used as a reference.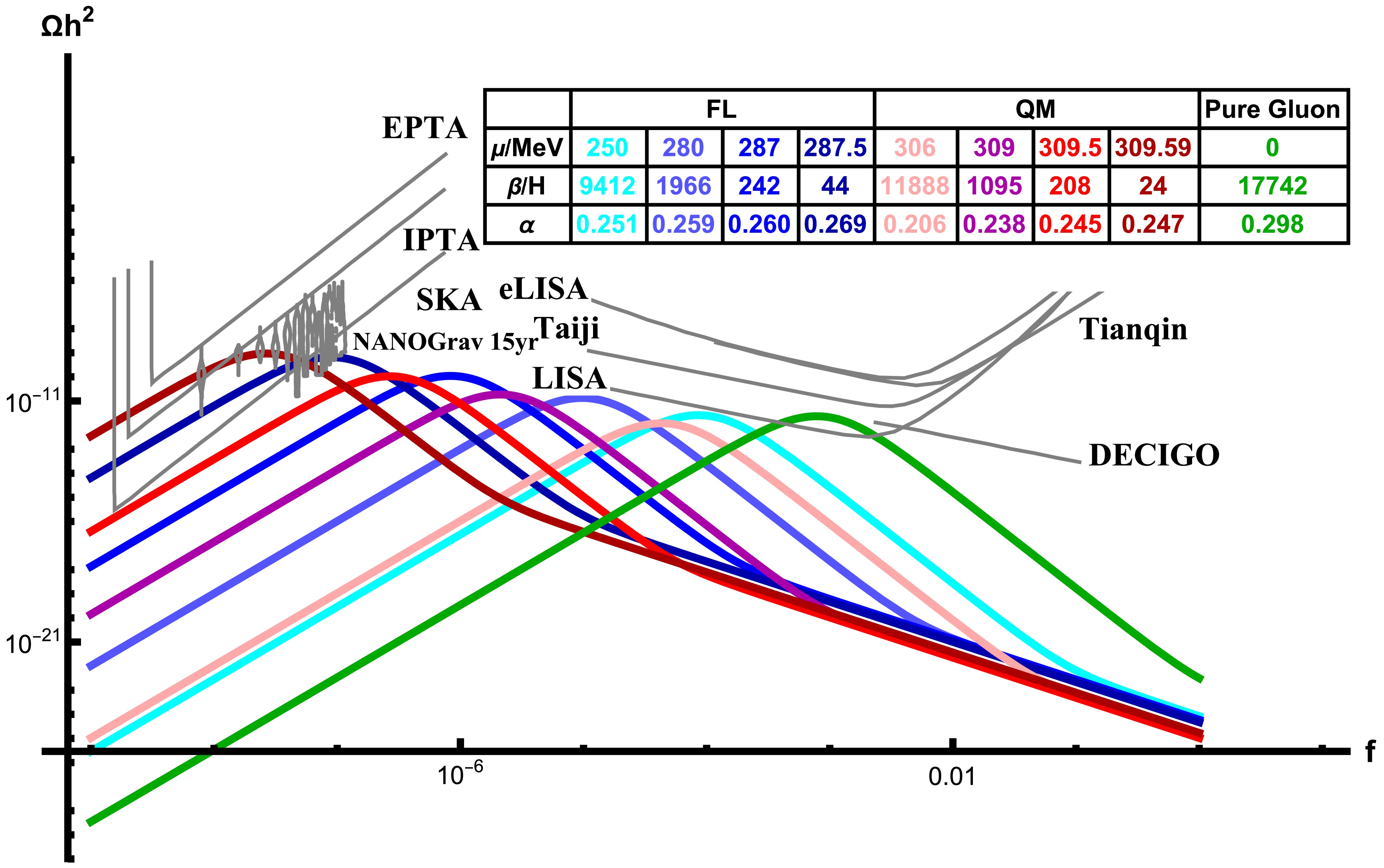

Figure 3.  (color online) The GW spectra from first-order phase transitions in the FL model and the QM model with different chemical potential. The pure gluon system at zero chemical potential is used as a reference.

It is noticed that in the pure gluon system without the quark chemical potential, we have $ \beta/H\sim 10^4 $ and the produced GWs fall in the LISA detection window. When the chemical potential increases, the transition rates in the FL model and the QM model decrease significantly and the produced GWs move to a lower frequency. In the high baryon density region with $ \mu/T\sim 10 $, the transition rate $ \beta/H $ can reach the order of $ 10^1 $, the produced nanohertz GWs can be detected by SKA, IPTA and EPTA, coinciding with the NanoGrav data.

It has been observed that there is an interesting property of the phase transition rate or decay rate of the false vacuum at high baryon density. We provide an explanation here.

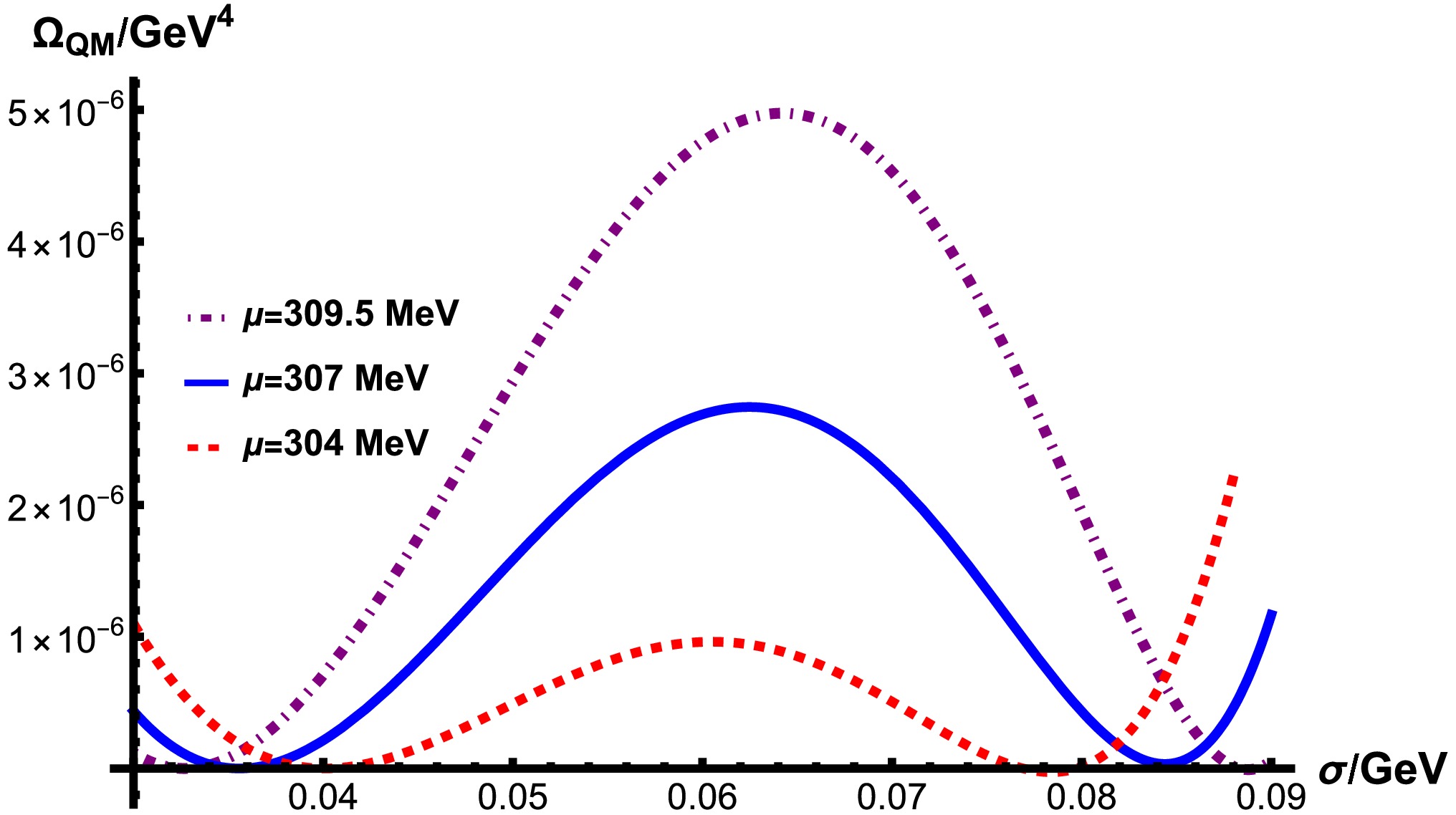
As shown in Fig. 4 where the QM model is taken as an example, a larger chemical potential μ results in a larger bounce action for the same supercooling and a smaller transition rate in the same model. In other words, a larger μ leads to a slower phase transition and a lower peak frequency of the GW spectra. The influence of μ can be understood in an intuitive way stemming from the experience in the Nambu–Jona-Lasinio (NJL) model. A repulsive vector interaction effectively generate a chemical potential, e.g., see Refs. [63−65]. This can be extended to treat μ as an effective repulsive vector interaction, which creates a potential barrier. As the chemical potential increases further, the potential barrier will be raised, and the system will experience a stronger first-order phase transition. The changes of the potential barrier as the chemical potential μ increases are shown in Fig. 5. When the potential barrier is so high that the false vacuum is unlikely to decay despite two degenerate vacua, the system reaches the CNP. Therefore, the false vacuum of quark matter cannot decay and persists as the PQNs over cosmological time scales.

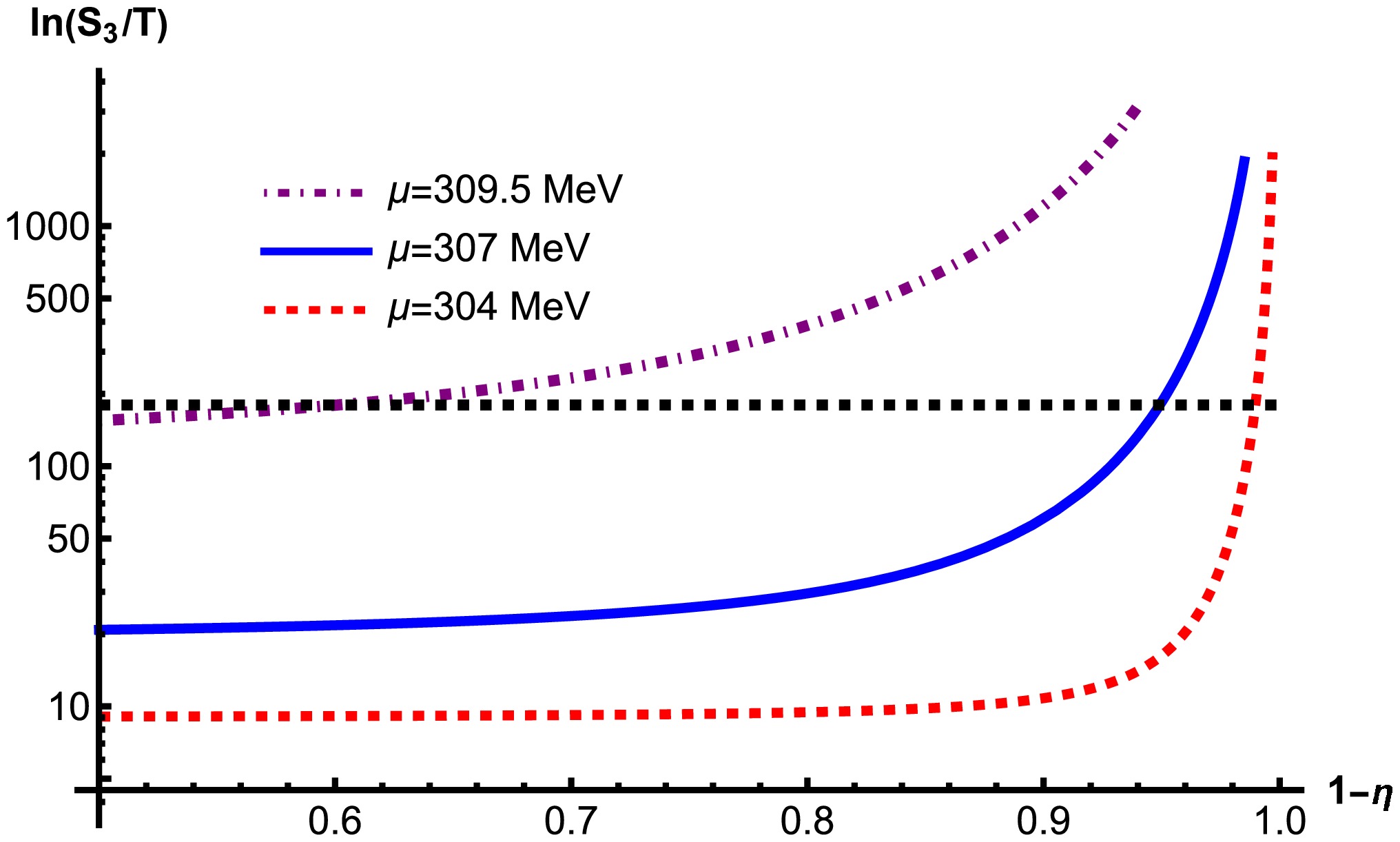
Figure 4.  (color online) $ S_3/T $ with different chemical potential μ in the QM model. The black dashed line is for 180. The supercooling is defined as $ \eta=1-\dfrac{T}{T_c}. $

Figure 5.  (color online) The potential barrier with different chemical potential μ in the QM model.

These PQNs are different from the ones proposed by Witten in 1984. In Ref. [20], during a completable first-order phase transition, there exists some sites at which the false vacuum statistically does not decay and the false vacuum is squeezed by the true vacuum bubbles until the formation of the droplets of quark matter. The size of the PQNs can be estimated by assuming the number of the nucleation during the phase transition and assuming the baryon excess they contain [20, 66]. The droplets of ud quark matter or the stranglets with the s quark are possibly more stable than the normal nuclear matter [20, 67, 68] with lower energy per baryon number than the normal nucleon considering the strong, weak and electromagnetic interactions and can act as exotic nuclei [69]. While in this paper, the PQNs with high chemical potential are generated before the QCD phase transition by the Affleck-Dine baryogenesis, and on the contrary, prefer a first-order phase transition during which the bubble nucleation cannot start to persistently survive. Meanwhile, the PQNs are not immortal unless the chemical potential is as large as $ \mu_c $ and will not be diluted. If $ \mu>\mu_c $, the quark matter is more stable than the hadrons with lower vacuum energy and if $ \mu_c>\mu>\mu_{CNP} $, the quark matter is metastable but does not decay immediately due to the high potential barrier. The size of the PQNs is not constrained by the phase transition itself and the false vacuum will eventually decay to the normal nuclear matter at very low temperature due to the quantum nucleation. Therefore, resembling the electroweak phase transitions with extreme super cooling mechanism to produce the nanohertz GWs [37, 70−73], these persistent dense nuggets will decay at an extremely slow rate at very low temperature. Because of a slow phase transition, the nanohertz GWs may also be generated later and inhomogeneous remaining cold matter may collapse into primordial black holes [74]. The long-lived false vacuum can also survive as seeds of compact stars, dramatically accelerating the evolution of compact stars as well as the formation of galaxies. Thus it is possible for the long-lived false vacuum in the compact structures partly formed by the PQNs to slowly decay to the normal matter and leave cosmic implications. This scenario is shown in Fig. 6.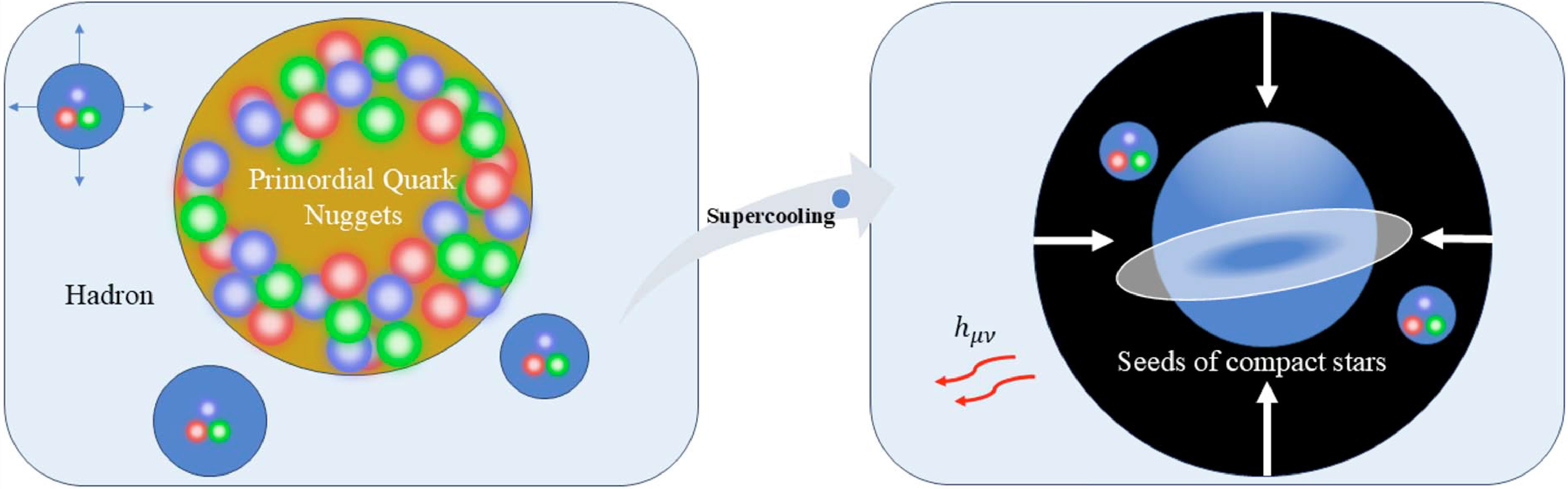

Figure 6.  (color online) The left panel shows that the chiral phase transition happens in the background while the PQNs remain in the early Universe. The right panel shows that the chiral phase transition finally happens inside the PQNs slowly after further supercooling and due to the imhomogeneity from the slow phase transition, the PQNs serve as the seeds of compact stars or galaxies and sources of GWs.

Many effective QCD model calculations have shown that first-order QCD phase transitions at high temperatures are characterized by a large transition rate with a magnitude of $ \beta/H \sim 10^4 $, and the GWs typically fall within the LISA detection window. In this work, we investigate the possibility of producing nanohertz GW spectra from first-order deconfinement and chiral phase transitions using two simple yet representative models, i.e., the FL model and the QM model, at high baryon chemical potential.

Our studies show that the baryon chemical potential enhances the potential barrier between the false and true vacuum and can significantly reduce the transition (or decay) rate. The decay rate is infinite at the CEP and drops to zero at the CNP. The nanohertz GWs can be produced in a narrow window of high baryon chemical potential when the transition rate is in the order of $ \beta/H \sim 10^1 $. When the chemical potential is larger than $ \mu_{CNP} $, the false vacuum is unlikely to decay and can persist over cosmological time scales. These remaining PQNs differ from the PQNs or strangelets proposed by Witten in 1984.

Furthermore, the PQNs will become the seeds of compact stars or structures, which may help to explain the high red-shift massive galaxies observed by the James Webb Space Telescope. The PQNs can survive to low temperature at which vacuum decay prevails thermal decay, the corresponding phase transition will eventually happen due to the quantum effect at an extremely slow rate, turning dense quark matter into normal baryon matter and possibly generating nanohertz GWs and inhomogeneity. The phase transition is likely to erupt most parts of the baryon matter with cold sparse core remaining. Ejected matter is likely to form halos around central matter or disperse around, forming structures. Besides, secondary signals such as electromagnetic and gravitational radiation from accretion might also be observed in the late Universe. Our results can be extended straightforwardly to high density of QCD-like dark matter [66] and the corresponding PQNs may constitute dark matter [75].

It is worthy of mentioning that considering the diquark condensation, i.e., the color superconducting phase at high baryon density [76−78], the first-order phase transition line at high μ and low temperature might be changed. Furthermore, the effect from the (primordial) magnetic field in the QCD phase transition should also be taken into account in the future [79, 80].

We thank Y.D. Chen, F. Gao and J. Schaffner-Bielich for helpful discussions.