-
At the forefront of global research, the investigation of exotic atomic nuclei-characterized by a neutron-to-proton number ratio significantly deviating from that observed in stable nuclei-unveils unique nuclear properties and contributes to our understanding of the origins of chemical elements obtained through stellar nucleosynthesis [1–6], with the distinctive physical properties of sodium isotopes becoming a focal point in nuclear physics research. These isotopes exhibit various exotic phenomena, including the island of inversion, shell evolution, changes in nuclear magic numbers, neutron halos, and shape decoupling between core and valence nucleons in deformed halo nuclei. The occurrence of these phenomena is intricately linked to the exceptional physical properties of sodium isotopes. The island of inversion in sodium isotopes has been a fascinating topic in nuclear physics since the 1970s. Near the traditional magic number
$ N=20 $ , it has been discovered that the ground states of unstable nuclei of Ne, Na, and Mg isotopes exhibit strong deformations [7–12]. A decrease in the single-particle gap between the$ s-d $ shell and$ p-f $ shell in these nuclei leads to the rearrangement of the single-particle structure in this region [13–17], resulting in the disappearance of the traditional magic number$ N=20 $ , known as the "island of inversion."Thibault et al., for the first time, observed the disappearance of magic numbers in neutron-rich nuclei 31,32Na in 1975 through direct mass measurements using an online mass spectrometer [7]. They detected abnormal experimental masses and anomalously large binding energies of neutron-rich Na isotopes near
$ N=20 $ , clearly indicating the disappearance of the magic number. Additionally, anomalies in the nuclear radii of sodium isotopes [8], anomalies in the spectroscopy of unstable Na isotopes [9, 10], large quadrupole moments in neutron-rich Na isotopes [18], and low-lying first excited states with large$ B(E2) $ transition probabilities observed in 31Na [19] provide unambiguous experimental results indicating the disappearance of the magic number$ N=20 $ .The transformation of sodium isotope chains from normal to intruder ground state form represents a major discovery in nuclear physics [20–22]. Investigations on experimental electromagnetic moments and energy levels of neutron-rich Na isotopes reveal that the transition from normal to intruder ground state occurs fully at 30Na, following a strong normal-intruder mixing already occurring at 29Na [21]. The low-energy level structure of 29Na is significantly influenced by
$ fp $ intruder configurations, as revealed through β-delayed γ spectroscopy [23]. The existence of intruder states in 30Na with low excitation energies dominated by the$ 2p2h $ configurations is supported based on Monte Carlo shell model calculations with the SDPF-M interaction in the$ sdpf $ valence space [24]. In 2010, Doornenbal et al. presented the excited states of 32,33Na for the first time and observed a decaying γ ray in 31Na consistent with the known$ (5/2^{+}_1)\longrightarrow3/2^{(+)}_{g.s.} $ transition, finding that its excited state belongs to a rotational band [25] formed by a$ 2p2h $ intruder configuration in the "island of inversion."Apart from exploring the island of inversion in sodium isotopes, physicists have undertaken systematic theoretical investigations into other ground state properties. Magnetic dipole and electric quadrupole moments, deformation parameter
$ \beta_{2} $ , root-mean-square (rms) charge, and matter radii of odd-even nuclei 21–41Na were obtained with the$ ab \; initio $ EEdf1 interaction applied in the$ sd + pf $ model space [26]; accordingly, the relationship between the neutron skin thickness and the electromagnetic moments for the exotic nucleus 31Na was explored. The level structure of 25Na at high excitation energy/high spin regime has been studied by γ ray spectroscopy and Doppler shifts lifetime measurements following 12C(18O,$ \alpha\rho $ )25Na reactions [27]. Higher-spin negative-parity states ($ I^{\pi} = 3/2^{-} $ ) of 25Na caused by neutron excitations or occupations in the$ pf $ shell have been detected.To further understand the nuclear structure and properties of sodium isotopes, physicists have conducted many theoretical studies to determine the location of the neutron drip line for Na [28–30]. Using the WS4 model [31], Gogny-Hartree-Fock-Bogoliubov (HFB) calculations with the D1S force [32], HFB-21 calculations [33], and relativistic continuum Hartree-Bogoliubov [34], the neutron drip line of Na is determined to be at 37Na, 35Na, 37Na, and 45Na, respectively. Moreover, the macroscopic model [35], complex shell model [16], and FRDM [36] model all predict 39Na as the most neutron-rich bound sodium isotope. HFB calculations based on SkM, SLy4, UNEDF0, SkMext1, and UNEDF0ext1 forces [37] suggest that the drip line exists at 41Na, 37Na, 39Na, 39Na, and 39Na, respectively. Furthermore, in 2023, deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc) calculations [38] with PC-PK1 [39], PC-F1 [40], NL3*[41], NLSH[42], and PK1 [43] endorse the drip line at 41Na, 39Na, 41Na, 39Na, and 41Na, respectively. These results underline the differences in the location of the neutron drip line for sodium isotopes predicted using different theoretical models or the same model with different parameter sets, providing a theoretical basis for experimental investigations.
Moreover, a series of experimental studies have been conducted on sodium to determine the location of its neutron drip line [44, 45]. In 2019, Ahn et al. observed one event for 39Na on the beryllium target using the projectile fragments of an intense 48Ca beam at 345 MeV/nucleon at the RIKEN Radioactive Isotope Beam Factory in Japan [46]. In 2022, Ahn et al. achieved an experimental breakthrough by identifying 39Na [47], which is believed to be an extremely neutron-rich sodium nucleus.
Consequently, the focus of both experiment and theory has shifted to exploring the ground state properties of 39Na, owing to the researchers' curiousity about whether it exhibits unique structures, such as a halo structure, the Borromean structure, and the quenched
$ N = 28 $ shell closure. The exploration of this extremely neutron-rich nucleus 39Na has aroused great interest from theoretical physicists. The HFB method and various Skyrme interactions [37] were used to obtain the two-neutron separation energies of sodium isotopes, revealing that 39Na is prolate deformed ($ \beta_{2} = 0.35 $ ) and has a unique deformed halo structure. By solving the Skyrme-HFB equation within deformed coordinate paces with the${\rm{SkM}}^{*}_{\rm ext1}$ and UNEDF0ext1 forces, systematic two-neutron separation energies, rms neutron radii, and density distributions were obtained, confirming 39Na as a promising candidate for a two-neutron deformed halo nucleus [48]. The DRHBc presents weakly bound 39,41Na as deformed halo nuclei with shape decoupling [38]. As far as deformed neutron halos are concerned, 39Na is a two-neutron halo nucleus with a Borromean structure [38], characterized by weak binding, small two-neutron separation energy, and a larger radius than adjacent isotopes. Additionally, 41Na and 43Na may also be classified as two-neutron halo nuclei.In this study, we utilize the DRMF-CMR-BCS to explore the ground state properties of neutron-rich sodium isotopes. The DRMF-CMR-BCS can provide resonant states of real physics, which do not change with the size of the basis or space in numerical calculations. The DRMF-CMR-BCS not only yields the energies and widths of the resonant states for deformed nuclei but also thoroughly explores unique halo structures [49]. The theoretical formalism of the DRMF-CMR-BCS theory is presented in Sec. II. In Sec. III, the numerical details and results of deformed odd-even nuclei 35–43Na are presented. The structures of 39Na, 41Na, and 43Na are discussed in subsections A, B, and C, respectively. The study is summarized in Sec. IV.
-
In this section, we introduce the formula of the DRMF-CMR-BCS model used to explore the structure of exotic nuclei. We first delve into the theoretical formalism of RMF [50–52]. In the RMF theory, nucleons are characterized as Dirac particles, which interact via photons and mesons. The effective Lagrange density is expressed as follows:
$ \begin{aligned}[b] \mathcal{L} \;=&\;\bar{\psi}[{\rm i}\gamma ^{\mu }\partial _{\mu }-M-g_{\sigma }\sigma -g_{\omega }\gamma ^{\mu }\omega _{\mu }-g_{\rho }\gamma ^{\mu }\vec{\tau}\vec{\rho}_{\mu }]\psi \\ &-\bar{\psi}[\frac{1}{2}e\gamma ^{\mu }(1-\tau _{3})A_{\mu }]\psi +\frac{1}{2} (\partial _{\mu }\sigma \partial ^{\mu }\sigma -m_{\sigma }^{2}\sigma ^{2}) \\ &-\frac{1}{4}\omega ^{\mu \nu }\omega _{\mu \nu }+\frac{1}{2}m_{\omega }^{2}\omega ^{\mu }\omega _{\mu }-\frac{1}{3}g_{2}\sigma ^{3}-\frac{1}{4} g_{3}\sigma ^{4} \\ &-\frac{1}{4}\vec{\rho}^{\mu \nu }\vec{\rho}_{\mu \nu }+\frac{1}{2}m_{\rho }^{2}\vec{\rho}^{\mu }\vec{\rho}_{\mu }+\frac{1}{4}c_{3}(\omega ^{\mu }\omega _{\mu })^{2} \\ &-\frac{1}{4} F^{\mu \nu} F_{\mu \nu}. \end{aligned} $

(1) The field-tensors for the mesons and photon are defined as follows:
$ \begin{align} \omega ^{\mu \nu } &=\partial ^{\mu }\omega ^{\nu }-\partial ^{\nu }\omega ^{\mu }, \\ \vec{\rho}^{\mu \nu } &=\partial ^{\mu }\vec{\rho}^{\nu }-\partial ^{\nu } \vec{\rho}^{\mu }, \\ A^{\mu \nu } &=\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }. \end{align} $

$ g_{\sigma } $ ,$ g_{\omega } $ , and$ g_{\rho } $ are the coupling constants of the isoscalar-scalar σ, isoscalar-vector ω, and isovector-vector ρ mesons, respectively. The masses of these coupling constants are$ m_{\sigma } $ ,$ m_{\omega } $ , and$ m_{\rho } $ , respectively. The classical variational principle yields the following Dirac equation describing the motion of a nucleon:$ \left[ \vec{\alpha}\cdot \vec{p}+\beta \left( m+S\right) +V\right] \psi =\varepsilon _{i}\psi $

(2) and the densities of mesons and photons are described as follows:
$ \begin{aligned}[b] \rho _{s} &=\sum\limits_{i=1}^{A}\bar{\psi}_{i}\psi _{i},\rho _{v}=\sum\limits_{i=1}^{A}\psi _{i}^{\dagger }\psi _{i}, \\ \rho _{3} &=\sum\limits_{i=1}^{A}\psi _{i}^{\dagger }\tau _{3}\psi _{i},\rho _{c}=\sum\limits_{p=1}^{Z}\psi _{p}^{\dagger }\psi _{p}. \end{aligned} $

(3) For axisymmetric and reflection symmetric systems, the parity π and third component of total angular momentum
$ m_{j} $ are good quantum numbers. The expansion of the Dirac spinor according to the spherical configurations is expressed as follows:$ \psi_{m_{j}}(\vec{r})=\frac{1}{r} \sum\limits_{l j}\left(\begin{array}{c} {\rm i} G^{l j}(r) Y_{j m_{j}}^{l}\left(\Omega_{r}\right) \\ -F^{l j}(r) Y_{j m_{j}}^{\tilde{l}}\left(\Omega_{r}\right) \end{array}\right) , $

(4) with
$ \tilde{l}=2j-l $ .$ Y_{j m_{j}}^{l}\left(\Omega_{r}\right) $ denoting the spin spherical harmonics. The densities are crucial for the research of deformed halo nuclei. Substituting Eq. (4) into Eq. (3) yields the scalar and vector densities. Accordingly, the radial density distributions are calculated as follows:$ \rho_{s}(r, \theta)=\sum\limits_{\lambda}\frac{2\lambda +1}{4\pi r^{2} }P_{\lambda}(\cos\theta) \sum\limits_{i(lj)(lj)^{\prime }}\nu_{i}^{2}\left( G_{i}^{lj}G_{i}^{(lj)^{\prime }}-F_{i}^{lj}F_{i}^{(lj)^{\prime }}\right) A\left( \lambda ,(lj)^{\prime },(lj),m_{j}\right), $ 
(5) $ \rho_{\nu}(r, \theta)=\sum\limits_{\lambda}\frac{2\lambda +1}{4\pi r^{2}}P_{\lambda}(\cos\theta) \sum\limits_{i(lj)(lj)^{\prime }}\nu_{i}^{2}\left( G_{i}^{lj}G_{i}^{(lj)^{\prime }}+F_{i}^{lj}F_{i}^{(lj)^{\prime }}\right) A\left( \lambda ,(lj)^{\prime },(lj),m_{j}\right) , $

(6) with
$\begin{aligned}[b] & A\left( \lambda ,(lj)^{\prime },(lj),m_{j}\right) \notag \\=&\int {\rm d}\Omega Y_{jm_{j}}^{l}(\cos \theta )^{\ast }P_{\lambda }(\cos \theta )Y_{j^{\prime }m_{j}}^{l^{\prime }}(\cos \theta ) \notag \\=&\int {\rm d}\Omega Y_{jm_{j}}^{\tilde{l}}(\cos \theta )^{\ast }P_{\lambda }(\cos \theta )Y_{j^{\prime }m_{j}}^{\tilde{l}^{\prime }}(\cos \theta ), \\\lambda = &0,2,4,\dots \end{aligned} $

Here,
$ \nu_i^2 $ represents the actual occupation numbers of particles at the i-level. In order to obtain the resonances, the Dirac Eq. (2) is transformed into momentum representation,$ \int {\rm d}\vec{k}^{\prime }\langle \vec{k}\left| H \right|{{\vec{k}}^{\prime }}\rangle \psi(\vec{k}^{\prime }) =\varepsilon \psi(\vec{k}) , $

(7) where
$ H=\vec{\alpha}\cdot \vec{p}+\beta \left(m+S\left(\vec{r}\right) \right) +V\left(\vec{r}\right) $ , and$ \psi (\vec{k}) $ denotes the momentum wave functions. The momentum wave function$ \psi (\vec{k}) $ describing axially deformed nuclei can be expressed as follows:$ \psi(\vec{k}) =\psi _{m_{j}}(\vec{k})=\sum\limits_{lj}\left( \begin{array}{c} f^{lj}(k)\phi _{ljm_{j}}\left( \Omega _{k}\right) \\ g^{lj}(k)\phi _{\tilde{l}jm_{j}}\left( \Omega _{k}\right) \end{array} \right) , $

(8) with
$ \phi _{ljm_{j}}\left(\Omega _{k}\right) =\sum\limits_{{{m}_{s}}}{ \langle lm\frac{1}{2}{{m}_{s}}\left\vert j{{m}_{j}}\rangle \right. }{Y}_{lm}(\Omega _{k})\chi _{m_{s}} $ . Here,$ \chi _{m_{s}} $ is the spin wave function, and$ Y_{lm}(\Omega _{k}) $ denotes spherical harmonics. Substituting wave function Eq. (8) into Eq. (7), the following Dirac equation is obtained:$ \begin{aligned}\\[-5pt]\left\{ \begin{array}{c} Mf^{lj}(k)-kg^{lj}(k)+\sum\limits_{l^{\prime }j^{\prime }}\int k^{\prime 2}{\rm d}k^{\prime }V^+\left( l^{\prime },j^{\prime },p,q,l,j,m_{j},k,k^{\prime }\right) f^{l^{\prime }j^{\prime }}(k^{\prime })=\varepsilon f^{lj}(k), \\ -kf^{lj}(k)-Mg^{lj}(k)+\sum\limits_{l^{\prime }j^{\prime }}\int k^{\prime 2}{\rm d}k^{\prime }V^-\left( \tilde{l ^{\prime }},j^{\prime },p,q,\tilde{l} ,j,m_{j},k,k^{\prime }\right) g^{l^{\prime }j^{\prime }}(k^{\prime })=\varepsilon g^{lj}(k), \end{array} \right. \end{aligned}$ 
(9) with
$ V^+\left(l^{\prime } ,j^{\prime },p,q,l,j,m_{j},k,k^{\prime }\right) =(-)^{l}i^{l+l'}\frac{2}{\pi}\int r^{2}{\rm d}r[V(r)+S(r)]j_{l}(kr)j_{l'}(k'r)\sum\limits_{m_{s}}\langle lm|Y_{pq}(\Omega_{r})|l'm'\rangle\langle lm\frac{1}{2}m_{s}|jm_{j}\rangle\langle l'm'\frac{1}{2}m_{s}|j'm_{j}\rangle, $

$ V^-\left(\tilde{l}^{\prime } ,j^{\prime },p,q,\tilde{l},j,m_{j},k,k^{\prime }\right) =(-)^{\tilde{l}}i^{\tilde{l}+\tilde{l}'}\frac{2}{\pi}\int r^{2}{\rm d}r[V(r)-S(r)]j_{\tilde{l}}(kr)j_{\tilde{l}'}(k'r)\sum\limits_{m_{s}}\langle \tilde{l}\tilde{m}|Y_{pq}(\Omega_{r})|\tilde{l}'\tilde{m}'\rangle\langle \tilde{l}\tilde{m}\frac{1}{2}m_{s}|jm_{j}\rangle\langle \tilde{l}'\tilde{m}'\frac{1}{2}m_{s}|j'm_{j}\rangle. $

The solution of Eq. (7) is obtained by solving the eigenvalues of the symmetric matrix depicted in Eq. (9). For exotic nuclei close to drip lines, the Fermi surface is very close to the continuum threshold; therefore, the valence nucleons are easliy scattered into the continuum. It is applicable to use the BCS approximation to assess the contribution of the pairings presented here. The pairing correlations after considering resonances can be treated using the gap equation, which is described as follows:
$ \sum\limits_{b}\frac{1}{\sqrt{\left( \varepsilon _{b}-\lambda \right) ^{2}+\Delta ^{2}}}+\sum\limits_{r}\int g_{r}(\varepsilon )\frac{1}{\sqrt{(\varepsilon -\lambda )^{2}+\Delta ^{2}}}{\rm d}\varepsilon =\frac{2}{G}, $

(10) and the particle number equation is:
$ \begin{aligned}[b]&\sum\limits_{b}\left( 1-\frac{\varepsilon _{b}-\lambda }{\sqrt{\left( \varepsilon _{b}-\lambda \right) ^{2}+\Delta ^{2}}}\right)\\& +\sum\limits_{r}\int g_{r}(\varepsilon )\left( 1-\frac{\varepsilon -\lambda }{\sqrt{(\varepsilon -\lambda )^{2}+\Delta ^{2}}}\right) {\rm d}\varepsilon =N, \end{aligned} $

(11) where G is the pairing strength, and N is the particle number. Here,
$ g_{r}(\varepsilon)=\dfrac{1}{\pi }\dfrac{\Gamma _{r}/2}{\left(\varepsilon -\varepsilon _{r}\right) ^{2}+\Gamma _{r}^{2}/4} $ .$ \varepsilon_{b} $ and$ \varepsilon_{r} $ are the energy eigenvalues of H for the bound and resonant states, respectively.$ \Gamma _{r} $ is the width of resonant states of H. The occupation probabilities for the bound states and resonances can be obtained using Eqs. (10) and (11). The densities described in Eqs. (5) and (6) are modified as follows:$ \begin{aligned}[b]\\[-9pt] \rho _{s}\left( r,\theta \right) \; =\;&\sum\limits_{\lambda }\frac{2\lambda +1 }{4\pi r^{2}}P_{\lambda }\left( \cos \theta \right) \sum\limits_{b\left( lj\right) \left( lj\right) ^{\prime }}v_{b}^{2}\left( G_{b}^{lj}G_{b}^{\left( lj\right) ^{\prime }}-F_{b}^{lj}F_{b}^{\left( lj\right) ^{\prime }}\right) A\left( \lambda ,\left( lj\right) ^{\prime },\left( lj\right) ,m\right) \\ &+\sum\limits_{\lambda }\frac{2\lambda +1}{4\pi r^{2}}P_{\lambda }\left( \cos \theta \right) \sum\limits_{r\left( lj\right) \left( lj\right) ^{\prime }}\int g_{r}(\varepsilon )v_{r}^{2}{\rm d}\varepsilon \left( G_{r}^{lj}G_{r}^{\left( lj\right) ^{\prime }}-F_{r}^{lj}F_{r}^{\left( lj\right) ^{\prime }}\right) A\left( \lambda ,\left( lj\right) ^{\prime },\left( lj\right) ,m\right), \end{aligned} $ 
(12) $ \begin{aligned}[b] \rho _{v}\left( r,\theta \right) \; =\;&\sum\limits_{\lambda }\frac{2\lambda +1 }{4\pi r^{2}}P_{\lambda }\left( \cos \theta \right) \sum\limits_{b\left( lj\right) \left( lj\right) ^{\prime }}v_{b}^{2}\left( G_{b}^{lj}G_{b}^{\left( lj\right) ^{\prime }}+F_{b}^{lj}F_{b}^{\left( lj\right) ^{\prime }}\right) A\left( s,\left( lj\right) ^{\prime },\left( lj\right) ,m\right) \\ &+\sum\limits_{\lambda }\frac{2\lambda +1}{4\pi r^{2}}P_{\lambda }\left( \cos \theta \right) \sum\limits_{r\left( lj\right) \left( lj\right) ^{\prime }}\int g_{r}(\varepsilon )v_{r}^{2}{\rm d}\varepsilon \left( G_{r}^{lj}G_{r}^{\left( lj\right) ^{\prime }}+F_{r}^{lj}F_{r}^{\left( lj\right) ^{\prime }}\right) A\left( \lambda ,\left( lj\right) ^{\prime },\left( lj\right) ,m\right). \end{aligned} $

(13) The BCS approximation is used to dispose of the pairing correlations. Then, Eqs. (10) and (11) are solved for a given pairing strength G or energy gap Δ. The Δ is used based on an empirical formula
$ \Delta=12/\sqrt{A} $ for the neutron and proton pairings [53]. The occupation probabilities$ v ^{2} $ can be obtained by solving Eqs. (10) and (11). The densities$ \rho _{s} $ and$ \rho _{\nu } $ are obtained by Eqs. (5) and (6), respectively, along with$ \rho _{3} $ and$ \rho _{c} $ . The sources in Eq. (3), which are composed of these densities, are used to calculate the meson fields and new potentials. This process is repeated until the iteration converges. -
We have delved into the ground state properties of neutron-rich sodium isotopes using the DRMF-CMR-BCS theory. To assess the influence of continuum and deformation effects on the halo structure under DRMF-CMR-BCS calculations with various effective interactions, we have examined four commonly used effective interactions: NL3 [54], NL3*, PK1, and NLSH. Before presenting our research findings, we provide a brief overview of the numerical details. The set of coupled equations is iteratively solved based on initial guesses for the potentials V and S. To obtain both the bound and resonant states, Eq. (2) is transformed into the complex momentum representation in Eq.(9). The Dirac equation, Eq. (9), is solved through the coupled-channel method. Here, the wave functions in momentum representation, denoted as
$ f(k) $ and$ g(k) $ , are expanded by different channels labeled as$ lj $ . The summation over$ lj $ presented in Eq. (9) is confined to a finite range$ N_{c}=8 $ , where$ N_{c} $ denotes the number of spherical configurations employed. In our calculations, we consistently use$ N_{c}=8 $ in every block with the determined$ \Omega_{\pi} $ . The truncated momentum$ k_{\text{max}} $ expressed in Eq. (9) is set to$ k_{\text{max}}=4.0 $ fm−1.The results for the ground state of 35,37,39,41,43Na from self-consistent DRMF-CMR-BCS calculations using four different effective interactions are presented in Table 1. The table includes the two-neutron separation energies (
$ S_{2n} $ ), quadrupole moments of proton and neutron ($ Q_p $ ,$ Q_n $ ), and rms proton and neutron radii ($ R_p $ ,$ R_n $ ), along with their differences ($ R_n-R_p $ ). From Table 1, the spin-parities ($ \Omega^{\pi} $ ) of the ground states for 35Na, 37Na, 39Na, and 41Na are$ 3/2^{-} $ ,$ 1/2^{-} $ ,$ 5/2^{-} $ , and$ 1/2^{-} $ , respectively. For 43Na, the spin-parity of the ground state of a single neutron is$ \Omega^{\pi}=1/2^{-} $ with NL3 and NL3* and$ \Omega^{\pi}=3/2^{-} $ with PK1 and NLSH.Nuclei $\Omega^{\pi}/N$ 

$ S_{2n} $ /MeV

$ Q_p $ /fm2

$ Q_n $ /fm2

$ R_p $ /fm

$ R_n $ /fm

$ R_n-R_p $ /fm

35Na $ 3/2^{-} $ 

NL3 5.298 47.331 83.451 3.048 4.150 1.102 $ 3/2^{-} $ 

NL3* 4.395 46.921 81.865 3.050 4.189 1.139 $ 3/2^{-} $ 

PK1 6.585 47.455 75.241 3.027 4.281 1.254 $ 3/2^{-} $ 

NLSH 4.479 47.589 95.578 3.025 4.019 0.993 37Na $ 1/2^{-} $ 

NL3 2.293 50.707 96.404 3.078 4.380 1.303 $ 1/2^{-} $ 

NL3* 2.149 50.527 95.107 3.080 4.418 1.337 $ 1/2^{-} $ 

PK1 2.344 50.805 72.860 3.055 4.573 1.518 $ 1/2^{-} $ 

NLSH 1.339 49.968 100.334 3.050 4.296 1.245 39Na $ 5/2^{-} $ 

NL3 1.015 50.908 112.106 3.098 4.470 1.371 $ 5/2^{-} $ 

NL3* 0.891 50.851 110.830 3.101 4.503 1.402 $ 5/2^{-} $ 

PK1 0.597 51.086 78.935 3.075 4.721 1.647 $ 5/2^{-} $ 

NLSH 0.705 50.099 59.334 3.066 4.794 1.729 41Na $ 1/2^{-} $ 

NL3 0.152 49.832 123.700 3.117 4.370 1.253 $ 1/2^{-} $ 

NL3* 0.027 49.824 121.504 3.121 4.408 1.288 $ 1/2^{-} $ 

PK1 -0.174 50.051 102.058 3.092 4.578 1.486 $ 1/2^{-} $ 

NLSH -0.432 48.647 99.707 3.081 4.580 1.499 43Na $ 1/2^{-} $ 

NL3 -0.417 48.647 99.707 3.128 4.404 1.277 $ 1/2^{-} $ 

NL3* -0.529 46.289 96.307 3.132 4.453 1.321 $ 3/2^{-} $ 

PK1 -1.020 46.537 93.869 3.104 4.498 1.395 $ 3/2^{-} $ 

NLSH -0.926 44.337 76.316 3.088 4.558 1.469 Table 1. Two-neutron separation energy (
$ S_{2n} $ ), quadrupole moments of proton and neutron distributions ($ Q_p $ ,$ Q_n $ ), root-mean-square proton radius ($ R_m $ ), root-mean-square neutron radius ($ R_n $ ), and their differences ($ R_n-R_p $ ) for isotopes 35,37,39,41,43Na obtained from self-consistent DRMF-CMR-BCS calculations with various effective interactions. Additionally,$ \Omega^{\pi}(N) $ represents the spin-parity of the ground state in odd-even nuclei 35–43Na.In Table 1, the calculated two-neutron separation energies for 35,37Na are presented, indicating that these nuclei are bound. The calculated
$ S_{2n} $ for 35Na is 5.298 MeV with NL3, 4.395 MeV with NL3*, 6.585 MeV with PK1, and 4.479 MeV with NLSH. Similarly, 37Na is bound with NL3 ($ S_{2n} $ = 2.293 MeV), NL3* ($ S_{2n} $ = 2.149 MeV), PK1 ($ S_{2n} $ = 2.344 MeV), and NLSH ($ S_{2n} $ = 1.339 MeV). Our calculations successfully reproduce the Borromean feature of 39Na with four different effective interactions. The calculated$ S_{2n} $ values for 39Na obtained using NL3, NL3*, PK1, and NLSH are 1.015 MeV, 0.891 MeV, 0.597 MeV, and 0.705 MeV, respectively. For 41Na, the calculated$ S_{2n} $ is 152 KeV with NL3 and 27 KeV with NL3*, whereas the value is –174 KeV with PK1 and –432 KeV with NLSH. In contrast, 43Na is determined to be unbound with NL3 ($ S_{2n} $ = –417 KeV), NL3* ($ S_{2n} $ = –529 KeV), PK1 ($ S_{2n} $ = –1.202 MeV), and NLSH ($ S_{2n} $ = –926 KeV). The analysis of two-neutron separation energies suggests that, according to calculations with NL3 and NL3*, the two-neutron drip line nucleus for Na isotopes is 43Na. However, calculations conducted with PK1 and NLSH indicate that the two-neutron drip line nucleus is 41Na.To date, the quadrupole moments for the odd-even nuclei 35–43Na have not been experimentally determined; however, numerous theoretical calculations have provided corresponding
$ \beta_2 $ values. Solving the Skyrme-HFB equation in deformed coordinate spaces with SkM${\rm{SkM}}^{*}_{\rm ext1}$ forces [48] yields$ \beta_2 $ values of 0.36, 0.33, 0.32, and 0.29 for the odd-even nuclei 35–41Na, respectively. Additionally, HFB calculations with various Skyrme interactions[37] suggest that 39Na exhibits prolate deformation with$ \beta_2\approx 0.35 $ . In the DRHBc framework with the effective interaction PK1 [38],$ \beta_2 $ values for 39,41Na are approximately 0.45 and 0.37, respectively. Table 1 presents the calculated quadrupole moments of proton and neutron distributions in the ground states for the odd-even nuclei 35–43Na using four different effective interactions. The$ \beta_2 $ values obtained in our approach for these nuclei consistently yield positive values, indicating prolate shapes. This observation aligns with similar trends in other theoretical calculations [37, 38, 48].The nuclear radius is a crucial observational parameter that sheds light on the properties of atomic nuclei. While the rms proton and neutron radii for odd-even nuclei 35–43Na have yet to be experimentally determined, Table 1 provides a comprehensive display of these radii and their differences in 35,37,39,41,43Na. Notably, 39Na stands out with a larger neutron radius compared to its neighboring isotopes, suggesting that it can potentially be classified as a neutron halo nucleus. Examining Table 1, it becomes apparent that the rms proton and neutron radii, determined using four different effective interactions, exhibit an increasing trend with growing neutron numbers. However, the rms neutron radii of 41,43Na are smaller than that of 39Na. The reasons for this intriguing observation are further elucidated in the subsequent discussion.
The computation results for odd-even nuclei 35–43Na depend on the chosen effective interaction and number of considered resonant states. In this analysis, we account for the impact of five resonant states on pairing correlations in deformed odd-even nuclei. Therefore, it becomes crucial to establish a suitable integration contour to capture the involvement of these five resonant states at specific deformation values. Following a methodology similar to that presented in Ref. [55], the contour is composed of three segments that are defined by four points in the complex momentum plane:
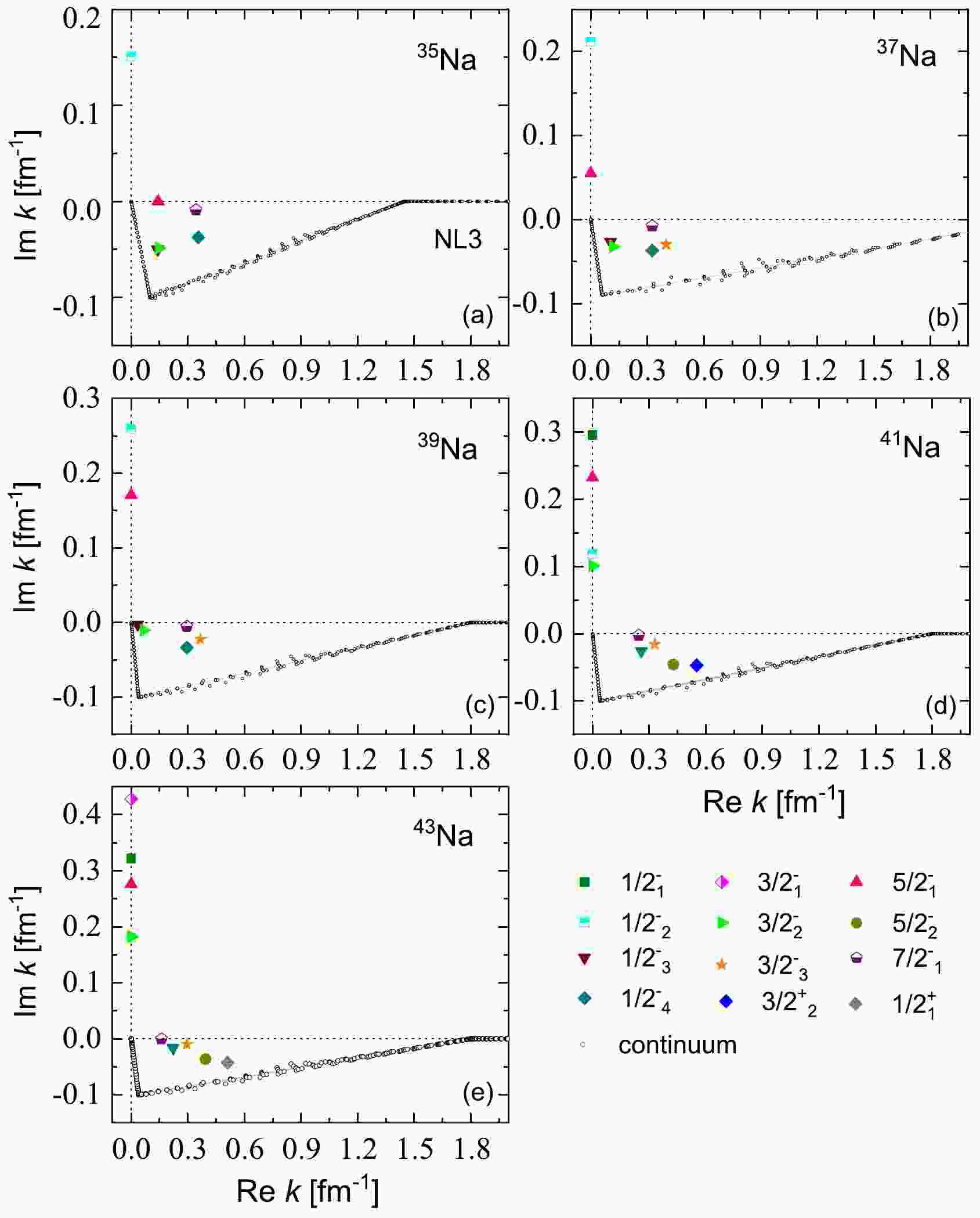
$ k_1 = 0.0 $ ,$ k_2 $ and$ k_3 $ , and$ k_\text{max} = 4.0 $ (all in fm-1). Notably, the values of$ k_2 $ and$ k_3 $ are selected differently for 35,37,39,41,43Na. Specifically, for 35Na,$ k_2 $ and$ k_3 $ are set to$ (0.1-i0.1) $ and$ 1.45 $ , respectively. For 37Na, these points are set to$ (0.06-i0.09) $ and 2.45, respectively. As for 39,41,43Na,$ k_2 $ and$ k_3 $ are established as$ (0.04-i0.1) $ and 1.8 (all in fm-1), respectively. The discretization of the contour is achieved through Gauss-Legendre quadrature, employing a total of 120 grid points.All bound and resonant states of odd-even nuclei 35–41Na at the ground state deformation are visualized in Fig. 1 utilizing the NL3 effective interaction. The single-particle neutron states of 35,37,39,41,43Na, specifically
$ \Omega^{\pi} = 1/2^{-}_1 $ ,$ 1/2^{-}_2 $ ,$ 1/2^{-}_3 $ ,$ 1/2^{-}_4 $ ,$ 1/2^{+}_1 $ ,$ 3/2^{-}_1 $ ,$ 3/2^{-}_2 $ ,$ 3/2^{-}_3 $ ,$ 3/2^{+}_2 $ ,$ 5/2^{-}_1 $ ,$5/2^{-}_2,\; 7/2^{-}_1$ at ground state deformation, are presented in the complex momentum planes in Fig. 1(a) to Fig. 1(e). From Fig. 1, the bound states manifest along the imaginary axis. The resonant states, in contrast, are distinctly separated from the continuum in the fourth quadrant, while the continuum adheres to the integration contour.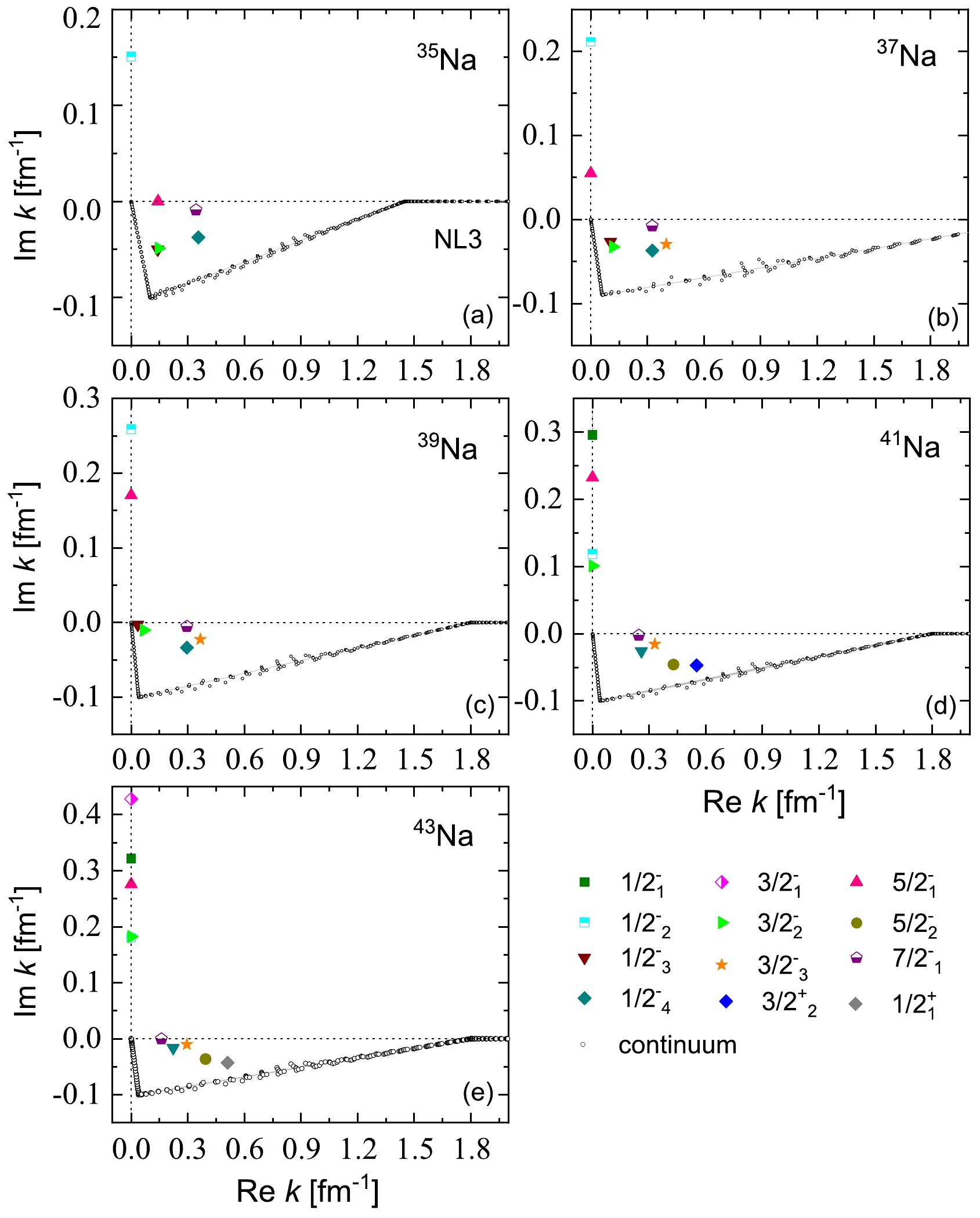
Figure 1. (color online) Single-neutron spectra in odd-even nuclei 35–43Na at ground state deformation for all bound and resonant states considered on the complex momentum plane. Each single-particle neutron state is labeled with
$ \Omega^{\pi}_{i} $ , where π is the parity, Ω is the projection of the angular momentum on the symmetry axis, and i is used to order the state in each$ \Omega^{\pi} $ -block. The bound and resonant states of different quantum numbers are marked with different colored and shaped labels. The continuous spectrum is marked with black open circles.To gain a more intuitive understanding of the ground state properties in odd-even nuclei 35–41Na, we conduct RMF-CMR-BCS calculations using the NL3 effective interaction. The resulting single neutron levels of 35,37,39,41,43Na are presented in Fig. 2. In this computation, we focus on the five resonant levels around the Fermi surface, considering 4, 6, 6, 8, and 7 bound levels for 35,37,39,41,43Na, respectively. The energy levels for the resonant states are depicted with error bars, where the position and width of each level are represented by the center line and height of the bar, respectively. In an axially deformed system, the parity π and third component of angular momentum Ω serve as good quantum numbers. To easily identify the neutron levels, these levels are labeled as
$ \Omega^{\pi}_{i} $ , where the levels are ordered within each$ \Omega^{\pi} $ -block, and i is used as a marker. The position of the chemical potential for neutrons, denoted by λ, is indicated by the dotted line.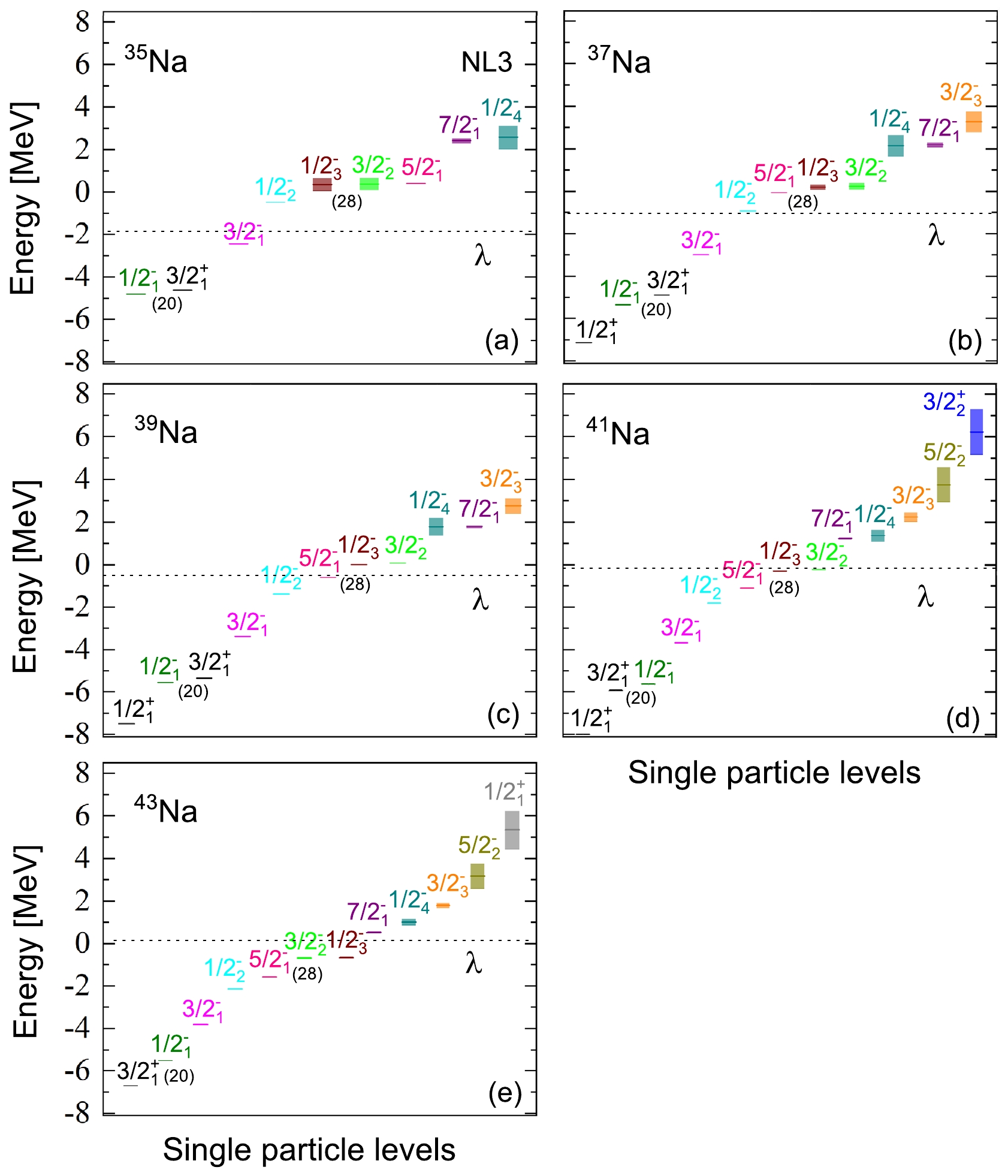
Figure 2. (color online) Available single-neutron levels around Fermi surface including the bound states and resonant states in odd-even nuclei 35–41Na. For the resonant states, the energy levels are shown with error bars. The center line of the bar corresponds to the position of energy level, and the height of the bar corresponds to the width of the energy level. The quantum numbers of angular momentum, parity, and i are labeled as
$ \Omega ^{\pi }_{i} $ , i is used for ordering the state in each$ \Omega^{\pi} $ -block. λ is the chemical potential marked by the dotted line.From Fig. 2(a) to Fig. 2(e), a noticeable trend emerges: the lowering of the
$ 1/2^{-}_{1} $ orbital leads to the collapse of the$ N = 20 $ shell closure in 35,37,39,41,43Na. Additionally, the collapse of the$ N = 28 $ shell closure is attributed to the lowering of the$ 1/2^{-}_{3} $ and$ 3/2^{-}_{2} $ orbitals. The stable prolate deformation observed in odd-even nuclei 35–41Na is likely a contributing factor to the collapse of both the$ N = 20 $ and$ N = 28 $ shell closures. According to Fig. 2, five narrow resonances with energies below 6.5 MeV appear in 35,37,39Na. Notably, all these resonances exhibit relatively small widths and relatively long lifetimes. Additionally, for 41Na, the resonant states$ 5/2^{-}_2 $ and$ 3/2^{+}_2 $ , as well as for 43Na, the resonant states$ 5/2^{-}_2 $ and$ 1/2^{+}_1 $ , are broad resonances, while the resonant states in the other nuclei are characterized by narrow widths.Neutron halos typically manifest in weakly bound nuclei, where valence neutrons occupying lower l-orbitals near the continuum threshold are easily scattered into the continuous spectrum. Fig. 3 presents the occupation probabilities of single neutron orbitals near the Fermi surface in odd-even nuclei 35–41Na, employing the NL3 effective interaction. The vertical dotted line indicates the position of the chemical potential. The formula of occupation probabilities
$ P^{m_{j}} $ is as follows: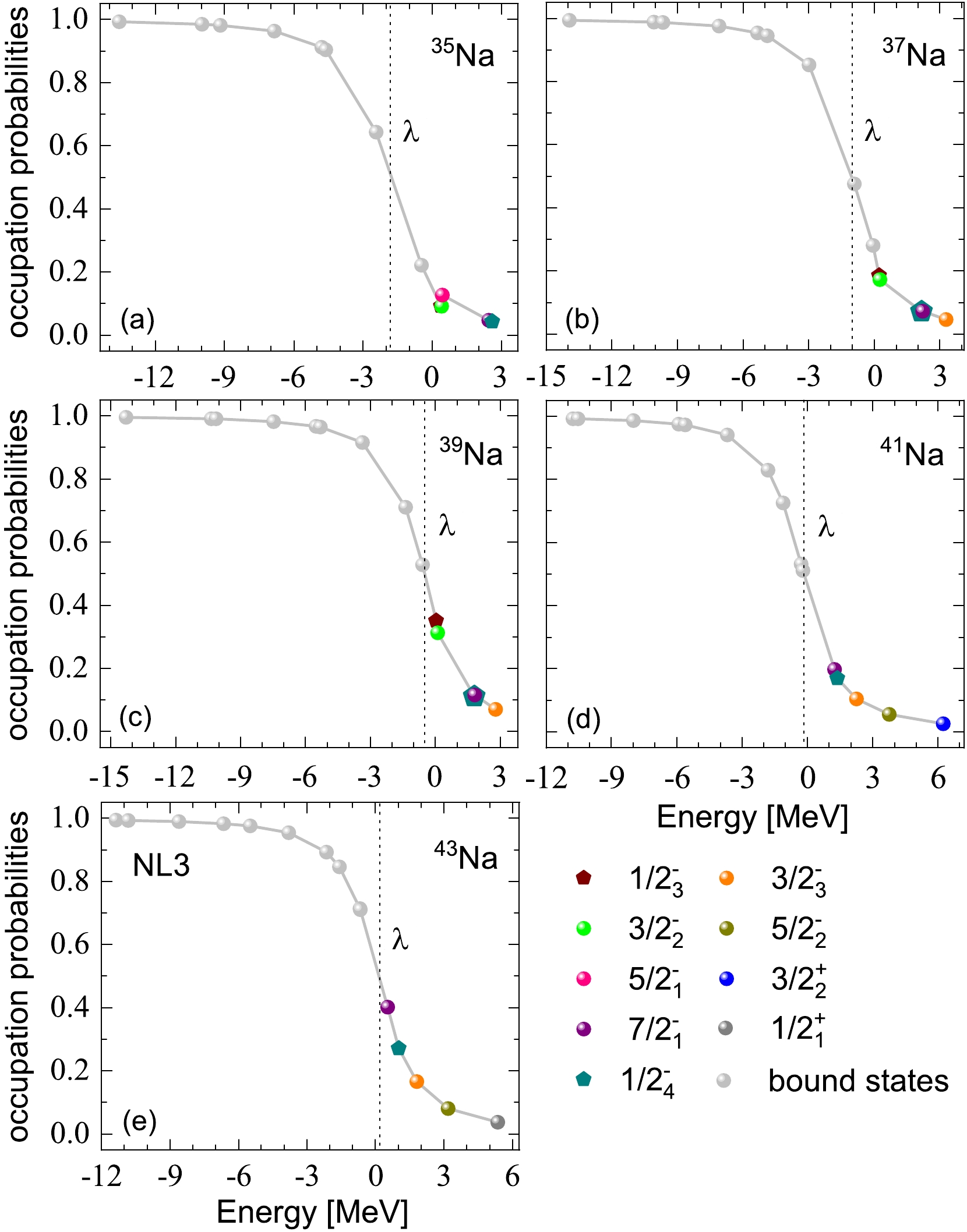
Figure 3. (color online) Occupation probabilities of single particle orbitals around the Fermi surface in odd-even nuclei 35–41Na. The bound orbitals are denoted as gray circles. The resonant orbitals are marked as solid circles with different colors. The chemical potential λ labels the position of the Fermi surface.
$ \begin{aligned}[b] P^{m_{j}} \;=\;\;&\operatorname{Re}(\int \widetilde{\psi}_{m_{j}}(\vec{k}) \psi_{m_{j}}(\vec{k}) \mathrm{\rm d} \vec{k} ) \\ \;=\;\;& \operatorname{Re}(\int \sum\limits_{lj} [f^{l j}(k) f^{l j}(k)+g^{l j}(k) g^{l j}(k)] k^{2} \mathrm{\rm d} k). \end{aligned} $

(14) In Fig. 3(a) to Fig. 3(e), the occupation probabilities of 35,37,39,41,43Na gradually decrease with increasing energy for all orbitals. However, exceptions exist, such as the
$ 5/2^{-}_1 $ orbital of 35Na and the$ 7/2^{-}_1 $ orbital of 37,39Na. The energy and occupation probabilities of these orbitals are slightly higher than those of their adjacent orbitals ($ 3/2^{-}_2 $ of 35Na and$ 1/2^{-}_4 $ of 37,39Na). This discrepancy may be attributed to the significantly smaller widths of the$ 5/2^{-}_1 $ orbital of 35Na and the$ 7/2^{-}_1 $ orbital of 37,39Na compared to those of their adjacent orbitals. Despite the decreasing occupation probabilities with increasing energies, the occupancies of these resonant orbitals should not be disregarded. In our calculations, the number of neutrons occupying these resonant orbitals is approximately 2.48, potentially contributing to the appearance of a halo in 39Na. For 41Na (or 43Na), the neutron number occupying weakly bound and resonant orbitals is approximately 6.3 (or 8.2), with 5.2 (or 6.3) of these neutrons being in weakly bound orbitals and others in the continuum. These results provide valuable insights into the neutron occupation patterns and potential halo formation in the specified odd-even nuclei.For a clear visual observation of the exotic structure of odd-even nuclei 35–41Na, two-dimensional neutron density distributions for the ground states of sodium isotopes, calculated with the effective interaction NL3, are depicted in Fig. 4. The density profiles illustrate the shape evolution with the mass number A; observe that the density distributions of 39,41,43Na exhibit more significant spatial expansions compared to the adjacent nucleus 37Na. The total neutron density distributions for 39,41,43Na are specifically highlighted in Fig. 4(c) to Fig. 4(e). Note that these density distributions are characterized by a pronounced diffusion. The configurations of 39,41,43Na will be further presented and discussed in the subsequent section.
-
The ground state of 39Na exhibits a notable gap between the bound levels
$ 3/2^{-}_1 $ and$ 1/2^{-}_2 $ , as illustrated in Fig. 2. This gap serves to divide the total neutron density into distinct core and halo components. Specifically, the levels$ 3/2^{-}_1 $ and those below are considered deeply bound levels constituting the core, while the halo component arises from the weakly bound and resonant levels. The neutron density distributions for the total, core, and halo components of 39Na are delineated in Fig. 5(a), Fig. 5(b), and Fig. 5(c), respectively. The density distributions for the deeply bound levels depicted in Fig. 5(b) are less diffuse, indicating a more concentrated spatial distribution. Conversely, the density distributions contributed by the weakly bound and resonant levels depicted in Fig. 5(c) are comparatively diffuse, signifying a more spread-out spatial distribution. Notably, the core of 39Na exhibits a prolate shape, while the neutron halo manifests an oblate shape. This observation indicates a shape decoupling between the core and halo in the odd-even nucleus 39Na with a two-neutron halo. This finding aligns with the predictions stated in Ref. [38].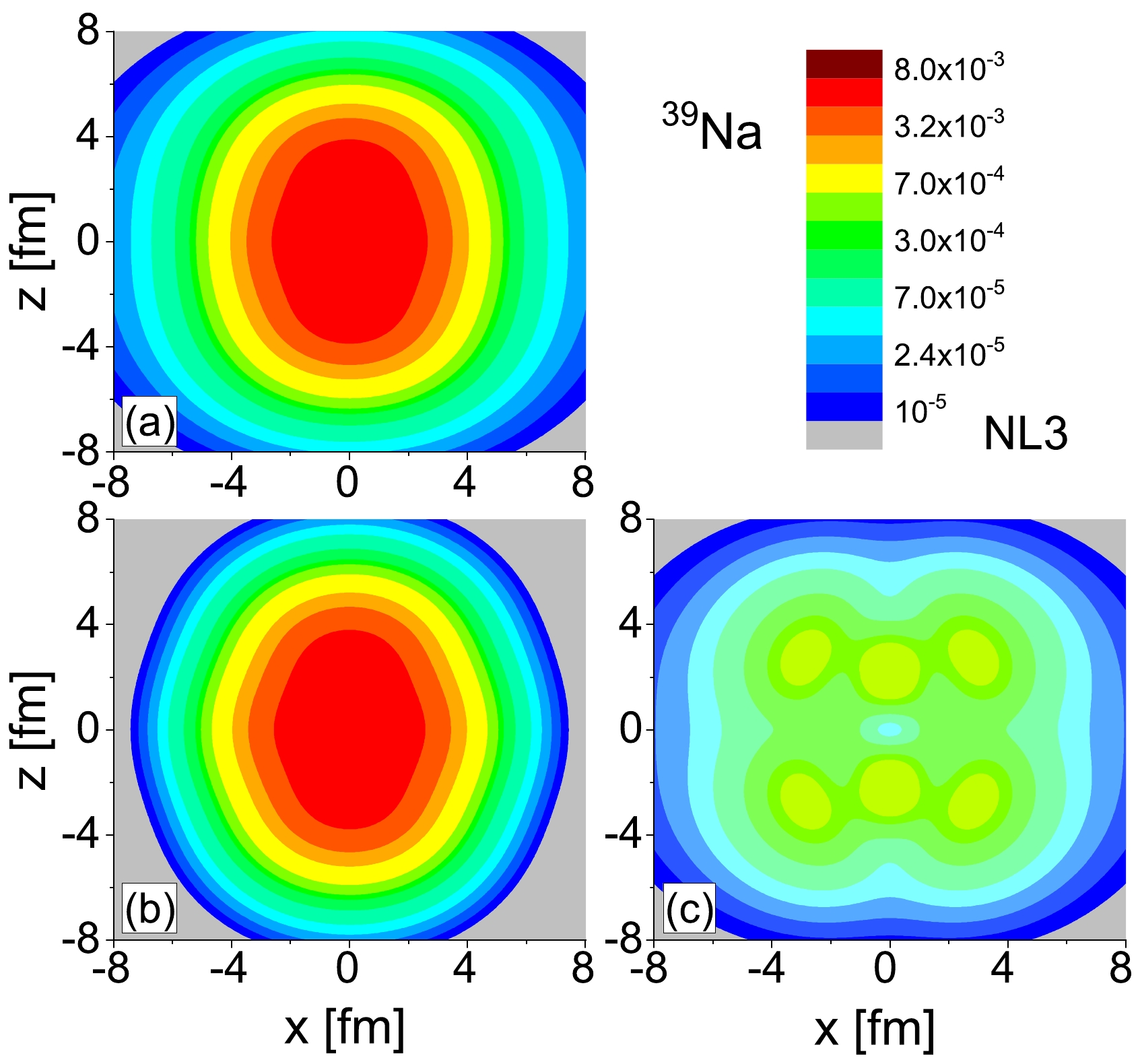
Figure 5. (color online) Matter neutron density distributions for odd-even nuclei 39Na. Subfigure (a) displays the total neutron density distributions. Subfigure (b) displays the density distributions contributed by these neutrons in the deeply bound levels, and (c) displays those in the weakly bound and resonant levels.
To comprehend the impact of different interactions on the ground state properties and unusual structures of sodium isotopes, the neutron density distributions of the core and halo for 39Na are plotted using four different effective interactions in Fig. 6. The single neutron spectrum of 39Na obtained with these four effective interactions reveals a significant gap between the
$ 3/2^{-}_1 $ and$ 1/2^{-}_2 $ orbitals. This gap is utilized to segregate the total neutron density into the halo and core components. The halo component arises from the$ 1/2^{-}_2 $ orbital and those above it, while the$ 3/2^{-}_1 $ orbital and those below it contribute to the core. Figure 6 demonstrates that the density distributions of the core and halo, obtained using four different effective interactions (NL3, NL3*, PK1, and NLSH), exhibit a prolate and oblate shape, respectively. This observation indicates a shape decoupling between the core and halo in 39Na within the framework of DRMF-CMR-BCS calculations using these different effective interactions. Notably, the results of the DRMF-CMR-BCS calculations obtained using the NL3 interaction are similar to those obtained with NL3*, PK1, and NLSH.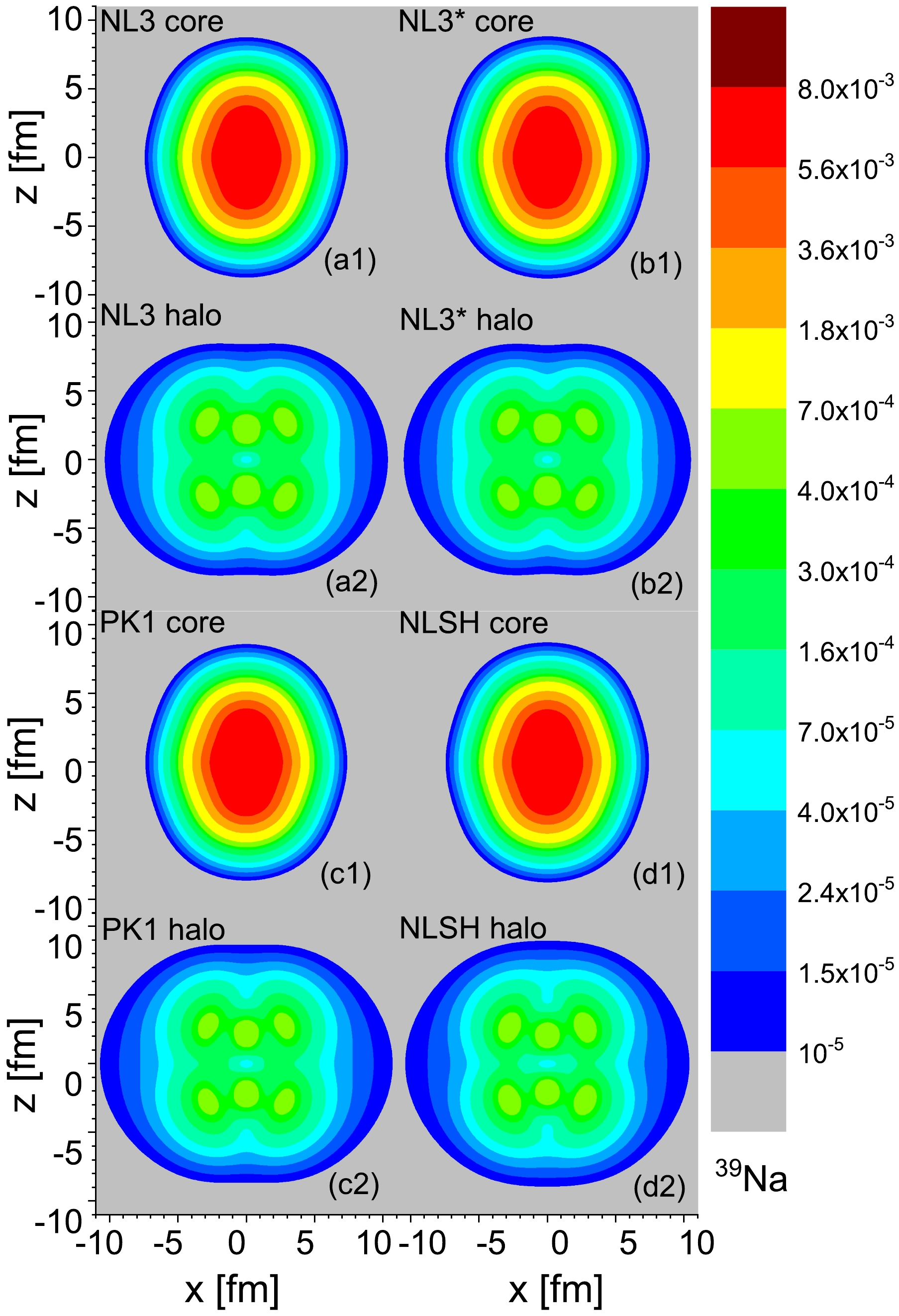
Figure 6. (color online) Neutron density distributions of the core and halo for 39Na based on the DRMF-CMR-BCS calculations obtained with four effective interactions. Subfigures (a1)-(d1) display the density distributions contributed by these neutrons occupying the deeply bound levels, and (a2)-(d2) display those in the weakly bound and resonant levels.
In Fig. 7, the densities of the core and halo for 39Na, calculated with four different effective interactions in the DRMF-CMR-BCS framework, are resolved into spherical, quadrupole, and hexadecapole components. Examining Fig. 7(a2) to Fig. 7(d2) for the four effective interactions (NL3, NL3*, PK1, and NLSH), it is evident that the quadrupole components of the halo consistently exhibit negative values. This correspondence signifies an oblate shape for the halo of 39Na, as illustrated in Fig. 6(a2) to Fig. 6(d2). Conversely, the quadrupole components of the core consistently display positive values in Fig. 7(a1) to Fig. 7(d1), aligning with the prolate shape observed in the density distribution of the core in Fig. 6(a1) to Fig. 6(d1). Additionally, the density distributions of the halo consistently exhibit visible hexadecapole components in Fig. 7(a2) to Fig. 7(d2). These findings collectively indicate to a shape decoupling between the core and the halo in 39Na; notably, this shape decoupling appears to be independent of the specific effective interactions employed.
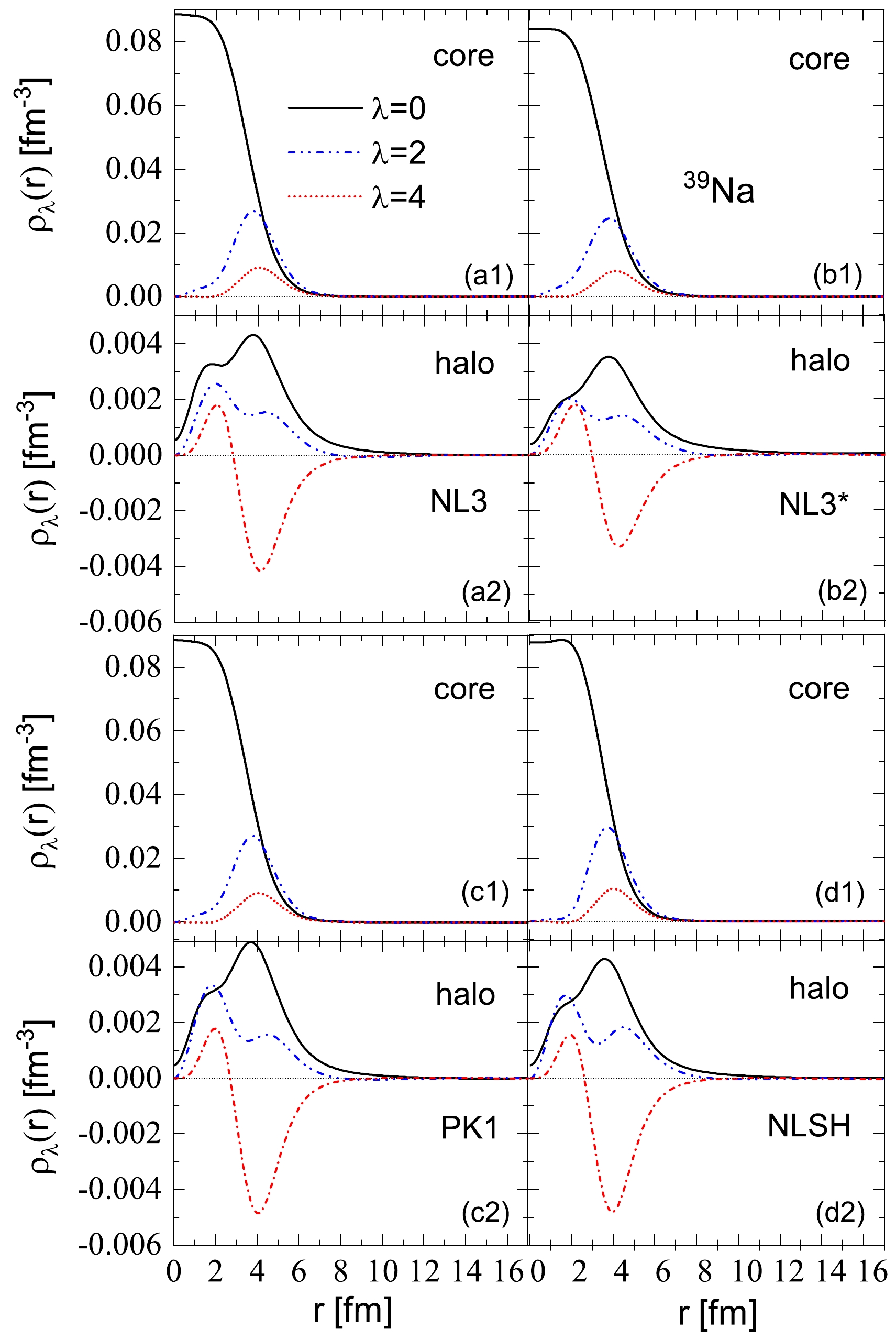
Figure 7. (color online) DRMF-CMR-BCS calculations with four effective interactions: decomposition of the neutron density of 39Na into spherical (
$ \lambda = 0 $ ), quadrupole ($ \lambda = 2 $ ), and hexadecapole ($ \lambda = 4 $ ) components for the core ((a1)-(d1)) and halo ((a2)-(d2)) are marked by the black solid, blue dash-dot, and red short dot lines, respectively.To gain a deeper understanding regarding the influence of resonant states on deformed halo formation, Fig. 8 presents the total neutron density distributions as well as the density distributions of the neutron core and neutron halo for 39Na. Similar to Fig. 5, each panel decomposes the levels into core and halo parts. The neutron halo component comprises weakly bound and resonant levels with energies above
$ 1/2^{-}_2 $ and contributes to the matter density distribution of the neutron halo. In contrast, the neutron core component consists of deeply bound levels with energies below$ 3/2^{-}_1 $ and contributes to the matter density distribution of the neutron core. In each subfigure of Fig. 8, the levels contributing to the neutron core remain consistent, while the levels contributing to the neutron halo vary. This facilitates a detailed examination of the impact of different resonant states on the formation of the neutron halo in 39Na.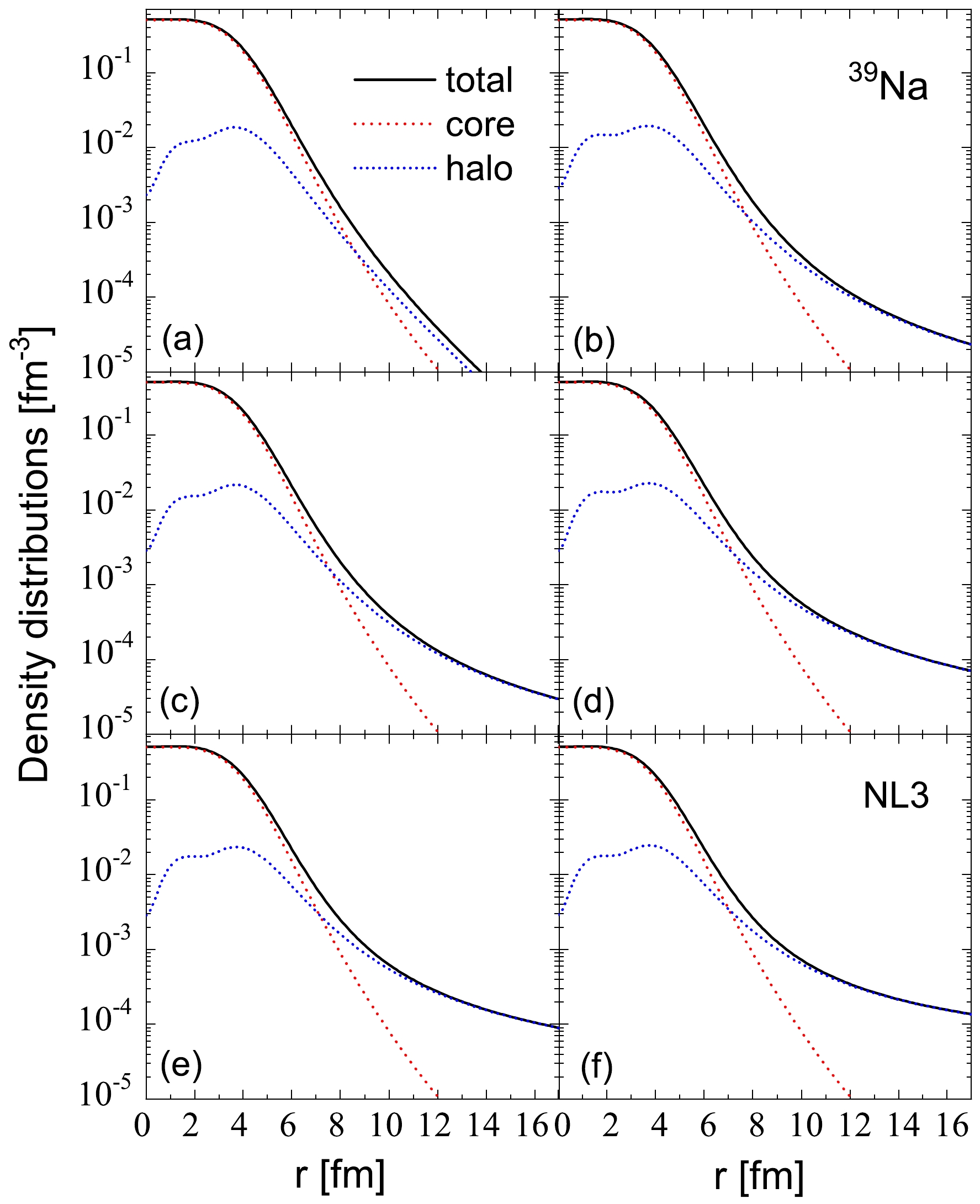
Figure 8. (color online) Total neutron density distributions, density distributions of neutron core, and neutron halo in 39Na, which are marked by the black solid, red dash-dot, and blue short dot lines, respectively. The density distributions of neutron halo in the different subfigures correspond to the different number of resonant levels occupied.
In Fig. 8, the density distribution of the neutron halo is analyzed, with contributions from two weakly bound levels,
$ 1/2^{-}_2 $ and$ 5/2^{-}_1 $ , shown in Fig. 8(a). These density distributions for the weakly bound levels are not highly diffuse, indicating a relatively modest contribution to the halo. The subsequent subfigures sequentially depict the neutron halo density distributions, each incorporating an increasing number of resonant levels. Figure 8(b) includes contributions from weakly bound levels$ 1/2^{-}_2 $ and$ 5/2^{-}_1 $ alongside one resonant level, namely,$ 1/2^{-}_3 $ . Figure 8(c) features contributions from weakly bound levels$ 1/2^{-}_2 $ and$ 5/2^{-}_1 $ alongside two resonant levels, namely,$ 1/2^{-}_3 $ and$ 7/2^{-}_1 $ . Figure 8(d) displays contributions from weakly bound levels$ 1/2^{-}_2 $ and$ 5/2^{-}_1 $ alongside three resonant levels, namely,$ 1/2^{-}_3 $ ,$ 7/2^{-}_1 $ , and$ 3/2^{-}_2 $ . Figure 8(e) depicts contributions from weakly bound levels$ 1/2^{-}_2 $ and$ 5/2^{-}_1 $ alongside four resonant levels, namely,$ 1/2^{-}_3 $ ,$ 7/2^{-}_1 $ ,$ 3/2^{-}_2 $ , and$ 3/2^{-}_3 $ . Figure 8(f) showcases contributions from weakly bound levels$ 1/2^{-}_2 $ and$ 5/2^{-}_1 $ alongside five resonant levels, namely,$ 1/2^{-}_3 $ ,$ 7/2^{-}_1 $ ,$ 3/2^{-}_2 $ ,$ 3/2^{-}_3 $ , and$ 1/2^{-}_4 $ .In Fig. 8(b) to Fig. 8(f), both the total neutron density distributions and density distributions of the neutron halo become progressively more diffuse as the number of resonant levels increases from one to five. This trend suggests that a higher number of occupied resonant levels by valence neutrons further supports the formation of a deformed neutron halo. Particularly noteworthy is the contribution of the resonant levels
$ 1/2^{-}_3 $ or$ 3/2^{-}_2 $ [see Fig. 8, transitioning from (a) to (b) or from (c) to (d)]. In these cases, the total neutron density distributions and density distributions of the neutron halo become significantly diffuse, indicating a substantial contribution to the halo in 39Na from these specific resonant levels. Note that the BCS approximation used to handle pairing correlations has a limitation regarding the convergence of wave functions for resonant states in coordinate space. This limitation is addressed by introducing a cutoff in the tail of the wave functions for resonant states, a method consistent with previous studies such as that reported in Ref. [49]. Importantly, this approach does not significantly impact the calculated results within the current precision.In Fig. 9, the ratios of the neutron density distributions of the weakly bound and resonant orbitals to the total neutron density distributions for 39Na are analyzed. The density distributions of the two weakly bound orbitals, namely,
$ 1/2^{-}_2 $ and$ 5/2^{-}_1 $ , are not highly diffuse, as clearly seen in Fig. 9. While the neutron density distribution of the resonant orbital$ 7/2^{-}_1 $ is relatively diffuse, the dominance of the$ 1f_{7/2} $ shell (99.5%) hinders the formation of halos due to the strong centrifugal barrier of the f component. The neutron density distributions of the two narrow resonant orbitals, namely,$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ , exhibit both high diffusion and relatively high occupation probabilities (0.3506 and 0.3134, respectively). The$ 1/2^{-}_3 $ orbital is distributed almost evenly between the$ 2p_{3/2} $ (53.0%) and$ 2p_{1/2} $ (36.6%) shells, while the$ 3/2^{-}_2 $ orbital is dominated by the$ 2p_{3/2} $ shell (89.8%). This leads to a diffuse matter density distribution. On the other hand, the neutron density distributions of the two narrow orbitals, namely,$ 1/2^{-}_4 $ and$ 3/2^{-}_3 $ , are diffuse, but their occupation probabilities are relatively small (0.1112 and 0.0709, respectively). These orbitals are dominated by the$ 1f_{5/2} $ shell (71.7% and 93.2%, respectively) with a significant mixing with the$ 2p_{1/2} $ shell (about 24.7% in the$ 1/2^{-}_4 $ orbital). Due to their large angular momentum and high centrifugal barrier of the f component, they contribute less to the halo. These observations suggest that 39Na is most likely a neutron halo primarily contributed to by the$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ orbitals. The strong mixing of the$ 2p_{1/2} $ shell with the$ 1f_{5/2} $ shell, correlated with quadrupole deformation, results in a ground state deformation in 39Na. The total proton, neutron, and matter density distributions of 39Na are presented in the bottom panel of Fig. 9, where the total proton density approaches zero for larger values of r. Additionally, the neutron density contributions from the resonant orbitals$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ dominate the long tail of the total density distribution.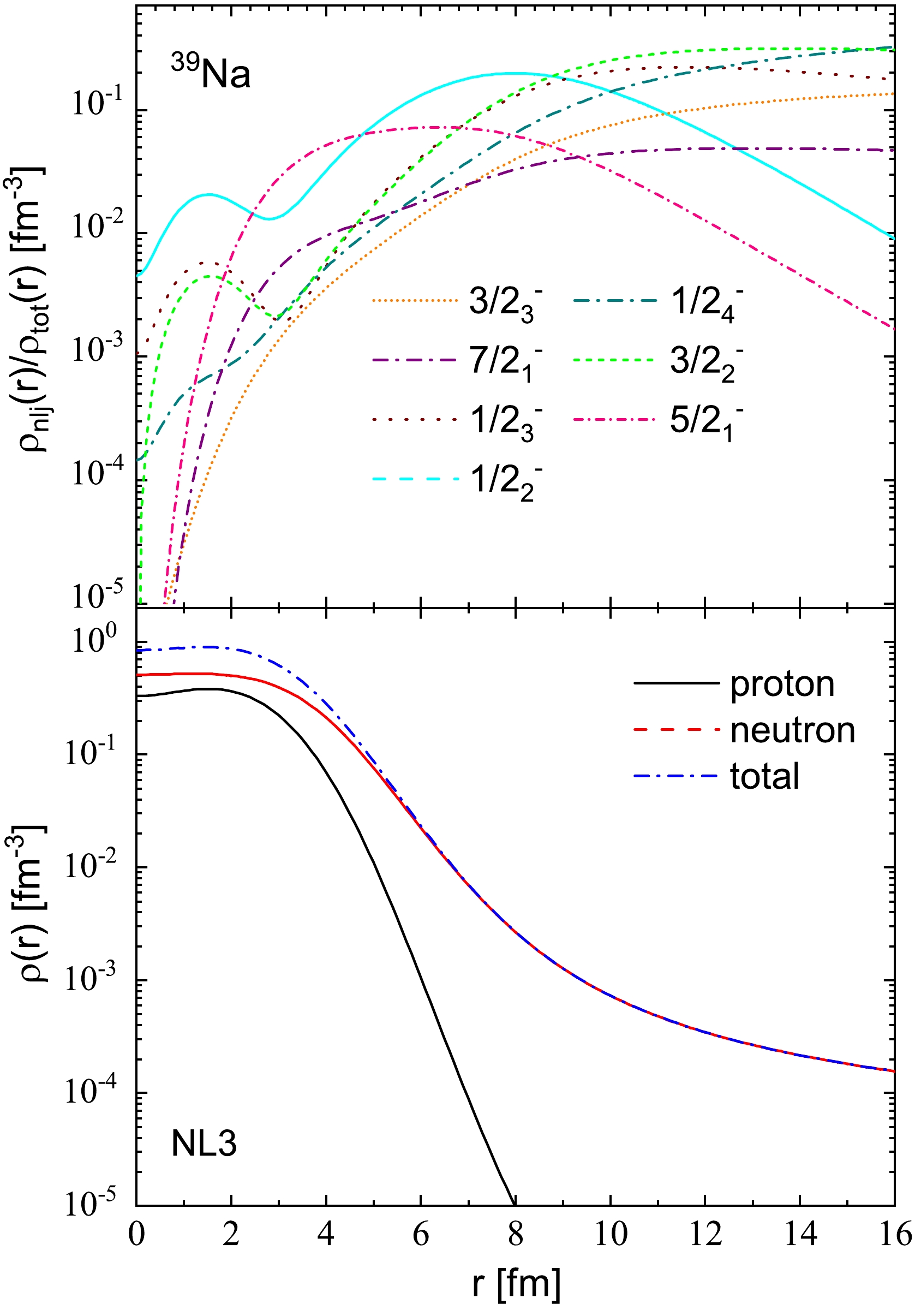
Figure 9. (color online) Ratios of the density distributions of single neutron orbitals to the total density distributions for the weakly bound and resonant levels for 39Na are presented in the top panel. These levels are the same as those in Fig. 2(c). The proton, neutron, and total matter densities are shown in the bottom panel, represented by the black solid, red dot, and blue dashed lines, respectively.
-
In Fig. 10, the neutron density distributions of 41Na, obtained from the DRMF-CMR-BCS calculations with the NL3 effective interaction, are presented. The total neutron densities are decomposed into the core and halo parts, as illustrated in Fig. 10(b) and Fig. 10(c), respectively. Notably, the neutron density of the halo part extends significantly farther than that of the core part, indicating the presence of a neutron halo in 41Na. The distinctive shapes of the halo and core density distributions are evident in Fig. 10, revealing a pronounced oblate shape for the halo and prolate shape for the core. This observation points to a shape decoupling phenomenon in 41Na, where the core and halo exhibit different deformation characteristics.
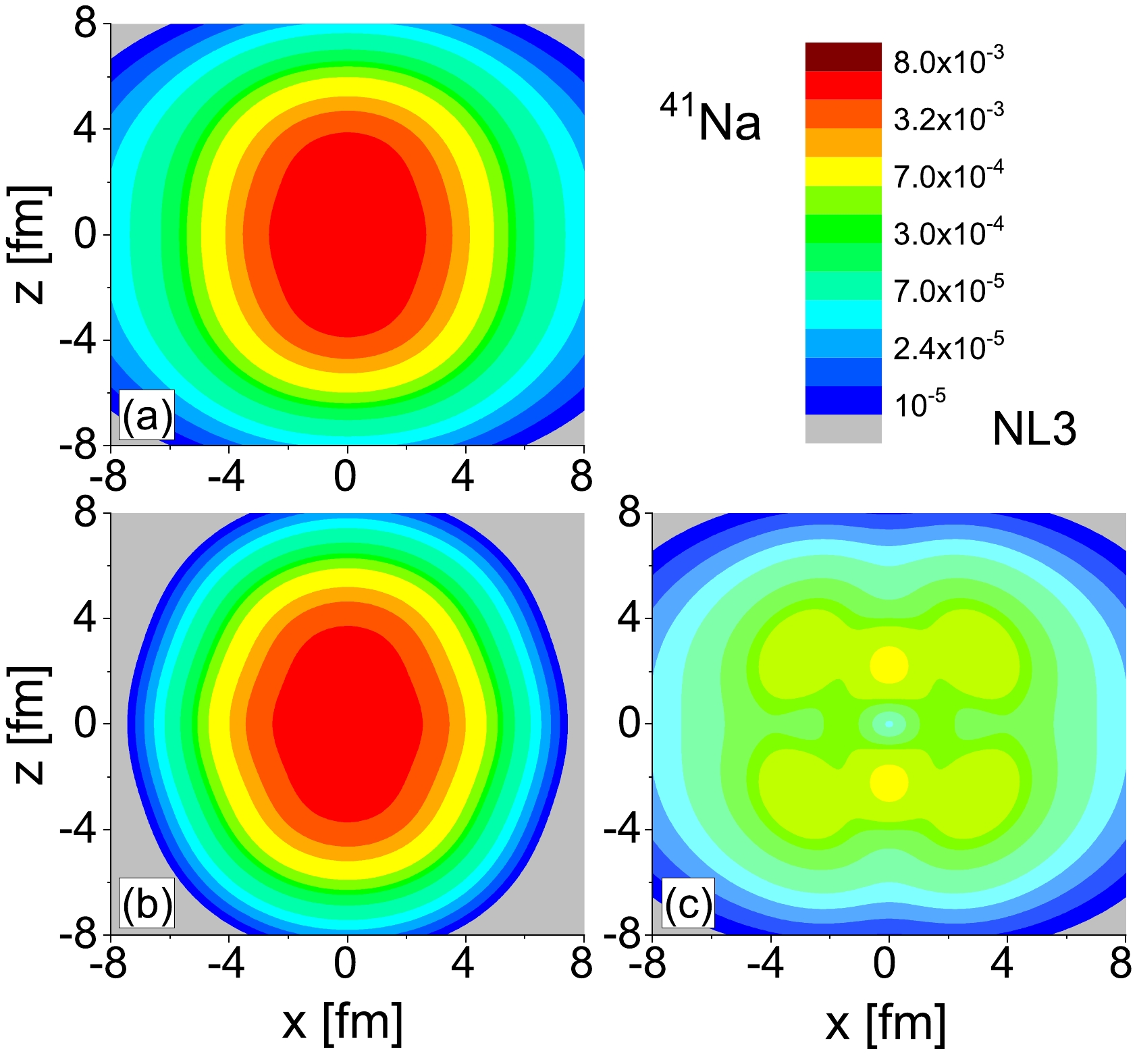
Figure 10. (color online) Matter neutron density distributions for odd-even nuclei 41Na. Subfigure (a) displays the total neutron density distributions. Subfigure (b) displays the density distributions contributed by these neutrons in the deeply bound levels, and (c) displays those in the weakly bound and resonant levels.
The ratios of neutron density distributions for weakly bound and resonant orbitals to the total neutron density distributions in 41Na are depicted in Fig. 11. As shown in Fig. 11, the density distributions of the two weakly bound orbitals, namely,
$ 5/2^{-}_1 $ and$ 1/2^{-}_2 $ , are not diffuse. In contrast, the weakly bound orbitals$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ with a lower angular momentum exhibit diffuse characteristics, and their occupancy probabilities are relatively high (0.5318 and 0.5109, respectively). The orbital$ 1/2^{-}_3 $ is distributed between the$ 2p_{3/2} $ and$ 2p_{1/2} $ shells (50.0% and 39.2%, respectively), while the$ 2p_{3/2} $ shell in the orbital$ 3/2^{-}_2 $ is notably pronounced (92.1%). Therefore, their contributions to the matter density are relatively substantial. The neutron density distribution of the resonant orbital$ 7/2^{-}_1 $ is diffuse, but its contribution to the total density tail is minimal due to its large angular momentum and high centrifugal barrier. The neutron density distribution of the broad resonant orbital$ 3/2^{+}_2 $ , located far from the Fermi surface, is relatively diffuse. However, its occupancy probability is quite small (0.0263), and it is predominantly associated with the$ 1h_{9/2} $ shell (81.9%). The substantial centrifugal barrier of the h component does not favor the formation of halos.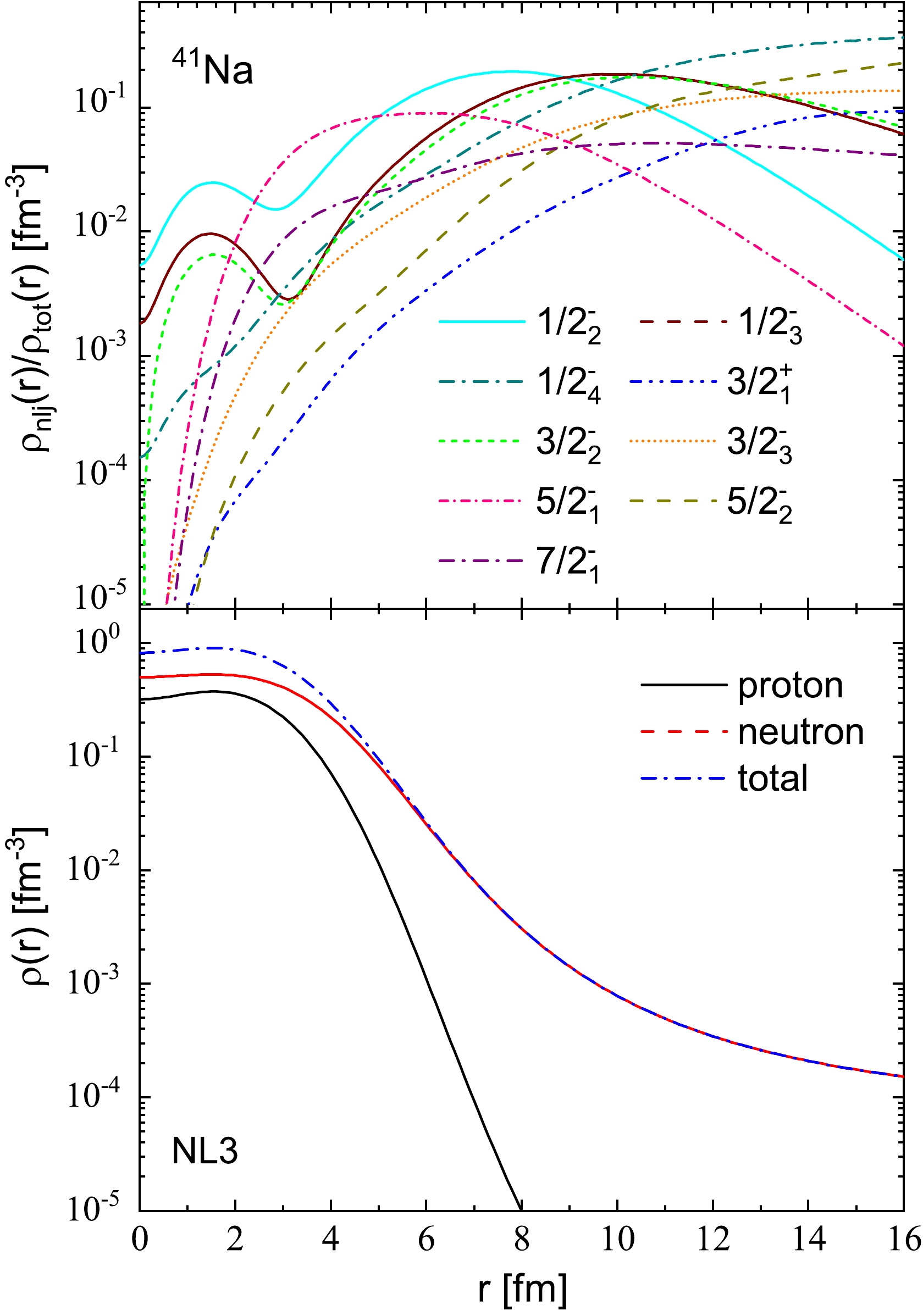
Figure 11. (color online) The ratios of the density distributions of single neutron orbitals to the total density distributions for the weakly bound and resonant levels for 41Na in the top panel. These levels are the same as those presented in Fig. 2(c). The proton, neutron, and total matter densities are shown in the bottom panel, represented by the black solid, red dot, and blue dashed lines, respectively.
While the neutron density distributions of the broad resonant orbital
$ 5/2^{-}_2 $ and narrow orbitals$ 3/2^{-}_3 $ and$ 1/2^{-}_4 $ are highly diffuse, their occupancy probabilities remain small (0.0554, 0.1054, and 0.1693, respectively). All three are predominantly associated with the$ 1f_{5/2} $ shell (95.9%, 93.9%, and 76.5%, respectively), with a mixing of approximately 20.6% in the$ 1/2^{-}_4 $ orbital with the$ 2p_{1/2} $ shell. This composition makes it challenging for them to form halos. Thus, the two weakly bound orbitals, namely,$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ , make significant contributions to the halo formation in 41Na. The substantial mixing of the$ 2p_{1/2} $ shell with the$ 1f_{5/2} $ shell results in the ground state deformation of 41Na. In the bottom panel of Fig. 11, the total proton, neutron, and matter density distributions of 41Na are plotted. Evidently, the total proton density approaches zero as r increases. The occupancy of valence neutrons on the weakly bound orbitals$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ is the primary factor contributing to the extended tail of the total density. -
Figures 12(a), (b), and (c) present the neutron density profiles for the total, core, and halo regions of 43Na, respectively. The considerable extension observed in the neutron density profile of the halo strongly suggests the presence of a neutron halo. Notably, the halo density profile of 43Na exhibits an oblate shape, while the core appears to have a prolate shape.

Figure 12. (color online) Matter neutron density profiles for odd-even nuclei 43Na. Subfigure (a) displays the total neutron density profiles. Subfigure (b) displays the density profiles contributed by these neutrons in the deeply bound levels, and (c) displays those in the weakly bound and resonant levels.
Next, we delve into the analysis of the halo structure in 43Na. Figure 13 illustrates the ratios of the neutron density profiles of weakly bound and resonant orbitals to the total neutron density profiles for 43Na. In Fig. 13, the density profiles of the two weakly bound orbitals, namely,
$ 5/2^{-}_1 $ and$ 1/2^{-}_2 $ , do not exhibit diffusion. Conversely, the weakly bound orbitals$ 3/2^{-}_2 $ and$ 1/2^{-}_3 $ , with lower angular momentum, display diffusion, and their occupation probabilities are substantial (0.7141 and 0.7110, respectively). The$ 2p_{3/2} $ shell in the orbital$ 3/2^{-}_2 $ is particularly significant (88.2%), while the orbital$ 1/2^{-}_3 $ is evenly distributed between the$ 2p_{3/2} $ and$ 2p_{1/2} $ shells (42.8% and 45.3%, respectively). Consequently, their contributions to the formation of the neutron halo are substantial.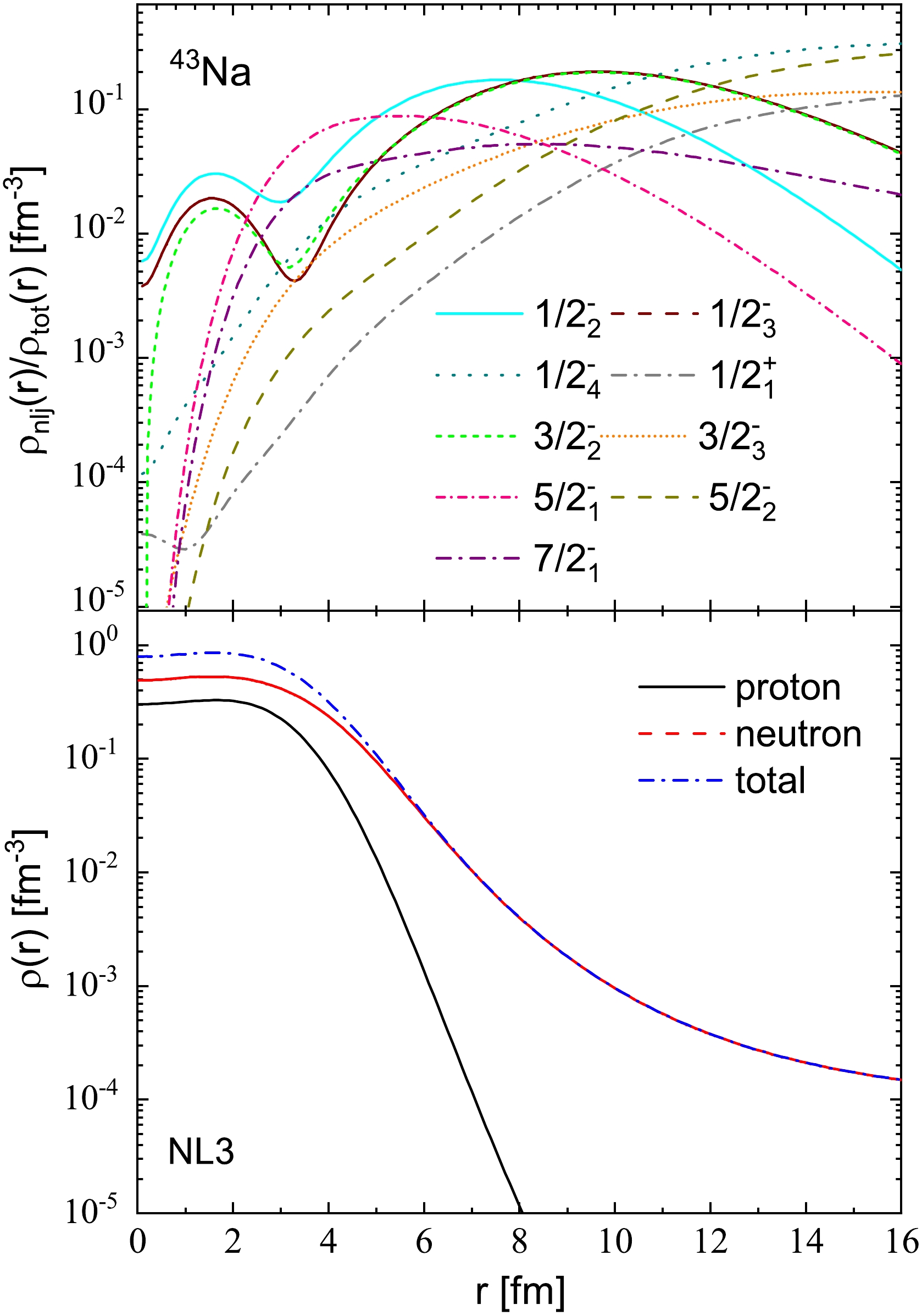
Figure 13. (color online) Ratios of the density profiles of single neutron orbitals to the total density profiles for the weakly bound and resonant levels for 43Na are presented in the top panel. These levels are the same as those depicted in Fig. 2(c). The proton, neutron, and total matter densities are shown in the bottom panel, represented by the black solid, red dot, and blue dashed lines, respectively.
The neutron density profiles of the broad resonant orbital
$ 5/2^{-}_2 $ and narrow orbitals$ 3/2^{-}_3 $ and$ 1/2^{-}_4 $ exhibit diffusion, with small occupation probabilities (0.0807, 0.1660, and 0.2714, respectively). All three are entirely governed by the$ 1f_{5/2} $ shell (96.3%, 95.0%, and 83.3%, respectively). Moreover, the$ 2p_{1/2} $ shell (14.9%) is mixed in the$ 1/2^{-}_4 $ orbital. The significant centrifugal barrier of the f component hinders the formation of a halo. The neutron density profile of the broad resonant orbital$ 1/2^{+}_1 $ , located far from the Fermi surface, is reasonably diffuse, but its occupancy probability is minimal (0.0372), with the largest proportion associated with the$ 1h_{9/2} $ shell (81.8%), making it difficult to form a halo.The neutron density profile of the resonant orbital
$ 7/2^{-}_1 $ is diffuse, yet its substantial angular momentum and high centrifugal barrier do not favor the halo formation. The principal contributors to the halo formation in 43Na are the weakly bound orbitals$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ , which are occupied by valence neutrons. This pattern closely resembles the situations observed in 39Na and 41Na. A significant mixing between the$ 2p_{1/2} $ and$ 1f_{5/2} $ shells induces ground state deformation in 43Na. In the bottom panel of Fig. 13, the total proton, neutron, and matter density profiles of 43Na are presented. The total proton density diminishes towards zero as r increases, and the weakly bound orbitals$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ , occupied by valence neutrons, contribute to the formation of an elongated tail in the total density. Overall, the halo structure of 39Na predominantly originates from the resonant orbitals$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ , while in 41Na and 43Na, the halo structures mainly stem from the weakly bound orbitals$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ . The density distributions of the two orbitals, namely,$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ , in 39Na are more diffuse compared to those in 41,43Na. This observation elucidates why the rms radius of 39Na is slightly larger than those of 41,43Na. -
In summary, our investigation focused on the ground-state properties of neutron-rich sodium isotopes, spanning 35–43Na. We utilized the DRMF-CMR-BCS theory with four effective interactions (NL3, NL3*, PK1, and NLSH) and employed the coupled-channel method to solve the Dirac equation in the complex momentum representation. Our approach provided a reasonably accurate description of several properties of odd-even nuclei 35–43Na, including two-neutron separation energies, quadrupole moments of proton and neutron distributions, as well as the root-mean-square proton and neutron radii. This methodology allowed us to explore the nuanced interplay of continuum and deformation effects on halo structures, particularly considering the influence of the chosen effective interaction and resonant states in our analysis.
Analyzing the single-neutron spectra in odd-even nuclei 35–43Na, depicted on the complex momentum plane, revealed the existence of bound states along the imaginary axis and resonant states separated from the continuum. Focusing on 35–41Na at ground state deformation using the NL3 effective interaction, our analysis demonstrated the collapse of the
$ N = 20 $ and$ N = 28 $ shell closures, indicative of stable prolate deformation. Notably, in 39Na, the collapse of the$ N = 20 $ shell closure was associated with the lowering of the$ 1/2^{-}_{1} $ orbital, contributing to the emergence of a neutron halo.Further investigation into the structure of 39Na identified the shape decoupling between the prolate core and oblate neutron halo, a feature consistent across various effective interactions (NL3, NL3*, PK1, and NLSH). The formation of the neutron halo was influenced by the occupancy of specific resonant states, particularly the
$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ orbitals, resulting in a diffuse matter density distribution. Continuing our exploration regarding the structure of 41Na, we observed a pronounced oblate neutron halo accompanied by a prolate core. The neutron density distributions highlighted a shape decoupling, underscoring the contrasting deformation characteristics of the core and halo. The contributions of weakly bound and resonant orbitals, such as$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ , were crucial in understanding the halo formation in 41Na. Moving forward, we extended our analysis to the case of 43Na, which displayed a distinctive halo structure with an oblate halo and a prolate core. Examining weakly bound and resonant orbitals, we observed diffusion in$ 3/2^{-}_2 $ and$ 1/2^{-}_3 $ , driven by the$ 2p_{3/2} $ shell, contributing significantly to the halo. Broad resonant orbitals, such as$ 5/2^{-}_2 $ , exhibit diffusion but face hindrance due to the centrifugal barrier of the$ 1f_{5/2} $ shell. The key contributors to the halo were the weakly bound orbitals$ 1/2^{-}_3 $ and$ 3/2^{-}_2 $ , echoing patterns seen in 39Na and 41Na. This sheds light on the nuanced interplay between the shell configurations, angular momentum, and nuclear structure in exotic sodium isotopes.In conclusion, our study provides valuable insights into the complex interplay among continuum effects, deformation, and resonant states in shaping the ground-state properties of neutron-rich sodium isotopes. The observed shape decoupling and influence of specific orbitals on halo formation contribute to our understanding of exotic nuclear structures in these isotopes.
Exploration of the ground state properties of neutron-rich sodium isotopes using the deformed relativistic mean field theory in complex momentumrepresentations with BCS pairings
- Received Date: 2023-11-20
- Available Online: 2024-04-15
Abstract: This study explores the ground-state characteristics of neutron-rich sodium isotopes, encompassing two-neutron separation energies, root-mean-square radii, quadrupole moments of proton and neutron distributions, single-particle levels of bound and resonant states, and neutron density distributions and shapes. Simultaneously, special attention is paid to the distinctive physical phenomena associated with these isotopes. The deformed relativistic mean field theory in complex momentum representations with BCS pairings (DRMF-CMR-BCS) employed in our research provides resonant states with real physics, offering insights into deformed halo nuclei. Four effective interactions (NL3, NL3*, PK1, and NLSH) were considered to assess the influence of continuum and deformation effects on halo structures. Calculations for odd-even nuclei 35–43Na revealed the dependence on the chosen effective interaction and number of considered resonant states. Neutron occupation patterns near the Fermi surface, particularly in orbitals





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: