0νββ decay nuclear matrix elements under Left-Right symmetric model from the spherical quasi-particle random phase approximation method with realistic force

As a rare and unobserved process, the neutrinoless double beta ($ 0\nu\beta\beta $) decay attracts attention from communities of nuclear and particle physics. This second-order weak process, with an even-even nucleus decaying to its neighbor with two additional protons and two emitted electrons, has no neutrinos in its products. This differs from the other mode of double beta decay, namely two-neutrino double beta decay, which has been observed for years. The absence of neutrinos in the decay product indicates that this process is a lepton-number-violating ($ \Delta L=2 $) process, and its discovery suggests new physics beyond the particle standard model.

The neutrino is the lightest Fermion ever known in our universe. It is still surrounded by many unsolved puzzles, including the origin of its mass, its mass hierarchy, and whether it is a Dirac or Majorana particle [1]. The $ 0\nu\beta\beta $ decay is key to our understanding of these problems. Accurately calculated nuclear matrix elements (NMEs) are particularly important in the search for $ 0\nu\beta\beta $ decay, as the half-lives of this process depend on its NMEs, which describe the nuclear transition during this process. It is crucial to extract the so-called effective neutrino mass $ |m_{\beta\beta}| $ or other new physics parameters from the measured half-life of $ 0\nu\beta\beta $ depending on the underlying mechanisms, once the process is observed. There are a large number of nuclear calculations with different many-body approaches focusing on the determination of NMEs, for instance, the works from the large-scale shell model (LSSM) [2−4], the quasi-particle random-phase approximation (QRPA) [5−11], the interacting boson model (IBM) [12, 13], and energy-density functional (EDF) theory [14−17]. However, a significant challenge remains: NMEs derived from different nuclear models can differ by as much as a factor of three [18, 19]. A promising avenue for reducing the discrepancy in calculations of NMEs is to develop ab initio methods, which is still a challenging task, especially for heavier nuclei [20].

Most of the above calculations focus on the neutrino mass mechanism, where the only new physics ingredient introduced is the neutrino mass term. These mass terms most probably come from the so-called neutrino see-saw mechanism; they are usually embedded in much more complicated new physics models. One such model, which could naturally incorporate this mechanism, is an extension to the standard model, the Left-Right symmetric model (LRSM). Within the framework of LRSM, besides the usual neutrino mass mechanism, there are more underlying mechanisms for $ 0\nu\beta\beta $-decay from the q part of the neutrino propagator besides the mass part. The q term of the neutrino propagator generally induces the η mechanism associated with the mixing of left- and right-handed gauge bosons and the λ mechanism related to the mass ratio of these two bosons. However, there is also the so-called "Master Formula" [21] derived from effective field theory (EFT) calculations, which claims that with a "complete non-redundant operator basis" consisting of nine independent long-range NMEs and six independent short-range NMEs, everything in $ \beta\beta $-decay can be calculated, including diagrams analogous to λ and η mechanisms [22]. Therefore, with these rapid developments of EFT studies, current calculations, as well as those concerning λ and η mechanisms mentioned later [23−30], which do not follow the "Master Formula", become meaningless and superfluous.

Despite these controversies, we focus our attention on the study of these NMEs. For these extra NMEs of LRSM, there have been fewer studies and inadequate nuclear many-body calculations compared to those of the mass mechanism. The existing limited calculations adopt different many-body approaches, including LSSM [23], QRPA [24−26], and projected Hartree-Fock Bogolyubov (PHFB) [27]. More recently, several new calculations of NMEs relevant to LRSM have been conducted. These include evaluations of the NMEs associated with the mass and λ mechanisms, using LSSM [28, 29] and QRPA [30] approaches, which incorporate higher-order nucleon currents based on the improved formalism from Ref. [31]. It was found that including pseudoscalar contributions enhances qGT matrix elements significantly in Ref. [28, 29]. Additionally, the competition of contributions in the decay rate between the mass and λ mechanisms was also discussed in the QRPA calculations [30] based on relevant calculated NMEs. The MM components in the q terms have often been considered suppressed and hence neglected in previous calculations. However, recent work using the LSSM approach [32] has shown that these MM components are essential for the calculations of relevant LRSM NMEs. Till now, such QRPA calculations that incorporate these MM components in LRSM NMEs are still absent.

Generally speaking, we still lack a thorough investigation of the LRSM NMEs from various calculations, and the calculations for these NMEs are far from abundant. Therefore, in this work, we calculate the NMEs for the LRSM using the pn-QRPA approach, employing a large model space and realistic NN interactions, for all the mechanisms mediated by light neutrinos, the mass, η, and λ mechanisms.

This article is structured as follows: we begin with a brief introduction to the underlying formalism of the LRSM and the formalism of the QRPA method. Next, we present the results of the NMEs and discuss the various contributions of these terms. Furthermore, we will also examine the influence of different SRC parametrizations. Finally, we draw our conclusions.

Ignoring the contribution from heavy neutrinos, the $ 0\nu\beta\beta $ half-life for the LR symmetric model with λ and η mechanisms can be written as [31−33]:

Here, $ m_{\beta\beta}=\sum_j U_{ej}^2 m_j $ is the effective neutrino mass. Parameters such as $ \left< \lambda \right> $ and $ \left< \eta \right> $ are given in [31]: $ \left< \lambda \right>=|\lambda\sum_{j}U_{ej}T_{ej}^* (g_V^\prime /g_V)| $ and $ \left< \eta \right>=|\eta\sum_{j}U_{ej}T_{ej}^*| $. The two phase angles are $ \psi_1 = {\rm{arg}}\left[\left(\sum_j m_j U^2_{ej}\right) \left(\sum_j U_{ej}T_{ej}^* (g_V^\prime /g_V) \right)^* \right] $ and $ \psi_2 ={\rm{arg}}\left[\left(\sum_j m_j U^2_{ej}\right) \left(\sum_j U_{ej}T_{ej}^*\right)^* \right] $. U and T are the constituents of a generalized 6×6 Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix [34]. It is typically assumed that $ g_V \approx g_V^\prime $, leading to $ \psi_1 \approx \psi_2 $.

The explicit forms of coefficients $ C^\prime $s, which are combinations of nuclear matrix elements (NMEs) and phase-space factors (PSFs), can also be found in Ref. [32], with $ G_{01,02,03}={\cal{G}}_{01,02,03} $, $ G_{04,05,06}={\cal{G}}_{04,05,06}/(m_e R) $, and $ G_{07,08,09,10,11}={\cal{G}}_{07,08,09,010,011}/(m_e R)^2 $:

With $ M_{m} $, $ M_{\omega} $, $ M_{q} $, $ M_{R} $, and $ M_{P} $ explicitly included, these NMEs may consist of different parts:

These different parts of the NMEs, $ M_I $, can be written in a general form:

where Is are different parts in eq. (3). $ |0_i^+\rangle $ and $ |0_f^+\rangle $ represent the ground states of the initial and final nuclei. The distance r is defined as $ |{\boldsymbol{r}}_m - {\boldsymbol{r}}_n| $, and $ r_+ $ is given by $ |({\boldsymbol{r}}_m + {\boldsymbol{r}}_n)/2| $, where $ {\boldsymbol{r}}_{m(n)} $ are the coordinates of the two decaying nucleons, labeled as m or n, respectively.

For the mass, q, R, and P terms, the neutrino potentials $ h_I(r, r_+) $ in (4) are expressed in the form:

where $ E_i $ ($ E_f $) is the ground state energy of the initial (final) nucleus, and $ E_m $ is the energy of the intermediate nucleus. In order to account for the characteristics of nuclear force at short distances, which are missing in the nuclear wave functions from many-body calculations, a short-range correlation (SRC) function $ f_{src}(r)=1-ce^{-ar^2}(1-br^2) $ [35, 36] is introduced in the calculations of neutrino potentials (5). In our work, we apply the Argonne V18 and CD-Bonn parametrizations of the SRC, where the parameters a, b, and c in the $ f_{src} $ are taken from Ref. [37]. The effects of SRC on the NMEs will be discussed later. With the inclusion of pseudo-scalar and weak-magnetism terms, as a usual convention, the $ f', s $ functions in the neutrino potentials are given by the following form [32]. For the mass term:

for the q term:

and for the R and P terms:

where $ R=1.2A^{1/3} $ is the nuclear radius, and $ j_{\lambda} $ ($ \lambda=0,1,2,3 $) is the spherical Bessel function of order λ. Considering the effects of finite nucleon size, the vector, axial-vector, weak-magnetism, and induced pseudo-scalar momentum-dependent form factors in the $ f_I $ function are considered:

We take $ g_V=1.0 $ and $ g_A=1.27 $ in this work. $ m_\pi $ and $ m_N $ are the pion and nucleon masses, respectively. The anomalous nucleon magnetic moment is $ \mu_p - \mu_n \approx 3.71 $. The cutoffs are $ \Lambda_V=0.85 $ GeV and $ \Lambda_A=1.086 $ GeV, respectively.

In the above equations, the superscripts for different components such as AA, AP, PP, and MM refer to the contributions from different combinations of products of different components of the axial-vector nuclear current [31].

Note that we change the definition of $ M^{0\nu}_q $, due to the fact that earlier calculations only included the axial-vector induced current, such as Pseudo-Scalar and weak magnetism terms, were neglected. If these terms are included, we find that a factor of 1/3 should be absorbed in the definition of $ M_{qGT}^{AA} $ in the sense that we treat $ M_{q} $ on equal footing as $ M_{m} $ or $ M_{\omega} $. In general, $ M_{qGT}=\frac{1}{3}M_{qGT}^{o} $, $ M_{qF}=M_{qF}^{o} $, and $ M_{qT}=-2M_{qT}^{o} $, where the NME parts with the superscript o refer to those defined in [30, 32, 33]. In the meantime, the corresponding phase space factors are also changed by dividing by a factor of 1/3.

For the neutrino potential $ h_I (r) $ with $ I=\omega F $, $ \omega GT $, and $ \omega T $ in ω terms, the expressions differ slightly from those in (5).

Here, the $ f^{\prime} $ functions of the ω term are:

Meanwhile, the operator $ {\cal{O}}_I $ in the NMEs can be expressed as:

where $ \hat{{\boldsymbol{r}}}={\boldsymbol{r}}/r $ and $ \hat{{\boldsymbol{r}}}_+={\boldsymbol{r}}_+/r_+ $.

To calculate these NMEs, certain many-body approaches are needed. In this work, the spherical proton-neutron quasi-particle random-phase approximation (pn-QRPA) with realistic force is employed. Although the QRPA approach lacks higher-order many-body correlations, it can incorporate a larger model space in the calculations compared to the nuclear shell model. Within the QRPA framework, we choose the BCS vacua as the initial and final ground states of the parent and daughter nucleus, while the virtual states of the intermediate odd-odd nucleus can be expressed as one phonon excitations:

Here, m refers to the index of the intermediate states, and $ A_{pn}^\dagger{(JM)} = {[\alpha_p^\dagger \alpha_n^\dagger]_{JM}} $ is the two-quasi-particle creation operator. The vacuum state $ |0\rangle $ is approximated as the BCS vacuum [5].

The forward X and backward Y amplitudes are obtained by solving the following equations:

These amplitudes are the key inputs for the calculation of NMEs. The ω represents the corresponding energy eigenvalues. The matrices A and B are defined as follows:

where $ J^{\pi} $ denotes the angular momentum and parity of virtual intermediate states. The $ E_p $ and $ E_n $ are the quasi-particle energies of the proton and neutron, respectively. They are obtained from solving the BCS equations [5]. G and F are G-matrix elements derived from the Brückner G-matrix equations.

The parameters $ g_{pp} $'s and $ g_{ph} $ are the renormalized strengths for the two-body residual interaction of the particle-particle and particle-hole channels, respectively. The $ g_{ph} $ is traditionally fixed to reproduce the experimental position of the giant Gamow-Teller resonance (GTGR) strength, and $ g_{ph}=1 $ is used in the current calculation. For the particle-particle channel, there are two kinds of interaction matrix elements: isoscalar (T=0) and isovector (T=1). Following the procedure in the work [8], we employ two parameters $ g_{pp}^{T=0} $ and $ g_{pp}^{T=1} $ to renormalize these two interaction strengths, which should be adjusted independently. These two parameters are typically fixed in the $ 2\nu\beta\beta $ calculations. The isoscalar parameter $ g_{pp}^{T=0} $ is determined by fitting the measured half-life of $ 2\nu\beta\beta $ decay. Meanwhile, the isovector parameter $ g_{pp}^{T=1} $ is adjusted so that the Fermi NME $ M^{2\nu}_F $ vanishes, thereby restoring the isospin symmetry in $ 2\nu\beta\beta $ [8, 38].

With the solutions of the pn-QRPA equations and summing over all the intermediate states, the NMEs of $ 0\nu\beta\beta $ decay can be expressed as:

where $ k_i $ and $ k_f $ label the different pnQRPA solutions corresponding to the initial and final even-even nuclei. The one-body transition densities in $ M_I^{0\nu} $ can be expressed as:

where the BCS occupation and vacancy amplitudes $ v^{(i)}(v^{(f)}) $, $ u^{(i)}(u^{(f)}) $ are derived from the solutions of BCS equations for the initial (final) even-even nucleus. These amplitudes contain important pairing information relevant to this nuclear process. The overlap of the intermediate states between the initial nucleus and the final nucleus can be expressed as:

where $ \langle BCS_f | BCS_i \rangle $ is the overlap factor between the initial and final BCS vacua, which is usually set to unity.

In this work, we calculate $ 0\nu\beta\beta $ NMEs for eight nuclei: ⁷⁶Ge, ⁸²Se, ⁹⁶Zr, ¹⁰⁰Mo, ¹¹⁶Cd, ¹²⁸Te, ¹³⁰Te, and ¹³⁶Xe. The single-particle levels are obtained from a Coulomb-corrected Woods-Saxon potential. We adopt a single-particle model space comprising 8 major oscillator shells (N=0−7). This model space is sufficiently large to incorporate all relevant valence orbitals for the nuclei of interest, and the contribution from higher oscillator shells (N>7) is negligible.

The G-matrix elements obtained from realistic NN potential (CD-Bonn) are employed for the pairing interaction in the BCS method for ground states and residual interaction in the QRPA equation for intermediate states. The BCS model is adopted to account for the residual isovector pairing interactions among nucleons (neutron-neutron and proton-proton). Typically, the strength of the pairing interactions $ g_{pair} $ as an overall factor multiplied by the G-matrix elements is adjusted to reproduce the phenomenological pairing gaps from the five-point formula [39], with the experimental masses taken from Ref. [40]. The residual interaction of the particle-particle channel of the QRPA phonon is divided into two parts, as mentioned above, isoscalar and isovector parts, with corresponding renormalization factors $ g_{pp} $'s. These renormalized parameters are presented in Table 1, where the average value of pairing strength $ \langle g_{pair}\rangle $ is close to $ g_{pp}^{T=1} $ as predicted in [8].

	$ g_{pair,i}^{p} $	$ g_{pair,i}^{n} $	$ g_{pair,f}^{p} $	$ g_{pair,f}^{n} $	$ \left< g_{pair}\right> $	$ g_{pp}^{T=1} $	$ g_{pp}^{T=0} $
76Ge	0.84	0.94	0.87	0.97	0.91	0.92	0.59
82Se	0.78	0.94	0.83	0.99	0.89	0.91	0.60
96Zr	0.81	0.66	0.87	0.82	0.79	0.85	0.63
100Mo	0.89	0.81	0.91	0.83	0.86	0.87	0.63
116Cd	0.87	0.81	0.73	0.77	0.80	0.77	0.66
128Te	0.77	0.87	0.81	0.87	0.83	0.86	0.57
130Te	0.74	0.84	0.80	0.87	0.81	0.87	0.58
136Xe	0.69	0.90	0.77	0.80	0.79	0.83	0.53

Table 1.  The proton and neutron pairing strength $ g_{pair} $ for the initial and final nuclei, as well as their average value $ \langle g_{pair} \rangle $, are considered. The isovector and isoscalar particle-particle parameters $ g_{pp}^{T=1} $ and $ g_{pp}^{T=0} $ pertain to the residual interaction.

In Tables 2 and 3, the $ 0\nu\beta\beta $-decay NMEs for eight nuclei obtained from our pn-QRPA approach are presented. For each nucleus, NMEs without SRC are tabulated, as well as results with the Argonne-V18 (AV18) and CD-Bonn SRC parametrizations consistently obtained from the corresponding nuclear force [37]. In this work, for the sake of comparison with various calculations, the factor $ g_A (0) $ and $ g_V (0) $ are both set to one for each component such as AA, AP, PP, and MM, while the MM components are divided by $ g_A^2 $ ($ g_A=1.27 $) when adding to the total GT and Tensor NMEs.

		76Ge				82Se				96Zr				100Mo
		AV18	CD-Bonn	w/o		AV18	CD-Bonn	w/o		AV18	CD-Bonn	w/o		AV18	CD-Bonn	w/o
$ M_{F} $		−1.482	−1.600	−1.522		−1.360	−1.463	−1.390		−1.033	−1.108	−1.057		−1.952	−2.090	−1.994
$ M_{GT} $	AA	5.567	6.101	5.869		4.853	5.319	5.104		2.426	2.746	2.623		5.087	5.677	5.433
	AP	−2.126	−2.362	−2.342		−1.890	−2.096	−2.075		−1.165	−1.306	−1.299		−2.226	−2.487	−2.468
	PP	0.718	0.811	0.820		0.639	0.721	0.728		0.414	0.469	0.476		0.780	0.884	0.895
	MM	0.819	1.000	1.092		0.725	0.882	0.963		0.479	0.586	0.642		0.897	1.096	1.200
	total	4.667	5.169	5.024		4.051	4.491	4.353		1.971	2.272	2.198		4.197	4.753	4.604
$ M_{T} $	AP	−0.989	−0.986	−0.960		−0.931	−0.928	−0.905		−0.743	−0.742	−0.723		−1.296	−1.293	−1.261
	PP	0.362	0.360	0.349		0.338	0.337	0.327		0.272	0.271	0.263		0.478	0.477	0.462
	MM	−0.239	−0.239	−0.228		−0.221	−0.221	−0.212		−0.178	−0.178	−0.169		−0.311	−0.311	−0.296
	total	−0.775	−0.774	−0.752		−0.730	−0.728	−0.709		−0.582	−0.581	−0.564		−1.011	−1.009	−0.982
$ M_{\omega F} $		−1.458	−1.571	−1.499		−1.333	−1.432	−1.365		−1.001	−1.072	−1.025		−1.877	−2.007	−1.921
$ M_{\omega GT} $	AA	5.494	6.005	5.795		4.835	5.281	5.085		2.645	2.952	2.840		5.268	5.830	5.611
	AP	−2.095	−2.327	−2.309		−1.867	−2.070	−2.050		−1.167	−1.305	−1.299		−2.207	−2.462	−2.446
	PP	0.707	0.799	0.808		0.631	0.711	0.718		0.410	0.465	0.472		0.769	0.871	0.882
	MM	0.805	0.983	1.076		0.714	0.870	0.950		0.473	0.580	0.636		0.883	1.080	1.183
	$ \omega_+ $ total	4.604	5.087	4.961		4.041	4.462	4.342		2.182	2.471	2.407		4.378	4.909	4.781
	$ \omega_- $ total	3.607	3.868	3.627		3.156	3.383	3.164		1.595	1.752	1.619		3.283	3.570	3.315
$ M_{\omega T} $	AP	−0.958	−0.956	−0.931		−0.903	−0.901	−0.878		−0.710	−0.708	−0.689		−1.242	−1.239	−1.208
	PP	0.351	0.350	0.339		0.329	0.328	0.318		0.260	0.260	0.252		0.459	0.458	0.444
	MM	−0.232	−0.232	−0.221		−0.216	−0.215	−0.206		−0.171	−0.171	−0.164		−0.299	−0.299	−0.286
	$ \omega_+ $ total	−0.752	−0.750	−0.729		−0.708	−0.706	−0.688		−0.555	−0.554	−0.538		−0.969	−0.967	−0.941
	$ \omega_- $ total	−0.464	−0.463	−0.455		−0.440	−0.440	−0.432		−0.343	−0.341	−0.336		−0.597	−0.596	−0.587
$ M_{qF} $		−0.944	−0.971	−0.857		−0.886	−0.910	−0.806		−0.704	−0.722	−0.647		−1.355	−1.387	−1.247
$ M_{qGT} $	AA	1.419	1.484	1.325		1.217	1.273	1.130		0.465	0.504	0.415		1.129	1.201	1.030
	AP	2.869	2.992	2.740		2.547	2.654	2.428		1.436	1.510	1.368		2.827	2.964	2.692
	PP	−1.271	−1.329	−1.226		−1.136	−1.186	−1.094		−0.693	−0.728	−0.670		−1.330	−1.395	−1.284
	MM	−2.172	−2.362	−2.256		−1.932	−2.098	−2.001		−1.247	−1.360	−1.301		−2.361	−2.571	−2.456
	$ q_+ $ total	4.364	4.611	4.237		3.826	4.042	3.705		1.981	2.130	1.919		4.091	4.365	3.961
	$ q_- $ total	1.671	1.682	1.440		1.431	1.440	1.223		0.435	0.443	0.306		1.163	1.176	0.915
$ M_{qT} $	AA	3.510	3.504	3.414		3.306	3.300	3.219		2.590	2.585	2.520		4.393	4.385	4.273
	AP	−1.873	−1.869	−1.799		−1.746	−1.743	−1.680		−1.394	−1.390	−1.340		−2.448	−2.443	−2.355
	PP	0.561	0.560	0.532		0.517	0.515	0.490		0.414	0.413	0.393		0.726	0.724	0.689
	MM	0.214	0.215	0.200		0.194	0.196	0.179		0.156	0.156	0.142		0.266	0.268	0.247
	$ q_+ $ total	2.065	2.062	2.022		1.956	1.951	1.919		1.513	1.511	1.485		2.506	2.499	2.453
	$ q_- $ total	2.331	2.328	2.271		2.196	2.194	2.140		1.707	1.705	1.662		2.836	2.831	2.760
	RGT	8.873	11.240	12.756		8.045	10.165	11.510		5.632	7.151	8.137		10.679	13.536	15.376
	RT	−2.783	−2.780	−2.646		−2.641	−2.638	−2.514		−2.239	−2.237	−2.131		−3.950	−3.947	−3.762
	P	−0.672	−0.682	−0.630		−0.635	−0.643	−0.598		−0.153	−0.155	−0.149		0.354	0.360	0.329

Table 2.  $ 0\nu\beta\beta $-decay NMEs for ⁷⁶Ge, ⁸²Se, ⁹⁶Zr, and ¹⁰⁰Mo from pn-QRPA calculations. The results are obtained in the model spaces (N=0-7). For each nucleus, there are three kinds of NMEs presented in the table, which are only different in the SRC. Here, AV18 (CD-Bonn) represents the results calculated with the Argonne (Charge-dependent Bonn) type SRC parametrizations, and w/o denotes the results without SRC.

		116Cd				128Te				130Te				136Xe
		AV18	CD-Bonn	w/o		AV18	CD-Bonn	w/o		AV18	CD-Bonn	w/o		AV18	CD-Bonn	w/o
$ M_{F} $		−1.354	−1.427	−1.361		−1.532	−1.651	−1.568		−1.304	−1.408	−1.336		−0.629	−0.681	−0.642
$ M_{GT} $	AA	3.485	3.773	3.612		5.169	5.712	5.464		4.318	4.790	4.575		2.450	2.697	2.571
	AP	−1.280	−1.408	−1.387		−2.125	−2.365	−2.341		−1.827	−2.035	−2.015		−1.020	−1.130	−1.115
	PP	0.425	0.476	0.477		0.736	0.832	0.839		0.639	0.721	0.729		0.353	0.397	0.399
	MM	0.470	0.569	0.616		0.839	1.023	1.116		0.729	0.889	0.970		0.396	0.480	0.522
	total	2.921	3.193	3.085		4.300	4.813	4.654		3.581	4.028	3.890		2.028	2.261	2.179
$ M_{T} $	AP	−0.528	−0.527	−0.514		−1.309	−1.306	−1.277		−1.180	−1.177	−1.151		−0.586	−0.584	−0.572
	PP	0.195	0.194	0.189		0.464	0.463	0.450		0.418	0.417	0.406		0.206	0.205	0.200
	MM	−0.125	−0.125	−0.120		−0.293	−0.293	−0.281		−0.264	−0.264	−0.253		−0.129	−0.129	−0.124
	total	−0.410	−0.410	−0.400		−1.026	−1.025	−1.001		−0.925	−0.924	−0.902		−0.460	−0.459	−0.449
$ M_{\omega F} $		−1.261	−1.329	−1.271		−1.521	−1.635	−1.559		−1.305	−1.404	−1.338		−0.625	−0.674	−0.640
$ M_{\omega GT} $	AA	3.384	3.659	3.515		5.211	5.732	5.506		4.394	4.849	4.652		2.431	2.667	2.555
	AP	−1.246	−1.371	−1.352		−2.103	−2.338	−2.316		−1.813	−2.018	−1.999		−0.996	−1.104	−1.090
	PP	0.414	0.464	0.466		0.726	0.820	0.828		0.631	0.713	0.720		0.344	0.387	0.390
	MM	0.458	0.555	0.603		0.827	1.007	1.100		0.720	0.877	0.958		0.386	0.468	0.510
	$ \omega_+ $ total	2.836	3.097	3.004		4.347	4.838	4.700		3.658	4.087	3.966		2.018	2.240	2.170
	$ \omega_- $ total	2.268	2.408	2.256		3.322	3.589	3.336		2.766	3.000	2.779		1.540	1.660	1.538
$ M_{\omega T} $	AP	−0.521	−0.520	−0.507		−1.257	−1.254	−1.226		−1.133	−1.130	−1.105		−0.563	−0.561	−0.549
	PP	0.192	0.191	0.186		0.447	0.446	0.434		0.403	0.402	0.391		0.199	0.198	0.193
	MM	−0.123	−0.123	−0.118		−0.284	−0.283	−0.271		−0.256	−0.256	−0.244		−0.126	−0.125	−0.120
	$ \omega_+ $ total	−0.406	−0.405	−0.394		−0.985	−0.983	−0.960		−0.888	−0.887	−0.865		−0.442	−0.440	−0.431
	$ \omega_- $ total	−0.252	−0.252	−0.248		−0.633	−0.632	−0.623		−0.571	−0.569	−0.563		−0.286	−0.285	−0.282
$ M_{qF} $		−1.051	−1.068	−0.978		−0.968	−0.996	−0.878		−0.808	−0.832	−0.730		−0.373	−0.385	−0.330
$ M_{qGT} $	AA	0.934	0.968	0.870		1.237	1.302	1.138		1.003	1.060	0.917		0.602	0.631	0.551
	AP	1.804	1.870	1.714		2.761	2.885	2.624		2.334	2.442	2.216		1.352	1.409	1.281
	PP	−0.786	−0.817	−0.754		−1.274	−1.333	−1.226		−1.093	−1.144	−1.052		−0.624	−0.651	−0.599
	MM	−1.285	−1.389	−1.320		−2.229	−2.422	−2.311		−1.932	−2.100	−2.003		−1.069	−1.158	−1.103
	$ q_+ $ total	2.749	2.881	2.649		4.106	4.357	3.968		3.441	3.659	3.323		1.992	2.107	1.916
	$ q_- $ total	1.155	1.159	1.011		1.342	1.353	1.103		1.046	1.055	0.839		0.667	0.671	0.549
$ M_{qT} $	AA	1.780	1.777	1.732		4.696	4.687	4.589		4.223	4.217	4.128		2.129	2.126	2.083
	AP	−1.010	−1.008	−0.973		−2.346	−2.342	−2.265		−2.114	−2.110	−2.041		−1.038	−1.035	−1.003
	PP	0.296	0.296	0.282		0.658	0.657	0.626		0.592	0.590	0.563		0.287	0.288	0.274
	MM	0.111	0.110	0.100		0.236	0.239	0.218		0.213	0.213	0.193		0.103	0.104	0.096
	$ q_+ $ total	0.998	0.997	0.978		2.862	2.855	2.815		2.569	2.564	2.530		1.315	1.314	1.294
	$ q_- $ total	1.136	1.133	1.103		3.154	3.151	3.085		2.834	2.829	2.770		1.443	1.442	1.413
	RGT	5.816	7.303	8.218		10.822	13.675	15.488		9.459	11.953	13.537		5.183	6.526	7.364
	RT	−1.671	−1.669	−1.593		−4.028	−4.024	−3.848		−3.643	−3.640	−3.481		−1.809	−1.807	−1.730
	P	0.307	0.313	0.287		−0.420	−0.427	−0.391		−0.335	−0.341	−0.311		−0.385	−0.390	−0.363

Table 3.  The same as in Tables 2, but for ¹¹⁶Cd, ¹²⁸Te, ¹³⁰Te, and ¹³⁶Xe.

As in most calculations, in the light neutrino mass mechanism, the GT parts dominate the NMEs, with the largest contribution coming from the AA components. $ M_{F} $ contributes about 1/3 from the naive analysis with Fierz rearrangement, and the reduction from $ M_{T} $ is about 10-20% as in most QRPA calculations. Different behaviors for these two parts are observed in most Shell Model calculations [23], where smaller $ M_F $ and negligible $ M_T $ are observed.

A lot of QRPA calculations have been done for the light neutrino mass mechanism, either from the QRPA with realistic forces [8, 9] or with the so-called self-consistent calculations based on the Skyrme density functional [11]. Our results are close to those from the realistic force since we are using the same residual interactions, while these results are generally smaller than that of Skyrme DFT; the reason for this still needs to be investigated through comparative studies.

While the NME differs for different many-body approaches, for different nuclei, the NME also varies. Their difference could be as large as a factor of two. Our calculations show that ⁷⁶Ge has the largest NME, almost twice as large as the smallest one from ¹³⁶Xe.

Concerning the ω terms, their differences from the mass terms arise only from the energy denominator (eq.(10)), and since $ M^{0\nu} $ is less sensitive to the intermediate states' excitation energies than the NME for $ 2\nu\beta\beta $-decay. As a result, $ M_{\omega F} $, $ M_{\omega GT} $, and $ M_{\omega T} $ are quite close to the corresponding terms of the mass terms. The difference for the GT part is less than 10% and for the Fermi part is less than 7%, etc.

As observed in LSSM calculations [32], the q term behaves quite differently from the mass term, as different components contribute differently. In fact, as stated above, we absorb the factor 1/3 into the definition of $ M_{qGT} $, in this sense that the q term can be written in a uniform form as sums of the Fermi, GT, and Tensor parts like that for the mass and ω terms. The Fermi NME is reduced by 20-50% compared to its counterpart in the mass term. Meanwhile, for the GT part, the AA components in q terms are largely hindered by a factor of 1/3 as explained above. Unlike the mass term, now AP components are the dominant ingredients for the GT part, about twice as large in magnitude as other components. In this sense, earlier calculations [24] with contributions only from AA components may give an incomplete estimation over the NMEs for the qGT part. The MM component from induced weak magnetic current, which emerges as a subleading order contribution according to Naive Dimension Analysis (NDA) from Chiral effective field theory, is expected to be suppressed. However, as first discovered in LSSM calculations, it appears as a leading order contribution with a similar magnitude as the AA or AP components; the reason for such enhancement is discussed in [32]. Its contribution to the total NME depends on the type of nuclear current, since there is a sign difference of weak-magnetism current for V-A and V+A currents. So the MM component comes out as an enhancement to cancel the contribution from the PP component or as a cancellation to cancel the contribution from the AA component. In general, compared to counterparts in the mass term, all components besides the AA component are getting enhanced in magnitude due to contributions from higher exchange momenta.

However, the most significant difference between the q term and the mass term is from the tensor part. For the mass term, the tensor part comes out as a sub-leading order contribution with roughly 10% corrections to the GT part. But for the q term, the qT part could be as important as qGT in QRPA calculations, as was already observed in [24], and now our calculation confirms this with more components included. For the qT part, the AA component dominates the NME, while the AP component gives a reduction of about 50% to that of AA. The PP and MM components are smaller; they give a correction of about 10%. The overall contributions of qT could be as important as qGT.

We also find that the mass term and the q term are weakly correlated, given that their ratios are nearly nucleus-independent, although for different nuclei their individual values are quite different.

For the R term, $ M_{RGT} $ is larger than other parts such as $ M_{GT} $ and $ M_{qGT} $ for each nucleus and has the largest value in all LRSM NMEs. The large values of the $ M_{RGT} $ were also reported in previous QRPA calculations [24] and LSSM calculations [32]. The same situation occurs with the RT parts, which also have magnitudes significantly larger than the corresponding parts of the mass and ω terms.

Finally, for the $ M_{P} $ term, it can be found that they are the smallest terms in magnitude for all LRSM NMEs, and their contributions to the decay rates should be negligible. This suppresses the p-wave effect [33] and makes the R term dominate the η mechanism [32]. The results from the current calculation and previous LSSM calculation suggest that we can safely neglect this term and simplify the expression in eq.(2) if limited accuracy is required.

In the final part, we focus our discussion on the effects of the SRC on the NMEs. As stated above, the SRC originates from the strong repulsive core of the nuclear force, which alters the short-range behaviors of various operators such as the two-body operator for $ 0\nu\beta\beta $-decay. To understand its effect on NMEs besides the absolute values of NMEs with or without SRCs presented in Table 2, 3, we give explicitly the ratios of NME with different SRC parametrizations to that without any SRC in Table 4.

		76Ge	82Se	96Zr	100Mo	116Cd	128Te	130Te	136Xe
F	AV18	0.97	0.98	0.98	0.98	0.99	0.98	0.98	0.98
	CD-Bonn	1.05	1.05	1.05	1.05	1.05	1.05	1.05	1.06
GT	AV18	0.93	0.93	0.90	0.91	0.95	0.92	0.92	0.93
	CD-Bonn	1.03	1.03	1.03	1.03	1.04	1.03	1.04	1.04
T	AV18	1.03	1.03	1.03	1.03	1.03	1.03	1.03	1.03
	CD-Bonn	1.03	1.03	1.03	1.03	1.02	1.02	1.02	1.02
$ \omega F $	AV18	0.97	0.98	0.98	0.98	0.99	0.98	0.98	0.98
	CD-Bonn	1.05	1.05	1.05	1.04	1.05	1.05	1.05	1.05
$ \omega GT_+ $	AV18	0.93	0.93	0.91	0.92	0.94	0.92	0.92	0.93
	CD-Bonn	1.03	1.03	1.03	1.03	1.03	1.03	1.03	1.03
$ \omega T_+ $	AV18	1.03	1.03	1.03	1.03	1.03	1.03	1.03	1.03
	CD-Bonn	1.03	1.03	1.03	1.03	1.03	1.02	1.02	1.02
$ \omega GT_- $	AV18	0.99	1.00	0.99	0.99	1.01	1.00	1.00	1.00
	CD-Bonn	1.07	1.07	1.08	1.08	1.07	1.08	1.08	1.08
$ \omega T_- $	AV18	1.02	1.02	1.02	1.02	1.02	1.02	1.02	1.02
	CD-Bonn	1.02	1.02	1.02	1.02	1.02	1.01	1.01	1.01
qF	AV18	1.10	1.10	1.09	1.09	1.07	1.10	1.11	1.13
	CD-Bonn	1.13	1.13	1.12	1.11	1.09	1.13	1.14	1.17
$ qGT_+ $	AV18	1.03	1.03	1.03	1.03	1.04	1.03	1.04	1.04
	CD-Bonn	1.09	1.09	1.11	1.10	1.09	1.10	1.10	1.10
$ qT_+ $	AV18	1.02	1.02	1.02	1.02	1.02	1.02	1.02	1.02
	CD-Bonn	1.02	1.02	1.02	1.02	1.02	1.01	1.01	1.02
$ qGT_- $	AV18	1.16	1.17	1.42	1.27	1.14	1.22	1.25	1.21
	CD-Bonn	1.17	1.18	1.45	1.29	1.15	1.23	1.26	1.22
$ qT_- $	AV18	1.03	1.03	1.03	1.03	1.03	1.02	1.02	1.02
	CD-Bonn	1.03	1.03	1.03	1.03	1.03	1.02	1.02	1.02
RGT	AV18	0.70	0.70	0.69	0.69	0.71	0.70	0.70	0.70
	CD-Bonn	0.88	0.88	0.88	0.88	0.89	0.88	0.88	0.89
RT	AV18	1.05	1.05	1.05	1.05	1.05	1.05	1.05	1.05
	CD-Bonn	1.05	1.05	1.05	1.05	1.05	1.05	1.05	1.04
P	AV18	1.07	1.06	1.03	1.08	1.07	1.07	1.08	1.06
	CD-Bonn	1.08	1.07	1.03	1.09	1.09	1.09	1.10	1.07

Table 4.  The ratios between matrix elements with and without SRC.

Let's first focus on the mass term. For $ M_{GT} $, the AV18 SRC reduces the NME by about 4%-9% in magnitude, while the CD-Bonn SRC enhances the NME by about 4%. The deviation between these two SRCs is about 10%, which agrees with other calculations [37]. For $ M_{F} $, the deviation due to the different SRCs is around 5%-8%, which is a little less than the variations observed in $ M_{GT} $. For $ M_{T} $, the uncertainties arising from various SRC parametrizations range from 1% to 3%, indicating that the effect of SRC on $ M_T $ is negligible. Similar behaviors are observed for the ω term, as it is essentially the same as the mass term. An enhancement of the q-term is observed for both SRC parametrizations; the magnitudes are generally around 10% for the Fermi and GT parts, but there are exceptions for the $ qGT- $ part for certain nuclei, where this enhancement could go as high as 40%. This is mostly caused by cancellations among different components. On the other hand, the important tensor part from the q term seems not affected by the SRC, and the inclusion of SRC changes the NME by only a few percent. The same applies to the P term; the general effects of SRC are below 10%.

Finally, we consider the effect of SRC on the R term. While the effect of SRC on the tensor part is smaller (around 5%), a drastic reduction is observed for the RGT part, especially for the Argonne SRC. The effects of SRC on RGT have similar but milder effects as the case of the heavy neutrino mass mechanism in various literature [8, 10]. While the CD-Bonn SRC leads to a reduction of about 10%, the Argonne SRC has much wilder effects, with a reduction of about 30% observed in our calculations, and it seems that such reduction is nucleus-independent.

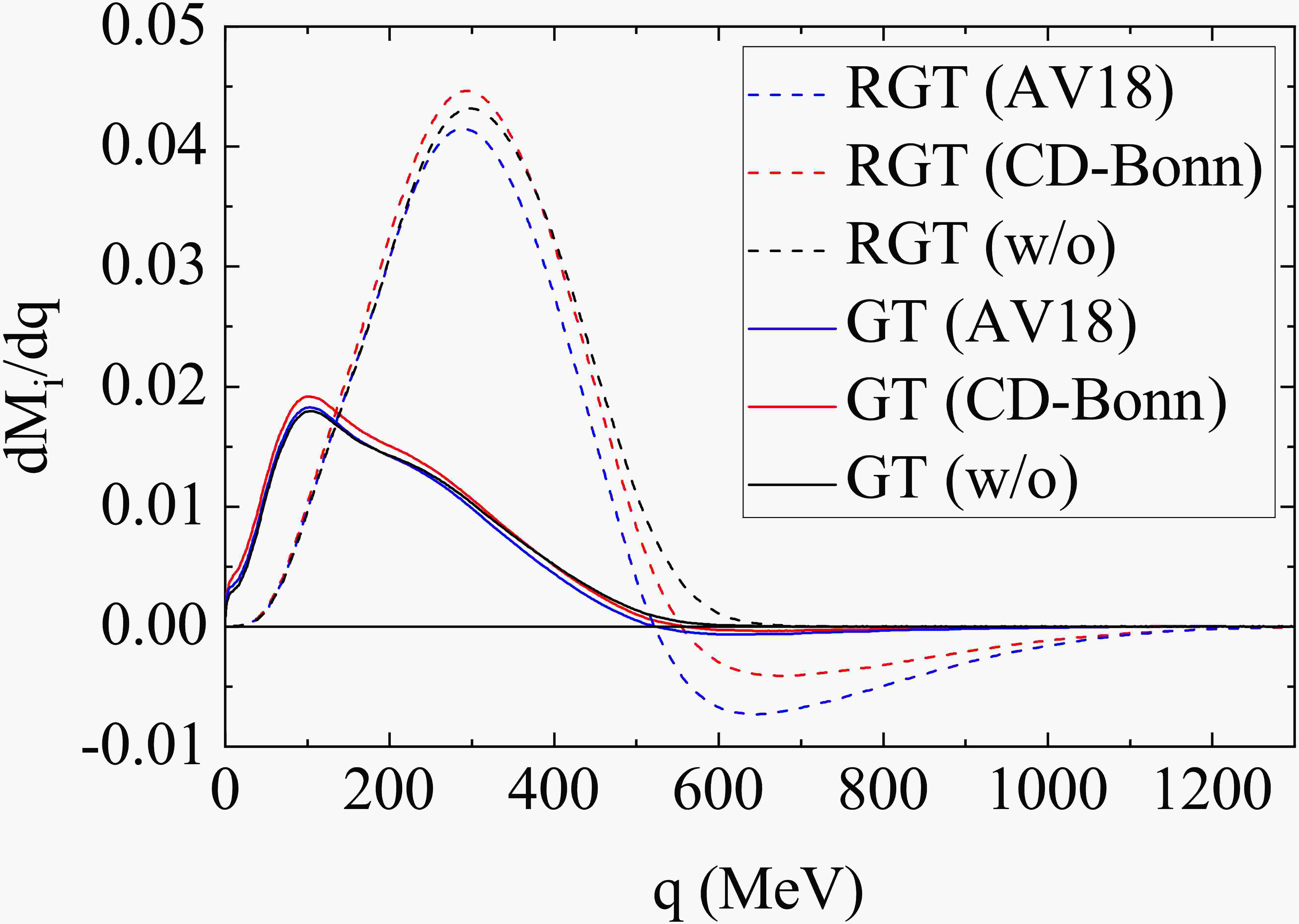
To understand the origin of this large reduction of SRC on the RGT part, we present the transfer momentum distributions of the matrix elements $ M_{RGT} $ and $ M_{GT} $ in Fig. 1, by comparing the results with or without SRC. One can clearly see that for $ M_{GT} $, the largest contribution comes from the momentum around 100 MeV ($ m_\pi $), whereas for $ M_{RGT} $, the major contribution is dominated by the region where momentum is around 300 MeV. This is mainly due to an additional $ q^2 $ multiplied by the spherical Bessel function $ j_0 (qr) $ in the integrand (8), which enhances the contribution from higher transfer momentum. This implies the importance of short-range contributions for this part of NME, which is why the SRC, which alters the short-range behavior of various operators, plays an important role here. As shown in Fig. 1, there is a notable difference in the results with or without SRC in the region where q > 600 MeV for $ M_{RGT} $. When the SRC is not included, we see no contribution to $ M_{RGT} $ from these high momenta, similar to what is seen for the GT part in the mass mechanism. But if the SRC is included, the behavior for $ M_{GT} $ and $ M_{RGT} $ differs greatly; a strong cancellation appears in this high momentum region for the latter. Meanwhile, a cancellation is barely observed for $ M_{GT} $. Therefore, from Fig. 1, we find that the reduction from SRC for $ M_{RGT} $ mainly comes from a drastic distortion of the transition strength distributions as a function of exchange momentum. The magnitude of the changes from the two SRC's differs by about 20 percent. Compared to the CD-Bonn SRC, the AV18 SRC reduces the strength at the low q peak and enhances the high q reduction. While for the CD-Bonn SRC, the reduction at high q overwhelms the enhancement at low q, contrary to the case of $ M_{GT} $. This emphasizes the importance of correctly describing the short-range behaviors of the nuclear force.

Figure 1.  (Color online) The GT and RGT parts of NMEs for ⁷⁶Ge as functions of momentum transfer q. 'AV18' ('CD-Bonn') represents the results obtained with Argonne (CD-Bonn) SRC parametrization, and 'w/o' represents the results without SRC included.

In this work, the nuclear matrix elements of $ 0\nu\beta\beta $ under the LR symmetric model are calculated using the QRPA approach for eight nuclei: ⁷⁶Ge, ⁸²Se, ⁹⁶Zr, ¹⁰⁰Mo, ¹¹⁶Cd, ¹²⁸Te, ¹³⁰Te, and ¹³⁶Xe. The weak-magnetism components of the nucleon current are incorporated for NME calculations. We find that these components in the q term play an important role, although they are usually considered to be suppressed. This conclusion is consistent with the previous LSSM calculation [32]. The R term becomes the largest term for all LR symmetric model NMEs; hence, its contribution to decay rates is also important. Furthermore, we discuss the effect of different SRC parametrizations on the NME. We find that certain parts of the NME (e.g., $ M_{RGT} $) are more sensitive to the SRC than others due to a large reduction from the high exchange momentum region.

We also want to thank the anonymous referee for their useful suggestions, although they noted that our studies are outdated and unnecessary.