Investigation of decay mechanisms and associated aspects of exotic Nobelium isotopes using the Skyrme energy density formalism

Superheavy elements and their synthesis has become an important field of research in recent years. Till now elements up to Z = 118 and their corresponding isotopes has been synthesized. Investigating the superheavy nuclei beyond Fermium has received much attention in last few decades because these nuclei are classified as transfermium elements, whose stability is mostly governed by the influence of shell effects. The quest for the heaviest element in the nuclear landscape has yielded many surprises and expanded our understanding of nuclear reactions which further attributed to play a pivotal role in the extension of the Periodic Table is achieved through the synthesis of new elements and isotopes. Numerous theoretical and experimental endeavors have been conducted to explore various reaction conditions and the mechanisms that govern their subsequent decay [1−9].

The disintegration of a compound nucleus formed through various low-energy heavy ion reactions is a fascinating topic, since it facilitates the production of new isotopes that are not naturally present. Furthermore, these mechanisms provide us with a thorough understanding of numerous nuclear reaction aspects and their associated structural impacts. Decay dynamics is extensively exercised to explore the compound (CN) and non-compound nucleus (nCN) decay mechanisms. The equilibrated state of the composite system in a heavy-ion reaction (HIR) is influenced upon several factors, including the mass asymmetry of the entrance channel $ (\alpha) $ and the Businaro-Gallone mass asymmetry $ (\alpha_{BG}) $ [10], the incident energy required to overcome the Coulomb barrier, the product of charges of projectile and target $ Z_PZ_T $, deformations and orientations, as well as shell effects.

As the colliding massive nuclei experiences an enhancement in the Coulomb repulsion, it may result in decay of the composite system. When a composite system reaches full equilibrium, it undergoes a process where the projectile and target merge completely, resulting in the formation of a CN stage. Further, the stage can then decay into two possible outcomes: the evaporation residue (ER) or fusion-fission (ff) fragments. Whereas, a non-equilibrated fused system i.e. nCN undergoes separation by transferring only small number of nucleons. Consequently, different decay mechanisms emerge such as quasi fission (QF), fast fission (FF), pre-equilibrium fission (PEF) etc [11].

The fusion cross-sections in superheavy elements are significantly suppressed by a non-equilibrium process i.e. quasi fission (QF). The process involves the formation of a di-nuclear system, which then divides into two fragments resembling fission, with the original kinetic energy being mostly or entirely dissipated. Quasi fission process occurs rapidly, typically 10⁻²¹ s, prior to the formation of a compact compound nucleus. Quasi fission can be classified into two categories based on the shell effects of fission fragments. Asymmetric quasi fission occurs when there are proton shell closures at Z = 28 and 82, as well as neutron shell closures at N = 50 and 126. On the other hand, symmetric quasi fission occurs when there are shell closures at Z = 50 and N = 82. Fast fission (FF) is a nuclear chain reaction mechanism that occurs when the potential barrier is eliminated due to a significant centrifugal force, especially at high angular momentum. Therefore, these processes are examined in order to comprehend the decay dynamics of heavy-ion induced reactions in heavy and superheavy mass region.

The estimation of lifetime can provide a comprehensive indication of the nuclear reaction mechanism. The attributes of the fissioning nucleus, such as its fissility and excitation energy, are crucial in determining the lifetime of the decay process. Processes such as QF often happens within a brief time scale of around 10⁻²¹ s to 10⁻²⁰ s, whereas ff takes place over longer duration's, ranging from roughly 10⁻²⁰ s to 10⁻¹⁶ s. The synthesis of the heavy and superheavy elements are strongly hindered by the nCN processes that results in fast splitting of the compound nucleus hence, the a lot efforts are done to study the timescales of such processes. This work aims to assess the time scales of QF and fusion-fission (ff) using DCM and compare the results with dinuclear system (DNS). Further, lifetimes in the DNS approach has greatly influenced by the charge number of the projectile and target nuclei, beam energy etc and the DNS lifetime should be enough to transform into the complete fusion of the interaction nuclei. Hence, the lifetime calculations are carried and results are compared for the both approaches. Extensive study is to investigate the decay mechanisms of CN and nCN. Few examples of such are as followed [12−25]. Further, to study the nuclear interaction potential, the Skyrme energy density formalism (SEDF) is used with the frozen density approximations, adopting the GSkI parameters. The Skyrme Hamiltonian density comprises distinct components that highlight the finite characteristics of nuclei. Recent advancements in the Skyrme Hamiltonian density have incorporated supplementary terms which are particularly useful for investigating nuclei that are highly responsive to the isospin-rich area and nuclei with a neutron-proton asymmetry [26]. The SEDF has been successfully applied in the light and heavy mass regions and it would be interesting to investigate the effect of SEDF nuclear potential in the superheavy mass regions and explore its properties. The Nobelium nuclei comes in the super heavy mass region. Hence, it would be interesting to study its properties within the domain of SEDF.

Recent studies related to Nobelium nuclei are as follows: fusion-fission analysis of ^12C+²⁴⁸Cm and ¹⁶O+²⁴⁴Pu nuclear reactions across the Coulomb barrier by Vijay et al. [27] and further, evaporation residue cross-section in the decay of ²⁵⁴No^* formed in ²⁰⁶Pb+⁴⁸Ca by Niyti et al. [28]. Recently, Yu-Hai Zhang et al. studied the production cross sections of ^243-248No isotopes in fusion reactions [29]. Also, the different decay modes and half-life of Nobelium isotopes are investigated by T. Bayram et al.[30]. More can be found in the references [31, 32].

There has been a significant increase in interest in CN and nCN mechanisms in recent years. This is primarily because these reactions hold potential for synthesizing a wide range of heavy and superheavy elements. Identifying the impact of CN and nCN processes in different decay channels has consistently been a challenge. This is primarily because the experimental evidences of these channels either overlap or their contribution is not as conspicuous. Here, in this work, The Dynamical cluster-decay model (DCM) using the SEDF with GSkI parameter sets, are used to analyze the respective contributions of different fission decay mechanisms in the processes of CN and nCN in ²⁴⁸No^* and ²⁵⁰No^* isotopes of Z=102 nucleus over a range of centre-of-mass energies around the Coulomb barrier in reference to the experimental finding of E. M. Kozulin et al. [33] and G. N. Knyazheva et al. [34]. Further, the fission peaks and the reaction cross-sections are studied by including deformation effect up to quadrupole $ (\beta_2) $ deformations. One can also observe the effect of octupole deformation in the fission peaks within the low-energy range at different excitation energies [35, 36].

The organisation of this document is as follows: In Section II, provides the explanation of the theoretical framework employed in this study. Specifically, the Skyrme energy density formalism (SEDF) [26, 56, 57], in reference to the Dynamical cluster-decay model (DCM), and the $ \ell $-summed Wong model [68]. Additionally, the probability of compound nucleus formation (P_CN) using an energy-dependent function is considered [33, 71, 72], and we examine the lifetimes using a theoretical approach derived from dinuclear system (DNS) calculations [73, 74]. Section III comprises the findings and analysis, while Section IV provides a concise summary of the work.

To investigate the various nuclear mechanisms the Quantum Mechanical Fragmentation Theory (QMFT) based [37−39] Dynamical cluster-decay model (DCM) [12, 13, 18−25] is worked out in the terms of collective coordinates of mass and charge asymmetry, relative separation coordinate 'R', deformations $ \beta_{\lambda i }$($\lambda$ = 2, 3, 4 and i = 1, 2), orientations of the deformed fragments $ \theta_i $ (i=1,2), and the neck parameter $ (\Delta R) $. The mass and charge asymmetry are stated as follows, respectively:

where $ A_i $ and $ Z_i $ (where i=1,2) represent the mass and charge numbers of the respective fragments and A_CN and Z_CN, is mass and charge of Compound nucleus. The temperature-dependent collective potential energy, or fragmentation potential, can be expressed using the relative spacing R and $ \eta $-coordinates as:

Here $ V_{LDM} $ corresponds to the liquid drop part of the binding energy of Davidson et al. [40] and $ \delta U $ is the shell corrections from Myers and Swiatecki [41], the value of $ T_0 $ =1.5 MeV is taken from classical work of Jensen and Damgaard [42], $ V_C $, $ V_N $ and $ V_\ell $ is the Coulomb, nuclear interaction and angular momentum-dependent potential for deformed and oriented nuclei.

The preformation probability of decaying fragments in $ \eta $-coordinates at $ R=R{_a} $ is determined by solving the stationary Schrodinger equation as:

with the ground and excited state solutions given by $ {\nu} $ = 0,1,2.... and the smooth hydrodynamical mass parameter represented by $ B_{\eta \eta} $.[43].

On the other hand, the barrier penetration probability P of decaying fragments is determined by WKB integral

with

regarding the two turning points. TKE denotes the total kinetic energy and $ Q_{eff} $ is the effective Q value.

In context to the compound nucleus decay, the following postulate is employed to describe the occurrence of the initial turning point.

The influence of neck formation, the neck length parameter denoted as $ \Delta R (T) $ is accounted by [45−48]. The radii are taken from [59−63].

The temperature T is related to the excitation energy $ E^*_{CN} $, through the semi-empirical statistical relation as [44] :

For this system, we have used a = 9, the entrance channel Q-value, denoted as $ Q_{in} $, is calculated using the equation $ Q_{in} $ = $ B_1 + B_2 - B_{CN} $, where $ B_1 $, $ B_2 $, and $ B_{CN} $ represent the binding energies of the target, projectile, and compound nucleus, respectively [49].

For the multipole-multipole interaction between two separated nuclei, the Coulomb potential can be expressed as given in references [50−52].

The equation accounts for the influence of nuclear deformation on the radius vector $ R_i $ is

Here i=1,2, $ \lambda $=2,3,4 and the variable $ \alpha_i $ represents the angle formed between the symmetry axis and the radius vector $ R_i $ of the colliding nuclei.

In the above expression, the T-dependence nuclear radius term $ R_{0i} (T) $ is given as

Here, $ R_{0i} $ =1.28$ A_{i}^{1/3} $ −0.76 + 0.8$ A_{i}^{-1/3} $ in fm.

The angular momentum effects impart additional energy to the rotational motion, and the corresponding rotational potential is computed in the references as [53, 54]. Finally, in terms of $ P_0 $ and $ P $ co-ordinates, the decay cross-sections are computed.

where $ \mu $ is the reduced mass.

The collective clusterization process within the domain of DCM is used to calculate the cross-section of values compound nucleus (CN) processes such as evaporation residue and fusion-fission (i.e $ \sigma_{ER} $ and $ \sigma_{ff} $) as

and for the non-compound nucleus (nCN) processes such as Quasi fission and fast fission using the formula as

Where $ P_{ic} $ is the penetration probability.

Here, $ P_0 $ is calculated by solving Schrodinger wave equation for fission fragments for angular momentum varying from $ \ell_{Bf} $ to $ \ell_{max} $ and barrier penetration probability is considered to be maximum (i.e. P=1).

The $ V_C $ and $ V_\ell $ are widely comprehended within the field, however the $ V_N $ lacks a specific definition. Numerous theoretical frameworks exist for the computation of nuclear interaction potentials. In this study, the Skyrme energy density formalism (SEDF) based $ V_N $ is intended to examine the stability of the heavy and superheavy mass area.

The semi-classical extended Thomas Fermi (ETF) approach [55] based, nucleus-nucleus interaction potential in SEDF is described as

i.e.,the potential of the interaction between two nuclei can be characterised as a function of the separation distance. $ V_N(R) $ denotes the difference in the expected energy value, referred to as E, between the colliding nuclei when they are overlapping at a finite separation distance R, and when they are completely separated at R = $ \infty $.

The Skyrme Hamiltonian density is precisely given as [26, 57]

Here, the nuclear density, kinetic energy density, and spin-orbit density are depicted by $ \rho = \rho_n + \rho_p $, $ \tau = \tau_n + \tau_p $ and $ {\bf{J}} = {\bf{J}}_n + {\bf{J}}_p $ and m denotes the nucleon mass. The Skyrme force parameters such as $ \alpha_i $, $ x_1 $, $ x_2 $, $ t_1 $, $ t_2 $, $ t_3 $,$ W_0 $ and $ A $ are fitted by Agrawal et al. [56, 57] referring to the modified version implemented for Skyrme interactions, including GSkI, GSkII, and SSk Skyrme interactions.

The densities in this study are determined using the frozen density approximation [58].

with $ \rho_i = \rho_{in} + \rho_{ip} $, $ \tau(\rho_i) = \tau_1in(\rho_{in}) + \tau_ip(\rho_{ip}) $ and $ {\bf{J}}(\rho_i) = {\bf{J}}(\rho_{in}) + {\bf{J}}(\rho_{ip}) $.

Nuclear density $ {\rho}_i $ is calculated using the two-parameter Fermi density distribution, as shown in [59, 60]

with central density

Here $ R_{i} $ is the nuclear radius and $ a_{i} $ is the surface thickness parameters [59−63]. Further, the T-dependence in the nuclear radii $ R_{i} $ has been discussed in Eq.(9) and the T-dependence in the surface thickness parameter $ a_{i} $ is introduced as [64, 65]

In the context of the $ V_N $, we adopt the slab approximation of semi-infinite nuclear matter with parallel surfaces in the x-y plane. The slab is in motion along the z-direction and is separated by a distance s, with a minimum separation value denoted as $ s_{0} $ [66, 67].The expression for the interaction potential $ V_N $(R) between two distant nuclei, where $ R $ = $ R_1 + R_2 + s $, is provided as

$ \overline{R} $ is the mean curvature radius, and $ e (s) $is the interaction energy per unit area between the two slabs.

Moreover, $ V_{P}(R) $ and $ V_{J}(R) $ represent the components of the nuclear interaction potential that are independent and dependent on the spin density, respectively.

In this work, we have used two different approximations in order to calculate the reaction cross-sections. The WKB approximation and the Hill-wheeler approximations are two different approaches developed to calculate the barrier transmission probabilities. The Hill-wheeler approximation is a purely parabolic barrier and is widely appreciated for its simplicity and numerical efficiency in calculations. Although, at above barrier energies the cross-sections marge for both the approximations. Hence, in next subsection, we have applied Hill-Wheeler approximation to compute the capture cross-sections.

The cross-section for fusion/capture between two orientated and deformed nuclei can be determined by considering the orientation angles $ \theta_i $ and the center of mass energy $ E_{c.m.} $ of the collision in $ \ell $-summed Wong model [68] is calculated as follows in terms of angular momentum $ \ell $ partial waves:

$ P_\ell $ is the transmission coefficient for each $ \ell $, which characterizes the penetration of barrier, and $ \ell_{max} $ is the maximum angular momentum, with $ k = \sqrt{\dfrac{2\mu E_{c.m.}}{\hbar^2}} $ and $ \mu $ as the reduced mass [70].

Probability of Compound nucleus formation P_CN:

Probability of completely fused compound system after the capture stage is referred as Probability of Compound nucleus formation (P_CN). In the superheavy mass region, the probability of formation of compound nucleus diminish as the atomic number increases. Here, the energy dependence of fusion probability approximated by a simple relation as [33, 71, 72].

where $ V_{B}^{*} $ is the compound nucleus excitation energy at $ E_{c.m.} $ $ \approx $ Coulomb barrier, $ E^{*} $ is the compound nucleus excitation energy and $ \Delta $ = 4 MeV considered for these calculations. Moreover, the parameters used in calculating the value $ P^{'}_{0} $ is taken from Ref. [72].

Fusion-fission (ff) and Quasi fission (QF) lifetimes:

Further, the lifetimes for fusion-fission (ff) and quasi fission (QF) are examined using the theoretical approach and is given by [73, 74].

where $ \lambda_{ff \mid QF} $ is the fission fusion or quasi fission decay constant and is expressed as

Here, $ \omega_m $ is the frequency of the harmonic oscillator, $ \omega_{ff \mid QF} $ refers to the frequency of the inverted harmonic oscillator, $ B_{ff \mid QF } $ is the barrier corresponding to the fusion-fission and Quasi fission, $ \Gamma $ denotes an average width taken as 2 MeV and T is the temperature taken in MeV.

The DCM equations are employed for the computation of cross-sections pertaining to different CN and nCN processes, as well as the determination of lifetimes associated with fusion-fission (ff) and quasi fission (QF), as elaborated in section III.

During heavy ion processes, the nuclei make contact with one other as a result of Coulomb interactions. In context to the centre-of-mass system, if the projectile possesses sufficient energy and the appropriate angular momentum, there exists a possibility that the nuclei could penetrate the Coulomb barrier and become confined within the potential well. This results in the attainment of the stage where the compound nucleus is in a state of complete equilibrium, also known as the CN process. Alternatively, if the captured system does not undergo significant evolution within the fusion pocket, mechanisms for example quasi fission (QF) and fast fission (FF) become relevant. In the present analysis, we have carried out our calculations to investigate the decay mechanisms of ²⁴⁸No^* and ²⁵⁰No^* isotopes of $ Z=102 $ Nobelium nuclei over the broad range of centre-of-mass energies near and above the Coulomb barrier. The Dynamical cluster-decay model (DCM) is used to examine the contributions of CN (compound nucleus) and nCN (non-compound nucleus) in fission. The interaction potential is obtained by applying the Skyrme energy density formalism (SEDF) with GSkI force parameters. The included deformations extend up to the quadrupole ($ \beta_2 $) moment, with the optimum orientation $ \theta_{i}^{opt} $. The detailed analysis to study the decay mechanism (ff, QF, FF) of the potential energy surfaces (PES), preformation factor $ P_0 $, penetrability P, neck length parameters and scattering potential V(R) is carried out. Further, the capture cross-sections, are studied using the $ \ell $-summed Wong model was used to compare it with the existing experimental data. Moreover, the decay cross-sections for the above stated processes is obtained and compared with the available experimental findings [33, 34]. Beside this, fusion-fission and quasi fission lifetime are estimated and the compound nucleus formation probability P_CN is worked out.

Here, we will discuss the decay of the ²⁴⁸No^* composite system formed via ⁴⁰Ca + ²⁰⁸Pb reaction. Fig. 1 shows the scattering potential at $ \ell = 0\hbar $ for ⁴⁰Ca + ²⁰⁸Pb reaction at centre mass energy $ E_{c.m.} = 187.03 $ MeV with respect to range R (fm). It is crucial to note that the first turning point $ R_a $ (which is equal to $ R_1 + R_2 + \Delta R $) represents the distance between the nuclei at which the fragments are assumed to have already preformed and begin to penetrate the interaction barrier. Similarly, $ R_b $, second turning point is the point at which the process of penetrating through the interaction barrier is fully completed. The quasi fission barriers is marked and is defined as the potential difference between the barrier $ V_B $ and the potential at the first turning point $ V(R_a) $, which depends on the angular momentum of the incoming channel at the specified incident energy.

Figure 1.  (color online) The calculated Scattering potential V (MeV) as a function of range R (fm) for the entrance channel of ²⁴⁸No^* nuclei at $ \ell = 0 \hbar $ at $ E_{c.m} $ = 187.03 MeV.

To evaluate the impact of different mechanisms on the superheavy nuclei synthesis, we have computed the probability of compound nucleus formation $ (P_{CN}) $ for both ²⁴⁸No^* and ²⁵⁰No^* nuclei. If the value of P_CN ~ 1, then the reaction is classified as a compound nucleus (CN) reaction. The deviation of P_CN from unity impart the potential to investigate the significance of the non-compound nucleus (nCN) process. The calculated P_CN for the two isotopes of i.e. ²⁴⁸No^* and ²⁵⁰No^* of Z=102 nuclei with three different entrance channels i.e ⁴⁰Ca+²⁰⁸Pb, ⁴⁴Ca+²⁰⁶Pb and ⁶⁴Ni+¹⁸⁶W comes out to be 3.40 × 10⁻⁵, 1.94 × 10⁻⁵ and 1.06 × 10⁻⁵ respectively. The value of P_CN being less than 1 in the calculated data suggests the existence of nCN processes. Hence, the contributions of $ \sigma_{ff} $, $ \sigma_{QF} $ and $ \sigma_{FF} $, are obtained so that dynamics of superheavy system be understood.

The experimental findings are employed to assess the ff, QF and FF cross-sections for the ²⁴⁸No^* and ²⁵⁰No^* nuclei. These calculations are performed via the DCM framework. Additionally, the $ \sigma_{capture} $ are studied by utilizing the $ \ell $-summed Wong model. The calculations are carried out by taking into account the hot optimum orientations at the energies around the barrier of the decay fragments. Initially, the research and discussion is carried out for ²⁴⁸No^* nucleus. Fig. 2, illustrates the fragmentation potential V (MeV) regarding the decay of ²⁴⁸No^* nucleus at three $ E_{c.m.} $ = 187.03,209.67 and 239.03 MeV for the $ \ell_{max} $ values of angular momentum obtained from the most probable fragment for which the penetrability becomes equal to one (i.e. P = 1). The T-dependent collective potential energy calculation provides information about the relative contributions of potential decay fragments. (i) From the figure, it is evident that with increase in temperature, the magnitude of fragmentation potential enhances whereas the structure remains similar as we move from lower energies to the higher excitation energies. (ii) The most probable decaying fragments are clearly indicated in the figure and can be seen that the decay fragments remains same independent of expectation energy. (iii) The angular momentum for the highest $ E_{c.m.} $ is more than for the other $ E_{c.m.'s} $, which could be attributed to the fact that higher $ E_{c.m.} $ takes more angular momentum to decay. (iv) The configuration of fragmentation potential for light mass fragments (LPs) and intermediate mass fragments (IMFs) and the fission region remains nearly similar at extreme energies.

Figure 2.  (color online) Fragmentation potential V$ (A_2) $ for the nuclear system ²⁴⁸No^* formed in ⁴⁰Ca + ²⁰⁸Pb reaction system at $ E_{c.m.} $ = 187.03,209.67 and 239.03 MeV, using the fixed value pf $ \Delta R $'s for the maximum $ \ell_{max} $ values of angular momentum.

Fig. 3, delves deeper into the examination of decay by plotting the preformation probability $ (P_{0}) $ based on the fragment mass $ A_{i} $ (i = 1,2). The analysis illustrates that the fission contribution becomes more pronounced as the $ \ell $ values increase. When examining the preformation profile at different $ E_{c.m.} $, it is clear that the value of $ P_0 $ varies, while the distribution of mass for the fission fragments remains nearly equal and exhibits an asymmetric nature, regardless of the $ E_{c.m.} $. It is crucial to note that these secondary peaks can be linked to the potential occurrence of QF. Further, the most probable fragments and their complimentary fragments observed on the asymmetric peaks remain similar as we move from the lowest to the highest $ E_{c.m.} $. Also, It is noteworthy to emphasize that the fragment with maximum probability to be preformed is ¹²⁰Sn and its complementary fragment ¹²⁸Te. Both emitted fragments are in close proximity to the magic numbers Z = 50 and N = 82, and hence the shell effects are instrumental for the asymmetric fission distribution.

Figure 3.  (color online) Fragment preformation probability $ P_0 $ against the fragment mass $ A_i $ (i=1,2) for the decay of ²⁴⁸No^* nuclei by including the $ \beta_2 $-deformation effects, plotted at fixed neck-length parameter and highest value of angular momentum.

Hence, following our understanding of the potential for fragmentation and the analysis of preformation, our next objective is to examine the conflicting processes of CN and nCN decay in the ²⁴⁸No^* nucleus. The recent investigation involved conducting an experiment on Z = 102 nucleus using ⁴⁰Ca + ²⁰⁸Pb reaction, and different decay mechanisms were explored and addressed by DCM. The $ \sigma_{capture} $ incorporate the contributions from CN and nCN process, i.e $ \sigma_{capture} = \sigma_{CN} + \sigma_{nCN} $. The current study focuses on the $ \sigma_{capture} $ for the ²⁴⁸No^* nucleus corresponding the $ E_{c.m.} $ is calculated using the $ \ell $-summed Wong Model and the $ \ell_{max} $ values are determined via the sharp cutoff model [82]. Table 1, clearly demonstrates that $ \sigma_{capture} $ exhibit an increase as the $ E_{c.m.} $ increases. The conclusions derived within the theoretical approach align with the experimental data. Additionally, the formation of a compound system involves two components: the evaporation residue (ER) cross-section and the fusion-fission (ff) cross-section. Mathematically, this can be expressed as $ \sigma_{CN} = \sigma_{ER} + \sigma_{ff} $. Alternatively, we can address the hindrance in the CN formation by considering the nCN cross sections $ (\sigma_{nCN}) $, which take into account the contributions of both QF and FF processes. In other words, we can express $ \sigma_{nCN} $ as the sum of $ \sigma_{QF} $ and $ \sigma_{FF} $. An effort is put forth to examine the CN-fission. The fragments chosen for ²⁴⁸No^* nuclei within the limits of A/2 ± 20, which indicate a favorable correspondence with the existing data.

$ E_{c.m.} $ (MeV)	$ E^*_{CN} $ (MeV)	T (MeV)	$ \ell_{max} $ $ (\hbar) $	$ \Delta R $ (fm)	$ \sigma_{2n}^{DCM} $ (nb)	$ \sigma_{ff}^{DCM} $ (mb)	$ \sigma_{ff}^{Expt.} $ (mb)	$ \Delta R_{QF} $ (fm)	$ \sigma_{QF}^{DCM} $ (mb)	$ \sigma_{QF}^{Expt.} $ (mb)	$ \Delta R_{FF} $ (fm)	$ \sigma_{FF}^{DCM} $ (mb)	$ \sigma_{FF}^{Expt.} $ (mb)	$ \sigma_{capt.}^{DCM} $ (mb)	$ \sigma_{capt.}^{Expt.} $ (mb)
187.03	49	1.35	123	2.14	0.00771	160.11	159	2.27	53.49	53	-	-	-	212.0	212
209.67	73	1.64	134	2.21	11.3	306.25	305	2.29	62.90	62	1.58	253.35	253	627.35	620
238.19	101	1.93	147	2.22	442	280.23	280	2.30	79.10	79	1.77	575.44	572	939.96	931

Table 1.  The DCM measured Evaporation residue cross-section $ \sigma_{2n} $, fusion-fission $ \sigma_{ff} $, quasi fission $ \sigma_{QF} $, fast fission $ \sigma_{FF} $ cross sections and capture $ \sigma_{capt.} $ cross section calculated using $ \ell $-summed Wong Model for ²⁴⁸No^* nucleus at different centre of mass energies $ E_{c.m.} $ along with relevant fitted neck length $ \Delta R $, Temperatures T and $ \ell_{max} $ values compared with experimental data.

The phenomenon known as QF, the projectile is captured by the target nucleus and a non-equilibrated compound system is formed. This system remains confined within the potential well for a brief duration. The QF contributions are calculated by taking in consideration the most probable fragments that appears on the shoulders of the preformation probability $ P_0 $ from the Fig. 3, and their complementary fragments, and further taking into account the preformation probability of each fragment on the peak and distributing the probability among all the considered fragments. The FF process results in the formation of a mononucleus that has successfully withstood the QF process. The angular momentum of the mononucleus is significant. At high angular momentum, the rotating system's fission barrier becomes insignificant due to the enhanced rotational energy. Therefore, a highly energetic and rapidly rotating nucleus experiences rapid fission, resulting in the production of two fission fragments which have a resemblance to those produced in the fast fission process. For fission fragments ($ A_2 $ = 90-124 and the complementary fragments), the Schrodinger equation must be solved in order to find the preformation probability $ P_0 $ for FF. The $ \ell $values range from $ \ell_{Bf} $ to $ \ell_{max} $, where $ \ell_{Bf} $ denotes the angular momentum at which the fission barrier ceases to exist. In this case, the possibility of barrier penetration is deemed to be maximal, i.e. P = 1. Clearly, one can observe from Table 1, that the contribution of CN process of ff first increases and then decreases as we move from lowest to the highest $ E_{c.m.} $ whereas in nCN processes i.e. QF and FF contribution is large at higher energies. Further, Table 1 provides the estimated cross sections for the DCM, together with the associated values of $ \Delta R $, temperatures T, $ \ell_{max} $ values, $ E^*_{CN} $ and $ E_{c.m.} $, and the $ \sigma_{capture} $ by employing the $ \ell $-summed Wong model for the decay of the ²⁴⁸No^* nucleus. The DCM-derived cross sections processes such as of ff, QF and FF and capture cross section, demonstrate excellent concordance with the experimentally obtained data at all energy levels. Also, we have obtained the 2n channel evaporation cross-sections for ²⁴⁸No^* nuclei. The aforementioned observed cross sections are determined by the optimization of the $ \Delta R $. Accounting for the contribution of $ \Delta R $ in the decay process is crucial because it leads to shape elongation in the compound system, resulting in the development of a neck between the nascent fragments. The presence of a neck region in the dinuclear system allows for a free movement of nucleons between the nuclei. This creates an opportunity for significant exit channels by altering the interaction barrier [85, 86]. The flow of mass drift and the adjustment of the barrier are governed by the neck length $ \Delta R $. According to Fig. 4, there is a clear correlation between an increase in the $ \Delta R $ with an increased $ E_{c.m.} $. Further, as a result of its lower barrier characteristics, the extended GSkI force necessitates a greater $ \Delta R $ value, but it remains within the maximum allowable value. The $ \Delta R $ may give an idea about the temporal scale of the fragments reaction time. The reaction time will be faster when the value of $ \Delta R $ is higher. As the QF process takes place faster than the ff and FF, hence $ \Delta R $ is slightly higher for QF than the ff and FF.

Figure 4.  (color online) Neck length parameter $ \Delta R $ (fm) in context to the centre of mass energy $ E_{c.m.} $ (MeV) optimized for fusion-fission (ff), quasi fission (QF) and fast fission (FF) using the GSkI Skyrme force.

Further, the study examines the impact of different entrance channel mass asymmetry on the synthesis of ²⁵⁰No^* nucleus. This is done by considering two different incoming channels: ⁴⁴Ca + ²⁰⁶Pb and ⁶⁴Ni + ¹⁸⁶W, at different $ E_{c.m.} $ = 187.04 MeV and 231.38 MeV. The comparison of the fragmentation potential V (in MeV) is presented with fragment mass, shown in Fig. 5. The fragmentation potential shows a roughly identical variation for both entrance channels, with a slightly greater magnitude seen for the ⁴⁴Ca + ²⁰⁶Pb case compared to the ⁶⁴Ni + ¹⁸⁶W case. The deformation effect shows asymmetric nature of the fragmentation potential for both the considered entrance channels in the analysis. According to the calculations based on DCM, the fragmentation characteristics of ER, IMF, heavy HMF and fission fragments are found to be nearly identical. This means that the choice of entrance channel does not have any significant impact on the fragmentation behavior. Furthermore, the minima in the fragmentation potential for both entrance channels exhibit a similar pattern. The results are elucidated in relation to the relative preformation probability $ P_0 $. Fig. 6 illustrates the computed preformation probability for the decay of ²⁵⁰No^* at different $ \ell_{max} $ values and their corresponding $ E_{c.m.'s} $. One can observe that preformation probability show slight variation in magnitude for the different entrance channels whereas the structure remains almost similar and even overlaps each other in fission region irrespective of the choice of entrance channels. Additionally, both cases demonstrate almost symmetrical fission peaks, and the contributing fission fragments remains same. Also, the fragments with maximum probability to be preformed i.e ¹²²Sn and its complementary fragment ¹²⁸Te are close to Z = 50 and N = 82 magic shell closure. Table 2, gives the information related to the various decay modes and their corresponding cross-sections, $ \ell_{max} $ values, neck length parameter for both the incoming channels using the GSkI force parameters. Table 2, clearly demonstrates that the $ \ell_{max} $ values and the $ \Delta R $ are comparable for both incoming channels. This suggests that the decay of ²⁵⁰No^* is not influenced by the entrance channel effect. The calculations demonstrate the extent of the contribution of the CN (ff) process is higher in the case of the ⁴⁴Ca + ²⁰⁶Pb reaction, while the nCN (QF) process appears to compete with ff in the ⁶⁴Ni + ¹⁸⁶W reaction channel. Ultimately, the investigation of the decay of ²⁵⁰No^* resulting from the collision of ⁴⁴Ca and ⁶⁴Ni beams with ²⁰⁶Pb and ¹⁸⁶W targets, respectively, was carried out using the DCM framework, taking into account the impact of deformation. From the findings, it can be concluded that the decay process remains unaffected by the specific approach of formation or the range of excitation energ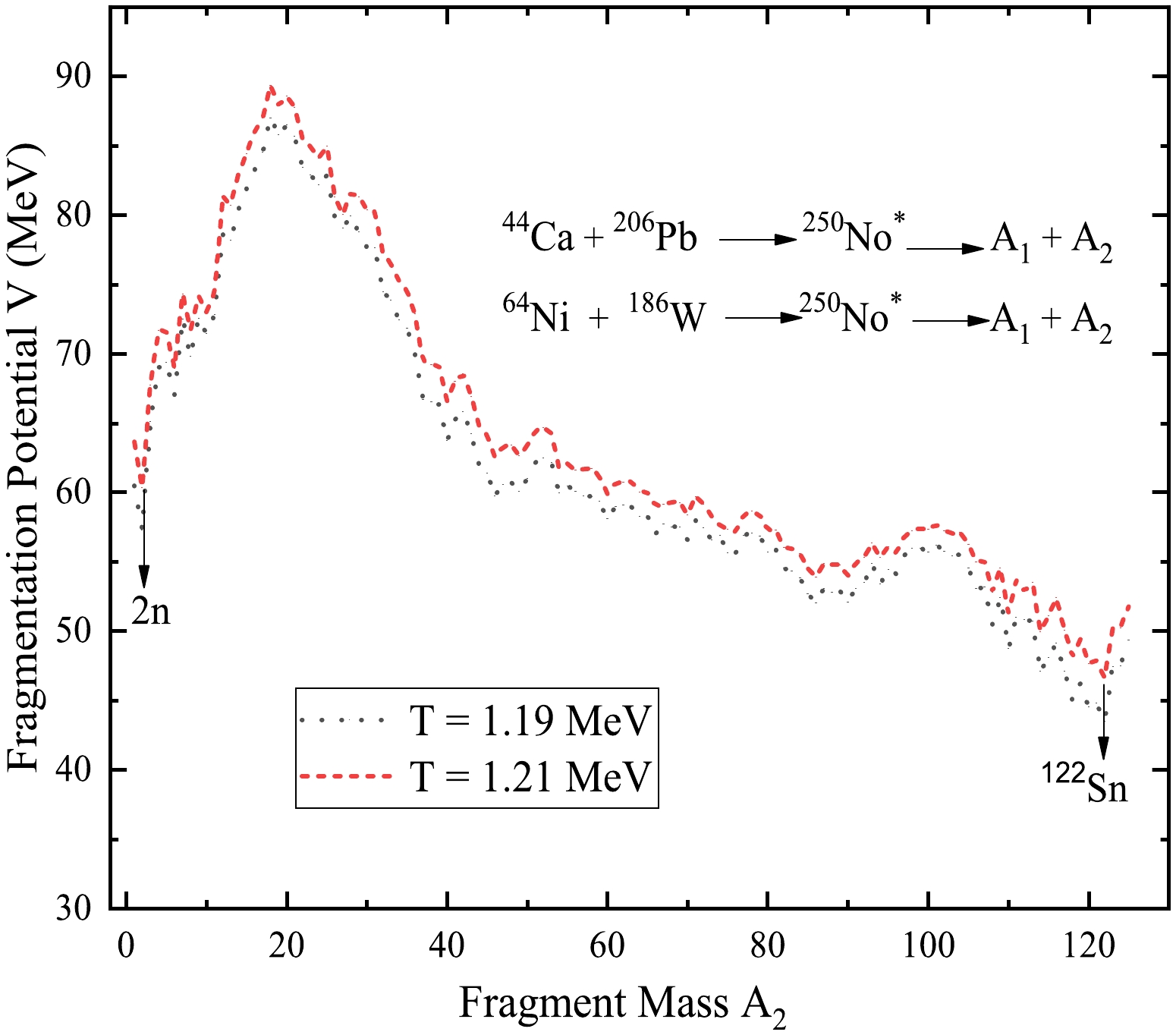y.

Figure 5.  (color online) Variation of Fragmentation potential V$ (A_2) $ for the parent nucleus ²⁵⁰No^* formed in ⁴⁴Ca + ²⁰⁶Pb and ⁶⁴Ni + ¹⁸⁶W reaction channels at $ \ell_{max} $ values and best fitted values of neck length parameter $ \Delta R $.

Figure 6.  (color online) Same as Fig.5 but for Preformation probability $ P_0 $ varies with fragment mass $ A_i $ (i=1,2).

Reaction	$ E_{c.m.} $ (MeV)	$ E^*_{CN} $ (MeV)	T (MeV)	$ \ell_{max} $ $ (\hbar) $	$ \Delta R_{ff} $ (fm)	$ \sigma_{ff} $ (mb)	$ \Delta R_{QF} $ (fm)	$ \sigma_{QF} $ (mb)	$ \sigma_{capt.} $ (mb)
44Ca + 206Pb	187.04	38.69	1.19	85	2.19	109.34	2.33	27.23	140
64Ni + 186W	231.38	40	1.21	86	2.10	22.54	2.41	66.99	89.7

Table 2.  The DCM-calculated fusion fission $ \sigma_{ff} $, quasi fission $ \sigma_{QF} $, fast fission $ \sigma_{FF} $ cross sections and capture $ \sigma_{capt.} $ cross section calculated using $ \ell $-summed Wong Model in the decay of $ ^{250}No^* $ nucleus formed formed in ⁴⁴Ca + ²⁰⁶Pb and ⁶⁴Ni + ¹⁸⁶W reaction channels at different centre of mass energies $ E_{c.m.} $ with the best fitted neck length $ \Delta R $, Temperatures T and $ \ell_{max} $ values.

This subsection focus on the lifetimes in reference to ff and QF. Fission is a dynamic phenomenon where the nucleus undergoes deformation until it reaches a point of scission. An induced fission process has time scale of greatest significance, both theoretically and experimentally. Understanding the lifetime of this process is crucial for comprehending the nuclear reaction process. The overall duration of a fission process can be conceptually separated into two primary components: the time required for the nucleus to cross the saddle point, and the time it takes for the nucleus to deform from the saddle point to the scission point. While the QF barrier depends upon $ Z_1Z_2 $ product, which in turn influence its lifetime. Hence, the available time may not be adequate for the conversion into a compound nucleus, resulting in the occurrence of the QF process. Hence, the duration of a partially equilibrated nuclear complex ought to be briefer compared to that of a fully equilibrated compound nuclear channel. The fission rate and fission lifetime for the asymmetric reaction such as ⁴⁰Ca + ²⁰⁸Pb, ⁴⁴Ca + ²⁰⁶Pb and symmetric ⁶⁴Ni + ¹⁸⁶W reactions are calculated which leads to the formation of ²⁴⁸No^* and ²⁵⁰No^* of Z=102 nucleus.Table 3, shows the comparison of ff and QF lifetime $ \tau_{ff} $ / $ \tau_{QF} $ using the excitation energy $ E^*_{CN} $ within the DCM and DNS approaches [73, 74]. The DCM and DNS approaches uses different parameters to calculate the lifetime thus leading to the difference in magnitude. In DCM the lifetime depends on three major factors i.e. Preformation probability $ P_0 $, penetrability P and barrier assault frequency $ \nu_0 $ whereas in DNS approach is greatly influenced by the charge number of the projectile and target nuclei, beam energy etc. One can observe from the Table 3 that, the calculations carried out for the DNS cases are in agreement with the trend that lifetime goes on decreasing with the increase in the excitation energy $ E^*_{CN} $ whereas in DCM analysis the lifetime remains almost constant. There is a noticeable trend that ff and QF lifetime $ \tau_{ff} $ / $ \tau_{QF} $ decreases with increase in the $ E^*_{CN} $. Therefore, the stability of a massive compound nucleus decreases as its excitation energy increases, primarily because the fission barrier is reduced. On comparing the lifetimes obtained using the DCM and DNS approaches one may differ of few magnitude is observed for the ff channel, whereas the quasi fission lifetimes are almost similar for both the approaches. Thus, The chance for survival of the large compound nucleus diminishes as the fission barrier falls with increasing $ E^*_{CN} $ of the resulting compound system.

Reaction	$ E_{c.m.} $ (MeV)	$ E^*_{CN} $ (MeV)	T (MeV)	$ \tau_{ff} $ (DCM) (sec−1)	$ \tau_{ff} $ (DNS) (sec−1)	$ \tau_{QF} $ (DCM) (sec−1)	$ \tau_{QF} $ (DNS) (sec−1)
40Ca + 208Pb	187.03	49	1.35	1.64 × 10−16	4.98 × 10−19	3.42 × 10−21	5.41 × 10−21
	209.67	73	1.64	6.91 × 10−16	2.39 × 10−19	3.68 × 10−21	3.12 × 10−21
	238.19	101	1.93	1.52 × 10−15	1.45 × 10−19	3.93 × 10−21	2.14 × 10−21
44Ca + 206Pb	187.04	38.69	1.19	5.49 × 10−17	1.50 × 10−18	3.01 × 10−21	1.46 × 10−20
64Ni + 186W	231.38	40	1.21	4.85 × 10−17	1.18 × 10−18	1.18 × 10−21	1.41 × 10−21

Table 3.  Comparison of Fusion-fission lifetime $ \tau_{ff} $ and Quasi fission lifetime $ \tau_{QF} $ for different reactions which are used for the formation of ²⁴⁸No^* and ²⁵⁰No^* at different excitation energies within the DCM and DNS approach.

Within the context of The Dynamical cluster-decay model (DCM), the competing decay mechanisms fusion-fission (ff), Quasi fission (QF) and Fast fission (FF) leading to ^248,250No^* isotopes of Z=102 nucleus reactions are investigated using Compound nucleus (CN) and Non-compound nucleus (nCN) processes. The investigation is conducted at incident energies around the barrier taking into account the quadrupole deformation using the optimum orientation approach.The calculated ff, QF, FF, and capture cross sections exhibit a satisfactory level of concordance with the experimental data. The existence of the nCN channel is regulated by the capture process. Compound nucleus formation probability $ (P_{CN} < 1) $ clarifies that nCN processes such as QF and FF compete with compound nucleus ff process. A comparative analysis is conducted to assess the fragmentation and preformation profiles of the isotopes ²⁴⁸No^* and ²⁵⁰No^*. The contribution of QF and FF start competing with the ff process at energies around the barrier due the diminishing of fission barrier. The most probable fragments in mass distribution have been identified near the magic shell closure Z=50 and N=82 leading to presence of asymmetric fragmentation. Finally, the ff and QF lifetimes are estimated and compared with DNS approach.