-
In the past few years, nuclei in the rare-earth region with A ~ 150-160 have been extensively investigated using different nuclear spectroscopic techniques. These nuclei have shown a number of phenomena that challenge our understanding of nuclear structure studies. They are known to have medium to large prolate deformation, β2 = 0.1–0.3 [1], and also exhibit rotational bands built on different multi-quasiparticle orbitals. Reflection-asymmetric deformation, parity doublets, octupole correlations, and K-isomerism are some of the properties that make this region of the Segre chart a rich hunting ground for both experimental and theoretical studies. In addition to these results, the A~150-160 region also offers the opportunity to study the emergence of collective behavior, such as rotations, from a single particle regime. The Z= 61 Promethium (Pm) nuclei lie well within this region and provide a good testing ground for the theoretical models. These nuclei have attracted a considerable amount of research attention because of their large prolate deformation (β2~0.3) [2-4]. Regarding the nuclear shell structures of neutron-rich 151-161Pm nuclei, in particular, information about their excited states is rather scarce. On the theoretical front , very few studies have been reported that aim to understand their structure. Some of the prominent research studies on these isotopes include Refs. [3-15], among which the work carried out by Liu et al. [3], Yokoyama et al. [4], and Bhattacharyya et al. [5] has been reported very recently and inspired us to take up this study. In their experimental work, Bhattacharyya et al. [5] extended the spectroscopic information on the rotational band structures in odd-A 151-155Pm isotopes to considerably higher spins, whereas the level schemes for 157Pm and odd-odd 152,154,156Pm were reported for the first time in their work. However, the probable spin, parity, and the initial and final states of 152,154,156Pm were only tentatively assigned in their work, and the level energies were also given with respect to a reference level; still, it provided a solid base for further studies. Bhattacharyya et al. also explored the possibility of the presence of reflection asymmetric shapes in these nuclei and concluded that the existence of octupole deformed shapes in neutron-rich Pm isotopes beyond N ≥ 90 is implausible. Later on, Liu et al. [3] employed the cranked shell model with pairing correlations treated by a particle-number-conserving method (PNC-CSM) to investigate the rotational bands in 153-157Pm. The results of their work not only accounted reasonably well for the available experimental data [5, 6], but also provided valuable information regarding the configuration and band head spin of 154, 156Pm nuclei, which can serve as a motivation for further experiments concerning these two nuclei. Conversely, Yokoyama et al. observed rotational bands with similar energies in 159Pm and 161Pm and also constructed their preliminary level scheme. They also suggested that neutron-rich Pm isotopes have a prolate type of deformation. These studies are definitely encouraging, but more information is required on the experimental as well as theoretical front to completely understand the nuclear structure of 151-161Pm isotopes.
The present study aims to provide additional information on the nuclear structure of these neutron-rich odd-mass 151-161Pm and odd-odd 154,156Pm nuclei. The theoretical framework of the projected shell model (PSM) [16] will be used for this purpose. From the wave functions obtained in the PSM calculations, we obtain various observables, such as B(E2) and B(M1) transition probabilities, which can provide a deeper understanding of the structure of these Pm isotopes. Physical insights provided from this particular model have already proven useful for understanding A = 150 nuclei [17-22]. The organization of this paper is as follows: in Section 2, we briefly review the PSM. The results, including the yrast energy spectra and M1 and E2 transition probabilities, are presented and discussed in Sections 3 and 4 for odd-mass and odd-odd Pm isotopes, respectively. The main conclusions are summarized in Section 5.
-
The PSM method is an extension of the shell model approach based on the angular momentum projection technique. For details of this model, readers may refer to the review article of Hara and Sun [16] and to the published computer code [23]. The PSM is built over a deformed mean field, in which pairing effects are incorporated through a Bogolyubov transformation to quasiparticle states. Starting from a deformed basis not only makes the shell model calculations for heavynuclei feasible, but at the same time, it makes physical interpretation of the complex systems easier and clearer. In the present work, we have assumed that the deformed single-particle states have axial symmetry.
The Hamiltonian used in the present work consists of a sum of schematic (quadrupole-quadrupole + monopole + quadrupole-pairing) forces that represent different kinds of characteristic correlations between active nucleons. The total Hamiltonian is of the form:
$\hat H = {\hat H_0}{\rm{ }} - {\rm{ }}\frac{1}{2}\chi \sum\limits_{\mu} {} \hat Q_{\mu} ^{{\dagger }}{\hat Q_{\mu} } - {G_M}{\hat P^{{\dagger }}}\hat P - {G_Q}\sum\limits_{\mu} {\hat P_{\mu} ^{{\dagger }}} {\hat P_{\mu} },$

(1) where the first term in Eq. (1),
${\hat H_0}$ , is the harmonic-oscillator single-particle Hamiltonian, which in particular contains a proper spin-orbit force, whose strengths (i.e., the Nilsson parameters κ and μ) are taken from Refs. [24-26].This single-particle term is given by
${\hat H_0}{\rm{ = }}\sum\limits_{\alpha} {c_{\alpha} ^{\dagger} {E_{\alpha} }} {c_{\alpha} },$

(2) where
$c_{\alpha} ^{\dagger} $ and$c_{\alpha} ^{}$ are the single-particle creation and annihiliation operators, respectively, labeled by a set of the spherical harmonic-oscillator quantum numbers,$\alpha = N, $ $ j,\, m$ .${E_{\alpha} }$ is the single-particle energy, given by${E_{\alpha} } = \hbar \omega \left[ {N - 2\kappa \hat l.\hat s - \kappa \mu \left( {{{\hat l}^2} - {{\left\langle {\hat l} \right\rangle }^2}} \right)} \right].$

(3) Note that the value of l is known when N and j are specified. ω is the harmonic-oscillator parameter, which incorporates the principle of volume conservation for nuclei deformed from spherical shapes; s and l represent the intrinsic nucleon spin and orbital angular momenta in the stretched co-ordinate basis. κ and μ are the Nilsson parameters.
The remaining terms in Eq. (1) are residual quadrupole-quadrupole, monopole, and quadrupole–pairing interactions, respectively. The operators appearing in Eq. (1) are defined as in Ref. [27], and the interaction strengths are determined as follows:
● The Q.Q interaction strength χ is adjusted by the self-consistent relation such that the input quadrupole deformation ε2 and that resulting from the HFB procedure agree with each other.
● All pairing interactions are assumed to occur between like nucleons (i.e., the isovector type). The monopole pairing strength, GM, first introduced by Dieterich et al. [28], is given by
${G_M} = {\rm{ }}\left( {{G_1} \mp {G_2}\frac{{N - Z}}{A}} \right)\frac{1}{A}$ , where “+ (-)” is for protons (neutrons). The choice of the strengths G1 and G2 depends on the size of the single-particle space in the calculation.● The quadrupole pairing strength, GQ, is assumed to be proportional to GM, and is generally set at approximately 1/5th of the monopole pairing constant, GM, allowing a ±10% variation to obtain the best representation of the experimental observations.
The next step is to diagonalize the Hamiltonian in the shell model space spanned by a selected set of projected multi-quasiparticle
$\left\{ {{\rm{ }}\hat P_{MK}^I\left| {{\phi _{\kappa} }} \right\rangle } \right\}$ states, where${\rm{ }}\left\{ {\hat P_{MK}^I} \right\}$ is the angular momentum projection operator that projects the quantum numbers I, M and is defined as${\rm{ }}\hat P_{MK}^I = \frac{{2I + 1}}{{8{\pi ^2}}}\int {{\rm d}\Omega D_{MK}^I} \left( \Omega \right)\hat R\left( \Omega \right).$

(4) Here,
$\hat R(\Omega )$ is the rotational operator,$D_{MK}^I(\Omega )$ is the D function [29] (irreducible representation of the rotation group), and Ω is the Euler angle. The D-functions form a complete set of functions in the parameter space of Ω. For the present study, the multi-quasiparticle states are chosen as$\left| {{\phi _{\kappa} }} \right\rangle = \left\{ {a_{\pi} ^{\dagger} \left| 0 \right\rangle ,a_{\pi} ^{\dagger} a_{{\nu _1}}^{\dagger} a_{{\nu _2}}^{\dagger} \left| 0 \right\rangle } \right\},$

(5) for odd-mass Pm and
$\left| {{\phi _{\kappa} }} \right\rangle = \left\{ {{\rm{ }}a_{{\upsilon _i}}^{{\dagger }}a_{{\pi _j}}^{{\dagger }}\left| 0 \right\rangle } \right\},$

(6) for odd-odd Pm nuclei, where a† is the quasiparticle (qp) creation operator, ν (π) denotes the neutron (proton) Nilsson quantum numbers, which run over low-lying orbitals, and
$\left| 0 \right\rangle $ is the Nilsson + BCS vacuum (0-qp state).Finally, the many-body wave function, which is a superposition of projected (angular momentum) multi-quasiparticle states, can be written as
$\left| {\Psi _{IM}^{\sigma} } \right\rangle = \sum\limits_{K\kappa } {f_{{\kappa _{}}}^{\sigma} \hat P_{MK}^I} \left| {{\phi _{\kappa} }} \right\rangle, $

(7) where the coefficients
$f_{\kappa} ^{\sigma} $ are the weights of the basis state κ, which are determined by diagonalization of the shell model Hamiltonian in the space spanned by the projected basis states given above. This leads to the eigenvalue equation (for a given spin I), which is given by$\sum\limits_{\kappa '} {\left\{ {{\rm{ }}H_{\kappa {\rm{ }}\kappa '}^I - E_{\sigma ,I}^{}{\rm{ }}N_{\kappa {\rm{ }}\kappa '}^{}} \right\}} {\rm{ }}f_{\kappa '}^{\sigma ,I} = 0,$

(8) with normalization condition
$\sum\limits_{\kappa \kappa '} {f_{\kappa} ^{\sigma ,I}{N_{\kappa \kappa '}}} f_{\kappa '}^{\sigma ',I'} = {\delta _{\sigma \sigma '}}{\delta _{I{\rm{ }}I'}},$

(9) where the Hamiltonian and norm matrix elements,
$H_{\kappa {\rm{ }}\kappa '}^I$ and$N_{\kappa {\rm{ }}\kappa '}^I$ , are defined, respectively, as$H_{\kappa {\rm{ }}\kappa '{\rm{ }}}^I = \left\langle {\mathop \phi \nolimits_{\kappa} } \right|\hat H{\rm{ }}{\hat P_{{K_{\kappa} }{{K'}_{\kappa '}}}}\left| {\mathop \phi \nolimits_{\kappa '} } \right\rangle \;\;\;{\rm{and}}\;\;\; \mathop N\nolimits_{\kappa {\rm{ }}\kappa '{\rm{ }}}^I = \left\langle {\mathop \phi \nolimits_{\kappa} } \right|\hat P_{{K_{\kappa {\rm{ }}}}K'{}_{\kappa '}}^{\rm{I}}\left| {\mathop \phi \nolimits_{\kappa '} } \right\rangle. $

(10) The projection of an intrinsic state
$\left| {{\phi _k}} \right\rangle $ on a good angular momentum generates a rotational energy of a band (or the band energy)${E_{\kappa} }(I) = \frac{{\langle {\varphi _{\kappa} }|\hat H\hat P_{K{\rm{ }}K}^I|{\varphi _{\kappa} }\rangle }}{{\langle {\varphi _{\kappa} }|\hat P_{K{\rm{ }}K}^I|{\varphi _{\kappa} }\rangle }} = \frac{{H_{\kappa \kappa }^I}}{{N_{\kappa \kappa }^I}},$

(11) which can be plotted as a function of spin for various bands, and important physics can be inferred from these plots.
-
The Shell model space in the present work is truncated by fitting the energy window around the neutron and proton Fermi surfaces at 4.50 MeV for the 1–quasiparticle and 9.50 MeV for the 3–quasiparticle basis states. The value of the quadrupole deformation parameter, ε2, is set as ~0.3 for all the nuclei under study, which is in agreement with the values given in Refs. [2-4]. In our meanfield Nilsson potential, which provides the optimal deformed basis, the hexadecapole deformation, ε4, has also been included and is set as ~ -0.090. The values of G1 and G2 are taken as 21.00 MeV and 10.70 MeV, respectively. The value of GQ in our work is set to be 0.16 times GM. The Nilsson parameters κ and µ are set according to the values given in Ref. [24]. In addition, in the present calculations, the three major shell single-particle configurations consist of N = 3, 4, 5 for protons and N = 4, 5, 6 for neutrons.
-
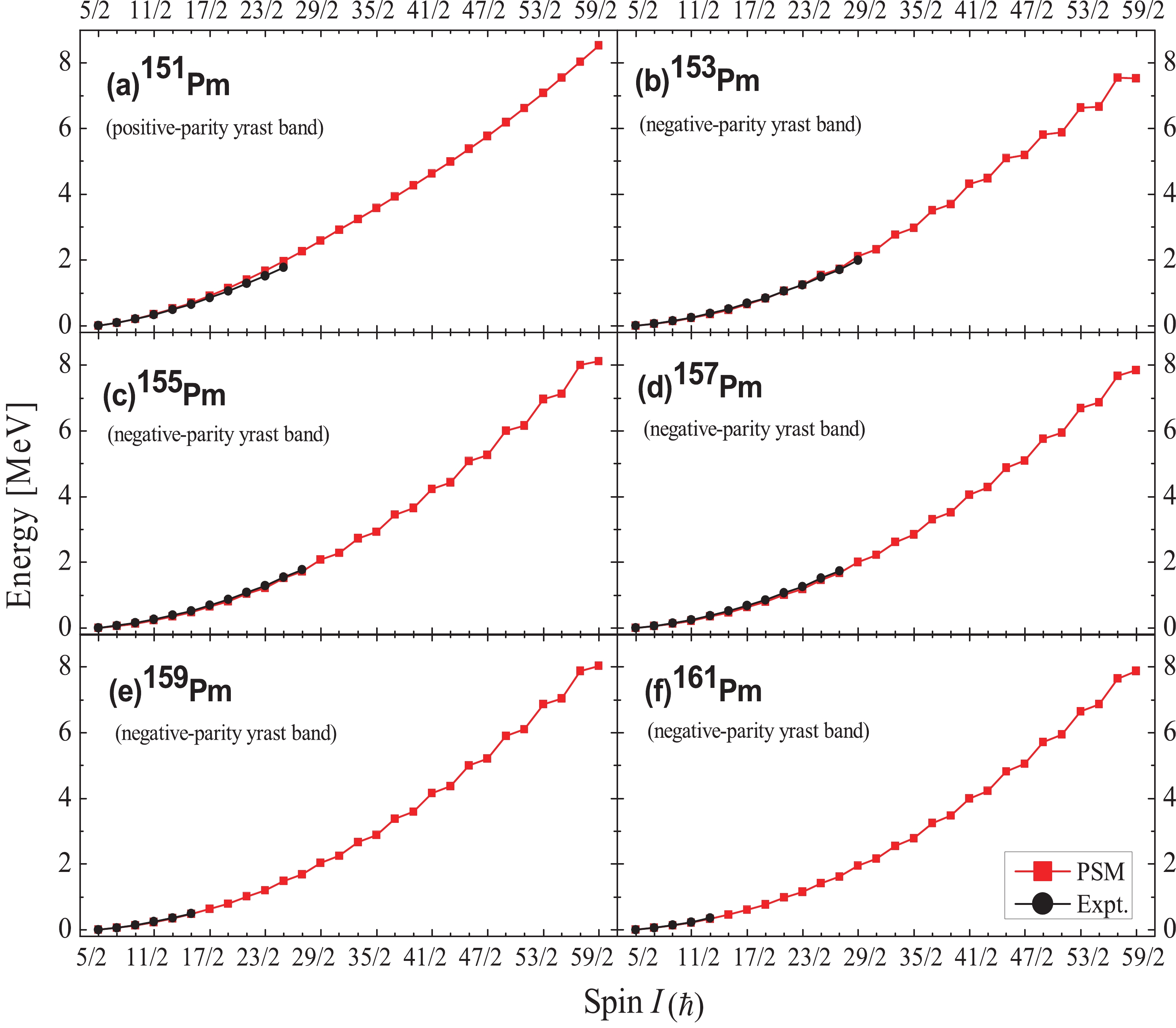
For the present study, the experimental data for the odd-mass 151-161Pm isotopes are taken from Refs. [3-5] and the NNDC database [30, 31]. The ground-state band in 151Pm [30] is reported to have a band head with spin and parity, Kπ = 5/2+, whereas all other odd-mass Pm isotopes under study have a ground-state band with a band head at Kπ = 5/2−. Note that the experimental data is sparse for these odd mass Pm isotopes. The maximum reported spin is 31/2− for 151Pm [30], 29/2− for 153Pm [5], 27/2− for 155, 157Pm [5, 31], 15/2− for 159Pm [4], and in case of 161Pm, the experimental data is available only up to a spin of 13/2− [4]. However, through our PSM calculations, we have been able to extend the yrast level scheme and obtained the higher energy levels up to a spin of 59/2ћ for all of these isotopes. Note that the ground-state bands of all of these odd-mass Pm isotopes, except for 151Pm, are negative parity bands, while 151Pm has a positive-parity band. However, a negative parity band in addition to the ground-state positive-parity band has also been reported in 151Pm, which is built on Kπ = 5/2− at an excitation energy of 0.117 MeV with respect to the ground state.
Our PSM calculations successfully reproduced the band-head spin and parity for all of these isotopes. The PSM energies for the ground-state yrast bands under study are plotted against the spin for the 151-161Pm isotopes in Figs. 1(a-f), whereas the excited negative-parity band of 151Pm is presented in Fig. 1(g). The available experimental data are also presented in the same figures for comparison. It is clear from the figures that the calculated PSM data reproduced the available experimental data with a satisfactory degree of agreement, where the maximum gap between the experimental and calculated energy levels is only ~0.124 MeV in the case of 153Pm for the 29/2− state, which proves the efficiency of the set of input parameters used in the PSM Hamiltonian to give a comprehensive description of the nuclear structure in this mass region.
It is worth mentioning here that the nuclei under study are located at the boundary of the octupole deformed lanthanide region [32, 33]. In fact, many research groups [10-12] have pointed out the presence of octupole deformation in 151Pm, whereas the possibility of the presence of a reflection asymmetric shape at N = 92 has also been reported in 153Pm [34]. However, Bhattacharyya et al. [5] in their recently documented work stated that the observed band structures of odd-A Pm isotopes do not show any indication of the presence of octupole deformation beyond N = 90. As the present PSM calculations have been performed using an axially symmetric Hamiltonian, the extent of agreement between the PSM results and the experimental data supports the findings of Bhattacharya et al. One more interesting feature of these nuclei is that the energy levels of the negative-parity bands for all Pm isotopes considered in the present work are very close to each other, indicating that the addition of a pair of high-j neutrons does not significantly affect the deformation of these nuclei. However, the addition of a pair of neutrons to 151Pm changes the Kπ of the yrast band from 5/2+ in 151Pm to 5/2− in 153Pm. This provides an idea regarding how the addition of neutrons in the high-j orbitals affects the energies of the proton orbitals under the same deformation.
-
A band diagram serves as a very useful tool for analyzing the PSM results. These are quite informative and can help unravel the intrinsic quasi-particle structures of the observed bands. Band diagrams are the plots of unperturbed energies before configuration mixing. In a band diagram, the rotational behavior of each configuration, as well as its relative energy compared with other configurations, can be easily visualized. In the present calculations, our configuration space is built by thirty-eight quasiparticle (qp) bands, out of which there are six 1-qp (1-quasiproton) bands and thirty-two 3-qp (1-quasiproton plus a pair of 2-
quasineutron ) bands. However, we have plotted only a few of the most important ones very close to the Fermi level in an energy window of approximately 5 MeV to illustrate the important physics. Moreover, we have marked each band with the corresponding qp configuration. Band diagrams for the yrast bands of 151-161Pm are shown in Figs. 2(a-g). The yrast band is also plotted in these figures to provide a clear understanding of how different bands interact to give rise to the yrast states. It is clearly visible from these figures that the 1-quasiproton band with the configuration 1πh11/2[5/2], |K|=5/2 is the dominant band affecting the formation of the ground-state yrast band in the odd-mass 153-161Pm isotopes and the negative-parity yrast band in 151Pm. The ground-state yrast band in 151Pm (which is a positive-parity band) is the band having the configuration 1πg9/2[5/2], K=5/2 originating from the πg7/2 orbital, which gives rise to the yrast spectra in the low- and mid-spin range.
The observation made in the present work is in agreement with the experimental results reported for these isotopes, which suggests that the yrast ground band in 151Pm is 5/2+ based on the 5/2+[413] configuration [12], whereas the non-yrast structure (negative-parity band) in 151Pm is reported to be based on a 5/2−[532] Nilsson configuration originating from the πh11/2 orbital. Furthermore, in the case of 153Pm, the yrast ground-state band built on K = 5/2− is also known to be constituted from the 5/2−[532] Nilsson orbital [35], which originates from the deformation driving πh11/2 orbital. Bhattacharyya et al. [5] suggested the same 5/2[532] configuration assignment for the observed negative-parity bands in 155,157Pm. A similar band structure to that of 153,155Pm is predicted for 159,161Pm by Yokoyama et al. [4]. This is very well reproduced by the present PSM calculations.
The other important thing that should be noted here is the very late occurrence or absence of band crossing in most of these isotopes. Their ground-state band is mostly dominated by the 1-qp bands. For the negative-parity band in 151Pm, the 1-qp band is crossed by a 3-qp band having the configuration 1πh11/2[5/2]+ 2νi13/2[−3/2,5/2], |K|= 7/2 at a spin of 45/2−, whereas the crossing is predicted at a spin of 49/2− in 153Pm. For 155Pm, the band crossing is further delayed and occurs at aspin of 53/2−, where the 1-qp 1πh11/2[5/2], |K|=5/2 band is crossed by a 3-qp 1πh11/2[1/2]+ 2νi13/2[5/2, −7/2], |K|= −1/2 band. Moving to higher-N/Z Pm isotopes, no band crossing is observed up to a spin of 59/2−. There may be a crossing occurring at higher spins than 59/2−, but we restrict our study to a spin of 59/2− only, as the experimental data have not been reported for such higher spins.
For the positive-parity ground state band in 151Pm, the 1-quasiproton band, 1πg9/2[5/2], |K|=5/2, is crossed by the 3-qp band identified to have the configuration 1πg9/2[5/2]+ 2νi13/2[-3/2,5/2], |K|= 7/2 at a spin of 43/2+, whereafter its interaction with another 3-qp band with |K| = 1/2 gives rise to the yrast spectra for the rest of the spins. The band structure of the ground-state band of 151Pm is quite different from the band structures of the other odd-mass Pm isotopes under study. One possible reason may be the presence of octupole correlation resulting from he closely lying 5/2−[532] and 5/2+[413] bands that originate from the g7/2 and h11/2 proton orbitals. However, our study is restricted to axial symmetry only, so we cannot comment on this in detail. Also, in the low-spin range, odd-mass 153-161Pm has almost the same band structure, which explains the presence of levels of nearly the same energies in their ground-state bands.
-
In the PSM approach, the eigenvalues of energy, along with the amplitude of wave functions, are obtained by diagonalization of the total Hamiltonian. Schematic analysis of the probability amplitude of various n-qp configurations for odd-mass 151-161Pm isotopes was performed in the present work. The average probability amplitudes of 1-qp and 3-qp configurations were plotted versus spin, and the results are displayed in Figs. 3(a-g) respectively.
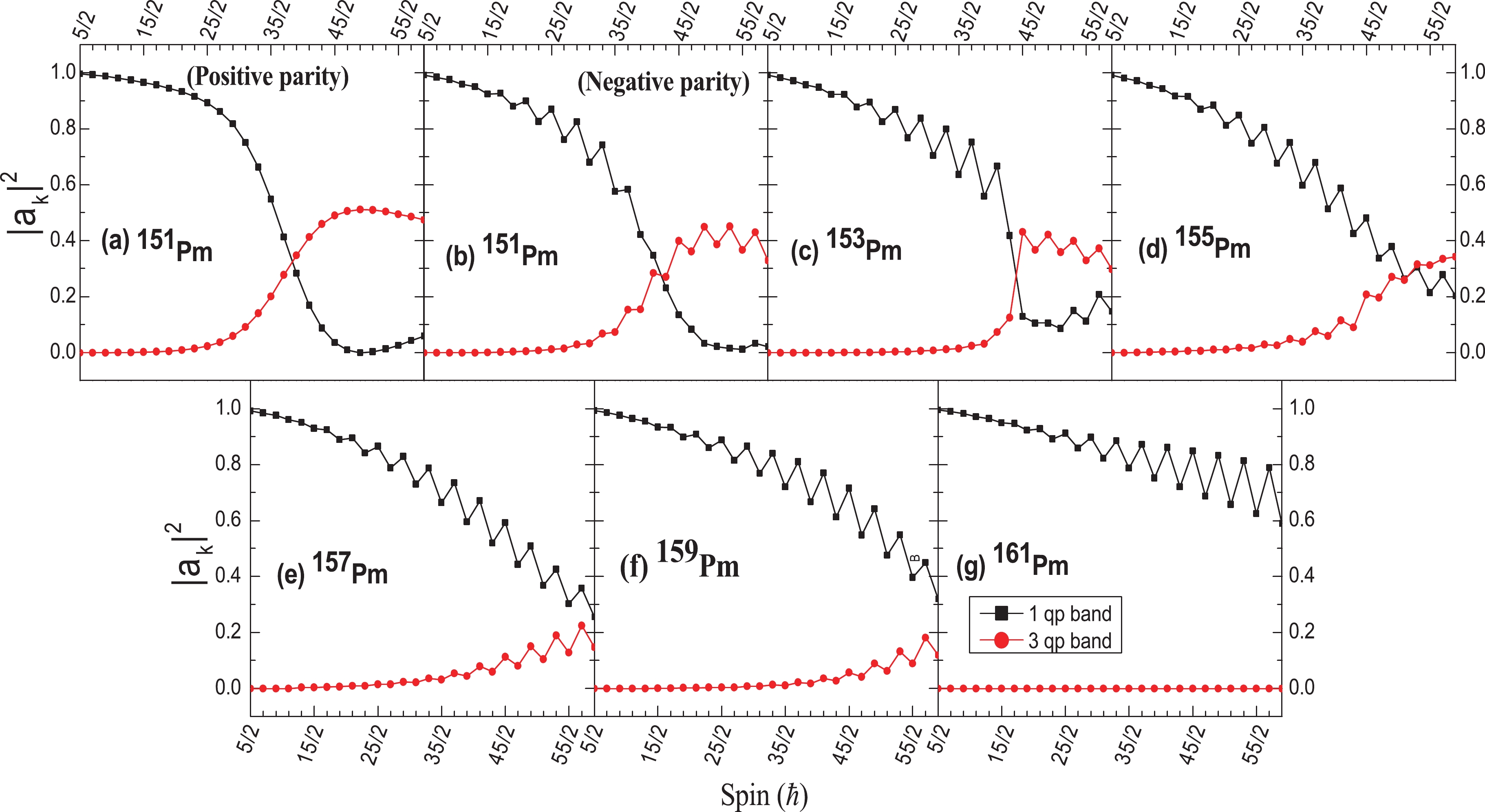
Figure 3. (color online) Probability amplitude of various projected K-configurations in the wave functions of the yrast bands for 151-161Pm.
For these Z=61 isotopes, it is clear from the probability amplitude plots that the lower spins of the ground-state bands arise solely from the contribution of the 1-qp configurations, whereas the contribution from the 3-qp configurations at higher spins for 151,153, & 155Pm isotopes is also predicted by the present PSM calculations. For the 157-161Pm isotopes, the dominance of the 1-qp configurations over the whole spin range, up to 59/2−, is established from the present analysis. Also, the absence of crossing between the 1-qp and 3-qp bands in these 157,159,161Pm isotopes, as depicted by the band diagrams [Fig. 2(e-g)], is supported by analysis of the amplitude of the wave functions of these qp configurations.
-
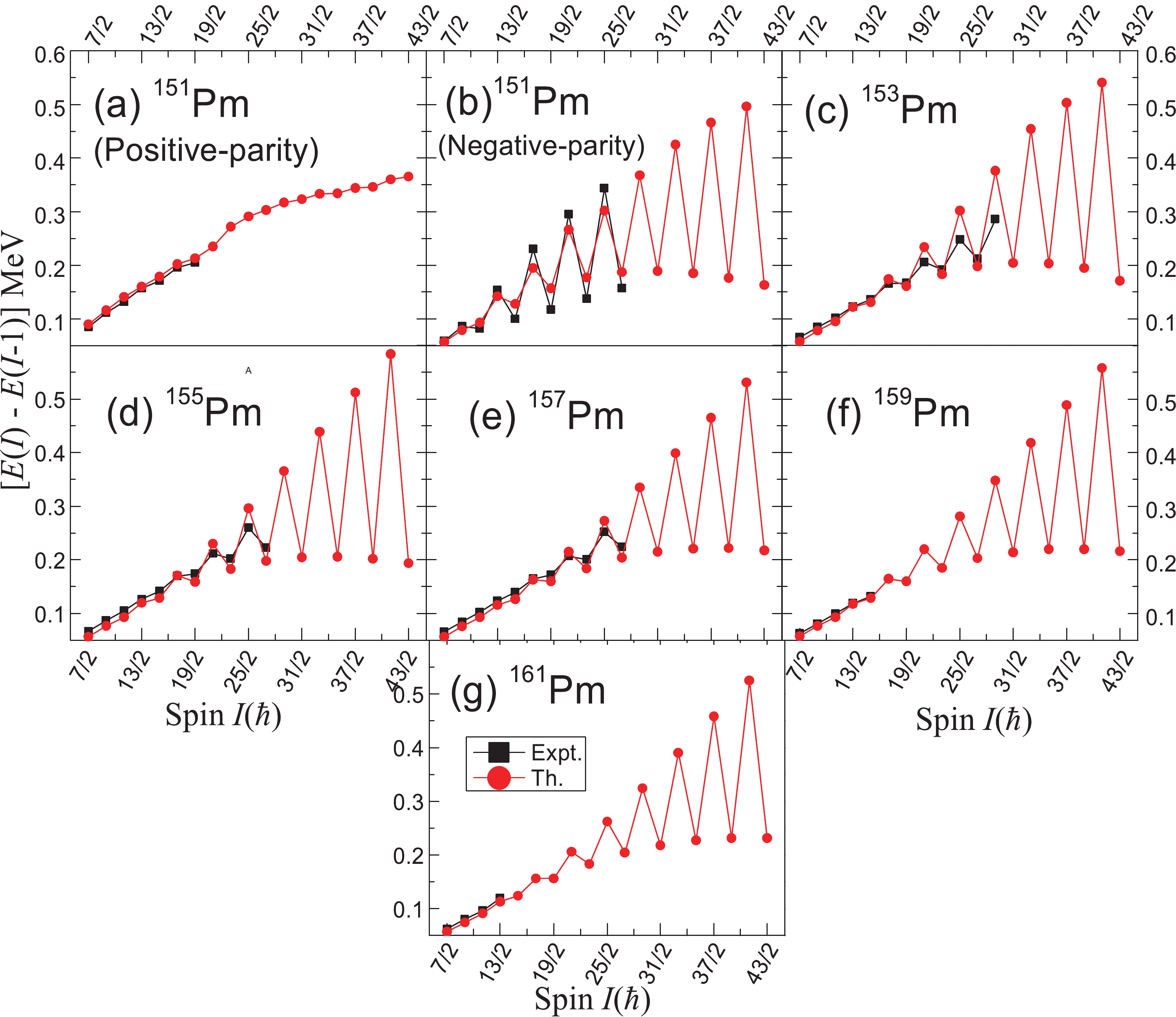
The transition energies [E(I) −E(I − 1)] of the states in the yrast bands of the odd-A Pm isotopes under study are presented in Figs. 4(a-g) as a function of spin I. It is evident from the figures that staggering in the energies of odd-even spin states is present for all of these nuclei. In the case of 151Pm, the positive-parity ground-state band shows small shifts in the energies of odd-even states, whereas the energy staggering is more prominent in the negative-parity band (1πh11/2[5/2]) of 151Pm corresponding to the 5/2−[532] orbital. The amount of staggering further increases in this case as we move toward the high-spin domain. The rest of the Pm isotopes (odd-A 153-161Pm) show a similar trend of variation of the quantity [E(I) −E(I − 1)] versus spin for their ground bands, where in the low-spin range, the extent of staggering is small, becoming moderate in the mid-range spin range; then, in the high-spin domain, this odd-even energy difference becomes quite large, with a maximum difference of ~0.4 MeV. However, no sign of inversion of the staggering pattern is found in the present analysis for any of these isotopes. The staggering pattern shown by the yrast bands in these nuclei are very much in accordance with the staggering pattern shown by the probability amplitude of the wave functions [Figs. 3(a-g)].
-
The electromagnetic transition probabilities calculated using PSM contain detailed information on the nuclear wave function, which can aid in enhancing our knowledge of the nuclear structure of the nuclei under study. The reduced electric quadrupole transition probability B(E2) from an initial state (Ii = I) to a final state (If = I - 2) is given by [36]
$B(E2, I \to I - 2) = \frac{{{e^2}}}{{2I + 1}}{\left| {{\rm{ }}\left\langle {{\psi ^{I - 2}}} \right|{\rm{ }}\left| {{\rm{ }}{{\hat Q}_2}{\rm{ }}} \right|{\rm{ }}\left| {{\psi ^I}} \right\rangle {\rm{ }}} \right|^2}.$

The E2 transitions from Ii = I to If = I-2 are of interest; therefore, the operator
${\hat Q_2}$ is related to the quadrupole operator by${\hat Q_{2{\rm{ }}\nu }}{\rm{ }} = {\rm{ }}e_{\nu} ^{{\rm{eff}}}\sqrt {\frac{5}{{16\pi }}} Q_{\nu} ^2,\;\;\;\;{\hat Q_{2{\rm{ }}\pi }}{\rm{ }} = {\rm{ }}e_{\pi} ^{{\rm{eff}}}\sqrt {\frac{5}{{16\pi }}} Q_{\pi} ^2.$

(12) The standard values of effective charges that are used in these expression are
${\rm{ }}e_{\nu} ^{{\rm{eff}}}$ = 0.5e for neutrons and${\rm{ }}e_{\pi} ^{{\rm{eff}}}$ = 1.5e for protons. However, these values of effective charges may be adjusted to take into consideration the effects of core polarization.The reduced magnetic transition probability can also be calculated using PSM wave functions. Magnetic dipole transition strengths are sensitive to the single-particle attributes of the nuclear wave function. The reduced magnetic dipole transition probability B(M1) is computed as
$ B\left( {M1,I \to I - 1} \right) = \frac{{\mu _N^2}}{{2I + 1}}{\rm{ }}{\left| {{\rm{ }}\left\langle {{\psi ^{I - 1}}} \right.\left| {{\rm{ }}\left| {{{\hat M}_1}} \right|{\rm{ }}} \right|{\rm{ }}\left. {{\psi ^I}} \right\rangle {\rm{ }}} \right|^2}, $

(13) where the magnetic dipole operator is defined as
$\hat {\rm M}_{{{\rm{ }}1}}^{\tau} = g_l^{\tau} {\hat j^{\tau} } + \left( {g_s^{\tau} - g_l^{\tau} } \right){\rm{ }}{\hat s^{\tau} },$

(14) where τ is either π or ν, and gl and gs are the orbital and spin gyromagnetic factors, respectively. The standard free values of gl and gs for protons and neutrons are
$ g_{l}^{\pi }=1,g_{l}^{\nu }=0,g_{s}^{\pi }=5.586,\ \ {\rm{and}}\ \ g_{s}^{\nu }=-3.826. $

However, in the PSM calculations, the free values of
$g_l^{\pi} $ &$g_l^{\nu} $ are used, whereas$g_s^{\pi} $ &$g_s^{\nu} $ are generally damped by a factor of 0.75 from the free-nucleon values to account for the core-polarization and meson-exchange current corrections [37]. Also, as the configuration space is sufficiently large, we do not use any core contribution.The reduced matrix element of an operator
$\hat O$ ($\hat O$ is either$\hat Q$ or$\hat M$ ) is expressed by$ \begin{split} \left\langle {{\psi ^{{I_f}}}} \right.\left\| {{\rm{ }}{{\hat O}_L}{\rm{ }}} \right\|\left. {{\rm{ }}{\psi ^{{I_i}}}} \right\rangle = \sum\limits_{{\kappa _i},{\kappa _f}} {f_{{I_i}{\kappa _i}}^{{\sigma _i}}} f_{{I_f}{\kappa _f}}^{{\sigma _f}}\sum\limits_{{M_i},{M_f},M} {{\rm{ }}( - 1)} {{\rm{ }}^{{I_f} - {M_f}}}{\rm{ }} \end{split} $

$ \begin{split}&\quad\quad\times\left( {{\rm{ }}\begin{array}{*{20}{c}} {{{\rm{I}}_{\rm{f}}}} \\ {{\rm{ - }}{{\rm{M}}_{\rm{f}}}} \end{array}{\rm{ }}\begin{array}{*{20}{c}} {\rm{L}} \\ {\rm{M}} \end{array}{\rm{ }}\begin{array}{*{20}{c}} {{{\rm{I}}_{\rm{i}}}} \\ {{{\rm{M}}_{\rm{i}}}} \end{array}} \right)\\ &\quad\quad\times \left\langle {{\phi _{{\rm{ }}{\kappa _f}}}} \right|\hat P_{{K_{{\kappa _f}}}{M_f}}^{{I_f}}{\hat O_{L{\rm{ }}M}}\hat P_{{K_{\kappa {}_i}}{M_i}}^{I_i^{}}\left| {{\phi _{{\kappa _{\rm{i}}}}}} \right\rangle \end{split}. $

(15) Reduced transition probabilities, B(E2)’s and B(M1)’s, have been calculated for the yrast band in 151-161Pm isotopes using the PSM wave functions according to Eqs. (11) and (13). The results are presented in Tables 1 and 2, respectively for B(E2) and B(M1).
151Pm 153Pm 155Pm Transition B(E2↓)(Positive-parity Yrast) Transition B(E2↓)(Negative-parity) Transition B(E2↓) Transition B(E2↓) 9/2+ →5/2+ 3.50 9/2ˉ →5/2ˉ 0.306 9/2ˉ →5/2ˉ 3.03 9/2ˉ →5/2ˉ 0.096 11/2+→7/2+ 0.788 11/2ˉ→7/2ˉ 1.35E-4 11/2ˉ→7/2ˉ 0.67 11/2ˉ→7/2ˉ 0.341 13/2+→9/2+ 0.0909 13/2ˉ→9/2ˉ 0.0962 13/2ˉ→9/2ˉ 0.0732 13/2ˉ→9/2ˉ 0.563 15/2+→11/2+ 0.0057 15/2ˉ→11/2ˉ 0.266 15/2ˉ→11/2ˉ 0.0066 15/2ˉ→11/2ˉ 0.724 17/2+→13/2+ 0.11 17/2ˉ→13/2ˉ 0.431 17/2ˉ→13/2ˉ 0.102 17/2ˉ→13/2ˉ 0.858 19/2+→15/2+ 0.265 19/2ˉ→15/2ˉ 0.571 19/2ˉ→15/2ˉ 0.239 19/2ˉ→15/2ˉ 0.941 21/2+→17/2+ 0.422 21/2ˉ→17/2ˉ 0.687 21/2ˉ→17/2ˉ 0.376 21/2ˉ→17/2ˉ 1.02 23/2+ →19/2+ 0.565 23/2ˉ →19/2ˉ 0.78 23/2ˉ →19/2ˉ 0.499 23/2ˉ →19/2ˉ 1.06 25/2+→ 21/2+ 0.690 25/2ˉ→ 21/2ˉ 0.858 25/2ˉ→ 21/2ˉ 0.606 25/2ˉ→ 21/2ˉ 1.13 27/2+→ 23/2+ 0.797 27/2ˉ→ 23/2ˉ 0.919 27/2ˉ→ 23/2ˉ 0.698 27/2ˉ→ 23/2ˉ 1.139 29/2+→ 25/2+ 0.889 29/2ˉ→ 25/2ˉ 0.973 29/2ˉ→ 25/2ˉ 0.776 29/2ˉ→ 25/2ˉ 1.19 Table 1. Calculated B(E2↓) values (in e2b2) for odd-A 151-161Pm isotopes.
151Pm 153Pm 155Pm Transition B(M1↓) (Positive-parity Yrast) Transition B(M1↓) (Negative-parity) Transition B(M1↓) Transition B(M1↓) 7/2+→5/2+ 0.052 7/2ˉ→5/2ˉ 5.84E-6 7/2ˉ→5/2ˉ 0.082 7/2ˉ→5/2ˉ 0.0853 9/2+ →7/2+ 0.000021 9/2ˉ →7/2ˉ 0.124 9/2ˉ →7/2ˉ 1.1E-4 9/2ˉ →7/2ˉ 0.123 11/2+→9/2+ 0.151 11/2ˉ→9/2ˉ 0.189 11/2ˉ→9/2ˉ 0.0075 11/2ˉ→9/2ˉ 0.142 13/2+→11/2+ 0.244 13/2ˉ→11/2ˉ 0.227 13/2ˉ→11/2ˉ 0.012 13/2ˉ→11/2ˉ 0.154 15/2+→13/2+ 0.305 15/2ˉ→13/2ˉ 0.25 15/2ˉ→13/2ˉ 0.015 15/2ˉ→13/2ˉ 0.16 17/2+→15/2+ 0.348 17/2ˉ→15/2ˉ 0.265 17/2ˉ→15/2ˉ 0.017 17/2ˉ→15/2ˉ 0.166 19/2+→17/2+ 0.379 19/2ˉ→17/2ˉ 0.274 19/2ˉ→17/2ˉ 0.0185 19/2ˉ→17/2ˉ 0.167 21/2+→19/2+ 0.403 21/2ˉ→19/2ˉ 0.28 21/2ˉ→19/2ˉ 0.0196 21/2ˉ→19/2ˉ 0.171 23/2+→21/2+ 0.421 23/2ˉ→21/2ˉ 0.282 23/2ˉ→21/2ˉ 0.0205 23/2ˉ→21/2ˉ 0.17 25/2+ →23/2+ 0.436 25/2ˉ →23/2ˉ 0.284 25/2ˉ →23/2ˉ 0.0213 25/2ˉ →23/2ˉ 0.174 27/2+→25/2+ 0.445 27/2ˉ→25/2ˉ 0.282 27/2ˉ→25/2ˉ 0.0219 27/2ˉ→25/2ˉ 0.171 29/2+→27/2+ 0.454 29/2ˉ→27/2ˉ 0.2826 29/2ˉ→27/2ˉ 0.0226 29/2ˉ→27/2ˉ 0.176 Table 2. Calculated B(M1↓) values (in
$ {\mu }_{N}^{2} $ ) for odd-A 151-161Pm isotopes.Prior to this work, no information had been reported on experimental as well as theoretical fronts regarding the reduced transition probabilities for these nuclei. Through the present calculations, we have been able to obtain the data concerning reduced transition probabilities for the yrast energy states up to a spin of 59/2. However, in Tables 1 and 2, we have provided results up to a spin of 29/2 only. Regarding the B(E2) transition probabilities, the PSM predicts that the quadrupole electric transition probabilities for these isotopes tend to decrease first and then increase gradually, possibly because of the decrease in the pairing correlations at smaller angular momentum. Conversely, the B(M1) transition probabilities show a similar increasing pattern for all of these isotopes. These values are obtained from the PSM wave functions and depend on the band structure of the nuclei. Here, a general trend for the B(E2) and B(M1) transition probabilities has been predicted by calculation for these isotopes. Although we would like to wait for some experimental data to be reported in the near future to make a final comment on this tendency and on the efficacy of our model for describing the nuclear structure properties of these rare earth nuclei, still, the data obtained in the present calculations can serve as a good base for future experimental as well as theoretical studies.
-
Manal Mahmoud Sirag [38] pointed out that the spectroscopic information for high-spin states of odd-odd nuclei near A = 150–170 provides a suitable insight for studying the interplay between single-particle and collective motion, and for probing the residual neutron-proton interaction. Still, very little information has been reported for the odd-odd nuclei in comparison with the even-even and odd-mass nuclei in this region for various reasons, including the presence of long-lived isomers in odd-odd nuclei
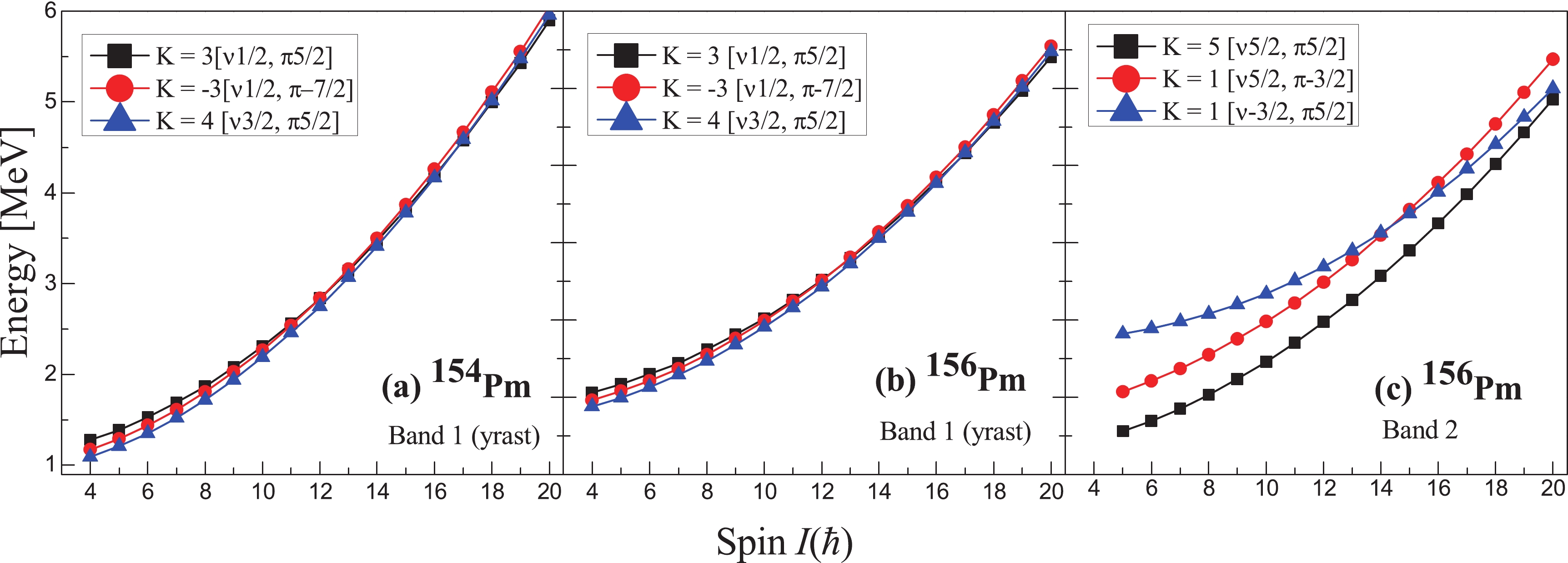
. In particular, regarding the neutron-rich odd-odd Pm isotopes, the amount of experimental data is rather sparse. Recently, Bhattacharyya et al. [5] reported the in-beam measurements of prompt γ rays of neutron-rich 152,154,156,158Pm isotopes. However, no firm spin and parity assignment or initial and final states were established in this work, as a result of which proper configurations could not been assigned for the 2-qp rotational bands in these odd-odd Pm isotopes. Recently, Liu et al. [3] in their theoretical work made configuration and bandhead spin assignments for the three 2-quasiparticle bands in 154,156Pm. In their work, for the 2-qp band in 154Pm, the configuration was assigned as π5/2−[532] $\otimes $ ν3/2−[521] (Kπ = 4+) with the bandhead spin 4ħ. In 156Pm, the configurations of the two 2-quasiparticle bands were assigned as π5/2−[532]$\otimes $ ν3/2−[521] (Kπ = 4+) with the bandhead spin 4ħ, and π5/2+[413]$\otimes $ ν5/2+[642] (Kπ = 5+) with the bandhead spin 5ħ, respectively, where the Kπ = 4+ band was predicted to be the lowest band.In the present work, we attempted to further understand the structure of these two odd-odd isotopes of Pm with A=154 and 156. Through our PSM calculations, we have been able to reproduce the bandhead spins and parities of the ground-state bands (lowest bands) in 154,156Pm as recommended by Liu et al. [3]. Additionally, one more band, ‘Band2’ of 156Pm with higher excitation energy than the ground-state band, was also obtained in the calculations. The results are presented in Fig. 5, where comparison of the PSM results with the experimental level schemes of these isotopes taken from Ref. [5] shows a good degree of agreement.

Figure 5. (color online) PSM data on yrast bands of 154,156Pm in comparison with the experimental data [3]. A side band, 'Band 2' of 156Pm, is also presented.
The band diagrams of 154,156Pm are presented in Fig. 6. In the diagrams for these odd-odd isotopes, the projected energies are shown for 2-quasiparticle configurations (with K = Kν ± Kπ). Careful analysis of the band diagrams of 154,156Pm reveals that the yrast bands of both these isotopes have composite structures because of the mixing of three very closely lying bands. In the case of 154Pm, there are three 2-qp bands with bandheads K = 3, -3, and 4 lying very close to each other with an energy gap of ~0.5 MeV; these interact with each other to give rise to the yrast band in this nucleus. However, it is the band with configuration |K| = 4[ν3/2, π5/2] (neutron from the 3/2−[521] orbital and proton from 5/2−[532] orbital) that dominates the contribution toward the yrast band, thereby assigning the configuration |K| = 4[ν3/2, π5/2] to the ground-state band. A very similar band diagram is obtained for 156Pm, where the same configuration (|K| = 4[ν3/2, π5/2]) for the yrast ground-state band as that of 154Pm is predicted by the PSM calculations. Further, for the excited band of 156Pm, the main contribution comes from the |K| = 5[ν5/2, π5/2] band; thus, this configuration is assigned to the excited band of the 156Pm where the quasineutron band arises from the 5/2+[642] neutron orbit and the quasiproton band comes from the 5/2+[413] orbital. The configurations assigned to these 2-qp bands in the present work are found to be in accordance with the work of Liu et al. [3]. The information on the transition probabilities, B(M1) and B(E2), has also been extracted for these odd-odd nuclei, and the results are presented in Tables 3 and 4. This is the first time that such detailed data have been reported for these properties of odd-odd Pm isotopes, making this subject appropriate for further experimental verification.
Transition B(E2↓) 154Pm 156Pm Band 1 Band 1 Band 2 6+ → 4+ 1.21 1.24 7+ → 5+ 0.969 1.01 1.57 8+ → 6+ 0.742 0.785 1.46 9+ → 7+ 0.55 0.598 1.27 10+ →8+ 0.359 0.411 1.08 11+→ 9+ 0.247 0.291 0.917 12+ → 10+ 0.137 0.172 0.774 13+ → 11+ 0.089 0.111 0.653 14+ → 12+ 0.052 0.0679 0.55 15+ → 13+ 0.0344 0.042 0.461 16+ → 14+ 0.023 0.029 0.387 17+ → 15+ 0.0159 0.0189 0.323 18+ → 16+ 0.0118 0.0148 0.271 19+ → 17+ 0.0086 3.5E-4 0.224 20+ →18+ 0.00696 1.47E-4 0.189 Table 3. Calculated B(E2↓) values (in e2b2) for 154,156Pm isotopes
Transition B(M1↓) 154Pm 156Pm Band 1 Band 1 Band 2 5+ → 4+ 0.0378 0.0442 6+ → 5+ 0.1733 0.179 0.194 7+ → 6+ 0.259 0.275 0.307 8+ → 7+ 0.437 0.444 0.378 9+ → 8+ 0.342 0.378 0.424 10+ →9+ 0.542 0.579 0.455 11+→ 10+ 0.205 0.257 0.476 12+ → 11+ 0.44 0.508 0.491 13+ → 12+ 0.0579 0.0855 0.501 14+ → 13+ 0.3 0.359 0.509 15+ → 14+ 0.0106 0.0176 0.515 16+ → 15+ 0.2 0.2392 0.519 17+ → 16+ 0.0014 0.00245 0.522 18+ → 17+ 0.136 0.156 0.524 19+ → 18+ 2E-4 1.979E-5 0.526 20+ →19+ 0.0937 2E-4 0.527 Table 4. Calculated B(M1↓) values (in
$ {\mu }_{N}^{2} $ ) for 154,156Pm isotopes -
The nuclear structure properties of odd-mass 151-161Pm and odd-odd 154,156Pm isotopes have been studied using the theoretical framework of the Projected Shell Model and using an axial (prolate) deformation of ~0.3. The correspondence between the experimental and calculated levels was investigated using the electromagnetic properties, which allowed us to establish the degree of reliability of the wave functions obtained in this work. The calculations described the fine details of the experimental data quantitatively and qualitatively, and, wherever the experimental data are not available, general trends are reproduced.
The level schemes of the odd-mass 151-161Pm nuclei were obtained up to a spin of 59/2 in this work. The late occurrence of the band crossing between the 1-qp and the 3-qp band was observed for 151,153,155Pm, whereas no crossing was found to occur for the rest of the odd-mass Pm isotopes. Moreover, the yrast band in 157,159,161Pm was found to have only 1-qp characteristics up to the calculated spin of 59/2ћ with the configuration assignment of 1πh11/2[5/2], |K|=5/2. For the odd-odd 154,156Pm nuclei, PSM calculations helped to understand their structure in some detail. The previously assigned configurations of one 2-qp band (π5/2−[532]
$\otimes $ ν3/2−[521] (Kπ = 4+)) in 154Pm and two 2-qp (π5/2−[532]$\otimes $ ν3/2−[521] (Kπ = 4+) and π5/2+[413]$\otimes $ ν5/2+[642] (Kπ = 5+)) bands in 156Pm has been confirmed in the present work.The present calculations also endorse the absence of octupole correlations in these nuclei. Furthermore, signature-splitting is present in the yrast energy states of these nuclei in middle- and higher-spin ranges, but signature inversion is not found to occur up to the calculated values of spin. The data regarding the transition probabilities for all these nuclei under study were reported for the first time in this work. As no prior information is available for these properties of the Pm isotopes under study, the results are promising for future experimental verification.
Systematic study of odd-mass 151-161Pm and 154,156Pm isotopes using projected shell model
- Received Date: 2020-04-03
- Available Online: 2020-09-01
Abstract: Inspired by the availability of recent experimental as well as theoretical data on the energy levels of odd-mass 151-161Pm and odd-odd 154,156Pm, we applied the theoretical framework of the projected shell model to further understand the nuclear structure of these nuclei. The calculations closely reproduced the experimental data reported for the yrast bands of these isotopes by assuming an axial (prolate) deformation of ~0.3. Other properties along the yrast line, such as transition energies and transition probabilities, have also been discussed. Band diagrams are plotted to understand their intrinsic multi-quasiparticle structure, which turn out to be dominated by 1-quasiparticle bands for the odd-mass Pm isotopes and 2-quasiparticle bands for the doubly-odd Pm isotopes under study. The present study not only confirms the recently reported experimental/theoretical data, but also extends the already available information on the energy levels and adds new information regarding the reduced transition probabilities.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: