-
The Circular Electron Positron Collider (CEPC) [1] is a particle physics research program of great scientific significance and has great potential. The concept of the CEPC is developed in the context of many international large colliders, such as the Large Hadron Collider (LHC) at the European Center for Nuclear Research (CERN). In contrast to previous colliders with high energy consumption and costs as well as the pressure of data processing and storage, the CEPC has unique features and advantages. Firstly, the CEPC is an electron collider in which positrons and electrons collide with each other to produce high-energy particle events. Unlike hadron collisions, electron collisions produce particle events that are much clearer and more controllable, facilitating precise measurements and particle identification. Secondly, the CEPC plans to build a highly detailed detector that will be able to capture and record all the important information in particle collisions, providing physicists with a large amount of data to study the behavior of elementary particles. In addition, the CEPC will invest significant effort in improving data processing and storage techniques to cope with the high density of collision data. Finally, the CEPC has a much brighter and cleaner experimental environment. The standard model (SM) observables can be studied with unprecedented precision, and the precision of many electroweak observables can be improved by an order of magnitude or more. Therefore, the CEPC offers an unmatched opportunity for precision measurements and searches far beyond the standard model (BSM) physics.
Among the many new physics (NP) scenarios, a class of models can predict the existence of leptophilic gauge boson
$ Z_x $ ; this kind of new neutral gauge boson arises due to the extension of a group in the standard model (SM) with the$ U(1)_{L_x-L_y} $ for$ x, y \in \{e, \mu, \tau \}$ [2−4]. The global symmetry$ U(1)_{L_x-L_y} $ can be introduced to the SM, which is anomaly-free, without any additional particles [5, 6]. When the$ U(1)_{L_x-L_y} $ gauge symmetry is spontaneously broken, the leptophilic gauge boson$ Z_x $ gains mass. This class of models can be a good solution to solve some problems in the SM, such as the neutrino mass and mixing problem [7−9], the dark matter dark energy problem [9−12], and the muon anomalous magnetic moment problem [13−15]. In our paper, we discuss the possibility of probing this class of the leptophilic gauge boson$ Z_x $ at the CEPC.The study of the leptophilic gauge boson
$ Z_x $ is an important step in exploring NP. The$ Z_x $ boson can be produced at current collider experiments. For example, at the LHC, the leptophilic gauge boson$ Z_x $ is mainly produced via the Drell-Yan process, where the$ Z_x $ is radiated from the final-state leptons; the constraints on the$ Z_x $ boson can be given via the processes$ pp\rightarrow 4\ell, 3\ell+ E_T^{miss}, 2\ell+E_T^{miss} $ , or$ 1\ell+E_T^{miss} $ [16−19]. At the KEKB collider, the leptophilic gauge boson$ Z_x $ is produced via the process$ e^+e^-\rightarrow \mu^+\mu^-Z_x(Z_x\rightarrow \mu^+\mu^-) $ in the framework of the$ U(1)_{L_\mu-L_\tau} $ model in the small mass range$ M_{Z_x}<10 $ GeV [20]. The processes$ e^+e^-\rightarrow Z_x\rightarrow \ell^+\ell^- $ or$ q\bar{q} $ [21] and$ e^+e^-\rightarrow \gamma Z_x(\rightarrow \ell^+\ell^-, \mu^+\mu^-) $ [22] can also be used to search for the$ Z_x $ boson at the LEP and BABAR. Most of the LHC (and Tevatron) bounds coming from resonance searches do not directly apply to such a neutral leptophilic sector. The relevant collider constraints of the$ U(1)_{L_e-L_\mu} $ model mainly come from the LEP and are generally much weaker than the direct LHC constraints applicable for hadrophilic resonances [23]. Therefore, the future$ e^+e^- $ colliders are uniquely capable of probing the leptophilic gauge boson$ Z_x $ to unprecedented mass and coupling values. Previous studies [24, 25] have investigated the sensitivity of the process$ e^+e^-\rightarrow Z_x \gamma $ to explore the leptophilic gauge boson$ Z_x $ in future$ e^+e^- $ colliders. In general, properties of any new particle can be studied via different processes, even for the same collider experiments. Furthermore, we find that there are few studies that search for the gauge boson$ Z_x $ predicted by the$ U(1)_{L_e-L_\mu} $ model via four-lepton final state processes at future$ e^+e^- $ colliders; hence, we propose searching for this kind of leptophilic gauge boson$ Z_x $ via the processes$ e^+e^-\rightarrow \ell^+\ell^-Z_x(Z_x\rightarrow \ell^+\ell^-) $ and$ e^+e^-\rightarrow \ell^+\ell^-Z_x (Z_x\rightarrow \nu_\ell\bar{\nu_\ell}) $ at the 240 GeV CEPC. We expect these processes to give better sensitivities in the certain mass range.The remainder of the paper is organized as follows. Section II briefly introduces the
$ U(1)_{L_e-L_\mu} $ model and summarizes the constraints of existing experiments on the model. Based on the details of the analysis of the$ Z_x $ signal processes$ e^+e^-\rightarrow \ell^+\ell^-Z_x(Z_x\rightarrow \ell^+\ell^-) $ and$ e^+e^-\rightarrow \ell^+\ell^-Z_x (Z_x\rightarrow \nu_\ell\bar{\nu_\ell}) $ and the relevant SM backgrounds, the sensitivity projections of the CEPC to the$ U(1)_{L_e-L_\mu} $ model parameter space are presented and compared with other experimental results in Section III. Finally, the conclusion and discussion are given in Section IV. -
The
$ U(1)_{L_x-L_y} $ model [2−4] comprises the SM gauge group$ SU(3)_C\otimes SU(2)_L\otimes U(1)_Y $ expanding a$ U(1)_{L_x-L_y} $ group without introducing an anomaly. This surprising feature is the main motivation considered here. For convenience, in Table 1, we list the lepton charges for the$ U(1)_{L_x-L_y} $ models. Here, e, μ, and τ are three generations of charged leptons;$ \nu_e $ ,$ \nu_\mu $ , and$ \nu_\tau $ represent the corresponding left-handed neutrinos, respectively.Model Charge $ e,\nu_e $ 

$ \mu, \nu_\mu $ 

$ \tau, \nu_\tau $ 

$ L_e-L_\mu $ 

$ 1 $ 

$ -1 $ 

$ 0 $ 

$ L_e-L_\tau $ 

$ 1 $ 

$ 0 $ 

$ -1 $ 

$ L_\mu-L_\tau $ 

$ 0 $ 

$L_e-\dfrac{1}{2}(L_{\mu}+L_{\tau})$ 

$ -1 $ 

$ L_e-\dfrac{1}{2}(L_\mu+L_\tau) $ 

$ 1 $ 

$ -\dfrac{1}{2} $ 

$ \dfrac{1}{2} $ 

$ L_e+2(L_\mu+L_\tau) $ 

$ 1 $ 

$ 2 $ 

$ 2 $ 

Table 1. Lepton charges corresponding to the
$ U(1)_{L_x-L_y} $ models.The Lagrangian part of the
$ U(1)_{L_e-L_\mu} $ model can be written as$ \begin{aligned}[b] \mathcal{L}(Z_x)=\;&-g'Z_x{^{\alpha}}[Q_e(\bar{e}\gamma_\alpha e+\bar{\nu_e}\gamma_\alpha P_L \nu_e)+Q_\mu(\bar{\mu}\gamma_\alpha \mu+\bar{\nu_\mu}\gamma_\alpha P_L \nu_\mu)\\ &+Q_\tau(\bar{\tau}\gamma_\alpha \tau+\bar{\nu_\tau}\gamma_\alpha P_L \nu_\tau)]-\frac{1}{4}Z_x{_{\mu\nu}}Z_x{^{\mu\nu}}+\frac{1}{2}m_{Z_x}^2Z_x{^\mu} Z_x{_\mu}, \end{aligned} $

(1) where the gauge coupling constant is denoted as
$ g' $ ;$ P_L=\dfrac{1}{2}(1-\gamma_5) $ is the left chirality projector; and$ Q_e $ ,$ Q_\mu $ , and$ Q_\tau $ correspond to the charges of leptons of three generations in the$ U(1)_{L_e-L_\mu} $ model. The$ Z_x- $ field strength tensor can be written as$ \begin{array}{*{20}{l}} Z_x{_{\mu\nu}}=\partial_{\mu} Z_x{_\nu}-\partial_{\nu} Z_x{_\mu}. \end{array} $

(2) Before we discuss the experimental constraints on the gauge boson
$ Z_x $ , we present the decays of the$ Z_x $ boson. The partial decay width of$ Z_x\rightarrow \ell^+\ell^-(\nu_\ell\bar{\nu_\ell}) $ for a single flavor lepton is given by$ \Gamma(Z_x\rightarrow \ell^+ \ell^-)=\frac{(g'Q_\ell)^2M_{Z_x}}{12\pi}\left(1+\frac{2m_\ell^2}{M^2_{Z_x}}\right)\sqrt{1-\frac{4m_\ell^2}{M_{Z_x}^2}}, $

(3) $ \Gamma(Z_x\rightarrow \nu_\ell\bar{\nu_\ell})= \frac{(g'Q_\ell)^2M_{Z_x}}{24\pi}. $

(4) In the
$ U(1)_{L_e-L_\mu} $ model, the gauge boson$ Z_x $ can only couple to two flavor leptons; therefore, the decay channels of the$ Z_x $ boson are as follows:$ \begin{array}{*{20}{l}} Z_x\rightarrow e^+ e^-,~ Z_x\rightarrow \mu^+ \mu^-,~ Z_x\rightarrow \nu_e\bar{\nu_e},~ Z_x\rightarrow \nu_\mu\bar{\nu_\mu}. \end{array} $

(5) Since
$ M_{Z_x} \gg M_\ell $ , we can neglect the mass of the lepton in Eq. (3), which gives the total width of the gauge boson$ Z_x $ as$ \begin{array}{*{20}{l}} \Gamma_{Z_x}\simeq\dfrac{g'^2}{4\pi}M_{Z_x}. \end{array} $

(6) There are two possible ways to discover the
$ Z_x $ boson. On the one hand, the$ Z_x $ boson is heavy at the current energy, and we would need a higher energy to find it. On the other hand, it may be that the$ Z_x $ mass is very small, and the coupling to the particles in the SM is weak (similar to the search for the Higgs boson); hence, researchers search for it by directly or indirectly producing it at future colliders. In our work, we prefer the latter .When the boson$ Z_x $ has a small mass, the τ mass is heavy and unstable, and we mainly consider that the$ Z_x $ boson couples only to the e and μ subsets and their corresponding neutrinos in the$ U(1)_{L_e-L_\mu} $ model. Some existing constraints on the leptophilic gauge boson mass$ M_{Z_x} $ and coupling$ g' $ in the$ U(1)_{L_e-L_\mu} $ model are summarized in Ref. [26]. The LEP bounds give the most stringent bounds in the larger mass range$ M_{Z_x} \leq 10^3 $ GeV at$ 1\sigma(2\sigma) $ via$ e^+e^-\rightarrow \ell^+\ell^- $ processes. CMS investigated the final state$ 4\mu $ for the case that all muons originate from the decay of an (almost) on-shell Z boson, offering good sensitivity for$ 10 $ GeV$ <M_{Z_x} < 60 $ GeV. The strongest constraints on the coupling$ g' $ with the$ 10-60 $ GeV mass range come from the LHC at a 95% confidence level (CL). The$ g' $ can be as low as$ 2\times10^{-2} $ [19, 23]. The production of a muon-antimuon pair in the scattering of muon neutrinos in the Coulomb field of a target nucleus gives a strong bound, e.g., neutrino trident production [27, 28]. A combination of measurements of the trident cross section from CHARM-II [29], CCFR [30], and NuTeV [31] imposes a bound of$g'\lesssim1.9\times10^{-3} M_{Z_x}/{\rm GeV}$ on the$ U(1)_{L_e-L_\mu} $ model [23]. The sensitivities from$ (g-2)_e $ and$ (g-2)_\mu $ on$ g' $ in the$ U(1)_{L_e-L_\mu} $ model are also considered; their results are in the range$ 0.2-1 $ and$ 4\times10^{-2}-1 $ , respectively [23, 32−40]. Hence, we propose the process$ e^+e^-\rightarrow \ell^+\ell^-Z_x(Z_x\rightarrow \ell^+\ell^- $ or$ \nu_\ell\bar{\nu_\ell}) $ in the$ U(1)_{L_e-L_\mu} $ model with$ 10 $ GeV$ \leq M_{Z_x} \leq 60 $ GeV to progress further in the search for expected sensitivities of the$ Z_x $ boson at the$ \sqrt{s}=240 $ GeV CEPC. -
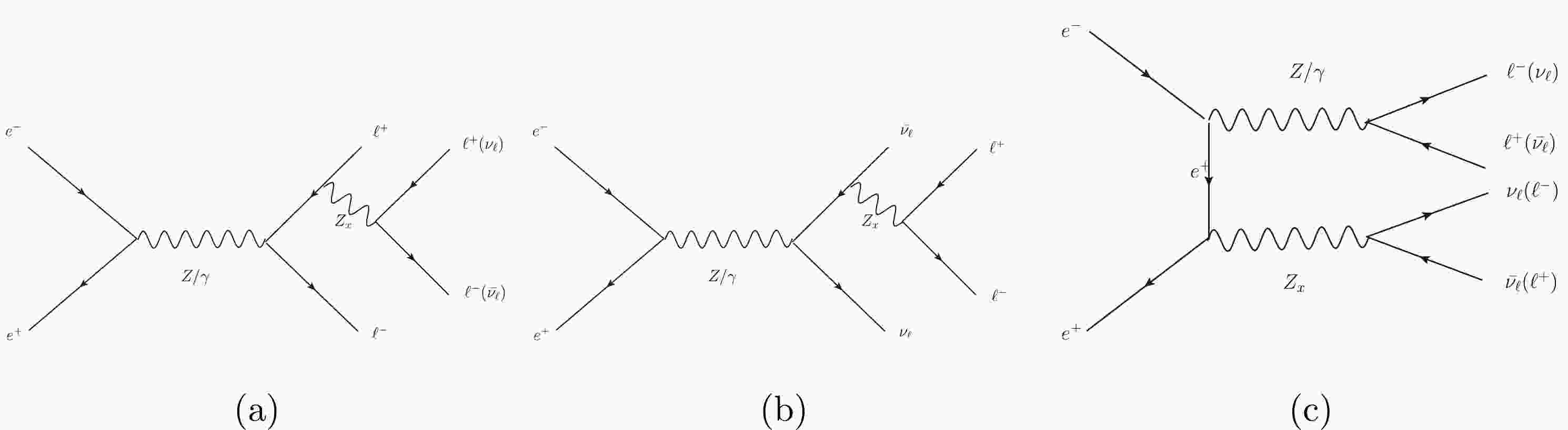
The main Feynman diagrams of the signal process
$ e^+e^-\rightarrow \ell^+\ell^-Z_x(Z_x\rightarrow \ell^+\ell^- $ or$ \nu_\ell\bar{\nu_\ell}) $ are shown in Fig. 1, which can be expanded into the following four processes:$ e^+e^-\rightarrow e^+e^-Z_x(Z_x\rightarrow e^+e^-)\rightarrow e^+e^-e^+e^- $ ,$e^+e^-\rightarrow \mu^+\mu^-Z_x (Z_x \rightarrow \mu^+\mu^-)\rightarrow \mu^+\mu^-\mu^+\mu^-$ ,$e^+e^-\rightarrow e^+e^-Z_x(Z_x\rightarrow \nu_e\bar{\nu_e})\rightarrow e^+e^- \nu_e\bar{\nu_e}$ , and$ e^+e^-\rightarrow \mu^+\mu^-Z_x(Z_x\rightarrow \nu_\mu\bar{\nu_\mu})\rightarrow \mu^+\mu^-\nu_\mu\bar{\nu_\mu} $ . In Fig. 2, we present the cross sections of four signaling processes and the corresponding backgrounds. The numerical results for the cross sections are imposed on the basic cuts. We make the transverse momenta of the leptons$ P_T(\ell) $ greater than 10 GeV, and the absolute value of the lepton pseudorapidity$ \eta_\ell $ needs to be less than 2.5. These basic cuts are then summed up as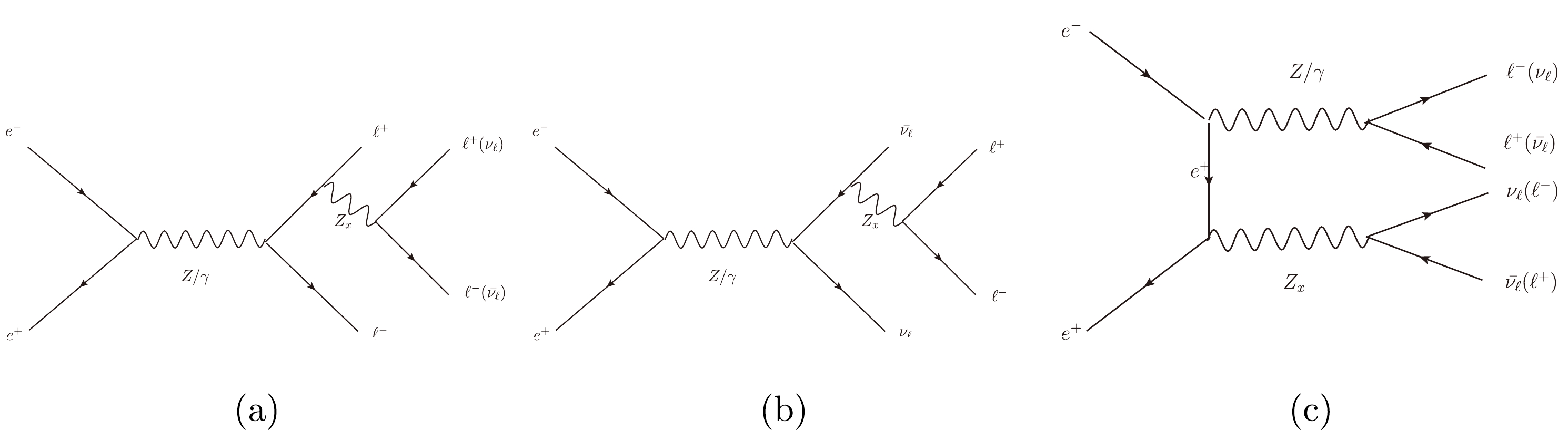
Figure 1. Main Feynamn diagrams for the process
$ e^+e^-\rightarrow \ell^+\ell^-Z_x(Z_x\rightarrow \ell^+\ell^- $ or$ \nu_\ell\bar{\nu_\ell}) $ within$ \ell \in \{e, \mu\} $ .
Figure 2. (color online) Cross sections of the signal and background processes as functions of the mass
$ Z_x $ when the coupling limits$ g'=0.01 \;\; \mathrm{GeV^{-1}} $ .$ \begin{array}{*{20}{l}} P_T(\ell)>10\; \mathrm{GeV},&&\mid\eta_\ell\mid<2.5. \end{array} $

(7) When the leptophilic gauge boson
$ Z_x $ decays to a pair of neutrinos, the beam polarizations can help further suppress the SM backgrounds to enhance the signals [41]. Therefore, in the right panel of Fig. 2, we show the polarized cross sections of the$ e^+e^-\rightarrow \ell^+\ell^-\nu_\ell\bar{\nu_\ell} $ processes with the beam polarization configurations$ (P_{e^+}, P_{e^-})= (-30\%, +80\%) $ . The solid lines represent the signal cross sections, and the dashed lines represent the SM background cross sections. The cross section ranges of signal processes$ e^+e^-\rightarrow e^+e^-\nu_e\bar{\nu_e} $ and$ e^+e^-\rightarrow \mu^+\mu^-\nu_\mu\bar{\nu_\mu} $ for$ 10~{\rm GeV} \leq $ $ M_{Z_x}\leq 60 $ GeV are$ 3.24\times10^{-4} \;\; - \;\; 1.6\times10^{-3} $ pb and$ 1.7\times10^{-4} \;\; - \;\; 2.24\times10^{-4} $ pb , respectively, with$g'=0.01 \mathrm{GeV^{-1}}$ . For the above two processes, the background cross sections are 0.04823 pb and 0.03663 pb, respectively.The left panel shows the
$ Z_x $ boson decaying to a pair of leptons. We consider the effect of polarization on the process$ Z_x\rightarrow \ell^+\ell^- $ , but the variations in the cross sections are not significant; hence, we do not impose beam polarizations on the cross sections. The solid-red and solid-black lines represent the cross sections of the signal processes$ e^+e^-\rightarrow e^+e^-e^+e^- $ and$ e^+e^-\rightarrow \mu^+\mu^-\mu^+\mu^- $ , respectively. The numerical results are$ 2.31\times10^{-4} \; - \; 4.24\times10^{-4} $ pb and$ 2.49\times10^{-5} \; - \; 8.91\times10^{-5} $ pb, respectively, in the mass range$ 10 $ GeV$ \leq M_{Z_x}\leq 60 $ GeV when the coupling constant$ g'=0.01 \;\; \mathrm{GeV^{-1}} $ . The dashed-red and dashed-black lines represent the cross sections of the background processes$ e^+e^-\rightarrow e^+e^-e^+e^- $ (0.01477 pb) and$e^+e^-\rightarrow \mu^+\mu^-\mu^+\mu^-$ (0.001899 pb), respectively. The cross sections of signals in the parameter region are smaller than the cross sections of corresponding SM backgrounds.Next, we used FeynRules [42] to simulate the signals to produce a model file output in the UFO format. Then, all signal and background events were simulated using MadGraph5 [43]; the parton shower and hadronization were carried out with Pythia8 [44], while the detector simulation was performed using MadAnalysis5 [45] and Delphes3 [46]. In our analysis, we generate, in each case, 10k signal events in an interval where the mass of
$ Z_x $ increases in order from 10 GeV to 60 GeV, with 500k events for backgrounds. -
To further improve event selection, the signal and background distributions of the angular separation
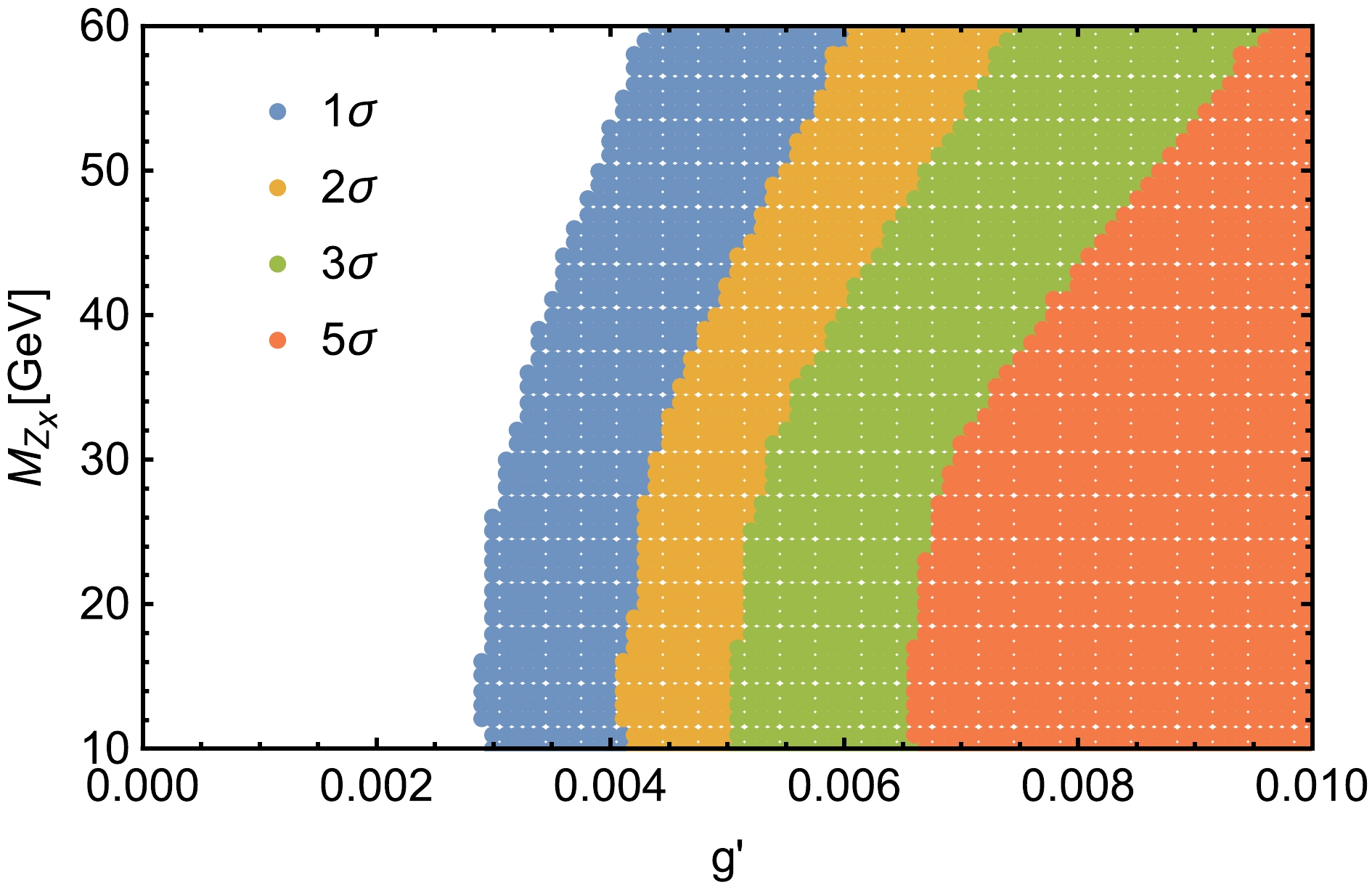
$ \triangle R $ between two muons, which is defined as$ \triangle R= \sqrt{(\triangle\phi)^2+(\triangle\eta)^2} $ , and invariant masses$ M(\mu^+, \mu^-) $ are shown in Fig. 3. We can see that the background and signal have very distinctive characteristics. In particular, for the distribution of invariant masses$ M(\mu^+, \mu^-) $ , the peaks in$ M(\mu^+, \mu^-) $ still denounce the presence of signals, making the distinction against the smooth background easy. We select$ M(\mu^+, \mu^-)-M_{Z_x}\leq5 $ .$ \triangle R $ is greater than$ 0.5 $ for$ Z_x $ mass from 10 GeV to 30 GeV and greater than 0.7 when the$ Z_x $ mass is in the mass range$ 30 \;\; - \;\; 60 $ GeV for the process$ e^+e^-\rightarrow \mu^+\mu^-\mu^+\mu^- $ . Based on the characteristics of the kinematic distributions, the selected cuts are listed in Table 2. After these improved cuts are applied, the SM background is significantly depressed. We take a signal benchmark point every 10 GeV in the$ 10 \;\; - \;\; 60 $ GeV mass interval and display the cross sections of the signal and background after applying the above selection cuts for these benchmark points for$ g'=0.01 \;\; \mathrm{GeV^{-1}} $ at the 240 GeV CEPC with$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ in Table 3. We also show the statistical significance (SS) in the last column of Table 3, which is defined as${SS} = {S}/\sqrt{{S}+{B}}$ , where${S}$ represents the number of signal events, and${B}$ represents the number of background events. The$ 1\sigma $ ,$ 2\sigma $ ,$ 3\sigma $ , and$ 5\sigma $ regions in the$ g' $ -$ M_{Z_x} $ plane are plotted in Fig. 4. The expected bounds on$ g' $ can reach$ 6.2\times10^{-3} $ ($ 8.1\times10^{-3} $ )$ \mathrm{GeV^{-1}} $ at$ 3\sigma \;\; (5\sigma) $ levels. For the same signal process for the mass$ M_{Z_x}<10 $ GeV, Ref. [20] provides the upper limit on$ g' $ at SS$ =1\sigma $ level; however, we can provide the SS at$ 3\sigma \;\; (5\sigma) $ levels for the mass range$ 10-60 $ GeV. Thus, the CEPC has the potential to discover the$ Z_x $ boson in the considered mass range.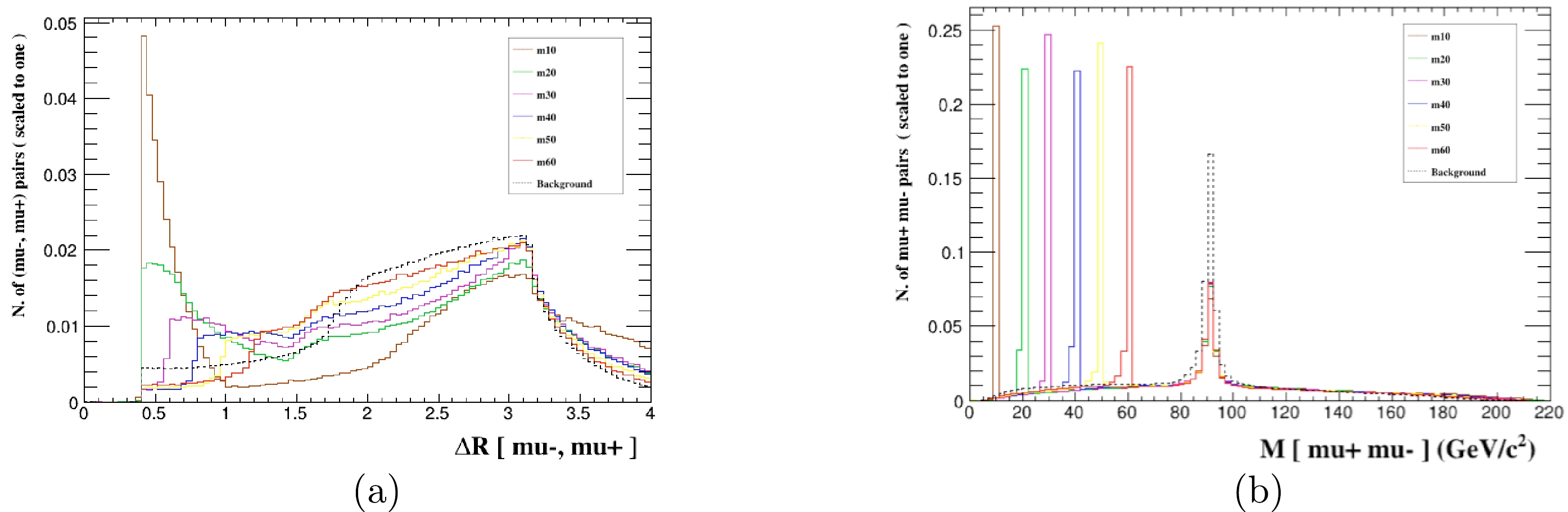
Figure 3. (color online) Normalized distributions of
$ \triangle R $ (a) and$ M(\mu^+, \mu^-) $ (b) from the signal and background events for different$ M_{Z_x} $ benchmark points for the process$ e^+e^-\rightarrow \mu^+\mu^-\mu^+\mu^- $ at the CEPC with$ \sqrt s=240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ .Cut Mass $10 \;\mathrm {GeV}\leq M_{Z_x}\leq30 \;\mathrm{GeV}$ 

$30 \;\mathrm{GeV} < M_{Z_x}\leq60 \;\mathrm{GeV}$ 

Cut1 $ \triangle R>0.5 $ 

$ \triangle R>0.7 $ 

Cut2 $ M(\mu^+, \mu^-)-M_{Z_x}\leq5 $ 

$ M(\mu^+, \mu^-)-M_{Z_x}\leq5 $ 

Table 2. Improved cuts for the process
$e^+e^-\rightarrow $ $ \mu^+\mu^-\mu^+\mu^-$ .Cross sections for signal (background)/fb $ M_{Z_x} $ /GeV

Basic cuts Cut1 Cut2 SS 10 $ 2.4852\times10^{-2} $ 

$ 2.4804\times10^{-2} $ 

$ 2.3443\times10^{-2} $ 

4.7640 (1.899) (1.894) (0.112) 20 $ 6.7516\times10^{-2} $ 

$ 6.7369\times10^{-2} $ 

$ 6.3763\times10^{-2} $ 

7.4520 (1.899) (1.894) (0.346) 30 $ 8.2532\times10^{-2} $ 

$ 8.2393\times10^{-2} $ 

$ 7.8353\times10^{-2} $ 

7.1090 (1.899) (1.894) (0.601) 40 $ 8.7872\times10^{-2} $ 

$ 8.7711\times10^{-2} $ 

$ 8.3870\times10^{-2} $ 

6.4464 (1.899) (1.894) (0.864) 50 $ 8.8983\times10^{-2} $ 

$ 8.8865\times10^{-2} $ 

$ 8.5551\times10^{-2} $ 

5.8548 (1.899) (1.894) (1.109) 60 $ 8.8160\times10^{-2} $ 

$ 8.8096\times10^{-2} $ 

$ 8.5297\times10^{-2} $ 

5.3669 (1.899) (1.894) (1.325) Table 3. Cross sections of the signal and background after imposing the improved cuts for
$ g'=0.01 \;\; \mathrm{GeV^{-1}} $ at the CEPC with$ \sqrt s=240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ for the process$e^+e^-\rightarrow $ $ \mu^+\mu^-\mu^+\mu^-$ .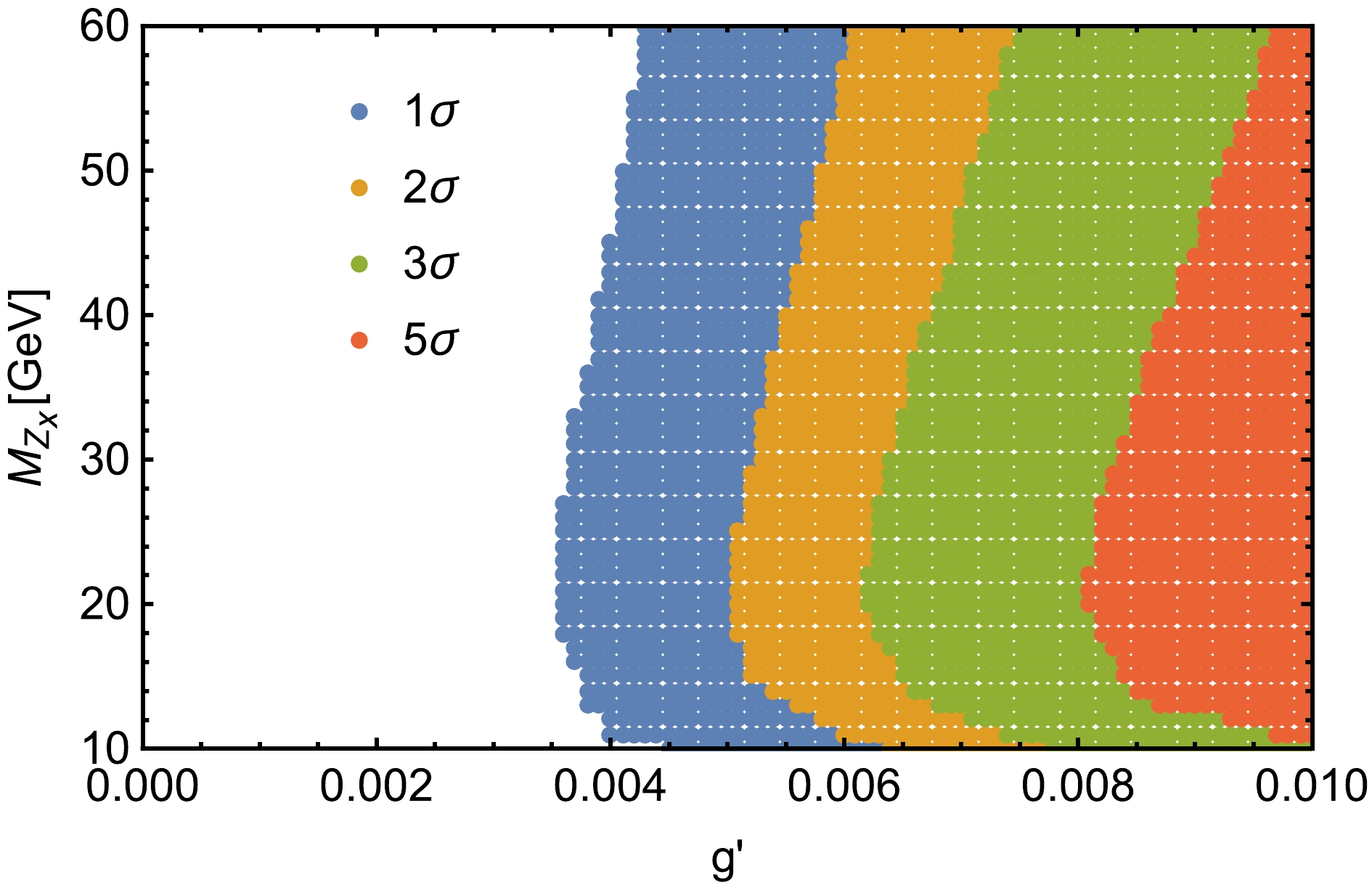
Figure 4. (color online)
$ 1\sigma $ ,$ 2\sigma $ ,$ 3\sigma $ , and$ 5\sigma $ regions for the process$ e^+e^-\rightarrow \mu^+\mu^-\mu^+\mu^- $ at the CEPC with$ \sqrt s = 240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ in the$ g' $ -$ M_{Z_x} $ plane.For the case where the gauge boson
$ Z_x $ decays into a pair of electrons, the kinematic distributions of the signal process$ e^+e^-\rightarrow e^+e^-e^+e^- $ ,$ \triangle R $ ,$ \eta_{e^-} $ ,$ \eta_{e^+} $ , and$ M(e^+, e^-) $ are shown in Fig. 5. The mass of$ Z_x $ is greater than 40 GeV, and the distributions of the peaks of$ \eta_{e^-} $ and$ \eta_{e^+} $ are shifted. Therefore, we divide the mass range into two segments of$ 10-40 $ GeV and$ 40 \;\; - \;\; 60 $ GeV when we select the effective cuts. Ultimately, we summarize the specific cuts in Table 4. After applying improved cuts, the cross sections of the signal and the background are shown in Table 5. We also present the regions of SS at$ 1\sigma $ ,$ 2\sigma $ ,$ 3\sigma $ , and$ 5\sigma $ levels in Fig. 6. As can be seen from the figure, the sensitivity projections of$ Z_x $ become weaker with increasing mass, and there is a significant dip at$ M_{Z_x}=30 $ GeV with $ g'=5\times10^{-3} \;\; \mathrm{GeV^{-1}} $ . By comparing the above two processes, the four-electron final state is more sensitive to discovering the$ Z_x $ boson.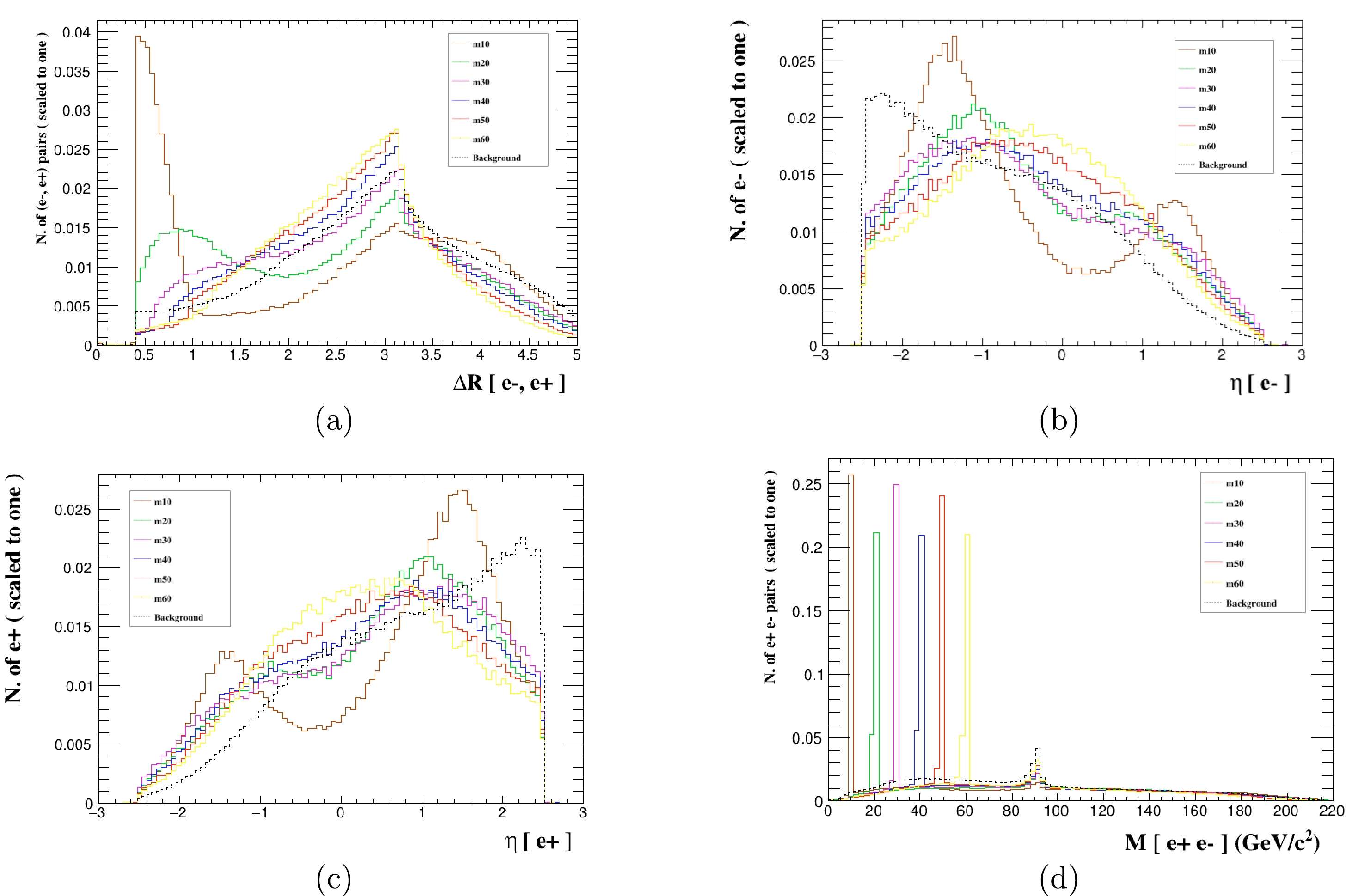
Figure 5. (color online) Normalized distributions of
$ \triangle R $ (a),$ \eta_{e^-} $ (b),$ \eta_{e^+} $ (c), and$ M(e^+, e^-) $ (d) from the signal and background events for different$ M_{Z_x} $ benchmark points for the process$ e^+e^-\rightarrow e^+e^-e^+e^- $ at the CEPC with$ \sqrt s=240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ .Cut Mass $10\;\mathrm{GeV}\leq M_{Z_x}\leq40 \;\mathrm{GeV}$ 

$40 \; \mathrm{GeV} < M_{Z_x}\leq60 \; \mathrm{GeV}$ 

Cut1 $ \triangle R>0.7 $ 

$ \triangle R>1 $ 

Cut2 $ \eta_{e^-}>-1.4 $ 

$ \eta_{e^-}>-1.1 $ 

Cut3 $ \eta_{e^+}<1.4 $ 

$ \eta_{e^+}<1.1 $ 

Cut4 $ M(e^+, e^-)-M_{Z_x}\leq5 $ 

$ M(e^+, e^-)-M_{Z_x}\leq5 $ 

Table 4. Improved cuts for the process
$e^+e^-\rightarrow $ $ e^+e^-e^+e^-$ .Cross sections for signal (background)/fb $ M_{Z_x} $ /GeV

Basic cuts Cut1 Cut2 Cut3 Cut4 SS 10 $ 0.2317 $ 

$ 0.2178 $ 

$ 0.1965 $ 

$ 0.1784 $ 

$ 0.1533 $ 

10.7950 (14.77) (14.18) (12.30) (10.77) (0.9745) 20 $ 0.3526 $ 

$ 0.3360 $ 

$ 0.3124 $ 

$ 0.2905 $ 

$ 0.2465 $ 

10.9270 (14.77) (14.18) (12.30) (10.77) (2.602) 30 $ 0.4241 $ 

$ 0.4061 $ 

$ 0.3765 $ 

$ 0.3495 $ 

$ 0.3027 $ 

10.2330 (14.77) (14.18) (12.30) (10.77) (4.596) 40 $ 0.3876 $ 

$ 0.3698 $ 

$ 0.3323 $ 

$ 0.2984 $ 

$ 0.2674 $ 

8.3090 (14.77) (14.11) (11.27) (9.133) (5.532) 50 $ 0.3261 $ 

$ 0.3108 $ 

$ 0.2839 $ 

$ 0.2588 $ 

$ 0.2357 $ 

6.6985 (14.77) (14.11) (11.27) (9.133) (6.696) 60 $ 0.2672 $ 

$ 0.2544 $ 

$ 0.2338 $ 

$ 0.2148 $ 

$ 0.1984 $ 

5.3463 (14.77) (14.11) (11.27) (9.133) (7.508) Table 5. Cross sections of the signal and background after imposing the improved cuts for
$ g'=0.01 \;\; \mathrm{GeV^{-1}} $ at the CEPC with$ \sqrt s=240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ for the process$e^+e^-\rightarrow $ $ e^+e^-e^+e^-$ . -
If the
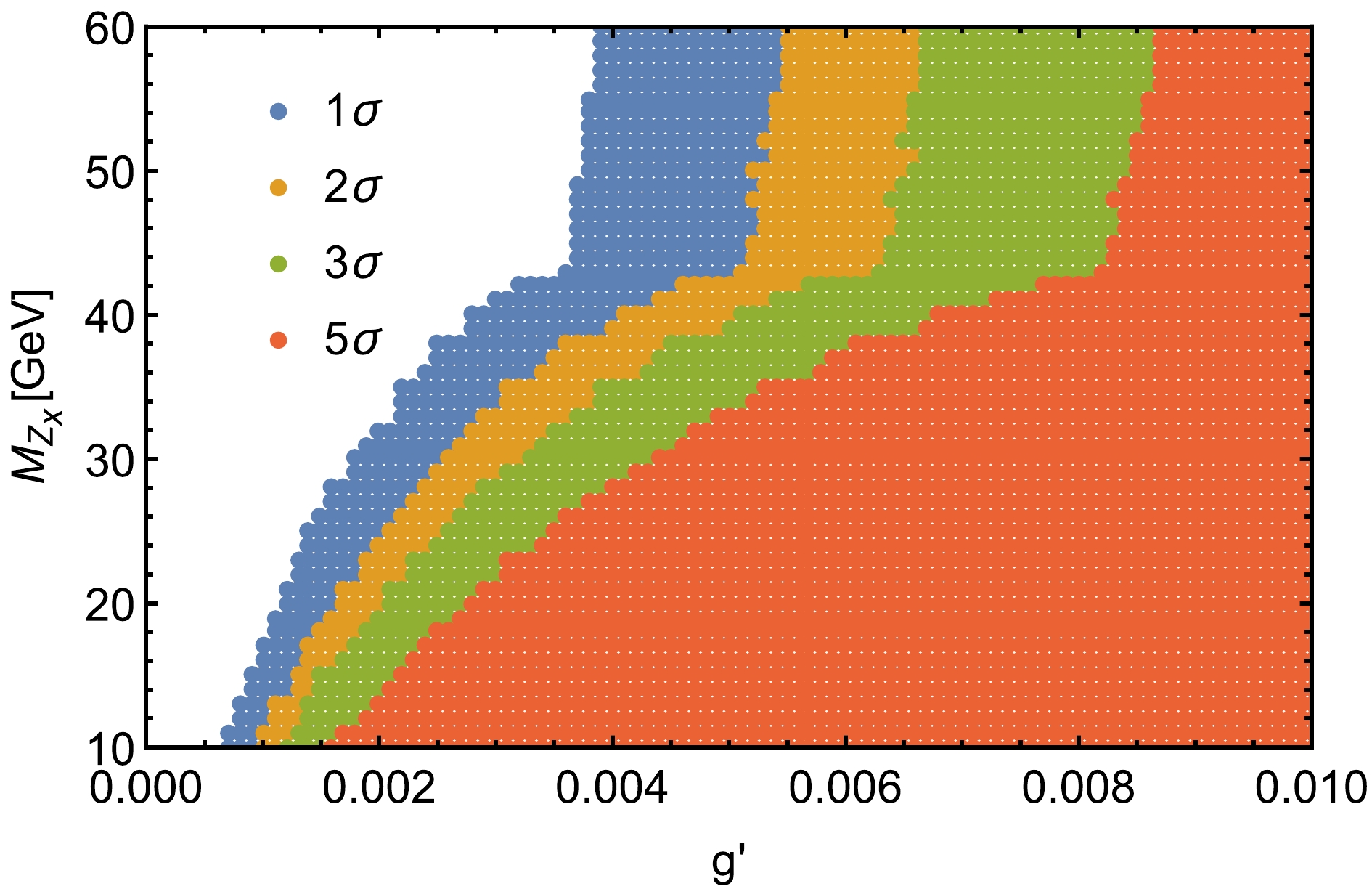
$ Z_x $ boson decays to a pair of neutrinos, the processes$ e^+e^-\rightarrow e^+e^-\nu_e\bar{\nu_e} $ and$ e^+e^-\rightarrow \mu^+\mu^-\nu_\mu\bar{\nu_\mu} $ have larger cross sections compared to those for the case when the$ Z_x $ boson decays to a pair of leptons. For the process$ e^+e^-\rightarrow \mu^+\mu^-\nu_\mu\bar{\nu_\mu} $ , according to the kinetic distributions in Fig. 7, the transverse momentum$ P_T(\ell) $ , invariant mass$ M(\mu^+, \mu^-) $ , angular separation$ \triangle R $ between two muons, and transverse energy$ E_T $ are improved cuts, as presented in Table 6 for the entire mass range$ M_{Z_x}=10 \;\; - \;\; 60 $ GeV. Optimized cuts might preserve as many signal events as possible. Then, we provide the signal and background cross sections after imposing the optimized cuts for the process in Table 7. We can see that, when the background is suppressed by two orders of magnitude, the signal is substantially preserved. Figure 8 shows the SS =$1\sigma,\; 2\sigma,\; 3\sigma,\; 5\sigma$ ranges in the$ g' $ -$ M_{Z_x} $ plane; the constraints on the$ Z_x $ boson are very strict with the coupling constant$ g' $ reaching$ 6.7\times10^{-3} \;\; \mathrm{GeV^{-1}} $ at SS$ = 5\sigma $ .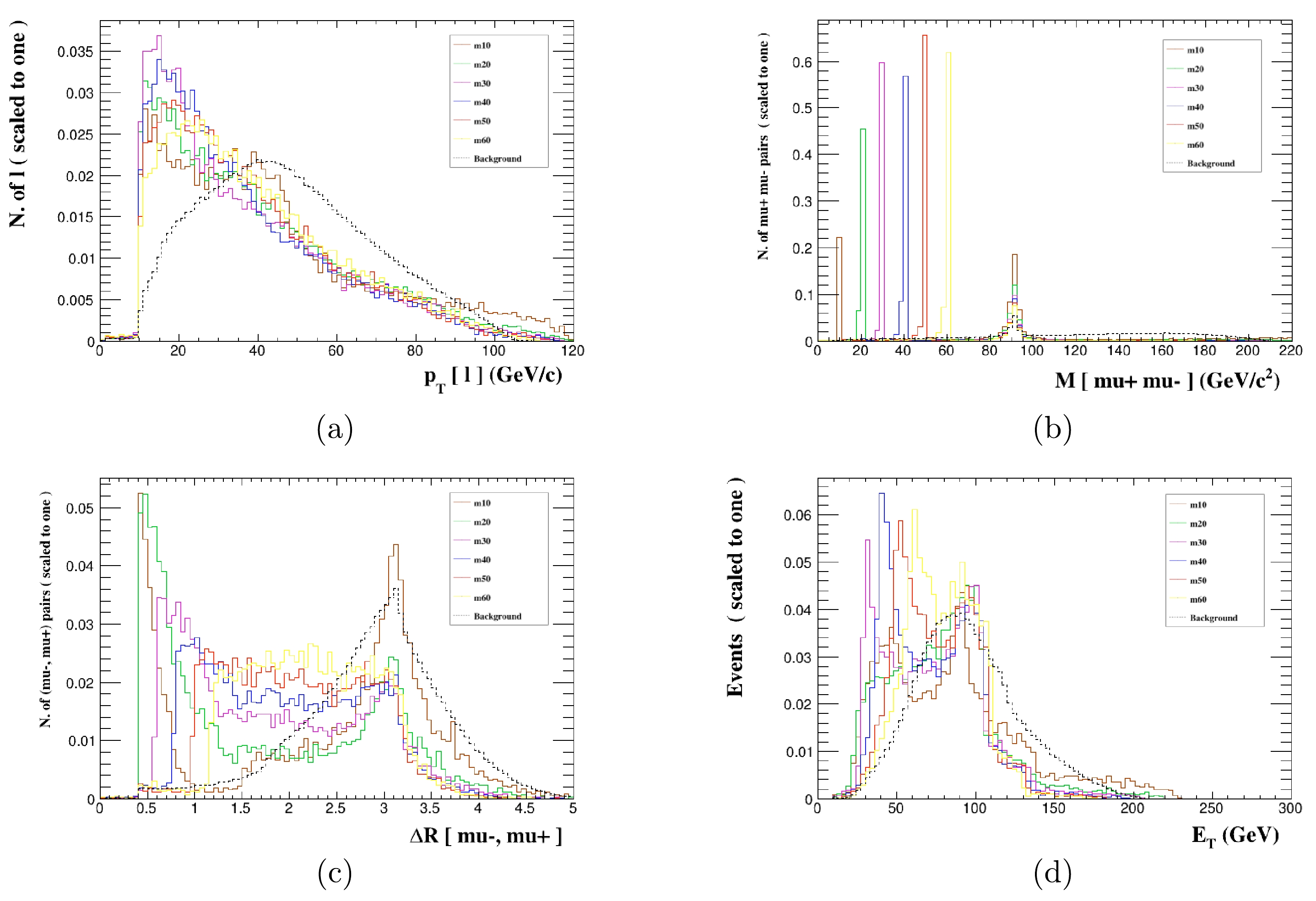
Figure 7. (color online) Normalized distributions of
$ P_T(\ell) $ (a),$ M(e^+, e^-) $ (b),$ \triangle R $ (c), and$ E_T $ (d) from the signal and background events for different$ M_{Z_x} $ benchmark points for the process$ e^+e^-\rightarrow \mu^+\mu^-\nu_\mu\bar{\nu_\mu} $ at the CEPC with$ \sqrt s=240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ .Cut Mass $10 \; \mathrm{GeV}\leq M_{Z_x}\leq60 \; \mathrm{GeV}$ 

Cut1 $ P_T(\ell)>5 $ 

Cut2 $ \mid M(\mu^+, \mu^-)-M_{Z_x}\mid\leq5 $ 

Cut3 $ \triangle R<4 $ 

Cut4 $ E_T<150 $ 

Table 6. Improved cuts for the process
$e^+e^-\rightarrow $ $ \mu^+\mu^-\nu_\mu\bar{\nu_\mu}$ .Cross sections for signal (background)/fb $ M_{Z_x} $ /GeV

Basic cuts Cut1 Cut2 Cut3 Cut4 SS 10 $ 0.1708 $ 

$ 0.1706 $ 

$ 0.03665 $ 

$ 0.03665 $ 

$ 0.03665 $ 

5.4300 (36.63) (36.59) (0.2205) (0.2205) (0.2200) 20 $ 0.2122 $ 

$ 0.2215 $ 

$ 0.1054 $ 

$ 0.1054 $ 

$ 0.1054 $ 

10.1420 (36.63) (36.59) (0.4993) (0.4993) (0.4985) 30 $ 0.2216 $ 

$ 0.2215 $ 

$ 0.1317 $ 

$ 0.1317 $ 

$ 0.1317 $ 

11.0030 (36.63) (36.59) (0.6723) (0.6721) (0.6711) 40 $ 0.2229 $ 

$ 0.2215 $ 

$ 0.1317 $ 

$ 0.1317 $ 

$ 0.1414 $ 

10.8980 (36.63) (36.59) (0.8064) (0.8056) (0.8046) 50 $ 0.2205 $ 

$ 0.2204 $ 

$ 0.1467 $ 

$ 0.1467 $ 

$ 0.1467 $ 

10.5890 (36.63) (36.59) (0.9205) (0.9195) (0.9195) 60 $ 0.2153 $ 

$ 0.2153 $ 

$ 0.1443 $ 

$ 0.1443 $ 

$ 0.1443 $ 

9.9480 (36.63) (36.59) (1.037) (1.036) (1.034) Table 7. Cross sections of the signal and background after imposing the improved cuts for
$ g'=0.01 \;\; \mathrm{GeV^{-1}} $ at the CEPC with$ \sqrt s=240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ for the process$e^+e^-\rightarrow $ $ \mu^+\mu^-\nu_\mu\bar{\nu_\mu}$ .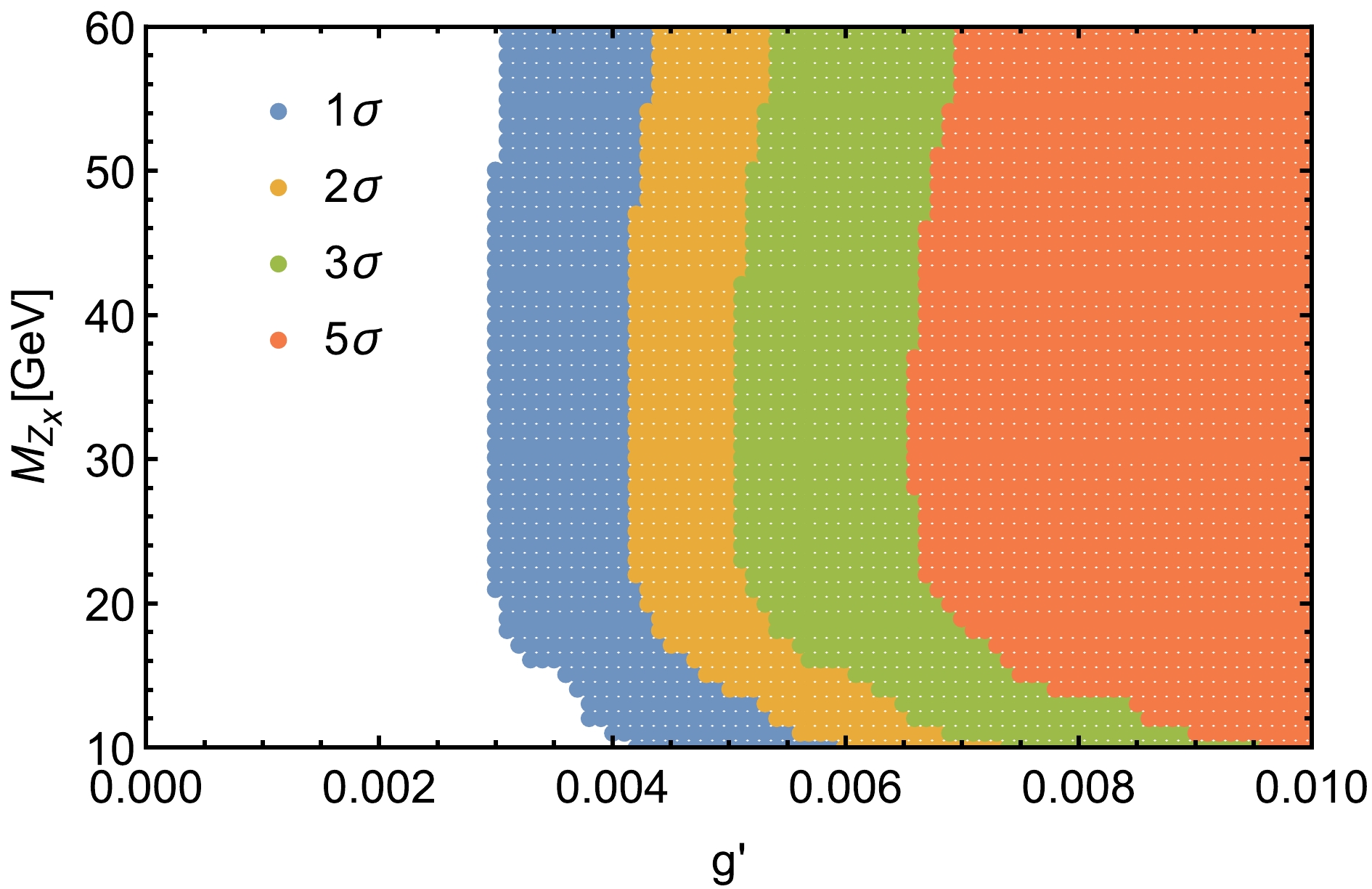
Figure 8. (color online)
$ 1\sigma $ ,$ 2\sigma $ ,$ 3\sigma $ and$ 5\sigma $ regions for the process$ e^+e^-\rightarrow \mu^+\mu^-\nu_\mu\bar{\nu_\mu} $ at the CEPC with$ \sqrt s = 240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ in the$ g' $ -$ M_{Z_x} $ plane.When
$ Z_x $ decays to$ \nu_e\bar{\nu_e} $ , the peak distribution of the$ e^+ $ energy for the signal process$ e^+e^-\rightarrow e^+e^-\nu_e\bar{\nu_e} $ is clearly demarcated from the background in Fig. 9. For the low mass range$ M_{Z_x}=10 \;\; - \;\; 40 $ GeV, the$ e^+ $ energy retains more signals after applying the cuts. On the contrary, for the large mass range$ M_{Z_x}=40 \;\; - \;\; 60 $ GeV, the signal events of the invariant mass$ M(e^+, e^-) $ outnumber the signal events of$ E(e^+) $ after improving cuts; therefore, we add to the effective cuts at$ M_{Z_x}=40 $ GeV, as shown in Table 8. Finally, Table 9 presents the cross sections of the signal and background after the improved cuts are imposed on the$ e^+e^-\rightarrow e^+e^-\nu_e\bar{\nu_e} $ process, and we plot$ 1\sigma $ ,$ 2\sigma $ ,$ 3\sigma $ and$ 5\sigma $ ranges in Fig. 10. The sensitivity projections of the$ Z_x $ boson that we obtain are very strict for the process, especially in the region of mass$ M_{Z_x}=10 \;\; - \;\; 40 $ GeV. In contrast to the three processes mentioned above, this process is more sensitive to the$ Z_x $ boson.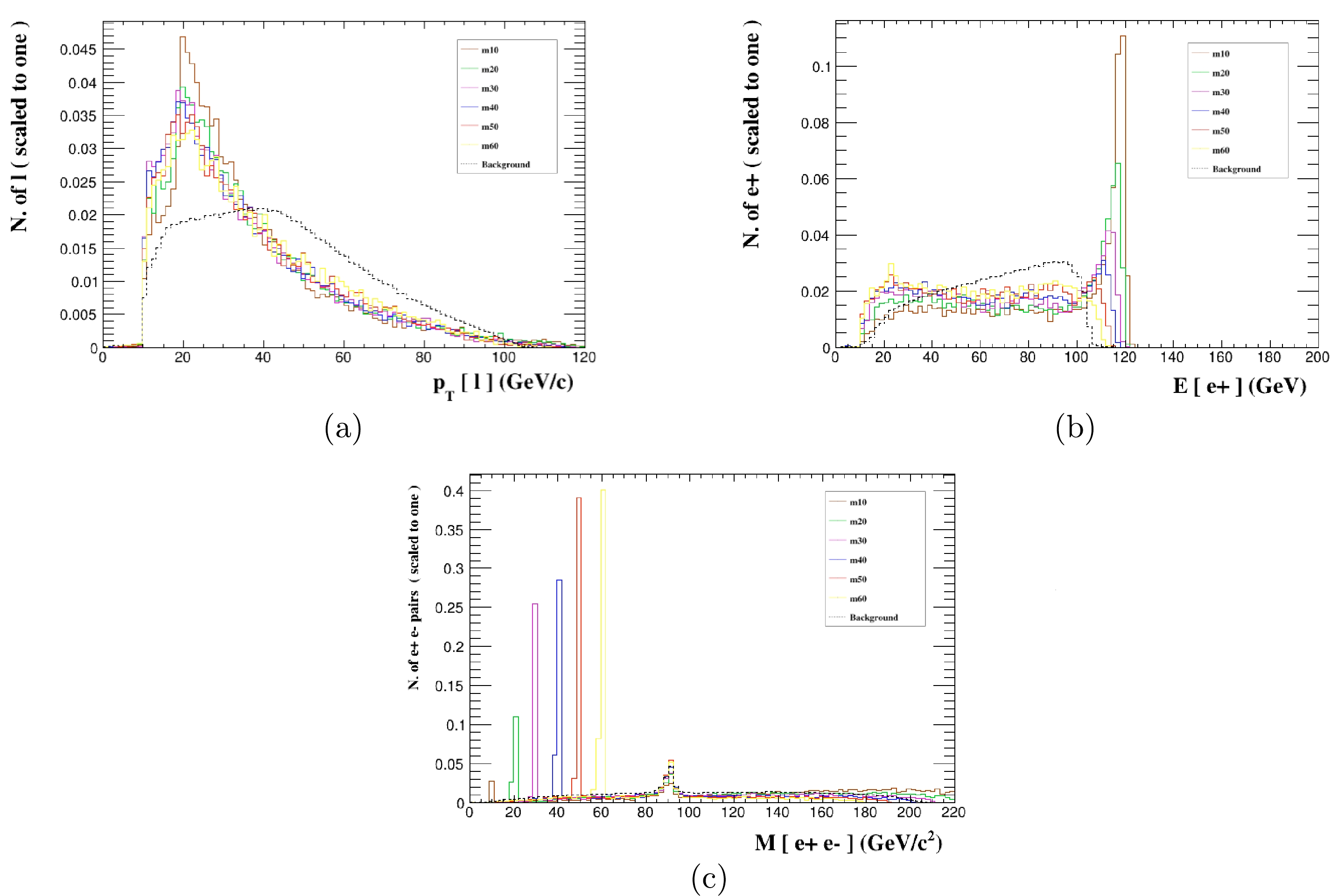
Figure 9. (color online) Normalized distributions of
$ P_T(\ell) $ (a),$ E(e^+) $ (b), and$ M(e^+, e^-) $ (c) from the signal and background events for different$ M_{Z_x} $ benchmark points for the process$ e^+e^-\rightarrow e^+e^-\nu_e\bar{\nu_e} $ at the CEPC with$ \sqrt s=240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ .Cut Mass $10 \;\mathrm{GeV}\leq M_{Z_x}\leq40 \;\mathrm{GeV}$ 

$40 \;\mathrm{GeV} < M_{Z_x}\leq60 \;\mathrm{GeV}$ 

Cut1 $ P_T(\ell)>5 $ 

$ P_T(\ell)>5 $ 

Cut2 $ E(e^+)>110 $ 

$ \mid M(e^+, e^-)-M_{Z_x}\mid\leq5 $ 

Table 8. The improved cuts for the process
$e^+e^-\rightarrow $ $ e^+e^-\nu_e\bar{\nu_e}$ .Cross sections for signal (background)/fb $ M_{Z_x} $ /GeV

Basic cuts Cut1 Cut2 SS 10 $ 1.6011 $ 

$ 1.5658 $ 

$ 0.49924 $ 

51.6830 (48.23) (46.75) (0.02334) 20 $ 0.8491 $ 

$ 0.8312 $ 

$ 0.1709 $ 

28.9830 (48.23) (46.75) (0.02334) 30 $ 0.5879 $ 

$ 0.5761 $ 

$ 0.06803 $ 

16.7940 (48.23) (46.75) (0.02334) 40 $ 0.4583 $ 

$ 0.4491 $ 

$ 0.02810 $ 

9.2220 (48.23) (46.75) (0.02334) 50 $ 0.3755 $ 

$ 0.3677 $ 

$ 0.1192 $ 

7.3630 (48.233) (46.75) (1.522) 60 $ 0.3247 $ 

$ 0.3172 $ 

$ 0.1187 $ 

6.6180 (48.23) (46.75) (0.1187) Table 9. Cross sections of the signal and background after imposing the improved cuts for
$ g'=0.01 \;\; \mathrm{GeV^{-1}} $ at the CEPC with$ \sqrt s=240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ for the process$e^+e^-\rightarrow $ $ e^+e^-\nu_e\bar{\nu_e}$ . -
Recently, there have been many studies related to the leptophilic gauge boson
$ Z_x $ . The search for the mass range of$ 10-500 $ GeV$ Z_x $ in the$ U(1)_{L_\mu-L_\tau} $ model is widely studied at the LHC. However, the search for a small mass of$ Z_x $ is very limited in the$ U(1)_{L_e-L_\mu} $ model at the future$ e^+e^- $ colliders. It is evident that there is still a large parameter space around the electroweak scale for us to explore the$ Z_x $ boson [23]. Thus, we can search for the$ Z_x $ predicted by the$ U(1)_{L_e-L_\mu} $ model at the CEPC to facilitate the extension of the sensitivity of$ Z_x $ or stricter couplings. In our study, we investigate the prospects of the CEPC to unravel the NP associated with a new weak interaction, and the gauge boson$ Z_x $ only couples to the e and μ subsets in the$ U(1)_{L_e-L_\mu} $ model.We investigated the sensitivity of the CEPC with
$ \sqrt s=240 $ GeV and$ \mathcal{L}=5.6 \;\; \mathrm{ab^{-1}} $ to the coupling parameter$ g' $ for$ M_{Z_x}=10-60 $ GeV. As can be seen from the four processes explored in the previous sections, the expected bounds of the process$ e^+e^-\rightarrow e^+e^-\nu_e\bar{\nu_e} $ on$ g' $ can reach$ 1.0\times10^{-3} $ ($ 1.6\times10^{-3} $ )$ \mathrm{GeV^{-1}} $ for$ M_{Z_x}=10-40 $ GeV at$ 3\sigma $ ($ 5\sigma $ ); these are the strictest constraints on the$ U(1)_{L_e-L_\mu} $ model. However, in the$ Z_x $ mass range of$ 40-60 $ GeV, the strictest constraints come from the process$ e^+e^-\rightarrow \mu^+\mu^-\nu_\mu\bar{\nu_\mu} $ , and the expected bounds on$ g' $ can reach$ 5.1\times10^{-3} $ ($ 6.7\times10^{-3} $ )$ \mathrm{GeV^{-1}} $ at$ 3\sigma $ ($ 5\sigma $ ). Compared to the other three processes, the process$ e^+e^-\rightarrow \mu^+\mu^-\mu^+\mu^- $ is less constrained.In conclusion, the expected sensitivities of the four processes to the parameter space of the
$ U(1)_{L_e-L_\mu} $ models are different. However, when we compare our numerical results in Fig. 2 with those in Ref. [23], they are not experimentally excluded except from the process$ e^+e^-\rightarrow \mu^+\mu^-\mu^+\mu^- $ . At the same time, Ref. [24] indicates that the sensitivity to$ g' $ for the process$ e^+e^-\rightarrow Z_x\gamma $ can be as low as$ 5\times10^{-3} $ in the mass range of$ 10-60 $ GeV at the$ 2\sigma $ level. Our results can reach$ 1\times10^{-3} $ for$ M_{Z_x}=10 $ GeV via the process$ e^+e^-\rightarrow e^+e^-\nu_e\bar{\nu_e} $ , and the constraints from the process$ e^+e^-\rightarrow \mu^+\mu^-\nu_\mu\bar{\nu_\mu} $ can reach$ 4.2\times10^{-3} $ at the$ 2\sigma $ level in the entire mass range of$ 10-60 $ GeV. Our numerical results align with those of Ref. [24], as the same conclusions are applicable to the process$ e^+e^-\rightarrow e^+e^-e^+e^- $ . Hence, searching for the$ Z_x $ boson predicted by the$ U(1)_{L_e-L_\mu} $ model at the 240 GeV CEPC via processes$ e^+e^-\rightarrow \ell^+\ell^-Z_x(Z_x\rightarrow \nu_\ell\bar{\nu_\ell} $ or$ \ell\ell) $ can enhance the sensitivity projections to the parameter space and promote further exploration of future$ e^+e^- $ colliders for the$ U(1)_{L_e-L_\mu} $ model, providing more opportunities for further discoveries regarding the leptophilic gauge boson$ Z_x $ . -
Yan-Yu Li would like to thank Han Wang for very useful discussions.
Searching for the light leptophilic gauge boson Zx via four-lepton final states at the CEPC
- Received Date: 2023-12-05
- Available Online: 2024-04-15
Abstract: We investigate the possibility of detecting the leptophilic gauge boson






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

























 DownLoad:
DownLoad: