Coupled channel analysis of neutron transfer in ^6,7Li induced reactions around the Coulomb barrier

The atomic nucleus is a complex many-body system. Understanding the internal degrees of freedom is essential for comprehending nuclear structure characteristics such as single-particle and collective states, clustering, and pairing correlations [1]. The information about the internal degrees of freedom is obtained from direct nuclear reactions, such as elastic scattering, inelastic scattering, and nucleon transfer, which are necessary to understand the stability of nuclei. Transfer reactions are also an effective method for producing neutron-rich nuclei [2, 3]. Further, the availability of radioactive beams has enabled us to investigate direct nuclear reactions in regions far from stability [4, 5].

Over the past decades, transfer reactions have been extensively studied. Single nucleon transfer provides insights into the shell structure, while two nucleon transfer reactions are particularly useful for exploring pairing correlations [6, 7]. The optical potential and spectroscopic factors are essential parameters for calculating transfer cross sections. Stripping reactions like $ (d,p) $ [8, 9] and $ (t,d) $ [10] are extensively used in nuclear structure studies to investigate the spectroscopic factor. $ ^{6} $Li and $ ^{7} $Li are commonly recognized as weakly bound nuclei having cluster structure, such as $ d+\alpha $ and $ t+\alpha $. Thus, a similar reaction mechanism can be expected for ($ ^{6} $Li, $ ^{5} $Li) and $ (d, p) $ reactions, as well as ($ ^{7} $Li, $ ^{6} $Li) and $ (t, d) $ reactions, assuming that the α particle does not participate in the neutron transfer process. Consequently, the same structural information can be obtained using ($ ^{6} $Li, $ ^{5} $Li) and ($ ^{7} $Li, $ ^{6} $Li) reactions. Spectroscopic factors were traditionally determined by comparing calculated and measured transfer reaction cross sections. However, this experimental approach can introduce ambiguities due to the chosen optical potentials and coupling scheme used in the calculations. With the remarkable increase in computing power, detailed nuclear structure calculations, such as large-scale shell-model computations, are being used to determine spectroscopic factors. Moreover, significant progress has been made in reaction theory. The distortion of the incoming and outgoing scattering waves is now effectively managed by using double-folding optical potentials (OP), such as the São Paulo potential (SPP) in the transfer reactions [11, 12].

Since direct transfer and breakup do not require tunneling through the barrier, their excitation functions do not decrease as rapidly as the fusion excitation function at sub-barrier energies. Consequently, the cross sections for these processes may be larger than the fusion cross sections. In the $ ^{6,7} $Li+$ ^{198} $Pt systems, measurements have shown that the direct reaction cross section is significantly larger than the fusion cross section at sub-barrier energies for $ ^{6} $Li+$ ^{198} $Pt [13]. For $ ^{7} $Li+$ ^{198} $Pt, it was found that both one- and two-neutron stripping and one-neutron pickup reactions play significant roles [14]. Similarly, large transfer cross sections have been observed in $ ^{6,7} $Li+$ ^{197} $Au and $ ^{6} $Li+$ ^{181} $Ta reactions [15, 16]. The derived excitation function drops less steeply compared to the complete fusion excitation function at low energy in one-neutron stripping reactions of $ ^{6} $Li+$ ^{96} $Zr. Experimental findings involving neutron-halo nuclei such as $ ^{6,8} $He [17−19] indicate that one- and two-neutron transfer channels are the predominant non-elastic processes below the Coulomb barrier and remain significant at energies above the barrier.

However, the mechanism behind the transfer of nucleons between a projectile and a target still has multiple aspects to be understood. It becomes more complicated due to the processes such as sequential transfers and inelastic excitations that can occur before or after the transfer, alongside the typically dominant direct cluster transfer. With more nucleons involved, possible interactions escalate, further complicating the understanding of the reaction mechanism. In the literature, it is commonly observed in $ ^{6,7} $Li-induced reactions that the measured excess cross sections in $ pxn $- or $ \alpha xn $-channels compared to the theoretical predictions are primarily attributed to incomplete fusion (ICF), with direct transfer often being overlooked [20−24]. Besides the breakup process, which is associated with the low binding energies of α particles, the significance of neutron transfer has been highlighted due to its substantial contribution to the production of inclusive α cross sections [25, 26]. Although numerous studies have concentrated on the breakup process, the role of neutron transfer still needs to be explored. Measurements of neutron transfer cross sections using weakly bound projectiles are limited, and available data are sparse [26−32].

In this study, we have investigated one-neutron transfer in the $ ^{6} $Li+$ ^{93} $Nb and $ ^{7} $Li+$ ^{115} $In systems, as well as two-neutron transfer in the $ ^{7} $Li+$ ^{181} $Ta system, utilizing the coupled reaction channel (CRC) formalism. We have analyzed the impact of coupling between various reaction channels and studied the relative contributions from the transfer path to understand the reaction mechanism. The article is organized as follows: The explanation of formalism, shell model, and CRC calculations are outlined in Sect. II. Section II D presents a discussion, and our work is summarized and concluded in Sect. III.

The theoretical formalism for one-neutron transfer is discussed in this section. The formalism for two-neutron transfer is similar to that of one-neutron transfer, with a distinction that the pair of neutrons behave like a single quasi-particle and the transition potential is assumed to act on the relative motion between the correlated neutron pair and the core.

For one-neutron transfer in the reaction ($ a + A \rightarrow b + B $), the wave functions of the entrance and exit channels can be represented as $ \Psi_{\alpha}(R,\zeta_{i},\zeta_{j}) $ and $ \Psi_{\beta}(R',\zeta_{k},\zeta_{l}) $. Here, $R $ and $R' $ denote the center of mass coordinates between the projectile and the target in the entrance and exit channels. The intrinsic coordinates of a and b are denoted by $ \zeta_{i} $ and $ \zeta_{k} $, while those of A and B are represented by $ \zeta_{j} $ and $ \zeta_{l} $, respectively. Consequently, the transfer matrix elements, which are used to calculate the coupling terms that arise from the transfer of particles, can be expressed as follows:

Here, $ \left| {\Psi_{\alpha}} \right\rangle = \sum_{ij}\left| {\phi_{a_i}\phi_{A_j}\chi_{\alpha}} \right\rangle $ and $ \left\langle {\Psi_{\beta}} \right| = \sum_{kl}\left\langle {\phi_{b_{k}}\phi_{B_{l}}\chi_{\beta}} \right| $. The symbol ϕ represents the intrinsic wave functions of the nuclei, while $ \chi_{\alpha} $ and $ \chi_{\beta} $ denote the relative motion wave functions in entrance and exit channels. $ {a_i}, {A_j}, b_{k} $, and $ B_{l} $ are all the quantum numbers required to specify the state of the a, A, b, and B nuclei.

The residual interaction, in the prior form, is given by $ W_{\alpha} = U_{c}(R_{c}) + \nu(r') - U(R) $. Here, $ U_{c}(R_{c}) $, where $ R_{c} $ denotes the distance between centers of nuclei, represents the core-core potential. The optical potential $ U(R) $ is used to generate the corresponding distorted waves. Both $ U_{c}(R_{c}) $ and $ U(R) $ are complex potentials defined to describe the scattering between core nuclei and between the projectile and target in the entrance channel. The term $ U_{c}(R_{c}) - U(R) $ is called the residual remnant potential. $ \nu(r') $ is the real potential that binds the valence nucleon to the core.

In this work, we have used São Paulo potential (SPP) as the optical potential, which is derived from a double-folding form

In this equation, $ r_{i} $ (i=1,2) represents the vector that connects the center of mass of nucleus i to the respective volume element, while R connects the centers of masses of the two nuclei. $ \rho_{1} $ and $ \rho_{2} $ being the matter densities of the colliding nuclei, and $ \nu_{NN}(R-r_{1}+r_{2}) $ is the nucleon-nucleon M3Y interaction [33, 34]. The SPP is given by $ V^{SP}(R,E) $ = $ V_{F}(R)e^{-4v^2/c^2} $ [35], where v is the relative velocity between the colliding nuclei, and c is the speed of light.

The intrinsic wave functions for nucleus B consisting of core A and a valence particle ν are expressed as follows:

where $ \phi_{lsj}(r) $ is the bound wave function of the valence particle with quantum numbers $ (l,s,j) $. The spectroscopic amplitudes, $ A^{IJ}_{lsj} $, are connected to the spectroscopic factors $ S^{IJ}_{lsj} $, where $ S^{IJ}_{lsj} $ = $ |A^{IJ}_{lsj}|^2 $. Spectroscopic factors represent the probability of finding the valence particle ν in a single-particle state defined by $ (l, s, j) $, coupled to a core A with spin I. The core wave function is denoted by $ \phi_{A}^{I}(\zeta_{j}) $. To calculate transfer amplitudes, CRC codes typically require the spectroscopic factors and quantum numbers $ (l, s, j) $ of the valence particle to construct the wave functions of the composite particle, along with the coupling potentials for valence-core and core-target interactions.

The spectroscopic amplitudes for the projectile and target overlaps are essential for performing microscopic CRC calculations. These amplitudes were obtained through shell-model calculations using the NuShellX code [36]. For the system $ ^{6} $Li+$ ^{93} $Nb, to acquire the one-neutron spectroscopic information for the target overlaps, the calculations are employed with $ sn $ model space and the effective interaction $ snet $. In this model space, $ ^{56} $Ni nucleus is considered a closed core, and the 1$ f_{5/2} $, 2$ p_{3/2} $, 2$ p_{1/2} $, 1$ g_{9/2} $, 1$ g_{7/2} $, 2$ d_{5/2} $, 2$ d_{3/2} $, and 3$ s_{1/2} $ orbitals are treated as the valence space for neutrons and protons. However, constraints were necessary due to our computational limitations in performing the shell-model calculations with such a large valence space. Consequently, we imposed some restrictions and considered the nucleus $ ^{88} $Sr as a closed core instead of $ ^{56} $Ni. This truncation made the accessible valence orbitals for neutrons 1$ g_{7/2} $, 2$ d_{5/2} $, 2$ d_{3/2} $, and 3$ s_{1/2} $, and for protons, the accessible valence orbitals became 2$ p_{1/2} $, 1$ g_{9/2} $, 1$ g_{7/2} $, 2$ d_{5/2} $, 2$ d_{3/2} $, and 3$ s_{1/2} $. For the projectile overlaps, both 1p$ _{3/2} $ and 1p$ _{1/2} $ components of the neutron bound to $ ^{6} $Li were included with spectroscopic factors of 0.43 and 0.29 [37]. Table 1 presents the spectroscopic amplitudes used in the one-neutron transfer calculations related to the target overlaps. Table 2 compares the excitation energies derived from the $ snet $ interactions and the experimental values.

Initial State	j	Final State	Spect. Ampl.
$ ^{93} $Nb$ _{g.s.}(9/2^{+} $)	$ 2d_{5/2} $	$ ^{92} $Nb$ _{g.s.}(7^{+} $)	0.7265
	$ 1g_{7/2} $		0.0520
$ ^{93} $Nb$ _{g.s.}(9/2^{+} $)	$ 2d_{5/2} $	$ ^{92} $Nb$ _{0.136}(2^{+} $)	0.5372
	$ 1g_{7/2} $		0.06
$ ^{93} $Nb$ _{g.s.}(9/2^{+} $)	$ 2d_{3/2} $	$ ^{92} $Nb$ _{0.286}(3^{+} $)	0.0557
	$ 2d_{5/2} $		0.3951
	$ 1g_{7/2} $		0.01
$ ^{93} $Nb$ _{g.s.}(9/2^{+} $)	$ 3s_{1/2} $	$ ^{92} $Nb$ _{0.357}(5^{+} $)	0.1575
	$ 2d_{3/2} $		0.0374
	$ 2d_{5/2} $		0.4287
	$ 1g_{7/2} $		0.0245
$ ^{93} $Nb$ _{g.s.}(9/2^{+} $)	$ 3s_{1/2} $	$ ^{92} $Nb$ _{0.480}(4^{+} $)	0.1034
	$ 2d_{3/2} $		0.0361
	$ 2d_{5/2} $		0.3763
	$ 1g_{7/2} $		0.0346
$ ^{93} $Nb$ _{g.s.}(9/2^{+} $)	$ 2d_{3/2} $	$ ^{92} $Nb$ _{0.501}(6^{+} $)	0.0412
	$ 2d_{5/2} $		0.3681
	$ 1g_{7/2} $		0.0264

Table 1.  Spectroscopic amplitudes used in one-neutron transfer CRC calculations for $ ^{6} $Li+$ ^{93} $Nb reaction, where j is the spin of the neutron orbitals.

Nucleus	$ j^{\pi} $	Energy (MeV)
		Experimental	$ snet $ interaction
$ ^{92}\text{Nb} $	$ 7^+ $	0.0	0.0
	$ 2^+ $	0.136	0.168
	$ 3^+ $	0.286	0.316
	$ 5^+ $	0.357	0.288
	$ 4^+ $	0.480	0.431
	$ 6^+ $	0.501	0.459
$ ^{93}\text{Nb} $	$ 9/2^+ $	0.0	0.0
	$ 1/2^- $	0.031	0.171
	$ 5/2^+ $	0.809	1.053
	$ 5/2^- $	0.810	1.066

Table 2.  Comparison of experimental and NuShellX results for $ ^{92}\text{Nb} $ and $ ^{93}\text{Nb} $ spectra using the $ snet $ interactions. The spin and parity of states are denoted by $ j^\pi $.

In this study, we have analyzed the experimental excitation functions of the residues $ ^{92m} $Nb, populated in $ ^{6} $Li+$ ^{93} $Nb reactions [21], and $ ^{116m} $In in $ ^{7} $Li+$ ^{115} $In reactions. The experiment for $ ^{7} $Li+$ ^{115} $In system was performed at the BARC-TIFR Pelletron facility in Mumbai, India. The off-beam γ-spectroscopy technique was adopted, and the radionuclides used in the current analysis were identified following their characteristic γ-rays and the decay curve. The measured cross sections of $ ^{92m} $Nb and $ ^{116m} $In were significantly underpredicted by the calculations from PACE4 and EMPIRE nuclear reaction codes, which are based on equilibrium and pre-equilibrium reaction processes. Consequently, we examined their production via one-neutron transfer channel. CRC calculations were carried out in the framework of FRESCO code [38].

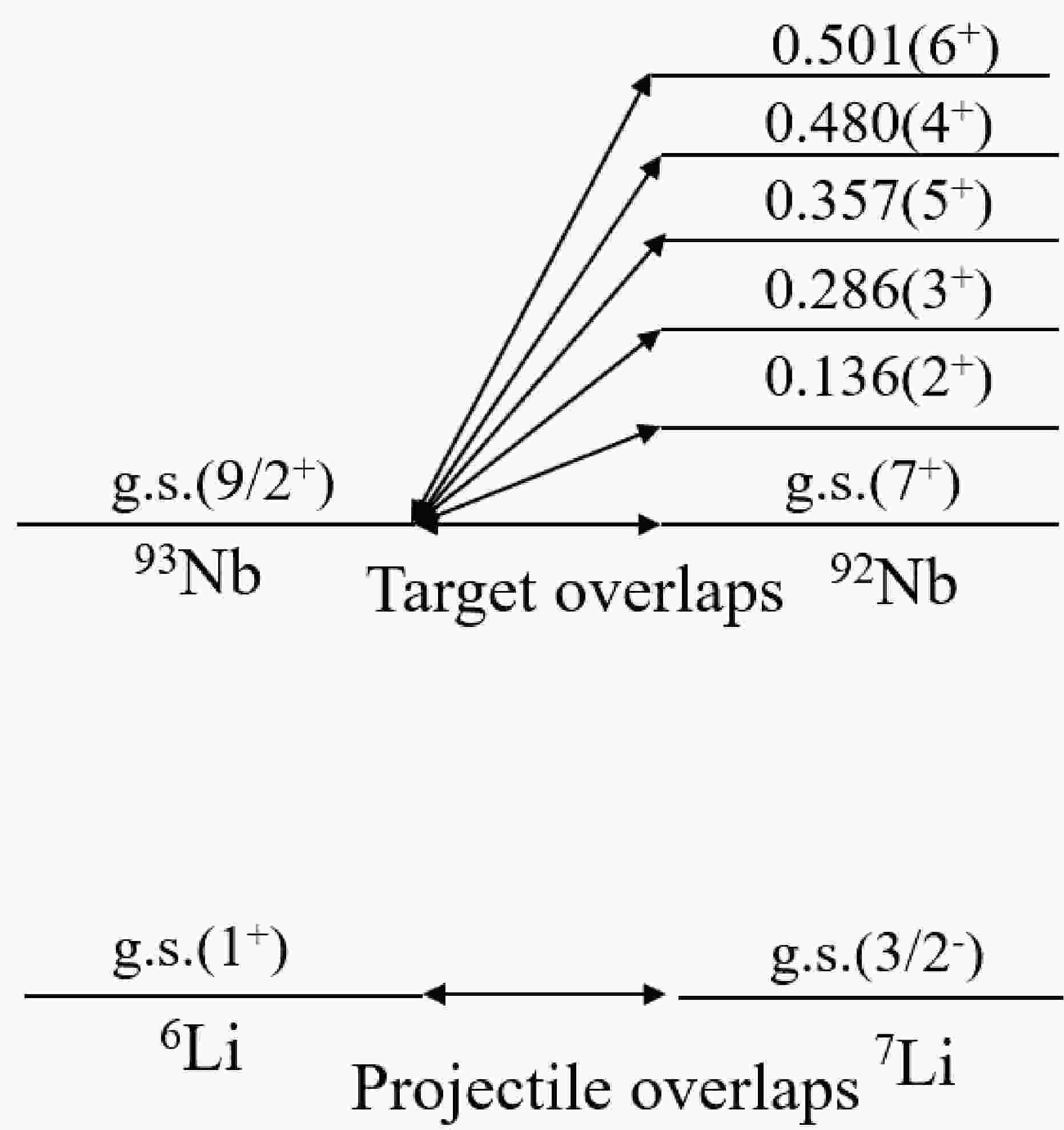
For the transfer of neutron in $ ^{6} $Li+$ ^{93} $Nb reaction, the coupling scheme adopted is shown in Fig. 1. The calculations employed double-folding SPP [11, 12] for both the real and imaginary parts of the optical potential ($ U(R) $ = ($ N_r $ + $ iN_i $)$ V^{SP}(R)) $. In the entrance partition, the strength coefficients for the real and imaginary potentials were set to $ N_r $ = $ N_i $ = 0.6, following the previous studies [28, 29, 39−41] to account for flux loss due to dissipative and breakup channels [40, 41] and the repulsive nature of the real part of the breakup polarization potential [42−45]. In the exit partition, the SPP was used for real and imaginary components with strength coefficients $ N_r $ = 1.0 and $ N_i $ = 0.78 [46], respectively. The coefficient value 0.78 has been proven effective for describing the elastic scattering cross section for various systems, spanning a wide range of masses and energy [47]. The prior form of potential with full complex remnant terms and non-orthogonality corrections were included in the calculations. Woods-Saxon form factor with a radius of 1.27$ A^{1/3} $ fm and a diffuseness of 0.65 fm for both lighter and heavier nuclei, where A represents the mass of the core nucleus, were utilized to generate single-particle wave functions. The depths were adjusted to reproduce the binding energies of the particle-core composite system, and a spin-orbit component was also included.

Figure 1.  Coupling scheme considered in the one-neutron transfer calculation for $ ^{6} $Li+$ ^{93} $Nb reaction. The energies of states are in MeV.

In $ ^{7} $Li+$ ^{115} $In reaction, the spectroscopic amplitudes for target overlaps were set equal to 1.0, as accurately determining these amplitudes requires a large model space, which is challenging to handle computationally. The coupling scheme depicted in Fig. 2 was employed in the calculations. Table 3 provides the spectroscopic data related to the target overlaps. For these calculations, the SPP was used for both the real and imaginary parts of the optical potential. The strength coefficients for real and imaginary potentials were set to $ N_r $ = $ N_i $ = 0.6 in the entrance partition. In the final partition, the SPP was utilized for the real and imaginary parts with strength coefficients of $ N_r $ = 1.0 and $ N_i $ = 0.78, respectively. Calculations were performed using the post form of the potential, including full complex remnant term and non-orthogonality corrections. The potentials binding the transferred particles were of the Woods-Saxon type, with a radius of 1.27$ A^{1/3} $ fm for (both) lighter and heavier nuclei and a diffuseness of 0.65 fm. The spin-orbit interaction was also included.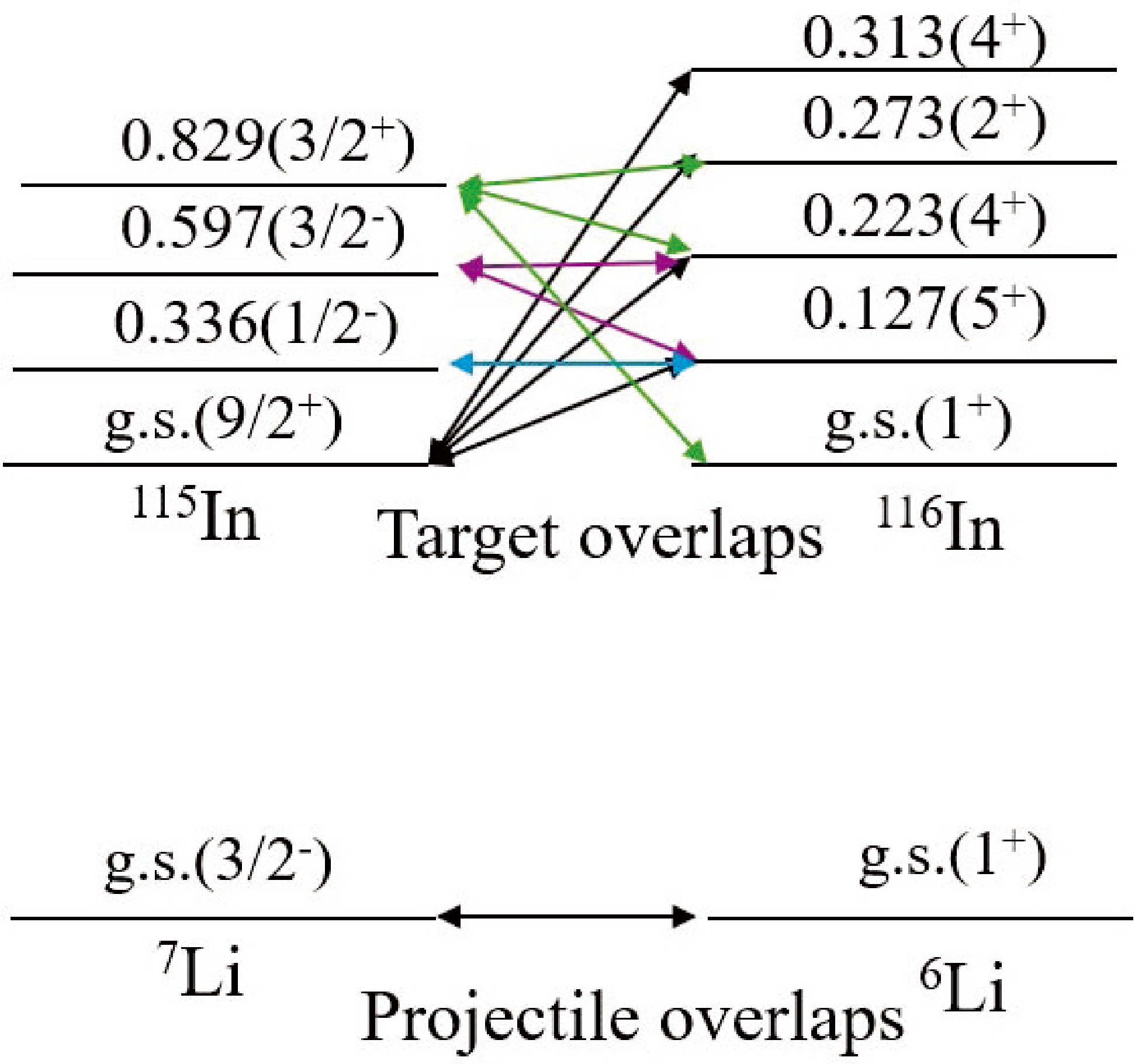

Figure 2.  Coupling scheme considered in one-neutron transfer calculations for $ ^{7} $Li+$ ^{115} $In reaction. The energies of states are in MeV.

Initial State	j	Final State	Spect. Ampl.
$ ^{115} $In$ _{g.s.}(9/2^{+} $)	$ 3s_{1/2} $	$ ^{116} $In$ _{0.127}(5^{+} $)	1.0
	$ 2d_{3/2} $		1.0
	$ 2d_{5/2} $		1.0
$ ^{115} $In$ _{g.s.}(9/2^{+} $)	$ 3s_{1/2} $	$ ^{116} $In$ _{0.223}(4^{+} $)	1.0
	$ 2d_{3/2} $		1.0
	$ 2d_{5/2} $		1.0
$ ^{115} $In$ _{g.s.}(9/2^{+} $)	$ 2d_{5/2} $	$ ^{116} $In$ _{0.273}(2^{+} $)	1.0
$ ^{115} $In$ _{g.s.}(9/2^{+} $)	$ 3s_{1/2} $	$ ^{116} $In$ _{0.313}(4^{+} $)	1.0
	$ 2d_{3/2} $		1.0
	$ 2d_{5/2} $		1.0
$ ^{115} $In$ _{0.336}(1/2^{-} $)	$ 1h_{11/2} $	$ ^{116} $In$ _{0.127}(5^{+} $)	1.0
$ ^{115} $In$ _{0.597}(3/2^{-} $)	$ 1h_{11/2} $	$ ^{116} $In$ _{0.127}(5^{+} $)	1.0
$ ^{115} $In$ _{0.597}(3/2^{-} $)	$ 1h_{11/2} $	$ ^{116} $In$ _{0.223}(4^{+} $)	1.0
$ ^{115} $In$ _{0.829}(3/2^{+} $)	$ 3s_{1/2} $	$ ^{116} $In$ _{g.s.}(1^{+} $)	1.0
	$ 2d_{3/2} $		1.0
	$ 2d_{5/2} $		1.0
$ ^{115} $In$ _{0.829}(3/2^{+} $)	$ 2d_{5/2} $	$ ^{116} $In$ _{0.223}(4^{+} $)	1.0
$ ^{115} $In$ _{0.829}(3/2^{+} $)	$ 3s_{1/2} $	$ ^{116} $In$ _{0.273}(2^{+} $)	1.0
	$ 2d_{3/2} $		1.0
	$ 2d_{5/2} $		1.0

Table 3.  Spectroscopic amplitudes used in one-neutron transfer CRC calculations for $ ^{7} $Li+$ ^{115} $In reaction, where j is the spin of the neutron orbitals.

In order to study the production of $ ^{183} $Ta through the two-neutron transfer channel in $ ^{7} $Li+$ ^{181} $Ta reaction [23], we have examined the simultaneous transfer of two neutrons using the extreme cluster approach, where the spectroscopic amplitudes for target and projectile overlap were taken as unity. This approach considers the transition potential to act on the relative motion between the correlated nucleon pair and the core. This approach treats the pair of nucleons as a single quasi-particle. The wave function of the cluster is derived from the energy conservation relation of the harmonic oscillator [1]:

Here, $ n_i $ and $ l_i $ represent the principal quantum number and orbital angular momentum of individual nucleons. The symbols $ n,l $ and $ N,L $ denote the corresponding quantities for the motion of the nucleons relative to each other and to the core. In the extreme cluster approximation, the two-nucleon cluster is assumed to be in the $ 1s $ internal state ($ n=1,l=0 $) with an intrinsic spin $ S=0 $ (anti-parallel spin configuration).

In Ref. [23], $ ^{183} $Ta produced in $ ^{7} $Li+$ ^{181} $Ta reaction is identified using offline γ-spectroscopy technique, and the measured cross section of $ ^{183} $Ta is compared with the calculated results from EMPIRE using GC, GSM, and EGSM level densities. The calculations underestimate the experimental data by 4 to 5 orders of magnitude. Consequently, we examined the production of $ ^{183} $Ta through the two-neutron transfer channel. The coupling scheme shown in Fig. 3 was used in the calculations. The initial and final bound state wave functions for the di-neutron system were generated using a Woods-Saxon potential, with a radius of 1.30 fm and diffuseness of 0.70 fm. The depth of the potential was adjusted to match the two-neutron separation energy. The finite range transfer calculations were performed using the post form of the interaction potential, incorporating the full complex remnant term and non-orthogonality corrections. The SPP was employed as the optical potential for both real and imaginary components. A strength coefficient of 0.6 was applied to real and imaginary parts in the entrance partition. In the final partition, the imaginary part was scaled by a factor of 0.78. We have also used the spin-orbit interaction term.

Figure 3.  Coupling scheme considered in the two-neutron transfer calculation for $ ^{7} $Li+$ ^{181} $Ta reaction. The energies of states are in MeV.

However, the nucleus $ ^{5} $Li is unstable and decays into $ ^{4} $He and a proton. For the overlap $ \langle ^7\text{Li} | ^5\text{Li} \rangle $, we have considered the first step in the CRC calculations, where the ground-state resonance of $ ^{5} $Li is formed and subsequently decays. If this resonance exists for a sufficient duration, it can be treated as a bound state in CC calculations. It is a standard method in CC calculations for explaining broad resonances, such as those in $ ^{6} $Li and $ ^{7} $Li [48].

We performed the CRC calculations using the code FRESCO to confirm that the residues $ ^{92m} $Nb, $ ^{116m} $In, and $ ^{183} $Ta result from transfer reactions. These calculations examined the production of $ ^{92m} $Nb via one-neutron pickup in $ ^{6} $Li-induced reaction on $ ^{93} $Nb, $ ^{116m} $In via one-neutron stripping in $ ^{7} $Li-induced reaction on $ ^{115} $In, and $ ^{183} $Ta via two-neutron stripping in $ ^{7} $Li-induced reaction on $ ^{181} $Ta. The results of these calculations are presented in Figs. 4, 5, and 6 and are compared with the experimental data. The solid black line represents the CRC calculations, incorporating the SPP potential with parameters $ N_r $=$ N_i $=0.60 for the entrance channel and $ N_r $=1.0, $ N_i $=0.78 for the exit channel in all three reactions. The figures indicate that the calculations closely match the experimental data in all cases. The CRC calculations using the extreme cluster model describe the data well for transferring two neutrons in $ ^{7} $Li-induced reaction on $ ^{181} $Ta, indicating the dominance of the one-step reaction mechanism.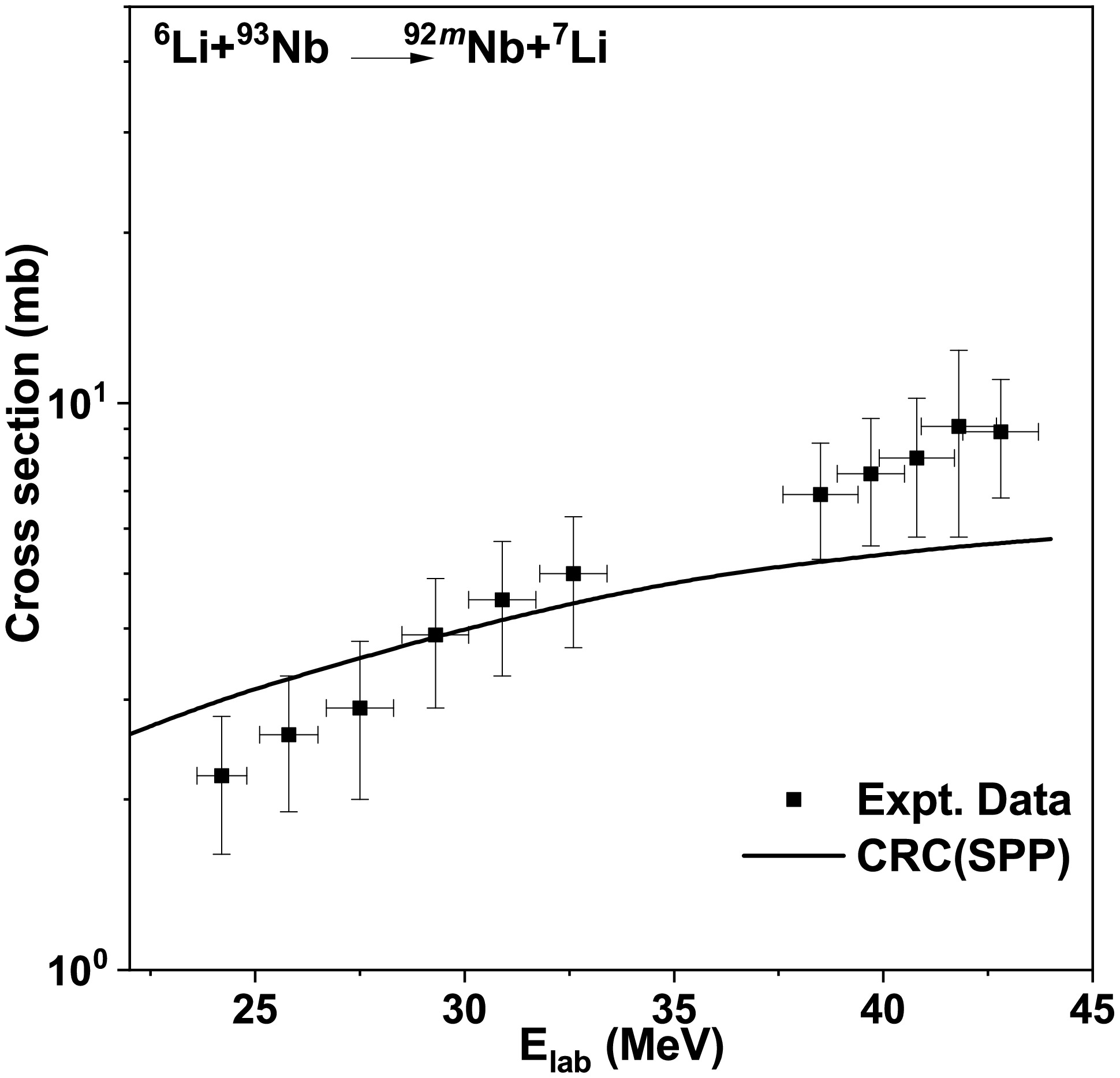

Figure 4.  Comparison between experimental [21] and theoretical excitation function for the reaction $ ^{93} $Nb($ ^{6} $Li,$ ^{7} $Li)$ ^{92m} $Nb.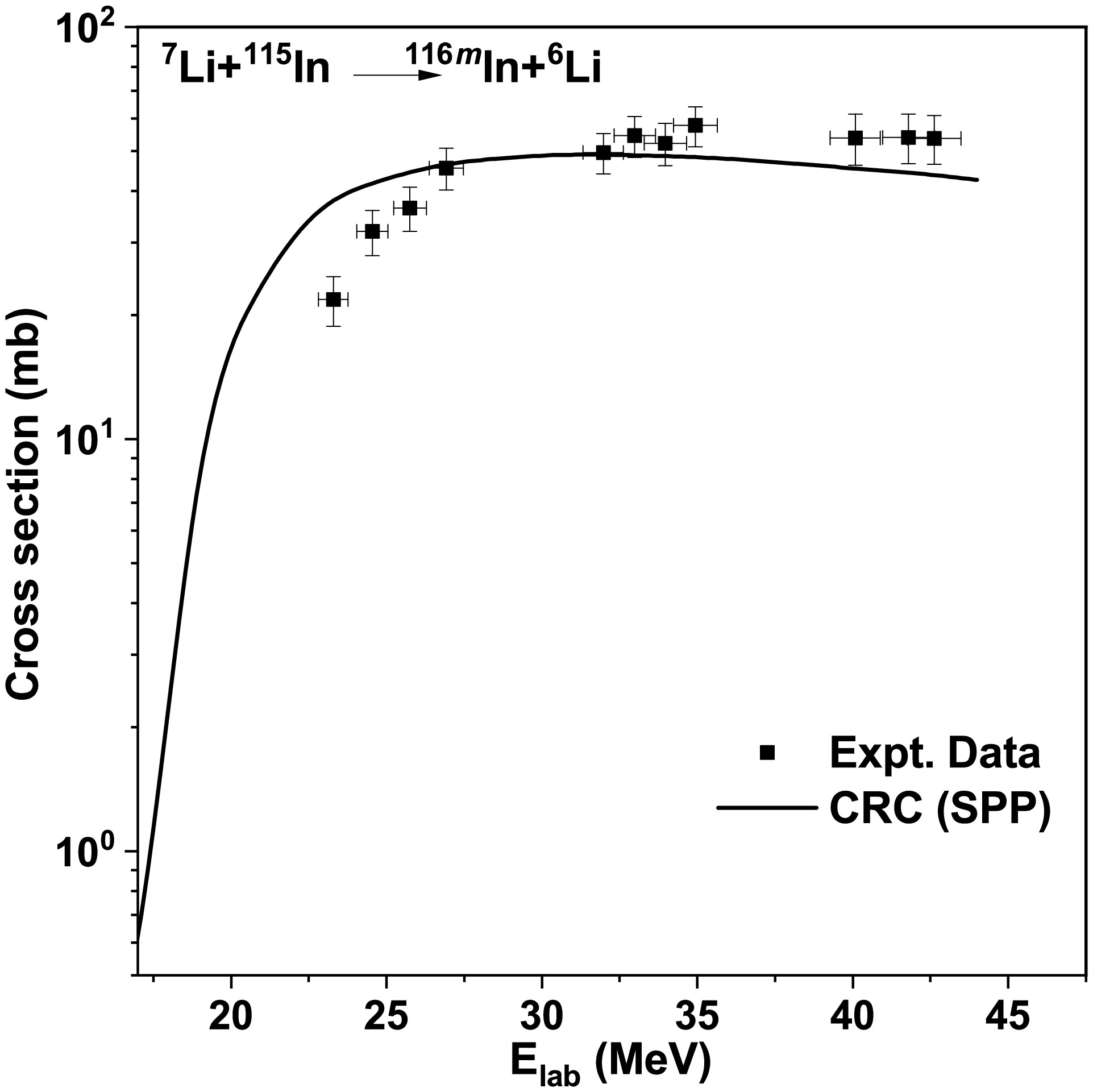

Figure 5.  Comparison between experimental and theoretical excitation function for the reaction $ ^{115} $In($ ^{7} $Li,$ ^{6} $Li)$ ^{116m} $In.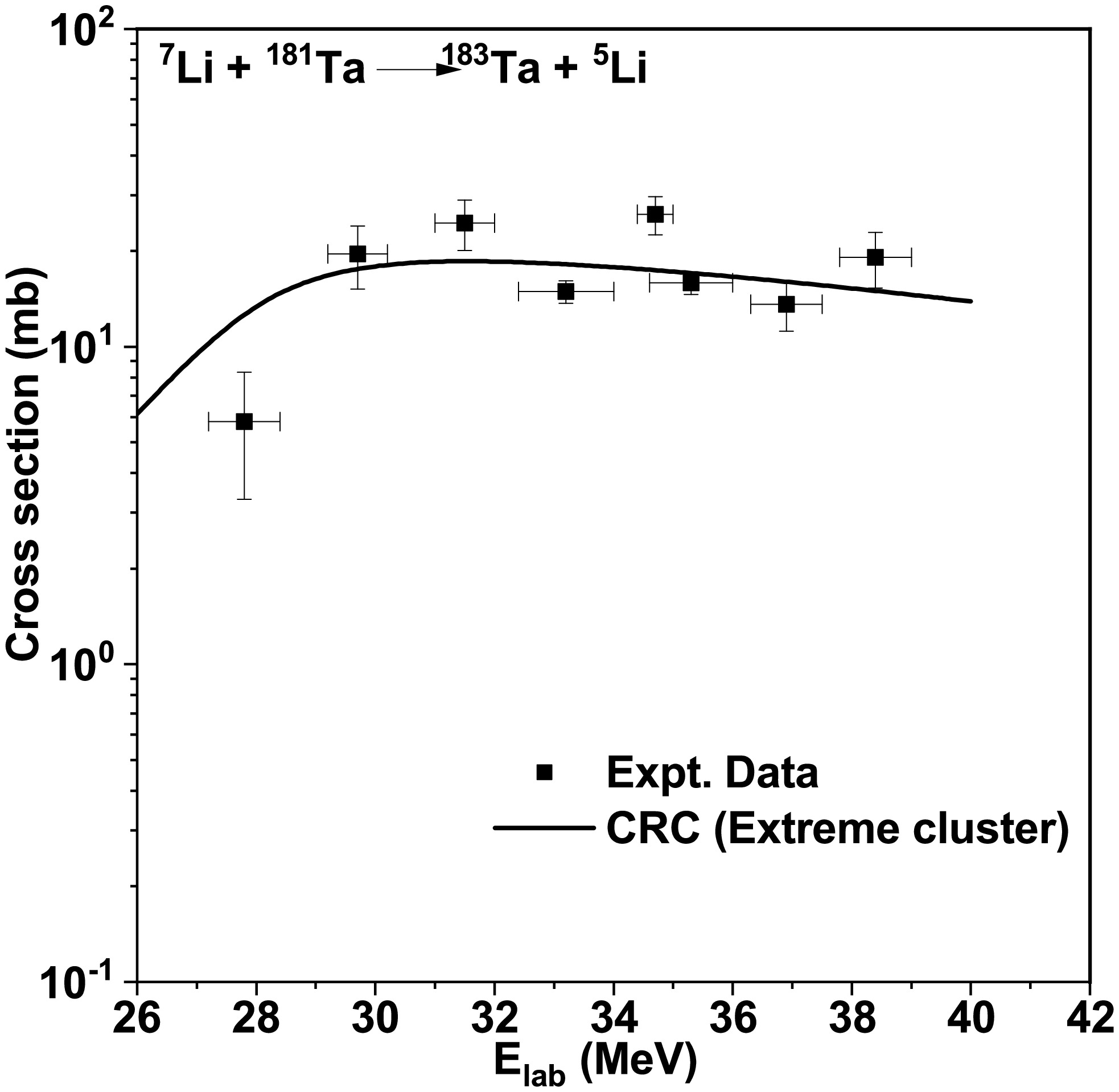

Figure 6.  Comparison between experimental [23] and theoretical excitation function for the reaction $ ^{181} $Ta($ ^{7} $Li,$ ^{5} $Li)$ ^{183} $Ta.

Although the SPP has been utilized as the optical potential, the single-particle states were generated using Woods-Saxon form factors for projectile and target overlaps. These form factors have three parameters: depth, reduced radius, and diffuseness. The sensitivity of the transfer cross section to changes in the reduced radius has been analyzed and is presented in Figs. 7, 8, and 9. The excitation functions for transfer in all three reactions have been studied at three reduced radii values: 1.20 fm, 1.25 fm, and 1.3 fm, commonly reported in the literature. It is clear that increasing or decreasing these parameters for both the projectile and target form factors leads to a corresponding increase or decrease in the transfer cross section compared to the average value of this parameter. Based on this analysis, the value of r used is 1.27 fm for one-neutron transfer reactions and 1.30 fm for two-neutron transfer reactions.

Figure 7.  The impact of variations in the reduced radius of the form factor of the projectile and target overlaps on one-neutron transfer cross section for $ ^{93} $Nb($ ^{6} $Li,$ ^{7} $Li)$ ^{92m} $Nb reaction. Experimental data taken from Ref. [21].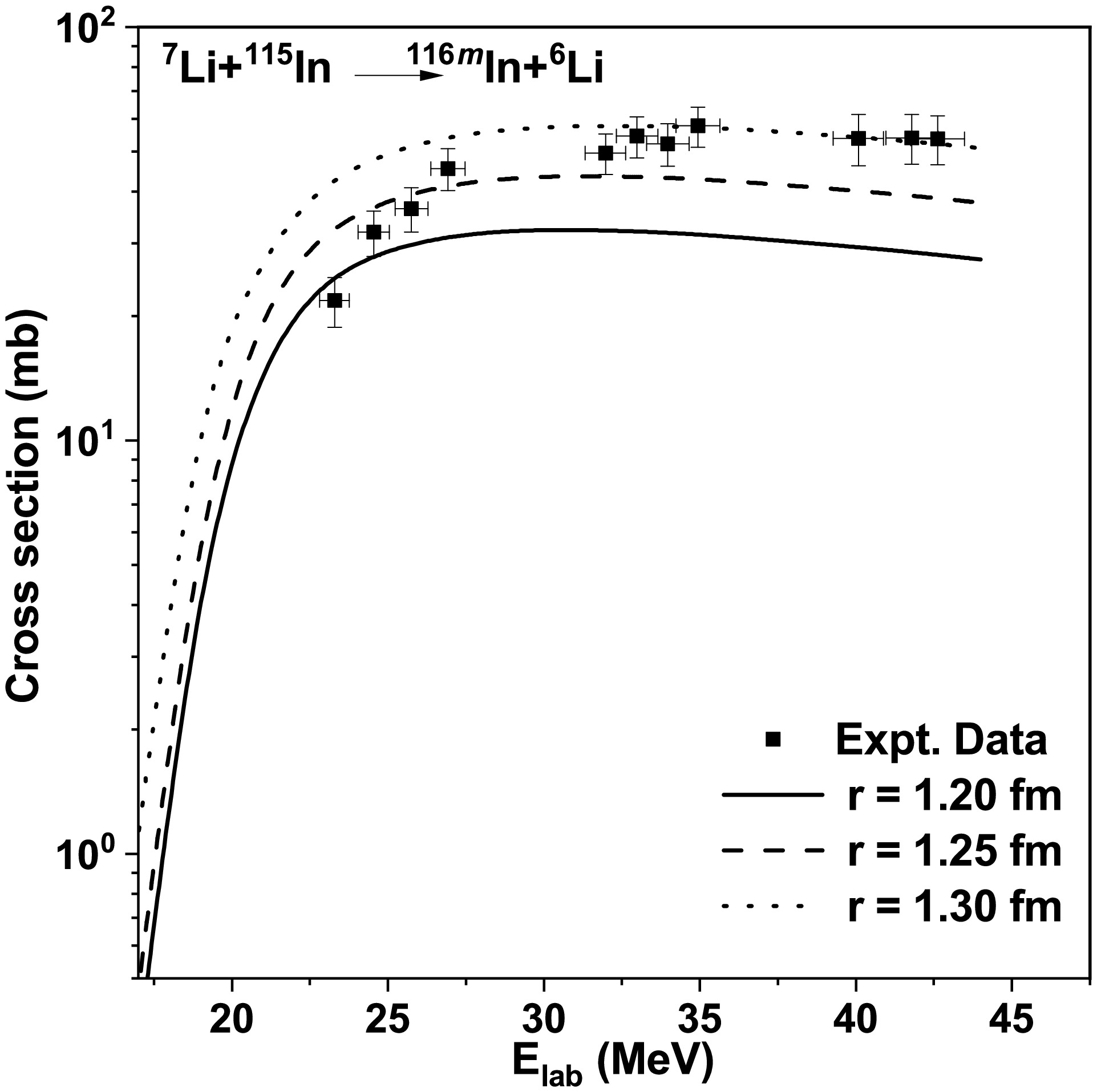

Figure 8.  The impact of variations in the reduced radius of the form factor of the projectile and target overlaps on one-neutron transfer cross section for $ ^{115} $In($ ^{7} $Li,$ ^{6} $Li)$ ^{116m} $In reaction.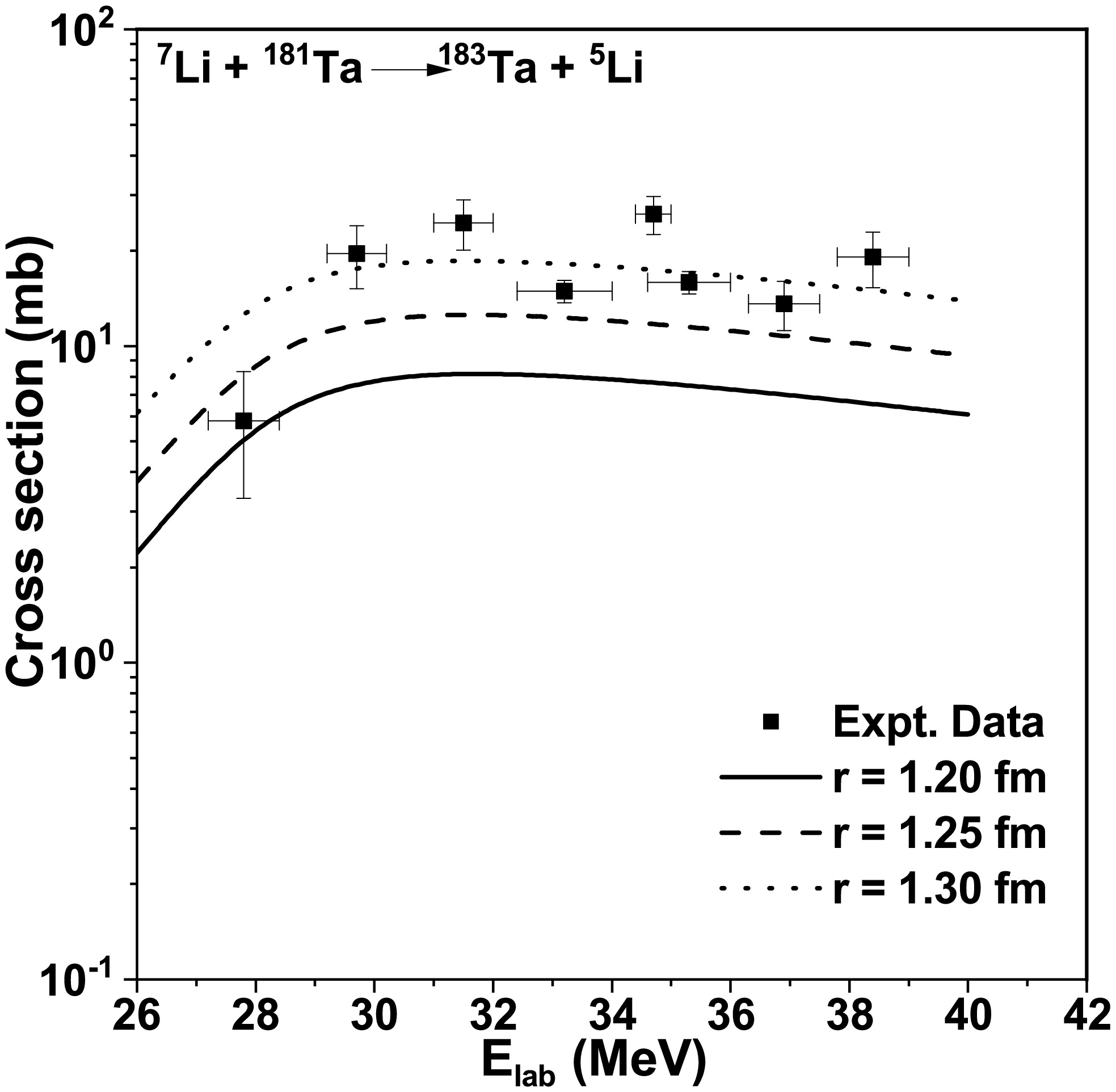

Figure 9.  The impact of variations in the reduced radius of the form factor of the projectile and target overlaps on two-neutron transfer cross section for $ ^{181} $Ta($ ^{7} $Li,$ ^{5} $Li)$ ^{183} $Ta reaction. Experimental data taken from Ref. [23].

Individual transitions were not measured since the nuclei of interest were measured using the γ-spectroscopy. Understanding the individual transitions and the population pattern of transfer products, as derived from experiments, will offer a deeper insight into the underlying reaction mechanism.

We conducted CRC calculations to understand the mechanism of one-neutron transfer in $ ^{93} $Nb($ ^{6} $Li,$ ^{7} $Li)$ ^{92m} $Nb and $ ^{115} $In($ ^{7} $Li,$ ^{6} $Li)$ ^{116m} $In reactions and two-neutron transfer in $ ^{181} $Ta($ ^{7} $Li,$ ^{5} $Li)$ ^{183} $Ta reaction. The double folding SPP was utilized, with the adopted imaginary potential $ W(R) $ = $ N_i $ $ \times $ $ V_{SPP} $. We thoroughly examined the one-neutron transfer in $ ^{6} $Li+$ ^{93} $Nb and $ ^{7} $Li+$ ^{115} $In reactions, as well as the two-neutron transfer in $ ^{7} $Li+$ ^{181} $Ta reaction, including the low lying excited states of both projectile and the target. The simultaneous transfer of two neutrons in the $ ^{7} $Li+$ ^{181} $Ta reaction was studied using the extreme cluster model. The optimal values of $ N_i $ for the initial and final partitions were found to be 0.6 and 0.78 for all three systems. A reasonable agreement between experimental and theoretical cross sections has been achieved in this study. The impact of the reduced radius of the form factor of the projectile and the target on transfer cross sections has also been studied. More systematic studies of multinucleon transfer channels within the CRC framework would help constrain potential parameters and reduce uncertainties in state selection. Identifying γ-transitions in coincidence with reaction products will allow for a more precise choice of states to include in the calculations, leading to a deeper understanding of the transfer mechanisms.

The authors sincerely thank the colleagues from the TASISPEC Lab for their support, Mr. Chandra Kumar for valuable discussions, and Dr. Erica N. Cardozo regarding FRESCO calculations.