Towards New Elements: Production of Superheavy Elements with ⁵⁰Ti and ⁵⁴Cr

Ever since Dmitri Mendeleev introduced the periodic table of elements in 1869 [1], and Glenn Seaborg subsequently synthesized the first elements beyond naturally occurring uranium [2], the search for the limits of element existence and the investigation of the properties of superheavy elements (SHE) have stood as an important frontier in modern nuclear physics [3]. Today, the exploration of the region of SHE exhibiting enhanced stability and the quest to discover new elements remain active fields of research in both theoretical and experimental nuclear physics [4−14].

In early research, it was discovered that nuclei with neutron and/or proton numbers of 2, 8, 20, 28, 50, 82, and 126 exhibit particularly high stability, known as magic numbers [15]. The nuclear shell model explains these magic numbers as resulting from completely filled nucleon shells [16]. Nuclei with these nucleon numbers are referred to as semi-magic or doubly-magic, such as $^{4}\text{He}$, $^{48}\text{Ca}$, and $^{208}\text{Pb}$, with $^{208}\text{Pb}$ being the heaviest known doubly-magic nucleus and the heaviest stable nuclide. Early calculations predicted that the next shell closures might occur at $ Z = 114 $ and $ N = 184 $, with nuclei around these numbers potentially having lifetimes ranging from minutes to millions of years, leading to the concept of an island of stability [17, 18]. Although element 118 has been successfully synthesized in laboratories, the exact location and extent of the island of stability on the chart of nuclides remain uncertain. The discovery of stable SHE will provide important insights into chemistry and physics, and the production of new SHE is one of the key focuses in this field.

Presently, the primary method for producing SHE with $ Z \geq 114 $ is through fusion reactions using doubly magic $^{48}\text{Ca}$ beams [19]. In these reactions, the beam nuclei fuse with target nuclei of appropriate actinide elements to reach proton numbers $ Z = 114 - 118 $. Unfortunately, to reach higher atomic numbers, continuing to use the $^{48}\text{Ca}$ beam for synthesis is not feasible, as current technology is unable to produce sufficient quantities (around 10 to 20 mg) of trans-Cf targets [20]. Thus, to achieve $ Z > 118 $, beams heavier than $^{48}\text{Ca}$ are required. Several experimental groups have attempted to synthesize new elements with $ Z \geq 119 $ using the following reactions: $^{64}\text{Ni}+^{238}\text{U}$ [21], $^{55}\text{Fe}+^{244}\text{Pu}$ [22], $^{50}\text{Ti}+^{249}\text{Cf}$ [23], $^{50}\text{Ti}+^{249}\text{Cf}$ [23], $^{54}\text{Cr}+^{248}\text{Cm}$ [24]. However, none of these experiments have resulted in successful synthesis to date. A key challenge in current experimental and theoretical research is to identify the most promising nuclear reactions and the optimal beam energy, which are critical for the successful production of new elements with $ Z > 118 $ [3]. It is absolutely crucial to choose the beam energy that corresponds to the maximum cross-section. Even a slight deviation of just a few MeV in the experimental settings can result in a significant decrease in the production rate [11].

Numerous theoretical models have studied the production rates of SHE. The majority of these models can reasonably reproduce the excitation functions of known fusion reactions induced by $^{48}\text{Ca}$ beams and predict the cross-sections for the production of new elements with $ Z > 118 $ using beams heavier than $^{48}\text{Ca} $ [25−41]. These studies largely agree that reactions with $^{50}\text{Ti}$ and $^{54}\text{Cr}$ beams are the most promising for the production of SHE with $ Z = 119 $ and 120. It is worth noting that the predicted cross-sections differ significantly. For example, in the $^{50}\text{Ti} + ^{249}\text{Cf}$ reaction, the predicted maximum cross-sections range from a few fb to several hundred fb. Moreover, the proposed beam energies corresponding to the maximum cross-sections differ by tens of MeV. This is because different theoretical models are based on different physical assumptions, leading to different predicted values. Also, these predictions are very sensitive to parameters like nuclear mass, fission barriers, and others, which is also why the results differ so much [42]. Considering the very small cross-sections for the production of elements with $ Z > 118 $ and the inconsistency in current theoretical predictions (particularly regarding the optimal beam energy), hastily conducting production experiments for new elements could result in experimental failure and lead to a waste of resources. Thus, it is crucial for both theory and experiment to focus on testing new production mechanisms, first testing the use of $^{50}\text{Ti}$ and $^{54}\text{Cr}$ to produce SHE with larger cross-sections, and then exploring the production of $ Z > 118 $ SHE with smaller cross-sections.

Several experiments to test new reaction mechanisms have been carried out. In Ref. [11], the $^{244}\text{Pu}(^{50}\text{Ti}, xn)^{294-x}\text{Lv}$ reaction was studied at Lawrence Berkeley National Laboratory's 88-Inch Cyclotron. The production cross-section was measured to be $\sigma_{\text{prod}} = 0.44^{+0.28}_{-0.58}$ pb, with a center-of-target center-of-mass energy of 220(3) MeV. Recently, it was reported that a new isotope, $^{288}\text{Lv}$, was produced in the $^{238}\text{U}(^{54}\text{Cr}, 4n)^{288}\text{Lv}$ reaction using a $^{54}\text{Cr}$ beam [43]. However, there have been no published papers on the measured production cross-section so far. Theoretically, a systematic investigation of the excitation functions for the production of SHE (not limited to $ Z > 118 $ SHE) using $^{54}\text{Cr}$ and $^{50}\text{Ti}$ can provide validation and reference for experimentally testing new reaction mechanisms.

This work is based on the dinuclear system (DNS) model [44]. The DNS model assumes that the fusion reaction of superheavy elements (SHE) consists of three steps: first, the capture process of the colliding system overcoming the Coulomb barrier; second, the dinuclear system evolves through nucleon or cluster transfer until an excited compound nucleus is formed, which is called the fusion process; and finally, the compound nucleus de-excites by emitting neutrons, which is called the survival process. The production cross section is the product of these three processes, which can be expressed as [45]:

Here, $ \sigma_{cap} $ is the capture cross-section, $ P_{cn} $ is the fusion probability, and $ W_{sur} $ is the survival probability. The capture cross-section can be written as:

The transmission probability $ T\left({{E_{c.m.}},J} \right) $ can be calculated using the Hill-Wheeler formula [46]. Considering the coupling channel effect through the potential barrier distribution function, the transmission probability can be written as:

The barrier distribution function is taken as an asymmetric Gaussian form:

Here, $ B_m = \dfrac{{B_s + B_0}}{2} $, where $ B_0 $ represents the height of the Coulomb barrier at the waist-to-waist orientation, and $ B_s $ is the minimum height of the Coulomb barrier with variance of dynamical deformation. N is the normalization constant. $ \Delta_2 = \left(B_0 - B_s \right)/2 $. The value of $ \Delta_1 $ is an empirical value. In this study, we adopt a value of 2 MeV, which is in reasonable agreement with existing experimental data.

For the fusion process, Adamian et al. used the Fokker-Planck equation to describe the diffusion process of nucleon transfer [44, 45, 47, 48]. They investigated the reaction mechanism for the production of SHE and successfully reproduced experimental measurement data [49−52]. In this work, a master equation with two variables was established and solved numerically to calculate the fusion probability [52]. This method avoids the harmonic oscillator approximation to the DNS potential energy surface [53−56]. The time evolution of the distribution probability function, $ P\left({Z_1,N_1,E_1,t} \right) $, at time t to find $ Z_1 $ protons and $ N_1 $ neutrons in fragment 1 with excitation energy $ E_1 $, can be described by the following master equation:

Here, $ W_{{Z_1}, {N_1}; {Z'_1}, {N_1}} $ represents the mean transition probability from the channel $ (Z_1, N_1) $ to $ (Z'_1, N_1) $, while $ d_{{N_1}, {Z_1}} $ denotes the microscopic dimension corresponding to the macroscopic state $ (Z_1, N_1) $. The sum includes all possible proton and neutron numbers of fragment 1, but the model considers only a single nucleon transfer, such that $ (N'_1 = N_1 \pm 1, Z'_1 = Z_1 \pm 1) $. The evolution of the double nuclear system along the distance R between the nuclei leads to quasifission. The quasifission rate $ \Lambda^{qf} $ and fission rate $ \Lambda^{fs} $ are estimated using the one-dimensional Kramers formula. The fusion probability can be expressed as:

$ N_{BG} $ and $ Z_{BG} $ represent the neutron number and charge number at the Businaro-Gallone (BG) point. The interaction time $ \tau_{\text{int}} $ refers to the duration of the interaction process during the diffusion at the bottom of the potential pocket, which is evaluated using the deflection function method.

The probability of survival when emitting $ x_n $ neutrons can be expressed as:

In the formula, $ E_{CN}^* $ represents the excitation energy of the compound nucleus. $ P\left({E_{CN}^*,x,J} \right) $ is the realization probability of emitting x neutrons, which is addressed in detail in Ref. [57]. $ {\Gamma _n} $ and $ {\Gamma _f} $ represent the partial wave decay widths of evaporating neutrons and fission, respectively.

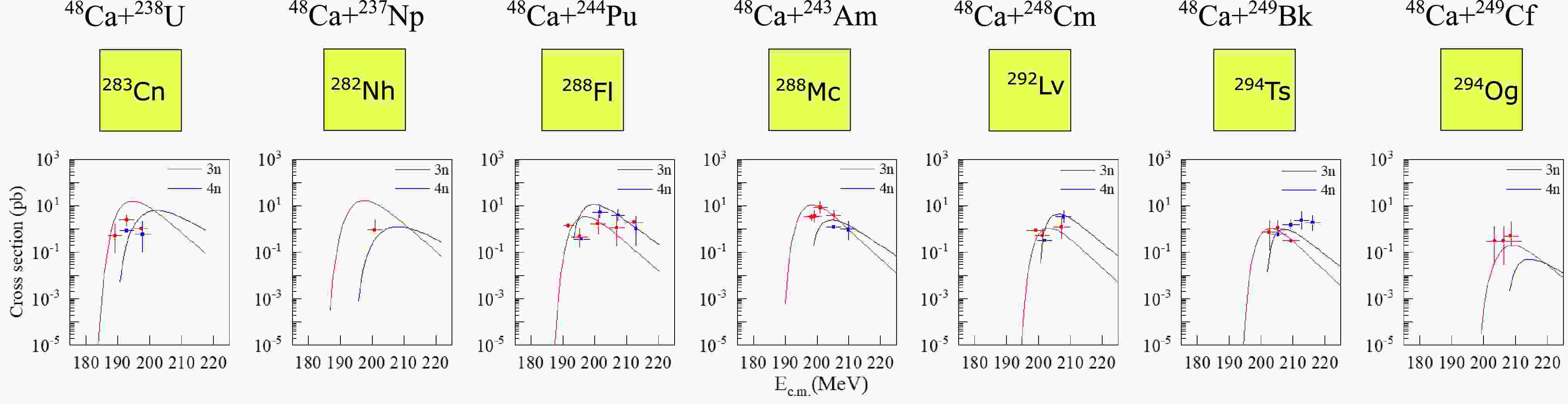
To test the ability of the DNS model to reproduce existing experimental data, we systematically calculated the production cross sections for isotopes with $ Z = 112-118 $ in $ ^{48} $Ca-induced reactions and compared them with the corresponding experimental data. The experimental data is taken from Ref. [10, 58−62]. Figure 1 shows the comparison of the calculated reaction cross sections with the experimental data for a series of reactions. It can be seen that the cross sections calculated by the DNS model can well describe the experimental values within the error range. Notably, the nuclear mass, neutron separation energy, and fission barrier used in the model are taken from Ref. [6], and the same parameters will be used in all the following calculations without any further adjustments.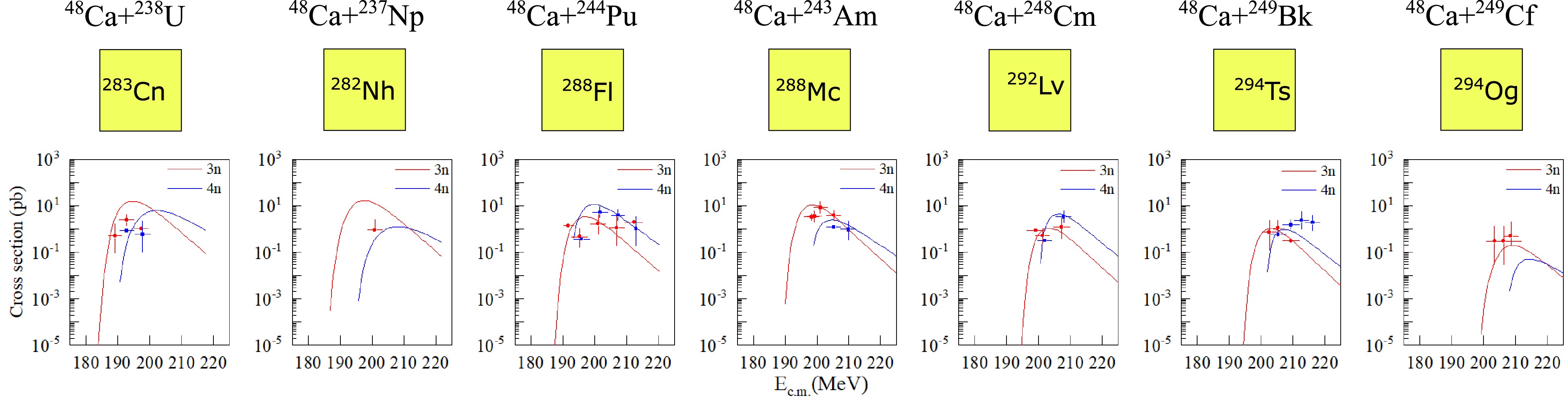

Figure 1.  (color online) Excitation function curves for the production of SHE with $ Z = 112{-}118 $ using $ ^{48} $Ca beams are presented. The red solid line represents the 3n exit channel, and the blue solid line represents the 4n exit channel. The red circles and blue squares represent experimental data for the 3n and 4n exit channels, respectively.

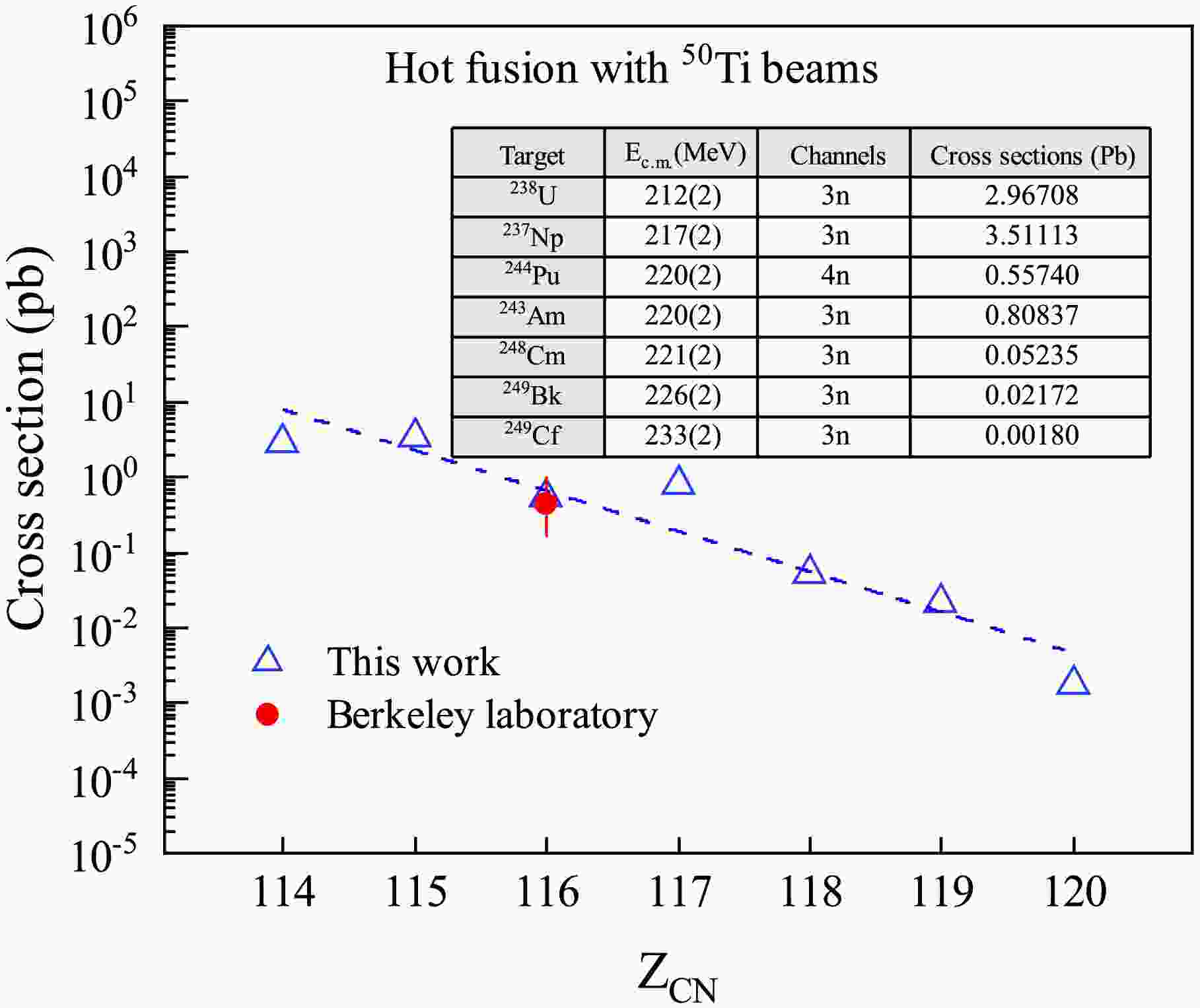
In Fig. 2, we present predictions of the maximum cross sections for the production of SHE with $ Z = 114{-}120 $ using $ ^{50} $Ti beams. One can see that as the atomic number of the compound nucleus ($ Z_{\text{CN}} $) increases, the maximum cross section generally decreases. In addition, most reactions show maximum cross sections in the 3n exit channels, while the $ ^{50} $Ti + $ ^{244} $Pu reaction has its maximum cross section in the 4n exit channels. We predict that the production cross section for this reaction is $ \sigma_{\mathrm{prod}} = 0.55 $ pb, with a center-of-target center-of-mass energy of 220(2) MeV. The experimental result shows a production cross section of $ \sigma_{\mathrm{prod}} = 0.44^{+0.28}_{-0.58}$ pb at a center-of-target center-of-mass energy of 220(3) MeV. Our results, whether for the center-of-mass energy, maximum cross section, or exit channel, are in remarkable agreement with the experimental data reported in Ref. [11].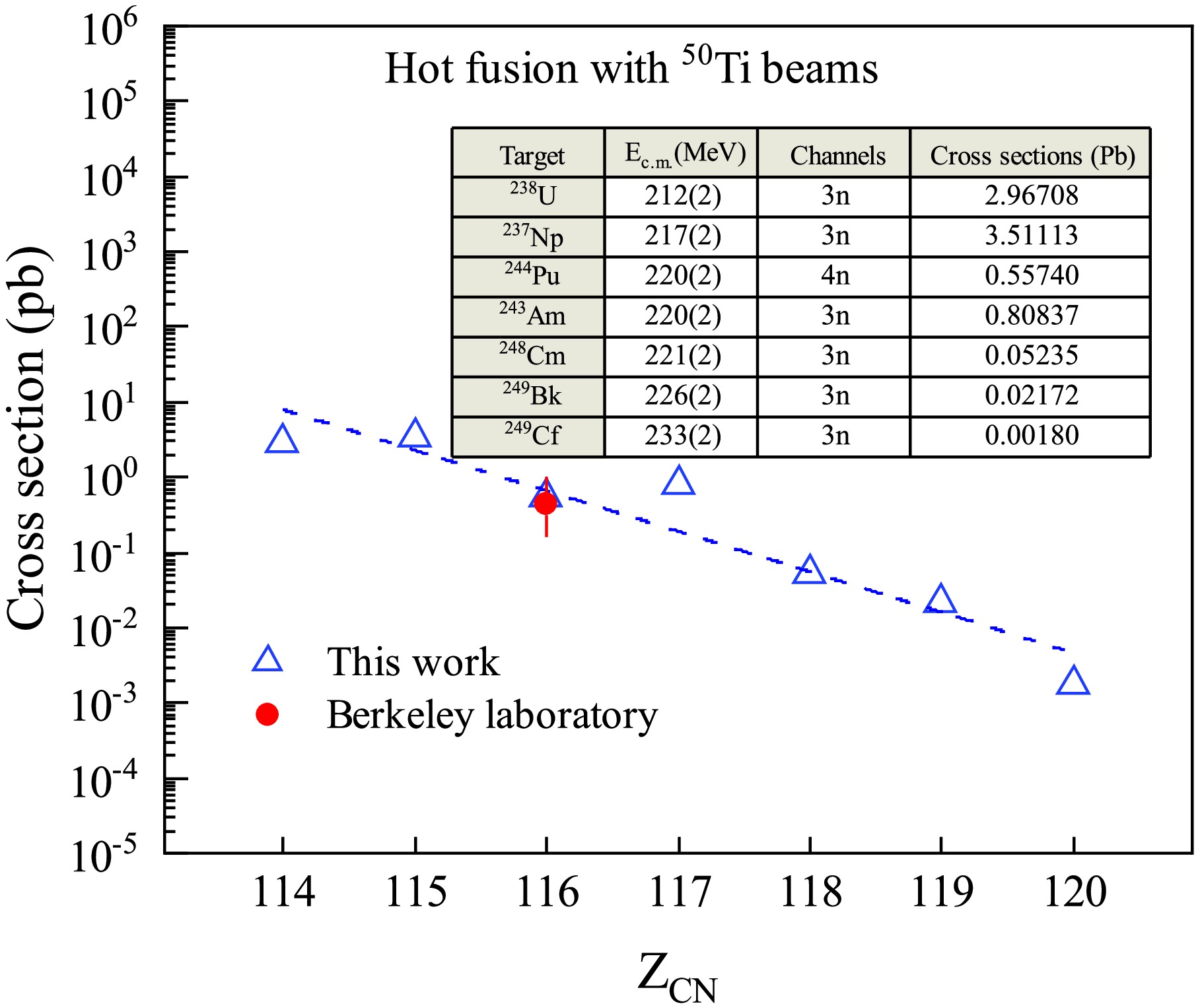

Figure 2.  (color online) Theoretical predictions (blue triangles) of the maximum cross sections for the production of SHE $ Z = 114{-}120 $ from the 3n or 4n exit channels with $ ^{50} $Ti beams, and experimental results (red circles) for $ ^{244} $Pu($ ^{50} $Ti, $ xn $)$ ^{294-x} $Lv from Ref. [11].

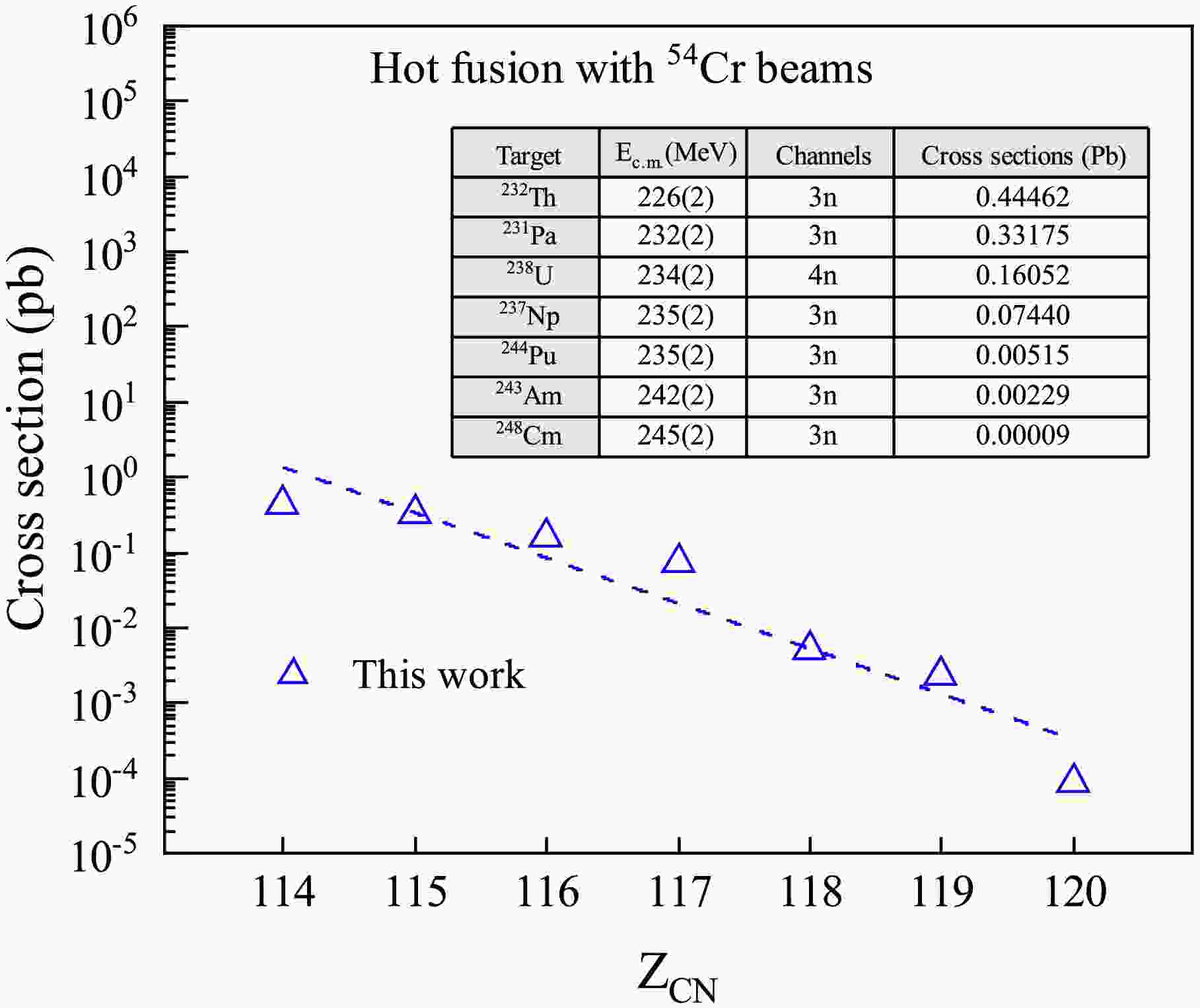
In Fig.3, we present predictions of the maximum cross sections for the production of SHE with $ Z = 114{-}120 $ using $ ^{54} $Cr beams. The results obtained with $ ^{50} $Ti beams are very similar, showing that the cross section generally decreases as the $ Z_{\text{CN}} $ increases. Additionally, most reactions show maximum cross sections in the 3n exit channels, while the $ ^{54} $Cr + $ ^{238} $U reaction has its maximum cross section in the 4n exit channels. We predict that the production cross section for this reaction is $ \sigma_{\mathrm{prod}} = 0.16 $ pb, with a center-of-target center-of-mass energy of 234(2) MeV. The experimental result for this reaction has not yet been published [43], and we look forward to further experimental validation.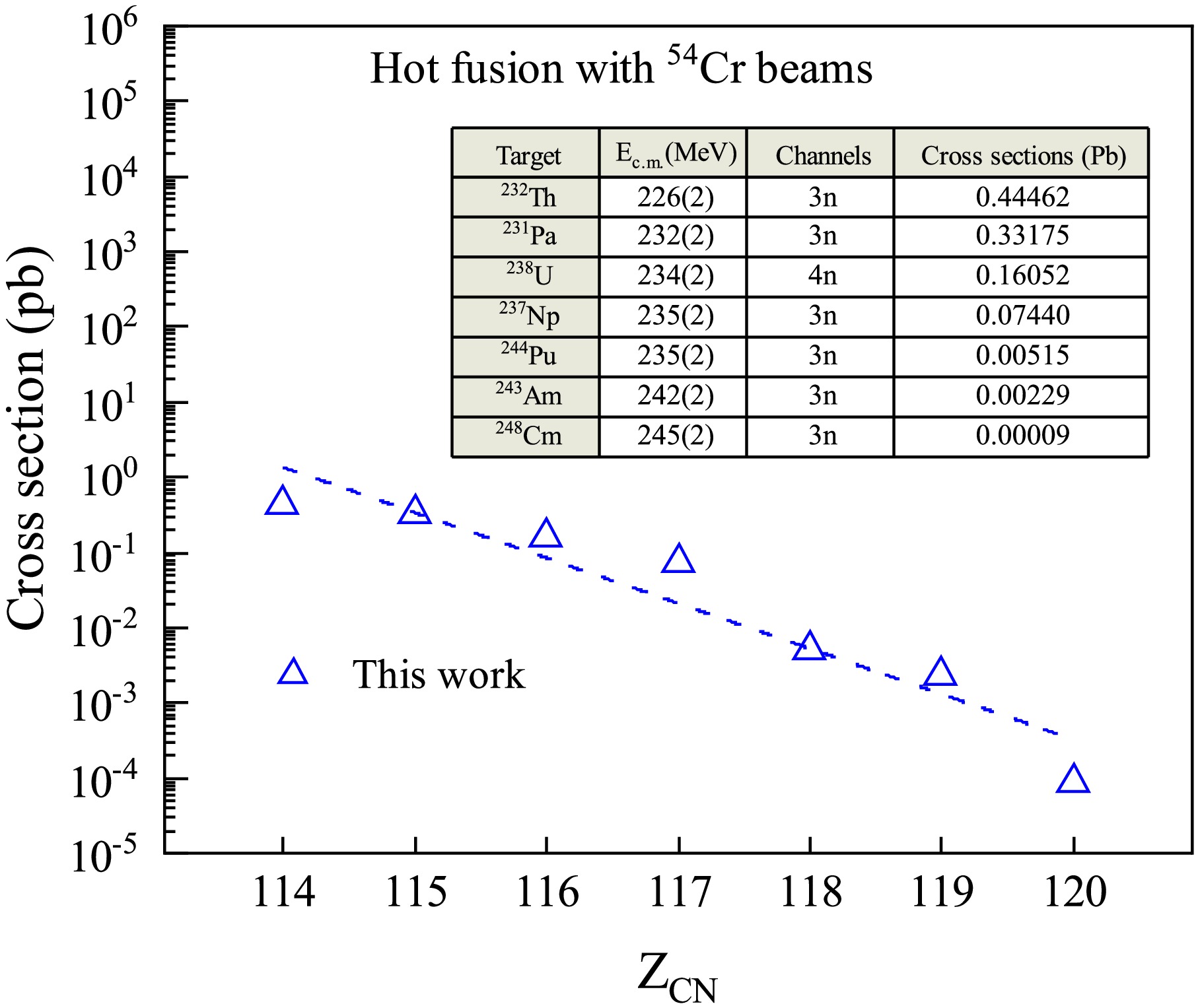

Figure 3.  (color online) Theoretical predictions (blue triangles) of the maximum cross-sections for the production of SHE $ Z = 114{-}120 $ from the 3n or 4n exit channels with $ ^{54} $Cr beams.

The production of SHE $ Z = 114{-}118 $ with a $ ^{48} $Ca beam has been investigated, and corresponding experimental cross sections have been reported. For SHE $ Z = 114 $, the $ ^{48} $Ca + $ ^{244} $Pu reaction in the 3n exit channel produced a cross section of $ 8.0^{+7.4}_{-4.5} $ pb [63], while the predicted cross sections for $ ^{50} $Ti + $ ^{238} $U and $ ^{54} $Cr + $ ^{232} $Th in the same exit channel are 2.96 pb and 0.44 pb, respectively. For SHE $ Z = 115 $, the $ ^{48} $Ca + $ ^{243} $Am reaction yielded 4 pb [64], with predicted values of 3.51 pb and 0.33 pb for $ ^{50} $Ti + $ ^{237} $Np and $ ^{54} $Cr + $ ^{231} $Pa, respectively. For SHE $ Z = 116 $, the $ ^{48} $Ca + $ ^{248} $Cm reaction produced $ 3.3^{+2.5}_{-1.4} $ pb [58], while the predicted cross sections for $ ^{50} $Ti + $ ^{244} $Pu and $ ^{54} $Cr + $ ^{238} $U are 0.55 pb and 0.16 pb, respectively. The $ ^{48} $Ca + $ ^{249} $Bk reaction for SHE $ Z = 117 $ yielded $ 1.1^{+1.2}_{-0.6} $ pb [62], with predictions of 0.80 pb and 0.07 pb for $ ^{50} $Ti + $ ^{237} $Am and $ ^{54} $Cr + $ ^{237} $Np, respectively. Finally, the $ ^{48} $Ca + $ ^{249} $Cf reaction for SHE $ Z = 118 $ produced $ 0.5^{+1.6}_{-0.3} $ pb [10], with predicted values of 0.052 pb and 0.005 pb for $ ^{50} $Ti + $ ^{248} $Cm and $ ^{54} $Cr + $ ^{244} $Pu, respectively. These results indicate that as the projectile beam becomes heavier, the production cross section for the same $ Z_{\text{CN}} $ decreases, suggesting that $ ^{50} $Ti is more probable than $ ^{54} $Cr to produce new SHE.

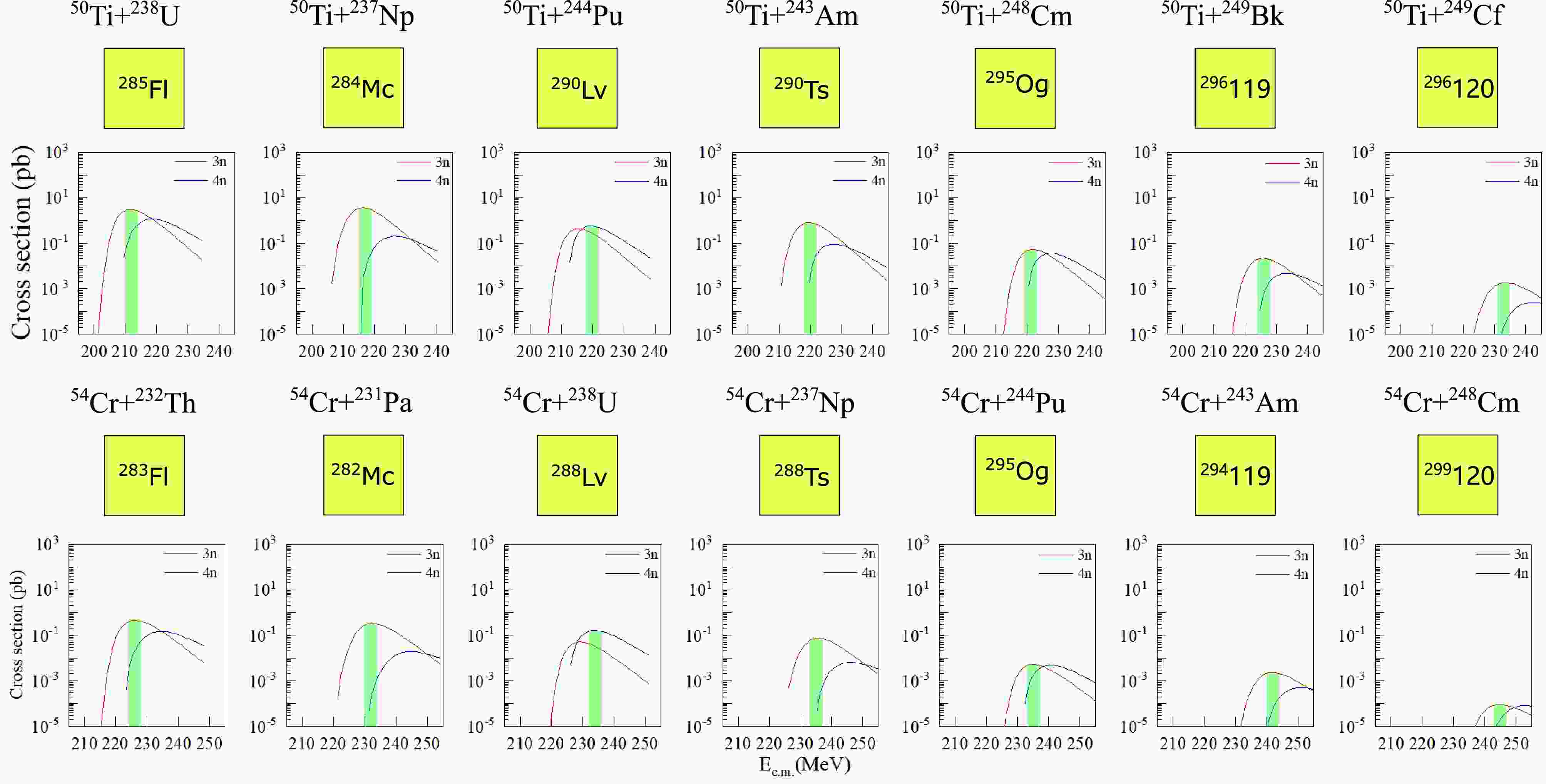
In Fig. 4, we present the excitation function curves for the production of SHE with $ Z = 114{-}120 $ using $ ^{50} $Ti and $ ^{54} $Cr beams. These results are of great importance for experimentally producing SHE with cross sections that are more easily measurable using $ ^{50} $Ti and $ ^{54} $Cr, thereby testing new production mechanisms. We note that the maximum cross section for the $ ^{50} $Ti + $ ^{243} $Am reaction occurs in the 3n exit channel, with the production cross section predicted to be 0.80 pb at a center-of-mass energy of 220(2) MeV. This cross section is larger than the previously reported production cross section for the $ ^{50} $Ti + $ ^{244} $Pu reaction. Thus, we recommend conducting experiments using $ ^{50} $Ti beams for this reaction to further test the new reaction mechanisms.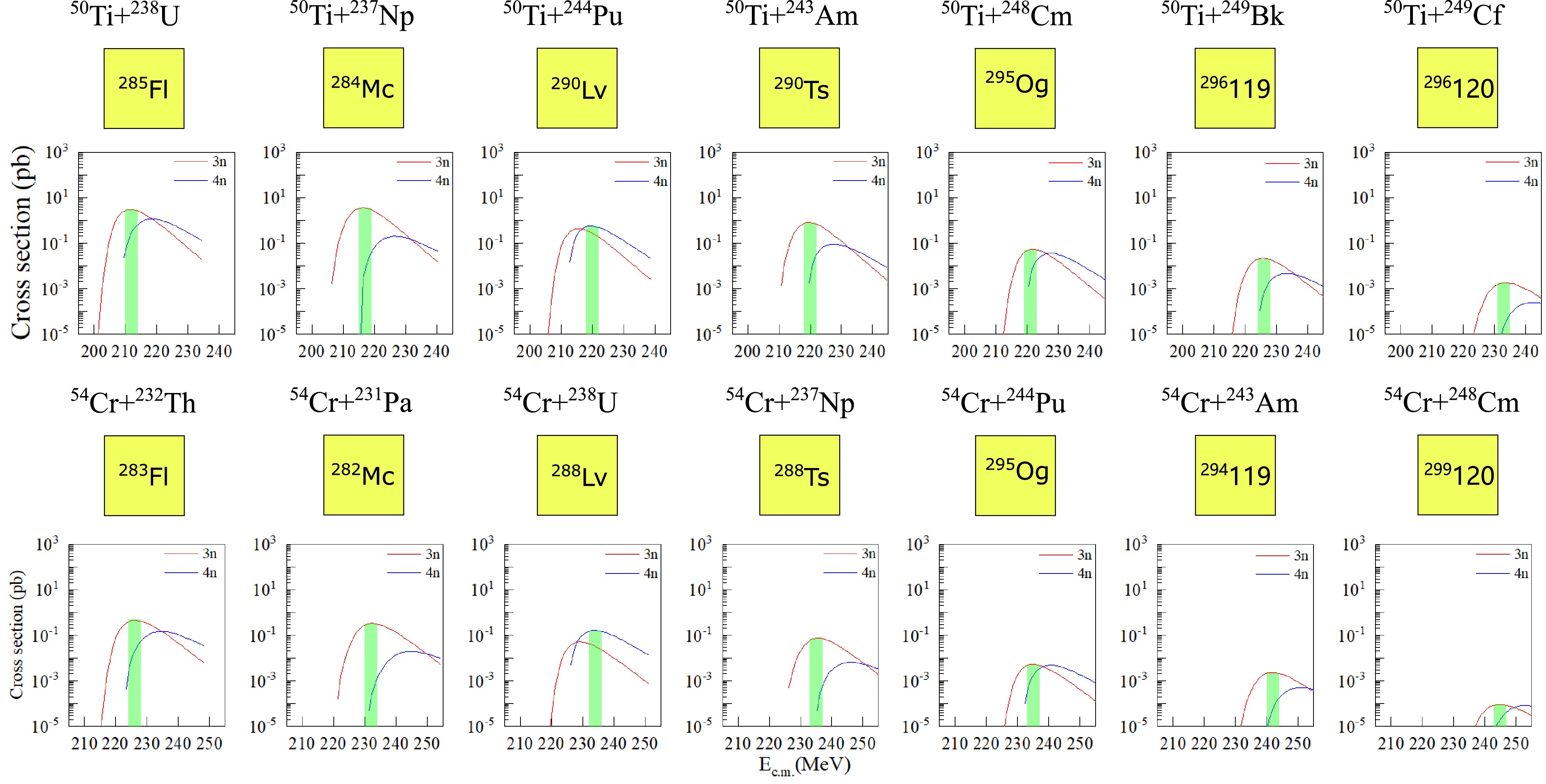

Figure 4.  (color online) Excitation function curves for the production of SHE with $ Z = 114{-}120 $ using $ ^{50} $Ti and $ ^{54} $Cr beams are shown. The red solid line represents the 3n exit channel, and the blue solid line represents the 4n exit channel. The shaded area (green) indicates the distribution of center-of-mass energy corresponding to the maximum production cross-section.

According to the current theoretical investigation, the $ ^{50}\text{Ti} $ beam is the most promising method for producing the new SHE. It is predicted that at a center-of-target center-of-mass energy of 226(2) MeV ($ E^* \approx 35 $ MeV), the maximum production cross section for the $ \mathrm{^{249}Bk}(\mathrm{^{50}Ti}, \, 3n)\, \mathrm{^{296}119} $ reaction is 21.72 fb. This cross section is very close to that for the production of Nh ($ Z = 113 $) in the $ \mathrm{^{209}Bi}(\mathrm{^{70}Zn}, \, n)\, \mathrm{^{278}Nh} $ reaction, where only three $ \mathrm{^{278}Nh} $ nuclei were registered in over 500 days of beam time, with a production cross section of $ 22^{+20}_{-13} $ fb [65, 66]. For the production of $ Z=120 $, it is predicted that at a center-of-target center-of-mass energy of 233(2) MeV ($ E^* \approx 37 $ MeV), the maximum production cross section for the $ \mathrm{^{249}Cf}(\mathrm{^{50}Ti}, 3n), \mathrm{^{296}120} $ reaction is 1.80 fb. In Ref. [23], neither was detected at cross-section sensitivity levels of 65 and 200 fb for the $ ^{50}\text{Ti} + ^{249}\text{Bk} $ and $ ^{50}\text{Ti} + ^{249}\text{Cf} $ reactions, respectively. The excitation energy for the $ ^{50}\text{Ti} + ^{249}\text{Bk} $ reaction was chosen to be $ E^* = 43.2 $ MeV, about 8 MeV higher than the optimal energy from our work, which may explain the undetectability due to the rapid drop in cross section. The excitation energy for the $ ^{50}\text{Ti} + ^{249}\text{Cf} $ reaction was $ E^* = 37.6 $ MeV, close to our optimal value, but due to the cross section being only 1.80 fb, it is difficult to detect. For the upcoming experiment on the production of the new element $ Z=119 $ via the $ ^{50}\text{Ti} + ^{249}\text{Bk} $ reaction, selecting the correct excitation energy that corresponds to the maximum cross section is absolutely crucial.

In summary, we have conducted a theoretical study of the production cross sections for elements $ Z=114-120 $ using $ ^{50}\text{Ti} $ and $ ^{54}\text{Cr} $ beams. Our results are in good agreement with recent experimental data for the $ \mathrm{^{244}Pu}(\mathrm{^{50}Ti}, \mathit{x}n), \mathrm{^{294-\mathit{x}}Lv} $ reaction. We find that, as the beam mass increases, the production cross section for the same ($ Z_{\text{CN}} $) decreases. Before embarking on new element production experiments, we recommend testing the $ ^{50} $Ti + $ ^{243} $Am reaction to gain further insights into the production mechanism. For the $ \mathrm{^{249}Bk}(\mathrm{^{50}Ti}, \mathit{x}n), \mathrm{^{299-\mathit{x}}119} $ reaction, we predict a production cross section of 21.72 fb at 226(2) MeV, while for the $ \mathrm{^{249}Cf}(\mathrm{^{50}Ti}, \mathit{x}n), \mathrm{^{299-\mathit{x}}120} $ reaction, it is 1.80 fb at 233(2) MeV. These findings provide valuable reference points for the design and validation of future SHE production experiments.