-
By combining observational data from radio pulsar observatories [1−4], gravitational wave (GW) signals [4, 5], short gamma-ray bursts [6], and kilonovae [7], meaningful celestial constraints on the stiffness of the equation of state (EOS) for compact stars can be derived. While extremely stiff (high-density) EOSs have been ruled out by experimental nucleon flow data [8] and gravitational wave observations due to their incompatibility with neutron star radii constraints [9], exceedingly soft high-density EOSs are also disfavored due to their inability to reproduce massive neutron stars [10, 11] and sufficiently massive accretion disks required for short gamma-ray bursts and kilonova emissions [12]. Observations of massive neutron stars, with masses around 2
$ M_\odot $ [1−3], suggest that their EOS must be relatively stiff, thereby constraining possible non-nucleonic degrees of freedom in neutron star matter [10, 13, 14]. On the other hand, the celestial constraints on the nuclear EOS cannot be completely exempt from the degeneracy arising from non-nucleonic degrees of freedom and some celestial factors. For instance, studies on bosonic dark matter-admixed neutron stars show consistency with maximum mass and tidal deformability constraints [15, 16]. Furthermore, extensive research on the non-Newtonian gravitational effect in neutron stars and strange stars suggests the possibility of soft high-density EOSs supporting massive compact stars [17−22]. Such an effect is often simulated by the exchange of weakly interacting light bosons beyond the standard model, potentially altering gravitational interactions and affecting EOS constraints.In particular, a neutral, weakly coupled spin-1 gauge boson, proposed in supersymmetric extensions of the Standard Model [23, 24], has been suggested as a candidate boson that modifies the inverse-square law of gravity [22, 25, 26]. Many terrestrial experiments have been conducted to search for it [27]. It has also been used as the interaction propagator of the MeV dark matter to explain the 511 keV gamma-ray emission from the galactic bulge [28−33]. More interestingly, the introduction of a vector gauge boson of the U(1) symmetry, referred to as the U boson, can significantly stiffen the soft EOS of asymmetric nuclear matter, influencing the structure of neutron stars [20, 25, 34−36]. Such stiffening is advantageous, as the softening of the EOS due to spontaneous phase transitions in the interior core of neutron stars must be compensated to sustain large-mass stars.
Vector bosons, including the vector meson and U boson, are involved in density fluctuation and collective modes as a response to the perturbation of nuclear systems. The collective modes can be used to constrain the properties of nuclear EOS. For instance, the nuclear matter compression modulus [37−39], the symmetry energy [40, 41], and the effective mass of the nucleon [42, 43] are correlated tightly with the isoscalar giant multipole resonances, the isovector giant dipole resonance, and the isoscalar giant quadrupole resonance, respectively. It is interesting to investigate how changes in these bosonic mediators, associated with nuclear matter stiffness, influence the collective excitation modes. As a collective mode, zero-sound mode in nuclear matter has been investigated in some early works [44−49]. Recently, we have demonstrated that the relativistic mean-field (RMF) model with a stiff EOS facilitates the emergence of zero-sound modes at high densities [50, 51]. The zero sound in nuclear matter is found to be intimately linked to the stiffness of the EOS. Namely, the occurrence of zero sound prefers a stiff EOS, regardless of whether the matter is symmetric or asymmetric. Though the soft EOS models, on the other hand, do not support the occurrence of zero sounds, stiffening the EOS by adjusting the
$ c_3 $ parameter of the vector meson self-interaction term, which increases the repulsive interaction, facilitates the revival of zero-sound modes at high densities. In light of the role of the vector meson in reviving the zero sound, it is interesting to examine whether the EOS stiffening induced by the U boson can have a similar effect on the occurrence of zero-sound modes. By doing so, we can examine whether the relationship is consistent between various EOS stiffenings and the occurrence of zero sound.The following facts may further highlight the significance of this work. Zero sounds, as potential candidates for Goldstone bosons, may annihilate into neutrino-antineutrino pairs via
$ Z^0 $ boson exchange [52]. This mechanism may yield an additional neutrino emission channel, potentially affecting the cooling behavior and long-term evolution of neutron stars [53, 54]. Moreover, the dual properties of the vector U-boson in modifying the EOS and gravity may bridge the relation between the zero sound and modified gravity in a dense astrophysical medium. Such investigations can shed new light on the fundamental aspects and correlated relationships of new physics beyond the Standard Model.In this work, we investigate the effects of the U boson on zero-sound modes in nuclear matter and neutron star matter using the relativistic random phase approximation (RRPA) method based on the RMF models. The RRPA formulations have been widely and successfully applied to study various collective modes in finite nuclei [37, 55−59]. It is necessary to mention that the zero sound obtained with the RRPA is consistent with those from Landau's kinetic theory [46, 60]. The structure of the remaining paper is as follows. In Sec. II, we briefly introduce the RMF models and the RRPA formalism. Sec. III presents numerical results and discussions. Lastly, a summary is given in Sec. IV.
-
By combining observational data from radio pulsar observatories [1−4], gravitational wave (GW) signals [4, 5], short gamma-ray bursts [6], and kilonovae [7], meaningful celestial constraints on the stiffness of the equation of state (EOS) for compact stars can be derived. While extremely stiff (high-density) EOSs have been ruled out by experimental nucleon flow data [8] and gravitational wave observations due to their incompatibility with neutron star radii constraints [9], exceedingly soft high-density EOSs are also disfavored due to their inability to reproduce massive neutron stars [10, 11] and sufficiently massive accretion disks required for short gamma-ray bursts and kilonova emissions [12]. Observations of massive neutron stars, with masses around 2
$ M_\odot $ [1−3], suggest that their EOS must be relatively stiff, thereby constraining possible non-nucleonic degrees of freedom in neutron star matter [10, 13, 14]. On the other hand, the celestial constraints on the nuclear EOS cannot be completely exempt from the degeneracy arising from non-nucleonic degrees of freedom and some celestial factors. For instance, studies on bosonic dark matter-admixed neutron stars show consistency with maximum mass and tidal deformability constraints [15, 16]. Furthermore, extensive research on the non-Newtonian gravitational effect in neutron stars and strange stars suggests the possibility of soft high-density EOSs supporting massive compact stars [17−22]. Such an effect is often simulated by the exchange of weakly interacting light bosons beyond the standard model, potentially altering gravitational interactions and affecting EOS constraints.In particular, a neutral, weakly coupled spin-1 gauge boson, proposed in supersymmetric extensions of the Standard Model [23, 24], has been suggested as a candidate boson that modifies the inverse-square law of gravity [22, 25, 26]. Many terrestrial experiments have been conducted to search for it [27]. It has also been used as the interaction propagator of the MeV dark matter to explain the 511 keV gamma-ray emission from the galactic bulge [28−33]. More interestingly, the introduction of a vector gauge boson of the U(1) symmetry, referred to as the U boson, can significantly stiffen the soft EOS of asymmetric nuclear matter, influencing the structure of neutron stars [20, 25, 34−36]. Such stiffening is advantageous, as the softening of the EOS due to spontaneous phase transitions in the interior core of neutron stars must be compensated to sustain large-mass stars.
Vector bosons, including the vector meson and U boson, are involved in density fluctuation and collective modes as a response to the perturbation of nuclear systems. The collective modes can be used to constrain the properties of nuclear EOS. For instance, the nuclear matter compression modulus [37−39], the symmetry energy [40, 41], and the effective mass of the nucleon [42, 43] are correlated tightly with the isoscalar giant multipole resonances, the isovector giant dipole resonance, and the isoscalar giant quadrupole resonance, respectively. It is interesting to investigate how changes in these bosonic mediators, associated with nuclear matter stiffness, influence the collective excitation modes. As a collective mode, zero-sound mode in nuclear matter has been investigated in some early works [44−49]. Recently, we have demonstrated that the relativistic mean-field (RMF) model with a stiff EOS facilitates the emergence of zero-sound modes at high densities [50, 51]. The zero sound in nuclear matter is found to be intimately linked to the stiffness of the EOS. Namely, the occurrence of zero sound prefers a stiff EOS, regardless of whether the matter is symmetric or asymmetric. Though the soft EOS models, on the other hand, do not support the occurrence of zero sounds, stiffening the EOS by adjusting the
$ c_3 $ parameter of the vector meson self-interaction term, which increases the repulsive interaction, facilitates the revival of zero-sound modes at high densities. In light of the role of the vector meson in reviving the zero sound, it is interesting to examine whether the EOS stiffening induced by the U boson can have a similar effect on the occurrence of zero-sound modes. By doing so, we can examine whether the relationship is consistent between various EOS stiffenings and the occurrence of zero sound.The following facts may further highlight the significance of this work. Zero sounds, as potential candidates for Goldstone bosons, may annihilate into neutrino-antineutrino pairs via
$ Z^0 $ boson exchange [52]. This mechanism may yield an additional neutrino emission channel, potentially affecting the cooling behavior and long-term evolution of neutron stars [53, 54]. Moreover, the dual properties of the vector U-boson in modifying the EOS and gravity may bridge the relation between the zero sound and modified gravity in a dense astrophysical medium. Such investigations can shed new light on the fundamental aspects and correlated relationships of new physics beyond the Standard Model.In this work, we investigate the effects of the U boson on zero-sound modes in nuclear matter and neutron star matter using the relativistic random phase approximation (RRPA) method based on the RMF models. The RRPA formulations have been widely and successfully applied to study various collective modes in finite nuclei [37, 55−59]. It is necessary to mention that the zero sound obtained with the RRPA is consistent with those from Landau's kinetic theory [46, 60]. The structure of the remaining paper is as follows. In Sec. II, we briefly introduce the RMF models and the RRPA formalism. Sec. III presents numerical results and discussions. Lastly, a summary is given in Sec. IV.
-
By combining observational data from radio pulsar observatories [1−4], gravitational wave (GW) signals [4, 5], short gamma-ray bursts [6], and kilonovae [7], meaningful celestial constraints on the stiffness of the equation of state (EOS) for compact stars can be derived. While extremely stiff (high-density) EOSs have been ruled out by experimental nucleon flow data [8] and gravitational wave observations due to their incompatibility with neutron star radii constraints [9], exceedingly soft high-density EOSs are also disfavored due to their inability to reproduce massive neutron stars [10, 11] and sufficiently massive accretion disks required for short gamma-ray bursts and kilonova emissions [12]. Observations of massive neutron stars, with masses around 2
$ M_\odot $ [1−3], suggest that their EOS must be relatively stiff, thereby constraining possible non-nucleonic degrees of freedom in neutron star matter [10, 13, 14]. On the other hand, the celestial constraints on the nuclear EOS cannot be completely exempt from the degeneracy arising from non-nucleonic degrees of freedom and some celestial factors. For instance, studies on bosonic dark matter-admixed neutron stars show consistency with maximum mass and tidal deformability constraints [15, 16]. Furthermore, extensive research on the non-Newtonian gravitational effect in neutron stars and strange stars suggests the possibility of soft high-density EOSs supporting massive compact stars [17−22]. Such an effect is often simulated by the exchange of weakly interacting light bosons beyond the standard model, potentially altering gravitational interactions and affecting EOS constraints.In particular, a neutral, weakly coupled spin-1 gauge boson, proposed in supersymmetric extensions of the Standard Model [23, 24], has been suggested as a candidate boson that modifies the inverse-square law of gravity [22, 25, 26]. Many terrestrial experiments have been conducted to search for it [27]. It has also been used as the interaction propagator of the MeV dark matter to explain the 511 keV gamma-ray emission from the galactic bulge [28−33]. More interestingly, the introduction of a vector gauge boson of the U(1) symmetry, referred to as the U boson, can significantly stiffen the soft EOS of asymmetric nuclear matter, influencing the structure of neutron stars [20, 25, 34−36]. Such stiffening is advantageous, as the softening of the EOS due to spontaneous phase transitions in the interior core of neutron stars must be compensated to sustain large-mass stars.
Vector bosons, including the vector meson and U boson, are involved in density fluctuation and collective modes as a response to the perturbation of nuclear systems. The collective modes can be used to constrain the properties of nuclear EOS. For instance, the nuclear matter compression modulus [37−39], the symmetry energy [40, 41], and the effective mass of the nucleon [42, 43] are correlated tightly with the isoscalar giant multipole resonances, the isovector giant dipole resonance, and the isoscalar giant quadrupole resonance, respectively. It is interesting to investigate how changes in these bosonic mediators, associated with nuclear matter stiffness, influence the collective excitation modes. As a collective mode, zero-sound mode in nuclear matter has been investigated in some early works [44−49]. Recently, we have demonstrated that the relativistic mean-field (RMF) model with a stiff EOS facilitates the emergence of zero-sound modes at high densities [50, 51]. The zero sound in nuclear matter is found to be intimately linked to the stiffness of the EOS. Namely, the occurrence of zero sound prefers a stiff EOS, regardless of whether the matter is symmetric or asymmetric. Though the soft EOS models, on the other hand, do not support the occurrence of zero sounds, stiffening the EOS by adjusting the
$ c_3 $ parameter of the vector meson self-interaction term, which increases the repulsive interaction, facilitates the revival of zero-sound modes at high densities. In light of the role of the vector meson in reviving the zero sound, it is interesting to examine whether the EOS stiffening induced by the U boson can have a similar effect on the occurrence of zero-sound modes. By doing so, we can examine whether the relationship is consistent between various EOS stiffenings and the occurrence of zero sound.The following facts may further highlight the significance of this work. Zero sounds, as potential candidates for Goldstone bosons, may annihilate into neutrino-antineutrino pairs via
$ Z^0 $ boson exchange [52]. This mechanism may yield an additional neutrino emission channel, potentially affecting the cooling behavior and long-term evolution of neutron stars [53, 54]. Moreover, the dual properties of the vector U-boson in modifying the EOS and gravity may bridge the relation between the zero sound and modified gravity in a dense astrophysical medium. Such investigations can shed new light on the fundamental aspects and correlated relationships of new physics beyond the Standard Model.In this work, we investigate the effects of the U boson on zero-sound modes in nuclear matter and neutron star matter using the relativistic random phase approximation (RRPA) method based on the RMF models. The RRPA formulations have been widely and successfully applied to study various collective modes in finite nuclei [37, 55−59]. It is necessary to mention that the zero sound obtained with the RRPA is consistent with those from Landau's kinetic theory [46, 60]. The structure of the remaining paper is as follows. In Sec. II, we briefly introduce the RMF models and the RRPA formalism. Sec. III presents numerical results and discussions. Lastly, a summary is given in Sec. IV.
-
In the RMF approach, the Lagrangian can generally be given as [61−63]:
$ \begin{aligned}[b] {\cal{L}}=\;& \bar{\psi}\left[{\rm i} \gamma_{\mu} \partial^{\mu}-M+g_{\sigma} \sigma-g_{\omega} \gamma_{\mu} \omega^{\mu}-g_{\rho} \gamma_{\mu} \tau_{3} b_{0}^{\mu}\right] \psi \\ &+\frac{1}{2}\left(\partial_{\mu} \sigma \partial^{\mu} \sigma-m_{\sigma}^{2} \sigma^{2}\right)-\frac{1}{3} g_{2} \sigma^{3}-\frac{1}{4} g_{3} \sigma^{4}\\ &-\frac{1}{4} F_{\mu \nu} F^{\mu \nu}+\frac{1}{2} m_{\omega}^{2} \omega_{\mu} \omega^{\mu}+\frac{1}{4} c_{3}\left(\omega_{\mu} \omega^{\mu}\right)^{2}\\ &-\frac{1}{4} B_{\mu \nu} B^{\mu \nu}+\frac{1}{2} m_{\rho}^{2} b_{0 \mu} b_{0}^{\mu}\\ & +4 \Lambda_{V} g_{\rho}^{2} g_{\omega}^{2} \omega_{\mu} \omega^{\mu} b_{0 v} b_{0}^{\nu}+{\cal{L}}_{u}, \end{aligned} $

(1) where
$ \psi, \sigma, \omega, b_0 $ are the fields of the nucleon, the scalar, vector, and isovector-vector mesons, respectively, with their masses$ M, m_\sigma, m_\omega $ , and$ m_\rho $ .$ F_{\mu \nu} $ and$ B_{\mu \nu} $ are the respective strength tensors of the vector mesons$ \omega $ and$ \rho $ , respectively:$ F_{\mu \nu}=\partial_{\mu} \omega_{\nu}-\partial_{\nu} \omega_{\mu}, \quad B_{\mu \nu}=\partial_{\mu} b_{0 v}-\partial_{\nu} b_{0 \mu}. $

(2) In Eq. (1), the additional Lagrangian
$ {\cal{L}}_{u} $ of the light vector U boson, which is postulated to account for the possible fifth force or modification to Newtonian gravity [17, 22, 64, 65], is included to comparatively check the repulsive role in the zero-sounds in nuclear matter. Similar to the form of the vector meson,$ {\cal{L}}_{u} $ is written as [20]$ {\cal{L}}_{u}=-\bar{\psi} g_{u} \gamma_{\mu} u^{\mu} \psi-\frac{1}{4} U_{\mu \nu} U^{\mu \nu}+\frac{1}{2} m_{u}^{2} u_{\mu} u^{\mu}, $

(3) where
$ g_u $ ,$ m_u $ , and$ U_{\mu \nu} $ are the coupling constant, mass, and strength tensor of the U boson, which is in a form similar to that of the$ \omega $ meson.The nonlinear equations of motion for nucleons and mesons are deduced from the standard Euler-Lagrange formula. In the mean-field approximation, meson fields in uniform nuclear matter are replaced by their expectation values, obtained through iteration. With these mean fields, the effective meson masses
$ m_{i}^{*} $ , which are derived from the second derivative of the Lagrangian, are given as follows:$ \begin{aligned} &m_{\sigma}^{* 2}=m_{\sigma}^{2}+2 g_{2} \sigma_{0}+3 g_{3} \sigma_{0}^{2}, \end{aligned} $

(4a) $ \begin{aligned} &m_{\omega}^{* 2}=m_{\omega}^{2}+3 c_{3} \omega_{0}^{2}+8 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} b_{0}^{2} , \end{aligned} $

(4b) $ \begin{aligned} &m_{\varrho}^{* 2}=m_{\varrho}^{2}+8 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0}^{2}. \end{aligned} $

(4c) The resulting energy density
$ \varepsilon $ and pressure P of nuclear matter are written as follows:$ \begin{aligned}[b] \varepsilon=\;& \sum_{i=p, n} \frac{2}{(2 \pi)^{3}} \int^{k_{F_{i}}} {\rm d}^{3} k E_{i}^{*}+\frac{1}{2} m_{\omega}^{2} \omega_{0}^{2}+\frac{1}{2} m_{\sigma}^{2} \sigma_{0}^{2} \\ &+\frac{1}{2} m_{\rho}^{2} b_{0}^{2}+\frac{1}{3} g_{2} \sigma_{0}^{3}+\frac{1}{4} g_{3} \sigma_{0}^{4}+\frac{3}{4} c_{3} \omega_{0}^{4}+\frac{1}{2}\frac{g_{u}^{2}}{m_{u}^{2}}\rho_B^2\\ &+12 \Lambda_{V} g_{\rho}^{2} g_{\omega}^{2} \omega_{0}^{2} b_{0}^{2}, \end{aligned} $

(5) $ \begin{aligned}[b] P=\;& \frac{1}{3} \sum_{i=p, n} \frac{2}{(2 \pi)^{3}} \int^{k_{F_{i}}} {\rm d}^{3} k \frac{{\bf{k}}^{2}}{E_{i}^{*}}+\frac{1}{2} m_{\omega}^{2} \omega_{0}^{2}-\frac{1}{2} m_{\sigma}^{2} \sigma_{0}^{2}\\ &+\frac{1}{2} m_{\rho}^{2} b_{0}^{2}-\frac{1}{3} g_{2} \sigma^{3}-\frac{1}{4} g_{3} \sigma^{4}+\frac{1}{4} c_{3} \omega_{0}^{4} +\frac{1}{2}\frac{g_{u}^{2}}{m_{u}^{2}}\rho_B^2\\ &+4 \Lambda_{V} g_{\rho}^{2} g_{\omega}^{2} \omega_{0}^{2} b_{0}^{2}, \end{aligned} $

(6) with
$ E_{i}^{*}=\sqrt{{\bf{k}}^{2}+\left(M_{i}^{*}\right)^{2}} $ . -
In the RMF approach, the Lagrangian can generally be given as [61−63]:
$ \begin{aligned}[b] {\cal{L}}=\;& \bar{\psi}\left[{\rm i} \gamma_{\mu} \partial^{\mu}-M+g_{\sigma} \sigma-g_{\omega} \gamma_{\mu} \omega^{\mu}-g_{\rho} \gamma_{\mu} \tau_{3} b_{0}^{\mu}\right] \psi \\ &+\frac{1}{2}\left(\partial_{\mu} \sigma \partial^{\mu} \sigma-m_{\sigma}^{2} \sigma^{2}\right)-\frac{1}{3} g_{2} \sigma^{3}-\frac{1}{4} g_{3} \sigma^{4}\\ &-\frac{1}{4} F_{\mu \nu} F^{\mu \nu}+\frac{1}{2} m_{\omega}^{2} \omega_{\mu} \omega^{\mu}+\frac{1}{4} c_{3}\left(\omega_{\mu} \omega^{\mu}\right)^{2}\\ &-\frac{1}{4} B_{\mu \nu} B^{\mu \nu}+\frac{1}{2} m_{\rho}^{2} b_{0 \mu} b_{0}^{\mu}\\ & +4 \Lambda_{V} g_{\rho}^{2} g_{\omega}^{2} \omega_{\mu} \omega^{\mu} b_{0 v} b_{0}^{\nu}+{\cal{L}}_{u}, \end{aligned} $
(1) where
$ \psi, \sigma, \omega, b_0 $ are the fields of the nucleon, the scalar, vector, and isovector-vector mesons, respectively, with their masses$ M, m_\sigma, m_\omega $ , and$ m_\rho $ .$ F_{\mu \nu} $ and$ B_{\mu \nu} $ are the respective strength tensors of the vector mesons$ \omega $ and$ \rho $ , respectively:$ F_{\mu \nu}=\partial_{\mu} \omega_{\nu}-\partial_{\nu} \omega_{\mu}, \quad B_{\mu \nu}=\partial_{\mu} b_{0 v}-\partial_{\nu} b_{0 \mu}. $
(2) In Eq. (1), the additional Lagrangian
$ {\cal{L}}_{u} $ of the light vector U boson, which is postulated to account for the possible fifth force or modification to Newtonian gravity [17, 22, 64, 65], is included to comparatively check the repulsive role in the zero-sounds in nuclear matter. Similar to the form of the vector meson,$ {\cal{L}}_{u} $ is written as [20]$ {\cal{L}}_{u}=-\bar{\psi} g_{u} \gamma_{\mu} u^{\mu} \psi-\frac{1}{4} U_{\mu \nu} U^{\mu \nu}+\frac{1}{2} m_{u}^{2} u_{\mu} u^{\mu}, $
(3) where
$ g_u $ ,$ m_u $ , and$ U_{\mu \nu} $ are the coupling constant, mass, and strength tensor of the U boson, which is in a form similar to that of the$ \omega $ meson.The nonlinear equations of motion for nucleons and mesons are deduced from the standard Euler-Lagrange formula. In the mean-field approximation, meson fields in uniform nuclear matter are replaced by their expectation values, obtained through iteration. With these mean fields, the effective meson masses
$ m_{i}^{*} $ , which are derived from the second derivative of the Lagrangian, are given as follows:$ \begin{aligned} &m_{\sigma}^{* 2}=m_{\sigma}^{2}+2 g_{2} \sigma_{0}+3 g_{3} \sigma_{0}^{2}, \end{aligned} $
(4a) $ \begin{aligned} &m_{\omega}^{* 2}=m_{\omega}^{2}+3 c_{3} \omega_{0}^{2}+8 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} b_{0}^{2} , \end{aligned} $
(4b) $ \begin{aligned} &m_{\varrho}^{* 2}=m_{\varrho}^{2}+8 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0}^{2}. \end{aligned} $
(4c) The resulting energy density
$ \varepsilon $ and pressure P of nuclear matter are written as follows:$ \begin{aligned}[b] \varepsilon=\;& \sum_{i=p, n} \frac{2}{(2 \pi)^{3}} \int^{k_{F_{i}}} {\rm d}^{3} k E_{i}^{*}+\frac{1}{2} m_{\omega}^{2} \omega_{0}^{2}+\frac{1}{2} m_{\sigma}^{2} \sigma_{0}^{2} \\ &+\frac{1}{2} m_{\rho}^{2} b_{0}^{2}+\frac{1}{3} g_{2} \sigma_{0}^{3}+\frac{1}{4} g_{3} \sigma_{0}^{4}+\frac{3}{4} c_{3} \omega_{0}^{4}+\frac{1}{2}\frac{g_{u}^{2}}{m_{u}^{2}}\rho_B^2\\ &+12 \Lambda_{V} g_{\rho}^{2} g_{\omega}^{2} \omega_{0}^{2} b_{0}^{2}, \end{aligned} $
(5) $ \begin{aligned}[b] P=\;& \frac{1}{3} \sum_{i=p, n} \frac{2}{(2 \pi)^{3}} \int^{k_{F_{i}}} {\rm d}^{3} k \frac{{\bf{k}}^{2}}{E_{i}^{*}}+\frac{1}{2} m_{\omega}^{2} \omega_{0}^{2}-\frac{1}{2} m_{\sigma}^{2} \sigma_{0}^{2}\\ &+\frac{1}{2} m_{\rho}^{2} b_{0}^{2}-\frac{1}{3} g_{2} \sigma^{3}-\frac{1}{4} g_{3} \sigma^{4}+\frac{1}{4} c_{3} \omega_{0}^{4} +\frac{1}{2}\frac{g_{u}^{2}}{m_{u}^{2}}\rho_B^2\\ &+4 \Lambda_{V} g_{\rho}^{2} g_{\omega}^{2} \omega_{0}^{2} b_{0}^{2}, \end{aligned} $
(6) with
$ E_{i}^{*}=\sqrt{{\bf{k}}^{2}+\left(M_{i}^{*}\right)^{2}} $ . -
In the RMF approach, the Lagrangian can generally be given as [61−63]:
$ \begin{aligned}[b] {\cal{L}}=\;& \bar{\psi}\left[{\rm i} \gamma_{\mu} \partial^{\mu}-M+g_{\sigma} \sigma-g_{\omega} \gamma_{\mu} \omega^{\mu}-g_{\rho} \gamma_{\mu} \tau_{3} b_{0}^{\mu}\right] \psi \\ &+\frac{1}{2}\left(\partial_{\mu} \sigma \partial^{\mu} \sigma-m_{\sigma}^{2} \sigma^{2}\right)-\frac{1}{3} g_{2} \sigma^{3}-\frac{1}{4} g_{3} \sigma^{4}\\ &-\frac{1}{4} F_{\mu \nu} F^{\mu \nu}+\frac{1}{2} m_{\omega}^{2} \omega_{\mu} \omega^{\mu}+\frac{1}{4} c_{3}\left(\omega_{\mu} \omega^{\mu}\right)^{2}\\ &-\frac{1}{4} B_{\mu \nu} B^{\mu \nu}+\frac{1}{2} m_{\rho}^{2} b_{0 \mu} b_{0}^{\mu}\\ & +4 \Lambda_{V} g_{\rho}^{2} g_{\omega}^{2} \omega_{\mu} \omega^{\mu} b_{0 v} b_{0}^{\nu}+{\cal{L}}_{u}, \end{aligned} $

(1) where
$ \psi, \sigma, \omega, b_0 $ are the fields of the nucleon, the scalar, vector, and isovector-vector mesons, respectively, with their masses$ M, m_\sigma, m_\omega $ , and$ m_\rho $ .$ F_{\mu \nu} $ and$ B_{\mu \nu} $ are the respective strength tensors of the vector mesons$ \omega $ and$ \rho $ , respectively:$ F_{\mu \nu}=\partial_{\mu} \omega_{\nu}-\partial_{\nu} \omega_{\mu}, \quad B_{\mu \nu}=\partial_{\mu} b_{0 v}-\partial_{\nu} b_{0 \mu}. $

(2) In Eq. (1), the additional Lagrangian
$ {\cal{L}}_{u} $ of the light vector U boson, which is postulated to account for the possible fifth force or modification to Newtonian gravity [17, 22, 64, 65], is included to comparatively check the repulsive role in the zero-sounds in nuclear matter. Similar to the form of the vector meson,$ {\cal{L}}_{u} $ is written as [20]$ {\cal{L}}_{u}=-\bar{\psi} g_{u} \gamma_{\mu} u^{\mu} \psi-\frac{1}{4} U_{\mu \nu} U^{\mu \nu}+\frac{1}{2} m_{u}^{2} u_{\mu} u^{\mu}, $

(3) where
$ g_u $ ,$ m_u $ , and$ U_{\mu \nu} $ are the coupling constant, mass, and strength tensor of the U boson, which is in a form similar to that of the$ \omega $ meson.The nonlinear equations of motion for nucleons and mesons are deduced from the standard Euler-Lagrange formula. In the mean-field approximation, meson fields in uniform nuclear matter are replaced by their expectation values, obtained through iteration. With these mean fields, the effective meson masses
$ m_{i}^{*} $ , which are derived from the second derivative of the Lagrangian, are given as follows:$ \begin{aligned} &m_{\sigma}^{* 2}=m_{\sigma}^{2}+2 g_{2} \sigma_{0}+3 g_{3} \sigma_{0}^{2}, \end{aligned} $

(4a) $ \begin{aligned} &m_{\omega}^{* 2}=m_{\omega}^{2}+3 c_{3} \omega_{0}^{2}+8 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} b_{0}^{2} , \end{aligned} $

(4b) $ \begin{aligned} &m_{\varrho}^{* 2}=m_{\varrho}^{2}+8 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0}^{2}. \end{aligned} $

(4c) The resulting energy density
$ \varepsilon $ and pressure P of nuclear matter are written as follows:$ \begin{aligned}[b] \varepsilon=\;& \sum_{i=p, n} \frac{2}{(2 \pi)^{3}} \int^{k_{F_{i}}} {\rm d}^{3} k E_{i}^{*}+\frac{1}{2} m_{\omega}^{2} \omega_{0}^{2}+\frac{1}{2} m_{\sigma}^{2} \sigma_{0}^{2} \\ &+\frac{1}{2} m_{\rho}^{2} b_{0}^{2}+\frac{1}{3} g_{2} \sigma_{0}^{3}+\frac{1}{4} g_{3} \sigma_{0}^{4}+\frac{3}{4} c_{3} \omega_{0}^{4}+\frac{1}{2}\frac{g_{u}^{2}}{m_{u}^{2}}\rho_B^2\\ &+12 \Lambda_{V} g_{\rho}^{2} g_{\omega}^{2} \omega_{0}^{2} b_{0}^{2}, \end{aligned} $

(5) $ \begin{aligned}[b] P=\;& \frac{1}{3} \sum_{i=p, n} \frac{2}{(2 \pi)^{3}} \int^{k_{F_{i}}} {\rm d}^{3} k \frac{{\bf{k}}^{2}}{E_{i}^{*}}+\frac{1}{2} m_{\omega}^{2} \omega_{0}^{2}-\frac{1}{2} m_{\sigma}^{2} \sigma_{0}^{2}\\ &+\frac{1}{2} m_{\rho}^{2} b_{0}^{2}-\frac{1}{3} g_{2} \sigma^{3}-\frac{1}{4} g_{3} \sigma^{4}+\frac{1}{4} c_{3} \omega_{0}^{4} +\frac{1}{2}\frac{g_{u}^{2}}{m_{u}^{2}}\rho_B^2\\ &+4 \Lambda_{V} g_{\rho}^{2} g_{\omega}^{2} \omega_{0}^{2} b_{0}^{2}, \end{aligned} $

(6) with
$ E_{i}^{*}=\sqrt{{\bf{k}}^{2}+\left(M_{i}^{*}\right)^{2}} $ . -
In the RRPA method, one can, in principle, involve the particle-hole and particle-antiparticle excitations of the fermions through various polarization tensors, while within the framework of the RMF models, the particle-antiparticle excitations are usually ignored in a no-sea approximation [37]. The interacting polarization is determined through the Dyson equation. For instance, the interacting longitudinal component of the vector polarization tensor
$ \Pi_{\mu\nu} $ , which is usually used to search for the collective modes, is given as$ \tilde{\Pi}_{L}={\Pi}_{L}+{\Pi}_{L}D_{L}\tilde{\Pi}_{L}, $

(7) where the polarization
$ \Pi_{L} $ and meson propagator$ D_{L} $ are in matrix form. The lowest-order longitudinal polarization$ \Pi_L $ in nuclear matter is written as$ \Pi_{L}=\left(\begin{array}{*{20}{c}} \Pi_{s}^{n}+\Pi_{s}^{p} & \Pi_{m}^{p} & \Pi_{m}^{n} \\ \Pi_{m}^{p} & \Pi_{00}^{p} & 0 \\ \Pi_{m}^{n} & 0 & \Pi_{00}^{n} \end{array}\right), $

(8) where the individual polarization entries are given by:
$ \begin{aligned} {\rm{i}} \Pi_{s}^a\left(q, q_{0}\right) =\int \frac{{\rm d}^{4} p}{(2 \pi)^{4}} {\rm{Tr}}[G^a(p) G^a(p+q)] , \end{aligned} $

(9a) $ \begin{aligned} {\rm{i}} \Pi_{m}^a\left(q, q_{0}\right) =\int \frac{{\rm d}^{4} p}{(2 \pi)^{4}} {\rm{Tr}}\left[G^a(p) \gamma_{0} G^a(p+q)\right] , \end{aligned} $

(9b) $ \begin{aligned} {\rm{i}} \Pi_{00}^a\left(q, q_{0}\right) =\int \frac{{\rm d}^{4} p}{(2 \pi)^{4}} {\rm{Tr}}\left[G^a(p) \gamma_{0} G^a(p+q) \gamma_{0}\right], \end{aligned} $

(9c) With
$ Tr $ indicating the trace over Dirac indices and$ a=p,n $ , the fermion Green function reads$ \begin{aligned}[b] G_a(k)=\;&\left(\gamma_{\mu}k^{\mu}+M^{*}_a\right) \left[\frac{1}{k_{\mu}^{ 2}-M_a^{* 2}+{\rm i}\varepsilon}\right.\\ &\left.+\frac{{\rm i} \pi}{E_{ka}^{*}} \delta\left(k_{0}-E_{ka}^{*}\right) \theta\left(k_{Fa}-|\boldsymbol{k}|\right)\right], \end{aligned} $

(10) where
$ M_a^{*}=M_a-g_{\sigma}\sigma_{0} $ is the nucleon effective mass, and$ k_{F} $ is the Fermi momentum.With the crossing coupling term of the
$ \rho $ and$ \omega $ mesons in Eq. (1), the meson propagator$ D_{L} $ is given as [50, 66]$ D_{L}=\left(\begin{array}{*{20}{c}} \chi_{\sigma} & 0 & 0 \\ 0 & \tilde{\chi}_{\omega}+\tilde{\chi}_{\varrho}+2 \tilde{\chi}_{\omega \varrho} & \tilde{\chi}_{\omega}-\tilde{\chi}_{\varrho} \\ 0 & \tilde{\chi}_{\omega}-\tilde{\chi}_{\varrho} & \tilde{\chi}_{\omega}+\tilde{\chi}_{\varrho}-2 \tilde{\chi}_{\omega \varrho} \end{array}\right). $

(11) Expressions for the various meson propagators with nonlinear meson couplings are provided as follows:
$ \begin{aligned} \chi_{\sigma}=\frac{g_{\sigma}^{2}}{q_{\mu}^{2}-m_{\sigma}^{*2}}, \end{aligned} $

(12a) $ \begin{aligned} \chi_{\omega}=\frac{g_{\omega}^{2}\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)}{\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)-\left(16 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0} b_{0}\right)^{2}} , \end{aligned} $

(12b) $ \begin{aligned} \chi_{\varrho}=\frac{g_{\varrho}^{2}\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)}{\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)-\left(16 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0} b_{0}\right)^{2}} , \end{aligned} $

(12c) $ \begin{aligned} \chi_{\omega \varrho}=\frac{-16 \Lambda_{V} g_{\omega}^{3} g_{\varrho}^{3} \omega_{0} b_{0}}{\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)-\left(16 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0} b_{0}\right)^{2}}, \end{aligned} $

(12d) $ \begin{aligned} &\tilde{\chi}_{i}=\frac{q_{\mu}^{2}}{q^{2}}\chi_{i},\quad i=\omega,\rho. \end{aligned}$

(12e) When the vector repulsion of the U boson is included,
$ \chi_{\omega} $ is replaced by$ \chi_{V}^\prime $ to modify the Dyson equation.$ \chi_{V}'=\chi_{\omega}+\chi_{u},\quad \chi_{u}=\frac{g_{u}^{2}}{q_{\mu}^{2}-m_{u}^{2}}. $

(13) The nuclear systems undergo transitions at small-amplitude density fluctuations by encountering the zeros of the following dielectric function.
$ \varepsilon_L={\rm{det}}\left(1-D_{L} \Pi_{L}\right)=0. $

(14) -
In the RRPA method, one can, in principle, involve the particle-hole and particle-antiparticle excitations of the fermions through various polarization tensors, while within the framework of the RMF models, the particle-antiparticle excitations are usually ignored in a no-sea approximation [37]. The interacting polarization is determined through the Dyson equation. For instance, the interacting longitudinal component of the vector polarization tensor
$ \Pi_{\mu\nu} $ , which is usually used to search for the collective modes, is given as$ \tilde{\Pi}_{L}={\Pi}_{L}+{\Pi}_{L}D_{L}\tilde{\Pi}_{L}, $

(7) where the polarization
$ \Pi_{L} $ and meson propagator$ D_{L} $ are in matrix form. The lowest-order longitudinal polarization$ \Pi_L $ in nuclear matter is written as$ \Pi_{L}=\left(\begin{array}{*{20}{c}} \Pi_{s}^{n}+\Pi_{s}^{p} & \Pi_{m}^{p} & \Pi_{m}^{n} \\ \Pi_{m}^{p} & \Pi_{00}^{p} & 0 \\ \Pi_{m}^{n} & 0 & \Pi_{00}^{n} \end{array}\right), $

(8) where the individual polarization entries are given by:
$ \begin{aligned} {\rm{i}} \Pi_{s}^a\left(q, q_{0}\right) =\int \frac{{\rm d}^{4} p}{(2 \pi)^{4}} {\rm{Tr}}[G^a(p) G^a(p+q)] , \end{aligned} $

(9a) $ \begin{aligned} {\rm{i}} \Pi_{m}^a\left(q, q_{0}\right) =\int \frac{{\rm d}^{4} p}{(2 \pi)^{4}} {\rm{Tr}}\left[G^a(p) \gamma_{0} G^a(p+q)\right] , \end{aligned} $

(9b) $ \begin{aligned} {\rm{i}} \Pi_{00}^a\left(q, q_{0}\right) =\int \frac{{\rm d}^{4} p}{(2 \pi)^{4}} {\rm{Tr}}\left[G^a(p) \gamma_{0} G^a(p+q) \gamma_{0}\right], \end{aligned} $

(9c) With
$ Tr $ indicating the trace over Dirac indices and$ a=p,n $ , the fermion Green function reads$ \begin{aligned}[b] G_a(k)=\;&\left(\gamma_{\mu}k^{\mu}+M^{*}_a\right) \left[\frac{1}{k_{\mu}^{ 2}-M_a^{* 2}+{\rm i}\varepsilon}\right.\\ &\left.+\frac{{\rm i} \pi}{E_{ka}^{*}} \delta\left(k_{0}-E_{ka}^{*}\right) \theta\left(k_{Fa}-|\boldsymbol{k}|\right)\right], \end{aligned} $

(10) where
$ M_a^{*}=M_a-g_{\sigma}\sigma_{0} $ is the nucleon effective mass, and$ k_{F} $ is the Fermi momentum.With the crossing coupling term of the
$ \rho $ and$ \omega $ mesons in Eq. (1), the meson propagator$ D_{L} $ is given as [50, 66]$ D_{L}=\left(\begin{array}{*{20}{c}} \chi_{\sigma} & 0 & 0 \\ 0 & \tilde{\chi}_{\omega}+\tilde{\chi}_{\varrho}+2 \tilde{\chi}_{\omega \varrho} & \tilde{\chi}_{\omega}-\tilde{\chi}_{\varrho} \\ 0 & \tilde{\chi}_{\omega}-\tilde{\chi}_{\varrho} & \tilde{\chi}_{\omega}+\tilde{\chi}_{\varrho}-2 \tilde{\chi}_{\omega \varrho} \end{array}\right). $

(11) Expressions for the various meson propagators with nonlinear meson couplings are provided as follows:
$ \begin{aligned} \chi_{\sigma}=\frac{g_{\sigma}^{2}}{q_{\mu}^{2}-m_{\sigma}^{*2}}, \end{aligned} $

(12a) $ \begin{aligned} \chi_{\omega}=\frac{g_{\omega}^{2}\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)}{\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)-\left(16 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0} b_{0}\right)^{2}} , \end{aligned} $

(12b) $ \begin{aligned} \chi_{\varrho}=\frac{g_{\varrho}^{2}\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)}{\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)-\left(16 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0} b_{0}\right)^{2}} , \end{aligned} $

(12c) $ \begin{aligned} \chi_{\omega \varrho}=\frac{-16 \Lambda_{V} g_{\omega}^{3} g_{\varrho}^{3} \omega_{0} b_{0}}{\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)-\left(16 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0} b_{0}\right)^{2}}, \end{aligned} $

(12d) $ \begin{aligned} &\tilde{\chi}_{i}=\frac{q_{\mu}^{2}}{q^{2}}\chi_{i},\quad i=\omega,\rho. \end{aligned}$

(12e) When the vector repulsion of the U boson is included,
$ \chi_{\omega} $ is replaced by$ \chi_{V}^\prime $ to modify the Dyson equation.$ \chi_{V}'=\chi_{\omega}+\chi_{u},\quad \chi_{u}=\frac{g_{u}^{2}}{q_{\mu}^{2}-m_{u}^{2}}. $

(13) The nuclear systems undergo transitions at small-amplitude density fluctuations by encountering the zeros of the following dielectric function.
$ \varepsilon_L={\rm{det}}\left(1-D_{L} \Pi_{L}\right)=0. $

(14) -
In the RRPA method, one can, in principle, involve the particle-hole and particle-antiparticle excitations of the fermions through various polarization tensors, while within the framework of the RMF models, the particle-antiparticle excitations are usually ignored in a no-sea approximation [37]. The interacting polarization is determined through the Dyson equation. For instance, the interacting longitudinal component of the vector polarization tensor
$ \Pi_{\mu\nu} $ , which is usually used to search for the collective modes, is given as$ \tilde{\Pi}_{L}={\Pi}_{L}+{\Pi}_{L}D_{L}\tilde{\Pi}_{L}, $
(7) where the polarization
$ \Pi_{L} $ and meson propagator$ D_{L} $ are in matrix form. The lowest-order longitudinal polarization$ \Pi_L $ in nuclear matter is written as$ \Pi_{L}=\left(\begin{array}{*{20}{c}} \Pi_{s}^{n}+\Pi_{s}^{p} & \Pi_{m}^{p} & \Pi_{m}^{n} \\ \Pi_{m}^{p} & \Pi_{00}^{p} & 0 \\ \Pi_{m}^{n} & 0 & \Pi_{00}^{n} \end{array}\right), $
(8) where the individual polarization entries are given by:
$ \begin{aligned} {\rm{i}} \Pi_{s}^a\left(q, q_{0}\right) =\int \frac{{\rm d}^{4} p}{(2 \pi)^{4}} {\rm{Tr}}[G^a(p) G^a(p+q)] , \end{aligned} $
(9a) $ \begin{aligned} {\rm{i}} \Pi_{m}^a\left(q, q_{0}\right) =\int \frac{{\rm d}^{4} p}{(2 \pi)^{4}} {\rm{Tr}}\left[G^a(p) \gamma_{0} G^a(p+q)\right] , \end{aligned} $
(9b) $ \begin{aligned} {\rm{i}} \Pi_{00}^a\left(q, q_{0}\right) =\int \frac{{\rm d}^{4} p}{(2 \pi)^{4}} {\rm{Tr}}\left[G^a(p) \gamma_{0} G^a(p+q) \gamma_{0}\right], \end{aligned} $
(9c) With
$ Tr $ indicating the trace over Dirac indices and$ a=p,n $ , the fermion Green function reads$ \begin{aligned}[b] G_a(k)=\;&\left(\gamma_{\mu}k^{\mu}+M^{*}_a\right) \left[\frac{1}{k_{\mu}^{ 2}-M_a^{* 2}+{\rm i}\varepsilon}\right.\\ &\left.+\frac{{\rm i} \pi}{E_{ka}^{*}} \delta\left(k_{0}-E_{ka}^{*}\right) \theta\left(k_{Fa}-|\boldsymbol{k}|\right)\right], \end{aligned} $
(10) where
$ M_a^{*}=M_a-g_{\sigma}\sigma_{0} $ is the nucleon effective mass, and$ k_{F} $ is the Fermi momentum.With the crossing coupling term of the
$ \rho $ and$ \omega $ mesons in Eq. (1), the meson propagator$ D_{L} $ is given as [50, 66]$ D_{L}=\left(\begin{array}{*{20}{c}} \chi_{\sigma} & 0 & 0 \\ 0 & \tilde{\chi}_{\omega}+\tilde{\chi}_{\varrho}+2 \tilde{\chi}_{\omega \varrho} & \tilde{\chi}_{\omega}-\tilde{\chi}_{\varrho} \\ 0 & \tilde{\chi}_{\omega}-\tilde{\chi}_{\varrho} & \tilde{\chi}_{\omega}+\tilde{\chi}_{\varrho}-2 \tilde{\chi}_{\omega \varrho} \end{array}\right). $
(11) Expressions for the various meson propagators with nonlinear meson couplings are provided as follows:
$ \begin{aligned} \chi_{\sigma}=\frac{g_{\sigma}^{2}}{q_{\mu}^{2}-m_{\sigma}^{*2}}, \end{aligned} $
(12a) $ \begin{aligned} \chi_{\omega}=\frac{g_{\omega}^{2}\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)}{\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)-\left(16 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0} b_{0}\right)^{2}} , \end{aligned} $
(12b) $ \begin{aligned} \chi_{\varrho}=\frac{g_{\varrho}^{2}\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)}{\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)-\left(16 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0} b_{0}\right)^{2}} , \end{aligned} $
(12c) $ \begin{aligned} \chi_{\omega \varrho}=\frac{-16 \Lambda_{V} g_{\omega}^{3} g_{\varrho}^{3} \omega_{0} b_{0}}{\left(q_{\mu}^{2}-m_{\varrho}^{*2}\right)\left(q_{\mu}^{2}-m_{\omega}^{*2}\right)-\left(16 \Lambda_{V} g_{\omega}^{2} g_{\varrho}^{2} \omega_{0} b_{0}\right)^{2}}, \end{aligned} $
(12d) $ \begin{aligned} &\tilde{\chi}_{i}=\frac{q_{\mu}^{2}}{q^{2}}\chi_{i},\quad i=\omega,\rho. \end{aligned}$
(12e) When the vector repulsion of the U boson is included,
$ \chi_{\omega} $ is replaced by$ \chi_{V}^\prime $ to modify the Dyson equation.$ \chi_{V}'=\chi_{\omega}+\chi_{u},\quad \chi_{u}=\frac{g_{u}^{2}}{q_{\mu}^{2}-m_{u}^{2}}. $
(13) The nuclear systems undergo transitions at small-amplitude density fluctuations by encountering the zeros of the following dielectric function.
$ \varepsilon_L={\rm{det}}\left(1-D_{L} \Pi_{L}\right)=0. $
(14) -
In our work, we adopt two well-fitting but relatively soft parameter sets, TM1 and FSUGarnet, to investigate the impact of the U boson on zero-sound modes. To improve the consistency of neutron star radius predictions in the TM1 model with observational data, we soften the symmetry energy by introducing an isoscalar-isovector (
$ \omega-\rho $ ) coupling term ($ \Lambda_V $ ) [50, 63, 67]. The modified TM1 model is referred to as TM1w02. The parameters and saturation properties of these two models are listed in Table 1.$ g_{\sigma} $ $ g_{\omega} $ $ g_{\rho} $ $ m_{\sigma} $ $ m_{\omega} $ $ m_{\rho} $ $ g_{2} $ $ g_{3} $ $ c_{3} $ $ \Lambda_{V} $ $ \rho_{0} $ $ K_0 $ $ M^{*}/M $ $ E_{\rm sym} $ TM1w02 10.029 12.614 5.277 511.198 783.000 770 7.233 0.618 71.31 0.02 0.145 281.20 0.63 30.7 FSUGarnet 10.505 13.700 6.945 496.939 782.500 763 9.576 -7.207 137.981 0.04338 0.153 229.628 0.58 30.9 Table 1. Parameters and saturation properties for the parameter sets TM1w02 and FSUGarnet. The meson masses
$ m_i (i=\sigma,\omega,\rho $ ), the incompressibility$ K_0 $ , and the symmetry energy$ E_{\rm sym} $ are in units of MeV. The saturation density$ \rho_0 $ is in units of$ \rm {fm^{-3}} $ .In Fig. 1, the pressure as a function of the energy density of symmetric nuclear matter is shown with the inclusion of the U boson in parameter sets TM1w02 and FSUGarnet. The EOS trajectories are depicted for a set of ratios
$ g_u^2/m_u^2 $ . In the RMF approximation, the contribution of the U boson is determined linearly by the ratio of the coupling constant to its mass, i.e.,$ g_u/m_u $ , as seen in Eqs. (5) and (6). The actual values of$ g_u $ and$ m_u $ lack sufficient constraints and are largely uncertain. As argued by Krivoruchenko et al. [17],$ m_u\leq30 $ MeV and the$ g_u^2/m_u^2 $ value of the U boson should be less than about 300 GeV-2, which roughly corresponds to the value of the ordinary vector$ \omega $ meson. To escape detection in terrestrial measurements on nuclei, it was pointed out that the mass of the weakly coupled U boson is on the order of 1 MeV [20]. In this work, the ratio is chosen to be beneath 300 GeV-2. It is observed that the inclusion of the U boson can significantly stiffen the nuclear EOS with the TM1w02 and FSUGarnet. This is physically evident since the vector U boson provides additional repulsion in addition to the vector mesons.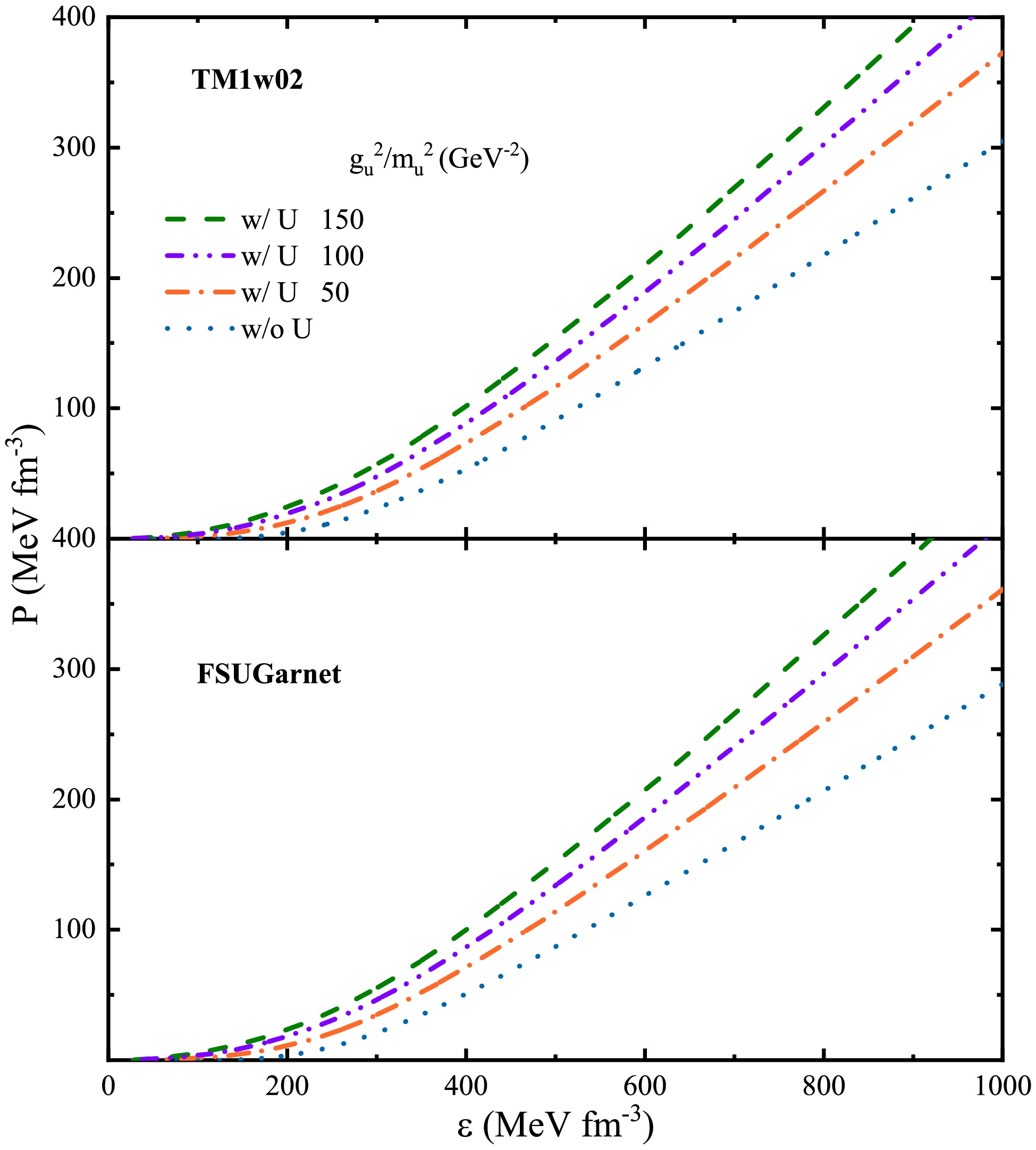
Figure 1. (color online) The relationship between pressure and energy density for various equations of state (EOS) with different
$ g_u^2/m_u^2 $ in TM1w02 and FSUGarnetZero sounds are determined by the zeros of the dielectric function and are the collective modes following the dispersion relation with the zero-energy limit. At small momentum transfer q, zero sounds have similar properties, and for numerical conciseness, the momentum
$ q = 10 $ MeV is typically chosen in our calculations. In previous studies [50], it has been found that zero-sound modes at lower densities (typically$ \rho_B \lesssim 2\rho_0 $ ) are dominated by the$ \rho $ meson and are referred to as isovector-dominated or isospin zero-sound modes. These modes are highly insensitive to the stiffness of the EOS. In contrast, zero-sound modes that emerge at higher densities are primarily governed by the$ \sigma $ and$ \omega $ mesons and are thus termed isoscalar-dominated zero-sound modes. The occurrence of these high-density modes has been shown to be strongly correlated with the EOS stiffness in both symmetric and asymmetric nuclear matter. In soft EOS models, these modes emerge only when the nonlinear self-interaction term of the$ \omega $ meson ($ c_3\omega_0^4 $ , see Eq. (1)) is reduced to yield a stiffer EOS. In this work, we examine whether the EOS stiffening induced by the U boson can have a similar effect on the occurrence of isoscalar-dominant zero-sound modes and further revisit the relationship between high-density zero-sound modes and the stiffness of the EOS. In contrast to the RMF EOS, the mass and coupling constant of the U boson are both contributive in RPA (see Eq. (13)). As mentioned above, the mass of the weakly coupling U boson is roughly of the order of 1 MeV [20]. Without loss of generality, the U boson mass is assumed to be 2 MeV or 4 MeV in the present RPA calculation, given the ratio$ g_u^2/m_u^2 $ beneath 300 GeV-2.It is interesting to examine how the U boson-induced modification to the EOS affects the behavior of zero sound. As shown in Figs. 2 and 3, the isoscalar-dominated zero-sound modes arise in the models TM1w02 and FSUGarnet at high density due to the stiffening role of the U boson in the EOS. Without the inclusion of the U boson, such isoscalar-dominated modes do not appear in these models at high density; only isovector-dominated zero-sound modes, mainly driven by the
$ \rho $ meson, emerge at lower densities, which are generally insensitive to the stiffness of the EOS. This results from the fact that the U boson provides an excess repulsion to overwhelm the attractive interaction at high density. The reproduction of the zero-sound modes by the U boson repulsion is similar to that caused by stiffening the repulsion of the$ \omega $ meson [50], providing additional evidence that the occurrence of zero-sound modes can signal the stiffness of the nuclear EOS. As the EOS becomes stiffer by increasing the coupling term of the U boson, we can see from the inset of Figs. 2 and 3 that the high-density zero-sound modes start to appear at$ g_u^2/m_u^2 = 95 $ (200) GeV-2 in TM1w02 (FSUGarnet), with the region expansion of zero-sound modes for larger coupling strength. It is worth noting that the coupling constant of the U boson for the onset of zero sounds in FSUGarnet is larger than that in TM1w02. This difference is mainly attributed to the larger coupling coefficient$ \Lambda_V $ between the$ \omega $ and$ \rho $ mesons, which increases the effective mass of the$ \rho $ meson but suppresses the magnitude of the$ \rho $ meson propagator. Consequently, this leads to a suppression of the contribution of the$ \chi_u \chi_\rho $ term to the vector part of the dielectric function, and a larger coupling constant of the U boson is needed for compensation. The onset of isoscalar-dominated zero-sound modes occurs at a slightly higher baryon density in FSUGarnet than in TM1w02, due to differences in their scalar meson self-interactions and effective meson masses, which affect the delicate balance between vector repulsion and scalar attraction. This balance plays a crucial role in determining the zeros of the dielectric function and thus the emergence of collective modes.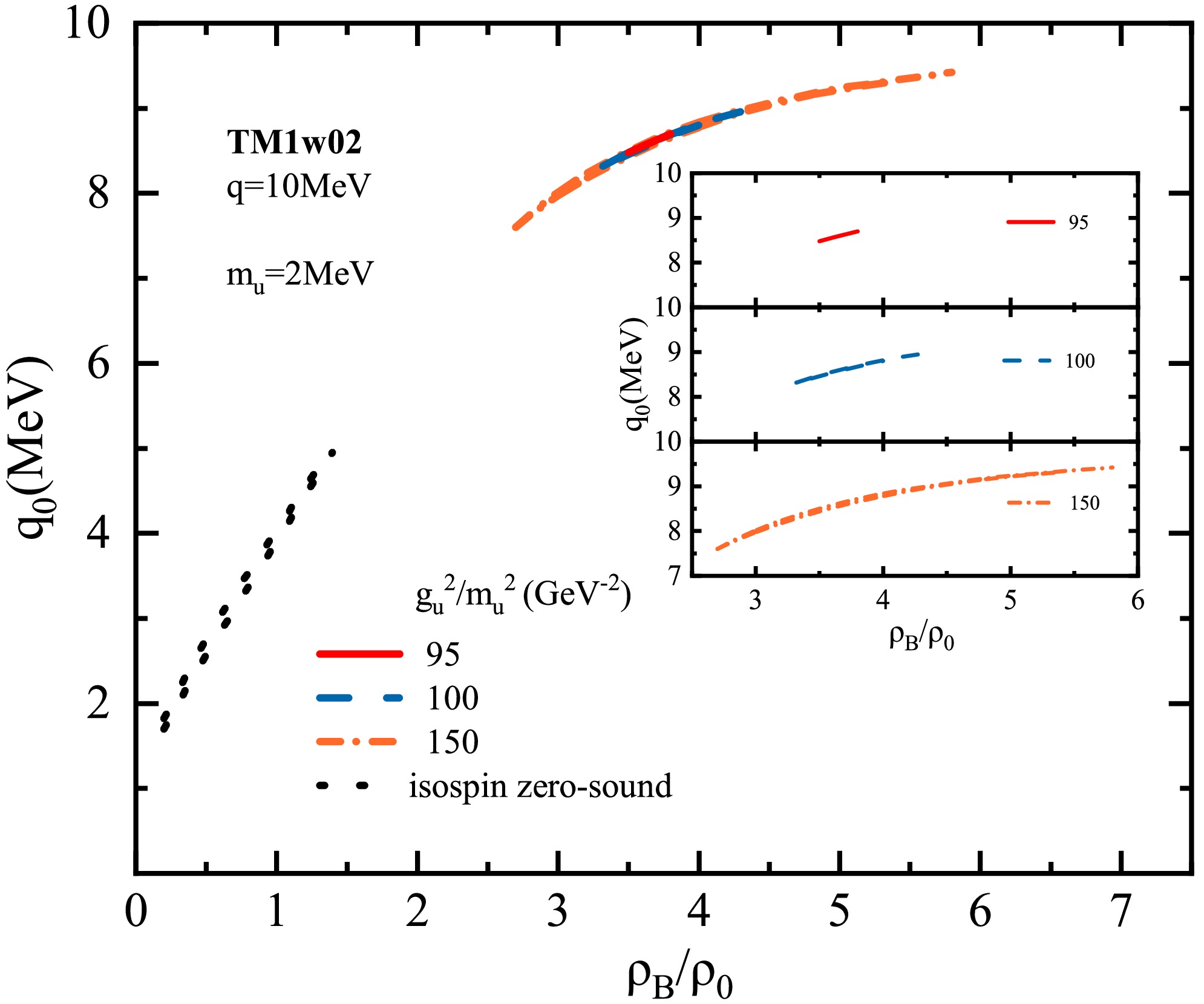
Figure 2. (color online) Isospin zero-sound modes (at low density) and isoscalar dominated zero-sound modes (at high density) in symmetric nuclear matter with the TM1w02 model. The U boson is included with varying coupling ratio parameters
$ g_u^2/m_u^2 $ , and its mass is fixed at 2 MeV. The inset separately shows isoscalar dominated zero-sound modes for different U boson coupling parameters.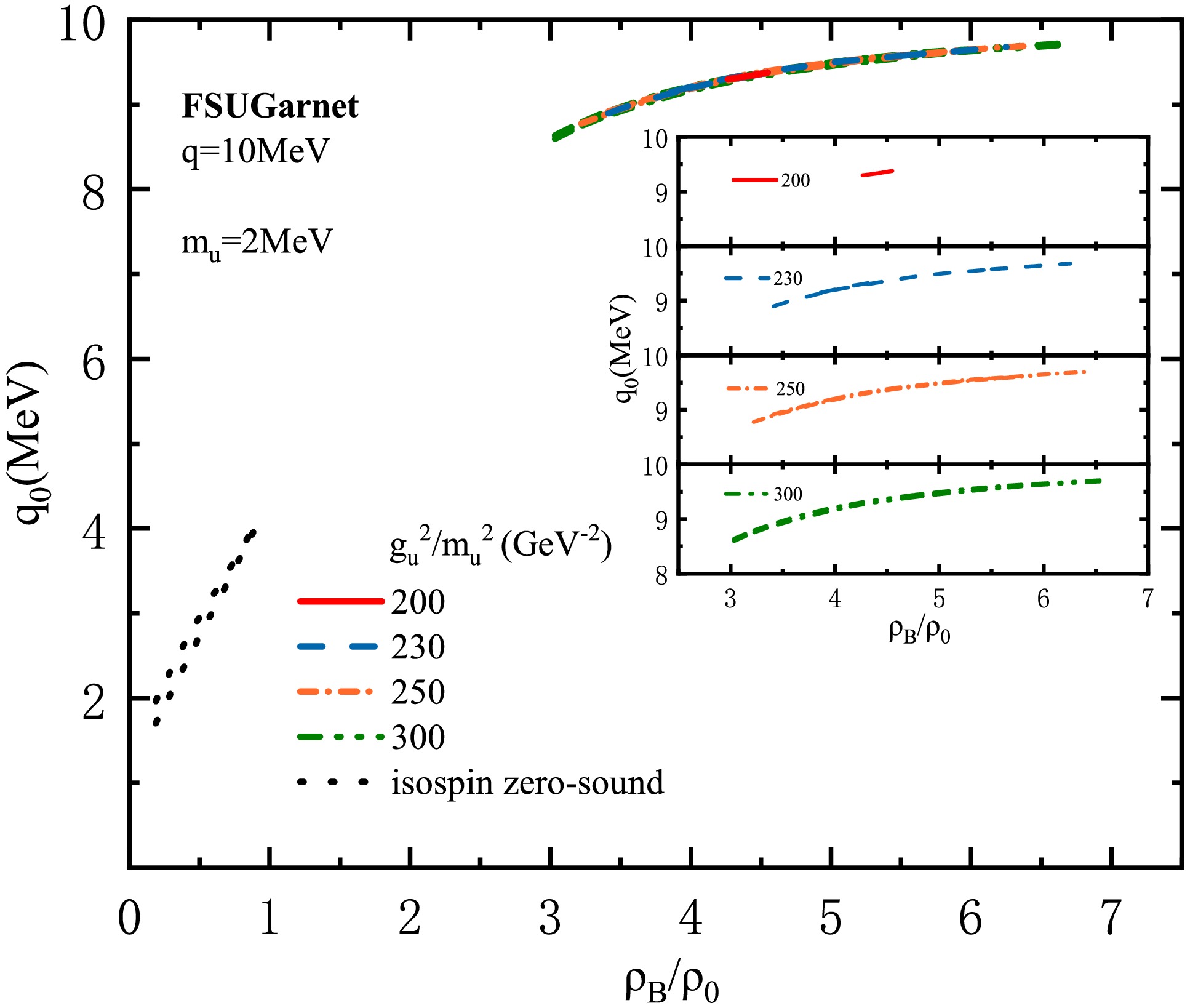
Figure 3. (color online) The same as in Fig. 2, but for the RMF model FSUGarnet with different U boson coupling strengths.
For isovector-dominated zero-sound modes, their behavior is independent of the stiffness of the EOS, and therefore the introduction of the U boson has no impact on them.
Figure 4 shows that when the mass of the U boson is fixed at 4 MeV, the values of
$ g_u^2/m_u^2 $ , at which the isoscalar-dominated zero-sound modes begin to appear, are 50 (100) GeV-2 for TM1w02 (FSUGarnet). The reduction in the threshold value of$ g_u^2/m_u^2 $ is evident. As shown in Eq. (13), the magnitude of$ \chi_u $ is proportional to both the mass$ m_u $ and the ratio$ g_u^2/m_u^2 $ . As$ m_u $ increases, the$ g_u^2/m_u^2 $ decreases for the same$ \chi_u $ required by the emergence of isoscalar-dominated zero-sound modes.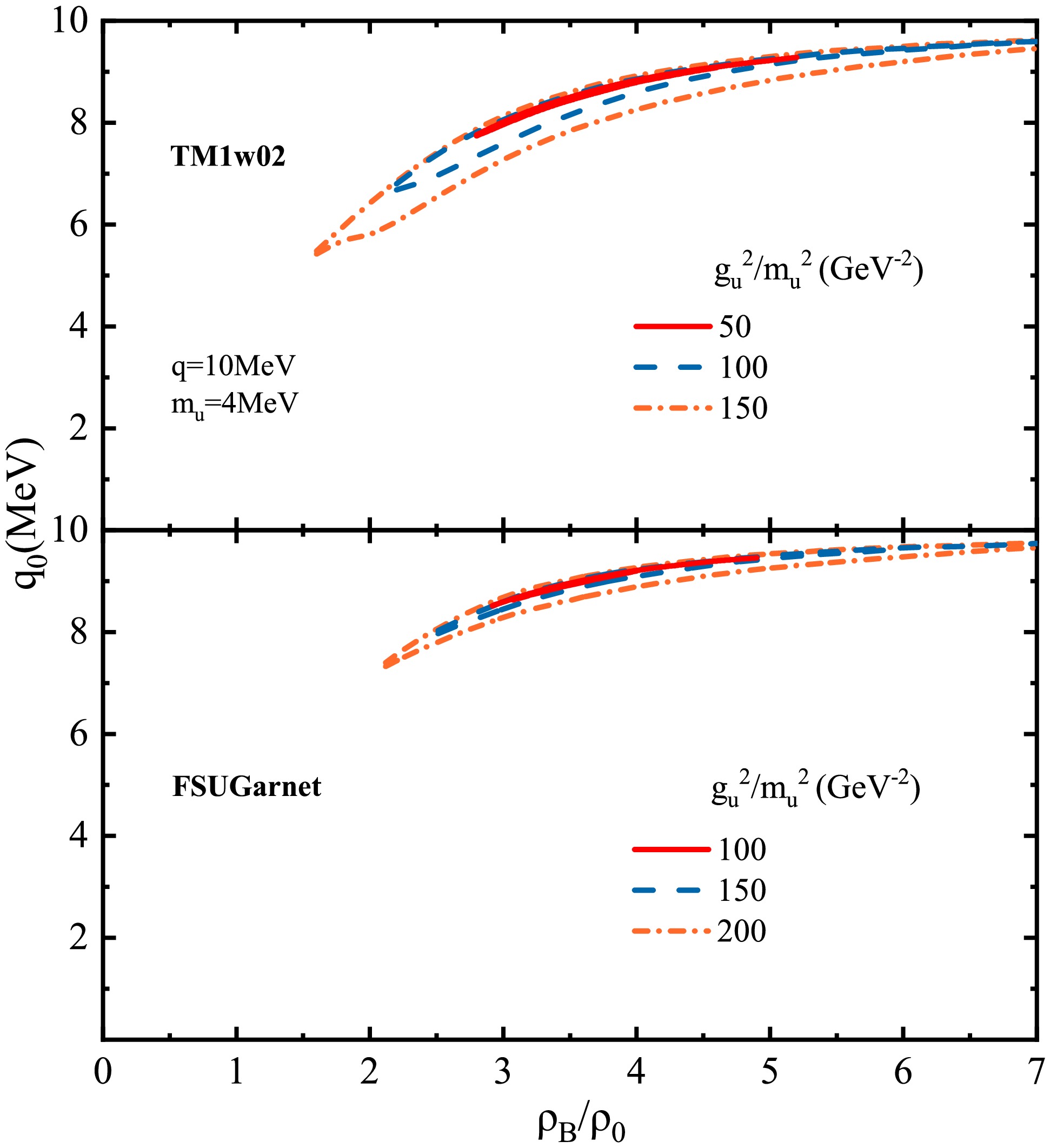
Figure 4. (color online) Isoscalar-dominated zero-sound modes in symmetric nuclear matter with the TM1w02 and FSUGarnet models. The mass of the U boson is fixed at 4 MeV.
In contrast to the case in symmetric matter, the distinction between isoscalar and isovector dominated zero-sound modes becomes blurred in asymmetric matter. For the soft EOS models, such as TM1w02, the emergence of zero-sound modes in asymmetric nuclear matter similarly requires stiffening the EOS. As shown in Fig. 5, the inclusion of the U boson enables the appearance of zero-sound modes in asymmetric matter. Notably, a lower isospin asymmetry parameter
$ \alpha $ ($ \alpha=(\rho_n-\rho_p)/\rho_B $ ) leads to a lower onset density of the zero-sound modes, as isospin asymmetry influences the delicate balance of the dielectric function. Similar to symmetric matter, in asymmetric matter, the larger the U boson coupling, the wider the density range over which zero-sound modes appear, as shown in Fig. 6 for the TM1w02 model. Note that Fig. 6 adopts$ m_u = 4\; {\rm{MeV}} $ , while Fig. 5 uses$ m_u = 2\; {\rm{MeV}} $ , for which zero-sound modes appear only when$ g_u^2 / m_u^2 \gtrsim 150\; $ GeV−2. Unlike the case in symmetric matter, where zero sound consists of the undamped (the one with larger$ q_0 $ ) and damped branches, multiple zero-sound branches appear in asymmetric matter. Among them, the branch with the largest$ q_0 $ is undamped, while the others are damped. Therefore, it can be concluded that the stiffening of the EOS by the U boson allows zero-sound modes to emerge in both symmetric and asymmetric matter.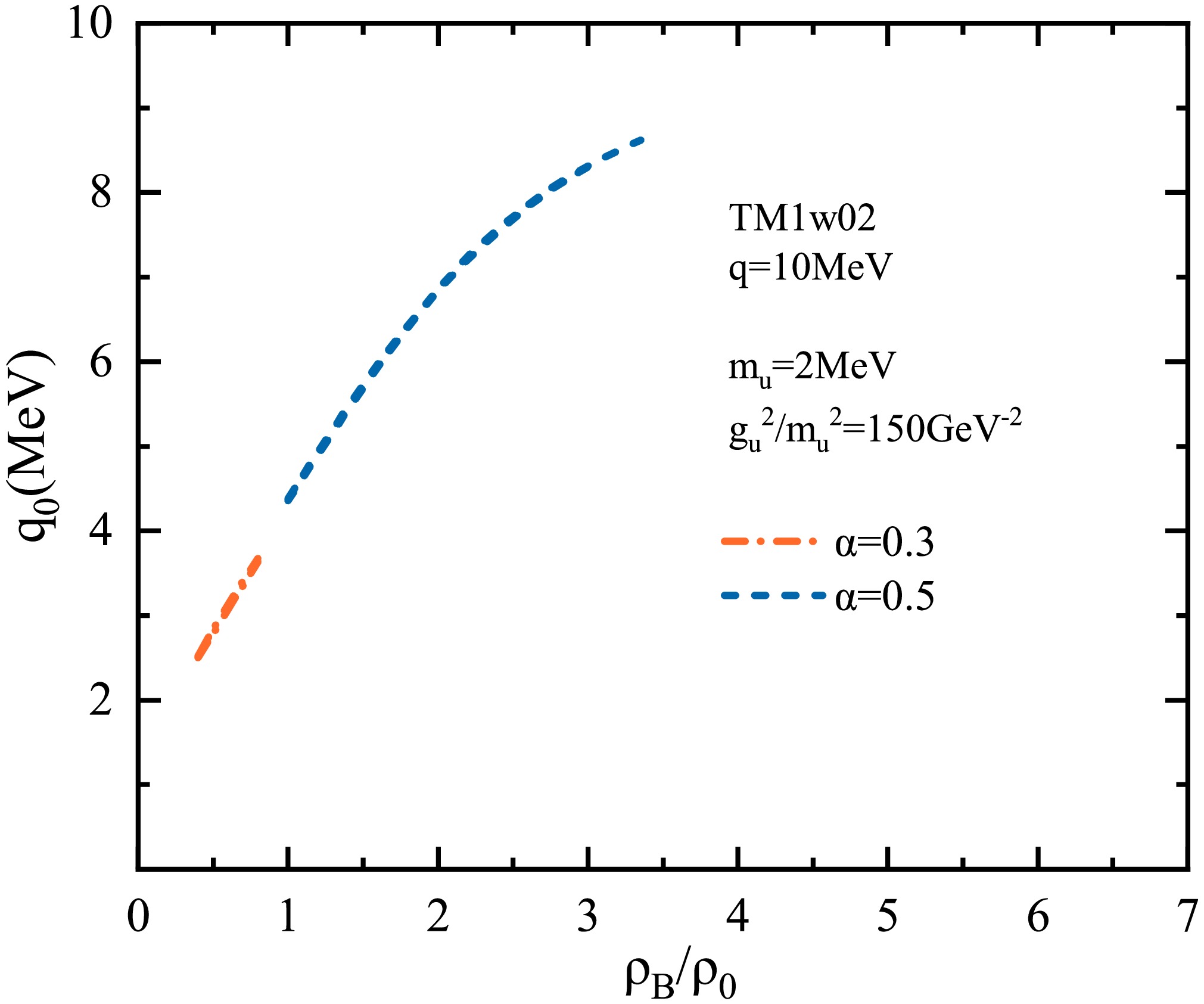
Figure 5. (color online) Zero sound in asymmetric nuclear matter
$ (\alpha =0.3, 0.5) $ with TM1w02. The mass of the U boson is set to 2 MeV, and the interaction ratio$ g_u^2/m_u^2 $ is set to 150$ \rm {GeV^{-2}} $ .
Figure 6. (color online) Zero sounds in asymmetric nuclear matter with TM1w02 for various
$ g_u^2/m_u^2 $ . The mass of the U boson is fixed at 4 MeV. The left panels represent the results with$ \alpha = 0.3 $ , and the right panels with$ \alpha = 0.5 $ . The orange lines represent the undamped branches of zero sound, and the green lines represent the damped branches.Furthermore, we investigate the effect of the U boson on zero-sound modes in the
$ \beta $ -equilibrated neutron star matter. Zero-sound modes in neutron star matter can possibly be associated with neutron star cooling and pulsar radiation [52]. Investigating the correlation between zero sound and the stiffness of the EOS is essential for understanding astrophysical phenomena in the multimessenger era. Figure 7 shows the zero-sound modes in neutron star matter with various$ g_u^2/m_u^2 $ . We can see that the damped zero-sound modes are similar across different values of$ g_u^2/m_u^2 $ , showing little sensitivity to the degree of EOS stiffening, whereas the undamped modes exhibit significant dependence on the coupling strength of the U boson. As$ g_u^2/m_u^2 $ increases, the range for the undamped zero-sound modes gradually extends to higher densities.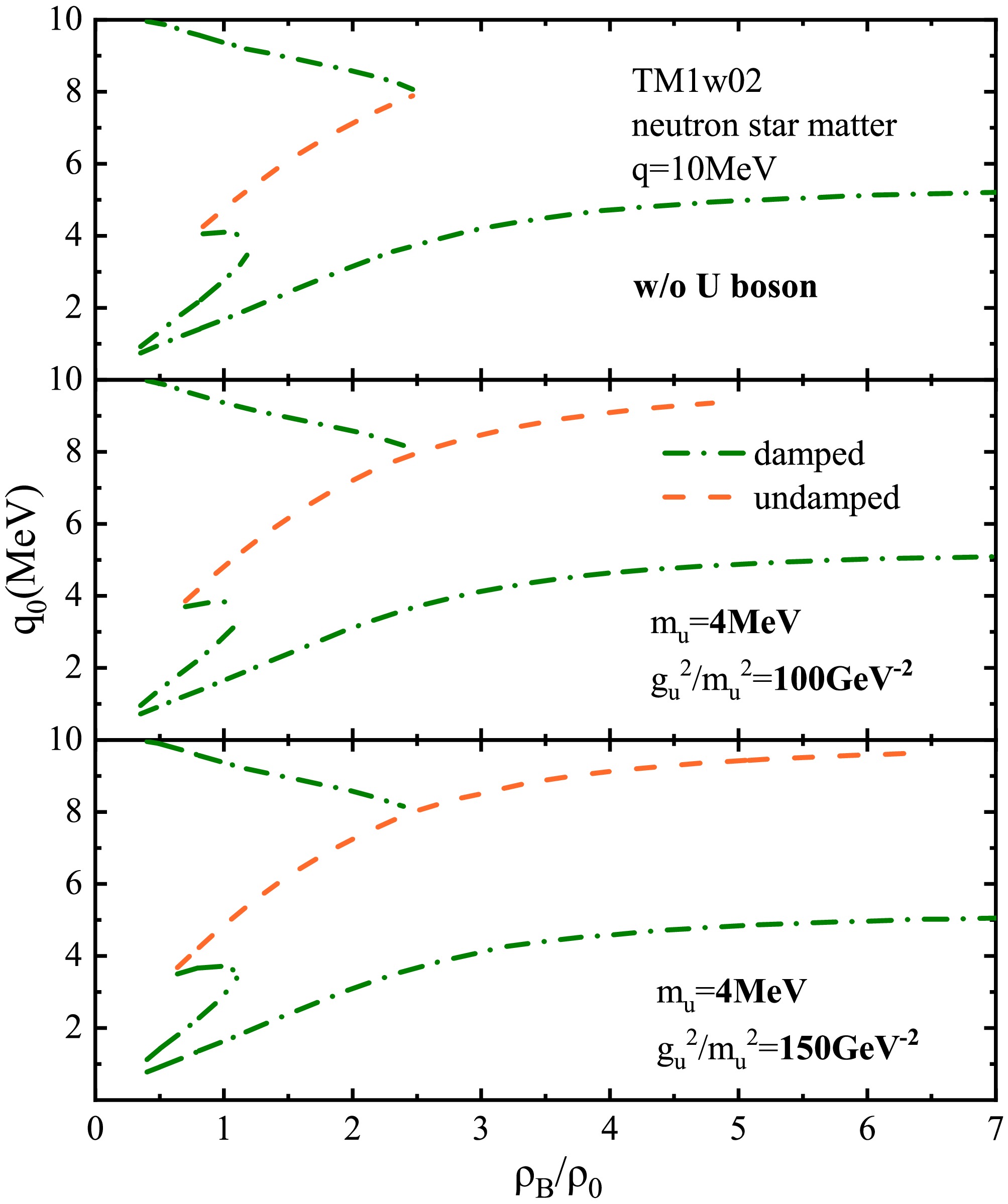
Figure 7. (color online) The same as in Fig. 6, but for neutron star matter.
It is worth noting that the repulsion of the U boson results in an increase in the predicted maximum mass of neutron stars. This is advantageous in satisfying the lower limit of the maximum mass of neutron stars around
$ 2M_\odot $ [2, 3]. Meanwhile, the additional repulsion of the U boson also tends to increase the predicted neutron star radii [18, 20], potentially exceeding observational bounds. This tension can be alleviated by adopting a density-dependent U boson coupling to merely reduce the star radius [68]. Moreover, the zero-sound modes have been proposed as potential Goldstone bosons that possibly couple to neutrino emission channels via$ Z^0 $ -boson exchange [52]. Thus, it suggests that facilitating the onset of zero sound by the U boson may affect neutron star cooling and long-term evolution through additional neutrino emission, which warrants further investigation.Lastly, it is necessary to point out that in the FSUGarnet model, the dependence of the zero sound on the U boson repulsion in asymmetric nuclear matter and neutron star matter is similar to that in the TM1w02 model, although a larger
$ g_u^2/m_u^2 $ is needed for the FSUGarnet model as in symmetric matter. To save space, the results with the FSUGarnet model are not presented here. -
In our work, we adopt two well-fitting but relatively soft parameter sets, TM1 and FSUGarnet, to investigate the impact of the U boson on zero-sound modes. To improve the consistency of neutron star radius predictions in the TM1 model with observational data, we soften the symmetry energy by introducing an isoscalar-isovector (
$ \omega-\rho $ ) coupling term ($ \Lambda_V $ ) [50, 63, 67]. The modified TM1 model is referred to as TM1w02. The parameters and saturation properties of these two models are listed in Table 1.$ g_{\sigma} $ 

$ g_{\omega} $ 

$ g_{\rho} $ 

$ m_{\sigma} $ 

$ m_{\omega} $ 

$ m_{\rho} $ 

$ g_{2} $ 

$ g_{3} $ 

$ c_{3} $ 

$ \Lambda_{V} $ 

$ \rho_{0} $ 

$ K_0 $ 

$ M^{*}/M $ 

$ E_{\rm sym} $ 

TM1w02 10.029 12.614 5.277 511.198 783.000 770 7.233 0.618 71.31 0.02 0.145 281.20 0.63 30.7 FSUGarnet 10.505 13.700 6.945 496.939 782.500 763 9.576 -7.207 137.981 0.04338 0.153 229.628 0.58 30.9 Table 1. Parameters and saturation properties for the parameter sets TM1w02 and FSUGarnet. The meson masses
$ m_i (i=\sigma,\omega,\rho $ ), the incompressibility$ K_0 $ , and the symmetry energy$ E_{\rm sym} $ are in units of MeV. The saturation density$ \rho_0 $ is in units of$ \rm {fm^{-3}} $ .In Fig. 1, the pressure as a function of the energy density of symmetric nuclear matter is shown with the inclusion of the U boson in parameter sets TM1w02 and FSUGarnet. The EOS trajectories are depicted for a set of ratios
$ g_u^2/m_u^2 $ . In the RMF approximation, the contribution of the U boson is determined linearly by the ratio of the coupling constant to its mass, i.e.,$ g_u/m_u $ , as seen in Eqs. (5) and (6). The actual values of$ g_u $ and$ m_u $ lack sufficient constraints and are largely uncertain. As argued by Krivoruchenko et al. [17],$ m_u\leq30 $ MeV and the$ g_u^2/m_u^2 $ value of the U boson should be less than about 300 GeV-2, which roughly corresponds to the value of the ordinary vector$ \omega $ meson. To escape detection in terrestrial measurements on nuclei, it was pointed out that the mass of the weakly coupled U boson is on the order of 1 MeV [20]. In this work, the ratio is chosen to be beneath 300 GeV-2. It is observed that the inclusion of the U boson can significantly stiffen the nuclear EOS with the TM1w02 and FSUGarnet. This is physically evident since the vector U boson provides additional repulsion in addition to the vector mesons.
Figure 1. (color online) The relationship between pressure and energy density for various equations of state (EOS) with different
$ g_u^2/m_u^2 $ in TM1w02 and FSUGarnetZero sounds are determined by the zeros of the dielectric function and are the collective modes following the dispersion relation with the zero-energy limit. At small momentum transfer q, zero sounds have similar properties, and for numerical conciseness, the momentum
$ q = 10 $ MeV is typically chosen in our calculations. In previous studies [50], it has been found that zero-sound modes at lower densities (typically$ \rho_B \lesssim 2\rho_0 $ ) are dominated by the$ \rho $ meson and are referred to as isovector-dominated or isospin zero-sound modes. These modes are highly insensitive to the stiffness of the EOS. In contrast, zero-sound modes that emerge at higher densities are primarily governed by the$ \sigma $ and$ \omega $ mesons and are thus termed isoscalar-dominated zero-sound modes. The occurrence of these high-density modes has been shown to be strongly correlated with the EOS stiffness in both symmetric and asymmetric nuclear matter. In soft EOS models, these modes emerge only when the nonlinear self-interaction term of the$ \omega $ meson ($ c_3\omega_0^4 $ , see Eq. (1)) is reduced to yield a stiffer EOS. In this work, we examine whether the EOS stiffening induced by the U boson can have a similar effect on the occurrence of isoscalar-dominant zero-sound modes and further revisit the relationship between high-density zero-sound modes and the stiffness of the EOS. In contrast to the RMF EOS, the mass and coupling constant of the U boson are both contributive in RPA (see Eq. (13)). As mentioned above, the mass of the weakly coupling U boson is roughly of the order of 1 MeV [20]. Without loss of generality, the U boson mass is assumed to be 2 MeV or 4 MeV in the present RPA calculation, given the ratio$ g_u^2/m_u^2 $ beneath 300 GeV-2.It is interesting to examine how the U boson-induced modification to the EOS affects the behavior of zero sound. As shown in Figs. 2 and 3, the isoscalar-dominated zero-sound modes arise in the models TM1w02 and FSUGarnet at high density due to the stiffening role of the U boson in the EOS. Without the inclusion of the U boson, such isoscalar-dominated modes do not appear in these models at high density; only isovector-dominated zero-sound modes, mainly driven by the
$ \rho $ meson, emerge at lower densities, which are generally insensitive to the stiffness of the EOS. This results from the fact that the U boson provides an excess repulsion to overwhelm the attractive interaction at high density. The reproduction of the zero-sound modes by the U boson repulsion is similar to that caused by stiffening the repulsion of the$ \omega $ meson [50], providing additional evidence that the occurrence of zero-sound modes can signal the stiffness of the nuclear EOS. As the EOS becomes stiffer by increasing the coupling term of the U boson, we can see from the inset of Figs. 2 and 3 that the high-density zero-sound modes start to appear at$ g_u^2/m_u^2 = 95 $ (200) GeV-2 in TM1w02 (FSUGarnet), with the region expansion of zero-sound modes for larger coupling strength. It is worth noting that the coupling constant of the U boson for the onset of zero sounds in FSUGarnet is larger than that in TM1w02. This difference is mainly attributed to the larger coupling coefficient$ \Lambda_V $ between the$ \omega $ and$ \rho $ mesons, which increases the effective mass of the$ \rho $ meson but suppresses the magnitude of the$ \rho $ meson propagator. Consequently, this leads to a suppression of the contribution of the$ \chi_u \chi_\rho $ term to the vector part of the dielectric function, and a larger coupling constant of the U boson is needed for compensation. The onset of isoscalar-dominated zero-sound modes occurs at a slightly higher baryon density in FSUGarnet than in TM1w02, due to differences in their scalar meson self-interactions and effective meson masses, which affect the delicate balance between vector repulsion and scalar attraction. This balance plays a crucial role in determining the zeros of the dielectric function and thus the emergence of collective modes.
Figure 2. (color online) Isospin zero-sound modes (at low density) and isoscalar dominated zero-sound modes (at high density) in symmetric nuclear matter with the TM1w02 model. The U boson is included with varying coupling ratio parameters
$ g_u^2/m_u^2 $ , and its mass is fixed at 2 MeV. The inset separately shows isoscalar dominated zero-sound modes for different U boson coupling parameters.
Figure 3. (color online) The same as in Fig. 2, but for the RMF model FSUGarnet with different U boson coupling strengths.
For isovector-dominated zero-sound modes, their behavior is independent of the stiffness of the EOS, and therefore the introduction of the U boson has no impact on them.
Figure 4 shows that when the mass of the U boson is fixed at 4 MeV, the values of
$ g_u^2/m_u^2 $ , at which the isoscalar-dominated zero-sound modes begin to appear, are 50 (100) GeV-2 for TM1w02 (FSUGarnet). The reduction in the threshold value of$ g_u^2/m_u^2 $ is evident. As shown in Eq. (13), the magnitude of$ \chi_u $ is proportional to both the mass$ m_u $ and the ratio$ g_u^2/m_u^2 $ . As$ m_u $ increases, the$ g_u^2/m_u^2 $ decreases for the same$ \chi_u $ required by the emergence of isoscalar-dominated zero-sound modes.
Figure 4. (color online) Isoscalar-dominated zero-sound modes in symmetric nuclear matter with the TM1w02 and FSUGarnet models. The mass of the U boson is fixed at 4 MeV.
In contrast to the case in symmetric matter, the distinction between isoscalar and isovector dominated zero-sound modes becomes blurred in asymmetric matter. For the soft EOS models, such as TM1w02, the emergence of zero-sound modes in asymmetric nuclear matter similarly requires stiffening the EOS. As shown in Fig. 5, the inclusion of the U boson enables the appearance of zero-sound modes in asymmetric matter. Notably, a lower isospin asymmetry parameter
$ \alpha $ ($ \alpha=(\rho_n-\rho_p)/\rho_B $ ) leads to a lower onset density of the zero-sound modes, as isospin asymmetry influences the delicate balance of the dielectric function. Similar to symmetric matter, in asymmetric matter, the larger the U boson coupling, the wider the density range over which zero-sound modes appear, as shown in Fig. 6 for the TM1w02 model. Note that Fig. 6 adopts$ m_u = 4\; {\rm{MeV}} $ , while Fig. 5 uses$ m_u = 2\; {\rm{MeV}} $ , for which zero-sound modes appear only when$ g_u^2 / m_u^2 \gtrsim 150\; $ GeV−2. Unlike the case in symmetric matter, where zero sound consists of the undamped (the one with larger$ q_0 $ ) and damped branches, multiple zero-sound branches appear in asymmetric matter. Among them, the branch with the largest$ q_0 $ is undamped, while the others are damped. Therefore, it can be concluded that the stiffening of the EOS by the U boson allows zero-sound modes to emerge in both symmetric and asymmetric matter.
Figure 5. (color online) Zero sound in asymmetric nuclear matter
$ (\alpha =0.3, 0.5) $ with TM1w02. The mass of the U boson is set to 2 MeV, and the interaction ratio$ g_u^2/m_u^2 $ is set to 150$ \rm {GeV^{-2}} $ .
Figure 6. (color online) Zero sounds in asymmetric nuclear matter with TM1w02 for various
$ g_u^2/m_u^2 $ . The mass of the U boson is fixed at 4 MeV. The left panels represent the results with$ \alpha = 0.3 $ , and the right panels with$ \alpha = 0.5 $ . The orange lines represent the undamped branches of zero sound, and the green lines represent the damped branches.Furthermore, we investigate the effect of the U boson on zero-sound modes in the
$ \beta $ -equilibrated neutron star matter. Zero-sound modes in neutron star matter can possibly be associated with neutron star cooling and pulsar radiation [52]. Investigating the correlation between zero sound and the stiffness of the EOS is essential for understanding astrophysical phenomena in the multimessenger era. Figure 7 shows the zero-sound modes in neutron star matter with various$ g_u^2/m_u^2 $ . We can see that the damped zero-sound modes are similar across different values of$ g_u^2/m_u^2 $ , showing little sensitivity to the degree of EOS stiffening, whereas the undamped modes exhibit significant dependence on the coupling strength of the U boson. As$ g_u^2/m_u^2 $ increases, the range for the undamped zero-sound modes gradually extends to higher densities.
Figure 7. (color online) The same as in Fig. 6, but for neutron star matter.
It is worth noting that the repulsion of the U boson results in an increase in the predicted maximum mass of neutron stars. This is advantageous in satisfying the lower limit of the maximum mass of neutron stars around
$ 2M_\odot $ [2, 3]. Meanwhile, the additional repulsion of the U boson also tends to increase the predicted neutron star radii [18, 20], potentially exceeding observational bounds. This tension can be alleviated by adopting a density-dependent U boson coupling to merely reduce the star radius [68]. Moreover, the zero-sound modes have been proposed as potential Goldstone bosons that possibly couple to neutrino emission channels via$ Z^0 $ -boson exchange [52]. Thus, it suggests that facilitating the onset of zero sound by the U boson may affect neutron star cooling and long-term evolution through additional neutrino emission, which warrants further investigation.Lastly, it is necessary to point out that in the FSUGarnet model, the dependence of the zero sound on the U boson repulsion in asymmetric nuclear matter and neutron star matter is similar to that in the TM1w02 model, although a larger
$ g_u^2/m_u^2 $ is needed for the FSUGarnet model as in symmetric matter. To save space, the results with the FSUGarnet model are not presented here. -
In our work, we adopt two well-fitting but relatively soft parameter sets, TM1 and FSUGarnet, to investigate the impact of the U boson on zero-sound modes. To improve the consistency of neutron star radius predictions in the TM1 model with observational data, we soften the symmetry energy by introducing an isoscalar-isovector (
$ \omega-\rho $ ) coupling term ($ \Lambda_V $ ) [50, 63, 67]. The modified TM1 model is referred to as TM1w02. The parameters and saturation properties of these two models are listed in Table 1.$ g_{\sigma} $ 

$ g_{\omega} $ 

$ g_{\rho} $ 

$ m_{\sigma} $ 

$ m_{\omega} $ 

$ m_{\rho} $ 

$ g_{2} $ 

$ g_{3} $ 

$ c_{3} $ 

$ \Lambda_{V} $ 

$ \rho_{0} $ 

$ K_0 $ 

$ M^{*}/M $ 

$ E_{\rm sym} $ 

TM1w02 10.029 12.614 5.277 511.198 783.000 770 7.233 0.618 71.31 0.02 0.145 281.20 0.63 30.7 FSUGarnet 10.505 13.700 6.945 496.939 782.500 763 9.576 -7.207 137.981 0.04338 0.153 229.628 0.58 30.9 Table 1. Parameters and saturation properties for the parameter sets TM1w02 and FSUGarnet. The meson masses
$ m_i (i=\sigma,\omega,\rho $ ), the incompressibility$ K_0 $ , and the symmetry energy$ E_{\rm sym} $ are in units of MeV. The saturation density$ \rho_0 $ is in units of$ \rm {fm^{-3}} $ .In Fig. 1, the pressure as a function of the energy density of symmetric nuclear matter is shown with the inclusion of the U boson in parameter sets TM1w02 and FSUGarnet. The EOS trajectories are depicted for a set of ratios
$ g_u^2/m_u^2 $ . In the RMF approximation, the contribution of the U boson is determined linearly by the ratio of the coupling constant to its mass, i.e.,$ g_u/m_u $ , as seen in Eqs. (5) and (6). The actual values of$ g_u $ and$ m_u $ lack sufficient constraints and are largely uncertain. As argued by Krivoruchenko et al. [17],$ m_u\leq30 $ MeV and the$ g_u^2/m_u^2 $ value of the U boson should be less than about 300 GeV-2, which roughly corresponds to the value of the ordinary vector$ \omega $ meson. To escape detection in terrestrial measurements on nuclei, it was pointed out that the mass of the weakly coupled U boson is on the order of 1 MeV [20]. In this work, the ratio is chosen to be beneath 300 GeV-2. It is observed that the inclusion of the U boson can significantly stiffen the nuclear EOS with the TM1w02 and FSUGarnet. This is physically evident since the vector U boson provides additional repulsion in addition to the vector mesons.
Figure 1. (color online) The relationship between pressure and energy density for various equations of state (EOS) with different
$ g_u^2/m_u^2 $ in TM1w02 and FSUGarnetZero sounds are determined by the zeros of the dielectric function and are the collective modes following the dispersion relation with the zero-energy limit. At small momentum transfer q, zero sounds have similar properties, and for numerical conciseness, the momentum
$ q = 10 $ MeV is typically chosen in our calculations. In previous studies [50], it has been found that zero-sound modes at lower densities (typically$ \rho_B \lesssim 2\rho_0 $ ) are dominated by the$ \rho $ meson and are referred to as isovector-dominated or isospin zero-sound modes. These modes are highly insensitive to the stiffness of the EOS. In contrast, zero-sound modes that emerge at higher densities are primarily governed by the$ \sigma $ and$ \omega $ mesons and are thus termed isoscalar-dominated zero-sound modes. The occurrence of these high-density modes has been shown to be strongly correlated with the EOS stiffness in both symmetric and asymmetric nuclear matter. In soft EOS models, these modes emerge only when the nonlinear self-interaction term of the$ \omega $ meson ($ c_3\omega_0^4 $ , see Eq. (1)) is reduced to yield a stiffer EOS. In this work, we examine whether the EOS stiffening induced by the U boson can have a similar effect on the occurrence of isoscalar-dominant zero-sound modes and further revisit the relationship between high-density zero-sound modes and the stiffness of the EOS. In contrast to the RMF EOS, the mass and coupling constant of the U boson are both contributive in RPA (see Eq. (13)). As mentioned above, the mass of the weakly coupling U boson is roughly of the order of 1 MeV [20]. Without loss of generality, the U boson mass is assumed to be 2 MeV or 4 MeV in the present RPA calculation, given the ratio$ g_u^2/m_u^2 $ beneath 300 GeV-2.It is interesting to examine how the U boson-induced modification to the EOS affects the behavior of zero sound. As shown in Figs. 2 and 3, the isoscalar-dominated zero-sound modes arise in the models TM1w02 and FSUGarnet at high density due to the stiffening role of the U boson in the EOS. Without the inclusion of the U boson, such isoscalar-dominated modes do not appear in these models at high density; only isovector-dominated zero-sound modes, mainly driven by the
$ \rho $ meson, emerge at lower densities, which are generally insensitive to the stiffness of the EOS. This results from the fact that the U boson provides an excess repulsion to overwhelm the attractive interaction at high density. The reproduction of the zero-sound modes by the U boson repulsion is similar to that caused by stiffening the repulsion of the$ \omega $ meson [50], providing additional evidence that the occurrence of zero-sound modes can signal the stiffness of the nuclear EOS. As the EOS becomes stiffer by increasing the coupling term of the U boson, we can see from the inset of Figs. 2 and 3 that the high-density zero-sound modes start to appear at$ g_u^2/m_u^2 = 95 $ (200) GeV-2 in TM1w02 (FSUGarnet), with the region expansion of zero-sound modes for larger coupling strength. It is worth noting that the coupling constant of the U boson for the onset of zero sounds in FSUGarnet is larger than that in TM1w02. This difference is mainly attributed to the larger coupling coefficient$ \Lambda_V $ between the$ \omega $ and$ \rho $ mesons, which increases the effective mass of the$ \rho $ meson but suppresses the magnitude of the$ \rho $ meson propagator. Consequently, this leads to a suppression of the contribution of the$ \chi_u \chi_\rho $ term to the vector part of the dielectric function, and a larger coupling constant of the U boson is needed for compensation. The onset of isoscalar-dominated zero-sound modes occurs at a slightly higher baryon density in FSUGarnet than in TM1w02, due to differences in their scalar meson self-interactions and effective meson masses, which affect the delicate balance between vector repulsion and scalar attraction. This balance plays a crucial role in determining the zeros of the dielectric function and thus the emergence of collective modes.
Figure 2. (color online) Isospin zero-sound modes (at low density) and isoscalar dominated zero-sound modes (at high density) in symmetric nuclear matter with the TM1w02 model. The U boson is included with varying coupling ratio parameters
$ g_u^2/m_u^2 $ , and its mass is fixed at 2 MeV. The inset separately shows isoscalar dominated zero-sound modes for different U boson coupling parameters.
Figure 3. (color online) The same as in Fig. 2, but for the RMF model FSUGarnet with different U boson coupling strengths.
For isovector-dominated zero-sound modes, their behavior is independent of the stiffness of the EOS, and therefore the introduction of the U boson has no impact on them.
Figure 4 shows that when the mass of the U boson is fixed at 4 MeV, the values of
$ g_u^2/m_u^2 $ , at which the isoscalar-dominated zero-sound modes begin to appear, are 50 (100) GeV-2 for TM1w02 (FSUGarnet). The reduction in the threshold value of$ g_u^2/m_u^2 $ is evident. As shown in Eq. (13), the magnitude of$ \chi_u $ is proportional to both the mass$ m_u $ and the ratio$ g_u^2/m_u^2 $ . As$ m_u $ increases, the$ g_u^2/m_u^2 $ decreases for the same$ \chi_u $ required by the emergence of isoscalar-dominated zero-sound modes.
Figure 4. (color online) Isoscalar-dominated zero-sound modes in symmetric nuclear matter with the TM1w02 and FSUGarnet models. The mass of the U boson is fixed at 4 MeV.
In contrast to the case in symmetric matter, the distinction between isoscalar and isovector dominated zero-sound modes becomes blurred in asymmetric matter. For the soft EOS models, such as TM1w02, the emergence of zero-sound modes in asymmetric nuclear matter similarly requires stiffening the EOS. As shown in Fig. 5, the inclusion of the U boson enables the appearance of zero-sound modes in asymmetric matter. Notably, a lower isospin asymmetry parameter
$ \alpha $ ($ \alpha=(\rho_n-\rho_p)/\rho_B $ ) leads to a lower onset density of the zero-sound modes, as isospin asymmetry influences the delicate balance of the dielectric function. Similar to symmetric matter, in asymmetric matter, the larger the U boson coupling, the wider the density range over which zero-sound modes appear, as shown in Fig. 6 for the TM1w02 model. Note that Fig. 6 adopts$ m_u = 4\; {\rm{MeV}} $ , while Fig. 5 uses$ m_u = 2\; {\rm{MeV}} $ , for which zero-sound modes appear only when$ g_u^2 / m_u^2 \gtrsim 150\; $ GeV−2. Unlike the case in symmetric matter, where zero sound consists of the undamped (the one with larger$ q_0 $ ) and damped branches, multiple zero-sound branches appear in asymmetric matter. Among them, the branch with the largest$ q_0 $ is undamped, while the others are damped. Therefore, it can be concluded that the stiffening of the EOS by the U boson allows zero-sound modes to emerge in both symmetric and asymmetric matter.
Figure 5. (color online) Zero sound in asymmetric nuclear matter
$ (\alpha =0.3, 0.5) $ with TM1w02. The mass of the U boson is set to 2 MeV, and the interaction ratio$ g_u^2/m_u^2 $ is set to 150$ \rm {GeV^{-2}} $ .
Figure 6. (color online) Zero sounds in asymmetric nuclear matter with TM1w02 for various
$ g_u^2/m_u^2 $ . The mass of the U boson is fixed at 4 MeV. The left panels represent the results with$ \alpha = 0.3 $ , and the right panels with$ \alpha = 0.5 $ . The orange lines represent the undamped branches of zero sound, and the green lines represent the damped branches.Furthermore, we investigate the effect of the U boson on zero-sound modes in the
$ \beta $ -equilibrated neutron star matter. Zero-sound modes in neutron star matter can possibly be associated with neutron star cooling and pulsar radiation [52]. Investigating the correlation between zero sound and the stiffness of the EOS is essential for understanding astrophysical phenomena in the multimessenger era. Figure 7 shows the zero-sound modes in neutron star matter with various$ g_u^2/m_u^2 $ . We can see that the damped zero-sound modes are similar across different values of$ g_u^2/m_u^2 $ , showing little sensitivity to the degree of EOS stiffening, whereas the undamped modes exhibit significant dependence on the coupling strength of the U boson. As$ g_u^2/m_u^2 $ increases, the range for the undamped zero-sound modes gradually extends to higher densities.
Figure 7. (color online) The same as in Fig. 6, but for neutron star matter.
It is worth noting that the repulsion of the U boson results in an increase in the predicted maximum mass of neutron stars. This is advantageous in satisfying the lower limit of the maximum mass of neutron stars around
$ 2M_\odot $ [2, 3]. Meanwhile, the additional repulsion of the U boson also tends to increase the predicted neutron star radii [18, 20], potentially exceeding observational bounds. This tension can be alleviated by adopting a density-dependent U boson coupling to merely reduce the star radius [68]. Moreover, the zero-sound modes have been proposed as potential Goldstone bosons that possibly couple to neutrino emission channels via$ Z^0 $ -boson exchange [52]. Thus, it suggests that facilitating the onset of zero sound by the U boson may affect neutron star cooling and long-term evolution through additional neutrino emission, which warrants further investigation.Lastly, it is necessary to point out that in the FSUGarnet model, the dependence of the zero sound on the U boson repulsion in asymmetric nuclear matter and neutron star matter is similar to that in the TM1w02 model, although a larger
$ g_u^2/m_u^2 $ is needed for the FSUGarnet model as in symmetric matter. To save space, the results with the FSUGarnet model are not presented here. -
In this work, we have studied the effects of a light vector U boson on zero-sound modes in nuclear matter and neutron star matter using the RRPA method. By employing two typical RMF models with a soft high-density EOS, our results show that the stiffening of the EOS by the U boson promotes the emergence of zero-sound modes at high densities.
In symmetric nuclear matter, low-density isovector zero-sound modes are not affected by the U boson, whereas the isoscalar-dominated zero-sound modes at high density are recreated in the RMF models with a soft EOS through the inclusion of the repulsion provided by the U boson. The larger coupling strength of the U boson further broadens their density range for zero sound to the high-density end.
In asymmetric nuclear matter, the role of the U boson in recreating zero-sound modes in RMF models with a soft EOS is similar to that in symmetric matter. The repulsion provided by the U boson supports the emergence of multiple zero-sound branches, either damped or undamped. Moreover, the inherent isospin asymmetry disrupts the balance of the different terms in the dielectric function, resulting in a blurred distinction between isovector- and isoscalar-dominated zero-sound modes.
In neutron star matter, multiple zero-sound modes in RMF models with a soft EOS are recovered by the U boson, similar to that in asymmetric nuclear matter. Interestingly, the presence of the U boson extends the density region for undamped zero-sound modes. If zero sounds couple to neutrino emission, the U boson that facilitates the creation of zero sounds may affect neutron star dynamics.
In comparison to zero sound creation through EOS stiffening by adjusting the
$ \omega $ self-interaction strength, the inclusion of the U boson achieves similar consequences. This confirms the unambiguous role of stiffening the high-density EOS in resulting in the appearance of zero sounds. As the deviation from the inverse square law of gravity due to the inclusion of the U boson can be alternatively expressed by its modification to the EOS [18], our study implies that the zero sound facilitated by the U boson in dense matter may be correlated with modified gravity, which would make the study of zero sound in dense matter particularly informative. -
In this work, we have studied the effects of a light vector U boson on zero-sound modes in nuclear matter and neutron star matter using the RRPA method. By employing two typical RMF models with a soft high-density EOS, our results show that the stiffening of the EOS by the U boson promotes the emergence of zero-sound modes at high densities.
In symmetric nuclear matter, low-density isovector zero-sound modes are not affected by the U boson, whereas the isoscalar-dominated zero-sound modes at high density are recreated in the RMF models with a soft EOS through the inclusion of the repulsion provided by the U boson. The larger coupling strength of the U boson further broadens their density range for zero sound to the high-density end.
In asymmetric nuclear matter, the role of the U boson in recreating zero-sound modes in RMF models with a soft EOS is similar to that in symmetric matter. The repulsion provided by the U boson supports the emergence of multiple zero-sound branches, either damped or undamped. Moreover, the inherent isospin asymmetry disrupts the balance of the different terms in the dielectric function, resulting in a blurred distinction between isovector- and isoscalar-dominated zero-sound modes.
In neutron star matter, multiple zero-sound modes in RMF models with a soft EOS are recovered by the U boson, similar to that in asymmetric nuclear matter. Interestingly, the presence of the U boson extends the density region for undamped zero-sound modes. If zero sounds couple to neutrino emission, the U boson that facilitates the creation of zero sounds may affect neutron star dynamics.
In comparison to zero sound creation through EOS stiffening by adjusting the
$ \omega $ self-interaction strength, the inclusion of the U boson achieves similar consequences. This confirms the unambiguous role of stiffening the high-density EOS in resulting in the appearance of zero sounds. As the deviation from the inverse square law of gravity due to the inclusion of the U boson can be alternatively expressed by its modification to the EOS [18], our study implies that the zero sound facilitated by the U boson in dense matter may be correlated with modified gravity, which would make the study of zero sound in dense matter particularly informative. -
In this work, we have studied the effects of a light vector U boson on zero-sound modes in nuclear matter and neutron star matter using the RRPA method. By employing two typical RMF models with a soft high-density EOS, our results show that the stiffening of the EOS by the U boson promotes the emergence of zero-sound modes at high densities.
In symmetric nuclear matter, low-density isovector zero-sound modes are not affected by the U boson, whereas the isoscalar-dominated zero-sound modes at high density are recreated in the RMF models with a soft EOS through the inclusion of the repulsion provided by the U boson. The larger coupling strength of the U boson further broadens their density range for zero sound to the high-density end.
In asymmetric nuclear matter, the role of the U boson in recreating zero-sound modes in RMF models with a soft EOS is similar to that in symmetric matter. The repulsion provided by the U boson supports the emergence of multiple zero-sound branches, either damped or undamped. Moreover, the inherent isospin asymmetry disrupts the balance of the different terms in the dielectric function, resulting in a blurred distinction between isovector- and isoscalar-dominated zero-sound modes.
In neutron star matter, multiple zero-sound modes in RMF models with a soft EOS are recovered by the U boson, similar to that in asymmetric nuclear matter. Interestingly, the presence of the U boson extends the density region for undamped zero-sound modes. If zero sounds couple to neutrino emission, the U boson that facilitates the creation of zero sounds may affect neutron star dynamics.
In comparison to zero sound creation through EOS stiffening by adjusting the
$ \omega $ self-interaction strength, the inclusion of the U boson achieves similar consequences. This confirms the unambiguous role of stiffening the high-density EOS in resulting in the appearance of zero sounds. As the deviation from the inverse square law of gravity due to the inclusion of the U boson can be alternatively expressed by its modification to the EOS [18], our study implies that the zero sound facilitated by the U boson in dense matter may be correlated with modified gravity, which would make the study of zero sound in dense matter particularly informative. -
We acknowledge the Big Data Computing Center of Southeast University for providing facility support for the partial numerical calculations in this study.
-
We acknowledge the Big Data Computing Center of Southeast University for providing facility support for the partial numerical calculations in this study.
-
We acknowledge the Big Data Computing Center of Southeast University for providing facility support for the partial numerical calculations in this study.
Correlation between Zero-Sound modes and nuclear equation of state stiffness detected by light vector boson
- Received Date: 2025-05-12
- Available Online: 2026-01-15
Abstract: We investigate zero-sound modes in nuclear matter and neutron star matter using the relativistic random phase approximation (RRPA), focusing on the role of a light vector U boson in stiffening the nuclear equation of state (EOS). The occurrence of zero sound is closely linked to the stiffness of the nuclear EOS. The additional vector repulsive potential induced by the U boson results in the occurrence of zero sound at high densities in models with a soft high-density EOS, and the density range for zero sound extends to higher densities with larger coupling strength of the U boson. This confirms the unambiguous role of stiffening the high-density EOS in resulting in the appearance of zero sound.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
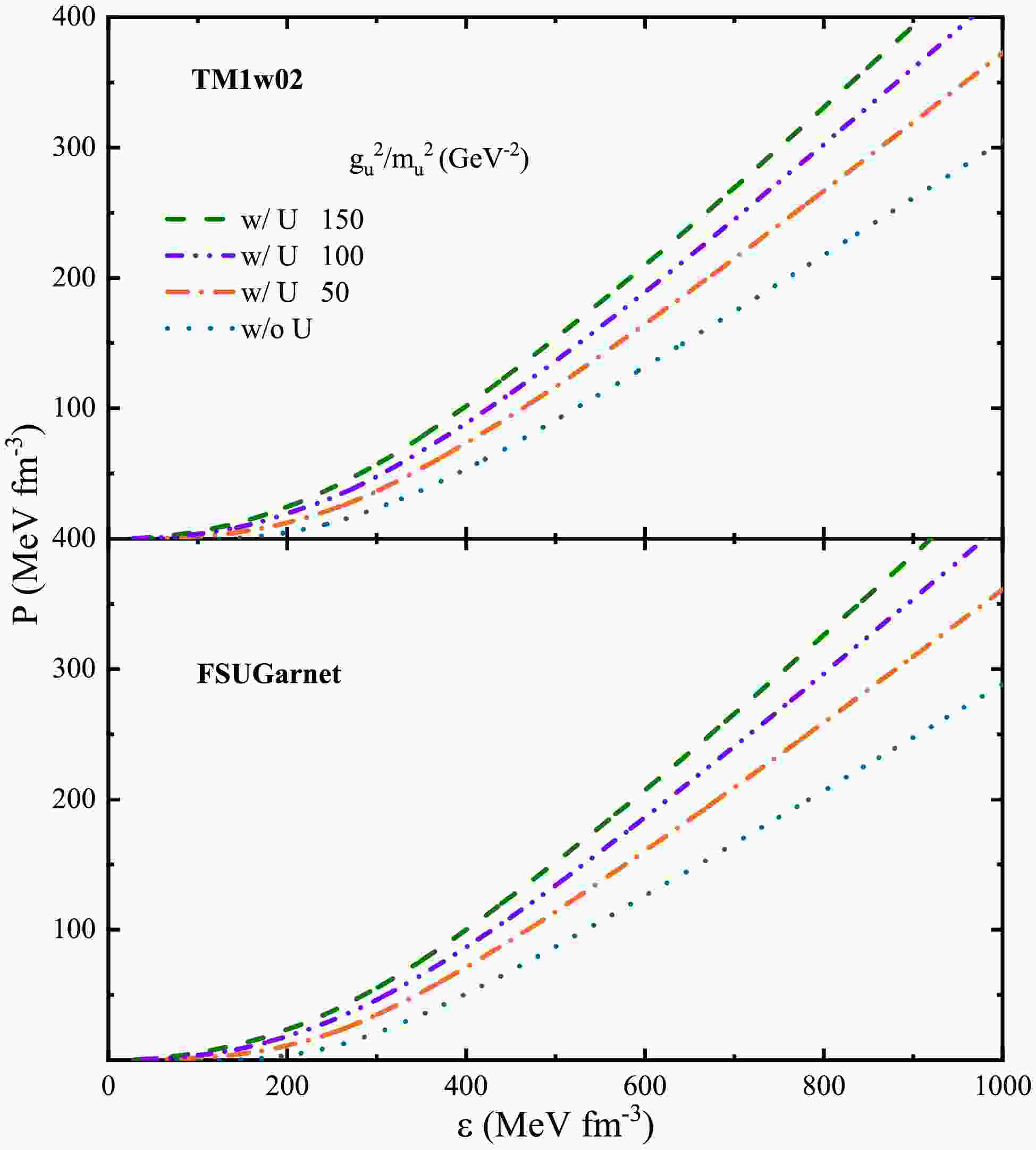













 DownLoad:
DownLoad: