Thermodynamic phase transition and Joule-Thomson expansion of a quantum corrected black hole in AdS spacetime

Owing to the inconsistency between general relativity (GR) and quantum theory, as well as issues such as singularities [1−5], quantum gravity has long been a subject of extensive interest. One approach to achieve spacetime quantization is non-commutative geometry [6−13], which is characterized by the commutation relation among spacetime coordinate operators $ [\hat{x^{\mu}},\hat{x^{\nu}}] = {\rm i}\theta^{\mu\nu} $, where $ \theta^{\mu\nu} $ is an anti-symmetric constant matrix. Smailagic showed that noncommutative effects eliminated the point-like mass distribution [2, 3], a phenomenon that may circumvent the black hole (BH) singularity problem. Inspired by this, Nicolini and Nozari, respectively, proposed that the point mass distribution model (represented by the Dirac delta function) can be replaced by either a Gaussian or Lorentzian distribution [14, 15]. In addition, the effective field theory (EFT) and loop quantum gravity (LQG) are candidate theories for quantum gravity. In Ref. [16] the authors analyzed low-energy one-loop quantum corrections to the Schwarzschild geometry. In their approach, GR is treated as a quantum field theory (QFT) within the framework of the EFT, indicating that, at low energies, the degrees of freedom organize themselves as quantum fields governed by a local Lagrangian [17]. Similarly, LQG has received significant attention [18−25]. In LQG, the minimal fundamental units of spacetime are suggested as a series of discrete, elementary loops. One interesting result is that, by studying the gravitational collapse of spherically symmetric dust matter in LQG, researchers have constructed a quantum corrected Schwarzschild BH and found that it can be interpreted as the formation of a white hole [26−28].

The BH discussed in this paper was proposed in a recent study that aimed to address the longstanding issue of general covariance in quantum gravity models. It is suggested that the classical GR could be modified by Hamiltonian constraint formulation [29−31]. In this approach, an issue arose: how to keep the general diffeomorphism covariance of spacetime theory [32]. Recently, this problem was effectively addressed in the framework of spherically symmetric vacuum gravity [33]. In the study of Zhang et al. [33], general covariance is rigorously formulated into a set of constraint equations. Based on this formulation, the authors derived the equations of motion for the effective Hamiltonian constraint, which depends on a quantum parameter ξ. Furthermore, they provided two candidate forms for the effective Hamiltonian constraint, each corresponding to a quantum corrected Schwarzschild spacetime. In this study, we investigate the thermodynamics of one such static, spherically symmetric quantum corrected BH.

The thermodynamics of anti-de Sitter (AdS) BHs in the extended phase space is a novel and highly intriguing subject. Within this framework, the cosmological constant term in the Einstein equation is interpreted as the energy-momentum tensor of a special "vacuum static ideal fluid," and it is assumed that the BH achieves phase equilibrium with the vacuum fluid, thereby acquiring pressure [34]. To ensure that the BH exhibits a positive pressure, the cosmological constant is required to be negative, indicating that the BH resides in an AdS spacetime. Consequently, the AdS BH is effectively regarded as a unique thermodynamic system, which has been extensively discussed in the academic community. In 1983, Hawking first investigated the thermodynamics of Schwarzschild-AdS BHs, revealing the existence of phase transitions within these systems [35]. This pioneering work is widely regarded as the inception of the field of AdS BH thermodynamics. Numerous studies have explored the thermodynamics of AdS BHs [36−49]. The thermodynamic properties of BHs are influenced by several additional parameters, such as electric charge [50−53], nonlinear magnetic charge [54−56], dark matter [57, 58], nonlinear electrodynamics models [59−65], noncommutative geometry [66−69], lower or higher-dimensional gravity theories [70−73], and various other modified gravity models [74]. Moreover, as a candidate theory for reconciling gravity and quantum physics, the AdS/CFT correspondence offers a novel perspective on the thermodynamics of BHs in AdS spacetime [75, 76]. Several BHs exhibit thermodynamic properties analogous to those of a van der Waals system, indicating a profound connection among gravitational theory, quantum physics, and thermodynamics, and thereby revealing a richer array of physical properties for these enigmatic objects.

The remainder of this paper is organized as follows. In Sect. II, we introduce the quantum corrected BH, which is the focus of this study. Under the assumption that this quantum gravity decouples from the cosmological constant, we derive the BH metric in AdS spacetime and compute its thermodynamic functions as well as the corrected first law. Sect. III provides a detailed investigation into the thermodynamic phase transitions and critical phenomena of the BH. The isobaric heat capacity and Gibbs free energy of the BH are described in Sect. IV and Sect. V, respectively. In Sect. VI, we present a detailed investigation of the constant mass expansion of the BH and illustrate its inversion curve. Finally, the summary and outlook of this study are presented in Sect. VII. Our study will demonstrate the influence of the quantum correction parameter on the thermodynamics of the conventional Schwarzschild-AdS BH, thereby enriching the results of research on quantum BH thermodynamics and providing a valuable reference for subsequent investigations.

For computational convenience, natural units $ G = \hbar = c = k_{B} = 1 $ are adopted throughout this paper.

The BH considered in this study is a quantum corrected BH, described by a static spherically symmetric spacetime [33]

with $ f\left(r\right) $ being

where ξ is a quantum parameter, which is considered to be on the order of the Planck length $ \ell_{p} $. This BH corresponds to an equivalent energy distribution given by

Assuming that this quantum gravity decouples from the cosmological constant Λ, the Einstein equation with Λ is given by

where $ T_{\mu\left(\Lambda\right)}^{\nu} = -\frac{\Lambda}{8\pi}\delta_{\mu}^{\nu} $ represents an equivalent energy-momentum tensor corresponding to the contribution of the cosmological constant term. Thus, the metric of this quantum corrected BH in AdS spacetime is obtained as

The BH solution satisfies $ f\left(r_{+}\right) = 0 $, where $ r_{+} $ is the event horizon radius. The mass of BH could be solved

where

Here, we discard the positive-sign branch because this branch does not reduce to the Schwarzschild-AdS case as $ \xi\to0 $, but instead diverges to infinity. It is required that $ \alpha\geqslant0 $, which yields

On the other hand, the existence of the BH requires $ M > 0, r_+ > 0,\ \Lambda < 0 $ (AdS spacetime), which reduces this parameter constraint to

or

where $ \beta = 9M+\sqrt{81M^{2}+3\xi^{2}} $. The condition of the existence of the BH is shown in Fig. 1.

Figure 1.  (color online) Condition of the existence of the BH in $ \left(r_{+},M\right)$ coordinates. The orange region signifies the parameter range in which BH solutions exist, whereas the remaining areas indicate the absence of BH solutions.

The temperature of the BH is defined by its surface gravity as follows:

In the extended phase space, the energy-momentum tensor $ T_{\mu\left(\Lambda\right)}^{\nu} $ contributed by the cosmological constant is regarded as an equivalent “vacuum static ideal fluid.” It is assumed that the BH reaches a phase equilibrium with this fluid, acquiring its pressure. The pressure of the BH is

Eq. (8) provides the maximum pressure of the BH as follows:

According to the studies in references, when the energy-momentum tensor outside the BH event horizon explicitly includes the mass M of the BH, the first law of BH thermodynamics takes the corrected form [55, 77−79]

where the correction function W is

The entropy of the BH is the Bekenstein-Hawking function [80, 81] given by

The thermodynamic volume of the BH is

The equation of state of the BH is solved from Eq. (11)

The $ P-r_{+} $ diagram of the BH consists of two branches, corresponding respectively to the positive-sign branch $ P_{+} $ (Fig. 2) and negative-sign branch $ P_{-} $ in the above function (Fig. 3).

Figure 2.  (color online) $ P_{+}-r_{+}$ diagram of the BH. The black point "critic" is the critical point. We set $ \xi=1$.

Figure 3.  (color online) $ P_{-}-r_{+}$ diagram of the BH. The black point ''critic'' is the critical point. We set $ \xi=1$.

In particular, there exists a critical temperature

When $ T>T_{c} $, the small BH phase ($ r_{+}<r_{1}\left(T\right) $) and large BH phase ($ r_{+}>r_{2}\left(T\right) $) become distinctly separated, and no phase transition occurs. $ r_{1}\left(T\right) $ and $ r_{2}\left(T\right) $ are the smaller and larger positive real roots of the equation with parameter T

respectively.

When $ T = T_{c} $, the small BH-large BH phase transition occurs at the critical radius

At the critical point, BH reaches its critical pressure

Note that, in this case, the critical point cannot be determined using the conventional critical point condition $ \partial P/\partial r_{+} = \partial^{2} P/\partial r_{+}^{2} = 0 $. As evident from Fig. 2 and Fig. 3, the critical behavior of this type of BH is entirely different from that of a Van der Waals fluid. At the critical point, $ {\rm d}P/{\rm d}r_{+}\big|_{r_{+c}^{-}}\neq {\rm d}P/{\rm d}r_{+}\big|_{r_{+c}^{+}} $, indicating that $ \mathrm{d}P/\mathrm{d}r_+ $ does not exist. Nevertheless, only when $ T<T_{c} $, there exists a solution of $ \mathrm{d}P/\mathrm{d}r_+=0 $, which corresponds to the phase transition.

This critical point yields a dimensionless constant

So this quantum corrected BH shows a larger critical ratio than Van der Waals system ($ \dfrac{3}{8} $) [52]. Furthermore, note that the equation of state $ P_{-} $ shown in Fig. 3 reduces to the Schwarzschild-AdS case in the limit $ \xi\to0 $. In Fig. 3, during an isothermal expansion process, the pressure of the small BH increases rather than decreases, signifying that it corresponds to an unstable phase. In contrast, the pressure of the large BH decreases with increasing radius. However, the situation in the BH phase diagram presented in Fig. 2 is opposite, where the small BH corresponds to the stable phase, whereas the large BH corresponds to the unstable phase. This characteristic arises owing to the quantum parameter ξ, and this feature does not occur in the ordinary Schwarzschild-AdS BH. The $ P_{-}-r_{+} $ diagram of the BH for different quantum parameters ξ is shown in Fig. 4.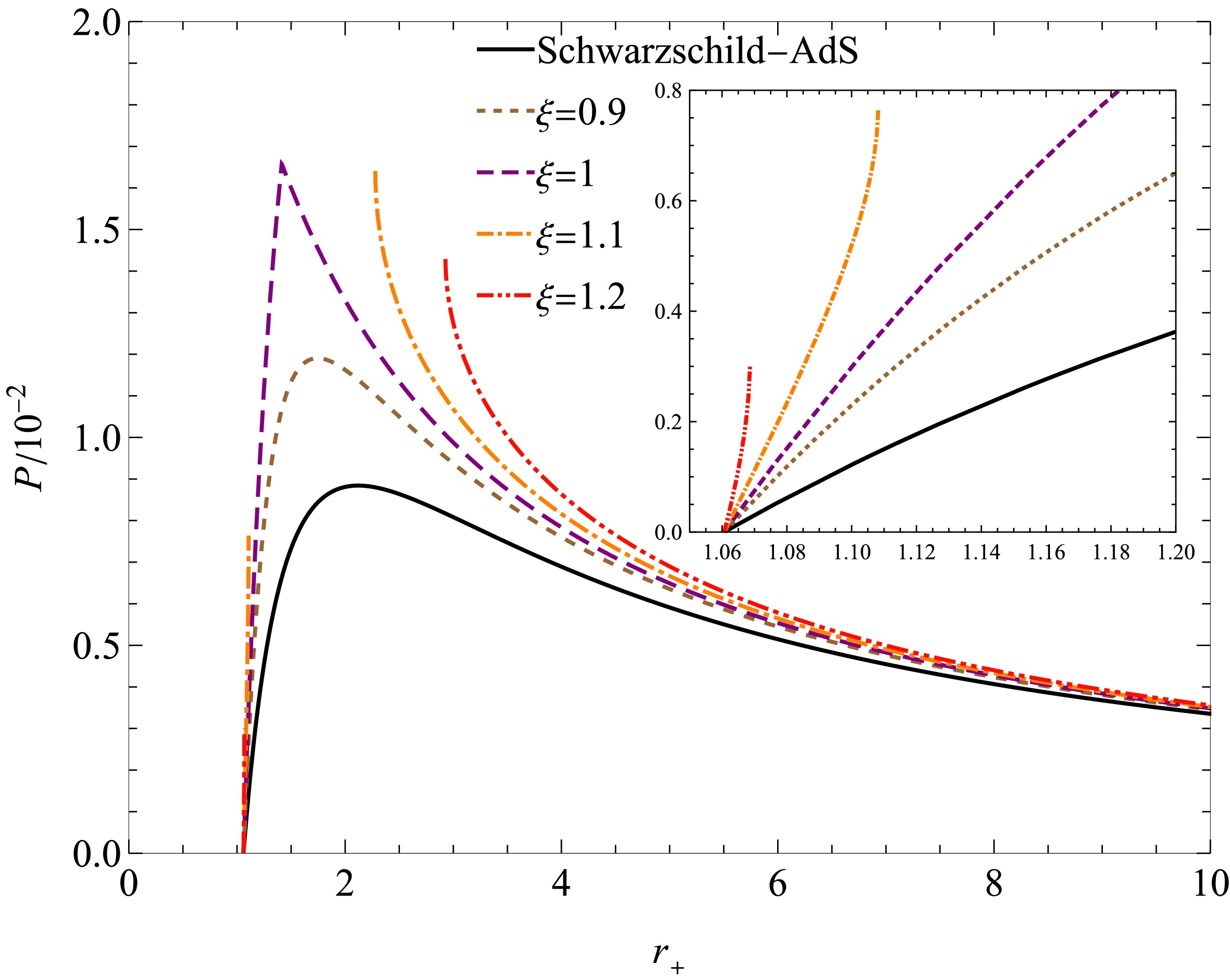

Figure 4.  (color online) $ P_{-}-r_{+}$ diagram of the BH for different quantum parameters ξ. The black line corresponds to the Schwarzschild-AdS BH ($ \xi=0$). We set $ T=T_{c} \; \left(\xi=1\right)$.

Specifically, when $ P_{-} = 0 $, the horizon radius of the BH is independent of the size of the quantum parameter ξ

which is also the result of the Schwarzschild-AdS BH.

The phase transition occurs at

The variation in the BH phase transition pressure $ P_{pt} $ with respect to the phase transition temperature $ T_{pt} $ is illustrated in Fig. 5. Thus, the critical temperature represents the maximum phase transition temperature. Moreover, if we consider only the BH pressure as shown in Fig. 3, then the critical pressure will also correspond to the maximum phase transition pressure. This characteristic is analogous to that observed in the Van der Waals system.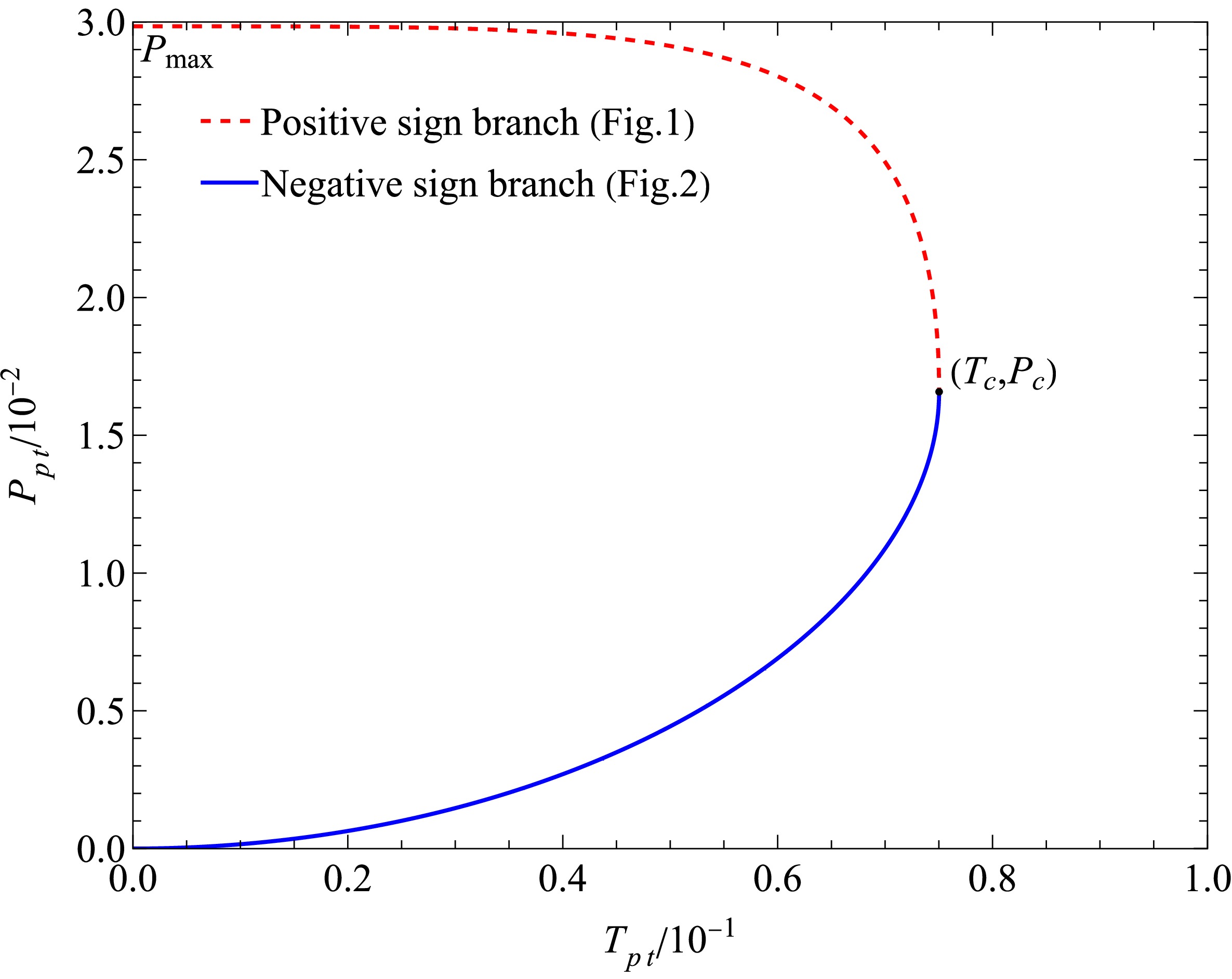

Figure 5.  (color online) Phase transition points in $T-P$ coordinates. The point $\left(T_{c},P_{c}\right)$ is the critical point. We set $\xi=1$.

The $ T-r_{+} $ diagram of the BH is shown in Fig. 6 and Fig. 7. It is evident that the BH exhibits a small BH-large BH phase transition similar to that of the Schwarzschild-AdS BH. The BH pressure initially increases with the horizon radius (corresponding to the small BH phase) and subsequently decreases (corresponding to the large BH phase). This phase transition, in contrast to that observed in Van der Waals fluids, occurs instantaneously at the maximum pressure point.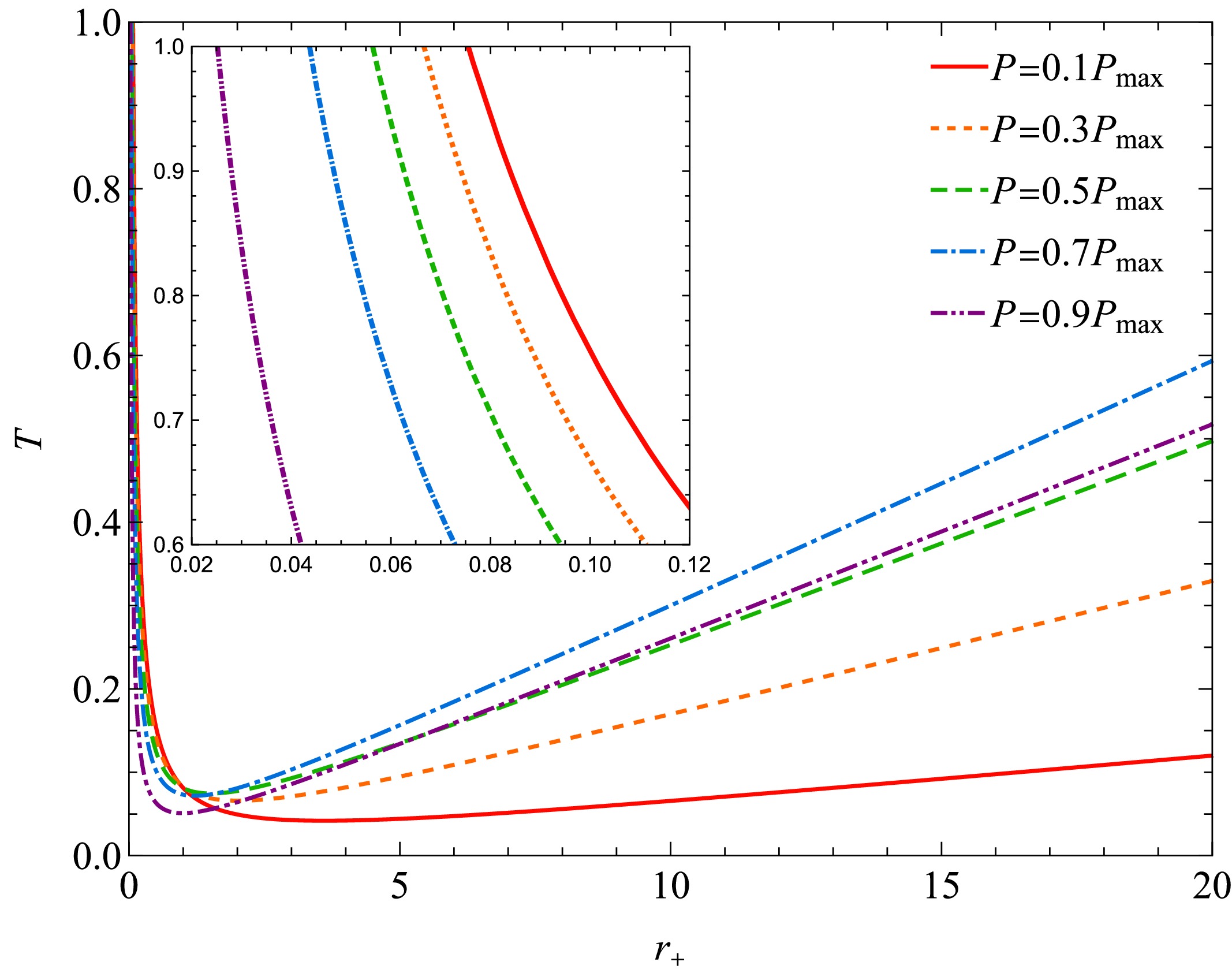

Figure 6.  (color online) $T-r_{+}$ curve of the BH corresponding to the isobaric process. We set $\xi=1$.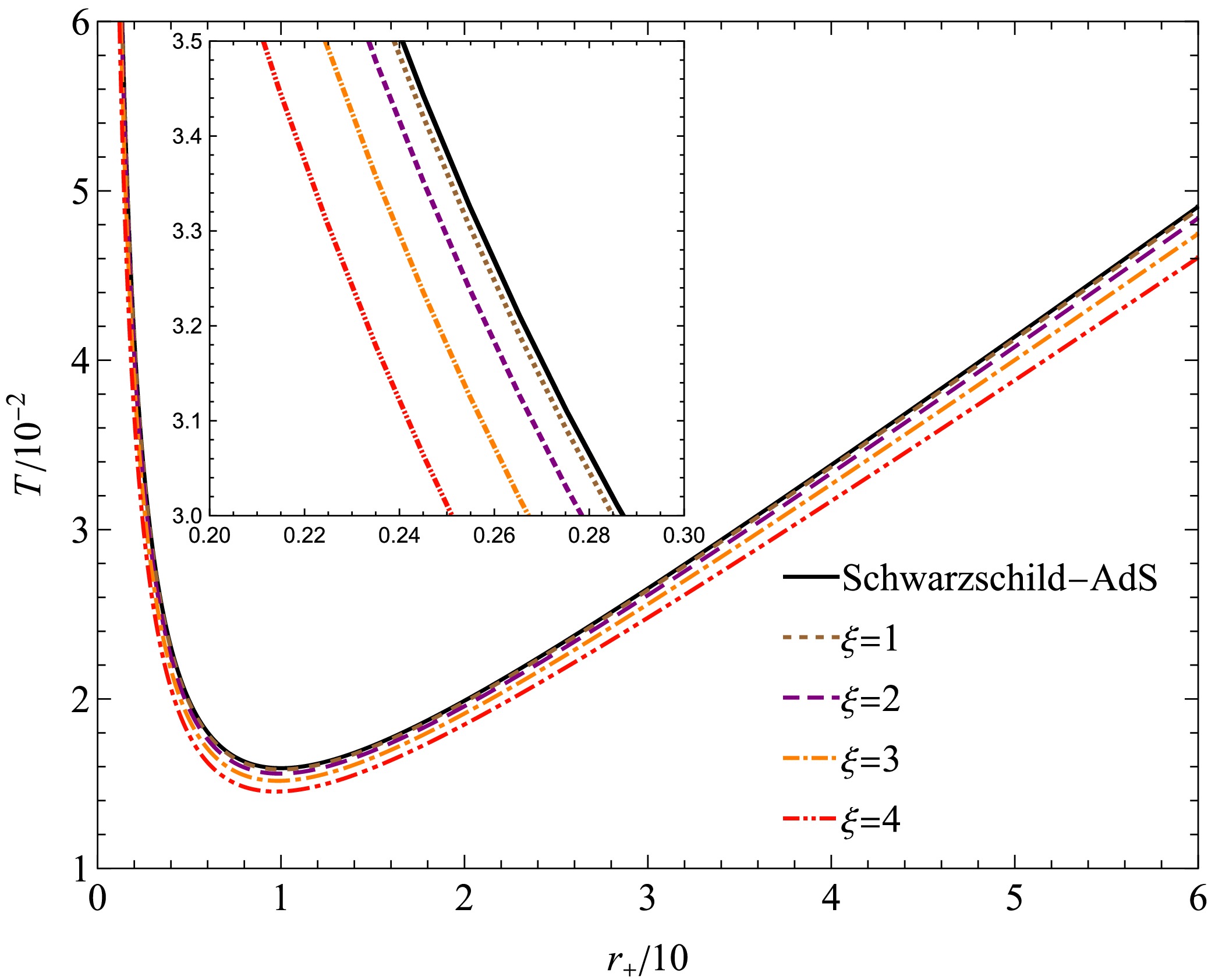

Figure 7.  (color online) $T-r_{+}$ diagram of the BH for different quantum parameters $\xi$. The black line ($\xi=0$) represents the Schwarzschild-AdS BH. We set $\Lambda=-0.01$.

In particular, phase separation does not occur in the $ T-r_{+} $ diagram of the BH. It can be verified that $ T>0 $ always holds. When $ P=P_{\mathrm{max}} $, the BH is an extremal BH, consistently maintaining a zero temperature $ T\equiv0 $. For any given pressure, the BH temperature always undergoes a small BH-large BH phase transition. The temperature of the small BH decreases as the horizon radius increases, whereas the large BH exhibits the opposite behavior.

The phase transition temperature $ T_{pt} $ satisfies

Using this condition, one could prove that, at $ P = P_{c} $, $ T_{pt} $ has its maximum

From the perspective of the $ T-r_{+} $ diagram, this also demonstrates that BHs with temperatures exceeding the critical temperature cannot undergo phase transitions.

According to

the isochoric heat capacity of the BH is zero

The isobaric heat capacity of the BH is

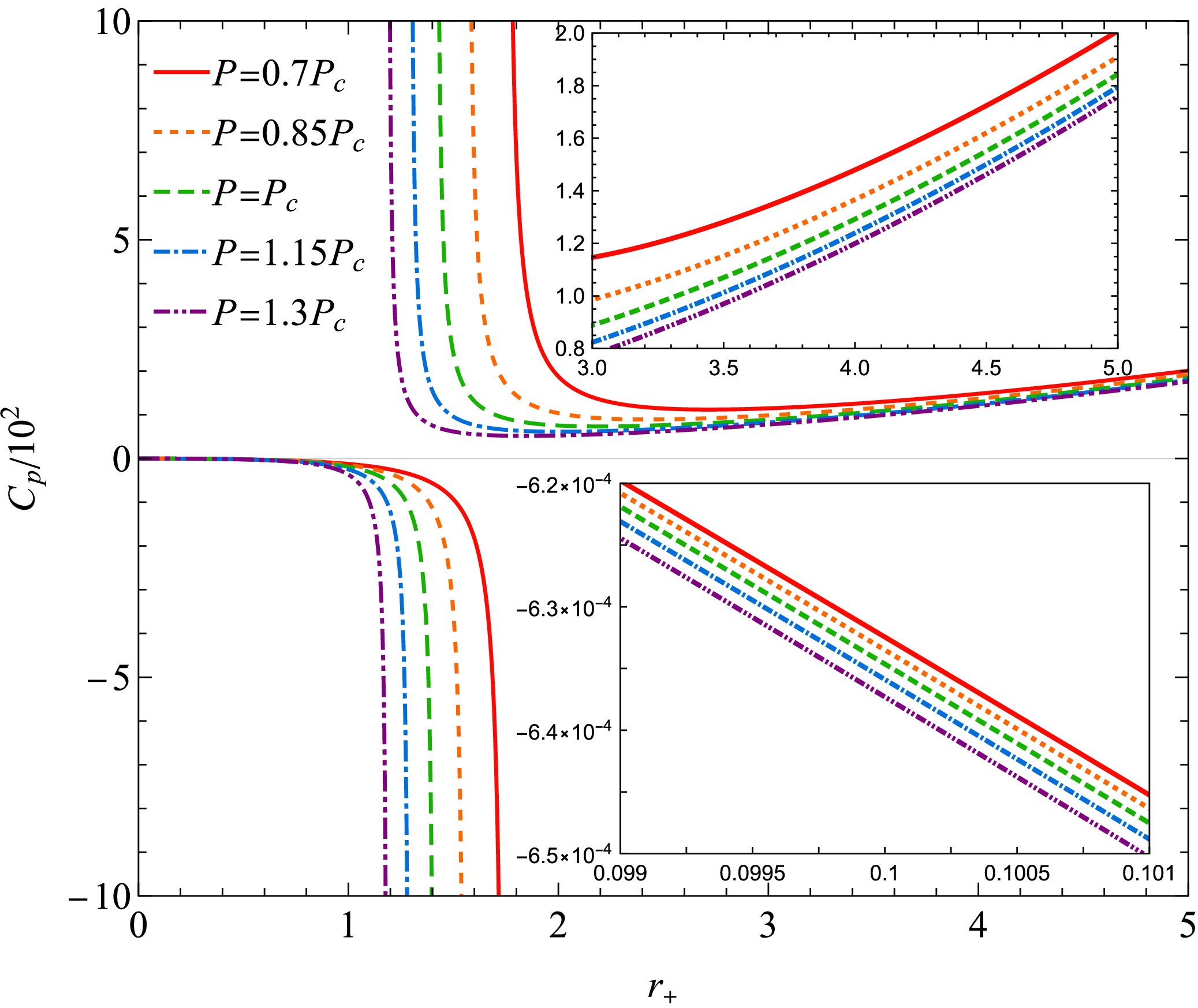
The heat capacity as a function of the horizon radius is presented in Fig. 8 and Fig. 9. In comparison with Fig. 6, it is evident that the small BH, satisfying $ \partial T/\partial r_{+}<0 $, exhibits a negative heat capacity, corresponding to an unstable phase, whereas the large BH, described by $ \partial T/\partial r_{+}>0 $, displays a positive heat capacity, indicating a stable phase. At the phase transition point, the heat capacity diverges to infinity. Moreover, when the horizon radius is sufficiently small, the heat capacity exhibits asymptotic behavior as follows: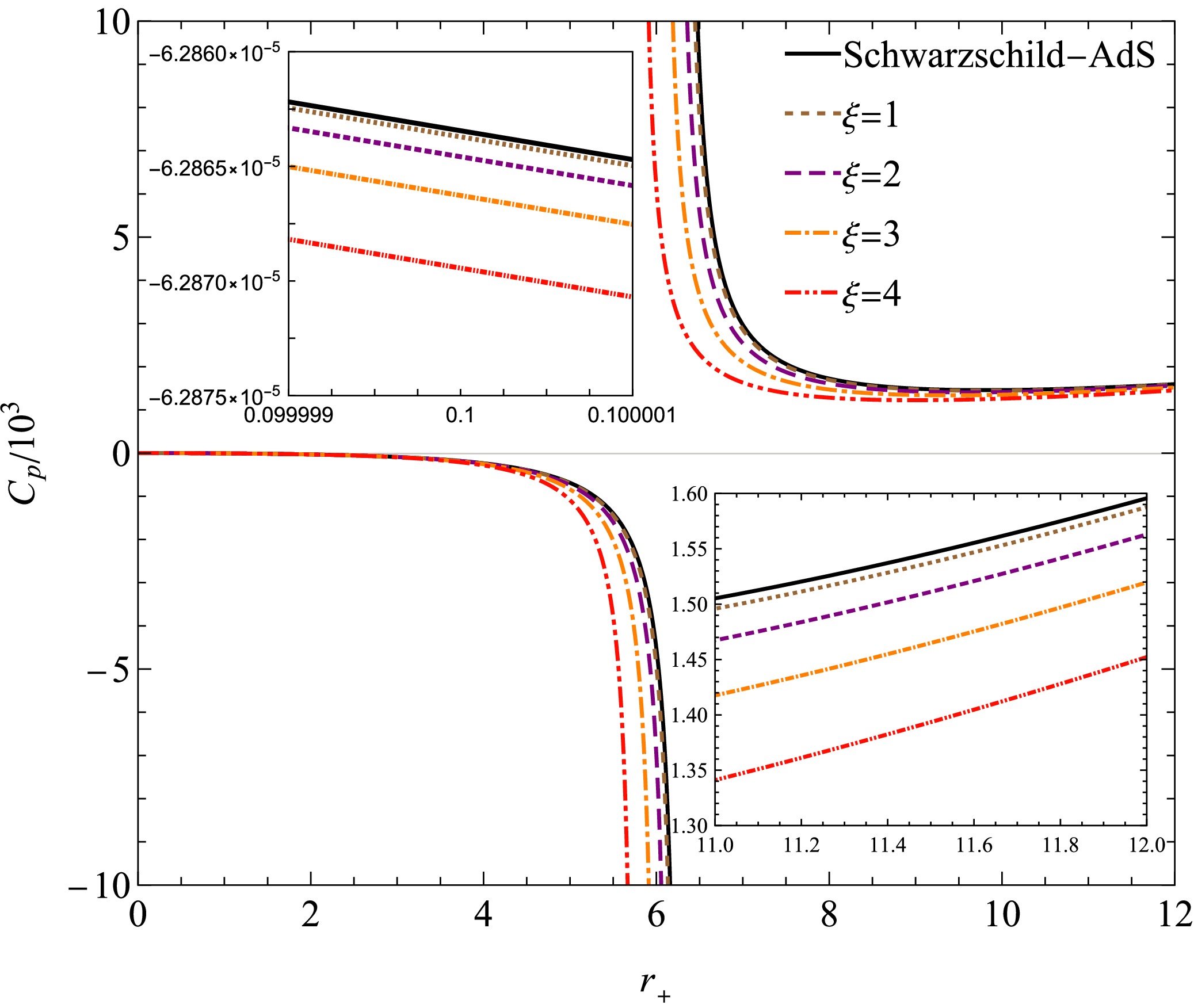

Figure 8.  (color online) Isobaric heat capacity for different quantum parameters ξ. The black line represents the Schwarzschild-AdS BH. We set $P=0.001$.

Figure 9.  (color online) Isobaric heat capacity for different pressures. We set $\xi=1$.

In the limit, as $ r_{+}\to\infty $, the isobaric heat capacity of the BH exhibits a quadratic divergence

The Gibbs free energy of the BH is given by

The differential form of G can be calculated as

which yields

The phase transition satisfies $ C_{p} = \infty $; hence, in the $ G-T $ diagram of the BH, the points at which $ \partial G/\partial T = \infty $ are exactly the phase transition points.

Specifically, when $ P<P_{c} $, there exists a point at which

shown as orange line ($ P = 0.5P_{c} $) and lightblue line ($ P = 0.75P_{c} $) in Fig. 10. When $ P<P_{c} $, the $ G-T $ curve of the BH resembles a swallowtail diagram, indicating the phase transition. However, it cannot be concluded that phase transitions occur only when $ P<P_{c} $. As previously analyzed, phase transitions can still occur even for $ P\geq P_{c} $, where the phase transition point is characterized by the condition $ \partial G/\partial T = \infty $, or equivalently, $ C_{p} = \infty $. Moreover, owing to the corrected first law, the swallowtail structure of the BH deviates from that of the Schwarzschild-AdS BH or Van der Waals fluid. Only when P is sufficiently small, or equivalently, when ξ is sufficiently small, does the $ G-T $ curve of the BH closely resemble the swallowtail behavior observed in the Schwarzschild-AdS case.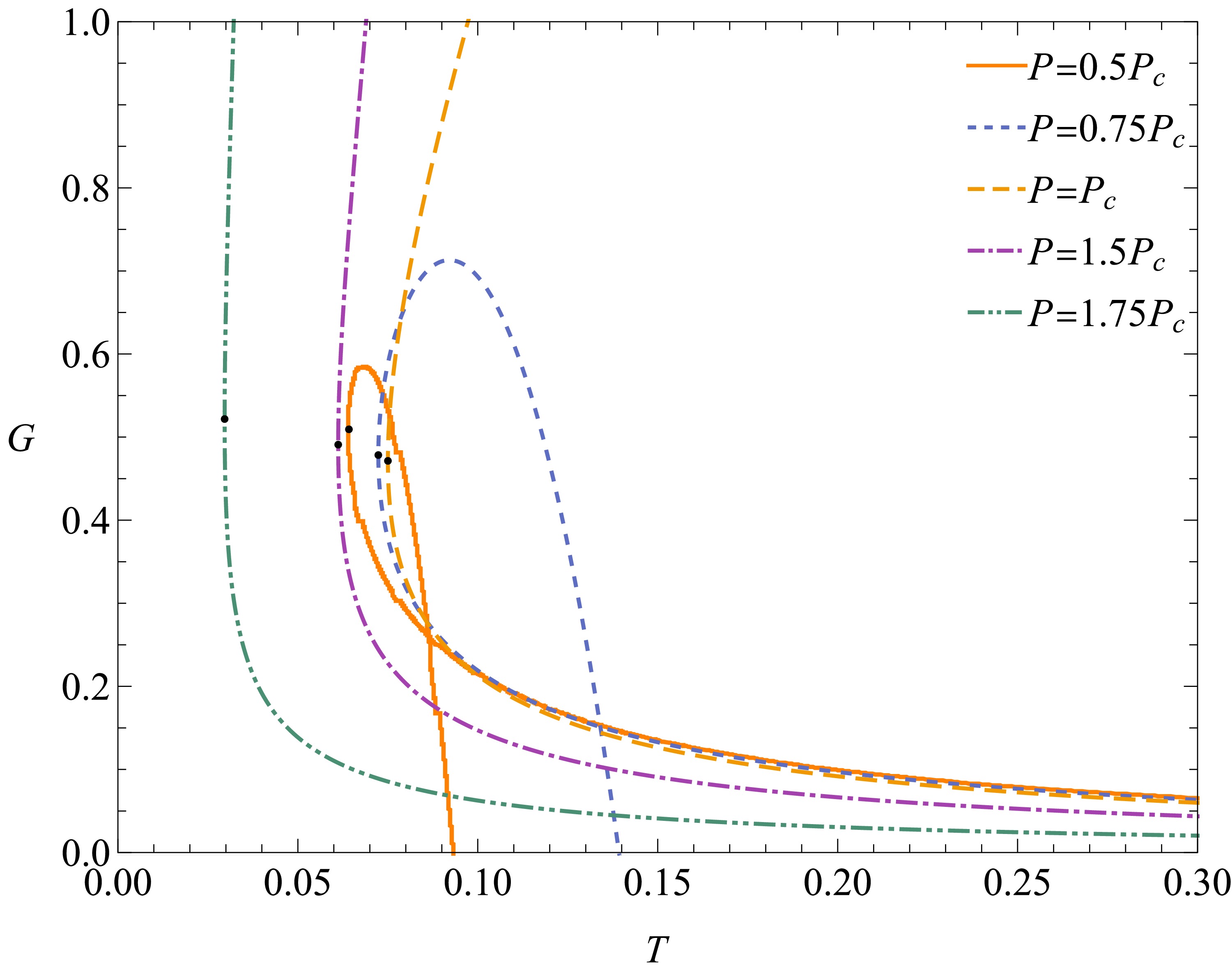

Figure 10.  (color online) Gibbs free energy of the BH for different pressures. The black points in the figure are phase transition points. We set $ \xi=1$.

Figure 11 shows the Gibbs free energy of the BH at a fixed pressure for various values of the quantum parameter ξ. When $ \xi = 0 $, the $ G-T $ curve of the BH reverts to that of the Schwarzschild-AdS case. As ξ increases, the $ G-T $ curve near the phase transition point becomes progressively smoother. Moreover, when ξ is further increased such that the pressure exceeds the critical pressure, the $ G-T $ curve of the BH deviates significantly from the Schwarzschild-AdS scenario.

Figure 11.  Gibbs free energy of the BH for different quantum parameters ξ. We set $ P=5/216\pi$ (the critical pressure for $ \xi=1.5$).

The Joule-Thomson process of BHs refers to their constant mass expansion process $ \mathrm{d}M=0 $. In several AdS BHs, the Joule-Thomson process exhibits striking similarities: during the constant mass expansion, the pressure continuously decreases while the temperature changes accordingly. The inversion curve partitions the $ T-P $ plane into distinct cooling and heating regions, and as the BH mass increases, the BH traverses increasingly broader ranges of pressure and temperature [53, 67, 69, 72, 73, 79, 82−89].

For the convenience of studying the constant mass expansion of the BH, we first rewrite the BH temperature and pressure in terms of the horizon radius and BH mass as parameters

The Joule-Thomson coefficient is given by

By setting $ \mu_{JT} = 0 $, one can obtain the inversion mass $ M_{i} $

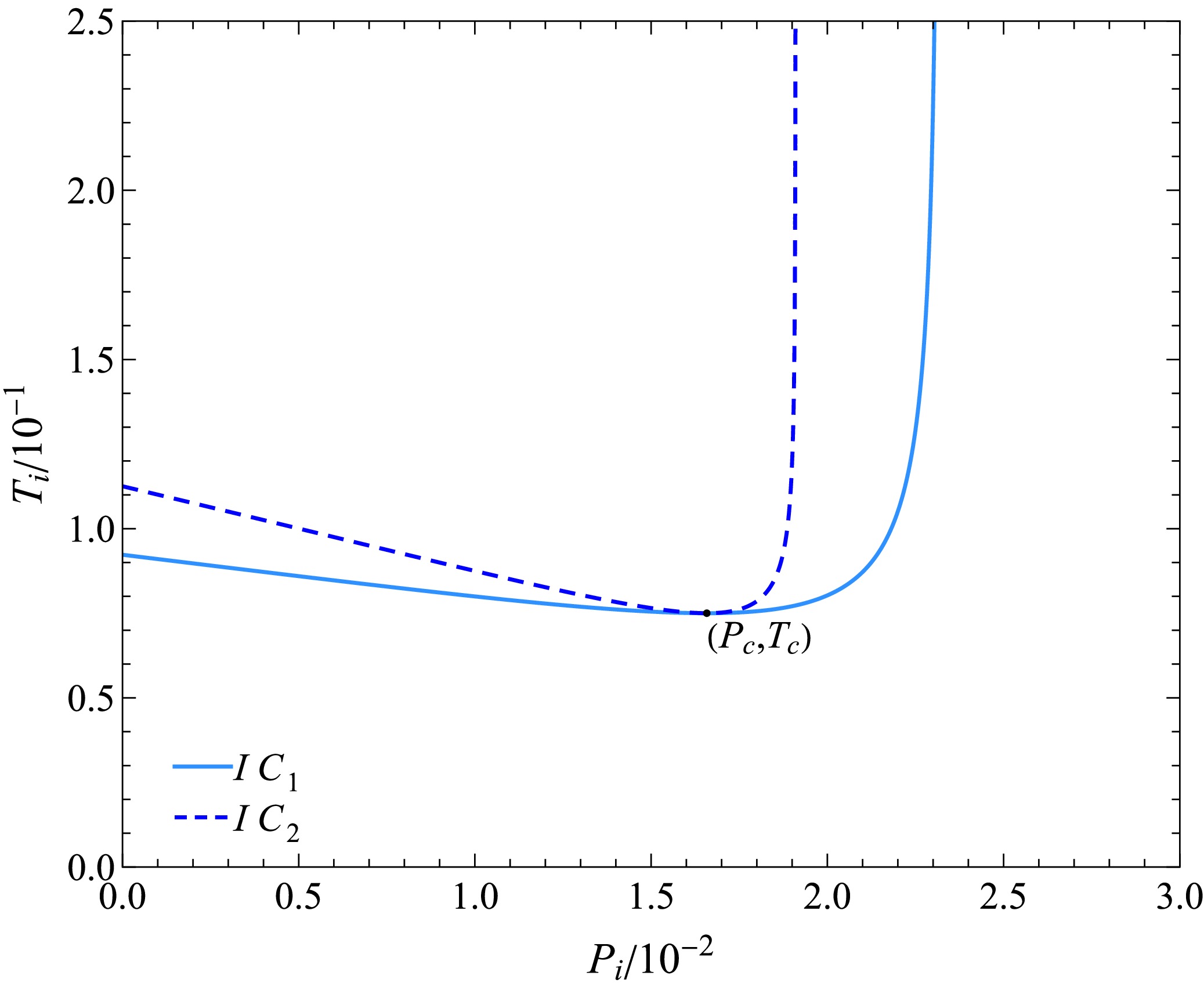
where $ r_{i} $ is the inversion radius. Thus, the inversion curve of the BH is divided into two branches (Fig. 12): for a given inversion radius, $ M_{i}^{1} $ induces the first branch ($ IC_{1} $), whereas $ M_{i}^{2} $ induces the second branch ($ IC_{2} $). $ IC_{1} $ and $ IC_{2} $ are exactly tangent at their minimum points $ T_i^{\mathrm{min}} $, and aside from the tangency point, $ T_{i}^{1}<T_{i}^{2} $ is identically satisfied. The phenomenon of multiple branches emerging in the inversion curve has also been observed in other types of BHs. For AdS BHs in quasitopological electromagnetism, the inversion curve may exhibit up to three branches [90]. Moreover, the inversion pressure and inversion temperature at this tangency point exactly coincide with the critical pressure and critical temperature of the BH. That is, $ T_i^{\rm min}=T_c $.

Figure 12.  (color online) Inversion curves of the BH. We set $ \xi=1$.

In the limit, as $ r_{+}\to\infty $, $ IC_{1} $ and $ IC_{2} $ both exhibit a maximum inversion pressure

This results in two constants that are independent of the quantum parameter ξ

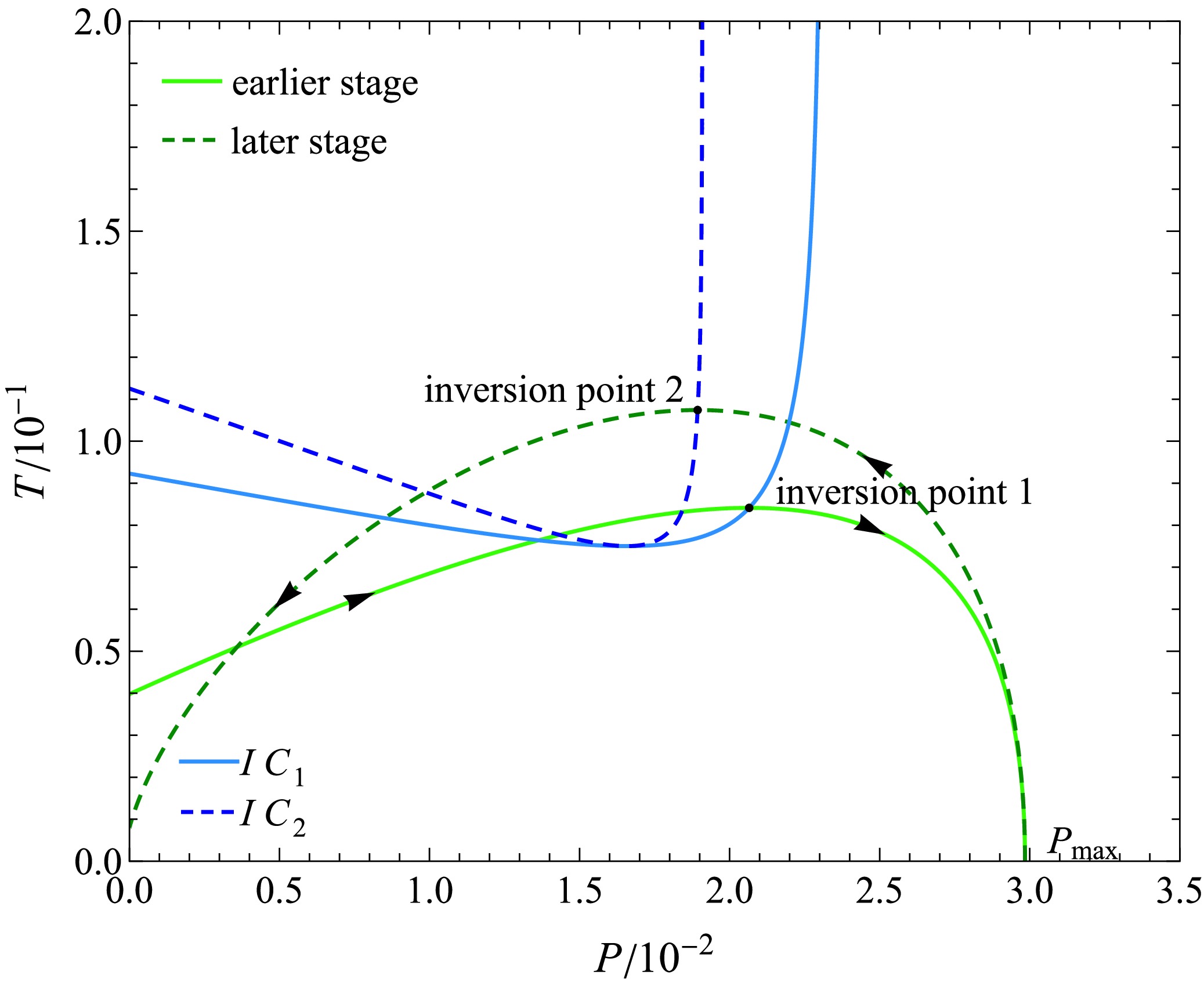
Figure 13 depicts the constant-mass expansion process of the BH. In the figure, the arrows indicate the direction of increasing horizon radius $ r_{+} $, representing the expansion process of the BH. The constant-mass expansion of the BH can be divided into two distinct stages. In the earlier stage, the pressure increases until reaching the maximum pressure $ P_{\rm max} $ of the BH; in the later stage, the pressure decreases. The black dots in the figure denote the inversion points experienced by the BH in each stage.

Figure 13.  (color online) Joule-Thomson expansion of the BH. We set $ \xi=1$, $ M=5$.

Note that, as the BH pressure increases rather than decreases during the pre-expansion stage, using the sign of $ \mu_{JT} $ to differentiate between the cooling and heating processes is no longer appropriate. More accurately, the sign in $ \left(\partial T/\partial V\right)_{M} $ (or equivalently, $ \left(\partial T/\partial r_{+}\right)_{M} $) should be employed to distinguish between the cooling and heating processes.

Thus, as depicted in Fig. 13, during both the earlier and later stages, the BH initially undergoes a heating phase before transitioning into a cooling phase at the inversion point.

Moreover, considering that, for a given inversion radius $ r_{i} $, $ M_{i}^{1}>M_{i}^{2} $ always holds, and $ M_{i}^{1}\left(r_{i}\right) $, $ M_{i}^{2}\left(r_{i}\right) $ are both increasing functions, for a constant mass process, the BH necessarily first passes through the inversion point on $ IC_{1} $, followed by that on $ IC_{2} $. In other words, $ IC_{1} $ precisely corresponds to the inversion points experienced by the BHs in the earlier stage, whereas $ IC_{2} $ pertains to the inversion points attainable by BHs in the later stage. In addition, since a given point in the $ \left(P,T\right) $ plane may correspond to several distinct BH phases, the inversion curve does not, by itself, partition the $ \left(P,T\right) $ plane into separate cooling and heating regions. In other words, in a constant- mass process, the intersection of the expansion and inversion curves is not necessarily the inversion point. This peculiar feature is also similar to that of the BH discussed in Ref. [90].

The earlier and later stages of the BH are connected at the point of maximum pressure $ P_{\rm max} $, at which the horizon radius $ r_{+} $ is

where $ \gamma = \sqrt{81M^{2}+6\xi^{2}}-9M $.

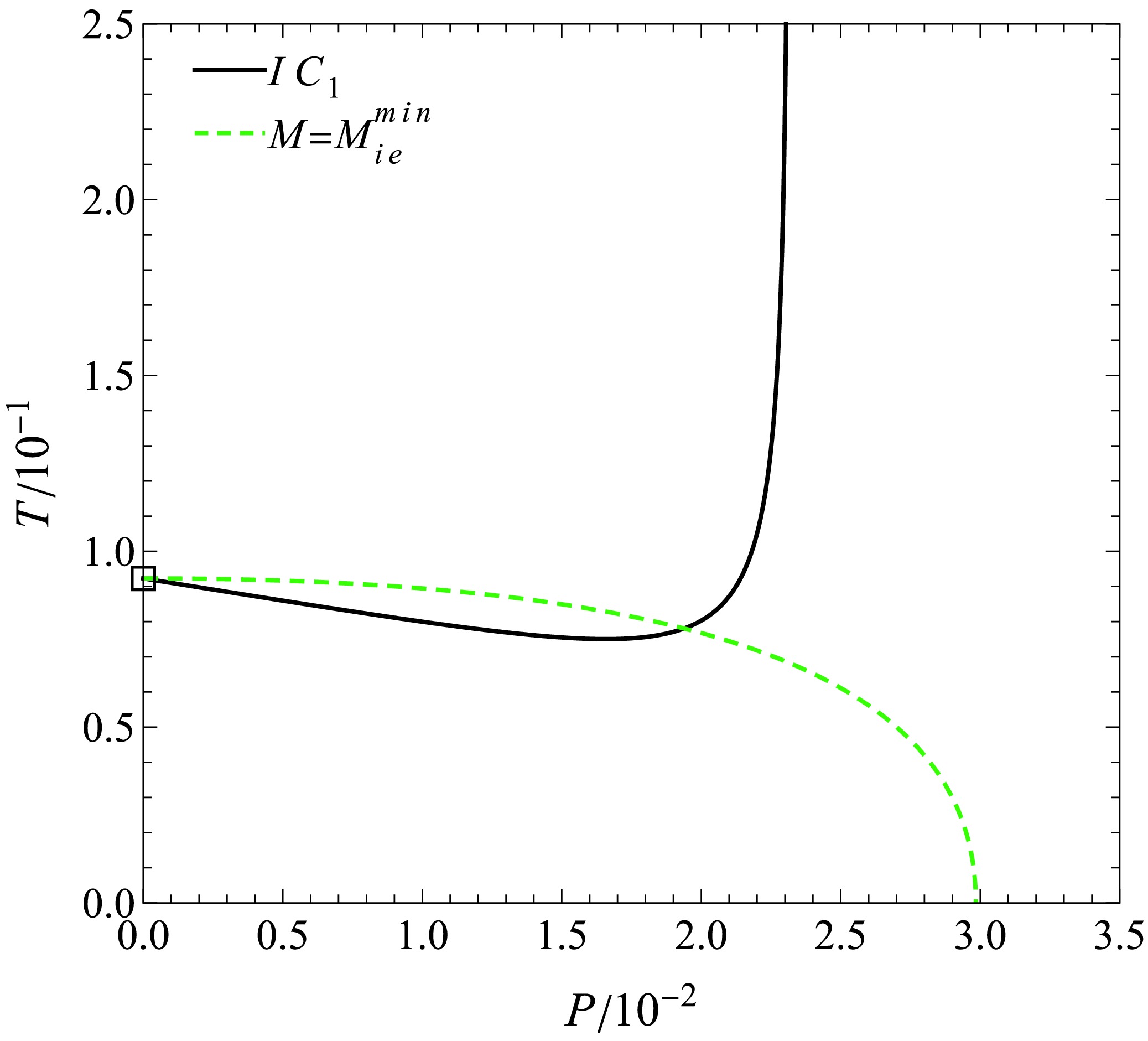
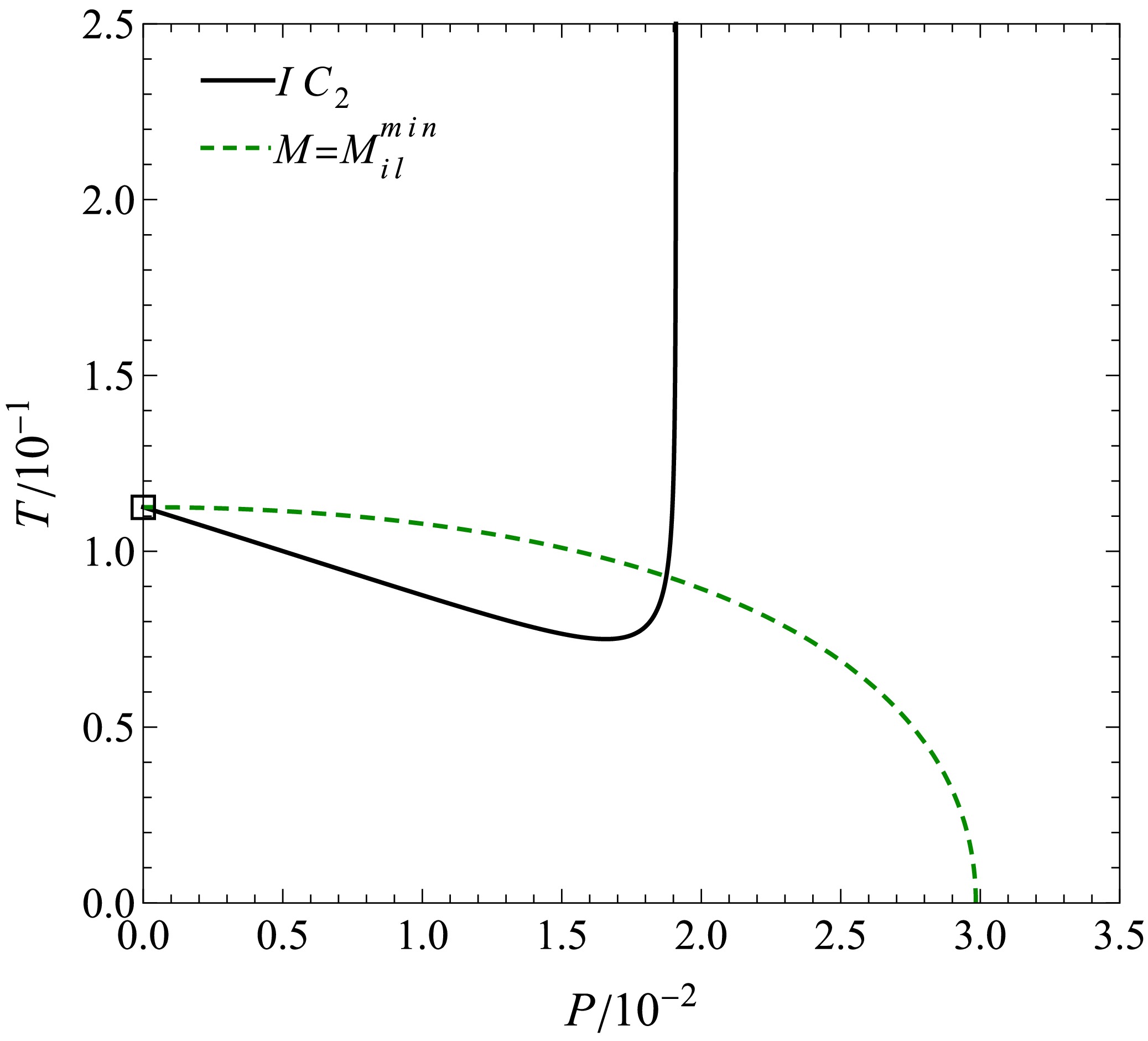
Fig. 14 and Fig. 15 depict the $ T-P $ diagrams for BHs with varying masses during the earlier and later stages of expansion, respectively. For sufficiently small BH masses, no inversion point exists. By setting $ P_{i} = 0 $, the minimum inversion mass $ M_{i}^{\rm min} $ for each case can be determined as follows: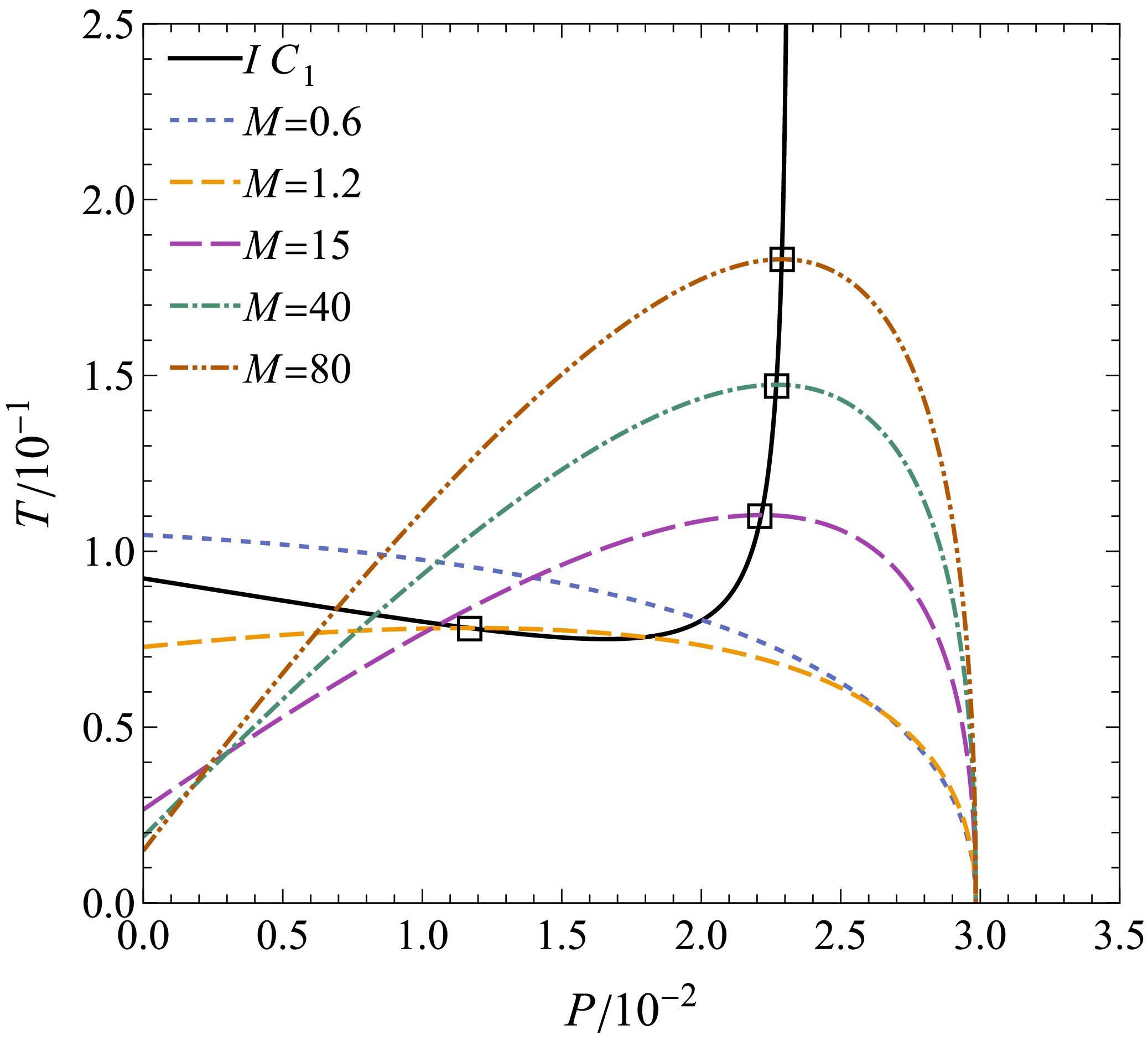

Figure 14.  (color online) Earlier stage of constant mass expansion of the BH. The points circled by small squares in the figure denote the inversion points. We set $ \xi=1$.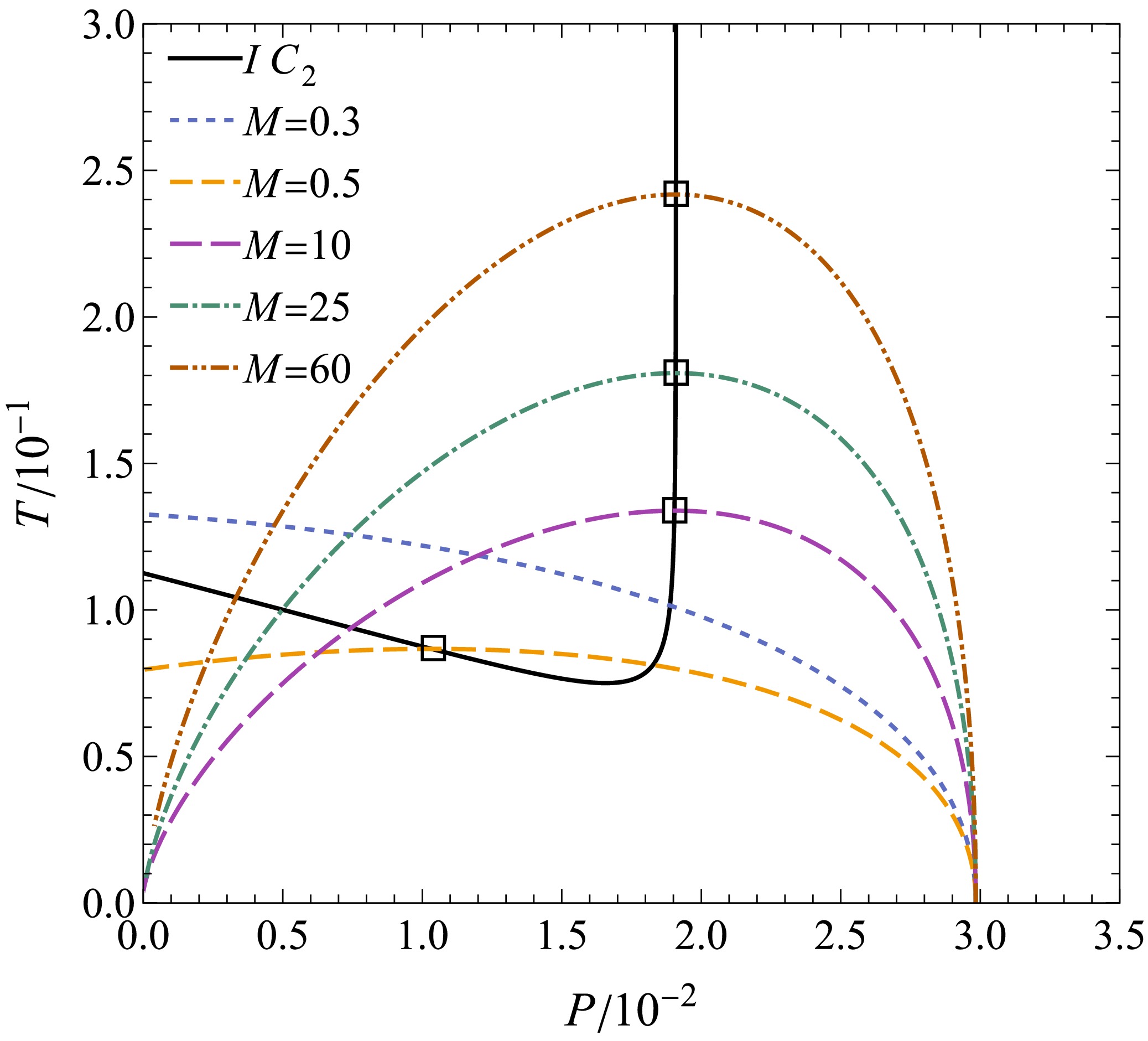

Figure 15.  (color online) Later stage of constant mass expansion of the BH. The points circled by small squares in the figure denote the inversion points. We set $ \xi=1$.

The minimum inversion mass can also be derived from Eq. (40) and Eq. (41) directly:

In Fig. 14 and Fig. 15, the first constant mass curve does not exhibit an inversion point, because

As shown in Fig. 16 and Fig. 17, the BHs with $ M_{i}^{\min} $ reach their critical points at $ P = 0 $.

Figure 16.  (color online) Earlier stage of constant mass expansion for BH with $ M_{ie}^{\mathrm{min}} $. The points circled by small squares in the figure denote the inversion points. We set $ \xi=1$.

Figure 17.  (color online) Later stage of constant mass expansion for BH with $ M_{il}^{\mathrm{min}} $. The points circled by small squares in the figure denote the inversion points. We set $ \xi=1$.

In this article, we investigated the thermodynamics in the extended phase space of a quantum corrected BH proposed recently. Our analysis demonstrates that the phase transition behavior of the BH is analogous to that of conventional Schwarzschild-AdS BH. In particular, there exists a critical temperature $ T_{c} $ such that, for any BH with a temperature exceeding $ T_{c} $, the small and large BH phases become separated, and no phase transition occurs. Owing to the effect of the quantum parameter ξ, the BH equation of state $ P\left(T,r_{+}\right) $ bifurcates into two branches with opposite stability properties. One branch converges to the Schwarzschild-AdS BH as $ \xi\to0 $, and it is associated with a phase transition pressure lower than the critical pressure $ P_{c} $, whereas the other branch exhibits a phase transition pressure greater than $ P_{c} $, which is not observed in conventional Schwarzschild-AdS BHs.

The temperature and heat capacity $ C_{p} $ of the BH closely resemble those of the Schwarzschild-AdS BH. Specifically, the small BH phase exhibits a negative heat capacity, indicating an unstable configuration, whereas the large BH phase shows a positive heat capacity, corresponding to a stable state. Moreover, the BH does not exhibit any region of negative temperature. In addition, owing to the corrected first law, the Gibbs free energy curve $ G-T $ in the vicinity of the BH phase transition point becomes smooth, thereby deviating from the behavior observed in conventional Schwarzschild-AdS BHs.

In addition, we conducted a detailed study of the Joule-Thomson expansion process of the BH. Our analysis reveals that the constant mass expansion process of the BH has two stages. In the earlier stage, the BH pressure increases with expansion until it reaches its maximum value; subsequently, during the later stage, the pressure gradually decreases. Consequently, the inversion curve of the BH splits into two branches, corresponding to the inversion points that may be experienced in the earlier and later stages, respectively. Moreover, each expansion stage is associated with a minimum inversion mass $ M_i^{\min} $, below which any BH undergoing a constant mass expansion process (in either stage) will not exhibit an inversion point.

We hope that these findings can offer novel insights into the interplay between quantum corrections and classical BH thermodynamics, and serve as a valuable reference for future research.

Our study is based on the assumption that the quantum gravity theory responsible for generating this quantum corrected BH decouples from the cosmological constant. This assumption, also adopted in Ref. [79], is generally regarded as valid, as the cosmological constant, being a constant, typically does not interact with other fields. Nevertheless, some modified gravity models suggest that the cosmological constant may be linked to other interactions. For instance, in Ref. [91], the authors constructed a gravastar in non-commutative BTZ geometry, finding that the non-commutativity parameter plays the role of the cosmological constant for gravastar formation and stability. If this theory is correct, the cosmological constant might be suggested as a non-commutative effect. In the context of Lorentz symmetry breaking theories, researchers have found that the choice of the self-interaction potential in the Kalb-Ramond field differs between the cases of zero and nonzero cosmological constants [92]. It is foreseeable that the cosmological constant may no longer be merely a constant term but instead could couple with various modified gravity models. In addition, although the quantum parameter ξ is presumed to be extremely small, its precise value remains undetermined. One approach is to estimate ξ by comparing the observed BH shadow radius with the theoretical value predicted for a Schwarzschild BH [32, 93, 94]. However, this method can only constrain ξ to be on the order of the Schwarzschild radius, which is evidently much larger than the Planck length $ \ell_{p} $. Therefore, seeking alternative methods to constrain this quantum parameter more precisely represents an interesting and worthwhile topic for future research.

Moreover, unlike most other AdS BHs, the phase structure of the BH investigated in this study exhibits significant deviations from that of the van der Waals system. It remains an important issue for future investigations to uncover the deeper physical mechanisms responsible for this phenomenon, as well as to explore whether other quantum effects could result in similar thermodynamic properties.

We want to thank School of Physical Science and Technology, Lanzhou University.