HTML
-
In recent years, the process of exploring unseen components of our cosmos has received considerable interest from numerous scientists. The investigation of different cosmic datasets has shown that dark energy (DE) plays a dominant role in the accelerating growth of our universe [1]. Theories and astrophysical observations related to cosmology and the early universe indicate that approximately 68% of the whole universe is made up of DE [2, 3], which can be described by a quintessential field or a repulsive cosmological parameter
$ \Lambda>0 $ [4−8]. Moreover, there exists another mysterious object termed dark matter (DM), which is supposed to compose at least 27% of matter content of the universe. Such matter consists of only weakly interacting particles and, as a result, does not interact with light and electromagnetic forces. Various experimental studies have investigated DM directly, but until now, no appreciative outcome has been obtained [9]. Hence, modified theories of gravity can be used to investigate the unusual characteristics of DM. These theories are derived from Einstein's general theory of gravity [10].Milgrom [11] was among the pioneers to modify Newtonian gravity to Modified Newtonian Dynamics (MOND). The MOND model may be used to explore the rotating curves of galaxies, but it may not be implemented for the gas density and temperature profiles of galaxy clusters without DM [12]. An extended version of MOND in tensor-vector-scalar gravity (TeVeS) is assumed to be a possible replacement for general relativity without DM [13]. In the case of a nonrelativistic weak acceleration limit, the model mentioned above gives rise to MOND, whereas its nonrelativistic strongly accelerating framework is Newtonian. In contrast to conventional scalar-tensor theories like Horndeski or DHOST, where no-hair theorems impose strict limitations on black hole solutions, the framework of modified gravity (MOG) introduces a massive vector field interacting with the scalar field. This interaction leads to a modified gravitational structure not subject to the same constraints as purely scalar-tensor frameworks. As a result, MOG does not fall into the classes of such theories.
An alternative DM model, the scalar-tensor-vector gravity (STVG), was introduced in [14]. Along with the matter action and Einstein-Hilbert term, the fields of three massive vectors and scalars are added to the action. This theory can be used to analyze the solar system, gravitational lensing, and rotational curves of galaxies, as well as the dynamics of galaxy clusters in the absence of DM [15]. By investigating MOG black holes (BHs), Moffat [16] deduced that the dimensionless parameter α (which describes the gravitational field’s strength) increases the shadow radius. By studying Kerr-MOG BHs, Lee and Han [17] found that α contributes to the radius of the innermost stable circular orbit (ISCO). Recently, Khan and Ren observed the shadow cast by BHs under the existence of a cosmological constant (Λ) and found that the quintessential DE intensity of the quintessence field (γ) and Λ contribute to the shadow radius [18, 19].
The weak gravitational lensing properties of Schwarzschild-MOG BHs in the presence of plasma medium were studied in [20]. The dynamics of test-charged and magnetized particles near regular and Schwarzschild BHs and magnetic fields in MOG were explored in Refs. [21−26]. S2 star tests [27], twin QPOs around regular BHs [28], vacuum and plasma magnetospheres of rotating magnetized neutron stars, and death line conditions of radio-loud pulsars have also been investigated in MOG [29].
A magnetic field around BHs has crucial consequences for the accretion process and charged matter. It was found that BHs possess an accretion disk generated by a conducting plasma, and their motion could constitute a regular magnetic field. Recent findings show the existence of strong magnetic fields near a supermassive BH in the Galaxy center that are not associated with the accretion disk [30]. Hence, BHs could be immersed in an external magnetic field with a composite formation near a BH's horizon. At the same time, their nature could be simple and close to a magnetic field of homogeneous nature at a larger, finite distance [31]. Kovar et al. [32] observed that a BH in the equatorial plane of a magnetar could be submerged in a homogeneous magnetic field if the magnetar is placed at a distant location. Therefore, in the current study, we focus on a BH immersed in a uniform external magnetic field, also called the Wald solution of the magnetized BH [33].
In relativistic astrophysics, the dynamics of both electrically charged and neutral test particles near BHs are of considerable interest. In particular, charged-particle dynamics are much more interesting because they play a crucial role in understanding the consequences of the magnetic field on the accretion process. The equations of electrically charged particle dynamics outlined by the Reissner-Nordström or Kerr-Newman spacetime can easily be separated and integrated [34]. Such dynamical motion of particles has been studied in various articles [35−39]. By examining the dynamics of the particles around a magnetized BH, Konoplya [40] deduced that the tidal charge strongly influences the motion of masses and the massless motion of particles. An abundant and detailed investigation of the charged particle motion in magnetized BHs can be found in [41−47]. Particle collision in the ergosphere and the dynamics of particles have been examined in Kerr and Kerr-Newman-Kasuya BHs, respectively [48−50]. Recently, by studying charged particle dynamics around the Kerr BH in a split monopole magnetic field, Khan and Chen investigated the position of stable circular orbits and deduced that the positive magnetic field increases the stability of effective potential [51].
The weak magnetic field has negligible effects on the motion of neutral particles or the background geometry. However, the magnetic field has a notable impact on the trajectory of a charged test particle. Thus, for charged test particles with charge q and mass m revolving near a BH of mass M that is enveloped in a magnetic field of intensity B, a dimensionless quantity
$ {\cal{B}}=qB GM/mc^4 $ may be defined as the relative Lorenz force [52, 53]. This quantity could also have a significant value in an inadequate magnetic field, owing to the greater amplitude of a particular charge$ q/m $ . A "charged particle" may refer to any material, ranging from electrons to some charge inhomogeneity revolving in an accretion disk's innermost location [54].One of the most realistic energy release processes from rotating BHs is the classical Penrose process, which Penrose suggested in 1969 [55]. The main idea is that a neutral particle decays into two neutral parts at the ergoregion of a rotating Kerr BH, and one part falls down the BH center with negative energy. At the same time, the other part leaves the region with a positive energy that is higher than the initial ("mother") particle's energy. In recent years, several approaches and modifications of Penrose processes have been developed in gravity theories. For example, the magnetic and electric Penrose processes have been suggested in Refs. [56−64], considering the decayed particles are spinning and charged.
Our primary objective in this work is to examine charged-particle dynamics and particle acceleration near a Kerr-MOG BH drowned in a nearby homogeneous magnetic field. The remainder of our article is organized as follows. In Section II, we briefly review the Kerr-MOG BH spacetime and its horizons. Section III investigates charged-particle motions around a Kerr-MOG BH. Section IV explores particle acceleration in the MPP. Finally, in Section V, we present concluding remarks. Throughout this paper, the geometrical unit system is used and
$ G_N=c=1 $ is assumed. -
The gravitational field action in the STVG theory includes GR
$ S_{G} $ , matter (pressure-less)$ S_{M} $ , vector field$ S_{\Phi} $ , and scalar field$ S_{S} $ terms [65]:$ \begin{aligned} S = S_{G}+S_{\phi}+S_{S}+S_{M}\ , \end{aligned} $

(1) where
$ \begin{aligned} & S_{G} = \frac{1}{16\pi}\int \frac{1}{G} (R+2 \Lambda) \sqrt{-g}{\rm d}^4x, \end{aligned} $

(2) $ \begin{aligned} & S_{\Phi} = -\frac{1}{4\pi} \int \left[{\cal{K}} + {\rm{V}}(\Phi)\right] \sqrt{-g}{\rm d}^4x\ , \end{aligned} $

(3) $ \begin{aligned}[b] S_{S} =\;& \int \frac{1}{G} \Bigg[\frac{1}{2} g^{\alpha \beta} \left( \frac{\nabla_{\alpha}G \nabla_{\beta}G}{G^2} + \frac{\nabla_{\alpha}\mu \nabla_{\beta}\mu}{\mu^2} \right)\\ &- \frac{V_{G}(G)}{G^2} -\frac{V_{\mu}(\mu)}{\mu^2} \Bigg] \sqrt{-g}{\rm d}^4 x\ , \end{aligned} $

(4) $ \begin{aligned} & S_{M} = -\int (\rho \sqrt{u^{\mu}u_{\mu}}+{\cal{Q}}u^{\mu}\Phi_{\mu})\sqrt{-g}d^4 x + J^{\mu} \Phi_{\mu}\ , \end{aligned} $

(5) where
$ R = g^{\mu\nu} R_{\mu\nu} $ is the Ricci scalar, Λ is the cosmological constant,$ g\equiv $ det$ (g_{\mu\nu}) $ is the determinant of the metric tensor,$ \nabla_{\alpha} $ is the covariant derivation, and$ V(G) $ and$ V(\mu) $ represent potentials associated with the two scalar fields, G and μ, respectively.$ {\cal{Q}} $ is the gravitational source charge,$ {\cal{Q}}=\sqrt{\alpha G_N}M $ , and$ {\cal{K}} $ is the kinetic term for the vector field$ \Phi_{\mu} $ :$ \begin{aligned} {\cal{K}} = \frac{1}{4}B^{\mu\nu} B_{\mu\nu}\ , \end{aligned} $

(6) where
$ B^{\mu\nu} = \partial _{\mu} \Phi_{\nu} -\partial _{\nu} \Phi_{\mu}. $ The covariant current density is defined as$ \begin{aligned} J^{\mu} =\kappa T_M^{\mu\nu} u_{\nu}\ , \end{aligned} $

(7) where
$ T_M^{\mu\nu} $ is the energy-momentum tensor for matter with$ \kappa = \sqrt{\alpha G_N}, $ $ \alpha = (G-G_N) /G_N $ is a parameter defining the scalar field,$ G_N $ is the Newtonian gravitational constant,$u^{\mu} = {\rm d}x^{\mu} /{\rm d}\tau$ is a timelike velocity, and τ is the proper time along a timelike geodesic. The perfect fluid energy-momentum tensor for matter is given by$ \begin{aligned} T^{M\mu\nu} = (\rho_M + p_M) u^{\mu}u^{\nu} -p_Mg^{\mu\nu}\ , \end{aligned} $

(8) where
$ \rho_M $ and$ p_M $ are the density and pressure of matter, respectively. From Eqs. (7) and (8), using$ u_\mu u^\mu=-1 $ , we get$ \begin{aligned} J^{\mu}={k} \rho_M u^{\mu}\ . \end{aligned} $

(9) For the matter-free and pressureless MOG field (
$ T_M^{\mu\nu}=0 $ ) in the asymptotically flat (zero-cosmological constant) spacetime, the field equation takes the form$ \begin{aligned} G_{\mu\nu}=-\frac{8\pi G}{c^4}T^\Phi_{\mu\nu}\ , \end{aligned} $

(10) where
$ T^\Phi_{\mu\nu} $ is the tensor of the massive-vector field. Observational data from a galaxy and cluster dynamics show that the mass of the particles of the field Φ is approximately$ m_\Phi=2.6\times10^{-28} $ eV, which is almost zero [66]. One may assume that the vector field is an analog of the electromagnetic field, and its field tensor is defined as$ \begin{aligned} T^\phi_{\mu\nu}=-\frac{1}{4\pi}(B_\mu^\alpha B_{\nu \alpha} - \frac{1}{4} g_{\mu \nu} B^{\alpha\beta}B_{\alpha\beta}) \end{aligned} $

(11) with
$ \begin{aligned} & \Delta_\mu B^{\mu\nu}=0\ , \end{aligned} $

(12) $ \begin{aligned} & \Delta_\alpha B^{\mu\nu}+\Delta_\nu B^{\mu\alpha}+\Delta_\mu B^{\alpha\nu}=0\ . \end{aligned} $

(13) The above assumptions imply that the potential term of the action
$ S_\Phi $ is zero ($ {\rm{V}}(\phi)=(1/2)\mu \Phi_\mu\Phi^\mu=0 $ ), so it has only a kinetic term. One may consider the kinetic term to be a function of the massive-vector field invariant$ {\cal{B}}=B_{\mu\nu}B^{\mu\nu} $ as$ {\cal{K}}=f({\cal{B}}) $ . The Schwarzschild-MOG BH solution is obtained with the simple linear approximation$ {\cal{K}}={\cal{B}} $ . -
This section aims to study the Kerr-MOG BH submerged in an externally uniform magnetic field. The MOG field equations are axially symmetric, stationary, and asymptotically flat. In Boyer-Linquist coordinates, the spacetime geometry can be expressed as [67]
$ \begin{aligned} { {\rm{d}}} s^2 = g_{tt}{ {\rm{d}}}{t}^2 + g_{rr}{ {\rm{d}}}{r}^2 + g_{\theta\theta}{ {\rm{d}}}\theta^2 + g_{\phi\phi}{ {\rm{d}}}\phi^2 +2g_{t\phi}{ {\rm{d}}}{t}{ {\rm{d}}}\phi, \end{aligned} $

(14) with
$ \begin{aligned}[b] &g_{tt} = -\left(\frac{\Delta-a^{2}\sin^{2}\theta}{\rho^2}\right), \quad g_{rr} = \frac{\rho^2}{\Delta}, \quad g_{\theta\theta} = \rho^2,\\ &g_{\phi\phi} = \frac{\sin^{2}\theta}{\rho^2}\left[(a^{2}+r^{2})^{2}-a^{2}\sin^{2}\theta \Delta\right], \\ &g_{t\phi}=\frac{a\sin^{2}\theta}{\rho^2}\left[\Delta-(a^{2}+r^{2})\right] , \end{aligned} $

(15) where
$ \begin{aligned} \Delta = r^2 - 2GMr + a^2 + \alpha G_N G M^2, \quad \rho^2 = r^2 + a^2 \cos^2\theta. \end{aligned} $

(16) In the above expressions,
$ G=G_N(1+\alpha) $ and$ G_N $ define the constant of gravity and Newton's constant of gravity, respectively. The parameter α characterizes the coupling strength of the gravitational field in MOG. The parameter a represents the BH's spin, while the dimensionless parameter α describes the gravitational field strength. Moreover, M represents the BH's mass and could be related to the Arnowitt–Deser–Misner (ADM) mass by the relation$ {\cal{M}}_{\alpha}=(1+\alpha)M $ [68]. By incorporating the value of G and utilizing the dimensionless quantities$ r\rightarrow r/G_{N}M $ ,$ a\rightarrow a/G_{N}M $ , and$ \alpha \rightarrow \alpha/G_{N}M $ in Eq. (16), Δ takes the form$ \begin{aligned} \Delta=r^{2}-2(1+\alpha)r+a^{2}+\alpha(1+\alpha). \end{aligned} $

(17) In rotating spacetime, the vector potential can be extended as
$ \begin{aligned} \Phi_\mu=\frac{\sqrt{\alpha} Mr}{\rho^2}(-1,0,0,a \sin^2{\theta}). \end{aligned} $

(18) -
The spacetime metric in Eq. (14) simplifies to the Kerr spacetime for
$ \alpha=0 $ , Schwarzschild-MOG BH for$ a=0 $ , and Schwarzschild BH for$ \alpha=a=0 $ .From observations of the solar system, the restriction on the parameter α can be given by [14, 69]
$ \begin{aligned} \alpha_\odot < 1.5 \times 10^5 \;{\rm cm} \times \frac{c^2}{G_N M_\odot} \approx 1 . \end{aligned} $

(19) Moreover, different astrophysical observations have obtained various constraint values for the parameter α. For instance, Ref. [70] demonstrated that MOG can act as DM around the galactic cluster Abel 1689, with α set to 8.89, based on X-ray observations. Another constraint on α comes from analyzing data from gravitational wave events GW150914 and GW151226, which yields estimates of 2 to 8.3 [71]. The constraint from the NGC1277 galaxy observation, with no signs of DM effects, is obtained as
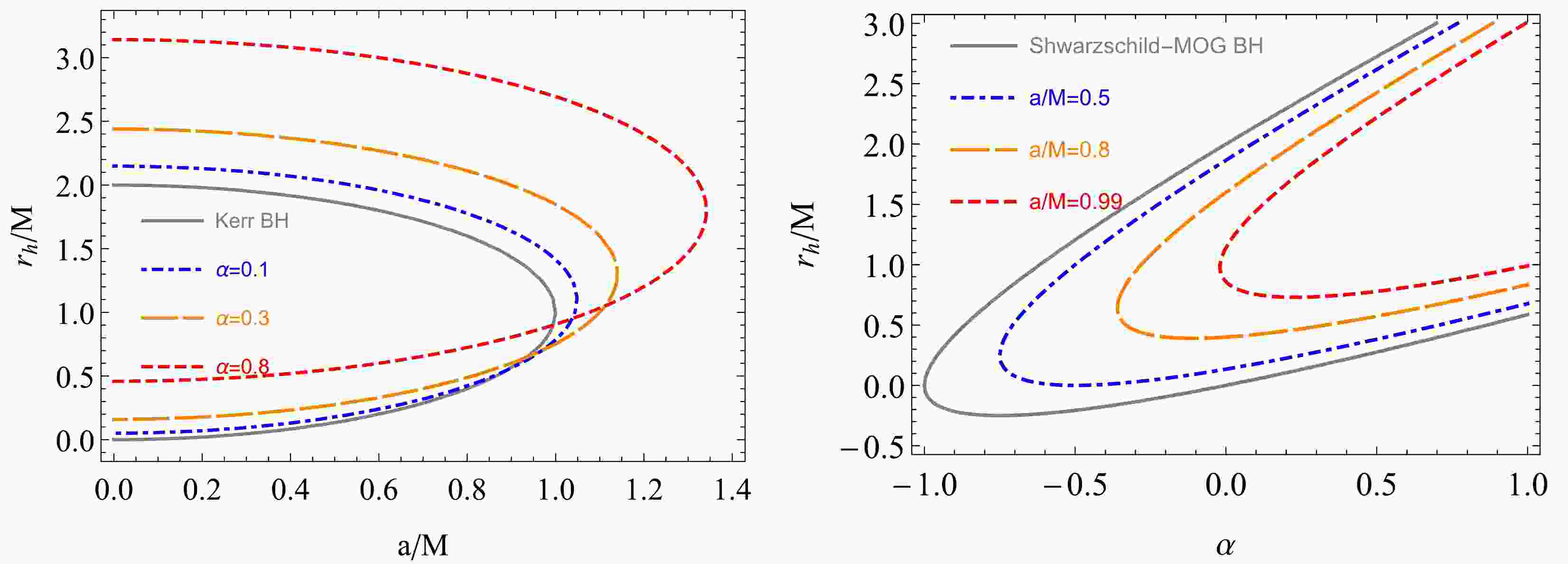
$ \alpha=16.61 $ [72]. Around Sagittarius A*, with a mass of$ 4.1 \times 10^6 M_{\odot} $ , α was found to be 0.055 [73]. By measuring the size of the supermassive BH at the center of the neighboring galaxy M87, located 26 Mpc away from the solar system, α was estimated to be$ 1.13^{+0.30}_{-0.24} $ [74]. Additionally, Ref. [66] set α to$ 8.89 \pm 0.34 $ using observational data from the rotation curve of the nearby galaxy. Recently, a critical value of the MOG parameter was found to be$ \sim 0.4 $ using the shadow of SrgA* BH [75].Figure 1 describes the geometric structure of BH horizons versus the spin parameter a on the left side and the parameter α on the right side. The graphical behavior shows that the Kerr and Schwarzschild-MOG BHs have the smallest and largest horizons, respectively. The graphs also depict that α increases the BH horizons, whereas a shrinks the horizons.

Figure 1. (color online) Graphical description of the BH horizons at various combinations of spin parameter a (left) and α (right).
One can obtain possible values of MOG and spin parameters that can provide a horizon in the spacetime of the Kerr-MOG BH by setting
$ \Delta=0 $ and$ \partial_r\Delta=0 $ .In Fig. 2, we demonstrate a set of values of α and a that correspond to BH (BH with a horizon) and no BH (an object without a horizon), where the blue line corresponds to BH solutions. The blue line implies that extreme values for the BH spin correspond to the maximum value of the MOG field parameter. The extreme values of
$ a_{\rm extr} $ are observed to increase with increasing$ \alpha_{\max} $ in quadratic form. In our subsequent analyses, we use these results to choose test values for spin and MOG parameters. -
We assume that the Kerr MOG BH is immersed in an external asymptotically uniform magnetic field and that the magnetic field B is orthogonal to the equatorial plane, oriented along the z axis. It is worse to note that the magnetic field could be expressed with the help of the electromagnetic 4-vector potential
$ {\cal{A}}_\mu $ using Wald's approach. Henceforth, its non-vanishing terms can be described as [47, 52]$ \begin{aligned} {\cal{A}}_t&=\frac{B}{2}(g_{t\phi}+2ag_{tt})-\frac{Q}{2}g_{tt}-\frac{Q}{2}, \end{aligned} $

(20) $ \begin{aligned} {\cal{A}}_{\phi}&=\frac{B}{2}(g_{\phi\phi}+2ag_{t\phi})-\frac{Q}{2}g_{t\phi}. \end{aligned} $

(21) The induced electrical charge Q is called the Wald charge. This explains the induced electric potential difference between the BH horizon and infinity due to the external magnetic field's presence and spacetime's rotation. The maximum induced BH charge produced due to the BH spin takes the Wald value (
$ Q_W=2aBM $ ) [33]. In principle, BHs with a maximum Wald charge possess the reduced electromagnetic potential as follows:$ \begin{aligned} {\cal{A}}_t=\frac{B}{2}g_{t\phi}-\frac{Q_W}{2},\quad {\cal{A}}_{\phi}=\frac{B}{2}g_{\phi\phi}. \end{aligned} $

(22) -
In this section, we separately discuss the effects of the electromagnetic and MOG interactions on the charged particle dynamics around the magnetized Kerr-MOG BH.
-
Here, we explore the phenomenological radiation called the gravitational-like counterpart to radiation. The equation of motion for massive test particles within the spacetime of the Kerr-MOG BH, as depicted in Ref. [16], is presented in a non-geodesic form
$ \begin{aligned} \frac{{\rm d}u^\mu}{{\rm d}s}+\Gamma^\mu_{\nu\lambda}u^\nu u^\lambda=\frac{\tilde q}{m}B^\mu_{\; \nu}u^\nu, \end{aligned} $

(23) where
$u^\mu={\rm d}x^\mu/{\rm d}s$ is the four-velocity of the particle, which can be normalized as$ u_\mu u^\mu=-1 $ , and$ \tilde{q}=\sqrt{\alpha}m $ . The four velocities are orthogonal to the four accelerations of the particle:$ w^\mu=\dfrac{Du^\mu}{ds} $ , that is,$ u_\mu w^\mu=0 $ . In Eq. (23), the radiation reaction forces' radiation is not considered. In Ref. [76], the Lorentz-Abraham-Dirac (LAD) equation [77] is modified for the radiation reaction by the STVG field for test particles in the form$ \begin{aligned}[b] \frac{Du^\mu}{ds}=\;&\frac{\tilde q}{m}B^\mu_{\; \nu}u^\nu+ \frac{1}{2}\tau_0 h^{\mu\lambda}R_{\lambda\nu}u^\nu\\ &+ \tau_0\frac{\tilde q}{m}\left(u^\alpha\nabla_\alpha B_{\; \nu}^\mu+\frac{\tilde q}{m}h^{\mu\lambda}B_{\lambda\alpha}B^\alpha_{\; \nu}\right)u^\nu\ , \end{aligned} $

(24) where
$ h^{\mu\nu}=g^{\mu\nu}+u^\mu u^\nu $ ,$ h_{\mu\nu}u^\nu=0 $ , and$ \tau_0=2{\tilde q}^2/(3m) $ is the damping time of the radiation. It is also shown that the damping time is approximately$ 10^{-66} $ s for electrons, while it is$ 10^{-60} $ s for protons, and on the order of$ 10^{-4} $ s for the scenario of a stellar-mass BH orbiting an SMBH [76]. This implies that one may neglect gravitational-like radiation in studies of the acceleration of protons up to ultra-high energies. -
The expression of the non-geodesic equation for charged particles around magnetized BHs containing the influence of external (electro)magnetic fields and the radiation reaction force reads [77]
$ \begin{aligned} \frac{{\rm d}u^\mu}{{\rm d}s}+\Gamma^\mu_{\nu\lambda}u^\nu u^\lambda = f^\mu_L +f^\mu_R. \end{aligned} $

(25) Here,
$ f^\mu_L=(q/m) F^{\mu}_{\,\,\,\nu} u^{\nu} $ is the Lorentz force by an external (electro)magnetic field, while$ f^\mu_R=(q/m) {\cal{F}}^{\mu}_{\,\,\,\nu} u^{\nu} $ is the self-force of the charged particle by the electromagnetic field emitted by the charged particle itself, including tail forces, which can be neglected [78]. The radiation reaction force takes the form [79]$ \begin{aligned}[b] f_R^\alpha =\;& \frac{q}{m} \Bigg[ \left(\frac{\partial F^{\alpha}_{\,\,\,\beta}}{\partial x^{\mu}} + \Gamma^{\alpha}_{\mu\nu} F^{\nu}_{\,\,\,\beta} - \Gamma^{\nu}_{\beta\mu} F^{\alpha}_{\,\,\,\nu}\right) u^\beta u^\mu \\& + \frac{q}{m} \left( F^{\alpha}_{\,\,\,\beta} F^{\beta}_{\,\,\,\mu} + F_{\mu\nu} F^{\nu}_{\,\,\,\sigma} u^\sigma u^\alpha \right) u^\mu \Bigg]. \end{aligned} $

(26) The qualitative analyses in Ref. [79] have shown that the ratio of the radiation reaction force
$ F_{\rm{RR}} \sim q^4 B^2/(m^2 c^4) $ to the Newton force is$ \begin{aligned} \frac{F_{\rm{RR}}}{F_{\rm{N}}} &\sim \frac{q^4 B^2 M G}{m^3 c^8} \simeq 10^3 \left(\frac{q}{e}\right)^4 \left(\frac{m_e}{m}\right)^3 \left( \frac{B}{10^8 {\rm{G}}}\right)^2 \left(\frac{M}{10 M_{\odot}}\right) \\ &\simeq \frac{1}{10^4} \left(\frac{q}{e}\right)^4 \left(\frac{m_p}{m}\right)^3 \left( \frac{B}{10^8 {\rm{G}}}\right)^2 \left(\frac{M}{10 M_{\odot}}\right), \end{aligned} $

(27) and in the Sgr A* case, the ratio for protons is [80, 81]
$ \begin{aligned} \frac{F_{\rm{RR}}}{F_{\rm{N}}} \simeq \frac{1}{10^{10}} \left(\frac{q}{e}\right)^4 \left(\frac{m_p}{m}\right)^3 \left( \frac{B}{10^2 {\rm{G}}}\right)^2 \left(\frac{M}{M_{SgrA*}}\right). \end{aligned} $

(28) The above estimations on radiation reaction forces in proton motion imply that one may also neglect the effects of the field radiated by protons on their motion. The revised scaling relation for radiation losses now includes a Lorentz factor dependence, reflecting significant losses for high-energy protons around stellar-mass black holes. However, these losses remain within bounds, allowing for an effective MPP for supermassive black holes. This process operates as a localized redistribution mechanism, balancing radiative losses with gravitational and magnetic energy contributions in the MOG framework, preserving the core dynamics of the MPP.
-
This section aims to explore the characteristics of the photon region around a Kerr-MOG BH by neglecting both electromagnetic and gravitational radiation by the particles, with the assumptions of
$ p^{\mu}p_{\mu}=-m^2 $ . Therefore, by applying the technique of separation of variables, the corresponding geodesic motion of the metric in Eq. (14) could be expressed by the Hamilton–Jacobi equation as$ \begin{aligned}[b] {\cal{H}} &= -\frac{\partial S}{\partial \tau}\\ &= \frac{1}{2}g_{\mu\nu}(P_\mu-q{\cal{A}}_\mu+\tilde{q}\Phi_\mu)(P_\nu-q{\cal{A}}_\nu+\tilde{q}\Phi_\nu)+\frac{1}{2}m^2, \end{aligned} $

(29) where
$ \tilde{q}=\sqrt{\alpha}m $ is the gravitational test particle charge. In Eq. (29),$ {\cal{H}} $ and S denote the Hamiltonian and Jacobi actions, respectively. Moreover,$ m^2 $ is the rest mass, while$ p_\mu={\partial S}/{\partial{x}^{\mu}} $ is the four-momentum of particles. Due to spacetime symmetry, the preserved energy and angular momentum may be described in the form$ \begin{aligned} -{\cal{E}}&=p_{t}=g_{tt}\dot{t}+g_{t\phi} \dot{\phi}+q{\cal{A}}_t+\tilde{q}\Phi_t, \end{aligned} $

(30) $ \begin{aligned} {\cal{L}}&=p_{\phi}=g_{t\phi}\dot{t}+g_{\phi\phi}\dot{\phi}+q{\cal{A}}_\phi+\tilde{q}\Phi_\phi. \end{aligned} $

(31) The dot denotes the derivative for the proper time τ. Therefore, by using
$ {\cal{E}}=E/m $ ,$ {\cal{L}}=L/m $ , and a particular charge$ \bar{q}=q/m $ , the Hamiltonian in Eq. (29) modifies to$ \begin{aligned} {\cal{H}}={\cal{H}}_p(r,\theta)+\frac{1}{2}g^{rr}p_r^2+\frac{1}{2}g^{\theta\theta}p_\theta^2, \end{aligned} $

(32) with
$ \begin{aligned}[b] {\cal{H}}_p(r,\theta)=\;&\frac{1}{2}\Big[g^{tt}({\cal{E}}=\bar{q} {\cal{A}}_t +\tilde{q}\Phi_t)^2+g^{\phi\phi}({\cal{L}}-\bar{q} {\cal{A}}_\phi -\tilde{q}\Phi_\phi)^2\\ &-2g^{t\phi}({\cal{E}}+\bar{q} {\cal{A}}_t +\tilde{q}\Phi_t)({\cal{L}}-\bar{q} {\cal{A}}_\phi -\tilde{q}\Phi_\phi)+1\Big]. \end{aligned} $

In the above expression,
$ {\cal{H}}_p(r,\theta) $ represents the potential part of the Hamiltonian. Utilizing Eqs. (30) and (31), the values of$ \dot{t} $ and$ \dot{\phi} $ can be obtained as$ \begin{aligned} &\dot{t}=-\frac{g_{t\phi}({\cal{L}}-\bar{q} {\cal{A}}_\phi-\tilde{q}\Phi_\phi)+g_{\phi\phi}({\cal{E}}+\bar{q} {\cal{A}}_t +\tilde{q}\Phi_t)}{g_{tt}g_{\phi\phi}-g_{t\phi}^2}, \end{aligned} $

(33) $ \begin{aligned} &\dot{\phi}=\frac{g_{tt}({\cal{L}}-\bar{q} {\cal{A}}_\phi-\tilde{q}\Phi_\phi)+g_{t\phi}({\cal{E}}+\bar{q} {\cal{A}}_t + \tilde{q}\Phi_t)}{g_{tt}g_{\phi\phi}-g_{t\phi}^2}. \end{aligned} $

(34) The energetic boundaries imposed by the
$ {\cal{H}}=0 $ constraint could restrict the charged test particle dynamics. By making use of the energy condition, the effective potential may be associated with the specific energy for circular orbits ($ \dot{r}=0 $ ) as$ {\cal{E}}={{\cal{U}}}_{eff}(r, \theta) $ , which, in the Kerr-MOG BH, simplifies to [43]$ \begin{aligned} {{\cal{U}}}_{eff}(r, \theta)=\frac{-\beta+\sqrt{\beta^2-4\delta \gamma}}{2\delta}, \end{aligned} $

(35) where
$ \delta = -g^{tt}, \beta= -2[g^{tt}(\bar{q}{\cal{A}}_t+\tilde{q}\Phi_t)-g^{t\phi}({\cal{L}}- \bar{q}{\cal{A}}_\phi- \tilde{q}\Phi_\phi)] $ , and$ \gamma =-g^{tt}(\bar{q}{\cal{A}}_t+\tilde{q}\Phi_t)^2+2g^{t\phi}(\bar{q}{\cal{A}}_t +\tilde{q}\Phi_t)({\cal{L}}-\bar{q}{\cal{A}}_\phi - \tilde{q}\Phi_\phi) - g^{\phi\phi}({\cal{L}}-\bar{q}{\cal{A}}_\phi-\tilde{q}\Phi_\phi)^2-1 \,. $ Magnetic fields around BHs produce chaotic behavior in charged particle dynamics, except in the equatorial plane. In the equatorial plane, the minima and maxima of
$ {{\cal{U}}}_{\rm eff} $ indicate stable and unstable circular orbits, respectively. The circular orbits of the Kerr-MOG BH can be distinguished into four different classes [53]: the prograde anti-Larmor orbit (PALO) for$ {\cal{L}}>0, {\cal{B}}>0 $ ; retrograde Larmor orbit (RLO) for$ {\cal{L}}<0, {\cal{B}}>0 $ ; prograde Larmor orbit (PLO) for$ {\cal{L}}>0, {\cal{B}}<0 $ ; and retrograde anti-Larmor orbit (RALO) for$ {\cal{L}}<0, {\cal{B}}<0 $ . Here,$ {\cal{L}}>0 $ and$ {\cal{L}}<0 $ denote the co-rotating and counter-rotating particles, respectively, while$ {\cal{B}}>0 $ and$ {\cal{B}}<0 $ define the repulsive and attractive Lorentz forces, respectively.The dynamics of charged particles can be bounded by the boundaries of their effective potential
$ \begin{aligned} {\cal{E}}= {{\cal{U}}}_{\rm eff}(r, \theta; {\cal{B}}, {\cal{L}}). \end{aligned} $

(36) The behavior of the effective potential (35) is investigated in Fig. 3, which allows us to illustrate the general features associated with the motion of charged particles without explicitly computing the equation of motion [31]. Also, the graphical behavior depicts that the magnetic field stabilizes the circular orbits (first column of Fig. 3). The particles coming from infinity with a higher spin parameter a require more energy to climb
$ {{\cal{U}}}_{\rm eff} $ compared to those with a smaller value of a, and vice versa for the parameter α (for details, see the second and last columns of Fig. 3). The middle and right panels show that circular orbits are initially unstable but become stable along x at a higher distance. It is also observed that the BH spin increases the instability, whereas α decreases the instability near the BH horizon. Furthermore, the circular orbit's instability at the horizon in the Kerr-MOG BH is higher than in the Schwarzschild-MOG BH. -
The Keplerian accretion disk could generate the trajectories of circular orbits near a BH, while the ISCO determines its lower boundary. One can obtain the boundaries of particle dynamics by investigating the properties of the effective potential
$ {{\cal{U}}}_{\rm eff}(r, \theta) $ . Therefore, the circular orbits of the charged test particle could be acquired using the stationary positions of the effective potential as$ \begin{aligned} \partial_r {{\cal{U}}}_{\rm eff}(r, \theta)=0, \quad \partial_\theta {{\cal{U}}}_{\rm eff}(r, \theta)=0. \end{aligned} $

(37) In the Schwarzschild BH, the local extrema of
$ {{\cal{U}}}_{\rm eff}(r, \theta) $ are located only on the equatorial plane. On the contrary, in our case (Kerr-MOG BH), the local extrema in the equatorial plane can also determine the circular orbits [31].In principle, charged particle motion near a BH immersed in a uniform external magnetic field is chaotic. Although charged particle trajectories near stable circular orbits still possess a structured nature [43], it has been observed that the charged particles also have structural trajectories on the equatorial plane. At the same time, their nature becomes chaotic as the angle of inclination of the beginning point varies from the equatorial plane (since the inclination of orbits changes in each period).
The characteristic of effective potential may provide various kinds of energetic boundaries (Eq. (36)). The graphical behavior of the test charged particle trajectories in the background of Schwarzschild, Kerr, and Kerr-MOG BHs are shown in the top, middle, and bottom rows of Fig. 4, respectively, in the absence of an external magnetic field (
$ {\cal{B}}=0 $ ). From Fig. 4, it can be observed that the Schwarzschild BH captures the test particle at the same value of other parameters. In contrast, in the case of Kerr and Kerr-MOG BHs, the test particle is trapped in some region around the BH. It starts circularly orbiting due to decreased gravitational forces in spacetime and increased centrifugal forces. This means that in the Kerr and Kerr MOG BH cases, the falling rate of accreting matter is smaller than that of the Schwarzschild BH. Furthermore, the presence of minor MOG effects makes the trajectories (bounded orbits) chaotic (unstable) and reduces the width between the turning planes due to the fifth interaction (MOG field). Meanwhile, its greater values result in particles falling into the BHs.
Figure 4. (color online) Test particle trajectories (solid curves) around BHs described by the shaded circle without considering external magnetic field (
$ {\cal{B}} $ ). Trajectories in the first, second, and third rows indicate the Schwarzschild, Kerr, and Kerr-MOG BHs, respectively. The fourth column corresponds to the$ 3D $ particle trajectories, whereas the first and second columns describe their$ 2D $ orientations. Using the principles of energy and angular momentum conservation, we can describe the$ 4D $ configuration space ($ t,x,y,z $ ) in a$ 2D $ graph (third column), where the motion boundary is plotted via the effective potential (dotted-dashed curves).In Figs. 4 and 5, we plot the charged particle trajectories in the close environment of the Kerr-MOG BH in the presence of an external asymptotically uniform magnetic field (with
$ {\cal{B}}\neq 0 $ ). We can observe various types of orbits with corresponding boundary conditions. The first one is related to the existence of an outer boundary, where the central magnetized BH should capture the charged particle. The second type is related to the existence of an inner boundary where the particle must escape to infinity. The third type is related to inner and outer boundaries, between which the charged particle is trapped around the BH and forms a toroidal region. The latest type is characterized by no inner and outer boundaries, where the BH can trap the particle or escape to infinity. The impact of the parameter α on particle trajectories can be explicitly observed in Figs. 4 and 5. Also, one can see from the first and second rows of Fig. 5 that the MOG field shrinks the region between the outer and inner boundaries and increases the chaos in the bounded orbits. However, the wideness of the region of the bounded orbits for negatively charged particles is smaller than that for positively charged particles.
Figure 5. (color online) Charged test particle trajectories (solid curves) around a Kerr-MOG BH with an external magnetic field (for details, see Fig. 4).
-
Particles within a neutral accretion disk can be ionized in various ways, such as particle disintegration or atom ionization due to particle collision in the hot and magnetized accretion disk. Another alternative possibility is connected with the accretion disk, which contains a quasineutral collection of ions and electrons as charged particles in circle-like orbits around a BH and photons. When the matter in the disk is sufficiently thick, the charged particles' principal free path becomes significantly shorter than that of the entire circumference of the orbits, and they travel together like a neutral entity. The plasma density decreases dramatically along the disk near the inner boundary, and charged particles are not further restricted by the surroundings and start floating independently, controlled entirely via the (electro)magnetic fields.
This particle ionization model, proposed by Stuchlík et al. in [82], naturally corresponds to the magnetic Penrose process (MPP) [56, 83], in which the initial neutral particle is divided into two charged particles. This straightforward ionization model may be used to investigate the destiny of ionized Keplerian disks [84], and if the magnetic influence is weak, it can be used to create modest oscillations of particles in circular orbits [53, 85]. The ionization process conserves both the charge and kinetic momentum of the particle [47]:
$ \begin{aligned} 0 = q_2 + q_3 , \quad {\pi}_{\alpha(1)} = {\pi}_{\alpha(2)} + {\pi}_{\alpha(3)}. \end{aligned} $

(38) It is possible to demonstrate that kinetic momentum remains unchanged during ionization using
$ \begin{aligned} p_{\alpha(1)} = p_{\alpha(2)} + p_{\alpha(3)}, \end{aligned} $

(39) because the electromagnetic effects balance out [82, 84]. In practical cases, one of the generated charged particles might be significantly heavier than the other; for example, in the ionization of atoms, the ion is much more massive than the electron. The gradually more massively charged product absorbs practically all the kinetic momentum of its predecessor's neutral particle, and the lower-charged product's dynamic impact may be ignored:
$ \begin{aligned} p_{\alpha(1)} \approx p_{\alpha(2)} \gg p_{\alpha(3)}. \end{aligned} $

(40) The neutral particle will be separated into two charged particles after ionization, and while their total mechanical momentum remains conserved, the charged particle will feel the effect of the electromagnetic field via the Lorentz force, and their trajectories will be significantly different from the neutral one, as shown in Fig. 6.

Figure 6. (color online) Particle acceleration near a magnetized spinning BH. In the left column, the electrically neutral particle (or in the absence of external magnetic fields) is shown by solid black curves, which lie along the inside edge of the accretion disk, decomposing into two charged particles: in the middle column, positively charged particles (blue curves), and in the right one, negatively charged particles (red curves). While the second particle (blue) gets stuck with excessive negative energy upon orbiting around the BH, the third particle (red) gains excessive energy via chaotic scattering and escapes along the magnetic field line.
In this section, we assume that the ionization event would take place close to the Kerr-BH equatorial plane but with some small perturbation
$ \theta_{0}\simeq\pi/2 $ , which allows the particle to also move in the vertical direction. The neutral parent particles appear to be in a spherical orbit with a starting location of$ x^\alpha $ and four-velocity of$ u_\alpha $ :$ \begin{aligned} x^\alpha&=(t,r,\theta,\phi)=(0,r_0,\theta_0,0), \end{aligned} $

(41) $ \begin{aligned} u_\alpha&=(u_t,u_r,u_\theta,u_\phi)=( {\cal{E}},0,0, {\cal{L}}). \end{aligned} $

(42) The particular energy
$ {\cal{E}} $ and angular momentum$ {\cal{L}} $ associated with neutral electrical particles adhering to circular orbits regulate the particle's motion constants [86]:$ \begin{aligned} {\cal{E}}&=\frac{r^{2} -2 (1+\alpha) r + \alpha \pm a \sqrt{(1+\alpha) r-\alpha} }{r {\cal{P}}} , \end{aligned} $

(43) $ \begin{aligned}[b] {\cal{L}} =\;&r^2 + a^2 \pm 2 a \sqrt{(1+\alpha) r-\alpha} \\ &\pm \frac{1}{r {\cal{P}}}\Big(\sqrt{(1+\alpha) r-\alpha}\pm a \alpha \Big), \end{aligned} $

(44) where
$ {\cal{P}}^2=r^2 -3(1+\alpha) r+2\alpha \pm 2a \sqrt{(1+\alpha) r-\alpha} $ . The inner edge of the Keplerian disks is situated at the ISCO, which can be obtained with the condition of${\rm d}^2 {{\cal{U}}}_{\rm eff}/{\rm d}r^2=0$ .Although the MPP is a regional decaying procedure, its energy balance can only be determined with the help of the electromagnetic field's local value. As a result, a simple estimation of an asymptotically homogeneous magnetic field compatible with a spinning axis could be utilized. The neutral particle (neutron) orbiting the central BH in a thin Keplerian disk or thick torus is in a bound state, and its energy is slightly lower than unity,
$ E_1<1 $ , where the value$ E_1=1 $ is reserved for a particle at rest located at infinity. Thus, the second particle's energy$ E_2 = p_{t2} - qA_t - \tilde{q}\Phi_t $ could be negative and of huge magnitude. The third particle's (proton) energy$ E_3 = p_{t3} + qA_t +\tilde{q}\Phi_t $ has the potential to be relatively high. MPP combined with chaotic dynamics in the combined gravitational and magnetic fields leads to the second charged particle trajectory [82], and the circular motion of the particles will be transmuted into linear motion alongside the lines of the magnetic field. Such a flow of charged particles may be used as a straightforward model for the relativistic jets (or particle winds) discovered in several active galactic nuclei and quasars. The BH instantly captures the second particle with significant negative energy, as illustrated in Fig. 6.The MPP of the charged particles that accelerate is depicted in Figs. 6 and 7 at various values of
$ {\cal{B}} $ and α. As previously discussed in [ ], the mechanism of chaotic scattering ensures that the ultra high-energy third particle can depart to infinity through magnetic field lines, while the particle with significant negative energy is instantly absorbed by the BH (see Figs. 6 and 7). Moreover, it should be observed that the chaotic nature increases in the case of a greater magnetic field value, and the particle escapes to infinity more quickly.
Figure 7. (color online) Identical scenario to that of Fig. 6 but with comparatively higher values of the magnetic field (
$ {{\cal{B}}} $ ) and MOG (α) parameters. -
In practical astrophysical situations, the arbitrary electromagnetic field near a BH is insufficient because its stress-energy tensor does not contribute to spacetime geometry. To contribute, the electromagnetic field energy density must be on the order of gravitational field density. Therefore, the requirement for the existence of a magnetic field having strength B and BH mass M is [87, 88]
$ \begin{aligned} B << B_{ {G}}=\frac{c^4}{G^{3/2} M_{\odot}} \left(\frac{{M}_{\odot}}{M}\right){\sim} 10^{19}{ \frac{{M}_{\odot}} {M} }\,{\rm{Gauss}}\, . \end{aligned} $

(45) However, it may significantly influence the motion of a charged particle. The interplay of the electromagnetic Lorentz force and gravitational attraction experienced by charged matter, symbolized by a specific charge,
$ q/m $ , could be expressed using the dimensionless "magnetic parameter"$ {\cal{B}} $ . Charged test particles may symbolize protons, electrons, ions, and massively charged anomalies, such as plasma objects or charged dust with specific charges$ q/m $ ranging from the electron maximum to zero. Due to the enormous magnitude of its specific charge, the magnetic field parameter$ {\cal{B}} $ for protons, ions, and, in particular, electrons can be enormous even in relatively weak magnetic fields, representing an essential impact of the electromagnetic Lorentz force on its dynamics even in weak magnetic fields. Results of an analogous study that involves protons and ions are listed in Table 1.$ M=10 M_{\odot} $ /

electron proton Fe+ charged dust $ {\cal{B}} = 0.1 $ 

$ 10^{-4} {\rm{G}} $ 

$ 0.4 {\rm{G}} $ 

$ 24 {\rm{G}} $ 

$ 10^{10} {\rm{G}} $ 

Table 1. Magnetic field strength B related to the magnetic parameter
$ {\cal{B}}=0.1 $ for different kinds of charged particles traveling near the BH$ M_{\rm{BH}}\sim{}10\; M_{\odot} $ .Suppose that the MPP is associated with an ionized Keplerian disk and a chaotic scattering approach. In this case, one might deduce that magnetized, revolving BHs could form jets headed toward infinity with exceptionally high velocities. As a result of the rotational energy extraction of BHs due to capturing electrons with significant negative energy, this is a fundamental procedure for a highly challenging Blandford-Znajek mechanism [56].
When the ionized disk rotates around a non-spinning BH (or a slowly spinning BH encircled by a relatively weak magnetic field), the MPP creates storms that cannot go on to infinity with acquired energy from the rotational motion of the encircling objects (which represents the Payne-Blandford procedure [89]). This chaotic scattering procedure results in the creation of jets caused by the conversion of revolving energy of matter initially revolving in the Keplerian disk; nevertheless, the energy associated with this transformation of circular motion energy to translational dynamic energy is smaller than that associated with electromagnetic field acceleration.
-
Cosmic rays are connected to the significant growth of particle energy. These are typically made up of high-energy ions or protons; their detected isotropic dispersion implies an extragalactic origin, which is why the production mechanism has long been contested. Inspections of Ultra-High-Energy Cosmic Rays (UHECRs) associated with energetic particles of
$ E > 10^{18} $ eV (on rare occasions, particles with energy$ E > 10^{21} $ eV are found, surpassing the GZK limit of$ 10^{19} $ eV owing to the interplay of cosmic microwave background) are of particular interest [47]. The study of particles with more enormous energy than the GZK limit necessitates strict distance limitations on the origin of such energetic particles.The extreme acceleration of particles with energies
$ E > 10^{21} $ eV can be difficult to explain. However, we may suggest a basic strategy centered on the MPP's ultra-efficient regime if it is near a supermassive BH surrounded by an abundant magnetic field. The charged particle's energy generated by the MPP in an extraordinarily efficient regime may be described as$ \begin{aligned} E_{\rm MPP}\simeq 1.3 (1+\alpha) \left(\frac{m_p}{m}\right) \left( \frac{q}{e} \right)\left(\frac{M}{10^{10} M_{\odot}}\right) \left(\frac{a B}{10^4 G} \right) 10^{21}\ {\rm eV} . \end{aligned} $

(46) Here, m and q represent the mass and charge of the test particle, respectively, whereas e and
$ m_p $ are the charge and mass of a proton, respectively. Protons possessing an energy of$ E > 10^{21} $ eV are undoubtedly possible even when$ a=0.8 $ , as supermassive BHs that possess mass$ M = 10^{10} M_{\odot} $ are contained in a magnetic field with strength$ B = 10^4 G $ and are quietly rotating. It is important to note that the energy of a photon may be calculated for the supermassive BH SgrA$ ^* $ , and the corresponding magnetic field observable in the galaxy's center is provided by$ \begin{aligned} E_{p}\simeq (1+\alpha)\left(\frac{q}{e} \right) \left( \frac{a}{0.4} \right) \left(\frac{B}{10^{2} G} \right) \left(\frac{M}{M_{\rm SgrA*}}\right) \left(\frac{m_p}{m} \right)10^{15.6}\ {\rm eV}. \end{aligned} $

(47) This quantity should be comparable to the well-known knee of the energy range in the gathered data, which is located at
$ E_{\rm knee} \sim 10^{15.6} $ eV, where the entire amount of particle flow detected is greatly reduced, implying the presence of an incredibly strong origin placed at a relatively close distance. The MPP on SgrA$ ^* $ recommends that the model be connected to the UHECR data knee at$ E \sim 10^{15.6} $ eV. -
The magnetic field has a profound influence on the astrophysical phenomena that occur in the vicinity of BHs and other compact objects. Even a small magnetic field may considerably affect the location of the inner edge of an ionized Keplerian accretion disk and the charged particle's trajectory if the particular particle's charge
$ q/m $ is sufficiently high. As GRMHD algorithms reveal, the real magnetic field near a BH may possess a relatively complex nature [90, 91]. Therefore, this article examines charged-particle motion and acceleration in MPP around a Kerr-MOG BH drowned in a uniform magnetic-field configuration.From the investigations of horizons, we observed that the Kerr BH has the smallest horizon, whereas the Schwarzschild-MOG BH has the largest horizon. Result graphs also showed that α contributes to the area of BH horizons, whereas a shrinks it. To gain information on the stability of a circular orbit, we explored its effective potential. Our study showed that an infinity-incoming particle with a higher value of a required more energy to climb the effective potential than its lower value, and vice versa for the parameter α. The second and third panels ofFig. 1 demonstrate that the circular orbits are initially unstable but become stable along the axes. We also observed that α results in a decreasing circular orbit instability near the horizon of the BH. The instability of circular orbits near the Kerr-MOG BH's horizons is higher than that of the Schwarzschild-MOG BH. Interestingly, the magnetic field contributes to the stability of circular orbits.
It has been observed that particles have structural trajectories on the equatorial plane, and their nature becomes chaotic as the inclination angle varies from that plane. In principle, charged particle dynamics around a magnetized BH reveal four feasible regimes of the ionized Keplerian disk behavior: surviving in consistent epicyclic motion, changing into a chaotic toroidal state, collapsing due to escaping along the magnetic field paths, and collapsing due to falling into the BHs. From the study of particle trajectories, we noticed that the Schwarzschild BH captures the test particle at fixed values of other parameters. In contrast, in the Kerr BH, the test particles may either escape to infinity or be trapped by the BH, while in the Kerr-MOG BH, the test particle is trapped in some region around the BH and starts orbiting it (see Fig. 4).
Our study found various types of boundary conditions. The first is related to the existence of an outer boundary, where the BH should capture the particle. The second type is associated with the existence of an inner boundary, where the particle must escape to infinity. The third type relates to inner and outer boundaries between which the charged particle is trapped around the BH and forms a toroidal region. The last type is characterized by no inner or outer boundaries, where the BH can trap the particle or escape to infinity. The impact of the parameter α on particle trajectories can be explicitly observed in Figs. 4 and 5.
We investigated an approach for supermassive BHs to be responsible for producing UHECRs and used a unique, ultra-efficient regime of MPP and ionization of neutral particles, including neutron-beta decaying at the horizon of a rotating BH. In investigating the MPP, we found that for a larger magnetic field, the behavior of orbits becomes more chaotic due to the particle escaping toward infinity more quickly, which is analogous to the findings of [87]. In addition, charged particles from an ionized Keplerian disk may be accelerated near Kerr-MOG BHs with an MPP efficiency of more than
$ 10^{10} $ , allowing protons to accelerate to the following energies:•
$ 10^{21} $ eV in the vicinity of a supermassive BH of mass$ M = 10^{10}M_{\odot} $ and$ B = 10^{4} $ G;•
$ 10^{19} $ eV in the vicinity of M$ 87 $ , a supermassive BH of mass$ M = 7\times 10^{9}M_{\odot} $ and$ B=10^{2} $ G; and•
$ 10^{15.6} $ eV in the vicinity of SgrA$ ^* $ , a supermassive BH of mass$ M = 4\times 10^{6}M_{\odot} $ and$ B=10 $ G.This approach may be used for neutron stars with small masses compensated by enormous magnetic fields. However, such directions will be left for future research. Because relativistic electrons lose synchrotron radiation
$ 10^{10} $ times quicker than protons, heavier elements of UHECRs appear more likely in this scenario.Magnetic field data at the event horizon scale are required to predict the candidates of supermassive BHs within the proposed framework. Few precise measurements are available, but future VLBI observations will likely increase this number. We believe that the proposed concept of a supermassive BH as a UHECR power engine opens up new avenues to understanding this unique high-energy phenomenon and its significance in various high-energy scenarios.
Note that the MOG and GR + EM theories share some mathematical isomorphisms, and the vector-scalar interactions in MOG contribute to additional degrees of freedom. These impact stability in ways that differ from purely electromagnetic effects, providing unique modifications to orbit dynamics in the MOG framework.
-
JR acknowledges the ERASMUS+ ICM project for supporting his stay at the Silesian University in Opava.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: