Charged black holes in the Kalb-Ramond background with Lorentz violation: null geodesics and optical appearance of a thin accretion disk

Before the Event Horizon Telescope (EHT) revealed images of supermassive black holes, Karl Schwarzschild provided the first exact solution to Einstein’s field equations in 1916 [1]. In 1963, Roy Kerr introduced the precise solution describing a rotating black hole [2]. The release of images depicting supermassive black holes such as M87* and Sgr A* at the centers of M87 and Milky Way galaxies, respectively, has confirmed the existence of black holes [3−5]. These images show a central dark region, referred to as the black hole shadow, along with a bright photon sphere [6−8]. Synge first proposed the concept of the black hole shadow in 1966 [9]. The observed dark disk encircled by a bright ring is attributed to the powerful gravitational lensing near the black hole [10]. Photons falling within the shadow are absorbed, whereas photons orbiting near the shadow may reach a distant observer multiple times and manifest as part of the bright photon ring. This ring is often considered the boundary of the black hole horizon or the critical curve [11, 12]. In the Schwarzschild spacetime, the bound photon orbit is located at $ r=3M $, corresponding to an impact parameter $ b=3\sqrt{3}M $. Consequently, the black hole shadow is demarcated by the region defined by this parameter.

Observations and theoretical research on black holes continue to expand [13−17]. When analyzing black hole shadows, the accretion flow plays a decisive role in visibility. Various methods focus on the influence of the accretion disk's geometry and optical depth on its shadow structure [18−20]. Many studies utilize a thin accretion disk, as employed by Gralla et al. [21], who classified photon trajectories near the shadow into direct rings, lensing rings, and photon spheres. Although realistic accretion streams are often not spherically symmetric, idealized spherical models aid in elucidating black hole shadows. Various corrections to general relativity in modified gravity theories can alter the shadow’s size and shape, facilitating novel tests of gravity. Additionally, black hole parameters such as charge and spin have a significant effect on shadows [22−28].

Black holes in the Kalb-Ramond background present an interesting scenario for exploring possible Lorentz symmetry violations [29−33]. Such a background may modify the spacetime geometry, black hole thermodynamics, and the behavior of matter and radiation around the event horizon [34, 35]. It may also alter the silhouette of the black hole shadow [36−41]. Because the Kalb-Ramond field emerges naturally in string theory, its study can deepen our understanding of fundamental physics [42−45]. Motivated by these considerations, we focus on examining the shadows and observational characteristics of a charged black hole in the Kalb-Ramond background, with the Lorentz violation parameter set to $ l=0.01 $. We study the observed intensity of the shadow under various charge values and thin accretion disk emission models.

The remainder of this paper is structured as follows. Section II derives the null geodesics of a charged black hole in the Kalb-Ramond background and explores the corresponding photon sphere radii. Section III applies a ray-tracing technique to evaluate the observational features of a thin accretion disk for different emission models. Section IV compares our results with the standard Reissner-Nordström black hole to highlight the effects of Lorentz violation. Section V summarizes our main findings.

In general relativity, the study of a charged black hole in the Kalb-Ramond field within a spherically symmetric background has a rich theoretical context. The Kalb-Ramond field, originally introduced in string theory as a two-form gauge field, can have significant implications for the properties of black holes. We start from the Kalb-Ramond field action [46, 47]:

where

Here, $ R $ refers to the Ricci scalar, $ \eta $ is the coupling constant, $ \xi_{1,2} $ denotes the non-minimal coupling constant between gravity and the Kalb-Ramond field, and $ \mathcal{L}_{\mathrm{M}} $ represents the Lagrangian of the electromagnetic field. To maintain invariance under Lorentz transformations, we assume that $ V\left(B^{\mu \nu} B_{\mu \nu} \pm b^2\right) $ depends on $ B^{\mu \nu} B_{\mu \nu} $.

The modified Einstein equation is obtained by varying the action with respect to the metric $ g^{\mu \nu} $ and is given by the following form:

Here, $ T_{\mu \nu}^{\mathrm{M}} $ is the energy-momentum tensor of the electromagnetic field, and $ T_{\mu \nu}^{\mathrm{KR}} $ is the effective energy-momentum tensor of the Kalb-Ramond field.

In the vacuum, the modified Einstein equation can be expressed as

When the cosmological constant $ \Lambda $ is set to zero, the metric describing a charged black hole in a spherically symmetric spacetime within the framework of the Kalb-Ramond field can be expressed as follows [48]:

where

Here, $ M $ and $ Q $ denote the mass and charge parameters, respectively. The Kalb-Ramond field originates from the rank-two antisymmetric tensor field in string theory, and the introduction of the Lorentz-violating parameter $ l $ in Eq. (9) is precisely derived from the Kalb-Ramond field. In the context of Lorentz symmetry violation, this parameter is used to modify the geometric properties and topological characteristics of spacetime. The strength of the Lorentz-violating effects is represented by the parameter $ l $ in Eq. (9). Such modifications are consistent with the framework of effective field theory, as similar terms can result from higher-dimensional operators or non-minimal couplings [29, 43, 44].

In string theory, the Kalb-Ramond field couples to the spacetime metric of black holes, potentially leading to Lorentz symmetry-violating corrections. These corrections influence the black hole solutions; consequently, the Kalb-Ramond field may affect key features of spacetime, such as the event horizon, photon sphere, and other important characteristics. To ensure that the Lorentz-violating effects remain perturbative and do not significantly alter the geometric structure of the black hole, we set the parameter in Eq. (9) to a small value ($ l=0.01 $) [29, 43, 44].

When $ l=0 $, this metric reduces to the Reissner-Nordström black hole. Further setting $ Q=0 $ recovers the Schwarzschild black hole. Throughout this work, we focus on the case $ l=0.01 $, leading to

The horizon radius of this charged black hole follows from

The largest positive root of Eq. (11) gives the event horizon. To ensure the black hole solution exists, $ Q $ must satisfy $ \dfrac{Q^2}{M^2} \leq (1-l)^3 $. Therefore, we restrict $ 0 \leq Q \leq 0.6 $.

Subsequently, we investigate the photon motion via the Euler-Lagrange equation

where $ \lambda $ is the affine parameter, and $ \dot{x}^\mu $ denotes the photon’s four-velocity. The Lagrangian $ \mathcal{L} $ is

Because the spacetime is spherically symmetric, we restrict photon motion to the equatorial plane $ \theta=0 $, where $ \dot{\theta}=0 $. The time-translation and $ \alpha $-rotational symmetries yield two conserved quantities:

The modification introduced by the Kalb-Ramond background primarily affects the conserved quantities of the system in terms of the parameter $ l $. As shown in Eq. (14), the parameter $ l $ has an impact on the conserved quantity $ E $ but has no effect on the conserved quantity $ l $.

Generally, the Hamiltonian form of the equation of motion is $\dot{x}^\mu=\dfrac{\partial H}{\partial p_\mu}, \dot{p}_\mu=-\dfrac{\partial H}{\partial x^\mu}$. By combining the corresponding conserved quantities and the specific spacetime background, we can obtain an equation of motion similar to that in the paper. For an axisymmetric spacetime, it is relatively more complex, and the Carter constant must be introduced to obtain the analytical form of the equation of motion. In this paper, it is a spherically symmetric spacetime, which is relatively simple. By combining the conserved quantities $ E $ and $ L $, as well as the null geodesic equation, we can describe the equation of motion of photons on the equatorial plane as

where "$ \pm $" indicates the motion direction. We define the impact parameter as $b_c=\dfrac{L}{E}=\dfrac{r^2\dot{\varphi}}{F(r)\dot{t}}$.

From Eq. (15), we have

with

The photon sphere radius $ r_p $ and critical impact parameter $ b_h $ (shadow radius as seen by a distant observer) satisfy

As shown in Fig. 1, the effective potential $V_{\rm eff}$ gradually increases from the event horizon radius $ r_h $, reaches its peak at the photon sphere radius $ r_p $, and then begins to decrease. Both plots in Fig. 1 show that, as the charge $ Q $ and Lorentz-violating parameter $ l $ increase, the peak value of the effective potential $V_{\rm eff}$ increases, and the radius of the photon sphere shrinks slightly. We find that $ l $ alters only the effective potential and does not transform the conditions for the stability of the photon sphere.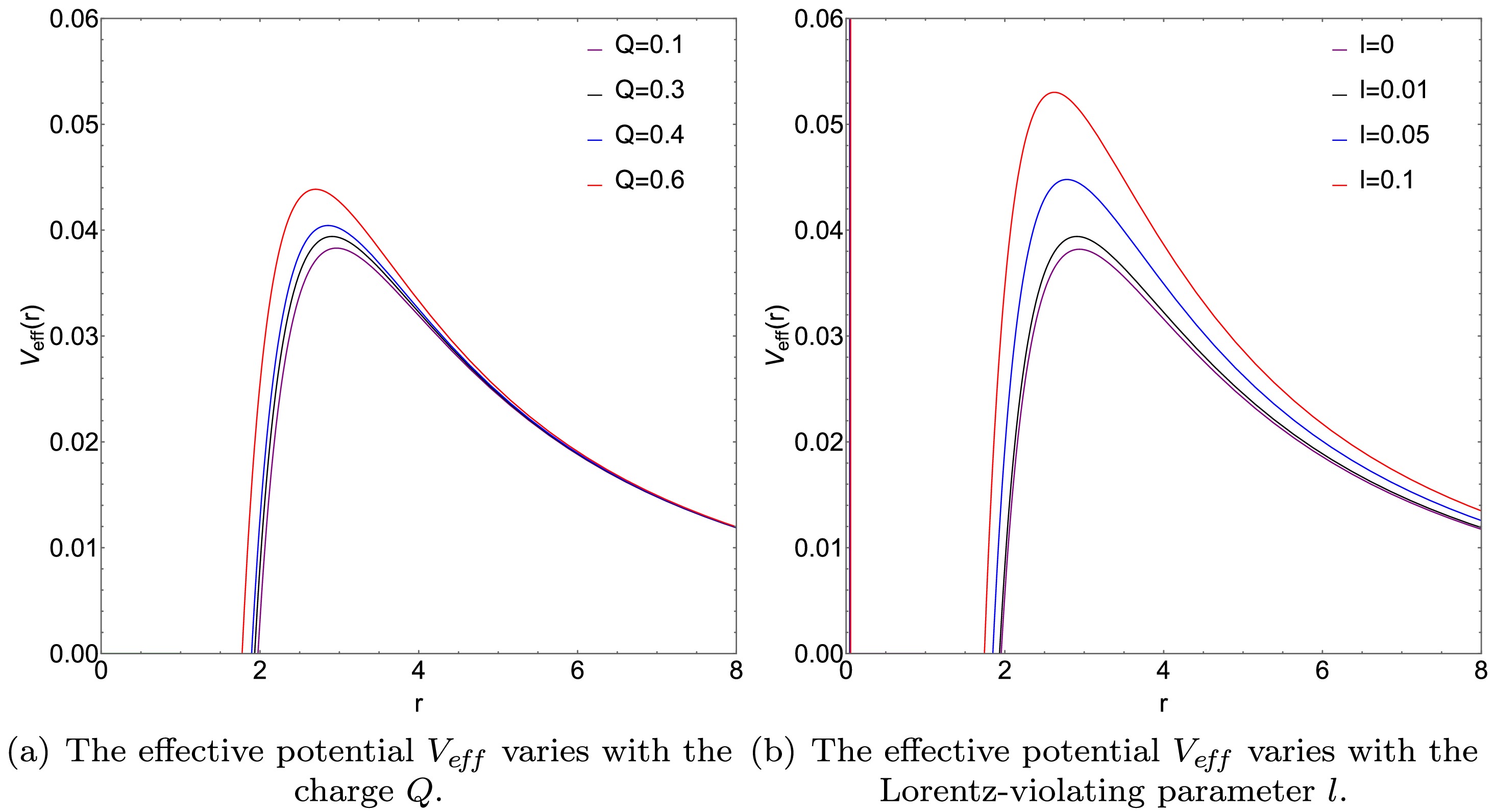

Figure 1.  (color online) With the mass $ M $ set to 1, the contours of the effective potential $V_{\rm eff}$ and the impact parameter $ b_c $ are presented.

By effectuating a Taylor expansion of the metric function presented in Eq. (9), we derive

Through the combination of Eq. (18) and (19), we can obtain the analytical expressions for $ r_p $ and $ b_h $

where

Through the photon sphere radius $ r_p $ and Eq. (19), we can obtain the shadow radius $ r_s $ as

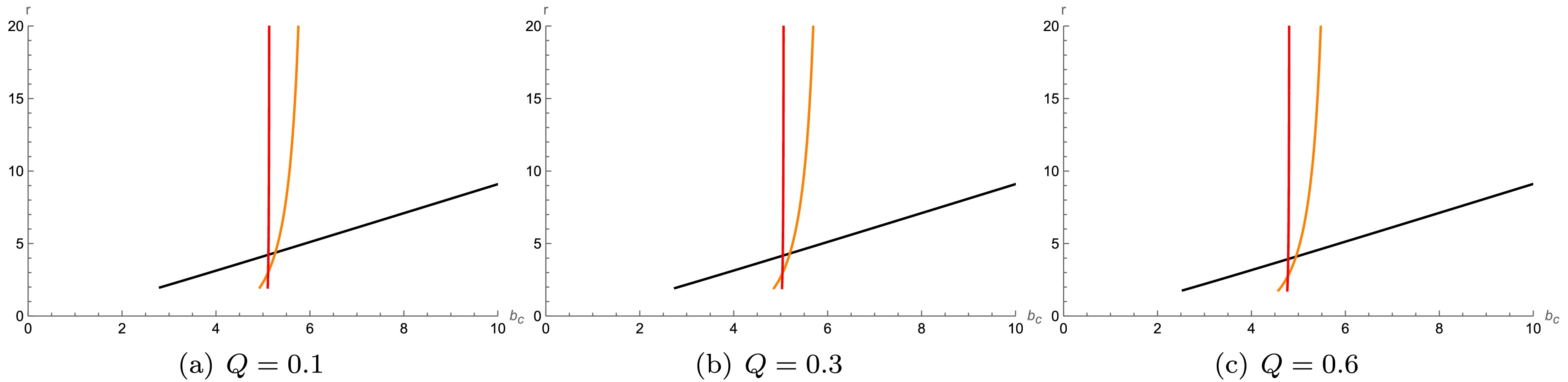
Subsequently, we fix the mass of the black hole at $ M = 1 $. Under this condition, the photon sphere radius $ r_p $, black hole shadow radius $ r_s $, and critical impact parameter $ b_h $ depend on $ Q $ and $ l $. From Fig. 2, we observe that as the parameters $ l $ and $ Q $ increase, they all exhibit a decreasing trend. As the parameters $ l $ and $ Q $ increase, they all exhibit a decreasing trend.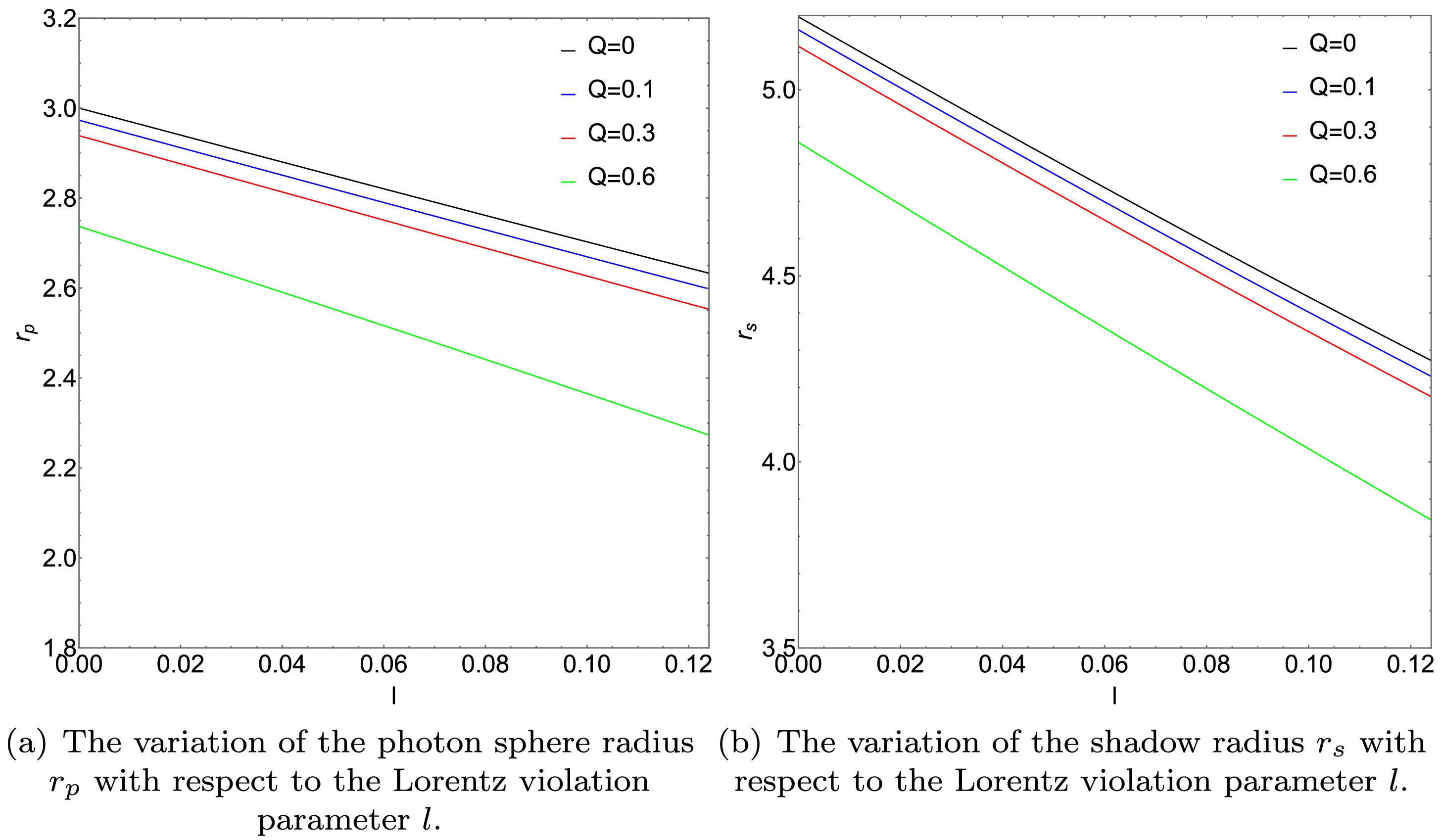

Figure 2.  (color online) Photon sphere radius $ r_p $ and shadow radius $ r_s $ as functions of the Lorentz-violation parameter $ l $ for a mass $ M $ of 1.

In Tables 1 and 2, we calculate a variation patterns of the values of $ b_h $, $ r_p $, and $ r_h $ within the Kalb-Ramond black hole. We can observe that the values of each parameters decrease as both $ Q $ and $ l $ increase. In Table 3, we discuss the change in the values of $ b_h $, $ r_p $, and $ r_h $ with $ Q $ in a Reissner-Nordström black hole. We also find a similar result, that is, each of these parameters decreases as $ Q $ increases.

$ l $	$ b_h $	$ r_p $	$ r_h $
0	5.11679	2.93875	1.95394
0.01	5.0378	2.90747	1.93297
0.05	4.72632	2.78228	1.84876
0.1	4.34993	2.62677	1.74261

Table 1.  Variation in $ b_h $, $ r_p $, and $ r_h $ for a standard Kalb-Ramond black hole ($ M=1 $ and $ Q=0.3 $) as functions of $ l $.

$ Q $	$ b_h $	$ r_p $	$ r_h $
0.1	5.1096	2.96318	1.97489
0.2	5.08295	2.94254	1.95938
0.3	5.0378	2.90747	1.93297
0.4	4.9729	2.85686	1.89470
0.5	4.88629	2.78891	1.84298
0.6	4.77487	2.70071	1.77515

Table 2.  Critical impact parameter $ b_h $, photon sphere radius $ r_p $, and event horizon radius $ r_h $ for a charged black hole in the Kalb-Ramond background ($ l=0.01, M=1 $) as functions of $ Q $.

$ Q $	$ b_h $	$ r_p $	$ r_h $
0.1	5.18748	2.99332	1.99499
0.2	5.16124	2.97309	1.97980
0.3	5.11679	2.93875	1.95394
0.4	1.91652	2.88924	5.05298
0.5	4.96791	4.82288	1.86603
0.6	4.85869	2.73693	1.80000

Table 3.  Variation in $ b_h $, $ r_p $, and $ r_h $ for a standard Reissner-Nordström black hole ($ M=1 $) as functions of $ Q $.

We introduce $u= {1}/{r}$. From Eq. (15), we can obtain

thus

Photons with $ b_c<b_h $ fall into the black hole, those with $ b_c=b_h $ perpetually orbit on the photon sphere, and those with $ b_c>b_h $ escape to infinity.

For an observer at infinity, we analyze trajectories governed by Eq. (24). Through transformation, we find

whose integral yields

We classify photon trajectories based on the number of times $ n $ they cross the equatorial plane:

We define: - Direct orbits if $ n<0.75 $, - Lensing orbits if $ 0.75<n<1.25 $, - Photon orbits if $ n>1.25 $.

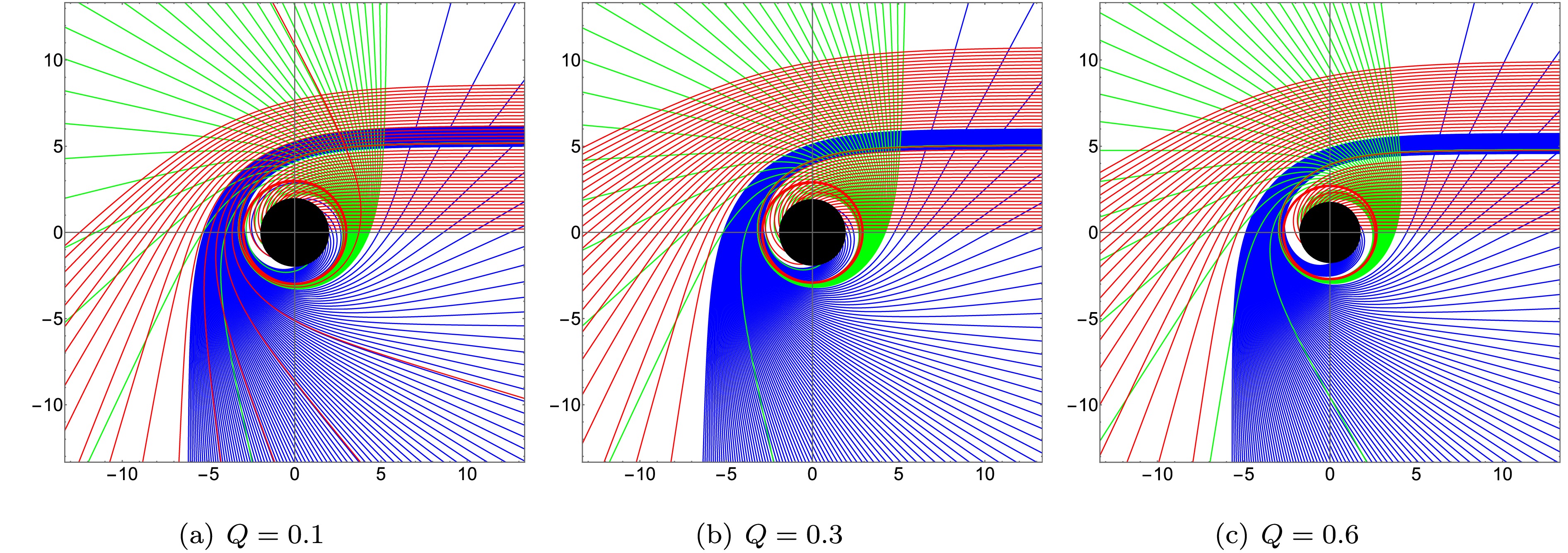
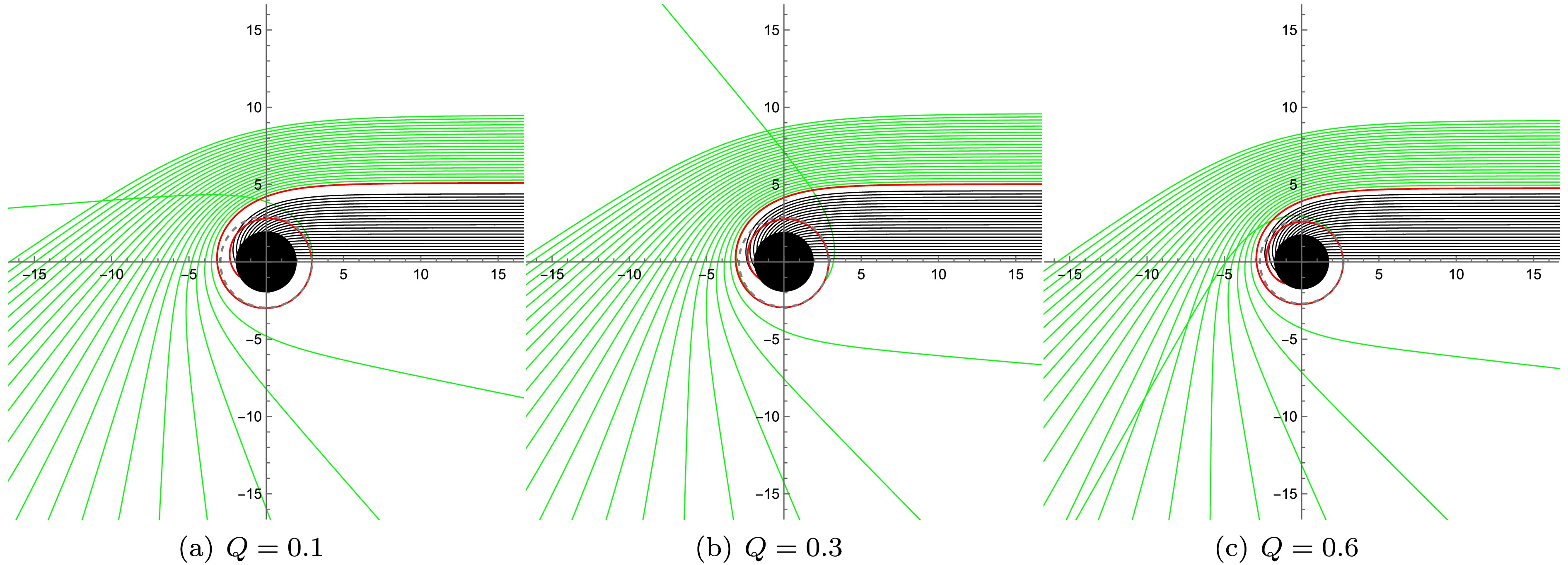
Figure 3 directly shows the classification of trajectories. As $ Q $ increases from 0.1 to 0.6, the relevant ranges of $ b_c $ for direct/lensing/photon orbits shrink, and the radius of the photon sphere decreases. Table 4 shows the corresponding calculation results. And Fig. 4 presents the photon trajectories with different collision parameters. Fig. 5 further depicts the photon orbits in polar coordinates, showing how a larger $ Q $ decreases both the photon sphere radii and horizon radius but slightly increases their thickness.

Figure 3.  (color online) Variation in the intersection number $ n $ with impact parameter $ b_c $ for $ M=1 $ and different values of $ Q $. Red curves represent direct orbits $ (n<0.75) $, blue curves lensing orbits $ (0.75<n<1.25) $, and green curves photon orbits $ (n>1.25) $.

Figure 5.  (color online) Photon trajectories for $ M=1 $ and different values of $ Q $. The black region represents the black hole horizon, the red circle is the photon sphere, and red/blue/green lines correspond to direct, lensing, and photon orbits, respectively.

Figure 4.  (color online) Polar-coordinate trajectories of photons for $ M=1 $ under different values of $ Q $. The black disk denotes the black hole horizon, and gray dashed circles mark the photon spheres.

Consider a thin accretion disk lying in the equatorial plane, observed from the north pole at infinity. The emission is assumed isotropic. The observed intensity is proportional to the number of disk-crossings. Through Liouville’s theorem [21],

Integrating over frequency gives

Summing over each intersection $ m $ with the disk yields

where $ r_m(b_c) $ is the transfer function identifying the radial position on the disk for each crossing.

Figure 6 plots the first three transfer functions. The slope of each curve is its demagnification factor. Direct emission ($ m=1 $) has a near-constant slope. Lensing ($ m=2 $) has a steeper slope, and the photon ring ($ m=3 $) exhibits an almost infinite slope. Hence, direct emission dominates the total observed intensity, whereas lensing and photon rings are strongly demagnified. As $ Q $ increases, all three curves shift to smaller radii. This analytical result is consistent with our numerical simulations, further supporting our conclusion.

Figure 6.  (color online) Transfer function for different $ Q $ values. Black curves correspond to direct rings, orange to lensing rings, and red to photon rings.

We consider three emission models:

1. Model A: Radiation starts from the innermost stable circular orbit ($ r_{\mathrm{ISCO}} $) with a quadratic decay [11]:

The ISCO in spherical symmetry is

2. Model B: Radiation starts from the photon sphere $ r_p $ and decays cubically [11]:

3. Model C: Radiation originates from the event horizon $ r_h $ with a certain arctangent-based decay [11]:

Figures 7, 8, and 9 show the emission intensity vs. $ r $, observed intensity vs. $ b_c $, and two-dimensional snapshots for Models A, B, and C, respectively, at different $ Q $ values.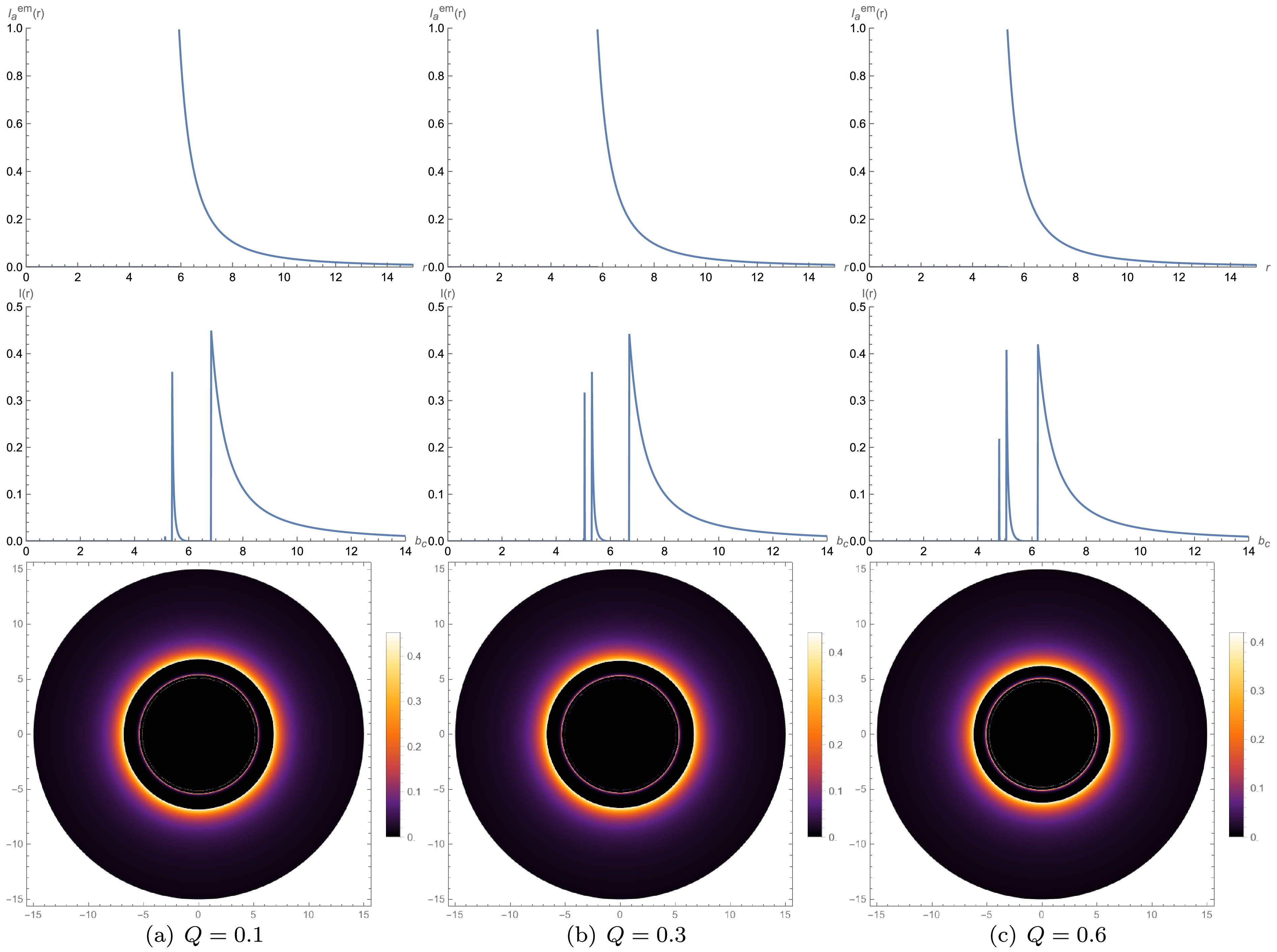

Figure 7.  (color online) Model A results, where radiation starts from $ r_{\mathrm{ISCO}} $. First row: emission intensity vs. $ r $. Second row: observed intensity vs. $ b_c $. Third row: two-dimensional appearance in the celestial plane.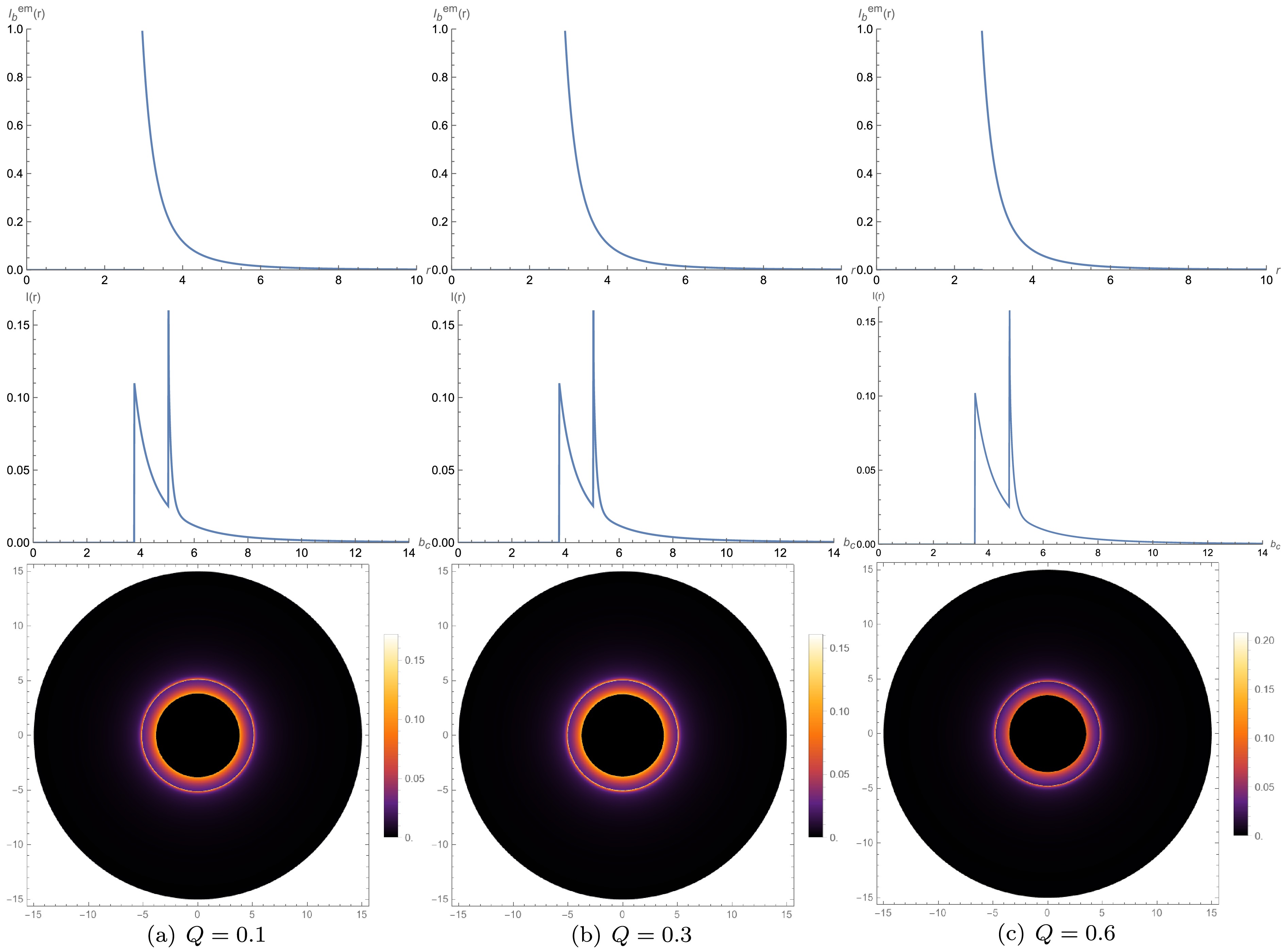

Figure 8.  (color online) Model B results, where radiation starts from $ r_p $, with the same plotting scheme as that of Fig. 7.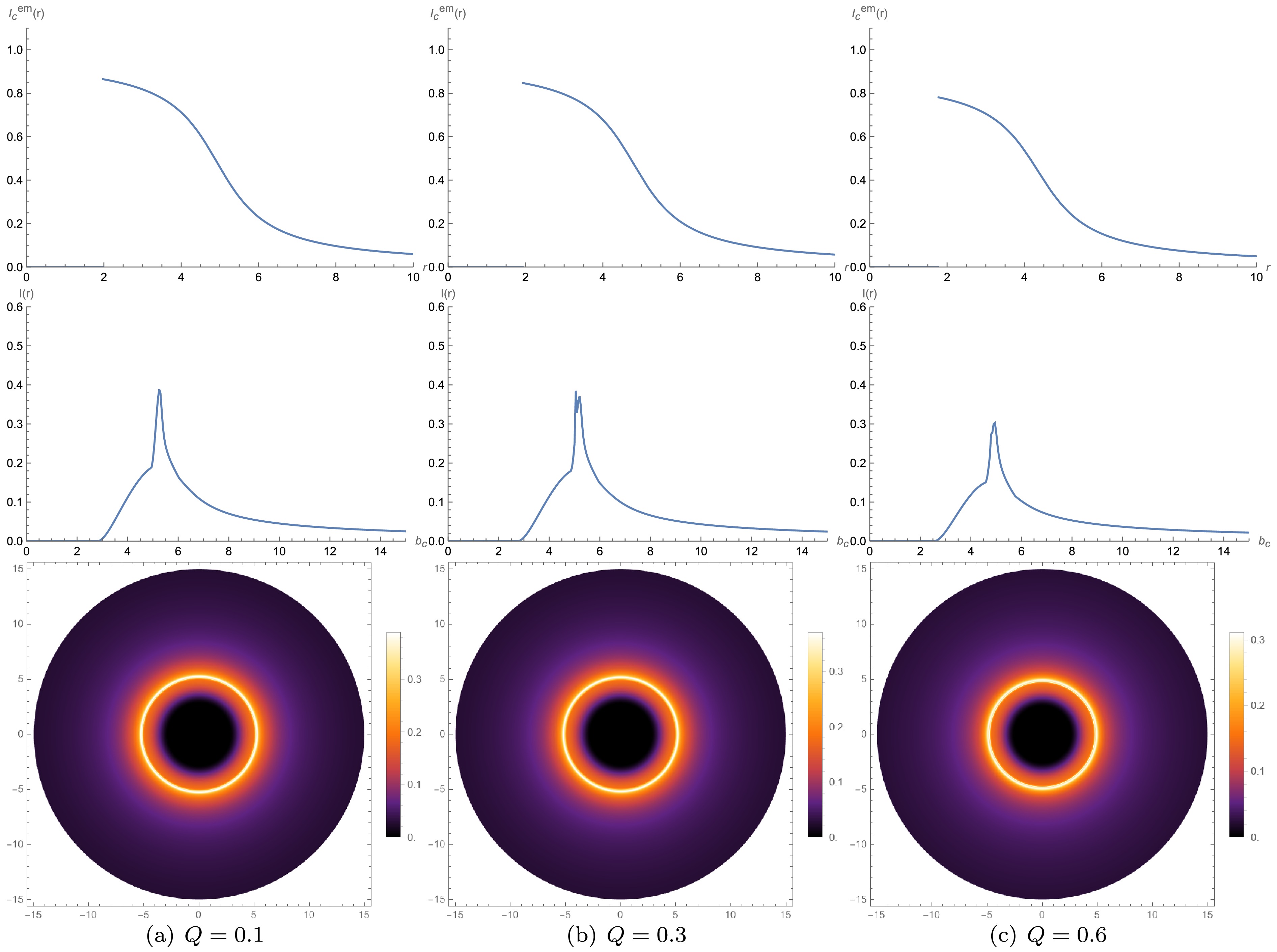

Figure 9.  (color online) Model C results, where radiation starts from $ r_h $, with the same plotting scheme as that of Fig. 7.

Using the first model, we have constructed Fig. 7. The first row of Fig. 7 represents the relationship between the emission intensity and $ r $. The emission intensity reaches a peak when $r=r_{\rm ISCO}$ and then rapidly decays to zero. When the charge quantity $ Q=0.1 $, the emission peak is at $ r \approx 5.92 \mathrm{M} $. When the charge quantity $ Q=0.3 $, the emission peak is at $ r \approx 5.78 \mathrm{M} $. When the charge quantity $ Q=0.6 $, the emission peak is at $ r \approx 5.32 \mathrm{M} $. We find that the larger the charge, the smaller the position of the curve peak, and the peak value decreases slightly.

This trend can be explained by the increasing gravitational influence of the charged black hole, which causes the emission region to contract. The decreased emission intensity with increasing $ Q $ also suggests a possible modification in the underlying emission mechanisms as the charge affects the photon trajectories.

The second row represents the relationship between the observed intensity by the observer and the impact parameter $ b_c $. The three images in the second row all have three peaks, which correspond to the photon sphere, lens ring, and direct ring as $ b_c $ increases. When the charge quantity $ Q=0.1 $, the observed intensity peaks occur at $ b_c \approx 5.12 \mathrm{M} $, $ b_c \approx 5.36 \mathrm{M} $, and $ b_c \approx 6.80 \mathrm{M} $. Similarly, when $ Q=0.3 $, the peaks of the observed intensities are located at $ b_c \approx 5.01 \mathrm{M} $, $ b_c \approx 5.30 \mathrm{M} $, and $ b_c \approx 6.67 \mathrm{M} $. For $ Q=0.6 $, the observed intensity peaks are also found at $ b_c \approx 4.78 \mathrm{M} $, $ b_c \approx 5.04 \mathrm{M} $, and $ b_c \approx 6.20 \mathrm{M} $. Additionally, as the charge quantity $ Q $ increases, the positions of the emission peak and observed intensity peak both shift inward.

In the region of the impact parameter $ b_c $ corresponding to these three rings, the photon sphere is the smallest, the lens ring is smaller, and the direct ring is the largest. Therefore, the direct ring contributes the most to the observed intensity, the photon sphere contributes the least, and the lens ring contributes slightly more than the photon sphere. Thus, the observed intensity is primarily derived from direct emission. At the same charge quantity $ Q $, the position of the emission peak is smaller than the observed peak position of the direct ring, a phenomenon caused by the gravitational lensing effect. The third row represents the appearance of a two-dimensional thin disk with different charge quantities $ Q $ in the celestial coordinate system. We can observe that each two-dimensional image has three rings, corresponding to the photon sphere, lens ring, and direct ring from the inside to the outside. Because the photon sphere contributes only slightly to the observed intensity, it forms a weak ring. The brightness of the lens ring is slightly greater than that of the photon sphere. The outermost direct ring is the brightest and widest because it is the main source of the total observed intensity.

In Fig. 8, we have plotted the emission intensity versus radius $ r $ for the second emission model, starting from the photon sphere, the intensity observed by the observer versus the impact parameter $ b_c $, and the two-dimensional image of the black hole starting from the photon sphere. From the emission intensity versus radius r graph, we know that no radiation occurs at point $ r<r_p $. At point $ r=r_p $, the radiation intensity reaches a peak. At point $ r>r_p $, the radiation intensity begins to decrease. When the charge quantity $ Q=0.1 $, the emission peak is at $r \approx 2.96 \, \mathrm{M}$. When the charge quantity $ Q=0.3 $, the emission peak is at $r \approx 2.90 \,\mathrm{M}$. When the charge quantity $ Q=0.6 $, the emission peak is at $r \approx 2.70 \,\mathrm{M}$. The first and second emission models follow the same pattern: the larger the charge quantity, the smaller the position of the peak of the emission intensity. The peak also slightly decreases. The observed intensity of the second model differs from the first model, as the second model starts radiating from the photon sphere. We find that the peaks of the photon sphere and the lens ring overlap, making them difficult to distinguish. The contribution of the lens ring to the observed intensity in the second model is greater than that in the first model, but similarly, the contribution of the photon sphere is the smallest, and the observed intensity still primarily results from direct emission. Examining the two-dimensional black hole images in the third row, we observe that the radiation regions of the photon sphere and the lens ring overlap. As $ Q $ increases, the range of the central area narrows, and the brightness of the rings also diminishes. With the increase in $ Q $, the position and peak of the emission intensity, as well as the ranges of the photon sphere, lens ring, and direct emission ring corresponding to the impact parameter $ b_c $, and the peaks of the observed intensity, all decrease.

The third model involves radiation starting from the black hole’s event horizon $ r_h $. By examining Fig. 9, we observe that the larger the charge quantity, the smaller the position of the emission intensity peak, and the peak value also slightly decreases. In this model, the observed intensity still primarily results from direct emission. Similar to the second model, the peaks of the photon sphere and the lens ring overlap, making them difficult to distinguish. However, compared with the first two models, the photon sphere and the lens ring contribute more significantly to the observed intensity. In the appearance of the two-dimensional thin disk, the bright photon sphere and the lens ring overlap to form a luminous area.

In each model, the emission intensity peaks near its start radius ($ r_{\mathrm{ISCO}} $, $ r_p $, or $ r_h $) and rapidly decays. For a distant observer, the direct ring provides the largest contribution to observed intensity, while lensing and photon sphere yield smaller (though non-negligible) contributions. As $ Q $ increases, both the peak value and its radial location shift inward.

Setting $ l=0 $ recovers the Reissner-Nordström solution [49]

The Lorentz-violating parameter $ l $ is tightly constrained and may be extremely close to zero. Here, we compare the charged black hole in the Kalb-Ramond background ($ l=0.01 $, $ l=0.05 $ and $ l=0.1 $) to Reissner-Nordström at $ Q=0.3 $.

From Table 1, as $ l $ increases, $ b_h $, $ r_p $, and $ r_h $ decrease for the Kalb-Ramond black hole. In contrast, Table 5 and Fig. 10 demonstrate that the photon sphere and lensing ring for the Kalb-Ramond black hole are narrower. As $ l $increases, the photon and lensing rings of the Kalb-Ramond black hole become progressively narrower, although their thickness slightly decreases. We observe that this behavior is in contrast to the result seen earlier, where an increase in $ Q $ leads to a different outcome. Lorentz violation enhances the gravitational pull, shrinking these rings. From their transfer functions, direct emission remains the primary contributor. The photon sphere of Reissner-Nordström is more prominent and thus easier to observe.

	Direct $ (n<0.75) $	Lensing $ (0.75<n<1.25) $	Photon $ (n>1.25) $
Reissner-Nordström	$ b_c<4.93142 $ or $ b_c>6.09956 $	$ 4.93142<b_c<5.10795 $ and $ 5.1499<b_c<6.09956 $	$ 5.10795<b_c<5.1499 $
$ l=0.01 $	$ b_c<4.85905 $ or $ b_c>5.97711 $	$ 4.85905<b_c<5.0294 $ and $ 5.06918<b_c<5.97711 $	$ 5.0294<b_c<5.06918 $
$ l=0.05 $	$ b_c<4.57161 $ or $ b_c>5.50608 $	$ 4.57161<b_c<4.71861 $ and $ 4.75055<b_c<5.50608 $	$ 4.71861<b_c<4.75055 $
$ l=0.1 $	$ b_c<4.21697 $ or $ b_c>4.95635 $	$ 4.21697<b_c<4.33787 $ and $ 4.36176<b_c<4.95635 $	$ 4.33787<b_c<4.36176 $

Table 5.  Range of $ b_c $ for direct, lensing, and photon orbits comparing Reissner-Nordström with Kalb-Ramond ($ l=0.01 $, $ l=0.05 $ , and $ l=0.1 $) black holes at $ Q=0.3 $.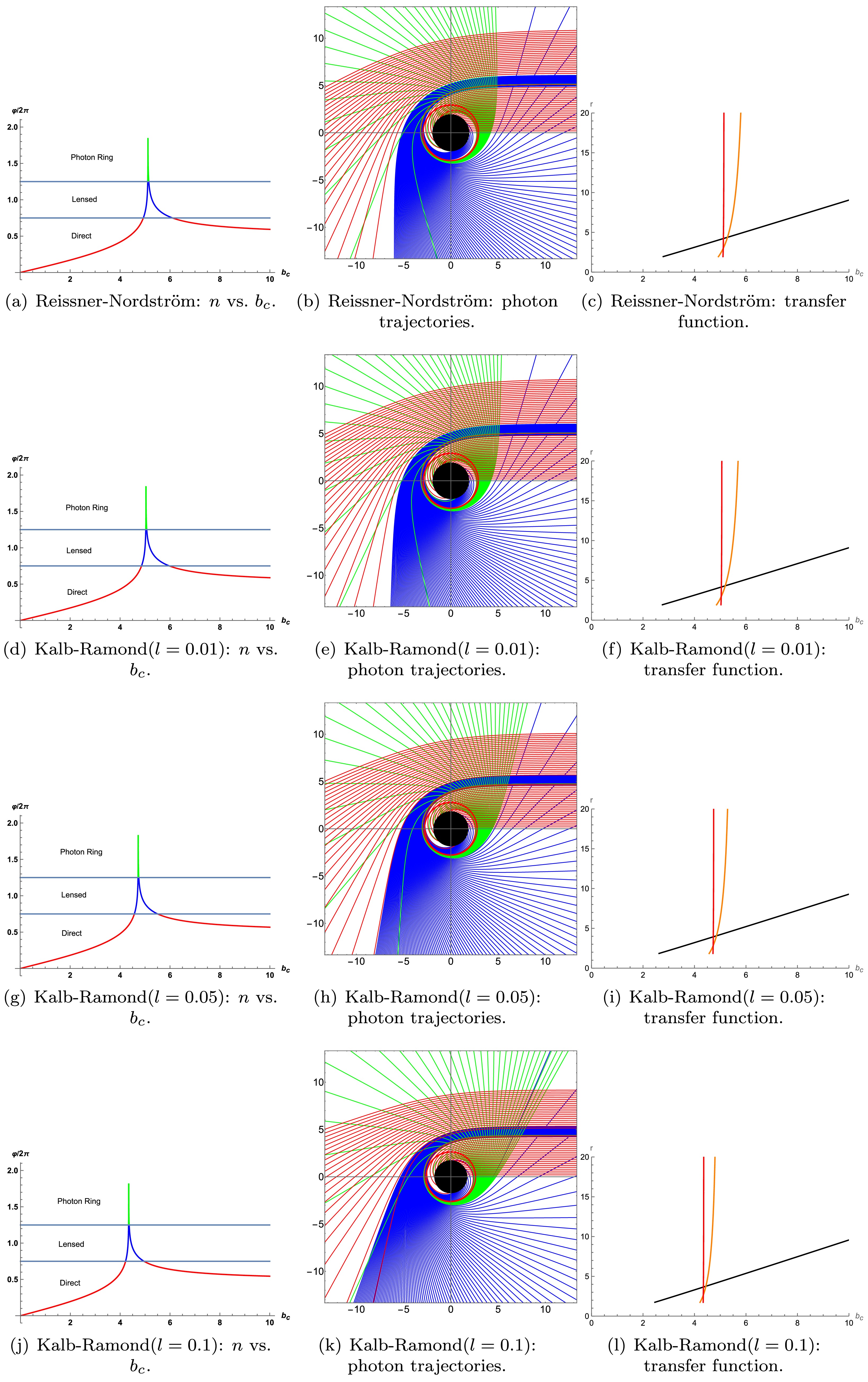

Figure 10.  (color online) Comparison of Reissner-Nordström ($ l=0 $) vs. Kalb-Ramond ($ l=0.01 $, $ l=0.05 $ and $ l=0.1 $) black holes at $ Q=0.3 $. The upper row shows $ n(b_c) $, photon trajectories, and transfer functions for Reissner-Nordström black holes; the following lines show the same scenario for Kalb-Ramond black holes ($ l=0.01 $, $ l=0.05 $ and $ l=0.1 $).

$ Q $	Direct $ (n<0.75) $	Lensing $ (0.75<n<1.25) $	Photon $ (n>1.25) $
0.1	$ b_c<4.93478 $ or $ b_c>6.03871 $	$ 4.93478<b_c<5.10164 $ and $ 5.13981<b_c<6.03871 $	$ 5.10164<b_c<5.13981 $
0.3	$ b_c<4.85905 $ or $ b_c>5.97711 $	$ 4.85905<b_c<5.0294 $ and $ 5.06918<b_c<5.97711 $	$ 5.0294<b_c<5.06918 $
0.6	$ b_c<4.21945 $ or $ b_c>5.50968 $	$ 4.21945<b_c<4.43842 $ and $ 4.50112<b_c<5.50968 $	$ 4.43842<b_c<4.50112 $

Table 4.  Range of $ b_c $ for direct, lensing, and photon orbits under different $ Q $ values.

Figures 11 and 12 compare the black hole images under three emission models. In all three models, the emission intensity reaches a peak and then decreases rapidly. The positions of the peak emission intensity for the Reissner-Nordström black hole in the three models are denoted as $ r \approx 5.87 \mathrm{M} $, $ r \approx 2.94 \mathrm{M} $, and $ r \approx 1.95 \mathrm{M} $, respectively. For the charged black hole in the Kalb-Ramond background with $ l=0.01 $, the positions of the peak emission intensity in the three models are denoted as $ r \approx 5.79 \mathrm{M} $, $ r \approx 2.89 \mathrm{M} $, and $ r \approx 1.92 \mathrm{M} $, respectively. When $ l=0.05 $, the corresponding peak positions are located at $ r \approx 5.53 \mathrm{M} $, $ r \approx 2.78 \mathrm{M} $, and $ r \approx 1.82 \mathrm{M} $ respectively. Moreover, when $ l=0.1 $, the corresponding peak positions respectively change to $ r \approx 5.21 \mathrm{M} $, $ r \approx 2.62 \mathrm{M} $, and $ r \approx 1.73 \mathrm{M} $. Through the above analysis, we can notice a pattern, that is, emission intensity of the black hole decreases as $ l $ increases. In addition, we also find that the peak emission intensity of the charged black hole in the Kalb-Ramond background with $ l $ is also slightly less than that of the Reissner-Nordström black hole. In each model, the peak emission intensities for the Lorentz-violating black hole are slightly smaller and occur at smaller radii. This shift indicates that Lorentz-violation leads to reduced emission strength and more compact emission regions.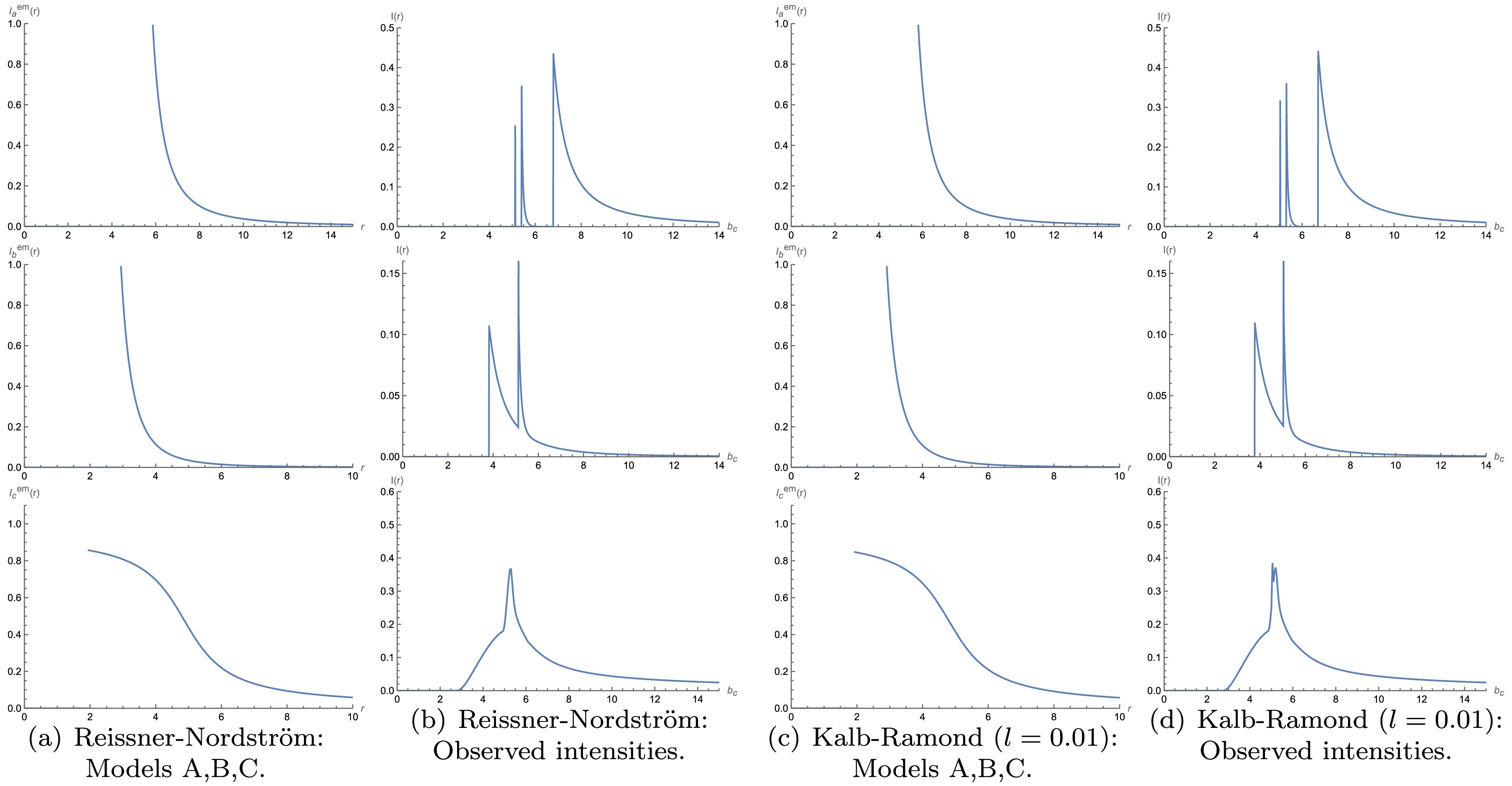

Figure 11.  (color online) Observational characteristics of a thin accretion disk around Reissner-Nordström ($ M=1 $, $ Q=0.3 $) and Kalb-Ramond black hole ($ l=0.01 $, $ M=1 $, $ Q=0.3 $) for Models A, B, and C. The first and third columns: emission intensity vs. $ r $. The second and fourth columns: observed intensity vs. $ b_c $.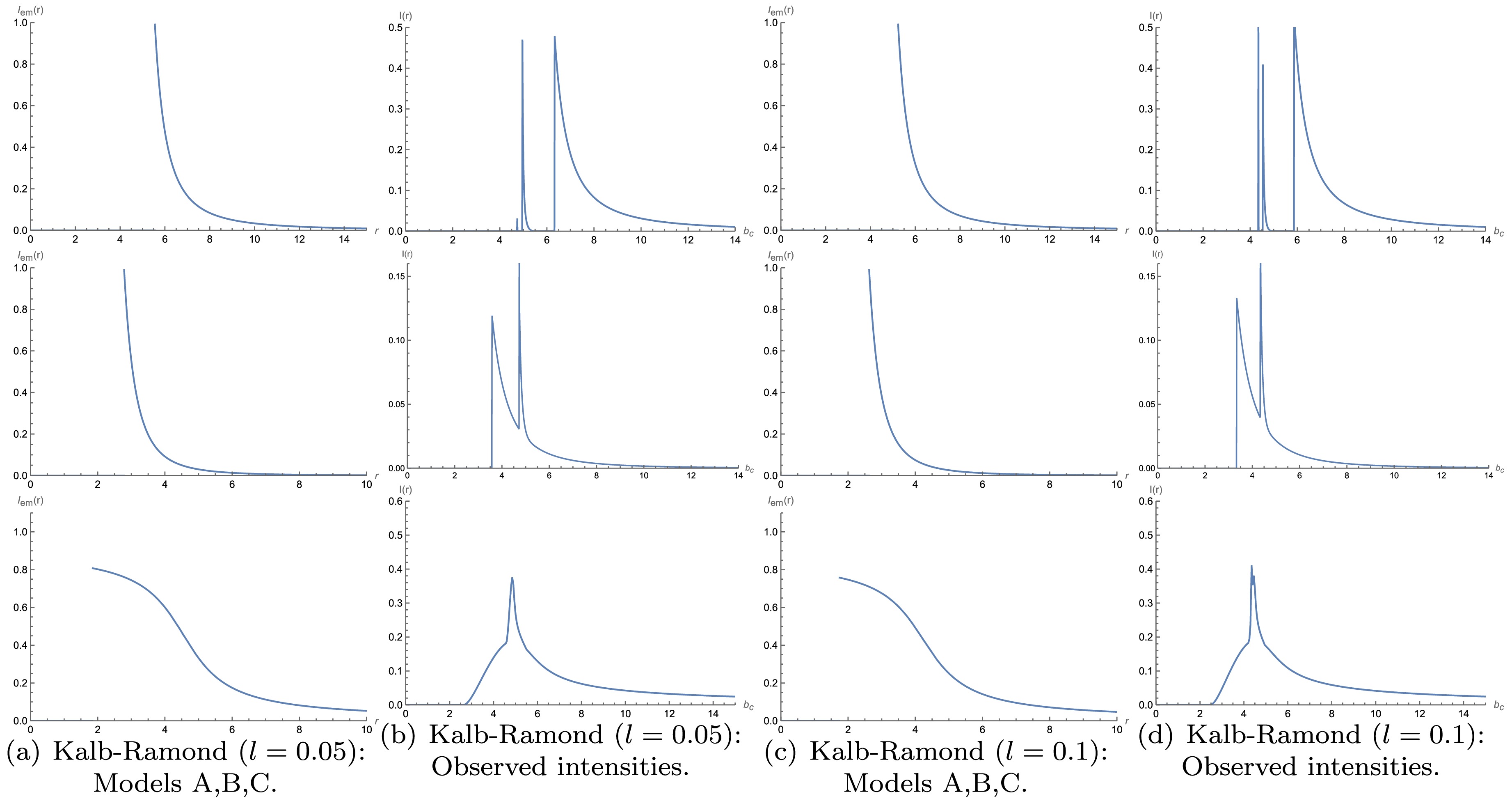

Figure 12.  (color online) Observational characteristics of a thin accretion disk around a Kalb-Ramond black hole ($ l=0.05 $, $ M=1 $, $ Q=0.3 $) and Kalb-Ramond black hole ($ l=0.1 $, $ M=1 $, $ Q=0.3 $) for Models A, B, and C. The plotting scheme is the same as that of Fig. 11.

We compare the observed intensity images in Figs. 11 and 12. For the observed intensity distribution of Model $\rm A$, in the case of the Reissner-Nordström black hole, the observed specific intensity reaches its peak at $ b_c \approx 5.10 \mathrm{M} $, corresponding to direct emission. A narrower and slightly lower peak appears at $ b_c \approx 5.38 \mathrm{M} $, corresponding to the lensing ring. An extremely narrow peak is observed at $ b_c \approx 6.75 \mathrm{M} $, which corresponds to the photon sphere. In the charged black hole within the Kalb-Ramond background with $ l=0.01 $, the corresponding positions shift to $ b_c \approx 5.01 \mathrm{M} $, $ b_c \approx 5.30 \mathrm{M} $, and $ b_c \approx 6.67 \mathrm{M} $, respectively.

When considering the observed intensity distribution of Model $\rm B$, within the Reissner-Nordström black hole, direct emission is observed at $b_c \approx 3.78 \mathrm{M} $, whereas the lensing ring makes its appearance at $ b_c \approx 5.12 \mathrm{M} $. In the charged black hole within the Kalb-Ramond background with $ l=0.01 $, these positions shift to $ b_c \approx 3.73 \mathrm{M} $ and $ b_c \approx 5.02 \mathrm{M} $, respectively. The emission regions of the photon sphere and lensing ring exhibit an overlapping pattern, and the peak intensity of the lensing ring is greater than that of the direct emission.

In Model $\rm C$, within the Reissner-Nordström black hole, the observed intensity distribution reveals that direct emission emerges around $ b_c \approx 2.85 \mathrm{M} $, whereas the lensing ring appears at approximately $ b_c \approx 5.26 \mathrm{M} $, overlapping with the direct emission. However, in a charged black hole influenced by the Kalb-Ramond background with $ l=0.01 $, these positions shift to $ b_c \approx 2.79 \mathrm{M} $ and $ b_c \approx 5.07 \mathrm{M} $, respectively. As $ l $ increases, both the peak intensity and its corresponding position gradually decrease.

Hence, Lorentz violation leads to smaller photon sphere, event horizon, and ISCO radii, all shifting inward. Under the same emission model, both the peak emiission intensity and its location move to smaller values, and the impact parameter ranges for the photon sphere, lensing ring, and direct ring diminish, suggesting that black holes with Lorentz violation are more difficult to detect.

Because black holes cannot be observed directly, its surrounding accretion material is crucial. This study analyzed the optical appearance of a charged black hole in the Kalb-Ramond background, focusing on Lorentz violation with $ l=0.01 $.

In a spherically symmetric setup, we examined the null geodesics, derived the effective potential, and computed the photon sphere radii, event horizon radii, and critical impact parameter. Under$ l=0.01 $, these quantities decreased with increasing $ Q $. Classifying photons by the number of equatorial-plane intersections yielded three trajectory types: direct, lensing, and photon orbits. Ray-tracing enabled us to determine the corresponding $ b_c $ranges, and the transfer function analysis indicated that direct emission dominates the total observed intensity, with lensing ring and photon sphere contributing significantly less.

Finally, we explored black hole shadows under three emission models; for each, we found that the emission intensity peaked at the starting radius and then decreased sharply. For an observer at infinity, direct emission was the principal source of brightness. As the values of $ l $ and $ Q $ increased, both the emission peak and observed intensity peak shifted inward, and their positions decreased slightly. Comparing with the Reissner-Nordström black hole, we confirmed that the Lorentz-violation parameter brought $ r_P $, $ r_h $, and $ r_{\mathrm{ISCO}} $ closer to the center, reducing and shifting the intensity peaks. These results suggested that black holes with Lorentz violation are comparatively more difficult to detect observationally owing to their diminished and more compact emission characteristics.

In this study, we employed three radiation models ($\rm A $, $\rm B $, and $\rm C $) to investigate the radiative properties of optically thin accretion disks. However, for optically thick accretion disks, the significant optical depth led to highly complex photon trajectories within the disk, involving multiple scattering and absorption events. This significantly increased the computational cost of numerical simulations, posing significant challenges for accurately modeling the radiation field. In future research, more advanced radiation models, such as general relativistic radiative transfer and Monte Carlo simulations, can be utilized to further explore the effects of multiple scattering and optical depth on black hole shadows and photon rings. These refined methodologies will provide deeper insights, enabling a better understanding of the observational characteristics of black holes and the radiative properties of accretion disks.

The critical value of $ l $ can be discussed using the shadow of the $\rm M87$ black hole detected by the Event Horizon Telescope. The diameter of the $\rm M87$ black-hole shadow in units of mass was obtained, that is $d_{\rm M 87} \equiv D \cdot \delta / M \approx 11 \pm 1.5$, where $ D $ and $ \delta $ are the angular size and distance of the $\rm M87$ black-hole shadow, respectively [22, 50−52]. Within the uncertainties of $ 1\delta $ and $ 2\delta $, we determined that the shadow diameters were in the regions $ 9.5 \sim 12.5 $ and $ 8 \sim 14 $. Therefore, this range could provide some upper or lower limits to the black-hole parameters. We assumed that, when $ Q=0.3 $, under the condition of an uncertainty of $ 1\delta $, the range of $ l $ could be calculated to be between $ -0.1423 $ and $ 0.04687 $. In contrast, under the condition of an uncertainty of $ 2\delta $, the corresponding value of $ l $ was between $ -0.2449 $ and $ 0.1486 $. In summary, the shadow of a black hole can effectively place certain observational constraints on its relevant parameters. This is of profound significance for delving deeper into the appearance characteristics of black holes in future observational studies.

This study primarily investigated the optical properties of charged black holes in the presence of a Kalb-Ramond field. The Kalb-Ramond field, originating from string theory, is a rank-two antisymmetric tensor field and constitutes an essential component of the theory. However, string theory also introduces other modifications, such as Dilaton fields. The introduction of the Dilaton field further modifies the geometry and thermodynamic quantities of black holes, playing a crucial role in string theory. Although the roles of the Dilaton and Kalb-Ramond fields differ in string theory, the methodologies employed in this study to analyze the Kalb-Ramond field—such as null geodesic analysis and ray-tracing techniques—can be extended to models incorporating the Dilaton field. The dynamical effects of the Dilaton field influence the geometry and topology of black holes, potentially affecting observable quantities such as the photon sphere, black hole shadow, and accretion disk. Therefore, the introduction of the Dilaton field may alter the shape and size of the black hole shadow, similar to the Lorentz-violating effects induced by the Kalb-Ramond field. Future research can further explore the impact of the Dilaton field on the photon sphere and black hole shadow and compare the results with our findings to gain deeper insights into these effects.