Bound states of ${\boldsymbol\eta, \boldsymbol\eta',{\boldsymbol D}^{\bf 0}}$, ${\bar{{\boldsymbol D}^{\bf 0}}}$, ${{\boldsymbol B}^{\bf 0}}$, ${\bar{{\boldsymbol B}^{\bf 0}}}$, ${\bar{{\boldsymbol K}^{\bf 0}}}$, and ϕ mesons with light and heavy nuclei within the chiral SU(3) model

The theory of strong interactions, quantum chromodynamics (QCD), has two well known properties: asymptotic freedom and confinement. The understanding of the low-energy non-perturbative regime of QCD poses extra challenges owing to a large value of the coupling constant. The properties of QCD, such as breaking of chiral symmetry and its expected restoration at high temperatures and baryon densities, play an essential role in our understanding of strong interaction physics. The study of the medium modification of hadron properties, particularly pseudoscalar and vector mesons, plays a pivotal role in revealing the nature of the partial restoration of the chiral symmetry at high temperatures and baryon densities. Heavy-ion collision experiments, for example, the large hadron collider (LHC) at CERN, Switzerland, and relativistic heavy-ion collider (RHIC) at BNL, USA, explore the regime of strongly interacting matter at high temperatures and low baryon densities, whereas future experimental facilities, for example, compressed baryon matter (CBM) experiment of FAIR, GSI, and the Nuclotron-based Ion Collider fAcility (NICA) at the Joint Institute for Nuclear Research (JINR), Russia, intend to explore the nature of interactions and phase transitions at high baryon densities and low/moderate temperatures. Extensive theoretical studies have been conducted using various approaches that explore the medium modification of hadron properties at finite temperatures and baryon densities [1−4].

An alternative technique in understanding the strongly interacting matter and role of chiral symmetry is the study of mesic nuclei, i.e., the bound states of mesons and nuclei, where strong interactions play a dominant role. In the formation of mesic nuclei, one of the nucleons in a given nuclei is replaced with a meson. This is complementary to mesic atoms in which mesons replace electrons in the atom, and Coulomb interactions are essential [5]. The formation of mesic nuclei for charged and neutral mesons has been studied using different approaches, for example, the quark meson coupling (QMC) model [6, 7], Nambu–Jona-Lasinio model (NJL) [8], and chiral unitary approach [9, 10]. Mesons with strong attractive interactions in the dense nuclear medium, i.e., whose mass decreases with an increase in the baryon density, and thus have deep attractive potential, may form the bound states with different nuclei.

The study of η and $ \eta' $ mesic nuclei elucidates not only the interactions of these mesons with nucleons in the nuclear matter but is also important to deepening our understanding on the behaviour of $ U_A(1) $ anomalies in dense media. Initial studies in the direction of η mesic nuclei were initiated by Haider and Liu [11]. In this study, through the analysis of $ \pi N \longrightarrow \eta N $ cross-sections and solving relativistic wave equations, the possibilities of existence of bound states of η mesons with nuclei having mass number $ A\geq 12 $ were studied. In [12], the Green function method was applied to study the $ \eta- ^{16} {\rm{O}}$ bound state. After these initial studies, the in-medium properties of η and $ \eta ' $ mesons and possibility of their bound state formation with different nuclei have been studied by different groups [13−19]. The formation of the $ \eta ' (958)- $nucleus bound state was investigated in the $ (p, d) $ reaction to explore the medium modification of $ \eta ' (958) $ mass [13]. Different collaborations have conducted many experiments to search for η mesic nuclei by studying reactions from heavy and light targets. Experiments at BNL [20] involved the reaction of $ \pi^+ $ with lithium, carbon, oxygen, and aluminium targets, whereas the Los Alamos Meson Physics Facility (LAMPF) considered $ ^{18} {\rm{O}}$ [21], but both had negative results. The photo-production process, induced by the reaction of the γ photon on $ ^{12} {\rm{C}}$, lead to the formation of the $ \eta- $nucleon bound state, as claimed by the Lebedev Physical Institute (LPI) group [22]. A deuteron induced reaction on carbon nuclei was studied at JINR to investigate the formation of η mesic nuclei through the decay of $ N^*(1535) $ resonance [23]. Along with heavy nuclei as targets, experimentalists are actively searching for the bound state of $ \eta- $ mesons with light nuclei; for example, WASA at the COSY collaboration through reaction channels $ pd \rightarrow {^{3} {\rm{He}}}$ 2 γ and $ pd \rightarrow {^{3} {\rm{He}}}$ 6 γ are searching for bound states of η with $ {^{3} {\rm{He}}}$ nuclei [24, 25]. Theoretically, using a few body $ \eta-NNN $ system, the existence of the $ {^{3} {\rm{He}}}$ η bound state was explored [26]. Recent reviews on the theoretical and experimental efforts on η and $ \eta' $ mesic nuclei are presented in Refs. [27, 28].

Investigating the medium modification of open charm D mesons has implications in understanding their production rate, the phenomenon of charmonium suppression that may elucidate the formation of QGP, and the possibility of formation of D [10, 29] and $ J/\psi $ mesic nuclei [30]. As the open charm D mesons have one light $ u/d $ quark or anti-quark as its content, these mesons can undergo significant mass modifications through the medium modification of light quark condensates. The medium modifications of charm mesons have been studied using QCD sum rules, the chiral $S U$(3) hadronic model, the coupled channel approach, the QMC model, etc. [31−39]. In Ref. [7], the bound states of $ D^-, D^0 $ and $ \bar{D^0} $ mesons in $ ^{208} {\rm{Pb}}$ were studied using the QMC model. Using D meson self-energies, calculated using the coupled channel approach, Garcia-Recio et al. studied the bound states of $ D^0 $ mesons with $ ^{12} {\rm{C}}$ and $ ^{208} {\rm{Pb}}$ [10]. The study of D meson bound states with the nuclei is also importrant for the $ \bar{\text{P}} $ ANDA experiment of the FAIR project [40]. The bound states of ω [41], $ J/\psi $ [30], $ \eta_c $ [42], and $ \eta_b $ [43] mesons with different nuclei have also been studied. Although the in-medium masses of bottom mesons have been studied using different approaches [44], the $ B- $mesic nuclei have not been explored except for one recent study using the QMC model [45].

Currently, understanding the medium modification of ϕ mesons is also an active topic owing to different results obtained from various experimental studies. In the KEK-PS E325 experiment, through the study of invariant mass spectra of $ e^{-}e^{+} $ pairs produced in a 12 GeV $ p+A $ reaction through the process $ p+A \rightarrow \phi + X \rightarrow e^{-}e^{+} + X ' $, a negative mass shift of 3.4% and decay width of 14.5 MeV were observed at nuclear saturation density [46]. Other experiments, for example, those conducted by the Laser-Electron Photon facility at SPring-8 (LEPS) [47] and CLAS collaboration JLab [48, 49], have reported significant modifications in the in-medium decay width without significant effects on the mass shift. The J-PARC E16 collaboration aims to investigate the mass modifications of ϕ mesons through the mass spectra of $ e^{-} e^{+} $ pairs, as in KEK, but with more high statistics and in the energy range of 50 GeV [50, 51]. Theoretically, the medium modifications of ϕ mesons have been studied using QCD sum rules, the coupled channel approach, the chiral hadronic model, the quark meson model, etc. [6, 52−60]. The negative mass shift for the ϕ mesons observed under various theoretical approaches and as reported by KEK-PS 325 [46] motivate to study the possibility of the formation of $ \phi- $ mesic nuclei [6]. At the JPARC experimental facility, plans are underway to investigate the mass shift of ϕ mesons through the ϕ meson-nuclei bound states using reactions $ \bar{p}p \rightarrow \phi \phi $ [61, 62].

In this study, we explore the formation of bound states of pseudoscalar mesons, $ \eta, \eta ', D^{0}, \bar{D^0}, B^{0}, \bar{B^0}, \bar{K^0} $ and the vector meson ϕ, whereas the bound states of ω, $ J/\psi $, $ \eta_c $, and $ \eta_b $ will be investigated in future work. For our current study, we use the chiral $S U$(3) hadronic mean field model, which is based on the low energy properties of QCD [63]. The chiral $S U$(3) model has been used to study the modification of properties of kaons [64−66], vector mesons ($ \omega, \rho $, and ϕ) [67], pseudoscalar η mesons [68, 69], D [38, 39, 70] and B mesons [71], charmonium [72], and bottomonium [73] in nuclear and strange hadronic matter. The optical potentials of mesons under study, calculated using the chiral effective model for different light and heavy nuclei, are used to solve the Klein Gordon equation in the momentum space to obtain the binding energies and decay width. Note that, throughout this paper, we use the mean field approximation to calculate the in-medium masses and optical potentials of different mesons. In the future, we may further improve the results by employing beyond mean field calculations, for example, including two loop contribution [74, 75].

The remainder of this paper is organized as follows. In Sec. II, we present the details of the chiral $S U $(3) model. Methods of obtaining the optical potentials of mesons in the environment of nuclei are discussed in Sec. III. The results and discussion are presented in Sec. IV. Finally, the summary and conclusion are presented in Sec. V.

To investigate the formation of mesic nuclei in this study, we use the chiral $S U$(3) hadronic mean-field model based on the nonlinear realization of chiral symmetry [63, 76−78]. In the chiral $S U$(3) model, the interactions between the nucleons are mediated through the exchange of the non-strange scalar meson σ, strange scalar meson ζ, scalar-isovector meson δ, vector meson ω, and vector-isovector meson ρ. The scalar field δ and vector field ρ contribute when a medium has finite isospin asymmetry. In this model, the scalar dilaton field, χ, known as the glueball field, is introduced to incorporate the broken scale invariance property of the QCD [63]. As discussed in the introduction, the QMC model, NJL model, chiral unitary approach, linear sigma model, etc., have been used to calculate the in-medium optical potentials, and hence, the possibility of the formation of mesic nuclei. The following are the important differences of the chiral $S U$(3) model from these approaches. In the QMC model, quarks are treated as fundamental degrees of freedom confined in hadrons through a bag potential. Quarks confined in baryons interact through the exchange of scalar and vector fields, which in turn modify the properties of baryons. In the QMC model, the in-medium masses of kaons and antikaons decrease as a function of the density of the nuclear matter. Repulsive interactions for kaons and attractive ones for antikaons contributed by the Weinberg Tomozawa term are not considered in this model (also for other pseudoscalar mesons). In the chiral unitary approach, coupled channel dynamics is employed to investigate the properties of antikaons and ϕ mesons. The coupled channel approach involves the coupling of $ \bar{K}N $ to $ \pi \Sigma $ and $ \pi \Lambda $ channels and is important for studying the dynamics of $ \Lambda(1405) $ resonance [79]. Such coupled channel effects are not considered in our present chiral model calculations. In the NJL model, calculations for the η and $ \eta' $ mesons, positive mass-shift for η, and negative mass-shift for $ \eta' $ have been observed [8]. In this model, interaction Lagrangian densities are expressed in terms of quark fields.

The Lagrangian density for the chiral $ S U$(3) hadronic mean-field model is expressed as [63]

In Eq. (1), ${\cal{L}}_{\text{kin}}$ represents the kinetic energy term for baryons and mesons and is given by

In Eq. (2), the first term represents the kinetic energy term for the baryon octet, B. The covariant derivative $ D_{\mu} $ appearing in this term is defined as $D_\mu B = \partial_\mu B + {\rm i} \left[\Gamma_\mu, B\right]$, with $\Gamma_{\mu}=-\dfrac{\rm i}{4}\left[u^{\dagger} \partial_{\mu} u-\partial_{\mu} u^{\dagger} u+\right.$ $ \left.u \partial_{\mu} u^{\dagger}-\partial_{\mu} u u^{\dagger}\right] $. Here, $u=\exp \left[\dfrac{\rm i}{\sigma_{0}} \pi^{a} \lambda^{a} \gamma_{5}\right]$ is the unitary transformation operator through which pseudoscalar mesons enter into the calculations. The second and third terms of Eq. (2) are the kinetic terms for the scalar and pseudoscalar mesons, respectively. The fourth and fifth terms represent the kinetic terms for the pseudoscalar singlet Y and dilaton field χ, respectively. The last two terms defined in terms of field tensors, $ V_{\mu \nu} $ and $ {\cal{A}}_{\mu \nu} $, represent the kinetic term of spin-1 vector and axial vector mesons, respectively.

Within the chiral $ S U$(3) model, to describe the interactions of nucleons through the exchange of scalar fields $ \sigma, \zeta $, and δ and vector fields ω and ρ, under the mean-field approximation, we define the following interaction Lagrangian:

where $ i = p,n $, and $ m_i^{*} $ is the effective mass of nucleons defined as

The coupling constants $ g_{\sigma i} $, $ g_{\zeta i} $, and $ g_{\delta i} $ describe the strength of interactions of nucleons with scalar fields. The term $ {\cal{L}}_{\text {0}} $ of Eq. (1) gives the self interaction of scalar mesons $ \sigma, \zeta $, and δ and the interactions for dilaton field χ. This term is expressed as

In Eq. (5), the last two terms account for scale breaking effects introduced in the chiral $ S U$(3) model through the dilation field $\chi $. In Eq. (1), the term $ {\cal{L}}_{\text {vec }} $ describes the self interactions of vector mesons through the Lagrangian density

The term $ {\cal{L}}_{S B} $ of Eq. (1) is the explicit symmetry breaking term and is given by

At zero temperature, the thermodynamic potential per unit volume of the grand canonical ensemble is expressed as

where $ E_i^*({\bf{k}}) = \sqrt{{\bf{k}}^2 + m_i^{*2}} $ and $ \mu_i^* = \mu_i - g_{\omega i} \omega-g_{\rho i} \tau_3 \rho $. In addition, the vacuum potential energy, $ {\cal{V}}_{\text{vac}} $, is subtracted from Eq. (8) to achieve the vanishing vacuum energy. The equations of motion for the non-strange σ, strange scalar ζ, scalar isovector δ, vector ω, vector-isovector ρ, and scalar dilaton χ fields are derived by minimizing the thermodynamic potential and are expressed as

and

respectively. In this study, we discuss the formation of bound states for the nuclei $ ^{12} {\rm{C}}$, $ ^{16} {\rm{O}}$, $ ^{40} {\rm{C}}{\rm{a}}$, and $ ^{208} {\rm{Pb}}$. As we shall describe later, the optical potentials of mesons required as input in the Klein Gordan equation for the study of bound states will depend upon the scalar fields $ \sigma, \zeta $, and δ. For nuclei with radius R, the values of scalar fields are required as a function of radial coordinator r, such that r varies from zero to R. For this, the coupled equations of motion for scalar and vector fields are solved for the baryon densities corresponding to these nuclei as a function of r. In this study, we consider the radial dependence of vector densities of nucleons through parameterization in the form of a harmonic oscillator or two parameter Fermi distribution function, as discussed below, and the second order derivative term of the form $ -\nabla^2 { \sigma}(r) $ in the field equations given above is not considered.

The total baryon density, $ \rho_B $, in a given nucleus is the sum of densities of protons and neutrons, i.e.,

For nuclei up to $^{18}{\rm O}$, we shall use the harmonic oscillator type density distribution, given as [80]

In contrast, for heavy nuclei, the two parameter Fermi distribution function is used in this study [80] and is expressed as

In Eqs. (16) and (17), $ \rho_{i,0} $ is the density of nucleons at the center of nuclei, and $ R_i $ and $ a_i $ are the radii and diffuseness parameters, respectively, corresponding to nucleons of type i. The values of these parameters for different nuclei are listed in Table 1 of Ref. [80]. For the nuclei with mass number A and having different number of protons, Z, and neutrons, N, the isospin asymmetry parameter I is given by $ I = (N-Z)/A $, which is further defined in terms of densities of nucleons as $ I = \dfrac{\rho_n(r) - \rho_p(r)}{2\rho_B(r)} $. The system of equations given by Eqs. (9) to (14) are solved for the densities in a given nuclei from center to surface, as given by Eq. (15). At zero temperature, the number density $ \rho_i $ and scalar density $ \rho_i^s $ are related to the Fermi momentum $ k_{F,i} $ through the relations

A	$ nl $	$ {\cal{E}}_{\cal{B}} $/MeV				Γ /MeV
		κ =0	κ = 0.5	κ =1		κ =0	κ = 0.5	κ =1
$ ^{12}_{6} {\rm{C}}$	$ 1s $	−0.511	−0.103	−		0.0	2.142	−
$ ^{16}_{8} {\rm{O}}$	$ 1s $	−1.72	−1.38	−0.458		0.0	3.775	8.094
$ ^{40}_{20} {\rm{C}}{\rm{a}}$	$ 1s $	−9.769	−9.538	−8.91		0.0	9.527	19.387
$ ^{208}_{82} {\rm{Pb}}$	$ 1s $	−20.642	−20.555	−20.309		0.0	12.987	26.046
	$ 1p $	−14.444	−14.303	−13.921		0.0	11.996	24.175
	$ 1d $	−7.244	−7.005	−6.392		0.0	10.621	21.656
	$ 2s $	−5.123	−4.74	−3.846		0.0	9.544	19.896

Table 1.  Values of binding energies, $ {\cal{E}}_{\cal{B}} $, and the full decay width, Γ, for η mesons in four nuclei with different mass numbers A for $ \kappa = 0, 0.5 $, and 1.

and

respectively. In these equations, $ \gamma_i $ is the degeneracy factor for the nucleons. To study the properties of mesons in infinite nuclear medium at zero temperature, we solve Eqs. (9) to (14) using the expressions of $ \rho_i $ and $ \rho_i^s $ given above. For finite temperature effects, $ \rho_i $ and $ \rho_i^s $ are defined as

and

respectively. Here, $ \beta = 1/T $.

To obtain the binding energy and absorption decay width of the mesic nuclei, we solve the Klein Gordon equation in the presence of local potential $ V(r) $, and it is expressed as

In this equation, μ is the reduced mass of the meson and nuclei under study. The local potential $ V(r) $ is complex in nature, i.e.,

where the real part $ U(r) $ is related to the mass shift of mesons, whereas the imaginary part $ W(r) $ relates to the absorption of mesons in the nuclei under consideration. For the real part, $ U(r) $, we write [5]

where $ \rho_0 $ denotes the baryon density at the center of nuclei, and $ \Delta m_\psi (\rho_0) $ $ [\psi = \eta, \eta ', D^{0}, \bar{D^0}, B^{0}, $ $ \bar{B^0}, \bar{K^0}, \phi ] $ is the mass shift at this density. Additionally, $ \rho_B(r) $ is the baryon density distribution inside the nuclei and is given by Eq. (15). The potential $ W(r) $ is related to the decay width $ \Gamma_0 $ through the relation [5]

In this study, the value of $ \Gamma_0 (\rho_0) $ for pseudoscalar mesons $\eta,\; \eta ', D^{0}, \bar{D^0}, B^{0}, \bar{B^0}$, and $ \bar{K^0} $ is calculated using the procedure adopted in the calculations within the QMC model [14]. Under this model, $ \Gamma_0 (\rho_0) $ is related to the mass shift $ \Delta m_\psi (\rho_0) $ through a parameter κ using the relation

The parameter κ imitates the absorption of mesons in the nuclear medium, and $ \Gamma_{\text{vac}} $ is the decay width in the vacuum. In this study, the contributions from the first term of the equation above are considered to estimate the contribution of imaginary part of the potential to the binding energy. We solve the Klein Gordon equation in the momentum space using the Fourier transformation and the partial wave decomposition method described in Refs. [81, 82] to obtain the complex energy eigenvalues $ \epsilon $, which are further related to the binding energy $ {\cal{E}}_{\cal{B}} $ and decay width Γ through the relations $ {\cal{E}}_{\cal{B}} = \text{Re}\,\epsilon - \mu $ and $ \Gamma = - 2\, \text{Im}\, \epsilon $, respectively. In the following, we briefly describe the calculations of the mass shift of $\eta,\; \eta ',\; D^{0},\; \bar{D^0},\; B^{0},\; \bar{B^0}$, $ \bar{K^0} $, and ϕ mesons, which are used as inputs to obtain the optical potentials of mesons in the environment of different nuclei.

In this section, we present the details of interaction Lagrangian density and dispersion relations to obtain the in-medium masses of pseudoscalar η and $ \eta^{\prime} $ mesons in the nuclear medium relevant for different nuclei. The physical states η and $ \eta^{\prime} $ result from the mixing of $ \eta_8 $ and $ \eta_0 $ states. The pseudoscalar $ \eta_8 $ appears in the octet of pseudoscalar mesons defined by [63]

where $ w = \sqrt{2}\sigma_{0}/\zeta_{0} $. For the pseudoscalar single $ \eta_0 $, we define

Within the chiral $S U $(3) model, for the pseudoscalar $ \eta_8 $, the interaction Lagrangian density is expressed as

where $ d' $ = $ 3d_1+d_2 $. Additionally, $ \sigma ' $ and $ \zeta ' $ are the fluctuations from the vacuum expectation values, i.e., $ \sigma ' = \sigma - \sigma_0 $ and $ \zeta ' = \zeta - \zeta_{0} $. The first term of Eq. (29) (mass term) corresponds to the explicit symmetry breaking and is obtained from the general term

In this equation, $ A_p $ is a diagonal matrix given by

The vacuum mass $ m_{\eta_8} $ of the $ \eta_8 $ meson deduced from Eq. (30) is identified as

where $ f = \sqrt{f_\pi^2 +2 \left(2f_K - f_\pi\right)^2} $. The second term of Eq. (29) is obtained from the general kinetic term of the pseudoscalar mesons (third term of Eq. (2)) and is also known as first range term in the chiral $S U $(3) model.

The last term of Eq. (29), in terms of $ d_1 $ and $ d_2 $, is obtained from the Lagrangian densities (known as $ d_1 $ and $ d_2 $ terms) [65, 66]:

In this study, for $ \eta_8 $mesons, from the Weinberg Tomozawa term, we do not obtain interaction terms with finite contributions unlike the case for kaons [65, 66] and D [38] mesons studied in the past using the present chiral $S U $(3) mean field model. These observations are also consistent with the calculations of η meson properties in the nuclear medium at zero temperature using chiral perturbation theory [83].

From the Lagrangian density given in Eq. (29), the equations of motion for $ \eta_8 $ is obtained, whose Fourier transformation leads to the dispersion relation

where $ \Pi_{\eta_8} $ denotes the $ \eta_8 $ meson's self-energy and is given by

At zero momentum ($ {\bf{k}} = 0 $), the effective mass $ m_{\eta_8}^{*} $ is expressed as

For the pseudoscalar singlet $ \eta_0 $, within the chiral $ S U$(3) hadronic mean field model, we write

Here, the first term is the kinetic energy term for pseudoscalar mesons. The second term is part of explicit symmetry breaking term and provides the finite mass to the pseudoscalar singlet. The last term of Eq. (37) is the extension of Eq. (30), in which the singlet Y is now included. This leads to the terms having mixing between $ \eta_0 $ and $ \eta_8 $ states. Explicitly, using Eq. (28) in Eq. (37), we obtain

where $ c= {2 \sigma_0}/{(\sqrt{2} \zeta_0 + \sigma_0)} $. In the last term of the above equation, the interaction terms corresponding to pure $ \eta_8 $ states, which are given in Eq. (29), are not repeated to avoid double counting. From Eq. (38), we observe that, unlike $ \eta_8 $, for the pure $ \eta_0 $ state, contributions from the in-medium interactions do not appear, i.e.,

From the mixed term (last term of Eq. (38)), we identify

The effective masses $ m_\eta^{*} $ and $ m_{\eta '}^{*} $ of physical η and $ \eta ' $ mesons are obtained through the diagonalization of the mass matrix

The parameter $ d ' $ is expressed in terms of the $ \eta-N $ scattering length, $ a^{\eta N} $. The expression for the scattering length $ a^{\eta N} $ calculated within chiral $ S U$(3) model is given by [68]

which can be rearranged to obtain the expression for $ d ' $. We calculate $ d' $ for the value of $ a^{\eta N} = $ 0.91 [83]. From the above calculated effective masses $ m_\eta^* $ and $ m_{\eta^{\prime}}^* $ of η and $ \eta^{\prime} $ mesons, the corresponding mass shift is calculated, which is used as input in Eqs. (24) and (26) to obtain the optical potentials of these mesons in the nuclei.

The effective masses of neutral $ D^{0} $ and $ \bar{D^{0}} $ mesons required in Eq. (24) to study the D mesic nuclei are obtained by extending the chiral $S U $(3) model to the $S U $(4) case [38, 84]. The mesons $ D^{0} $ and $ \bar{D^{0}} $ are the members of D $ (D^{+}, D^{0}) $ and $ \bar{D} $ $ (D^{-}, \bar{D^{0}}) $ doublets, respectively. From the Lagrangian density describing the interactions of D and $ \bar{D} $ mesons with nucleons in the nuclear medium, equations of motion are obtained whose Fourier transformation yields the dispersion relation

For the $ D^{0} $ mesons, the expression of the self-energy is given by

For $ \bar{D^0} $, we have

In Eqs. (44) and (45), $ \zeta_c^{\prime} $ denotes the fluctuations of the charm condensate $ ( c\bar{c}) $ from the vacuum expectation value and, being heavy in flavor, is considered zero in this study. From the dispersion relation, the effective mass for the D mesons (at zero momentum) is expressed as

The in-medium mass of D mesons calculated using the above relation is used in Eqs. (24) and (26) to obtain the real and imaginary optical potentials.

To study the formation of bound states corresponding to $ B^{0} $ and $ \bar{B^{0}} $ mesons, we generalize the chiral $S U $(3) model to the $S U $(5) sector as these bottom mesons are composed of one heavy b quark/antiquark. The pseudoscalar $ B^0 $ and $ \bar{B^{0}} $ mesons belong to the open bottom $ B(B^+,B^0) $ and $ \bar{B} (B^-, \bar{B^0}) $ meson doublets. In Ref. [44], the masses of open bottom mesons were calculated in nuclear and strange hadronic matter using the chiral effective model. For our present calculations, we require the mass shift of $ B^{0} $ and $ \bar{B^0} $ mesons in the nuclear medium at zero temperature obtained by solving the dispersion relation

For $ B^{0} $ and $ \bar{B^{0}} $ mesons, the self-energies are expressed by [44]

and

respectively. Similar to $ \zeta_c^{\prime} $, the fluctuations $ \zeta_b^{\prime} $ (corresponding the condensate, $ b\bar{b} $, of heavy b quark) appearing in Eqs. (48) and (49) are considered zero in the calculations of the mass shift of $ B^0 $ and $ \bar{B^{0}} $ mesons. At zero momentum, the in-medium masses of neutral B mesons required to obtain the mass shift, and hence the optical potentials in different nuclei, can be expressed as

The in-medium masses of kaons and antikaons have been studied using the chiral $S U $(3) model in nuclear [65, 66] and strange hadronic media [64]. In the nuclear matter, the effective mass of kaons $ (K^+, K^0) $ is observed to increase, whereas the mass of antikaons $ (K^-, \bar{K^0}) $ decreases as a function of density of the nuclear medium. Because the negative mass shift implies that the attractive optical potentials are required to form the bound states with nuclei, here we study the possible formation of bound states of $ \bar{K^0} $ mesons with light and heavy nuclei. Similar to Eqs. (43) and (47), within the chiral model, the effective mass of $ \bar{K^0} $ mesons will be obtained by solving the dispersion relation, for which the required self energy $ \Pi_{\bar{K^0}}(\omega,|{\bf{k}}|, \rho(r)) $ is expressed as [66]

To investigate the possibility of the formation of ϕ mesic nuclei, we calculate the effective masses and decay width of ϕ mesons using the effective Lagrangian, which considers the interactions of ϕ mesons with kaon $ K(K^{+},K^{0}) $ and antikaon $ \bar{K}(K^{-}, \bar{K^{0}}) $ isospin doublets. This interaction Lagrangian density is expressed as [85, 86]

Using this equation, the ϕ meson self-energy, $ \Pi_{\phi}^{*}(p) $, in the nuclear medium relevant for different nuclei is calculated for the decay process $ \phi \rightarrow K \bar{K} $ at the one-loop level. In Eq. (52), $ g_{\phi} $ represents the coupling constant. Because the contributions of $ \phi \phi $K$ \bar{K} $ interactions to the in-medium masses and decay width are smaller than those of ϕK$ \bar{K} $ interactions, we have not considered these interactions in our study on the interaction Lagrangian [86]. The in-medium mass of the ϕ meson is expressed in terms of real part of the self energy, $ \Pi_{\phi}^{*}(p) $, through the relation

In the above equation, $ m_{\phi}^{0} $ is the bare mass of the ϕ meson. Additionally, the real part of the self energy is expressed in terms of in-medium energies of kaons and antikaons as [60, 86]

where $ {\cal{P}} $ denotes the principal value of the integral. Moreover, $ E_{K}^{*}= $ $ \left(\vec{q}^{\,2}+m_{K}^{*^{2}}\right)^{1 / 2} $ and $ E_{\bar{K}}^{*}=\left(\vec{q}^{\,2}+m_{\bar{K}}^{*^{2}}\right)^{1 / 2} $, where $ m_{K}^{*}\left(=\frac{m_{K^{0}}^{*} + m_{K^{+}}^{*}}{2}\right) $ and $ m_{\bar{K}}^{*}\left(=\frac{m_{\bar{K}^{0}}^{*}+m_{K^{-}}^{*}}{2}\right) $ are the in-medium average masses of the kaon and antikaon doublets, respectively. The values of effective masses, $ m_{K^{+}}^{*}, m_{K^{0}}^{*}, m_{K^{-}}^{*} $, and $ m_{\bar{K}^{0}}^{*} $ are calculated in the nuclear medium using the chiral $ S U$(3) model [64, 66]. The integral in Eq. (54) is regularized by incorporating a phenomenological form factor with the cutoff parameter $ \Lambda_{c} $, i.e., [87]

For the ϕ meson, the value of decay width required in Eq. (25) is obtained from the imaginary component of its self energy. The decay width, expressed in terms of in-medium masses of ϕ mesons and masses of kaons and antikaons, is given by [88]

The value of coupling constant $ g_{\phi} $ is fixed to the empirical width of the ϕ meson in the vacuum and found to be $ 4.539 $. Additionally, the bare mass of the ϕ meson appearing in Eq. (53) is calculated by setting its vacuum mass to 1019.461 MeV.

We now discuss the possibility of the formation of mesic nuclei of various mesons through the numerical calculations of the optical potentials and binding energies. We shall calculate the optical potentials of $ \eta, \eta ' $, $ D^{0} $, $ \bar{D^{0}} $, $ B^0 $, $ \bar{B^0} $,$ \bar{K^{0}} $, and ϕ mesons in the medium relevant for the nuclei $ ^{12} {\rm{C}}$, $ ^{16} {\rm{O}}$, $ ^{40} {\rm{C}}{\rm{a}}$, and $ ^{208} {\rm{Pb}}$. As discussed in the previous section, the in-medium properties of mesons are calculated using the chiral $S U $(3) hadronic mean field model and extended to the $S U $(4) and $S U $(5) sectors to obtain the in-medium masses of charmed and bottom mesons [63]. The parameters $ k_0 $, $ k_2 $, and $ k_4 $ of the chiral $S U $(3) model appearing in Eq. (5) are fitted to reproduce the vacuum values of $ \sigma, \zeta $, and χ fields [63]. Furthermore, the vacuum values $ \sigma_0 $ and $ \zeta_0 $ are calculated using the values of the pion decay constant $ f_\pi = 93.3 $ and kaon decay constant $ f_K = 122 $ MeV through the relations $ \sigma_0 = -f_\pi $ and $ \zeta_0 = -\frac{1}{\sqrt{2}}(2f_K -f_\pi) $. The vacuum value of $ \chi_0 $ is constrained such that the binding energy $ -16 $ MeV for symmetric nuclear matter at a saturation density of $ \rho_0 =0.15 $ fm$ ^{-3} $ is reproduced. Moreover, the parameter $ k_3 $ is constrained through the masses of η and $ \eta ' $ mesons, and $ k_1 $ is fixed to give a mass of the order of $ m_\sigma \sim $ $ 500 $ MeV. The values of parameters $ d_1 = 2.56/m_K $ and $ d_2 = 0.73/m_K $ are fitted to empirical values of the kaon-nucleon scattering length [65, 66, 89].

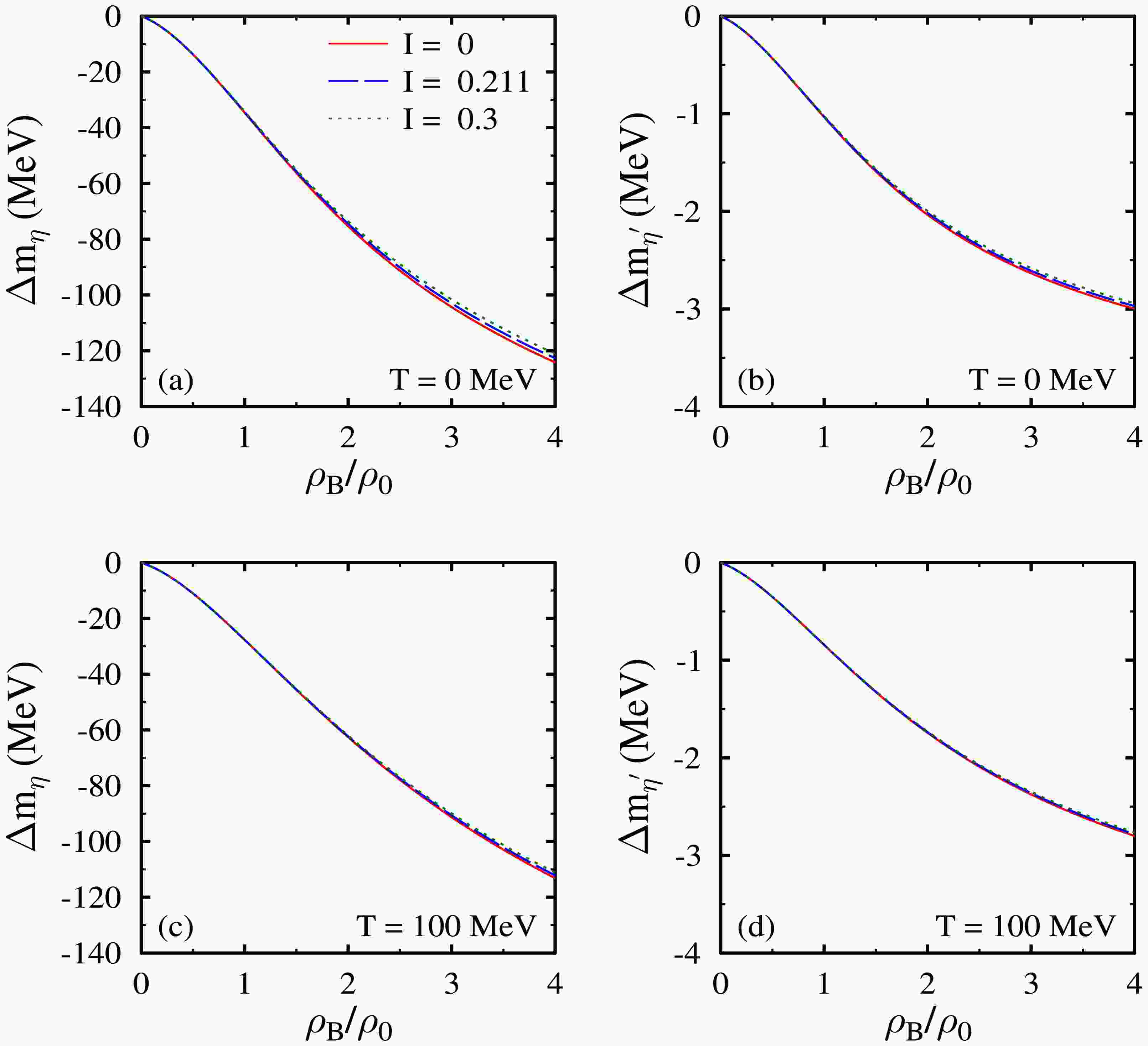
In this subsection, we explore the possibility of the formation of η and $ \eta ' $ mesic nuclei. Using Eq. (41), the mass shifts of pseudoscalar η and $ \eta ' $ mesons are calculated within the chiral $S U $(3) model. In Fig. 1, we show the mass shift of η and $ \eta ' $ mesons as a function of the baryon density $ \rho_B $ (in units of nuclear saturation density $ \rho_0 $) of the infinite nuclear medium for isospin asymmetry $ I = 0, 0.211 $, and $ 0.3 $ at temperatures $ T = 0 $ and $ 100 $ MeV. The isospin asymmetry $ I = 0.211 $ corresponds to the heavy nuclei $ ^{208} {\rm{Pb}}$ considered in this study for the bound state formation. As discussed earlier, for the calculations of η and $ \eta ' $ meson properties, we have considered the mixing of $ \eta_8 $ and $ \eta_0 $ states. The pseudoscalar η meson, which is a member of the octet, is observed to undergo a larger mass shift than the singlet $ \eta ' $. At the nuclear saturation density $ \rho_B = \rho_0 $, for isospin asymmetry $ I = 0(0.3) $ and temperature $ T = 0 $ MeV, the values of the mass shift $ \Delta m_\eta $ and $ \Delta m_\eta ' $ are observed to be $ -34.64 (-34.21) $ and $ -1.03 (-1.02) $ MeV, respectively. At the baryon density $ \rho_B= 4\rho_0 $, the above values of mass shift change to $ -124.15(-120.92) $ and $ -3.00 (-2.94) $ MeV. The finite isopsin asymmetry of the medium causes a lower decrease in the masses of η and $ \eta ' $, although the impact is small. An increase in the temperature of the nuclear medium from $ T = 0 $ to $ 100 $ MeV enhances the in-medium mass of these mesons. Furthermore, in the present chiral model calculations, compared with η mesons, the singlet $ \eta ' $ undergoes a significantly lower decrease in mass as a function of density of the nuclear medium. Recall that the in-medium masses of η and $ \eta ' $ mesons are obtained from the diagonalization of Eq. (41). Neglecting the off-diagonal terms (having very small contributions), $ m_{\eta}^{*} \sim m_{\eta_8}^{*} $ and $ m_{\eta{'}}^{*} \sim m_{\eta_0}^{*} $. As observed from Eq. (39), within the chiral $S U $(3) model, $ m_{\eta_0}^{*} = m_{\eta_0} $, i.e., $ \eta_0 $is not modified in the medium, and therefore, $ \eta ' $ mesons are not significantly modified in the present calculations (small modifications are stimulated through the diagonalization of Eq. (41).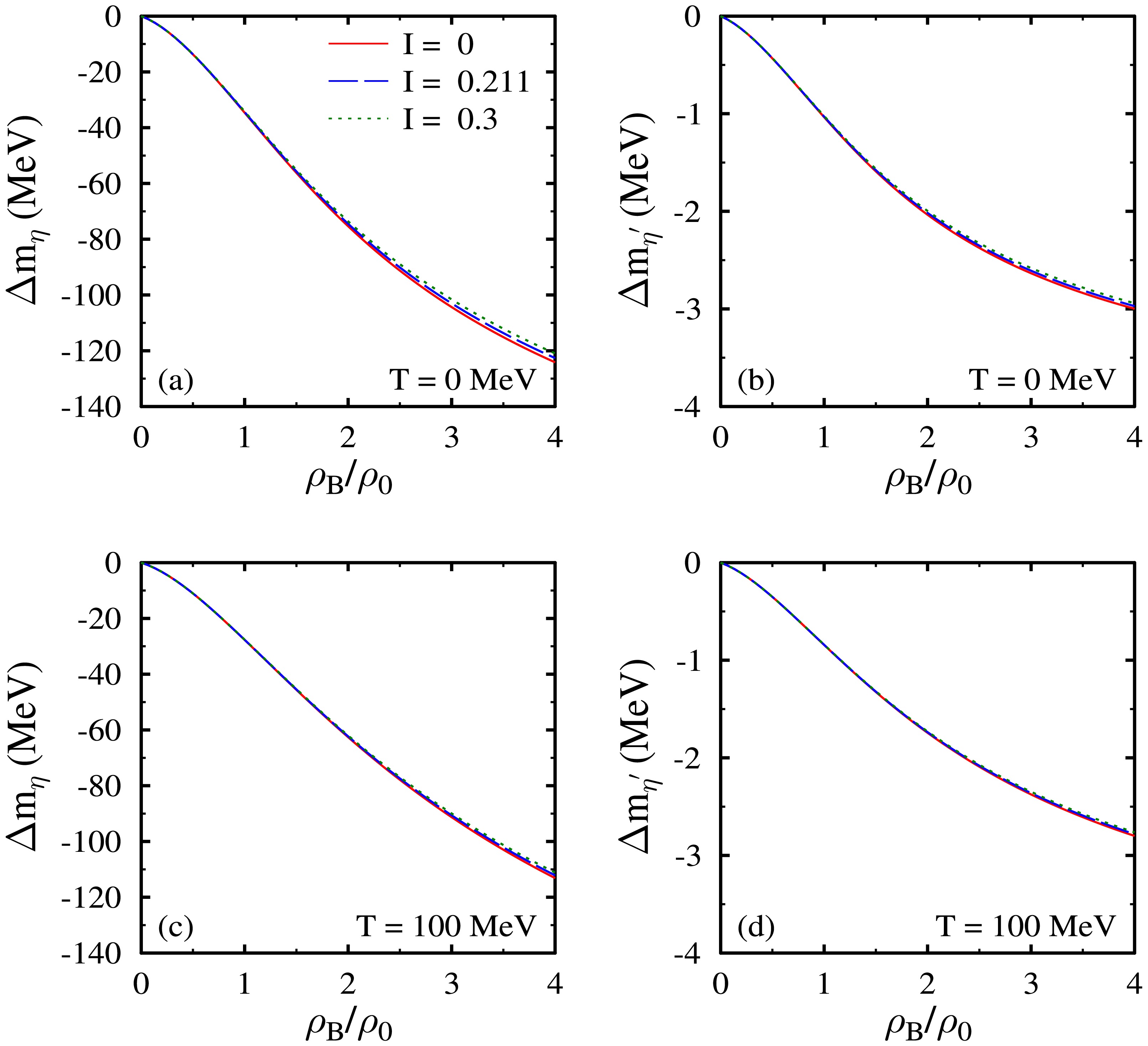

Figure 1.  (color online) Mass shift of η [in subplots (a) and (c)] and $ \eta^{\prime} $ [in subplots (b) and (d)] mesons as a function of density $ \rho_B $ (in units of nuclear saturation density $ \rho_0 $) of the nuclear medium for isospin asymmetries $ I = 0, 0.211 $, and $ 0.3 $. Results are shown for temperatures $ T = 0 $ and $ 100 $ MeV.

To study the bound states, we solve the Klein Gordon equation [Eq. (22)], which requires the optical potential corresponding to different nuclei under study as input. In Fig. 2, the real part of the optical potentials for η and $ \eta^\prime $mesons, calculated using Eq. (24), is plotted as a function of distance r from the center of the nuclei. The heavy nuclei are observed to have larger values of negative optical potentials than lighter nuclei. The imaginary optical potential, which corresponds to the absorption of mesons in the nuclei, is calculated using Eq. (25). Using the real and imaginary values of optical potential in the Klein Gordon equation, we calculate the binding energy and absorption decay width. For η mesons, the values of binding energies and decay width are listed in Table 1. For light nuclei $ ^{12} {\rm{C}}$, the negative values for the binding energies are observed only in the $ 1s $ state for the values of the phenomenological parameter $ \kappa = 0 $ and $ 0.5 $. As described earlier in Sec. III, through κ, we simulate the impact of imaginary optical potential on the formation of bound states. As the value of κ is increased to $ 1 $, no bound state is observed. For $ ^{16} {\rm{O}}$ and $ ^{40} {\rm{C}}{\rm{a}}$, the bound state formation in the $ 1s $ state may occur for all values of κ considered in this study. As observed from Table 1, for $ ^{208} {\rm{Pb}}$ nuclei, the negative values for the binding energies are observed not only for the $ 1s $ state but also for the other excited states, for example, $ 1p, 1d $, and $ 2s $. Owing to the larger value of the attractive optical potential (magnitude) of η meson with heavy $ ^{208} {\rm{Pb}}$ nuclei, the possibility of the formation of bound state is higher with these nuclei.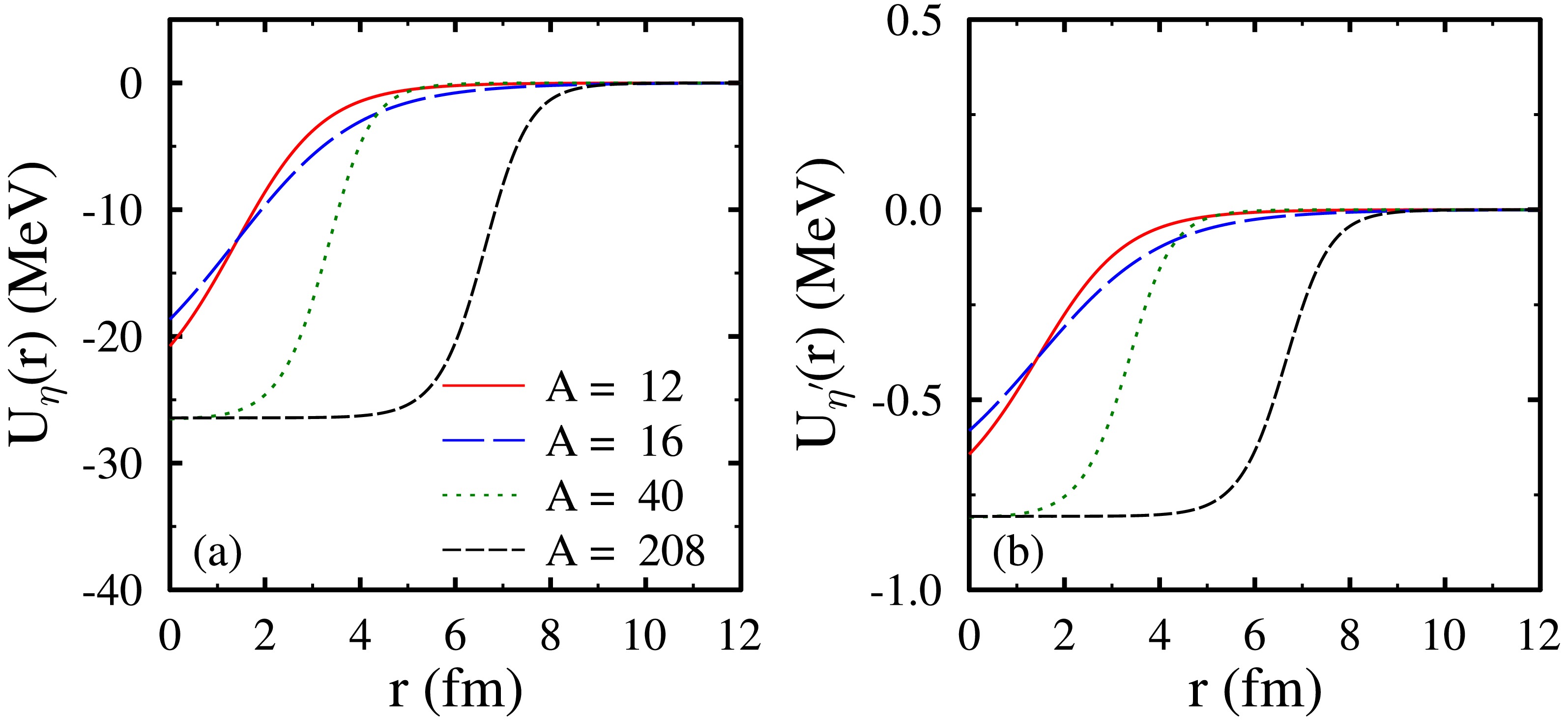

Figure 2.  (color online) Real optical potential $ U(r) $ of η [in subplot (a)] and $ \eta^{\prime} $ [in subplot (b)] mesons as a function of distance r from the center, for nuclei $ ^{12} {\rm{C}}$, $ ^{16} {\rm{O}}$, $ ^{40} {\rm{C}}{\rm{a}}$, and $ ^{208} {\rm{Pb}}$, with mass numbers $ A = 12, 16, 40 $, and $ 208 $, respectively.

As discussed earlier, in the present calculations, the $ \eta ' $ mesons are not observed to undergo an appreciable mass drop in the nuclear medium ($ \Delta m_{\eta '} = -1.03 $ MeV at $ \rho_B = \rho_0 $), and bound states are not observed for these pseudoscalar singlet mesons with any of the nuclei considered. The present results of η and $ \eta ' $ mesons can be compared with those of earlier studies using different approaches. In Ref. [14], the mass shifts of η and $ \eta ' $ mesons were calculated in the symmetric nuclear medium using the QMC model considering the $ \eta-\eta ' $ mixing. The values of mass shift were observed to be $ -63.6 $ and $ -61.3 $ MeV, respectively, at $ \rho_B =\rho_0 $. The binding energies and absorption decay width were calculated for light and heavy nuclei and were observed to form the bound states due to a significant mass drop. Using the coupled channel approach, the optical potential for $ \eta ' $ mesons was found to be $-(8.7 + 1.8 {\rm i})$ MeV at nuclear saturation density, $ \rho_0 $, and no bound state was observed in Ref. [9]. Bound states of η mesons were explored using the unitarized coupled channel approach in Ref. [17], considering the energy independent and dependent potentials. The binding energies obtained were larger than our present calculations. The feasibility of the formation of η and $ \eta ' $ meson bound states with nuclei has also been explored using the NJL model [8]. In Ref. [90], the relativistic field theoretical model under mean field approximation was used to study the $ \eta^{\prime} $ mesic nuclei through the direct coupling of the $ \eta^{\prime} $ meson with scalar mean field σ (interaction of form $ \sim g_{\sigma \eta^{\prime}} m_{\eta^{\prime}} \eta^{\prime 2}\sigma $). Assuming the partial restoration of chiral symmetry and $ 30 $% reduction in the chiral condensate to determine the coupling constant $ g_{\sigma \eta^{\prime}} $, the $ \eta^{\prime} $ meson was observed to undergo a mass drop of $ 80 $ MeV at nuclear saturation density from the vacuum value. Such larger mass drops lead to the formation of bound states with the nuclei $ ^{12} {\rm{C}}$, $ ^{16} {\rm{O}}$, and $ ^{40} {\rm{C}}{\rm{a}}$ considered in this study.

Now, we discuss the formation of bound states for neutral $ D^{0} $ and $ \bar{D^{0}} $ mesons with the nuclei within the chiral $S U $(3) hadronic mean field model. The mass shift of $ D^0 $ and $ \bar{D^0} $ mesons calculated using Eq. (46) are plotted in Fig. 3 as a function of the baryon density ratio $ \rho_B/\rho_0 $. As the figure shows, the in-medium masses of both $ D^0 $ and $ \bar{D^0} $ mesons decrease as a function of the density of the nuclear medium. Furthermore, the increase in the isospin asymmetry of the medium from zero to a finite value (which is relevant for studying nuclei with different numbers of protons and neutrons) decreases the magnitude of the mass shift for these neutral pseudoscalar mesons. At zero temperature and $ \rho_B = \rho_0 (4\rho_0) $, the values of mass shift for $ D^0 $ and $ \bar{D^0} $ mesons are observed to be $ -76.96 (-343.82) $ and $ -26 (-159.71) $ MeV in the symmetric nuclear medium, whereas for $ I = 0.3 $, these values change to $ -64.17 (-298.80) $ and $ -23.37 (-148.43) $ MeV, respectively. For temperature $ T = 100 $ MeV, the values of mass shift for $ D^0 $ and $ \bar{D^0} $ mesons are observed to be $ -64.92(-316.43) $ and $ -14.24(-129.53) $ MeV, respectively, in the symmetric nuclear medium at $ \rho_B = \rho_0 (4\rho_0) $.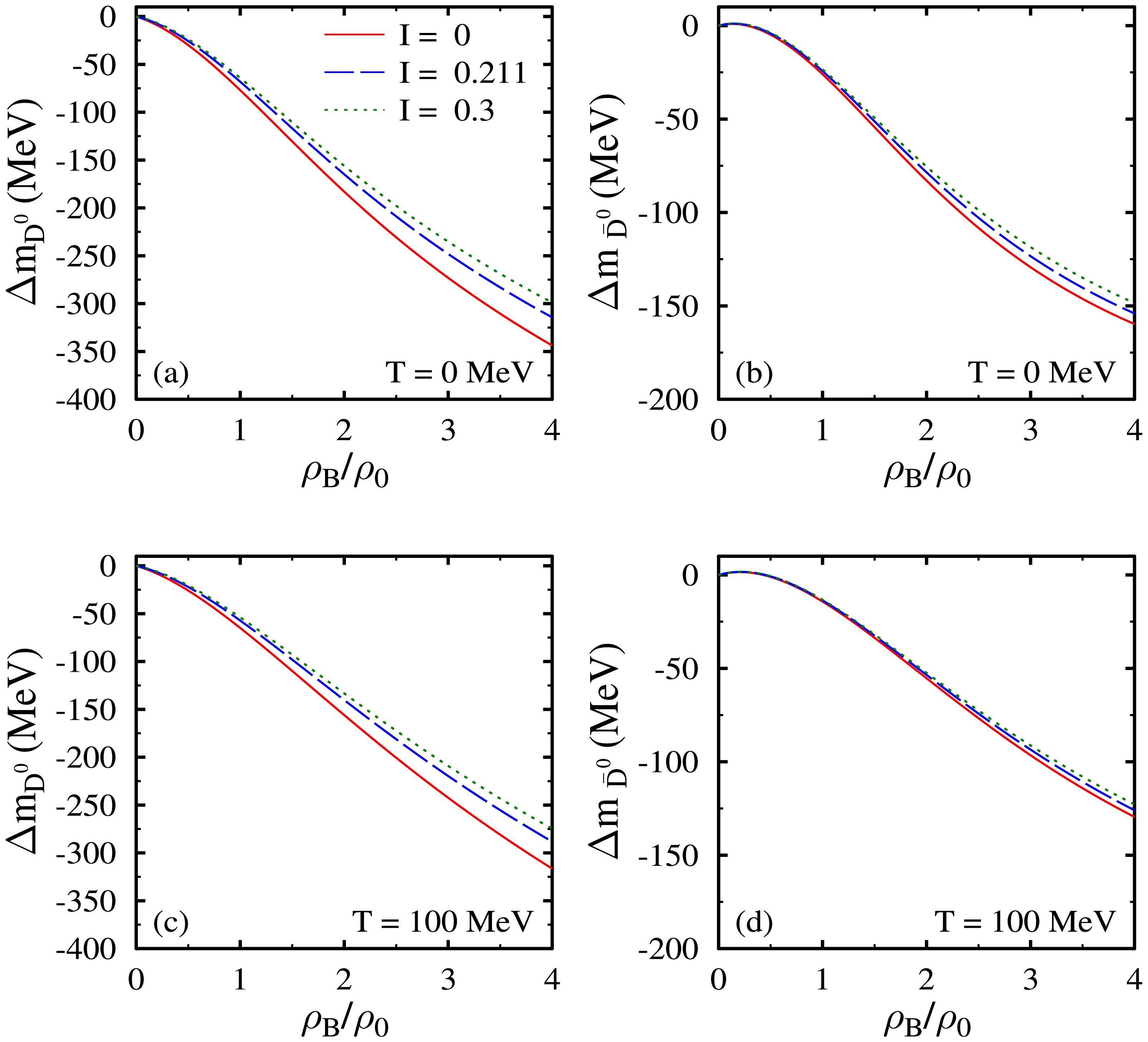

Figure 3.  (color online) Mass shift of $D^{0}$ [in subplots (a) and (c)] and $\bar{D^{0}}$ [in subplots (b) and (d)] mesons as a function of the baryon density$\rho_B$ (in units of nuclear saturation density $\rho_0$) of the nuclear medium for isospin asymmetry $I = 0, 0.211$, and $0.3$. Results are shown for $T = 0 $ and $100$ MeV.

Using the observed values of mass shift for $ D^{0} $ and $ \bar{D^0} $ mesons at the center of the given nuclei in Eq. (24), we calculate the real part of the optical potential and plot it in Fig. 4 as a function of r for the nuclei $ ^{12} {\rm{C}}$, $ ^{16} {\rm{O}}$, $ ^{40} {\rm{C}}{\rm{a}}$, and $ ^{208} {\rm{Pb}}$. As the figure shows, the depth of the optical potential (large negative value) is observed to be higher for $ D^{0} $ mesons than for $ \bar{D^{0}} $ mesons. For $ \bar{D^0} $ mesons, the optical potential $ U_{\bar{D^0}}(r) $ is observed to have positive values for a certain range of r, causing a bump, as shown in Fig. 4(b). In contrast, such positive values are not observed for the optical potential of $ D^{0} $ mesons. The observed difference is because of the opposite contribution of the Weinberg Tomozawa term for the $ D^{0} $ and $ \bar{D^{0}} $ mesons, as shown in Eqs. (44) and (45), respectively. The Weinberg Tomozawa term alone gives positive contribution to the optical potential of $ \bar{D^{0}} $ mesons, whereas the combined contribution of all other terms provides a negative value for $ U_{\bar{D^0}}(r) $. For a certain range of r, the positive contribution due to the Weinberg Tomozawa term dominates over the net negative contribution of other terms, causing an overall positive value of the optical potential for $ \bar{D^0} $ mesons. To understand this, in Fig. 4(c) and Fig. 4(d), we plot the optical potentials of $ D^0 $ and $ \bar{D^0} $ mesons, respectively, considering (i) the Weinberg Tomozawa term only and (ii) without the Weinberg Tomozawa term for $ ^{208} {\rm{Pb}}$. As shown in Fig. 4(c), for $ D^{0} $ mesons, the optical potentials from the Weinberg Tomozawa term have negative values, and therefore, unlike $ \bar{D^0} $ mesons, positive values are not observed for $ D^0 $ mesons.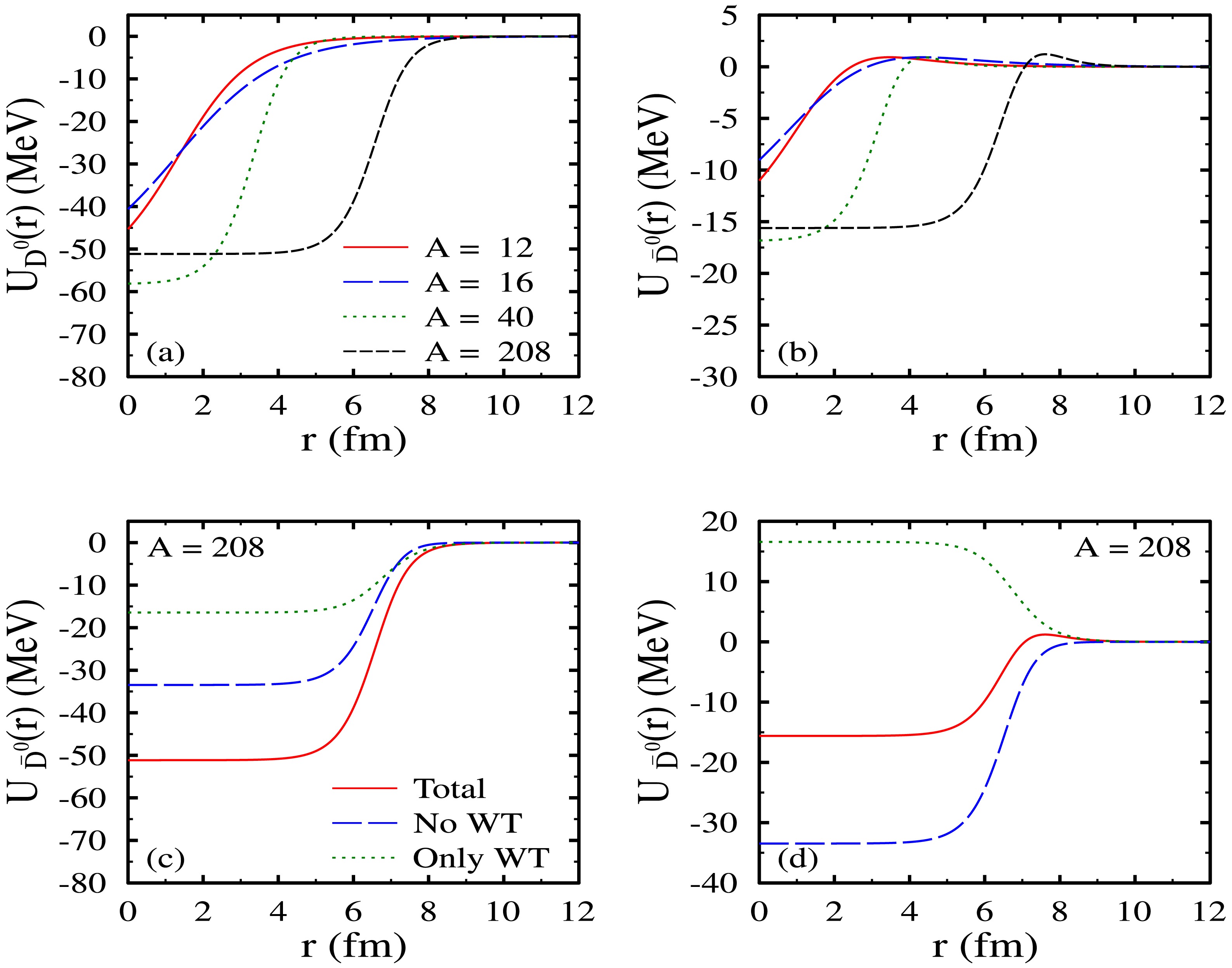

Figure 4.  (color online) Real optical potentials $ U(r) $ of $ D^0 $ [in subplot (a)] and $ \bar{D^{0}} $ [in subplot (b)] mesons as a function of distance r from the center for nuclei $ ^{12} {\rm{C}}$, $ ^{16} {\rm{O}}$, $ ^{40} {\rm{C}}{\rm{a}}$, and $ ^{208} {\rm{Pb}}$ with mass numbers $ A = 12, 16, 40 $, and $ 208 $, respectively. In subplots (c) and (d), optical potentials are plotted for $ A =208 $ considering the impact of the Weinberg Tomozawa (WT) term to the total optical potential.

The imaginary part of the optical potential, required to understand the absorption of mesons in the nuclei and its impact on the binding energy of neutral D mesic nuclei, is calculated using Eq. (25). The values of binding energy and decay width obtained by solving the Klein Gordon equation are given in Tables 2 and 3 for $ D^0 $ and $ \bar{D^0} $ mesons, respectively, for $ \kappa = 0, 0.5 $, and 1. As shown in Table 2, the bound states of $ D^0 $ mesons for $ ^{40} {\rm{C}}{\rm{a}}$ and $ ^{208} {\rm{Pb}}$ may be found not only for lower states $ 1s $ and $ 1p $ but also for other higher states when $ \kappa = 0 $ and $ 0.5 $. When the value of κ is increased to 1, the magnitude of binding energy is observed to be lower than the decay width value. This may cause a broadening of the peak and hindrance in the observation of the clear signature of bound states. Comparing the values of binding energies in Tables 2 and 3, the magnitudes of the binding energies for $ \bar{D^0} $ mesons are significantly lower than those of $ D^0 $ mesons. In Ref. [10], the bound states of $ D^{0} $ mesons were studied for several nuclei using the coupled channel approach. Comparing our results for $ ^{12} {\rm{C}}$, $ ^{40} {\rm{C}}{\rm{a}}$, and $ ^{208} {\rm{Pb}}$ with those of Ref. [10], the magnitudes of binding energies are observed to be higher in our case. The binding energies of $ D^0 $ and $ \bar{D^0} $ mesons for $ ^{208} {\rm{Pb}}$ nuclei are calculated using the QMC model and are found to be approximately $ -96 $ and $ -25 $ MeV, respectively [7].

A	$ nl $	$ {\cal{E}}_{\cal{B}} $/MeV				Γ /MeV
		κ =0	κ = 0.5	κ =1		κ =0	κ = 0.5	κ =1
$^{12}_{\phantom{1}6} {\rm{C} }$	1s	−25.965	−25.741	−25.118		0.0	18.731	37.748
	1p	−11.246	−10.811	−9.638		0.0	14.235	29.144
	2s	−0.935	–	–		0.0	–	–
$^{16}_{\phantom{1}8} {\rm{O} }$	1s	−29.11	−28.941	−28.474		0.0	19.504	39.224
	1p	−16.516	−16.184	−15.282		0.0	16.451	33.407
	1d	−3.884	−3.234	−1.619		0.0	12.057	25.31
	2s	−3.946	−3.152	−1.182		0.0	9.717	20.971
$ ^{40}_{20} {\rm{C}}{\rm{a}}$	1s	−47.743	−47.607	−47.22		0.0	27.865	55.842
	1p	−38.223	−38.016	−37.44		0.0	26.065	52.369
	1d	−27.642	−27.338	−26.509		0.0	23.945	48.313
	2s	−25.594	−25.233	−24.263		0.0	23.249	47.047
	2p	−14.212	−13.608	−12.07		0.0	19.93	40.966
	2d	−3.852	−2.7	−0.152		0.0	15.302	33.133
$^{208}_{\phantom{2}82} {\rm{Pb} }$	1s	−49.133	−49.073	−48.897		0.0	26.019	52.054
	1p	−46.417	−46.344	−46.135		0.0	25.734	51.507
	1d	−43.096	−43.008	−42.757		0.0	25.382	50.832
	2s	−41.77	−41.674	−41.401		0.0	25.235	50.554
	2p	−37.132	−37.008	−36.664		0.0	24.711	49.56
	2d	−32.078	−31.919	−31.486		0.0	24.102	48.414

Table 2.  Values of binding energies, $ {\cal{E}}_{\cal{B}} $, and full decay width, Γ, for $ D^0 $ mesons in four nuclei with different mass numbers A for $ \kappa = 0, 0.5 $, and 1.

A	$ nl $	$ {\cal{E}}_{\cal{B}} $/MeV				Γ/MeV
		κ =0	κ = 0.5	κ =1		κ =0	κ = 0.5	κ =1
$^{12}_{\phantom{1}6} {\rm{C} }$	1s	−1.633	−1.49	−1.102		0.0	2.539	5.306
$^{16}_{\phantom{1}8} {\rm{O} }$	1s	−2.142	−2.03	−1.726		0.0	2.756	5.694
$ ^{40}_{20} {\rm{C}}{\rm{a}}$	1s	−9.87	−9.801	−9.615		0.0	7.096	14.299
	1p	−4.25	−4.091	−3.676		0.0	5.674	11.637
$^{208}_{\phantom{2}82} {\rm{Pb} }$	1s	−13.541	−13.524	−13.479		0.0	7.646	15.313
	1p	−11.434	−11.403	−11.32		0.0	7.41	14.869
	1d	−8.887	−8.836	−8.701		0.0	7.101	14.29
	2s	−7.936	−7.869	−7.694		0.0	6.924	13.973
	2p	−4.607	−4.478	−4.164		0.0	6.303	12.881
	2d	−1.3	−1.007	−0.43		0.0	5.311	11.331

Table 3.  Values of binding energies, $ {\cal{E}}_{\cal{B}} $, and full decay width, Γ, for $ \bar{D^0} $ mesons in four nuclei with different mass numbers A for $ \kappa = 0, 0.5 $, and 1.

The bound states of B mesons with nuclei have not been studied sufficiently [44]. In this section, we discuss the formation of bound states of pseudoscalar $ B^{0} $ and $ \bar{B^{0}} $ mesons by calculating their optical potential using the chiral $S U $(3) model. In Fig. 5, the mass shift of these pseudoscalar mesons are plotted as a function of the baryon density $ \rho_B $ (in units of $ \rho_0 $) for isospin asymmetries $ I = 0, 0.211 $ and $ 0.3 $, at $ T = 0 $ and $ 100 $ MeV. Both pseudoscalar $ B^0 $ and $ \bar{B^0} $ mesons are observed to undergo appreciable mass drops at nuclear matter densities, whereas, for any given density, an increase in temperature from zero to finite values causes an increase in the mass, i.e., a lower drop in mass. However, the isospin asymmetry effects are not appreciable. In cold symmetric nuclear media, with $ \rho_B = \rho_0 $, the values of $ \Delta m $ for $ B^0 $ and $ \bar{B^0} $ mesons are observed to be $ -48.69 $ and $ -74.06 $ MeV, whereas at $ 4\rho_0 $, these values change to $ -356.40 $ and $ -453.28 $ MeV, respectively. As shown in Fig. 6, for given nuclei, at the center, the real part of optical potentials have larger values for $ \bar{B^{0}} $ mesons than for $ B^0 $ mesons. In case of $ B^0 $ mesons, the optical potentials have positive values for a certain range, whereas for $ \bar{B^{0}} $ mesons, this is not the case. This is because of the opposite contribution of the Weinberg Tomozawa term to $ B^0 $ and $ \bar{B^{0}} $ mesons (see the first term of Eqs. (48) and (49)). For $ B^0 $ mesons, the Weinberg Tomozawa term leads to positive values of optical potentials. The values of binding energy and decay width for these pseudoscalar mesons are given in Tables 4 and 5. As expected from the magnitude of mass drop for $ B^0 $ and $ \bar{B^0} $ mesons, the magnitude of binding energy with given nuclei is more for $ \bar{B^0} $ mesons as compared to $ B^0 $.

Figure 5.  (color online) Mass shift of $ B^{0} $ [in subplots (a) and (c)] and $ \bar{B^{0}} $ [in subplots (b) and (d)] mesons as a function of the density $ \rho_B $ (in units of nuclear saturation density $ \rho_0 $) of the nuclear medium for isospin asymmetry $ I = 0, 0.211 $, and $ 0.3 $. Results are shown for temperatures $ T = 0 $ and $ 100 $ MeV.

Figure 6.  (color online) Real optical potential $ U(r) $ of $ B^0 $ [in subplot (a)] and $ \bar{B^{0}} $ [in subplot (b)] mesons as a function of distance r from the center for nuclei $ ^{12} {\rm{C}}$, $ ^{16} {\rm{O}}$, $ ^{40} {\rm{C}}{\rm{a}}$, and $ ^{208} {\rm{Pb}}$ with mass numbers$ A = 12, 16, 40 $, and $ 208 $, respectively.

A	$ nl $	$ {\cal{E}}_{\cal{B}} $/MeV				Γ/MeV
		κ =0	κ = 0.5	κ =1		κ =0	κ = 0.5	κ =1
$^{12}_{\phantom{1}6} {\rm{C} }$	1s	−10.933	−10.845	−10.604		0.0	7.907	15.944
	1p	−4.572	−4.385	−3.886		0.0	5.989	12.285
	2s	−0.272	–	–		0.0	–	–
$^{16}_{\phantom{1}8} {\rm{O} }$	1s	−10.848	−10.789	−10.627		0.0	7.362	14.816
	1p	−5.789	−5.657	−5.302		0.0	6.133	12.486
	1d	−0.805	−0.513	–		0.0	4.274	–
	2s	−1.02	−0.662	–		0.0	3.274	–
$ ^{40}_{20} {\rm{C}}{\rm{a}}$	1s	−26.07	−26.032	−25.926		0.0	14.613	29.275
	1p	−22.064	−21.996	−21.809		0.0	13.928	27.954
	1d	−17.562	−17.456	−17.166		0.0	13.13	26.425
	2s	−16.627	−16.502	−16.166		0.0	12.902	26.009
	2p	−11.516	−11.316	−10.79		0.0	11.741	23.84
	2d	−6.481	−6.158	−5.352		0.0	10.282	21.205
$^{208}_{\phantom{2}82} {\rm{Pb} }$	1s	−31.71	−31.698	−31.665		0.0	16.342	32.691
	1p	−30.648	−30.632	−30.586		0.0	16.245	32.505
	1d	−29.347	−29.325	−29.263		0.0	16.125	32.277
	2s	−28.826	−28.802	−28.733		0.0	16.08	32.19
	2p	−26.996	−26.961	−26.868		0.0	15.91	31.867
	2d	−24.983	−24.938	−24.815		0.0	15.717	31.502

Table 4.  Values of binding energies, $ {\cal{E}}_{\cal{B}} $, and full decay width, Γ, for $ B^{0} $ mesons in four nuclei with different mass numbers A for $ \kappa = 0, 0.5 $, and 1.

A	$ nl $	$ {\cal{E}}_{\cal{B}} $/MeV				Γ/MeV
		κ =0	κ = 0.5	κ =1		κ =0	κ = 0.5	κ =1
$^{12}_{\phantom{1}6} {\rm{C} }$	1s	−25.403	−25.292	−24.986		0.0	16.151	32.455
	1p	−16.432	−16.222	−15.646		0.0	13.936	28.186
	1d	−7.473	−7.117	−6.171		0.0	11.205	22.994
	2s	−7.506	−7.101	−6.028		0.0	10.381	21.446
	2p	−1.086	−0.26	–		0.0	6.142	–
$^{16}_{\phantom{1}8} {\rm{O} }$	1s	−26.085	−26.014	−25.818		0.0	15.715	31.532
	1p	−19.262	−19.116	−18.717		0.0	14.435	29.096
	1d	−11.721	−11.471	−10.799		0.0	12.632	25.674
	2s	−10.487	−10.193	−9.407		0.0	11.52	23.535
	2p	−4.153	−3.645	−2.362		0.0	8.743	18.447
$ ^{40}_{20} {\rm{C}}{\rm{a}}$	1s	−45.779	−45.725	−45.572		0.0	24.844	49.743
	1p	−41.003	−40.917	−40.677		0.0	24.034	48.174
	1d	−35.617	−35.492	−35.146		0.0	23.119	46.409
	2s	−34.457	−34.317	−33.934		0.0	22.917	46.034
	2p	−28.121	−27.919	−27.371		0.0	21.716	43.749
	2d	−21.612	−21.326	−20.57		0.0	20.34	41.161
$^{208}_{\phantom{2}82} {\rm{Pb} }$	1s	−55.277	−55.252	−55.179		0.0	28.274	56.555
	1p	−54.102	−54.073	−53.986		0.0	28.164	56.343
	1d	−52.663	−52.627	−52.523		0.0	28.029	56.085
	2s	−52.09	−52.052	−51.941		0.0	27.981	55.992
	2p	−50.065	−50.017	−49.883		0.0	27.796	55.639
	2d	−47.833	−47.775	−47.612		0.0	27.59	55.244

Table 5.  Values of binding energies, $ {\cal{E}}_{\cal{B}} $, and full decay width, Γ, for $ \bar{B^0} $ mesons in four nuclei with different mass numbers A for $ \kappa = 0, 0.5 $, and 1.

Finally, in this subsection, we explore the formation of bound states for $ \bar{K^{0}} $ and ϕ mesons. Within the chiral $ S U$(3) model, among the neutral $ K^0 $ and $ \bar{K^0} $ mesons, only the latter is observed to undergo a mass drop as a function of the density of the nuclear medium [64−66]. Therefore, we consider the $ \bar{K^0} $ neutral meson only to explore the bound state formation. In Fig. 7, we show the variation in the mass shift for $ \bar{K^0} $ mesons as a function of baryon density $ \rho_B $ at temperatures $ T = 0 $ and 100 MeV. The plot of the real part of the optical potential $ U(r) $as a function of distance r from the center of the given nuclei of mass number A for $ \bar{K^0} $ mesons is given in Fig. 8. At $ I = 0 $ and $ T = 0 $ (100) MeV, the values of the mass shift for $ \bar{K^0} $ mesons are found to be $ -36.90 (-36.43) $ and $ -184.31 (-175.87) $ MeV at $ \rho_B = \rho_0 $ and $ 4\rho_0 $, respectively. For a given density of the medium, an increase in the isospin asymmetry enhances the mass drop for $ \bar{K^0} $ mesons, which is more appreciable at higher baryon densities. As Table 6 shows, for the nuclei $ ^{12} {\rm{C}}$, $ ^{18} {\rm{O}}$, and $ ^{40} {\rm{C}}{\rm{a}}$, the negative values of binding energies are observed only for the $ 1s $ state. Furthermore, when the value of κ is considered to be finite, the bound state of $ \bar{K^0} $ mesons with these nuclei may be difficult to observe owing to the comparable or larger value of decay width Γ.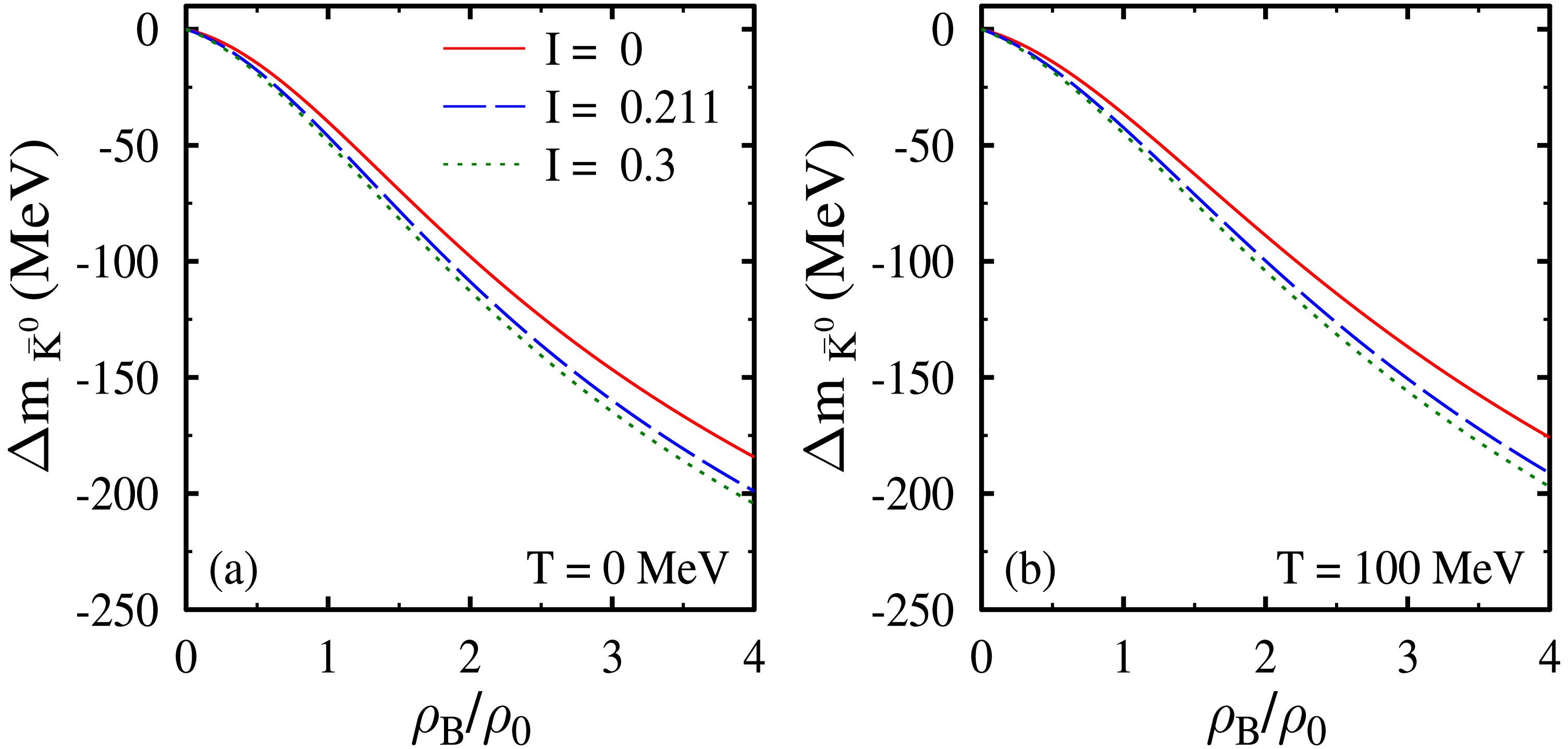

Figure 7.  (color online) Mass shift of $ \bar{K^{0}} $ mesons as a function of density $ \rho_B $ (in units of nuclear saturation density $ \rho_0 $) of the nuclear medium for isospin asymmetries $ I = 0, 0.211 $, and $ 0.3 $. Results are shown for temperatures $ T = 0 $ (subplot (a)) and $ 100 $ MeV (subplot (b)).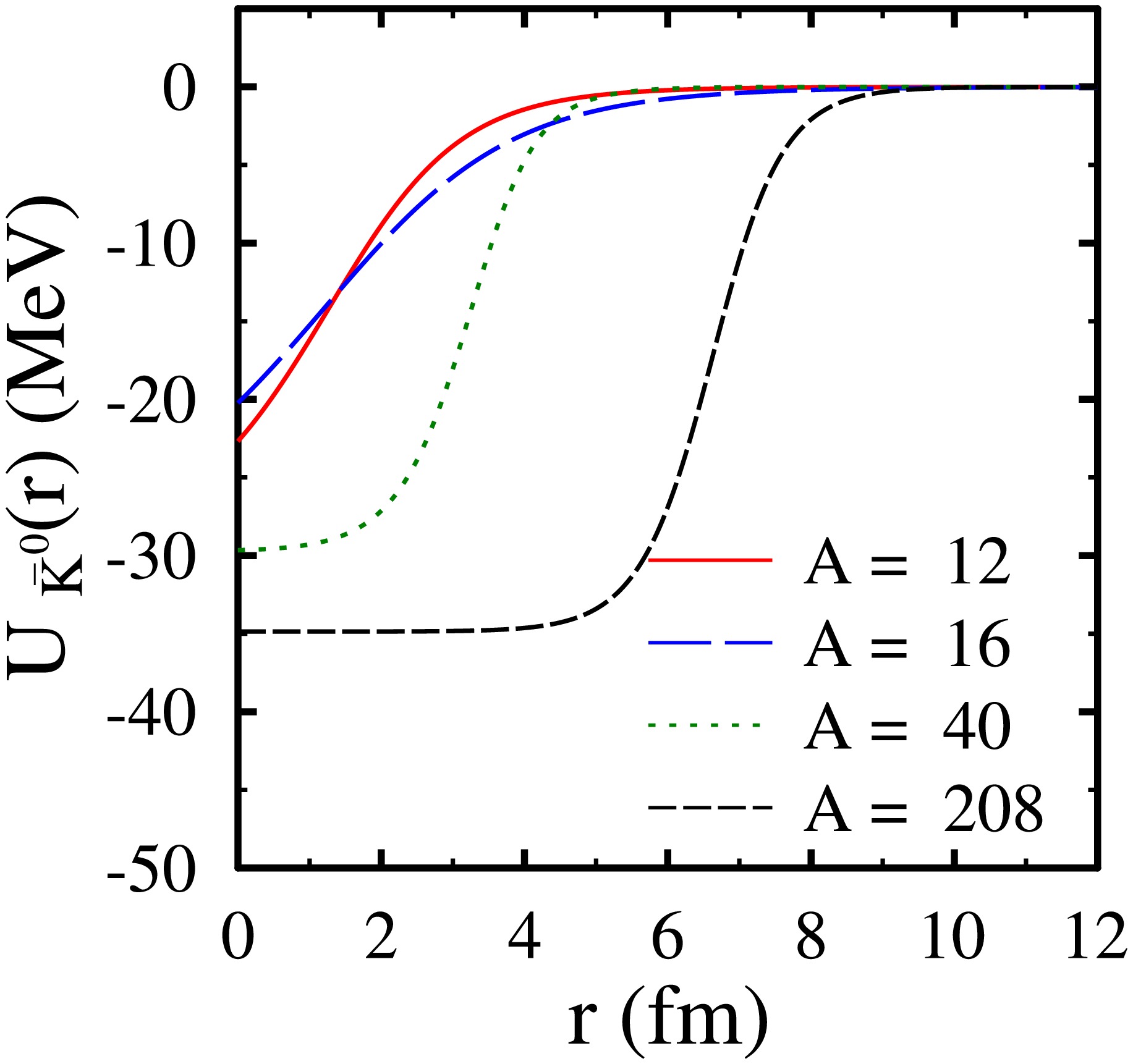

Figure 8.  (color online) Real optical potential $ U(r) $ of $ \bar{K^{0}} $mesons as a function of distance r from the center for nuclei $ ^{12} {\rm{C}}$, $ ^{16} {\rm{O}}$, $ ^{40} {\rm{C}}{\rm{a}}$, and $ ^{208} {\rm{Pb}}$ with mass numbers$ A = $ 12, 16, 40, and $ 208 $, respectively.

A	$ nl $	$ {\cal{E}}_{\cal{B}} $/MeV				Γ/MeV
		κ =0	κ = 0.5	κ =1		κ =0	κ = 0.5	κ =1
$^{12}_{\phantom{1}6} {\rm{C} }$	1s	−0.573	−0.128	–		0.0	2.368	–
$^{16}_{\phantom{1}8} {\rm{O} }$	1s	−1.84	−1.469	−0.462		0.0	4.071	8.731
$ ^{40}_{20} {\rm{C}}{\rm{a}}$	1s	−11.209	−10.949	−10.24		0.0	10.803	21.964
$^{208}_{\phantom{2}82} {\rm{Pb} }$	1s	−28.644	−28.509	−28.123		0.0	17.663	35.389
	1p	−21.387	−21.202	−20.688		0.0	16.485	33.146
	1d	−12.892	−12.621	−11.9		0.0	14.939	30.257
	2s	−10.123	−9.746	−8.799		0.0	13.919	28.501
	2p	−0.991	–	–		0.0	–	–

Table 6.  Values of binding energies, $ {\cal{E}}_{\cal{B}} $, and full decay width, Γ, for $ \bar{K^0} $ mesons in four nuclei with different mass numbers A for $ \kappa = 0, 0.5 $, and 1.

As discussed in Sec. III.E, the mass shift and decay width of ϕ meson are obtained in this study by calculating the self energy, which involves the interactions of ϕ mesons with K and $ \bar{K} $, at the one loop level. In Fig. 9, we have plotted the mass shift and decay width of ϕ mesons as a function of $ \rho_B/\rho_0 $. At $ T =0 $MeV, the values of mass shift $ \Delta m_{\phi}^* $ and decay width $ \ \Gamma_{\phi}^* $at baryon density $ \rho_B = \rho_0 (4\rho_0) $ are observed to be $ -2.00 (-20.28) $ and $ 4.96 (27.68) $ MeV, respectively, for a cutoff parameter of $ \Lambda_c = 3000 $ MeV. In Fig. 10, the real and imaginary optical potentials $ U_\phi(r) $ and $ W_\phi(r) $ of ϕ mesons are plotted as a function of distance r for the four nuclei ($ A = 12, 16, 40 $, and $ 208 $). As we observe a very small negative mass shift for the ϕ mesons, the bound states are not possible for these mesons within the present calculations, where the in-medium masses of K and $ \bar{K} $ mesons are evaluated using the chiral $S U $(3) model. In the chiral $S U $(3) model, the properties of kaons and antikaons are modified differently in the nuclear medium. The effective mass of kaons increases, whereas the mass of antikaons decreases as the density of the medium changes from zero to an finite value [64−66]. From Fig. 10, we observe that the real part of the optical potential remains mostly repulsive. This is because of the dominance of repulsive contributions of kaons as a function of r over the attractive contribution of antikaons to the in-medium masses of ϕ mesons. As discussed in Sec. III.E, average masses $ m_{K}^{*}\left(=\dfrac{m_{K^{0}}^{*} + m_{K^{+}}^{*}}{2}\right) $ and $ m_{\bar{K}}^{*}\left(=\dfrac{m_{\bar{K}^{0}}^{*}+m_{K^{-}}^{*}}{2}\right) $ are used in the calculations of self-energy of ϕ mesons given by Eq. (54). As shown in Fig. 11, average mass $ m_{K}^{*} $ remains repulsive (in-medium mass greater than vacuum mass ($ \sim $ 494 MeV)) as a function of r, whereas $ m_{\bar{K}}^{*} $ is attractive (in-medium mass less than vacuum mass ($ \sim $ 494 MeV)). For a certain range of r values, the increased dominance of the repulsive contribution causes a bump in the real part of the optical potential of ϕ mesons and a well in the imaginary part. In Ref. [6], the ϕ meson bound states were investigated considering the modification of kaons and antikaons within the QMC model. The in-medium masses of kaons and antikaons were considered to be the same in the nuclear medium and were observed to decrease as a function of the baryon density $ \rho_B $. Thus, the mass drop in the ϕ mesons was larger than that in our present calculations. For example, at$ \rho_B = \rho_0 $, $ \Delta m_\phi $ is observed to be $ \approx - 20 $ MeV for the cuttoff $ \Lambda_c = 2000 $ MeV. This larger mass drop in the ϕ meson masses also leads to the possibility of bound states in the calculations of Ref. [6]. However, as discussed above, in the chiral $ S U$(3) model considered in the present calculations, the in-medium mass of kaons increases, whereas the mass of antikaon decreases as a function of density of the nuclear medium. Actually, the effective masses of kaons and antikaons in the chiral $S U$(3) model are modified in the nuclear medium through the Weinberg Tomozawa, scalar meson exchange, and range terms [64−66]. As a function of the density of the nuclear medium, the leading order Weinberg Tomozawa term gives repulsive contributions to kaons and attractive ones to antikaons. Overall, this leads to an increase in the mass of kaons and a decrease in the mass of antikaons as function of $ \rho_B $. Because the in-medium masses of ϕ mesons are modified through the medium modifications of kaons and antikaons, their opposite behavior as a function of density leads to a small mass shift in the mass of ϕ mesons in the present calculations.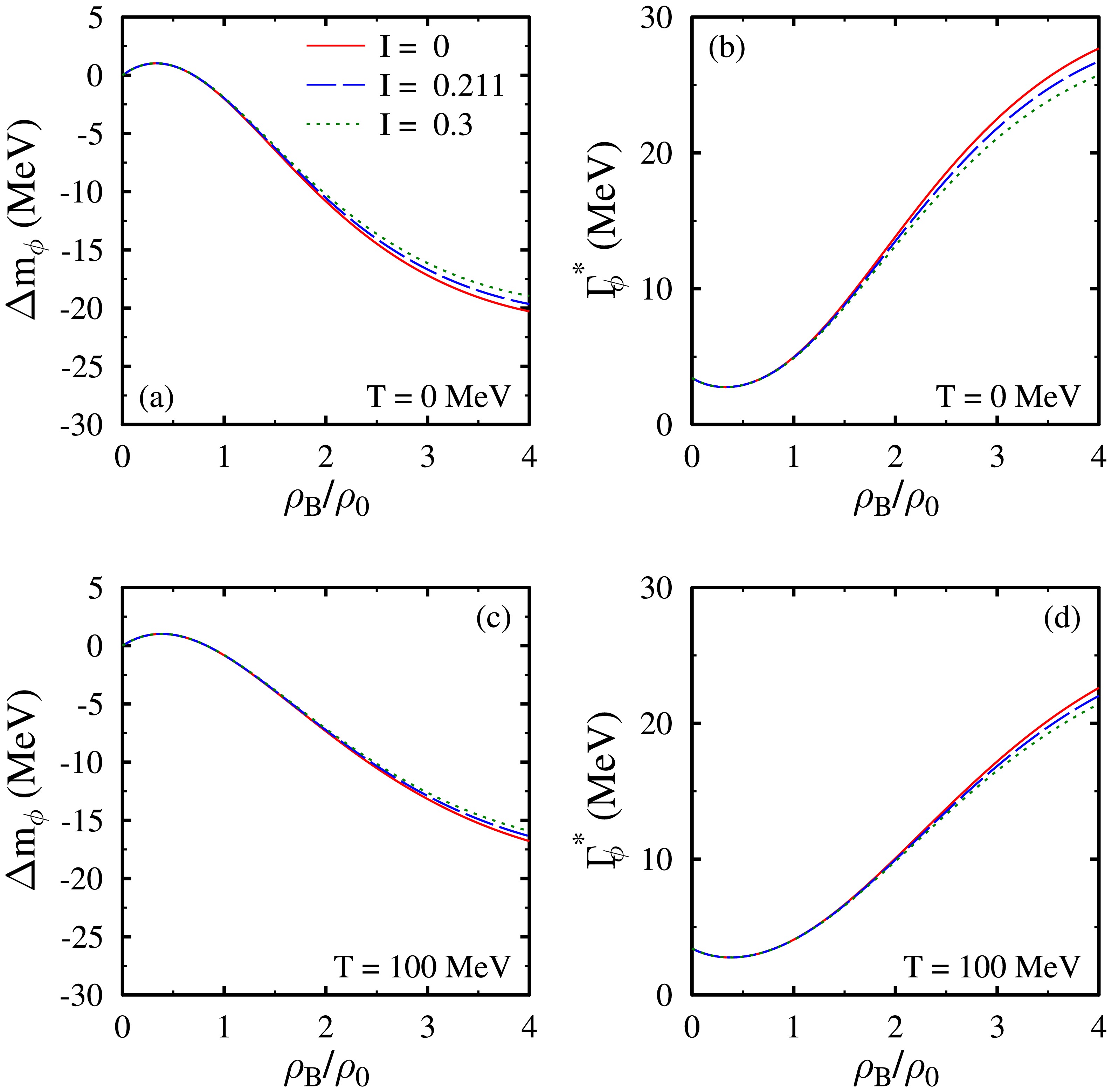

Figure 9.  (color online) Mass shift [in subplots (a) and (c)] and decay width [in subplots (b) and (d)] of ϕ mesons as a function of density $ \rho_B $ (in units of nuclear saturation density $ \rho_0 $) of the nuclear medium for isospin asymmetries $ I = 0, 0.211 $, and $ 0.3 $. Results are shown for temperatures $ T = 0 $ and $ 100 $ MeV.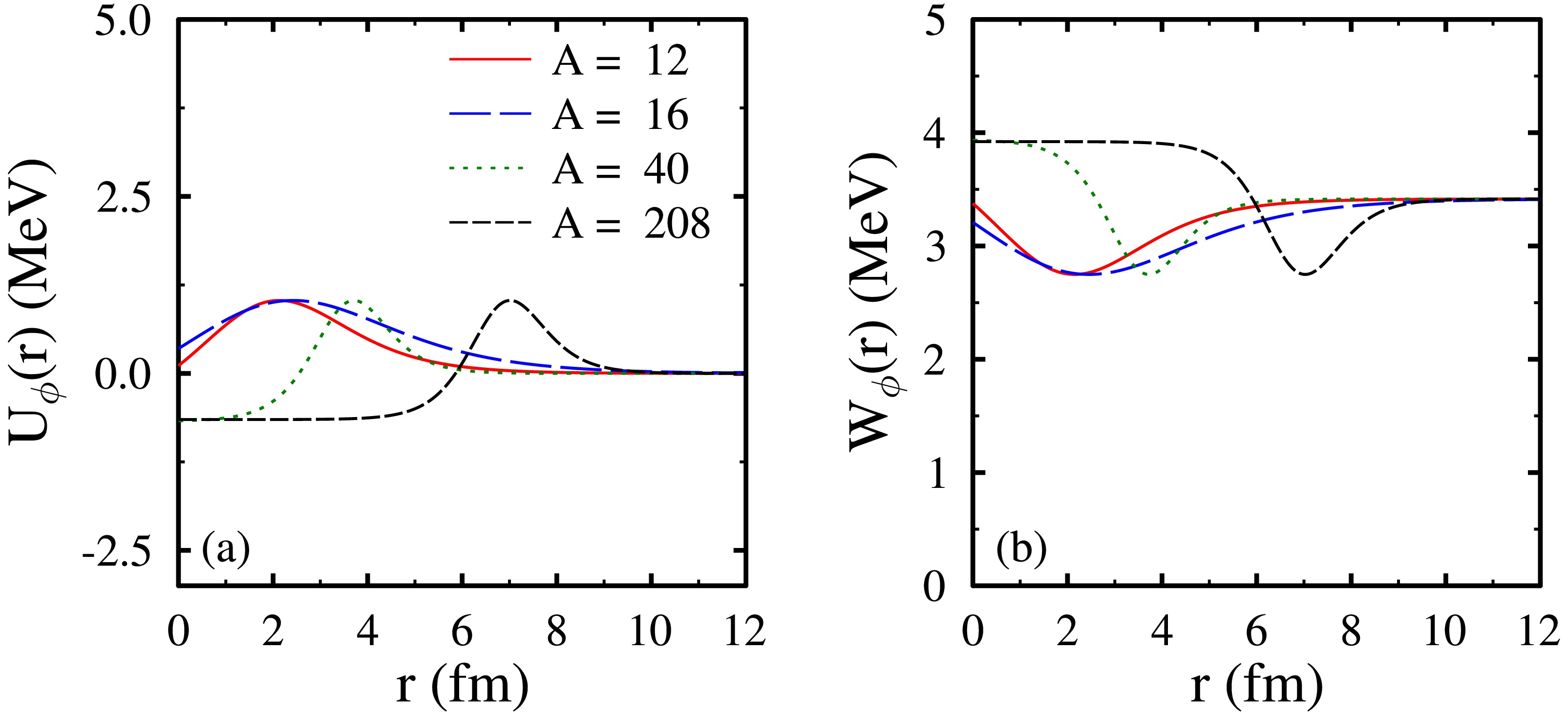

Figure 10.  (color online) Real optical potential $ U(r) $ [in subplot (a)] and imaginary optical potential $ W(r) $ [in subplot (b)] of ϕ mesons as a function of distance r from the center for the nuclei $ ^{12} {\rm{C}}$, $ ^{16} {\rm{O}}$, $ ^{40} {\rm{C}}{\rm{a}}$, and $ ^{208} {\rm{Pb}}$ with mass numbers$ A = 12, 16,, 40 $, and $ 208 $, respectively.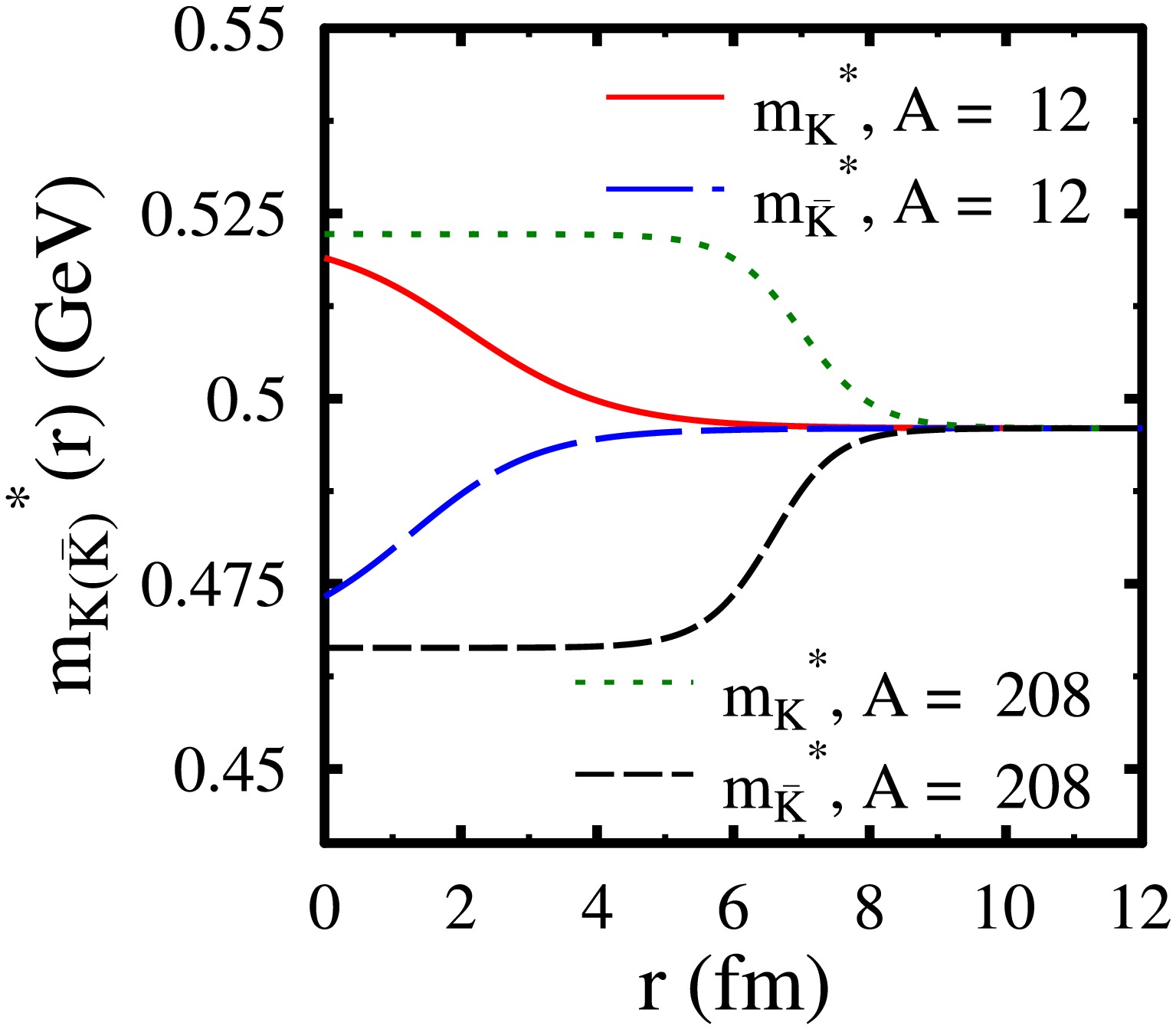

Figure 11.  (color online) Average effective masses $ m_{K}^{*}\left(=\frac{m_{K^{0}}^{*} + m_{K^{+}}^{*}}{2}\right) $ and $ m_{\bar{K}}^{*}\left(=\frac{m_{\bar{K}^{0}}^{*}+m_{K^{-}}^{*}}{2}\right) $ for kaons and antikaons as a function of distance r from the center for the nuclei $ ^{12} {\rm{C}}$ and $ ^{208} {\rm{Pb}}$ with mass numbers $ A = 12 $ and $ 208 $, respectively.

We investigated the possibility of the formation of bound states for neutral mesons $ \eta, \eta ' $, $ D^{0}, \bar{D^0} $, $ B^0, \bar{B^0} $, and $ \bar{K^0} $ and ϕ mesons with the nuclei $ ^{12} {\rm{C}}$, $ ^{16} {\rm{O}}$, $ ^{40} {\rm{C}}{\rm{a}}$, and $ ^{208} {\rm{Pb}}$. The binding energies for different mesons were calculated by solving the Klein Gordon equation considering the complex potential. The imaginary potential was introduced to understand the impact of absorption of mesons in the nuclei on the formation of bound states. The mass shifts for different mesons considered in this study were used to obtain the real and imaginary optical potentials for nuclei of different mass numbers. Except for vector ϕ mesons, the imaginary optical potentials for all other mesons were introduced through phenomenological prescription in terms of a parameter κ according to some previous studies [14].

To study the bound states for pseudoscalar η and $ \eta ' $ mesons within the chiral $S U $(3) model, we considered the mixing between the states $ \eta_{8} $ and $ \eta_0 $. We observed an appreciable mass drop for the η mesons, whereas the $ \eta ' $mass was observed to decrease significantly less. This led to the possibility of bound states of η mesons with the nuclei considered in this study, whereas for the $ \eta ' $ meson, no bound state was observed. Using the chiral $S U $(3) model, generalized to the $S U $(4) sector, we also elaborate on the formation of bound states for $ D^0 $ and $ \bar{D^0} $ mesons. For both $ D^0 $ and $ \bar{D^0} $ mesons, the mass drop observed at nuclear saturation density was such that it led to the formation of bound states. Between $ D^0 $ and $ \bar{D^0} $, the former was observed to undergo a larger mass drop, and this led to the formation of bound states with higher states. For $ B^0 $ and $ \bar{B^0} $ mesons, the obtained negative mass shift led to the formation of bound states for lower and excited states, particularly for nuclei with larger mass numbers A. In this study, we also observed that the pseudoscalar $ \bar{K^0} $ mesons could form bound states as a negative mass shift is observed within the chiral $ S U$(3) model. For vector ϕ mesons, the mass drop obtained in this study was not sufficiently large to form their bound states with the light and heavy nuclei. In Ref. [45], meson-nucleus bound states were studied using the QMC model. In the QMC model, quarks were treated as fundamental degrees of freedom and confined inside the nucleon bag. These confined quarks interacted through the exchange of scalar fields σ and δ and vector fields ω and ρ. In the chiral $ S U$(3) hadronic mean field model, hadrons were treated as point particles. As discussed earlier, the properties of nucleons in the chiral $S U $(3) hadronic mean field model were modified through the exchange of scalar mesons, $ \sigma, \zeta $, and δ and vector mesons ω and ρ. In the QMC model, the effective masses of different mesons in the nuclear medium were calculated through the energy of the static bag in which quarks and antiquarks are confined. In contrast, as explained in detail in Sec. III, in the chiral hadronic model, the interaction Lagrangian density, describing the interactions of mesons under study with the nucleons of the medium, was obtained. The dispersion relations were obtained from the interaction Lagrangian to calculate the optical potentials of mesons in the nuclear medium. In Ref. [45], the possibilities of bound states for K, D, and B mesons were explored, whereas, in this paper, the bound states of $ \eta, \eta^{\prime} $, and ϕ mesons with different nuclei were also considered.

We did not consider the effect of finite density and temperature of the nuclear medium on the binding energy of mesic nuclei. An estimate of this can be obtained considering the following picture: in the formation of mesic nuclei in a nuclear medium at finite temperature, the medium effects can be incorporated by replacing the vacuum mass of mesons with the in-medium value in the calculation of binding energy (appearing in definitions of reduced mass μ [in Eq. (22)] and the real and imaginary part of optical potentials [Eqs. (24) and 25)] at a given density and temperature. As an example, consider the formation of $ D^{0} $ mesic nuclei in a nuclear medium with $ \rho_B = \rho_0 $ and $ T = 100 $ MeV, at which the mass of the $ D^{0} $ meson is found to be $ 1799.57 $ MeV. Using this value, the mass shift $ \Delta m_\psi (\rho_0) $ at the center of $ ^{208}_{\phantom{2}82} {\rm{Pb}}$ nuclei is found to be $ -42.29 $ MeV. This can be compared with the value $ -64.98 $ MeV, which is calculated without considering the impact of the nuclear medium on the formation of bound states, and the mass of $ D^{0} $ in free space is 1864 MeV (see Fig. 4(a)). Using the modifications due to finite density and temperature, the values of binding energy for $ 1s $ and $ 1p $ states change to $ -40.10 $ and $ -37.41 $ MeV and can be compared with the values $ -49.133 $ and $ -43.096 $ MeV given in Table 2. Thus, we observe a decrease in the magnitude of the binding energy at a finite density and temperature of the medium. The decrease in the magnitude of binding energy is also expected for other cases in which bound states with different mesons are formed owing to attractive interactions in the medium. The many-body effects that may impact the density distributions of protons and neutrons inside the nuclei and cause additional attractive interaction and absorption [91] will be investigated in a future study. The present investigations on the formation of meson-nuclei bound states will be significant for the experiments of $ \bar{\text{P}} $ ANDA at FAIR, WASA at COSY, and J-PARC facilities.