Neutrino-nucleus reaction cross sections in supernova explosion

During the early stages of core-collapse supernova explosions, numerous high-speed neutrinos are emitted from proto-neutron stars, forming shock waves. The shock waves engage in neutrino-nucleus reactions with nuclei present in the outer layers of the stars, triggering the synthesis of novel elements in a process recognized as the neutrino-nucleosynthesis process. Our study specifically focuses on the electron-neutrino induced reactions, characterized by the reaction $\nu_{e}+ (Z,~ A)$$\rightarrow (Z,~ A+ 1)$$ +e^{-} $, which represents the inverse process of electron capture (EC) decay and is the predominant neutrino-nucleus interaction. In contrast to the strong or electromagnetic interactions of other major nucleosynthesis processes, such as the s-, r-, and γ-processes, neutrino-nucleus reactions are dominated by weak interactions with very small cross sections on the order of magnitude of 10^-42 cm². Despite the diminutive cross sections, the large neutrino flux generated by supernova explosions can induce numerous neutrino-nucleus reactions, significantly impacting elemental abundances. The neutrino-process occurring in core-collapse supernovas markedly influences the synthesis of some rare isotopes, including the exceedingly proton-rich nuclei associated with the p-process [1−4]. These nuclei cannot be produced by the s- and r-processes, underscoring the indispensable role of neutrino-nucleus reactions in unraveling the origin of p-process nuclei.

In network calculations for stellar nucleosynthesis, the ν-process that occurs during core-collapse supernova explosions represents an indispensable nuclear process. The cross sections of neutrino-nucleus reactions provide essential input information for estimating the abundance of ν-process nuclei, which is crucial for gaining a deeper understanding of the exotic properties of neutrinos and studying the dynamic mechanisms associated with stellar collapse [5]. The calculation of neutrino-nucleus reaction cross sections largely depends on nuclear models. In 1990, Woosley et al. [6] utilized a simple interpolation between node kernels based on mass number A to obtain cross sections related to giant resonance responses. Subsequently, a theoretical analysis of the shell model was used to estimate the cross sections of neutrino-nucleus reactions [7]. In 1999, Kolbe et al. [8] selected a hybrid approach of the shell model (Hybrid model), which has been proven to correctly describe the GT strength distribution and total strength for $ ^{56} {\rm{Fe}}$ and can reliably evaluate neutrino-induced cross sections on nuclei in the iron mass range. In 2010, the quasiparticle random-phase approximation (QRPA) model was adopted as a method of describing the cross sections of the interactions between neutrinos and atomic nuclei [9]. In 2020, the nuclear gross theory of beta decay (GTBD) was employed to evaluate the cross section of neutrino-nucleus reactions [10]. The GTBD model is a microscopic model that combines the β amplitude function of independent particles associated with the Fermi gas model with statistical arguments phenomenologically, and it considers the pairing and shell effects. This methodology not only accurately reproduces existing experimental data but also extends its predictive prowess to the properties of unknown atomic nuclei located far from the stability line [11].

In this study, we employ the GTBD model to estimate the cross sections of $ ^{12} {\rm{C}}$$ (\nu_{e},e^{-})^{12} {\rm{N}} _{\rm{g.s.}} $, $ ^{16} {\rm{O}}$$ (\nu_{e},e^{-})^{16} {\rm{F}}$, $ ^{56} {\rm{Fe}}$$ (\nu_{e},e^{-})^{56} {\rm{C}}{\rm{o}}$, and $ ^{208} {\rm{Pb}}$$ (\nu_{e},e^{-})^{208} {\rm{Bi}}$ reactions. The reliability of the GTBD model is verified by comparing our results with other theoretical results. Based on this foundation, we introduce a semi-empirical parametrization formula to describe the spectrum-weighted cross section for neutrino-nucleus reactions at a certain neutrino temperature. The efficacy of the formula is meticulously assessed through the computation of the maximum relative deviation, ensuring that is consistent with the results calculated using the theoretical equation. This parametric formula is similar to that of the nuclear astrophysical reaction rate in the REACLIB database [12], thereby enhancing its utility for network calculations pertinent to astrophysics nucleosynthesis processes. The adoption of such a formula streamlines computational work and improves the efficiency of predicting nucleosynthesis yield.

Forty years ago, Takahashi and Yamada [13] proposed the GTBD model, which is used to describe the overall characteristics of allowed decay processes. The GTBD model is a statistical model that can be integrated to represent the transition matrix of nuclear energy levels. It is more convenient and feasible than microscopic models, which are complex and require tedious computational work. After years of development, the GTBD model has undergone significant evolution and can be used to systematically explain the properties of stable atomic nuclei. It is also widely used to describe the decay half-lives and properties of many atomic nuclei participating in nuclear synthesis far from the β-stable line [14]. According to the GTBD model, the cross section of the neutrino-nucleus reaction is primarily determined by the incident energy of neutrinos, the energy and momentum distribution of emitted electrons, and the transition matrix elements of the initial and final states of a system. It is expressed as [10, 15]

where the Fermi weak coupling constant is denoted as ${G_{\rm F}} = 1.166 \times {10^{ - 11}}\;{\rm{Me}}{{\rm{V}}^{{\rm{ - 2}}}}$. The energy $ {E_{\rm{e}}} $ and momentum $ {P_{\rm{e}}} $ of the emitted electrons are represented by ${E_e} = {E_{{\nu _e}}} - E$ and $ {P_e} = \sqrt {E_e^2 - m_e^2} $, respectively. E represents the transition energy from the ground state of the parent nucleus to a certain resonant state of the daughter nucleus, and $ E_{\nu} $ is the energy of the incident neutrino. The Coulomb correction factor $ F_{\rm {c}} $ for electrons and nuclei interactions can be determined using either the Fermi function [16] or Modified Effective Momentum Approximation (MEMA) [17]. Because the Fermi function method may overestimate the Coulomb corrections at high lepton energies, and MEMA may overestimate it at low energies, this study utilizes both correction factors to calculate cross sections accordingly. Additionally, we adopt the common practice of selecting the smaller of the two Coulomb correction factors across the entire energy range [17−19]. The Fermi function $F\left( {{Z_f},{E_e}} \right)$ is given by

where $ \gamma = {[1 - {(\alpha {Z_f})^2}]^{1/2}} $, $ y = \alpha {Z_f}{E_e}/{P_e} $, and $ Z_{f} $ is the number of protons in the daughter nucleus. $ R = 1.2{A^{1/3}} $ denotes the radius of the daughter nucleus. $ \alpha = 1/137 $ is the fine structure constant.

For the MEMA, this approximation involves using an effective momentum $ P_{\rm{eff}} = \sqrt{E_{\rm{eff}}^2-m_e^2} $, where $ E_{\rm{eff}} = E_e-V_C(0) $, $ V_C(0) = -3Z_f\alpha/2R $ is the Coulomb potential at the origin, and $ F_{\rm{MEMA}} = E_{\rm{eff}}P_{\rm{eff}}/E_eP_e $ [18].

The effective interaction constants of vector and axial-vector are $ {g_V} = {g_A} = 1 $. The matrix elements of the Fermi (F) and Gamow-Teller (GT) transitions are determined using the following equation:

where X = F or GT to represent the Fermi or GT transition, respectively. Additionally, $ {\varepsilon _{\min}} $ corresponds to the lowest single particle energy of the parent nucleus, and $ {\varepsilon _{\max}} $ represents the energy of its highest occupied state. The transition matrix element $ \left| {{M_X}{{(E)}^2}} \right| $ provides an average effect over a range of excitation energies. ${\rm d}N_{1}/{\rm d}\varepsilon$ represents the energy level density of a single particle, dominated by the Fermi gas model of the parent nucleus [15]:

for $ \beta^{-} $, $ N_{1} $ is the number of neutrons in the parent nucleus, and for EC, $ N_{1} = Z $. ${\varepsilon _{\rm F}}$ is the Fermi energy of a nucleon:

$ {M_n} $ and $ M_n^* $ are the mass and effective mass of the nucleon, respectively, $ {r_0} = 1.25(1 + 0.65{A^{ - 2/3}}) $, and $ M_n^*/M_n = 0.6 + 0.4{A^{ - 1/3}} $ according to [15].

Accounting for the Pauli blocking constraint, the weight function $ W(E,\varepsilon ) $ is defined within the range of $ 0 \le W(E,\varepsilon ) \le 1 $. $ {D_X}(E,\varepsilon ) $ represents the probability of a nucleon undergoing β transition at single particle energy ε, normalized to $\int_{ - 1}^{ + 1} {{D_X}(E,\varepsilon )}{\rm d}E = 1$. The β decay probabilities of all the nucleons with different ε are the same if $ {D_X}(E,\varepsilon ) = {D_X}(E) $ is energy independent [13]. $ {D_X}(E) $ follows a Gaussian distribution [11] :

$ E_{X} $ and $ {\sigma _X} $ represent the resonance energy and corresponding standard deviation, respectively. When the isospin serves as an appropriate quantum number, the total Fermi strength ${\left| {{M_{\rm F}}(E)} \right|{\rm{d}}E = N - Z}$ is completely determined by the isospin similar states (IAS) in the daughter nucleus. However, owing to Coulomb force effects, when the isospin does not remain conserved as a quantum number, the Fermi resonance energies split. We adopt the method proposed by Takahashi and Yamada for estimation [13]:

for $ \beta^{-} $ decay, $ Z_{1} $ represents the number of protons in the parent nucleus. For $ \beta^{+} $ decays and EC, $ Z_{1} $ signifies the number of protons in the daughter nucleus. The total GT intensity of the $ ({\nu _e},{e^ - }) $ channel depends on the Ikeda summation rule $\int \left| {{M_{\rm GT}}(E)} \right|{\rm d}E \simeq 3(N - Z)$, but its distribution must be determined by calculation or measurement. The experimental results from charge exchange reaction (p, n) indicate that the wide resonances near IAS significantly contribute to the GT transition strength [20,21]. Takahashi and Yamada et al. [13] used an approximation of $ {E_{{\rm{GT}}}} \simeq {E_F} $, whereas $ {\sigma _{{\rm{GT}}}} $ is expressed as ${\sigma_{{\rm{GT}}}} = \sqrt {{\sigma _{\rm F}}^2 + {\sigma _N}^2}$, and the parameter $ {\sigma _N} $ represents the energy diffusion resulting from spin-dependent nuclear forces, with each decay mode demonstrating distinct values [10]. For even-even, even-odd, odd-even, and odd-odd parent nuclei, the respective values of $ {\sigma _N} $ for $ \beta^{+} $ decay or EC are 9.9, 11.8, 12.2, and 10.4. For $ \beta^{-} $ decay, the values for $ {\sigma_N} $ are 15.8, 7.2, 16.5, and 15.8, respectively [10].

For Fermi transitions, we use Eq. (7). However, for GT resonance, we use the following equation to estimate $ E_{\rm GT} $ [13]:

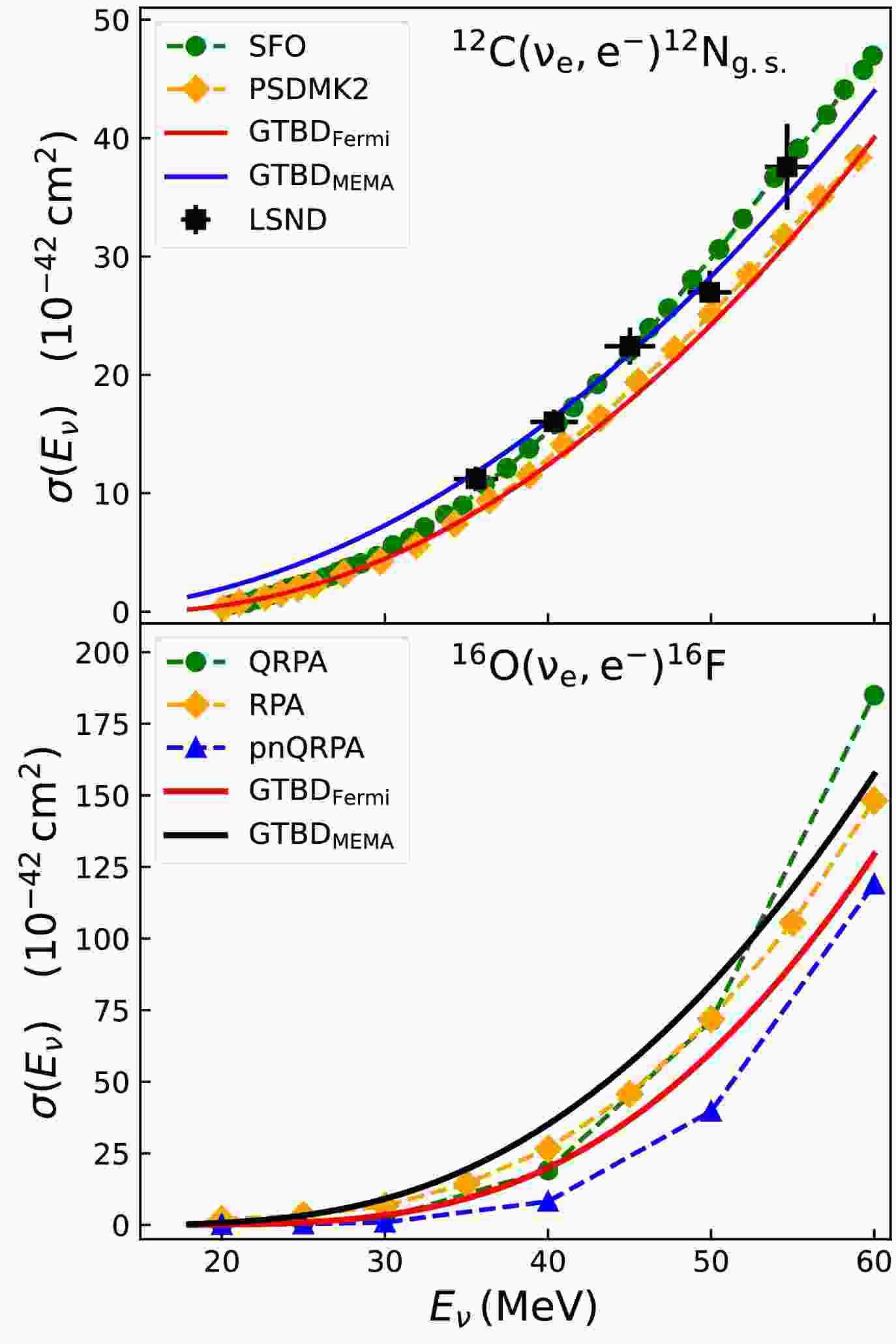
The computational procedure was executed using Python code. We have computed the cross sections for the $ ^{12} {\rm{C}}$$ (\nu_{e},e^{-})^{12} {\rm{N}} _{\rm{g.s.}} $ and $ ^{16} {\rm{O}}$$ (\nu{_e},e^{-})^{16} {\rm{F}}$ reactions as functions of neutrino energy. Following the suggestion of references [17−19], we applied the minimum Coulomb corrections. The calculations showed that the Coulomb corrections using the Fermi function are consistently smaller than those using the MEMA method across the entire energy range, as shown in Fig. 1. Therefore, the Coulomb corrections for these reactions were determined using the Fermi function in the subsequent analysis. Two experiments on direct measurement of neutrino-$ ^{12} {\rm{C}}$ interaction cross sections were performed by KARMEN [22−24] and LSND Collaborations [25, 26]. The neutrino sources are the positive muon decay, the monoenergetic muon neutrino beam, resulting from stopped positive pion decay (DAR) and muon neutrino flux, produced by positive pion decay in flight (DIF). In the top panel of Fig. 1, we compare the results obtained from the GTBD model with the experimental data from LSND and the results from two different Hamiltonians of the new shell model. The maximum relative deviations of the $ {\rm{GTBD}}_{\rm{Fermi}} $ results compared with the experimental data, SFO, and PSDMK2 Hamiltonian results are 30%, 40%, and 20%, respectively, across the entire energy range. In addition, we conducted a comparative analysis of the cross sections for the $ ^{16} {\rm{O}}$$ (\nu_{e},e^{-})^{16} {\rm{F}}$ reaction calculated using the GTBD model and other models, including QRPA [27], RPA [28], and pnQRPA [29]. The analysis indicated that the results of $ {\rm{GTBD}}_{\rm{Fermi}} $ lie within the range of results from other models and are consistent with the observed trend of cross section variation as a function of neutrino energy. Across the entire energy range, QRPA and RPA results are up to 1.4 and 1.9 times those of $ {\rm{GTBD}}_{\rm{Fermi}} $, respectively. Meanwhile, $ {\rm{GTBD}}_{\rm{Fermi}} $ results are up to 2.5 times those of the pnQRPA model.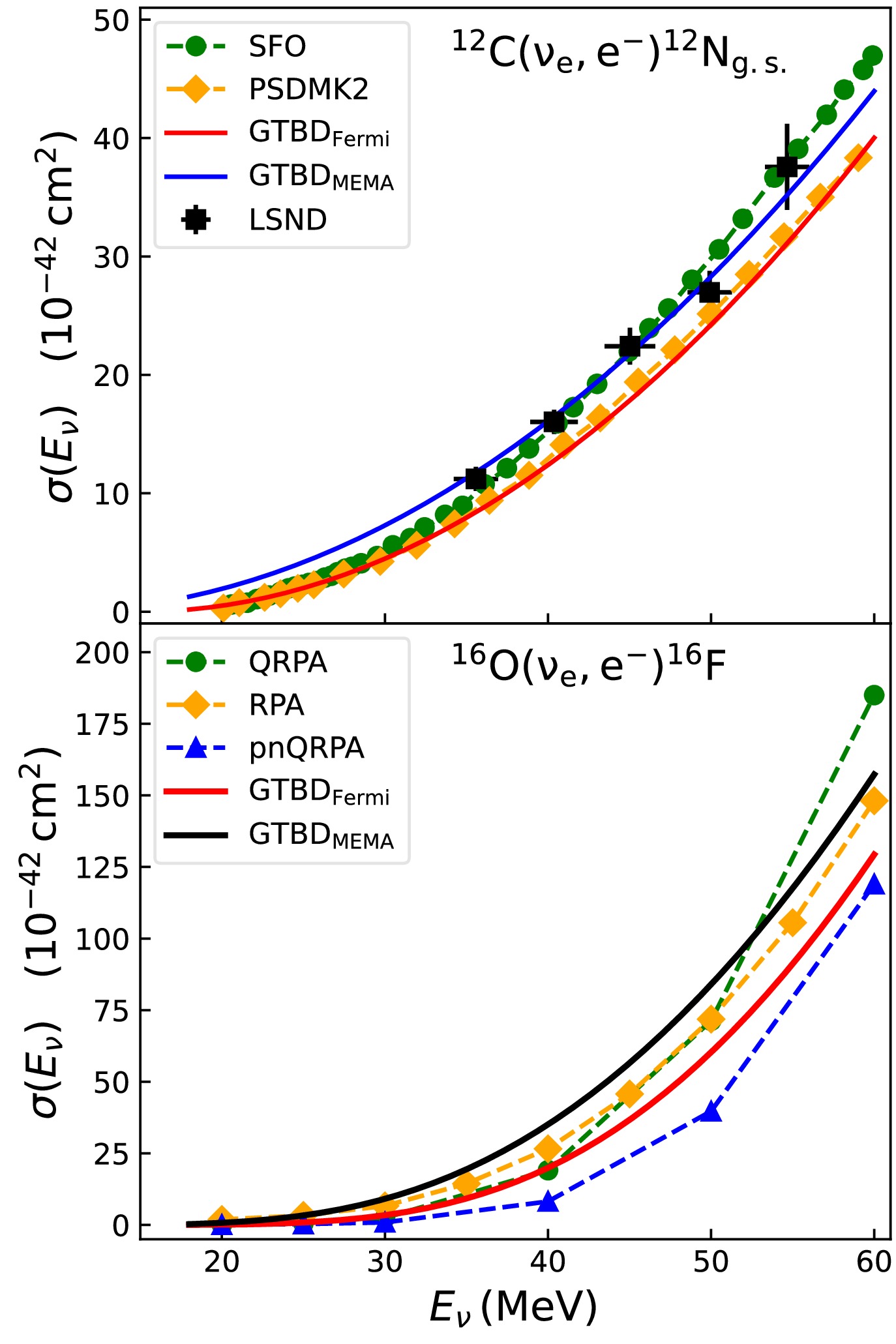

Figure 1.  (color online) Cross sections of the $^{12}{\rm{C}}$$(\nu_{e},e^{-})^{12}{\rm{N}} _{\rm{g.s.}}$ (top panel) and $^{16}{\rm{O}}$$(\nu_{e},e^{-})^{16}{\rm{F}}$ (bottom panel) reactions as a function of neutrino energy.

The cross section of $ ^{56} {\rm{Fe}}$$ (\nu_{e},e^{-})^{56} {\rm{C}}{\rm{o}}$ varying with the incident neutrino energy are shown in Fig. 2. The green dotted, orange dotted, blue dotted, purple dotted, red solid, and black solid lines represent the results predicted by the QRPA [27], Hybrid [30], RPA [28], pnQRPA [29], $ {\rm{GTBD}}_{\rm{Fermi}} $, and $ {\rm{GTBD}}_{\rm{MEMA}} $ models, respectively. The cyan solid line indicates the cross sections calculated using the minimum value of Coulomb corrections derived from the Fermi function and MEMA method. For the $ ^{56} {\rm{Fe}}$$ (\nu_{e},e^{-})^{56} {\rm{C}}{\rm{o}}$ reaction, the Fermi function is effective at low neutrino energies, whereas the MEMA method is preferable at high neutrino energies. Through a combination of these methods, minimal Coulomb corrections can be achieved across different energy ranges [17−19]. Therefore, the Fermi function is used for $ E_\nu<50 $ MeV, and the MEMA method is applied for $ E_\nu\geq50 $ MeV. The $ {\rm{GTBD}}_{\rm{min}} $ cross section result is most appropriate for subsequent calculations. As the neutrino energy increases within the range of $ 7.5 \leq E_{\nu} \le 50\;{\rm{MeV}} $, the discrepancy between the $ {\rm{GTBD}}_{\rm{min}} $ model and results of other models gradually decreases as the energy increases. The results of the $ {\rm{GTBD}}_{\rm{min}} $ model lie between those of the other models. Specifically, the average relative deviations between $ {\rm{GTBD}}_{\rm{min}} $ and the QRPA, Hybrid, RPA, and pnQRPA models are 50%, 21%, 55%, and 45%, respectively. Within the higher energy band of $50 < {E_\nu } \le 100 {\rm{MeV}}$, the predictions of the $ {\rm{GTBD}}_{\rm{min}} $ model fall within the envelope of cross section values projected by the four theoretical models. The largest discrepancy is observed between the QRPA and pnQRPA results, with a maximum difference of 76%. The QRPA and pnQRPA models fundamentally compute the cross sections at discrete energy levels and the transition strength distributions corresponding to each occupied state, informed by the shell configuration, spin parity of the nucleus, and nucleon-nucleon interaction parameters. In contrast, the GTBD model differs from these models, offering a description of the continuous transition.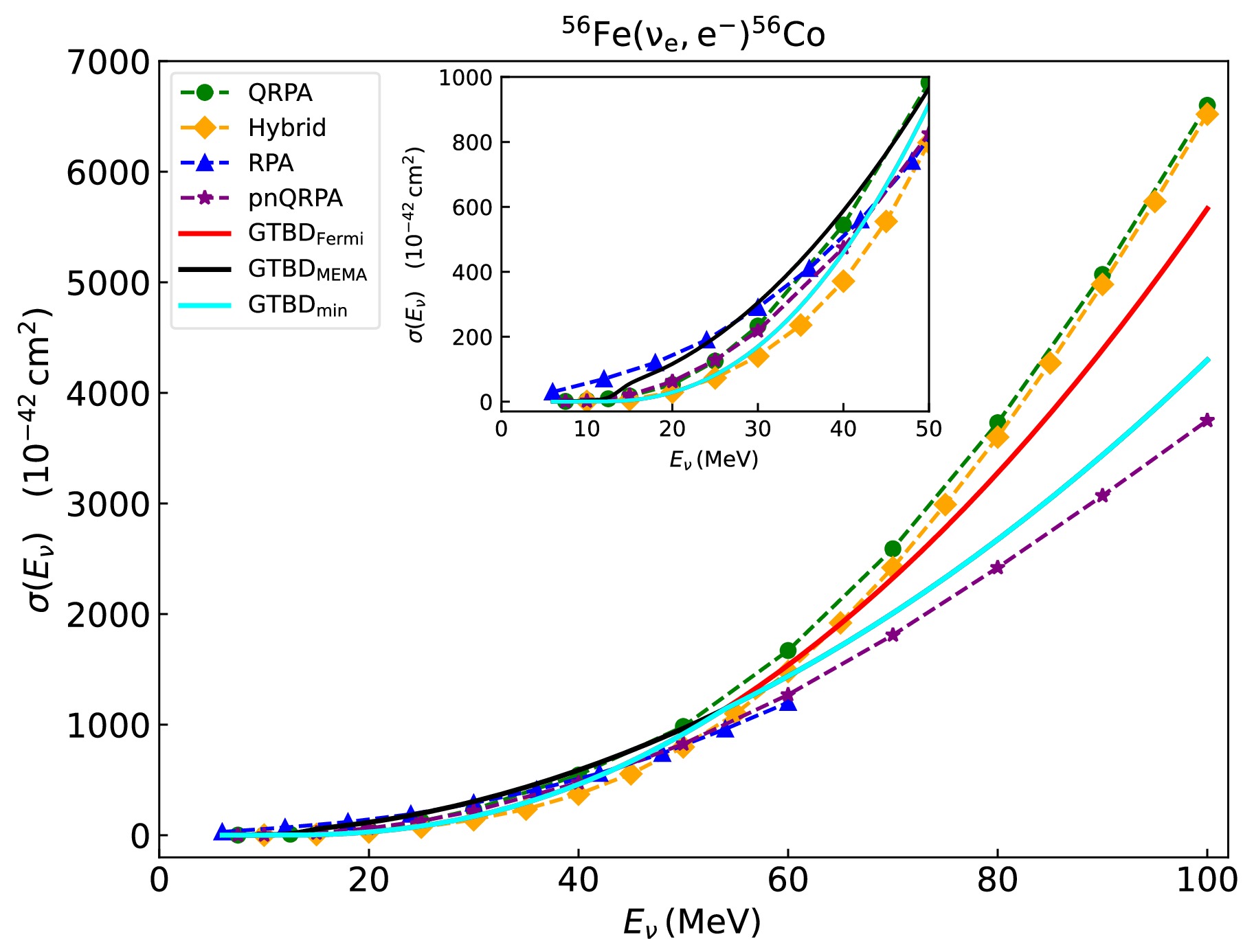

Figure 2.  (color online) Cross sections of the $^{56}{\rm{Fe}}$$(\nu_{e},e^{-})^{56}{\rm{C}}{\rm{o}}$ reaction predicted by the QRPA [27], Hybrid [30], RPA [28], pnQRPA [29], and GTBD (Fermi function or MEMA) models, respectively. ${\rm{GTBD}}_{\rm{min}}$ represents Coulomb corrections using the Fermi function at low neutrino energies and the MEMA method at high neutrino energies. The inset shows the cross sections at low energies to display the differences among the model calculations clearly.

Figure 3 shows the cross section of the $ {}^{{\rm{208}}}{\rm{Pb(}}{\nu _e}, {e^ - } ) {}^{{\rm{208}}}{\rm{Bi}} $ reaction. Similarly, we compare the cross sections calculated using the GTBD model with the results calculated using the QRPA [27], Hybrid [30], and RPA models [28], and the Hybrid model used here is actually RPA for all the multipolarities. For the $ {}^{{\rm{208}}}{\rm{Pb(}}{\nu _e},{\rm{ }}{e^ - }{\rm{)}}{}^{{\rm{208}}}{\rm{Bi}} $ reaction, which has a large charge number Z, we consider Coulomb corrections using the Fermi function at low neutrino energies and the MEMA method at high neutrino energies. The Fermi function is adopted for $ E_\nu<33 $ MeV, whereas the MEMA method is used for $ E_\nu\geq33 $ MeV. This approach provides a more reasonable calculation of the cross sections. As the figure shows, when the neutrino energy is $ 5 \le {E_\nu } \le 40\;{\rm{MeV}} $, the discrepancies between the results of the $ {\rm{GTBD}}_{\rm{min}} $ model and those of the QRPA, Hybrid, and RPA models become increasingly pronounced with the increase in neutrino energy, culminating in maximum relative discrepancies of 87%, 50%, and 90%, respectively. Given the inherent complexity of the various theoretical models, compounded by variations in parameter selection and the conditions of application, we expect that the computed data across models will manifest some degree of variance. Notably, the maximum relative discrepancy between the RPA and QRPA models is estimated to be approximately 145%. In the absence of experimental data on neutrino-nucleus reactions, discerning the superior accuracy of any given theoretical calculation in predicting cross sections remains a challenge. Within the astrophysical energy range of interest, the predictions of the GTBD model fall within the range of discrepancies among other theoretical models. Therefore, the GTBD model is a viable alternative for cross section computations in neutrino-nucleus interactions.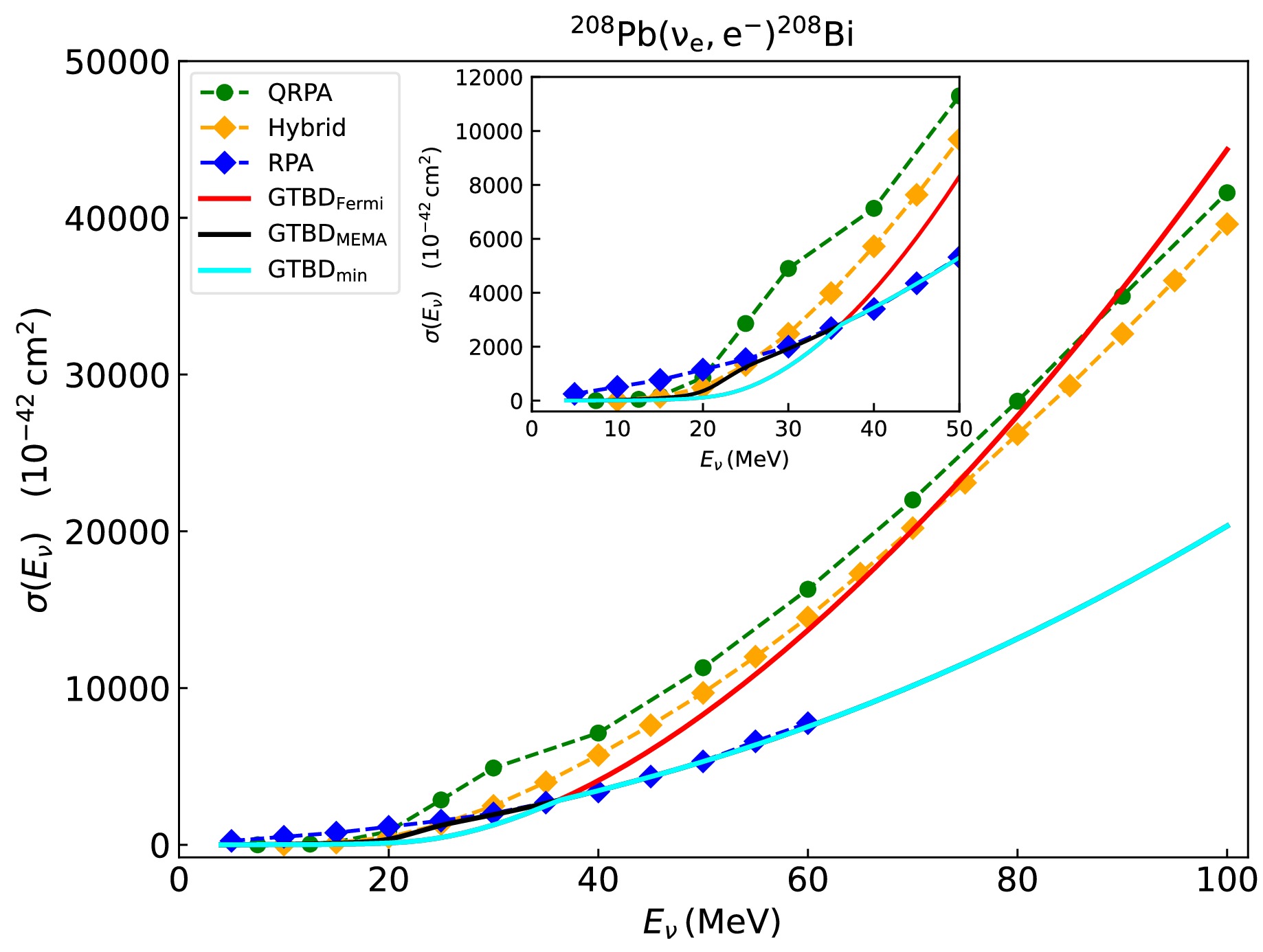

Figure 3.  (color online) Cross sections of the $ ^{208} {\rm{Pb}}$$ (\nu_{e},e^{-})^{208} {\rm{Bi}}$ reaction calculated using the QRPA [27], Hybrid [30], RPA [28], and GTBD models. $ {\rm{GTBD}}_{\rm{min}} $ represents the cross section calculated when the Coulomb correction is minimized by the Fermi function and MEMA method in the GTBD model. The inset shows the cross sections at the neutrino energies less than 50 MeV.

The spectrum-weighted cross section of neutrino-nucleus reactions is the corresponding cross section averaged over the neutrino spectrum of the neutrino stream, which can be expressed as [9]

where $ {E_{{\rm{th}}}} $ is the threshold energy of the reaction, which is equal to the Q value of the nuclear decay. $ \Phi_\nu ({E_\nu },{T_\nu}) $ is the supernova explosion neutrino spectrum, which can be assumed to approximately follow the Fermi-Dirac distribution [29]. It is expressed as follows [2]:

where N is the normalization coefficient $ N = 0.5546 $, and $ {T_\nu } $ represents the neutrino temperature; previous studies have suggested that the appropriate electron neutrino temperature is ${T_\nu } = 4~{\rm{ MeV}}$ [6, 31]. In a follow-up study, Sieverding et al. corrected this by using results from current supernova simulations and suggested that the electron neutrino temperature was ${T_\nu } = 2.8~{\rm{ MeV}}$ [32−34]. If the influence of the mutual conversion between electron neutrinos and other flavor neutrinos is considered, the neutrino temperature will likely increase to a higher value of ${T_\nu } = $ 6 MeV [35]; μ represents the chemical potential $ \mu = 0 $.

The spectrum-weighted cross sections of neutrino-nucleus reactions are temperature-related physical quantities. Although the spectrum-weighted cross section at different neutrino temperatures can be calculated using Eq. (10), the calculation involves the physical parameters of the reaction cross section and the supernova explosion energy spectrum at different neutrino temperatures, and this requirement for extensive computer processing time leads to low computational efficiency. To solve this problem, we propose a transformation of the spectrum-weighted cross section into a semi-empirical parameterized formula that correlates with neutrino temperature following the approach of the nuclear astrophysical reaction rates compilation [12, 36, 37]. This approach enables stellar model calculation programs to access parameters such as the neutrino energy spectrum and cross section, thereby enhancing computational efficiency. Owing to the lack of an analytical expression for the spectrum-weighted cross section, this study utilizes approximate methods or numerical integration to derive a parameterized representation. The cross sections are calculated using the minimum value of Coulomb corrections obtained from the Fermi function and the MEMA method and are expressed as $ \sigma \left( {{E_\nu }} \right)\sim C(E_{\nu}-E_{\rm{th}})^{2} $, where C is a constant. By taking the logarithm of both sides of Equation (10), we can express the relationship as follows:

Subsequently, Eq. (12) is transformed by applying the substitution $ x = {E_\nu}/{T_\nu} $. The integral is then defined as $f_n = \displaystyle\int_{E_{\rm{th}}/T_\nu}^\infty \dfrac{x^n}{\exp(x)+1}{\rm d}x$, which leads to the following formulation:

After numerically solving the integral part of Eq. (13) and fitting the results with a polynomial related to the neutrino temperature $ T_{\nu} $, we conducted extensive validations and found that the integral results are correlated with the constant term, –1, –2, –3, –4, and logarithmic terms of the neutrino temperature. Based on these findings, we derive the relationship between the neutrino spectrum-weighted cross section and neutrino temperature as follows:

To evaluate the difference between the results obtained from the semi-empirical parametrization formula (14) and the theoretical Eq. (10), we define the relative deviation r as the evaluation indicator:

$ R_{\rm{th}} $ denotes the numerical value derived from theoretical calculations, whereas $ {R_{\rm{fit}}} $ represents the value obtained through the semi-empirical parametrization formula. The parameter r encapsulates the discrepancy between the fitted data and theoretical dataset; a lower r value indicates a superior fit. The maximum relative deviation $ r_{\rm{max}} $ signifies the extent of the greatest divergence between the fitting and theoretical values across a dataset.

Figure 4 depicts the spectrum-weighted cross sections for six neutrino-nucleus reactions, $ ^{\rm 56}{\rm{Fe}}(\nu_{e},e^{-})^{\rm 56}{\rm{Co}} $, $ ^{74}{\rm{Ge}}{({\nu_e},{\rm{ }}{e^ - })^{74}}{\rm{As}} $, $ ^{94}{\rm{Zr}}{({\nu_e},{\rm{ }}{e^ - })^{94}}{\rm{Nb}} $, $ ^{102}{\rm{Ru}}{({\nu_e}, {e^-})^{102}}{\rm{Rh}} $, $ ^{108}{\rm{Pd}}{({\nu_e}, {e^ - })^{108}}{\rm{Ag}} $, and $ ^{208}{\rm{Pb}}{({\nu_e}, {e^ - })^{208}}{\rm{Bi}} $, as a function of neutrino temperature. The figure displays a temperature range of 1−8 MeV, which covers the range of neutrino temperatures typically associated with core-collapse supernova explosions. We employ Eq. (14) to fit the spectrum-weighted cross sections of six neutrino-nucleus reactions, calculated using the theoretical weighted cross sections (Eq. (10)) based on the GTBD model. The resultant fitting parameters are presented in Table 1. Parameter errors primarily result from the interdependencies among parameters and their inherent uncertainties. The covariance matrix derived from the least squares fitting process encompasses the correlations and variances of these parameters. The diagonal elements of the matrix represent the variances of the parameters, with their square roots corresponding to the standard errors. The uncertainties of the parameterized formula are indicated by the shaded areas in Fig. 4. Because the fitting error is smaller than the discrepancies among the computational results from various theoretical models, our focus lies on the maximum deviation between the results calculated using the parameterized and theoretical formulas. We calculated the theoretical results of the spectrum-weighted cross sections using Eq. (10) and compared them with the results obtained from the semi-empirical parameterized formula (14). The maximal relative deviations between the parameterized formula calculations and the theoretical weighted cross sections were observed to be $ r_{\rm{max}} = $ 0.54%, 0.47%, 0.35%, 0.55%, 0.61%, and 1%, respectively. The majority of medium or heavy atomic nuclei exhibit a maximum relative variation of less than 1%. The goodness of fit for the six reactions exceeds 0.99, underscoring the universal applicability and accuracy of the parameterized formula across most reactions.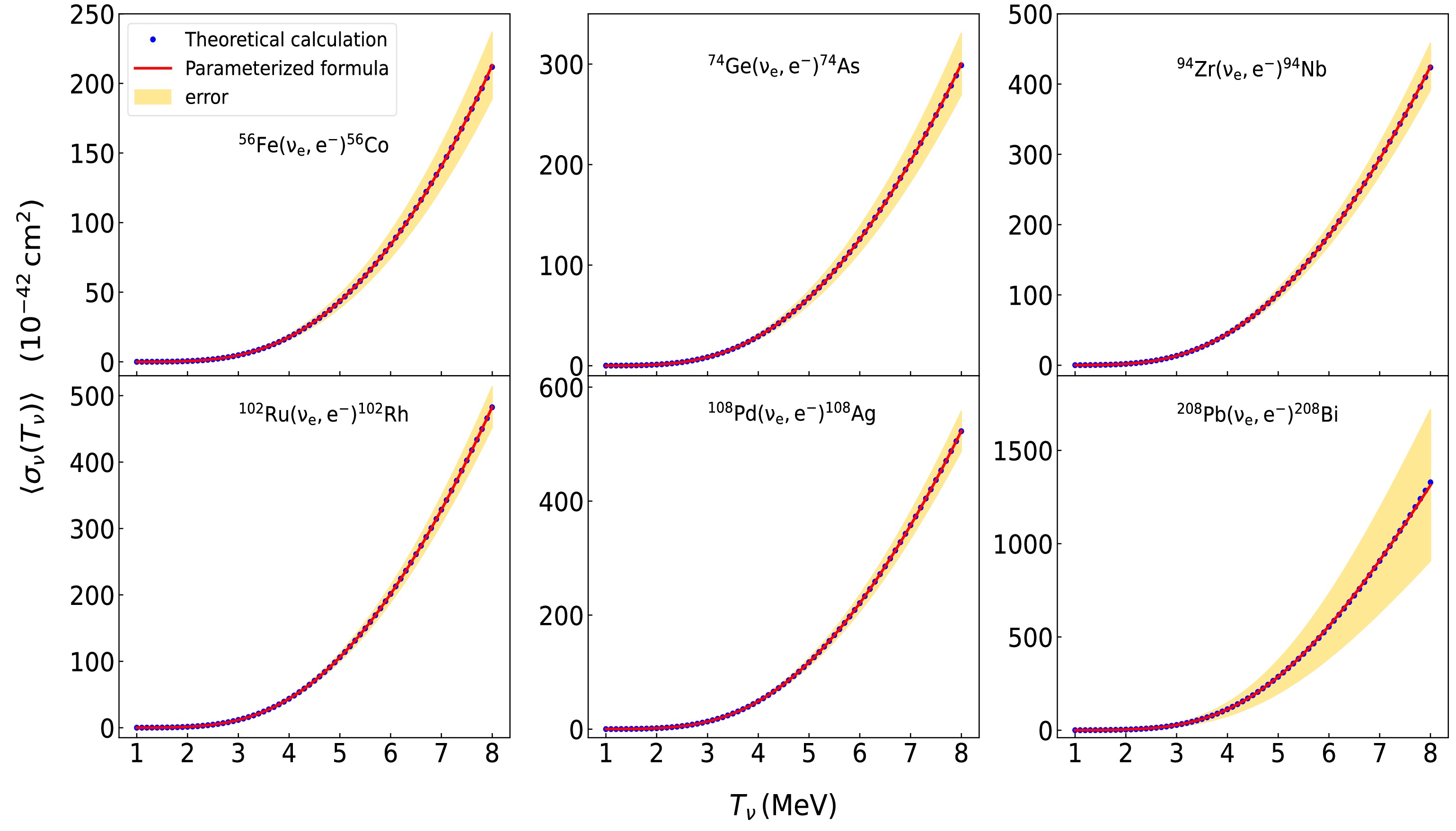

Figure 4.  (color online) Fitting results of spectrum-weighted cross sections of different neutrino-nucleus reactions. The blue circles indicate the results calculated using the GTBD model based on the theoretical equation for the spectrum-weighted cross sections. The red solid lines represent the results from the semi-empirical parametric formula. The orange shaded area indicates the uncertainty range of the semi-empirical parametric formula.

reaction	$a_{1}$	$a_{2}$	$a_{3}$	$a_{4}$	$a_{5}$	$a_{6}$
$^{56}{\rm{Fe}}{({\nu_e},{\rm{ }}{e^ - })^{56}}{\rm{Co}}$	3.00±0.11	–10.07±0.39	–1.64±0.73	5.22±0.73	–1.88±0.28	1.75±0.04
$^{74}{\rm{Ge}}{({\nu_e},{\rm{ }}{e^ - })^{74}}{\rm{As}}$	3.96±0.10	–10.93±0.36	0.67±0.03	5.50±0.66	–2.35±0.25	1.49±0.03
$^{94}{\rm{Zr}}{({\nu_e},{\rm{ }}{e^ - })^{94}}{\rm{Nb}}$	5.06±0.08	–12.39±0.27	1.25±0.51	6.35±0.51	–3.09±0.19	1.21±0.02
$^{102}{\rm{Ru}}{({\nu_e},{\rm{ }}{e^ - })^{102}}{\rm{Rh}}$	6.48±0.06	–17.03±0.22	4.98±0.41	6.40±0.41	–4.13±0.16	0.84±0.02
$^{108}{\rm{Pd}}{({\nu_e},{\rm{ }}{e^ - })^{108}}{\rm{Ag}}$	6.79±0.07	–17.50±0.23	5.75±0.44	6.06±0.43	–4.10±0.16	0.75±0.02
$^{208}{\rm{Pb}}{({\nu_e},{\rm{ }}{e^ - })^{208}}{\rm{Bi}}$	15.11±0.31	-43.61±1.08	49.13±2.02	-29.49±2.00	6.73±0.76	–1.53±0.10

Table 1.  Parameters of semi-empirical parametrization formulas for neutrino-induced nuclear reactions.

In this study, we successfully developed a computational code to calculate the cross sections of neutrino-nucleus reactions using the GTBD. This code enables users to conveniently obtain the relevant reaction cross sections by merely inputting the parameters of the target neutrino-nucleus reaction. To verify the precision of the GTBD model in estimating cross sections, we utilized this model to compute the cross sections of $ ^{12} {\rm{C}}$$(\nu_{e}, e^{-})^{12} {\rm{N}} _{\rm{g.s.}}$, $ ^{16} {\rm{O}}$$ (\nu_{e},e^{-})^{16} {\rm{F}}$, $ ^{\rm 56}{\rm{Fe}}(\nu_{e},e^{-})^{\rm 56}{\rm{Co}} $, and $ ^{\rm 208}{\rm{Pb}}(\nu_{e},e^{-})^{\rm 208}{\rm{Bi}} $ reactions. We conducted a comparative analysis of the predictions of the GTBD model with those of the QRPA, Hybrid, RPA, and pnQRPA models. For the $ ^{12} {\rm{C}}$$ (\nu_{e},e^{-})^{12} {\rm{N}} _{\rm{g.s.}} $ reaction, we assessed the spectrum-weighted cross section using the neutrino spectrum produced by the decay of muons at rest. Low-energy neutrino beams can be obtained at the Spallation Neutron Source (SNS) facility [38], where muon decay at rest results in a significant flux of $ \nu_e $. This neutrino spectrum is referred to as the Michel spectrum, represented by $\Phi_{\rm{M}}(E_{\nu_e}) = \dfrac{12}{E_{0}^4}E_{\nu_{e}}^2(E_{0}-E_{\nu_{e}})$ [39]. In the GTBD model, when considering the Coulomb distortion of leptons using the Fermi function, the spectrum-weighted cross section derived from the Michel spectrum is calculated to be $ \langle \sigma_{\nu_{e}} \rangle = 7.0 \times 10^{-42} $ cm². This value is 30% smaller than the experimental measurements from LSND ($ (9.1 \pm 0.4 \pm 0.9) \times 10^{-42} $ cm²) [40], E225 ($ (10.5 \pm 1.0 \pm 1.0) \times 10^{-42} $ cm²) [41], and KARMEN ($ (9.1 \pm 0.5 \pm 0.8) \times 10^{-42} $ cm²) [22]. For the $ ^{\rm 56}{\rm{Fe}}(\nu_{e},e^{-})^{\rm 56}{\rm{Co}} $ reaction, the cross section was calculated using the GTBD model with the minimum value of the Coulomb correction. The spectrum-weighted cross section was calculated using the Michel spectrum to be $ 290\times 10^{-42} $cm², a result that agrees well with the experimental measurement of $(256 \pm 108 \pm 43) \times 10^{-42}$ cm² obtained by the KARMEN collaboration [42], and it is well within the error range of experiment data. The cross sections predicted using the GTBD model are consistent with the results of these theoretical models within an order of magnitude. Considering the current scarcity of experimental data on neutrino-nucleus reactions and the current status of theoretical computations, the GTBD model provides a viable predictive tool for calculating neutrino-nucleus reaction cross sections during supernova explosions. For the $ ^{208}{\rm{Pb}}{({\nu_e},{\rm{ }}{e^ - })^{208}}{\rm{Bi}} $ reaction, by convoluting with the approximate distribution of the supernova explosions observation spectrum, we obtained an spectrum-weighted cross section of $ 2.85\times 10^{-40} $ cm². For 100 kT of $ ^{208} {\rm{Pb}}$, the number of nucleons are $ 2.91 \times 10^{33} $. Over a period of one year, with an ideal detector and 100% detection efficiency, the observable event count is 26.

We also introduced a parameterized method for obtaining the spectrum-weighted cross sections of neutrino-nucleus reactions at specific temperatures. The semi-empirical parameterized formula includes six undetermined coefficients, which are ascertained by fitting to the cross section data derived from theoretical calculations. After testing with six neutrino-nucleus cross sections, we found that the relative deviations are controlled below 1% for medium or heavy mass nuclei. These results fully substantiate the effectiveness and reliability of the parameterized formula in reproducing the spectrum-weighted cross sections of neutrino-nucleus reactions. Furthermore, applying the formula is beneficial for establishing a database of neutrino-nuclear reactions. It provides neutrino-nucleus cross section data for nuclear astrophysics reaction networks, significantly improving retrieval efficiency in these calculations.