New approach to studying alpha decay and cluster radioactivity using an extended form of the Sextic potential

Alpha decay is an important source of information in the study and understanding of nuclear structure. It was first demonstrated in 1896 by Henri Becquerel and theoretically described independently by Gamow [1] and Condon and Gurney [2, 3] through the phenomenon of quantum tunneling. Moreover, the emission of particles heavier than alpha or cluster radioactivity, which is of great importance in modern nuclear physics, was described by Sandescu et al. [4] in 1980 and received its first experimental confirmation by Rose and Jones [5] with observation of the emission of ¹⁴C by the nucleus of ²²³Ra. Subsequently, other more massive particles, such as ²⁰O, ²³Fe, ^24,25,26Ne, ^28,30Mg, and ^32,34Si, emitted by heavy elements in the trans-lead region have been experimentally detected. In the nuclear decay model, the α particle or cluster is preformed inside the parent nucleus, where it is under the action of an effective potential, and then collides with the well-restricted Coulomb barrier created by the Coulomb-type interaction between the α particle and daughter nucleus. The particle eventually crosses the barrier with a tunneling probability, which is then used to estimate the decay half-life. Several methods can be used to determine this probability, such as the Born distorted wave approximation [6], the WKB approximation [7−11], coupled channel approaches [12, 13], the Coulomb Proximity Potential Model (CPPM) [14], and modified two-potential approaches [15, 16].

Some of these methods, notably the Wentzel-Kramers-Brillouin (WKB) approximation and the Coulomb Proximity Potential Model (CPPM), as well as unified (alpha and cluster) models, such as the Universal Decay Law (UDL)[17, 18], Ni's empirical formula[19], and Scaling law [20], are the most commonly used in the study of alpha decay and radioactivity of clusters. These methods differ in the way they consider the nuclear interactions between the daughter nucleus and preformed cluster. For example, in the WKB method, nuclear interactions are represented by microscopic and phenomenological potentials; in the case of the CPPM, we have nuclear proximity potentials [14, 21], and for the unified law, they are completely neglected because the distance between the daughter nucleus and cluster is assumed to be sufficiently large. If we want to determine the nature of the dynamics of our preformed system in the parent nucleus within the framework of a unified potential model (alpha decay and cluster radioactivity), we must take into account the effective potential, which guarantees the dynamics between the particle and daughter nucleus in the parent nucleus. Therefore, it plays an important role in the decay mechanism and is the combination of three interactions: nuclear, Coulomb, and centrifugal. The Coulomb and centrifugal potentials pose no problem here because they are well known in the literature, whereas the one we do not know is the nuclear potential. It is worth emphasizing that the underlying decay process takes place at the nuclear level. Thus, it is important, if not necessary, that the expression of the half-life takes into account the properties of the nuclear potential. Moreover, with the discovery of new forms of decay in large particle accelerators (Dubna, Berkeley GSI, GANIL and RIKEN) [22−24], there has been growing interest in finding the fields that best describe the strong nuclear interaction between the daughter nucleus and α particle or cluster of the preformed system that is a radioactive nucleus. Many studies have considered a variety of potentials, including the depth potential, Wood-Saxon potential, Cosh potential proposed by Buck et al. [25−29], and modified harmonic oscillator potential introduced by Bayrak et al. [7]. From a molecular perspective, the Morse potential was studied by Koyuncu [30]. Other models with equally interesting potentials have also been explored, such as the double-folding model proposed by Satchler and Love [31] to describe the collision of heavy ions and successfully applied to alpha decay by Delion et al. [32−37]. We also mention the works of Ismaiel et al. [38] and Soylu et al. [39] with a nuclear potential $ \alpha-\alpha $ cluster with single-folding to describe the interaction between the daughter nucleus and cluster.

With the same aim of proposing a suitable nuclear potential model for decay processes, several studies have also been conducted on the simple and deformed relativistic mean-field (RMF) with microscopic R3Y and phenomenological M3Y nucleon-nucleon (NN) potentials [40−48]. The results obtained are in good agreement with experimental data and provide important information on the nuclear structure. However, we see from the literature that singular power potentials, such as Davidson [49], Sextic [50, 51], Kratzer [52], Killingbeck [53], have not been explored in the context of alpha and cluster decay. However, they are attracting increasing interest due to their ability to describe nucleon-nucleon interaction systems in a very satisfactory manner in many areas of physics, including molecular, nuclear, and particle physics. The case of the Sextic potential, considered as a realistic model of nuclear interaction, would be particularly interesting to study, as it is possible to obtain an analytical solution with the WKB method. Moreover, it is a potential that allows nuclear interactions involving a large number of nucleons in coherent motion to be interpreted as vibrations and rotations of the nuclear surface for medium and heavy nuclei. Because α decay is subject to nucleon-nucleon interactions, it would be interesting to study the effects of this type of potential and to observe what information it can give us about the nuclear structure. Henceforth, the aim of this paper is to study the α and cluster decay half-lives of 263 atomic-α nuclei located in the region $ 52\leq Z\leq 107 $ for alpha and in the region $ 86\leq Z\leq 96 $ for clusters in the presence of an extended form of the Sextic potential [54]. To this end, we used the Wentzel-Kramers-Brillouin (WKB) approximation to determine and account for the effect of the effective potential between daughter nuclei and clusters in the expression of the decay half-life calculations.

The remainder of this paper is organised as follows: in Sec. II we determine the expression of the decay half-life α in the presence of the extended form of the Sextic potential in the WKB structure, in Sec. III numerical results and discussion are presented, and finally in Sec. IV we present our conclusions.

The standard form of the effective potential in the model of decay of the parent nucleus, which governs the interaction between the daughter nucleus and alpha particle, is given by the following relation:

This expression of the effective potential is the combination of three fields: nuclear, Coulomb, and centrifugal. Of these three interaction fields, the forms of the Coulomb and centrifugal potentials are well known from literature. The standard centrifugal potential is given by [11, 55, 56]

where $ \mu=A_{1}A_{2}/A $ is the reduced mass of the nuclear system, and $A,\; A_{1}$, and $ A_{2} $ are the atomic masses of the parent nucleus, daughter nucleus, and alpha particle, respectively. l is the orbital angular momentum of our system, which results from the rotation of the daughter nucleus and alpha particle about their centre mass. We take $ l=0 $ because data are available on favorable and unfavorable α-transitions for the case of odd-A or odd-odd nuclei. Inside the parent nucleus, the Coulomb potential is generated by the interaction of the daughter nucleus of point charge $ Z_{1}e $ with the preformed particle of charge $ Z_{2}e $ distributed on a sphere of uniform radius $ R_C $ [7, 8, 29]. Thus, we have

where $ R_{C}=1.07\left(A_{1}^{1/3}+A_{2}^{1/3}\right) $ in fm [7]; $ Z_{1} $ and $ Z_{2} $ denote the charge numbers of the daughter nucleus and alpha particle, respectively. We do not know the correct form of the nuclear potential because no mathematical equation is written for the nuclear force. The very first nuclear potential proposed in the literature was the depth potential introduced by Buck et al. to describe the interaction between the α particle and daughter nucleus. It has the peculiarity of offering a single degree of freedom and allows us to obtain analytical relations between the observables, energy Q, half-life $ T_{1/2} $, and parameters of the potential. However, it is not suitable for describing the α-core interaction. It has no confinement dependence on the position of the nucleus and cluster and does not take coupling phenomena into account. This potential is therefore not very suitable for obtaining more information about the dynamics between the elements of the nuclear system. In this study, we use the extended form of the Sextic potential to represent the nuclear interaction, which was constructed from the Sextic and Davidson potentials [54]:

where $ a, b,c $, and d are free and real parameters of the potential. This potential is widely used in literature: in molecular physics to describe the bonds between the atoms of the molecule ammonia$ NH_{3} $ [57, 58] and in nuclear physics to describe the energy levels of the deformed states in Bohr's Hamiltonian [50, 54]. In Figs. 1 and 3, we plot the effective potential using the extended form of the Sextic potential as the nuclear potential ($ r>0 $). It takes the form of a finite and symmetric double well, where we can see the properties of a repulsive nucleus and a short-range attractive force described between the turning points $ R_{1} $ and $ R_{2} $. These properties are indeed characteristics of the nucleon-nucleon interaction. Given the properties proposed by this form of Sextic potential, it may be very reasonable to use it to describe the nuclear interaction inside the parent nucleus between the daughter nucleus and α particle. Therefore, the physical system describing the nuclear decay mechanism in our model is as follows: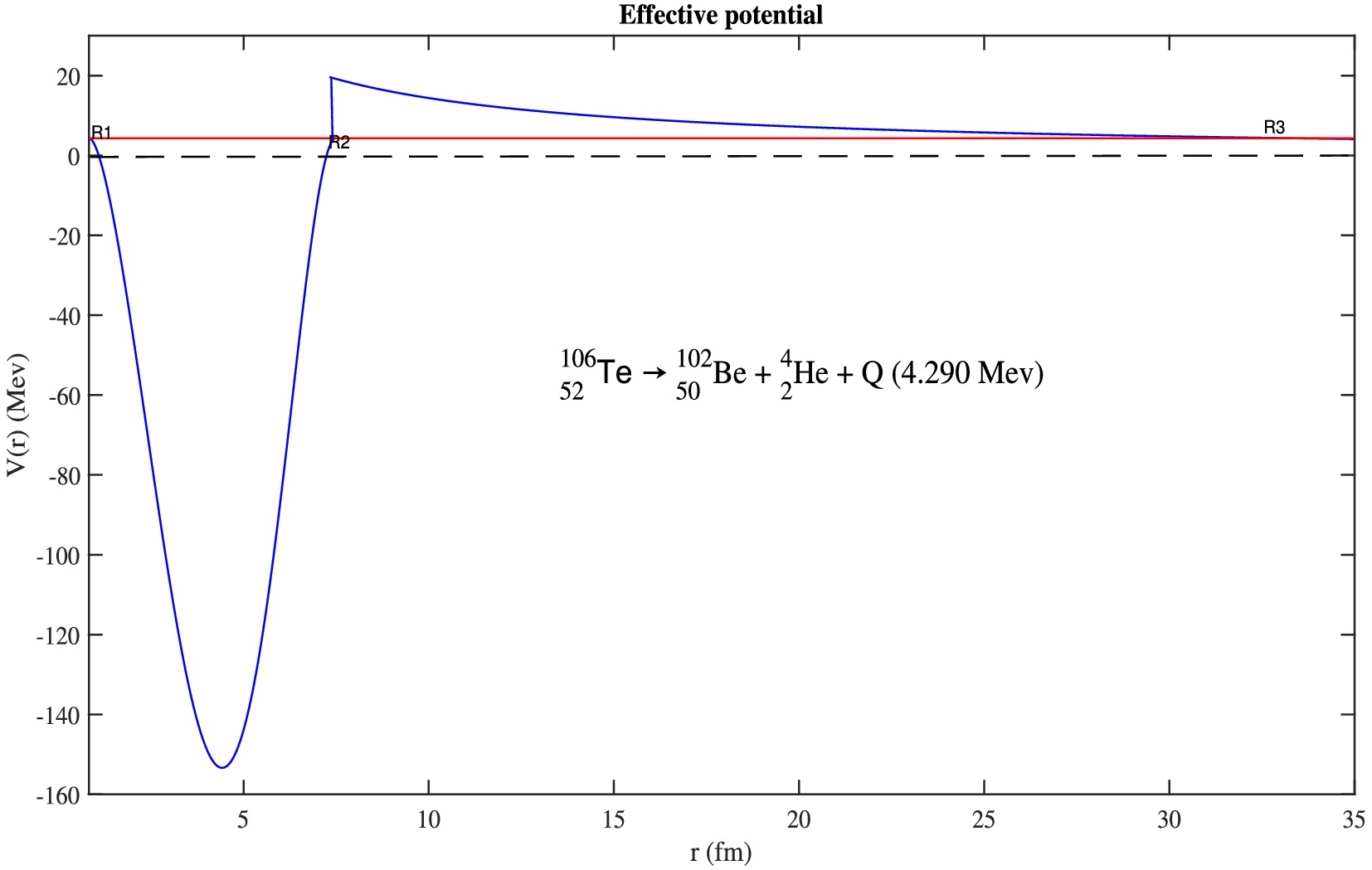

Figure 1.  (color online) Variation $ (r:0\rightarrow \infty) $ in the effective potential of the Tellurium 106 nucleus between the nucleus and Coulomb radii $ R_{1} $, $ R_{2} $, and $ R_{3} $ with released energy Q.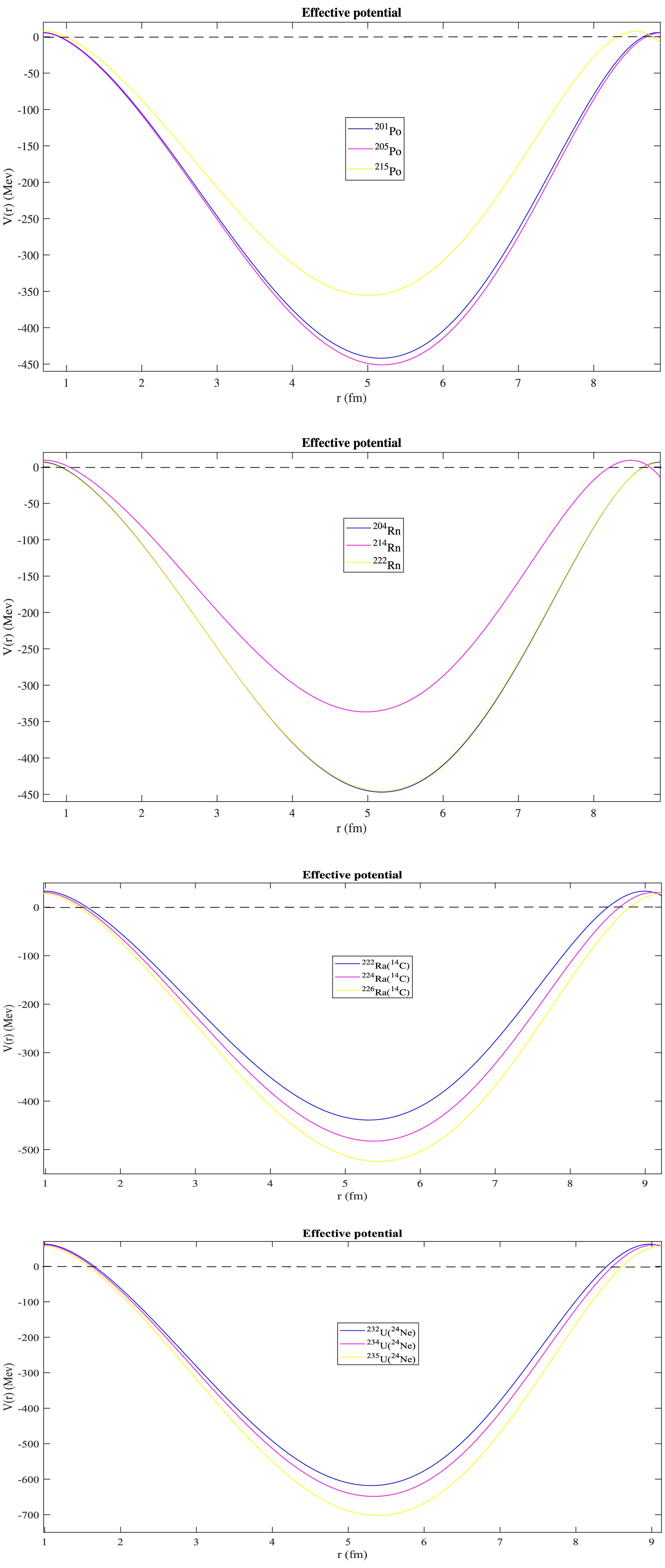

Figure 3.  (color online) Effective potential as a function of nuclear radius in the range bounded by $ R_{1} $ and $ R_{2} $ for polonium (Po), radon (Rn), radium (Ra), and uranium (U).

In this study, the potential at $ R_{2} $ is divided into two parts. This choice has also been made in other works [7], and the main aim of this approach is to take into account the nuclear and centrifugal potentials in the probability of tunneling through the Coulomb barrier. $ R_{2} $ is given by the equation $V_{\rm eff}(r)=Q$. Our current model has three major advantages: it provides an analytical solution with the spherical Coulomb potential, it is more realistic than the model of Buck et al. [25], and it gives the analytical expression of the normalization factor to guarantee the total probability of finding the alpha particle or cluster in a given state. The weakness of our model is that it has a discontinuity at the $ R_2 $ turning point between the potential well and top of the barrier. In addition, it does not take into account the effects of nuclear deformation [8] because many nuclei are not spherical like those in the neutron-rich region. This discontinuity can be removed by inserting the inverted harmonic oscillator potential at the top of the barrier, as proposed in the work of Delion et al. [59]. To preserve the simplicity of our approach, we do not take into account the quadrupole, octupole, or hexadecapole deformation in our nuclear potential.

The semi-empirical relationship between the decay constant and probability of penetration or Gamow factor is given by [7]

where $ P_{1} $is the cluster pre-formation factor in the parent nucleus. It is a very important parameter in the α decay model and should be specific to each nucleus. However, for consistency with literature, we take $ P_{1}=1 $ for even-even nuclei, $ P_{1}=0.6 $ for odd-even and even-odd nuclei, and $ P_{1}=0.35 $ for odd-odd nuclei [8]. F is the normalization factor, and G is the action integral or Gamow factor. The normalization factor is obtained from the expression [7, 8, 27]

where $k(r)=\sqrt{\dfrac{2\mu}{\hbar^{2}}\left(Q-V_{\rm eff}(r)\right)}$ is the wave number of the nuclear region, and Q is the energy released during the decay. From a quantum mechanical perspective, alpha decay is described as a preformed alpha particle in the nucleus crossing the Coulomb barrier by tunneling. This tunneling probability is calculated using the semi-classical WKB approximation [7, 10, 60−62]:

where $K(r)=\sqrt{\dfrac{2\mu}{\hbar^{2}}\left(V_{\rm eff}(r)-Q\right)}$ is the wave number in the barrier region of the effective potential. $ R_{1},R_{2} $, and $ R_{3} $ are the turning points between the potential and Q energy released during the decay reaction. $ R_{1} $ and $ R_{2} $ define the nuclear potential region, while $ R_{2} $ and $ R_{3} $ define the Coulomb barrier. $ R_{2} $ is a very important point as it allows us to take into account the effects of the nuclear potential on the tunneling probability. $ R_3 $ is a constant point where the nuclear interaction is zero and the distance beyond which the alpha particle is considered to be radiation [33]. These points are obtained by solving the equation $V_{\rm eff}(r)=Q$ [7, 19, 63].

Let us change the variable $ X=r^{2} $ to reduce the order of our equation at the turning point:

We also perform a quantization transformation, similar to that proposed in the structure of the Extended Nikiforov-Uvarov (ENU) method [64] to reduce the degrees of freedom of our nuclear potential (the equation at the turning point must be of second degree at most to obtain two turning points). Assuming here that our equation can be written in quadratic form,

If we proceed by identification, we obtain the following system:

From these different quantification transformations, we can derive constraints on the parameters b and c of the nuclear potential with the decay energy Q. This allows us to determine the value of these parameters and reduce the degrees of freedom of the system.

Thus, our equation at the turning points is reduced to

where $ R_{1}=\sqrt{X_{1}} $ and $ R_{2}=\sqrt{X_{2}} $. $ X_{1} $ and $ X_{2} $ are the solutions to Eq. (15).

where $ R_{3}> R_{2}>R_{1}\geq0 $.

The wave number of the nuclear region can be rewritten as follows:

We obtain an analytical expression for the normalization factor of the form [65]

and the Gamov factor is given by the expression

The half-life is obtained from its relationship with the decay constant [7, 30]: $ T_{1/2}=\hbar \ln(2)/\Gamma $. Therefore, it is written as follows:

In science, to validate a new theoretical model based on the numerical results it produces, it is necessary for these to converge with experimental results. However, it must also be compared with existing models in the literature.

-Universal Decay Law (UDL)

This is a law proposed by Qi et al. [17] to describe alpha and cluster decay within the framework of R-matrix theory, using a set of adjustable parameters. In this model, R is the distance between the corresponding centres of mass of the cluster and daughter nuclei, which should be large enough for the nuclear interaction to be negligible.

where μ is the reduced mass of the system; Q is the energy released during the decay; $ Z_c $ and $ Z_d $ are the atomic numbers of the cluster and daughter nuclei, respectively; $ A_c $ and $ A_d $ are the mass numbers of the cluster and daughter nuclei, respectively; and a, b, and c are empirical parameters that can be adjusted according to the nuclear decay described.

-Formula of Ni et al. for alpha and cluster decay

Based on the semi-classical WKB approximation, in 2008, Ni et al. [19] proposed a parametric formula for the calculation of nuclear decay half-lives. This unified formula for alpha and cluster decay has the following form:

where μ is the reduced mass of the system; Q is the energy released during the decay; $ Z_c $ and $ Z_d $are the atomic numbers of the cluster and daughter nuclei, respectively; and a, b, and c are empirical parameters that can be adjusted according to the nuclear decay described.

In this section, we present the numerical results obtained in the calculation of α and cluster decay half-lives in the presence of an extended form of the Sextic potential. We systematically studied the half-lives of 263 parent nuclei in the region $ 52\leq Z\leq 107 $ and 21 emitting parent nuclei ¹⁴C, ²⁰O, ²³Fe, ^24,25,26Ne, ^28,30Mg, and ^32,34Si. In the analytical expression for calculating the half-lives, we had three free parameters: the preformation factor $ P_1 $ and real coefficients a and d of the nuclear potential. The parameter a is the coupling constant. It allows us to characterize the grouping of nucleons in the parent nucleus, in particular, the nature of the preformed cluster of our model, giving the possibility to describe the alpha decay and radioactivity of the clusters. The parameter d is a constant for the diffusion of nuclear forces between nucleons. These nuclear potential parameters are obtained for each decay path (alpha decay and cluster radioactivity) through implementation of the fitting procedure. For the purposes of quantitative analysis, we use the formula for the logarithmic standard deviation as follows [7, 8, 39]:

where m, $T_{j}^{\rm exp}$, and $T_{j}^{\rm exp}$ are the number of parent nuclei, experimental half-life, and theoretical half-life, respectively. We found optimal nuclear parameters $ a_{\alpha}=-5.287 $ and $ d=-0.0125 $ for 263 parent nuclei that explain the α decay mechanism by using the RMS deviation and obtained a total standard deviation of $ \sigma=0.51 $. It is obvious that the alpha and cluster decay mechanisms differ in the size of the emitted particle. For alpha decay, we have $ Z =2 $ and mass number $ A=4 $ with a decay energy ranging from $ 2 $ to $ 9 $ MeV; for cluster decay, we have $ Z > 2 $ and mass number $ A>4 $ with a decay energy ranging from $ 10 $ to $ 90 $ MeV. The different parameters of the nuclear potential for each variety of cluster are depicted in Table 1.

Cluster	a	d
α	$ -5.287 $	$ -0.0125 $
C $ (Z=6) $	$ -22.553 $	$ -0.0125 $
O $ (Z=8) $	$ -32.826 $	$ -0.0125 $
Fe $(Z=9)$	$ -44.814 $	$ -0.0125 $
Ne$ (Z=10) $	$ -46.313 $	$ -0.0125 $
Mg $ (Z=12) $	$ -58.625 $	$ -0.0125 $
Si$ (Z=14) $	$ -66.425 $	$ -0.0125 $

Table 1.  Free parameters of the nuclear potential used in this study.

In Table 4, we calculate the decay half-lives of 263 α-emitting parent nuclei and 21 cluster emitters from the ground state to the ground state transitions and compare them with experimental results. In the calculation, the reduced mass μ of the daughter nucleus-cluster system, decay energy Q, and experimental half-lives $T^{\rm exp}_{1/2}$ are taken from NUBASE 2020 [66−69]. In this new database, recommended experimental values of nuclear properties are reported with associated uncertainties in the form of standard deviations. As a result, the quality of this information already provides greater precision in the evaluation of our theoretical results, as the parameters derived from the model are strongly correlated with the experimental data. The first column shows the symbols of the parent nuclei and the second column the decay energy. The third and fourth columns show the decimal logarithms of the experimental and theoretical half-lives, respectively. The fifth column shows the logarithmic ratio of the present model. It could be observed that the model produces results that are in very good agreement with the experimental data, producing better results than those obtained by Denisov et al. [70] with an error of $ \sigma=0.62 $ . Those proposed by the Universal Decay Law (UDL) have an error of $ \sigma=0.71 $ [30], and those proposed by Royer have an error of $ \sigma=1.1130 $. In addition, our model has two degrees of freedom on the effective potential, the UDL model has three free empirical parameters ($ a=0.4314 $, $ b=-0.4087 $, and $ c=-25,7725 $) [17, 18], and the model proposed by Koyuncu with Morse potential ($ D_{e} $: dissociation energy, a: paramter that changes the width of the potential well, and $ r_{e} $: equilibrium distance [30]) and that of Denisov et al. [70] have several free potential parameters. In this respect, the proposed model provides increased accuracy with reduced degrees of freedom. This reduction in degrees of freedom also allows us to reduce the uncertainty in the effective potential of the nuclear system in the decay model. The results are summarized in Table 2 for a total of 263 α-emitting nuclei.

Nucleus	Q	$\log\left(T^{\rm exp}_{1/2}\right)$	$\log\left(T^{\rm theo}_{1/2}\right)$	σ		Nucleus	Q	$\log\left(T^{\rm exp}_{1/2}\right)$	$\log\left(T^{\rm theo}_{1/2}\right)$	σ
$^{106}_{ {\phantom{1}52} } {\rm{Te} }$	4.290	−4.15	−4.13	0.02		$^{157}_{\phantom{1}70} {\rm{Yb}}$	4.622	3.89	3.44	0.45
$^{107}_{\phantom{1}52} {\rm{Te}}$	4.010	−2.35	−2.56	0.21		$^{158}_{\phantom{1}70} {\rm{Yb}}$	4.170	6.63	6.20	0.43
$^{108}_{\phantom{1}52} {\rm{Te}}$	3.420	0.49	0.57	−0.08		$^{156}_{\phantom{1}72} {\rm{Hf}}$	6.026	−1.63	−2.15	0.52
$^{109}_{\phantom{1}52} {\rm{Te}}$	3.198	2.06	2.32	−0.26		$^{157}_{\phantom{1}72} {\rm{Hf}}$	5.880	−0.91	−1.36	0.45
$^{113}_{\phantom{1}53} {\rm I\phantom{e}}$	2.707	9.30	7.39	1.91		$^{158}_{\phantom{1}72} {\rm{Hf}}$	5.404	0.81	0.65	0.16
$^{112}_{\phantom{1}54} {\rm{Xe}}$	3.330	2.53	2.43	0.10		$^{160}_{\phantom{1}72} {\rm{Hf}}$	4.901	2.77	2.66	0.11
$^{113}_{\phantom{1}54} {\rm{Xe}}$	3.087	3.89	4.42	−0.53		$^{162}_{\phantom{1}72} {\rm{Hf}}$	4.416	5.80	5.44	0.36
$^{114}_{\phantom{1}56} {\rm{Ba}}$	3.592	1.77	1.73	0.04		$^{174}_{\phantom{1}72} {\rm{Hf}}$	2.494	22.80	24.10	−1.30
$^{144}_{\phantom{1}60} {\rm{Nd}}$	1.901	22.86	23.75	−0.89		$^{159}_{\phantom{1}74} {\rm W}$	6.451	−2.09	−2.69	0.60
$^{145}_{\phantom{1}61} {\rm{Pm}}$	2.322	17.30	17.90	−0.60		$ ^{160}_{\phantom{1}74}{\rm W} $	6.066	−0.99	−1.50	0.51
$^{146}_{\phantom{1}62} {\rm{Sm}}$	2.529	15.51	15.72	−0.21		$^{162}_{\phantom{1}74} {\rm W}$	6.678	0.46	0.32	0.14
$^{147}_{\phantom{1}62} {\rm{Sm}}$	2.311	18.52	18.91	−0.39		$^{164}_{\phantom{1}74} {\rm W}$	5.278	2.38	1.93	0.45
$^{148}_{\phantom{1}62} {\rm{Sm}}$	1.987	23.34	23.99	−0.65		$^{166}_{\phantom{1}74} {\rm W}$	4.856	4.74	4.35	0.39
$^{147}_{\phantom{1}63} {\rm{Eu}}$	2.991	10.98	11.45	−0.47		$^{180}_{\phantom{1}74} {\rm W}$	2.515	25.75	25.72	0.03
$^{148}_{\phantom{1}63} {\rm{Eu}}$	2.694	14.70	14.88	−0.18		$^{160}_{\phantom{1}75} {\rm{Re}}$	6.698	−2.02	−2.93	0.91
$^{148}_{\phantom{1}64} {\rm{Gd}}$	3.271	9.37	9.31	0.06		$^{162}_{\phantom{1}75} {\rm{Re}}$	6.119	−0.96	−0.84	−0.12
$^{149}_{\phantom{1}64} {\rm{Gd}}$	3.099	13.27	11.30	1.97		$^{163}_{\phantom{1}75} {\rm{Re}}$	5.926	−0.22	−0.31	0.09
$^{150}_{\phantom{1}64} {\rm{Gd}}$	2.807	13.75	13.91	−0.16		$^{162}_{\phantom{1}76} {\rm{Os}}$	6.767	−2.73	−3.01	0.29
$^{151}_{\phantom{1}64} {\rm{Gd}}$	2.652	15.03	15.93	−0.90		$^{166}_{\phantom{1}76} {\rm{Os}}$	6.143	−0.52	−0.74	0.22
$^{152}_{\phantom{1}64} {\rm{Gd}}$	2.203	21.53	22.02	−0.49		$^{168}_{\phantom{1}76} {\rm{Os}}$	5.815	0.62	0.61	0.01
$^{150}_{\phantom{1}66} {\rm{Dy}}$	4.351	3.08	3.18	−0.10		$^{169}_{\phantom{1}76} {\rm{Os}}$	5.713	1.59	1.30	0.29
$^{151}_{\phantom{1}66} {\rm{Dy}}$	4.179	4.28	4.27	0.01		$^{170}_{\phantom{1}76} {\rm{Os}}$	5.536	1.79	1.65	0.14
$^{152}_{\phantom{1}66} {\rm{Dy}}$	3.727	6.93	6.86	0.07		$^{172}_{\phantom{1}76} {\rm{Os}}$	5.224	3.98	3.63	0.35
$^{153}_{\phantom{1}66} {\rm{Dy}}$	3.559	8.39	8.38	0.01		$^{173}_{\phantom{1}76} {\rm{Os}}$	5.055	5.03	4.28	0.75
$^{154}_{\phantom{1}66} {\rm{Dy}}$	2.945	13.98	13.80	0.18		$^{174}_{\phantom{1}76} {\rm{Os}}$	4.871	5.34	5.30	0.04
$^{152}_{\phantom{1}67} {\rm{Ho}}$	4.507	3.13	2.86	0.27		$^{186}_{\phantom{1}76} {\rm{Os}}$	2.821	22.80	22.78	0.02
$^{154}_{\phantom{1}67} {\rm{Ho}}$	4.041	6.57	5.69	0.88		$^{166}_{\phantom{1}77} {\rm{Ir}}$	6.722	−1.95	−2.24	0.29
$^{152}_{\phantom{1}68} {\rm{Er}}$	4.934	1.06	0.83	0.23		$^{169}_{\phantom{1}77} {\rm{Ir}}$	6.119	−0.11	−0.23	0.12
$^{153}_{\phantom{1}68} {\rm{Er}}$	4.802	1.85	1.53	0.32		$^{170}_{\phantom{1}77} {\rm{Ir}}$	6.230	0.08	−0.64	0.72
$^{154}_{\phantom{1}68} {\rm{Er}}$	4.279	4.68	4.43	0.25		$^{176}_{\phantom{1}77} {\rm{Ir}}$	5.260	2.60	3.65	−1.05
$^{155}_{\phantom{1}68} {\rm{Er}}$	4.118	6.16	5.69	0.48		$^{177}_{\phantom{1}77} {\rm{Ir}}$	5.082	4.70	4.59	0.11
$^{153}_{\phantom{1}69} {\rm{Tm}}$	5.248	0.21	0.26	−0.05		$^{168}_{\phantom{1}78} {\rm{Pt}}$	6.990	−2.70	−3.21	0.51
$^{155}_{\phantom{1}69} {\rm{Tm}}$	4.572	3.06	3.23	−0.17		$^{170}_{\phantom{1}78} {\rm{Pt}}$	6.707	−1.85	−2.24	0.39
$^{156}_{\phantom{1}69} {\rm{Tm}}$	4.345	5.12	4.79	0.32		$^{171}_{\phantom{1}78} {\rm{Pt}}$	6.607	−1.35	−1.66	0.31
$^{154}_{\phantom{1}70} {\rm{Yb}}$	5.474	−0.36	−0.95	0.59		$^{174}_{\phantom{1}78} {\rm{Pt}}$	6.183	0.03	−0.26	0.23
$^{155}_{\phantom{1}70} {\rm{Yb}}$	5.338	0.30	−0.12	0.43		$^{176}_{\phantom{1}78} {\rm{Pt}}$	5.884	1.22	1.00	0.22
$^{156}_{\phantom{1}70} {\rm{Yb}}$	4.810	2.42	2.41	0.01		$^{177}_{\phantom{1}78} {\rm{Pt}}$	5.642	2.33	2.25	0.08
$^{178}_{\phantom{1}78} {\rm{Pt}}$	5.573	2.45	2.58	−0.13		$^{206}_{\phantom{2}84} {\rm{Po}}$	5.327	7.14	7.03	0.11
$^{180}_{\phantom{1}78} {\rm{Pt}}$	5.276	4.24	4.05	0.19		$^{207}_{\phantom{2}84} {\rm{Po}}$	5.215	8.00	7.67	0.33
$^{181}_{\phantom{1}78} {\rm{Pt}}$	5.150	4.86	4.48	0.38		$^{210}_{\phantom{2}84} {\rm{Po}}$	5.407	7.08	6.20	0.88
Continued on next page

Table 4.  Evaluation and comparison between the decimal logarithm of theoretical and experimental half-lives for 263 parent atomic nuclei located in the $ 52\leq Z\leq 107 $ region.

Works	$\sigma \ (\rm error)$	Ref.
Our	$ 0.51 $	This work
Denisov et al.	$ 0.62 $	[70]
UDL	$ 0.71 $	[30]
Royer	$ 1.1130 $	[10]

Table 2.  Standard deviation $(\rm RMS)$ of the decimal logarithm for different models.

Besides the reduced number of real parameters proposed by our model, the probable reason for the excellent results obtained by the model in the evaluation of half-lives here is that nuclear interactions are not neglected and are materialized by the extended Sextic potential. This is in contrast to notable models, such as those of UDL [17] and Ni et al. [19], which opt for sufficiently large distances between the cluster and daughter nucleus to neglect nuclear interactions. Moreover, the potential used in this work is a combination of several interactions that have previously had great success in the field of nuclear physics, namely, the Davidson potential [49] and Sextic potential [50, 51]. We considered them simultaneously to describe nuclear decay. This may explain why our model combining these two potentials also gives better results than those of Denisov et al. [70], who proposed the Woods-Saxon potential, although they took into account the effects of quadrupole and hexadecapole deformation of the daughter nucleus. We also compared the results obtained for the cluster decay half-lives (¹⁴C, ²⁰O, ²³Fe, ^24,25,26Ne, ^28,30Mg and ^32,34Si) with the experimental data (Table 3) and with the results of Ni et al. [19], who proposed a unified formula for alpha and cluster half-lives (Table 4). The choice of different clusters emitted here is particularly interesting because they are particles emitted by parent nuclei in the trans-lead region (with atomic numbers ranging from 86 to 96) and lead to daughter nuclei with so-called magic ($ Z=82 $) or neighbouring ($ Z=81-83 $) atomic numbers. This means that the emission of these clusters in this region of the atomic map is an important phenomenon in understanding the effects of nuclear layer closure and pairing.

Works	$\sigma \ (\rm error)$	Parameters	Ref.
Our	$ 0.461 $	a, $ d=-0.0125 $	This work
Ni et al.	$ 0.489 $	$ a =0.38617 $, $ b =-1.08676 $, $ c_{e-e}=-21.37195 $, $ c_{e-A}=-20.11223 $	[19]

Table 3.  Standard deviation $(\rm RMS)$ and free parameters.

The obtained results are in agreement with the experimental data and provide an improved description of cluster decay compared to that of Ni et al. for a reduced number of parameters. Moreover, they provide information on the dynamics between the daughter nucleus and cluster.

To better appreciate the results, we plot the logarithmic differences between the experimental and theoretical half-lives in Fig. 2. It can be seen that the majority of the 263 points lie within the $ \pm 0.5 $ interval. Meanwhile, almost all the points lie within the $ \pm 1 $ interval. At the same time, we note that some large deviations (9) persist for the nuclei of $\rm ^{176}Ir$, $\rm ^{206}At$, $\rm ^{218}Pa$ (odd-odd),$\rm^{113}I$, $\rm ^{231}Pa$, $\rm ^{261}Bh$ (odd-even), $\rm ^{149}Gd$ (even-odd), and $\rm ^{174}Hf$, $\rm ^{246}Cf$(even-even). This set of discrepancies provides a basis for discussion with the results of other major models, such as those of UDL and Denisov et al. Similar discrepancies are found for the same nuclei in the models of UDL and Denisov et al. and even those of Koyuncu with the potential of Morse [30], suggesting a general problem due to a lack of physical consideration. Given that alpha and cluster decay are asymmetric phenomena [30], our current model does not take into account the asymmetry either in terms of the nuclear potential or in the evaluation of the preformation factor of odd and odd-A nuclei. Furthermore, the discrepancies observed for the odd and odd-A nuclei can also be attributed to unfavorable transitions $ (l\neq0) $between the fundamental states because, in this study, we investigated the favorable cases $ (l=0) $ neglecting the centrifugal potential. Meanwhile, the discrepancies observed for the two even nuclei are probably due to exceptionally low decay energy in the case of the $\rm ^{174}Hf$ nucleus, which requires a more careful approach to determine the WKB tunneling probability of the alpha particle across the Coulomb barrier. In the case of $\rm ^{246}Cf$, which is a neutron-rich heavy nucleus, a study of the effects of nuclear deformation, which are pronounced for neutron-rich heavy and superheavy nuclei (as in the study of Coban et al. [8]), and a study of the interactions between nucleons (protons and neutrons), which give rise to spin-orbit and spin-spin effects that cause the energy levels to be subdivided into finer sublevels, are required. These effects might be the reason for the discrepancies observed between the experimental and theoretical half-lives of the nuclei mentioned above. However, to preserve the simplicity of our model, we do not consider deformed potential forms and the effect of fine structure.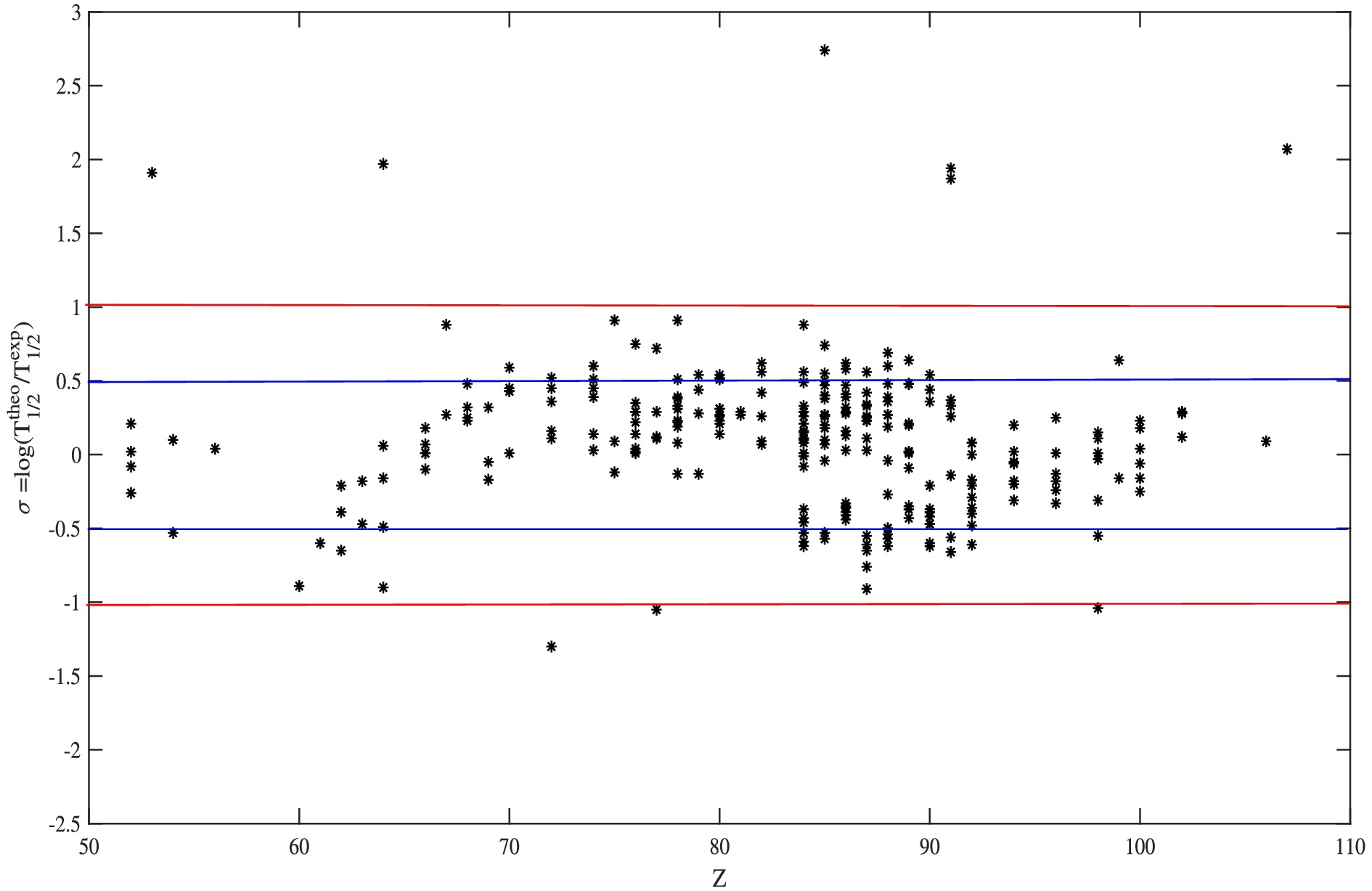

Figure 2.  (color online) Difference between the logarithms of the experimental and theoretical α decay half-lives of 263 atomic nuclei as a function of the charge number Z.

In Fig. 3, we plot the effective potential of the isotopes of the $\rm Po$, $\rm Rn$, $\rm Ra$, and U nuclei using Eq. (5) between the turning points $ R_{1} $ and $ R_{2} $. The curves take on the appearance of wells of different depths for each isotope, reflecting the nucleon-nucleon interaction. Thus, they highlight the degree of stability of each isotope relative to the others. These observations are consistent with the experimental data: the deeper the well, the less unstable the nucleus, and the longer the half-life. This interpretation would justify the greater depth (on the order of 600 MeV for molecular state binding depths or energies proposed by Koyuncu) of cluster-emitting nuclei ($\rm Ra$ and U). Our potential model offers greater freedom to consider the instability state of each radioactive nucleus. This is not the case with the models of Buck et al. [25] and Bayrak et al. [7], which propose an average value for the potential well for all nuclei. From the model, we also obtain information about the shape of the experimental well for each nucleus from the parameters b and c, which depend on the decay energy Q.

Figure 4 plots the decimal logarithm of the α and cluster decay half-lives of the isotopes Pt, Hg, Po, At, Rn, Ra, Th, and U in our model as a function of $ Q^{-1/2} $. It can be observed that there is a linear correlation between the decimal logarithm and inverse of the square root of the decay energy Q, consistent with the law formulated by Geiger and Nuttal [71−73]. This was also confirmed for cluster emission.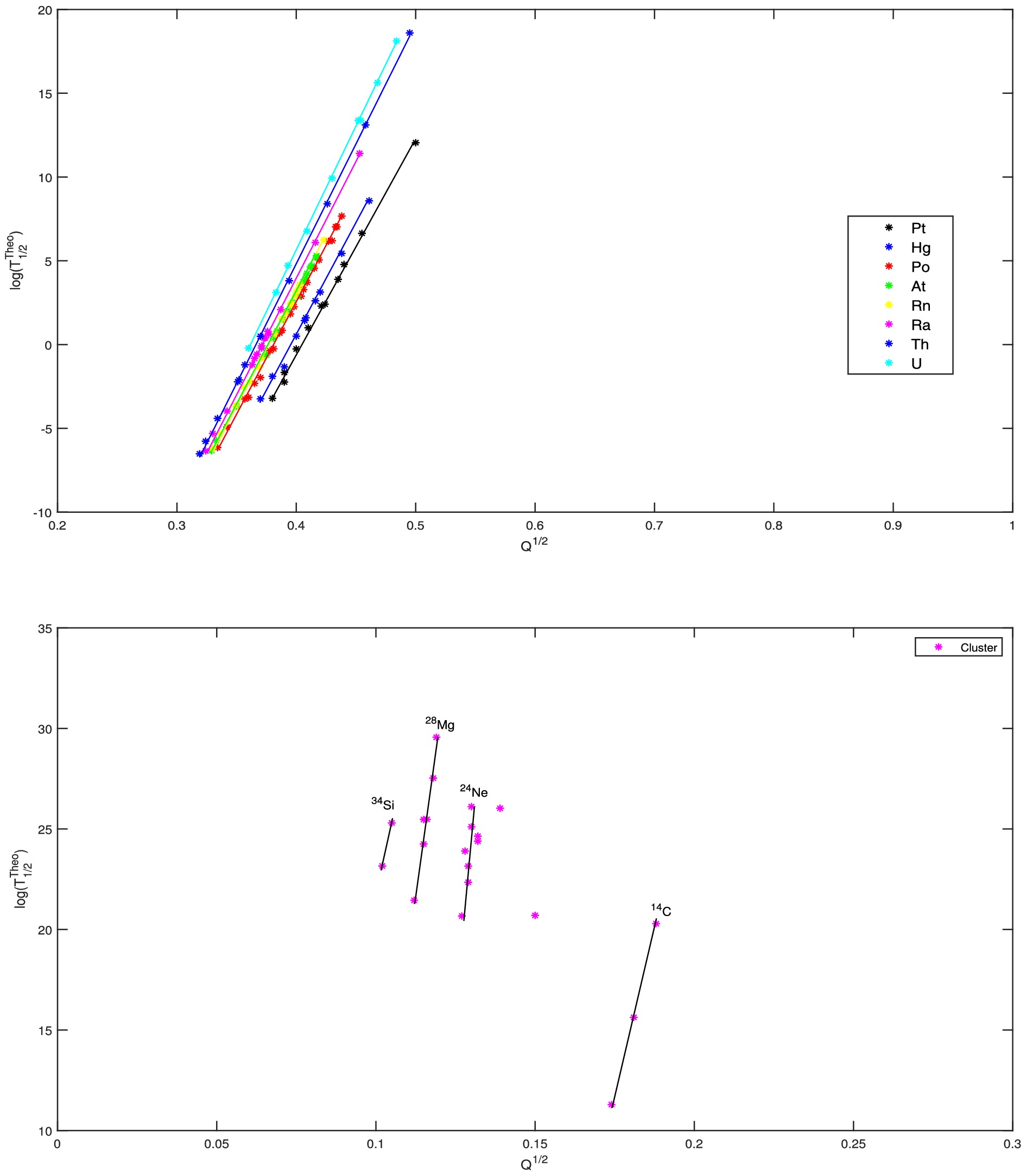

Figure 4.  (color online) Linear correlation of the logarithm of the α and cluster decay half-lives with the decay energy $Q^{-1/2}$ for the nuclei Pt, Hg, Po, At, Rn, Ra, Th, and U.

From the results in Table 2, we can examine other alpha emitters and clusters in regions of the nuclear map beyond the 263 nuclei studied and apply our model to other nuclear systems. We can extend our model to evaluate the half-lives of the entire nuclear map for all existing alpha emitters and clusters, considering that once the parameter a has been defined for each cluster, it is possible to evaluate the half-lives of the emitting parent nuclei of these clusters. It is also conceivable that our model could be used to study other analogous physical phenomena, such as spontaneous nuclear fission. Nevertheless, it would be important to take into account the strong effects of asymmetry and the deformation of the daughter nucleus when studying nuclei in the trans-lead and superheavy regions in the model, particularly at the level of the nuclear potential.

In this study, we systematically investigated the decay half-lives of 263 α-emitting nuclei in the region $ 52\leq Z\leq 107 $ and some cluster emitters in the presence of an extended form of the Sextic potential using the WKB method. We show that this type of potential, which is a combination of the Davidson and Sextic potentials in addition to having an analytical solution with the spherical Coulomb potential, is suitable for describing the nuclear interaction between the daughter nucleus and cluster. As alpha decay is sensitive to the surface of the effective potential, this potential allowed us to account for the effects of the nuclear potential on the action integral G through the $ R_{2} $turning point. A set of constraints between the parameters of the nuclear potential and experimental observables was also obtained, highlighting a link between the shape of the nuclear potential and observed half-life. We found a reduced set of real parameters of the potential that explains the mechanism of α decay and cluster radioactivity. The obtained results are in very good agreement with the experimental data. Given the good results obtained with this form of nuclear potential, we believe that it is possible to explore more exotic structures, such as nuclear molecules [74].

The authors would like to thank the referees for their insights and constructive suggestions and comments.