Constraining vector dark matter and dark photon with degenerate mass in a hidden local SU(2) model

Understanding of dark matter (DM) nature is one of the greatest challenges in physics. The existence of DM definitely requires physics beyond the standard model (SM), which we call the dark sector. In fact, various candidates of DM are considered from new physics models. One promising candidate of DM is a massive stable particle that weakly interacts with the SM sector, as its relic density can be explained via thermal production. Such a DM has been searched for by direct detection, indirect detection, and collider experiments. However we do not have any clear evidence of DM yet, and the nature of dark sector is an open question.

One attractive scenario is to consider the dark sector as the hidden gauge sector, as the SM is also described by gauge symmetry. We consider hidden gauge symmetry where SM particles are neutral but fields in the dark sector including DM are charged under it. In this scenario, we can explain stability of DM by a remnant symmetry after spontaneous symmetry breaking of hidden gauge symmetry [1, 2]. In particular, it is interesting to consider the minimal non-Abelian group $ S U(2)_H $ as hidden gauge symmetry. In the minimal scenario [3], $ S U(2)_H $ is broken by the vacuum expectation value (VEV) of the $ S U(2)_H $ doublet scalar Φ, and dark gauge bosons are DM candidates whose stability is guaranteed by remaining custodial symmetry ¹. Interestingly, we can have kinetic mixing between $ S U(2)_H $ and $ U(1)_Y $ gauge fields if we introduce the dimension-6 operator of $ (\Phi^\dagger \sigma^a \Phi)X^a_{\mu \nu} B^{\mu \nu} $, where $ X_{\mu \nu} $ and $ B_{\mu \nu} $ are the gauge field strengths of $ S U(2)_H $ and $ U(1)_Y $, respectively, and $ \sigma^a $ is the Pauli matrix on the $ S U(2)_H $ representation space [31, 32] ². A dimension-5 operator is also possible by introducing the $ S U(2)_H $ triplet scalar [9, 10, 20, 29]. With such a mixing, we obtain both a complex vector DM $ X^\pm $ and a dark photon Z′ [35, 40] from the $ S U(2)_H $ gauge sector, where the stability of DM is guaranteed by remnant $ U(1) $ symmetry from the custodial one. The dark photon can be a mediator between the dark sector and SM particles; some interesting phenomenology associated with dark photons has been considered [36−45]. In previous works [3, 32], for a model with minimal field contents, DM-scalar interactions are mainly considered in explaining DM relic density in which the new scalar boson plays the role of mediator between the SM and dark sectors via mixing with the Higgs boson, but it is also possible to obtain observed relic density via the $ X^+X^- \to Z' Z' $ process, as discussed in Ref. [31]. Although the masses of DM and Z′ are degenerate, the process is possible in the early Universe [34]; we also note that DM and Z′ masses are not completely degenerate due to Z-Z′ mixing in this model, although it would be a small effect. In this case, degenerate dark gauge bosons, DM and Z′, play a dominant role in dark matter physics and would give more stringent constraints on the gauge sector, including the kinetic mixing parameter. Thus, it is worth exploring this scenario to constrain gauge coupling, DM/Z' mass, and kinetic mixing parameter, taking into account current experimental constraints obtained from both DM and dark photon physics.

In this work, we discuss the $ S U(2)_H $ gauge sector, introducing only one $ S U(2)_H $ doublet scalar and the effective operator providing $ S U(2)_H $ and $ U(1)_Y $ kinetic mixing. We then estimate the relic density of DM $ X^\pm $, focusing on the $ X^+X^- \to Z' Z' $ process, and search for the parameter region explaining observations. In addition, we discuss constraints on the kinetic mixing from dark photon (Z′) physics and DM direct detection by calculating the DM-nucleon scattering cross-section. The model provides a simple framework in which DM and dark photons appear from one non-Abelian gauge sector predicting their almost degenerate mass. This framework realizes stable DM and mediator particles between the dark sector and SM in an economical manner. It is thus interesting to explore phenomenological constraints from DM as well as dark photon (Z′) physics taking into account current experimental data.

The remainder of this paper is organized as follows. In Sec. II, we introduce the model and formulate mass eigenvalues and eigenstates in the scalar/gauge sector and relevant interactions. In Sec. III, we discuss the relic density of DM, constraints from dark photon physics, and direct detection of DM. Finally, we provide a conclusion in Sec. IV.

We consider a model with the hidden sector described by hidden $ S U(2)_H $ gauge symmetry, where we introduce the $ S U(2)_H $ doublet scalar field Φ to break the symmetry spontaneously. The new scalar field Φ will develop a vacuum expectation value (VEV) $ v_\Phi $, which can be written, without the loss of generality, as

where $ G^\pm_H $ and $ G_H $ correspond to massless Nambu-Goldstone (NG) bosons that are absorbed by $ S U(2)_H $ gauge bosons. In the scalar sector, we also have the SM Higgs field H given by

where v is the VEV of H, and $ \{w^\pm, G_Z \} $ correspond to NG bosons absorbed by the SM massive gauge bosons $ \{W^\pm, Z \} $. The fermion sector is considered to be the same as the SM, and we do not focus on fermions in this work.

The renormalizable Lagrangian in the model is

where $ X^a_{\mu \nu} (a=1,2,3) $ is the gauge field strength for $ S U(2)_H $, $ \mathcal{L}\mathrm{_{SM}} $ is the Lagrangian of the SM without scalar potential, and $ \mathcal{V} $ is the scalar potential including the SM Higgs field H. The explicit form of the scalar potential is given by

The covariant derivative of Φ is given by

where $ g_H $ is gauge coupling associated with $ S U(2)_H $, and $ \sigma^a $ is the Pauli matrix acting on the representation space of $ S U(2)_H $. In addition to the renormalizable Lagrangian, we introduce a gauge-invariant effective interaction of

where $ B_{\mu \nu} $ is the gauge field strength of $ U(1)_Y $, and Λ represents a high-energy scale ³. After Φ developing its VEV, the effective Lagrangian provides a kinetic mixing term such that

indicating mixing between the third component of the $ S U(2)_H $ gauge field $ X^3_\mu $ and $ U(1)_Y $ gauge field $ B_\mu $. The kinetic terms of $ X^3_\mu $ and $ B_\mu $ can be diagonalized by the transformation

where $ r=\dfrac{1}{\sqrt{1 - \epsilon^2}} $. We then obtain the Lagrangian for gauge sector as

where $ i=1,2 $, and $ W^{\alpha}_{\mu \nu} $ is the gauge field strength of the$ S U(2)_L $ gauge field $ W^{\alpha}_\mu (\alpha =1-3) $.

Here, we consider the scalar sector in the model and derive mass eigenvalues with corresponding eigenstates. The VEVs v and $ v_\Phi $ can be obtained from the scalar potential in Eq. (4), requiring stationary conditions $ \partial V/\partial v = \partial V/\partial v_\Phi = 0 $ that provide

Here, we require $ \mu_H^2, \mu_\Phi^2 < 0 $ to make the square of VEVs positive definite.

After spontaneous symmetry breaking, we obtain the mass matrix for the CP-even neutral scalar as

We obtain mass eigenvalues by diagonalizing the mass matrix such that

where we identify $ m_h = 125 $ GeV as the mass of the SM Higgs boson. The mass eigenstates and relevant mixing angle are obtained as

where h is identified as the SM Higgs boson. In this analysis, we assume that scalar mixing is negligibly small, choosing tiny $ \lambda_{H \Phi} $, and we focus on the effect of gauge interactions.

After spontaneous breaking of electroweak and hidden gauge symmetries, we obtain mass terms of electrically neutral gauge fields, including the SM ones, as follows:

where $X_\mu^\pm = \dfrac{1}{\sqrt{2}} (X^1_\mu \mp {\rm{i}} X^2_\mu)$ and $ \tilde{Z}_\mu = \cos \theta_W W^3_\mu - \sin \theta_W \tilde{B}_\mu $, with $ \theta_W $ being the Weinberg angle. The squared mass parameters are given by

Thus, the $ \tilde{Z}_\mu $ and $ \tilde{Z}'_\mu $ fields mix as a consequence of kinetic mixing effect, while $ X^\pm_\mu $ is the mass eigenstate with mass $ m_X $. We obtain mass eigenvalues by diagonalizing the mass matrix for $ \tilde{Z} $ and $ \tilde{Z}' $ as

The mass eigenstates are given by

In our analysis, we consider χ to be tiny by choosing $ \epsilon $ sufficiently small, as the Z-Z′ mixing is strongly constrained by the electroweak precision tests. Thus, we take $ \tan \chi \simeq \sin \chi \simeq \chi $ hereafter. In addition, gauge boson masses can be approximated as $ m_Z \simeq m_{Z_{\rm SM}} $ and $ m_{Z'} \simeq m_X $ for small $ \epsilon $.

The gauge interactions among $ X^\pm $ and Z′ can be obtained from the Lagrangian of Eq. (9) as

where we adopt the approximations of $ r \simeq 1 $ and $ \cos \chi \simeq 1 $. In addition, Z′ can interact with the SM particles through Z-Z′ mixing. The interactions between Z′ and SM fermions f can be written as

where $ T_3 $ is the diagonal generator of $ S U(2)_L $, $ Q_f $ is the electric charge, and Y is hypercharge. In the model, Z′ decays into SM particles, while $ X^\pm $ is stable and can be a DM candidate. In addition, we have DM-photon and DM-Z interactions from the effective term of Eq. (6) such that

where $ A_\mu $ is the photon field, and we ignore Z-Z′ mixing effect because it is negligibly small. We notice that coupling $ g_H $ appears instead of electromagnetic coupling e for DM-photon interaction.

In this section, we consider the phenomenology of DM, such as its relic density and DM-nucleon scattering cross-section for direct detection.

The relic density of DM is estimated by solving the Boltzmann equation for number density $ n_X $ of $ X^\pm $:

where $ \langle \sigma \rangle $ is the thermal average of the DM annihilation cross-section, H is the Hubble parameter, and $ n_{X_{\mathrm{eq}}} $ is the number density of $ X^\pm $ in thermal equilibrium. Relic density $ \Omega_X h^2 $ can be estimated approximately as follows [46, 47]:

where $ M\mathrm{_{Pl}}\simeq1.22\times10^{19} $ is the Planck mass, $ x_f = m_X/T_f $ with $ T_f $ is freeze out temperature, and $ g^*(x_f) $ is the effective relativistic degrees of freedom at $ T_f $. The factor $ J(x_f) \equiv \int_{x_f}^\infty \mathrm{d}x \dfrac{\langle \sigma v \rangle}{x^2} $

where $ K_{1}(\sqrt{s}x/m_X) $ and $ K_2(x) $ denote the modified Bessel functions of the second kind of order-1 and -2, respectively. The dominant contribution to the cross-section comes from the s-channel diagram for the process $ X^+X^- \to Z'Z' $, providing $ \sigma v \sim {\rm few} \times g_H^4 $ from rough estimation. ⁴

Here, we adopt micrOMEGAs code [52] to estimate relic density by implementing relevant interactions in the model. In estimating relic density, the relevant parameters in the model are DM(Z′) mass $ m_X $, new gauge coupling $ g_H $, and scalar mass $ m_\phi $. In this work, we consider ϕ as heaver than $ X^\pm $ and Z′ so that a DM annihilation mode including ϕ in final states is forbidden kinematically. Thus, the DM annihilation process in our scenario is solely

Here, we fix $ m_\phi = 1.5 m_X $ for simplicity ⁵ and search for a parameter region on the $ \{m_X, g_H \} $ plane that can provide observed DM relic density. Note also that we compare the numerical results with analytical ones using Eq. (24), applying the dominant contribution of $ \sigma v \sim {\rm few} \times g_H^4 $, and confirm the consistency. Here, we consider mass range of DM (dark photons) as follows:

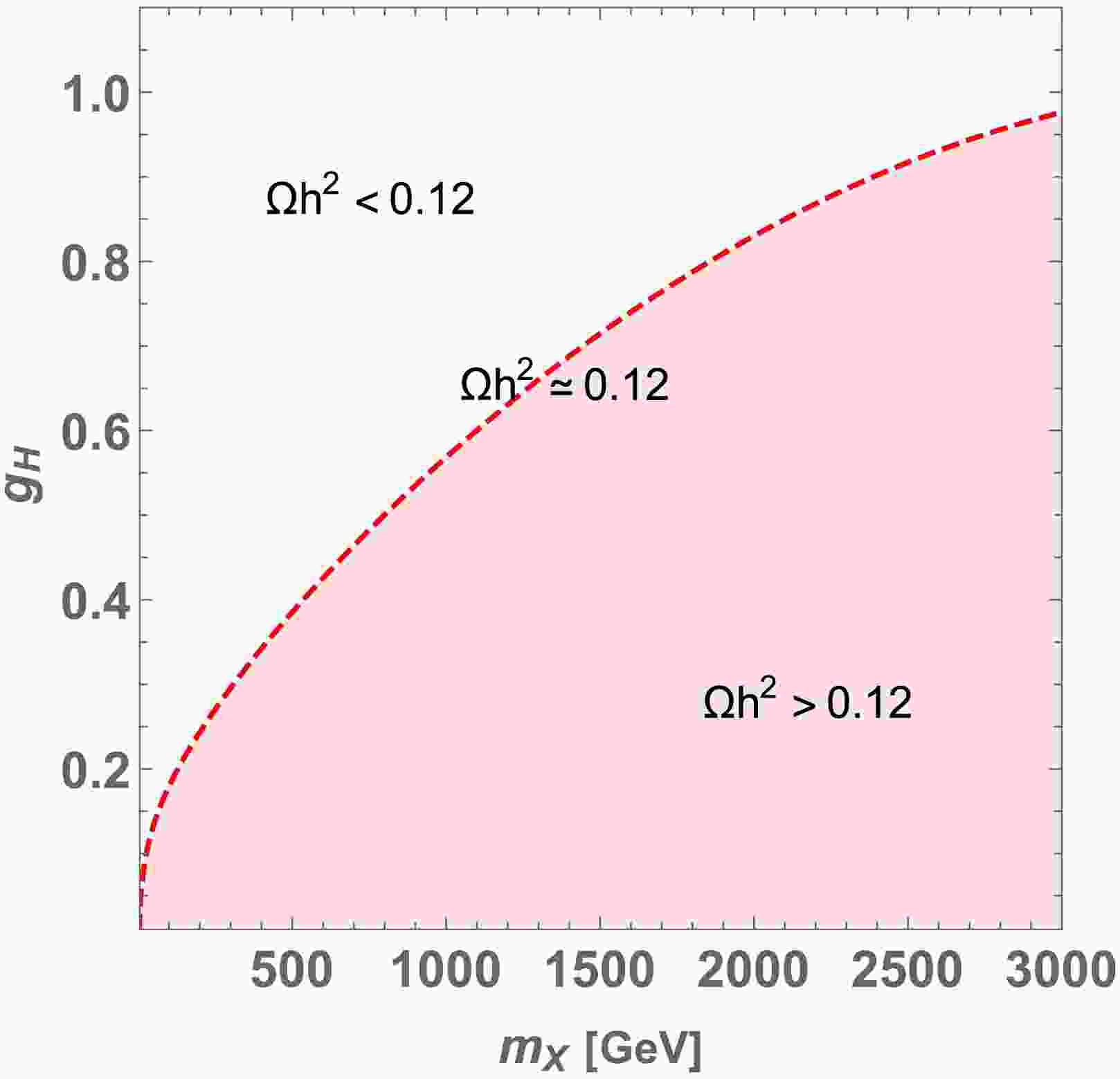
Here, the region $ m_{X} \in [1, m_Z] $ GeV is light WIMP like the DM case, where Z′ is also lighter than Z and more dark photon-like. The region $ m_{X} \in [m_Z, 3000] $ corresponds to the heavy WIMP DM case, and Z′ is heavier than Z. Note that the $ m_X \simeq m_{Z'} \sim m_{Z} $ region is strongly constrained by Z-Z′ mixing, as we discuss below.

In Fig. 1, we show the regions providing $ \Omega h^2 < 0.12 $, $ \Omega h^2 \simeq 0.12 $, and $ \Omega h^2 > 0.12 $ on the $ \{m_X, g_H \} $ plane. The red dashed curve indicate the parameters explaining observed relic density. The shaded region is excluded because relic density is over-abundant, while the white region provides smaller relic density. We find that observed relic density can be obtained by gauge coupling $ g_H \in [0.01, 1] $ for DM mass of 1 to 3000 GeV.

Figure 1.  (color online) The red dashed curve indicates parameter $ \{m_X, g_H \} $ realizing observed relic density $ \Omega h^2 \simeq 0.12 $. The shaded region is excluded because DM is over-abundant.

Here, we summarize the constraints on kinetic mixing parameter $ \epsilon $ from dark photon searches, the thermalization condition of DM, and mili-charged DM interaction.

Constraints from Z-Z^′ mixing:

The kinetic mixing parameter is constrained by Z-Z′ mixing from analysis of the electroweak precision test (EWPT). The Z-Z′ mixing is typically constrained as $ |\sin \chi| \lesssim 10^{-3}-10^{-4} $ when the Z′ boson comes from local $ U(1) $ symmetry, especially a subgroup of GUT symmetry like $ SO(10) $ and $ E_6 $ [48]. In the model, Z-Z′ mixing is given by Eq. (19). We then adopt the conservative bound of $ |\sin \chi| < 10^{-4} $ and estimate the upper bound of $ |\epsilon| $. In Fig. 2, we show the contour of $ \sin \chi $ on the $ \{m_{Z'}, |\epsilon| \} $ plane. We find that the $ |\epsilon| $ value is strongly constrained around $ m_{Z'} \sim m_{Z} $ as the mixing is enhanced.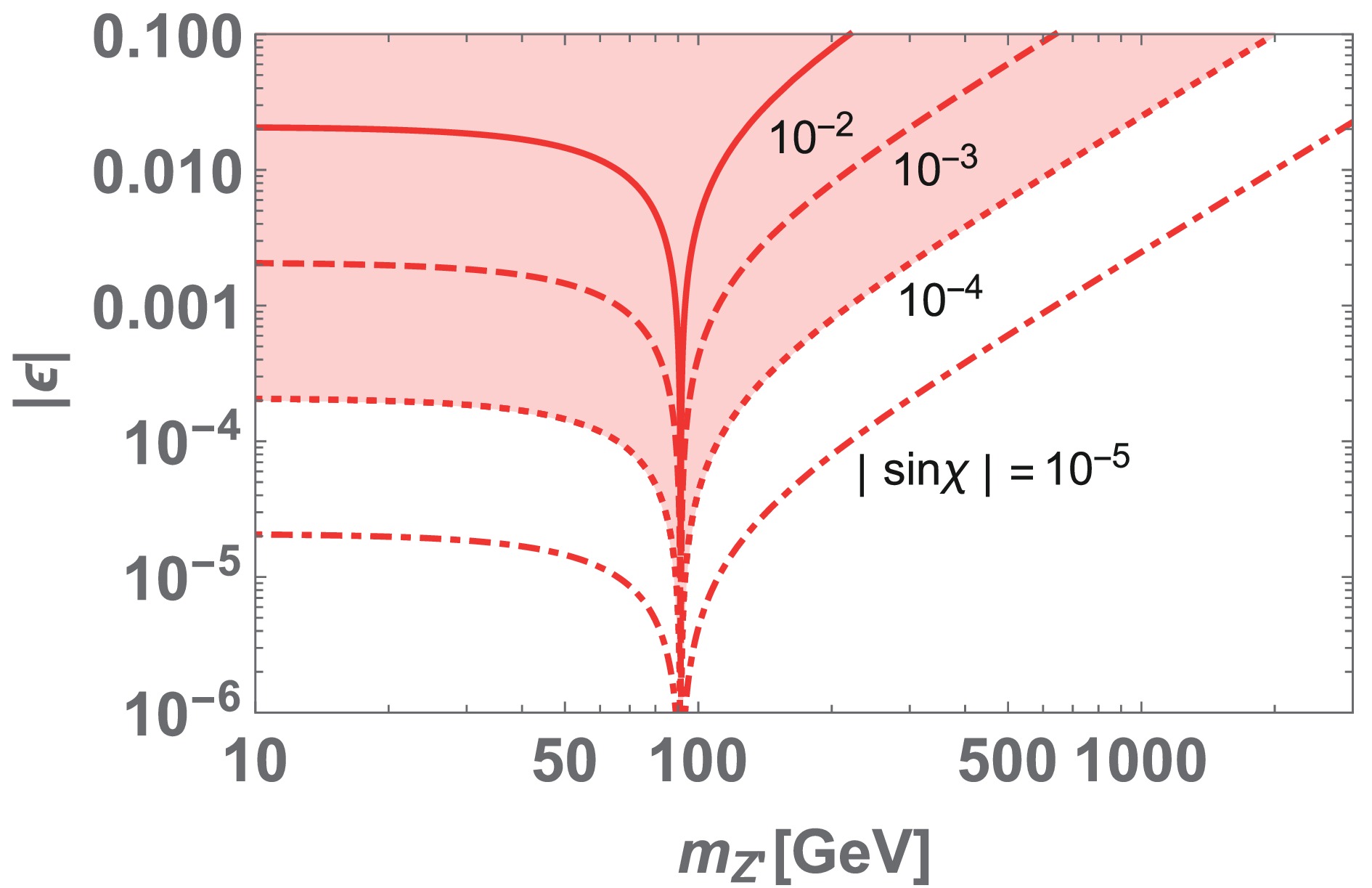

Figure 2.  (color online) Contours showing the value of Z-Z′ mixing $ |\sin \chi| $ on the $ \{m_{Z'}, |\epsilon| \} $ plane.

Constraints from dark photon search:

In the mass range (i) of interest, $ \epsilon $ is constrained by BaBar [53, 54] and LHCb [55] experiments that search for dark photons. The BarBar experiment searches for the process $ e^+ e^- \to \gamma Z' $, where Z′ is considered to decay into visible modes $ \{e^+ e^-, \mu^+ \mu^-, \text{light mesons} \} $ or invisible mode such as neutrinos and DM states. The LHCb experiment searches for dark photons that are produced in proton-proton collision and decay into $ \mu^+ \mu^- $ pairs. We apply constraints from these experiments for the allowed range of $ \epsilon $, where we use the DARKCAST code to extract the limit [38].

In addition, we take into account Z′ searches at the LHC for the $ m_{Z'} \gtrsim \mathcal{O}(100) $ GeV region. The most stringent constraints are obtained from dilepton resonance searches associated with the process $ pp \to Z' \to \ell^+ \ell^- (\ell = e, \mu) $ [49, 50]. We estimate the cross-section for the process by applying CalcHEP 3.8.10 [51], implementing relevant interaction among Z′ and the SM fermions in Eq. (21). The estimated cross-section is compared with the upper limit given in Ref. [50] to estimate a bound on kinetic mixing parameter $ \epsilon $.

DM thermalization condition:

We require particles in the dark sector, DM and dark photons, to be in thermal equilibrium before freeze-out of DM to guarantee our relic density calculation. In addition, dark photon lifetime should be smaller than $ \mathcal{O}(1) $s to avoid inconsistency with Big Bang Nucleosynthesis. In the model, the dark sector is thermalized in the early Universe via dark photon decays into electrons. Then, we impose the condition that the decay rate is larger than the Hubble rate at freeze-out. This condition can be written as [36, 45]

We adopt this condition as a lower bound of $ \epsilon $ in the analysis below.

Constraint from mili-charged DM interaction:

Unlike in the Abelian hidden $ U(1) $ case, we have DM-photon interaction (Eq. (22)) that arises from the effective interaction (Eq. (6)). We thus comment on constraints from DM-Baryon scattering for milli-charged DM [56] through the interaction. In this case, the cross-section is $ \sigma_X = \sigma_{X0} v^2 $, where v is DM-Baryon relative velocity. It is suppressed by $ v^2 $ factor compared to the milli-charged fermion DM case $ (\sigma_F = \sigma_{F0} v^4) $ due to the momentum factor appearing from the derivative in the interaction of Eq. (6). Therefore, the constraint is not severe, and the DM direct detection experiment provides a stronger constraint, as estimated below.

In the model, DM $ X^\pm $ interacts with nucleons via a Z′ exchange process through interactions in Eqs. (20) and (21). In addition, $ X^\pm $ have interactions with the SM Z boson via Z-Z′ mixing, where the relevant interaction for DM-nucleon scattering is

where we included Eq. (22) for the third term inside the square bracket. Thus, we must take into account both Z′ and Z boson exchange diagrams to obtain the DM-nucleon scattering cross-section. Here, vector type interaction among $ Z(Z') $ and nucleons can be obtained as

where p and n indicate proton and neutron, respectively, and we approximate $ \cos \chi \simeq 1 $. We then calculate diagrams and obtain the DM-nucleon scattering cross-section in the non-relativistic limit such that

where $ m_N $ denote nucleon mass $ (N=p, n) $. Here, we consider the average of the DM-nucleon scattering cross-section $ (\sigma_{nX}+\sigma_{pX})/2 $ and compare it with experimental constraints to estimate the upper limit of $ \epsilon $. In estimating the cross-section, we adopt $ g_H $ to explain relic density $ \Omega h^2 \simeq 0.12 $ in Fig. 1 for each DM (dark photon) mass.

In Fig. 3, we show constraints on $ \epsilon $ on the $ \{m_X, \epsilon \} $ plane. Some colored regions above the curves are excluded by direct detection experiments, as indicated by labels, where the strongest limits are from LZ [57], Xenon1T (2020) [58], and DarkSide-50 [59] for the mass ranges $ m_X \gtrsim 10 $ GeV, 3 GeV $ \lesssim m_X \lesssim $ 10 GeV, and 1 GeV $ \lesssim m_X \lesssim $ 3 GeV, respectively; we also show constraints from Xenon1T(2018) [60] and PandaX-4T [61]. In addition, we show the excluded region from Z-Z′ mixing and the dilepton search at the LHC, as discussed in the previous section. In the gray region, $ \epsilon $ is too small for DM and dark photons to be thermalized before freeze out. The $ \epsilon $ value below the blue dotted curve provides the DM-nucleon cross-section in the neutrino floor, and this is difficult to explore by direct detection. In the left plot, we also indicate the excluded region by dark photon searches by LHCb and BarBar. We find that the direct detection cross-section gives us much stronger constraints than dark photon searches when DM (dark photons) is relatively light. Future DM direct detection experiments can also explore the allowed region, unless it is above the region of the neutrino floor.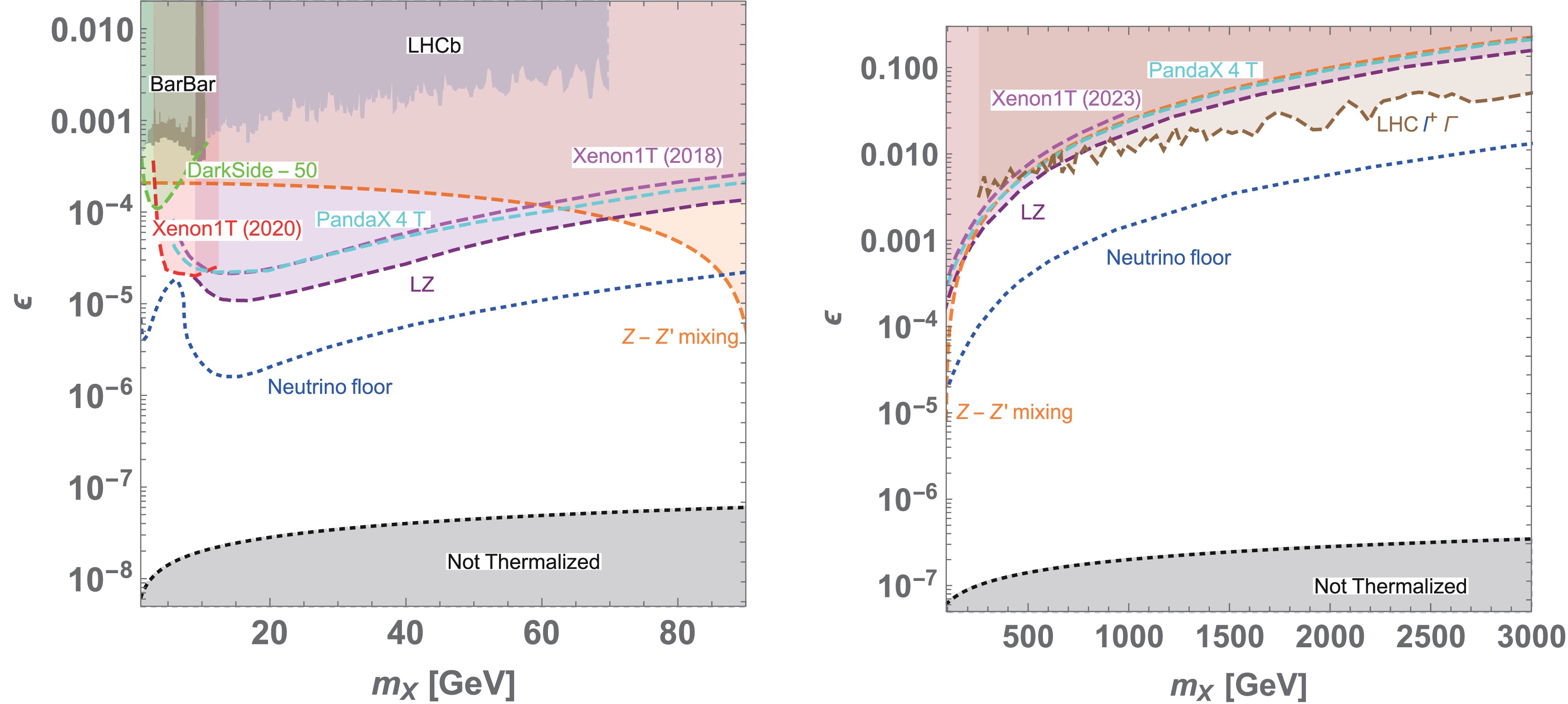

Figure 3.  (color online) Constraints on $ \epsilon $. The colored regions above the curves are excluded by direct detection experiments, Z-Z′ mixing, and dilepton search at the LHC, as indicated by labels. The left and right plots show different DM mass regions. In the gray region labeled as "Not Thermalized", $ \epsilon $ is too small for DM and dark photons to be thermalized before freeze out. In the left plot, the regions labeled as LHCb and BarBar are excluded in dark photon searches by these experiments. The $ \epsilon $ value below the blue dotted curve provides the DM-nucleon cross-section in the neutrino floor.

In this paper, we discussed DM and dark photons from a hidden $ S U(2)_H $ model with minimal new field content: the $ S U(2)_H $ doublet scalar field, introducing a dimension-6 effective operator among $ S U(2)_H $ and $ U(1)_Y $ gauge fields and the doublet. The effective operator induces kinetic mixing between these gauge fields after spontaneous gauge symmetry breaking, and one component of $ S U(2)_H $ gauge field becomes dark photon Z′, while the other two components become vector DM $ X^\pm $. Note that $ X^\pm $ and Z′ have almost degenerate mass in the model.

Then, we considered the scenario in which the relic density of DM is explained by the $ X^+ X^- \to Z' Z' $ process, as it is determined by gauge interaction only and more constrained due to the fixed mass relation between $ X^\pm $ and Z′. Numerically analyzing the Boltzmann equation, we searched for the parameter region that satisfies observed relic density. It was found that $ \mathcal{O}(0.01) $ to $ \mathcal{O}(1) $ gauge coupling of $ S U(2)_H $ can realize the relic density in the DM (dark photon) mass range of $ \sim $1 GeV to $ \sim 3 $ TeV. We also discussed relevant constraints from DM and dark photon physics to constrain the kinetic mixing parameter. In addition, the cross-section of DM-nucleon scattering via dark photon exchange was estimated to explore constraints from DM direct detection. As a result, we found that direct detection searches can provide the strongest constraint on the kinetic mixing parameter, and further parameter spaces will be tested in the future unless the cross-section is above neutrino floor. The model could also be tested in future collider experiments, such as the LHC and lepton colliders, considering new scalar bosons in addition to Z′ and $ X^\pm $. For example, $ pp(e^+e^-) \to Z \phi $ production is realized via scalar mixing. The new scalar ϕ would decay into $ Z'Z' $ and $ X^+X^- $ with the same branching ratio if kinematically allowed. Because we predict almost degenerate masses of Z′ and $ X^\pm $, detailed analysis of the signals from the process can explore the model. Detailed study of collider physics is beyond the scope of this paper and is left for future work.