Anisotropic flow, flow fluctuation, and flow decorrelation in relativistic heavy-ion collisions: the roles of sub-nucleon structure and shear viscosity

One of the most significant discoveries in relativistic heavy-ion collisions performed at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) is the creation of the strongly-coupled Quark-Gluon Plasma (QGP). This novel hot and dense nuclear matter exhibits perfect fluid-like transport properties, as characterized by an extremely low ratio of shear viscosity to entropy density $ ({\eta_v/s}) $ [1−5]. The use of a relativistic hydrodynamic approach [6−11] at the early high-temperature stage and microscopic hadronic cascades [12−14] at the later low-temperature stage has been very successful in describing the dynamical space-time evolution of heavy-ion collisions.

Strong (anisotropic) collective flow is one of the most important pieces of evidence for the formation of QGP and has attracted significant attention over the past decades. It refers to the azimuthal anisotropy of the final produced particles, stemming from the initial state spatial anisotropy converting to the final state momentum anisotropy as a result of strong interaction among the QGP constituents [15−20]. The final-state anisotropies are typically observed by performing a Fourier analysis of the azimuthal angle distribution of the final state particles relative to the event-plane angle $ \Psi_{{n}} $, i.e.,

where the Fourier coefficient $ v_n $ is called the n-th order harmonic flow. Early works [8, 21−23] have indicated that the anisotropic flow $ v_n $ is sensitive to the initial state and transport properties of the QGP medium, such as specific shear viscosity $ {(\eta_v / s)} $ and bulk viscosity $ {(\zeta / s)} $. To quantitatively extract and constrain the intrinsic properties of QGP, the state-of-the-art Bayesian inference method [23−26] has been widely utilized in the heavy ion research community. This involves calibrating hydrodynamics calculations, e.g., the particle yield and flow magnitude, with experimental data from the LHC and RHIC.

One of the interesting features of anisotropic flow is its event-by-event fluctuations. These fluctuations originate partly from the varying positions of nucleons within nuclei in each event. Such fluctuations could further result in the phenomenon of factorization breaking (or the decorrelation effect) of the anisotropic flow [7, 27−32]. A common method for studying the factorization breaking effect is to construct two-particle correlations using flow vectors. This method takes into account the combined contributions from the flow magnitude and flow angle [29, 30, 33−35]. The factorization breaking effect has been confirmed in Au+Au collisions at the RHIC, as well as in Xe+Xe and Pb+Pb collisions at the LHC [28, 33, 36]. Recently, the ALICE Collaboration has developed new observables based on four-particle correlations, which can separately measure the contributions from the flow magnitude and flow angle in the transverse plane [36, 37]. Similar observables have also been defined by the ATLAS Collaboration to separate the contributions from the flow magnitude and flow angle along the longitudinal direction [33]. Distinguishing the contributions from the flow magnitude and flow angle offers a unique opportunity to understand and constrain the fundamental properties of the QGP medium.

Another important source of flow fluctuation is the initial sub-nucleon structure (the constituent quark). This was first studied in particle production mechanisms in A+A collisions. It was found that the multiplicity at mid-rapidity scales linearly with the number of quark participants in large collision systems [38−44], which rules out the conventional two-component ansatz in the initial Glauber model. A later study [45] based on MCKLN (TRENTO) + USPhydro indicated that flow harmonics may not be very sensitive to underlying microscopic sub-nucleon fluctuations in Pb+Pb collisions. However, the same study also claimed that flow fluctuations play a key role in small systems: the eccentricities in high multiplicity p+Pb collisions at $ \sqrt{s_{NN}} $=5.02 TeV depend strongly on these fluctuations. More recently, hydrodynamic models based on the IP-Glasma initial condition [46, 47] with three gluonic hot spots have been able to quantitatively describe experimental flow data in p+Au, d+Au, and He3+Au collisions [48, 49]. However, models without sub-nucleon fluctuations fail to achieve this. This further confirms the necessity of considering sub-nucleon fluctuations in hydrodynamics model calculations. This effect could even exist in proton-proton collisions, where the size and substructure of the proton may influence the production of vector mesons (e.g., $ J/\Psi $) [50, 51] and generation of hadron anisotropies [52] with respect to the reaction plane. However, it is still an open question as to how the effects of sub-nucleon fluctuations can be detected from the flow observables in A+A collisions. In this study, we aim to explore the impacts of shear viscosity and sub-nucleon structure on flow fluctuations and decorrelations.

Our paper is organized as follows. In Sec. II, we introduce the setup of the event-by-event (3+1)-dimensional CLVisc viscous hydrodynamics framework. In Sec. III, the $ p_T $differential flow observables are constructed based on two-particle and four-particle correlations. In Sec. IV, we present our numerical results for the elliptic flow fluctuation for identified particles and the angle and magnitude decorrelations of elliptic flow for charged particles. The summary is presented in Sec. IV.

In this study, we utilize the event-by-event (3+1)-dimensional CLVisc viscous hydrodynamics framework [6, 7, 53], which includes the fluctuating TRENTO initial condition [54−56], second-order dissipative hydrodynamics evolution, and Cooper-Frye hadronic sampler, to simulate the space-time evolution of the QGP medium and hadron production in Pb+Pb collisions at$ \sqrt{s_{NN}} $=5.02 TeV at the LHC.

The theoretical descriptions of the initial states of the QGP created in relativistic heavy-ion collisions from the first principle remain a significant challenge. In this study, we employ the parameterized initial condition model, TRENTO [54−56], to phenomenally simulate the initial space-time distribution of the QGP fireball. In the TRENTO initial condition, the positions of nucleons are sampled following Woods-Saxon distributions. Unlike in the traditional Glauber model [57], the collisional probability of nucleons is determined by the effective parton cross-sections, which are tuned to fit the inelastic nucleon cross-section. Recently, the sub-nucleon degree of freedom has been incorporated into the TRENTO model, which provides a possible approach to investigate the substructures of nucleons and extra sources of flow fluctuations [24, 45, 50, 51, 58]. Once the positions of wounded nucleons are determined, one can obtain the thickness functions of the projectile and target nuclei as follows:

Here, $ T_p $ is the thickness function originating from each wounded nucleon with Gaussian form, and $ w_i $ is a random weight taken from a gamma distribution to account for the multiplicity fluctuations in p+p collisions. Naturally, one may define the reduced thickness function by considering the generalized average of the thickness functions of two nuclei,

where the parameter p characterizes the different approximations for the entropy deposition. In the new version of the TRENTO initial condition model, the sub-nucleon structure is included. The positions of constituent partons are assumed to follow a Gaussian distribution within the nucleons, and the same entropy deposition function is used as the nucleons. In this study, we choose an IP-Glasma-like entropy deposition, i.e., $ p=0 $ [23, 24]. The number of constituent partons is set to 3. The Gaussian widths are set to 0.5 fm for nucleons and 0.2 fm for partons. By utilizing the scale factor K, the initial transverse entropy profile is assumed to be

where the factor K can be tuned to fit the final particle yield ${{\rm d}N/{\rm d}{\eta}}$ in the most central collisions. Additionally, we assume the initial proper time $ \tau_0 $ to be 0.6 fm. For the longitudinal direction, we use the following plateau-like envelope function:

In this study, we take the parameters $ {\eta_{\rm{flat}}}=1.7 $ and $ {\eta_{\rm{gw}}}=2.0 $.

After the initial entropy density distribution has been constructed, the (3+1)-dimensional CLVisc viscous hydrodynamics model is used to simulate the space-time evolution of the QGP fireball. The following energy-momentum conservation equation is solved:

where $ T^{\mu\nu} $is the energy-momentum tensor of the QGP system. Because the QGP medium is not fully in local thermal equilibrium, we also solve the evolution of the shear tensor and bulk pressure using the second-order Israel-Stewart equation [59],

Here, D is the covariant derivative, and $ \theta=\partial_{\mu}u^{\mu} $ is the expansion rate. The traceless symmetric tensor is defined as $ \pi^{\langle\mu \nu\rangle}=\Delta_{\alpha \beta}^{\mu \nu}\pi^{\alpha \beta} $ with second-order symmetric projection operator $ \Delta_{\alpha \beta}^{\mu \nu}=\dfrac{1}{2}\left(\Delta_\alpha^\mu \Delta_\beta^\nu+\Delta_\alpha^\nu \Delta^\mu{ }_\beta\right)-\dfrac{1}{3} \Delta^{\mu \nu} \Delta_{\alpha \beta} $. $ \tau_{\pi} $ and $ \tau_\Pi $ are the relaxation times of the shear tensor and bulk pressure, respectively. $ \delta_{\Pi \Pi},\lambda_{\Pi \pi},\delta_{\pi \pi},\tau_{\pi \pi},\varphi_1 $ are second-order transport coefficients. The values of relaxation time and transport coefficients are summarized in Table 1.

$ \tau_{\Pi} $	$ \delta_{\Pi \Pi} $	$ \lambda_{\Pi \pi} $
$ \dfrac{\zeta(T)}{15\left(\dfrac{1}{3}-c_s^2\right)^2(e+p)} $	$ \dfrac{2}{3} \tau_{\Pi} $	$ \dfrac{4}{5}\left(1-c_s^2\right) \tau_{\Pi} $
$ \tau_\pi $	$ \delta_{\pi \pi} $	$ \tau_{\pi \pi} $	$ \varphi_1 $
$ \dfrac{{5\eta_v}}{T} $	$ \dfrac{4}{3} \tau_\pi $	$ \dfrac{5}{7}\tau_\pi $	$ \dfrac{9}{70} \dfrac{4}{e+p}\tau_\pi $

Table 1.  Transport coefficients for the second-order Israel-Stewart equation of motion.

In this study, the specific shear viscosity $ {\eta_v}/s $ is taken as 0.16, the temperature dependence of bulk viscosity $ {\zeta/s(T)} $ is taken from Ref. [26], and the equation of state is taken from the HotQCD Collaboration [60]. When the temperature of the QGP fluid cell drops down to the freezeout temperature ($ T_\mathrm{frz} $=150 MeV), the momentum of the thermal hadrons is obtained using the Cooper-Frye prescription,

where the thermal equilibrium term $ f_{\rm{{eq}}} $ and out-of-equilibrium correction $ \delta f_{\rm{shear}} $ are given as

Here, we ignore the correction related to bulk pressure because it has been confirmed [22, 61] that the bulk pressure correction, $ \delta f_{\rm{bulk}} $, has a significant contribution (approximately 20%) only to the yield and mean $ p_T $ of protons, while it is almost insensitive to the yield and mean $ p_T $ of pions and kaons. Moreover, different forms of viscous correction can result in varying transport coefficients [23, 24]. However, these different forms do not qualitatively alter the model results. Therefore, in this study, we consider only the widely accepted shear tensor correction, $ \delta f_{\rm{shear}} $. After the thermal hadrons are produced, they undergo resonance decay procedures. Once again, the direct resonance decay primarily affects protons and has a slight impact on pions and kaons [22, 61]. Therefore, neglecting the afterburner stage can be a reasonable approximation for qualitative studies, especially at LHC energies, and it also saves a significant amount of CPU hours. The centrality classes are determined from the total entropy at midrapidity at the initial time $ \tau_0 $ within the TRENTO initial condition. To improve the statistics, we run 2000 hydrodynamics events and oversample 3000 times for each hydrodynamics event at each centrality bin.

Under the assumptions that the flow vector follows a 2-dimensional Gaussian distribution and that the effect of collision geometry is dominant compared to that of the flow fluctuations, the two-particle and four-particle correlations can be written as follows [62]:

where $ \langle v_{{n}}\rangle $ and $ \sigma_{{v}_{{n}}} $ are the mean and fluctuation of the anisotropic flow coefficient $ v_n $, respectively. Using the above formula, the mean flow $ \langle v_{{n}}\rangle $ and flow fluctuation $ \sigma_{{v}_{{n}}} $ can be estimated via $ v_{{n}}\{2\} $ and $ v_{{n}}\{4\} $ as

The relative flow fluctuation $ F\left(v_{{n}}\right) $ can be calculated as [63]

Note that the relative flow fluctuation can also be quantified by the ratio $ v_2\{4\}/v_2\{2\} $.

Based on the standard multiple cumulant method [64−66], the $ p_T $ differential flow coefficient can be defined via two-particle correlation as follows:

where the single brackets denote event averages, and the double angle brackets denote averages over both particles and events. $ \phi_1^a $ denotes the azimuthal angles of final particles from some specific $ p_T $ range, $ {\Psi_{{n}}(p_T)} $ is the corresponding $ p_T $ differential event-plane angle, $ \phi_1 $ and $ \phi_2 $ are the azimuthal angles of final particles (without $ p_T $ constraint), and $ \Psi_{{n}} $ stands for the $ p_T $-integrated event plane angle. Because of event-by-event fluctuation, the$ p_T $ differential event plane $ {\Psi_{{n}}(p_T)} $ does not always align with the $ p_T $ integrated $ \Psi_{{n}} $. Therefore, the above differential flow coefficient includes the decorrelation effect. Following the standard procedure, the $ \eta $-gap technology is utilized in this study to eliminate short-range correlations.

One may also define the $ p_T $ differential flow coefficient using the four-particle correlation method, as follows:

where $ d_n\{4\}(p_T) $ is related to the fourth-order $ p_T $ differential cumulant and $ c_n\{4\} $ corresponds to the fourth-order $ p_T $ integrated cumulant, as described in Refs. [64−66].

To separate the flow angle and flow magnitude fluctuations in the $ {p_T} $-dependent flow vector, ALICE collaboration [36, 37] has recently proposed a new set of four-particle correlation functions,

and

where $ A_{n}^f $ ($ M_{n}^f $) denotes the decorrelation between the $ p_T $differential flow angle (magnitude) and $ p_T $integrated flow. If the$ p_T $differential flow is the same as the $ p_T $ integrated flow, $ A_{n}^f $ and $ M_{n}^f $ should be unity. It should be noted that the flow angle decorrelation $ A_{n}^f $ should be less than or equal to unity because of the cosine function in the definition. However, $ M_{n}^f $ does not have such an upper limit, owing to the fact that it involves not only the covariance between the $ p_T $ differential flow and $ p_T $ integrated flow but also their relative fluctuations.

In this section, we present the numerical results for the $ p_T $ differential flow coefficients, flow fluctuation, flow angle, and magnitude decorrelations in Pb+Pb collisions at $ \sqrt{s_{NN}} $=5.02 TeV. These results are based on the (3+1)-dimensional CLVisc hydrodynamics framework with fluctuating TRENTO and AMPT initial conditions [67]. We first focus on the $ p_T $ differential flow and flow fluctuations of identified particles in various centrality intervals and study the effects of shear viscosity. Later, we discuss the granularity of initial state fluctuations by considering the nucleon and sub-nucleon structures in the initial condition. Finally, we demonstrate the hydrodynamic description of flow angle and flow magnitude fluctuations and their dependence on the initial condition model, shear viscosity, and sub-nucleon structure.

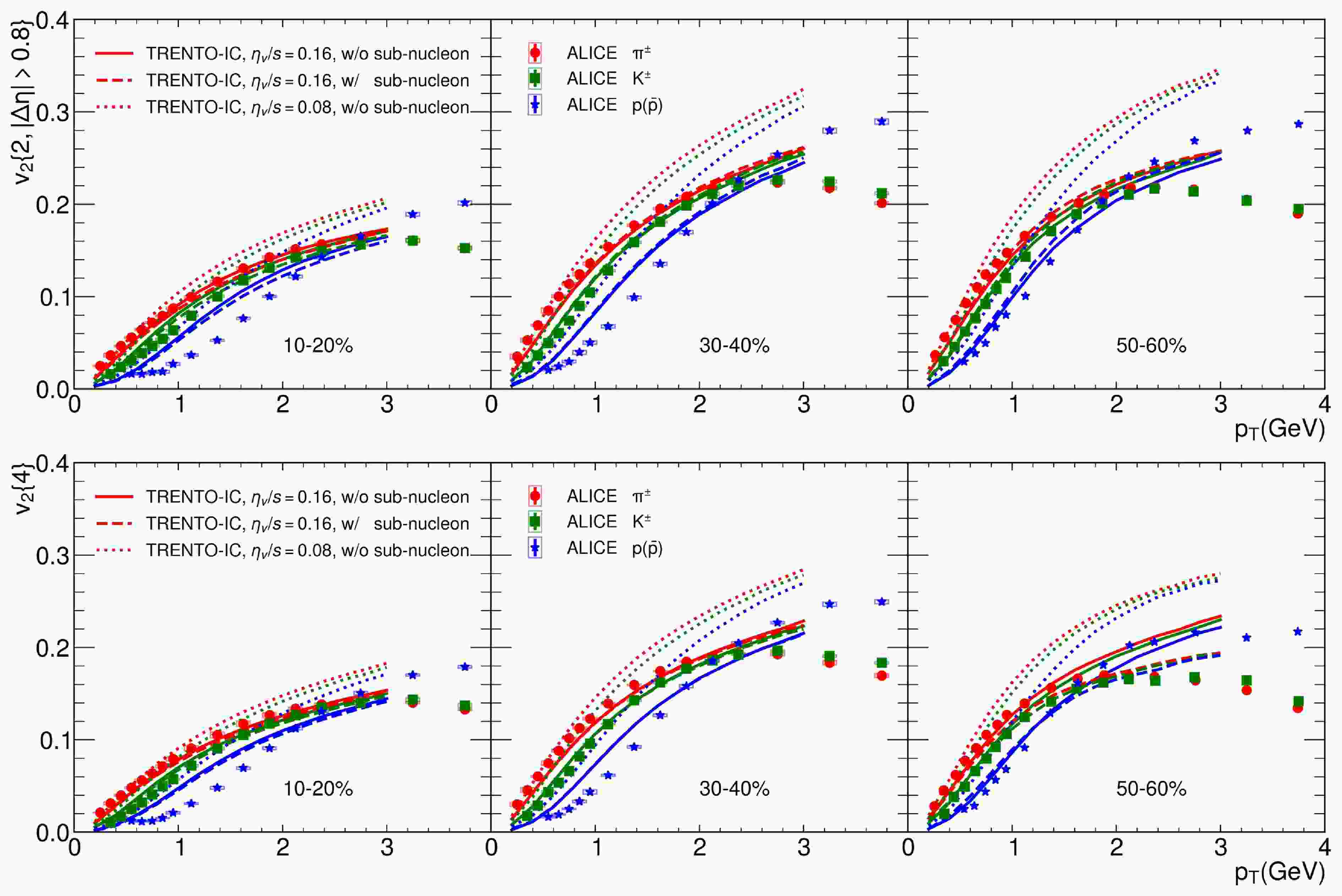
In Fig. 1, we show $ {p_T} $ differential $ {v_2\{2\}} $ with rapidity gap $ \vert \Delta {\eta} \vert > 0.8 $ (upper) and $ p_T $ differential $ {v_2\{4\}} $ (lower panel) for identified particles ($ {\pi^\pm, K^\pm, p+\bar{p}} $) in Pb+Pb collisions at $ \sqrt{s_{NN}} $= 5.02 TeV. The subfigures from left to right refer to three centrality classes: 10%−20%, 30%−40%, and 50%−60%, respectively. The experimental data from the ALICE collaboration [63] are shown for comparison. For CLVisc hydrodynamics simulations, the effects of shear viscosity and sub-nucleon structure are shown in the figure. First, we observe that hydrodynamics calculations with shear viscosity $ \eta_v/s $ = 0.16 can describe the $ {v_2\{2\}} $ and $ {v_2\{4\}} $ of $ \pi^{\pm} $ and $ K^{\pm} $ up to 2.5 GeV. However, compared to the experimental data, our model overestimates the values for protons at low transverse momentum. This deviation increases from peripheral to central collisions. This can be attributed to the absence of a hadronic afterburner in our calculations, which would produce more blue shift effects for protons but have mild effects on $ \pi^{\pm} $ and $ K^{\pm} $. Second, we observe that the $ {v_2\{2\}} $ and $ {v_2\{4\}} $ of identified particles show a weak dependence on the sub-nucleon structure, except for $ {v_2\{4\}} $ in peripheral collisions. In peripheral collisions, the collision systems are smaller and tend to be influenced more by the sub-nucleon structure. To further illustrate this, we present in Fig. 2 the energy density distribution in the transverse plane at proper time $ \tau_0 $=0.6 fm in Pb+Pb collisions at $ \sqrt{s_{NN}} $=5.02 TeV with and without the sub-nucleon structure. One can see that large hot spots split into many small hot spots after the sub-nucleon structure is considered. Because of competition among the many small hot spots, the underlying geometry of the collision zone does not fully convert into the final anisotropic flow after hydrodynamics evolution. This explains the suppression of $ v_2\{4\} $ when sub-nucleon fluctuations are included. In contrast, $ v_2\{2\} $ also includes contributions from fluctuations (in addition to the underlying collision geometry). The decrease in event-averaged anisotropy and the increase in fluctuations (as shown in Fig. 3) effectively cancel each other out, resulting in an unchanged $ v_2\{2\} $.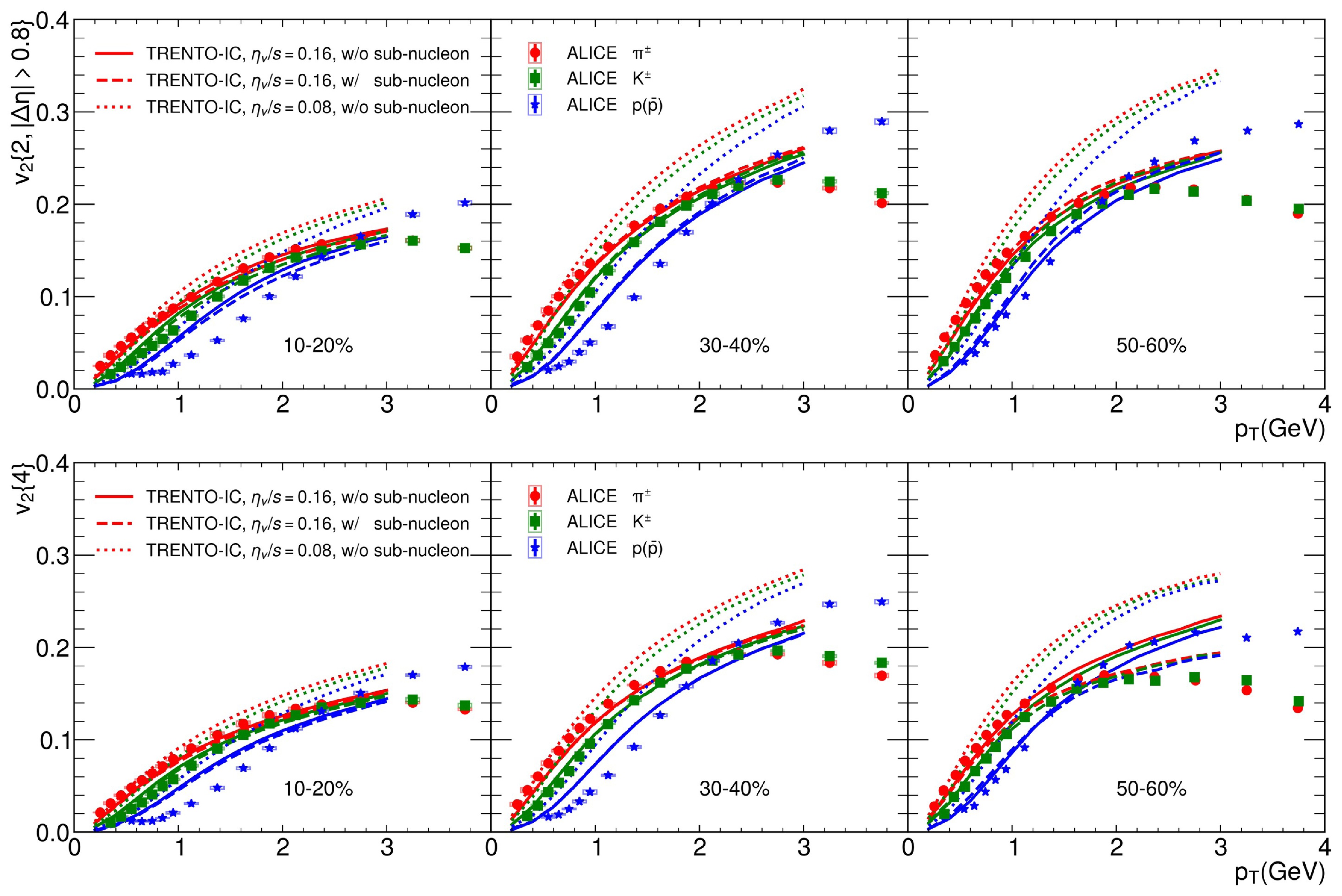

Figure 1.  (color online) Elliptic flow, $ v_2\{2\} $ (with $ \vert \Delta {\eta} \vert > 0.8 $) and $ {v_{{2}}\{4\}} $, for identified particles as a function of transverse momentum $ p_T $ in Pb+Pb collisions at $ \sqrt{s_{NN}} $ = 5.02 TeV for 10%−20%, 30%−40%, and 50%−60% centrality classes. Solid and dotted lines represent the results from hydrodynamics simulations with the TRENTO initial condition for $ \eta_v/s $=0.16 and $ \eta_v/s $=0.08, respectively. The blue dashed line represents the hydrodynamics result with sub-nucleon structure in the TRENTO initial condition and $ \eta_v/s=0.16 $. Data are taken from ALICE collaboration (errors for 50%−60% are absent) [63].

Figure 2.  (color online) Initial energy density at $ \tau_0 $ = 0.6 fm and $ \eta_s $ = 0 in Pb+Pb collisions at $ \sqrt{s_{NN}} $=5.02 TeV. From left to right are 0−5%, 10%−20%, and 30%−40% centrality classes. The upper panel shows the initial conditions with the nucleon size 0.5 fm, while the bottom panel shows the initial conditions with the sub-nucleon structure (i.e., the nucleon consists of three constituent quarks with size 0.2 fm).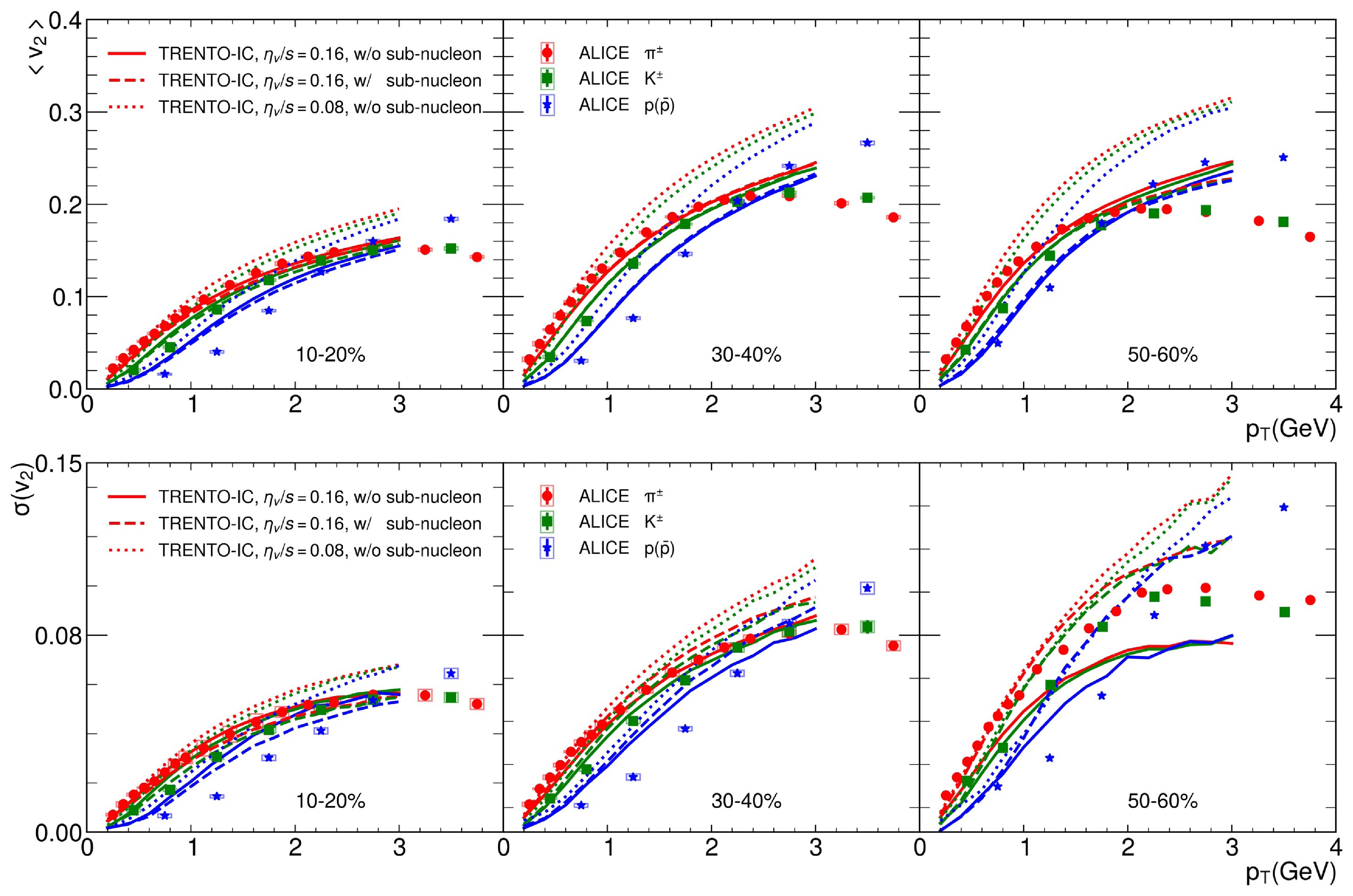

Figure 3.  (color online) Mean flow $ \langle {v_2} \rangle $ and flow fluctuation $ {v_2(\sigma_{v_2})} $) for identified particles as functions of transverse momentum $ p_T $ in Pb+Pb collisions at $ \sqrt{s_{NN}} $= 5.02 TeV for 10%−20%, 30%−40%, and 50%−60% centrality classes. Solid and dotted lines represent the hydrodynamics results with the TRENTO initial condition for $ \eta_v/s $=0.16 and $ \eta_v/s $=0.08, respectively. The blue dashed line represents the hydrodynamics result with the sub-nucleon structure in the TRENTO initial condition and $ \eta_v/s=0.16 $. Data are taken from ALICE collaboration (errors for 50%−60% are absent) [63].

In Fig. 3, we present the mean value $ {\langle v_2\rangle} $ and standard deviation $ {\sigma_{v_2}} $ of the elliptic flow $ {v_2} $ as functions of $ {p_T} $ for the same particle species, centrality interval, and model setup as in Fig. 1. One can see that the mean flow value $ {\langle v_2\rangle} $ and flow fluctuation $ {\sigma_{v_2}} $ exhibit similar $ {p_T} $ dependence and mass ordering behavior as those exhibited by the two-particle and four-particle elliptic flows ($ v_2\{2\} $ and $ v_2\{4\} $). The solid curves with shear viscosity $ \eta_v/s $=0.16 can better describe the trends of $ {\langle v_2\rangle} $ and $ {\sigma_{v_2}} $data up to 2-3 GeV for $ \pi^{\pm} $, $ K^{\pm} $. Similar to $ v_2\{2\} $ and $ v_2\{4\} $, both $ {\langle v_2\rangle} $ and $ {\sigma_{v_2}} $ are also suppressed by the shear viscosity. This can be understood from Fig. 4 , which shows the energy density distribution on the transverse plane at proper time $ \tau $= 3 fm in Pb-Pb collisions at $ \sqrt{s_{NN}} $=5.02 TeV with different values of shear viscosity: $ \eta_v/s=0.16 $ and $ \eta_v/s=0.08 $. One can clearly see that the larger shear viscosity has stronger smearing power and therefore results in a more isotropic structure. In addition, we observe from Fig. 3 that the mean flow $ {\langle v_2\rangle} $ is insensitive to the effect of the sub-nucleon structure. However, the flow fluctuation $ {\sigma(v_2)} $ shows very interesting dependence on the sub-nucleon structure. In central collisions, $ {\sigma(v_2)} $ is suppressed by the sub-nucleon structure, but in peripheral collisions, it is actually enhanced by the sub-nucleon structure. This can be understood as follows. From Fig. 2, one can see that, for larger systems (i.e., more central collisions), the inclusion of the sub-nucleon structure can generate many small hot spots, which can partially cancel the flow developed by each hot spot. By contrast, for smaller systems (i.e., more peripheral collisions), the flow pattern can be easily influenced by the sub-nucleon structure (fluctuation).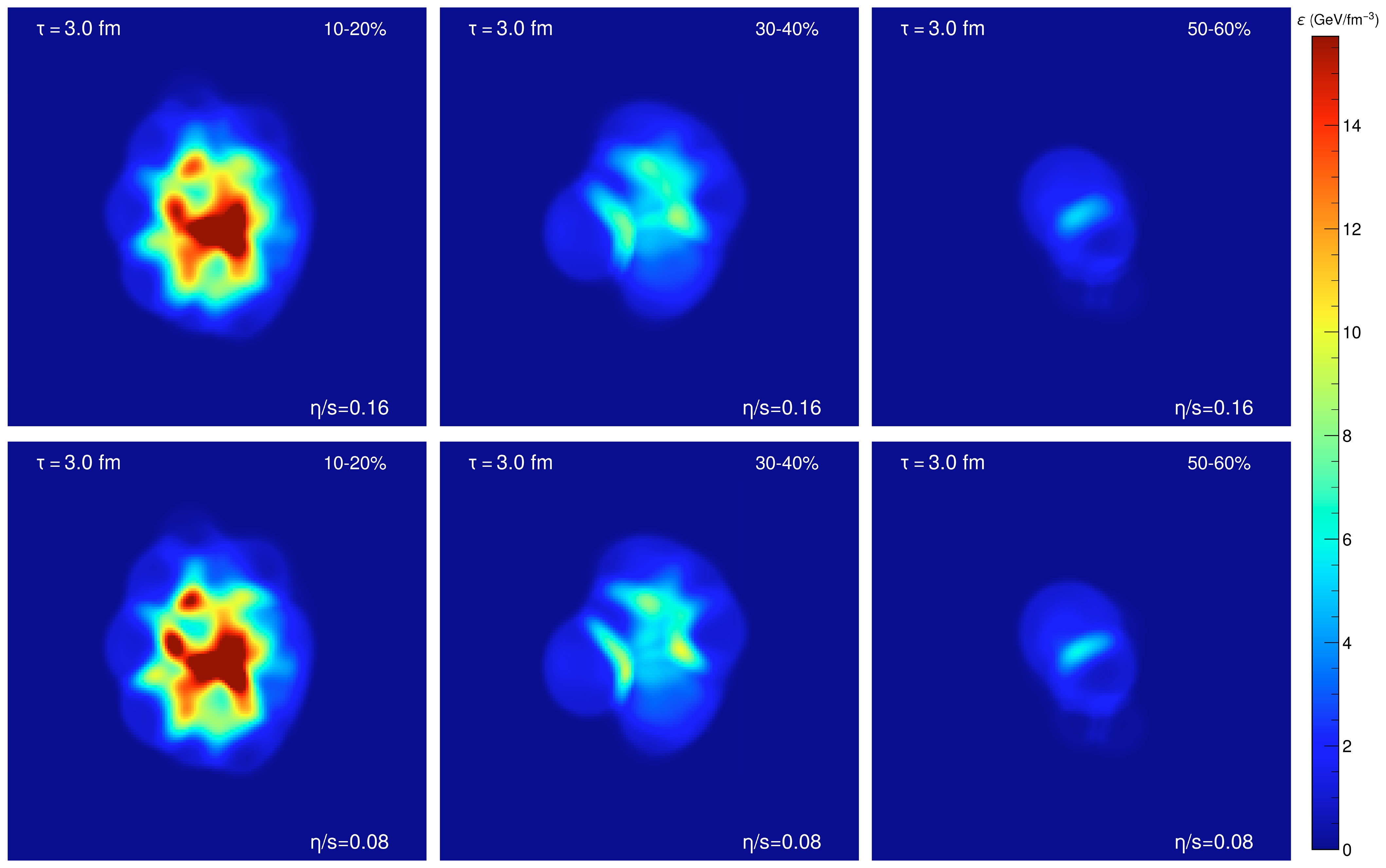

Figure 4.  (color online) Energy density in the transverse plane at proper time $ \tau $ =3 fm in Pb+Pb collisions at $ \sqrt{s_{NN}} $= 5.02 TeV. From left to right are 0−5%, 10%−20%, and 30%−40% centrality classes. The upper panels are for $ {\eta_v/s} $=0.16, while the bottom panels are for $ {\eta_v/s} $ = 0.08.

To further understand the fluctuation of elliptic flow $ v_2 $, Fig. 5 shows the effect of shear viscosity and sub-nucleon structure on the $ p_T $ dependence of the multi-particle cumulant ratio $ {v_2\{4\}/v_2\{2\}} $ and the relative fluctuation function $ F({v_2}) $ in Pb+Pb collisions at $ \sqrt{s_{NN}} $=5.02 TeV for different centrality classes. One can see that, in central collisions, $ {v_2\{4\}/v_2\{2\}} $ and $ F(v_2) $ do not show strong $ p_T $ dependence, while in peripheral collisions, the relative flow fluctuations show quite different $ p_T $ dependences for different model setups. The dashed curves with shear viscosity $ \eta_v/s $=0.16 and the sub-nucleon structure in the initial condition model can better describe the trends of $ {v_2\{4\}/v_2\{2\}} $ and $ F(v_2) $ data up to 2−3 GeV. If one removes the sub-nucleon structure (as shown by the solid curves), the relative fluctuation becomes smaller, resulting in larger values for $ {v_2\{4\}/v_2\{2\}} $ and smaller values for $ F(v_2) $. Meanwhile, the $ p_T $ dependence of the relative flow fluctuations also becomes reverse in peripheral collisions. For the viscosity effect, if one increases the value of the shear viscosity to entropy density ratio ($ \eta_v/s $), both flow and flow fluctuation become smaller because of the smearing characteristics of the viscosity. This leads to a different viscosity dependence for relative flow fluctuation in a different centrality. In central collisions, shear viscosity increases the relative flow fluctuation, while in peripheral collisions, the shear viscosity tends to suppress the relative flow fluctuation, especially in the large $ p_T $ region (the low $ p_T $ region is more similar to central collisions). Finally, we observe that the meson–baryon grouping of $ F(v_2) $ and $ v_2\{4\}/v_2\{2\} $, as seen in the experimental data from ALICE, can be qualitatively reproduced by incorporating sub-nucleon structures in the initial conditions or by considering a smaller shear viscosity in the hydrodynamic phase. This suggests that the $ p_T $-differential flow fluctuations of identified hadrons can further constrain the initial conditions and transport properties of the QGP medium in heavy-ion collisions.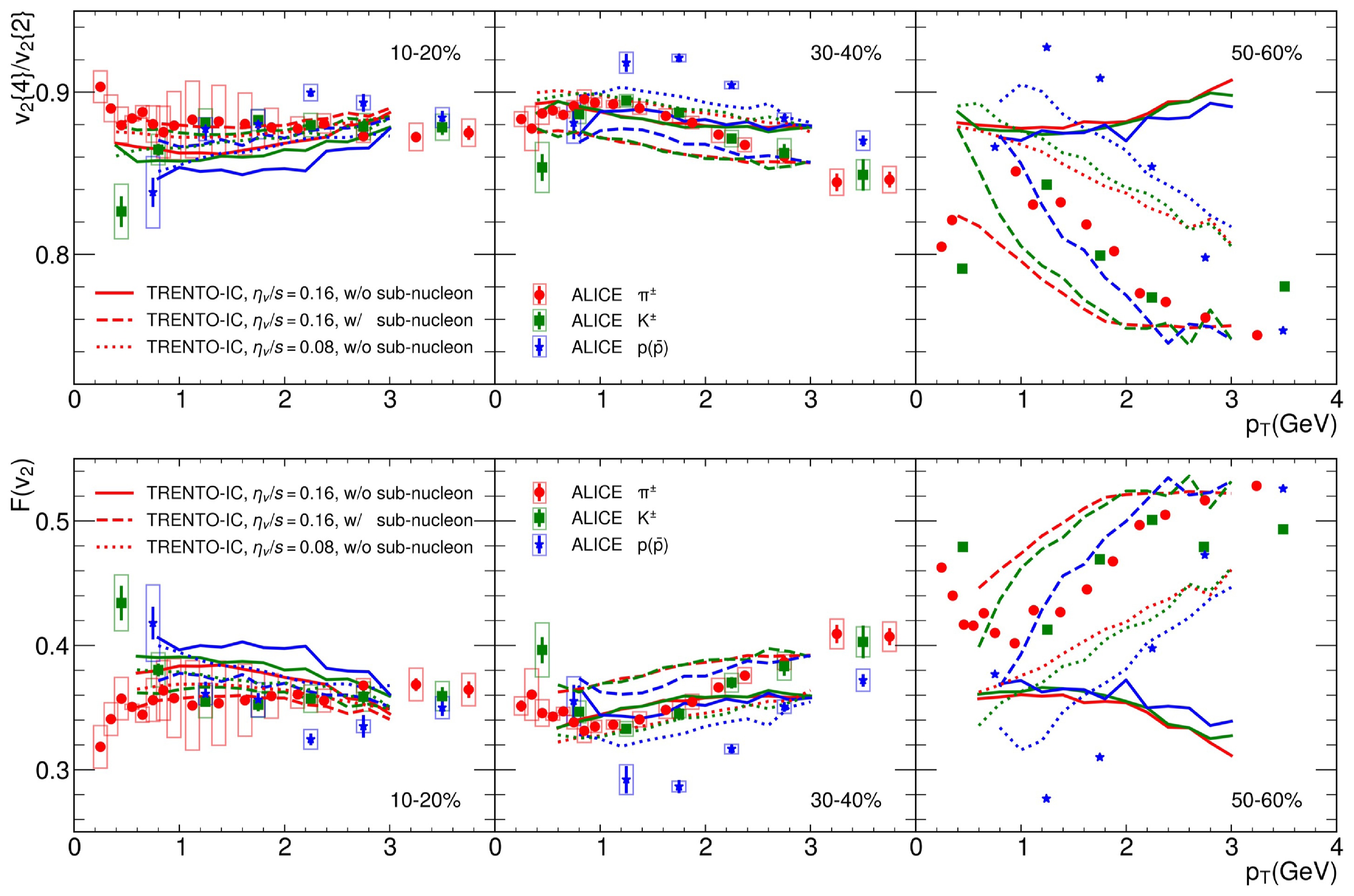

Figure 5.  (color online) Multi-particle cumulant ratio $ {v_2\{4\}/v_2\{2\}} $ and relative flow fluctuation $ F({v_2}) $ for identified particles as functions of transverse momentum $ p_T $ in Pb+Pb collisions at $ \sqrt{s_{NN}} $= 5.02 TeV for 10%−20%, 30%−40%, and 50%−60% centrality classes. Solid and dotted lines represent the hydrodynamics results with the TRENTO initial condition for $ \eta_v/s $ = 0.16 and $ \eta_v/s $= 0.08, respectively. The blue dashed line represents the hydrodynamics result with the sub-nucleon structure in the TRENTO initial condition and $ \eta_v/s=0.16 $. Data are taken from ALICE collaboration (errors for 50%−60% are absent) [63].

To better understand the flow fluctuation and decorrelation, the ALICE collaboration has proposed two new sets of $ p_T $ dependent decorrelation observables ($ {A_2^f} $ and $ {M_2^f} $) based on the four-particle correlation method, which can separate the contributions from flow angle and flow magnitude decorrelation. Figure 6 presents the flow angle and flow magnitude decorrelation $ {A_2^f} $ and $ {M_2^f} $ as functions of the associated particle transverse momentum $ {p_T^a} $ in Pb+Pb collisions at $ \sqrt{s_{NN}} = 5.02 $ TeV for several centrality classes (0−5%, 10%−20%, and 30%−40%). The effects of shear viscosity and sub-nucleon structure are also shown in the figure. We first observe that the deviation of flow angle decorrelation $ {A_2^f} $ from unity increases with the transverse momentum $ p_T^a $, consistent with experimental data. This indicates that the flow angle for higher $ p_T $ particles is more decorrelated from the $ p_T $ integrated flow angle. This can be understood from the fact that low $ {p_T} $ particles originate mainly from the inner part of the QGP medium and participate longer in hydrodynamic expansion; therefore, they carry more information about the $ p_T $ integrated event plane. By contrast, high $ {p_T} $ particles come mainly from the edges of the QGP fireball and experience shorter hydrodynamics evolution; thus, they carry less information about the overall flow. The flow magnitude decorrelation $ {M_2^f} $ shows similar $ {p_T^a} $ dependence to $ A_2^f $ in the 0−5% and 10%−20% centrality classes. However, in the 30%−40% centrality class, the value of $ {M_2^f} $ may become larger than unity at high $ p_T^a $. As has been mentioned before, $ M_{n}^f $ not only depends on the covariance between the $ p_T $ differential flow magnitude and the $ p_T $ integrated flow but also involves their relative fluctuations. Therefore, it is not necessarily bounded to unity. $ M_{n}^f >1 $ might indicate that a strong positive correlation exists between the $ p_T $ differential flow magnitude and $ p_T $ integrated flow magnitude, and/or that the relative fluctuation for the $ p_T $ differential flow magnitude is very large (at certain $ p_T $). Another interesting feature is that the decorrelation effect (i.e., the deviation from unity) for both the flow angle and flow magnitude is the largest in central collisions because of a lack of underlying anisotropy for the collision zone. For the effect of viscosity, we find that the flow angle decorrelation, $ A_2^f $, is not sensitive to shear viscosity, aligning with results from AMPT [68] and hydrodynamics studies [37]. However, the flow magnitude decorrelation, $ M_2^f $, shows only a slightly stronger dependence on shear viscosity in the most central collisions, consistent with AMPT simulation in [68] but significantly different from the results of TRENTO+MUSIC simulations [37]. This may be because shear viscosity tends to have a similar smearing effect on flow angles across different $ p_T $ values, whereas the flow magnitude is more significantly influenced by shear viscosity. For the initial condition effect, the flow angle decorrelation $ A_2^f $ does not show much dependence on initial condition. However, the AMPT initial conditions give a completely different $ p_T $ dependence for flow magnitude decorrelation $ {M_2^f} $ compared to that obtained with the TRENTO initial conditions in the 10%−20% and 30%−40% centrality classes. In comparison with findings from the full AMPT calculations [36, 37], the results from the AMPT initial condition combined with hydrodynamics demonstrate a similar trend, indicating that both flow angle and flow magnitude decorrelation originate from the initial condition. One possible explanation is that the initial partons come mainly from excited strings and mini-jets in the AMPT initial condition. As a result, the AMPT initial condition produces a stronger initial flow than the TRENTO initial condition, which in turn leads to a stronger correlation of flow magnitude in the large-$ p_T $ region, causing flow magnitude decorrelation $ {M_2^f} >1 $. As for the granularity of the initial state, our result indicates that the sub-nucleon structure has negligible effect on flow angle and magnitude decorrelations owing to the relatively large system size compared to the size of sub-nucleon fluctuation.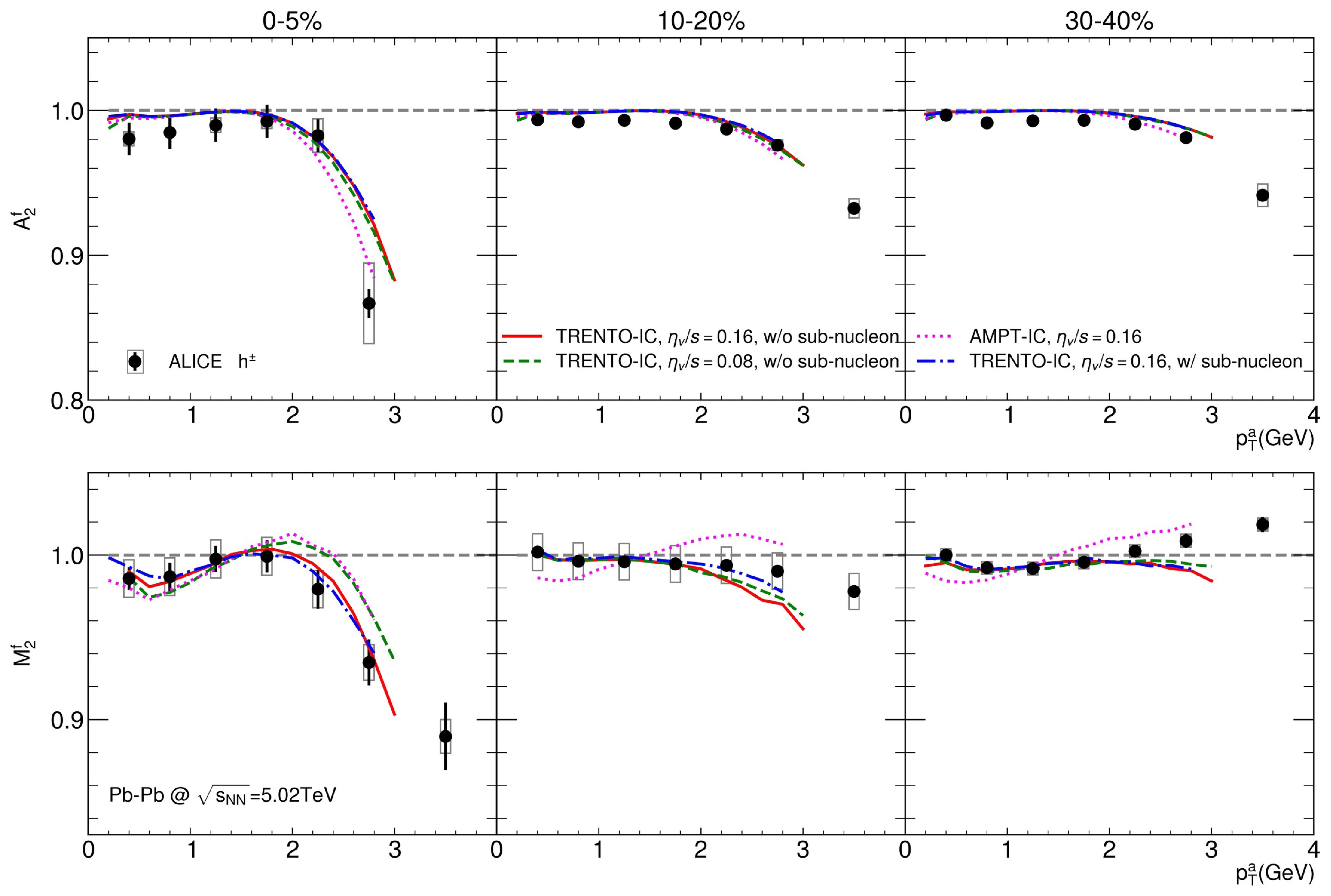

Figure 6.  Flow angle decorrelation $ A_2^f $ and flow magnitude decorrelation $ M_2^f $ for charged particles as functions of transverse momentum $ p_T $ in Pb+Pb collisions at $ \sqrt{s_{NN}} $= 5.02 TeV for 0−5%, 10%−20%, and 30%−40% centrality classes. Solid red line and dashed green line represent the hydrodynamics results with the TRENTO initial condition for $ \eta_v/s $ = 0.16 and $ \eta_v/s $ = 0.08, respectively. The blue dash-dotted line represents the hydrodynamics result with the sub-nucleon structure in the TRENTO initial condition and $ \eta_v/s $ = 0.16. The pink dotted line signifies the AMPT initial condition and $ \eta_v/s $ = 0.16. Data are taken from ALICE collaboration [36].

In this study, we performed a systematic investigation on elliptic flow coefficients, flow fluctuation, and flow decorrelation in Pb+Pb collisions at $ \sqrt{s_{NN}} $=5.02 TeV based on the (3+1)-Dimensional CLVisc hydrodynamics framework with the TRENTO (and AMPT) initial conditions. In particular, we studied the effect of shear viscosity and sub-nucleon structure on these flow observables.

Our numerical results with shear viscosity $ \eta_v/s=0.16 $ can reasonably describe the experimental data on two-particle $ v_2\{2\} $ and four-particle $ v_2\{4\} $, mean flow $ {\langle v_2\rangle} $ , and flow fluctuation $ {\sigma_{v_2}} $ for $ \pi^{\pm} $ and $ K^{\pm} $ particles. For protons, our result overestimates the elliptic flow and flow fluctuation because of the absence of hadronic afterburner in the simulation. Shear viscosity tends to suppress the elliptic flow coefficient and flow fluctuation, owing to its smearing effect on the local density fluctuation. In addition, the flow coefficients appear to be insensitive to the sub-nucleon structure, while the flow fluctuation does depend on the sub-nucleon structure: it tends to be suppressed by the sub-nucleon structure in central collisions but enhanced in peripheral collisions. Our result considering the sub-nucleon structure can better describe the experimental data on the relative flow fluctuation observables, such as $ {v_2\{4\}/v_2\{2\}} $ and $ F({v_2}) $, measured by the ALICE Collaboration at the LHC.

We further studied the effects of the shear viscosity, sub-nucleon structure, and initial condition on flow angle and flow magnitude decorrelations ($ {A_2^f} $, $ {M_2^f} $) using the four-particle correlation method as proposed by the ALICE Collaboration. We found that the decorrelation effect for both the flow angle and flow magnitude is the largest in most central collisions. Also, the flow angle decorrelation effect increases with transverse momentum. In addition, the flow angle decorrelation is insensitive to shear viscosity and only slightly depends on the initial condition in most central collisions, whereas the flow magnitude decorrelation shows sensitivity to both shear viscosity and initial condition. In particular, the AMPT initial condition yields a very different behavior for the flow magnitude decorrelation as compared to that obtained with the TRENTO initial condition.

In the future, it would be interesting to investigate additional sources of flow fluctuation and decorrelation, such as hadronic afterburner and hydrodynamic thermal fluctuation [69−71]. Additionally, performing a Bayesian analysis based on calibrations that include flow fluctuation and decorrelation observables can further help constrain the transport properties and initial structure of the QGP produced in relativistic heavy-ion collisions.