Systematic studies of odd-even staggering in isotopic cross sections with new difference formulas

At many existing and future nuclear facilities, projectile fragmentation, spallation, and fission reactions over a wide energy range (from tens of MeV/nucleon to several GeV/nucleon) are the most important experimental techniques used to produce and study exotic isotopes away from stability [1]. As an example, many isotopes between the neutron and proton drip-lines have been produced by intermediate-energy fragmentation, spallation, and fission reactions at the A1900 separator at MSU [2−5], the Fragment Separator (FRS) at GSI [6−10], the BigRIPS separator at RIKEN [11−15], and the RIBLL-CSR facility at IMP [16−21]. Reliable isotopic cross sections from these reactions are required for designing nuclear physics experiments and understanding the reaction mechanism. In addition, accurate spallation cross sections are key input parameters for simulating the propagation of cosmic-ray nuclei in the galaxy and understanding the origin of the galactic cosmic-ray [22−24]. Last, but not least, these cross sections are also useful for many other applications, e.g., the design of accelerator-driven subcritical reactor systems, radiation protection in space, and cancer therapy with protons or heavy ions [25].

Many projectile fragmentation, spallation, and fission reaction experiments (see, e.g., Refs. [26−46]) demonstrate that isotopic cross sections (yields) present an enhanced production of even-Z isotopes with respect to the neighboring odd-Z ones, the so-called odd-even staggering (OES). Because of only A or Z identification in most of these experiments (see, e.g., Refs. [27, 28, 31, 36, 37]) and very large uncertainties in many previous experimental data, the OES was not quantitatively and accurately studied for isotopic cross sections of many exotic nuclei far from the valley of β stability. Recently, quantitative OES studies were performed by using accurate yields of some neutron-deficient nuclei produced by fragmentation reactions (⁵⁸Ni,⁷⁸Kr+Be) measured in Refs. [17, 18] with a heavy-ion storage ring at IMP [16]. According to these OES studies for limited neutron-deficient nuclei, a universal OES is observed in their cross sections measured in several fragmentation reactions [17, 18]. However, OES studies for neutron-rich nuclei were missing until our recent OES studies in Refs. [47, 48]. Comparisons of OES in about 5000 cross sections accurately measured in approximately 30 reaction systems at different energies confirm that this OES appears to depend on neither the projectile-target combinations nor the projectile energy. Recent fragmentation experiments at the RIBLL-CSR facility indicate new opportunities for the OES studies [19, 21, 49−52]. For example, our new experimental data measured at RIBLL-CSR also support the universality of this OES [19]. This universal OES observed in extensive experimental cross sections seems to originate from the OES of the particle-emission threshold energies in excited nuclei during the final evaporation phase [17, 18, 35, 53].

In our previous studies [17−19, 47, 48, 54], the following 3rd-order difference OES (3D-OES) formula was often employed to calculate the 3rd-order OES magnitudes of experimental cross sections (centered at $ Z+1/2 $):

where $ Y(Z,N) $ stands for the production cross section (yield) of a particular nucleus with an atomic number Z and a neutron number N. In this 3D-OES formula, cross sections of four neighboring nuclei along a constant isospin $ T_{z}=(N-Z)/2 $ chain are required. Although this 3D-OES formula is generally very useful, it may not be suitable in some cases, and thus, other formulas would be needed. For instance, when only three consecutive experimental data (along a constant $ T_{z} $ chain) are available approaching the drip-lines, the 3D-OES formula cannot be applied and a lower-order difference formula should be employed. Additionally, for cases of cross sections with large uncertainties, some higher-order difference formulas may be much better, considering that the OES magnitudes calculated by higher-order formulas should be much smoother when more experimental data points are used in their calculations. Therefore, further systematic investigations and comparisons of the OES with other difference formulas are obviously very welcome, and this will be carried out in this work.

Similar to the above-mentioned 3D-OES formula [Eq. (1)] widely used in our previous publications [17−19, 47, 48, 54], we propose the following 2nd, 4th, and 5th-order difference OES (2D, 4D, and 5D-OES) formulas for deriving the OES magnitudes [$ D_{\text{CS}}^{(2)} $, $ D_{\text{CS}}^{(4)} $, and $ D_{\text{CS}}^{(5)} $, respectively] in the measured isotopic cross sections of several consecutive nuclei along a constant $ T_{z} $ chain:

$ Y(Z) $, the simplification of $ Y(Z,N = Z + 2T_{z}) $, is the production cross section (yield) of one nucleus with an atomic number Z and a neutron number $ N = Z + 2T_{z} $. The 2D and 4D-OES magnitudes are centered at Z, whereas the 3D and 5D-OES ones are centered at $ Z+1/2 $. This small shift does not affect our OES studies in this work. Both the 3D-OES formula and these new OES formulas with different orders can be derived from the finite difference calculus. To study the performance of these new OES formulas, they will be validated with thousands of accurate experimental data.

In the following, these new 2D, 4D, and 5D-OES formulas will be applied to investigate the OES magnitudes in extensive accurate cross sections measured in various fragmentation and spallation reaction systems (see, e.g., Refs. [5−10, 17, 18, 20, 26, 55−57]). As in our previous investigations with the 3D-OES formula in Refs. [47, 48], systematic OES studies will be performed for many isotopes with (N − Z) from –3 to 23 over a broad range of atomic numbers (Z ≈ 3−50). Furthermore, the average values of these OES magnitudes ($ D_{\text{CS}}^{(2)} $, $ D_{\text{CS}}^{(4)} $, and $ D_{\text{CS}}^{(5)} $) in experimental datasets measured in different reaction systems at various energies will be evaluated and adopted as the new (2nd, 4th, and 5th-order, respectively) OES evaluations. Finally, these new 2nd, 4th, and 5th-order OES evaluations as well as the 3rd-order OES ones presented in our previous publications [47, 48] will be quantitatively compared.

Recently, extensive cross sections have been accurately measured in many different fragmentation or spallation reactions: 140 MeV/nucleon ^40,48Ca+Be/Ta [5], 140 MeV/nucleon ^58,64Ni+Be/Ta [5], ⁵⁶Fe+p at 300, 500, 750, 1000, and 1500 MeV/nucleon [6], 1000 MeV/nucleon ¹³⁶Xe+p [7], 1000 MeV/nucleon ^124,136Xe+Pb [8], 1000 MeV/nucleon ¹¹²Sn+¹¹²Sn [9], 500 MeV/nucleon ¹³⁶Xe+d [10], 483 MeV/nucleon ⁷⁸Kr+Be [17], 463 MeV/nucleon ⁵⁸Ni+Be [18], 57 MeV/nucleon ⁴⁰Ar+Be/Ta [20], 650 MeV/nucleon ⁵⁸Ni+Be [26], 64 MeV/nucleon ⁸⁶Kr+Be/Ta [55], 1000 MeV/nucleon ²⁰⁸Pb+p [56], and 140 MeV/nucleon ⁴⁰Ar+Ni/Ta [57].

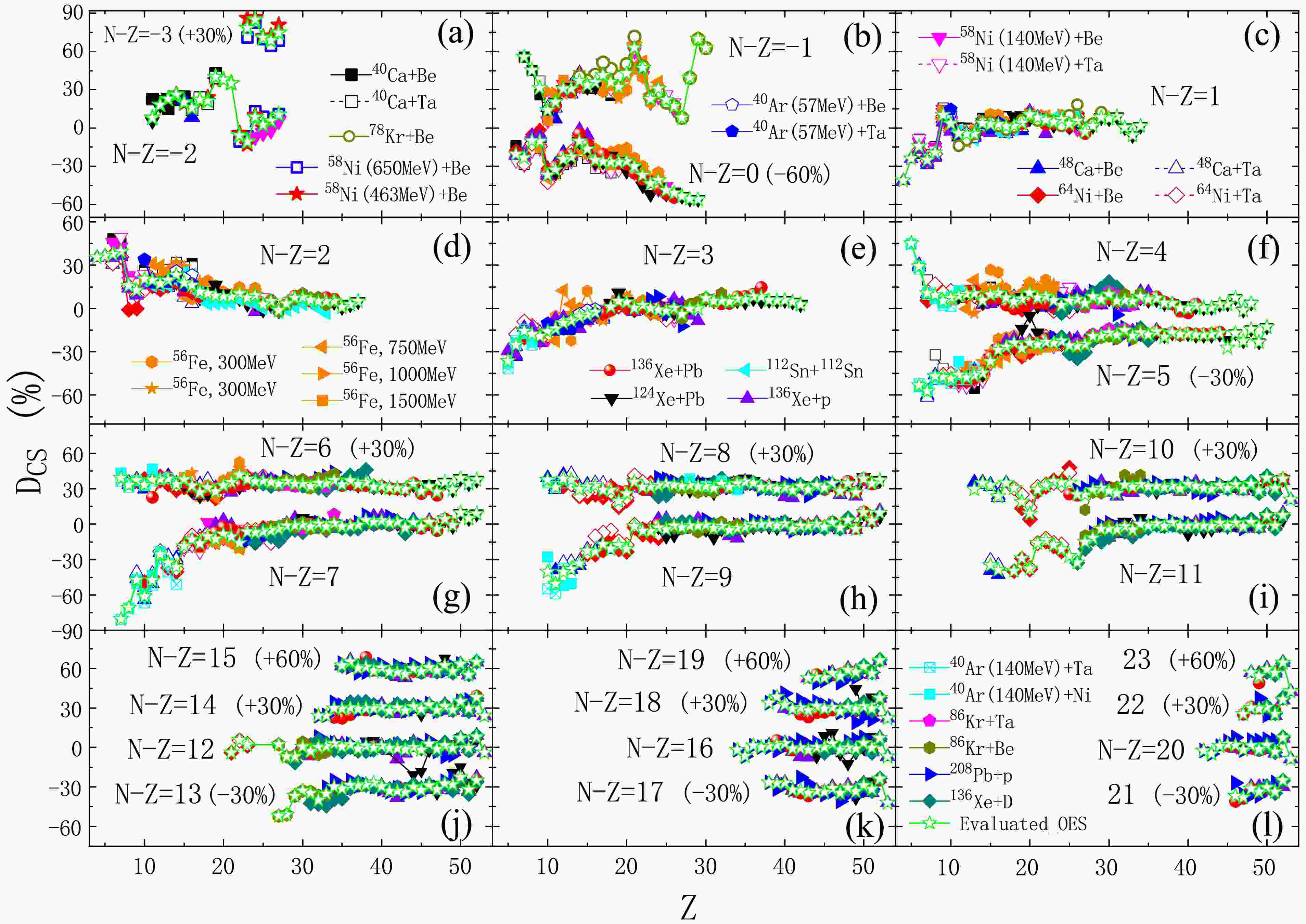
The relative uncertainties of these experimental datasets are less than 15% in most cases, although they are larger than 20% for a few experimental data produced by ⁵⁸Ni+Be at 650 MeV/nucleon reported in Ref. [26]. These accurate experimental cross sections are used in this work to avoid possible spurious staggering structures caused by large errors in experimental data. The OES magnitudes ($ D_{\text{CS}}^{(2)} $, $ D_{\text{CS}}^{(4)} $, and $ D_{\text{CS}}^{(5)} $) in the above accurate experimental cross sections are calculated using Eqs. (2)−(4) for extensive fragments with (N − Z) from –3 to 23 over a very wide range of atomic numbers (Z ≈ 3−50).

Figure 1 displays the 2D-OES magnitudes $ D_{\text{CS}}^{(2)} $ for many fragments with (N − Z) from –3 to 23, which are calculated by the 2D-OES formula [Eq. (2)] using the cross sections measured in the above-mentioned fragmentation or spallation reactions with different projectile-target combinations over a wide energy range [5−10, 17, 18, 20, 26, 55−57]. In general, the 2D-OES magnitudes obtained from different reaction systems at various energies are consistent within their uncertainties. Deviations in few experimental data can be explained by their large uncertainties. For instance, the absolute error of $ D_{\text{CS}}^{(2)} $ derived from 140 MeV/nucleon ⁴⁰Ar+Ni/Ta [57] is larger than 10% for N − Z = 9 nuclei around Z = 10, where some deviations occur. Similar to $ D_{\text{CS}}^{(3)} $, the $ D_{\text{CS}}^{(2)} $ is almost positive for all measured neutron-deficient fragments with (N − Z) from –3 to 0. Considering that the OES is mainly dominated by the lowest value from the neutron- or proton-separation energy [17, 18], this positive $ D_{\text{CS}}^{(2)} $ can be explained by a large proton separation energy for even-Z nuclei but a small one for odd-Z nuclei. Strong shell effects are clearly observed for the $ D_{\text{CS}}^{(2)} $ of N − Z = −2 nuclei near Z = 20 and N − Z = −1 nuclei at Z = 20 and 28. For neutron-rich fragments with (N − Z) from 1 to 23, the $ D_{\text{CS}}^{(2)} $ of odd-A (even-A) ones presents a transition from a large negative (positive) value to a small value around 0 as Z increases. For light neutron-rich nuclei with odd-A (e.g., N − Z = 1, 3, 5, 7, and 9), a large negative $ D_{\text{CS}}^{(2)} $ means an enhanced production of odd-Z ones and is caused by their large neutron separation energy, whereas it is small for even-Z ones. For light neutron-rich nuclei with even-A (e.g., N − Z = 2, 4, and 6), even-Z ones have a large neutron separation energy and thus show a large positive $ D_{\text{CS}}^{(2)} $. These evolution tendencies of $ D_{\text{CS}}^{(2)} $ along a constant isospin chain are almost the same as those of $ D_{\text{CS}}^{(3)} $ reported in Refs. [47, 48]. However, small local staggering structures are displayed for $ D_{\text{CS}}^{(2)} $ of some nuclei (e.g., $ D_{\text{CS}}^{(2)} $ around Z = 50 in Fig. 1), which have not been observed for $ D_{\text{CS}}^{(3)} $ [47, 48].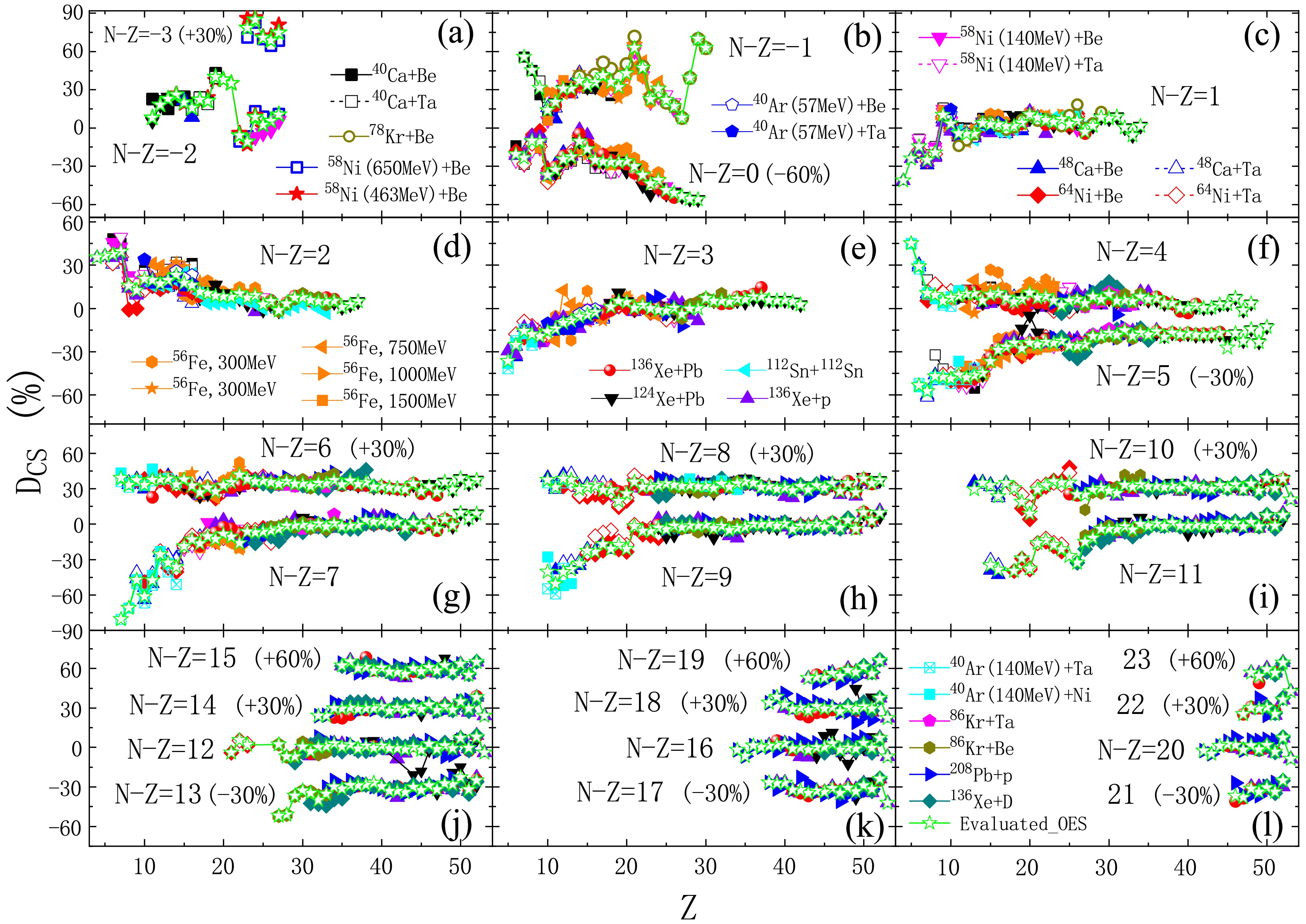

Figure 1.  (color online) Odd-even staggering (OES) magnitudes calculated by the 2D-OES formula [Eq. (2)] using isotopic cross sections measured in 28 reaction systems at different energies, i.e., 463 MeV/nucleon ⁵⁸Ni+Be [18], 650 MeV/nucleon ⁵⁸Ni+Be [26], 140 MeV/nucleon ^40,48Ca+Be/Ta [5], 140 MeV/nucleon ^58,64Ni+Be/Ta [5], ⁵⁶Fe+p at 300, 500, 750, 1000, and 1500 MeV/nucleon [6], 1000 MeV/nucleon ¹³⁶Xe+p [7], 483 MeV/nucleon ⁷⁸Kr+Be [17], 1000 MeV/nucleon ^124,136Xe+Pb [8], 1000 MeV/nucleon ¹¹²Sn+¹¹²Sn [9], 57 MeV/nucleon ⁴⁰Ar+Be/Ta [20], 64 MeV/nucleon ⁸⁶Kr+Be/Ta [55], 500 MeV/nucleon ¹³⁶Xe+d [10], 1000 MeV/nucleon ²⁰⁸Pb+p [56], and 140 MeV/nucleon ⁴⁰Ar+Ni/Ta [57]. The evaluated 2nd-order OES magnitudes (green open stars) are derived from the weighted average of the above measured OES magnitudes using Eq. (5). For clarity, experimental error bars (approximately 8% in most cases) are not shown. For N − Z = −3, 0, 5, 6, 8, 10, 13, 14, 15, 17, 18, 19, 21, 22, and 23, OES magnitudes have been shifted by the constant values given in brackets.

For the above experimental cross sections of many fragments with (N − Z) from −3 to 23, their 4D-OES magnitudes $ D_{\text{CS}}^{(4)} $ calculated by the 4D-OES formula in Eq. (3) are presented in Fig. 2. The 4D-OES magnitudes obtained from many isotopic cross sections measured in 28 different reaction systems are also in a good agreement. The evolution tendency of $ D_{\text{CS}}^{(4)} $ along a constant isospin chain is very similar to that of $ D_{\text{CS}}^{(3)} $ reported in Refs. [47, 48]. Compared to $ D_{\text{CS}}^{(2)} $ in Fig. 1, the variation of $ D_{\text{CS}}^{(4)} $ along a constant $ T_{z} $ chain is much smoother. This is reasonable because five neighboring experimental data points are used in the calculations of $ D_{\text{CS}}^{(4)} $, whereas only three neighboring ones are used in $ D_{\text{CS}}^{(2)} $ calculations.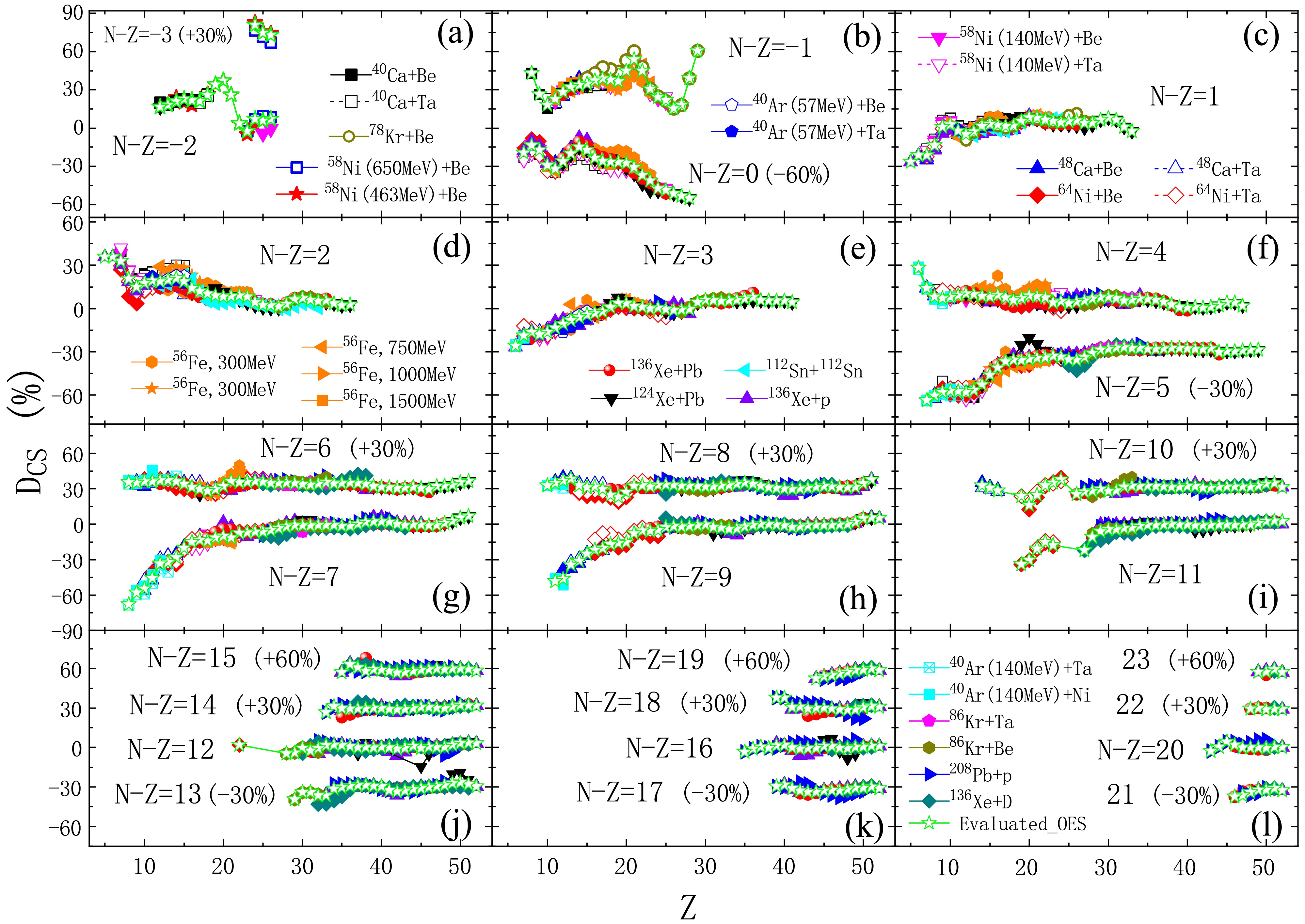

Figure 2.  (color online) Similar to Fig. 1, but for OES magnitudes calculated by the 4D-OES formula [Eq. (3)] using experimental data of 28 different reaction systems. The evaluated 4th-order magnitudes (green open stars) are obtained from the weighted average of the above measured OES values using Eq. (5). For N − Z = −3, 0, 5, 6, 8, 10, 13, 14, 15, 17, 18, 19, 21, 22, and 23, OES magnitudes have been shifted by the constant values given in brackets.

Finally, the 5D-OES formula [Eq. (4)] is also applied to calculate the 5D-OES magnitudes $ D_{\text{CS}}^{(5)} $ of the above experimental cross sections for extensive fragments with (N − Z) from −3 to 23, as shown in Fig. 3. The 5D-OES magnitudes $ D_{\text{CS}}^{(5)} $ derived from different experimental datasets agree very well with each other. The evolution tendency of $ D_{\text{CS}}^{(5)} $ along a constant isospin chain is almost the same as that of $ D_{\text{CS}}^{(4)} $ shown in Fig. 2 as well as $ D_{\text{CS}}^{(3)} $ reported in Refs. [47, 48]. Among the OES magnitudes with different orders, the 5D-OES magnitudes $ D_{\text{CS}}^{(5)} $ in Fig. 3 are the smoothest along a constant isospin chain, according to all the results shown in Figs. 1−3.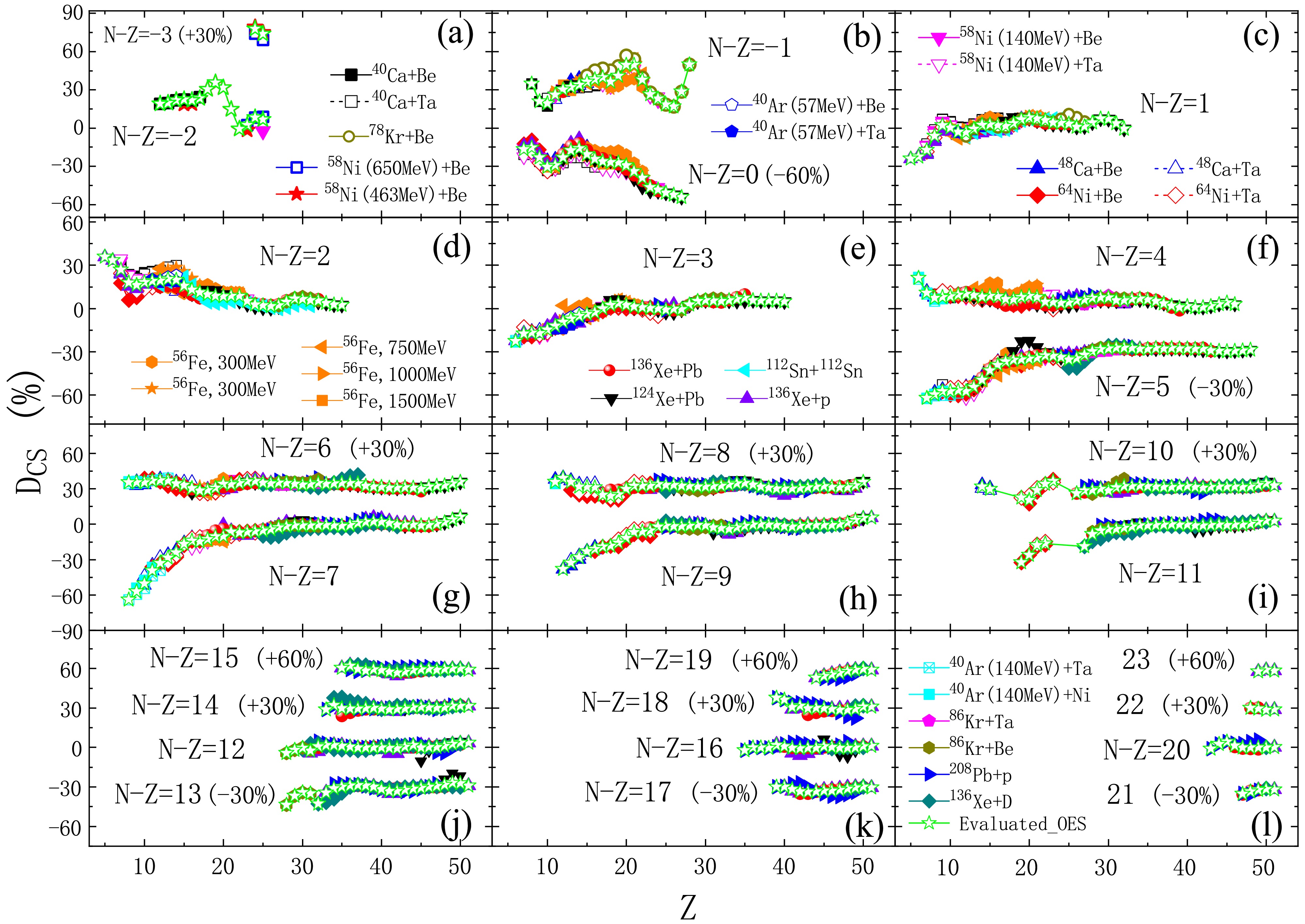

Figure 3.  (color online) Similar to Fig. 1, but for OES magnitudes calculated by the 5D-OES formula [Eq. (4)] using experimental data of 28 different reaction systems. The evaluated 5th-order magnitudes (green open stars) are calculated from the weighted average of the above measured OES values using Eq. (5). For N − Z = −3, 0, 5, 6, 8, 10, 13, 14, 15, 17, 18, 19, 21, 22, and 23, OES magnitudes have also been shifted by constant values.

All the above comparisons of the 2D, 4D, and 5D-OES magnitudes in Figs. 1, 2, and 3, respectively, derived from approximately 4200 accurate cross sections measured in 28 different fragmentation or spallation reactions over a broad energy range, support that the 2D, 4D, and 5D-OES magnitudes are almost independent of the projectile-target combinations and of the projectile energy. In other words, these 2D, 4D, and 5D-OES magnitudes, namely, $ D_{\text{CS}}^{(2)} $, $ D_{\text{CS}}^{(4)} $, and $ D_{\text{CS}}^{(5)} $, show a universality for different fragmentation and spallation reaction systems. A similar universality has also been observed in the 3D-OES magnitude investigated in Refs. [47, 48].

Quantitative evaluations of the OES magnitudes are very useful for accurately calculating cross sections of fragmentation, spallation, and projectile fission reactions using empirical formulas [54, 58] as well as some OES relations, e.g., those recently proposed by Mei [59, 60]. In our recent publications [47, 48], the 3D-OES evaluations were derived from extensive accurate experimental data, considering the universality of the 3D-OES magnitudes observed in different fragmentation and spallation reactions. In the following, similar OES investigations will be performed to obtain the 2D, 4D, and 5D-OES evaluations.

For a specific fragment with atomic number Z and neutron number N, the weighted average of the OES magnitudes in different experimental datasets is adopted as the evaluated OES magnitude, following the method used for 3D-OES evaluations in Refs. [47, 48]. The evaluated 2D, 4D, and 5D-OES magnitudes can be calculated by the following equation:

where the superscript j = 2, 4, and 5 respectively represents the order of difference. $ D^{(j)}_{i} $ and $ \sigma^{(j)}_{i} $ are the OES magnitude and its error, respectively, derived from one experimental dataset (denoted by i), and n is the total number of different experimental datasets. These evaluated 2D, 4D, and 5D-OES magnitudes are also presented in Figs. 1, 2, and 3, respectively (see the green open stars). These evaluated OES magnitudes are in an excellent agreement with the OES magnitudes derived from various experimental data, as shown in Figs. 1−3. For the evaluated OES magnitudes, an error of approximately 7% is estimated by comparing these evaluated OES magnitudes with those derived from accurate experimental data measured in different reaction systems. The OES magnitudes evaluated from extensive experimental data are very useful for accurate calculations of the isotopic cross sections with several OES relations proposed by Mei [59, 60] as well as some fragmentation and spallation models, including OES correction factors (e.g., FRACS [54] and SPACS [58]).

Finally, these evaluated 2D, 4D, 5D, and (previous) 3D-OES magnitudes are compared. The differences between these evaluated OES magnitudes are displayed in Fig. 4. The differences between the evaluated 5D and 3D-OES magnitudes ($ D_{\text{eval}}^{(5)}-D_{\text{eval}}^{(3)} $), those between the evaluated $ D_{\text{eval}}^{(4)} $ and $ D_{\text{eval}}^{(3)} $, and those between the evaluated $ D_{\text{eval}}^{(2)} $ and $ D_{\text{eval}}^{(4)} $, are shown in panels (a), (b), and (c) of Fig. 4, respectively. The absolute values of the differences between these evaluated OES magnitudes with different orders are very small, less than 5% in most cases. In addition, the distributions of ($ D_{\text{eval}}^{(5)}-D_{\text{eval}}^{(3)} $) and ($ D_{\text{eval}}^{(4)}-D_{\text{eval}}^{(3)} $) seem to be narrower than that of ($ D_{\text{eval}}^{(2)}-D_{\text{eval}}^{(4)} $). These comparisons demonstrate that the evaluated 2D, 3D, 4D, and 5D-OES magnitudes are generally consistent and all the difference formulas with different orders, namely, Eqs. (1)−(4), are applicable to the systematic OES studies of measured isotopic cross sections.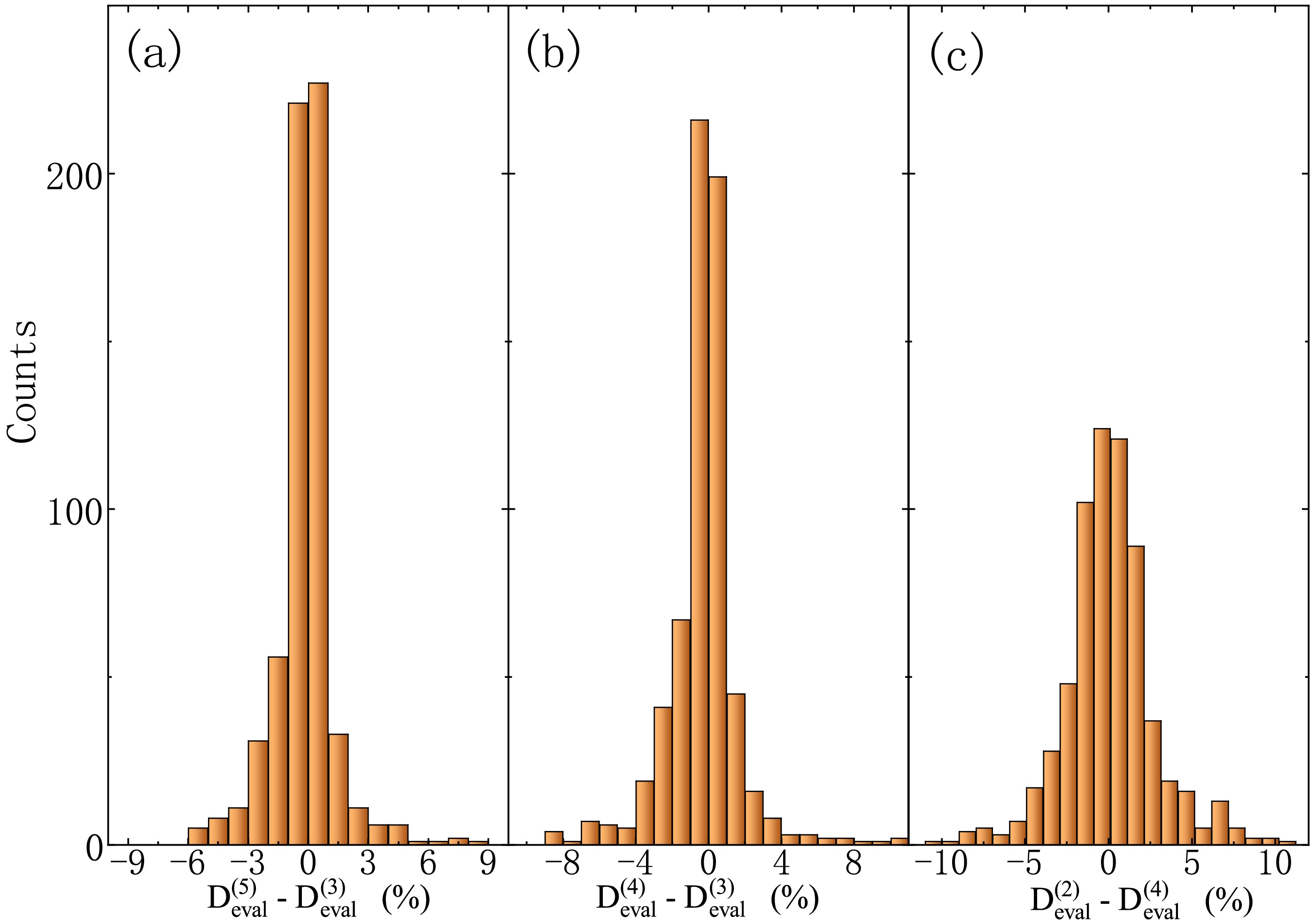

Figure 4.  (color online) (a) Differences between the evaluated 5D and 3D-OES magnitudes, namely, $ D_{\text{eval}}^{(5)}-D_{\text{eval}}^{(3)} $. (b) Differences between the evaluated 4D and 3D-OES magnitudes ones, namely, $ D_{\text{eval}}^{(4)}-D_{\text{eval}}^{(3)} $. (c) Differences between the evaluated 2D and 4D-OES magnitudes, $ D_{\text{eval}}^{(2)}-D_{\text{eval}}^{(4)} $.

In summary, three new difference formulas [Eqs. (2)−(4)] are proposed to quantitatively investigate the 2nd, 4th, and 5th-order OES magnitudes (namely, the $ D_{\text{CS}}^{(2)} $, $ D_{\text{CS}}^{(4)} $, and $ D_{\text{CS}}^{(5)} $, respectively) in extensive experimental cross sections. Approximately 4200 accurate cross sections measured in 28 different fragmentation or spallation reactions over a wide energy range are used to validate these formulas. Comparisons of the $ D_{\text{CS}}^{(2)} $, $ D_{\text{CS}}^{(4)} $, and $ D_{\text{CS}}^{(5)} $ derived from different reaction systems confirm that these OES magnitudes with different orders seem to be universal for different reaction systems at various energies, which was first observed for the $ D_{\text{CS}}^{(3)} $ in our previous works [47, 48]. Additionally, the 2nd, 4th, and 5th-order OES evaluations (i.e., $ D_{\text{eval}}^{(2)} $, $ D_{\text{eval}}^{(4)} $, and $ D_{\text{eval}}^{(5)} $) are calculated by Eq. (5) using the OES magnitudes, namely, $ D_{\text{CS}}^{(2)} $, $ D_{\text{CS}}^{(4)} $, and $ D_{\text{CS}}^{(5)} $, respectively, extracted from many accurate experimental data measured in different reaction systems over a broad energy range. Finally, the 2nd, 4th, 5th, and (previous) 3rd-order OES evaluations are also compared. These comparisons indicate that the OES evaluations with different orders are generally in a good agreement and that all the difference formulas with different orders are very suitable for systematic investigations of the OES in isotopic cross sections. These evaluated OES magnitudes with different orders can be applied to accurately calculate cross sections of fragmentation, spallation, and projectile fission reactions by using some OES relations, e.g., four OES relations recently proposed by Mei [59, 60], as well as some empirical formulas including OES factors, e.g., FRACS [54] and SPACS [58].