-
One of the current problems of modern high-energy physics is the study of strong interactions at extremely high temperatures and energy densities reached in relativistic heavy-ion collisions (for a recent review, see for instance [1] and references therein). This includes the investigation of properties of created quark-gluon plasma (QGP) and dynamics of quark-hadron phase transition, as well as the analysis of the mechanisms of multiparticle production. The particular interest of this subject is conditioned by the intensive experimental studies conducted at the Large Hadron Collider (LHC). The maximum energies currently achieved in laboratory conditions at the LHC allow for probing the high-temperature QGP state, whose properties are similar to those of ''proto-matter'' in Early Universe. Future experiments with heavy-ion beams at intermediate energies in Nuclotron-based Ion Collider fAcility (NICA) and Facility for Antiproton and Ion Research (FAIR) are expected to have a significant impact on the study of dynamics of the quark-hadron phase transition, including search for the ''critical point'', near their boundary. Both aforementioned tasks are complementary.
Among various physical observables, event-by-event (EbyE) fluctuations of conserved quantities such as net-baryon, net-strangeness, and net-electric charge are considered sensitive tools to characterize the thermodynamic properties and critical behavior of hot and dense matter produced in relativistic heavy-ion collisions [2, 3]. In particular, the net-charge fluctuations are proportional to the square of the charges in the system, and may be quantified in terms of D [4, 5] and Σ [6−8] variables.
A dramatic decrease of the EbyE fluctuations of the net charges in local regions of a phase space was predicted by many theoretical investigations [2, 4, 9, 10] as a prominent signal of QGP formation, provided that the final-state charge fluctuations survive the hadronization. Note that these fluctuations are related to the charge distribution in the plasma state and not to the phase transition from plasma to hadrons. The main question is how and why the initial distributions can survive during the QGP hadronization stage [11, 12].
Experimental studies of net-charge fluctuations in heavy-ion collisions, including measurements of their dependencies on rapidity interval and event centrality, were conducted by the NA49 Collaboration at CERN Super Proton Synchrotron (SPS) [13, 14], STAR Collaboration at BNL Relativistic Heavy Ion Collider (RHIC) [15], and ALICE [16, 17] and CMS [18] Collaborations at CERN LHC. The corresponding experimental data are poorly described by existing theoretical models.
In the present study, phenomenological analysis of
$\rm Pb$ +$\rm Pb$ data for net-charge fluctuations at LHC energies was performed in terms of the strongly intensive quantities D and Σ. The advantage of using these strongly intensive quantities is that they are independent of both system volume and fluctuations [6, 7]. The paper is organized as follows. To simulate heavy-ion collisions, we selected the two-component Monte Carlo HYDJET++ model [19]. Their final state represents a superposition of the soft-“thermal” and hard states resulting from multi-parton fragmentation. Recently [20], we presented a modification of this model through the inclusion of explicit event-by-event charge conservation using a statistical approach. This modification allows for describing the experimentally observed centrality dependence of widths of the charge balance function in$\rm Pb$ +$\rm Pb$ collisions at the LHC center-of-mass energy of 2.76 TeV per nucleon pair. Basic features of the default version of HYDJET++ and its modification for exact EbyE charge conservation are presented in Sec. II. Section III discusses the relation between the charge balance function and net-charge fluctuations, first established in [5]. In Sec. IV, the results obtained for the net-charge fluctuations in$\rm Pb$ +$\rm Pb$ collisions at a center-of-mass energy of 5.02 TeV per nucleon pair using the HYDJET++ model are compared with ALICE data [17] and with the predictions of other Monte Carlo models, such as HIJING [21−23] and AMPT [24−26]. Conclusions are drawn in Sec. V. -
The HYDJET++ model (Hydrodynamics with JETs) was designed as a Monte Carlo (MC) event generator [19, 27] for simulation of heavy-ion collisions at (ultra)relativistic energies. It consists of two parts describing the soft and hard processes, respectively. The soft sector of HYDJET++ is the adapted version of the FASTMC model [28, 29] and represents a relativistic hydrodynamic parametrization of hypersurfaces of chemical and thermal freeze-out under given freeze-out conditions. Although the model includes the option that both freeze-outs can occur simultaneously in a single freeze-out scenario, much better agreement with experimental data is obtained in a scenario with separated chemical and thermal freeze-outs. The simulation of a single event begins by calculating the effective fireball volume
$V_{\rm eff}$ , which depends on the mean number of participating nucleons for a given impact parameter b, i.e., the collision centrality. This impact parameter is determined from the Glauber multiple scattering model. For the most appropriate scheme with separate freeze-outs, the composition of particles in the system is frozen at the chemical freeze-out stage according to the predictions of statistical thermal models [30, 31]. The system continues to expand and cools to the point of thermal freeze-out, where the mean free path of hadrons exceeds the size of the system. At this stage, two- and many-body decays of resonances are taken into account as final state interactions (FSIs). The table of resonances included in HYDJET++ from the model SHARE [32] is notably rich. It contains more than 360 mesonic and baryonic states, including the charmed ones. To manage the decays of resonances, HYDJET++ employs its own original routine.The hard sector of the model deals with the propagation of hard partons through an expanding quark-gluon plasma. The approach, which takes into account both gluon radiation due to parton rescattering and partonic collisional losses, is based on the PYQUEN (PYTHIA QUENched) model of parton energy losses [33]. The number of jets is generated in accordance with a binomial distribution, whereas their average number in a nuclear collision with a given impact parameter b is calculated as a product of the number of binary nucleon-nucleon (NN) collisions and integral cross-section of the hard process in NN collisions with minimum transverse momentum transfer
$p_T^{\rm min}$ . This is an important free parameter of the HYDJET++ model, because partons created in (semi) hard subprocesses with momentum transfer below$p_T^{\rm min}$ are considered to be in thermal equilibrium. The products of their hadronization are added to the spectra of soft particles.The simultaneous consideration of soft and hard processes allows HYDJET++ to describe aspects such as centrality and transverse momentum dependence of the differential elliptic and triangular flow of hadrons in heavy-ion collisions at energies of RHIC and LHC [34−36], violation of the mass hierarchy and violation of the constituent quark scaling (NCQ) of these differential flows at intermediate and high values of
$ p_T $ [35, 37, 38], peculiarities of factorization of dihadron angular harmonics (ridge) [39], and higher flow harmonics [35, 38] and their EbyE fluctuations [40]. However, to reproduce both the centrality dependence and the width of the balance functions of charged particles, the model requires modification. -
The generation of hadron species in the soft sector of HYDJET++ proceeds within the framework of the grand canonical ensemble (GCE), similar to other statistical models of hadron-resonance gas. Therefore, the correlations between hadrons arise because of decays of resonances and jet fragmentation. These correlation mechanisms appear insufficient to describe features of the balance functions of charged hadrons in
$\rm Pb$ +$\rm Pb$ collisions at LHC energies. To reproduce this signal, the model was extended in [20]. The modified version of HYDJET++ takes into account exact conservation of the net electric charge in the system of colliding nuclei on the EbyE basis.Next, we describe the algorithm for the hadronic system with zero net electric charge. All hadrons of the soft component are generated according to the GCE prescription, i.e., unlike-sign charges are initially uncorrelated. Then, half of the charged hadrons are randomly discarded. A Monte Carlo realization of this procedure assumes that each directly produced charged hadron is either removed with probability 50% from the particle spectrum or remained untouched. Then, for each of the remaining hadrons, its counterpart with opposite electric charge and similar transverse momentum is generated. As reported in [20], this procedure does not change the pseudorapidity, angular, and transverse momentum spectra of charged particles for statistics of at least 1000 events. The azimuthal angle
$ \phi_2 $ and rapidity$ \eta_2 $ of newly produced particles are distributed around the azimuthal angle$ \phi_1 $ and rapidity$ \eta_1 $ of the initial hadron following a Gauss normal distribution,$ { } P_{\mu,\sigma}(x) = \frac{1}{\sqrt{2 \pi} \sigma} \exp{\left[ - \frac{(x - \mu)^2}{2 \sigma^2} \right]} \ , $

(1) where
$ x = (\phi_2,\eta_2) $ ,$ \mu = (\phi_1,\eta_1) $ , and$ \sigma = (\sigma_\phi, \sigma_\eta) $ . Both dispersions,$ \sigma_\phi $ and$ \sigma_\eta $ , characterize the strength of the charge correlations of the produced hadrons. Their values are free parameters of the modified model and should be fixed by comparison with the available experimental data on the balance functions. The described procedure is relevant for the midrapidity region of heavy-ion collisions at RHIC and LHC energies. For lower energies, this procedure was recently generalized to systems with non-zero net electric charge [41]. -
Concerning HIJING (Heavy Ion Jet INteraction Generator) [21−23], it is a Monte Carlo event generator designed for description of jet and mini-jet production, and associated particle production in high energy hadronic (
$ hh $ ), hadron-nucleus ($ hA $ ), and nuclear (A+A) collisions. Recall that jets with large transverse momenta are one of the hard probes of heated nuclear matter. The sources of these jets are particles that arise during the hadronization of quarks and gluons. Before hadronization, quarks and gluons propagate in the nuclear medium, which can include both hadrons and a quark component. In this case, the energy loss of a quark during collisions with particles of the medium and during bremsstrahlung depends on the properties of the medium. This phenomenon, known as “jet quenching", can serve as a signature of quark-gluon plasma. Another important process is the formation of mini-jets. It is estimated that mini-jets contribute up to 50% of the transverse energy in central collisions of heavy ions. Mini-jets with medium transverse momenta have shorter path lengths in the parton medium and are more likely to dissipate in the background, losing memory of the initial correlations and changing their characteristics when interacting with the medium. Thus, HIJING incorporates several mechanisms such as multiple mini-jet production, soft excitation, nuclear shadowing of parton distribution functions, and jet interactions in dense hadronic matter.To describe hadron production in relativistic collisions, HIJING relies on a two-component model developed initially for
$ hh $ interactions [42−45] and extended to A+A collisions [46−48]. This two-component model treats the parton interactions in high-energy$ hh $ collisions as (semi-)hard with jet production if the transverse momentum of the jet is larger than the characteristic cut-off parameter$ p_0 $ , and as soft in the opposite case. To generate kinematic variables for each hard scattering, HIJING uses subroutines of PYTHIA [44, 49], whereas for string fragmentation JETSET routine [50] of the Lund model [51, 52] is employed. Further details of the model can be found in [21−23].Regarding AMPT (A Multi-Phase Transport) [24−26], it is a hybrid transport model designed for the description of
$ pA $ and A+A collisions at relativistic and ultra-relativistic energies. It consists of four main parts. To generate the initial conditions, such as production of hard mini-jet partons and soft strings, the model employs results from HIJING. The further rescattering of partons is governed by Zhang's parton cascade (ZPC) [53], which manages the two-body parton interactions within the framework of perturbative quantum chromodynamics (pQCD). Two scenarios are used to hadronize partons when they stop interacting. In the first scenario, partons are recombined with parent strings, which convert into hadrons according to the Lund fragmentation model [51, 52]. The second scenario assumes the melting of strings into partons at the initial stage and hadronization of partons at the end of the parton cascade within the quark coalescence model. Finally, hadronic matter propagates and develops a hadron cascade described by the ART (A Relativistic Cascade) model [54, 55].In our calculations, we used the AMPT model with string melting. Other parameters of the model were extracted from [56].
-
In relativistic heavy-ion collisions, one can denote the net charge as
$ Q = N_+ - N_- $ , the total number of charged particles as$N_{\rm ch} = N_+ + N_-$ , and the ratio of positive to negative charges as$ R = \dfrac{N_+}{N_-} $ . Then, the following relation between the variances$ \langle \delta R^2 \rangle $ and$ \langle \delta Q^2 \rangle $ can be established, provided that$\langle N_{\rm ch} \rangle \gg \langle Q \rangle$ [4]:$ { } \langle N_{\rm ch}\rangle \langle \delta R^2 \rangle = D = 4 \frac{\langle \delta Q^2 \rangle}{\langle N_{\rm ch} \rangle} \ . $

(2) Here, D is the final observable measure of fluctuations [2, 4]. This measure can be linked to the event-by-event fluctuations by calculating the second moment, which is the difference between the relative charged particle multiplicities
$ \nu_{+-} $ and statistical fluctuations$ \nu_{+-,\text{stat}} $ $ { } \nu_{+-,\text{dyn}} = \nu_{+-} - \nu_{+-,\text{stat}} \ , $

(3) $ \nu_{+-} = \left\langle \left( \frac{N_+}{\langle N_+ \rangle} - \frac{N_-}{\langle N_- \rangle} \right)^2 \right\rangle \ , $

(4) $ \nu_{+-,\text{stat}} = \frac{1}{\langle N_+ \rangle} + \frac{1}{\langle N_- \rangle} \ . $

(5) Therefore, the fluctuation measure D is expressed as [4]
$ { } D = 4 \frac {\langle \delta Q^2 \rangle} {\langle N_{\rm ch} \rangle} = \langle N_{\rm ch} \rangle \nu_{+-,\text{dyn}} + 4 \ . $

(6) From Eqs. (3) and (4), we can derive another expression for
$ \nu_{+-,\text{dyn}} $ $ { } \nu_{+-,\text{dyn}} = \frac{\langle N_+^2 \rangle - \langle N_+ \rangle} {\langle N_+ \rangle^2} + \frac{\langle N_-^2 \rangle - \langle N_- \rangle} {\langle N_- \rangle^2} - 2 \frac{\langle N_+ N_- \rangle}{\langle N_+ \rangle \langle N_- \rangle} \ , $

(7) which means that the correlations are negative when the covariance term dominates.
Another measure is the strongly intensive quantity (SIQ), suggested in [6] for the analysis of particle multiplicity correlations and fluctuations in high-energy A+A collisions. It characterizes the second moment of random extensive variables used to study fluctuations and correlations in a physical system.
For two extensive quantities A and B, the strongly intensive quantity
$ \Sigma [A,B] $ reads$ { } \Sigma [A,B] = \frac{1}{C_\Sigma} \bigg[ \langle B \rangle \omega[A] + \langle A \rangle \omega[B] - 2(\langle AB \rangle - \langle A \rangle \langle B \rangle ) \bigg] \ , $

(8) where
$ { } \omega[A] = \frac{\langle A^2 \rangle - \langle A \rangle^2} {\langle A \rangle}\ , \quad \omega[B] = \frac{\langle B^2 \rangle - \langle B \rangle^2} {\langle B \rangle} \ . $

(9) For particle charged multiplicities
$ A = N_+ $ and$ B = N_- $ , we have$ C_\Sigma = \langle N_+ \rangle + \langle N_- \rangle $ and$ \begin{aligned}[b] \Sigma [N_+, N_-] =\;& \left\{ \langle N_-\rangle \frac{\langle N_+^2\rangle - \langle N_+ \rangle^2}{\langle N_+ \rangle} + \langle N_+ \rangle \frac{\langle N_-^2\rangle - \langle N_- \rangle^2}{\langle N_- \rangle } -\right. \\ &\bigg. - 2 (\langle N_+ N_- \rangle - \langle N_+ \rangle \langle N_- \rangle ) \bigg\} \bigg/ \bigg( \langle N_+ \rangle + \langle N_- \rangle \bigg) \ . \end{aligned} $

(10) Comparing this with the result obtained using Eq. (7), we have that
$ { } \frac{\langle N_+ \rangle + \langle N_- \rangle }{\langle N_+ \rangle \langle N_- \rangle} (\Sigma [N_+, N_-] - 1) = \nu_{+-,\text{dyn}} \ . $

(11) It is possible to demonstrate that the strongly intensive quantity
$ \Sigma [N_+, N_-] $ is related to the integral of the balance function$ B(\Delta\eta) $ [20] through the equation$ { } \Sigma [N_+, N_-] = 1 - \int B(\Delta\eta){\rm d}\Delta\eta \ . $

(12) Here, we define the charge balance function as
$ { } B(\Delta\eta) = \frac{1}{2}\left\{\frac{\langle N_{+-} \rangle - \langle N_{++} \rangle}{\langle N_+ \rangle} + \frac{\langle N_{-+}\rangle - \langle N_{-} \rangle} {\langle N_- \rangle}\right\}\ , $

(13) where
$ N_{+-} = N_{+-}(\Delta\eta) $ is the number of pairs of unlike-sign charged particles separated by the relative pseudorapidity$ \Delta\eta $ , and$ N_+ $ is the number of positively charged particles within pseudorapidity window$ |\eta| < H $ . Other terms in Eq. (13) are defined similarly. From this point onward, we assume that within the rapidity window,$ \langle N_+ \rangle = \langle N_- \rangle = \dfrac{\langle N_\text{ch} \rangle}{2} $ ; thus, Eq. (13) can be integrated over$ \Delta\eta $ and reduced to$ \int B(\Delta\eta){\rm d}\Delta\eta = \frac{1}{\langle N_\text{ch} \rangle} \bigg\{2 \langle N_{+-} \rangle - \langle N_{++} \rangle - \langle N_{-}\rangle\bigg\} \ , $

(14) where the number of charged particle pairs no longer depends on the relative rapidity. Under the same assumption of charge balance, the term
$ \Sigma[N_+, N_-] - 1 $ in Eq. (10) can be rewritten using relations$ \langle N_{+-} \rangle = \langle N_+N_- \rangle $ ,$ \langle N_{++} \rangle = \langle N_+(N_+ - 1) \rangle $ etc., and simplified as$ \begin{aligned}[b] \Sigma[N_+, N_-] - 1 =\;& \frac{\langle N_+ \rangle \langle N_- \rangle}{\langle N_+\rangle + \langle N_- \rangle} \\&\times \left\{\frac{\langle N_{++} \rangle}{\langle N_+\rangle^2} + \frac{\langle N_{-} \rangle}{\langle N_- \rangle^2} - 2 \frac{\langle N_+N_- \rangle}{\langle N_+\rangle \langle N_-\rangle}\right\} \\ =\;& \frac{1}{\langle N_\text{ch}\rangle}\bigg\{ \langle N_{++}\rangle + \langle N_{-}\rangle - 2\langle N_{+-}\rangle\bigg\} \ . \end{aligned} $

(15) Note that combining Eqs. (14) and (15), Eq. (12) is obtained.
An important property of a strongly intensive quantity is its independence on volume and volume fluctuations. It is worth noting that
$ \Sigma[N_+, N_-] $ is equal to unity in case of independent emission of particles in the so-called independent particle model [7, 8].The D and Σ variables measure both net-charge fluctuations and correlations. Some apparent sources of correlations are resonance decays in final state and production of (mini)jets, which are not thermalized in QGP. Moreover, the trivial correlations of particles caused by charge conservation have to be accounted for, given that the predictions for the magnitudes of fluctuations were derived using a grand canonical ensemble where charge is conserved on average. The correction for global charge conservation of
$\nu_{(+-,{\rm dyn})}$ proposed in [5] reads$ \nu_{+-,\text{dyn}}^\text{corr} = \nu_{+-,\text{dyn}} + \frac{4}{\langle N_{\rm tot} \rangle}\ , $

(16) where
$\langle N_{\rm tot} \rangle$ is the total charged multiplicity in full phase space. Another approach to correct the D magnitude is derived in [9],$ D^{\text{corr}} = (\nu_{+-,\text{dyn}}\langle N_{\rm ch}\rangle + 4)/ (C_{\mu}C_{\eta}) \ , $

(17) where
$ C_{\mu} = \langle N_{+}\rangle^{2} /\langle N_{-}\rangle^{2} $ and$C_{\eta} = 1- \langle N_{\rm ch}\rangle /\langle N_{\rm tot}\rangle$ . -
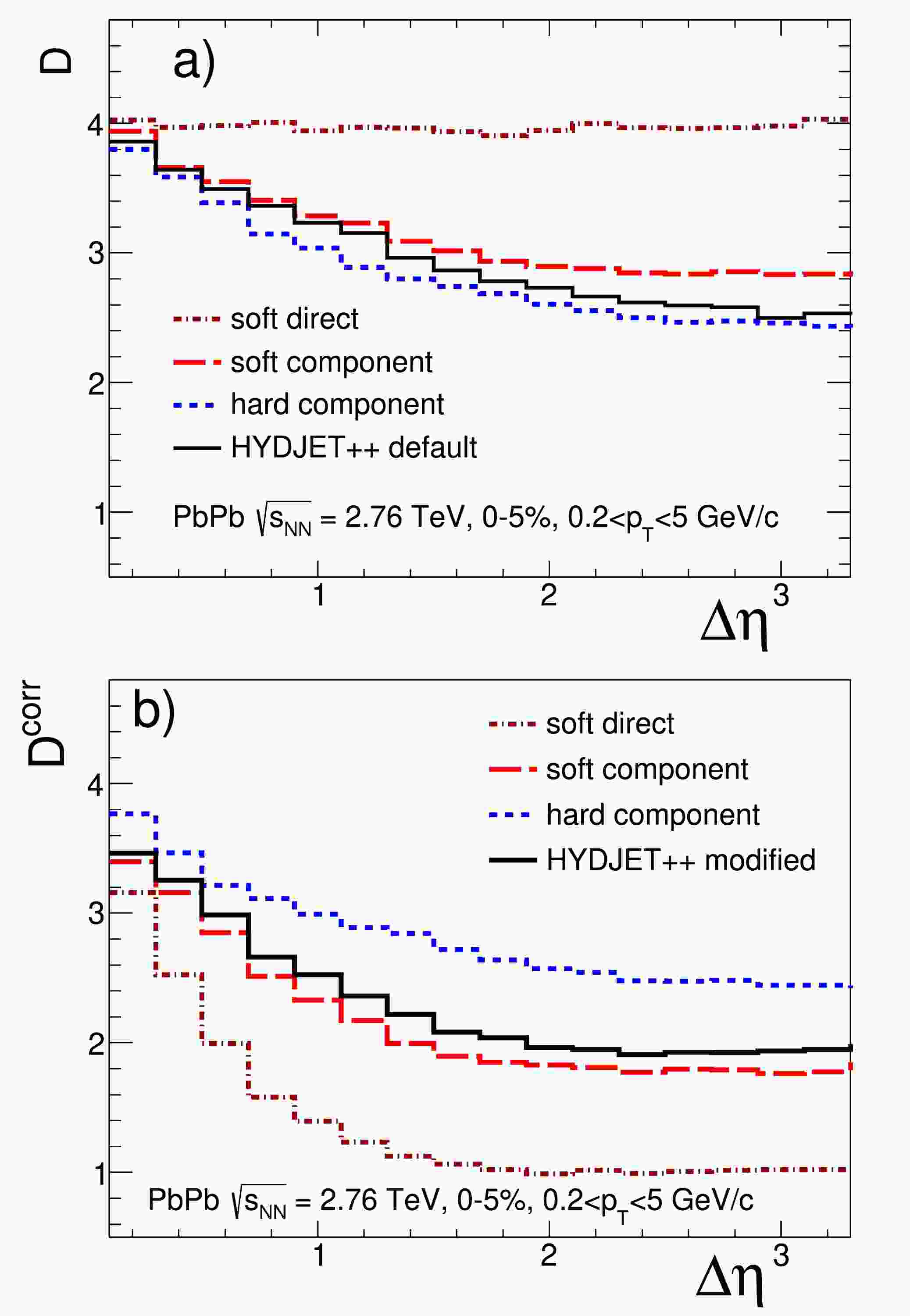
The soft part of the HYDJET++ model represents a grand canonical ensemble. Thus, the correction for global charge conservation is not needed. The primordial, or direct, hadron production in the soft component corresponds to independent particle emission and is expected to be similar to the D value predicted for a hadron gas, i.e.,
$ D = 4 $ or$ \Sigma = 1 $ . This is observed in Fig. 1(a) for the directly produced hadrons. The correlations of charged hadrons in jets are stronger than those for resonances, and typically result in even smaller values of D (Σ). Note, however, that the hard component of HYDJET++ is corrected for global charge conservation during the jet fragmentation process (see Eq. (16)). The correction is more dramatic for larger phase space. We checked that the hard component of the D-measure exhibits low sensitivity to partial thermalization owing to jet quenching and to the electrical charge of the initial parton, gluon or quark.
Figure 1. (color online) D and
$D^{\rm corr}$ represented as a function of the$\Delta\eta$ window for the HYDJET++ model-generated Pb+Pb collisions at$\sqrt s = 2.76$ TeV with centrality of 0−5% for each component: soft (red dashed line), hard (blue dotted line), for direct soft hadrons (brown dash-dotted line) together with the resulting total value (full black line); (a) HYDJET++ calculations in default mode; (b) modified model calculations.Some models experience difficulties to describe the data. Model calculations usually provide higher values of D (Σ). Moreover, experimental results exhibit centrality dependence not reproduced by the models. The low value of D may arise either from the small net-charged fluctuations due to more uniformly distributed charges in a QGP or from the strong
$ (+-) $ correlations. The modifications in the HYDJET++ model were introduced to describe the width of the experimental BF. In particular, the$ (+-) $ pair production of direct hadrons was employed in the soft component, implying strong correlations (with short correlation length) among unlike-sign charged hadrons. Such correlations sufficiently reduce the values of D, as shown in Fig. 1(b). Note that, in this case, the resonance decays dilute the correlations, thus increasing the D magnitude, in contrast to the situation with hadron gas, where resonance decays decrease the D magnitude. This effect of resonance decays may also be valid for the case of QGP fluctuations. Therefore, the magnitude of fluctuations for the QGP may be increased by● resonance decays in the final state
● contribution of non-thermalized, or partially thermalized, hard mini-jets, which are still present within the considered low
$ p_{T} $ interval,$ 0.2 < p_{\rm{T}} < 5 $ GeV/c.To date, the corrected values of D experimentally measured are larger than the expectations for QGP.
Collisions of lead beams at the LHC give rise to events with the highest multiplicity of produced particles. A comparison of the AMPT, HIJING, and HYDJET++ models with the experimental values of
$ D^{\text{corr}}(\Delta\eta) $ in central 0−5% Pb+Pb collisions at$ \sqrt{s} = 2.76 $ TeV [16] is depicted in Fig. 2(a). The$ 0.2 < p_{\rm{T}} < 5 $ GeV/c transverse momentum range was used in the calculations, similar to the experimental data. Note that the HIJING and modified HYDJET++ models are corrected for global charge conservation, while the AMPT and HYDJET++ default models are not corrected, given that the global electric charge is not conserved, in general, in each individual event. For instance, as pointed out in [57, 58], violation of the electric charge conservation in the AMPT model occurs because of two reasons. One reason is that, in some many-body decays of resonances and many hadronic interactions, the electric charge of each hadron in the final state is set randomly [57]. The second reason is that the hadronic cascade in the ART model treats only charged kaons as explicit particles, discarding the neutral ones.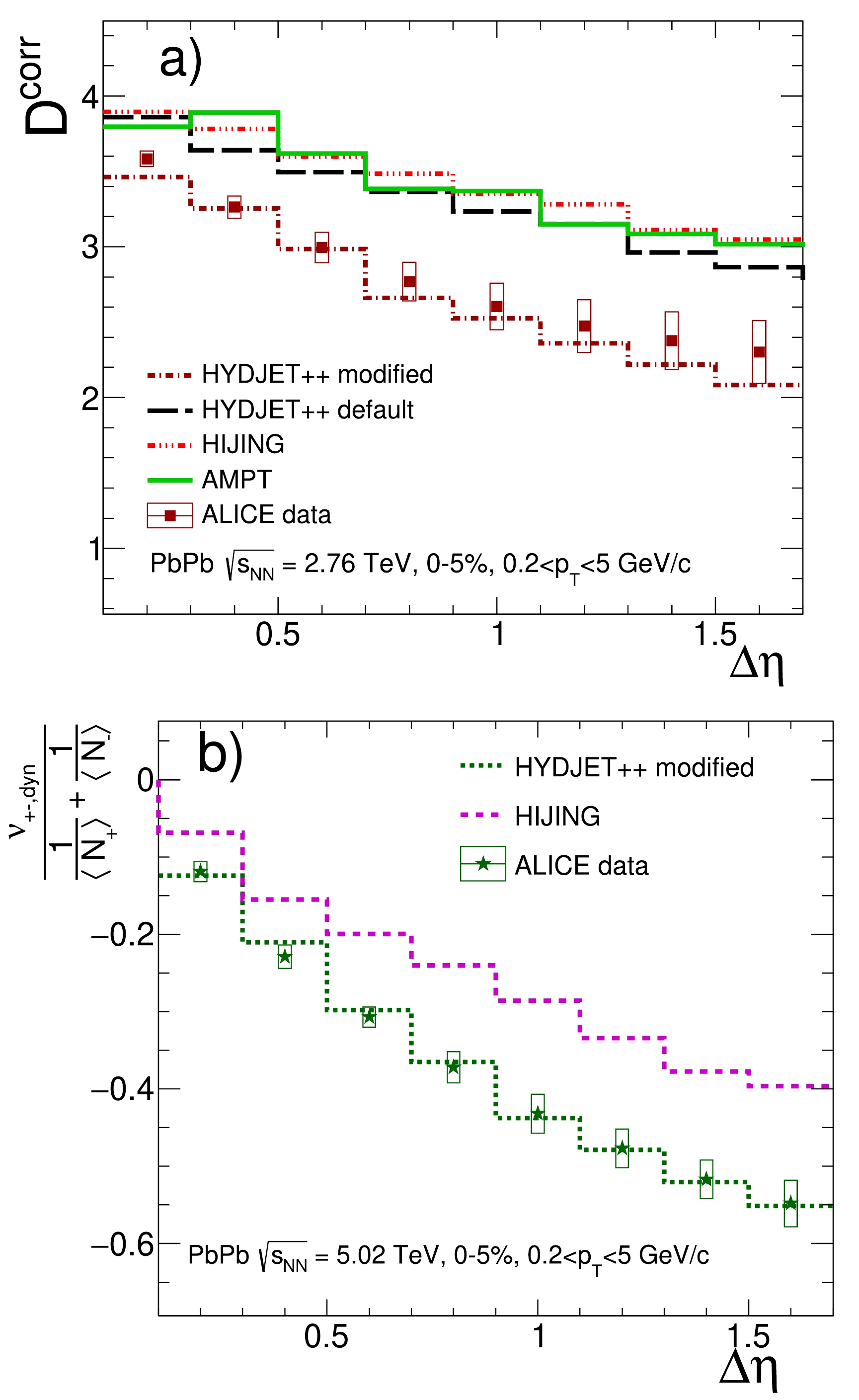
Figure 2. (color online) (a) D and
$D^\text{corr}$ represented as a function of the$\Delta\eta$ window for the HYDJET++ (dashed histogram), HYDJET++ modified (dash-dotted), AMPT (full), and HIJING (dotted-dash) model-generated Pb+Pb collisions at 2.76 TeV with centrality of 0−5%, in comparison with data (squares). These data were extracted from [16]; (b)$ \nu_{+-,\text{dyn}}\,\bigg/ \left( \dfrac{1} {\langle N_+\rangle} + \dfrac{1}{\langle N_-\rangle} \right) $ as a function of$\Delta\eta$ for the HYDJET++ modified (dotted histogram) and HIJING (dashed) model-generated Pb+Pb collisions at 5.02 TeV with centrality of 0−5% in comparison with data (stars) extracted from [17].The corrected values of
$ D^{\text{corr}} $ were obtained as averaged values provided by Eqs. (16) and (17), as performed for experimental data processing. A comparison of model results with experimental$ \Sigma -1 $ values, expressed as$ { } \nu_{+-,\text{dyn}}\,\bigg/ \left( \dfrac{1} {\langle N_+\rangle} + \dfrac{1}{\langle N_-\rangle} \right) $ for central 0−5% Pb+Pb collisions at$ \sqrt{s} = 5.02 $ TeV [17], is presented in Fig. 2(b).A comparison with experimental centrality dependence of measured fluctuation values (D and
$ \Sigma-1 $ ) for Pb+Pb collisions at$ \sqrt{s} = 2.76 $ TeV [16] and$ \sqrt{s} = 5.02 $ TeV [17] is displayed in Fig. 3. The centrality dependence in ALICE data is represented as a function of$ \langle N_{\rm part}\rangle $ and$\langle {\rm d}N_{ch}/{\rm d}\eta\rangle$ . The model results correspond to centralities of 0−5%, 20%−30%, and 50%−60%, respectively. The pseudorapidity windows are chosen to be symmetric around$ \eta = 0 $ . Note that the results for the$ { } \nu_{+-,\text{dyn}}\,\bigg/ \left( \dfrac{1} {\langle N_+\rangle} + \dfrac{1}{\langle N_-\rangle} \right) $ variable for both AMPT and default HYDJET++ models are not shown here because the data are not corrected for global charge conservation. Note also that the HYDJET++ model with modifications qualitatively describes the data. The strength of pair correlations was adjusted to describe the BF widths, whereas the D-measure is connected to the integral of the balance function, where both the width and amplitude of BF are important. To quantitatively describe the data, the strength of the pair correlations$ weta \equiv \sigma_{\eta} $ (see Eq. (1)) was reduced as listed in Table 1.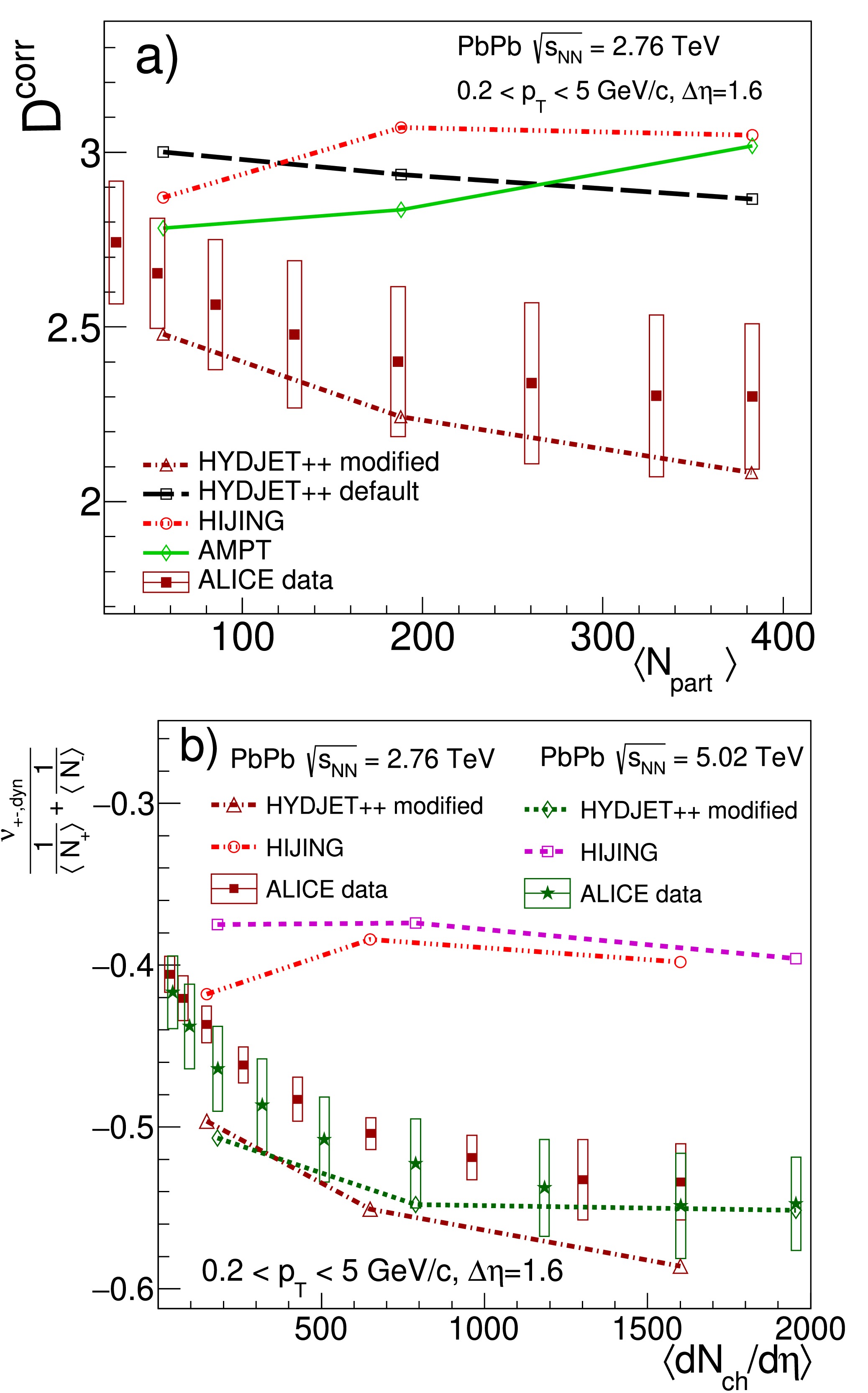
Figure 3. (color online) (a) D and
$D^\text{corr}$ represented as a function of$N_{\rm part}$ for the HYDJET++ (open squares), HYDJET++ modified (open triangles), AMPT (open diamonds), and HIJING (open circles) model-generated Pb+Pb collisions at 2.76 TeV in comparison with ALICE data (full squares) extracted from [16]; the lines are drawn to facilitate visualization; (b)$ \nu_{+-,\text{dyn}}\,\bigg/ \left( \dfrac{1} {\langle N_+\rangle} + \dfrac{1}{\langle N_-\rangle} \right) $ represented as a function of$\Delta\eta$ for the HYDJET++ modified (open triangles and open diamonds) and HIJING (open circles and open squares) model-generated Pb+Pb collisions at 2.76 TeV and 5.02 TeV, respectively, in comparison with ALICE data (full squares and full stars) extracted from [16] and [17]; again, the lines are drawn to facilitate visualization.Centrality 0−5% 20%−30% 50%−60% HYDJET++ modified weta 0.35 0.5 1 HYDJET++ new tune weta 0.5 0.7 1.1 Table 1. Values of previous and newly tuned parameter weta.
Results of calculations made with previous and newly tuned parameters are displayed in Fig. 4. The HYDJET++ model adequately reproduces experimental data both for
$ D^{\text{corr}} $ and$ \Sigma[N_+, N_-] - 1 $ . Therefore, it can be concluded that the main shortcoming of various models when it comes to reproducing data is either the use of a grand canonical ensemble to describe multiparticle production, which is the case of macroscopic statistical models (e.g., HYDJET++ default), or the random distribution of electric charge for secondary hadrons in microscopic transport models (e.g., AMPT). To solve this problem, it is necessary to take into account the pair production of hadrons of opposite sign (HYDJET++ modified).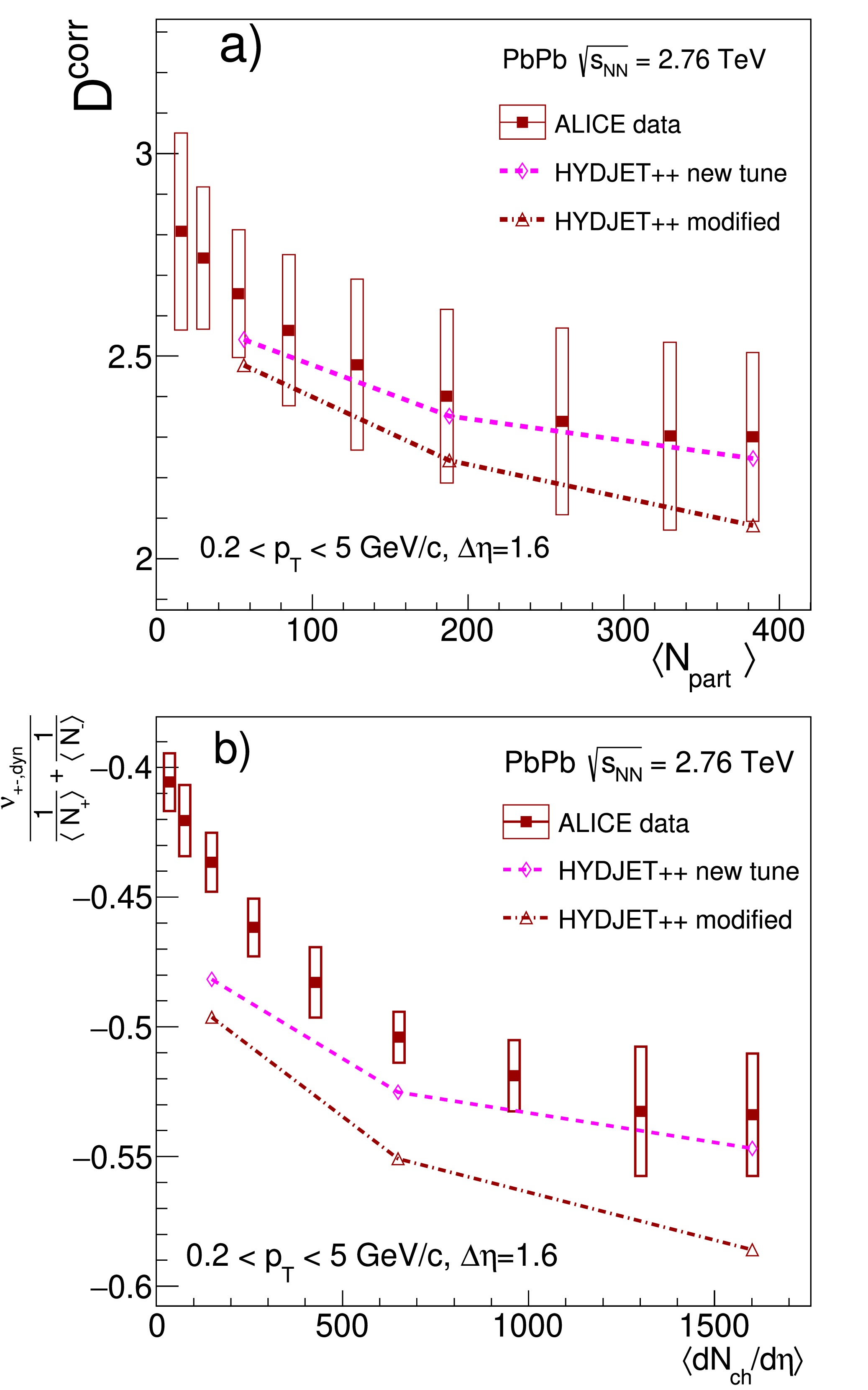
Figure 4. (color online) Same as Fig. 3, but with reduced correlation strength in the HYDJET++ model. Please, refer to the main text for further details.
We also checked that the new parametrization does not affect the widths of the balance functions of charge particles studied using the HYDJET++ model [20]. Recall that the charge balance function is defined as
$ B(\Delta \eta) = \frac{1}{2} \Big[\frac{\langle N_{+-}(\Delta \eta) \rangle - \langle N_{++}(\Delta \eta)\rangle }{\langle N_+ \rangle } + \frac{\langle N_{-+}(\Delta \eta)\rangle - \langle N_{-}(\Delta \eta) \rangle }{\langle N_- \rangle }\Big]\ , $

(18) where
$ \langle N_{+-}(\Delta \eta) \rangle $ is the average number of unlike-charge pairs with particles separated by the relative pseudorapidity$ \Delta \eta = \eta_{+}-\eta_{-} $ , and this is also the case for$ \langle N_{-+}(\Delta \eta) \rangle $ ,$ \langle N_{++}(\Delta \eta) \rangle $ , and$ \langle N_{-}(\Delta \eta) \rangle $ .Variations of the width of the balance function of charged hadrons for the correlations studied as functions of relative pseudorapidity
$ \Delta \eta $ with centrality in${\rm Pb}$ +${\rm Pb}$ collisions at$ \sqrt{s} = 2.76 $ TeV are shown in Fig. 5. Note that the deviations of model calculations with newly tuned parameters from those presented in [20] lie within a 7% accuracy limit.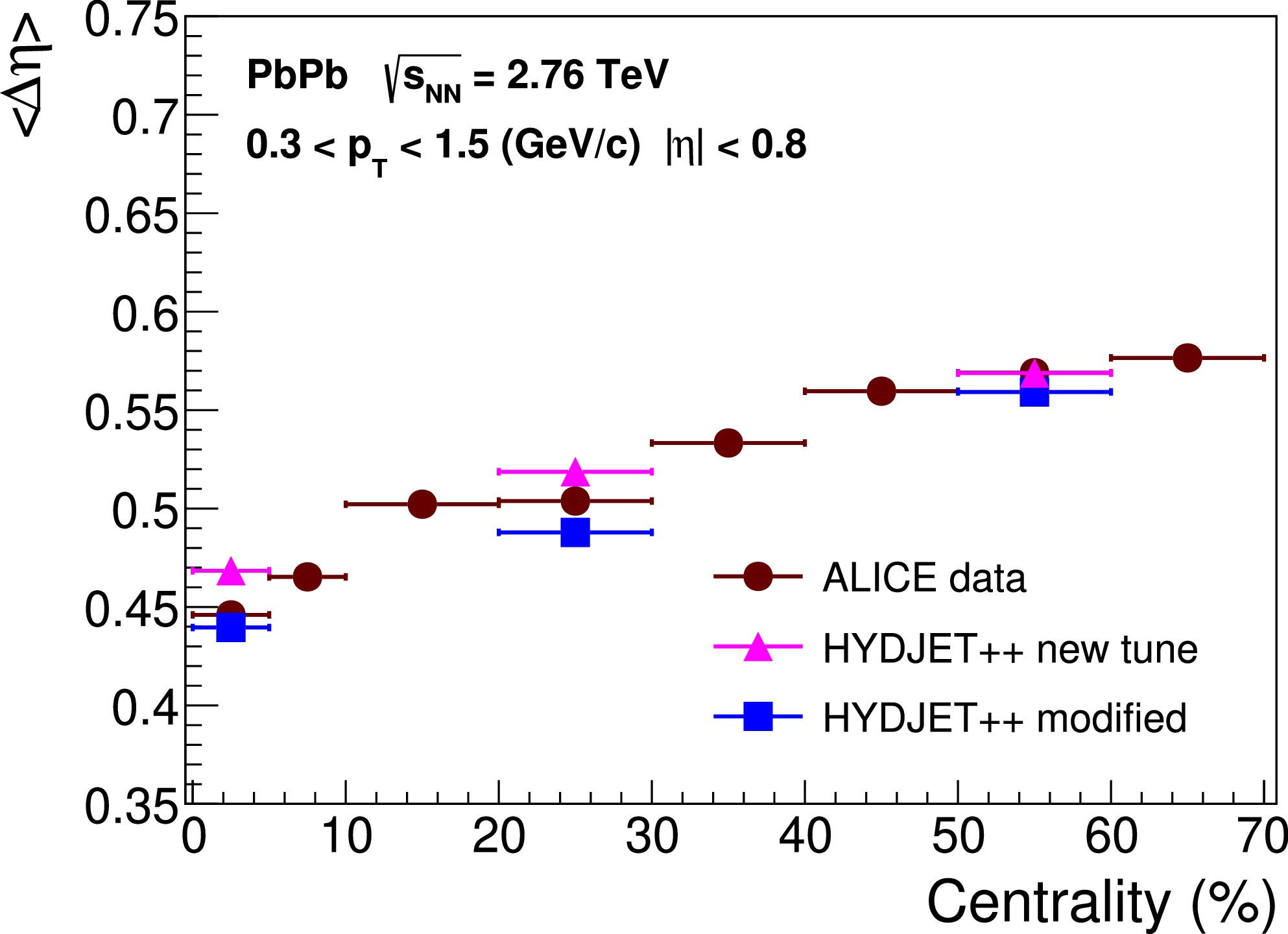
Figure 5. (color online) Centrality dependence of the width of the balance function of charged hadrons in Pb+Pb collisions at
$\sqrt s = 2.76$ TeV for the correlations studied in terms of relative pseudorapidity$\Delta \eta$ . The model calculations with modified (squares) and newly tuned (triangles) versions of the HYDJET++ model are compared with ALICE data (circles) extracted from [59].Recently [18], the CMS Collaboration presented preliminary data on the net-charge fluctuations in
${\rm Pb}$ +${\rm Pb}$ collisions at$ \sqrt{s} = 5.02 $ TeV for a wide range of relative pseudorapidity up to$ \Delta \eta = 4.8 $ . The analysis was performed in terms of the variable D. The default HYDJET++ model fails to accurately replicate the data, as shown in Fig. 6. In contrast, the modified version of HYDJET++ reproduces the experimentally measured values up to$ \Delta \eta = 1.5 $ but overestimates them at larger pseudorapidities. The discrepancy may be explained by a possible shift of the strength of pair correlations$ \sigma_{\eta} $ at large rapidities. Note also that the CMS data are not corrected for the effect of global charge conservation, which is more prominent at large values of$ \Delta \eta $ . This effect might reveal itself differently in data and in model calculations. In other words, for a fixed value of$ \sigma_{\eta} $ , the effect of charge fluctuations due to directly produced hadrons decreases with increasing$ \Delta \eta $ , given that an increasingly smaller fraction of charged hadrons from each generated pair will not fall within the considered range of pseudorapidity. It is this exclusion from the observation zone that provides the net-charge fluctuations of direct hadrons. This important question deserves further investigation.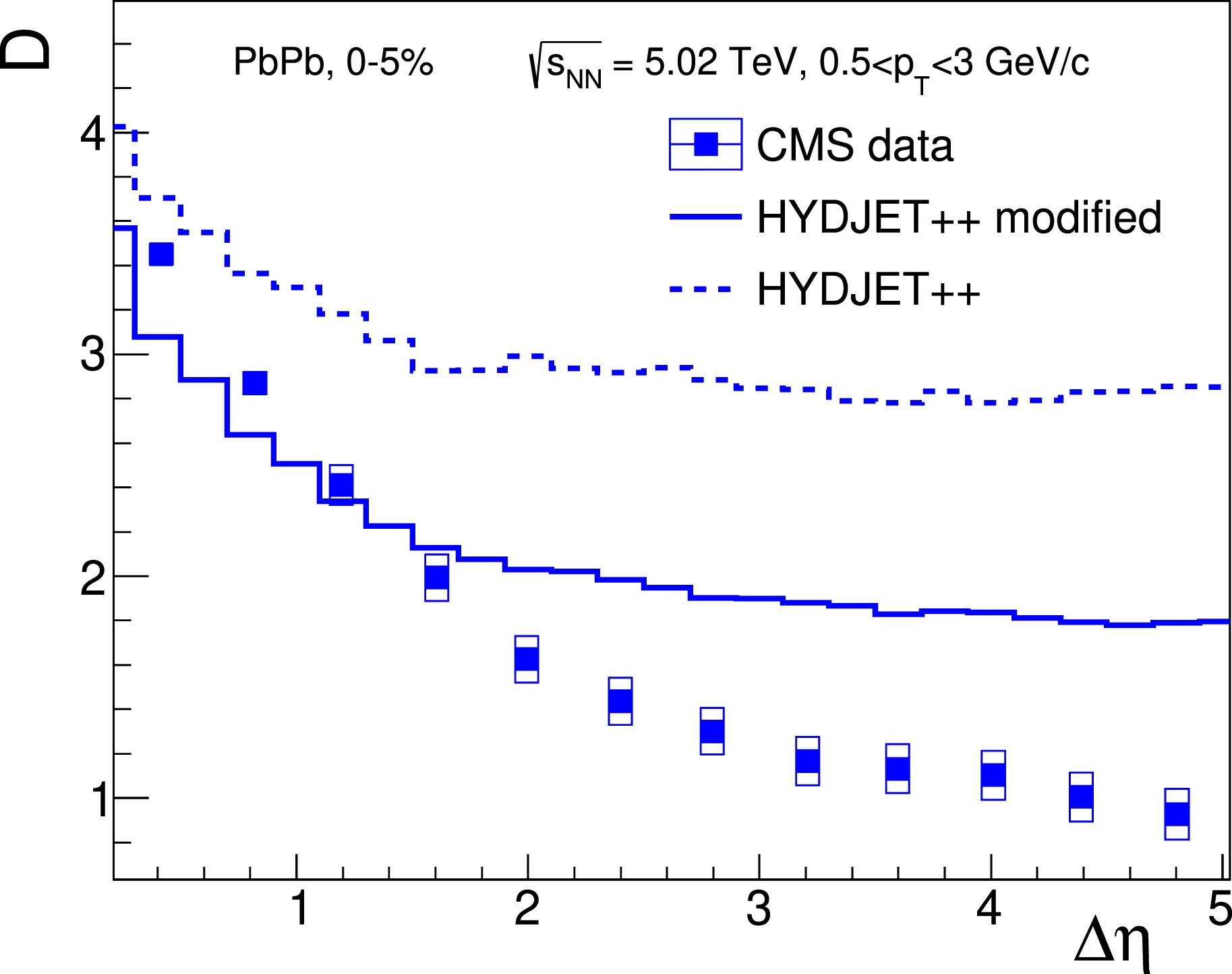
Figure 6. (color online) D as a function of
$\Delta \eta$ in Pb+Pb central (0 − 5%) collisions at$\sqrt s = 5.02$ TeV. The squares represent CMS data extracted from [18]; HYDJET++ calculations for the default and modified versions are shown by dashed and solid histograms, respectively. -
Fluctuations of the net electric charge of particles are studied in
${\rm Pb}$ +${\rm Pb}$ collisions at LHC energies of$ \sqrt{s} = 2.76 $ TeV and 5.02 TeV within the framework of several models designed for description of nucleus-nucleus interactions at (ultra)relativistic energies. The following conclusions can be drawn from our study.The values of quantitative measures of these fluctuations, namely D and Σ, obtained from the HYDJET++, ampt, and HIJING models, exceed the corresponding experimental values and are more consistent with the fluctuations corresponding to those of a hadronic gas. The discrepancy is attributed to the treatment of multiparticle production within the grand canonical ensemble approach rather than the canonical one, which accounts for the explicit charge conservation in each individual event.
A modified version of the HYDJET++ model with pair-production of oppositely charged hadrons on the freeze-out hypersurface, in contrast to independent generation of hadron species in the "default" version of the model, properly describes the data. This is achieved by introducing a new model parameter, namely charge correlation length at the formation stage of direct hadrons. This effectively considers the mechanisms of occurrence of the charge correlations. In this case, the charge correlation length decreases when going from the peripheral collisions to the central ones. This behavior of the parameters D and Σ corresponds to fluctuations attributed to those of the quark-gluon plasma. This modification and the corresponding parameters allow describing the width of the balance function of unlike-sign charged hadrons in lead-lead collisions at energies of
$ \sqrt{s} = 2.76 $ TeV and 5.02 TeV.It has been established that the decay of resonances in the case of initially strong correlations of the directly produced hadrons with unlike charges, i.e., with a correlation length less than that for resonances, causes blurring of these correlations and, hence, increase of the parameter
$ D (\Sigma) $ . In contrast, in case of absence of charge correlations between directly produced hadrons, which corresponds to an infinite correlation length, decays of resonances lead to smaller values of$ D (\Sigma) $ . -
Fruitful discussions with L.V. Bravina and A.I. Demyanov are highly appreciated.
Modeling net-charge fluctuations in heavy-ion collisions at the LHC
- Received Date: 2024-08-14
- Available Online: 2025-01-15
Abstract: Analysis of Pb+Pb data for net-charge fluctuations at LHC energies using the HYDJET++ model is presented. The strongly intensive quantities D and Σ were used to remove the effects related to system volume fluctuations. We employed two versions of HYDJET++ for the analysis. The first one is the standard or default version, whereas the second one is a modification that takes into account explicit event-by-event conservation of the electric net-charge of produced particles. The inclusion of the canonical net-charge conservation in the model allows for better description of the experimental data obtained by the ALICE and CMS Collaborations. A comparison with calculations from other models is also presented.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: