-
The imposition of gauge invariance in the standard model (SM) requires introducing gauge bosons. Because the Lagrangian involving a Higgs doublet in the SM is invariant under the
$S U(2)_L\otimes U(1)_Y$ gauge transformation, electroweak gauge bosons acquire nonzero masses through spontaneous symmetry breaking (SSB). This SSB mechanism also provides mass to all massive particles in the SM. Therefore, high-precision measurements of gauge boson masses are crucial for testing the SM and searching for new physics (NP) phenomena. The 2022 CDF II measurement [1] of the W boson mass was approximately$ 7\sigma $ away from the SM prediction [2]:$ M_W^{\rm{SM}}=80354\pm7\;{\rm{MeV}}, $

(1) $ M_W^{\rm{CDF\;II}}=80433.5\pm9.4\;{\rm{MeV}}. $

(2) Moreover,
$ M_W^{\rm{CDF\;II}} $ is not compatible with the world average,$ M_W^{\rm{Average}}=80377\pm12\;{\rm{MeV}}, $

(3) which is based on the measurements at LEP-2 [3], Tevatron [4, 5], and the LHC [6, 7]. The measured W boson mass anomaly at CDF II has prompted numerous studies attempting to explain it within various NP models [8–32]. In a recent update, the ATLAS collaboration reported a measurement of the W boson mass based on data from proton-proton (pp) collisions at a center-of-mass energy
$ \sqrt s=7\;{\rm{TeV}} $ [33]:$ M_W^{\rm{ATLAS}}=80360\pm 16\;{\rm{MeV}}. $

(4) Interestingly, the updated result from the ATLAS collaboration agrees with the SM prediction, with no observed deviation. This underscores the importance of obtaining a proper W boson mass that can satisfy experimental measurements in NP models, which is crucial for NP phenomenology studies.
Among the various NP models, those with an extra
$ U(1) $ gauge group, such as the$ U(1)_{B-L} $ extended SM, minimal supersymmetric model (MSSM) with local$ B-L $ gauge symmetry [34–41], and MSSM with a$ U(1)_X $ local gauge group [42–46], have attracted the attention of physicists. In these NP models, the introduction of a new$ Z' $ gauge boson corresponding the extra$ U(1) $ gauge group and new introduced gauge couplings can contribute to the oblique parameters S, T, and U at tree level and consequently impact the theoretical predictions of the W boson mass. Therefore, determining the appropriate gauge coupling strength and the new$ U(1) $ gauge group charges of the particle fields that can satisfy the high-precision measurements of the W boson mass is crucial in these NP models. In this study, we conduct a general analysis of the W boson mass in NP models with a new extra$ U(1) $ gauge group, and the obtained results can be applied to all such NP models.The paper is organized as follows. The S, T, and U parameters and W boson mass in NP models with an extra
$ U(1) $ local gauge group are calculated in Sec. II. The numerical results are presented and analyzed in Sec. III. Finally, a summary is provided in Sec. IV. -
For convenience, the newly introduced
$ U(1) $ local gauge group can be defined as$ U(1)_X $ ($ X=B,\;L,\;B-L $ , etc, where B refers to the baryon number, and L refers to the lepton number), that is, the local gauge group of this type of NP model is extended to$S U(3)_C\otimes S U(2)_L\otimes U(1)_Y\otimes U(1)_X$ . Owing to the presence of two Abelian groups, gauge kinetic mixing can occur and be induced through RGEs even when set to zero at$ M_{\rm{GUT}} $ [47–52]. This leads to the covariant derivatives in this type of NP model being expressed as$D_\mu=\partial_\mu-{\rm i}\left(\begin{array}{*{20}{c}} {Y,} &{ X}\end{array}\right)\left(\begin{array}{*{20}{c}}{g_Y, }& {g_{Y X}} \\ {g_{X Y},} & {g_X}\end{array}\right)\binom{B_\mu}{Z_\mu^{\prime}},$

(5) where Y and X are the hypercharge and
$ U(1)_X $ charge, respectively,$ g_Y $ is the measured hypercharge coupling constant,$ g_X $ is the coupling constant corresponding to the$ U(1)_X $ gauge group,$ g_{YX} $ is the coupling constant arising from the gauge kinetic mixing effect, whereas$ g_{XY} $ can always be rotated to 0 as long as the two Abelian gauge groups are unbroken.The kinetic terms of vector bosons
$ \Pi_{33}(p^2) $ ,$ \Pi_{00}(p^2) $ ,$ \Pi_{30}(p^2) $ , and$ \Pi_{WW}(p^2) $ can be defined by the effective Lagrangian [53]$ \begin{aligned}[b] {\cal{L}}_{\rm{oblique}}=\;& -\frac{1}{2}W_\mu^3 \Pi_{33}(p^2)W^{3\mu}-\frac{1}{2}B_\mu \Pi_{00}(p^2)B^\mu\\ &-W_\mu^3 \Pi_{30}(p^2)B^\mu-W_\mu^+\Pi_{WW}(p^2)W^{-\mu}. \end{aligned}$

(6) $ \Pi_{ij}(p^2) $ ($ ij=33,\;00,\;30,\;WW $ ) in Eq. (6) can be expanded at$ p^2=0 $ because NP is generally considered very heavy, and$ \Pi_{ij}(p^2) $ can be written as$ \Pi_{ij}(p^2)=\Pi_{ij}(0)+p^2 \Pi'_{ij}(0)+\cdot\cdot\cdot, $

(7) where the higher order terms can be safely neglected. The oblique parameters
$ S,\;T,\;U $ are defined as$\begin{aligned}[b]& S=4s_Wc_W\Pi'_{30}(0),\;T=\frac{\Pi_{33}(0)-\Pi_{WW}(0)}{M_W^2},\;\\ &U=4s_W^2[\Pi'_{33}(0)-\Pi'_{WW}(0)],\end{aligned} $

(8) where
$ s_W\equiv \sin \theta_W,\;c_W\equiv \cos \theta_W $ , and$ \theta_W $ is the Weinberg angle.Generally, the Π matrix of neutral vector bosons can be written in the basis
$ (B_\mu,\;W^3_\mu,\;Z'_\mu) $ as$ \left(\begin{array}{*{20}{c}} {p^2-M_W^2 t^2 }&{ M_W^2 t }&{ -M_W^2 t t'}\\ {M_W^2 t }&{ p^2-M_W^2 }&{ M_W^2 t'}\\ {-M_W^2 t t' }&{ M_W^2 t' }&{ p^2-M_{Z'}^2}\end{array}\right), $

(9) where
$ t=g_{Y}/g_2 $ , and$ t'=(g_{YX}+2X_H g_X)/g_2 $ . It is obvious that there is a nonzero$ Z-Z' $ mixing effect even when$ X_H=0 $ because of the existence of the kinetic mixing effect. In general, the kinetic mixing effect can also be described by the kinetic mixing parameter$ \epsilon $ $ L=-\frac{1}{4}B_{\mu\nu}B^{\mu\nu}-\frac{1}{4}X_{\mu\nu}X^{\mu\nu}-\frac{\epsilon}{2}B_{\mu\nu}X^{\mu\nu}+\frac{1}{2}M_Z^2 B_\mu B^\mu+\frac{1}{2}M_{Z'}^2 X_\mu X^\mu. $

(10) The kinetic terms of the above Lagrangian can be normalized by
$ K=\left(\begin{array}{*{20}{c}}{-k_1} & {k_2}\\ {k_1} &{ k_2}\end{array}\right), $

(11) where
$ k_1=1/\sqrt{1-2\epsilon} $ , and$ k_2=1/\sqrt{1+2\epsilon} $ . The normalization arises the nonzero mixing terms of the mass matrix for$ (B_\mu,\;X_\mu) $ $ \left(\begin{array}{*{20}{c}}{k_1^2 (M_{Z'}^2+M_Z^2) }&{ k_1k_2 (M_{Z'}^2-M_Z^2)}\\ {k_1k_2 (M_{Z'}^2-M_Z^2) }&{ k_2^2 (M_{Z'}^2+M_Z^2)}\end{array}\right). $

(12) Combining Eqs. (9) and (12), we obtain
$ \epsilon\approx\frac{1}{2}-\frac{(g_{YX}+2X_H g_X)^2M_W^4}{2g_2^2M_{Z'}^4}. $

(13) Hence, it is equivalent to describe the kinetic mixing effect using Eqs. (9) and (12), and we take the forms defined in Eq. (9) to conduct the following analysis.
The gauge couplings involving charged leptons can be written as
$\begin{aligned}[b] {\cal{L}}=\;& -{\rm i} \bigg[\left(-\frac{1}{2}g_2W^3_\mu+Y_L g_Y B_\mu+Y_L g_{YX} Z'_\mu+X_L g_B Z'_\mu \right)\bar e_L e_L\\ &+(g_Y Y_E B_\mu+g_B X_E Z'_\mu+g_{YX} Y_E Z'_\mu)\bar e_R e_R \bigg] \end{aligned}$

(14) $ Y_L $ and$ Y_E $ are the hypercharges of the left-handed and right-handed components of leptons, respectively, which can be normalized as$Y_L=- {1}/{2}$ and$ Y_E=-1 $ . Moreover,$ X_L,\;X_E,\;X_H $ are the$ U(1)_X $ charges of the left-handed components of leptons, right-handed components of leptons, and scalar doublets, respectively. Because the most strict constraints originate from the precision measurements performed at$ e^+e^- $ colliders (such as LEP1 and LEP2), we choose to eliminate the neutral currents involving charged leptons in Eq. (14), which can be achieved by redefining the vector fields$ \begin{aligned}[b] B_\mu=\; &\tilde B_\mu-c_Y Z'_\mu,\;\;W_\mu^3=\tilde W_\mu^3-c_W Z'_\mu,\\ Z'_\mu=\; & \tilde Z'_\mu+\frac{1}{p^2-M_{Z'}^2}\{[(p^2-M_W^2 t^2)A_Y+M_W^2 tA_W+M_W^2 tt']\tilde B_\mu\\ &+[M_W^2 tA_Y+(p^2-M_W^2)A_W-M_W^2 t']\tilde W^3_\mu\},\\ A_Y=\; & \frac{g_X X_E+g_{YX}Y_E}{g_1 Y_E},\;\;A_W= \frac{2}{g_2}(Y_L g_Y c_Y-X_L g_B-Y_L g_{YX}). \end{aligned} $

(15) Then, the oblique parameters
$ S,\;T,\;U $ can be obtained from Eq. (8) as$\begin{aligned}[b] S=\; &\frac{8 s_W^2 M_W^2 g_X}{M_{Z'}^2}\Bigg[\frac{1}{g_Y^2}(g_X X_E-g_{YX})\\ &+\frac{g_X}{g_2^2}(X_E-2X_L)\Bigg](X_E-X_L+X_H),\end{aligned} $

(16) $ T=\frac{4g_X^2M_W^2}{g_2^2 M_{Z'}^2}(X_E-X_L+X_H)^2, $

(17) $ U=\frac{-8g_X^2M_W^2}{g_2^2 M_{Z'}^2}(X_E-2X_L)(X_E-X_L+X_H). $

(18) As shown in Eqs. (16)−(18),
$ S=T=U=0 $ when$ X_E-X_L+X_H=0 $ , which indicates that the leptonic Yukawa couplings are invariant under$ U(1)_X $ symmetry in this case, eliminating the need for a model to generate the lepton masses. For nonzero$ X_E-X_L+X_H $ , other mechanisms are needed to generate the lepton masses, such as the$ U(1)_H $ model [54]. In addition, we approximately neglect the Z couplings to neutrinos or quarks in our calculations because they are measured considerably less accurately than Z couplings to charged leptons, and all effects involving charged leptons are included in the approximation. The W boson mass with a local$ U(1)_X $ gauge group can be written as [55, 56]$ M_W^2=(M_W^{\rm{SM}})^2+\frac{c_W^2 M_Z^2}{c_W^2-s_W^2}\Big(-\frac{1}{2}S+c_W^2 T+\frac{c_W^2-s_W^2}{4s_W^2}U\Big). $

(19) Eqs. (16)−(18) indicate that the
$ U(1)_X $ charges of leptons, denoted as$ X_E $ and$ X_L $ , can affect the theoretical predictions for the W boson mass. Consequently, we consider$ X_E $ and$ X_L $ as free parameters to explore their effects in the following analysis. Typically,$ X_E $ and$ X_L $ are subject to constraints enforced by chiral anomaly cancellations. For NP models with an extra$ U(1)_X $ local gauge group, there are four distinctive chiral anomaly cancellation patterns per generation [20],$ \sum\limits_{f}X_f=\sum\limits_{f}(X_f)^3=\sum\limits_{f}(X_f)^2Y_f=\sum\limits_{f}X_f(Y_f)^2=0. $

(20) Here, f represents various fermion species, encompassing the left-handed lepton doublet
$ \hat L $ , left-handed quark doublet$ \hat Q $ , right-handed lepton singlets$ \hat E $ and$ \hat N $ (heavy neutrinos), and right-handed quark singlets$ \hat u $ and$ \hat d $ . It is evident from Eq. (20) that the phenomena of chiral anomaly cancellations can be realized by assigning approximate values to$ X_N $ ,$ X_Q $ ,$ X_u $ , and$ X_d $ while considering$ X_E $ and$ X_L $ as unconstrained. We focus on illustrating the effects of an extra$ U(1)_X $ local gauge group on the W boson mass; hence, we do not explore the chiral anomaly cancellations in detail for different$ X_E $ and$ X_L $ in specific NP models. -
Based on the calculations in Sec. II, the numerical results are presented in this section. As input parameters [57],
$ M_W^{\rm{SM}} $ is taken as$80.354\;\;{\rm{GeV}}$ , the Z boson mass is$ M_Z=91.1876\;{\rm{GeV}} $ , the fine-structure constant$\alpha_{em}(m_Z)= 1/128.9$ , and the fermion coupling constant$G_F= 1.1664\times10^{-5}~{\rm{GeV}}^{-2}$ .The large amount of data collected at the LHC on the
$ Z' $ gauge boson provides great potential for its direct search. To date, ATLAS [58] and CMS [59] have conducted direct searches for the$ Z' $ gauge boson through the channel$ pp\to Z'\to e^+e^-,\;\mu^+\mu^- $ based on the data collected in proton$ - $ proton collisions at a centre-of-mass energy of$ 13\;{\rm{TeV}} $ . In addition, there is a measurement of the$ t\bar t $ pair production cross section with$ 35.9\;{\rm{fb}}^{-1} $ data from CMS [60] and$ 139\;{\rm{fb}}^{-1} $ data from ATLAS [61] through the channel$ pp\to Z'\to t\bar t $ , and ATLAS [62] has presented a search for new resonances decaying into a pair of jets through the channel$ pp\to Z'\to q\bar q $ , including$ b\bar b $ . Although the$ Z' $ gauge boson has not been observed so far, severe constraints are set on the$ Z' $ boson mass, which depends on the$ U(1) $ symmetry and the corresponding gauge coupling strength generally. For example, for a sequential SM (SSM), the latest experimental constraint on the$ Z'_{\rm SSM} $ boson (which has the same fermion couplings as the SM Z boson) mass is$ M_{Z'}\gtrsim5.1\;{\rm{TeV}} $ [58, 59]. For an$E_6-$ motivated grand unification model, the additional gauge bosons are required to be heavier than approximately$ 4.1\;{\rm{TeV}} $ for$ Z'_{\Psi} $ and$ 4.6\;{\rm{TeV}} $ for$ Z'_{\chi} $ experimentally [58, 59].The new
$ Z' $ boson can also make contributions to$ B_s-\bar B_s $ mixing and the$ B_s\to\mu^+\mu^- $ process, depending on the additional$ U(1) $ symmetry. For example, the contributions from the$ Z' $ boson to$ B_s\to\mu^+\mu^- $ for$ U(1)_{B-L} $ symmetry are highly suppressed by its heavy mass [63], whereas the$ Z' $ boson can make important contributions to$ B_s-\bar B_s $ mixing and$ B_s\to\mu^+\mu^- $ at tree level for$ U(1)_{L_\mu-L_\tau} $ symmetry [64] and the flavor dependent$ U(1)_F $ symmetry [65, 66]. In addition, probing the newly introduced$ Z' $ boson in future will also depend on$ U(1) $ symmetry and the relevant couplings. For example,$ Z' $ will be produced at the LHC if$ Z' $ has nonzero couplings with quarks, indicating that searches for high-mass dielectron, dimuon, and dijet resonances at the future HL-LHC are effective in probing the$ Z' $ boson directly.$ Z' $ has the potential to be probed by di-muon production at future high-energy electron-positron linear colliders if$ Z' $ has nonzero couplings with charged leptons [67], and$ Z' $ may also be produced at future muon colliders [68–70] in this case. In the following analysis, we consider the constraints on the$ Z' $ gauge boson mass$ M_{Z'} $ and$ M_{Z'}/g_X $ as [71–73]$ M_{Z'}\geq4.2\;{\rm{TeV}},\;\frac{M_{Z'}}{g_X}\geq6\;{\rm{TeV}}. $

(21) The kinetic mixing effect appears in any NP model with two Abelian groups. We focus on the effects of
$ g_{YX} $ on$ M_W $ by first eliminating neutral currents involving charged leptons. Taking$ X_E=-1/2 $ and$ X_L=-1 $ , the results of$ M_W $ versus$ g_{YX} $ are plotted for$ X_E-X_L+X_H= $ 1/2, 1, 3/2 in Figs. 1 (a), (b), and (c), respectively, where the gray areas denote the ATLAS$ 2\sigma $ interval, the green areas denote the CDF II$ 2\sigma $ interval, the black, red, and blue lines denote the results for$ M_{Z'}= $ 4.2, 7, 10 TeV, respectively, and the solid, dashed, and dotted lines denote the results for$ g_X= $ 0.1. 0.4, 0.7, respectively. The figure shows that large$ g_X $ ,$ g_{YX} $ , and$ X_E-X_L+X_H $ combined with a small$ M_{Z'} $ can effectively explain the measured$ M_W $ at CDF II, whereas that measured at ATLAS prefers small$ g_X $ ,$ g_{YX} $ , and$ X_E-X_L+X_H $ and a large$ M_{Z'} $ . In addition, a positive$ g_{YX} $ can increase the theoretical prediction of$ M_W $ , whereas a negative$ g_{YX} $ suppresses the contributions from the$ U(1)_X $ gauge group to$ M_W $ . The effects of$ g_{YX} $ are clearly affected by the values of$ M_{Z'} $ ,$ g_X $ , and$ X_E-X_L+X_H $ ;$ g_{YX} $ influences$ M_W $ drastically when$ M_{Z'} $ is small and$ g_X $ and$ X_E-X_L+X_H $ are large. This can be clearly understood because the effects of introducing a$ U(1)_X $ local gauge group are highly suppressed by large$ M_{Z'} $ or very small$ g_X $ , and the leptonic Yukawa couplings approach invariance under$ U(1)_X $ symmetry as$ X_E-X_L+X_H $ approaches$ 0 $ . Because the kinetic mixing constant$ g_{YX} $ may significantly affect the theoretical predictions of$ M_W $ , the constraints on$ M_{Z'}/g_X $ from a high-precision W boson mass in NP models with an extra local$ U(1) $ gauge group would be relaxed partly by considering the contributions from$ g_{YX} $ .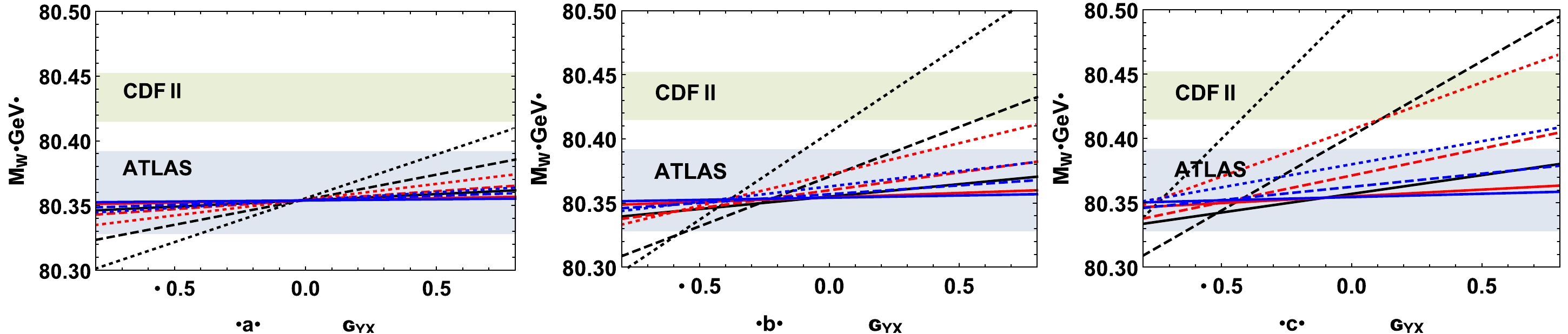
Figure 1. (color online) Taking
$ X_E=-1/2 $ and$ X_L=-1 $ , the results of$ M_W $ versus$ g_{YX} $ are plotted for$ X_E-X_L+X_H=1/2 $ (a),$ 1 $ (b), and$ 3/2 $ (c), where the gray areas denote the ATLAS$ 2\sigma $ interval, the green areas denote the CDF II$ 2\sigma $ interval, the black, red, and blue lines denote the results for$ M_{Z'}=4.2,\;7,\;10\;{\rm{TeV}} $ , respectively, and the solid, dashed, and dotted lines denote the results for$ g_X=0.1.\;0.4,\;0.7 $ , respectively.To observe the effects of
$ X_E,\;X_L,\;X_H $ on the W boson masses, we take$ g_B=0.6 $ and$ M_{Z'}=5\;{\rm{TeV}} $ and scan the following parameter space:$\begin{aligned}[b] g_{YX} = & (-0.8,0.8),\;X_E=\left(-\frac{3}{2},\frac{3}{2}\right),\\ X_L = & \left(-\frac{3}{2},\frac{3}{2}\right),\;X_H=\left(-\frac{3}{2},\frac{3}{2}\right). \end{aligned} $

(22) The allowed results of
$ X_E,\;X_L $ for$ X_E-X_L+X_H= 1/2,\;1,\;3/2 $ are plotted in Figs. 2(a1), (b1), and (c1), respectively, where the blue points are obtained by considering the W boson mass measured at CDF II in the$ 2\sigma $ interval, and the red points are obtained by considering the W boson mass measured at ATLAS in the$ 2\sigma $ interval. To illustrate the effects of kinetic mixing on the allowed results of$ X_E,\;X_L $ , the results of scanning$ g_{YX} $ in the range$g_{YX}=(-0.4, 0.4)$ are plotted in Figs. 2(a2), (b2), and (c2). By comparing Figs. 2 (a1), (b1), and (c1) with Figs. 2 (a2), (b2), and (c2), the allowed ranges of$ X_E,\;X_L $ for$ g_{YX}= (-0.4,~0.4) $ are found to be narrower than those for$g_{YX}=(-0.8, 0.8)$ , because in the chosen parameter space,$ g_{YX} $ clearly affects the numerical results, as concluded above. For NP models with an extra$ U(1) $ local gauge group, the ranges of$ X_E $ ,$ X_L $ would be limited more strictly by the W boson mass measured at CDF II for smaller$ X_E-X_L+X_H $ , whereas the ranges of$ X_E $ ,$ X_L $ would be limited more strictly by that measured at ATLAS for larger$ X_E-X_L+X_H $ . The W boson mass measured at CDF II or ATLAS can be satisfied with appropriate values of$ X_E $ ,$ X_L $ ,$ X_H $ ,$ g_{YX} $ ,$ g_{X} $ , and$ M_{Z'} $ .
Figure 2. (color online) Taking
$ g_B=0.6 $ ,$ M_{Z'}=5\;{\rm{TeV}} $ , the allowed results of$ X_E,\;X_L $ for$ X_E-X_L+X_H=1/2 $ (a1),$ 1 $ (b1), and$ 3/2 $ (c1) are plotted, where the blue (red) points are obtained by considering the W boson mass measured at CDF II (ATLAS) in the$ 2\sigma $ interval. Similarly, the results obtained for$ g_{YX} $ scanning in the range$ g_{YX}=(-0.4,0.4) $ are plotted in Figs. 2 (a2), (b2), and (c2).Nonzero
$ X_L $ ,$ X_E $ , and$ g_{YX} $ may significantly affect the theoretical predictions of the branching ratio of$ Z\to l\bar l $ , which would be useful for testing models with an extra$ U(1) $ gauge group in future experiments. Generally,$ {\rm{Br}}(Z\to l\bar l) $ can be simplified by neglecting the final lepton masses as$ {\rm{Br}}(Z\to l\bar l)\approx \left(1+\frac{3\alpha_{em}}{4\pi}\right)(g_V^2+g_A^2)\frac{M_Z^3}{12\pi v^2\Gamma_Z}, $

(23) where
$ \Gamma_Z=2.4952\;{\rm{GeV}} $ [57],$ v=246.22\;{\rm{GeV}} $ [57], and$ \begin{aligned}[b] g_V=\;&-\frac{c_W}{2g_2}[c_W c_W'g_2-3c_W' s_W g_Y\\&+2s_W'(g_{YX}-g_X X_E-g_X X_L)],\\ g_A=\;&-\frac{c_W}{2g_2}[c_W c_W' g_2+c_W' s_W g_Y+2s_W'g_X(X_E-X_L)],\\ s_W'\approx\;&\frac{g_{YX}M_Z}{2g_X M_{Z'}},\;c_W'=\sqrt{1-s_W'^2}. \end{aligned} $

(24) To clearly observe the effects of
$ X_L $ ,$ X_E $ , and$ g_{YX} $ on$ {\rm{Br}}(Z\to l\bar l) $ , we take the points obtained in Fig. 2 as inputs and plot the results of$ {\rm{Br}}(Z\to l\bar l) $ versus$ g_{YX} $ in Fig. 3, where (a1), (b1), and (c1) present the results for$ X_E-X_L+X_H=1/2 $ ,$ 1 $ ,$ 3/2 $ , respectively; the blue (red) points are obtained by considering the W boson mass measured at CDF II (ATLAS) in the$ 2\sigma $ interval, and the black lines denote the SM prediction. Figures 3 (a2), (b2), and (c2) present the results for$ g_{YX} $ scanning in the range$ g_{YX}=(-0.4,0.4) $ . The figure clearly shows that$ g_{YX} $ affects the numerical results of$ {\rm{Br}}(Z\to l\bar l) $ significantly. The coupling$ Z l\bar l $ in NP models with an extra$ U(1) $ local gauge group decouples to that in the SM for$ g_{YX}=0 $ even with nonzero$ X_L $ and$ X_E $ , whereas$ {\rm{Br}}(Z\to l\bar l) $ may be modified acutely for large$ g_{YX} $ . This indicates that the kinetic mixing effect plays an important role in$ Z l\bar l $ coupling, and observing$ {\rm{Br}}(Z\to l\bar l) $ with high precision can help test and limit the additional gauge couplings.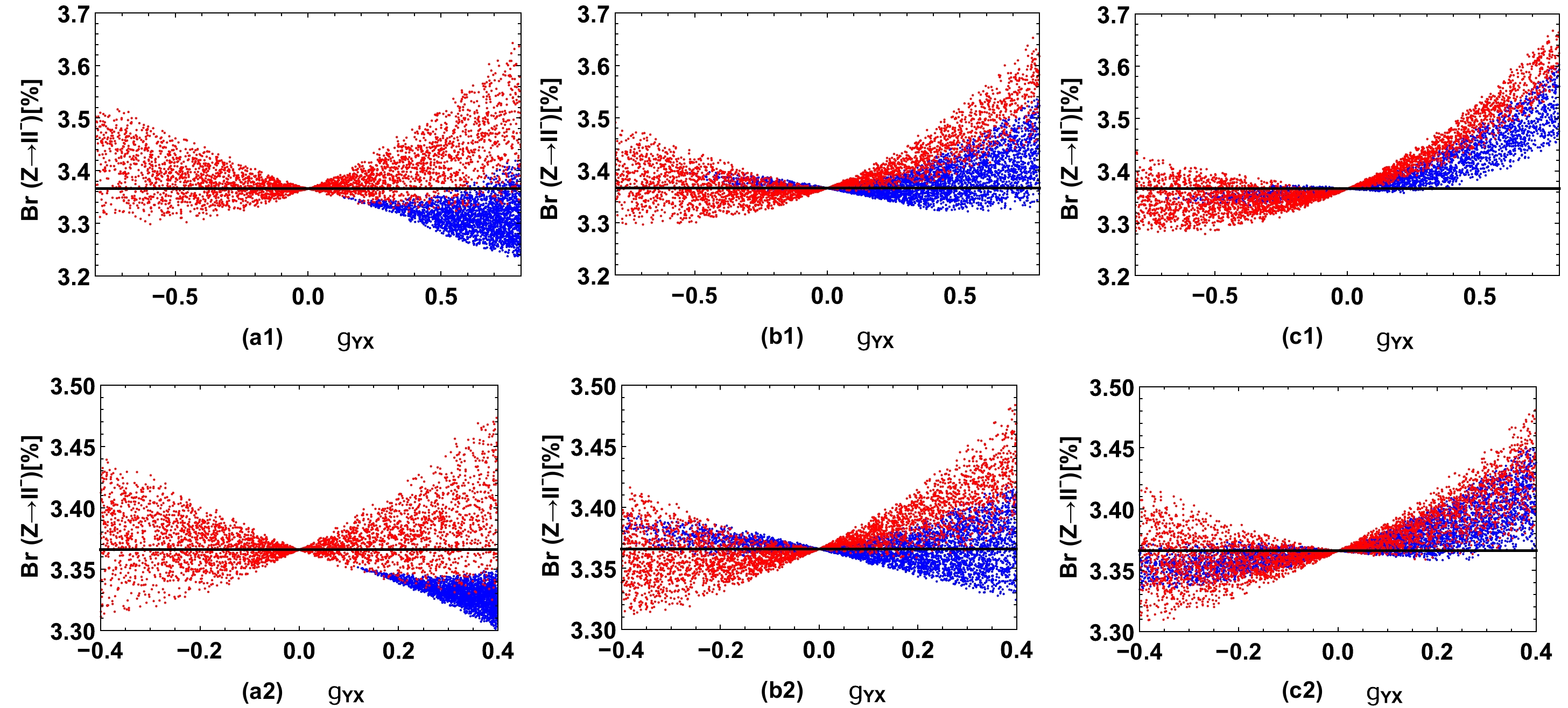
Figure 3. (color online) Taking
$ g_B=0.6 $ ,$ M_{Z'}=5\;{\rm{TeV}} $ and$ {\rm{Br}}(Z\to l\bar l) $ versus$ g_{YX} $ for$ X_E-X_L+X_H=1/2 $ (a1),$ 1 $ (b1), and$ 3/2 $ (c1) are plotted, where the blue (red) points are obtained by considering the W boson mass measured at CDF II (ATLAS) in the$ 2\sigma $ interval, and the black lines denote the SM prediction. Similarly, the results obtained for$ g_{YX} $ scanning in the range$ g_{YX}=(-0.4,0.4) $ are plotted in Figs. 3 (a2), (b2), and (c2). -
The contributions to the oblique parameters S, T, and U and the W boson mass are calculated in NP models with an extra
$ U(1) $ local gauge group. In such NP models, the newly introduced$ Z' $ gauge boson and leptonic gauge couplings can make significant contributions to S, T, and U and the W boson mass at tree level if we choose to eliminate neutral currents involving charged leptons. Hence, the precise measurements of the W boson mass are related closely to such NP models. Considering kinetic mixing effects (which arise in any NP model with two Abelian groups) in the calculations, the analytical results can be applied to all such NP models. Based on the numerical results analyzed above, the kinetic mixing effects can significantly affect the contributions to the W boson mass. Importantly, if the leptonic Yukawa couplings are invariant under the extra$ U(1) $ local gauge group, the contributions to S, T, and U and the W boson mass in such NP models can be eliminated by redefining the gauge boson fields through removing neutral currents involving charged leptons, even with nonzero kinetic mixing effects.
W boson mass in NP models with an extra U(1) gauge group
- Received Date: 2024-06-10
- Available Online: 2024-11-15
Abstract: The precise measurement of the W boson mass is closely related to the contributions of new physics (NP), which can significantly constrain the parameter space of NP models, particularly those with an additional






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: