Scissors vibration and its collective rotation in a microscopic investigation

The scissors mode in deformed nuclei is understood as a vibrational motion of the proton part with respect to the neutron part, in which their intrinsic orientations oscillate against each other. The idea of such a vibration was proposed in the 1970s by considering a two-rotor model comprising a proton one and a neutron one, with an angle allowed between their symmetry axes [1]. The scissors vibration is recognized experimentally as 1⁺ excitations with a strong M1 connection to the ground state and has been found extensively in deformed nuclei from various mass regions [2] since its first observation in ¹⁵⁶Gd [3]. Theoretically, the scissors mode can be described by geometric models (e.g., the two-rotor model [1, 4−6]), algebraic models (e.g., the interacting boson model [7]), and microscopic models, such as the shell model [8−10] and quasiparticle random phase approximation [11−14]. Although the microscopic descriptions provide observable parameters like the 1⁺ excitation energies and M1 strengths, which are compared with experimental data, showing the 'scissors-like' picture in the intrinsic frame is not straightforward. Therefore, the connection between the scissors vibration picture provided by the geometric models and the 1⁺ excitations described by the microscopic approaches remains unclear. As stated in Ref. [1], a detailed microscopic analyses of the two-rotor model is highly desirable.

Conversely, the rotational bands based on the scissors vibrational state are rarely studied. Experimentally populating the rotational excitations of the scissors mode is challenging, and only a few observations have been made [15]. In Ref. [15], it was observed that the 2⁺ member of the scissors band in ¹⁵⁶Gd stays exceptionally close to the 1⁺ band head, leading to the possible existence of a large moment of inertia (MoI) or a large odd-even splitting in the scissors bands. The possibility of a large MoI is qualitatively supported in Ref. [16], while that of odd-even splitting is suggested in Ref. [17]. In the latter work, the energy separation between the 1⁺ and 2⁺ members of the scissors band in ¹⁵⁶Gd is reproduced to a quantitative level, and the E2 and M1 strengths from the scissors excitations are also reasonably reproduced. The suggested odd-even splitting was found to be largely contributed by mixing with two-quasiparticle configurations; however, splitting also exists even without mixing. The reason for such a split is not given in detail in Ref. [17]. In most cases, odd-even splitting in rotational bands is recognized as signature splitting arising from the 'planar' orientation of the angular momentum [18], contributed by the collective rotor and the decoupled valence nucleons. However, for the scissors band, the orientation of the angular momentum with respect to the principle axes is not investigated.

This study aims to illustrate the scissors vibration and its collective rotation, based on the microscopic framework adopted in Ref. [17]. This framework was first proposed in Refs. [19, 20] as a generalization of the projected shell model [21, 22], with separate angular momentum projections for protons and neutrons. Such a projection treats the Euler angles of protons and neutrons independently, and the 'scissors' degree of freedom is introduced accordingly. In this work, the 'scissors' degree of freedom will be made explicit, enabling the visualization of the scissors vibration. Moreover, the angular momentum projection approach adequately describes collective rotations. In particular, the orientation of the angular momentum with respect to the intrinsic frame can be analyzed based on the so-called ''azimuthal plot'' extracted by the angular momentum projection, as can be found in a series of works discussing the ''exotic rotational modes'' of triaxial nuclei, i.e., the chiral rotation [23−28] and the wobbling motion [29, 30]. The analysis based on the azimuthal plot is also popular in particle-rotor model investigations, again for the chiral and wobbling motion [31−35], where it is also known as the spin coherent state map [33]. In the following, the azimuthal plot will be made for the scissors rotational bands to investigate their rotational behavior and obtain the origin of their odd-even splitting.

The remainder of the paper is organized as follows: Sec. II presents the model framework, the formalism for the illustration of the scissors vibration, and the azimuthal plot. In Sec. III, the formalism is applied to a well deformed nucleus ¹⁶⁸Er, and the scissors vibration/rotation features are discussed. Finally, Sec. IV gives a brief summary.

The model used in this work is the same as that used in Ref. [19]; however, it is presented here in an alternative way to visualize the scissors motion and its collective rotation. The model starts from a pairing-plus-quadrupole Hamiltonian adopted by the traditional projected shell model [21] and in Ref. [19]:

where

is the pairing-plus-quadrupole interaction among neutrons or protons, and

is the neutron-proton interaction of the quadrupole-quadrupole type. The basis for the diagonalization of the above Hamiltonian can be written as

in which $ |0_\nu\rangle(|0_\pi\rangle) $ represents the BCS vacuum for neutrons (protons) and $ P^{I_\nu}(P^{I_\pi}) $ is the angular momentum projector, acting on neutrons (protons) only. The subscript $ K=0 $ is used for the projector $ \hat{P}^I $ owing to the axial symmetry of the BCS vacuum. The neutron and proton vacua are projected to have spins $ I_\nu $ and $ I_\pi $, respectively, and the total spin I is then obtained by coupling the two. The values of $ I_\nu $ and $ I_\pi $ are cutoff at $ 30\hbar $. The overlap matrix for this non-orthogonal basis and the Hamiltonian matrix are calculated similarly to that in Ref. [19], after which the wave function

can be obtained by solving the standard Hill-Wheeler equation [36].

The angular momentum projector in (4) writes

in which the Euler angle Ω describes the relative orientation between laboratory frame and intrinsic frame. Therefore, with separate projections for neutrons and protons, the basis in (4) involves two independent Euler angles $ \Omega_\nu $ and $ \Omega_\pi $. The two independent Euler angles can be transformed into the set $ \{\Omega_\pi,\Omega_{\pi\nu}\} $, with $ \Omega_{\pi\nu} $ defined as

According to (7), $ \Omega_{\pi\nu} $ describes the relative orientation between the intrinsic frames of neutrons and protons, which should be connected with the scissors angle.

Using the transformation in (7), the integral over $\Omega_\nu,\;\Omega_\pi$ involved in the basis in (4) can be transformed into those over $\Omega_\pi,\;\Omega_{\nu\pi}$. The one over $ \Omega_\pi $ can then be rearranged into an angular momentum projector using (4), which gives the following:

Therefore, the separate projections for neutrons and protons in (4) becomes a projection $ \hat{P}^{I'}_{MK'} $ for the whole nucleus. Using (8), the basis in (4) becomes

Using the axial symmetry of $ |0_\nu\rangle $ and $ |0_\pi\rangle $, the integral over $ \alpha_{\pi\nu} $ and $ \gamma_{\pi\nu} $ in $ \Omega_{\pi\nu}=\{\alpha_{\pi\nu},\beta_{\pi\nu},\gamma_{\pi\nu}\} $ can be done explicitly, and the above equation can be reduced to

which contains a projection of the intrinsic state

In (11) the neutron part $ |0_\nu\rangle $ is shifted by an angle $ \beta_{\pi\nu} $ from the proton part, coinciding with the scissors-like picture. The angle $ \beta_{\pi\nu} $ is actually the scissors angle between the symmetry axes of protons and neutrons.

The expression (11) for the intrinsic state means that the 'scissors' is put in the intrinsic frame in such a way that the intrinsic axes coincide with the principle axes of the proton part, rather than the principle axes of the whole nucleus. Although the orientation of the intrinsic state does not change the calculated observable, describing the intrinsic motion with respect to the principle axes (for the whole system) might be convenient. Therefore, rotating the intrinsic state (11) by an Euler angle $ \Omega_{\text{PA}} $ is recommended to make its principle axes coincide with the intrinsic axes. The rotated intrinsic state can be written as

and according to the definition of the principle axes, $ \Omega_{\text{PA}} $ satisfies

It can be found that $ \gamma_{\text{PA}} $ is irrelevant and can be set to zero for convenience. The remaining two angles $ \alpha_{\text{PA}} $ and $ \beta_{\text{PA}} $ for $ \Omega_{\text{PA}} $ can be solved from the real and imaginary parts of (13), which gives

Therefore, the intrinsic state described in the frame of principle axes (12) becomes

Inserting

into (10), one obtains

in which the identity

is used. Using the basis in (17) the wave function can be written as

The above wave function in (19) can be interpreted as a generator-coordinate-method treatment for the generator coordinates $ \{\beta_{\pi\nu},K\} $, in which $ \hat{P}^I_{MK}|\Phi(\beta_{\pi\nu})\rangle $ is the generating wave function and the weight function is

In such an interpretation the collective wave function of $ \{\beta_{\pi\nu},K\} $ is

in which $ \mathcal{N}^{1/2} $ is the square root of the norm matrix

satisfying

Using (15) and (11) for the intrinsic state $ |\Phi(\beta_{\pi\nu})\rangle $, the norm matrix (22) can be formulated as

and it can be shown that

Using (25) and (20), the collective wave function in (21) becomes

The probability density distribution of $ \beta_{\pi\nu} $ and K can be obtained from (26) as

and

To get the so-called 'azimuthal plot' the orientation of the angular momentum with respect to the intrinsic frame is connected to the Euler angles as shown in Fig. 1 of Ref. [23], with $ M=I $ assumed in the wave function (19). The probability density distribution of the Euler angles can be obtained by treating $\beta_{\pi\nu},\; \Omega$ in (19) as generator coordinates, where Ω is involved in the projector $ \hat{P}^I_{MK} $ (see (6)). The generating function in this case is $ \hat{R}(\Omega)|\Phi(\beta_{\pi\nu})\rangle $ and the corresponding weight function is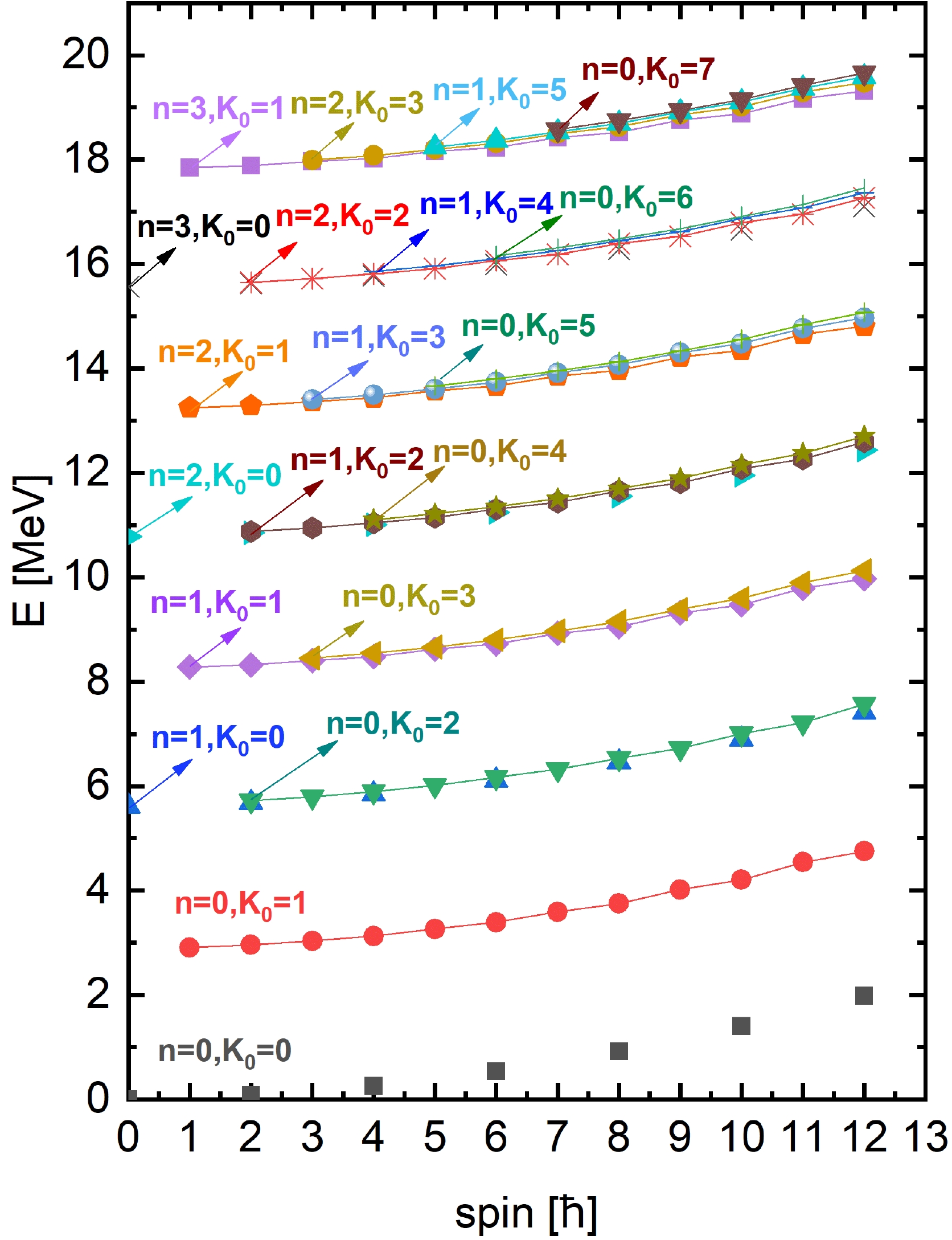

Figure 1.  (color online) Calculated spectra of scissors vibrations and their corresponding rotational bands, also shown in Ref. [19].

which can be obtained by inserting (6) into (19) and using $ M=I $. The norm matrix in this case can be connected to the previous one (24) via

and its square root $ \mathcal{M}^{1/2}(\beta_{\pi\nu},\Omega;\beta'_{\pi\nu},\Omega') $ can be obtained from (25) by

Using (29) and (31), the collective wave function of $ \{\beta_{\pi\nu},\Omega\} $ defined as

can be connected to that of $ \{\beta_{\pi\nu},K\} $:

and can be obtained easily once one gets (26). The probability density distribution of Ω, and therefore the azimuthal plot, can be obtained using (33).

The energy spectra of the scissors excitations obtained from the model framework given above are shown in Fig. 1 for a well deformed nucleus ¹⁶⁸Er given in Ref. [19]. An approximate equidistant behavior can be found in Fig. 1, consistent with the vibrational picture. The purpose for showing the figure here is to assign for each band two approximate quantum numbers n and $ K_0 $. The energy of the vibrational excitation (i.e., the energy of the band head) is approximately given as follows

as two bands with the same value of $ (2n+K_0) $ are near degenerate. The relation (34) is consistent with the interpretation by the two-rotor model [37] in terms of isotropical two-dimensional harmonic oscillator. Note that a phenomenological harmonic potential as a function of the scissors angle is assumed in Ref. [37], while the harmonicity arises naturally in the present model without any presupposition. However, the scissors vibration is harmonic only with sufficiently large deformation. For small deformations, the scissors motion has a large amplitude, and anharmonicity develops. The odd-even staggering mentioned above, existing in the $ n=0, K_0=1 $ band shown in Fig. 1, is shown explicitly in Fig. 2 in terms of the quantity $ S(I)=[E(I)-E(I-1)]/2I $.

Figure 2.  (color online) The odd-even staggering of the lowest scsissors band $ n=0, K_0=1 $, shown in terms of the quantity $ S(I)=[E(I)- E(I-1)]/2I $.

The E2 transitions between states in the lower-lying bands shown in Fig. 1 are given in Ref. [20]. Strong intra-band E2 transitions have been found along the scissors bands investigated, with a similar order to those of the ground state. The E2 transitions between different scissors bands are relatively small. Conversely, the strong M1 transitions take place only between neibouring scissors bands. The M1 transitions between states in the same scissors band are very small in accordance with the results shown in Ref. [17]. The $ B(M1) $ from the 1⁺ scissors state to the ground state is $ 3.53\; \mu_N^2 $, of the same order as that predicted in Ref. [17] for ¹⁵⁶Gd. Note that this M1 transition rate can be overestimated by the present model, as the fragmentation of the M1 strength due to mixing with quasiparticle excited states are not considered.

The probability density distribution of the angle $ \beta_{\pi\nu} $ between the symmetry axes of protons and neutrons (see (27)) is given in Fig. 3. All plots shown here are calculated for the band head, while the dependence on spin will be illustrated in Fig. 4. Panel (a) gives the distributions for $ n=0 $ with various $ K_0 $, where $ K_0=0 $ indicates the ground band, which peaks at $ \beta_{\pi\nu}=0 $, as expected. The bands with $ K_0>0 $ are scissors excitations with the most probable value of $ \beta_{\pi\nu} $ appearing at $ \beta_{\pi\nu}\neq0 $. The scissors angle $ \beta_{\pi\nu} $ for $ K_0=1 $ (the experimental 1⁺ scissors state) is approximately $ 10^\circ $, while the value increases with $ K_0 $, as shown in Fig. 3. Note that in the present case without a single-particle degree of freedom, the angular momentum component K can be generated only by breaking the axial symmetry, while the only way to do this in the present framework is to develop a scissors angle. In this sense, the increase of the most probable value of $ \beta_{\pi\nu} $ with $ K_0 $ is easy to understand. Finally, note that the probability density of $ \beta_{\pi\nu}=0 $ vanishes for all $ K_0\ne 0 $ owing to the implied axial symmetry.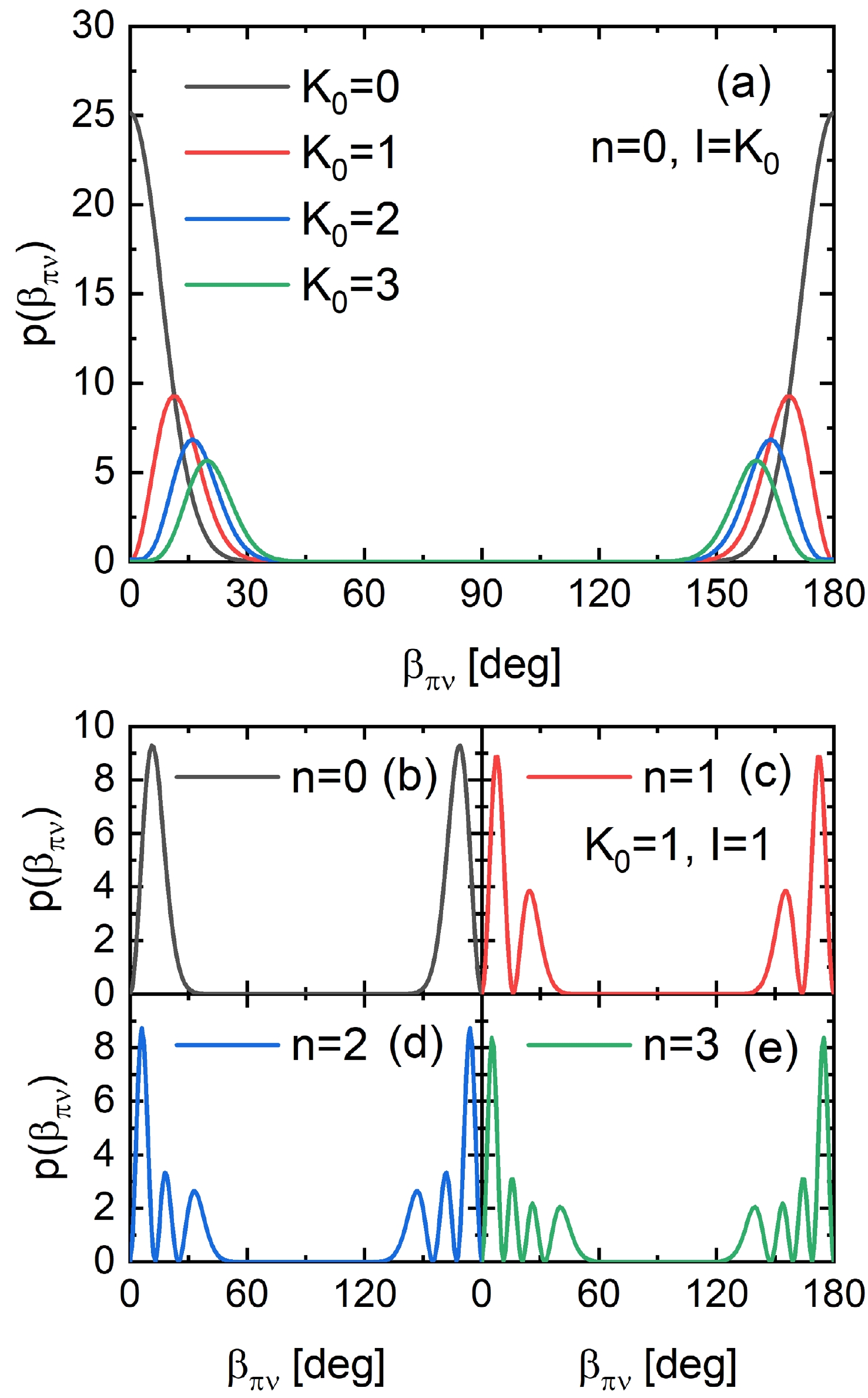

Figure 3.  (color online) Probability density distribution of the scissors angle $ \beta_{\pi\nu} $ between the symmetry axes of protons and neutrons calculated at the band head with various n and $ K_0 $.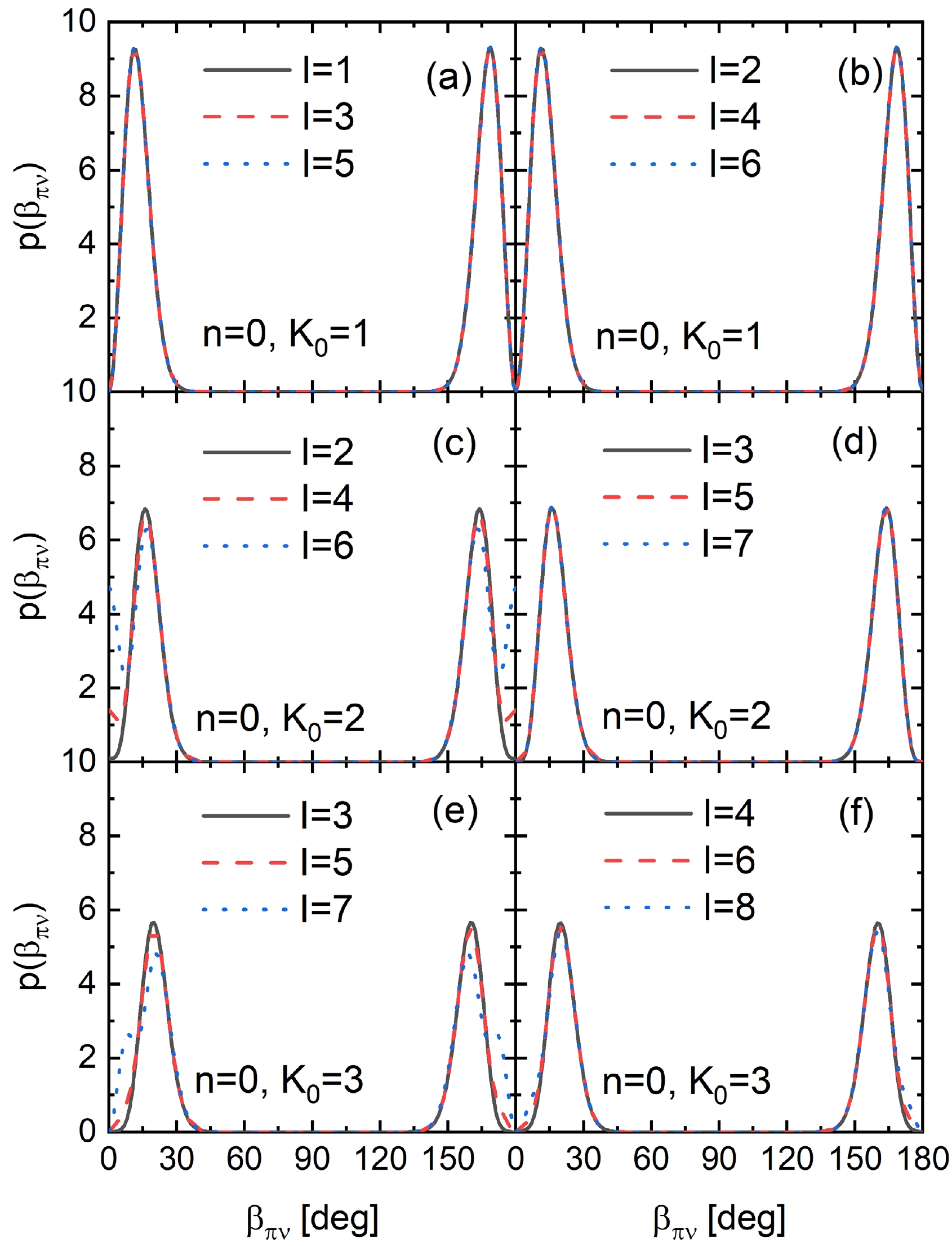

Figure 4.  (color online) Probability density distribution of the scissors angle $ \beta_{\pi\nu} $ between the symmetry axes of protons and neutrons calculated for scissors bands with $ n=0 $ and various $ K_0 $.

Panels (b)–(e) gives the distributions of $ \beta_{\pi\nu} $ for bands with $ K_0=1 $ and various n. Nodes exist in these distributions and it could be found that n is the number of nodes in the range $ \beta_{\pi\nu}\leqslant 90^\circ $, also in accordance with the isotropic harmonic oscillator interpretation [37]. (The cases of $ \beta_{\pi\nu}=0 $ with vanishing probability density are not included as a node.) One should be reminded here that the observed 1⁺ scissors band is in fact a zero-phonon state with $ n=0 $.

The evolution of the $ \beta_{\pi\nu} $ distribution with increasing spin is shown in Fig. 4. Panel (a) and (b) give results for the 1⁺ scissors band, for odd and even spins, respectively. The behavior of $ \beta_{\pi\nu} $ is found to have little dependence on spin and is almost the same for the odd and even spin members of the $ K_0=1 $ band. This implies that the scissors vibration is basically stable against the increasing frequency of collective rotation. Moreover, the odd-even splitting of the rotational energy suggested in Ref. [17] is not due to any difference in the intrinsic structure for odd and even spins.

Panels (c) and (d) in Fig. 4 show distributions of the scissors angle for the $ n=0, K_0=2 $ band, and for even and odd spins. The spin dependence of the $ \beta_{\pi\nu} $ distribution is then obtained for even spins. The probability density at $ \beta_{\pi\nu}=0 $ almost vanishes for the band head ($ I=2 $); however, it increases quickly with I. Conversely, the $ \beta_{\pi\nu} $ distribution for odd spins shows little spin dependence. The reason for such a difference can be found in Fig. 1. The $ n=0, K_0=2 $ band is near degenerate with the $ n=1, K_0=0 $ one, which has only even spin members. Therefore, the mixing between these two bands occurs only at even spins. The probability densities at $ \beta_{\pi\nu}=0 $ shown in panel (c) for $ I=4 $ and $ I=6 $ seem to arise from the $ n=1, K_0=0 $ band, since the probability density for $ \beta_{\pi\nu}=0 $ (corresponding to a single axially symmetric rotor) can be nonzero only if $ K=0 $. Similarly, the $ n=0, K_0=3 $ band, whose $ \beta_{\pi\nu} $ distributions are shown in panels (e) and (f), can mix with the band $ n=1,K_0=1 $, which has both even and odd spin members. Therefore, the spin dependence of the $ \beta_{\pi\nu} $ distribution can be found in even and odd spins. The mixing between scissors bands with different n and $ K_0 $ suggests the disturbance of the Coriolis effect to the harmonic oscillation, for which $ n, K $ are not exactly good quantum numbers.

This subsection presents an illustration of the scissors vibration in terms of the probability density distribution of the scissors angle $ \beta_{\pi\nu} $ between the symmetry axes of protons and neutrons. The scissors-like configuration can be illustrated by the non-vanishing values for $ \beta_{\pi\nu} $ with the largest probability density, as shown in above figures. The vibrational behavior of the scissors angle is reflected by the oscillating distribution shown in Fig. 3, with the number of nodes equal to n. The spin evolution of the $ \beta_{\pi\nu} $ distribution reflects the mixing between near degenerating bands with different n and $ K_0 $ and, therefore, demonstrates the development of anharmonicity owing to the Coriolis effect.

In this subsection, we will focus on the rotational behavior of the scissors mode. Unlike the ground state, the scissors-like configuration excited in axially symmetric nuclei is no longer axially symmetric [1]. Therefore, the scissors mode is allowed to rotate about various axes, as the axes perpendicular to the symmetry axis of the ground state are no longer equivalent. Bands with various K can arise from the collective rotation of the scissors mode, in a certain sense similar to the case of a triaxial rigid rotor. The value (to be exact, the probability distribution) of K is related to the choice of the rotational axis and, therefore, may provide some information on the rotational behavior of the scissors mode.

The distributions of K are discussed in Fig. 5 for representative bands with several n and $ K_0 $ (Note that a band denoted by $ K_0 $ can have admixtures of $ K\ne K_0 $.). Panel (a) gives the probability of $ K=K_0 $. The ground band $ n=0, K_0=0 $ is very pure in K, as expected, as is the 1⁺ scissors band $n=0,\;K_0=1$. The purity of K in the 1⁺ scissors band is the result of the axial symmetry of the ground state. When the symmetry axis of the neutrons (protons) deviates from that of the protons (neutrons), it has an orientation $ (\theta,\varphi) $ with respect to the latter. Owing to the axial symmetry of the ground state, the configuration with any value of φ is exactly equivalent. The symmetry corresponding to such an equivalence provides the conservation of the quantum number K in the scissors excitation. The Coriolis mixing is negligible for the 1⁺ scissors band that is not near degenerate with any other band, so K remains to a large extent as a good quantum number as spin increases.

Figure 5.  (color online) (a) Probability of $ K=K_0 $ in bands assigned to $ n=0 $ and various $ K_0 $. (b) Solid lines: Probability of $ K\neq K_0 $ in the bands assigned to $ K_0=2 $ and $ K_0=3 $ shown in Panel (a). Dashed lines: Probability of $ K=K_0 $ in bands assigned to $ n=1 $ that are near-degenerate with the bands assigned to $ K_0=2 $ and $ K_0=3 $ shown in solid lines.

The purity of K in the $n=0,\; K_0=2$ band fluctuates between odd and even spins. For odd spins it has a pure $ K=K_0 $ while for even ones K-mixing arises. This is similar to the odd-even difference arising in the $ \beta_{\pi\nu} $-distribution for this band, as shown in Fig. 4 (c) and (d). Therefore, the fluctuation observed here can also be attributed to band mixing, between near-degenerate bands $n=0, K_0=2$ and $n=1,\; K_0=0$, occurring only at even spins. The band $n=0,\;K_0=3$ also mixes with its near-degenerate partner $n=1,\;K_0=1$, with its probability of $ K=K_0 $ always less than 1.

The connection between K-mixing shown in Fig. 5 (a) and the mixing between near-degenerating bands can be further demonstrated in Fig. 5 (b). The solid lines in Fig. 5 (b) give the admixture of $ K=0 $ and $ K=1 $ in the $n=0,\;K_0=2$ and $n=0,\; K_0=3$ bands discussed above, respectively. In the $n=0,\;K_0=2$ band, the $ K=0 $ component comes from mixing with the $n=1,\;K_0=0$ band, and appears only for even spins. Consequently, the probability of $ K=0 $ fluctuates in a opposite phase to the probability of $ K=K_0=2 $ shown in panel (a). Similarly, the probability of $ K=1 $ in the $ n=0,K_0=3 $band, owing to mixing with the band $n=1,\;K_0=1$, also behaves opposite to the probability of $ K=K_0=3 $. The effect of band mixing also leads to impurity in K in the bands $n=1,\;K_0=0$ and $n=1,\;K_0=1$ that are mixed with the above ones, as can be found in the dashed lines in Fig. 5 (b). In panels (a) and (b), the K-mixing between near-degenerating bands increased with the spin, in accordance with the behavior of the Coriolis effect.

Besides the K-distribution, the method for rotating the scissors mode can be given in a more straightforward manner by the so-called azimuthal plot, which determines the polar and azimuthal angles of the angular momentum with respect to the intrinsic frame, defined here by the principle axes of the MoI, as described in Sec. II. The definition of the polar angle θ and the azimuthal angle φ are illustrated in Fig. 6. The azimuthal plot is invented for the analysis of the 'angular momentum geometry' in the chiral doublet bands and the wobbling bands, arising from the deviation of the total angular momentum from the principle axes due to the angular momenta contributed by the valence nucleons. In the present case without valence nucleons, the angular momentum may also deviate from the principle axes owing to the axial symmetry breaking with a finite scissors angle.

Figure 6.  (color online) Illustration of the polar angle θ and the azimuthal angle φ describing the orientation of the angular momentum with respect to the principle axes, denoted by 1, 2, and 3 here. The two dashed lines represent the symmetry axes for neutrons and protons, respectively, staying within the 1–3 plane. The red solid line represents the orientation of the angular momentum. The polar angle θ is the angle between the angular momentum and the 3-axis, while the azimuthal angle φ represents the angle between the 1-axis and the projection of the angular momentum on the 1–2 plane.

The azimuthal plot for the scissors band $n=0,\; K_0=1$ is shown in Fig. 7 for $ I=1-6\hbar $, with the definition of the angles θ and φ illustrated in Fig. 6. For the band head shown in panel (a), the angular momentum is generated by the scissors vibration rather than the collective rotation. The remaining panels in Fig. 7 show two types of orientation distributions for the angular momentum. The distributions for even spin members of this scissors band peak at $\theta=90^\circ,\;\varphi=90^\circ$, which corresponds to the 2-axis in Fig. 6. Such an axis can be described as the principle axis perpendicular to the scissors plane, i.e., the plane determined by the symmetry axes of protons and neutrons. Conversely, for odd spins, the distributions peak at $\theta=90^\circ, \varphi=0^\circ/180^\circ$, corresponding to the 1-axis in Fig. 6, i.e., the principle axis within the scissors plane. The rotation about the 2-axis is forbidden analytically for odd spins, as can be seen from the collective wave functions in Eqs. (26) and (33). Such a prohibition is governed by the signature property about the 2-axis and is therefore independent of the deformation parameter. In this sense, the odd-even flipping in the rotational axes of the scissors band is valid not only in the well deformed nuclei discussed here but also in the ones with moderate or soft deformations as long as the collective rotation can be defined.

Figure 7.  (color online) The so-called azimuthal plot showing the probability density distribution of the angles θ and φ illustrated in Fig. 6 for the 1⁺ scissors band with $ n=0 $. Panels (a)–(f) correspond to states with $ I=1-6\hbar $ in this band. The color with a larger wavelength represents a larger probability density. The color codes vary for different panels.

As the odd and even spin branches in the scissors band $n=0,\;K_0=1$ rotate about different axes, they might have different MoIs. In Fig. 3 in Ref. [17], it was shown that the even spin branch has a larger MoI than the odd spin one. Qualitatively, this is consistent with the expression given for the MoI by the two-rotor model in terms of the scissors angle. According to Ref. [4], the MoI about the principle axis perpendicular to the scissors plane (i.e., for the even spin branch) is the same as that of the axially symmetric rotor without the scissors degree of freedom. The MoI about the principle axis within the scissors plane (for odd spin) is reduced by the factor $ \cos^2(\beta_{\pi\nu}/2) $, where $ \beta_{\pi\nu} $ is the scissors angle. Therefore, the odd-even difference in MoI and, therefore, the odd-even splitting in the scissors band can be attributed to the flipping rotational axis between odd and even spins. The odd-even splitting due to the difference in MoI will increase with spin, as a result of the $ I(I+1) $ law, as predicted in Fig. 1. However, that does not mean a spin variation of the rotational behavior or the azimuthal plot. Finally, the splitting behavior of the scissors band is independent of the deformation parameter and is also valid for moderately deformed or soft nuclei.

Interestingly, the azimuthal plot for $n=0,\;K_0=2$ is shown in Fig. 8. Two nodes exist in all panels of Fig. 8, whereas only one exists in Fig. 7. This suggests that the number $ K_0 $ is related to the number of nodes in the azimuthal plot. Similar to the nodes in the scissors angle distribution, the nodes in the azimuthal plot may also be connected with a vibrational behavior, i.e., the oscillation (not necessarily harmonic) in the orientation of the angular momentum with respect to the intrinsic frame. The wobbling mode predicted for a triaxial rotor by Bohr and Mottelson is an example of such an oscillation [38].

Figure 8.  (color online) The same as Fig. 7 but for the $ n=0, $$ K_0=2 $ band.

Finally, the azimuthal plots for the band $n=1,\;K_0=1$ are given in Fig. 9, being very similar to those in Fig. 7 for the $n=0,\;K_0=1$ band. This suggests that the method of collective rotation of the scissors mode is almost independent of n or the phonon number of the scissors vibration. However, a slight difference can be found between Fig. 9 and Fig. 7, which becomes more apparent with increasing spin. This difference can again be attributed to the mixing of the $n=1,\;K_0=1$ band with its near degenerate partner $n=0,\;K_0=3$, which does not exist in the $ n=0 $ case.

Figure 9.  (color online) The same as Fig. 7, but for the $n=1, $$ K_0=1$ band.

This subsection discusses the rotational behavior of the scissors mode in terms of the K-distribution and the azimuthal plot. The quantum number K for the 1⁺ scissors band $n=0,\;K_0=1$ is very pure up to the largest spin considered, owing to the axial symmetry of the ground state and the absence of a strong Coriolis effect. For higher scissors bands, the purity of K is reduced owing to the mixing among near degenerate bands with the same $ (2n+K_0) $. The mixing that increases with spin suggests the development of anharmonicity due to the Coriolis effect. The so-called azimuthal plot for the 1⁺ scissors band $n=0,\;K_0=1$ suggests different rotational axes for its odd and even spin branches, leading to different MoIs and odd-even splitting that has been present before mixing with quasiparticle excitations, as is suggested in Ref. [17]. The splitting behavior is governed by the symmetry of the system and also exists in scissors bands with moderate or soft deformation. The azimuthal plots also illustrate the wobbling-like motion of the orientation of the angular momentum with respect to the principle axes, which is related to $ K_0 $ and almost independent of n.

This study illustrates the intrinsic motion and rotational behavior of the scissors mode based on an angular-momentum-projected model framework. The framework with independent projections for protons and neutrons can be understood as a generator-coordinate-method for the scissors angle and the Euler angles, so the motion in these degrees of freedom can be visualized by collective wave functions. States (bands) in the scissors spectra can be characterized by two quantum numbers n and $ K_0 $, with the excitation energy proportional to $ (2n+K_0) $, as a microscopic support to the picture of harmonic oscillation assumed by the two-rotor model. The intrinsic vibrational motion in the scissors angle can be illustrated by the oscillating structure in its probability density distribution, in which the number of nodes is related to the quantum number n. For the $n=0,\; K_0=1$ scissors band corresponding to the experimentally observed one, the intrinsic scissors vibration is very stable against the development of collective rotation. However, for bands with higher n or $ K_0 $, mixing among near-degenerate ones with equal $ (2n+K_0) $ appears and increases with spin, suggesting an increasing anharmonicity in the scissors vibration due to the Coriolis effect. Moreover, the choice of the rotational axis is based on the development of the scissors angle, even in nuclei with an axially symmetric ground state. The odd and even spin members of the 1⁺ scissors band are found to rotate about different axes with different MoI, which provides a possible explanation for the odd-even splitting behavior expected to exist extensively in scissors bands. For bands with higher $ K_0 $, wobbling-like motions of the intrinsic orientation of the angular momentum seem to occur, as oscillating structures can be found in the azimuthal plots with the number of nodes connected to $ K_0 $. The motion of the orientation of the angular momentum is almost independent of n, except for small Coriolis perturbations.

Notably, several important degrees of freedom are omitted in the present model framework, like multi-quasiparticle excitations, particle number projection, and shape mixing. The multi-quasiparticle excitations can be important, not only for high spins, in the scissors motion. For example, it has been found in Ref. [17] that the odd-even splitting of the scissors band can be enhanced by including two-quasiparticle configurations. Therefore, the coupling between quasiparticle excitations and the scissors motion should be investigated carefully in the future. However, the particle number projection is expected to be important only if the properties under investigation vary significantly from one nucleus to its neighbor. In the well deformed rare earth region discussed here, the structures between neighboring nuclei are quite similar, and the effect of particle number projection is assumed to be small. The shape mixing is expected to affect the scissors motion via its effect on the MoI, as the scissors motion is esentially the rotational motion of two interacting rotors. Therefore, the effect of shape mixing on the scissors motion might not be decisive as long as the 2⁺ energy of the ground state band, as a representation of the MoI, can be estimated by the minimum deformation, which is the case for most deformed nuclei, including the transitional ones.