-
The study of one-step and two-step transfer of nucleons and clusters in nuclear reactions may answer the question of the existence of multi-neutron systems, which is an important problem in nuclear physics. The problem of the existence of light neutron clusters (dineutron, tetraneutron, etc.) is over 60 years old, but it is still of interest for both theoretical and experimental studies [1−5]. A recent paper [6] reported that the observation of a resonance structure near the threshold for the formation of a four-neutron system corresponds to a quasi-bound tetraneutron cluster that manifests itself in the 8He+p→4He+p+4n reaction and lives for a very short time.
Concerning the problem of studying light neutron clusters, a dineutron is of great interest. The dineutron can be formed near the surface of neutron-rich nuclei [7]. The first attempt to observe an unstable dineutron, i.e., a system of two neutrons in the singlet state, was made by V. K. Voitovetskii et al. in reaction 2H(n,p)2n at En = 14 MeV from the spectrum of the protons [8]. In Ref. [9], the authors studied the decay of the 16Ве nucleus and obtained results that show the dineutron nature of the decay with a small angle of emission between two neutrons. The measured two-neutron separation energy for 16Ве was 1.35 MeV, which is consistent with calculations in the shell model. However, in these calculations, the authors did not take into account the interaction between the emitted neutrons, which can also explain the observed correlations of the emission angles of the two neutrons [10].
Two-neutron transfer reactions are a unique tool for studying the interaction between neutrons and confirming the existence of the dineutron clusters that manifest themselves during the interaction of two nuclei [11−15]. The difficulty in interpreting experimental data is that such reactions can proceed as both one-step and two-step neutron transfer processes, which cannot be separated experimentally [16]. In Ref. [17], the authors showed that the product nuclei are formed as a result of one-step transfer of two neutrons and that the contribution of this process is especially significant when low-lying excited states are populated in the formed nuclei. Thus, to describe experimental data, it is extremely important to take into account the probabilities of both one-step and two-step neutron transfer [18].
In the elastic scattering of 6He nuclei on 4He [19−22] and 4He on 6Li [23], an increase in the cross-section at backward angles was observed. The authors interpreted this increase as the existence of the dineutron cluster in the 6Не nucleus and the deuteron cluster in the 6Li nucleus. However, the optical model of elastic scattering could not describe this effect, while the calculation of the corresponding transfer cross-sections for dineutron and deuteron clusters within the framework of the distorted wave Born approximation (DWBA) method fully explained this behavior as the contribution of the channel of the transfer of a two-nucleon cluster.
Another interesting experimental result was obtained in Ref. [24] for the 6He+65Cu reaction at a beam energy of 22.6 MeV: the cross-section for the two-neutron transfer was found to be larger than that for one-neutron transfer. Thus, the authors concluded that “the dineutron configuration of 6He plays a dominant role in the reaction mechanism.”
Concerning the 9Be nucleus, it was revealed that the dineutron cluster manifests itself in the reaction channel 9Be(3He,7Be)5He [25, 26]. The 9Be(3He,6He)6Be reaction channel observed at forward angles corresponds to the transfer of three neutrons. The calculations reported in [25] within the framework of the coupled reaction channels (CRC) method showed that the two-step transfer mechanisms (n-2n and 2n-n) make a significant contribution to the cross-section, which is also an indirect evidence of the transfer of the dineutron cluster.
The present study is a part of our systematic studies of nucleon and cluster transfer in reactions with various projectiles on 9Be: d + 9Be [27] and 3He+9Be [25, 26]. Here, we studied reaction channels with the weakly bound projectile nucleus 6Li. The aim was to elucidate the manifestation of the cluster structure of 9Be in the studied reaction channels. In particular, we focused on the reaction channel 9Be(6Li,8Li)7Be to estimate whether a one-step or two-step transfer is the most probable mechanism of the transfer of two neutrons.
Section II provides a detailed description of the conducted experiment. Section III presents experimental cross-sections and their comparative analysis. Sections IV and V are devoted to the theoretical method employed to analyze the experimental data. Sections VI and VII present the results of the theoretical analysis of the experimental data.
-
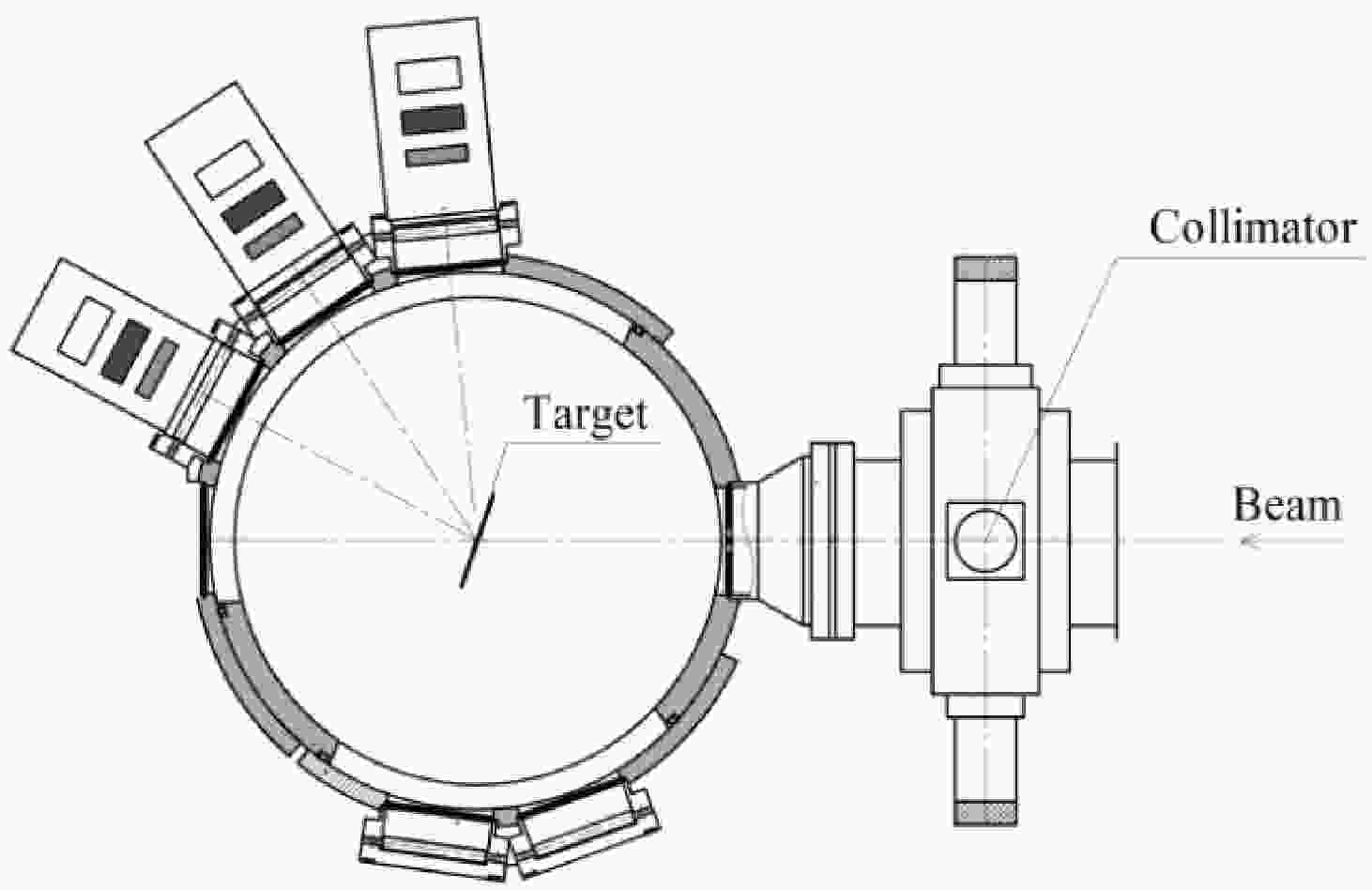
The experiment was performed at the Flerov Laboratory of Nuclear Reactions, Joint Institute for Nuclear Research, Dubna. An intense 6Li beam with an energy of 68 MeV was accelerated by the U-400 cyclotron and transported to the reaction chamber (Fig. 1) of the high-resolution magnetic analyzer MAVR [28].
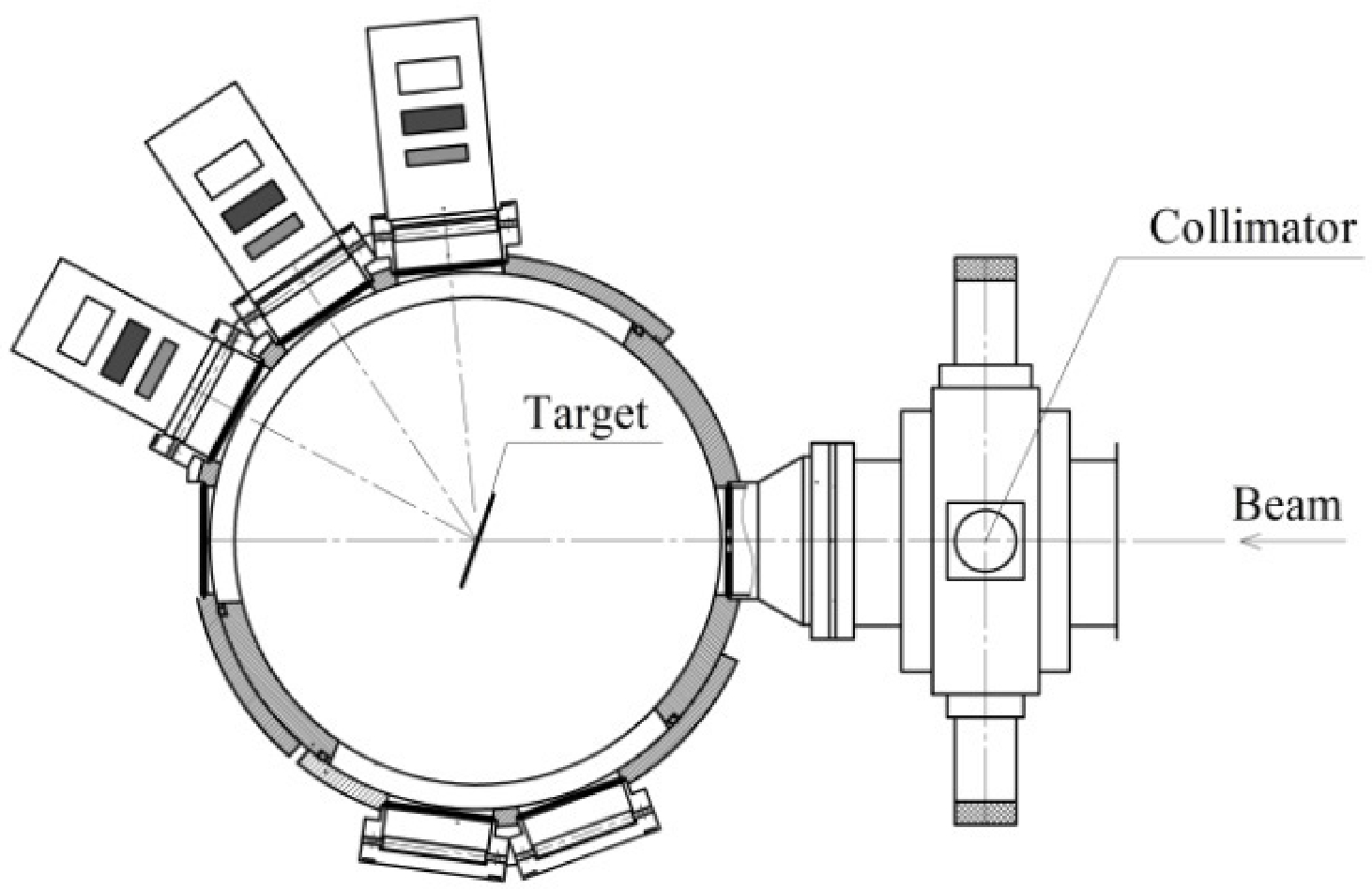
Figure 1. Reaction chamber with the 9Be foil target and three three-layer semiconductor telescopes (∆E1, ∆Е2, ER).
The beam profile was formed by the magnetic optics of the U-400 cyclotron supplemented by a system of diaphragms. The beam size was controlled by the profilometer installed in front of the reaction chamber; on a target, it was 5 mm × 5 mm at an intensity of 30 nA. The total number of particles passing through the target was determined by a Faraday cup and also monitored by elastic scattering.
The beam was focused onto the self-supporting 5-µm thick 9Be foil. The target purity was higher than 99%; a possible admixture of carbon and oxygen isotopes in the target material was not observed in the measured energy spectra.
Particle identification was done by measuring energy losses and residual energy in detectors (∆E-E method). For this purpose, three three-layer semiconductor telescopes were used, the first two thin detectors of which measured specific energy losses ∆E1, ∆Е2 (Fig. 1). Their thickness was 50 and 300 µm, respectively. The third detector ER was 3.2-mm thick and measured the residual energy of the reaction products after they passed through the first two detectors. The configuration of such telescopes made it possible to reliably identify reaction products from helium to boron isotopes in a wide energy range. Examples of identification matrices obtained by one of the telescopes used in the experiments are shown in Fig. 2. It can be seen that the reaction products were unambiguously identified.
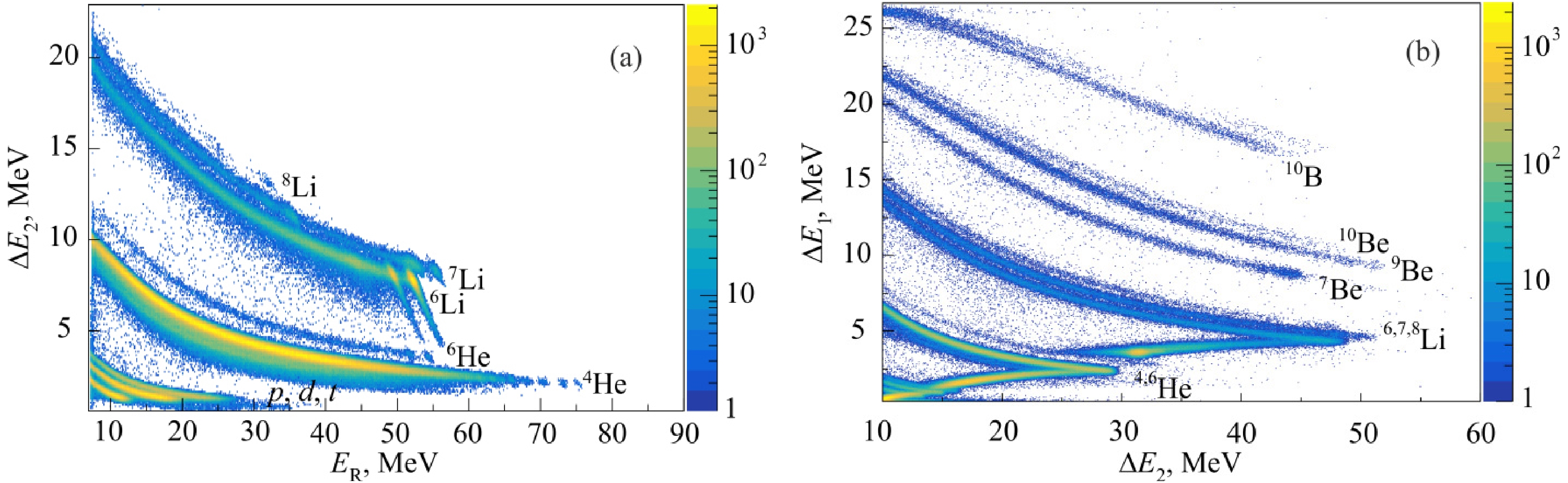
Figure 2. (color online) Examples of identification matrices obtained by one of the telescopes: (a) ∆E2- ∆ER at an angle of θlab= 16° and (b) ∆E1-∆E2 at θlab= 12°.
To measure the energy spectra and angular distributions of the nuclei emitted in the reaction, we used an inclusive method. The energy resolution of the detecting system was determined by the energy resolution of the 6Li beam and errors in measuring the energy losses of particles in the target material. In the case of registration of particles with Z = 1‒3, the energy resolution was ≈ 500 keV; for particles with Z = 4‒5, it was ≈ 1 MeV.
The excitation energy spectra corresponding to the energy of the states of the 9Be, 8Be, 7Be, and 8Li nuclei are shown in Figs. 3 and 4. The populated ground and first excited states are indicated. Note that the width of each peak of a state in the spectra was determined by three factors: natural width, instrument resolution of the spectrometer, and energy spread. Events corresponding to multibody exit channels make insignificant contributions to these peaks. The excited states of the complementary products corresponding to the two-body exit channels can be observed in the resulting energy spectra. The complementary products are as follows:
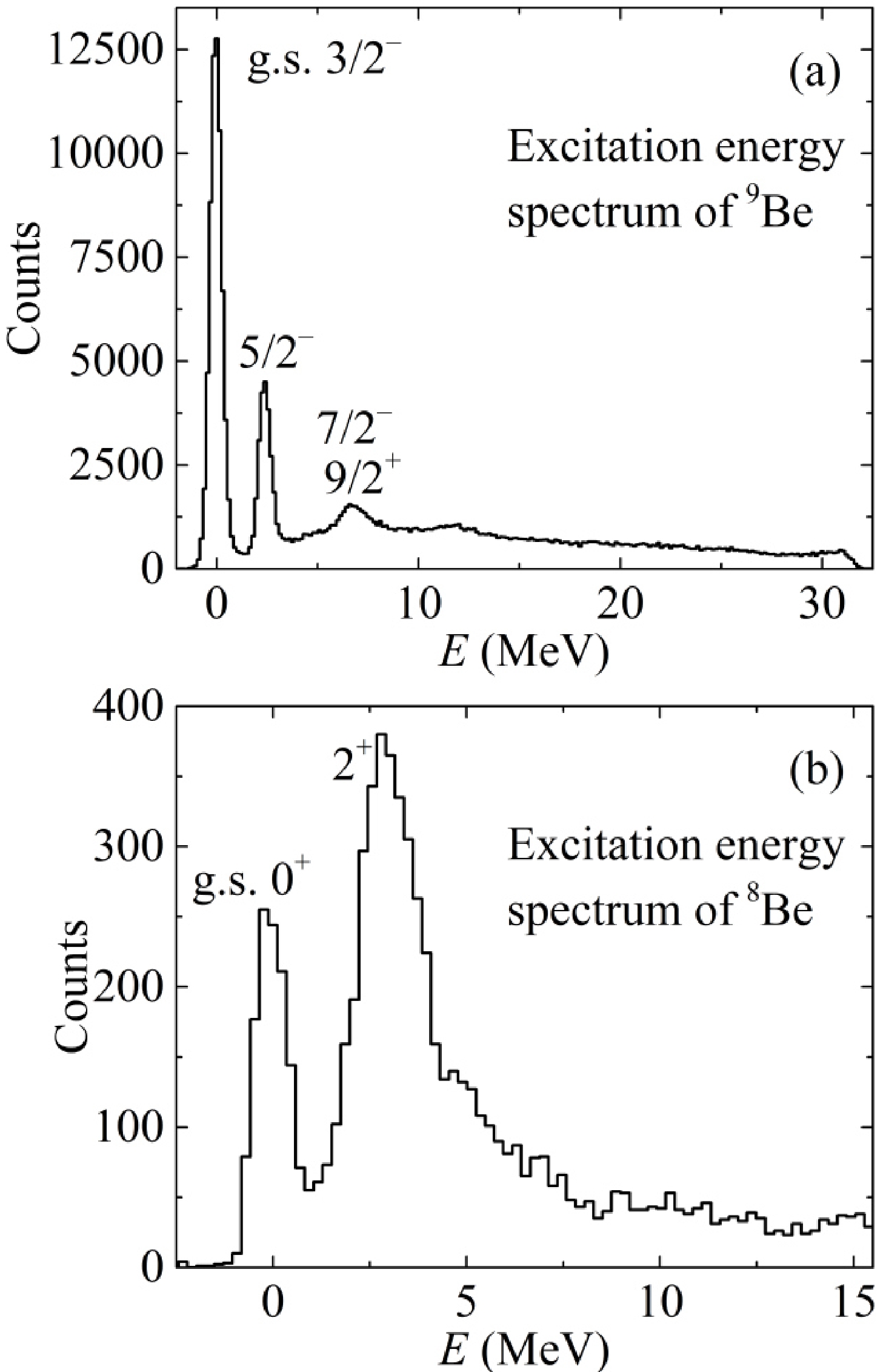
Figure 3. Excitation energy spectra for (a) 9Be in the case of detection of 6Li at an angle of θlab= 16° and (b) 8Be in the case of detection of 7Li at θlab= 14°.
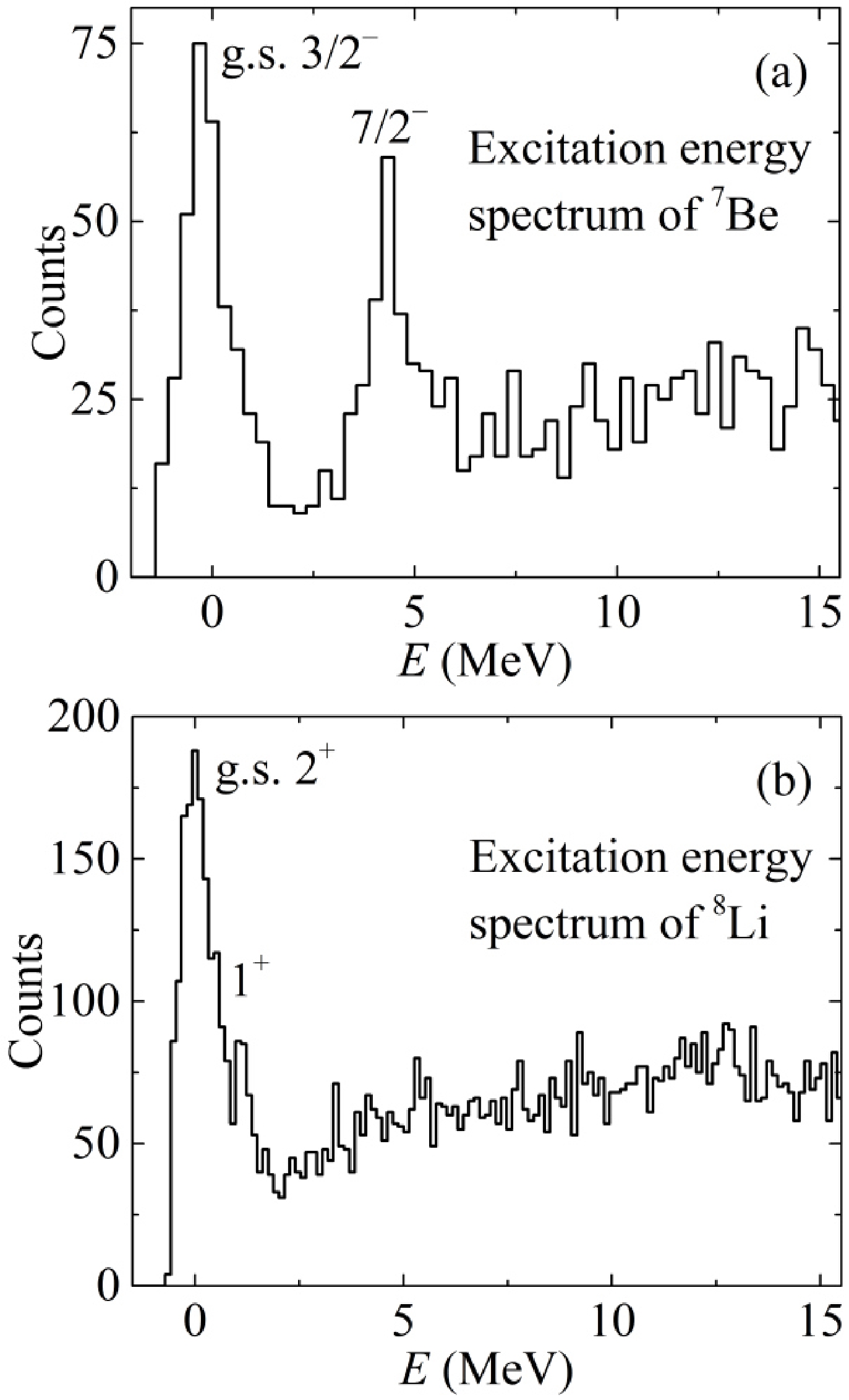
Figure 4. Excitation energy spectra for (a) 7Be in the case of detection of 8Li at an angle of θlab= 12° and (b) 8Li in the case of detection of 7Be at θlab= 16°.
– 9Ве in the reaction channel 9Be(6Li,6Li)9Be (in the case of detection of 6Li [Fig. 3(a)]);
– 8Ве in the reaction channel 9Be(6Li,7Li)8Be (in the case of detection of 7Li [Fig. 3(b)]);
– 7Ве in the reaction channel 9Be(6Li,8Li)7Be (in the case of detection of 8Li) [Fig. 4(a)];
– 8Li in the reaction channel 9Be(6Li,7Be)8Li (in the case of detection of 7Be [Fig. 4(b)]).
The narrow peak at 2.43 MeV in Fig. 3(a) is the first excited rotational level 5/2– of the 9Be nucleus. The next wide peak corresponds to overlapping of two excited levels (7/2–, 6.38 MeV) and (9/2+, 6.76 MeV) of 9Be. The narrow peak at 3.03 MeV in Fig. 3(b) is the first excited rotational level 2+ of the 8Be nucleus. For the 9Be and 8Be nuclei, the first rotational levels 5/2– and 2+ are populated with large probabilities. The single-particle excited levels of the 9Be nucleus are not observed because of the small neutron separation threshold (Table 1). For the 7Be nucleus [Fig. 4(a)], the first low-lying single-particle excited level (1/2–, 0.43 MeV) is not separated from the ground state peak, and the second single-particle excited level (7/2–, 4.57 MeV) is observed. Other single-particle excited levels of the 7Be nucleus are not observed because they are above the proton separation threshold (Table 1) and are populated with low probability. For the 8Li nucleus [Fig. 4(b)], the first low-lying single-particle excited level (1+, 0.98 MeV) is situated near the ground state peak. Other single-particle excited levels of the 8Li nucleus are not observed because they are above the neutron separation threshold (Table 1) and are populated with low probability.
Nucleus Alpha particle α /MeV Proton p /MeV Neutron n /MeV 8Li 6.1 12.4 2.03 7Be 1.59 5.6 10.7 8Be –0.092 17.3 18.9 9Be 2.46 16.9 1.66 Table 1. Particle separation energies for the 8Li and 7,8,9Be nuclei.
-
Differential cross-sections for each angle were obtained by considering solid angles of the telescopes, the thickness of the target, and the number of particles incident on the target. The experimental setup made it possible to measure the energy spectra of the reaction products in the range of angles 10°–83° in the laboratory system; the error in measuring the angle was ±1°. Angles greater than 83° could not be measured because of the design features of the scattering chamber. The measured angular distributions of the products of the reaction 6Li+9Be at an energy of 68 MeV are presented in Figs. 5, 6. The relative error in cross-section measurements is not larger than 20%. This error is predominantly due to the following factors: statistical errors in counting events, errors in target thickness determination, inaccuracies in solid angle values, and errors in beam intensity measurements.
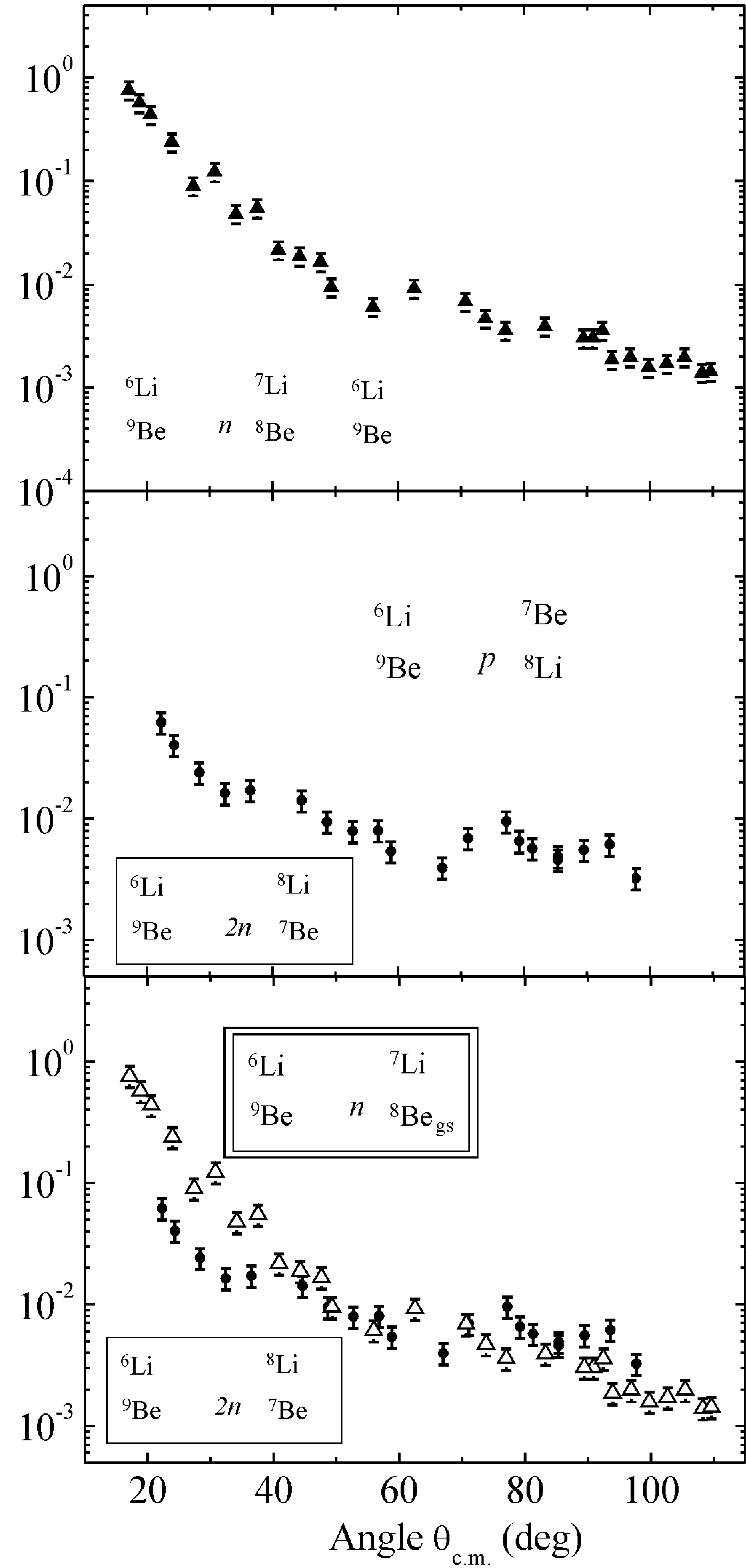
Figure 5. Experimental angular distributions for the products of the 6Li+9Be reaction at 68 MeV: (a) 7Li in exit channels 7Li+8Begs (triangles) and 7Li+8Be2+ (circles); (b) 8Li (circles) and 7Be (triangles) in exit channels 8Li gs+7Begs,1/2– and 7Begs+8Ligs,1+, respectively; (c) 7Li in exit channel 7Li+8Begs (empty triangles) and 8Li (circles) in exit channel 8Li gs+7Begs,1/2–. The transfer mechanisms are shown in insets.
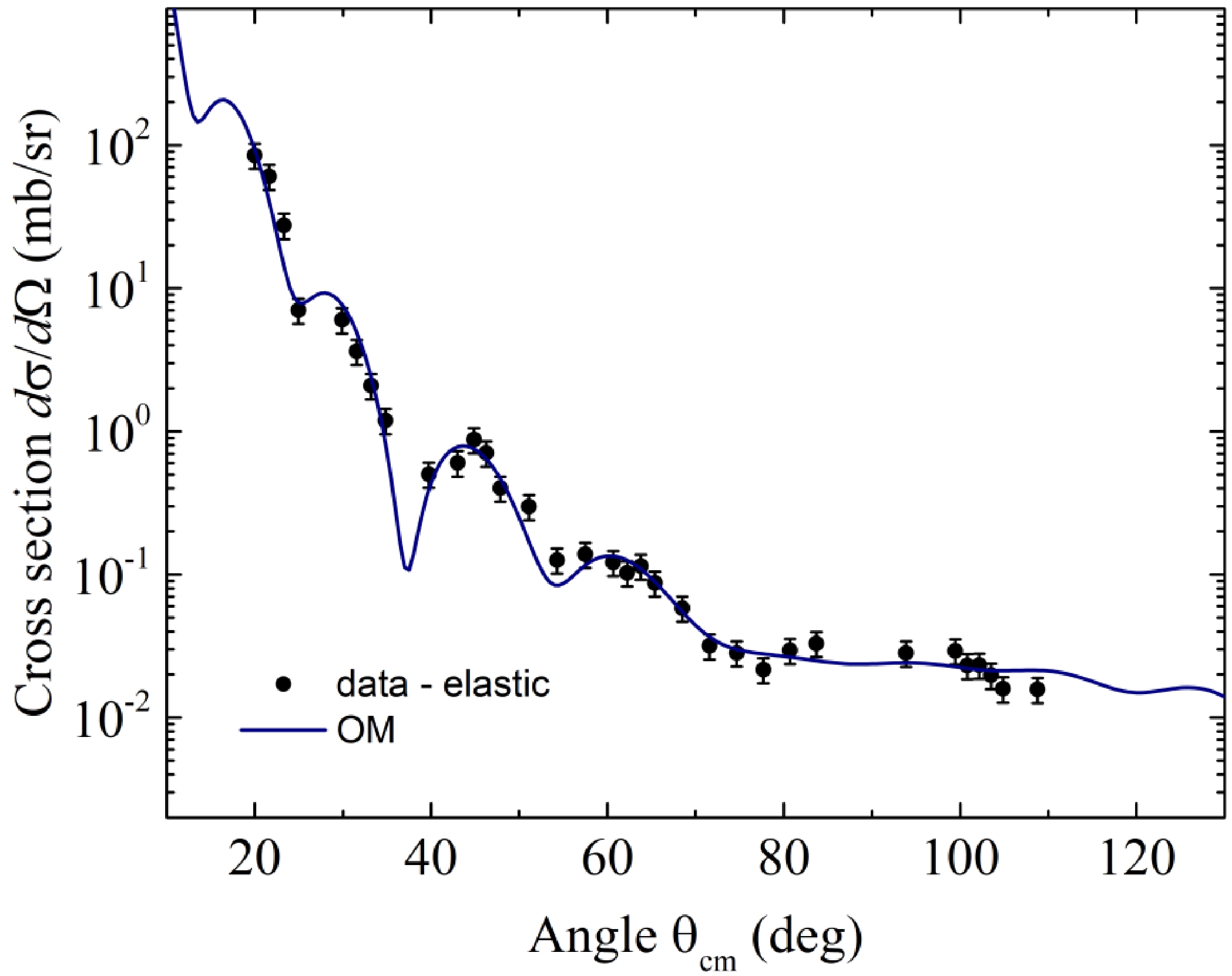
Figure 6. (color online) Angular distributions for the elastic scattering channel 9Be(6Li,6Li)9Be: experimental data (circles) and results of calculations (curves).
The relatively high cross-sections for the transfer of one neutron n from the weakly bound target nucleus 9Be [Fig. 5(a)] can be explained by the manifestation of its cluster structure (α+n+α) [27]. The differential cross-sections for the transfer of two neutrons in the reaction channel 9Be(6Li,8Li)7Be have comparable values with those for the reaction channels of the transfer of one neutron, 9Be(6Li,7Li)8Begs and 9Be(6Li,7Li)8Be2+. As can be seen from Fig. 5(c), the ratio σ1n/σ2n for the reaction channels 9Be(6Li,7Li)8Begs and 9Be(6Li,8Li)7Be at forward angles is approximately equal to 10 and smoothly decreases with increasing angle to ~ 1.
-
Experimental differential cross-sections for elastic scattering of 6Li on the 9Be nucleus are presented in Fig. 6. The experimental data were analyzed within the optical model using the Fresco code [29, 30]. The optical potential used in the calculations is expressed as
$ U\left( r \right) = - {V_{\text{V}}}f(r;{R_{\text{V}}},{a_{\text{V}}}) - {\rm i}{V_{\text{W}}}f(r;{R_{\text{W}}},{a_{\text{W}}}) + {V_{\text{C}}}\left( r \right) , $

(1) with the Woods-Saxon form-factors for both the real and imaginary parts expressed as
$ f(r;{R_{{\text{V,W}}}},{a_{{\text{V,W}}}}) = {\left\{ {1 + \exp \left[ {{{\left( {r - {R_{{\text{V,W}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {r - {R_{{\text{V,W}}}}} \right)} {{a_{{\text{V,W}}}}}}} \right. } {{a_{{\text{V,W}}}}}}} \right]} \right\}^{ - 1}} , $

(2) where
$ {R_{{\text{V,W}}}} = {r_{{\text{V,W}}}}\left( {A_{\text{p}}^{1/3} + A_{\text{t}}^{1/3}} \right) , $

(3) VV and VW are the depth parameters for the real and imaginary parts of the optical potential, respectively; rV,W and aV,W are geometric parameters; Ap and At are the mass numbers of the projectile and target nuclei, respectively; VC (r) is the Coulomb potential of a uniformly charged sphere with radius
$ {R}_{\text{С}}={r}_{\text{С}}\left({A}_{\text{p}}^{1/3}+{A}_{\text{t}}^{1/3}\right) . $

(4) In our calculations, we set rC = 0.717 fm.
The theoretical elastic scattering cross-section was fitted to the measured experimental data within the optical model using the SFresco code [30]. As a starting point for seeking the optical potential in our calculations, we used the parameters for the elastic scattering of 6Li+9Be at an energy of 50 MeV [31]. All six parameters, namely, depths VV,W and geometric parameters rV,W, aV,W, were varied. It can be seen that we achieved an excellent fit (χ2/N=1.418) of the experimental data (Fig. 6). The parameters of the potential expressed by Eq. (1) are listed in Table 2.
VV /MeV rV /fm aV /fm VW /MeV rW /fm aW /fm 152.20 0.698 0.624 12.36 1.388 0.930 Table 2. Parameters of the optical potential (1) for elastic scattering.
-
Theoretical analysis of the cross-sections for the transfer channels was performed using the DWBA method [32, 33] and the Fresco code [29, 30]. We calculated the one-step transfer using the prior formalism of the DWBA amplitude. For the two-step transfer of two neutrons, we used the second-order DWBA; a prior-post combination was chosen to avoid non-orthogonality terms [30, 32, 33]. According the DWBA formalism, the main ingredients required for calculations are the internal wave functions
$ \left( {{\phi _A},{\phi _b}} \right) $ ,$ \left( {{\phi _a},{\phi _B}} \right) $ for the nuclei in the transfer reaction A+b → a+B (A=a+x, B=b+x). The wave function for nucleus B with total spin J and spin projection M can be expressed as [30, 32, 33]$ \phi _B^{JM}\left( {\xi ,r} \right) = {\sum\limits_{Ilj} {A_{lsj}^{IJ}\left[ {\phi _b^I\left( \xi \right) \otimes {\varphi _{lsj}}\left( r \right)} \right]} _{JM}} , $

(5) where coefficients
$ A_{lsj}^{IJ} $ are the so-called coefficients of fractional parentage (CFP) or spectroscopic amplitudes, and their square moduli$ S_{lsj}^{IJ} = {\left| {A_{lsj}^{IJ}} \right|^2} $ are the spectroscopic factors [30, 32, 33]. These factors can be interpreted as a probability of finding the nucleon or cluster x in a single-particle state with quantum numbers l, s, j bound to core a or b with spin I [32]. Below, we denote the spectroscopic amplitude as Ax, where x is the nucleon or cluster with all its quantum numbers. All spectroscopic amplitudes Ax used in our calculations (Table 3) were taken from the shell model calculations reported in [13, 25, 34−37].A or B a or b x nlj Ax 7Li 6Li n 1p3/2 –0.735 7Li0.477 6Li n 1p3/2 0.329 8Li 6Li 2n 1d2 –0.667 8Li 7Li n 1p3/2 –0.478 7Be 6Li p 1p3/2 –0.735 7Be0.429 6Li p 1p3/2 –1.740 8Be 7Be n 1p3/2 –1.234 8Be3.03 7Be n 1p3/2 0.771 8Be3.03 7Be0.429 n 1p3/2 −0.655 9Be 8Li p 1p1/2 –0.375 9Be 8Be n 1p3/2 0.866 9Be 7Be 2n 2s0 0.247 The wave functions of the bound states of the nucleons and dineutron clusters x in the target and projectile nuclei were obtained using the Woods-Saxon potential. The potential depths were adjusted to reproduce the experimental binding energies of the nucleons and clusters [38], while the parameters a and r0 were fixed: a = 0.65 fm and r0 = 1.25A1/3 fm [13, 25, 39].
We adjusted only the potential parameters for the exit channels [40] while keeping the parameters for the entrance and intermediate channels as well as the spectroscopic amplitudes.
-
Experimental differential cross-sections for the 9Be(6Li,7Li)8Вegs and 9Be(6Li,7Li)8Вe3.03 channels in comparison with the DWBA calculations are shown in Fig. 7. For these reaction channels, we detected the 7Li nucleus, and the 8Be product was considered complementary to the detected one.
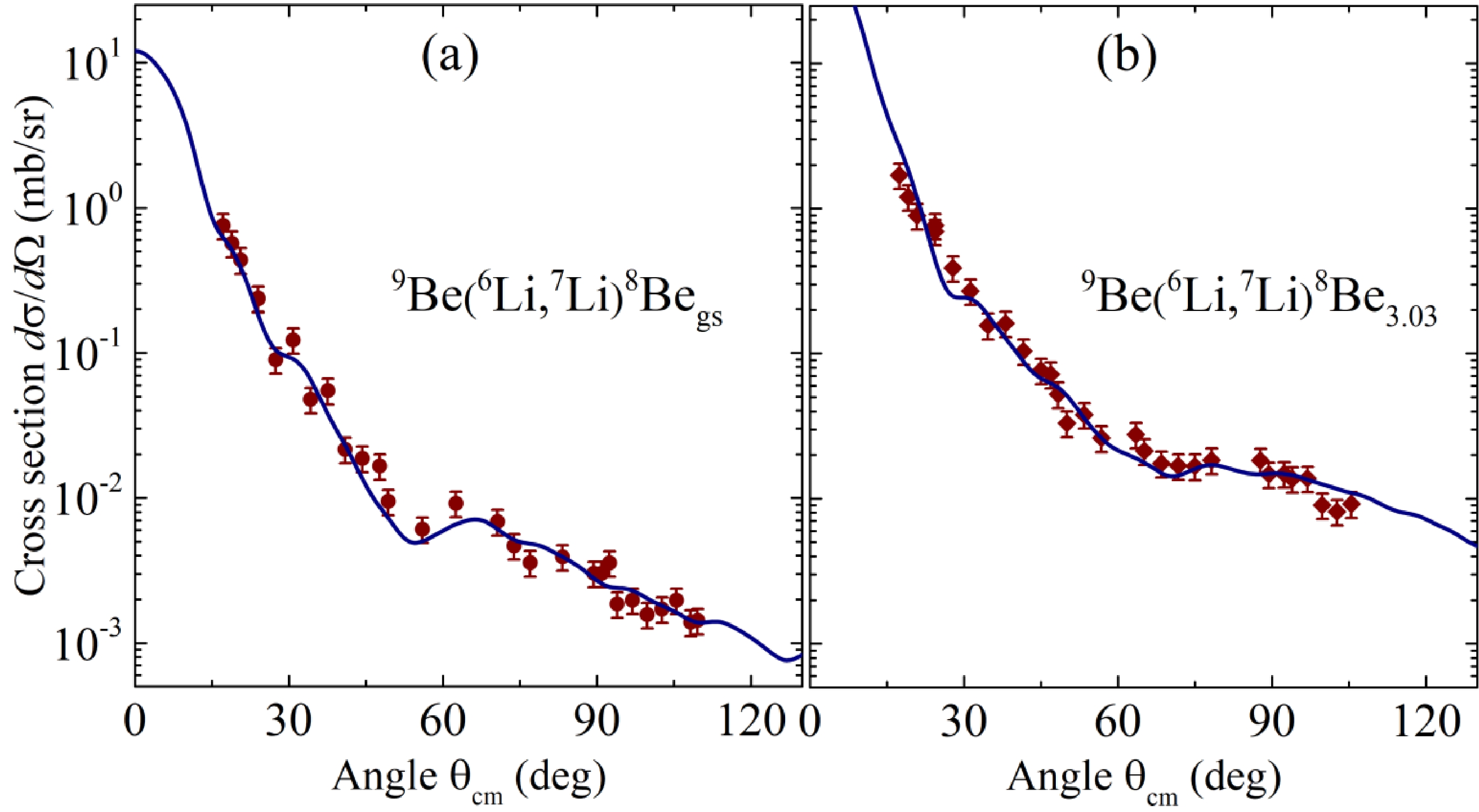
Figure 7. (color online) Experimental angular distributions for the neutron transfer channels (a) 9Be(6Li,7Li)8Вegs and (b) 9Be(6Li,7Li)8Вe3.03 (symbols) in comparison with the calculation results (curves).
The potential parameters describing the elastic scattering of 6Li+9Be (Table 2) were used for the entrance channel. For the 7Li+8Begs exit channel, we also used a potential in the Woods-Saxon form with the parameters obtained by fitting the calculation results to the experimental data on the angular distributions. The parameters recommended in [41] were used as initial parameters in the fitting procedure.
The parameters of the real part of the potential for the 7Li+8Begs exit channel were the same as those for the 7Li+8Be3.03 exit channel. However, owing to the fact that the values of the cross-sections for the 9Be(6Li,7Li)8Вe3.03 reaction channel are higher, we reduced the depth parameter VW of the imaginary part for the 7Li+8Be3.03 exit channel. To better reproduce the shape of the experimental angular distributions, we fitted the radius parameter rW of the imaginary part. As a result, an increased value of the radius parameter rW was obtained for the 7Li+8Be3.03 exit channel. Note that our DWBA calculations reproduce the experimental data well (Fig. 7). The obtained parameters of the optical potential are listed in Table 4.
Reaction channel VV /MeV rV /fm aV /fm VW /MeV rW /fm aW /fm rC /fm 7Li+8Be 152.20 0.669 0.853 30.50 1.008 0.809 0.677 7Li+8Be3.03 152.20 0.669 0.853 12.36 1.388 0.809 0.677 Table 4. Parameters of the optical potential (1) obtained for the specified exit channels.
-
Similar to the 9Be(6Li,7Li)8Be reaction channel, calculations were carried out for the 9Be(6Li,7Be)8Li reaction channel, in which the proton transfer occurs from the target nucleus to the projectile nucleus, leading to the exit channel 7Be+8Li. The spectroscopic amplitudes of the transferred proton used for the configurations 6Li+p and 8Li+p are listed in Table 3. The wave functions of the protons in the nuclei 7Be = 6Li+p and 9Be = 8Li+p were calculated by varying the depth of the Woods–Saxon potential to reproduce the binding energy exactly in the same manner as described in the previous section. It is worth mentioning that the binding energy of the proton p in the 9Ве nucleus is 16.9 MeV, which is comparable to the binding energy of two neutrons 2n in the 9Ве nucleus, 20.6 MeV.
The parameters of the Woods-Saxon potential for the 7Be+8Ligs and 7Be+8Li0.98 exit channels (Table 5) were obtained by fitting the calculation results to the experimental angular distribution at fixed potential parameters for the entrance channel (6Li+9Be, Table 2). The parameters reported in [42] were used as initial parameters in the fitting process.
Reaction channel VV /MeV rV /fm aV /fm VW /MeV rW /fm aW /fm rC /fm 7Be+8Ligs 125.50 0.657 0.853 12.25 0.888 0.809 0.664 7Be+8Li0.98 115.04 0.657 0.853 12.36 0.888 0.809 0.664 Table 5. Parameters of the optical potential (1) obtained for the specified exit channels.
The measured energy spectrum of 7Вe for the 9Be(6Li,7Вe)8Li reaction channel is shown in Fig. 4(b). Because of the relatively low energy resolution, the low-lying excited state of 8Li (1+, 0.98 MeV) is practically not resolved from the ground state. The results of the DWBA calculations for the transfer of a proton in the reaction channels 9Be(6Li,7Вe)8Ligs,0.98 are shown in Fig. 8. They are fairly close to the experimental angular distribution of the 7Вe nucleus. The solid blue curve in Fig. 8 represents an incoherent sum of the cross-sections for the ground state and the first excited state 0.98 of 8Li. The significant contribution of the reaction channel 9Be(6Li, 7Вe)8Li0.98 in the incoherent sum of the cross-sections is consistent with the measured energy spectrum of 7Be shown in Fig. 4(b).
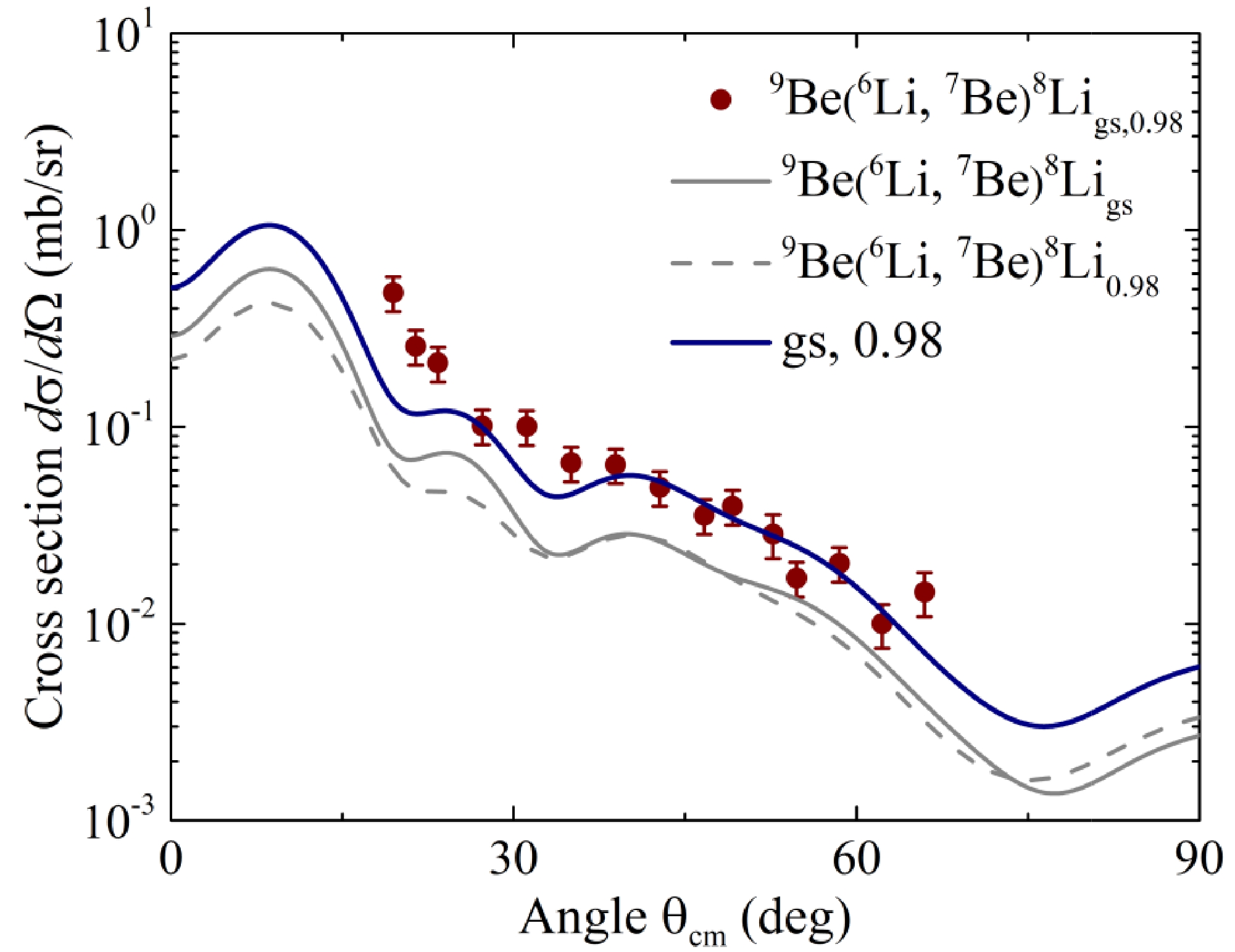
Figure 8. (color online) Experimental angular distribution of the reaction channels 9Be(6Li,7Вe)8Ligs,0.98 (circles) in comparison with the calculation results (curves).
The values of the experimental differential cross-sections at forward angles (three points at θcm=19.5°−23.4°) could not be described by the theoretical curve; this may be due to the presence of a contribution from the inelastic excitation of the 6Li projectile [43]. Nevertheless, the shape of the theoretical curve in this angular range is close to that of the experimental data.
A similar discrepancy between DWBA calculations and experimental data was observed in [43, 44]. This can be solved by adjusting the values of the spectroscopic amplitudes or reducing the imaginary part of the exit channel potential. However, in such a case, we would lose the overall agreement of the DWBA calculations with the experimental points. This fact indicates the need for more complex calculations that take into account inelastic excitations of the nuclei in the studied channels; this will be addressed in a future theoretical study.
The proton transfer, inverted with respect to the scattering angle, serves as an alternative to the two-neutron transfer mechanisms in the 9Be(6Li,8Li)7Be reaction channel [45]. Therefore, we included it in the calculations shown in Fig. 9. The one-step mechanism corresponds to the transfer of a di-neutron cluster 2n or a proton p, while the two-step mechanism corresponds to the two-step transfer of two neutrons n-n.
We used the same potential parameters from Table 5 for the 7Be+8Ligs and 8Ligs+7Be exit channels. The potential parameters obtained in Sections IV and V were used for the entrance channel (6Li+9Be, Table 2) and for the intermediate channels (7Li+8Begs and 7Li+8Be3.03 in the calculations for the n-n transfer, Table 4). The potential parameters for the exit channel 8Li+7Be0.429 were obtained by fitting the cross-section to reproduce the experimental data. As a starting point for seeking the potential, we used the parameters for the exit channel 7Li+8Begs (Table 4). The resulting parameters were as follows: VV= 155 MeV, rV = 0.669 fm, aV=0.853 fm, VW = 19.25 MeV, rW = 1.388 fm, and aW = 0.780 fm.
The spectroscopic amplitudes Ax for the nucleons and dineutron clusters included in the calculations are listed in Table 3. The higher value of Ax = 0.667 for the configuration 8Li=6Li+2n compared to Ax = 0.478 for the configuration 8Li=7Li+n may favor dineutron in the cluster transfer mechanism (i.e., one-step transfer of two neutrons) compared to the two-step mechanism of neutron transfer.
The differential cross-section for the 9Be(6Li,8Li)7Be reaction channel has the form of a coherent sum of two amplitudes,
$ \frac{{{d}\sigma }}{{{d}\Omega }}\left( {{\theta _{{\text{cm}}}}} \right) = {\left| {{f_{\text{I}}}\left( {{\theta _{{\text{cm}}}}} \right) + {f_{{\text{II}}}}\left( {{\theta _{{\text{cm}}}}} \right)} \right|^2} , $

(6) where
${f_{\text{I}}}\left( {{\theta_{{\text{cm}}}}} \right)$ and${f_{{\text{II}}}}\left( {{\theta_{{\text{cm}}}}} \right)$ are the amplitudes of the one-step and two-step transfer mechanisms, respectively [29, 30]:$ {f_{\text{I}}}\left( {{\theta_{{\text{cm}}}}} \right) = {f_{2n}}\left( {{\theta_{{\text{cm}}}}} \right) + {f_p}\left( {{\text{π }} - {\theta_{{\text{cm}}}}} \right),{f_{{\text{II}}}}\left( {{\theta_{{\text{cm}}}}} \right) = {f_{n - n}}\left( {{\theta_{{\text{cm}}}}} \right), $

(7) ${f_{2n}}\left( {{\theta_{{\text{cm}}}}} \right)$ and${f_p}\left( {\pi - {\theta_{{\text{cm}}}}} \right)$ are the amplitudes of the one-step transfer of two neutrons and proton, respectively;${f_{n - n}}\left( {{\theta_{{\text{cm}}}}} \right)$ is the amplitude of the two-step transfer of two neutrons. The experimental angular distribution of the 8Li nucleus for the reaction channel 9Be(6Li,8Li)7Вe in comparison with the calculation results is shown in Fig. 10(a). In Fig. 10(b), the DWBA calculations for each mechanism considered in the coherent sum [Eq. (6)] are presented separately: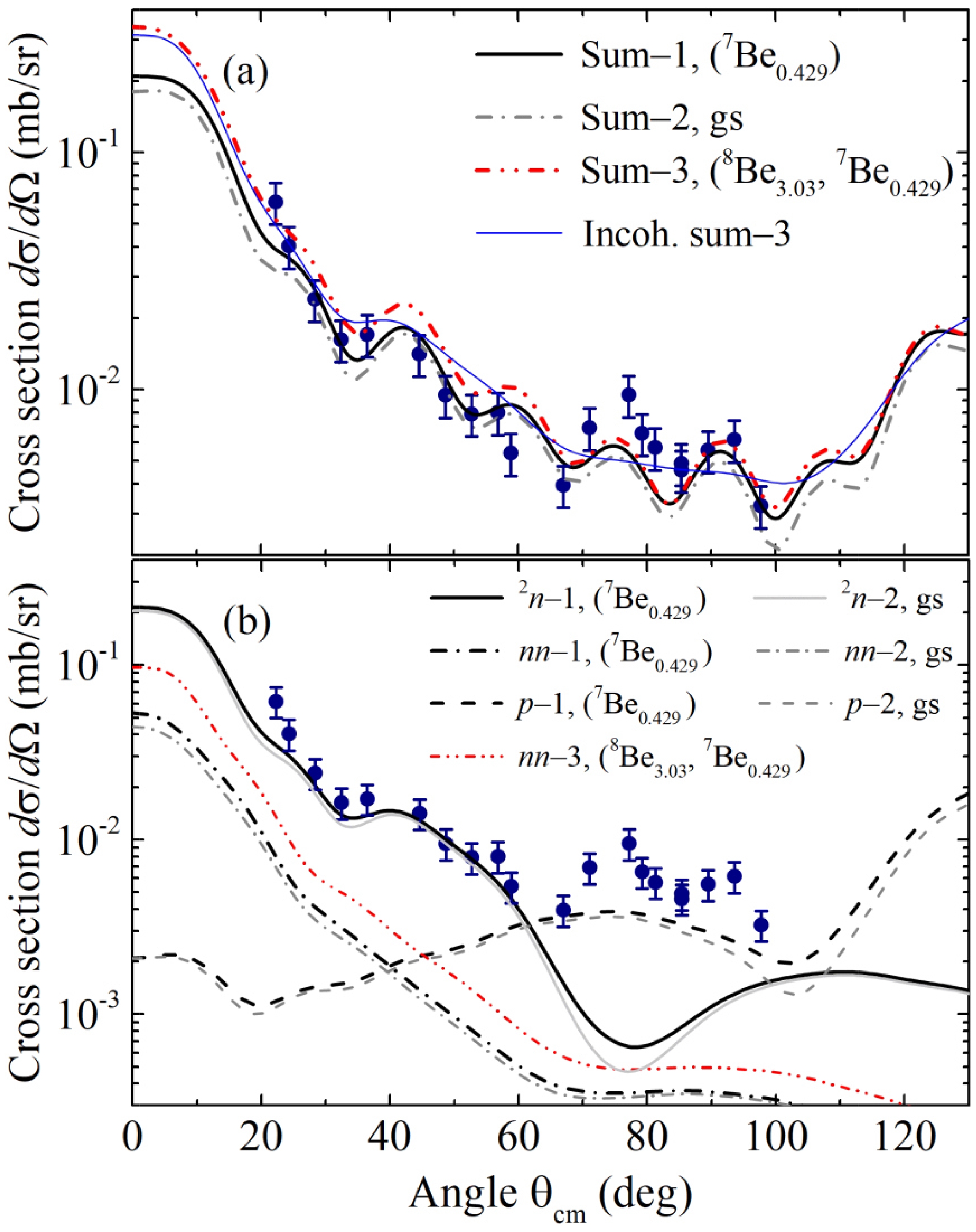
Figure 10. (color online) Experimental angular distribution of the 8Li nucleus for the nucleon transfer channels 9Be(6Li, 8Li)7Вegs,0.429 (circles) in comparison with the calculation results. The curves are the results of calculations including the excited states given in parentheses. (a) Sums of reaction mechanisms. (b) Contributions of nucleon and cluster transfer mechanisms taken into account in the calculations.
– for one-step transfer:
● 6Li+9Be → 8Ligs+7Begs,0.429 (2n–1 curve) – dineutrosn transfer included in the Sum-1 curve;
● 6Li+9Be → 8Ligs+7Begs (2n–2 curve) – dineutron transfer included in the Sum-2 curve;
● 6Li+9Be → 7Begs,0.429 +8Ligs (p–1 curve) – proton transfer included in the Sum-1 curve;
● 6Li+9Be → 7Begs +8Ligs (p–2 curve) – proton transfer included in the Sum-2 curve;
– for two-step n-n transfer:
● 6Li+9Be → 7Ligs+8Begs → 7Begs,0.429 +8Ligs (nn–1 curve) included in the Sum-1 curve;
● 6Li+9Be → 7Ligs+8Begs → 7Begs+8Ligs (nn–2 curve) included in the Sum-2 curve;
● 6Li+9Be → 7Ligs+8Begs,3.03 → 7Begs,0.429 +8Ligs (nn–3 curve) included in the Sum-3 curve.
The angular distributions of the 9Be(6Li,8Li)7Вegs,0.429 reaction channels in Fig. 10(a) have oscillations. These oscillations indicate the interference of the transfer mechanisms presented in Fig. 9. The dineutron transfer makes a relatively large contribution at forward angles, while in the range of angles 60°–130°, the proton transfer dominates [Fig. 10(b)]. The contribution of two-step neutron transfer is negligible in the entire range of angles, which is consistent with the results of [13, 18, 46, 47].
Similar oscillations due to the interference of two-neutron and α-transfer mechanisms in the reaction 14C(16O, 18O)12C were obtained in [45]. The incoherent sum yields a smoother angular distribution [45, 47], as shown by the thin solid curve in Fig. 10(a). It can be assumed that the characteristic features of two-neutron transfer reactions are the domination of the one-step transfer of two neutrons and the interference of the transfer mechanisms [18, 46, 48, 49].
Note that the 8Be3.03 state in the intermediate channel of the two-step neutron transfer provides a better description of the experimental points in the region of θcm=20°−30°; simultaneously, the calculated cross-sections in the region of θcm=45°−70° are slightly overestimated [Fig. 10(a)]. The excitation of the 8Be3.03 state in the intermediate channel does not have a strong effect on the calculation results for the 9Be(6Li,8Li)7Вe reaction channel. The same results were obtained in [13] for 9Be(7Be, 9Be)7Be.
The contribution of the 9Be(6Li,8Li)7Be0.429 channel is insignificant, which is consistent with the excitation energy spectrum of the 7Be nucleus [Fig. 4(a)]. However, taking into account the excitation of 7Be0.429 in the exit channel improves the theoretical description of the cross-sections [Fig. 10(a)]. Note that if we exclude all excitations from the calculations, the experimental differential-cross sections will be underestimated, for example, in the regions of angles θcm=0−25° and θcm=70°−85°, which indicates the importance of considering excitations of nuclei in the reaction.
Typically, the structure of the 8Li nucleus is considered in the two-body 7Li+n or three-body α+n+t theoretical models [50, 51]. The 9Be nucleus is usually represented as a system of two α-clusters and a neutron located with a high probability between them, i.e., α+n+α [52-54]. However, the large contribution of the dineutron transfer to the cross-sections [Fig. 10(b)] suggests that the 8Li and 9Be nuclei can manifest configurations corresponding to the two-body structures 6Li+2n and 7Be+2n, respectively. The contribution of the dineutron transfer mechanism in the range of angles 0–60° is approximately five times higher than the contribution of the mechanism of two-step transfer of two neutrons [46].
-
The energy and angular distributions for the 9Be(6Li, 6Li)9Be, 9Be(6Li,7Li)8Be, 9Be(6Li,8Li)7Be, and 9Be(6Li, 7Be)8Li channels in the 6Li+9Be reaction at an energy of 68 MeV were measured. The energy distributions of the detected nuclei reproduce the population scheme of the ground and low-lying excited states of complementary nuclei, which confirms the two-body nature of the reaction exit channels considered in this study.
The parameters of the Woods-Saxon optical potential were determined from the analysis of the experimental data on elastic scattering of 6Li+9Be. The consideration of elastic scattering as well as the one- and two-step transfer reaction mechanisms led to good agreement with the experimental data on the 9Be(6Li,8Li)7Be reaction channel. It was also shown that the dineutron transfer 2n makes a larger contribution to the cross-sections of the 9Be(6Li,8Li)7Be reaction channel at forward angles compared to proton transfer and two-step transfer of two neutrons. The proton transfer makes a contribution comparable to the dineutron transfer in the range of angles θcm=60°−130°. The contribution of two-step transfer of two neutrons is negligible in the entire range of angles. The oscillations in the angular distribution for the 9Be(6Li,8Li)7Вe reaction channel indicate the interference of the transfer mechanisms. The large contribution of the dineutron transfer to the cross-sections suggests that the 8Li and 9Be nuclei can manifest configurations corresponding to the two-body structures 6Li+2n and 7Be+2n, respectively.
Study of one-step and two-step neutron transfer in the reaction 6Li + 9Be
- Received Date: 2024-05-07
- Available Online: 2024-11-15
Abstract: This paper presents the results of experiments conducted to measure the cross-sections for elastic scattering and nucleon transfer channels in the 6Li+9Be reaction at an incident energy of 68 MeV: 9Be(6Li,6Li)9Be, 9Be(6Li,7Li)8Be, 9Be(6Li,7Li)8Be2+, 9Be(6Li,8Li)7Be, and 9Be(6Li,7Be)8Li. The objective of the study is to elucidate the manifestation of the cluster structure of 9Be. Theoretical analysis of the contributions of the one-step and two-step neutron transfer mechanisms is performed using the distorted wave Born approximation method with the Fresco code. Good agreement between the calculations and the experimental data is obtained for the channels of elastic scattering 9Be(6Li,6Li)9Be, neutron 9Be(6Li,7Li)8Be, and proton transfer 9Be(6Li,7Be)8Li, as well as for the transfer of two neutrons 9Be(6Li,8Li)7Be. The dineutron cluster transfer mechanism makes a dominant contribution to the 9Be(6Li,8Li)7Be reaction channel at forward angles.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: