-
High-energy experiments in hadron physics provide an important window for testing the theory of quantum chromodynamics (QCD), the strong interaction theory of the standard model. The study of the properties of the η meson provides a test of the basic symmetries of QCD in the standard model and even the possibility of a theoretical precedent beyond the standard model (BSM). In addition, the study of the η meson may provide a theoretical basis for anomalous behavior of basic symmetries. The first prediction of the η meson came from the Sakata model in the 1950s [1−5] and was finally completed by Gell-Mann and Ne'eman [6, 7], using an eightfold approach to fill in the last piece of the pseudoscalar meson octet. In 1961, the η meson was discovered in the three-pion resonance state [8], but due to isospin symmetry, Gell-Mann did not identify this channel. In addition to the traditional studies of η decay modes (see the recent review paper [9]), η also serves as a laboratory for searching for new weakly-coupled light particles at the GeV scale. These particles include dark photons and other hidden gauge bosons, light Higgs-like scalars, and axion-like particles. These particle states are predicted to be associated with dark matter and other matter beyond the SM frameworks and have become one of the most active research areas in phenomenology over the past decade [10−13].
Dark matter dominates the cosmic matter density, and its cosmological abundance and stability may indicate the existence of a dark sector with its own forces, symmetries, and spectrum of frequencies, perhaps as rich as the standard model [14]. Meson studies provide a unique opportunity to discover dark matter in the MeV-GeV mass range [15, 16]. From the perspective of symmetry, the symmetries of the standard model are extended at the level of dark matter. In particular, the extension of the SU(3)×SU(2)×U(1) gauge symmetry predicts new light vector bosons - dark photons
$A' $ . In this manner, searching for dark photons in experiments can utilize these couplings to explore the contributions of dark photons in electromagnetic interactions [17, 18]. Various experiments have been conducted to study the properties of dark photons, including Refs. [19−26]. In particular, it has been found that the study of meson decays can provide probes of dark photons, largely due to the significant number of meson events produced by large hadron colliders, which can provide a considerable number of decay modes. Inspired by Ref. [26], we will investigate the production of dark photons in conjunction with the rare decay process of η.Searching for light hidden particles through the study of η decay modes is feasible. In addition to η decay being a primary channel for searching for various exclusive hidden particles produced by proton beam dump [11, 27−31], one of the main reasons is that tagging η decay can easily distinguish between different models based on the other particles in final states. Therefore, existing high-energy colliders, as well as future ones, are crucial for searching for dark photon and dark matter candidates [17, 32]. The process of obtaining dark photons from η decay has been thoroughly analyzed and discussed in Ref. [33], and we integrated these perspectives into this study.
In this paper, we propose that in ultra-peripheral collisions (UPCs), it should be possible to find the channel where η decays into a dark photon and a classical photon, and we consider the light decay of the dark photon, ultimately leading to the reconstruction of events with a specific mass of the dark photon. The remainder of this paper is as organized follows: In Sec. II, we provide some information on the production of η in UPCs, including the equivalent photon approximation and a realistic model for the nuclear photon flux. We also describe the branching ratio of
$ \eta\to A^\prime \gamma $ . The main numerical results are presented in Sec. III, including the distribution of event yields with respect to the parameters at different center-of-mass energies. Finally, we present the main conclusions of this work, along with a brief discussion and outlook of the experimental aspects. -
The process of PbPb UPC producing η and decaying into
$A' $ is shown in Fig. 1, where the η meson is generated by the interaction of heavy-ion beam radiation. UPCs require the impact parameter of the two lead nuclei to be greater than twice the nuclear radius. In UPCs, the total cross-section of PbPb$\to $ PbPbη can be written in the well-known form from [34] with equivalent photon approximation [35]
Figure 1. (color online) Feynman diagram illustrating the production of dark photons in Pb-Pb ultraperipheral collisions. The cyan shading represents the unknown details of the η decay, and
$ \omega_{1(2)} $ denotes the energy of the photon fluxes radiated by the two lead nuclei. We only consider the case where dark photons decay into electron or muon pairs.$ \begin{aligned}[b]& \sigma\left({\rm PbPb\to Pb}\otimes\eta\otimes {\rm Pb};s\right)\\ =\;&\int{\rm{d}}^2{\bf{b}}_1{\rm{d}}^2{\bf{b}}_2{\rm{d}}W{\rm{d}}y\frac W2\hat{\sigma}\left(\gamma\gamma\to\eta;W\right) \\& \times N\left(\omega_1,{\bf{b}}_1\right)N\left(\omega_2,{\bf{b}}_2\right)\theta(|{\boldsymbol{b}}_{1}-{\bf{b}}_{2}|-2R_{\rm Pb}), \end{aligned} $

(1) where
$ W=\sqrt{4\omega_1\omega_2} $ represents invariant mass of the$ \gamma\gamma $ system, and y is the rapidity of η in the final state. The photon flux energy$ \omega_{1(2)} $ is written in terms of W and y as follows:$ \omega_1=\frac W2 {\rm e}^y\quad{\rm{and}}\quad\omega_2=\frac W2 {\rm e}^{-y}. $

(2) The step function in Eq. (1) serves as an absorption factor, excluding the overlap collisions of nuclei and thereby constraining the results within the UPC framework. It is important to emphasize that the step function represents the approximation of nuclei as hard spheres. To consider the electromagnetic distribution within the nuclei, besides introducing the electromagnetic form factor (as mentioned later), it may also be necessary to account for nuclear breakup, as referenced in [36]. This nuclear breakup can introduce significant corrections in the process of lepton pair production via photon-photon collisions [37, 38], but it is not the primary focus of our work. Moreover,
$ {\boldsymbol{b}}_{1} $ and$ {\boldsymbol{b}}_{2} $ represent the impact parameters. For nucleus, we choose$R_{\rm Pb} = r_0 A_{\rm Pb}^{1/3}$ with$ r_0 = 1.2 $ fm, and the mass number of lead is$A_{\rm Pb}=208$ . In particular,$ N(\omega,{\boldsymbol{b}}) $ is the equivalent photon flux for a given photon energy$ \omega $ and impact parameter b, which can be expressed in terms of the form factor$ F(q^2) $ for the equivalent photon source as follows:$ \begin{aligned}[b]N(\omega, b)=\;&\frac{Z^{2} \alpha_{e m}}{\pi^{2}} \frac{1}{b^{2} \omega} \Bigg[\int u^{2} J_{1}(u) \\&\times F\left(\sqrt{\frac{(b \omega / \gamma_L)^{2}+u^{2}}{b^{2}}}\right) \frac{1}{(b \omega / \gamma_L)^{2}+u^{2}} \ {\rm{d}} u\Bigg]^{2} , \end{aligned} $

(3) where Z is the atomic number of nucleus and
$ \alpha_{e m} $ denotes the fine structure constant.$ \gamma_L $ is the Lorentz factor, which is discussed below.$ J_n(u) $ is the first-kind Bessel function. Form factor is the Fourier transform of charge distribution in the nucleus. If one assumes tha$ \rho(r) $ is the spherical symmetric charge distribution, the form factor is a function of photon virtuality$ q^2 $ [39]:$ F\left(q^2\right)=\int \frac{4 \pi}{q} \rho(r) \sin (q r) r {\rm{d}} r=1-\frac{q^2\langle r^2\rangle}{3 !}+\frac{q^4\langle r^4\rangle}{5 !} \cdots. $

(4) Referring to Refs. [39, 40], the form factor function is given as
$ F(q)=\frac{\Lambda^{2}}{\Lambda^{2}+q^{2}} $

(5) with
$ \Lambda=0.088 $ GeV for nucleus [41−43]. Thus, the equivalent photon flux is written as$ \begin{aligned}[b]N(\omega,{b})=\;&\frac{Z^2 \alpha_{{\rm{em}}}}{\pi^2} \frac{1}{\omega}\Bigg[\frac{\omega}{\gamma_L} K_1\left(b \frac{\omega}{\gamma_L}\right)\\& -\sqrt{\frac{\omega^2}{\gamma_L^2}+\Lambda^2} K_1\left(b \sqrt{\frac{\omega^2}{\gamma_L^2}+\Lambda^2}\right)\Bigg]^2 . \end{aligned} $

(6) where
$ K_1 $ is the modified Bessel function of the second kind. Lorentz factor$ \gamma_L $ is computed as$ \gamma_L=\sqrt{s_{NN}}/2m_N $ , where$ m_N $ is the nucleon mass.The cross-section for the
$ \gamma\gamma\to\eta $ process can be calculated using the Low formula, given by [44]$ \hat{\sigma}(\gamma\gamma\to \eta; W^2)=8\pi^2(2J+1)\frac{\Gamma_{\eta\to\gamma\gamma}}{m_\eta}\delta(W^2-m_\eta^2), $

(7) where
$J=0 $ is η's spin, and$ \Gamma_{\eta\to \gamma\gamma} $ is the two-photon decay width of η. Moreover,$ m_\eta $ denotes the mass of the η meson.Based on Eqs. (1)−(7), the total cross-section of the process
${\rm Pb}{\rm Pb}\to {\rm Pb}\otimes\gamma {e}^+{e}^-(\mu^+\mu^-)\otimes{\rm Pb}$ is defined as$ \begin{aligned}[b]&\sigma({\rm Pb}{\rm Pb}\to {\rm Pb}\otimes\gamma {e}^+{e}^-(\mu^+\mu^-)\otimes{\rm Pb}; s) \\ =\;&\sigma\left({\rm PbPb}\to {\rm Pb}\otimes\eta\otimes {\rm Pb}\right)\\& \times {\cal{B}}(\eta\to A^{\prime}\gamma) \times{\cal{B}}(A^{\prime}\to e^+e^-(\mu^+\mu^-)), \end{aligned} $

(8) where s is the square of the center of mass energy of the PbPb system.
$ {\cal{B}}(\eta\to A^{\prime}\gamma) $ and$ {\cal{B}}(A^{\prime}\to e^+e^-(\mu^+\mu^-)) $ denote η decay to dark photons and dark photon decay to electron or muon pair, respectively.We first consider the branching ratios of dark photon decays to lepton pairs, specifically the branching ratios of the
$ A^\prime\to e^+e^- $ or$ A^\prime\to \mu^+\mu^- $ processes. Information on the mass-dependent decay branching ratios of the dark photon below the η meson mass threshold can be found in Ref. [33], indicating that for$ m_{A^\prime}<m_\eta $ , the dark photon mainly decays into the two aforementioned decay channels. We adopt the branching ratio results from [33] and present the branching ratios of the dark photon$ A'$ decaying into the two types of lepton pairs in Fig. 2.
Figure 2. (color online) Branching ratios of dark photon decaying into lepton pairs, including electron and muon pair final states. The curves come from Ref. [33].
It is important to emphasize that in this work, we only consider the dark photon decay below the η meson mass threshold. The appearance of decay channels with hadrons as final states leads to a reduction in the branching ratios for lepton pairs, which is beyond the scope of this study. Now, there is one remaining branching ratio related to the dark photon
$ {\cal{B}}(\eta\to A^{\prime}\gamma) $ that needs to be discussed, which is also the largest source of uncertainty in the current analysis. -
The dark photon is the benchmark model for gauge mediators accessible at low energies [18, 45, 46]. The gauge boson
$A' $ mixes with a photon through kinetic mixing and charge coupling [47, 48]. The kinetic mixing term is$ {\cal{L}}_{{\rm{kin}}.{\rm{mix}}.}=-\frac\varepsilon{2\cos\theta_W}{F}_{\mu\nu}^{\prime}{B}^{\mu\nu}, $

(9) where
$ {F}_{\mu\nu}^{\prime}({B}^{\mu\nu}) $ is the U(1)' (hypercharge U(1)Y) field strength tensor and$ \theta_W $ is the weak mixing angle. This will result in a kinetic mixing coupling between the fields of the standard model and the U(1)' field${\cal{L}}_{{\rm{int}}}=-e\varepsilon j_{{\rm{em}}}^\mu{A}_{\mu}^{\prime}$ . As the kinetic mixing parameter$ \varepsilon $ is constrained to be small, these couplings are far weaker than electromagnetism [9, 47−50]. The couplings are suppressed by$ \varepsilon $ . The NA62 collaboration at the CERN SPS has reported the results of the search for η decays to photons and dark photons$A' $ [25], improving the previous constraints on the dark photon mass$ m_{A^\prime} $ and coupling$ \epsilon^2 $ . However, there is currently no viable approach for the precise exploration of the parameter space of dark photons$ (m_{A^\prime},\varepsilon^2) $ .Based on previous studies of the decay mode of η into a classical photon and dark photon, we adopt the branching ratio form from Refs. [27, 29, 51−53]:
$ \begin{aligned}[b] {{\cal{B}}(\eta\to A^{\prime}\gamma)}=\;&{2\varepsilon^2{\cal{B}}(\eta\to\gamma\gamma)\left(1-m_{A^{\prime}}^2/m_\eta^2\right)^3}\\ &{\times\left|\bar{{F}}_{\eta\gamma^*\gamma^*}(m_{A^{\prime}}^2,0)\right|^2, }\end{aligned} $

(10) where
$ {\cal{B}}(\eta\to \gamma\gamma)$ =39.36% denotes the branching ratio of η decay to 2$ \gamma $ [54]. From Refs. [29, 53], the transition form factor$ \bar{F}_{\eta\gamma^*\gamma^*} \simeq 1 $ is used in our analysis.We now find that to calculate the total cross-section in Eq. (8), it is necessary to determine the values of the dark photon's mixing parameters
$ (m_{A^\prime},\varepsilon^2) $ . As mentioned earlier, there is currently no well-established method to tightly constrain these parameters with high precision. Following suggestions from literature reviews [9, 55−59], we limit the dynamical mixing parameter$ \varepsilon $ of the dark photon to$ 10^{-5}< \varepsilon <10^{-4} $ . We acknowledge that the strength of the dark photon coupling is constrained by existing and future experiments, and our results strongly depend on the choice of$ \varepsilon $ . -
We first simply examine the influence of the parameters
$ m_{A^\prime} $ and$ \varepsilon^2 $ on the results. For this purpose, we first calculate the rapidity distribution${\rm d}\sigma/{\rm d}y$ for the process PbPb$\to $ PbPbη, considering the$ \eta\to A^\prime \gamma $ and$A^\prime\to e^+e^-(\mu^+\mu^-)$ decay processes. As shown in Fig. 3, it is evident that the calculated results strongly depend on the chosen parameter space ($ m_{A^\prime},\varepsilon^2 $ ). Therefore, a high-precision determination of the properties of the dark photon in experiments is necessary. It can be seen from Eq. (10) that the cross-section is suppressed by the parameter$ \varepsilon^2 $ , and the smaller the mass of the dark photon$ m_{A^\prime} $ , the larger the cross-section. This indicates that in the collision process under study, there is a higher likelihood of producing low-mass dark photons in the final state. The dark photon decaying into different lepton pairs, such as$ e^+e^- $ or$ \mu^+\mu^- $ , is the reason for the different differential cross-sections under the same parameter settings. This can be observed in Fig. 2.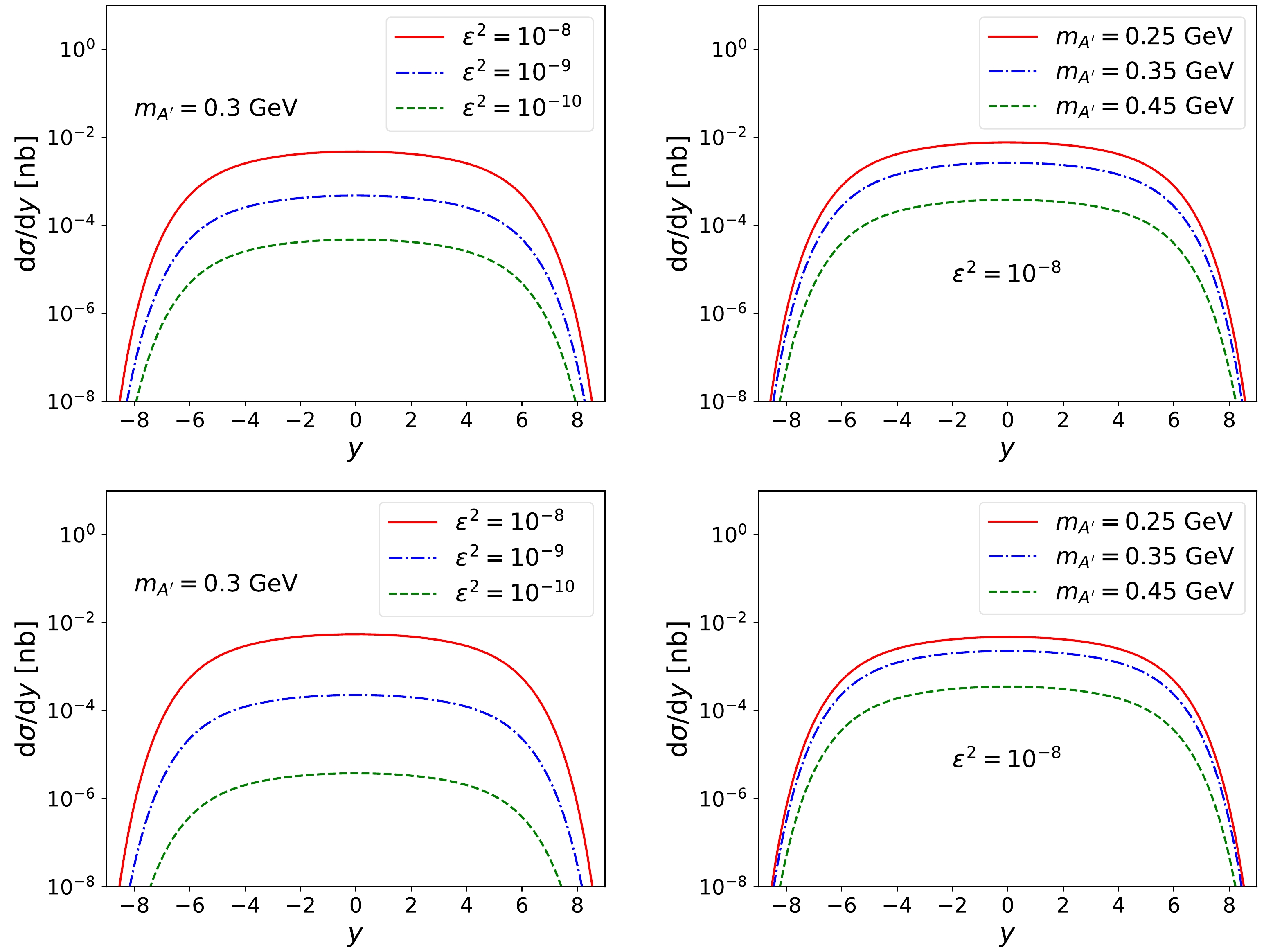
Figure 3. (color online) Rapidity distributions of the differential cross-sections
${\rm d}\sigma/{\rm d}y$ (in nb) at$ \sqrt{s}=5.5 $ TeV in PbPb UPCs. (upper panels) Considering the dark photon decay into the$ e^+e^- $ channel, we separately examined the cases with fixed$ m_{A^\prime}=0.3 $ GeV and fixed$ \varepsilon^2=10^{-8} $ . (lower panels) Considering the dark photon decay into the$ \mu^+\mu^- $ channel, we separately examined the cases with fixed$ m_{A^\prime}=0.3 $ GeV and fixed$ \varepsilon^2=10^{-8} $ .It is valuable to study the total cross-section of UPC and the number of detectable event signals in the detector. We assume the total cross-section within the detector's central rapidity interval (
$ |y|<2.0 $ ), which is a typical rapidity range for the CMS and ATLAS detectors at the LHC. We consider the ultra-peripheral PbPb collision scenarios in line with the future operation and upgrade plans of the LHC. Following the references, we estimate the total cross-section for the next run of the LHC at center-of-mass energies of$ \sqrt{s}=5.5 $ TeV, for the High-Luminosity LHC (HL-LHC) also at 5.5 TeV, for the High-Energy LHC (HE-LHC) at 10 TeV, and for the Future Circular Collider (FCC) at 39 TeV [60−62]. Furthermore, we assume that the luminosities for these collider plans correspond to a full year of operation at L = 3, 10, 10, and 110 nb-1 [26] and estimate the signal events for the production of dark photons decaying into electron and muon pairs.Figure 4 presents the total cross-section for the production of dark photons in PbPb collisions in the two-dimensional parameter space
$ (m_{A^\prime},\varepsilon^2) $ . The center-of-mass energy is set to$ \sqrt{s}=5.5 $ TeV, and we consider different lepton decay channels for the dark photon. Overall, both types of lepton decays of the dark photon show a trend of increasing total cross-section with increasing$ \varepsilon^2 $ and decreasing$ m_{A^\prime} $ . However, in the case of$ A^\prime\to e^+e^- $ , the cross-section exhibits a clear boundary around$ m_{A^\prime}\sim 2m_\mu $ (see left panel of Fig. 4). This is due to the possibility of the$ \mu^+\mu^- $ final state decay above the threshold of twice the muon mass.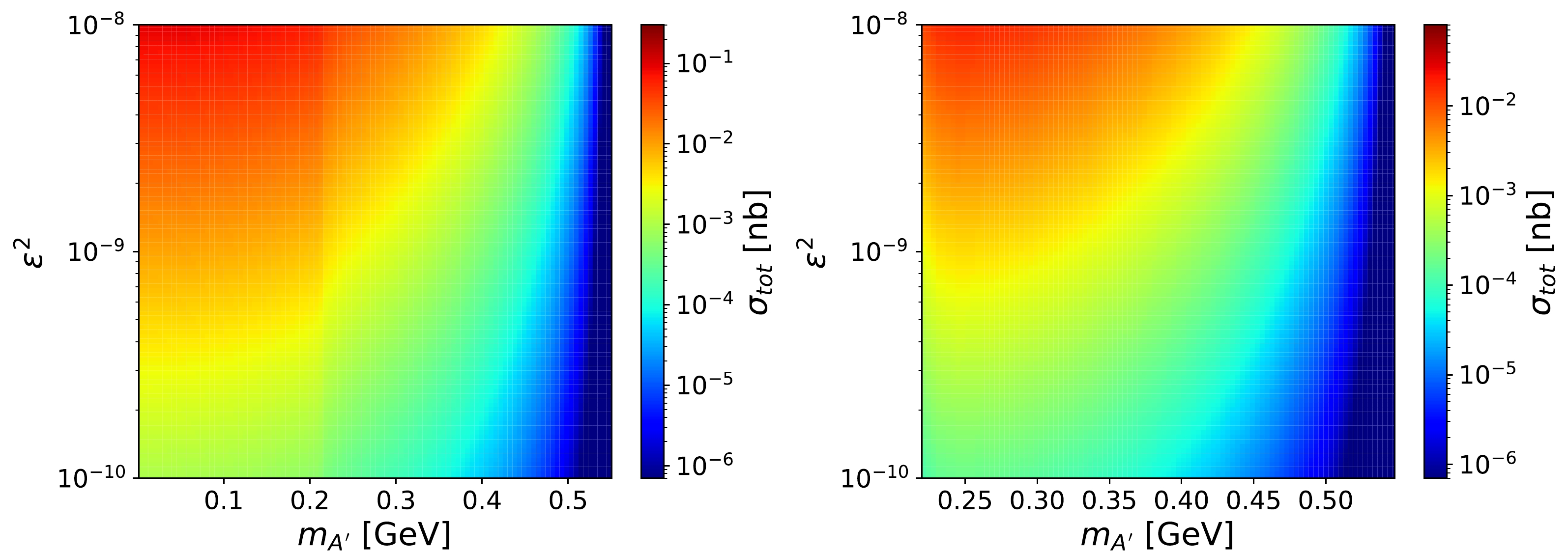
Figure 4. (color online) Cross-sections (in nb) for the dark photon production in PbPb collisions at
$ \sqrt{s}=5.5 $ TeV. The horizontal and vertical axes represent the values in the$ (m_{A^\prime}, \varepsilon^2) $ parameter space. The left and right panels are considered as the cases of A' decaying into$ e^+e^- $ and$ \mu^+\mu^- $ , respectively.These predicted cross-sections need to be considered and discussed in the context of the main background. Assuming the parameter choices
$ m_{A^\prime}=0.05 $ GeV,$ \varepsilon^2=10^{-8} $ for the$ A^\prime\to e^+e^- $ case and$ m_{A^\prime}=0.22 $ GeV,$ \varepsilon^2=10^{-8} $ for the$ A^\prime\to \mu^+\mu^- $ case, we estimate the main background$ \eta\to \gamma e^+e^-(\mu^+\mu^-) $ . First, we find the corresponding branching ratio from the Particle Data Group [54] to be$ {\cal{B}}(\eta\to \gamma e^+e^-(\mu^+\mu^-))=6.9(0.31)\times 10^{-3} $ . Next, we estimate the ratio of the PbPb cross-section with and without the intermediate dark photon at$ \sqrt{s}=5.5 $ TeV, using the detectable rapidity range of the central rapidity detector,$ |y|<2.0 $ . For$ A^\prime\to e^+e^- $ type, the resulting signal and background cross-sections are$ \sigma_{\rm{signal}}=0.0941 $ nb and$ \sigma_{\rm{background}}=84744.681 $ nb, respectively. For these cases, we have estimated and predicted that the signal-to-background ratio is$ 1.1\times 10^{-6} $ . The signal-to-background ratio for the decay of dark photons into muon pairs can be analyzed similarly, which gives the signal-to-background ratio$ 3.0\times 10^{-6} $ . One can observe that the main background from the decay is still quite significant. Of course, this ratio depends on the two parameters related to the dark photon discussed above. If we consider more complex couplings involving resonant states, such as considering intermediate states like vector mesons, the signal-to-noise ratio will be improved [63]. In meson decays, constraints on searching for dark photon signals in the invariant mass spectrum of electron-positron pairs are provided. The origin of the final state electron-positron pairs should be considered and reflected in the signal-to-noise ratio analysis. Moreover, we naively assume that the direct final state of$ \gamma e^+e^-(\mu^+\mu^-) $ is easily distinguishable in experiments so that such background noise can be removed, thus obtaining event selection related to the dark photon.Subsequently, we provide predictions for the number of signal events that could be achieved under the current experimental energy and luminosity conditions at the LHC, as well as the estimated signal yields for the HL-LHC, HE-LHC, and FCC facilities. Similar to the estimation method for the total cross-section, we simultaneously consider the dark photon decaying into
$ e^+e^- $ and$ \mu^+\mu^- $ , providing a two-dimensional distribution of signal yields with respect to the parameters$ (m_{A^\prime},\varepsilon^2) $ under various experimental conditions, as shown in Fig. 5.
Figure 5. (color online) Two-dimensional
$ (m_{A^\prime},\varepsilon^2) $ distribution for the number of events per year in PbPb collisions at the LHC, HL-LHC, HE-LHC, and FCC considering the central rapidity ranges (see text). The upper and lower panels are considered as the cases of A' decaying into$ e^+e^- $ and$ \mu^+\mu^- $ , respectively.The distribution of signal events clearly depends on the corresponding total cross-section distribution, following the same trend of variation. Although the signal yield generated under the current PbPb UPC experimental conditions at the LHC is limited, it is possible to reconstruct the dark photon production process by tracking rare η decays in the FCC facility. Furthermore, compared to
$ \pi^0\to A^\prime\gamma $ ,$ \eta\to A^\prime\gamma $ can raise the mass detection limit of the dark photon to near the η mass threshold, providing more options for dark photon mass selection. -
In this study, we investigated the production of dark photons from the decay of η mesons in UPCs at the LHC with different center-of-mass energies. We utilized the
$ \eta\to A^\prime \gamma $ branching ratio descriptions from Refs. [27, 29, 51−53] and the branching ratios of$A' $ decaying into lepton pairs from Ref. [33]. By performing numerical calculations, we estimated the total cross-section for producing dark photons in ultra-peripheral PbPb collisions at existing and planned future hadron colliders, as well as the signal yields, as depicted in Figs. 4−5.In theory, in addition to heavy ion beams, proton beams can also be used for UPC experiments; although the photon flux input of UPCs is proportional to the square of charge number
$ Z^2 $ of the beam particles, proton beams often have higher luminosity. However, higher luminosity implies larger pileup, which will make this measurement impossible in pp collisions [22, 24] (also see the review article [64]). Thus, the absence of pileup in PbPb collisions may make this system more beneficial to trigger on and reconstruct any UPCs compared to pp collisions. We also note that many studies have investigated the production of a large number of η decay events in pp collisions [24, 65], focusing on the perspective of strong interactions producing η. Our work serves as a complement to these studies by exploring the UPC process. It should be emphasized that high-precision measurements of the η decay channel often require a higher statistical yield of η mesons. In addition to existing heavy-ion colliders and the existing electron-ion collider at the Jefferson Lab, planned future η factories could significantly increase the yield of η mesons. A new experiment called REDTOP (Rare Eta Decays To Probe New Physics) [66] is being proposed, with the intent of collecting a data sample of the order of 1014 η (1012 η') for studying very rare decays. Moreover, the Primakoff process [67] at high-energy electron-ion colliders in the United States [68, 69] and China [70−72] can also yield a significant number of η mesons. In addition to the common two-photon decay channel, the measurement precision of rare η decays can also be significantly improved.In addition to the upgraded versions of the LHC mentioned in this work, which enhance the experimental energy and luminosity, detector upgrades are beneficial for tracking low-
$ p_T $ leptons and photons in the final state. The future ALICE 3 Run 5 and Run 6 experiments [73] have the potential to measure lower parameter space limits$ (m_{A^\prime},\varepsilon^2) $ , such as$ \varepsilon^2\simeq (4-10)\times 10^{-9} $ [58] in the η mass region. Furthermore, high-precision tracking performance at very low$ p_T $ can improve the efficiency of reconstructing and tracking lepton pairs. This work is likely to inspire more in-depth analyses, including cuts analysis typically considered by experimental collaborations. -
We are very grateful for the valuable discussion and communication about CMS experiment with Dr. Hao Qiu and Dr. Shuai Yang. We would like to express our gratitude to Dr. M. Williams for providing recent developments on dark photon decay and offering many constructive suggestions for our study.
Estimating the production of dark photons with η decay in high-energy collisions
- Received Date: 2024-06-11
- Available Online: 2024-10-15
Abstract: We propose searching for dark photon signals in the decay channel of η mesons, specifically through the leptonic decay (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: