-
Cosmological observations, such as the velocity dispersions of galaxies [1], Big Bang nucleosynthesis (BBN) [2, 3] and cosmic microwave background (CMB) [4], provide strong evidence for the existence of dark matter (DM) and baryon asymmetry in the universe. Cosmological measurements [5] indicate that the relic densities of dark matter (
$ \Omega_{{\rm{DM}}} $ ) and baryons ($\Omega_{B}$ ) are of the same order, i.e.,$\Omega_{{\rm{DM}}}= (5.36 \pm 0.06) \ \Omega_{B}$ , which implies that the dark matter and baryon asymmetry may stem from the same ultraviolet (UV) model [6].Recently, a model of B-Mesogenesis was proposed to simultaneously explain the origins of DM and baryon asymmetry by assuming that dark matter is charged under baryon number [7]. The Sakharov conditions are satisfied in the following ways. A long-lived particle produces bottom mesons and their anti-mesons out of the thermal equilibrium in the early universe. Then the neutral bottom mesons undergo
$ B^0-\overline B^0 $ and$ B_s^0-\overline B_s^0 $ oscillations, which naturally provide CP violation. Finally, the bottom mesons decay into an ordinary baryon with the baryon number$ B=+1 $ and a dark fermion ψ that is charged under baryon number with$ B=-1 $ ; thus, the visible baryon number is violated but the total baryon number is conserved. To preserve the DM and baryon asymmetry, the dark fermion ψ should decay into a dark Majorana fermion ξ and a dark scalar baryon ϕ. In this way, both the DM relic abundance and baryon asymmetry in the universe can be simultaneously explained by this model. Additionally, most of the new particles in this scenario exist at the GeV scale, which can be precisely examined at the current B-factories and hadron colliders or by experiments in the near future.This model has garnered significant interest from both theorists and experimentalists during the past a few years [8–22]. To explore the B-Mesogenesis scenario, most theoretical studies concentrate on the semi-invisible decays of B mesons. The BABAR and Belle experiments have measured the decay of bottom mesons into a baryon and a dark sector anti-baryon ψ, such as
$ B^0\to \Lambda^0\psi $ and$ B^+\to p\psi $ [19–21]. However, it is also possible for the bottom baryons to decay into a meson and a dark baryon, such as$ \Lambda_b(\Xi_b)\to P\bar{\psi} $ , with P denoting a light pseudo-scalar$ \pi,K $ meson, which was mentioned in the B-Mesogenesis proposal [7] and precisely estimated in a recent study [18]. However, for bottom baryons, there are two processes that have not ever been studied in the context of B-Mesogenesis, which are the fully invisible decay ($ \Lambda_b^0\to \xi\bar{\phi} $ ) and semi-invisible radiative decay ($ \Lambda_b^0\to\gamma\bar{\psi} $ ) of$ \Lambda_b^0 $ baryons. In particular, the fully invisible decay of$ \Lambda_b^0 $ yields a distinctive signal with which the stable dark particles in B-Mesogenesis can be explored. All these processes can be explored at future colliders with high accuracy. For instance, the upgrade of Belle-II [23] is expected to produce the bottom baryons pair at the threshold, while the LHCb can measure the signals with its vertices detector [24]. In addition, as the Circular Electron Positron Collider (CEPC) [25] and Future Circular Collider (FCC-ee) [26] will produce substantial bottom baryons, these rare decays of bottom baryons are expected to be explored at future lepton colliders. Therefore, to precisely probe B-Mesogenesis, systematic analyses of the invisible and semi-invisible decays of bottom baryons are crucial and may shed light on the study of dark matter and baryon asymmetry in the universe.Except for
$ \Lambda_b^0\to \xi\bar\phi $ , the fully invisible decays are also very interesting for neutron and hyperon decays, which share the same type of interaction as$ u_ad_bd_c\psi $ , where$ a,b,c $ represent the flavors of up- and down-type quarks. To explain the neutron lifetime puzzle (i.e., the discrepancy between the bottle method and the beam method), the idea of allowing neutrons to decay into dark matter was proposed [27]. The invisible decays of$ \Lambda^0 $ hyperons were also allowed for in the new physics models in a fashion similar to the B-Mesogenesis model and the ones for the neutron lifetime anomaly [12]. The BESIII collaboration has measured it as${\rm BR} (\Lambda^0\to {\rm{invisible}}) < 7.4 \times 10^{-5}$ [28]. The invisible decays of bottom baryons rely on the interaction with a bottom quark, which is beneficial for exploring B-Mesogenesis.When searching for new physics in the decays of hadrons, hadronic matrix elements are crucial for determining the observables, except for the interaction of UV models. Therefore, it is necessary to calculate the corresponding matrix elements to examine the new physics or constrain the parameters of a specific model of hadron decays. Because the matrix elements relate to the strong interaction, we need to utilize a perturbative or non-perturbative method to determine the hadronic matrix elements. In practice, the decays of
$ \Lambda_b(\Xi_b)\to P\bar{\psi} $ involve bottom baryon to light-meson transition form factors, which have been investigated recently in the light-cone sum rules (LCSR) method [18]. Because the baryon-to-meson form factors are a new kind of physical quantity, they require more detailed discussions in theoretical studies. Under the heavy quark limit, these matrix elements can also be estimated within the QCD factorization approach [29–32]. For example, this kind of form factor also emerges in the baryon and lepton number violation decays of$ \Lambda_b\to P\ell $ from a Leptoquark model, and have been studied recently within the QCD factorization [33]. Although the higher dimensional operators of the B-Mesogenesis model are different to those of the Leptoquark model, the bottom baryon to light meson transition form factors can be similarly determined within the QCD factorization. Our results suggest that the transition form factors can be factorized into a convolution of the perturbatively calculable hard-scattering kernel and the non-perturbative distribution amplitudes without endpoint divergence [33, 34]. The matrix elements involved in$ \Lambda_b^0\to\gamma\bar{\psi} $ can also be calculated within the same QCD factorization method, while those of$ \Lambda_b^0\to\xi\bar{\phi} $ can be estimated by directly relying on the matrix elements in the SM. With these matrix elements, we can calculate the branching ratios of invisible and semi-invisible decays of bottom baryons and predict the potential of exploring B-Mesogenesis using future measurements.This manuscript is organized as follows. In Sec. II, we briefly introduce the B-Mesogenesis scenario. In Sec. III, the hadronic matrix elements in the invisible and semi-invisible decays of
$ \Lambda_b $ and$ \Xi_b $ baryons are calculated within the QCD factorization approach. In Sec. IV, the sensitivities of the parameters of B-Mesogenesis are discussed for the invisible and semi-invisible decays of bottom baryons at future colliders. Finally, we conclude the study in Sec. V. -
As the relic densities of DM and net baryons are similar, they may arise from the same UV completion. In practice, B-Mesogenesis [7, 10–12], which assumes dark matter is charged under the baryon number, attempts to simultaneously explain the existence of DM and baryon asymmetry in the Universe. In particular, this scenario induces the decays of bottom baryons into dark baryons, which significantly violate the baryon number conservation in the visible regime. The corresponding Lagrangian is given by:
$ \begin{aligned}[b] {\cal{L}}_{\rm int} \supset \;& -y^R_{u_a d_b} \epsilon_{ijk} Y^{*}_i \bar{u}_{R a}^{j} d_{R b}^{k, {\cal{C}}} -y_{u_a d_b}^{L} \epsilon_{ijk} Y^*_{i} \bar{u}_{L a}^{j} d_{L b}^{k, {\cal{C}}} \\&- y_{\psi d_c} Y_i \bar{\psi} d_{R c}^{i, {\cal{C}}} -y_d\; \bar{\psi} \phi\xi +{\rm h.c.}. \end{aligned} $

(1) The u (d) represents the up-type (down-type) quarks, the indices
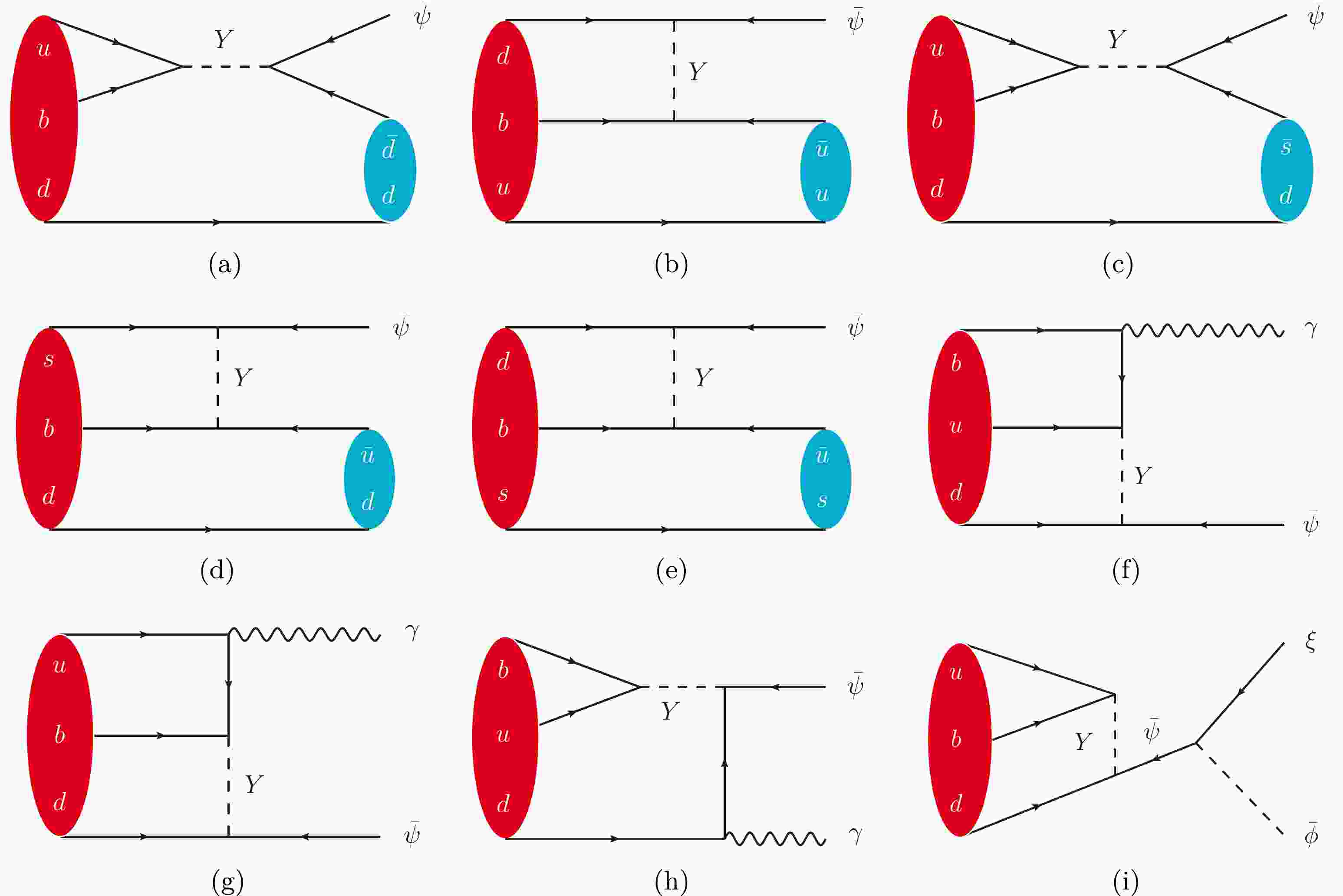
$ a,b,c $ ($ i,j,k $ ) denote the quark flavors (colors), L$ (R) $ represents the left-handed (right-handed) component of quarks,$ {\cal{C}} $ represents a charge conjugation, Y is a color-triplet scalar with electric charge$ Q_Y=-1/3 $ (which couples to ordinary quarks in the first two terms and to a right-handed quark and a dark fermion in the third term; it is a TeV-scale particle which will be integrated out in the bottom hadron decays), and ψ is a dark fermion with the baryon number$ B_\psi=-1 $ , which is a singlet under the standard model gauge group that can only couple to the right-handed down-type quarks under that color conservation. The total baryon number is conserved in the interaction of$ Y_i\bar\psi d_{R_c}^{i,{\cal{C}}} $ , while the visible baryon number is violated. This is illustrated in Fig. 1, in which ψ completely decays into stable dark matter, a dark scalar ϕ with$ B_{\phi}=-1 $ , and a dark Majorana fermion ξ. Their quantum numbers are summarized in Table 1.
Figure 1. (color online) The diagrammatic representations for the invisible and semi-invisible decays of bottom baryons in the B-Mesogenesis. (a) and (b) are the diagrams for the semi-invisible hadronic decay of
$ \Lambda_b^0\to \pi^0 \bar\psi $ , (c) for$ \Lambda_b^0\to K^0\bar\psi $ , (d) for$ \Xi_b^-\to \pi^-\bar\psi $ , (e) for$ \Xi_b^-\to K^-\bar\psi $ , (f,g,h) for the semi-invisible radiative decay of$ \Lambda_b^0\to \gamma\bar\psi $ , and (i) for the fully invisible decay of$ \Lambda_b^0\to \xi\bar\phi $ . The dark sector particles of$ \bar\psi $ and$ \bar \phi $ are charged under the baryon number of$ B_{\bar\psi, \bar\phi}=+1 $ , so that the total baryon number are conserved in these processes.Field S Q B Y 0 $ -\dfrac{1}{3} $ 

$ -\dfrac{2}{3} $ 

ψ $ \dfrac{1}{2} $ 

0 −1 ξ $ \dfrac{1}{2} $ 

0 0 ϕ 0 0 −1 Table 1. Quantum numbers for the new particles in B-Mesogenesis, including particle spin S, electric charge Q, and baryon number B.
If the mass of color-triplet scalar
$ M_Y $ is much heavier than that of bottom baryons, we can integrate out such particles and obtain an effective Lagrangian related to the (semi-)invisible decay, which is given by$ {\cal{L}}_{{\rm{EFT}}}= C^{L,R}_{u_ad_b,d_c}\; {{\cal{O}}}^{L,R}_{u_ad_b,d_c}+ C^{L,R^*}_{u_ad_b,d_c}\; \bar{{\cal{O}}}^{L,R}_{u_ad_b,d_c} , $

(2) where
$ C^{L,R}_{u_ad_b,d_c}=y^{L,R^*}_{u_a d_b} y^*_{\psi d_c}/M_{Y}^2 $ are the Wilson coefficients and the effective operators$ {\cal{O}}^{L,R}_{u_ad_b,d_c} $ and$ \bar{{\cal{O}}}^{L,R}_{u_ad_b,d_c} $ are given by$ \begin{aligned}[b]& {{\cal{O}}}^{L}_{u_ad_b,d_c}=\epsilon_{ijk} \left( \bar{u}_{La}^{i , {\cal{C}}}\; d_{Lb}^{j} \right)\left( \bar{\psi}^{{\cal{C}}}\; d_{Rc}^{k} \right), \\& \bar{{\cal{O}}}^{L}_{u_ad_b,d_c}=\epsilon_{ijk} \left( \bar{u}_{La}^{i}\; d_{Lb}^{j , {\cal{C}}} \right)\left( \bar{\psi}\; d_{Rc}^{k,{\cal{C}}} \right), \\& {{\cal{O}}}^{R}_{u_ad_b,d_c}=\epsilon_{ijk}\left( \bar{u}_{Ra}^{i, {\cal{C}}}\; d_{Rb}^{j} \right)\left( \bar{\psi}^{{\cal{C}}}\; d_{Rc}^{k} \right) ,\\& \bar{{\cal{O}}}^{R}_{u_ad_b,d_c}=\epsilon_{ijk} \left( \bar{u}_{Ra}^{i}\; d_{Rb}^{j , {\cal{C}}} \right)\left( \bar{\psi}\; d_{Rc}^{k , {\cal{C}}} \right). \end{aligned} $

(3) For convenience, we factorize out the external field ψ from the effective operators and rewrite the Lagrangian as
$ {\cal{L}}_{{\rm{EFT}}} = C^{L,R}_{u_ad_b,d_c}\; \bar{\psi}^{\cal{C}}\; {{\cal{O}}}^{'L,R}_{u_ad_b,d_c} + {\rm h.c.}, $

(4) where the operators
$ {\cal{O}}^{'L,R}_{u_ad_b,d_c} $ are expressed as$ {\cal{O}}^{'L}_{u_ad_b,d_c}=\epsilon_{ijk}\ d_{Rc}^k \left( \bar{u}_{La}^{i,{\cal{C}} }\; d_{Lb}^{j} \right), \quad {\cal{O}}^{'R}_{u_ad_b,d_c}=\epsilon_{ijk} \ d_{Rc}^k\left( \bar{u}_{Ra}^{i, {\cal{C}}}\; d_{Rb}^j \right). $

(5) -
With the effective Lagrangian for B-Mesogenesis shown in Eq. (4), we can systematically study the invisible and semi-invisible decays of bottom baryons. To explore B-Mesogenesis, we primarily focus on the exclusive decay modes of
$ \Lambda_b^0\to P^0\bar{\psi},\; \; \Xi_b^-\to P^-\bar{\psi},\; \; \Lambda_b^0\to\gamma\bar{\psi},\; \; \Lambda_b^0\to\xi\bar{\phi} . $

(6) The diagrammatic representation of these processes are shown in Fig. 1. In the heavy quark limit, we calculate the relevant diagrams and apply the QCD factorization method for these heavy baryon to meson transition form factors at the leading order of
$ \alpha_s $ . The non-perturbative inputs are the heavy baryon and light meson distribution amplitudes, and we restrict our calculation to the leading twist (twist-2) distribution amplitudes. Finally, the transition matrix elements defined by the effective operators$ {\cal{O}}^{'L,R}_{u_ad_b,d_c} $ can be represented as a convolution of the perturbative part with the leading twist heavy baryon and light meson distribution amplitudes. -
In this subsection, we construct the factorization formula and explicitly calculate the hadronic matrix elements of
$ \Lambda_b^0/\Xi_b^- \to P^{0,-}\bar{\psi} $ decays in the heavy quark limit. The relevant diagrams are shown in Fig. 2. Using the effective Lagrangian given in Eq. (4), one can express the decay amplitude for the operator$ {\cal{O}}^{'L,R}_{u_ad_b,d_c} $ as
Figure 2. (color online) The Feynman diagrams of the
$ \Lambda_b^0/\Xi_b^- \to P\bar{\psi} $ decays, where the bold line represents the b quark and the circle cross denotes the currents in the$ {\cal{O}}^{L,R} $ operators.$ {\rm i} {\cal{M}} = C^{L,R}_{u_ad_b,d_c} \bigg( \bar{v}_{\psi}^{{\cal{C}}}(q) \langle P(p)| {\cal{O}}^{'L,R}_{u_ad_b,d_c} |{\cal{B}}(p')\rangle \bigg), $

(7) where
$ v_{\psi} $ is the spinor of dark baryon$ \bar{\psi} $ with momentum$ q = p'-p $ , and$ {\cal{B}} $ represents$ \Lambda_b^0 $ or$ \Xi_b^- $ with momentum$ p'=m_{{\cal{B}}}v $ . The hadronic matrix elements can be parameterized in terms of two form factors:$ \begin{aligned}[b] \langle P(p)| {\cal{O}}^{'L,R}_{u_ad_b,d_c} |{\cal{B}}(p')\rangle =\;& P_R \Bigg( \zeta^{{\cal{B}} \to P(L,R)}_1(q^2) \\&+ \frac{\not {q}}{m_{{\cal{B}}}} \zeta^{{\cal{B}} \to P(L,R)}_2(q^2) \Bigg) u_{{\cal{B}}}(p').\end{aligned} $

(8) We will calculate the form factors working in the rest frame of the heavy baryon and choose two light-cone vectors along the fast-moving final state particles with the conventions of
$ n_\mu=(1,0,0,1),\quad \bar{n}_\mu=(1,0,0,-1),\quad v^\mu=(1,0,0,0). $

(9) Then the four-momentum of the final state particles can be written as
$ \begin{aligned}[b] q &=\bigg(E_q+|\vec{q}|,\; E_q-|\vec{q}|,\; 0 \bigg),\quad p=\bigg(E_p-|\vec{p}|,\; E_p+|\vec{p}|,\; 0 \bigg),\\ E_q &=\frac{m_{\cal{B}}^2+m^2_{\psi}-m_P^2}{2m_{\cal{B}}},\qquad \quad \; \, E_p=\frac{m_{\cal{B}}^2-m^2_{\psi}+m_P^2}{2m_{\cal{B}}},\\ |\vec{q}|&=|\vec{p}|=\frac{\sqrt{\left(m_{{\cal{B}}}^2 - (m_{\psi}+m_P)^2 \right)\left(m_{{\cal{B}}}^2 - (m_{\psi}-m_P)^2 \right)}}{2 m_{{\cal{B}}}}, \end{aligned} $

(10) with
$ p^\mu=(n\cdot p)\frac{\bar{n}^\mu}{2}+(\bar{n}\cdot p)\frac{n^\mu}{2}+p_{\perp}^\mu\equiv (n\cdot p,\bar{n}\cdot p,p_{\perp}) . $

(11) When computing the Feynman diagrams in the heavy quark limit, we list the momenta involved as
$ \begin{aligned}[b]& p'=(m_{\cal{B}},m_{\cal{B}},0),\quad q=(m_{\cal{B}},m_{\cal{B}}\lambda^2,0),\quad p=(m_{\cal{B}}\lambda^2,m_{\cal{B}},0),\\& k=(\Lambda_{{\rm{QCD}}},\Lambda_{{\rm{QCD}}},\Lambda_{{\rm{QCD}}}),\end{aligned} $

(12) where k corresponds to the momentum of the light spectator quark in the baryon. The parameter
$ \lambda\sim\dfrac{m_{\psi}}{m_{{\cal{B}}}}\sim \dfrac{m_P}{m_{\cal{B}}}\sim \dfrac{\Lambda_{{\rm{QCD}}}}{m_{\cal{B}}} $ , which vanishes in the heavy quark limit.When considering only the leading twist distribution amplitudes and the tree-level QCD calculations, the contribution of operator
$ {\cal{O}}^{'R}_{u_ad_b, d_b} $ in Eq. (4) to the transition matrix element always vanishes because there is an odd number of Dirac matrices between the two chiral projection matrices$ P_R=\dfrac{1+\gamma_5}{2} $ within the operator$ {\cal{O}}^{'R}_{u_ad_b, d_b} $ . For example, in the heavy quark limit, the Dirac structure of the$ \Lambda_b^0\to \pi^0\bar{\psi} $ transition amplitude shown in Fig. 2 (a) is given by$ {\rm i}{\cal{M}}\propto v_\psi^T {\mathcal{C}} P_R \left(\not {p} \gamma_5\right) \gamma_\mu \left(\not {\bar{n}}\gamma_5 {\mathcal{C}} \right) (\gamma^{\mu})^T x \not {p}^T P_{L,R} u_{\Lambda_b}, $

(13) where
$\left(\not {p} \gamma_5\right)$ and$\left(\not {\bar{n}}\gamma_5 {\mathcal{C}} \right)$ are the light-cone projectors corresponding to the leading twist distribution amplitudes of$ \Lambda_b^0 $ and$ \pi^0 $ , respectively [31, 35]. The subscripts of$ P_{L,R} $ correspond to the insertion of operators$ {\cal{O}}^{L}_{u_a d_b d_c} $ or$ {\cal{O}}^{R}_{u_a d_b d_c} $ . Because there is an odd number of Dirac matrices between$ P_R $ and$ P_{L,R} $ , the contribution of right-handed operators$ {\cal{O}}^{R}_{u_a d_b d_c} $ will vanish. The contributions of the right-handed operators in other semi-invisible decays of bottom baryons will vanish in the same way.In heavy quark limit, the transition amplitude in Eq. (7) also vanishes for operators
$ {\cal{O}}^{L}_{ud,b} $ and$ {\cal{O}}^{L}_{us,b} $ owing to the parity conservation. Taking$ \Lambda_b^0\to \pi^0 \bar{\psi} $ as an example, the partonic amplitude1 can be factorized as a product of two transition matrix elements in the spin space,$ {\rm i} {\cal{M}} \propto \langle\bar{\psi}(q)|\,\bar{\psi}^{{\cal{C}}} b_R \, | b(m_bv)\rangle\, \langle \bar{q} (xp)q(\bar{x}p)| \, \bar{u}^{{\cal{C}}}_L d_L \,|u(k_1) d(k_2)\rangle. $ We will find that there is a trace in the second matrix element in our calculation, which is always zero because there is an odd number of γ matrices. We find that$ \gamma_5 $ in the operator$ \bar{u}^{{\cal{C}}}_L d_L $ cannot contribute to the trace because there are only two independent Lorentz vectors in this process to contract with the 4-dimensional antisymmetric tensor$ \epsilon_{\mu\nu\rho\sigma} $ . Actually, the$ J^P $ quantum number of quark pair$ (ud) $ in the$ \Lambda_b^0 $ baryon is$ 0^+ $ in the leading twist approximation, and$ \langle q (xp)\bar{q}(\bar{x}p)| \, \bar{u}^{{\cal{C}}}_L d_L \,|u(k_1) d(k_2)\rangle $ describes a scalar decay into a pseudoscalar induced by a scalar operator, which violates parity conservation. The hadronic effects will not affect this conclusion cause the perturbative results in the final factorization formula are independent of the external state [37].In the following calculation, we only consider the contribution of the operators
$ {\cal{O}}^{'L}_{ub,d} $ and$ {\cal{O}}^{'L}_{ub,s} $ . Strange number conversed or violated processes are induced by the corresponding operators, which is summarized as$ \begin{aligned}[b] \Lambda_b^0 \to \pi^0 \bar{\psi} \quad {\rm{and}} \quad \Xi_b^- \to K^- \bar{\psi}, & \quad{\rm{induced\; by}}\; {\cal{O}}^{'L}_{ub,d} , \\ \Lambda_b^0 \to K^0 \bar{\psi} \quad {\rm{and}} \quad \Xi_b^- \to \pi^- \bar{\psi}, & \quad{\rm{induced\; by}}\; {\cal{O}}^{'L}_{ub,s} . \\ \end{aligned} $

(14) In the framework of the QCD factorization approach, the longitudinal momentum of the quarks in the energetic final state meson is at the scale of
$ m_b $ and the exchanged gluons have virtuality of order$ m_b\Lambda_{{\rm{QCD}}} $ , which can be treated perturbatively. Next, we calculate the hard-scattering contributions, such as the ones shown in Fig. 2. The decay amplitudes are expressed as$ {\rm i} {\cal{M}} = \eta_{\Delta s} C^{L}_{u_ad_b,d_c} \zeta^{{\cal{B}} \to P} \bigg( \bar{v}_{\psi}^{{\cal{C}}}(q) P_{R}\frac{\not {n}}{2}\, u_{{\cal{B}}}(p') \bigg), $

(15) where the sign factor
$ \eta_{\Delta s}=-1 $ for strange flavor conserved processes$ \Lambda_b^0\to\pi^0 $ and$ \Xi_b^-\to K^- $ , while$ \eta_{\Delta s}=+1 $ for strange flavor violated processes$ \Lambda_b^0\to K^0 $ and$ \Xi_b^-\to \pi^- $ . The convention for the sign factor arises from the inconsistency between the quark flavor order in the operator$ {\cal{O}} $ and the definition of the light-cone distribution amplitudes.The factorization formula of the form factor
$ \zeta^{{\cal{B}} \to P} $ is given by$\begin{aligned}[b] \zeta^{{\cal{B}} \to P} =\;&f_{P}f_{{\cal{B}}}^{(2)} \int_{0}^{\infty} {\rm d}\omega\,\omega\int_{0}^{1} {\rm d} u\int_{0}^{1}{\rm d}x {\cal{J}}^{{\cal{B}} \to P }\\&\times(x,u,\omega,\mu) \phi_{P}(x) \psi_{2}(u,\omega),\end{aligned} $

(16) where
$ f_{P({\cal{B}})} $ is the decay constant of particle$ P({\cal{B}}) $ ,$ {\cal{J}}^{{\cal{B}} \to P }(x,u,\omega,\mu) $ is the corresponding hard-scattering kernel, and$ \phi_P(x) $ and$ \psi_2(u,\omega) $ are the leading twist light-cone distribution amplitudes of the P meson and$ {\cal{B}} $ baryon [30, 38–40], respectively,$ \begin{aligned}[b]& \langle P(p)|\,[\bar{q}(t\bar{n})]_{A}\,[t\bar{n},0]\,[q(0)]_{B}\,|0\rangle \\=\;&\dfrac{{\rm i}f_{P}}{4}\,\bar{n}\cdot p\,\bigg[\,\dfrac{\not {n}}{2}\,\gamma_{5}\,\bigg]_{BA}\int_{0}^{1}{\rm d}x\,{\rm e}^{{\rm i}xt\bar{n}\cdot p}\,\phi_{P}(x,\mu), \end{aligned}$

(17) with the momentum fraction x of anti-quark
$ \bar{q} $ in the P meson, and$ \begin{aligned}[b] &\left\langle{0} \right|[u_{i}(t_{1}\bar{n})]_{A}\,[0,t_{1}\bar{n}]\,[d_{j}(t_{2}\bar{n})]_{B}\,[0,t_{2}\bar{n}]\,[b_{k}(0)]_{C}\left| {\Lambda_{b}^0(p')} \right\rangle \\ = &\,\dfrac{1}{6} \dfrac{\epsilon_{ijk}}{4}\,f_{\Lambda_{b}}^{(2)}(\mu)\,[u_{\Lambda_{b}}(p')]_{C}\,\bigg[\,\dfrac{\not {\bar{n}}}{2}\,\gamma_{5}\,C^{T}\,\bigg]_{BA}\int_{0}^{\infty} {\rm d} \omega\,\omega\\&\times\int_{0}^{1}{\rm d}u\,{\rm e}^{-{\rm i}\omega(t_{1}u+ t_{2}\bar{u})}\,\psi_{2}(u,\omega), \\ & \left\langle{0} \right|[d_{i}(t_{1}\bar{n})]_{A}\,[0,t_{1}\bar{n}]\,[s_{j}(t_{2}\bar{n})]_{B}\,[0,t_{2}\bar{n}]\,[b_{k}(0)]_{C}\left|{\Xi_{b}^-(p')} \right\rangle \\ = &\, \dfrac{1}{6}\dfrac{\epsilon_{ijk}}{4}\,f_{\Xi_{b}}^{(2)}(\mu)\,[u_{\Xi_{b}^-}(p')]_{C}\,\bigg[\,\dfrac{\not {\bar{n}}}{2}\,\gamma_{5}\,C^{T}\,\bigg]_{BA}\int_{0}^{\infty} {\rm d} \omega\,\omega\\&\times\int_{0}^{1}{\rm d}u\,{\rm e}^{-{\rm i}\omega(t_{1}u+t_{2}\bar{u})}\,\psi_{2}(u,\omega), \end{aligned} $

(18) where
$ \omega_i=(n\cdot k_i) $ represent the momentum components of the spectator quark. We use the convention$ \omega_1=u \omega $ ,$ \omega_2=\bar{u} \omega $ with$ \omega=\omega_1+\omega_2 $ , where u and$ \bar{u} $ represent the momentum fraction of the spectator quark in the light quark pair. In the heavy-quark limit, the coupling constants$ f_{{\cal{B}}} $ for$ \Lambda_b^0 $ and$ \Xi_b^- $ are respectively defined by [39]$ \begin{aligned}[b]& \epsilon_{ijk} \langle 0| u^{iT}_{\alpha}(0) d^{j}_{\beta}(0) b^{k}_{\gamma}(0) |\Lambda_b^0(p')\rangle \\\equiv \;&\frac{1}{4} \left\{ f_{\Lambda_b}^{(1)} [\gamma_5 C^{T}]_{\beta\alpha} + f_{\Lambda_b}^{(2)} [\not {v}\gamma_5 C^{T}]_{\beta\alpha}\right\} \left[u_{\Lambda_b}(p')\right]_{\gamma},\\ & \epsilon_{ijk} \langle 0| d^{iT}_{\alpha}(0) s^{j}_{\beta}(0) b^{k}_{\gamma}(0) |\Xi_b^-(p')\rangle \\\equiv\;& \frac{1}{4} \left\{ f_{\Xi_b}^{(1)} [\gamma_5 C^{T}]_{\beta\alpha} + f_{\Xi_b}^{(2)} [\not {v}\gamma_5 C^{T}]_{\beta\alpha}\right\} \left[u_{\Xi_b}(p')\right]_{\gamma}. \end{aligned} $

(19) The gauge links in Eq. (18) are used to preserve the gauge invariance,
$ [t\bar{n},0]={\rm{P}}\,{\rm{exp}}\bigg[\,{\rm i}g\int_{0}^{t}{\rm d} x\,\bar{n}\cdot A(x\bar{n})\,\bigg] , $

(20) which does not affect our calculations at the leading order of QCD. The leading-twist LCDAs of pseudoscalar mesons can be expanded using Gegenbauer polynomials [41],
$ \phi_{P}(x,\mu)=6x(1-x)\bigg[\,1+\sum\limits_{n=1}^{\infty}a_{n}^{P}(\mu)\,C_{n}^{(3/2)}(2x-1)\,\bigg], $

(21) and the leading-twist wave function for the
$ \Lambda_{b}^0 $ baryon is given by [38, 39, 42],$ \psi_{2}(u,\omega)=u\,(1-u)\,\omega^{2}\,\dfrac{1}{\omega_{0}^{4}}\,{\rm e}^{-\omega/\omega_{0}}. $

(22) In the limit of the SU(3) flavor symmetry, the wave function of
$ \Xi_b^- $ is the same as that of$ \Lambda_b^0 $ . Table 2 summarizes the numerical input parameters.$ m_{\Lambda_{b}}=5.6196\,{\rm{GeV}} $ 

[43] $ \quad\tau_{\Lambda_{b}}=1.471\,{\rm{ps}} $ 

[43] $ m_{\Xi_{b}}=5.7970\,{\rm{GeV}} $ 

[43] $ \quad\tau_{\Xi_{b}}=1.572\,{\rm{ps}} $ 

[43] $ \quad\omega_{0}=0.280\,_{-0.038}^{+0.047}\,{\rm{GeV}} $ 

[42] $ f_{\Lambda_{b}}^{(2)}(\mu_{0})=0.030\pm 0.005\,{\rm{GeV}}^{3} $ 

[42] $ f_{\pi}=0.1304\pm0.0002\,{\rm{GeV}} $ 

[40] $ f_{K}=0.1562\pm0.0007\,{\rm{GeV}} $ 

[40] $ a_{1}^{\pi}(\mu_{0})=0 $ 

[40] $ a_{2}^{\pi}(\mu_{0})=0.29\pm0.08 $ 

[40] $ a_{1}^{K}(\mu_{0})=-0.07\pm0.04 $ 

[40] $ a_{2}^{K}(\mu_{0})=0.24\pm0.08 $ 

[40] Table 2. Input parameters with renormalization scale
$ \mu_{0}=1\,{\rm{GeV}} $ .The corresponding hard-scattering functions are calculated as
$ \begin{align} {\cal{J}}^{\Lambda_{b}^0\to\pi^{0}}(x,u,\omega,\mu)&=\frac{1}{\sqrt{2}}\big({\cal{J}}_u(x,u,\omega,\mu)+{\cal{J}}_{\bar{u}}(x,u,\omega,\mu)\big),\\ {\cal{J}}^{\Lambda_{b}^0\to K^{0}}(x,u,\omega,\mu)&={\cal{J}}^{\Xi_{b}^-\to K^-}(x,u,\omega,\mu)={\cal{J}}_{\bar{u}}(x,u,\omega,\mu),\\ {\cal{J}}^{\Xi_{b}^-\to\pi^-}(x,u,\omega,\mu)&={\cal{J}}_u(x,u,\omega,\mu), \end{align} $

(23) with
$ {\cal{J}}_u(x,u,\omega,\mu)=\frac{1}{9}\frac{\pi\alpha_s(\mu)}{u \omega^2 x},\qquad {\cal{J}}_{\bar{u}}(x,u,\omega,\mu)=\frac{1}{9}\frac{\pi\alpha_s(\mu)}{\bar{u} \omega^2 x} , $

(24) where the
${1}/{\sqrt{2}}$ is the isospin factor from$ |\pi^0\rangle = \dfrac{1}{\sqrt{2}}(|u\bar{u}\,\rangle-|d\bar{d}\,\rangle) $ . The asymptotic behaviors of the leading twist light-cone distribution amplitudes in the endpoint region are$ \phi_P(x)\sim x(1-x),\qquad \psi_2(u,\omega)\sim u(1-u)\omega^2, $

(25) which will cancel the divergent behavior in the hard-scattering functions
$ {\cal{J}}_u(x,u,\omega,\mu) $ and$ {\cal{J}}_{\bar{u}}(x,u,\omega,\mu) $ . Then the convolution integral in Eq. (16) converges, as noted already in [33, 34]. Next, we assign the QCD coupling constants a value of$ \alpha_{s}(2\; {\rm{GeV}})\approx 0.3 $ and use the other inputs displayed in Table 2. The numerical results for the form factors are$ \begin{aligned}[b] \zeta^{\Lambda_{b}^0\to\pi^{0}} & =(1.43\,_{-0.54}^{+0.46})\times10^{-2}\;[{\rm{GeV}}^2],\\ \zeta^{\Lambda_{b}^0\to K^{0}} & =(1.23\,_{-0.47}^{+0.40})\times10^{-2}\;[{\rm{GeV}}^2], \\ \zeta^{\Xi_{b}^-\to K^-} & =(1.23\,_{-0.47}^{+0.40})\times10^{-2}\;[{\rm{GeV}}^2],\\ \zeta^{\Xi_{b}^-\to\pi^-} & =(1.01\,_{-0.38}^{+0.33})\times10^{-2}\;[{\rm{GeV}}^2]. \end{aligned} $

(26) The mass dimension of the form factors is
$ [\zeta]=2 $ , as the dimension of the baryon coupling constant is$ [f_{{\cal{B}}}]=3 $ .The form factors in Eq. (26) are related to the form factors
$ \zeta_1 $ and$ \zeta_2 $ resulting from the match between Eq. (15) and Eqs. (7) and (8):$ \eta_{\Delta s}\zeta^{{\cal{B}}\to P}=\zeta_1=-\zeta_2, $

(27) We use the heavy quark limit during the calculation of the heavy baryon to light meson transition form factors, and the reliability of our results is best when the momentum transfer
$ q^2=0 $ . In most of the calculations of heavy to light decays, (e.g.,$ B\to\pi \ell\bar{\nu}_{\ell} $ [36] or$ \Lambda_b\to\Lambda \ell\bar{\ell} $ [42]), the relevant form factors can be determined only at one or two values of$ q^2 $ using an assumed$ q^2 $ -dependence to obtain the numerical results at an arbitrary$ q^2 $ . The parameterization and extrapolation of the transition form factors have been extensively studied; thus, we introduce the simplest single-pole model to extrapolate the form factors$ \zeta_{1,2}(q^2=0) $ toward$ \zeta_{1,2}(q^2=m_{\psi}^2) $ [18, 44–46]:$ \zeta_{1,2}(q^2)=\frac{1}{1-q^2/m^2_{{\rm{pole}}}}\zeta_{1,2}(q^2=0). $

(28) Here,
$ \zeta_{1,2}(q^2=0) $ are obtained through the values in Eq. (26) and the relationship between$ \zeta^{{\cal{B}}\to P} $ and$ \zeta_{1,2} $ in Eq. (27). The denominator is introduced to describe the threshold behaviour below the onset of the continuum. The form factor has a pole at the mass of the lowest state that relates to the operators in Eq. (14). For instance,$ m_{\rm pole} $ is the mass of$ \Lambda_b^0\,(\frac{1}{2}^+) $ for the$ \Lambda_{b}^0\to\pi^{0} \,/\Xi^-_{b}\to K^{-} $ transition, as$ \Lambda_b^0\,(\frac{1}{2}^+) $ is the lowest state of operator$ {\cal{O}}^{'L}_{ub,d} $ , while$ m_{\rm pole} $ is the mass of$ \Xi_b^0\,(\frac{1}{2}^+) $ for the$ \Lambda_{b}^0\to K^{0}\,/\Xi^-_{b}\to \pi^{-} $ transition.Starting from Eqs. (7) and (8), the branching fractions of
$ {\cal{B}} \to P \bar{\psi} $ are expressed as$ \begin{aligned}[b] {\cal{BR}}({\cal{B}} \to P \bar{\psi})=\;&\frac{|\vec{q}_{\psi}|}{16 \pi \Gamma_{{\cal{B}}} }\left| C^L_{ub,d} \right|^2 \Bigg[ \zeta^2_1(q^2)+\zeta^2_2(q^2)\frac{m_\psi^2}{m_{{\cal{B}}}^2}\\ &+ \left(\zeta^2_1(q^2)+\zeta^2_2(q^2)\frac{m_\psi^2}{m_{{\cal{B}}}^2} \right)\frac{m_\psi^2-m_P^2}{m_{{\cal{B}}}^2}\\ & +4\zeta_1(q^2)\zeta_2(q^2)\frac{m_\psi^2}{m_{{\cal{B}}}^2} \Bigg], \end{aligned} $

(29) where
$ (u_ad_b,d_c) $ represents$ (ub,d) $ or$ (ub,s) $ for effective operators$ {\cal{O}}^{L}_{ub,d} $ or$ {\cal{O}}^{L}_{ub,s} $ ,$ |\vec{q}_{\psi}| $ is the momentum of dark baryon$ \bar{\psi} ,$ $ |\vec{q}_{\psi}|= \frac{\sqrt{(m_{{\cal{B}}}^2 - (m_{\psi}+m_P)^2)(m_{{\cal{B}}}^2 - (m_{\psi}-m_P)^2)}}{2 m_{{\cal{B}}}}, $

(30) and
$ \Gamma_{{\cal{B}}} $ ($ m_{{\cal{B}}} $ ) is the decay width (mass) of baryon$ {\cal{B}} $ . -
For the radiative decay processes
$ \Lambda_b^0 \to \gamma \bar{\psi} $ showed in Fig. 3, the decay amplitudes can be expressed as,
Figure 3. (color online) The Feynman diagram for
$ \Lambda_b^0 \to \gamma\bar{\psi} $ with the bold line representing the b quark.$ {\rm i} {\cal{M}} = C^{L,R}_{u_ad_b,d_c} \bigg( \bar{v}_{\psi}^{{\cal{C}}}(q) \langle \gamma(p)| {\cal{O}}^{'L,R}_{u_ad_b,d_c} |\Lambda_{b}^0(p')\rangle \bigg). $

(31) The transition amplitudes associated with the right-handed operators
$ {\cal{O}}_{ub,d}^{'R} $ and$ {\cal{O}}_{ud,b}^{'R} $ always vanish for the same reason as in the hadronic semi-invisible decays, which we have mentioned previously. The hadronic matrix elements in Eq. (31) can be parameterized in terms of two form factors:$ \begin{aligned}[b] \langle \gamma(p)| {\cal{O}}^{'L}_{u_ad_b,d_c} |\Lambda_{b}^0(p')\rangle =\;& P_R \Bigg( \zeta^{\Lambda_b \to \gamma}_1(q^2) \frac{\not {p}'}{m_{\Lambda_{b}}^2} {\rm i}\sigma^{\mu\nu}\\& + \zeta^{\Lambda_b \to \gamma}_2(q^2) \frac{\not {q}}{m_{\Lambda_{b}}^2} {\rm i}\sigma^{\mu\nu} \Bigg) u_{\Lambda_b}(p')\epsilon^{*}_{\mu}p'_{\nu}.\end{aligned} $

(32) In the heavy quark limit, the transition amplitude for operator
$ {\cal{O}}^{'L}_{ud,b} $ vanishes in our calculation. We can also arrive at this conclusion by considering the amplitude at the partonic level, which can be factorized as a product of two transition matrix elements in the spin space,$ {\rm i} {\cal{M}}\propto \langle\bar{\psi}(q)|\,\bar{\psi}^{{\cal{C}}} b_R \, | b(m_bv)\rangle\, \langle \gamma(p)| \, \bar{u}^{{\cal{C}}}_L d_L \,|u(k_1) d(k_2)\rangle $ . The second matrix element describes the transition of a quark pair into a photon, with an initial momentum k, transfer momentum r, and final state momentum p. Its amplitude is proportional to the polarization vector$ \epsilon_{\mu} $ of the photon. Considering momentum conservation ($ k+r=p $ ) and the on-shell condition ($ p^2=0 $ ), there are two independent Lorentz-invariant amplitudes proportional to$ p\cdot \epsilon $ and$ r\cdot \epsilon $ , respectively. In the heavy quark limit, we neglect the momentum$ k\sim $ $ \Lambda_{{\rm{QCD}}} $ of the spectator quarks. Therefore, the second transition matrix element must be proportional to$ p \cdot \epsilon=r\cdot \epsilon $ , which is zero after implementing the Ward Identity:$ p\cdot\epsilon=0 $ .The non-vanishing amplitude
$ \Lambda_b^0\to\gamma \bar{\psi} $ defined by$ {\cal{O}}_{ub,d}^{'L} $ is given by$ {\rm i} {\cal{M}} = C^{L}_{ub,d} \bar{v}_{\psi}^{{\cal{C}}}(q)P_R\bigg( \zeta^{\Lambda_{b}^0\to\gamma}_u \dfrac{\not {\bar{n}}}{2} \not {\epsilon}\dfrac{\not {n}}{2} + \zeta^{\Lambda_{b}^0\to\gamma}_d \dfrac{\not {n}}{2} \not {\epsilon} \dfrac{\not {\bar{n}}}{2} \bigg) u_{\Lambda_{b}}(p'), $

(33) The form factors can be factorized as
$ \zeta^{\Lambda_{b}^0\to\gamma}_{u,d } =f_{\Lambda_{b}}^{(2)}\int_{0}^{\infty}{\rm d} \omega\,\omega\int_{0}^{1}{\rm d} u{\cal{J}}_{u,d}^{\Lambda_{b}^0\to\gamma}(u,\omega,\mu)\psi_{2}(u,\omega), $

(34) where the index u (d) denotes the contributions of photons emitted from a u (d) quark. The photon radiation from a b quark is suppressed by
$ m_b $ in a heavy quark propagator. Furthermore,$ {\cal{J}}_{u,d}^{\Lambda_{b}^0\to\gamma}(u,\omega,\mu) $ is the hard-scattering kernel for the$ \Lambda_b \to \gamma $ transition,$ \begin{aligned}[b]& {\cal{J}}_u^{\Lambda_{b}^0\to\gamma}(u,\omega,\mu)=-\dfrac{1}{4}\bigg(\dfrac{Q_{u}(\mu)}{u\omega}\bigg),\\& {\cal{J}}_d^{\Lambda_{b}^0\to\gamma}(u,\omega,\mu)=-\dfrac{1}{4}\bigg(\dfrac{Q_{d}(\mu)}{\bar{u}\omega}\bigg), \end{aligned}$

(35) where the electric charges of the light quarks u and d are
$ Q_{u}(\mu)=\dfrac{2}{3}e(\mu) $ and$ Q_{d} (\mu)=-\dfrac{1}{3}e(\mu) $ , respectively. Combining Eqs. (31)−(33), we have$ \zeta_1^{\Lambda_{b}^0\to\gamma}=-\zeta_d^{\Lambda_{b}^0\to\gamma},\qquad \zeta_2^{\Lambda_{b}^0\to\gamma}=-\zeta_u^{\Lambda_{b}^0\to\gamma}+\zeta_d^{\Lambda_{b}^0\to\gamma}. $

(36) The numerical results for the form factors of the spectator processes
$ \Lambda_{b}^0\to\gamma\bar{\psi} $ are$ \begin{aligned}[b]& \zeta^{\Lambda_{b}^0\to\gamma}_{u}=-(5.49\,_{-1.30}^{+1.18}) \times 10^{-3}\;[{\rm{GeV}}^{2}] ,\\& \zeta^{\Lambda_{b}^0\to\gamma}_{d}=(2.74\,_{-0.65}^{+0.59}) \times 10^{-3} \;[{\rm{GeV}}^{2}], \end{aligned} $

(37) the input of which is shown in Table 2, with
$ \alpha_{em}\,(2\,{\rm{GeV}})\approx 1/133 $ [47]. The single-pole model is also used to describe the$ q^2 $ -dependence of form factor$ \zeta_{1,2}(q^2) $ ,$ \zeta_{1,2}(q^2)=\frac{1}{1-q^2/m^2_{\Lambda_b}}\zeta_{1,2}(q^2=0), $

(38) where
$ m_{\Lambda_b} $ is the mass of$ \Lambda_b^0\,(\frac{1}{2}^+) $ . Then, the branching ratio for$ \Lambda_{b}^0\to\gamma\bar{\psi} $ with operator$ {\cal{O}}_{ub,d}^{'L} $ is estimated as$ \begin{aligned}[b] {\cal{BR}}(\Lambda_b^0 \to \gamma \bar{\psi}) =\;&\frac{|\vec{q}_{\psi}|}{8 \pi m^2_{\Lambda_b} \Gamma_{\Lambda_b} }\frac{1}{2}\sum\limits_{{\rm{spin}}}^{}\left| {\cal{M}} \right|^2\\ =\;&\frac{|\vec{q}_{\psi}|}{8 \pi \Gamma_{\Lambda_b} }\left| C^L_{ub,d} \right|^2 \Bigg[\zeta_1^2(q^2)+ \bigg(\zeta^2_1(q^2)+\zeta^2_2(q^2) \bigg)\\&\times \frac{m_\psi^2}{m_{\Lambda_b}^2}+2\zeta_1(q^2)\zeta_2(q^2)\frac{m_\psi^2}{m_{\Lambda_b}^2} \Bigg], \end{aligned} $

(39) with
$ q^2=m_{\psi}^2 $ . -
Under the B-Mesogenesis scenario, the
$ \Lambda_b^0 \to \xi \bar{\phi} $ channel is governed by both effective operators$ {{\cal{O}}}_{ud,b}^{'L,R} $ and$ {{\cal{O}}}_{ub,d}^{'L,R} $ . The Feynman diagram is shown in Fig. 4. The decay amplitudes can be respectively expressed as
Figure 4. (color online) The Feynman diagram for
$ \Lambda_b^0 \to \xi\bar{\phi} $ process, with the bold line denoting the b quark.$ \begin{aligned}[b] {\rm i} {\cal{M}}_{ud,b}^{L,R} &= y_dC^{L,R}_{ud,b} \bigg(\bar{u}_{\xi}^{{\cal{C}}}(q) \frac{\not {p}'+m_{\psi}}{p'^{2}-m_{\psi}^2} \langle 0| {\cal{O}}^{'L,R}_{ud,b} |\Lambda_b^0(p') \rangle \bigg), \\ {\rm i} {\cal{M}}_{ub,d}^{L,R} &= y_dC^{L,R}_{ub,d} \bigg(\bar{u}_{\xi}^{{\cal{C}}}(q) \frac{\not {p}'+m_{\psi}}{p'^{2}-m_{\psi}^2} \langle 0| {\cal{O}}^{'L,R}_{ub,d} |\Lambda_b^0(p')\rangle \bigg), \end{aligned} $

(40) where
$ u_{\xi}(q) $ is the spinor for ξ with four-momentum q. To estimate the branching ratios of the invisible baryon decay, we first calculate the corresponding hadronic matrix elements in Eq. (40), which can be parameterized in terms of the coupling constants defined by$\begin{aligned}[b]& \langle 0| {\cal{O}}^{'L,R}_{ud,b} |\Lambda_b^0(p')\rangle = \lambda_{ud,b}^{L,R}\ P_R u_{\Lambda_b}(p'), \\& \langle 0| {\cal{O}}^{'L,R}_{ub,d} |\Lambda_b^0(p')\rangle = \lambda_{ub,d}^{L,R}\ P_R u_{\Lambda_b}(p').\end{aligned} $

(41) We found that the couplings
$ \lambda_{ud,b}^{L,R} $ and$ \lambda_{ub,d}^{L,R} $ could be related to the coupling$ f_{\Lambda_b}^{(1,2)} $ defined in Eq. (19) by multiplying the corresponding matrix element. For instance,$ \begin{aligned}[b]& \langle 0| {\cal{O}}^{'L,R}_{ud,b} |\Lambda_b^0(p')\rangle \\=\;& \epsilon_{ijk} \langle 0| \left[u^{i T}\, C P_{L, R}\, d^j \right]b_{R}^k | \Lambda_b^0\left(p'\right) \rangle \\ =\;&\sum\limits_{\rho} (CP_{L,R})^{\alpha\beta}(P_R)^{\rho\gamma} \left\{ \epsilon_{ijk} \langle 0| u^{iT}_{\alpha} d^{j}_{\beta} b^{k}_{\gamma} |\Lambda_b^0(p') \rangle \right\} \\ =\;& \frac{1}{4}\left\{ f^{(1)}_{\Lambda_b} {\rm{Tr}}[CP_{L,R}\gamma_5C^T]+ f^{(2)}_{\Lambda_b}{\rm{Tr}}[ CP_{L,R}\not {v}\gamma_5C^T ] \right\} P_R u_{\Lambda_b}(p'). \end{aligned} $

(42) The last line is the result of using Eq. (19). After the trace, we can obtain the relations,
$ \lambda^L_{ud,b} = -\frac{1}{2} f_{\Lambda_b}^{(1)}, \quad \lambda^R_{ud,b} = +\frac{1}{2} f_{\Lambda_b}^{(1)}. $

(43) The same operation can be used for
$ \lambda^{L,R}_{ub,d} $ , which results in$ \lambda^L_{ub,d} = -\frac{1}{4} f_{\Lambda_b}^{(2)}, \quad \lambda^R_{ub,d} = +\frac{1}{4} f_{\Lambda_b}^{(1)}.$

(44) For the numerical value of the couplings, we quote the result of the NLO QCD sum rules analysis in Ref. [48]:
$ f_{\Lambda_b}^{(2)}\approx f_{\Lambda_b}^{(1)} = 0.030 \pm 0.005 \; [{\rm{GeV}}^3]. $

(45) Then, we can estimate the branching ratios of the invisible baryon decay. Assuming the new physics individually exists in either the left-handed or right-handed component, the branching ratios of
$ \Lambda_b\to\xi\bar{\phi} $ are given by$ \begin{aligned}[b] {\cal{BR}}({\Lambda_b\to\xi\bar{\phi}})^{L,R}_{u_ad_b,d_c} =\;& \frac{\left|\vec{q}_{\xi}\right|}{8 \pi m_{\Lambda_b} \Gamma_{\Lambda_b}} \bigg(\left|y_d\right|^2 \left|C^{L,R}_{u_ad_b,d_c}\right|^2 \left|\lambda_{_{u_ad_b,d_c}}^{L,R}\right|^2 \bigg)\\&\times \frac{E_{\xi}\left( m_{\Lambda_b}^2 + m^2_{\psi} \right) + 2 m_{\Lambda_b} m_{\psi}m_{\xi}}{\left(m_{\Lambda_b }^2 -m_{\psi}^2\right)^2},\end{aligned} $

(46) where
$ (u_ad_b,d_c) $ represents$ (ud,b) $ or$ (ub,d) $ for different effective operators$ {\cal{O}}^{L,R}_{ud,b} $ and$ {\cal{O}}^{L,R}_{ub,d} $ according to the convention in Eq. (3), respectively;$ m_i\; (i=\Lambda_b^0,\bar{\psi},\bar{\phi},\xi) $ is the mass of particle i;$ \Gamma_{\Lambda_b} $ is the total width of heavy baryons; and$ \vec{q}_{\xi} $ and$E_{\xi} = \dfrac{m_{\Lambda_b}^2 + m_{\xi}^2 - m_{\phi}^2}{2m_{\Lambda_b}}$ are the momentum and kinetic energy of ξ in the heavy baryon$ \Lambda_b^0 $ rest frame, respectively. -
Using the hadronic matrix elements obtained in the section above, we can explore B-Mesogenesis via the invisible and semi-invisible decays of bottom baryons detectable at future lepton colliders. The reconstructions of the invisible and semi-invisible decays of bottom baryons are always difficult in experiments. However, these difficulties can be overcome by the double tag method [49]. In the
$ e^+e^- $ collisions, the initial energy is well known in each event. Assuming the detectors have a sufficient resolution, we reconstruct all the recoiling particles except for$ \Lambda_b^0/\Xi_b^{0,-} $ in the colliding event, which helps to determine the invariant mass of the bottom-baryon candidate using energy-momentum conservation. The production of a bottom baryon will be identified if the invariant mass is consistent with the mass of$ \Lambda_b^0/\Xi_b^{0,-} $ and if the conservation laws for the electric charge, baryon number, bottom number, and strange number are satisfied. Then we are able to measure the invisible and semi-invisible decays of bottom baryons. The double tag method has been widely used by BESIII, BABAR and Belle. For example, BESIII measured the absolute branching fraction of$ \Lambda_c^+\to \Lambda^0e^+\nu_e $ at the$ \Lambda_c^+\bar\Lambda_c^- $ threshold, which determines$ \Lambda_c^+ $ by reconstructing the charmed anti-baryon via its hadronic decays, such as$ \bar\Lambda_c^-\to \bar p K^+\pi^- $ [50]. It is also possible to use the double tag method at energies much higher than the baryon-antibaryon threshold. The Belle collaboration measured the absolute branching fractions of$ \Lambda_c^+ $ decays by reconstructing the recoiling$ D^{(*)-}\bar p\pi^+ $ system in the event of$ e^+e^-\to D^{(*)-}\bar p\pi^+\Lambda_c^+ $ at the colliding energy of approximately 10 GeV [51]. Therefore, the invisible and semi-invisible decays of$ \Lambda_b^0/\Xi_b^- $ can be measured using the double tag method at$ e^+e^- $ colliders, such as BelleII at the bottom baryon-antibaryon threshold, or CEPC and FCC-ee at a higher energy as well.In practice, to estimate the sensitivity of the parameters of B-Mesogenesis, we define the significance s of the signal at the 95% C.L. as
$ s=\frac{n_S}{\sqrt{n_S+n_B}} =\sqrt{n_S}=\sqrt{N_{{\cal{B}}}\times {\rm Br} ({\cal{B}}\to X)} =2, $

(47) where
$ n_S $ and$ n_B $ denote the numbers of signal and background events at future lepton colliders, respectively. The background events are negligible using the double tag method because the three kinds of processes studied in this work are all forbidden in the Standard Model by the visible baryon number violation. The branching fractions${\rm Br}({\cal{B}}\to X)$ with$ X=\pi\bar{\psi}, K\bar{\psi}, \gamma\bar{\psi}, \xi\bar{\phi} $ are given in Eqs. (29), (39), and (46), where$ N_{\cal{B}} $ represents the production number of bottom baryons detected by the double tag method, which is different from the total production of bottom baryons in the collisions. We assume an efficiency of reconstruction of 100% for pions, kaons, and photons in the semi-invisible decays. We also assume that the production number of bottom baryons in the double tag method is$ N_{\cal{B}}=N_{\Lambda_b,\Xi_b}=10^8 $ as a benchmark for future lepton colliders. The corresponding constraints can directly scale up to the results for the actual production number of bottom baryons at future lepton colliders, which are still indistinct in the current theoretical study.There are some constraints on the masses of dark particles under the B-Mesogenesis scenario. To prevent the decay of protons into dark particles, the masses of dark matter particles must satisfy
$ \begin{align} m_{\bar{\psi}} &> m_p -m_e-m_{\nu_e} \simeq 937.8\; {\rm{MeV}},\\ m_{\xi}+m_{\bar{\phi}} &> m_p -m_e-m_{\nu_e} \simeq 937.8\; {\rm{MeV}}, \end{align} $

(48) where the former prohibits
$ p\to \bar{\psi}e^+\nu_e $ decay and the latter prevents$ p \to \bar{\phi}\xi e^+\nu_e $ decay through an off-shell$ \bar{\psi} $ propagation. In addition, the stability of dark matter requires that the mass difference between the dark scalar$ \bar{\phi} $ and dark Majorana fermion ξ must obey [10]$ |m_{\xi}- m_{\bar{\phi}}| < m_p + m_e + m_{\nu_e} \simeq 938.8\ {\rm{MeV}}. $

(49) Otherwise, the dark particles could decay into each other by emitting a proton, an electron, and a neutrino, which will diminish the baryon asymmetry generated in the Universe.
-
First, we estimate the sensitivity required for B-Mesogenesis by searching for the semi-invisible decay of bottom baryons at future lepton colliders. Their branching ratios are only sensitive to the mass
$ m_\psi $ and Wilson coefficients$ |C^L_{ub,d}| $ or$ |C^L_{ub,s}| $ of the scenario. The constraints on the Wilson coefficients$ |C^L_{ub,d}| $ and$ |C^L_{ub,s}| $ versus$ m_\psi $ at the 95% C.L. are illustrated in Fig. 5, for which the production number of bottom baryons in the double tag method is assumed to be$ N_{\Lambda_b,\Xi_b}=10^8 $ . The constraints on the right-handed operators$ {\cal{O}}^R_{ud_a,d_b} $ are omitted because they could not project out the leading-twist wave function of the$ \Lambda_b $ and$ \Xi_b $ baryons.
Figure 5. (color online) The constraints on the Wilson coefficients at 95% C.L. versus
$ m_\psi $ in the semi-invisible decays of bottom baryons. The left panel illustrates the constraints on$ |C^L_{ub,d}| $ , while the right panel display the constraints on$ |C^L_{ub,s}| $ . The declines of the constraints at the tail result from the suppression of phase space. When dark fermion mass$ m_\psi $ close to the mass of$ \Lambda_b^0 $ baryon, the soft photon radiation in$ \Lambda_b^0\to\gamma\bar{\psi} $ channel will induce a serious infrared divergence, which invalid the leading order estimation in this region. Hence, we omit the constraints in$ \Lambda_b^0\to\gamma\bar{\psi} $ process when$ m_\psi>5 $ GeV (blue dot dashed line).For the
$ \Lambda_b(\Xi_b)\to P\bar{\psi} $ processes, we found that the semi-invisible decay$ \Lambda_b^0\to\pi^0\bar{\psi} $ is most sensitive to operator$ {\cal{O}}^L_{ub,d} $ , while the$ \Lambda_b\to K^0\bar{\psi} $ process is most sensitive to operator$ {\cal{O}}^L_{ub,s} $ . When assuming the production number of bottom baryons in the double tag method is$ N_{\Lambda_b,\Xi_b}= 10^8 $ , the constraints on the Wilson coefficients can reach$ {\cal{O}}(10^{-8}) $ GeV-2. The decline in the Wilson coefficients at the tail result from the suppression of phase space. The form factors and hadron mass in the semi-invisible decay are similar, and the constraints on the Wilson coefficients are similar in these processes.For the
$ \Lambda_b^0\to\gamma\bar{\psi} $ channel, the constraints on the Wilson coefficients can reach at least$ {\cal{O}}(10^{-7}) $ GeV-2. This constraint is looser than that in the hadronic semi-invisible decay in the small-mass region owing to the fact that the form factors of photon radiation are smaller than those of meson final states. However, in the large-mass region, the constraints will be tighter because of the evolution of the form factors. Moreover, when the dark fermion mass$ m_\psi $ is similar to the mass of initial baryons$ m_{\Lambda_b} $ , the divergence in the evolution of the form factors invalidates the estimation of the branching ratio. Therefore, we omit the constraints in the$ \Lambda_b^0\to\gamma\bar{\psi} $ channel when$ m_\psi>5\;{\rm{GeV}} $ .Finally, because the final state hadrons in the
$ \Xi_b^- $ semi-invisible decay are all electrically charged, these decay modes should be probed at future high-energy lepton colliders (i.e., CEPC or FCC-ee) using a displaced vertex method. Therefore, we expect a thorough exploration of these semi-invisible decays of bottom baryons to be conducted at future lepton colliders. -
As shown in Refs. [7, 13, 15–18], previous studies primarily focused on searching for the dark fermion ψ in the semi-invisible decay of bottom baryons or mesons. To keep the dark matter stable, B-Mesogenesis must involve a dark Majorana fermion ξ and a dark scalar baryon ϕ, and requires all the dark fermions ψ to completely decay into these two invisible particles, with
$ {\cal{BR}}(\psi\to \phi\xi)= $ 100%. Therefore, the coupling of$ y_d $ and the interaction of$ \bar\psi\phi\xi $ are very challenging to explore in the semi-invisible decays in which ψ is always on-shell. The width of ψ (depending on$ y_d $ ) cannot be measured in experiments because the final states ϕ and ξ are not measurable. On the contrary,$ \bar\psi $ is off-shell in the fully invisible decay of$ \Lambda_b^0\to\xi\bar{\phi} $ , as seen in Fig. 1 (i) or Fig. 4. Then the stable dark matter particle ξ or$ \bar\phi $ can be explored, and the interaction of$ y_d\bar\psi\phi\xi $ can be measured, as shown in the branching fraction of$ \Lambda_b^0\to\xi\bar{\phi} $ in Eq. (46). Therefore, we argue that the fully invisible decay of$ \Lambda_b^0\to\xi\bar{\phi} $ is crucial for probing B-Mesogeneisis, as it provides a distinctive signal that can be used to examine the stable dark particles in this scenario.Assuming the production number of
$ \Lambda_b^0 $ baryons using the double-tag method is$ N_{\Lambda_b}=10^8 $ , the constraints on the parameters$ |y_d\; C^{L,R}_{ud_a,d_b}| $ can be taken straight from Eq. (46), depending on the different masses of$ \bar\psi $ ,$ \bar\phi $ , and ξ. The constraints at the 95% C.L. are displayed in Fig. 6 and Fig. 7 for the variations of$ m_{\psi} $ and$ m_{\xi}+m_{\phi} $ , respectively.
Figure 6. (color online) The constraints on the parameters
$ |y_d\; C^{L,R}_{ud,b}| $ and$ |y_d\; C^{L,R}_{ub,d}| $ versus$ m_{\psi} $ from the invisible decay of$ \Lambda_b^0 $ with 95% C.L. We estimate the constraints in six different mass distribution of dark matters. The left and right panels illustrate the constraints related to operators$ {\cal{O}}_{ud,b}^{L,R} $ and$ {\cal{O}}_{ub,d}^{L,R} $ , respectively. The dark matter (DM) stability in Eq. (49) prohibits a large mass difference between dark fermion ξ and dark scalar$ \bar{\phi} $ , which imposes a truncation at large mass region if$ m_\phi\neq m_\xi $ . For the three cases where$ m_\xi+m_\phi=0.5 \,m_\psi $ (dashed line), there is another truncation at small$ m_\psi $ region to forbid the decay of proton into$ \xi\bar{\phi} $ through an off-shell$ \bar{\psi} $ particle.
Figure 7. (color online) The constraints on the parameters
$ |y_d\; C^{L,R}_{ud,b}| $ and$ |y_d\; C^{L,R}_{ub,d}| $ versus total mass$ m_{\xi\phi}=m_\xi+m_\phi $ with 95% C.L.. As the DM stability prohibits a large mass splitting of dark fermion and dark baryons, we estimate the constraints in three different mass distribution of dark matters.In Fig. 6, the constraints of the parameters depending on
$ m_{\psi} $ are given for$ |y_d\; C_{ud,b}^{L,R}| $ in the left panel, and for$ |y_d\; C_{ub,d}^{L,R}| $ in the right panel. We estimate the constraints in six different mass distributions of dark matter particles. Three cases of the masses of ξ and ϕ are shown as the blue, green, and red curves, with (i)$ m_{\xi}=m_{\phi}=0.49 \,m_{\psi} $ , (ii)$m_\xi= 0.90\,m_\psi$ ,$ m_\phi=0.08\,m_\psi $ , and (iii)$ m_\xi=0.08\,m_\psi $ ,$m_\phi= 0.90\,m_\psi$ , respectively. Because the stable dark particles ξ and$ \bar{\phi} $ carry most of the mass of$ \bar{\psi} $ , the decay of protons into$ \xi\bar{\phi} $ through off-shell$ \bar{\psi} $ particles is forbidden for$ m_\psi\simeq 1 $ GeV. In addition, to directly illustrate the dependence of the constraints on the mass distribution of dark particles, three other cases of$ m_\xi $ and$ m_\phi $ are shown as the orange, cyan, and magenta curves, with (i)$m_\xi=m_\phi = 0.25\,m_\psi$ , (ii)$ m_\xi=0.4\,m_\psi,\; m_\phi=0.1\,m_\psi $ , and (iii)$ m_\xi=0.1\,m_\psi, m_{\phi}=0.4\,m_\psi $ , respectively. For these cases, a truncation at the small-mass region was imposed to prevent the decay of protons into$ \xi\bar{\phi} $ . Because the DM stability in Eq. (49) prohibits a large mass difference between dark fermions ξ and dark scalar baryons ϕ, it also imposes a truncation at the large-mass region with a specific mass distribution. We found that the constraints on the parameters of B-Mesogenesis can reach$ {\cal{O}}(10^{-7}) $ GeV-2. Because the values of the form factors from the left- and right-handed operators are the same except for their signs, the constraints on the operators with different chirality are equal to each other. For the operators with different flavor structures, a factor of$ 2 $ in the constraint on$ |y_d\; C^{L,R}_{ub,d}| $ arises from the half suppression of the decay constants$ \lambda^{L,R}_{ub,d} $ in the comparison between Eqs. (43) and (44). In the allowed mass region, we found that the differences between the constraints for various mass distributions are very small, indicating that the fully invisible decay of$ \Lambda_b $ baryons is insensitive to the mass distribution of dark particles. The drop in the constraints at$ m_\psi $ values close to$ m_{\Lambda_b} $ arises from a nearly on-shell transition of$ \Lambda_b^0\to\bar{\psi} $ , which significantly enlarges the invisible decay rate.Similarly, the constraints on the parameters of the mass of
$ m_{\xi\phi}=m_\xi+m_\phi $ are shown in Fig. 7; the left and right panels correspond to$ |y_d\; C^{L,R}_{ud,b}| $ and$ |y_d\; C^{L,R}_{ub,d}| $ , respectively. The three cases of (i)$ m_\phi=m_\xi $ , (ii)$ m_\xi=m_\phi+ 0.9 \; {\rm{GeV}} $ , and (iii)$ m_\phi=m_\xi+0.9 \; {\rm{GeV}} $ are displayed as the blue, green, and red curves, respectively, with the mass of ψ fixed at 4.0 GeV. The curves are roughly flat in the region of$ m_{\xi\phi} $ between 1 GeV and 5 GeV. Furthermore, the differences between the three curves in each panel are also very small. These phenomena indicate that the constraints on the parameters are insensitive to the mass distribution of$ m_\xi $ and$ m_\phi $ . This is beneficial to the search for the stable particles in B-Mesogenesis. If there is a deviation in the semi-invisible decays of bottom baryons or mesons, the fully invisible decay of$ \Lambda_b^0 $ can further indicate the stable components that are inherent in B-Mesogenesis. The declines in the constraints within the large-mass region result from the suppression of phase space. -
The similar densities of baryons and dark matter in the universe imply that they may arise from the same UV complete model. B-Mesogensis, which assumes dark matter can be charged under the baryon number, attempts to simultaneously explain the origins of dark matter and baryon asymmetry. Since this model was proposed, most studies have primarily concentrated on exploring the semi-invisible decays of B mesons. However, both invisible and semi-invisible decays of bottom baryons are crucial for exploring B-Mesogenesis at the GeV scale. In particular, as B-Mesogenesis must involve a dark Majorana fermion and a dark scalar baryon to keep the DM and baryon asymmetry stable, the fully invisible decay of
$ \Lambda_b^0 $ yields a distinctive signal that can be used to directly probe the stable particles of this scenario. In addition, when exploring B-Mesogenesis in terms of the decays of bottom baryons, the hadronic matrix elements are vital for determining the physical observables. Accordingly, we systematically examined the hadronic semi-invisible decays of$ \Lambda_b^0\to \pi^0(K^0)\bar\psi $ and$ \Xi_b^-\to \pi^-(K^-)\bar\psi $ , the radiative semi-invisible decay of$ \Lambda_b^0\to \gamma\bar\psi $ , and the fully invisible decay of$ \Lambda_b^0\to \xi\bar\phi $ . The relevant hadronic matrix elements were calculated using the QCD factorization method in the heavy quark limit. Furthermore, we analyzed the sensitivities of the parameters of B-Mesogenesis by searching for the invisible and semi-invisible decays of bottom baryons at future lepton colliders. Assuming the production of bottom baryons in the double-tag method was$ N_{\Lambda_b,\Xi_b}=10^8 $ , we found that the constraints on the Wilson coefficients$ |C^{L}_{ub,d}| $ and$ |C^{L}_{ub,s}| $ in the semi-invisible decay of bottom baryons can reach$ {\cal{O}}(10^{-8}) $ GeV-2, while the constraints on$ |y_d\; C^{L,R}_{ud,b}| $ and$ |y_d\; C^{L,R}_{ub,d}| $ can reach$ {\cal{O}}(10^{-7}) $ GeV-2 from the fully invisible decay of$ \Lambda_b^0 $ . Although the invisible decay of$ \Lambda_b^0 $ baryons was sensitive to new physics parameters, this decay mode provides a distinctive signal with which the stable dark particles of B-Mesogenesis can be directly explored. -
We are grateful to Sheng-Qi Zhang and Man-Qi Ruan for useful discussions.
Invisible and semi-invisible decays of bottom baryons
- Received Date: 2024-04-07
- Available Online: 2024-08-15
Abstract: The similar densities of dark matter and baryons in the universe imply that they may arise from the same ultraviolet model. B-Mesogenesis, which assumes dark matter is charged under the baryon number, attempts to simultaneously explain the origin of baryon asymmetry and dark matter in the universe. In particular, B-Mesogenesis may induce bottom-baryon decays into invisible or semi-invisible final states, which provide a distinctive signal for probing this scenario. In this work, we systematically study the invisible decays of bottom baryons into dark matter and the semi-invisible decays of bottom baryons into a meson or a photon together with a dark matter particle. In particular, the fully invisible decay can reveal the stable particles in B-Mesogenesis. Some QCD-based frameworks are used to calculate the hadronic matrix elements under the B-Mesogenesis model. We estimate the constraints on the Wilson coefficients or the product of some new physics couplings with the Wilson coefficients according to the semi-invisible and invisible decays of bottom baryons detectable at future colliders.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: