-
Nuclear level density (NLD) is defined as the number of excited levels per unit energy at a given excitation energy. It plays a central role in aspects of nuclear reactions and nuclear structure, thereby influencing the behavior of stellar nucleosynthesis networks in nuclear astrophysics [1], the design of novel reactors [2], and applications of radioactive isotopes in applied nuclear physics [3]. Accurate predictions of NLD are crucial for understanding the properties and behavior of nuclei at high excitation states, which are prevalent in nuclear reactions and stellar processes.
Its theoretical model was first introduced by Bethe in 1936 [4], also known as the Fermi gas model (FGM). The FGM is based on the assumption that the excited levels of the nucleus are evenly spaced and that there are no collective levels; it is successful in estimating levels at high excitation energies and fails in the low energy region. Various phenomenological level density models, mostly based on the FGM, have been proposed to solve this problem, such as the back-shifted FGM (BSFGM) [5], Gilbert Cameron model (GCM) [6], and generalized superfluid model (GSM) [7, 8]. These phenomenological models with simplified assumptions are usually more computationally accessible but are limited to excitation energies above 5 MeV. Microscopic models, such as Hartree-Fock-Bardeen-Cooper-Schrieffer (HF-BCS) [9], Gogny-Hartree-Fock-Bogoliubov (Gogny-HFB) [10], and Skyrme-Hartree-Fock-Bogoliubov (Skyrme-HFB) [11], and density functional theory combinatorial models [12, 13], the Monte Carlo shell model [14], quasi-particle random phase approximation (QRPA) [15], and core-quasi particle coupling (CQC) model [16], have attempted to describe the NLD from more fundamental particle interactions with excitation energies ranging from 0 to 20 MeV. Thus, a high efficiency and unified predictive model is urgently required for the application of NLD. Machine learning can be used to achieve these goals.
Machine learning is based on a class of computer algorithms. These algorithms do not require coding for specific tasks. They can automatically extract features from large amounts of data. The application of machine learning technology to physics to solve unsolved scientific problems is currently a frontier of international, cross-disciplinary research methods. Bayesian neural networks (BNNs) represent such an alternative, offering a novel methodology that can handle the uncertainties inherent in both theoretical models and experimental data within a unified framework. In recent years, several groups have demonstrated how BNNs can obtain accurate models for predicting nuclear charge radii [17], atomic nucleus mass [18], half-life of decay [19], and fission yield [20], with the uncertainties. In addition, nucleon density distributions are calculated based on the deep neural network method [21–23], and level density parameters are estimated using an artificial neural network (ANN) [24] and feedback neural network (FNN) [25].
In this study, a BNN is used to train a set of NLDs that are uniformly described over a large range, considering the NLD calculated by the theoretical model and obtained experimentally using the Oslo method [26–28]. By training a neural network for the identification and reconstruction of the NLD, we can explore the model uncertainties in a comprehensive manner and provide a model-independent method for the study of the NLD. This approach using a BNN not only improves the descriptive power of models for complex nuclear systems, but also allows for a more precise and systematic way to quantify and understand the uncertainties in NLD predictions, which is crucial for the future development of nuclear physics.
-
A detailed description of the origins and development of BNNs goes beyond the scope of this study; for a detailed exposition, see Refs. [29–32]. The use ANNs in nuclear physics is mainly to estimate unknown properties of revelant exotic nuclei to astrophysics and began in the early 90s with the work of Clark and collaborators [33–36]. It continues to this day [37–41] with more sophisticated applications.
There are two main components in a BNN [29]: one is the ANN and the other is the Bayesian inference system. The ANN we use is a fully connected feed-forward ANN. The neural network function
$ f (x, \omega) $ with one hidden layer adopted here has the following form:$ f(x,\omega)=a+\sum\limits_{j=1}^Hb_j {\rm tanh}(c_j+\sum\limits_{i=1}^ld_{ij}x_i), $

(1) where the model parameters (or "connection weights") are collectively given by
$ \omega = (a, b_j, c_j, d_{ij}) $ , and x is the set of inputs$ x_i $ . The function above contains$ 1 + H(2 + I) $ parameters, where H is the number of neurons in the hidden layer, and I denotes the number of input variables. Here, tanh is a common form of the sigmoid activation function that controls the firing of the artificial neurons [42, 43].In the present case, we assume that the four sets of parameters
$ \omega = (a, b, c, d) $ are independent of each other and each of them obeys a Gaussian distribution centered around 0 with a width controlled by a hyperparameter. As shown in Ref. [29], the "gamma" probability distribution is used for the hyperparameter. Similarly, a Gaussian distribution is used for the likelihood:$ p(x,t|\omega)={\rm exp}(-\chi^2/2), $

(2) where the cost function
$ \chi^2(\omega) $ reads as$ \chi^2(\omega)=\sum\limits_{i=1}^N\left(\frac{t_i-f(x_i,\omega)}{\Delta t_i}\right)^2, $

(3) where N is the total number of data points,
$ t_i\equiv t(x_i) $ is the empirical value of the target evaluated at the ith input$ x_i $ , and$ \Delta t_i $ is the associated error. -
In this study, we propose a BNN model to investigate the NLD and verify whether it can be used to make reliable predictions. The training set used in the BNN contains 282 nuclides, including six theoretical NLD models (BSFGM, GCM, GSM, HF-BCS, Gogny-HFB, and Skyrme-HFB), with
$ 11\leq $ Z$ \leq 98 $ ,$ 24\leq $ A$ \leq 251 $ taken from the TALYS 1.95 code [44], and the experimental 53-nuclide database measured using the Oslo method [26–28]. Approximately 70000 data points are used for training set.In the BNN model, the input layer has five neurons, which are the number of protons Z, total number of masses A, neutron separation energy
$ Sn $ , and proton separation energy$ Sp $ and excitation energy E. There are two hidden layers, and the number of neurons per layer is 64 and 32. The output of the neural network is$ \mathrm{log}(\rho/\rho_c) $ , where$ \rho_c=1 $ MeV–1. For each training, the training set is randomly divided into two categories: training (80%) and validation (20%) parts. Finally, we use the mean absolute error (MAE) as the loss function.$ {\rm{MAE}} = \frac{1}{n} \sum\limits_{i=1}^{n} \left| y_i - \hat{y}_i \right|, $

(4) where n is the total number of data points,
$ y_i $ is the actual value for the ith data point,$ \hat{y}_i $ is the predicted value for the ith data point, and$ \left| y_i - \hat{y}_i \right| $ is the absolute difference between the actual and predicted values. -
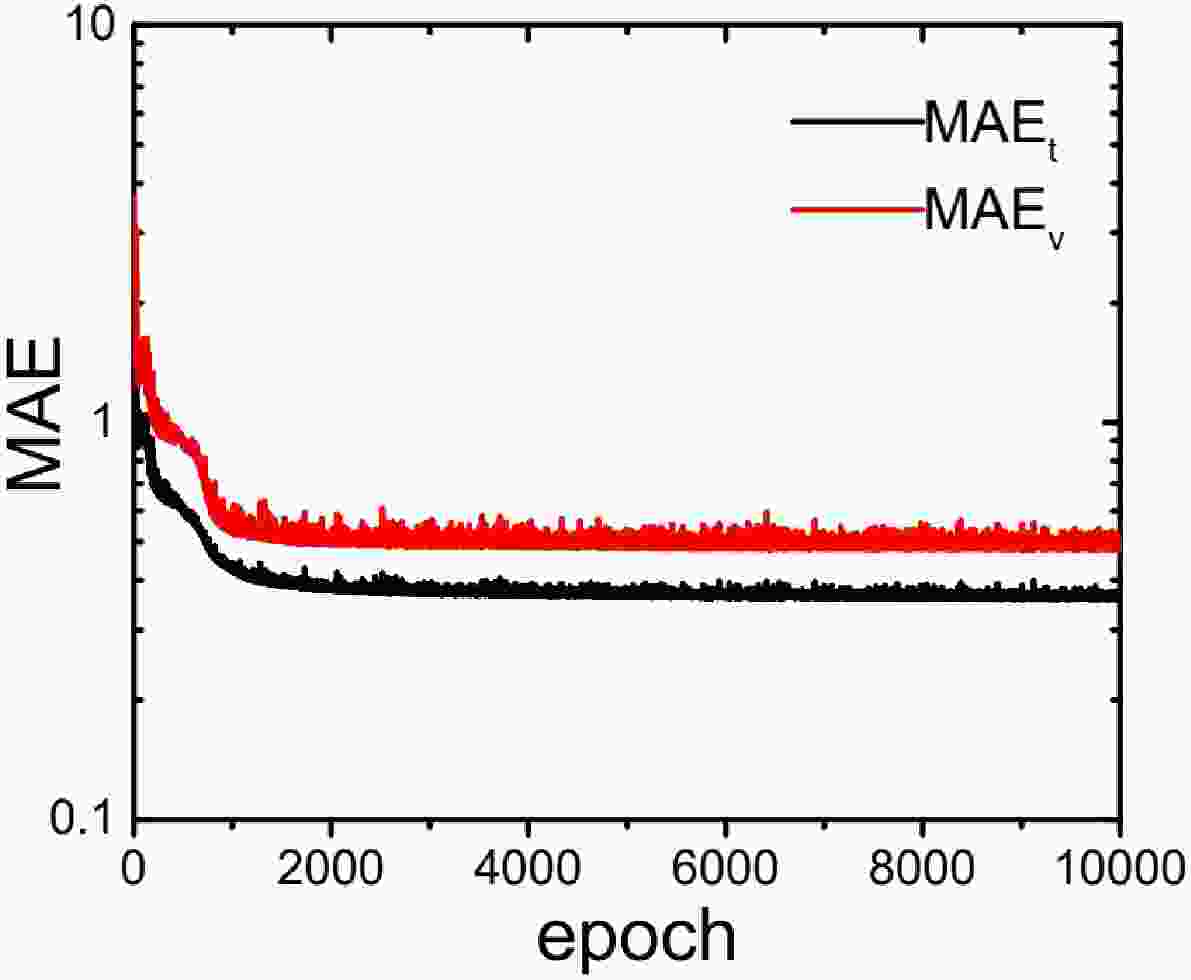
First, we check the MAE as a function of iteration epoch. There are 10000 epochs in the training processes in this study. The MAEs of both the training and validation parts of the total training set decrease steadily, as shown in Fig. 1. The convergence of the MAE of the training set indicates well trained data.

Figure 1. (color online) Mean absolute error of the training (MAEt) and validation parts (MAEv) of the training set.
To obtain the special BNN, we present the trained results of the BNN and the NLD data from theoretical calculations and experimental data in Fig. 2. The red solid lines are the mean values of the different nuclei, the dash lines and circles are the data of the models and Oslo experiment [26–28]. The pink band represents the 95% confidence interval, showing the uncertainty in the predictions of the BNN, which provides the uncertainty among all models and experimental data. As shown in Fig. 2, the BNN predictions mostly associate with the range of predictions of the NLD from other models across the entire excitation energy from 0 to 20 MeV, suggesting that the BNN is capable of learning and predicting the behavior of the training data. The uncertainties of all models obtained with the BNN model are smaller at lower excitation energies (
$ E<5 $ MeV). However, the uncertainties become wider in higher excitation energy regions ($ E>10 $ MeV), especially for heavy nuclei ($A > 100$ ) because of the greater uncertainty among the different model predictions in these areas for heavy nuclei. Because the depicted nuclei are part of the training set, this consistency is expected. A more rigorous test would include predictions for nuclei that are not in the training set.
Figure 2. (color online) Training of nuclear level density. The shadow region corresponds to the CI estimated at 95%.
For the test sets, the NLD of 233U-239U and experimental data with 63Ni, 70Ni, and 167Ho [26–28] are used. The MAEs of both the training and test sets are listed in Table 1. The MAEs of the test sets are smaller than that of the validation part in the training set; hence, the NLD prediction from the BNN is reliable.
MAE of training set MAE of test set training validation 233U-239U 63Ni 70Ni 167Ho 0.3590 0.4830 0.4329 0.1895 Table 1. Mean absolute error of the training and test sets.
In Fig. 3, the results of the NLD of 233U-239U are displayed as part of the test set, which were not included in the training set. The mean values of the level density of the BNN model predictions for Uranium isotopes are shown as red lines in the plots, which are similar to those of traditional models, suggesting that the model generalizes well beyond the training data. This is a positive indication of the model's robustness and its ability to infer the properties of unseen nuclides based on the patterns learned from the training set. The 95% confidence interval, represented by the pink shaded area, encapsulates the BNN predictions both from the theoretical models and the experimental data of the Oslo method. Moreover, the BNN predictions are closely aligned with those of theoretical models such as the GCM, BSFGM, GSM, HF-BCS, Skyrme-HFB, and Gogny-HFB. Except for HF-BCS, most theoretical models are in the range of the BNN predictions, which also find 243Pu in the training set. For most of the theoretical models, the model predictions are within a statistically reasonable range. The consistency within this interval indicates that the BNN uncertainty is reliable. The BNN model displays consistent performance across various isotopes of Uranium, which may be indicative of the model's ability to handle the systematic variations in nuclear properties across isotopes. Fig. 3 shows an increased spread in the predictions at higher excitation energies, which is typical for extrapolative predictions. This spread implies increased uncertainty and highlights areas where additional data or refinement of the model may be beneficial. The NLD from the BNN predictions using the experimental data points of the Oslo method for these isotopes, which were also not part of the training database, is particularly noteworthy. It demonstrates the potential utility of BNNs in predicting experimental outcomes.
To further test the predictions from the BNN models, we investigate the NLD for 63Ni, 70Ni, and 167Ho [26–28] in Fig. 4. The plots present the latest experimental data (black dots) and the predictions made using the BNN model (red line), along with the 95% confidence interval (shaded pink area). The BNN predictions are very closely aligned with the experimental data, which indicates that the BNN is capable of learning and predicting new experimental outcomes effectively. For all three nuclides, the 95% confidence interval encompasses nearly all the experimental data points, signifying that the BNN predictions are statistically reasonable and provide a credible estimate of the predictive uncertainty. We also find that the BNN offers a reliable method for predicting NLDs, even in the absence of theoretical models to guide predictions, especially in higher excitation energy regions, where BNN predictions remain consistent with experimental data, which are areas often challenging for theoretical models to reach. Although the BNN predictions match the experimental data, the confidence intervals also are wide at higher excitation energies, indicating greater uncertainty in the predictions in these regions. This could be due to sparse experimental data in these areas or the increased complexity of physical processes at these energies.
-
We study NLD using BNNs. NLD is a critical parameter in nuclear physics and is essential for understanding nuclear reactions and structures. Many theoretical models and experimental methods have been proposed; however, they each have their own limitations. In this study, a BNN is used to integrate and unify NLD data from a variety of sources, including phenomenological models, microscopic models, and experimental data from the Oslo method. The NLD achieved using the BNN not only reproduces the training data, but also gives very good predictions of the test data. In particular, the results show the capability of the BNN in predicting NLDs on new experimental data without comparable theoretical models. The application value of BNNs provides valuable guidance for future experimental and theoretical work.
In the future, these NLDs will be used as input for TALYS to calculate nuclear reaction cross sections, and the NLD uncertainties will be used to calculate covariance matrices for each reaction channel. In addition, the BNN method in this study will provide an opportunity for improving the predictions of NLD data when new measured data are available.
Uncertainties of nuclear level density estimated using Bayesian neural networks
- Received Date: 2024-03-22
- Available Online: 2024-08-15
Abstract: Nuclear level density (NLD) is a critical parameter for understanding nuclear reactions and the structure of atomic nuclei; however, accurate estimation of NLD is challenging owing to limitations inherent in both experimental measurements and theoretical models. This paper presents a sophisticated approach using Bayesian neural networks (BNNs) to analyze NLD across a wide range of models. It uniquely incorporates the assessment of model uncertainties. The application of BNNs demonstrates remarkable success in accurately predicting NLD values when compared to recent experimental data, confirming the effectiveness of our methodology. The reliability and predictive power of the BNN approach not only validates its current application but also encourages its integration into future analyses of nuclear reaction cross sections.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: