-
When examining the evolution of the universe, our current understanding suggests that it originated from the Big Bang. Since then, the universe has been continuously expanding. Scientists expect that the acceleration must decrease after some point. However, two simultaneous and independent investigations (the Supernova Cosmology Project and the High-Z Supernova Search Team) in 1998 showed that the rate of acceleration of the universe has been gradually increasing instead of decreasing. This was a baffling discovery as it shook our current understanding of how the universe works. A phantom force appears to be ripping the universe apart.
To understand and theoretically justify this observed phenomenon, researchers have proposed several different ideas. One idea is to consider an energy form with a positive energy density but negative pressure, known as dark energy. Alternatively, researchers have proposed modified versions of General Relativity (GR) that interpret this phenomenon as a geometric effect. This geometric modification enables the elimination of exotic or dark energy. Several modified gravity theories have been tested by researchers, including
$ f(\mathcal{R}) $ gravity [1, 2], teleparallel gravity [3],$ f(\mathcal{R},G) $ gravity [4], and unimodular gravity [5]. Several other studies have explored various modified gravity theories, which have been described in the following works [6−32].Harko et al. [33] considered the concept of weak coupling between geometry and matter and proposes a novel gravity theory known as
$ f(\mathcal{R},T) $ gravity, where R is the Ricci scalar, and T is the trace of the EM tensor. The Einstein-Hilbert (EH) action was modified using the function$ f(\mathcal{R},T) $ . However, note that the imperfect fluids can be attributed to the trace part. In$ f(\mathcal{R},T) $ theory, the$ f(\mathcal{R},T) $ function is adopted in various forms, such as$ f(\mathcal{R},T)= aR + 2bf(T) + c(f_1(R)+ f_2(T)) + d(f_2(R)f_3(T)) $ by tuning the constants a, b, c, and d (which can have values of$ 0,\; 1,\; 2.... $ ) with different sets of values, e.g.,$ f(T) $ ,$ f_2(T) $ ,$ f_3(T) $ ,$ f_1(R) $ , and$ f_2(R) $ , being some arbitrary functions. Recently, this theory of gravity has been widely used by researchers, particularly because of its effectiveness in explaining the late-time accelerated expansion of the universe. Several papers using$ f(\mathcal{R},T) $ gravity under various scenarios are available in the literature [34−45].The effectiveness of the modified gravity theories, including
$ f(\mathcal{R},T), $ is not limited to understanding the late-time behavior of the universe. They are essential in understanding compact objects with very high densities. Despite the efforts of several researchers over many years, these compact objects have not yet been completely understood. A particular aspect to understand is the behavior of matter distribution inside these objects. For theoretical modeling of these objects, we must determine solutions to Einstein's field equations. The matter distribution can be considered a perfect fluid, anisotropic, or charged distribution. Note that owing to the highly nonlinear nature of Einstein's field equations, very few perfect fluid interior solutions considering anisotropy can generalize the existing well-known solutions. However, a question that remains is, Can compact objects have anisotropic distribution at all?We can consider the possibility that owing to the extremely high density, the matter distribution can cease to be isotropic and anisotropy may emerge inside the compact objects. In a detailed review paper, Herrera and Santos [46] described the higher likelihood for compact stars to have an anisotropic matter distribution than an isotropic one. This can be due to several reasons, such as the exotic phase transitions. This triggers the release of large amounts of energy, for which the equation of state gets softened and thus dramatically alters the collapsing configurations. An example of such an exotic phase transition is the pion condensed state. Moreover, owing to energy dissipation in the form of massless (photons) or low-mass particles (like neutrinos), the matter distribution can become anisotropic during the stellar evolution, even if it was isotropic in the beginning [47].
Anisotropy can also be attributed to viscosity. When the Fermi energy is higher than the temperature, the dissipative forces are generally neglected, and the matter distribution is considered to be isentropic. However, when the matter density increases to
$10^{11} - 10^{12} \rm g/cm^3$ , this approximation breaks down because of neutrino trapping. The trapped neutrinos have a large mean free path, very high energy density, and a small radiative Reynolds number, which leads to local anisotropy. Ruderman [48] showed that when the density exceeds$10^{15} ~ \rm g/cm^3$ , the matter distribution no longer remains isotropic. In the given scenarios, the pressure can be decomposed into two distinct components, namely the tangential and radial pressure, leading to the emergence of pressure anisotropy. In this connection, the pressure anisotropy condition ($ P_t-P_r=g\,q^2\,r^2 $ ) was introduced by Herrera and Varela [49], where g is a non-zero constant.This paper adopts a particular concept called the vanishing complexity condition. The term "complexity" can sound very vague and ambiguous. Therefore, for quantitative analysis of a concept such as complexity, we must understand the methodology to quantify it. However, the notion of complexity differs for different fields of study. Researchers have attempted to define complexity in several ways [50−64]. Often, researchers have attempted to combine disequilibrium with information and define complexity as their product such that, if either of them approaches zero, complexity becomes zero. In this approach, both perfect crystal and ideal gas maintain zero complexity. However, this does not function perfectly in every scenario. Another method was adopted by Lopez-Ruiz et al. [56] to quantify complexity for self-gravitating systems [65−70]. Herrera [71] proposed a new concept of complexity that is specifically defined for self-gravitating systems generated by static and spherically symmetric spacetime as a result of several flaws in their technique. Later, this was expanded to include dynamic scenarios (see [72]).
The definition provided by Herrera [71] will be used in this article. Note that the complexity factor, a scalar measure used to define this concept of complexity, is unrelated to disequilibrium or entropy. As an alternative, itinvolves the Tolman mass, pressure anisotropy, and energy inhomogeneity. Two scenarios exist in which the vanishing complexity criterion can be satisfied: where both pressure anisotropy and energy inhomogeneity are zero and where they balance each other. Therefore, the very nature of the system is linked to the notion of the complexity factor. Although Herrera's concept [71] was initially developed within the framework of GR, it has also been applied to several modified theories of gravity, such as those described in [73−81]. Furthermore, this popular complexity approach was also applied in the gravitational decoupling scenario [82−85].
The remainder of this paper is organized as follows: Section II.A discusses
$ f(\mathcal{R},T) $ field equations, and Section III discusses the Einstein field equations in$ f(\mathcal{R},T) $ gravity. Section IV describes the anisotropic solution in$ f(\mathcal{R},T) $ gravity using the complexity formula. Section II.B presents the matching condition of the self-gravitating system, whereas the physical analysis is presented in Section V. We discuss the equation of state (EoS) for the dense matter in Sec. VI. Section VII provides concluding remarks. -
The integral action for the
$ f(\mathcal{R},T) $ formulation is given by$ S = \frac{1}{16\pi}\int \sqrt{-g} f(\mathcal{R},{T})\,d^{4}x+\int \sqrt{-g}\,{L}_{m}\,d^{4}x, $

(1) where relativistic units
$ G=c=1 $ , and the matter Lagrangian is represented by the symbol$ L_m $ . Let us now vary the action with respect to the metric tensor$ g^{\mu \nu} $ , which results in the following field equation:$ \begin{aligned}[b] 8\pi T_{\mu\nu} - T_{\mu\nu} f_{T}(\mathcal{R},{T})\, =\;& - \frac{1}{2} g_{\mu\nu}\,f(\mathcal{R},{T}) +\Box f_\mathcal{R} (\mathcal{R},{T})\,g_{\mu\nu} \\ &\left( -\nabla_{\mu} \nabla_{\nu}+\mathcal{R}_{\mu\nu} \right)f_\mathcal{R} (\mathcal{R},{T}), \end{aligned} $

(2) where
$ \partial f(\mathcal{R},T)/\partial \mathcal{R}=f_{\mathcal{R}}(\mathcal{R},T) $ and$ \partial f(\mathcal{R},T)/\partial T=f_{T}(\mathcal{R},T) $ .At this point, the EM tensor
$ T_{\mu \nu} $ and additional source$ \theta_{\mu \nu} $ can be expressed as$ T_{\mu\nu}=-2 \; {\partial{L}_m \over \partial g^{\mu\nu}}+g_{\mu\nu}{L}_m, $

(3) $ {\Theta_{\mu\nu}}= {g^{\gamma\,\epsilon}\; {\delta T_{\gamma\,\epsilon} \over \delta g^{\mu\nu}}}, $

(4) where the physical significance of the conceptual meaning of this unique tensor
$ \Theta_{\mu\nu} $ is discussed later. Consequently, after rearranging Eq. (2), the Einstein tensor$ G_{\mu\nu} $ can be expressed in the following form:$ \begin{aligned}[b] G_{\mu\nu}=\;&\frac{1}{f_{\mathcal{R}}\left(\mathcal{R},{T}\right)}\Big[8\pi T_{\mu\nu}+\frac{1}{2}\left(f\left(\mathcal{R},{T}\right)-\mathcal{R}\,f_{\mathcal{R}}\left(\mathcal{R},{T}\right)\right) \\ &\times g_{\mu\nu} -\left(g_{\mu\nu}\Box-\nabla_{\mu}\nabla_{\nu}\right)f_{\mathcal{R}}\left(\mathcal{R},{T}\right) \\ &- f_{{T}}\left(\mathcal{R},{T}\right) \left(T_{\mu\nu}+\Theta_{\mu\nu}\right)\Big].\end{aligned} $

(5) Now, the relevant conservation equation is given by
$ \begin{aligned}[b] \nabla^{\mu}T_{\mu\nu}=\;&\frac{f_{T}(\mathcal{R},{T})}{8\pi -f_{T}(\mathcal{R},{T})}\bigg[(\Theta_{\mu\nu}+T_{\mu\nu})\nabla^{\mu} \ln f_{T}(\mathcal{R},{T}) \\ & +\nabla^{\mu}\Theta_{\mu\nu}-\frac{1}{2}g_{\mu\nu}\nabla^{\mu}{T} \; \frac{8\pi \alpha\,\nabla^{\mu}\theta_{\mu\nu}}{f_{{T}}\left(\mathcal{R},{T}\right)} \bigg] . \end{aligned} $

(6) To characterize a spherically symmetric and static spacetime, we consider the most general line element, which is given by
$ \begin{array}{*{20}{l}} {\rm d}s^2_-=- H(r) \, {\rm d} t^{2}+W (r) {\rm d} r^{2} +r^{2}(\sin ^{2} \theta \, {\rm d} \phi ^{2}+ {\rm d} \theta ^{2}). \end{array} $

(7) For an anisotropic distribution, the tensor
$ T_{\mu\nu} $ can be expressed as follows:$ \begin{array}{*{20}{l}} T_{\mu\nu}=(p_t+\rho)u_\mu u_\nu-\left({p_t}-{p_r}\right)v_\mu v_\nu +{p_t}g_{\mu\nu}, \end{array} $

(8) where
$ u_\nu $ is the four-velocity, satisfying the conditions$ u^\mu u_\mu=-1 $ and$ u_\nu v^\nu =0 $ . Here, ρ is the matter density, and$ p_r $ and$ p_t $ are the radial and tangential pressures, respectively. Here, the Lagrangian is considered as$ {L}_m=-\mathcal{P} $ , where$\mathcal{P}=\dfrac{1}{3}(p_r+2p_t)$ [24]. The matter Lagrangian that appears in the field equations (5) and the conservation equations (6) can be realized according to the option made (see Ref. [86] for further information). However, in terms of GR, this decision would have no impact on the results of the observations. Therefore, selecting a certain form of the matter Lagrangian is extremely relevant when the matter field is characterized as a perfect fluid. Because it offers a recognized Lagrangian density, the option we mention here is consistent. Therefore, from Eq. (3), we obtain$ \frac{\delta\,T_{\mu \nu}}{\delta\,g^{\gamma \epsilon}}=\left(\frac{\delta\,g_{\mu \nu}}{\delta\,g^{\gamma \epsilon}}\right)\,L_{m}+g_{\mu \nu}\,\left(\frac{\partial\,L_{m}}{\partial\,g^{\gamma \epsilon}}\right)-2\,\frac{\partial^{2}\,L_{m}}{\partial\,g^{\mu \nu}\,\partial\,g^{\gamma \epsilon}}. $

(9) Now, using
$ \delta\,g_{\mu \nu}/\delta\,g^{\gamma \epsilon}=-g_{\mu\sigma}g_{\nu \zeta}\delta^{\sigma \zeta}_{\gamma \epsilon} $ , the above equation becomes$ \frac{\delta\,T_{\mu \nu}}{\delta\,g^{\gamma \epsilon}}=g_{\mu \nu}\,\left(\frac{\partial\,L_{m}}{\partial\,g^{\gamma \epsilon}}\right)-g_{\mu\sigma}\,g_{\nu \zeta}\,\delta^{\sigma \zeta}_{\gamma \epsilon}\,L_{m}-2\,\frac{\partial^{2}\,L_{m}}{\partial\,g^{\mu \nu}\,\partial\,g^{\gamma \epsilon}}. $

(10) Substituting Eq. (10) into Eq. (5), we obtain
$ \Theta_{\mu\nu}=-2\,T_{\mu\nu}+g_{\mu\nu}\,L_{m}- 2\,g^{\gamma \epsilon}\frac{\partial^{2}\,L_{m}}{\partial\,g^{\gamma \epsilon}\,\partial\,g^{\mu\nu}}. $

(11) Again, using Eq. (3) and
$ {L}_m=-\mathcal{P} $ , we ultimately obtain$ \begin{array}{*{20}{l}} \Theta_{\mu\nu}=-2\,T_{\mu\nu}-\mathcal{P}\,g_{\mu\nu}. \end{array} $

(12) Based on the research by Harko et al. [33], we assume that the function
$ f(\mathcal{R},T) $ can be represented in a linear form as$ \begin{array}{*{20}{l}} f(\mathcal{R},{T})=R+2\chi{T}, \end{array} $

(13) where the coupling constant χ is a dimensionless quantity. In the framework of astrophysical and cosmological solutions, the linear version of
$ f(\mathcal{R},T) $ is extremely successful (its accomplishments are outlined in the Introduction). Moreover, the anisotropic fluid distribution in GR context can be obtained when we incorporate$ \chi \rightarrow 0 $ in$ f(\mathcal{R},{T})=R $ [87].Eq. (5) can be rewritten by inserting the
$ f(\mathcal{R},T) $ function form (13) as$ \begin{aligned}[b] G_{\mu\nu}&=8\pi T_{\mu\nu} +\chi(2T_{\mu\nu}+2\mathcal{P} g_{\mu\nu}+{T}g_{\mu\nu}) \\ &= 8\pi\,\big( T_{\mu\nu}+\hat{T}_{\mu\nu}\big)=8\pi\,T^{\text{eff}}_{\mu\nu}, \end{aligned} $

(14) where we denote
$ \hat{T}_{\mu\nu} $ as$ \hat{T}_{\mu\nu}=\frac{\chi}{8\,\pi}\,(2T_{\mu\nu}+2\,\mathcal{P} g_{\mu\nu}+{T}g_{\mu\nu}), $

(15) with
$ {T}_{\mu\nu} $ as given by Eq. (8).As a result, we obtain the following from the conservation of (14):
$ \begin{array}{*{20}{l}} && \quad \nabla^{\mu} T^{\text{eff}}_{\mu\nu} =0\; \; \Rightarrow\; \; \nabla^{\mu}\big( T_{\mu\nu}+\hat{T}_{\mu\nu}\big)=0. \end{array} $

(16) In the subsequent analysis, when χ equals zero, the principle of EM conservation, which holds significant importance in Einstein's theory of gravity, can be reestablished.
-
In the self-gravitating
$ f(\mathcal{R},T) $ -gravity system, the interior spacetime should be matched with the exterior spacetime to construct the self-gravitating compact objects. Regarding the linear functional form of$ f(\mathcal{R},T) $ , we must match our interior spacetime with the spacetime generated from the exterior Schwarzschild solution at the boundary of the star. The exterior Schwarzschild spacetime is given by the following line element:$ \begin{aligned}[b] {\rm d} s^2_+= -\frac{{\rm d} r^2}{\bigg(\dfrac{2{{M}}}{r}-1\bigg)} +({\rm d}\theta^2+\sin^2\theta\,{\rm d}\phi^2) r^2+\bigg(\frac{2{{M}}}{r}-1\bigg)\,{\rm d}t^2, \end{aligned} $

(17) where M denotes the entire mass of the object when r equals R.
Currently, at the boundary (
$ r=R $ ), the smooth matching between the exterior spacetime$ds^2_+$ (17) and interior spacetime$ ds^2_- $ (7) ensures that both the first and second fundamental forms are satisfied throughout the surface. The first fundamental form requires the matching of the metric potentials generated by spacetimes$ ds^2_- $ and$ ds^2_+ $ , i.e.,$ \begin{array}{*{20}{l}} &&H^-|_{r=R}=H^+|_{r=R}\; \; \text{and}\; \; W^-|_{r=R}=W^+|_{r=R}.\; \; \; \end{array} $

(18) Clearly, it can be understood as
$ W^{-1}(R)=\frac{R-2M}{R},\; $

(19) $ H(R) =\frac{R-2M}{R}.\; $

(20) Moreover, the second fundamental form predicts that the radial pressure must be disappeared at the star's boundary, i.e.,
$ \begin{array}{*{20}{l}} p_{r}(R)=0. \end{array} $

(21) Conditions (19), (20), and (21) are required and sufficient to define the constants in the current solution.
-
The following set of differential equations is obtained from Eq. (14):
$ 8\pi \epsilon=\frac{1}{r^2}+\Bigg(\frac{W'}{W^2 r}-\frac{1}{W r^2}\Bigg), $

(22) $ 8\pi P_r=\Bigg(\frac{H'}{WHr}+\frac{1}{Wr^2}\Bigg)-\frac{1}{r^2}, $

(23) $ 8\pi P_t=\frac{-2W'H+2H'W-W'H'r}{4 H W^2 r} +\frac{H'^2+2H''H}{4 W H^2}, $

(24) where
$ 24\,\pi\,\epsilon = 24\,\pi\,\rho+\chi\,\left( 9\,\rho-2\,p_t-p_r \right),\; $

(25) $ 24\,\pi\,P_r = 24\,\pi\,p_r-\chi\,\left( 3\,\rho-2\,p_t -7\,p_r\right), $

(26) $ 24\,\pi\,P_t = 24\,\pi\,p_t-\chi\,\left( 3\,\rho-8\,p_t -p_r\right). $

(27) Because
$ G_{\mu \nu} $ satisfies the Bianchi identity i.e.,$ \nabla^{\mu} T^{\text{eff}}_{\mu\nu} =0 $ , we obtain$ -\frac{{\rm d}{P_r}}{{\rm d}r}-\frac{H'}{2H} (\epsilon+P_r) =\frac{2(P_r-P_t)}{r}, $

(28) which can be expressed in the following form:
$ \begin{aligned}[b]& -p^{\prime}_r-\frac{H^{\prime}}{2H}\,(\rho+p_r)+\frac{2}{r}\,(p_t-p_r)+\frac{\chi}{6\,(4\,\pi+\chi)}\\ &\times\left(3\rho^{\prime}-p^{\prime}_r-2p^{\prime}_t\right)=0. \end{aligned} $

(29) This is the Tolman-Oppenheimer-Volkoff (TOV) equation for an anisotropic matter distribution in the
$ f(\mathcal{R},T) $ -gravity system. Additionally, the metric function$ H(r) $ can be mathematically represented in the form of a mass function as$ H^{\prime}=H \frac{2m+8\pi P_r r^3}{r(r-2m)}, $

(30) where the mass function
$ m(r) $ is denoted by$ m(r)=4\pi \int^r_0 x^2\,\epsilon (x)\,{\rm d}x. $

(31) Subsequently, the final form of TOV equation is represented by
$ \frac{{\rm d}{P_r}}{{\rm d}r}=-\frac{m+4\pi P_r r^3}{r(r-2m)}\,({\epsilon}+{P_r})+\frac{2(P_t-P_r)}{r}. $

(32) -
In view of the self-gravitating system, the generalized definition of Herrera's complexity factor (
$ Y_{TF} $ ) in the context of$ f(\mathcal{R},T) $ -gravity is$ Y_{TF} = 8\pi (P_r-P_t)-\frac{4\pi}{2r^3} \int^r_0 x^3 \epsilon' (x) {\rm d} x. $

(33) Under the
$ f(\mathcal{R}, T) $ system of equations (22)–(24), we obtain the following form of$ Y_{TF} $ :$ Y_{TF}=\frac{rHH^\prime W^\prime+W(2H^{\prime}H-2rH^{\prime\prime}H+H^2)}{4rH^2W^2}. $

(34) Consequently, the condition of the complexity factor vanishes, i.e.,
$ Y_{TF}=0 $ yields$ \begin{array}{*{20}{l}} rHH^\prime W^\prime+W(2H^{\prime}H-2rH^{\prime\prime}H+H^2)=0. \end{array} $

(35) The above condition can be solved for H or W. Therefore, after integration with some manipulation, we obtain a relation between H and W:
$ H=\bigg(A\,\int r\, \sqrt{W} {\rm d} r +B\bigg)^2, $

(36) where the variables A and B represent the constants of integration.
The complexity criterion in
$ f(\mathcal{R}, T) $ -gravity is equivalent to the condition established in GR [84]. Thus, we can determine the analytic expression for the temporal metric function H by solving Eq. (36). If we examine the above system of equations in$ f(\mathcal{R},T) $ -gravity and the vanishing complexity factor, then any solution in GR will also be a solution for the$ f(\mathcal{R},T) $ system. Therefore, we require to observe only the coupling constant χ effect on the pressures$ p_r $ &$ p_t $ and density ρ. Hence, we determine the explicit expression for$ p_r $ &$ p_t $ and ρ in terms of the metric functions W and H with the coupling parameter χ as follows:$ \begin{aligned}[b] p_r=\;&\frac{1}{48 (\chi+2 \pi ) (\chi+4 \pi ) r^2 W^2 H^2} \big[W \{2 H r (-H'' \chi r \\&+10 H' \chi+24 \pi H')+H'^2 \chi r^2-16 H^2 (\chi+3 \pi ) (W-1)\} \\&+W' H \chi r (H' r+8 H)\big], \end{aligned} $

(37) $ \begin{aligned}[b]p_t=\;& \frac{1}{48 (\chi+2 \pi ) (\chi+4 \pi ) r^2 W^2 H^2} \Big[W \{2 H r (H'' (5 \chi+12 \pi ) r \\&+4 H' (\chi+3 \pi ))-H'^2 (5 \chi+12 \pi ) r^2+8 H^2 \chi (W-1)\} \\&-W' H r (H' (5 \chi+12 \pi ) r+4 H (\chi+6 \pi ))\Big], \end{aligned} $

(38) $ \begin{aligned}[b] \rho=\;&\frac{1}{48 (\chi+2 \pi ) (\chi+4 \pi ) r^2 W^2 H^2} \big[W \{2 H \chi r (H'' r+2 H') \\&-H'^2 \chi r^2+16 H^2 (\chi+3 \pi ) (W-1)\}+W' H r (16 H \\&\times (\chi+3 \pi )-H' \chi r) \big], \end{aligned} $

(39) which satisfies the following conservation equation:
$ \begin{aligned}[b]& -p^{\prime}_r-\frac{H^{\prime}}{2 H (p_r+\rho)}\,+\frac{2 (p_t-p_r)}{r}\, +\frac{\chi}{\,(24\,\pi+6\chi)}\\& \times\left(3\rho^{\prime}-p^{\prime}_r-2p^{\prime}_t\right)=0 . \end{aligned} $

(40) Eq. (40) is called the the modified TOV equation in
$f(\mathcal{R},T)$ -gravity.Surprisingly, Einstein's gravity and
$ f(\mathcal{R},T) $ gravity have the same complexity condition. Eq. (22) may be used to calculate the mass of the star, which is now mostly caused by the energy density of the matter. The mass m assumes a new shape as follows:$ m_{f}=4\pi\int_0^r{\rho\, r^2\,{\rm d}r}. $

(41) Here,
$ m_f $ denotes the mass in$ f(\mathcal{R},T) $ -gravity. In this context, the constant parameter χ is crucial to determining the stellar configuration. Traditionally, the$ f(\mathcal{R},T) $ -gravity theory with χ= 0 recovers the same physics as GR. Note that the bridge equation in this analysis, Eq. (36), contains the two essential integration constants A and B. By solving the matching conditions, we may derive the expression for these constants A and B in terms of the mass$ (M) $ and radius$ (R) $ . -
As we discussed earlier, we seek to observe the effect of the χ parameter on physical quantities after determining the solution of the anisotropic system. Because we have used the complexity factor condition to obtain our solution, we must define one metric function to obtain another metric function. Hence, we propose a Tolman-IV metric to construct our model as follows:
$ \begin{array}{*{20}{l}} W(r)=(1+ar^2+br^4), \end{array} $

(42) where a and b are constants, and their corresponding dimensions are
$ l^{-2} $ and$ l^{-4} $ . Furthermore, when a and b are both zero, we recover a flat spacetime metric.By substituting W into the complexity-free condition (36), we obtain the following expression for
$ H(r) $ after integration:$\begin{aligned}\\[-9pt] H(r)=\Bigg[A \bigg(\frac{1}{16 b^{3/2}}\Big[(a^2-4 b) \log (-2 b^{3/2} \sqrt{a r^2+b r^4+1} +a b+2 b^2 r^2)\Big]+\frac{1}{8b}\Big[(a+2 b r^2) \sqrt{a r^2+b r^4+1}\Big]\bigg) +B \Bigg]^2. \end{aligned}$ 
(43) After substituting Eqs. (42) and (43) into Eqs. (37)−(39), we calculate the explicit expressions for
$ \rho(r) $ ,$ p_r(r) $ , and$ p_t(r) $ as$ \begin{aligned}[b] \rho(r)=\;& \frac{1}{48 (\chi+2 \pi ) (\chi+4 \pi ) }\Bigg[\frac{1}{\rho_1(r)}\Big\{16 \chi \Big(A \left(a^2-4 b\right) \left[a^2 r^2+a \left(2 b r^4+3\right)+b r^2 \left(b r^4+5\right)\right] \sqrt{a r^2+b r^4+1} \\& \times \log \left(b \left(-2 \sqrt{b} \sqrt{a r^2+b r^4+1}+a+2 b r^2\right)\right)+2 \sqrt{b} \big\{a^4 A r^4+a^3 A r^2 \left(5 b r^4+4\right)+a^2 \big(8 b B r^2 \sqrt{a r^2+b r^4+1} \\& +3 A \left(3 b^2 r^8+8 b r^4+1\right)\big)+a b \left(8 B \left(2 b r^4+3\right) \sqrt{a r^2+b r^4+1}+A r^2 \left(7 b^2 r^8+38 b r^4+23\right)\right)+2 b \Big(4 b B r^2 \\& \times \left(b r^4+5\right) \sqrt{a r^2+b r^4+1}+A \left(b^3 r^{12}+9 b^2 r^8+11 b r^4+3\right)\Big)\big\}\Big)\Big\}+48 \pi \left(\frac{2 \left(a+2 b r^2\right)}{\left(a r^2+b r^4+1\right)^2}+\frac{a +b r^2}{a r^2+b r^4+1}\right)\Bigg],\end{aligned} $

(44) $ \begin{aligned}[b] p_r(r)=\;& \frac{1}{3 (\chi+2 \pi ) (\chi+4 \pi ) \rho_1(r)}\Big[-2 \sqrt{b} \Big\{A \left(a r^2+b r^4+1\right) \Big(b \left(\chi \left(4 a^2 r^4-19 a r^2-18\right)+3 \pi \left(4 a^2 r^4-13 a r^2-16\right)\right) \\& +a^2 \left(a \chi r^2+3 \pi \left(a r^2+1\right)\right)+b^2 r^4 \left(5 \chi \left(a r^2-4\right)+3 \pi \left(5 a r^2-14\right)\right)+2 b^3 (\chi+3 \pi ) r^8\Big)+8 b B \sqrt{a r^2+b r^4+1} \\& \times \left(a^2 (\chi+3 \pi ) r^2+a \left(2 b \chi r^4+\pi \left(6 b r^4+3\right)\right)+b r^2 \left(\chi \left(b r^4-1\right)+3 \left(\pi b r^4+\pi \right)\right)\right)\Big\}-A \left(a^2-4 b\right) \sqrt{a r^2+b r^4+1}\\& \times \left(a^2 (\chi+3 \pi ) r^2+a \left(2 b \chi r^4+\pi \left(6 b r^4+3\right)\right)+b r^2 \left(\chi \left(b r^4-1\right)+3 \left(\pi b r^4+\pi \right)\right)\right) \log \big[b \big(-2 \sqrt{b} \sqrt{a r^2+b r^4+1}+a\\& +2 b r^2\big)\big]\Big], \end{aligned} $

(45) $ \begin{aligned}[b] p_t(r)=\;& \frac{1}{6 (\chi+2 \pi ) (\chi+4 \pi ) \rho_1(r)}\Big[2 \sqrt{b} \Big(A \left(a r^2+b r^4+1\right) \Big\{b \left(\chi \left(4 a^2 r^4+35 a r^2+36\right)+24 \pi \left(3 a r^2+4\right)\right)+a^2 \left(a \chi r^2-6 \pi \right) \\& +b^2 r^4 \left(\chi \left(5 a r^2+34\right)+72 \pi \right)+2 b^3 \chi r^8\Big\}+8 b B \sqrt{a r^2+b r^4+1} \left(a^2 \chi r^2+a \left(2 b \chi r^4-6 \pi \right)+b r^2 \left(\chi \left(b r^4-1\right)-12 \pi \right)\right)\Big)\\& +A \left(a^2-4 b\right) \sqrt{a r^2+b r^4+1} \left(a^2 \chi r^2+a \left(2 b \chi r^4-6 \pi \right)+b r^2 \left(\chi \left(b r^4-1\right)-12 \pi \right)\right) \log \big[(b \big(-2 \sqrt{b} \sqrt{a r^2+b r^4+1}\\& +a+2 b r^2\big)\big]\Big],\; \end{aligned} $

(46) where
$ \begin{aligned}[b] \rho_1(r)=\;&\left(a r^2+b r^4+1\right)^{5/2} \Big[A \left(a^2-4 b\right) \log \left(b \left(-2 \sqrt{b} \sqrt{a r^2+b r^4+1}+a+2 b r^2\right)\right)+2 \sqrt{b} \big\{2 A b r^2 \sqrt{a r^2+b r^4+1} \\& +a A \sqrt{a r^2+b r^4+1}+8 b B\big\}\Big]. \end{aligned} $

-
In this article, the interior solution to field equations is determined within the context of
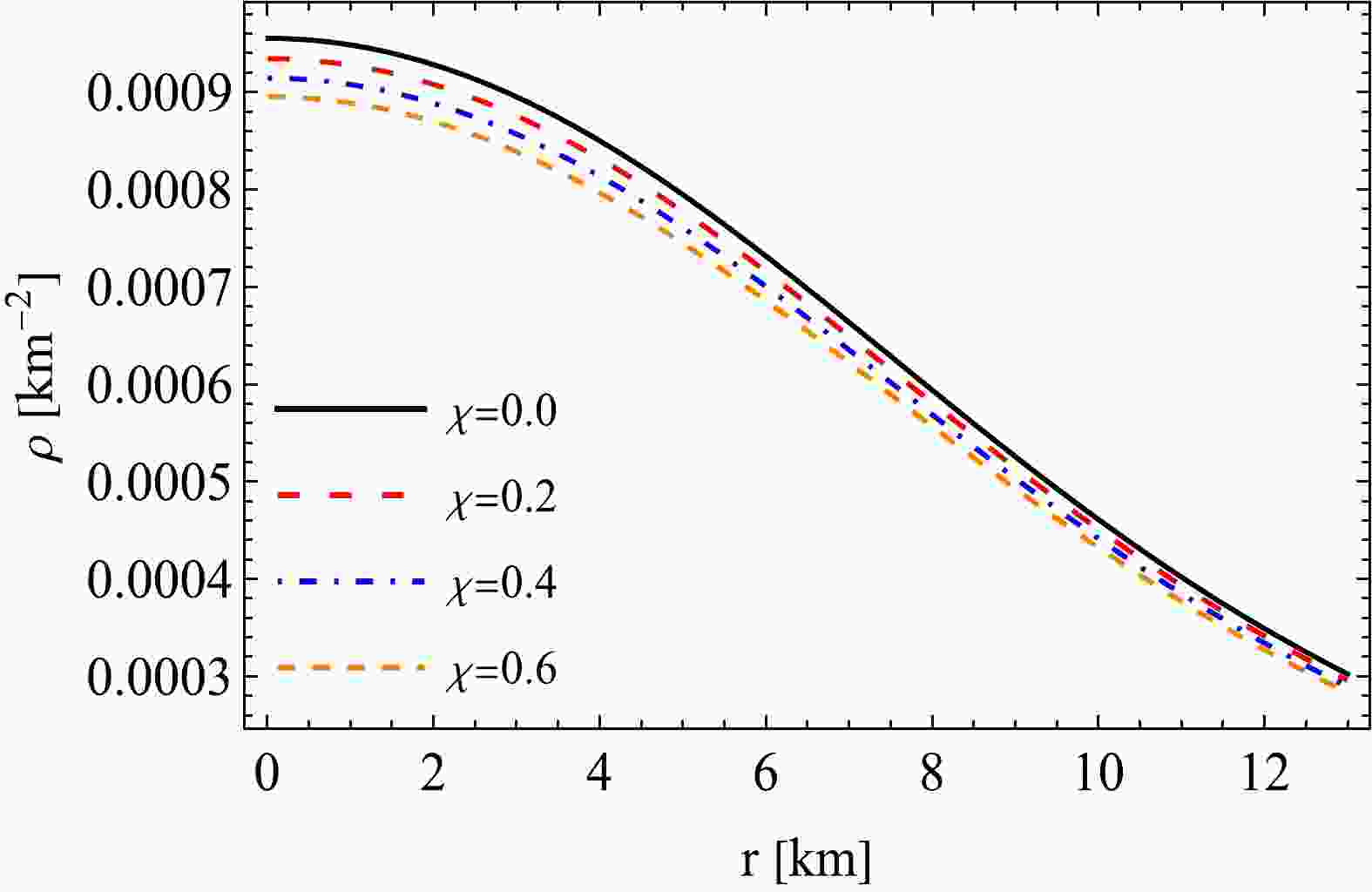
$ f(\mathcal{R}, T) $ gravity under vanishing complexity formalism. After determining the solution, we have conducted thorough physical examinations. This included analyzing stability, thermodynamic characteristics, and other aspects. First, let us analyze the effect of χ on thermodynamic parameters such as the density, pressure, and anisotropy. As we know, when χ is zero, we revert to the pure GR case, whereas, when it is non-zero,$ f(\mathcal{R},T) $ gravity is turned on.The variations of
$ \rho(r) $ ,$ p_r(r) $ ,$ p_t(r) $ , and$ \Delta(r) $ are highlighted in Figs. 1, 2, 3, and 4, respectively, for different values of χ. As the value of χ increases from$ 0.0 $ to$ 0.6 $ , the magnitudes of all thermodynamic parameters$ \rho(r) $ ,$ p_r(r) $ ,$ p_t(r) $ , and$ \Delta(r) $ decrease. The dependence on χ is more prominent at the center and diminishes towards the surface concerning the density and radial and tangential pressures. Additionally, all the curves for different values of χ converge to zero for the radial pressure as expected. From this observation, we can infer that in both GR and$ f(\mathcal{R},T) $ gravity, the radial pressure becomes zero at the surface, whereas the tangential pressure is still non-zero and positive. However, we observe that the effect of χ is more significant at the surface when considering the anisotropic factor. At the center, the anisotropy is zero in both GR and$ f(\mathcal{R},T) $ gravity. Hence, under the framework of$ f(\mathcal{R},T) $ gravity, the influence of χ on anisotropy is more pronounced at the surface, whereas it affects the pressure components and the density more near the center. The nature of the ρ reveals that it is maximum at the center and then continues decreasing toward the boundary (Fig. 1). This indicates that the core region has a higher energy density than the remainder of the body. Figs. 2 and 3 show that the radial and tangential pressures ($ p_r $ and$ p_t $ ) are greatest at the center and monotonically decrease outward. Fig. 4 shows that the anisotropic factor Δ is zero at the center and monotonically increases toward the border, indicating that the core has an isotropic distribution, whereas the surface is anisotropic. This indicates that the force generated by the pressure anisotropy (Δ) is directed outward, which makes the system stable and aids in avoiding gravitational collapse.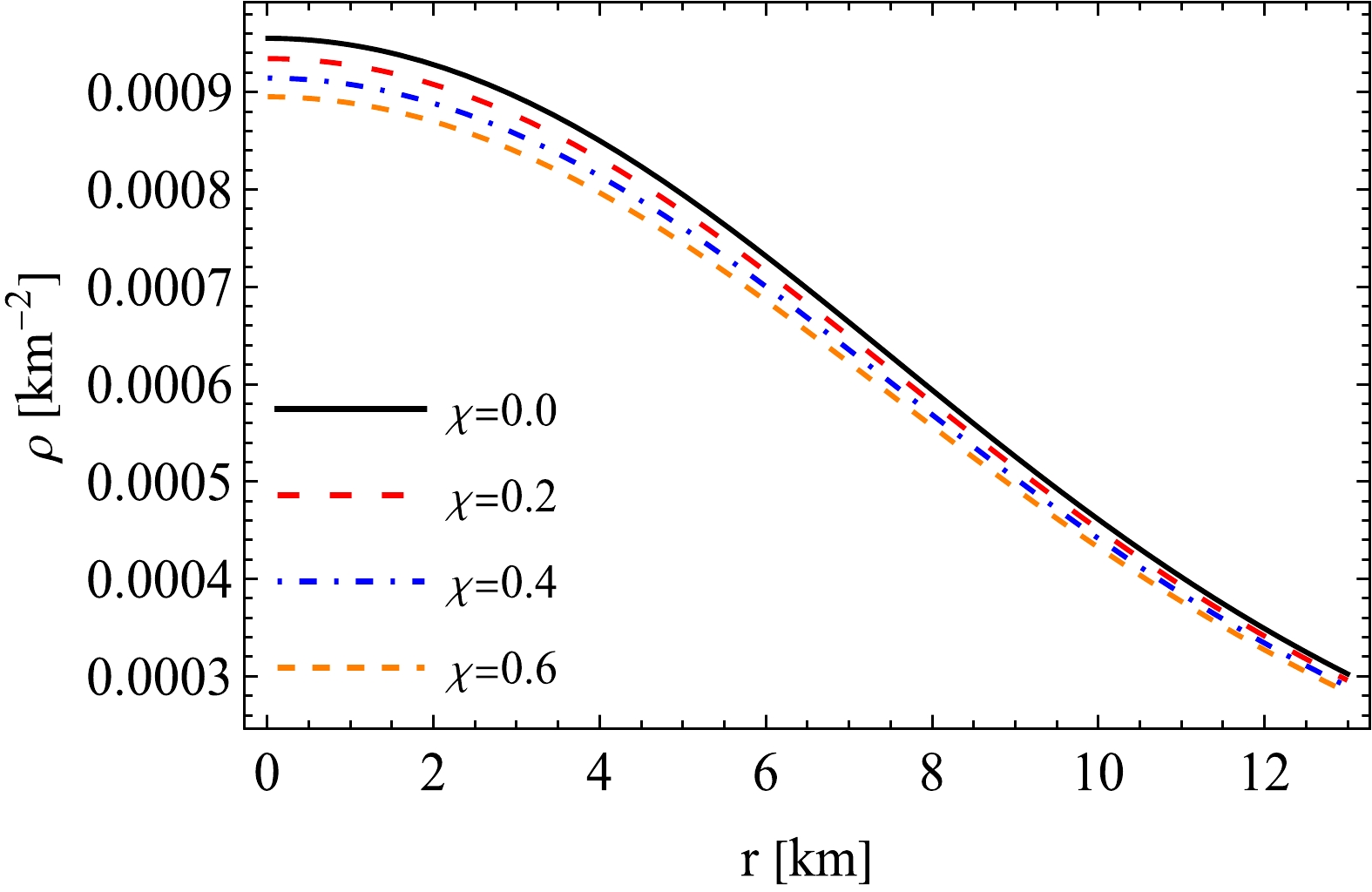
Figure 1. (color online) For different values of χ with constant values
$ a=0.008\; \text{km}^{-2} $ and$ b=0.00003 \; \text{km}^{-4} $ , the energy density ($ \rho\; \rm [km^{-2}]=\rho\times1.34\times10^{18}\; \rm [g/cm^3] $ ) is plotted against the radial coordinate (r).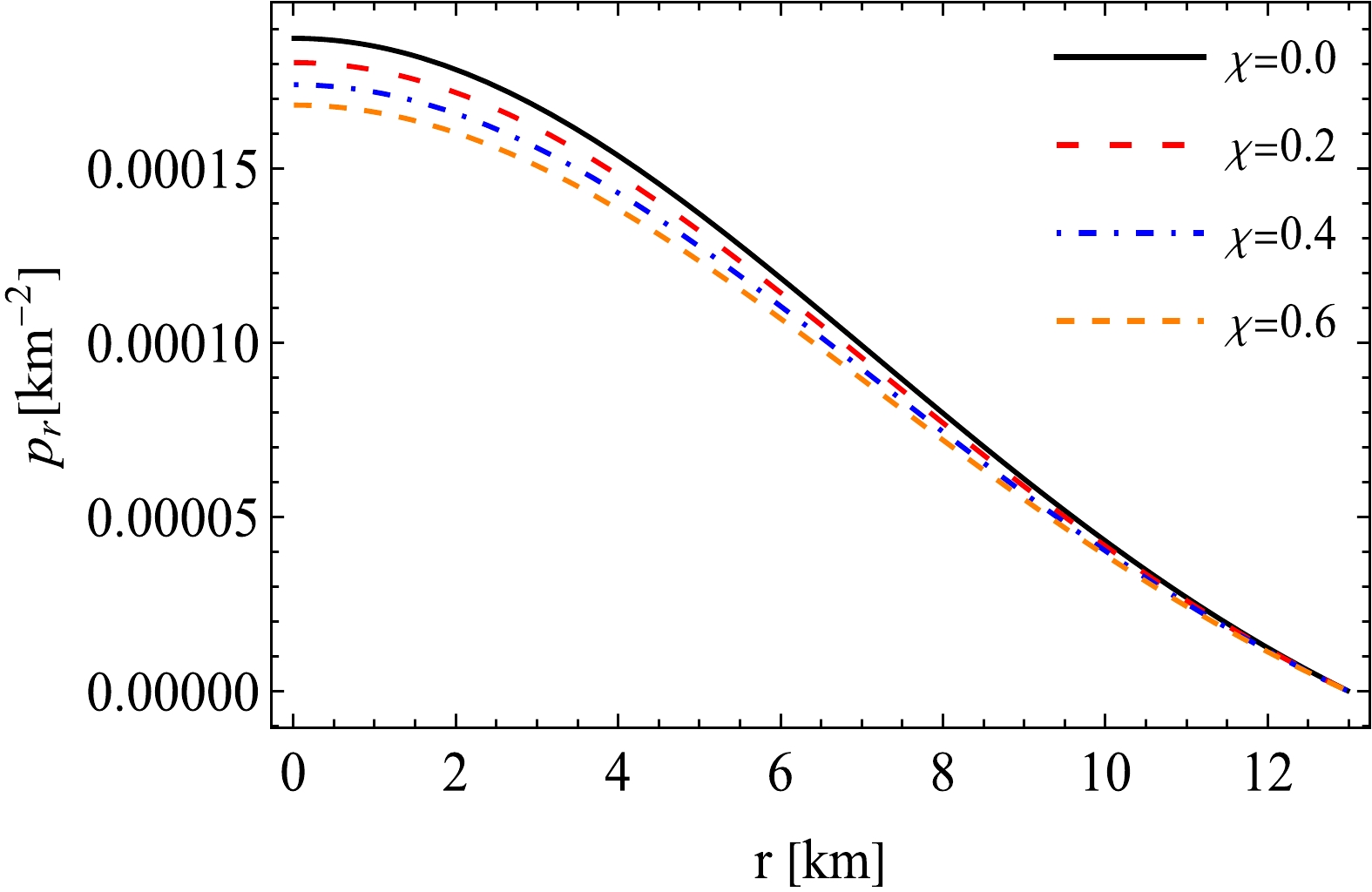
Figure 2. (color online) For different values of χ with constant values
$ a=0.008\; \text{km}^{-2} $ and$ b=0.00003 \; \text{km}^{-4} $ , the radial pressure ($p_r\; [{\rm km}^{-2}]=p_r\times1.09\times10^{39}\;\rm [dyne/cm^2]$ ) is plotted against the radial coordinate (r).
Figure 3. (color online) The same metric constant values as those in Fig. 2 are used to plot the tangential pressure (
$p_t\; [{\rm km}^{-2}]=p_t\times1.09\times10^{39}\;\rm [dyne/cm^2]$ ) vs radial coordinate (r) for different values of χ.
Figure 4. (color online) Utilizing the same values for constants as those listed in Fig. 2, we plot anisotropy (Δ) against radial coordinate (r) for different values of χ.
-
Any model must satisfy the causality criterion to represent a stable system. In other words, the speed of sound should never be faster than the speed of light. The subliminal radial and tangential components of the speed of sound (
$ {v}_r^2 $ and$ {v}_t^2 $ ) should always remain within the limits of$ 0 \le {v}_r^2 \le 1 $ and$ 0 \le {v}_t^2 \le 1 $ , respectively, if the speed of light c is scaled to unity. Figs. 5 and 6 show that both the radial and tangential components of velocities remain well within the permitted range, thereby proving that the causality criterion is satisfied. When χ is examined in relation to the velocity components,$ v_r $ and$ v_t $ decrease as χ increases.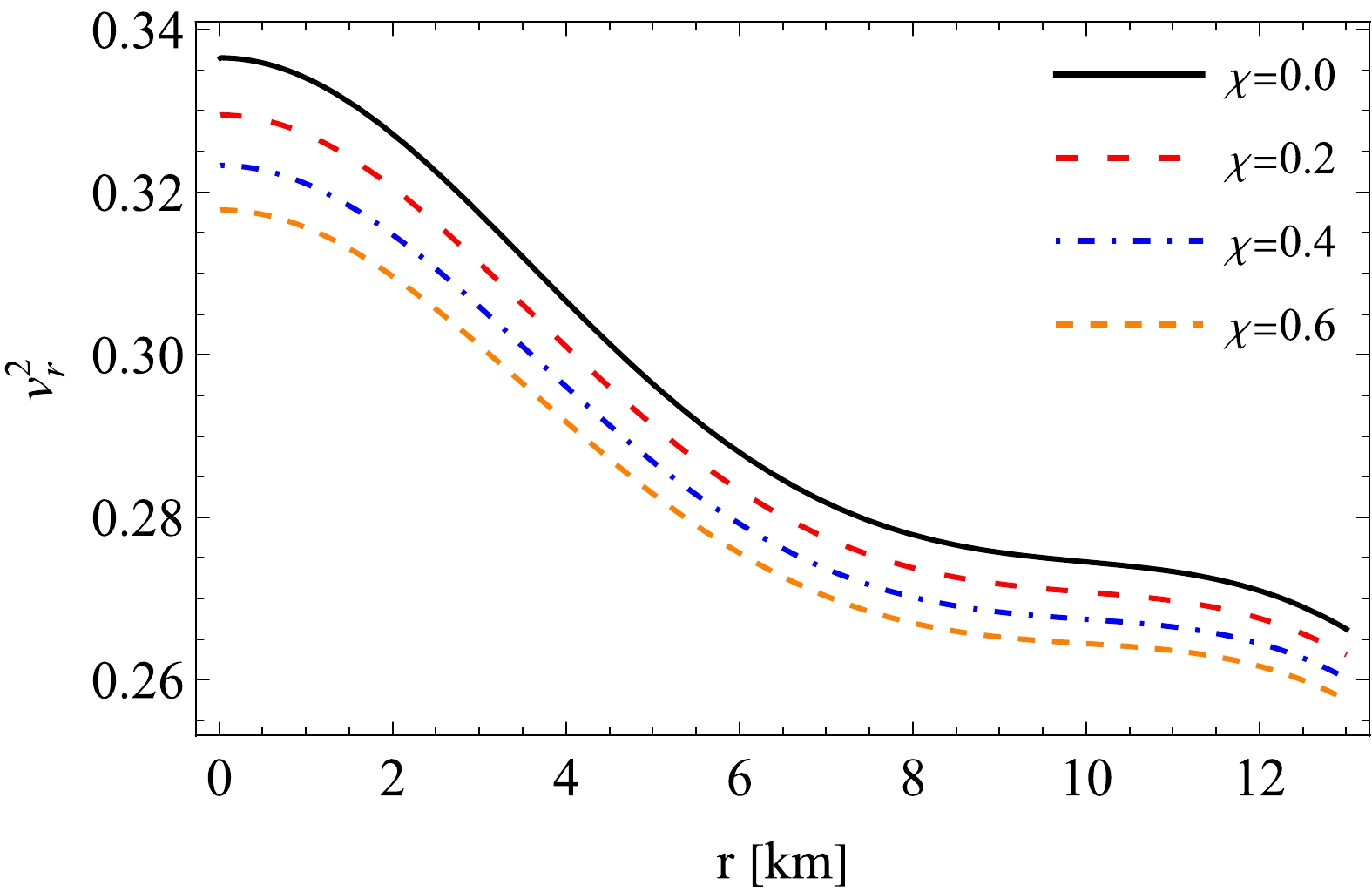
Figure 5. (color online) Radial velocity (
${v}^2_r$ ) versus radial coordinate r for different values of χ with constant values of$ a=0.008\; \text{km}^{-2} $ and$ b=0.00003 \; \text{km}^{-4} $ .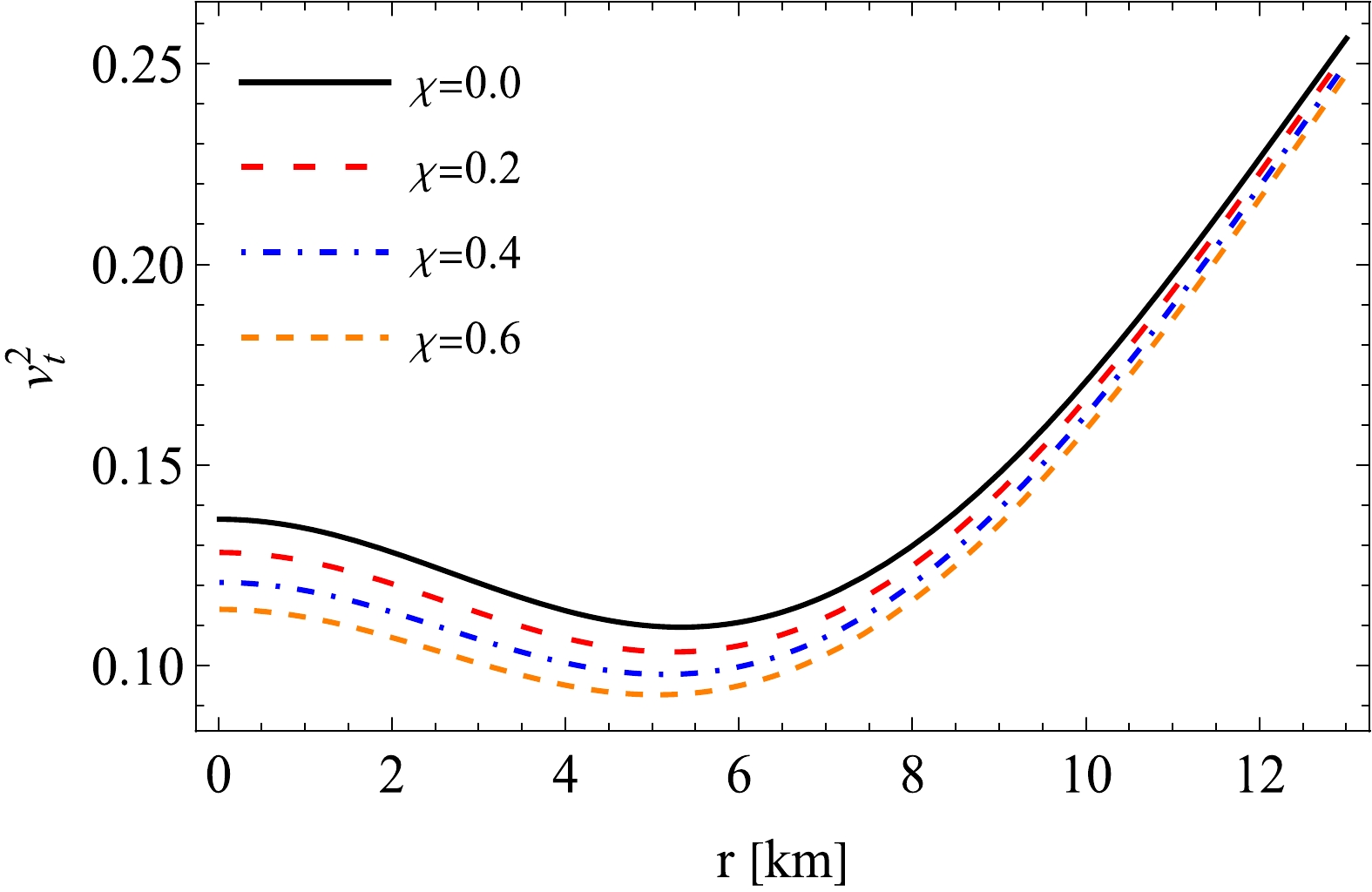
Figure 6. (color online) Utilizing the same values for constants as those listed in Fig. 5, we plot the tangential velocity (
${v}^2_t$ ) vs radial coordinate (r) for different values of χ. -
This subsection evaluates the stability of the model in relation to the cracking condition given by Herrera's [88] and Abreu's [89] criteria. It is tested via the subluminal radial and tangential sound velocity components, similar to the causality condition. Testing this condition becomes even more necessary when anisotropy is present. The cracking concept is expressed in terms of anisotropy
$ |\delta \Delta^{ \rm{tot}}| $ alongside the magnitude of perturbation of the energy density$ |\delta \epsilon| $ and their ratio$ \left|\dfrac{\delta \Delta^{ \rm{tot}}}{\delta \epsilon}\right| $ as$ \left|\frac{\delta {\Delta}}{\delta{\rho}}\right|\simeq\left| \frac{\delta\left({p}_{t}-{p}_{r}\right)}{\delta{\rho}}\right| \simeq\left| \frac{\delta{p}_{t}}{\delta{\rho}}-\frac{\delta{p}_{r}}{\delta{\rho}}\right|\simeq \left| {v}^{2}_{t}- {v}^{2}_r\right|. $

(47) The causality condition is fulfilled everywhere within this model; therefore, the
$0\leq {v}^{2}_{r}\leq 1$ and$0\leq {v}^{2}_{t}\leq 1$ conditions are fulfilled automatically. Now, the density also has to be greater than the magnitude of perturbation in anisotropy, i.e.,$|\delta \Delta^{ \rm{tot}}| \le |\delta \epsilon| \;\; \Longrightarrow \;\; | {v}^{2}_{t}- {v}^{2}_{r}|\leq 1$ . Moreover, the$ \left|\dfrac{\delta {\Delta}}{\delta{\rho}}\right|>0 $ region is unstable. Thus, regions based on stability are expressed as$ \begin{array}{*{20}{l}} 0\leq |{v}^{2}_{t}-{v}^{2}_{r}|\leq 1 = \left\{ \begin{array}{ll} -1\leq {v}^{2}_{t}-{v}^{2}_{r}\leq 0 \\ 0< {v}^{2}_{t}-{v}^{2}_{r}\leq 1, \end{array} \right.\; \; \; \; \end{array} $

(48) where the stable region is
$ -1\leq {v}^{2}_{t}-{v}^{2}_{r}\leq 0 $ (or$ 0\leq {v}^{2}_{r}-{v}^{2}_{t}\leq 1 $ ) and the unstable one is$ 0< {v}^{2}_{t}-{v}^{2}_{r}\leq 1 $ . However, when no sign change occurs in$ 0< {v}^{2}_{r}-{v}^{2}_{t}\leq 1 $ , this region is also marked as a stable region. Fig. 7 shows that the quantity$ {v}^{2}_{r}-{v}^{2}_{t} $ falls in the stable region of$ 0\leq {v}^{2}_{r}-{v}^{2}_{t}\leq 1 $ everywhere within the model. Therefore, the model can be considered stable everywhere in terms of the cracking condition. Additionally, the variation in$ {v}^{2}_{r}- {v}^{2}_{t} $ reveals that this amount reaches its maximum in the center, remains constant up to$ r \approx 3 $ , and gradually decreases as we approach to the boundary. Additionally, when χ increases, the difference between$ {v}^{2}_{r} $ and$ {v}^{2}_{t} $ can be observed near the center, whereas it becomes indistinguishable but remains stable near the boundary.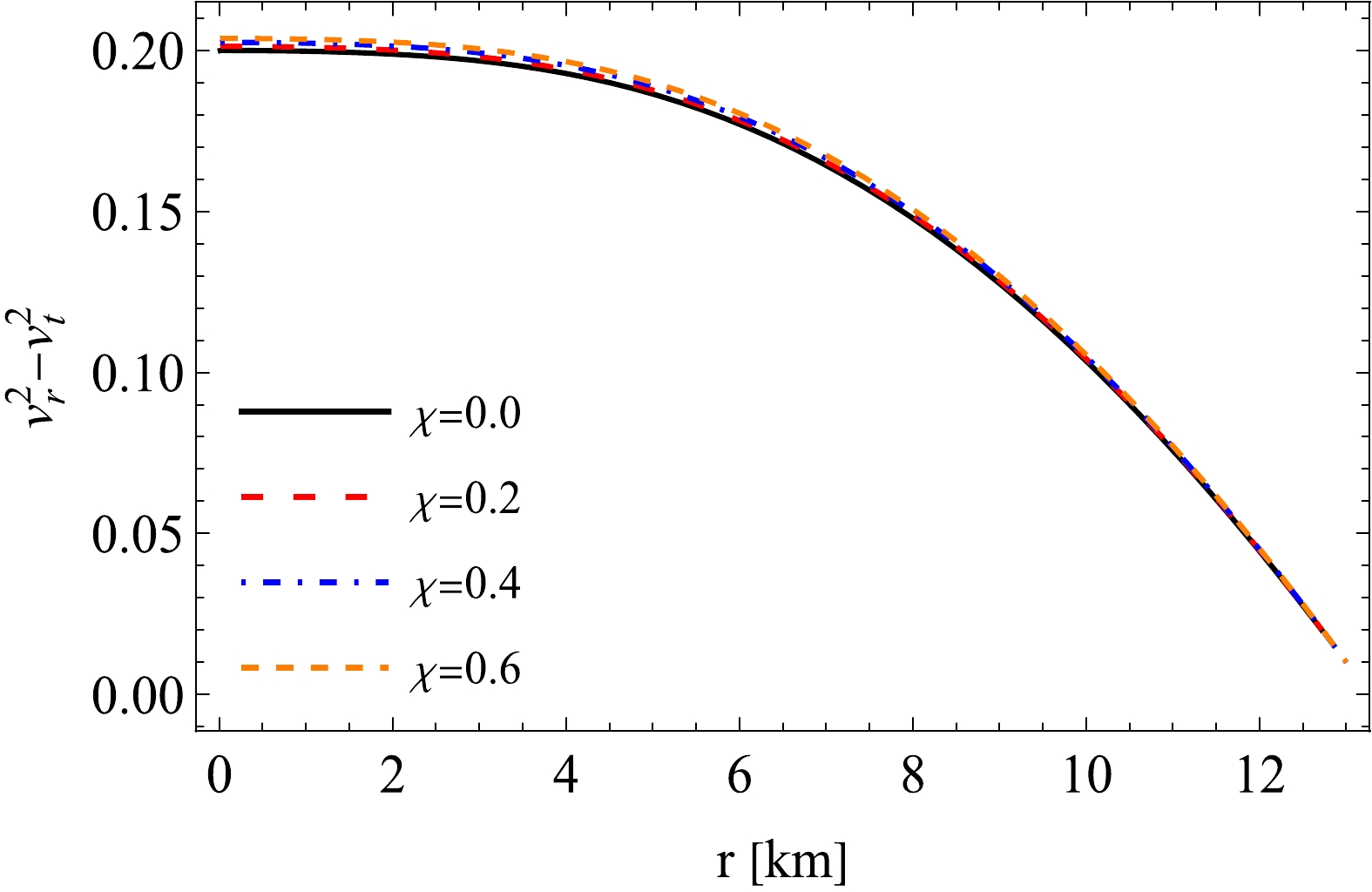
Figure 7. (color online) Stability analysis (
${v}^2_r- {v}^2_t$ ) versus radial coordinate r for distinct χ using same metric constant values as in Fig. 5. -
In analyzing collapsing stellar objects, the examination of the presence and consistency of a positive and well-defined EM tensor throughout the entire model is vital. For this, the following energy conditions are known as the null energy condition (NEC), weak energy condition (WEC), strong energy condition (SEC), dominant energy condition (DEC), and trace energy condition (TEC) [90]:
$ \text{NEC}:\; \; \rho+p_r \ge 0,\; \; \rho+p_t \ge 0, $

(49) $ \text{WEC} : \; \; \rho \ge 0,\; \; \rho+p_r \ge 0,\; \; \rho+p_t \ge 0, $

(50) $ \text{SEC}:\; \; \rho+p_r+2\,p_t \ge 0, $

(51) $ \text{DEC}:\; \; \rho \ge 0,\; \; \rho-p_r \ge 0,\; \; \rho-p_t \ge 0, $

(52) $ \text{TEC}:\; \; \rho-p_r-2p_t\ge 0. $

(53) Becauce ρ,
$ p_r $ , and$ p_t $ are considered to be positive everywhere within the model, the first three inequalities (NEC, WEC, and SEC) are automatically satisfied. In the present scenario, we must test only DEC and TEC within the stellar system. Hence, we plot Figs. 8−10 to examine the nature of the DEC and TEC. We observe that all the curves for$ \rho - p_r $ ,$ \rho - p_t $ , and$ \rho - p_r - 2p_t $ for different values of χ are similar, as all the values exhibit a peak at the central region and gradually diminish towards the outermost part. The magnitude values for$ \rho - p_r $ and$ \rho - p_t $ decrease as χ increases, whereas that for$ \rho - p_r - 2p_t $ initially increases slightly with χ near the center, but then decreases with χ as we move from the center. Fig. 10 shows that the TEC also remains positive everywhere within the model, which signifies that all the energy conditions are satisfied and the model behaves according to the energy conditions.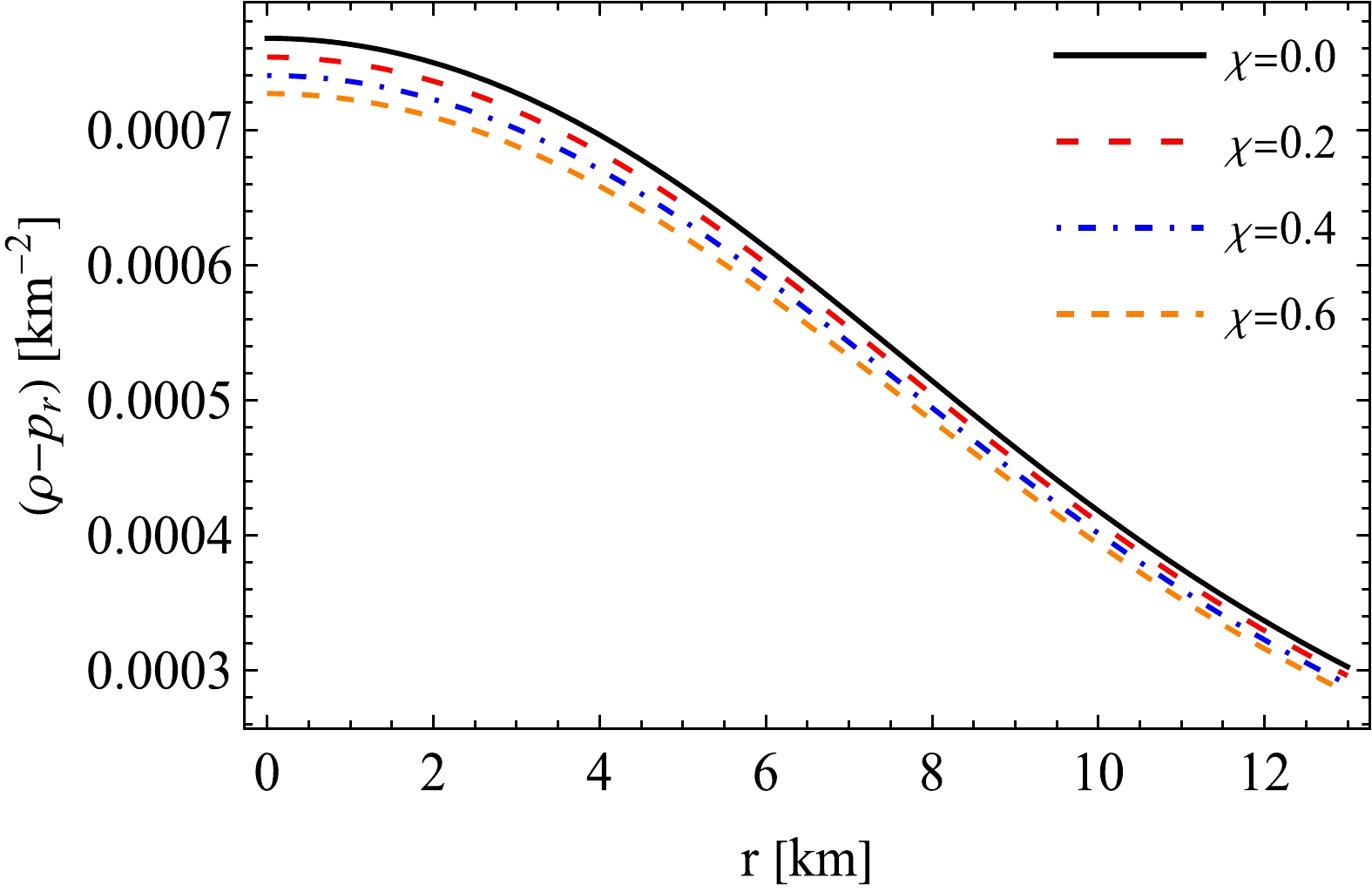
Figure 8. (color online) Dominant energy condition for radial pressure versus radial coordinate r for different values of χ using same metric constant values as in Fig. 5.

Figure 9. (color online) Dominant energy condition for tangential pressure versus radial coordinate r for different values of χ using same metric constant values as in Fig. 5.
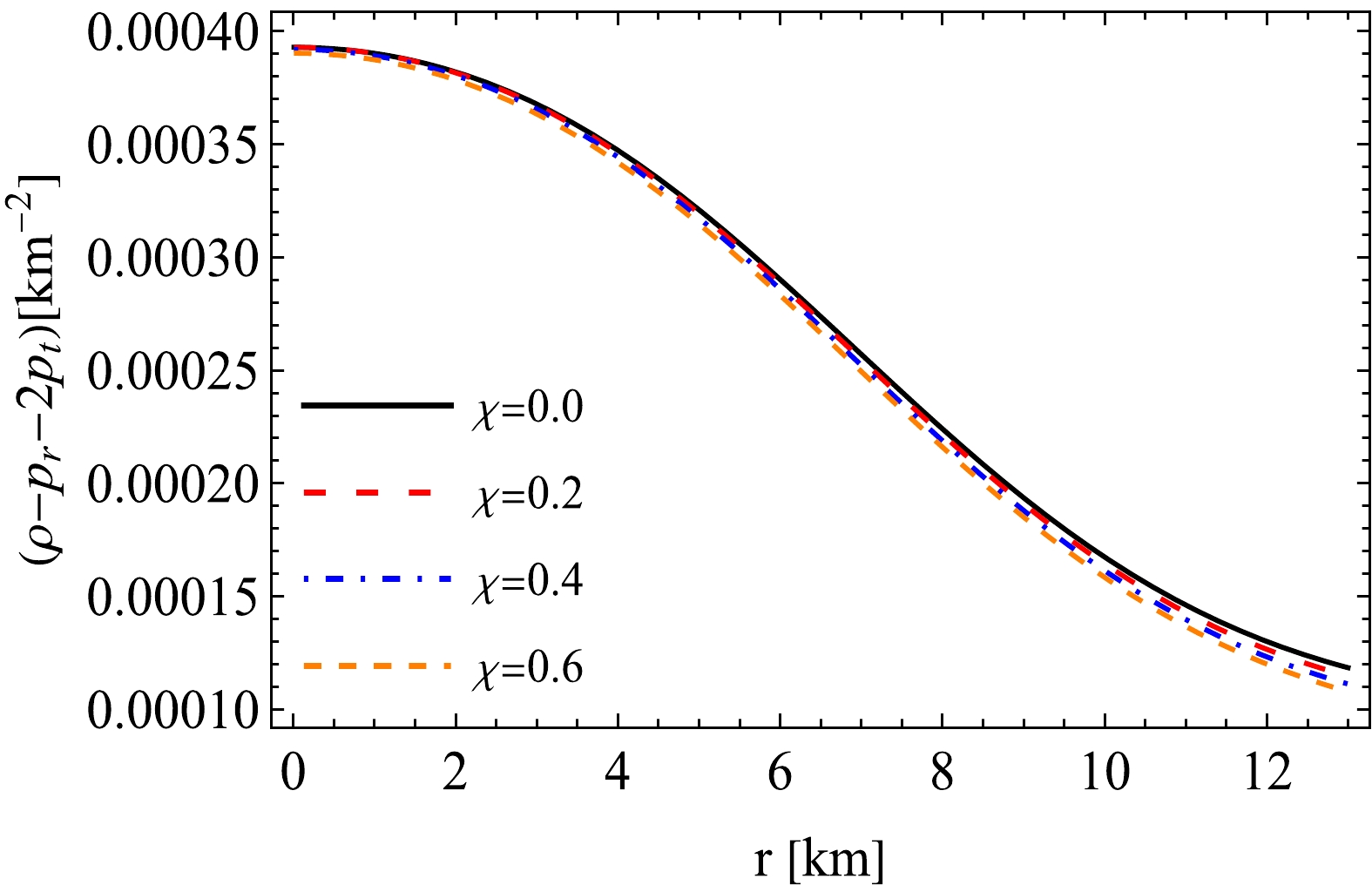
Figure 10. (color online) Trace energy condition versus radial coordinate r for different values of χ using same metric constant values as in Fig. 5.
-
This section discusses the stability of the model via the adiabatic index. In particular, when the matter distribution is anisotropic, the stability study with respect to the adiabatic index is crucial. The collapse requirement for ideal fluid distribution is provided as
$ \Gamma < 4/3 $ , which is related to the adiabatic index [91, 92]. This condition changes when the relativistic anisotropy is considered [93, 94] which is given by$ \Gamma < \frac{4}{3} + \bigg[\frac{8 \pi}{3} \frac{p_{r0} \rho_0}{|p^\prime_{r0}|} - \frac{4}{3} \frac{p_{r0}-p_{t0}}{|p^\prime_{r0}| r} \bigg]_{\max}. $

(54) The anisotropic correction is included in the third term, and the relativistic modification is introduced in the second term on the right-hand side. Heintzmann and Hillebrandt [91] demonstrated that the stable models must satisfy the requirement
$ \Gamma > 4/3 $ in the presence of the anisotropic factor ($ \Delta=p_t-p_r $ ). The adiabatic index is shown in Fig. 11, showing that Γ is always more than 2 throughout the model, which satisfies the stable range of$ \Gamma > 4/3 $ . Hence, the obtained solution is stable and well-behaved in terms of the adiabatic index. Examining the behavior of Γ, we find that Γ decreases monotonically in the range [0, 4.5] and increases rapidly towards the surface when$ r \ge 4.5 $ . Additionally, the value of Γ decreases with an increase in χ, which implies that the value of χ cannot be arbitrarily large for a stable model. Furthermore, the effect of χ is more pronounced near the center of the star, and it exhibits a negligible effect on Γ near the surface.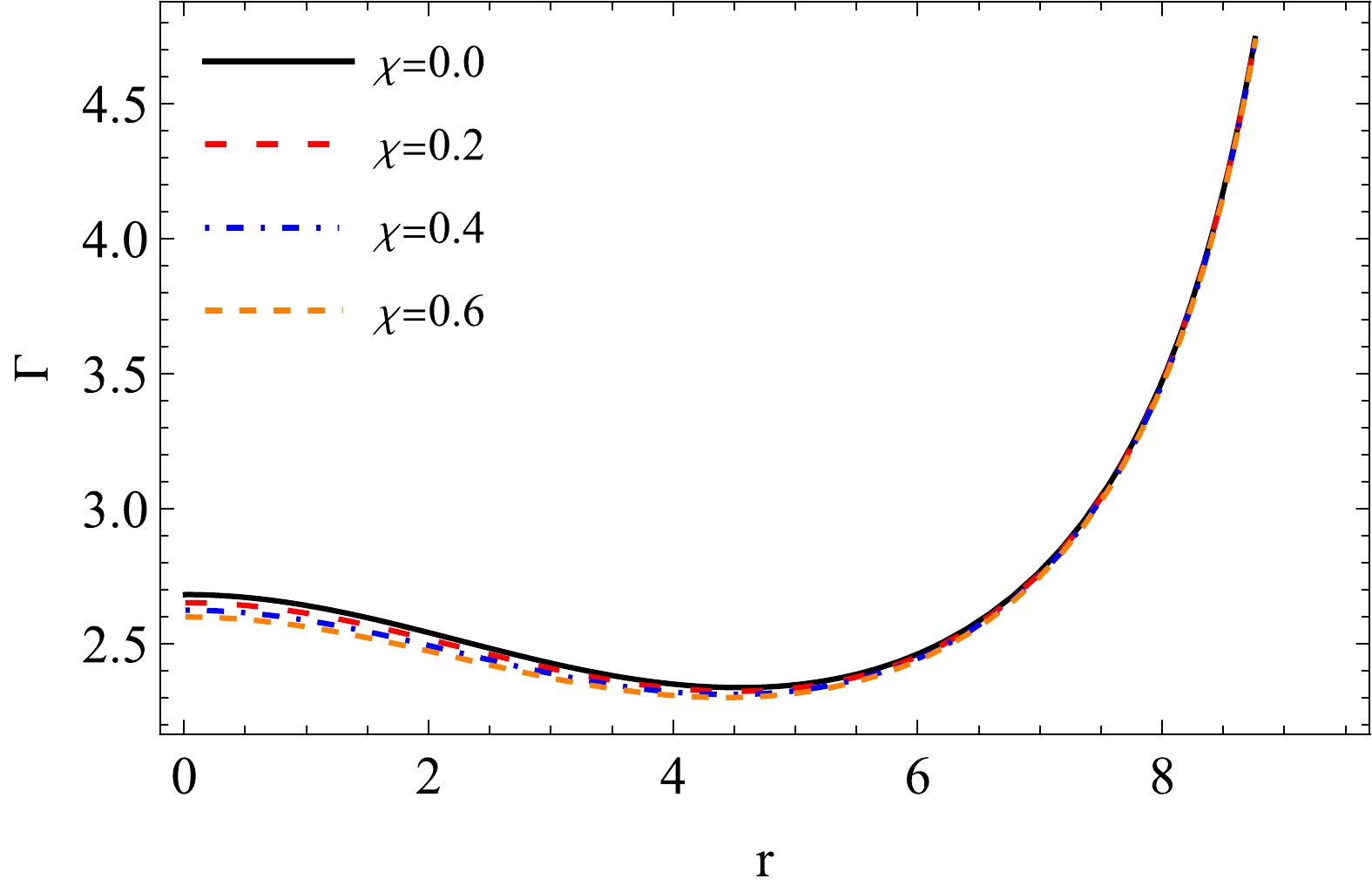
Figure 11. (color online) Adiabatic index versus radial coordinate r for different values of χ with constant values of
$ a=0.008\; \text{km}^{-2} $ and$ b=0.00003 \; \text{km}^{-4} $ .Sharma et al. [95] derived the formula for the adiabatic index Γ as
$\Gamma=\dfrac{n_b}{P} \dfrac{{\rm d}P}{{\rm d} n_b}$ , where$ n_b $ represents the baryon density. However, they presented the variation in Γ with respect to$ n_b $ rather than the radial vector r. Consequently, the adiabatic index does not exhibit a significant increase at large values of$ n_b $ , which differs from the observations in our current paper. If we examined the relationship between Γ and$ n_b $ instead of focusing on our current approach, we would have obtained exactly the same findings as Sharma et al. [95]. -
This subsection assesses the dynamical state of equilibrium of the model by employing the TOV equation. It is well-known that the stress energy tensor
$ T_{\mu\nu} $ is not conserved in the$ f(\mathcal{R},T) $ -gravity framework, i.e.,$ \nabla^\mu T_{\mu\nu}\ne 0 $ . Hence, the modified TOV equation within$ f(\mathcal{R},T) $ -gravity is derived using the Bianchi identity as follows:$ \begin{aligned}[b]& -p^{\prime}_r-\frac{H^{\prime}}{2H}\,(\rho+p_r)+\frac{2}{r}\,(p_t-p_r)+\frac{\chi}{6\,(4\,\pi+\chi)} \\& \times\left(3\rho^{\prime}-p^{\prime}_r-2p^{\prime}_t\right)=0.\end{aligned} $

(55) The aforementioned expression corresponds to the modified TOV equation, which provides the condition of equilibrium in the
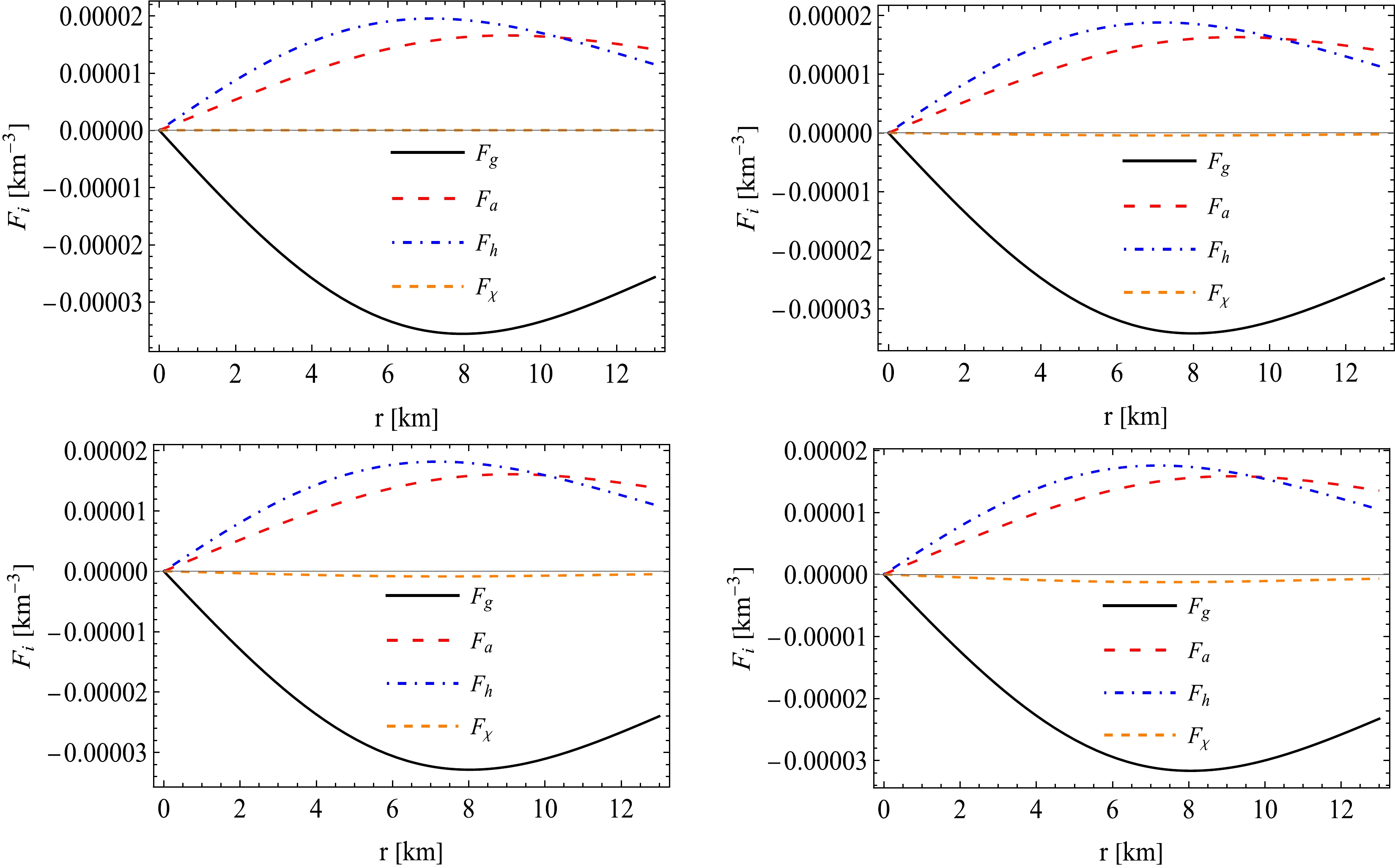
$ f(\mathcal{R},T) $ theory, and different forces such as$ F_g $ ,$ F_a $ ,$ F_h $ , and$ F_{\chi} $ can be defined by Eq. (55). The force$ F_a = \dfrac{2}{r}\,(p_t-p_r) $ denotes the anisotropic force, whereas$F_g = -\dfrac{H^{\prime}}{2 H}\,(\rho+p_r)$ expresses the gravitational force. The hydrostatic force is defined by$ F_h = -p^{\prime}_r $ , and the coupling force due to modified gravity is defined by$ F_{\chi} = \dfrac{\chi}{6\,(4\,\pi+\chi)}(3\rho^{\prime}-p^{\prime}_r-2p^{\prime}_t) $ . For the system to achieve a state of equilibrium, the sumof all forces acting upon should be equal to zero, which means that the equilibrium condition is$ F_a + F_h +F_g + F_\chi = 0 $ .Now, for the behaviour of the different forces, Fig. 12 shows that the parameter χ is essential in the coupling forces (
$ F_{\chi} $ ). As shown in the upper left panel of Fig. 12, in the scenario of pure GR where$ \chi=0 $ , the value of$ F_{\chi} $ is zero. However, for values of$ \chi=0.2, 0.4 $ , and$ 0.6 $ ,$ F_{\chi} $ assumes negative values. This observation indicates that the coupling force is characterized by an attracting nature, and its strength is directly proportional to the value of χ. Furthermore, all the forces$ F_a $ ,$ F_h $ ,$ F_{\chi} $ , and$ F_g $ have zero values at the center, and their magnitudes increase as we move towards the surface up to a certain point and then decrease near the surface. In contrast, in every instance, anisotropic and hydrostatic forces that are positive and repulsive balance out the gravitational force, which is inherently negative and attracting. Moreover, the attractive force$ F_{\chi} $ has a minimum impact on achieving equilibrium within the system compared with other forces. -
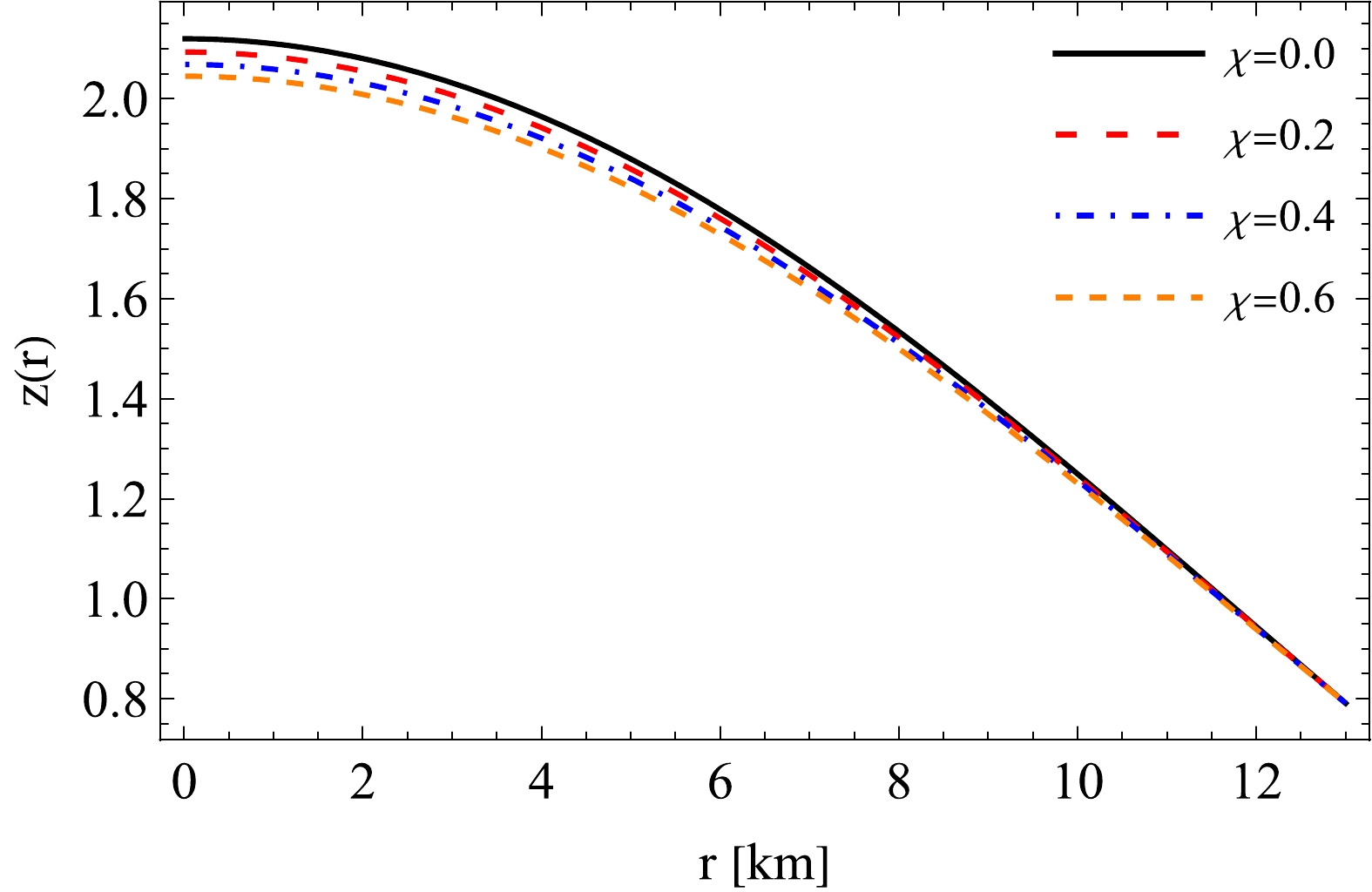
To analyse the phenomenon of gravitational redshift, we will employ the general relativistic effects. This effect can be quantified using the equation
$ z_s = \Delta \lambda/\lambda_{e} = \dfrac{\lambda_{0}-\lambda_{e}}{\lambda_{e}} $ , where$ \lambda_{e} $ represents the wavelength emitted at the surface of a nonrotating star, and$ \lambda_{0} $ corresponds to the observed wavelength received at a specific radial coordinate r. The gravitational redshift from the surface of the star, as detected by a distant observer in the weak-field limit where$ g_{tt}\rightarrow -1 $ , can be expressed as$ \begin{aligned}[b] z_S =\;& \uparrowvert g_{tt}(R) \uparrowvert ^{-1/2} -1= \uparrowvert g_{rr}(R) \uparrowvert ^{1/2}-1\\=\;& \sqrt{1+aR^2+bR^4}-1, \end{aligned} $

(56) The behavior of gravitational redshift is shown in Fig. 13. In this model, the calculated value of the surface redshift is
$ z_s=0.791321 $ , which is under the limit proposed in Refs. [96, 97]. -
In this subsection, we compare the dynamical behavior of the Tolman-IV model in the
$f(\mathcal{R},T)$ gravity framework using the complexity formalism with available observational results. Hence, we exploit observational measurements gathered during the GW190814 event and data from two-millisecond pulsars, namely PSR J1614-2230 and PSR J0952-0607. When embedded in$f(\mathcal{R},T)$ gravity, the Tolman-IV model provides an additional method of characterizing the gravitational dynamics of compact objects. We can examine the intricate behavior of this model and determine whether it is consistent with observed phenomena by using the complexity formalism.Here, we utilize the observational data that were collected during the GW190814 event. The LIGO and Virgo observatories have detected this gravitational wave event, which provides important information on the characteristics of the compact object involved in the merger. We may assess the validity of the Tolman-IV model in
$f(\mathcal{R},T)$ gravity by comparing its predictions with the observed data, considering the characteristics of this event. In this analysis, we also include data from two millisecond pulsars: PSR J1614-2230 and PSR J0952-0607. These pulsars have been investigated in detail, and their characteristics, including timing and mass data, offer useful constraints for evaluating theoretical theories. We may examine the predictions of the Tolman-IV model in$f(\mathcal{R},T)$ gravity and determine if they align with the observed characteristics of the pulsars by incorporating these pulsars into our comparison.In Fig. 14, we present the results of our analysis for various values of χ. The plot depicts the relationship between the total mass M (normalized in solar masses
$ M_{\odot} $ ) and radius R of the compact object candidates. We consider constant values for the parameters$ a=0.008 \text{km}^{-2} $ and$ b=0.00003 \; \text{km}^{-4} $ while varying the surface densities. The figure shows that the maximum mass value$ M_{\text{max}} $ gradually decreases as χ increases from 0 to 1. Tables 1 and 2 present the masses of the compact object candidates and their corresponding predicted radii for different values of χ. These tables consider two different surface densities. Our analysis demonstrates that the proposed model of compact stars can successfully reproduce the masses of the three mentioned neutron stars for various selected values of χ.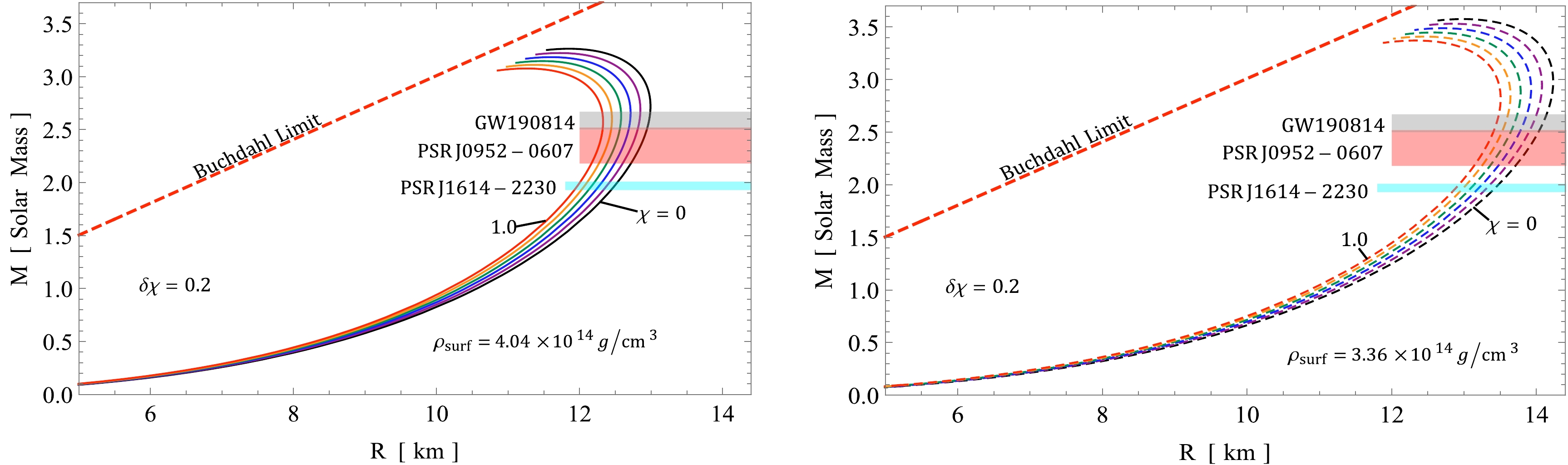
Figure 14. (color online)
$ M-R $ curve for distinct χ using same metric constant values as in Fig. 5 with different surface densities.Objects $\dfrac{M}{{M}_\odot}$ 

Predicted R km surface density $(\rho_{\rm surf})=4.04 \times 10^{14}~{\rm g/cm^3}$ 

$ \chi=0 $ 

$ \chi=0.2 $ 

$ \chi=0.4 $ 

$ \chi=0.6 $ 

$ \chi=0.8 $ 

$ \chi=1.0 $ 

PSR J1614-2230 [98] 1.97 $ \pm $ 0.04

12.48 $ _{-0.03}^{+0.06} $ 

12.38 $ _{-0.04}^{+0.04} $ 

12.27 $ _{-0.04}^{+0.06} $ 

12.17 $ _{-0.04}^{+0.04} $ 

12.07 $ _{-0.04}^{+0.05} $ 

11.98 $ _{-0.04}^{+0.04} $ 

PSR J0952-0607 [99] $ 2.35 \pm 0.17 $ 

12.85 $ _{-0.13}^{+0.10} $ 

12.74 $ _{-0.13}^{+0.08} $ 

12.61 $ _{-0.12}^{+0.08} $ 

12.49 $ _{-0.12}^{+0.08} $ 

12.39 $ _{-0.11}^{+0.05} $ 

12.27 $ _{-0.10}^{+0.05} $ 

GW190814 [100] 2.5−2.67 12.98 $ _{-0.03}^{+0.01} $ 

12.84 $ _{-0.02}^{+0.02} $ 

12.71 $ _{-0.02}^{+0.01} $ 

12.58 $ _{-0.01}^{+0.01} $ 

12.45 $ _{-0.01}^{+0.01} $ 

12.33 $ _{-0.02}^{+0.01} $ 

Table 1. Predicted radii of compact stars PSR J1614-2230, PSR J0952-0607, and GW190814 for the
$f(\mathcal{R},T)$ model (see Fig. 14).Objects $ \dfrac{M}{M_\odot} $ 

Predicted R km surface density $ (\rho_{\rm surf})=3.36 \times 10^{14}\; \rm g/cm^3 $ 

$ \chi=0 $ 

$ \chi=0.2 $ 

$ \chi=0.4 $ 

$ \chi=0.6 $ 

$ \chi=0.8 $ 

$ \chi=1.0 $ 

PSR J1614-2230 [98] 1.97 $ \pm $ 0.04

$ 13.45_{-0.08}^{+0.03} $ 

13.31 $ _{-0.04}^{+0.07} $ 

13.21 $ _{-0.05}^{+0.05} $ 

13.12 $ _{-0.07}^{+0.03} $ 

12.99 $ _{-0.06}^{+0.05} $ 

12.88 $ _{-0.04}^{+0.05} $ 

PSR J0952-0607 [99] $ 2.35 \pm 0.17 $ 

13.91 $ _{-0.20}^{+0.12} $ 

13.77 $ _{-0.19}^{+0.14} $ 

$ 13.65_{-0.18}^{+0.12} $ 

13.54 $ _{-0.18}^{+0.12} $ 

13.41 $ _{-0.16}^{+0.12} $ 

13.31 $ _{-0.18}^{+0.10} $ 

GW190814 [100] 2.5−2.67 14.09 $ _{-0.04}^{+0.05} $ 

13.97 $ _{-0.06}^{+0.03} $ 

13.83 $ _{-0.06}^{+0.04} $ 

13.69 $ _{-0.03}^{+0.04} $ 

13.57 $ _{-0.04}^{+0.03} $ 

13.45 $ _{-0.04}^{+0.04} $ 

Table 2. Predicted radii of compact stars PSR J1614-2230, PSR J0952-0607, and GW190814 for the
$f(\mathcal{R},T)$ model (see Fig. 14).Note that the secondary mass of the GW190814 event falls within the hypothesized lower "mass gap" of
$ (2.5-5) M_{\odot} $ , which is considered to exist between known neutron stars and black holes [101−104]. This secondary mass is heavier than the most massive pulsar in the Galaxy. It nearly surpasses the mass of the primary component of GW190425, which falls in the range of$ (1.61-2.52) M_{\odot} $ and is considered an outlier among the Galactic population of binary neutron stars [105]. Furthermore, the secondary mass of GW190814 is comparable to that of the millisecond pulsar PSR J1748-2021B, which has a claimed mass of$ 2.74_{-0.21}^{+0.21} M_{\odot} $ at a 68% confidence level [106]. This observation is significant because, in the context of the dynamical behavior of the Tolman-IV model in$f(\mathcal{R},T)$ gravity using the complexity formalism, our analysis with$ \chi=1 $ yields two compact stars with masses of$ 3.09 M_{\odot} $ and$ 3.41 M_{\odot} $ for$\rho_{\rm surf} = 4.04 \times 10^{14}\; {\rm g/cm}^3$ and$\rho_{\rm surf} = 3.36 \times 10^{14}\; {\rm g/cm}^3$ , respectively, thus falling within the hypothesized lower mass gap.Our findings are also consistent with the recent data for PSR J0952-0607, which has a mass of
$ 2.35_{-0.17}^{+0.17} M_{\odot} $ . This pulsar, known as the heaviest and fastest pulsar in the disk of the Milky Way, supports the potential presence of strange quark matter in its composition. PSR J0952-0607 is a binary millisecond pulsar with a rotation frequency of 707 Hz and was initially reported by Bassa et al. [107]. It is classified as a black widow binary owing to its low-mass (sub-stellar) companion, which is being irradiated and evaporated by the pulsar's luminosity. These comparisons and observations highlight the significance of the dynamical behavior of the Tolman-IV model in the$f(\mathcal{R},T)$ gravity framework using complexity formalism. Next, we compare the results of predicted radii of our$f(\mathcal{R},T)$ models with those obtained in GR using a realistic EoS. In this regard, Gangopadhyay et al. [108] predicted the radii for 12 pulsars using the strange star EoS, with masses ranging from$ 0.85\pm 0.15M_{\odot} $ to$ 1.97\pm 0.04M_{\odot} $ . In their study, the predicted radii for all 12 pulsars lay between$ 7.86 $ and$ 9.69 $ km. In our present study, the predicted radii range from$ 12 $ to$ 14 $ km, which is consistent with the study of Burgio et al. [109]. This analysis demonstrates that the predicted radii obtained in our study are larger than those predicted within the context of the strange star EoS. -
Several authors [110−112] have proposed a more plausible approximation of the EoS by expressing pressure p as a linear function of the energy density ρ, denoted as
$ p=p(\rho) $ . Furthermore, this linear correlation between p and ρ has an additional benefit as it guarantees the preservation of the causality requirement. We emphasize that our method effectively interprets the physical characteristics of celestial bodies without introducing any particular EoS. At the surface, denoted as$ r=R $ , the density is non-zero, whereas the radial pressure at the surface is zero. Subsequently, the EoSs$ p=p(\rho) $ , specifically$ p=\omega\,\rho $ or the polytropic EoS$ p=\omega\,\rho^{5/3} $ , do not align with the solution we have derived. When examining Eqs. (44)−(45), predicting an accurately well-known specific established EoS for dense matter becomes challenging because of the somewhat complicated relationship between pressure and density. To determine the approximate EoS for the interior structure of stars, we plot a graph (Fig. 15) that shows the relationship between pressures and density. This graph depicts the potential EoS for the present compact stellar object.
Figure 15. (color online) Variations in the radial pressure (
$ p_t $ ) and tangential pressure ($ p_t $ ) against the energy density (ρ) for different values of the$f(\mathcal{R},T)$ parameter χ.The curves representing the object's behavior from the surface to the core exhibit an almost linear pattern, with the curve increasing from areas of low density to areas of high density. This indicates a proportionate relationship between the radial pressure
$ p_r $ and density ρ. Additionally, a constant that is equal to the surface density must be included in the EoS. This ensures that no radial pressure occurs at the surface. Therefore, the behaviors shown in Fig. 15 (top panels) provide strong evidence that the approximate linear EoS may be expressed as follows:$ \begin{array}{*{20}{l}} p_r=\alpha \left(\rho-\rho_s\right). \end{array} $

(57) Let α represent a positive constant, and
$ \rho_s $ denote the surface density. Furthermore, Fig. 15 shows that$ p_r $ becomes zero when r is equal to R. This occurs owing to the equivalence of the energy density and surface energy density, which can be expressed as$ \rho(R)={\rho_s} $ . Furthermore, we can predict that the approximate relation between the tangential pressure and density using the anisotropy. The anisotropy factor Δ is introduced to incorporate the difference between the radial and tangential pressures in the system. It serves as a correction term ($ \pm\Delta $ ) that modifies the EoS for tangential pressure. Because$ p_t=p_r+\Delta $ , we may propose the EoS for the tangential pressure$ p_t $ as$ \begin{array}{*{20}{l}} p_t=\alpha \left(\rho-\rho_s\right)+\Delta. \end{array} $

(58) The proposed EoS for
$ p_t $ with Δ enables us to characterize the anisotropic pressure distribution within the system, encompassing deviations from isotropy. -
This paper derives an anisotropic interior solution for the field equations in the setting of the
$ f(\mathcal{R},T) $ -gravity theory. The solution is determined by imposing the constraint of the vanishing complexity factor, and it is utilized to describe compact objects that are of physical relevant.To assess the physical feasibility of the solution, we have conduccted a comprehensive physical examination. Here, the final remarks provide a concise summary of the findings analysis, which can be described as follows:
Upon examining the influence of the parameter χ on the physical parameters through Figs. 1–4, we observe that the value of the parameters ρ,
$ p_r $ ,$ p_t $ , and Δ decrease as χ increases. This suggests that the$ f(\mathcal{R},T) $ gravity model, having a zero complexity factor, has a lower density than the pure general relativity (GR) model. Consequently, the influence of anisotropic force on the equilibrium of the system exhibits an inverse relationship with the variable χ. Moreover, all the energy conditions are satisfied within the entire model (Figs. 1−10).The causality condition must be verified for any well-behaved model to guarantee that the sound velocity never surpasses the speed of light at every point within the model. The radial and tangential components of the velocity of sound (
$ {v}^2_r $ and${v}^2_t $ ) always remain within the stable ranges of$ 0 \le {v}^2_r \le 1 $ and$ 0 \le {v}^2_t \le 1 $ . Figures 5 and 6 show that the causality constraint is satisfied throughout the model. Subsequently, the stability of the structure is examined using the cracking condition and the adiabatic index, whereas the hydrostatic equilibrium condition is examined via the modified TOV equation. The stability analysis, as described by Herrera [88] and Abreu [89], is conducted to assess the cracking condition. The analysis revealed that the quantity$ {v}^{2}_{r}-{v}^{2}_{t} $ consistently falls within the stable range of$ 0\leq {v}^{2}_{r}-{v}^{2}_{t}\leq 1 $ (see Fig. 7). Consequently, the stability study is further conducted using the adiabatic index (Γ). Γ consistently remains within the stable range of$ \Gamma > 4/3 $ throughout the entire model (Fig. 11).In this study, we also have verified the hydrostatic equilibrium condition of an anisotropic model by employing a modified TOV equation. This equation considers the combined effects of various forces, namely
$ F_a,\; F_h, F_g $ , and$ F_\chi $ . Figure 12 shows that the sum of all forces is equal to zero for all values of χ, indicating the attainment of hydrostatic equilibrium. Finally, the mass-radius relationship and the predicted radii for PSR J1614-2230, PSR J0952-0607, and GW190814 are analyzed using the Tolman-IV model in$f(\mathcal{R},T)$ gravity with the complexity formalism. The comparison between the model's predictions and the observed properties of these compact stars is presented in Fig. 14 and Tables 1 and 2, enabling an evaluation of the agreement between the model and observational data. We generate a graph (Fig. 15) that shows the relationship between pressures, energy density, and anisotropy. This graph is used to estimate the linear equation of state (EoS), which is expressed as$ p_r=\alpha (\rho-\rho_s) $ and$ p_t=\alpha (\rho-\rho_s)+\Delta $ .As a final comment, we emphasize that the solution obtained through the utilization of the vanishing complexity formula in
$f(\mathcal{R},T)$ -gravity exhibits desirable properties. This solution will be further expanded in future projects through the execution of the gravitational decoupling technique. -
The authors MKJ and SKM acknowledge that this work is carried out under TRC Project (BFP/RGP/CBS/22/014). This study is also supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445). The authors are thankful to the Deanship of Graduate Studies and Scientific Research at University of Bisha for supporting this work through the Fast-Track Research Support Program. AE thanks the National Research Foundation of South Africa for the award of a postdoctoral fellowship.
Physical properties and maximum allowable mass-radius relation of complexity-free compact stellar objects within modified ${\boldsymbol f}({ \mathcal{\boldsymbol R}},{\boldsymbol T})$ gravity formalism
- Received Date: 2024-01-27
- Available Online: 2024-07-15
Abstract: This paper investigates the physical properties and predicted radii of compact stars generated by the Tolman-IV complexity-free model within the background of modified gravity theory, particularly the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: