-
The recent PREX-II experiment on measuring the neutron skin of
$ ^{208} $ Pb through parity violation in electron scattering [1, 2] extracted a neutron skin thickness of$ R_{\rm skin}^{208} $ =0.283$ \pm $ 0.071 fm [2], which is abnormally large and presents a serious challenge to current nuclear theories. Advanced ab initio calculations of$ ^{208} $ Pb predict a neutron skin thickness of approximately 0.14$ - $ 0.20 fm [3]. Previously, various measurements of neutron skins via nuclear reactions were conducted, resulting in neutron skins that did not significantly deviate from theory. The comprehensively inferred$ R_{\rm skin}^{208} $ is 0.17 fm by considering the constraints of astrophysical data [4]. The large$ R_{\rm skin}^{208} $ leads to a large radius and significant tidal deformability of neutron stars of 1.4 solar mass ($ M_\odot $ ), causing tensions with gravitational-wave observations in the GW170817 event [5]. A very recent measurement using ultrarelativistic heavy-ion collisions also extracted a neutron skin thickness of approximately 0.217 fm [6]. The neutron skin measurement is now an attractive and interdisciplinary topic in low and high energy nuclear physics and astrophysics.Extensive studies have been conducted on the consequences of thick neutron skins on the nuclear EoS [3−5, 7−14]. A thick neutron skin is related to a large density slope L of symmetry energy, which leads to large radii and tidal deformability of neutron stars. A serious issue concerns the ability of current nuclear theories to describe other finite nuclear properties, such as charge radii and dipole polarizability, but not neutron skin thickness [15]. However, the neutron skin of
$ ^{48} $ Ca [16] from the CREX experiment is slightly lower than theoretical estimations and is related to small L values. The$ R_{\rm skin}^{48} $ from ab initio calculations is in the range 0.12$ - $ 0.15 fm [17], whereas the experimental data is 0.121$ \pm $ 0.026 fm [16]. The PREX-II and CREX results imply contradictory EoSs, although experimental uncertainties are still large. The combined analysis of thick neutron skin and astronomical observations of neutron stars can even provide clues about the EoS of dense nuclear matter and phase transition behaviors from nuclear to quark matter [18].Neutron skin thickness is a one-body bulk observable, and density functional theory is, in this respect, a suitable tool for descriptions of heavy nuclei. The effective Skyrme energy density functionals have been widely used in studies of neutron stars and finite nuclei [19]. For example, the SLy4 force can reasonably describe neutron stars of maximum 2.0
$ M_\odot $ and tidal deformability [20] and is adopted as references in LIGO papers [21]. The tension between neutron skins and GW170817 observations is similar in relativistic mean field models [5]. Note that ab initio descriptions of nuclear matter from chiral effective field theory (χEFT) suffer from large uncertainties toward higher densities [22] owing to ambiguous many-body interactions. There have been many studies on neutron skins and symmetry energies based on existing Skyrme forces [8], and these Skyrme forces have been fitted with different physics motivations. It would be useful to study neutron skins and neutron stars with Skyrme forces refitted in a consistent manner.In this study, five new sets of extended Skyrme parameterizations are fitted with different weights of the PREX-II and CREX experiments. The fitting procedure and extended Skyrme force are described in the Methods section. The neutron skins are studied via the difference between neutron and proton density distributions. The resulting charge radii and nuclear matter properties are also discussed. Based on the EoS of different parameterizations, the mass-radius relations and tidal deformabilities of neutron stars are studied. Finally, the global calculations of nuclear binding energies and their influences on neutron drip-line locations are demonstrated. Possible clues to resolve neutron skin issues are also discussed.
-
In this study, we perform new optimizations of extended Skyrme forces by including the PREX-II and CREX measurements of neutron skins. The extension of Skyrme forces with an additional higher-order density dependent term is expected to provide better descriptions of finite nuclei and nuclear matter within a large range of densities [23]. The Skyrme interaction includes two-body and three-body interactions as follows [19]:
$ \begin{array}{*{20}{l}} V_{\rm Skyrme}={\sum\limits_{i<j}v_{ij}^{(2)}}+{\sum\limits_{i<j<k}v_{ijk}^{(3)}}. \end{array} $

(1) The low-momentum effective two-body interaction can be written as
$\begin{aligned}[b]{v_{ij}^{(2)}}=\;& t_{0}(1+x_{0}P_{\sigma})\delta({ \boldsymbol{r}}_i-{ \boldsymbol{r}}_j)\\ &+ \frac{1}{2}t_{1}(1+x_1P_{\sigma})[\delta({ \boldsymbol{r}}_i-{ \boldsymbol{r}}_j){\bf{k}}^2+{\bf{k'}}^2\delta({ \boldsymbol{r}}_i-{ \boldsymbol{r}}_j)] \\ &+ t_2(1+x_2P_{\sigma}){\bf{k'}}\cdot\delta({ \boldsymbol{r}}_i-{ \boldsymbol{r}}_j){\bf{k}} \\ &+ iW_0(\sigma_i+\sigma_j)\cdot{\bf{k'}}\times\delta({ \boldsymbol{r}}_i-{ \boldsymbol{r}}_j){\bf{k}}. \end{aligned} $

(2) The three-body interaction can be transformed into a density dependent two-body interaction, and an additional term is adopted in this study [23, 24].
$ \begin{aligned}[b] v_{ijk}^{(3)} =\;& \frac{1}{6}t_3(1+x_3P_\sigma)\rho(\boldsymbol{R})^\gamma\delta( \boldsymbol{r}_i- \boldsymbol{r}_j) \\ & +\frac{1}{6}t_{3E}(1+x_{3E}P_{\sigma})\rho(\boldsymbol{R})^{\gamma_E}\delta( \boldsymbol{r}_i- \boldsymbol{r}_j). \end{aligned} $

(3) In Eq. (2),
$ t_i $ ,$ x_i $ , and$ W_0 $ are parameters of the standard Skyrme interation. The spin-orbit term can be extended to include isospin dependence, and$ W_0 $ is replaced by$ b_4 $ and$ b_4' $ [25]. Moreover,$ t_{3E} $ and$ x_{3E} $ are additional high-order parameters. The power factor γ is$ 1/6 $ , which is similar to those of the SLy4 and SkM$ ^{*} $ forces, and the high-order power$ \gamma_E $ is$ 1/2 $ [23]. The effective mass is taken as$ m^{*}/m $ =0.8, whereas it is 0.68 for SLy4. In our study, systematic calculations are based on the self-consistent deformed Skyrme-Hartree-Fock+BCS (SHF-BCS) method [26]. The mixed pairing interaction [27] is adopted and the pairing strengths are$ V_p $ =400 MeV and$ V_n $ =340 MeV. The Hartree-Fock-BCS equations are solved by the SKYAX code in axial-symmetric coordinate-spaces [26].In the fitting procedure, we minimize the quantity
$ \begin{aligned}[b] \chi^2 =\;& \left(\frac{e_\infty+16.0}{0.2}\right)^2+\left(\frac{\rho_s-0.16}{0.005}\right)^2+\sum\limits_i\left(\frac{E(i)-E^{\rm exp}(i)}{2.0}\right)^2\\ & +\sum\limits_i\left(\frac{\sqrt{<r^2>_{\rm ch}(i)}-\sqrt{<r^2>_{\rm ch}^{\rm exp}(i)}}{0.02}\right)^2\\ & +{w_1(R^{48}_{\rm skin}-0.12)^2+w_2(R^{208}_{\rm skin}-0.28)^2}{}. \end{aligned} $

(4) Here,
$ e_\infty $ is the average energy per nucleon at the saturation density, the saturation density$ \rho_s $ is constrained to be approximately 0.16 fm$ ^{-3} $ , and$ E^{\rm exp}(i) $ and$ \sqrt{<r^2>_{\rm ch}^{\rm exp}(i)} $ denote the total binding energies and charge radii of selected nuclei, respectively. The selected nuclei are listed in our previous work [23]. The experimental binding energies are taken from [28] and the experimental charge radii are taken from [19]. In addition, the neutron skin thicknesses of$ ^{48} $ Ca and$ ^{208} $ Pb are included in the fitting, the experimental values of which are taken from CREX and PREX-2 [2, 16]. The nuclear matter properties are not explicitly included in the fitting; however, the incompressibility at$ \rho_s $ and the symmetry energy at 0.11 fm$ ^{-3} $ ($ \sim\dfrac{2}{3}\rho_s $ ) are loosely constrained. Considering the large uncertainties in neutron skin measurements, the fitting weights$ w_1 $ and$ w_2 $ in Eq. (4) are varied, as shown in Table 1. It is challenging for existing nuclear structure theories to simultaneously describe the thick neutron skin in$ ^{208} $ Pb and the thin neutron skin in$ ^{48} $ Ca. There is a competition in the fitting between neutron skin thickness and other nuclear observables. Thus, we obtain several sets of Skyrme parameters by changing the weights of the neutron skin constraints. The optimization is realized using the simulated annealing method with gradually decreasing temperatures, as shown in Refs. [23, 29]. We adjust$ t_2 $ ,$ t_3 $ ,$ x_2 $ ,$ x_3 $ ,$ x_{3E} $ ,$ b_4 $ , and$ b_4^{'} $ , and the remaining parameters are determined via relations in the equation of state.Parameters SkNS1 SkNS2 SkNS3 SkNS4 SkNS5 $ t_0 $ 

−2381.22 −2340.20 −2287.31 −2195.17 −2339.41 $ t_1 $ 

451.24 455.64 475.35 475.96 472.89 $ t_2 $ 

−399.65 −399.65 −465.37 −465.37 −462.58 $ t_3 $ 

12115.30 11564.79 10955.19 9849.11 11709.66 $ t_{3E} $ 

2477.62 2887.07 3217.65 3864.70 2620.65 $ x_0 $ 

0.431 2.41E-002 −0.303 −0.602 −0.649 $ x_1 $ 

−0.297 −0.309 −0.243 −0.243 −0.243 $ x_2 $ 

−0.729 −0.718 −0.763 −0.763 −0.763 $ x_3 $ 

0.640 −0.193 −0.874 −1.823 −1.414 $ x_{3E} $ 

6.20E-003 1.100 1.586 2.793 1.935 $ b_4 $ 

67.46 68.16 97.38 96.20 96.11 $ b_4^{'} $ 

93.96 98.69 74.60 82.04 79.35 γ 1/6 1/6 1/6 1/6 1/6 $ \gamma_E $ 

0.5 0.5 0.5 0.5 0.5 $ e_\infty $ 

−16.03 −16.03 −16.01 −16.02 −15.98 $ \rho_s $ 

0.1592 0.1605 0.1597 0.1592 0.1603 K 232.68 239.00 238.64 240.79 233.39 $ a_s^{0.16} $ 

32.941 35.614 34.624 36.468 36.964 $ a_s^{0.11} $ 

26.860 26.405 26.635 27.048 25.880 L 29.732 46.653 60.077 60.543 81.659 $ w_1 $ 

1000 5000 10000 5000 1000 $ w_2 $ 

1000 5000 10000 10000 20000 Table 1. Fitted parameters of the extended Skyrme interactions, obtained by varying the weights of the neutron skin measurements. The incompressibility K (MeV), symmetry energy
$ a_s $ (MeV), and slope L (MeV) of symmetry energy at the saturation density are listed. The symmetry energy at a density of 0.11 fm$ ^{-3} $ is also given. The fitting weights of neutron skins$ w_1 $ and$ w_2 $ are also listed.Using the new Skyrme-like interactions, the EoS of nuclear matter can be obtained. With the obtained EoS, the neutron star observations are calculated by solving the well-known Tolman-Oppenheimer-Volkoff (TOV) equation. With the calculated mass-radius relation of neutron stars, the gravitational-wave tidal deformability can also be calculated, as described in our previous work [20].
-
First, we obtain five different sets of Skyrme parameters by varying the fitting weights of neutron skin measurements, as shown in Table 1. Note that with increasing fitting weights of neutron skins, the deviations in binding energies increase. We loosely constrain the symmetry energy at 0.11 fm
$ ^{-3} $ , which is approximately 2/3 of the saturation density and is more relevant for finite nuclear properties [30]. However, the symmetry energy at 0.16 fm$ ^{-3} $ is not constrained and is significantly large with the thick neutron skin of$ ^{208} $ Pb. The incompressibility at the saturation density is not sensitive to the neutron skin thickness.Table 2 shows the results of the neutron skin thicknesses of
$ ^{48} $ Ca and$ ^{208} $ Pb with different Skyrme parameters. Parameters with a thicker neutron skin of$ ^{208} $ Pb also result in a thicker neutron skin of$ ^{48} $ Ca. The theoretical neutron skin thickness is larger than the CREX data, and there is a contradiction in descriptions of$ ^{48} $ Ca and$ ^{208} $ Pb. Current nuclear theories heavily underestimate$ ^{208} $ Pb and slightly overestimate$ ^{48} $ Ca. It is also difficult to understand the PREX-2 and CREX results simultaneously within relativistic mean-field models [32]. The PREX and CREX experiments are based on measurements of the weak charge of neutrons. The consideration of the weak mixing angle dependence, which is a key parameter in electroweak theory, may be a clue to explaining this contradiction [33]. The clustering at the nuclear surface may also affect the neutron skin; however, the role of clustering is very small in magic nuclei [34].SkNS1 SkNS2 SkNS3 SkNS4 SkNS5 Expt. $ R_{\rm skin}^{48} $ 

0.153 0.168 0.178 0.183 0.195 0.121±0.026 $ R_{\rm skin}^{208} $ 

0.186 0.220 0.247 0.259 0.284 0.283±0.071 $ R_{ch}^{48} $ 

3.55 3.54 3.53 3.52 3.51 3.48 $ R_{ch}^{208} $ 

5.51 5.51 5.50 5.48 5.47 5.50 -
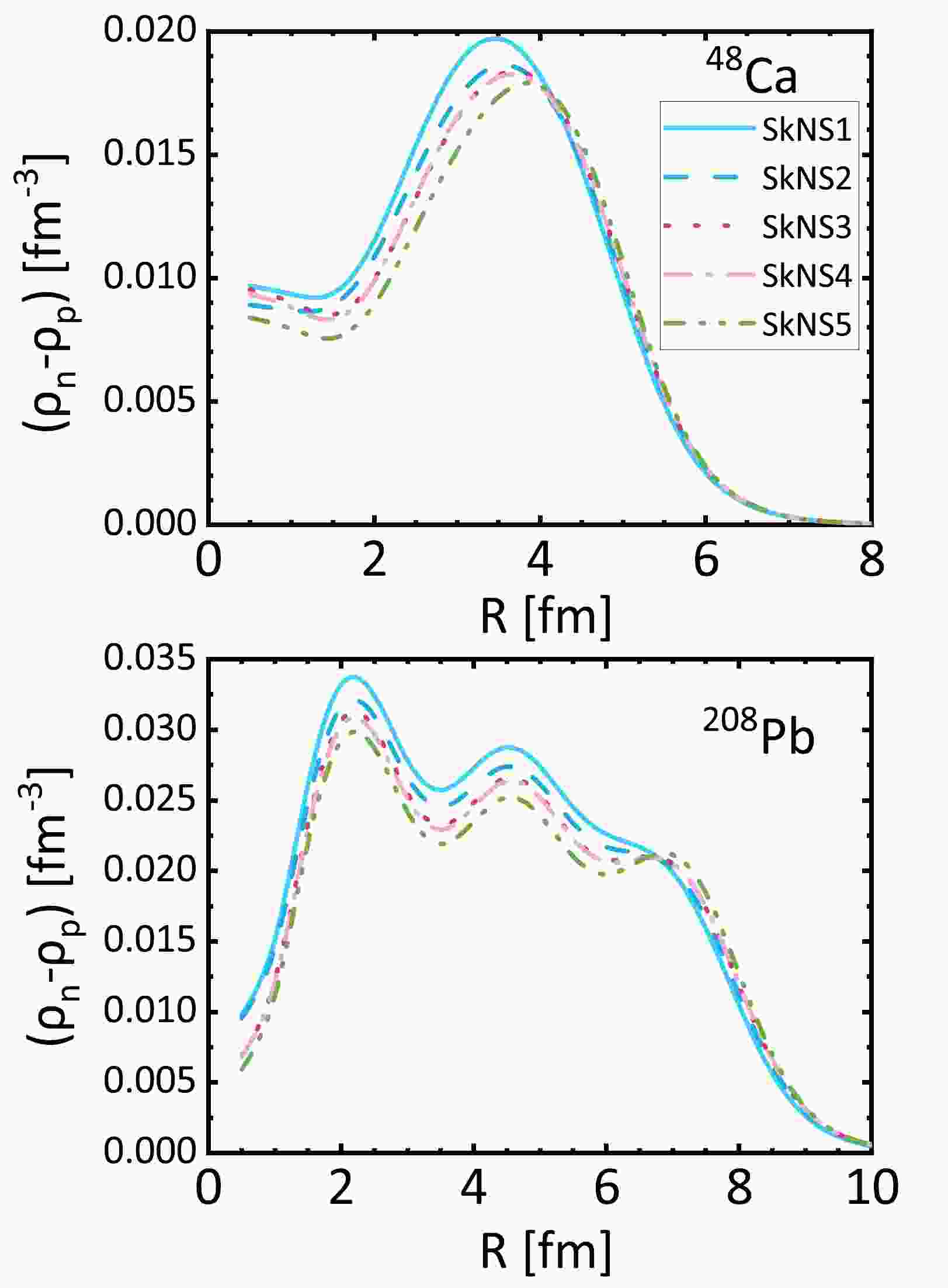
To study the properties of neutron skins, the density distributions can be obtained via self-consistent SHF-BCS calculations. It is known that SHF calculations are generally good at describing charge radii and proton density distributions, which can be obtained from electron scatterings. Figure 1 shows the differences between the proton and neutron density distributions of
$ ^{48} $ Ca and$ ^{208} $ Pb. The central neutron densities decrease with increasing neutron skin thickness. We expect to see more neutrons at the nuclear surface when the neutron skin is thick. However, the density differences at the surface are not significant. Generally, there are more neutrons than protons inside nuclei, and hence neutron skins at surfaces are strongly suppressed. The problem is that the optimization of binding energies and charge radii is not sensitive to the low density part of nuclear surfaces.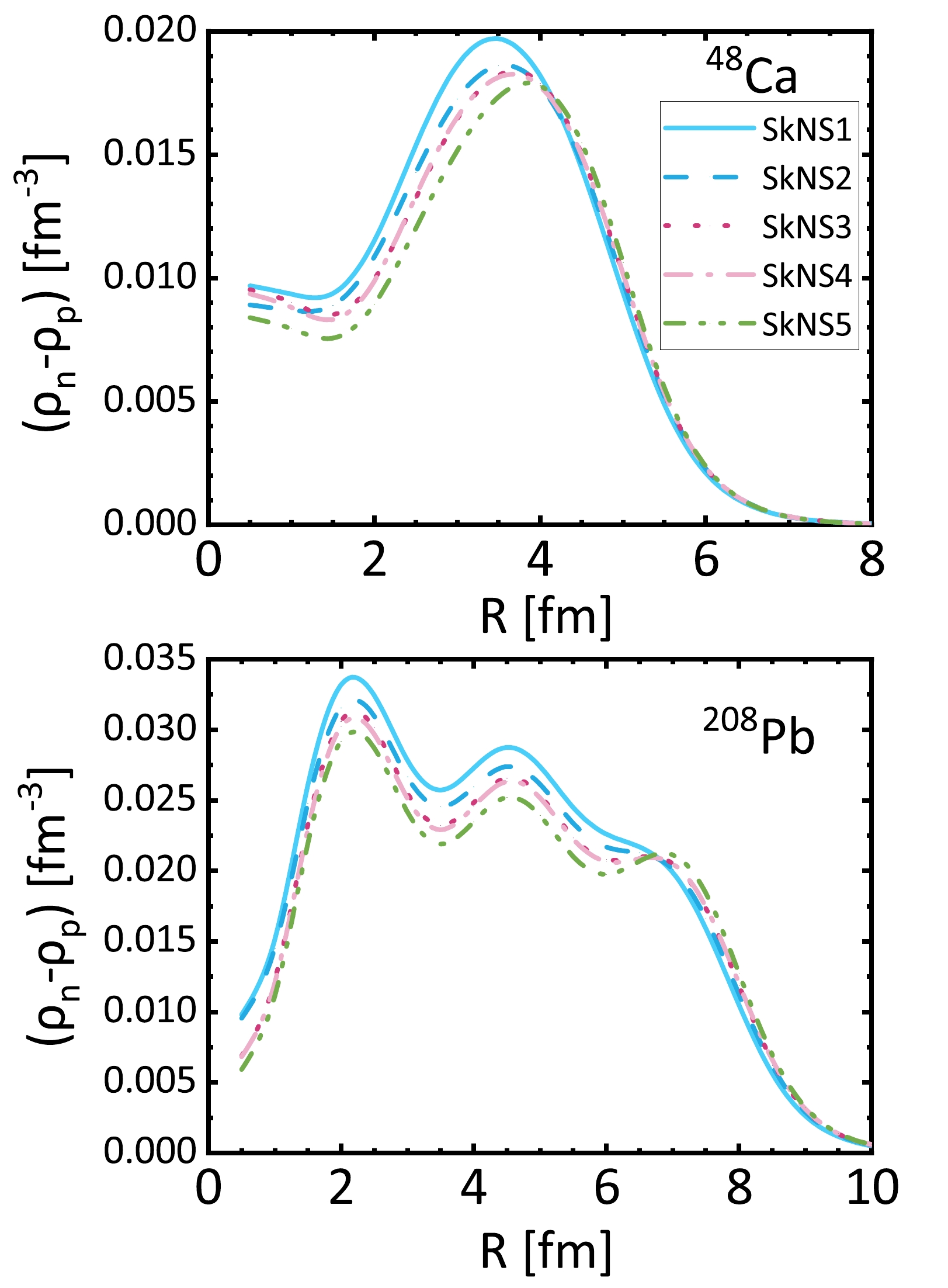
Figure 1. (color online) Calculated difference between neutron and proton densities,
$ \rho_n(r)-\rho_p(r) $ , of$ ^{48} $ Ca (a) and$ ^{208} $ Pb (b) using different Skyrme parameterizations.The charge radii of
$ ^{48} $ Ca and$ ^{208} $ Pb are also calculated, as shown in Table 2. The charge radii are calculated using the formula in Ref. [19], but without spin-orbit corrections. As shown, the charge radius of$ ^{48} $ Ca is larger than that of experiments [31]. If the neutron skin thickness of$ ^{208} $ Pb is forced to be thick, the charge radius of$ ^{208} $ Pb becomes smaller. This indicates that some physics is missing in the theoretical approach. In the fitting procedure, the thin neutron skin in$ ^{48} $ Ca corresponds to a large charge radius, and the large charge radius of$ ^{48} $ Ca has been a problem in other density functional calculations [35]. The inclusion of relativistic and spin-orbit corrections [36] would slightly improve the charge radius of$ ^{48} $ Ca. The strong weights of thick neutron skins may inevitably lead to reduced charge radii in the fitting. -
The properties of infinite nuclear matter associated with newly fitted interactions are studied, which are relevant to neutron star observations. Figure 2 shows the average energies per nucleon of symmetric and pure neutron matter. The difference between different parameter sets in symmetric matter is small, even at high densities. For neutron matter, a thicker neutron skin results in a stiffer EoS at higher densities. However, a thicker neutron skin results in lower energies at low densities. Note that the low density part is more relevant than the high density part to the neutron skins. Theoretical studies of the very low density part are also challenging owing to the emergence of clustering.
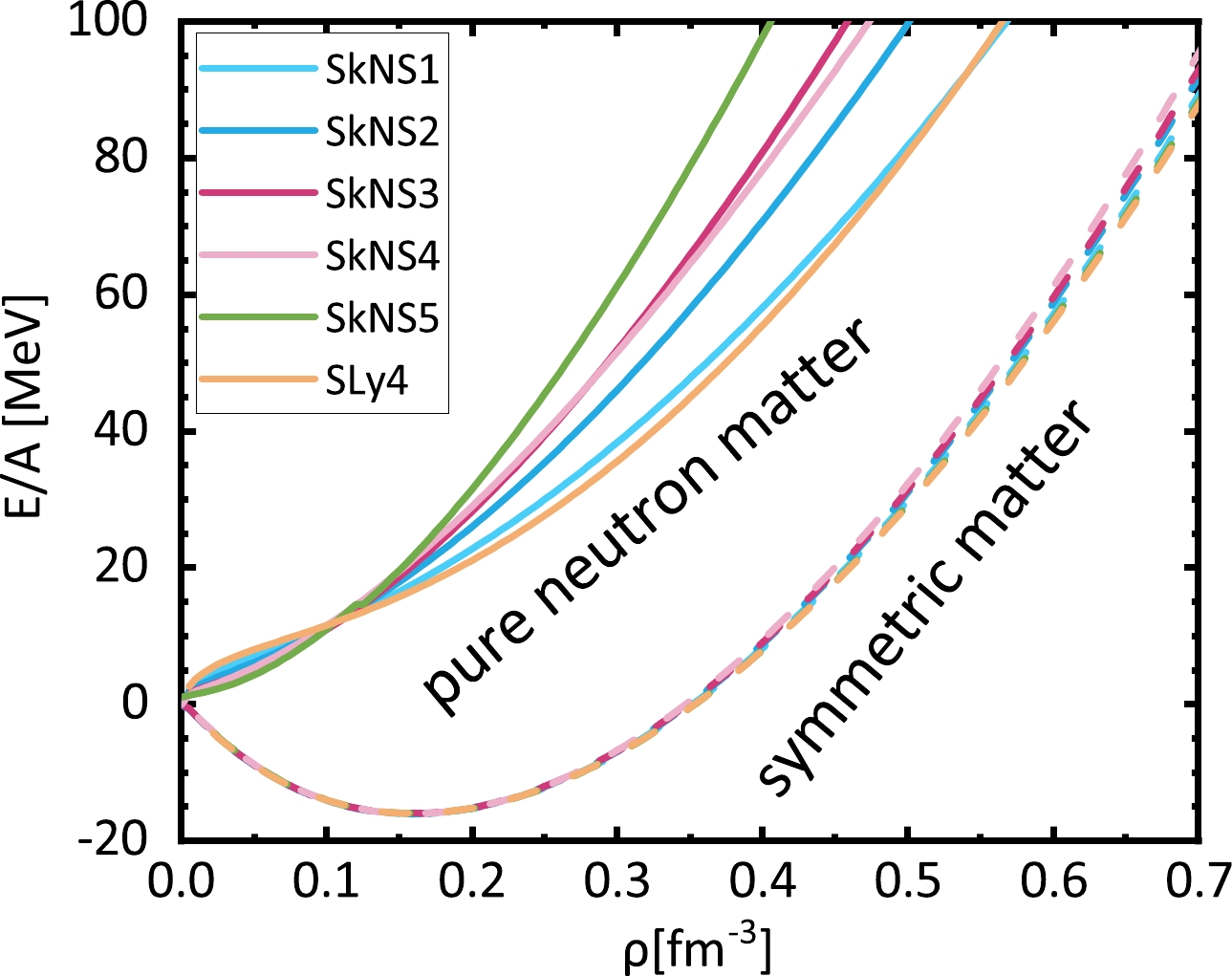
Figure 2. (color online) Density dependent energies of symmetric nuclear and pure neutron matter associated with different Skyrme interactions.
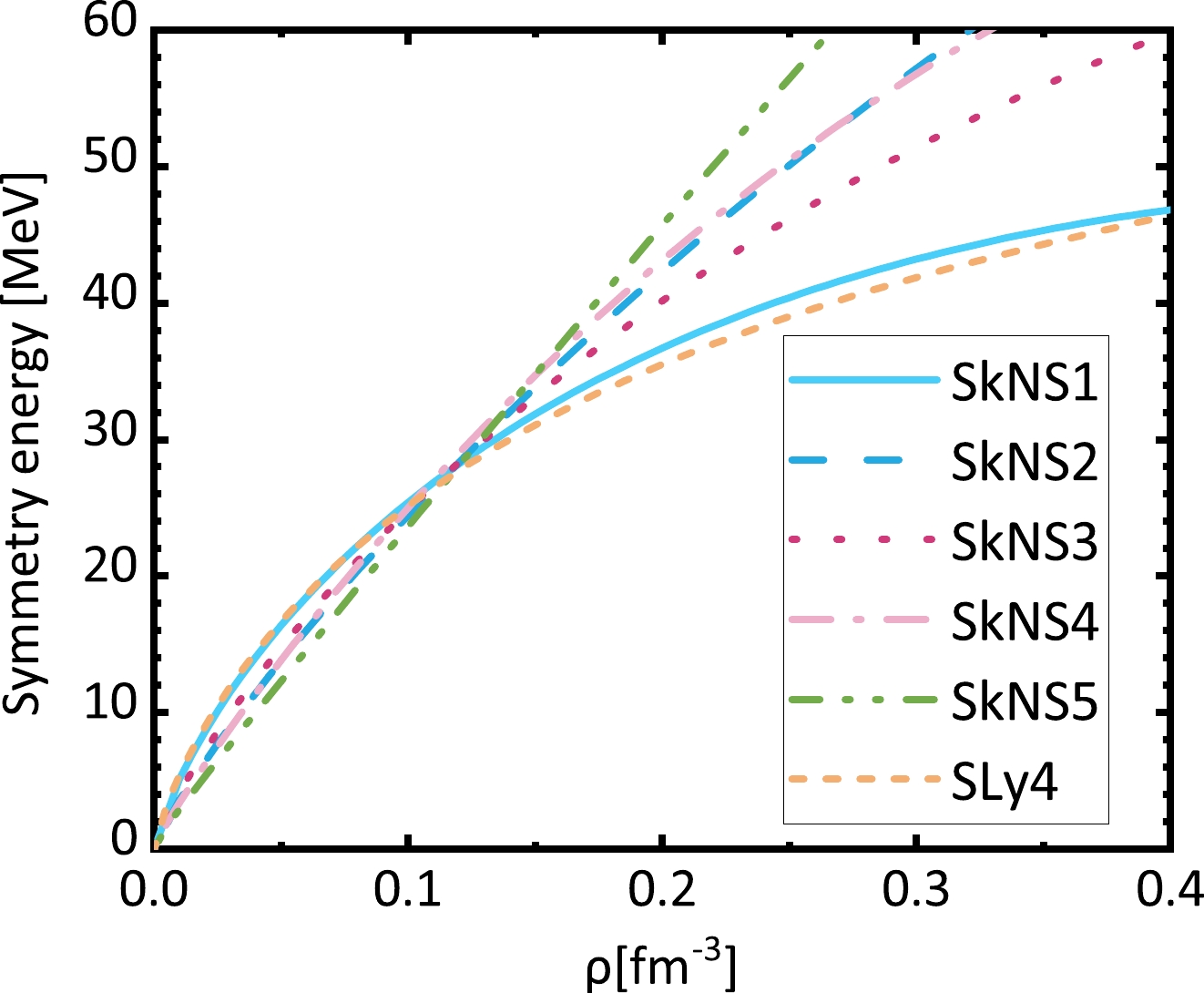
The density dependent symmetry energies are shown in Fig. 3. The symmetry energy is loosely constrained at 0.11 fm
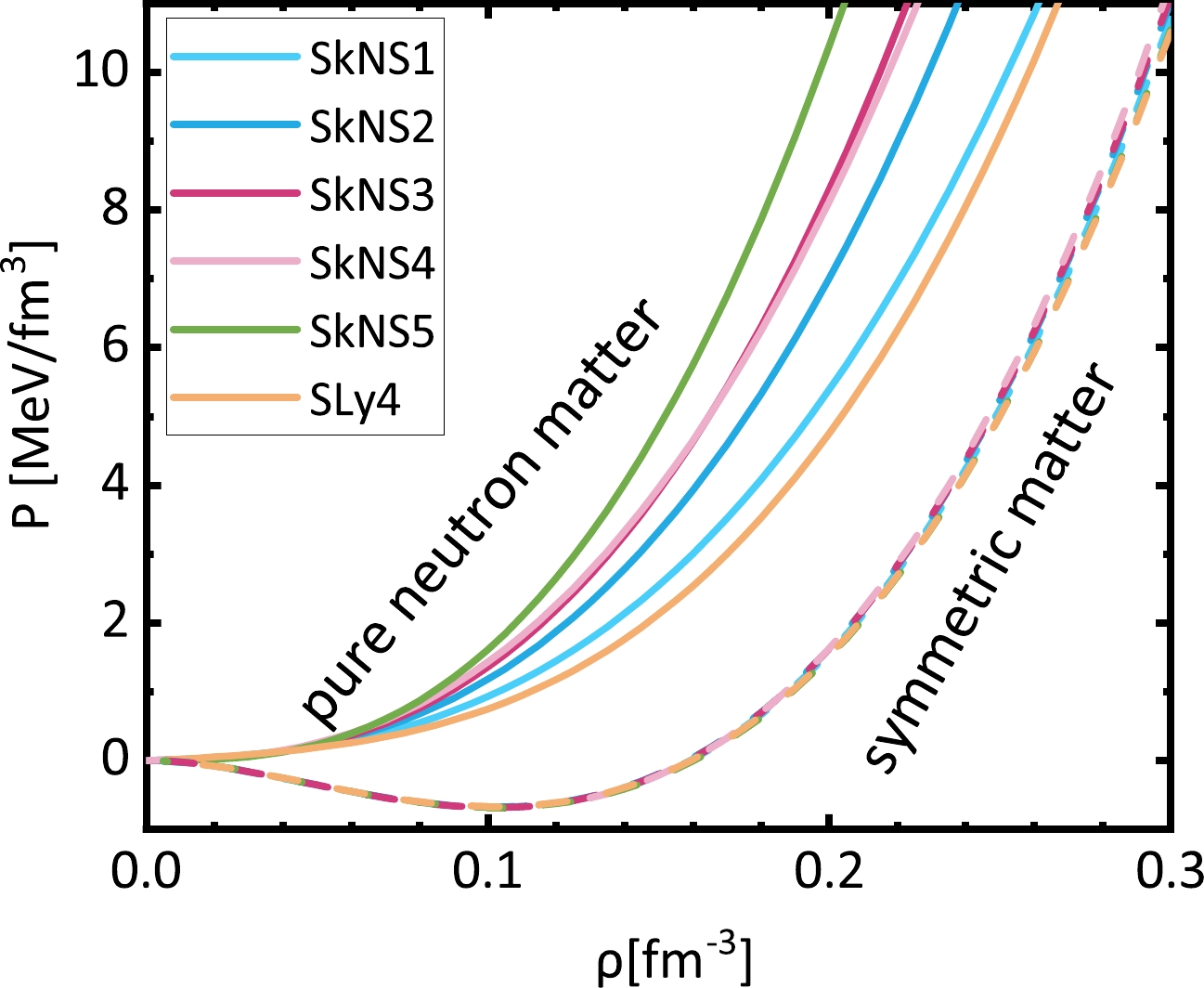
$ ^{-3} $ around 26.0 MeV, which is reasonable for descriptions of neutron drip lines [37]. Symmetry energies above the saturation density increase with increasing neutron skins. In contrast, symmetry energies decrease with increasing neutron skins below the saturation density. The actual correlated quantity is the slope L of the symmetry energy, which increases with the neutron skin thickness. The related pressure of nuclear matter is shown in Fig. 4. For the symmetric nuclear matter, the pressure from different interactions are similar. However, there are large discrepancies in pressure for pure neutron matter. A thicker neutron skin corresponds to higher pressure in the high density region. -
It is interesting to know the consequences of the neutron skin measurements on neutron star observations. Figure 5(a) shows the mass-radius relationships of neutron stars obtained by solving the TOV equation, based on EoSs related to different neutron skins. The EoS is calculated with β-equilibrium nuclear matter. At densities lower than 0.04 fm
$ ^{-3} $ , the EoS of the crust is taken from the online library [38]. The maximum masses are all close to 2.0$ M_\odot $ except that of SkNS4. Moreover, the maximum masses of all cases are within the causality limit. Generally, the radii of 1.4$ M_\odot $ increase with increasing neutron skin thickness. SkNS4 results in a very large radius and is beyond the GW170817 observations [21]. Indeed, SkNS4 is different from other interactions; the$ x_{3E} $ parameter is 2.793 and is beyond the usually adopted ranges. Note that the recently observed neutron star J0952-0607 has a mass of 2.35$ \pm $ 0.17$ M_\odot $ [39], which is the heaviest known neutron star and can be reached by some stiff non-relativistic interactions such as BSk21 to BSk25 [40, 41]. It is also not difficult for relativistic functionals to obtain such a massive neutron star [42].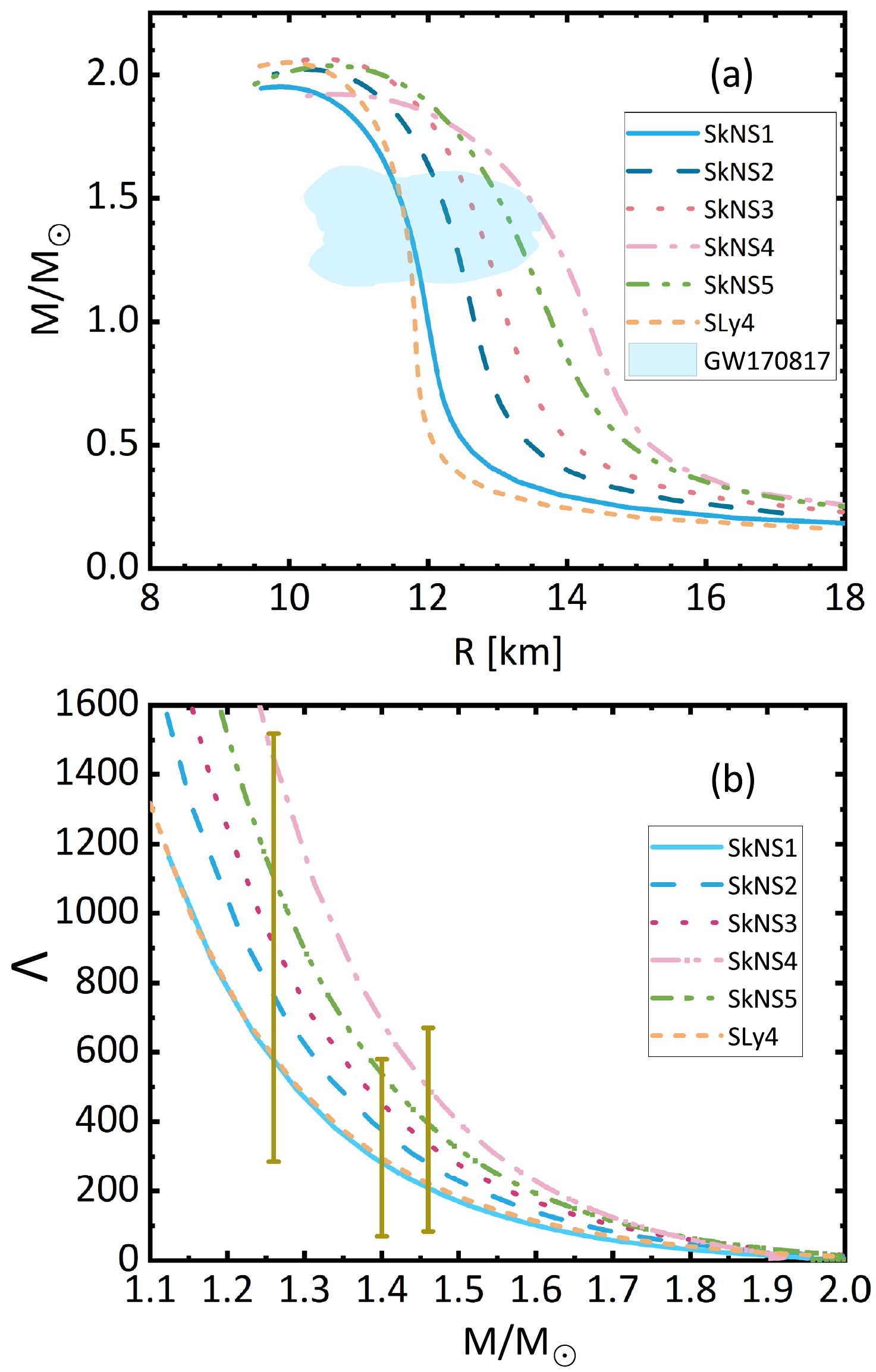
Figure 5. (color online) Mass-radius relationships of neutron stars calculated using our four Skyrme interactions. (a) Mass-radius relationships of neutron stars calculated with different Skyrme interactions. (b) Tidal deformability Λ of neutron stars associated with different Skyrme interactions. The tidal deformabilities of two neutron stars in GW170817 are 661
$ ^{+858}_{-375} $ and 255$ ^{+416}_{-171} $ [43]. The inferred Λ at 1.4$ M_\odot $ is$ 190_{-120}^{+390} $ [21].The tidal deformability Λ of neutron stars is a novel observable of gravitational waves, providing additional constraints on the EoS. Figure 5(b) displays the tidal deformability as a function of neutron star mass. There are two neutron stars in the GW170817 event. The inferred tidal deformability at 1.4 solar mass is approximately
$ \Lambda=190_{-120}^{+390} $ [21]. As shown, SkNS5 with a thick neutron skin of 0.284 fm is in tension with the upper limit of Λ. SkNS4 has the largest neutron star radius and its tidal deformability is too large. The comprehensive analysis obtains an upper limit of Λ at 519 [44], which presents an even bigger challenge to the thick neutron skin. The relativistic mean field calculations also present serious challenges to simultaneously describing the neutron skins and tidal deformability [5]. To reconcile with the thick neutron skin and neutron star observations, a modified speed of sound above the saturation density is needed [18]. -
Systematic calculations of the properties of finite nuclei are also performed with the associated Skyrme interactions, as shown in Fig. 6. There are 603 even-even nuclei to be calculated, and the root of mean square (rms) of the binding energies are 2.22, 2.41, and 3.21 MeV for SkNS1, SkNS2, and SkNS3, respectively. The smallest deviation is 2.15 MeV for SkNS4. The largest deviation is 4.45 MeV for SkNS5. Note that the global rms of the binding energies of SLy4 is approximately 4.37 MeV. Therefore, the results of the global binding energies are acceptable. There is an evident competition between neutron skin measurements and global binding energies. We find that there are overestimated shell effects in the binding energies, which can be alleviated by adopting a larger effective mass [45]. The binding energies of heavy nuclei associated with thick neutron skins are generally satisfied, even though the descriptions of light nuclei are not ideal. The rms of binding energies for
$ Z\geqslant 82 $ is approximately 2.2 MeV for SkNS3 and 1.6 MeV for SkNS4. Note that SkNS4 is much better in descriptions of finite nuclei that also have a considerable neutron skin thickness. This is because the parameter$ x_{3E} $ in SkNS4 is very different.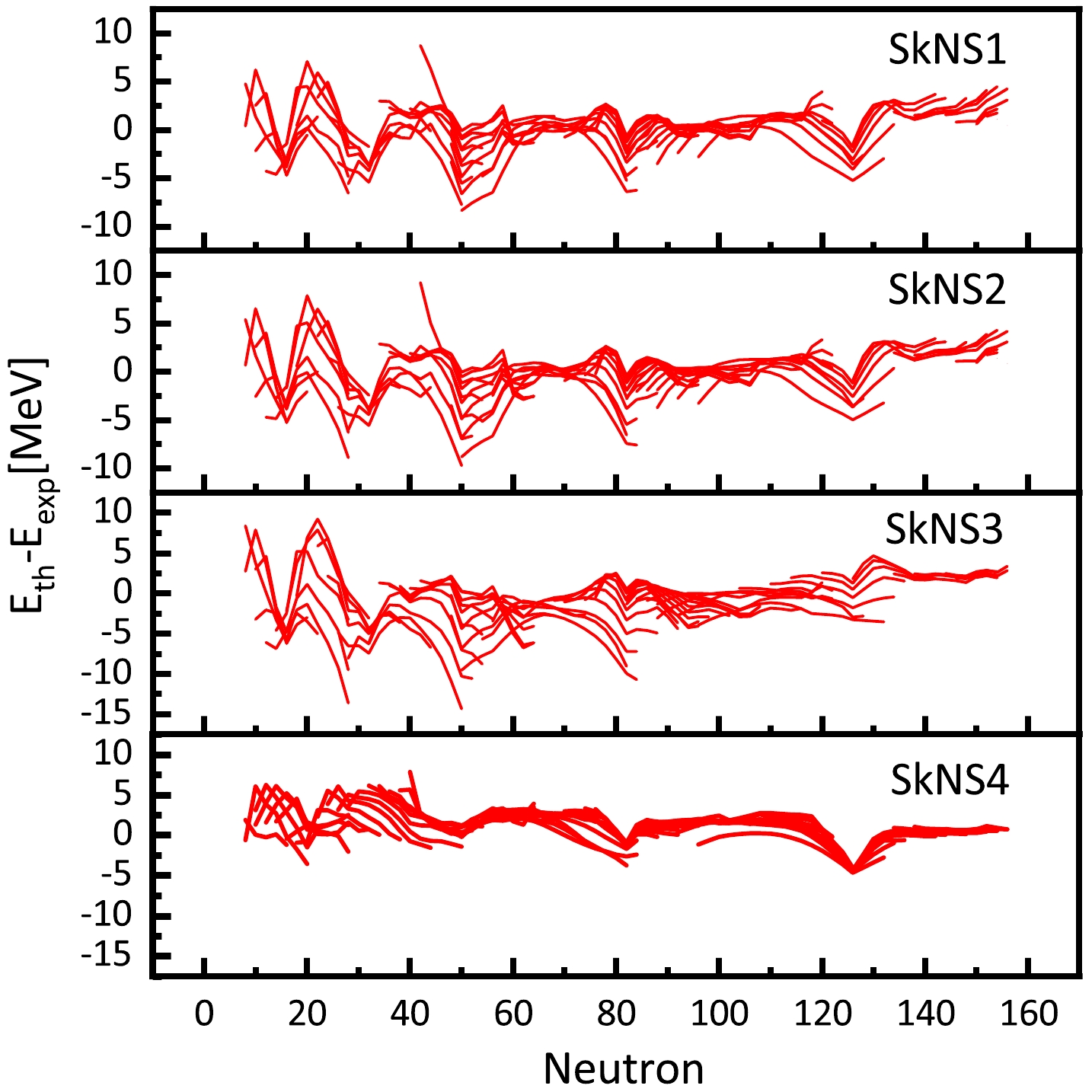
Figure 6. (color online) Binding energy difference between theoretical calculations and experiments for 603 even-even nuclei. The experimental data are taken from [26]. The calculations are based on the Hartree-Fock+BCS method with different Skyrme interactions.
The neutron drip-line locations of selected nuclei are also calculated with different interactions, as shown in Table 3. As shown, the neutron drip lines are extended with interactions associated with thick neutron skins. There is a significant extension in the neutron drip line of U isotopes. The extension of the neutron drip line is not a result of the large symmetry energy, which actually reduces the stability of neutron-rich nuclei, but is because of the small symmetry energy below the saturation density, as shown in Fig. 3. Again, we find that the SkNS4 results are different owing to the large
$ x_{3E} $ parameter. In the future, the simultaneous descriptions of neutron skins and other nuclear observables may be improved by increasing the searching range of x parameters in the fitting.SkNS1 SkNS2 SkNS3 SkNS4 SkNS5 Mg 32 32 32 32 34 Ca 50 54 56 56 58 Sn 124 124 126 124 132 Pb 186 186 190 188 202 U 206 204 224 216 240 Table 3. Calculated neutron numbers of the neutron drip-line locations of selected nuclei with different Skyrme interactions.
-
In summary, extended Skyrme interactions are refitted by considering the PREX-II and CREX measurements of neutron skin thickness in a consistent manner. Several new parameterizations are obtained by varying the fitting weights of neutron skins. The density distributions are studied, revealing that the inner neutron-proton density differences decrease with increasing neutron skin thickness. The properties of nuclear matter exhibit smaller symmetry energy below the saturation density and stiff symmetry energy at high density with increasing neutron skins. This results in larger radii and tidal deformability of neutron stars. In this respect, the PREX measurements are in tension with neutrons star observations. It is possible to reconcile the neutron skin measurements with neutron star observations by modifying the speed of sound above the saturation density. The thick neutron skins also undermine the descriptions of global binding energies and result in highly extended neutron drip lines. The results of SkNS4 indicate that the simultaneous descriptions of neutron skins and other nuclear observables may be improved by increasing the searching range of x parameters. Currently, there are large uncertainties in the neutron skin measurements; however, in the future, precise measurements of neutron skins are highly expected because of the significant consequences in understanding neutron stars and finite nuclei.
Implications of neutron skin measurements on Skyrme equations of state
- Received Date: 2023-12-01
- Available Online: 2024-06-15
Abstract: The recent measurements of neutron skins via parity violation in electron scattering have extracted an abnormally thick neutron skin for





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: