-
Quantum entanglement, one of the most prominent characteristics of a quantum system, has been shown to play an important role in many fields, such as quantum information, quantum computation, condensed matter physics, and black hole physics [1−7]. It demonstrates the mysterious non-classical correlation between quantum subsystems. Entanglement entropy, which is an important measure of quantum entanglement, has been extensively investigated. In particular, for a bipartite system, Page [6] discovered an important feature for the entanglement entropy between two subsystems, which is now sometimes referred to as "Page's theorem." It states that the average entanglement entropy of the smaller subsystem over random pure states is close to its maximal value, which is constrained by degrees of freedom in the subsystem. This typically means that the smaller subsystem is almost maximally entangled with the other subsystem. Inspired by this observation, Page originally noted that it may be applicable to the famous black hole information loss paradox [5, 7]. The core issue of this paradox is whether the evaporation process of a black hole due to Hawking radiation
1 , which is a semi-classical result in quantum field theory over a curved but classical spacetime, is fundamentally unitary at the complete quantum mechanical level. A complete quantum theory of gravity has not yet been established, and the microscopic description of a black hole with quantum states remains unknown. Nevertheless, Page suggests that random states may be chosen as the approximation of black hole states during the evaporation process2 . Under the condition that the black hole evaporation process is unitary, it is believed that Page's theorem is applicable to a system composed of a black hole and its radiation, and in principle, the typical entanglement entropy of the radiation subsystem as a function of its size should follow the so-called Page curve. This concept proposed by Page has stimulated considerable research to further understand the black hole information paradox by investigating the entanglement between a black hole and radiation. In particular, since the island paradigm was proposed in the holographic approach [12−14], reproducing the Page curve for the evaporation process of the black hole via holography has become a central method to argue that the information is released in the later half stage of radiation.Nevertheless, we know that the approximation with totally random states is not always sufficiently precise to describe the evolution of quantum entanglement in practice, because physically relevant systems usually have conserved charges, such as energy, momentum, and electric charge. In a system with conserved charges, the reduced Hilbert space is composed of quantum states that are subject to the conservation of charges and thus do not equal the tensor product of the Hilbert spaces [15, 16], each of which is separately defined on an individual subsystem. However, in this case, the entanglement entropy between two subsystems based on the reduced Hilbert space can still be computed, which is known as "symmetry-resolved (SR) entanglement entropy" [17, 18], and has been widely investigated from many theoretical aspects [19–74] and in experiments [75, 76]. It is important to note that, when computing the average SR entanglement entropy, the original Page's theorem is generally not applicable. Therefore, it is interesting to investigate the Page curve for SR entanglement entropy (SR Page curve) and compare it with the Page curves of systems without conserved charges. Some relevant work on this topic can be found in [77, 78].
It is well known that a stationary black hole is usually classically characterized by three conserved quantities, namely, the mass E, angular momentum J, and electric charge Q. When considering the evaporation of such a black hole, it is also natural to assume that these three quantities are conserved during the evaporation process. Therefore, one may apply SR entanglement entropy to describe the entanglement between the black hole and radiation. In principle, a refined Page curve may be obtained with a similar method introduced by Page, except that only the average value of entanglement entropy is considered over the non-factorized reduced Hilbert space [79]. However, note that for the evaporation of a charged black hole, such a calculation based on random states does not align with the semi-classical calculation of Hawking radiation and the Schwinger effect [8]. The key point is that the charge does not radiate out at the same rate as the mass [8, 80–83]. Specifically, if we were to randomly select states in the entire Hilbert space with a fixed global charge number, the average charge number of the subsystem (radiation part) would increase linearly with the number of particles (at least in the case of the typically simple qubit model, see Fig. 1). However, the semi-classical calculation of Hawking radiation and the Schwinger effect reveals that the evolution of the electric charge Q, mass E, and angular momentum J exhibits a distinct behavior during evaporation [8, 80–82]. In general, for a black hole, the rate of energy and angular momentum loss changes relatively slowly during the entire evaporation process [80], whereas the radiation rate of the electric charge Q depends on the stage of the black hole, which is specified by the parameter relations [8, 83]. For different parameter values, the evaporation rate of the charge Q varies dramatically, which as described in detail in Sec. III. Consequently, the random model, even at a qualitative level, fails to capture the charge distribution during the course of evaporation for a charged black hole. In this study, aiming to simulate the evaporation of a charged black hole, we analyze the SR entanglement entropy in a qubit model with conserved charges and obtain various refined Page curves that reflect the different behaviors of the black hole as it radiates its charge. We show that this model qualitatively reveals that the charge does not radiate out with a uniform rate during the evaporation of black holes.

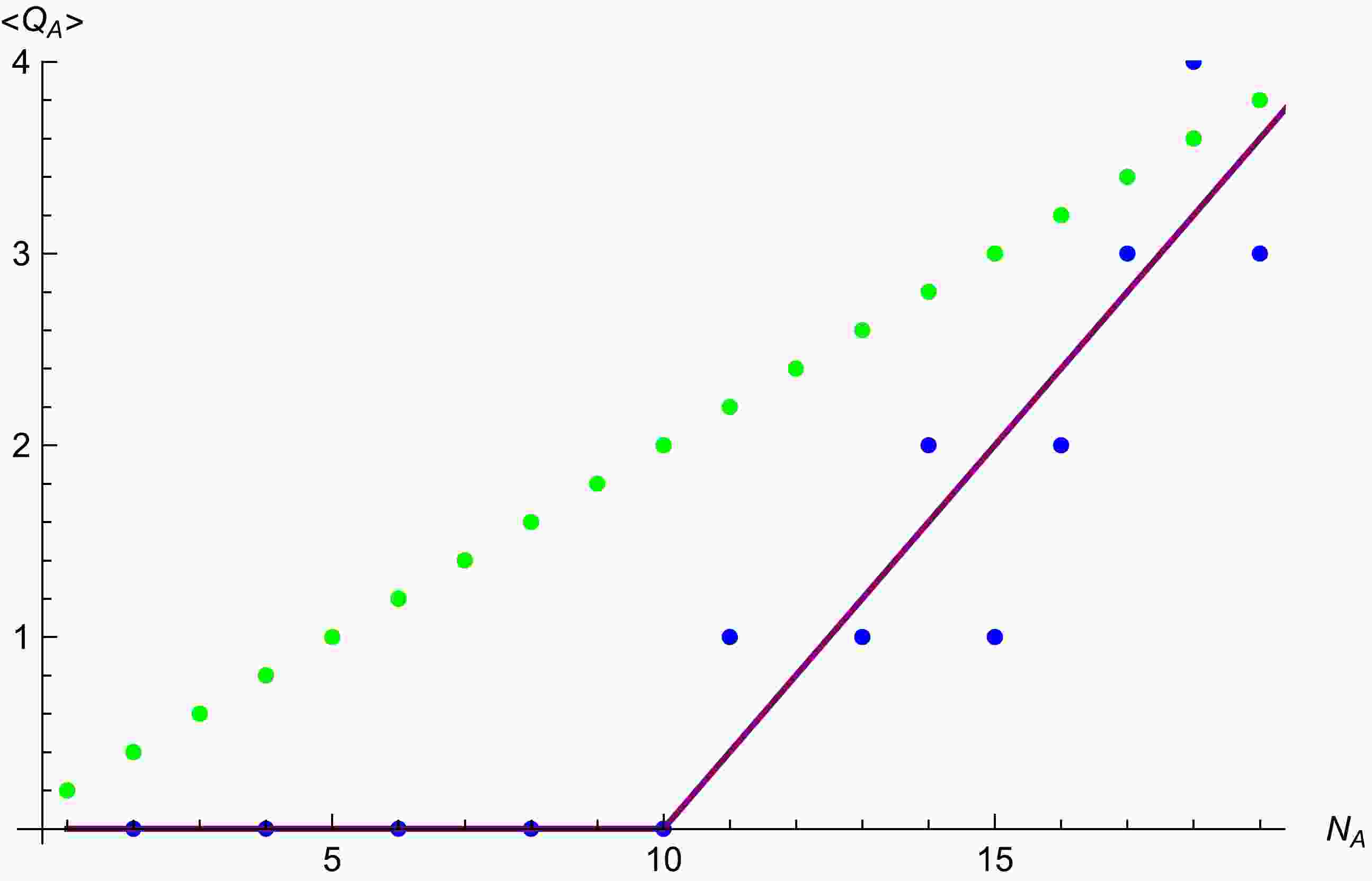
Figure 1. (color online) Average charge number
$ \langle Q_A \rangle $ over random states with particle number$ N_A $ in subsystems A under different evaporation patterns. (i) The green dotted line represents the average value over random states in Hilbert space$ {\cal{H_{AB}}}(Q=4) $ . (ii) The blue dotted line represents the average value over random states in the refined Hilbert space$ {\cal{H_{AB}}} $ . (iii) The purple solid line represents the average value over the random states in the refined Hilbert space$ {\cal{H_{AB}}} $ in the thermodynamic limit, where the coordinates ($ N_a $ ,$ \langle Q_A \rangle $ ) correspond to ($ N_a $ ,$ \langle Q_A\rangle $ )$ \times\frac{20}{N_{th}} $ as a result of normalization.The rest of this paper is organized as follows. In Sec. II, we review the calculation of the average entanglement entropy over totally random states in a system without conserved charges and the average SR entanglement entropy in a system with conserved charges. In Sec. III, we introduce a qubit model for the evaporation of a charged black hole and propose refined rules for selecting a random state with a conserved quantity to simulate the distribution of charges during the different stages of evaporation and obtain refined SR Page curves. In Sec. IV, we provide a discussion and the outlook for future research.
-
In this section, we review the general concept of the entanglement between two subsystems in a bipartite system described by a random pure quantum state. We first compute the average value of the entanglement entropy in a system without conserved charges and then address the SR entanglement entropy in a system with conserved charges.
-
Consider a bipartite system
$ A\cup B $ with the Hilbert space$ {\cal{H_{AB}}}={\cal{H_A}}\otimes {\cal{H_B}} $ , where$ {\cal{H_A}} $ and$ {\cal{H_B}} $ are the Hilbert space of subsystems A and B, respectively. Supposing the total system is described by a pure state$ \vert{\psi}\rangle $ , the entanglement entropy of A is defined by$ \begin{array}{*{20}{l}} S_A=-{\rm{Tr}}(\rho_A{\rm{ln}}\rho_A), \end{array} $

(1) where
$ \rho_A $ is the reduced density matrix by tracing B. Supposing the dimensions of$ {\cal{H_{A}}} $ and$ {\cal{H_{B}}} $ are$ d({\cal{H_{A}}})=d_{A} $ and$ d({\cal{H_{B}}})=d_{B} $ , respectively, the dimension of$ {\cal{H_{AB}}} $ is$ d({\cal{H_{AB}}})=d_{AB}=d_{A}d_{B} $ . Now, we intend to compute the average value of the entanglement entropy$ \langle S_A\rangle $ for random states in$ {\cal{H_{AB}}} $ . We must first find the uniform measure in$ {\cal{H_{AB}}} $ . For this purpose, we choose an orthogonal basis$ \{\vert{n}\rangle\} $ for a random state$ \vert{\psi}\rangle= \sum _{n=1}^{d_{AB}} c_{n} \vert{n}\rangle $ , and then the measure is just the uniform measure on the unit sphere of$ \mathbb{C}^{d_{AB}} $ , which is$ d\mu(\psi)=\delta(\sum _{n=1}^{d_{AB}} |c_{n}|^2-1) \prod_{n=1}^{d_{AB}} dc_n d\bar{c}_n $ .As a result, the average value of
$ S_A $ is obtained by integrating all the quantum states in the Hilbert space$ {\cal{H_{AB}}} $ $ \langle S_A\rangle=\int -{\rm{Tr}}(\rho_A{\rm{ln}}\rho_A) d\mu(\psi). $

(2) We can also transform the integration variables into eigenvalues of
$ \rho_A $ , the details of which can be found in [79]. The final result is$ \langle S_A \rangle= \Psi(d_{AB}+1)-\Psi(d_{B}+1)-\frac{d_{A}-1}{2d_{B}} $

(3) $\quad \quad\simeq \ln d_A-\frac{d_{A}}{2 d_{B}} ~\text { for }~ 1 \ll d_A \leq d_B, $

(4) where
$ \Psi(x)=\Gamma'(x)/\Gamma(x) $ is the so called Digamma function. The above result indicates that for a bipartite system described by pure states, the smaller subsystem is almost maximally entangled with the other subsystem. Therefore, the Page curve, which plots the entanglement entropy as a function of the size of the subsystem, first increases with the size of the subsystem up to its maximal value at$ d_A=d_B $ and then decreases with the size, because for a pure system, one always has$ \langle S_A \rangle=\langle S_B \rangle $ , which is now constrained by the size of the smaller subsystem B. Obviously, when the Hilbert space of the system is sufficiently large, the Page time is located at$ d_A=d_B $ , and the curve exhibits a symmetric behavior on both sides of the Page time. Note that this result is rooted at the uniform measure over the Hilbert space and thus does not depend on the details of evolution; in this sense, it may be treated as a model independent result. -
In a system with conserved charges, only the quantum states subject to these constraints are allowable, leading to a reduced Hilbert space that may be considerably smaller than the total Hilbert space. For instance, if a bipartite system contains a conserved charge
$ \hat{Q} $ , the total Hilbert space can be decomposed into the direct sum of the eigenspace of$ \hat{Q} $ ,$ {\cal{H_{AB}}=\sum\limits_Q{\cal{H_{AB}}}}(Q). $

(5) If the charge number Q is fixed and conserved in a system, only one sector needs to be considered:
$ {\cal{H_{AB}}}(Q) $ . One immediate difference for$ {\cal{H_{AB}}}(Q) $ is that it can no longer be factorized into the tensor product of two Hilbert spaces of the subsystems. Instead, it generally becomes the direct sum of the tensor products of the Hilbert spaces of subsystems with fixed charges,$ {\cal{H_{AB}}}(Q)=\sum\limits_{i=1}^{s} {\cal{H_{A}}}(q_i)\otimes{\cal{H_B}}(Q-q_i), $

(6) where s denotes the number of possible distributions of charges into two subsystems. In such a system, because
$ {\cal{H_{AB}}}(Q)\ne {\cal{H_A}}\otimes {\cal{H_B}} $ , more effort is required to ascertain the uniform measure over the Hilbert space. On account of the direct sum structure of$ {\cal{H_{AB}}}(Q) $ , we may write a random state in$ {\cal{H_{AB}}}(Q) $ as$ \vert{\psi}\rangle= \sum _{i=1}^s\sqrt{p_i} \vert{\phi_i}\rangle $ , with$ p_i\ge0 $ and$ \sum _{i=1}^s p_i=1 $ , where$ \vert{\phi_i}\rangle \in {\cal{H_{A}}}(q_i)\otimes{\cal{H_B}}(Q-q_i) $ . As for each distribution$ (q_i,Q-q_i) $ , the corresponding Hilbert space has the form of the tensor product. Therefore, in this situation, the entanglement entropy of subsystem A can be factorized into two parts,$ S_A=\sum\limits_{i=1}^s p_i(q_i) S_{A}(q_i)-\sum\limits_{i=1}^s p_i(q_i) \ln p_i(q_i). $

(7) Here,
$ S_A(q_i) $ represents the entanglement entropy within the factorized Hilbert space$ {\cal{H_{A}}}(q_i)\otimes{\cal{H_B}}(Q-q_i) $ for the state$ \vert{\phi_i}\rangle $ , which can be readily computed using the formula discussed in the previous subsection.The uniform measure is also factorized into two parts [79],
$ {\rm{d}} \mu_{Q}(\psi)={\rm{d}} \nu\left(p_{1}, \ldots, p_{s}\right) \prod\limits_{i=1}^s {\rm{d}} \mu\left(\phi_{i}\right)\,, $

(8) where
$ {\rm{d}} \nu\left(p_{1}, \ldots, p_{s}\right) $ is the multivariate beta distribution [79]. After the average integration, we obtain the final result for the average SR entanglement entropy [79]:$ \langle S_A \rangle_{ {}_Q}= \sum _{i=1}^s \frac{d_i}{d_{Q}} \big(\langle S_A(q_i) \rangle+\Psi(d_Q+1) -\Psi(d_i +1)\big), $

(9) where
$ d_i=d({\cal{H_{A}}}(q_i)\otimes{\cal{H_B}}(Q-q_i)) $ , and$ d_Q=\sum _{i=1}^sd_i $ . Then, in a similar manner as described in the previous subsection, we may obtain the SR Page curve as the sizes of A and B are changed. -
In this section, we consider a simple qubit model with conserved charges to simulate the evaporation of a charged black hole, with the assumption that the process of evaporation is unitary. As mentioned in Sec. I, based on the analysis of Hawking radiation and the Schwinger effect, charged black holes do not release their charge uniformly during evaporation [83]
3 . In fact, during evaporation, the black hole may undergo different phases depending on the black hole mass M and electric charge Q, as previously revealed in [8, 83]4 . Specifically, for the situations that are of primary interest in this study, when$ M> 2\times10^7M_{\odot} $ , where$ M_\odot $ denotes the mass of the Sun, the configuration space$ (M,Q) $ may be divided into two regions according to the characteristics of evaporation: the "mass dissipation zone" and "charge dissipation zone" [83]. When the charge-to-mass ratio of the black hole,$ Q/M $ , is considerably less than one and M is large, the black hole is in the "mass dissipation zone," and the black hole loses charges at a low rate${\rm d} Q(t)/{\rm d} M(t) < Q(t)/M(t)$ . Thus, the ratio$ Q(t)/M(t) $ becomes large as time t increases. Conversely, when$ Q/M $ is relatively close to one and M is small, the black hole is in the "charge dissipation zone," and the black hole loses charges via the Schwinger effect at the rate${\rm d}Q(t)/{\rm d}M(t) > Q(t)/M(t)$ such that the ratio$ Q(t)/M(t) $ decreases with the evaporation. As a result, if a charged black hole starts to evaporate from a certain region within the "mass dissipation zone", its electric charge may remain nearly unchanged until more than half of its mass is lost. Only when the mass decreases to an order similar to the charge (in natural units) will significant charge release begin and the black hole enter the "charge dissipation zone"5 . Therefore, we conclude that the non-uniform release of charge is a common phenomenon during the evaporation of charged black holes. Next, we apply a micro-level qubit model to simulate the evaporation of a charged black hole and propose refined rules to describe the charge release at a non-uniform rate and investigate how the Page curve in this scenario differs from that evaluated in the case with completely random states.We consider a qubit model composed of N qubits to simulate a charged black hole radiating out particles. We divide the system into two subsystems, A and B, corresponding to the radiation and charged black hole itself, respectively. For numerical analysis, we set the total number of qubits as
$ N=20 $ and require$ N_A+N_B=20 $ , where$ N_A $ and$ N_B $ are the number of qubits in A and B, respectively. Thus, the different partitions with$ N_A $ from$ 0 $ to$ 20 $ represent the different stages of evaporation from the initial state to the final state. The number$ N_B $ can be approximately considered a quantity analogous to the mass value M of the black hole, whereas$ N_A $ is the energy of radiation. Alternatively, because the black hole loses its mass and the energy of radiation becomes larger during evaporation, the number of qubits$ N_A $ may play a role in time as well. Next, we must introduce a quantity to simulate the charge of a black hole. Similar to the notion of spin, we assume each qubit may have a charge of either$ +1 $ or$ -1 $ ; hence, there is a 2-dimensional Hilbert space for each qubit. The total charge Q of the system is defined as the eigenvalue of the operator$ \hat{Q}=\sum _{i=1}^{N=20}{\sigma^i_z} $ .As a typical pattern of evaporation, we consider the system to have a total charge
$ Q=4 $ , which is used to simulate a black hole with an initially small charge-to-mass ratio. In the configuration with ($ N=20 $ ,$ Q=4 $ ), at the early stage of evaporation, subsystem B may fall into the “mass dissipation zone” due to$ Q_B\ll N_B $ . In this case, as a toy model, we stipulate that subsystem B does not release any charge until it shrinks to half its size, that is, to half the total number of qubits. This condition implies that when$ N_A $ is less than or equal to half of the total particles ($ \dfrac{N}{2} $ ), the Hilbert space of radiation is$ {\cal{H}}_A(q_i=0) $ , and correspondingly,$d({\cal{H_A}}(q_i=0))=\left(\begin{array}{*{20}{c}}{N_A}\\{{N_A}/{2}}\end{array}\right)$ . On the other hand, the Hilbert space of the black hole is$ {\cal{H}}_B(Q-q_i=4) $ , and correspondingly,$d({\cal{H_B}}(Q-q_i=4)) =\left(\begin{array}{*{20}{c}}{N-N_A}\\{(c{N-N_A+Q})/{2}}\end{array}\right)$ . After half of the black hole has evaporated, that is,$ N_A\ge \dfrac{N}{2} $ , we consider subsystem B to have entered the “charge dissipation zone” because$ Q_B/N_B $ is sufficiently large. For a qualitative description, we can require the charge to evaporate uniformly from the black hole afterward; therefore, the corresponding Hilbert space for radiation is${\cal{H_A}}\left(q_i= \dfrac{Q}{\left({N}/{2}\right)}\left(N_A-{N}/{2}\right)\right)$ with$ N_A $ from$ N/2 $ to N. Note that for a finite N, a technical problem may arise when$ N_A $ jumps to N with integer steps. For some$ N_A $ , the corresponding$q_i=\dfrac{Q}{\left({N}/{2}\right)} \left(N_A-{N}/{2}\right)$ is possibly not an integer; then, we must skip this step or demand its integer part be$ q_i $ . When plotting the figure to illustrate the evolution of entanglement entropy with small N, this may cause visible imprecision. However, we must emphasize that such imprecision does not appear anymore in the thermodynamic limit, which requires$N_{\rm th},\; Q_{\rm th}\rightarrow \infty$ , but keeping the ratio$\dfrac{Q_{\rm th}}{N_{\rm th}}= \dfrac{Q}{N}=\dfrac{4}{20}$ . We can simply follow the calculations mentioned above and then appropriately normalize the results.Now, we demonstrate our numerical results for
$ N=20 $ and$ Q=4 $ . For comparison, we depict the average charge and average entanglement entropy as functions of$ N_A $ for different patterns of evaporation in Figs. 1 and 2, respectively. In Fig. 1, three different patterns for the charge evaporation are shown. The blue dotted line represents the numerical results for$ N=20 $ , where we require that no charge is released before$N_A\le {N}/{2}$ , whereas after$N_A\ge {N}/{2}$ , the charge is released with a constant rate. The purple solid line represents the expected charge profile in the thermodynamic limit, with the same rules. It is noticed that for$ N=20 $ , the deviation from the case of thermodynamic limit with a perfect constant rate for$N_A\ge {N}/{2}$ is visible, but the deviation gradually disappears as N increases. As a comparison, the green dotted line represents another pattern, where the charge is released uniformly throughout the process of evaporation, which is obtained by computing the average value in the total Hilbert space$ {\cal{H_{AB}}}(Q=4) $ . Our main results are shown in Fig. 2, in which various Page curves are plotted for different patterns of evaporation. Evidently, in comparison with the Page curves with the random state approximation, the refined Page curves exhibit two prominent features. First, the refined Page time may shift from the middle point$ N_A=N/2 $ . Second, the refined Page curves exhibit asymmetric behavior on both sides of the Page time. Such features are understandable because, to match the non-uniform charge release from the black hole, we apply different rules to choose different sectors of the total Hilbert space before and after the middle point$ N_A= {N}/{2} $ , which disrupts the symmetry of the dimensions of the Hilbert space before and after the middle point NA = N/2. In addition, to construct the plot for$ N=20 $ (the blue dotted line), we apply an integer approximation to generate more data.
Figure 2. (color online) Average entanglement entropy
$ \langle S_A \rangle $ over random states with particle number$ N_A $ in subsystem A under different evaporation patterns. (i) Red solid line represents the average value over random states in the total Hilbert space$ {\cal{H_{AB}}}={\cal{H_A}}\otimes{\cal{H_B}}=\{\vert{-1}\rangle,\ \ \vert{ 1}\rangle\}^{\otimes 20} $ . (ii) The green dotted line represents the average value over random states in the Hilbert space$ {\cal{H_{AB}}}(Q=4) $ . (iii) The blue dotted line represents the average value over random states in the refined Hilbert space$ {\cal{H_{AB}}} $ . (iv) The purple solid line represents the average value over random states in the refined Hilbert space$ {\cal{H_{AB}}} $ in the thermodynamic limit, where the coordinates ($ N_a $ ,$ \langle S_A \rangle $ ) correspond to ($ N_a $ ,$ \langle S_A\rangle $ )$\times\frac{20}{N_{\rm th}}$ as a result of normalization.Note that we only consider some typical patterns of charged black hole evaporation with a specific set of parameters. One may also perform a similar analysis for other patterns (as mentioned in the first paragraph of Sec. III and footnote 4) with different discharge behaviors. Different constraints would need to be imposed on the original Hilbert space, and then, the reduced Hilbert space can be used to match different macroscopic evaporation patterns.
-
In this study, we apply symmetry-resolved entanglement entropy to plot the Page curve to understand the evaporation of charged black holes. Owing to the non-uniform rate of discharge during evaporation, we should not simply evaluate the average entanglement entropy over random states in a single Hilbert space for all time because this would lead to a uniform charge release. In a toy model, we compute the
$ SR $ entanglement entropy in a qubit system that simulates the charge distribution at different stages of evaporation for a charged black hole. After imposing restrictions on the Hilbert space of the system, we obtain a reduced Hilbert space for each stage of the evaporation and plot the refined$ SR $ Page curve for this qubit system. We observe that the refined$ SR $ Page curve exhibits two distinct features compared to the random cases, that is, it has a different Page time and displays asymmetric behavior on either side of the Page time.Although the qubit system as a toy model is too simple to describe the quantum states of a genuine charged black hole, we emphasize that considering the entanglement structure of random states in the qubit model grasps the essential idea of the unitary evolution of a quantum chaotic system, which exhibits a highly entangled behavior and may be viewed as analogous to a black hole. The refined SR Page curve obtained in this study matches the macroscopic phenomenon of the discharge during black hole evaporation and has helped to understand the release procedure of information from charged black holes at a microscopic level. Many aspects of this model can be improved in future. First, the analysis presented in this paper for charged black holes is somewhat qualitative. In a more realistic black hole, various types of particles may evaporate, the effects of which cannot be ignored. The evaporation rate for different particles can be derived from semi-classical calculations of radiation [8]. Second, to simplify the analysis, we only consider a linear relationship between charge and particle number release, whereas the actual quantitative relationship (e.g.,
${{\rm d}Q_A(t)}/{{\rm d}t}$ and${{\rm d}M_A(t)}/{{\rm d}t}$ ) would also depend on specific calculations of the details of the evaporation [81–83]. Third, it is also interesting to consider a system with multiple conserved charges, such as energy and angular momentum. We expect the Page curve will differ quantitatively in such situations. -
We are grateful to Kai Li, Wenbin Pan, Zhuoyu Xian, Zhangping Yu, and Hongbao Zhang for their helpful discussions. We also appreciate the anonymous reviewer for pointing out some ambiguous expressions in our previous manuscript.
Refined symmetry-resolved Page curve and charged black holes
- Received Date: 2023-11-06
- Available Online: 2024-05-15
Abstract: The Page curve plotted using the typical random state approximation is not applicable to a system with conserved quantities, such as the evaporation process of a charged black hole, during which the electric charge does not macroscopically radiate out with a uniform rate. In this context, the symmetry-resolved entanglement entropy may play a significant role in describing the entanglement structure of such a system. We attempt to impose constraints on microscopic quantum states to match the macroscopic phenomenon of charge radiation during black hole evaporation. Specifically, we consider a simple qubit system with conserved spin/charge serving as a toy model for the evaporation of charged black holes. We propose refined rules for selecting a random state with conserved quantities to simulate the distribution of charges during the different stages of evaporation and obtain refined Page curves that exhibit distinct features in contrast to the original Page curve. We find that the refined Page curve may have a different Page time and exhibit asymmetric behavior on both sides of the Page time. Such refined Page curves may provide a more realistic description for the entanglement between the charged black hole and radiation during the evaporation process.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: