-
Quantum complexity, a concept originating from quantum computation theory, is defined as the minimal number of quantum gates required to construct a target state from a reference state [1−5]. Complexity is believed to be a valuable tool for understanding the inside of a black hole horizon, particularly in addressing phenomena such as the firewall paradox and the horizon's transparency [6−9]. Properly defining complexity within the framework of quantum field theory has emerged as an interesting subject in research [10−16]. An alternative way to define complexity is through the geometric approach, which considers that lower bounds on the number of quantum gates may be provided by the length of the minimal geodesics of certain Finsler metric structures [17−23].
In contrast, according to the holographic principle [24−28], the complexity on the boundary field theory is dual to a gravitational quantity in the bulk, known as the holographic complexity. The first holographic dual, known as the complexity = volume (CV) conjecture, proposes that the holographic complexity is given by the regularized volume of the largest codimension on one surface crossing the Einstein Rosen bridge [29]. Another reliable proposal, known as the complexity = action (CA) conjecture, suggests that the holographic complexity is dual to the action of the Wheeler-DeWitt (WDW) patch, a specific spacetime region defined as the union of all spatial slices anchored at a given boundary time [30, 31]. Both of these conjectures have garnered significant attention and have been extensively investigated in numerous studies [32−56]. Nagasaki et al. recently conducted several studies on the influences of string velocity, horizon curvature, angular velocity, spacetime dimension, black hole mass, graviton mass, and Horndeski's parameters on the complexity growth, using the method of inserting a probe string in the bulk [57−64]. Considering that the case of charged black holes has not been explored, we extend previous research to investigate the complexity growth of charged hairy black holes, where, according to the holographic dictionary, introducing a charge to the black hole results in a corresponding chemical potential in the gauge theory.
In this study, we focus on an Einstein-Maxwell-scalar gravity system at finite temperature and chemical potential in D dimensions with charged hairy black hole solutions. Using the potential reconstruction method and appropriate choices for the gauge kinetic function and scale factor, this model can match the part features of the boundary strongly coupled gauge theory with real QCD. Our research aims to investigate the behavior of complexity growth in this model, assessing its capability to detect and characterize phase transitions and their corresponding phase structures. To study the complexity growth of this holographic QCD model, we introduce a probe fundamental string on the AdS spacetime. The effect of this string is given by the Nambu-Goto (NG) action, and we can investigate how the NG action growth is affected by the string velocity, chemical potential, and temperature, which is dual to the complexity growth from the CA conjecture.
The rest of this paper is organized as follows. In Sec. II, we review the Einstein-Maxwell-scalar gravity system in D spacetime dimensions. In Sec. III, we present the calculation for the NG action of the probe string and evaluate the effect of string velocity, chemical potential, and temperature on the NG action growth for the D = 4 and 5 cases. In the final section, we summarize our results and engage in further discussion.
-
In this section, we consider the holographic QCD model at finite temperature and chemical potential, previously investigated in [65, 66]. The following bulk action can be used to explore the Einstein-Maxwell-scalar system in D spacetime dimensions:
$ \begin{aligned}[b] \ S =& -\frac{1}{16\pi G_D }\int {\rm d}^D x \sqrt{-g} \Bigg [R-\frac{f(\phi)}{4}F_{MN}F^{MN}\\&-\frac{1}{2}\partial_M \phi \partial^M \phi-V(\phi) \Bigg]. \end{aligned} $

(1) $ {G_D} $ is the Newton constant in D dimensions, and it is fixed to one in the numerical computations. The field strength tensor of the$ U(1) $ gauge field$ A_M $ is denoted as$ F_{MN} $ . The potential of the scalar field ϕ is represented by$ V(\phi) $ , and the coupling between the scalar field and the$ U(1) $ gauge field is given by$ f(\phi) $ . To construct the charged hairy black hole solution, we adopt the following ansatz for the background metric, scalar field ϕ, and gauge field$ A_M $ [65]:$ \begin{aligned}[b] & {\rm d} s^{2}=\frac{L^2 {\rm e}^{2 P(z)}}{z^2} \left[ -g(z) {\rm d} t^2+\sum^{D-2}_{i=1} {\rm d} x_{i}^{2}+\frac{{\rm d}z^{2}}{g(z)} \right ],\\ & \phi=\phi(z),\ A_{M}=A_t (z)\delta^t_M. \end{aligned} $

(2) One can get the solution to the equations of motion from action (1), which can be summarized as follows:
$ \begin{aligned}[b] & \ A_t (z) = \widetilde{\mu} \int^{z_h}_z {\rm d}\xi \frac{{\rm e}^{-(D-4)P(\xi)}\xi^{D-4}}{f(\xi)},\\ \ &g (z) = 1+ \int^{z}_0 {\rm d} \xi {\rm e}^{-(D-2)P(\xi)} \xi^{D-2} [ C_{1}+K(\xi) ],\\ & C_{1}=-\frac{1+\displaystyle\int^{z_h}_0 {\rm d}\xi {\rm e}^{-(D-2)P(\xi)} \xi^{D-2} K(\xi)}{\displaystyle\int^{z_h}_0 {\rm d}\xi {\rm e}^{-(D-2)P(\xi)}\xi^{D-2}}, \end{aligned} $

$ \begin{aligned}[b] K(\xi)=&\int {\rm d}\xi \left[\widetilde{\mu}^2 \frac{\xi^{D-4}{\rm e}^{-(D-4)P(\xi)}}{L^2 f(\xi)} \right],\\ \phi(z)=& \int {\rm d} z \sqrt{2(D-2)\left[-P''(z)+P'(z)(P'(z)-\frac{2}{z})\right]}+C_{2},\\ V(z) = &-\frac{2z^{2}g(z) {\rm e}^{-2P(z)}}{L^2} \Bigg[\frac{(D-1)(D-2)}{2z^2}-\frac{3(D-2)}{4}\frac{g'(z)}{zg(z)}\\&+\frac{g''(z)}{4g(z)} +\frac{D-2}{2}P''(z) +(D-2)^2 \Bigg(-\frac{1}{z}+\frac{P'(z)}{2}\\&+\frac{3}{4(D-2)}\frac{g'(z)}{g(z)}\Bigg)P'(z)\Bigg], \end{aligned} $

(3) where z is the usual holographic radial coordinate, the horizon
$ z_h $ is determined by$ g(z_h)=0 $ , and the AdS radius L has been set to one. Here, we will choose the value of$ C_{2} $ such that ϕ approaches zero when it gets close to the asymptotic boundary$ z=0 $ . According to the holographic duality, the gauge field has the following near boundary behavior:$ A_t=\mu- \rho z^{D-3} $ , where the chemical potential and baryon density, respectively, are represented by μ and ρ. Based on the research in [65−67], our$ P(z) $ and$ f(z) $ will take the following form to give a good description of the QCD phenomenon$ \begin{array}{*{20}{l}} \ P(z)= -a\log(b z^2 +1), \ f(z)={\rm e}^{-(D-4)P(z)}. \end{array} $

(4) The parameters can be fixed as
$a=9.889,\; b=0.0358$ when D = 4, and$a=8.675, \; b=0.019$ when D = 5, while requiring the phase transition temperature$T_{\rm HP} = 270~\rm MeV$ at zero chemical potential for a pure gluon system. The D = 4 and 5 cases are only meant to be used as examples, and one can also study the case of higher dimensions. From the metric, the Hawking temperature, which would be the temperature of the D-dimensional system, ought to be$ \begin{aligned}[b] T=&\frac{z^{D-2}_h {\rm e}^{-(D-2)P(z_{h})}}{4\pi} \\&\times\Bigg[-K(z_h)+\frac{1+\displaystyle\int^{z_h}_0 {\rm d}\xi {\rm e}^{-(D-2)P(\xi)} \xi^{D-2} K(\xi)}{\displaystyle\int^{z_h}_0 {\rm d}\xi {\rm e}^{-(D-2)P(\xi)}\xi^{D-2}}\Bigg]. \end{aligned} $

(5) In this study, the phase transition temperature is fixed to study the complexity growth in D dimensions around the phase transition temperature.
-
Using the strategy in [57], in this section, we present an analysis of the NG action growth in the Einstein-Maxwell-scalar system with a probe string, which is a dual description of the complexity growth according to the CA conjecture. Now, we explore the effect of string motion in this spacetime geometry, for which we use the parameters τ and σ of the worldsheet as follows:
$ \begin{array}{*{20}{l}} \ t=\tau,\ \ r=\sigma, \ \phi=v\tau+\xi(\sigma). \end{array} $

(6) Here, the function
$ \xi(\sigma) $ specifies the shape of the string, and υ is the string velocity relative to the black hole. By integrating the square root of the determinant of the induced metric over the WDW patch, we obtain the time derivative of the NG action$ \begin{aligned}[b] \frac{{\rm d} S_{\rm N G}}{{\rm d} t}=&T_{s} \int_{z_{h}}^{\infty} {\rm d} \sigma \sqrt{-g_{\text {ind }}(\sigma)}\\=&T_{s} \int_{z_{h}}^{\infty} {\rm d} \sigma \sqrt{-g_{t t} g_{z z}-g_{z z} g_{x x} v^{2}-g_{t t} g_{x x} \xi^{\prime 2}}, \end{aligned} $

(7) where
$g_{tt}= -\dfrac{L^2 {\rm e}^{2 P_s(z)}}{z^2} g(z)$ ,$g_{xx}=\dfrac{L^2 {\rm e}^{2 P_s(z)}}{z^2}$ , and$g_{zz}= \dfrac{L^2 {\rm e}^{2 P_s(z)}}{z^2} \dfrac{1}{g(z)}$ .$ T_{s} $ is the fundamental string tension. The equation of motion for ξ is obtained by varying the above action:$ \frac{{\rm d}}{{\rm d} \sigma}\left(\frac{-g_{t t} g_{x x} \xi^{\prime}}{\sqrt{-g_{t t} g_{z z}-g_{z z} g_{x x} v^2-g_{t t} g_{x x} \xi^{\prime 2}}}\right)=0. $

(8) We define a constant as follows:
$ \ \Pi_{\xi}=\frac{-g_{tt}g_{xx} \xi'}{\sqrt{-g_{tt}g_{zz}-g_{zz}g_{xx}\upsilon^2-g_{tt}g_{xx}\xi'^{2}}}, $

(9) and
$ \xi'^{2} $ can now be resolved as$ \xi'^{2}=\frac{-g_{zz}(g_{tt}+g_{xx} \upsilon^2)\Pi^2_{\xi}}{g_{tt}g_{xx}(g_{tt}g_{xx}+\Pi^2_{\xi})}. $

(10) The numerator and denominator have to change signs at the same position. However, under this condition, we can find the critical point as
$ \begin{array}{*{20}{l}} \ g_{tt}(z_{c})=-g_{xx}(z_{c})\upsilon^2, \end{array} $

(11) and
$ \begin{array}{*{20}{l}} \ \Pi^2_{\xi}=-g_{tt}(z_{c})g_{xx}(z_{c}). \end{array} $

(12) By substituting the Eqs. (10), (11), and (12) into Eq. (7), the growth of the action can be expressed as
$ \frac{{\rm d} S_{N G}}{{\rm d} t}=T_s \int_{z_h}^{\infty} {\rm d} \sigma \sqrt{-\frac{g_{tt} g_{x x} g_{z z}\left(g_{t t}+g_{x x} v^2\right)}{g_{t t} g_{x x}+\left(g_{x x}\left(z_c\right)\right)^2 v^2}}. $

(13) We numerically solve the integral (13) and show how the string velocity, chemical potential, and temperature affect the NG action growth in D dimensions, as shown in the following figures.
As illustrated in Fig. 1, the correlation between the action growth and the string velocity at different chemical potentials can be analyzed. Notably, an increase in the chemical potential and a slower string movement leads to a larger action growth, while a faster string movement results in a reduced effect. The action growth reaches its maximum when the string velocity is zero, which means it is stationary. Several previous studies [57−64] have also observed a similar phenomenon. Additionally, a larger chemical potential results in a higher peak value of the action growth. As the dimension grows, the velocity dependent action growth becomes more gentle, resulting in a smoother slope. It can be inferred that in higher dimensions, the impact of the probe string is less sensitive.
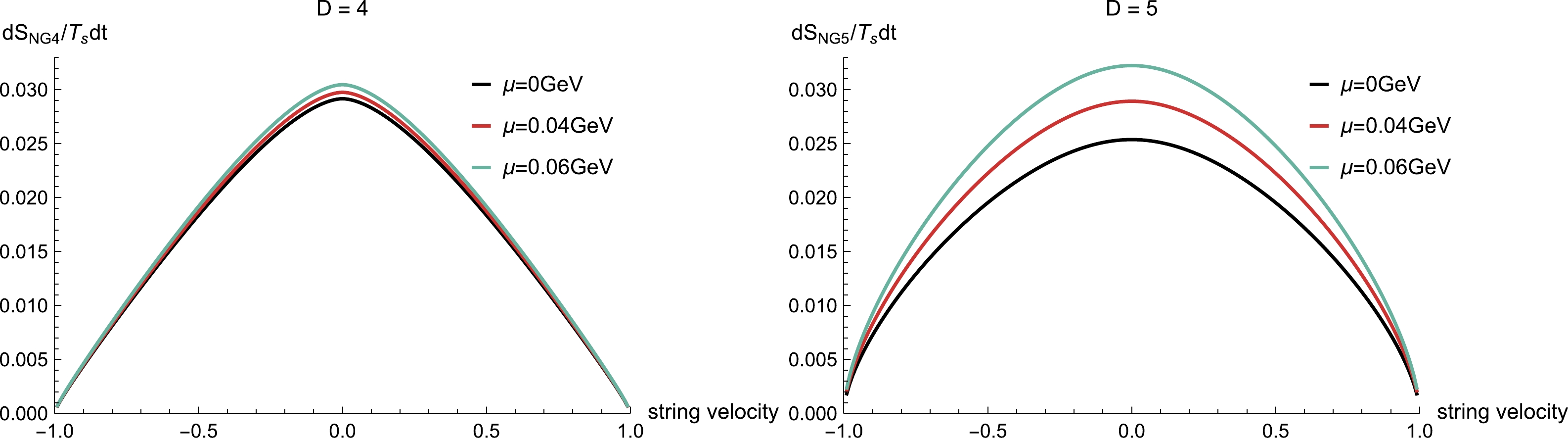
Figure 1. (color online) The action growth versus string velocity for different chemical potentials when
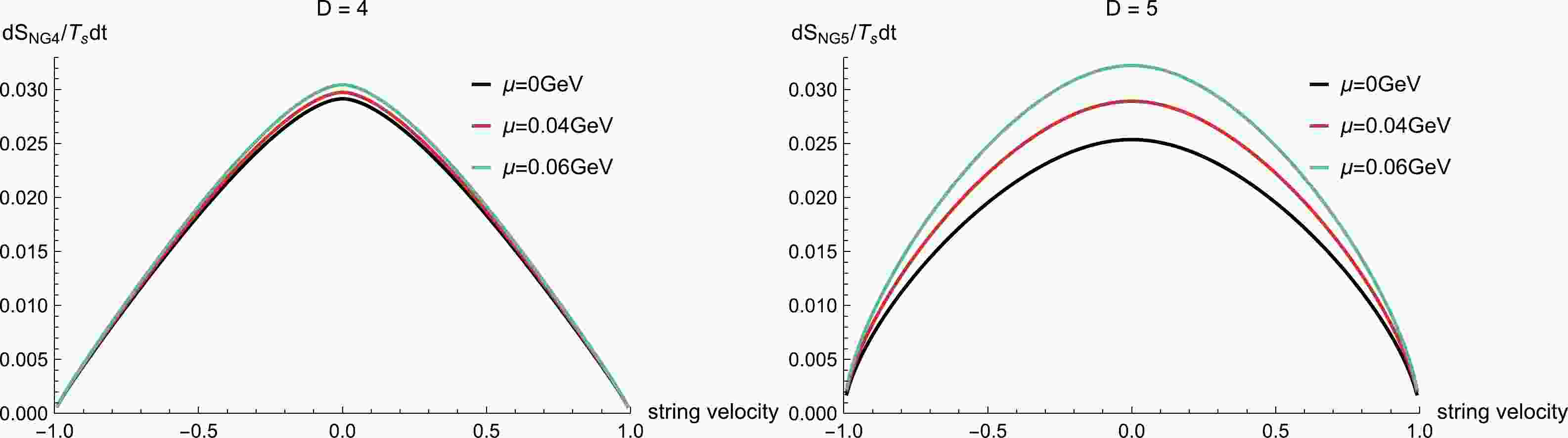
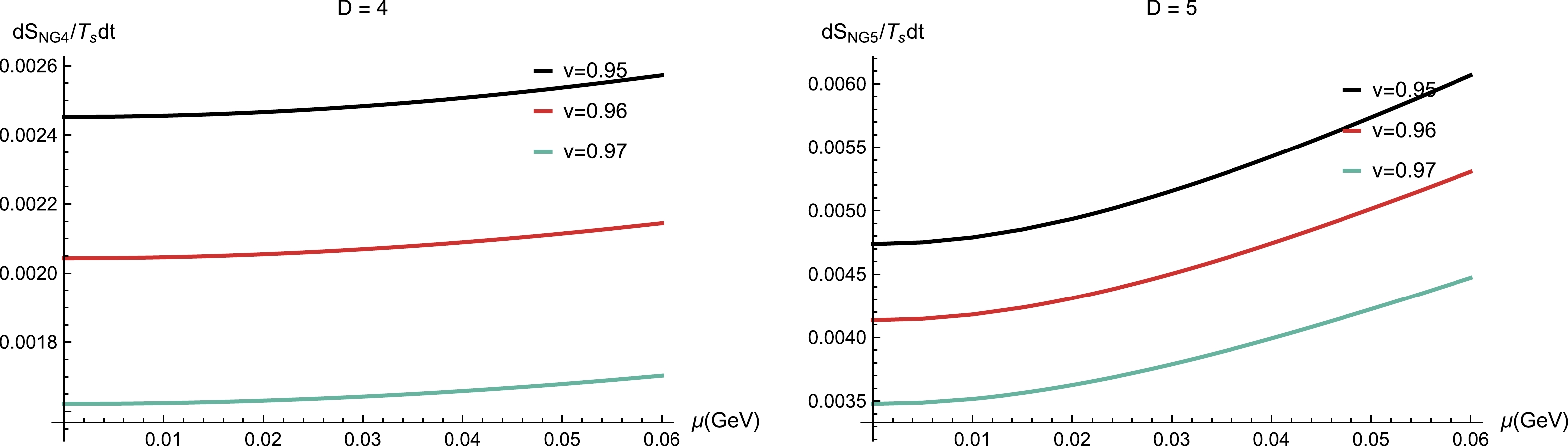
$T=0.27~\rm GeV$ in the D = 4 and 5 cases.The study presented in Fig. 2 demonstrates how action growth depends on the chemical potential for different string velocities close to the speed of light. The observed data suggests that a faster string results in smaller action growth, which agrees with the findings shown in Fig. 1. As a function of the chemical potential, in the vicinity of light speed, the action growth always increases monotonically. Fig. 3 shows how the action growth varies with the temperature for a fixed chemical potential when D = 4 and 5. Near the critical temperature, the action growth exhibits a multi-valued behavior within the range
$ 0<\mu<\mu_c $ , indicating the presence of a first-order phase transition. However, for$ \mu \geq \mu_c $ , it is single-valued, reflecting a shift from phase transition to crossover. Our results indicate a decrease in the phase transition temperature corresponding to increased chemical potential, which agrees with the lattice QCD results [68]. In addition, we notice that the action growth values are enhanced by the chemical potential for the D = 4 and 5 cases. Moreover, Fig. 3 reveals a remarkable similarity between complexity and thermal entropy, as illustrated in Fig. 10 of [66], potentially attributable to complexity’s behavior, which is similar to entropy, in satisfying the second law of thermodynamics [69]. -
In this study, we investigate the holographic complexity growth within a D-dimensional QCD model with a planar horizon, utilizing various consistent metric solutions previously explored in Refs. [65, 66]. This holographic model is an Einstein-Maxwell-scalar system that adopts suitable forms of the scale factor, gauge kinetic function, and optimized parameter values to fit the lattice results and reproduce the confinement/deconfinement transition. Our method involves using a probe string in the bulk background, contributing an NG term to the total action. We studied the growth of the NG action and its dependence on the string velocity, chemical potential, and temperature, which correspond to the complexity growth via the CA conjecture.
Here, we present the main findings of our study as follows. The complexity growth of the system is observed to be maximized when the probe string is at rest. As the velocity of the string increases, the complexity growth declines. This phenomenon is consistent with the results of previous studies [57−64], suggesting that it is a universal property of complexity. Moreover, the maximal value of the complexity growth rises with the chemical potential. With an increase in dimensionality, the rate of change in the complexity growth becomes more gradual. When approaching relativistic velocities, the complexity growth exhibits a monotonic increase as a function of the chemical potential. Furthermore, we investigate how the growth of complexity depends on the temperature at a fixed chemical potential and examine whether it reflects the phase transition when D = 4 and 5. Our results reveal that the growth of complexity exhibits a multi-valued behavior close to the transition temperature when
$ 0<\mu<\mu_c $ , while it displays a single-valued behavior for$ \mu \geq \mu_c $ , indicating the first-order transition becomes a crossover. The findings of our study suggest that complexity growth may serve as a special probe to characterize phase transitions, thereby contributing to a more comprehensive understanding of the phase structure.In heavy-ion collision experiments, particularly in non-central collisions, the emergence of a strong magnetic field and substantial angular momentum has been observed, highlighting the necessity of studying the complexity growth of nonzero total angular momentum and magnetic fields within the holographic model, which is a topic we aim to delve into in forthcoming research [70−73].
-
We thank Zi-qiang Zhang, Xun Chen, and Zhou-Run Zhu for their fruitful discussions.
Complexity growth in a holographic QCD model
- Received Date: 2023-10-10
- Available Online: 2024-03-15
Abstract: In this study, we utilize the complexity-action duality to study the evolution of complexity in a holographic QCD model at finite temperature and chemical potential. By inserting a fundamental string as a probe, we investigated the properties of complexity growth in this Einstein-Maxwell-scalar gravity system, which is affected by the string velocity, chemical potential, and temperature. Our results show that the complexity growth is maximized when the probe string is stationary, and it decreases as the velocity of the string increases. When the string approaches relativistic velocities, the complexity growth always increases monotonically with respect to the chemical potential. Furthermore, we find that the complexity growth can be used to identify phase transitions and crossovers in the model.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: