-
In recent years, there has been a lot of interest in studying the effects of breakdown on fusion reactions in heavy-ion collisions at the Coulomb barrier [1–3]. The total fusion cross-section is the sum of complete fusion (CF) and incomplete complete fusion (ICF) cross-sections. ICF is the sum of sequential complete fusion (SCF) and direct complete fusion (DCF). If all the projectile fragments fuse with the target, then it is said to be SCF. DCF is the process by which a complete projectile fuses with the target without any breakup. From an experimental perspective, an SCF cannot be distinguished from a DCF.
Experimental measurements of ICF and CF cross sections are challenging. During the cooling process, the excited compound nucleus releases charged particles, which is especially important in light reaction systems. Only the TF cross-section may be measured since the residues from ICF and CF cannot be differentiated. The decay of the excited compound nucleus through the emission of charged particles can be insignificant in heavy reaction systems, allowing for independent CF cross-section measurements. Experimentally, CF cross-sections have been measured [4–9].
Earlier researchers [10] investigated heavy-ion fusion cross sections from 16O+18O to 64Ni+124Sn at extreme sub barrier energies with a simple formula. Umar et al. [11] uncovered evidence of the barrier's energy dependency by comparing fusion cross-sections estimated from potentials, i.e., density-constrained n time-dependent Hartree-Fock approach obtained at different bombarding energies, with experimental data. The cold fusion reactions with
$ 104\le Z\le 112 $ show larger fusion cross-sections below the bass barrier with 9−15 MeV of excitation energy [12, 13]. Rajbongshi et al. [14] investigated the role of the hexadecapole deformation effect of nuclei in the lanthanide region near the sub-barrier fusion cross-sections. Sub-barrier fusion reactions enhance the production cross-sections [15, 16].Rowley and Hagino [17] examined the fusion cross sections of l60+154Sm and 12C+12C with generalized Wong and Hill-Wheeler formulae. Sedykh [18] proposed an empirical relation for the fusion cross-sections of heavy ions. Chushnyakova et al. [19] evaluated heavy ion fusion cross-sections with Hartree-Fock nuclear densities. Earlier studies show a detailed investigation of entrance channel parameters, deformation effect of projectile-target, optimal energy, possible projectile-target combinations, and rules for the selection of projectile-target combinations [20–30]. The production cross section has been measured for the fusion reaction of the 16O+27Al system at different bombarding energies using the time-of-flight technique [31]. Fusion processes are distinguished by their fusion cross-sections, described by three energy-dependent functions: Gamow-Sommerfield, geometric, and astrophysical S-factors [32]. Hence, the main aim of the present work is to propose an empirical relation for the astrophysical S-factor for 40,48Ca-induced fusion reactions. The fusion cross-sections obtained using three energy-dependent functions are compared with those of the available experimental data and fusion cross-sections obtained using Wong's formulae.
-
The fusion cross-section in terms of energy-dependent factors such as geometric, Gamow-Sommerfield, and astrophysical S-factor [33] is expressed as
$ \sigma_{\rm fus}(E)=\phi(E)G(E)S(E). $

(1) Here, the geometric factor ϕ term is inversely proportional to particle energy. G(E) is the Gamow-Sommerfield factor, which is the penetration factor. Further, the S-factor, also known as the astrophysical S-factor, is a strong energy-correlated quantity dependent on the boundary conditions between the nuclear potential and the Coulomb electrostatic field.
-
In the majority of the fusion cross-section expressions,
$ \phi=\dfrac{1}{E} $ . It is also denoted by the area occupied by a de-Broglie wavelength$ \rlap-{\lambda} $ or wavenumber k, which varies with energy and is expressed as$ \phi(E)=\pi\rlap-{\lambda}^2=\frac{\pi}{k^2}, $

(2) where
$ k=\sqrt{2\mu E/\hbar} $ and$ \mu = m_1m_2/(m_1+m_2) $ is the reduced mass of the system. The term$ \phi(E) $ in terms of two independent terms is expressed as$ \phi(E)=\pi\left(\frac{\hbar^2}{2\mu}\right)\frac{1}{E_{\rm cm}}. $

(3) -
The Gamow-Sommerfield factor G(E) is a penetration factor of the Coulomb barrier by the incident particle that characterizes the likelihood of incident/target nuclei undergoing fusion. It is represented by an exponential attenuation function [34] expressed as
$ G(E)=\frac{1}{\chi^2}={\rm exp}(-2\pi\eta_l), $

(4) the term
$ \eta_l $ in the above equation is the Sommerfield parameter, and it is expressed as$ \eta_l=\frac{1}{\pi}\int_{r_n}^{r_{\rm tp}}\left|k_l(r)\right|{\rm d}r, $

(5) where
$ k_l(r) $ is the wave number inside the nuclear well given by$ k_l(r)=\left[\frac{2\mu}{\hbar^2}(E-U(r))\right]^{1/2}, $

(6) here,
$ r_n $ and$ r_{tp} $ are the classical turning points. Under relativistic conditions, Eq. (4) [35] reduces as follows:$ G(E)=\frac{2\pi}{{\rm exp}(2\pi/ka_c)-1}, $

(7) here,
$a_c=\dfrac{\hbar^2}{k_eZ_1Z_2\mu {\rm e}^2}$ with$ k_e=\dfrac{1}{4\pi\epsilon_0} $ -
The S-factor is a function that characterizes the width and energy of a nuclear reaction's resonance peaks. According to Miley et al. [32], the S-factor for light projectiles, such as T(d, n)4He, 3He(d, p)4he, D(d, p)T, D(d, n)3He, T(t, 2n)4He, T(
$ {}^{3}, X)Y^* $ , and 11B(p, 24He)4He is defined as follows:$ S(E)=\frac{A_2}{(A_4-A_3E)^2+1}+A_5, $

(8) here,
$ A_2 $ ,$ A_3 $ ,$ A_4 $ . and$ A_5 $ are fitting constants [32]. However, in the present work, we have used experimental fusion cross-sections to evaluate the S-factor as follows;$ S(E)= \frac{\sigma_{\rm fus}}{G\phi}, $

(9) here,
$\sigma_{\rm fus}$ is the experimental fusion cross-section for 40,48Ca-induced fusion reactions. Further, the S-factor is studied as a function of entrance channel parameters. -
In constructing the empirical formulae, we considered about 22 fusion reactions with 40,48Ca as projectiles. These reactions are available in the existing literature [36–50]. The atomic and mass numbers of the compound nuclei vary between
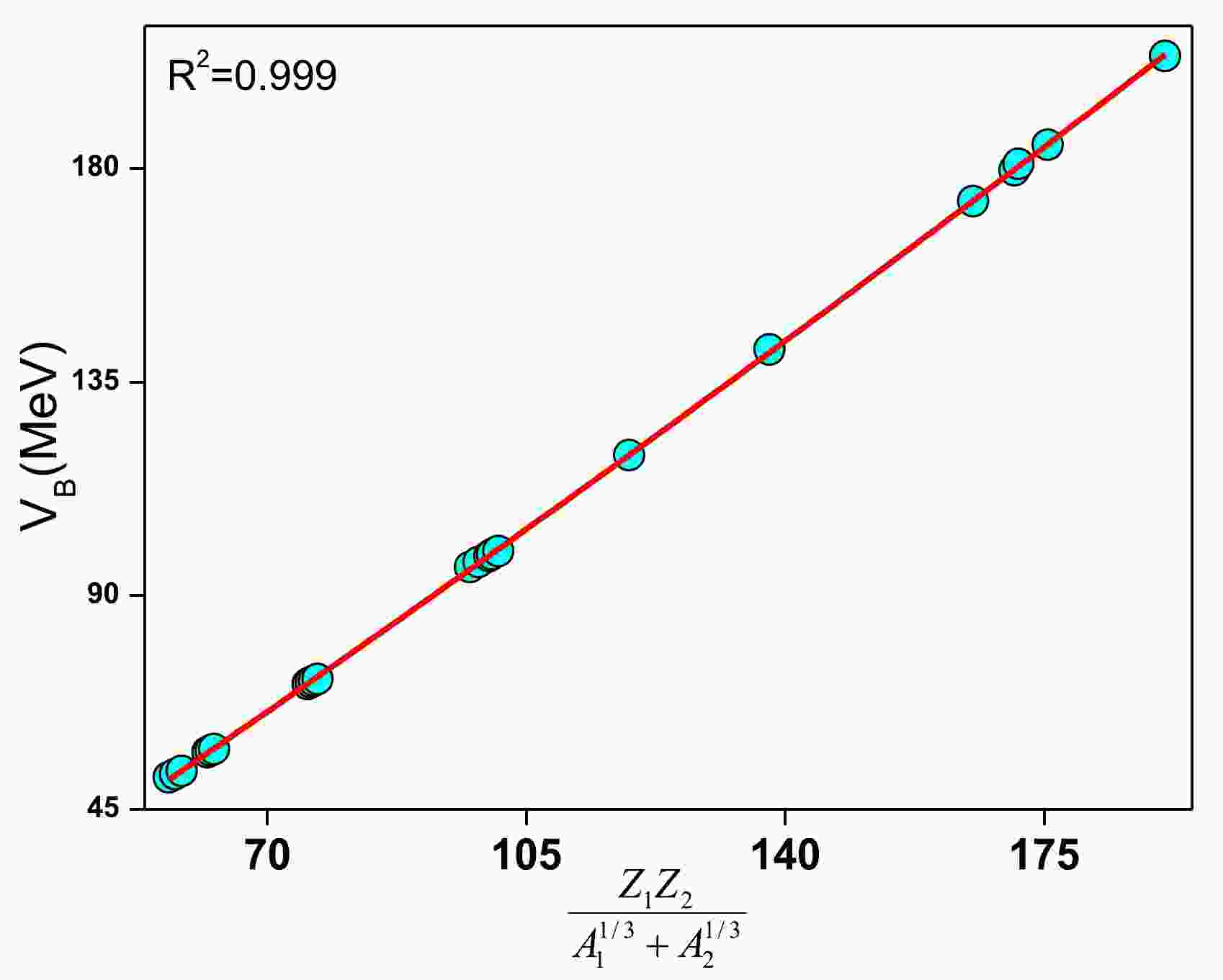
$ 40\le Z \le 112 $ and$ 88\le A\le 278 $ , respectively.The fusion barrier heights of 40,48Ca-induced fusion reactions are taken from nrv data [51]. Then, we plotted
$ V_{B} $ as a function of$ \dfrac{Z_1Z_2}{A_{1}^{1/3}+A_2^{1/3}} $ , as represented in Fig. 1. The scatter symbol represents the fusion barrier height for 48Ca-induced fusion reactions. The continuous line specifies the fitted equation for$ V_B $ as follows: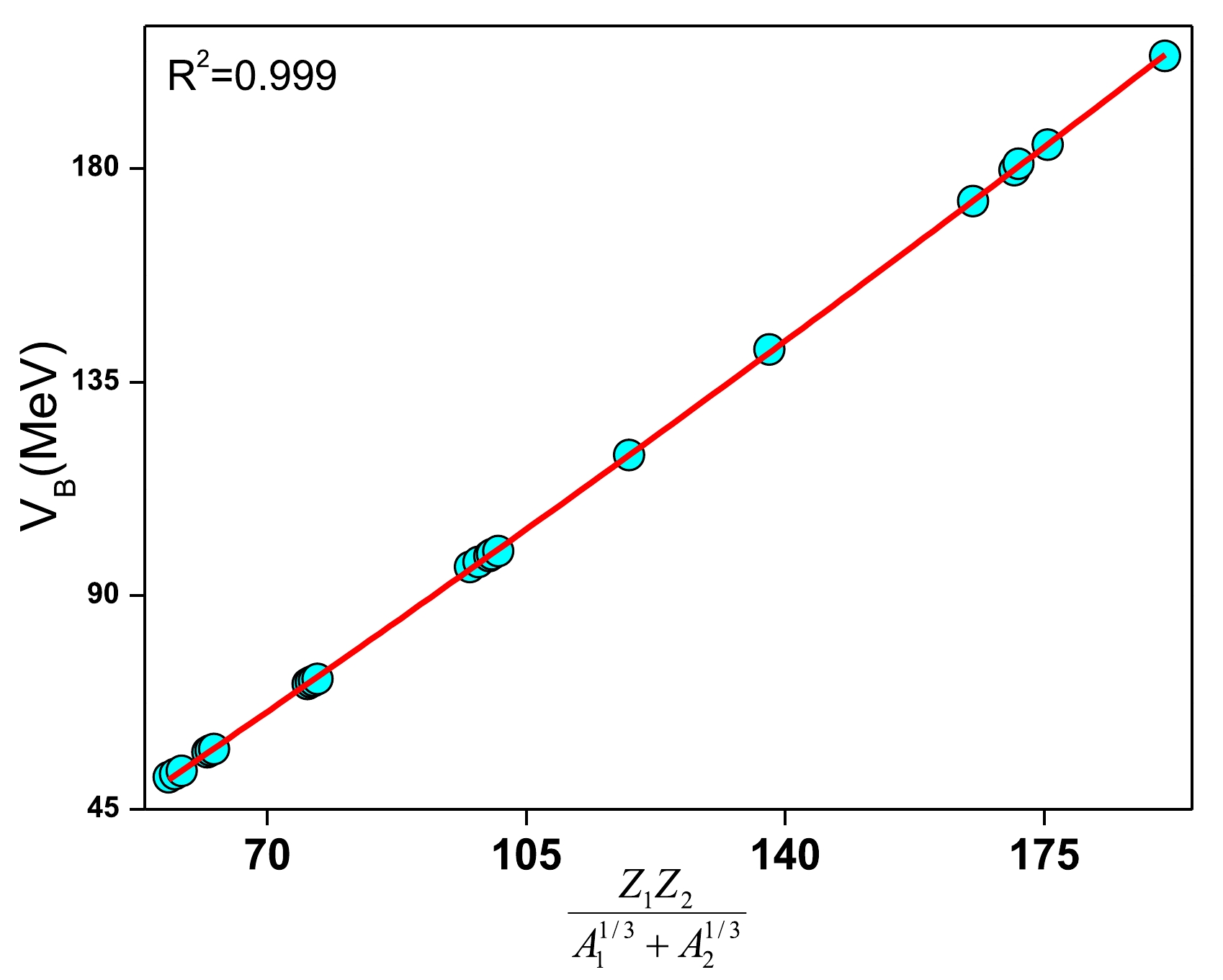
Figure 1. (color online) A plot of fusion barrier (
$ V_B $ ) as function of the Coulomb interaction parameter.)$ V_B=-7.62454+1.01166z+4.92881\times 10^{-4}z^2, $

(10) here,
$Z={Z_1Z_2}/({A_{1}^{1/3}+A_2^{1/3}})$ . The coefficient of determination is found to be$ R^2=0.999 $ , and$ R^2 $ is explained in detail in the following paragraph. Hence, the target fusion barriers are evaluated most accurately by simply inputting the atomic and mass number of the projectile and target fusion barriers is evaluated most accurately. In all our further investigations, we considered the above empirical relation for$ V_{B} $ . As an illustration, we considered the fusion reaction of 40Ca+46Ti and plotted the astrophysical S-factor as a function of$E_{\rm cm}/V_B$ [47], as shown in Fig. 2. The value corresponding to the S-factor increases exponentially and reaches a maximum value as$E_{\rm cm}/V_B$ increases. Hence, we tried to fit a suitable equation, i.e., a third-order polynomial equation fitted for S-factor values. The fitted equation as a function of$E_{\rm cm}/V_B$ is as follows;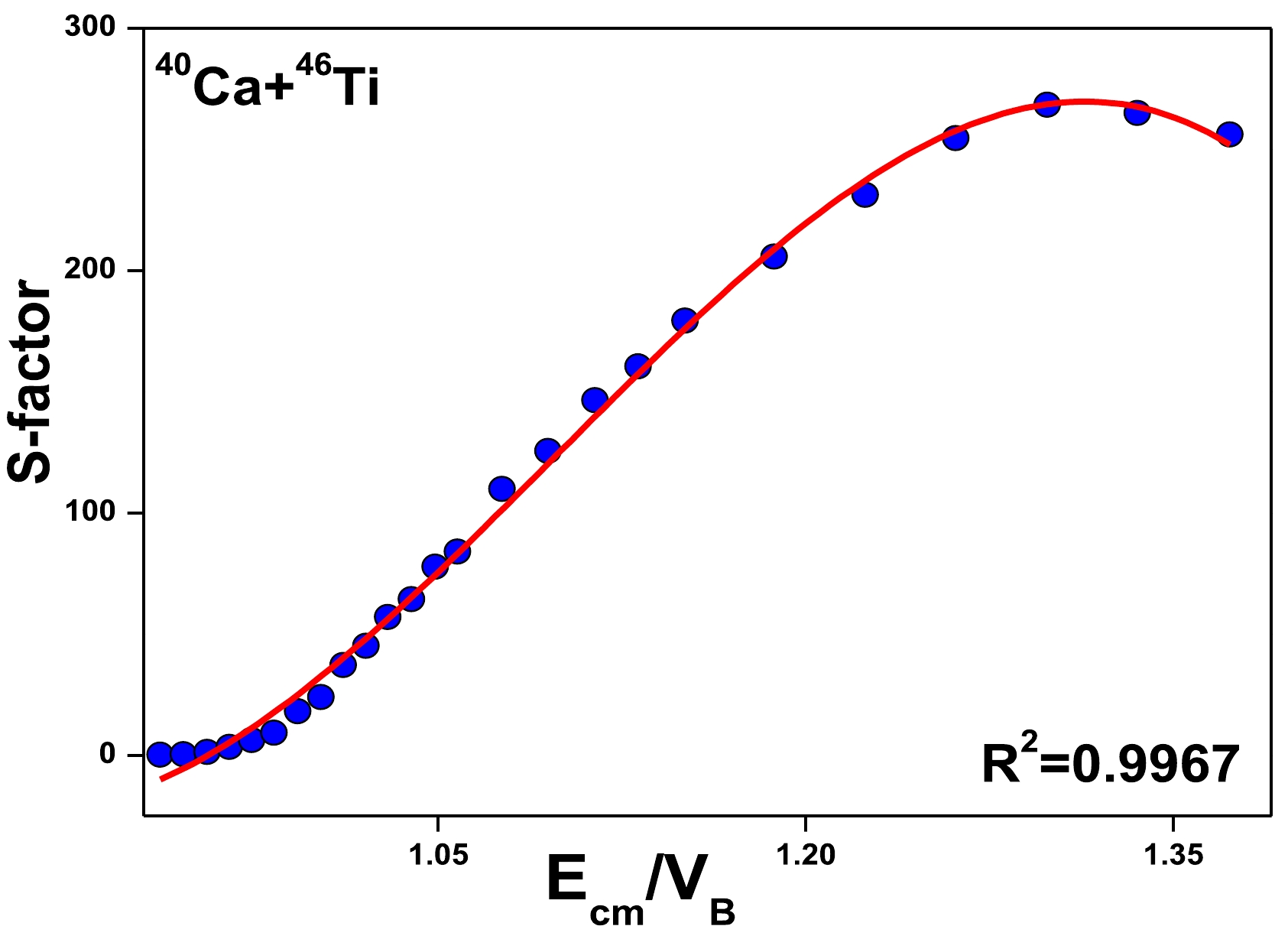
Figure 2. (color online) A plot of the astrophysical S-factor as a function of
$E_{\rm cm}/V_B$ for the fusion reaction of 40Ca+46Ti. The hollow circle specifies the S-factor obtained using experimental fusion cross-sections, and the continuous red line corresponds to the fitted equation.$ \begin{aligned}[b] S(E)^{PF}=&B_0+B_1\times \left(\frac{E_{\rm cm}}{V_B}\right)+B_2\times \left(\frac{E_{\rm cm}}{V_B}\right)^2\\&+ B_3\times \left(\frac{E_{\rm cm}}{V_B}\right)^3, \end{aligned} $

(11) here,
$ B_0 $ ,$ B_1 $ ,$ B_2 $ , and$ B_3 $ are the fitting constants. The hollow circle specifies the S-factor obtained using experimental fusion cross-sections, and the continuous red line corresponds to the fitted equation. The fitted equation is such that the coefficient of determination$ R^2\approx 1 $ . Where$ R^2=1-\dfrac{\sum_{i=1}^n(\hat y_i-y_i)^2}{\sum_{i=1}^n(y_i-\bar y_i)^2} $ . Here,$ y_i $ is the S-factor obtained using experimental fusion cross-sections,$ \bar y_i $ is the average value, and$ \hat{y}_i $ is the value obtained from the present fitted equation. If the value of$ R^2 $ is close to one, it means that the value produced from the present fit is comparable to the value obtained for the S-factor using$\sigma_{\rm fus}$ , Gamow-Sommerfield factor, and geometric factor. Accordingly, we obtained$ R^2=0.9967 $ for the fusion reaction of 40Ca+46Ti. Similarly, we explored all possible experimentally available 40,48Ca-induced fusion reactions available in the literature.Further, we emphasize the geometric factor, Gamow Sommerfield factor, S-factor, and fusion cross-sections as a function of
$E_{\rm cm}$ for the fusion reaction of 40Ca+46Ti. Figure 3 (a)−(d) shows three dependent factors: ϕ,$ G(E) $ , and S-factor on the fusion cross-sections. Figure 3 (d) corresponds to the fusion cross-sections obtained using S-factor, G(E), and ϕ as a function of$E_{\rm cm}$ . From the figure, the ϕ noticeably decreases with an increase in$E_{\rm cm}$ . Whereas, in the case of$ G(E) $ , the S-factor and$\sigma_{\rm fus}$ gradually increase with an increase in$E_{\rm cm}$ . Further, we extended our studies to all 40,48Ca-induced fusion reactions available in the literature [36–50]. Further, we gathered all fitting constants of 40,48Ca-induced fusion reactions, and these fitting constants were again plotted as a function of different entrance channel parameters. The different entrance channel parameters [25]: mass asymmetry$ \eta_A $ , charge asymmetry$ \alpha_Z $ , iso-spin asymmetry$ \Delta(N/Z) $ , charge product$ Z_1Z_2 $ , Coulomb interaction parameter$ (Z_1Z_2)/(A_1^{1/3}+A_2^{1/3}) $ , mean fissility$ \chi_m $ and$ Z^2/A $ . The plot of$ B_0 $ ,$ B_1 $ ,$ B_2 $ and$ B_3 $ , a function of the Coulomb interaction parameter (z), shows more systematic variation than all other studied entrance channel parameters. The best suitable fit corresponds to a fourth-order polynomial function. Consequently, we have fitted an empirical relation for$ B_0 $ ,$ B_1 $ ,$ B_2 $ , and$ B_3 $ as a function of the Coulomb interaction parameter, and it is given by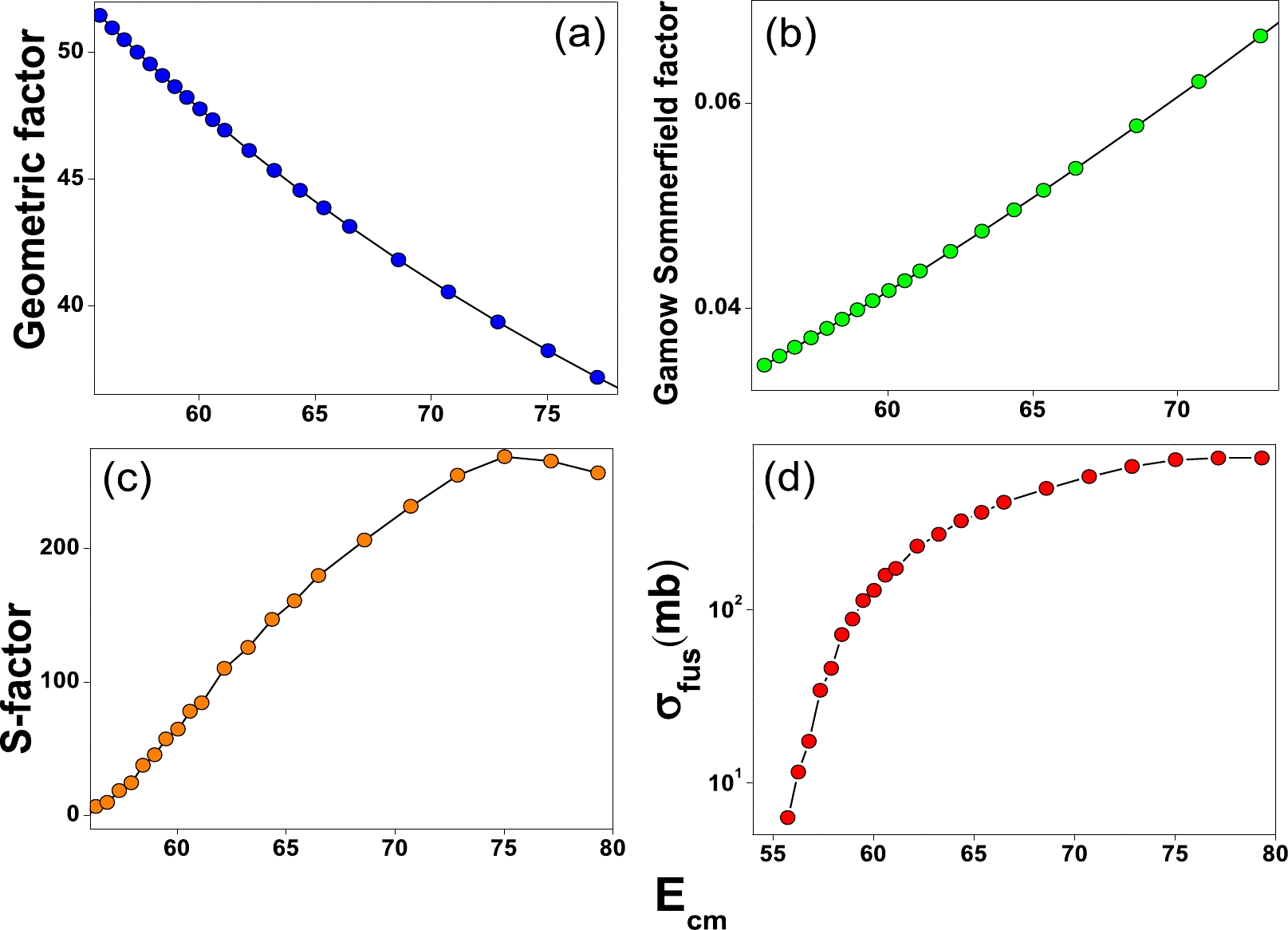
Figure 3. (color online) (a) Geometric factor, (b) Gamow Sommerfield factor, (c) astrophysical S-factor, and (d) fusion cross-sections as a function of the center of mass-energy for the fusion reaction of 40Ca+46Ti.
$ \begin{aligned}[b]& B_{0}=\sum_{i=0}^{4}B_{i0}z^i, \quad B_{1}=\sum_{i=0}^{4}B_{i1}z^i, \\& B_{2}=\sum_{i=0}^{4}B_{i2}z^i,\quad B_{3}=\sum_{i=0}^{4}B_{i3}z^i, \end{aligned} $

(12) here,
$ B_{i0} $ ,$ B_{i1} $ ,$ B_{i2} $ , and$ B_{i3} $ are the fitting constants whose values are tabulated in Table 1.Parameters Coulomb interaction regions $56.70\leq{}z\leq{}62.37$ 

$62.83\leq{}z\leq{}76.80$ 

$97.40\leq{}z\leq{}101.24$ 

$118.95\leq{}z\leq{}165.41$ 

$169.40\leq{}z\leq{}191.32$ 

B00 −28332537697.0978 −64435938215.0135 2203255720.78296 −656384034.537705 718103288.995812 B10 1899266991.06486 3565880041.22783 −89697465.9448795 18672321.6099274 −16198443.3275908 B20 −47716329.8469277 −73813845.3711374 1369263.5571222 −198214.503445243 136937.60578956 B30 532495.452482732 677530.491177697 −9289.07320486588 930.717074241155 −514.173351049124 B40 −2227.14309130892 −2327.24022733404 23.6292964092531 −1.63119412248294 0.723493714869457 B01 74155501865.1684 179936541485.059 −8062716463.75572 1013137999.93127 −2274900515.76646 B11 −4969960187.56886 −9957975694.56154 327450781.216016 −28819904.5885794 51341614.3086018 B21 124836976.199133 206136910.648799 −4986709.86432899 305920.755546077 −434246.147680954 B31 −1392842.15972741 −1892172.76748474 33749.8813175876 −1436.37270074054 1631.30728770228 B41 5824.31016914153 6499.61337173533 −85.6514768172259 2.51726251217576 −2.29651664486989 B02 −64538359422.0306 −166944972987.738 9503015946.60498 −521686292.017596 2360492170.49599 B12 4324462380.47212 9239263377.64448 −385301520.830439 14839439.5263792 −53294534.9065123 B22 −108599446.500798 −191264697.071673 5857989.12492678 −157510.753257383 450940.31810073 B32 1211412.51240851 1755710.90176198 −39581.4376985516 739.500655641065 −1694.67147551589 B42 −5064.55339797348 −6031.05442556466 100.286858383963 −1.29588145351538 2.38661560001902 B03 18836106053.3082 51455405399.732 −3630526068.45853 89644054.0631107 −806569328.034477 B13 −1261880703.88212 −2847777630.14262 147025738.783876 −2549897.67189143 18216456.6717986 B23 31683084.9748326 58954239.6708472 −2232687.02980118 27064.1525036251 −154184.167008323 B33 −353351.05279423 −541184.190230803 15068.1373241659 −127.05460664328 579.619434940112 B43 1476.96725249418 1859.07766520354 −38.1331586988069 0.222625894265698 −0.816532819909371 Table 1. Tabulation of fitting constants for different Coulomb interaction regions.
With the benefit of the empirical formula for the S-factor and derived fusion barrier height, we extend our studies to reproduce experimental fusion cross-sections. Hence, the fusion cross-section expression is as follows:
$ \begin{aligned}[b]\sigma_{\rm fus}=&\frac{2\pi^2\hbar^2}{2\mu E_{\rm cm}({\rm exp}(2\pi/ka_c)-1)}\Bigg[B_0+B_1\times \left(\frac{E_{\rm cm}}{V_B}\right)\\&+B_2\times \left(\frac{E_{\rm cm}}{V_B}\right)^2+B_3\times \left(\frac{E_{\rm cm}}{V_B}\right)^3\Bigg].\end{aligned} $

(13) Figure 4 (a)−(f) shows a comparison between fusion cross-sections obtained from the present work and Wong's formula with that of experimental fusion cross-sections for 40,48Ca-induced fusion reactions. In the case of Wong's formula [52, 53] the fusion cross-sections are evaluated as follows:
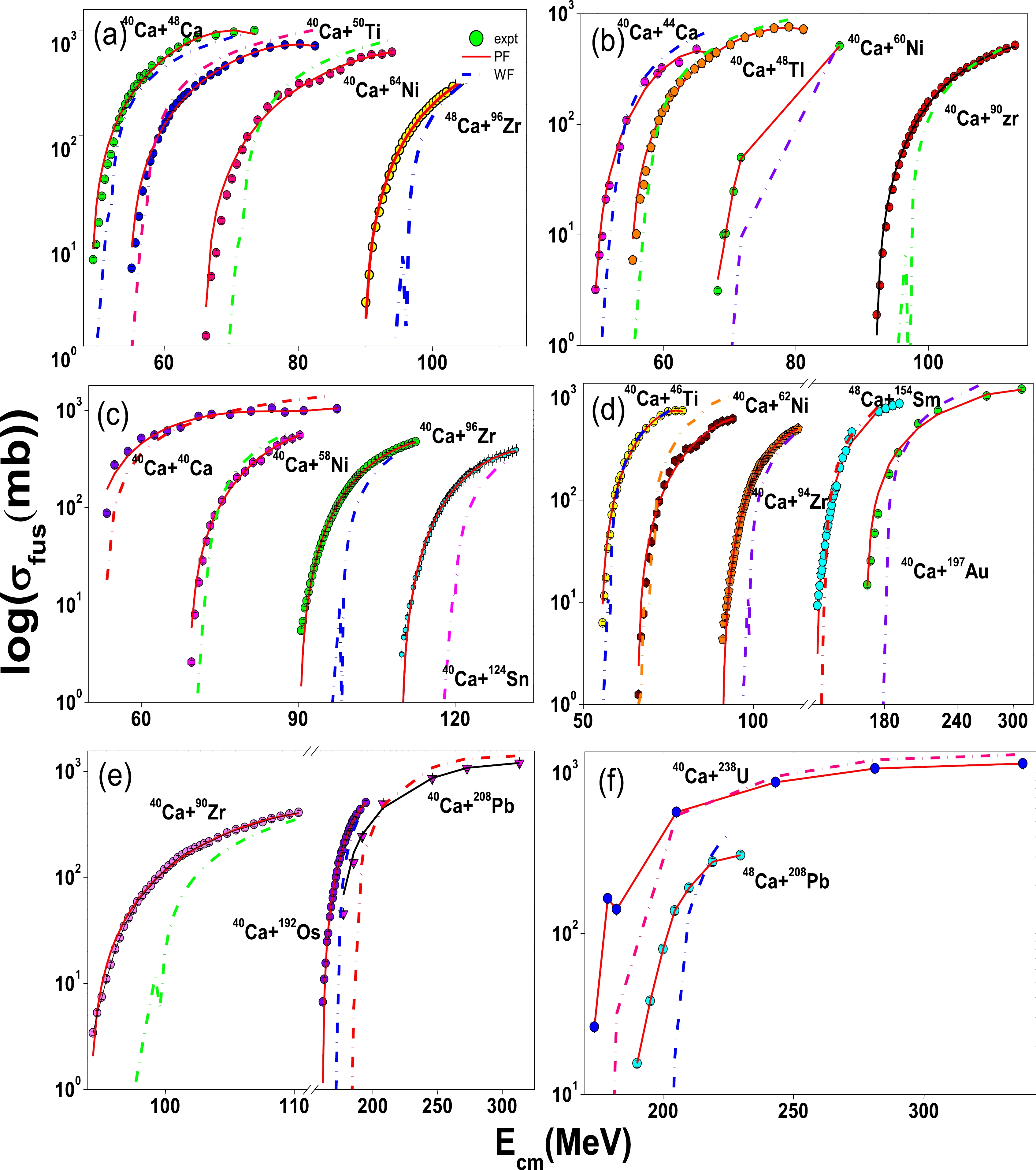
Figure 4. (color online) Comparison of fusion cross-sections obtained from the present work with those of the experimental fusion cross-sections and those obtained using Wong's formula for 40,48Ca-induced fusion reactions. Here, the scatter symbol specifies the experimental data. The continuous and dash-dot lines correspond to the fusion cross-sections obtained in the present work and using Wong's formula, respectively.
$ \sigma_{\rm fus}^{\rm Wong}= \left\{ \begin{array}{*{20}{l}} {\dfrac{R_B^2\hbar\omega}{2E_{\rm cm}}{\rm ln}\left[1+{\rm exp}\left(\dfrac{2\pi}{\hbar\omega}{\rm cm}-V_B)\right)\right], }&{\ E_{\rm cm} \le V_B} \\ {\pi R_{B}^2\left(1-\dfrac{V_B}{E_{\rm cm}}\right), }& {E_{\rm cm} \ge V_B } \end{array} \right. $

(14) here,
$ \hbar\omega $ ,$ R_{B} $ , and$ V_B $ are the inverted parabola, fusion barrier height, and barrier position. Further, a close examination of Fig. 4 (a) reveals that the fusion cross-sections obtained from the present work are in good agreement with those of available experimental values when compared to the fusion cross-sections estimated from the Wong formula. In all the studied fusion reactions, the cross-sections noticeably increase with an increase in$E_{\rm cm}$ . Further, the fusion cross-sections produced by the Wong formula below the fusion barrier are in good agreement with that of the experimental data. However, a larger deviation from the experimental value is observed when$E_{\rm cm}$ is above the fusion barrier. Hence, Wong's formula reproduces the experimental fusion cross-sections with less deviation when$E_{\rm cm}$ is below the fusion barrier compared to the above fusion barrier for the 40,48Ca-induced fusion reactions.Further, to check the applicability of the proposed empirical formula, the present formula is applied for fusion reactions, which were not considered when constructing the formula. To illustrate, we reproduced fusion cross-sections for the 48Ca+194Pt reaction and compared them with those of the experiments and Wong's formalism. The values produced by the present formula are close to those of the experiments when compared to Wong's formula, as shown in Fig. 5. Furthermore, we used the standard deviation as a goodness of fit measure. It defines how well the value obtained from the present fit agrees with the experimental data. The standard deviation is evaluated as follows:
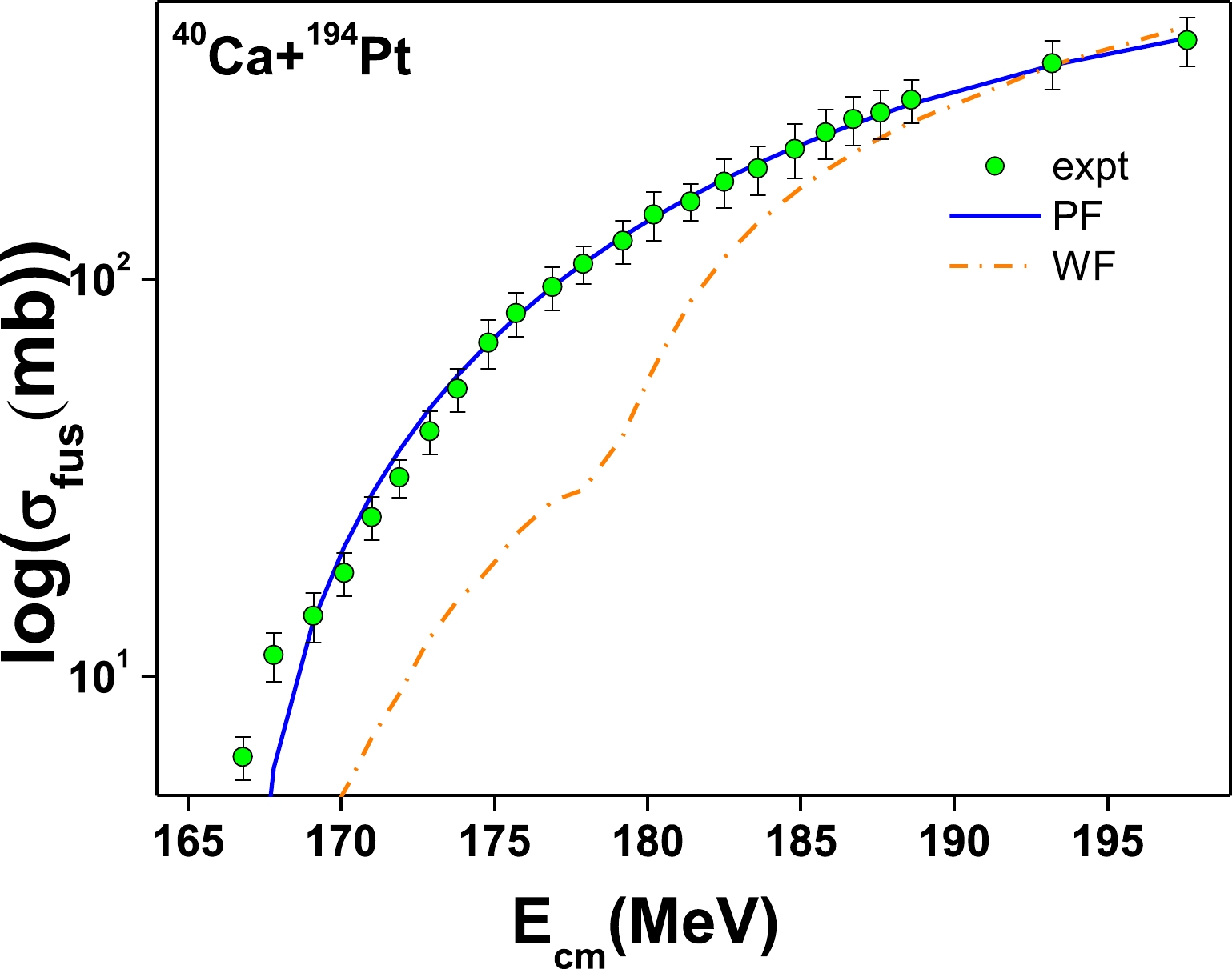
Figure 5. (color online) A comparison of the fusion cross-sections obtained using the present formula with those of the available experiment [54] and Wong's formula.
$ \sigma=\sqrt{\frac{1}{N-1}{\sum\limits_{i=1}^n (O_i-E_i)^2}}. $

(15) Here,
$ O_i $ is the observed value obtained from the present fit, and$ E_i $ is the experimental value. N is the total number of values considered in each fusion reaction. The standard deviation obtained using the present work and Wong's formula is also tabulated in Table 2. From the table, the standard deviation obtained using the present work is found to be smaller than that of Wong's formula for 40,48Ca-induced fusion reactions. Consequently, more accurate and exact fusion cross-sections may be predicted using the geometric factor, Gamow-Sommerfield factor, and empirical formula of the S-factor for 40,48Ca-induced fusion cross-sections.Reaction Range of $E_{\rm cm}$ /MeV

$\sigma_{\rm fus}^{PF}$ 

$\sigma_{\rm fus}^{\rm Wong}$ 

40Ca+48Ca 90.71-134.8 29.04 318.47 40Ca+44Ca 49.75-67.6 17.99 107.24 40Ca+40Ca 53.46-97.46 41.94 187.05 40Ca+50Ti 55.23-82.55 2.17 22.41 40Ca+48Ti 55.37-81.13 2.18 13.75 40Ca+46Ti 55.76-79.34 2.22 7.45 40Ca+64Ni 66.29-93.99 4.14 21.62 40Ca+62Ni 70-106.7 7.34 18.35 40Ca+60Ni 68.2-86.6 0.62 13.97 40Ca+58Ni 69.64-90.34 2.46 15.26 48Ca+96Zr 90.1-112.1 3.06 46.18 48Ca+90Zr 92.2-113.1 4.61 37.82 40Ca+96Zr 128.36-159.38 2.67 72.97 40Ca+94Zr 91.124-113.22 3.86 74.46 40Ca+90Zr 136.37-159.38 0.69 11.66 40Ca+124Sn 109.82-131.75 3.68 92.33 48Ca+154Sm 138.01-191.12 26.91 72.83 40Ca+192Os 161.2-194.5 5.31 76.97 40Ca+197Au 168.16-310.71 38.70 250.22 48Ca+208Pb 173.71-338.08 30.50 495.49 40Ca+208Pb 177.14-313.51 24.22 305.80 40Ca+238U 190.1-229.8 5.31 109.32 Table 2. Tabulation of the standard deviations obtained from the present formula (
$\sigma_{\rm fus}^{PF}$ ) and Wong's formula ($\sigma_{\rm fus}^{\rm Wong}$ ) with those of available experimental values. We also tabulated the range of$E_{\rm cm}$ considered in predicting the fusion cross-sections. -
In the present study, we investigated 40,48Ca-induced fusion cross-sections. The empirical formulae for the astrophysical S-factor are deduced using experimental fusion cross-sections, Gammow-factor (ϕ), and Gammow-Sommerfield factor G(E). Further, the fitting constants for each fusion reaction are made independent using the effect of entrance channel parameters. Accordingly, the S-factor reproduces experimental fusion cross-sections more accurately and precisely when compared to Wong's formula for 40,48Ca-induced fusion reactions. The present study contributes to predicting the fusion cross-sections for 40,48Ca-induced reactions leading to compound nuclei with atomic and mass numbers varying between
$ 40\le Z \le 112 $ and$ 88\le A\le 278 $ respectively.
Empirical model for fusion cross sections of Ca-induced reactions
- Received Date: 2023-07-24
- Available Online: 2024-03-15
Abstract: A new empirical formula for the astrophysical S-factor has been suggested as a function of the Coulomb interaction parameter, center of mass energy, and barrier height. About 22 fusion reactions with 40,48Ca as projectiles were considered for different targets, leading to compound nuclei with atomic and mass numbers varying between 40





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: