-
The symmetry energy and its slope in nuclear matter are crucial features of the equation of state (EOS) of asymmetric nuclear matter, which play important roles in nuclear physics [1−3] and neutron star properties [4−8]. Specifically, the density dependence of the symmetry energy can affect the occurrence of the non-nucleonic degrees of freedom in neutron stars [9−14]. In recent decades, numerous terrestrial experiments and astronomical observations have been attempted to constrain the symmetry energy. Experimental extractions based on a larger number of groups yield an average range of
$ 58.7\pm28.1 $ MeV or even a smaller range [15, 16]. It is, however, interesting to see that new experiments often break through the constrained ranges. For instance, measuring$ ^{208} $ Pb neutron skin thickness ($ 0.283\pm0.071 $ fm) through weak-interaction electron scattering suggests a wide range for the symmetry energy slope$ L =106\pm37 $ MeV [17, 18]. A recent study used the multimessenger resonant shattering flares to estimate L to be approximately$ 0<L<120 $ MeV [19]. On the other hand, fundamental symmetries and new methods have been proposed to constrain the symmetry energy [20−26]. Though it remains a challenge to resolve the uncertainty of the symmetry energy, one may employ this uncertainty to study its effect on physical observables, such as pulsar glitches [27, 28] and star tidal deformability [29, 30]. These astrophysical observations may constrain or even reduce the uncertainty.Understanding the causes of pulsar glitches is not a straightforward process. Initially, glitches were thought to come from starquakes [31], but this could not explain why they occur every three years. Later, a corequake model was established [32], but the solid core explanation still seemed unreasonable. The current explanation is that glitches are caused by sudden transfers of angular momentum between the neutron superfluid in the inner crust and the rest of the star [33−37]. After considering crustal entrainment in the Vela pulsar, the lower limit of the crustal inertia moment fraction
$ \Delta I/I $ needs to be increased from the original 1.6% to 7% [37−39].The crustal inertia moment fraction is usually regarded as being determined by the core-crust transition density and pressure and the star radius, which are all dependent on the density dependence of the symmetry energy [40−42]. The core-crust transition properties from homogeneous to inhomogeneous matter are crucial for understanding neutron star glitches. However, the calculation with the well-constrained models shows that reaching the required
$ \Delta I/I\geq7 $ % for the Vela pulsar is difficult only by changing the symmetry energy and/or slope within a reasonable range. Hence, it is necessary to consider novel variables that may increase the$ \Delta I/I $ .In the past, many theoretical models have been used to understand the properties of these core-crust transition densities [36, 42−48]. Here, we obtain the core-crust transition density
$ \rho_{t} $ through the relativistic random phase approximation (RRPA) method with the inclusion of the renormalized vacuum polarization in the relativistic Hartree approximation (RHA). The numerical results indicate a strong positive correlation between$ \rho_{t} $ and the mass of the σ meson induced by the scalar vacuum polarization [48]. In this work, we will perform a systematic and comparative study of the effects of the$ m_{\sigma} $ and the density dependence of the symmetry energy on the core-crust transition and the fraction of the moment of inertia$ \Delta I/I $ . In addition, our theoretical models will also be calibrated carefully using the constraints on the neutron star radii and maximum masses.The remainder of the paper is organized as follows. In Sec. II, we present the formalism that includes the Lagrangian, the RRPA equations, and relevant formulas for calculating the properties of neutron stars. The model Lagrangian is extended to include the scalar-vector coupling and ω-meson self-interacting terms and isoscalar-isovector coupling term to fit the maximum mass of neutron stars and adjust the slope of the symmetry energy, respectively. The results, including the impact of
$ m_\sigma $ , the symmetry energy, and the slope of the symmetry energy on$ \rho_{t} $ ,$ \Delta I/I $ , and the neutron star radius at$ 1.4M_{\odot} $ , are presented in Sec. III. Finally, a brief summary is given in Sec. IV. -
We added a nonlinear isoscalar-isovector coupling term in terms of the parameter
$ \Lambda_{v} $ [49] to our previous Lagrangian [48] to adjust the slope of the symmetry energy. Now, the interacting Lagrangian is written as$ \begin{aligned}[b] \mathcal{L}_{\rm int}=&\overline{\psi} [\gamma_{\mu}({\rm i}\partial^{\mu}-g_{\omega}\omega^{\mu} -g_{\rho} \boldsymbol{\tau\cdot b^{\mu}}+\frac{e}{2}(1+\tau_{3})A^{\mu}) \\ &-(M-g_{\sigma}\phi)]\psi+4g^{2}_{\rho}b_{\mu}\cdot b^{\mu}\Lambda_{v}g^{2}_{\omega}\omega_{\mu}\omega^{\mu}\\ &-U(\phi,\omega), \end{aligned} $

(1) where
$ U(\phi,\omega) $ is the nonlinear σ and ω meson self-interactions,$ U(\phi,\omega)=-\frac{1}{2}g_{\sigma\omega}\omega^{2}\phi^{2}+\frac{1}{3!}g_{2}\phi^{3} +\frac{1}{4!}g_{3}\phi^{4}+\frac{1}{4}c_{3}\omega^{4}. $

(2) The counterterms to renormalize the infinite nucleon self-energy are
$ \mathcal{L}_{CT}=\sum^{4}_{n=1}\dfrac{\alpha_{n}}{n!}\phi^{n} $ [50]. In addition, the one-loop contributions from the$ g_2 $ and$ g_3 $ terms need to be renormalized by introducing additional counterterms. Eventually, in RHA, the renormalized finite$U^{\rm Ren.}(\phi,\omega)$ is analogously given as [51]$ \begin{aligned}[b] U^{Ren.}( \phi,\omega)=&-\frac{1}{2}g_{\sigma\omega}\omega^{2}\phi^{2} +\frac{1}{3!}g_{2}\phi^{3}+\frac{1}{4!}g_{3}\phi^{4}\\&+\frac{1}{(8\pi)^{2}} \bigg[-\left(g_{2}\phi+\frac{g_{3}\phi^{2}}{2}\right) \tilde{m}^2_\sigma+\frac{1}{12}\frac{g^{4}_{2}\phi^{4}}{\tilde{m}^4_\sigma} \\& +\left(\tilde{m}^2_\sigma+g_{2}\phi+\frac{g_{3}\phi^{2}}{2}\right)^{2} \ln\left(1+\frac{g_{2}\phi+\frac{g_{3}\phi^{2}}{2}}{\tilde{m}^2_\sigma}\right) \\& -\frac{3}{2}\left(g_{2}\phi+\frac{g_{3}\phi^{2}}{2}\right)^{2} -\frac{(g_{2}\phi)^{2}}{3\tilde{m}^2_\sigma} \left(g_{2}\phi+\frac{3g_{3}\phi^{2}}{2}\right)\bigg], \end{aligned} $

(3) with
$ \tilde{m}^2_\sigma=m^{2}_{\sigma}-g_{\sigma\omega}\omega^{2} $ .The perturbation of nuclear matter can be described by the dressed polarization tensors, which are the solution to Dyson's equation. In a static system where the variable
$ q_0 $ of the dressed polarization tensors is set to zero, a uniform system may become unstable to small amplitude density fluctuations of momentum transfer q. This instability occurs when the following inequality is satisfied [52]:$ \begin{array}{*{20}{l}} \epsilon_L=\det[1-D_{L}(q)\Pi_{L}(q,q_{0}=0)]\leq 0, \end{array} $

(4) where the meson propagator
$ D_L $ and polarization tensor$ \Pi_L $ are in form of$ 4\times4 $ matrices. The core-crust transition density is determined as the largest density satisfying Eq. (4) for any q.The longitudinal polarization matrix is defined as
$ \begin{array}{*{20}{l}} \Pi_{L}={ \left( \begin{array}{cccc} \Pi^{e}_{00D}+\Pi^{e}_{00f} & 0 & 0 & 0 \\ 0&\Pi^{n}_{sD}+\Pi^{p}_{sD}+\Pi^{n}_{sf}+\Pi^{p}_{sf} &\Pi^{p}_{m} &\Pi^{n}_{m} \\ 0 &\Pi^{p}_{m} &\Pi^{p}_{00D}+\Pi^{p}_{00f}& 0 \\ 0 &\Pi^{n}_{m} & 0 &\Pi^{n}_{00D}+\Pi^{n}_{00f} \end{array} \right )}. \end{array} $ 
(5) Here, all the components in
$ \Pi_L $ include the renormalized Feynman part, whose explicit expression can be referred to Ref. [53]. The renormalized scalar polarization has special importance on matter stability, and it reads$ \begin{aligned}[b] \Pi_{sf}=&\frac{g^{2}_{\sigma}}{\pi^{2}}\sum\limits_{i=p,n}\bigg[\frac{m^{2}_{\sigma}-q^{2}}{8}-\frac{1}{2}(3M\Sigma_{s}-\frac{9}{2}\Sigma^{2}_{s}) \\&-\frac{3}{4}\int^{1}_{0}{\rm d}x(M^{*2}-M^{2})\ln \left(1+\frac{x(x-1)m^{2}_{\sigma}}{M^{2}}\right)\bigg] \\ &-\frac{3}{4}\int^{1}_{0}{\rm d}x(M^{*2}+x(x-1)q^{2})\ln\frac{x(x-1)q^{2}+M^{*2}}{x(x-1)m^{2}_{\sigma}+M^{2}}, \end{aligned} $

(6) where the renormalized scalar self-energy
$ \Sigma_{s} $ is given by$ \begin{aligned}[b] \Sigma_{s}=&\sum\limits_{i=p,n}\frac{g^{2}_{\sigma}}{m^{2}_{\sigma}}\frac{2}{(2\pi)^{3}} \int^{k_{F_{i}}}_{0}{\rm d}^{3}q\frac{M^{*}}{(q^{2}+M^{*2})^{1/2}}\\&-\frac{g^{2}_{\sigma}}{m^{2}_{\sigma}} \frac{1}{\pi^{2}}[M^{*3}\ln(\frac{M^{*}}{M})+M^{2}(M-M^{*}) \\ &-\frac{5}{2}M(M-M^{*})^{2}+\frac{11}{6}(M-M^{*})^{3}]. \end{aligned} $

(7) Together with the consistent relation
$ \Sigma_{s}=M-M^{*} $ , the nucleon effective mass$ M^* $ can be obtained numerically.The meson effective mass is defined by the second derivative of the Lagrangian against the meson field around its static and mean values
$ \begin{aligned}[b]& m^{*2}_{\sigma}=-\frac{\partial^{2}\mathcal{L}}{\partial\phi_0^{2}},\\ & m^{*2}_{\omega}=\frac{\partial^{2}\mathcal{L}}{\partial \omega^{2}_{0}},\\ & m^{*2}_{\rho}=\frac{\partial^{2}\mathcal{L}}{\partial b^{2}_{0}}. \end{aligned} $

(8) The photon and various meson propagators are explicitly given as follows [54]:
$ d_{g}=-\frac{e^{2}}{q^{2}}=-\frac{4\pi\alpha}{q^{2}}, $ 
(9) $ d_{\sigma}=\frac{g^{2}_{\sigma}((m^{*2}_{\rho}-q^{2})(m^{*2}_{\omega}-q^{2})-(16g_{\omega}g_{\rho}\Lambda_{v}W_{0}B_{0})^{2})} {(m^{*2}_{\rho}-q^{2})(m^{*2}_{\omega}-q^{2})(m^{*2}_{\sigma}-q^{2})-(16g_{\omega}g_{\rho}\Lambda_{v}W_{0}B_{0})^{2}(m^{*2}_{\sigma}-q^{2}) +(2g_{\sigma\omega}\omega_{0}\phi_{0})^{2}(m^{*2}_{\rho}-q^{2})}, $

(10) $ d_{\omega}=\frac{g^{2}_{\omega}(m^{*2}_{\rho}-q^{2})(m^{*2}_{\sigma}-q^{2})} {(m^{*2}_{\rho}-q^{2})(m^{*2}_{\omega}-q^{2})(m^{*2}_{\sigma}-q^{2})-(16g_{\omega}g_{\rho}\Lambda_{v}W_{0}B_{0})^{2}(m^{*2}_{\sigma}-q^{2}) +(2g_{\sigma\omega}\omega_{0}\phi_{0})^{2}(m^{*2}_{\rho}-q^{2})}, $

(11) $ d_{\rho}=\frac{g^{2}_{\rho}((m^{*2}_{\omega}-q^{2})(m^{*2}_{\sigma}-q^{2})+(2g_{\sigma\omega}\omega_{0}\phi_{0})^{2})} {(m^{*2}_{\rho}-q^{2})(m^{*2}_{\omega}-q^{2})(m^{*2}_{\sigma}-q^{2})-(16g_{\omega}g_{\rho}\Lambda_{v}W_{0}B_{0})^{2}(m^{*2}_{\sigma}-q^{2}) +(2g_{\sigma\omega}\omega_{0}\phi_{0})^{2}(m^{*2}_{\rho}-q^{2})}, $

(12) $ d_{\omega\rho}=\frac{-16g^{2}_{\omega}g^{2}_{\rho}\Lambda_{v}W_{0}B_{0}(m^{*2}_{\sigma}-q^{2})} {(m^{*2}_{\rho}-q^{2})(m^{*2}_{\omega}-q^{2})(m^{*2}_{\sigma}-q^{2})-(16g_{\omega}g_{\rho}\Lambda_{v}W_{0}B_{0})^{2}(m^{*2}_{\sigma}-q^{2}) +(2g_{\sigma\omega}\omega_{0}\phi_{0})^{2}(m^{*2}_{\rho}-q^{2})}, $

(13) $ d_{\sigma\omega}=\frac{2g_{\omega}g_{\sigma}g_{\sigma\omega}\omega_{0}\phi_{0}(m^{*2}_{\rho}-q^{2})} {(m^{*2}_{\rho}-q^{2})(m^{*2}_{\omega}-q^{2})(m^{*2}_{\sigma}-q^{2})-(16g_{\omega}g_{\rho}\Lambda_{v}W_{0}B_{0})^{2}(m^{*2}_{\sigma}-q^{2}) +(2g_{\sigma\omega}\omega_{0}\phi_{0})^{2}(m^{*2}_{\rho}-q^{2})}, $

(14) where
$ W_{0}\equiv g_{\omega}\omega_{0} $ , and$ B_{0}\equiv g_{\rho}b_{0} $ . The longitudinal propagator matrix in Eq. (4) now reads$ \begin{array}{*{20}{l}} D_{L}= \left( \begin{array}{cccc} d_{g} & 0 & -d_{g} & 0 \\ 0 & -d_{\sigma} & d_{\sigma\omega} & d_{\sigma\omega} \\ -d_{g} & d_{\sigma\omega}& d_{g}+d_{V}+2d_{\omega\rho} & d_{I} \\ 0 & d_{\sigma\omega}& d_{I} & d_{V}-2d_{\omega\rho} \end{array} \right), \end{array} $

(15) with
$ d_{V}=d_{\omega}+d_{\rho} $ , and$ d_{I}=d_{\omega}-d_{\rho} $ . Without the scalar-vector coupling$ g_{\sigma\omega} $ in Eqs. (10)−(15), the propagator matrix reduces to that in Ref. [52].Here, we specifically focus on a simple neutron star composition consisting merely of protons, neutrons, and electrons. The energy density of neutron star matter is given as
$ \begin{aligned}[b] \varepsilon=&\sum\limits_{i=p,n,e}\frac{2}{(2\pi)^{3}}\int^{k_{F_{i}}}_{0}{\rm d}^{3}q(q^{2}+M^{*2})^{1/2}\\ &+\frac{1}{2}m^{2}_{\omega}\omega^{2}+\frac{1}{2}m^{2}_{\rho}\rho^{2}+\frac{1}{2}m^{2}_{\sigma}\sigma^{2}+U^{\rm Ren.}(\phi)\\ &+12\Lambda_{v}g^{2}_{\rho}g^{2}_{\omega}\omega^{2}\rho^{2}+\varepsilon_{\rm vac}, \end{aligned} $

(16) where
$\varepsilon_{\rm vac}$ is the finite vacuum fluctuation energy density [50]. The pressure can be obtained from the thermodynamic relation:$p=\rho^2 \partial(\varepsilon/\rho)/\partial\rho$ .From the energy density, we can get the symmetry energy
$ E_{\rm sym}=\frac{1}{2}\frac{\partial^{2}(\varepsilon/\rho)}{\partial\delta^{2}}\Big|_{\delta=0}, $

(17) where
$ \delta=(\rho_{n}-\rho_{p})/\rho_{B} $ is the isospin asymmetry parameter. The slope of the asymmetry energy at saturation density is defined as$ L=3\rho_{0}\frac{\partial E_{\rm sym}}{\partial\rho}\Big|_{\rho_{0}}. $

(18) In the slow rotation scenario, the moment of inertia of a uniformly rotating axially symmetric neutron star is given by [55−57]
$ I\equiv\frac{J}{\Omega}=\frac{8\pi}{3}\int^{R}_{0}r^{4}{\rm e}^{-\nu(r)}\frac{\bar{\omega}(r)}{\Omega} \frac{(\varepsilon(r)+P(r))}{\sqrt{1-2GM(r)/r}}{\rm d}r, $

(19) where J is the angular momentum, Ω is a stellar frequency,
$ \nu(r) $ is the spherically symmetric metric function,$ \bar{\omega}(r) $ is the relative frequency, and$ M(r) $ and$ P(r) $ are the stellar mass and pressure profiles, respectively. The crustal moment of inertia is given as$ I_{cr}=\frac{8\pi}{3}\int^{R}_{R_{t}}r^{4}{\rm e}^{-\nu(r)}\frac{\bar{\omega}(r)}{\Omega} \frac{(\varepsilon(r)+P(r))}{\sqrt{1-2GM(r)/r}}{\rm d}r, $

(20) where
$ R_{t} $ is the radius from the star center to the transition density. These are the complete expressions of the moments of inertia, and the details can be referred to Ref. [55]. The fraction of the crustal moment of inertia$ \Delta I/I $ now reads$ \Delta I/I=\frac{I_{cr}}{I}. $

(21) In literature [58], there is a frequently used approximate expression for the fraction of moments of inertia
$ \begin{aligned}[b] \frac{\Delta I}{I}\cong&\frac{28\pi P_{t}R^{3}}{3M_{NS}\cdot c^{2}}\frac{(1-1.67\beta-0.6\beta^{2})}{\beta} \\ &\times \left[1+\frac{2P_{t}(1+5\beta-14\beta^{2})}{\rho_{t}Mc^{2}\beta^{2}}\right]^{-1}, \end{aligned} $

(22) where
$ \beta=GM_{NS}/Rc^{2} $ is the compactness parameter, and$ M_{NS} $ and R are the neutron star mass and radius, respectively. Equation (22) holds on the following conditions:$ P_{t}\ll \varepsilon_{t} $ ,$ M (R_{t})\simeq M $ , and$ \bar{\omega}(R_{t})\simeq\bar{\omega}(R) $ . -
Our models include the nonlinear σ meson self-interactions in the RHA to reduce the compression modulus, as well as the scalar-vector coupling (
$ g_{\sigma\omega} $ ) and ω-meson self-interacting ($ c_3 $ ) terms to increase the matter pressure and maximum mass of neutron stars. By including the parameters$ g_{\sigma\omega} $ and$ c_{3} $ , we have developed three parameterizations, namely, RHAn1c, RHAn2c, and RHAn3c, based on the previous ones without the coupling$ g_{\sigma\omega} $ and$ c_{3} $ [48]. All these models are carefully constrained by the saturation properties of nuclear matter; see Table 1. In Table 1, some properties of neutron stars are also listed, and the increase in the maximum mass of the neutron star can be observed due to the inclusion of the coupling parameters$ g_{\sigma\omega} $ and$ c_{3} $ . Note that analysis based on the available open-shell nuclei allows for incompressibility in a larger range of$ 250<\kappa<315 $ MeV, although it dwells well in the range of$ \kappa=240\pm20 $ MeV from the analysis of the isoscalar giant monopole resonances in closed shell nuclei such as$ ^{208} $ Pb [59−61]. Since the focus of our work is not the accuracy of incompressibility, we quote it in a reasonable range of$ 240\sim300 $ MeV. The pressures as a function of density, calculated using three nonlinear RHA parameter sets, are shown in Fig. 1. It can be seen that the curves of the nonlinear RHA parameter sets are consistent with the constraints of the collective flow data [62]. Moreover, we mention that the pressure of pure neutron matter obtained with current parametrizations is basically consistent with that from the microscopic chiral NN and 3N interactions at an applicable low density, as discussed in literature [48].Model $g_{\sigma}$ 

$g_{\rho}$ 

$g_{\omega}$ 

$g_{2}$ 

$g_{3}$ 

$g_{\sigma\omega}$ 

$c_{3}$ 

$M^{*}/M$ 

$\rho_{t}$ 

κ $R_{1.4}$ 

$M^{\rm max}_{NS}/M_{\odot}$ 

$M^{\rm max*}_{NS}/M_{\odot}$ 

RHAn1c 7.72 4.03 8.45 25.19 21.16 0.5 0.0 0.782 0.081 300 13.62 2.048 2.03 RHAn2c 7.59 4.06 7.96 35.58 39.24 0.5 -4.3 0.800 0.081 270 13.44 2.012 1.91 RHAn3c 7.47 4.10 7.39 51.11 88.90 7.0 -9.0 0.820 0.079 240 13.35 1.975 1.72 Table 1. Main parameters of RHAnc Models and properties of nuclear matter and neutron stars.
$M^{\rm max*}_{NS}$ is the maximum neutron star mass in RHAn Models without$ g_{\sigma\omega} $ and$ c_{3} $ . The masses of σ, ω, and ρ mesons are 512, 783, and 770 MeV, respectively. The parametrizations are constrained by the saturation properties, including the binding energy per nucleon$ E_{b}=-16 $ MeV, incompressibility κ, and vanishing pressure at saturation density$\rho_0=0.16~{\rm fm}^{-3}$ . The transition density$ \rho_{t} $ , incompressibility κ, and radius$ R_{1.4} $ of 1.4$ M_\odot $ star are in units of fm$ ^{-3} $ , MeV, and km, respectively.
Figure 1. (color online) Pressure as a function of density for symmetric nuclear matter. The blue area constraints are from the collective flow data [62].
With the EOS of the nonlinear RHA models as an input for neutron stars, the resulting mass versus radius relationship can be solved by the Tolman-Oppenhaimer-Volkoff equation. The mass-radius trajectories of neutron stars that include the composition of neutrons, protons, and electrons are depicted in Fig. 2. It shows that the star radii predicted by our models agree well with those extracted from the NICER measurements of the pulsars J0030+0451 and J0740+6620 [63−65]. Fig. 2 also shows the 68% and 95% confidence intervals for the relationship between mass and radius in Ref. [64]. The predicted maximum masses of neutron stars are within or close to the large-mass constraints.
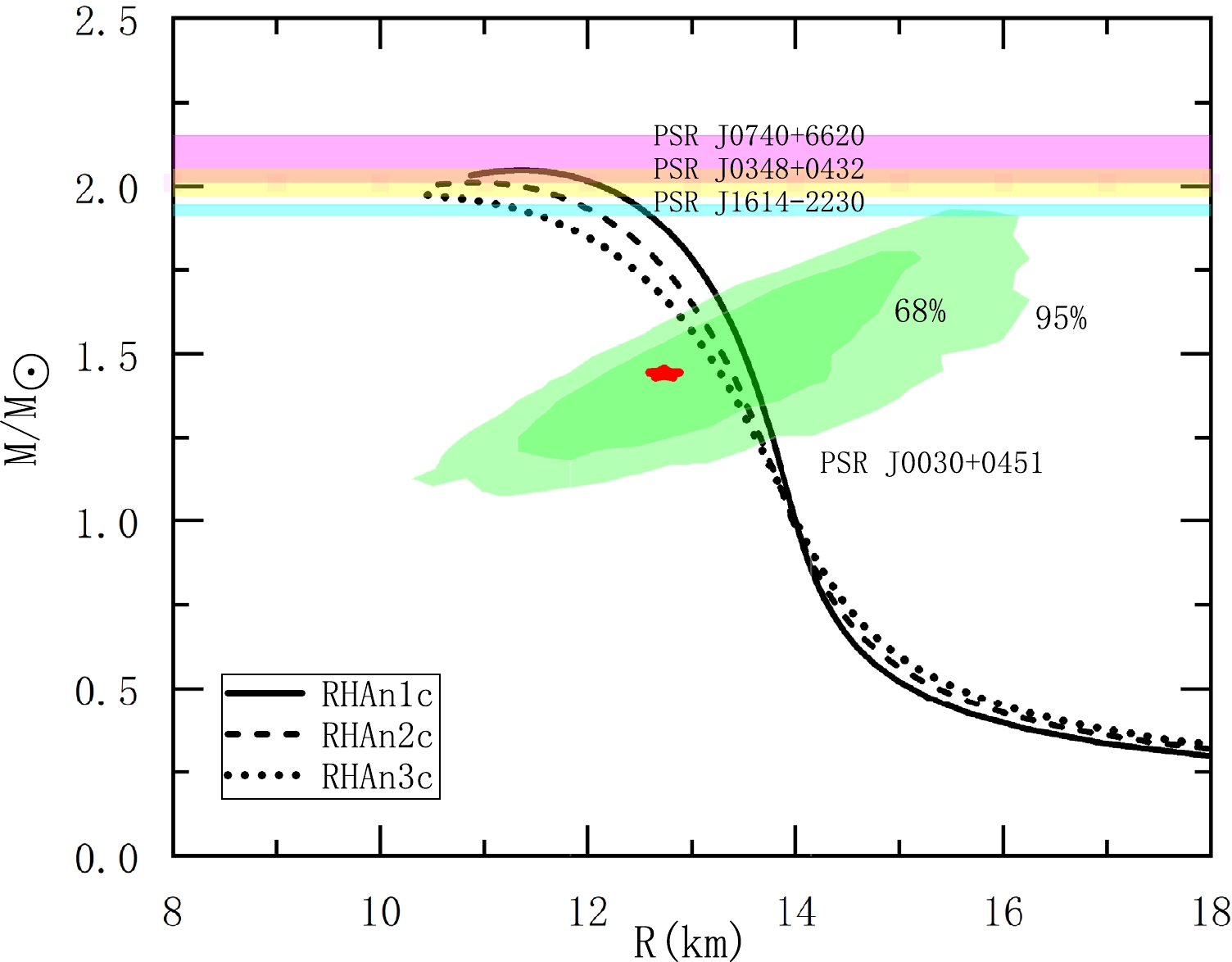
Figure 2. (colour online) The neutron star mass versus radius with three nonlinear RHA parameter sets. In Refs. [66−70], the astrophysical constraints of large mass neutron star observations are shown as horizontal shadow regions. The deep and light green areas represent 68% and 95% confidence intervals constrained by PSR J0030+0451 NICER analysis, respectively [64].
In nonlinear RHA models, the nucleon effective mass at saturation density is approximately 0.8M, which is quite larger than 0.6M in the usual relativistic mean field (RMF) models. The conversion of nucleon mass into energy and pressure is crucial for sustaining a large-mass neutron star. In order to reduce the nucleon effective mass, the isoscalar scalar-vector coupling (in terms of
$ g_{\sigma\omega} $ ) and ω-meson self-interaction (in terms of$ c_{3} $ ) terms are included for such conversion in light of the relevant fact that the σ and ω mesons are responsible predominantly for the reduction of nucleon mass and the repulsion needed for sufficient pressure, respectively. Thus, the nucleon effective mass can be reduced moderately with the inclusion of the coupling$ g_{\sigma\omega} $ and$ c_{3} $ , leading to a moderate increase in the maximum mass of the neutron star, as seen in Table 1. As a result, the maximum masses of neutron stars with the RHAn1c and RHAn2c agree well with astrophysical observations of massive neutron stars PSR J1614-2230 [66, 67], PSR J0348+0432 [68], and PSR J0740+6620 [69, 70]. The maximum mass of 1.975$ M_{\odot} $ with the RHAn3c is very close to 2$ M_{\odot} $ , albeit with a small deviation. The insufficient maximum mass can be understood from the tendency of nonlinear RHA models: as the incompressibility κ decreases, the nucleon effective mass increases, and the maximum mass of neutron star decreases. Note that the inclusion of muons can lead to moderate softening of the EOS and a small reduction of approximately 0.026$ M_{\odot} $ in the maximum neutron star mass.We now use these nonlinear RHA models to investigate the core-crust transition density
$ \rho_t $ . Fig. 3 shows the transition density as a function of$ m_\sigma $ in the nonlinear RHA models with and without the couplings$ g_{\sigma\omega} $ and$ c_3 $ . When the$ m_\sigma $ changes here or elsewhere, the saturation properties always remain unchanged by readjusting other parameters concerning the σ meson. The transition density$ \rho_t $ is sensitively dependent on the renormalization point ($ q^2_\mu=m_\sigma^2 $ ) of the scalar polarization$ \Pi_s $ when including the vacuum contribution in nonlinear RHA models [48]. Figure 3 clearly illustrates that the incorporation of the scalar-vector coupling ($ g_{\sigma\omega} $ ) and ω-meson self-interaction ($ c_{3} $ ) in the nonlinear RHA models has an almost negligible impact on the$ \rho_t-m_\sigma $ correlation.
Figure 3. (color online) Core-crust transition density
$ \rho_{t} $ as a function of$ m_\sigma $ in three nonlinear RHA models with and without the parameters$ g_{\sigma\omega} $ and$ c_{3} $ . Here,$ \Lambda_v=0 $ is taken, and the symmetry energy at saturation density is fixed at$E_{\rm sym}=33$ MeV.In our previous work [48], the effects of the symmetry energy and its slope on
$ \rho_t $ were briefly investigated; the symmetry energy and its slope L change with the density coherently without the freedom to adjust L. To systematically investigate the effects of the symmetry energy and its slope on$ \rho_t $ ,$ P_{t} $ , neutron star radius R, and$ \Delta I/I $ , an additional isoscalar-isovector coupling term in terms of the parameter$ \Lambda_{v} $ is included to reduce the slope of the symmetry energy through increasing the ρ meson effective mass. With the inclusion of the isoscalar-isovector coupling and readjustment of the parameter$ g_\rho $ , the symmetry energy at saturation density can be constrained within a small domain [49]. This modification enables us to adjust the slope of the symmetry energy separately. Thus, our results, as seen in the relation between$ \rho_t $ and L in Fig. 4 (a), align with previous studies [40−42] that establish an inverse correlation between$ \rho_t $ and L. In addition, the variation of$ \rho_t $ in a reasonable range of$ m_\sigma $ due to the vacuum contribution is comparable to that by changing the symmetry energy slope L in a large range. As shown in Fig. 4 (b),$ P_{t} $ is not a monotonous function of L. It first increases and then decreases with L. It can be observed from Fig. 4 (c) that increasing the slope L while keeping the symmetry energy unchanged leads to an increase in the radius of the canonical neutron star$ R_{1.4} $ and a decrease in the$ \rho_{t} $ in these RHAn models.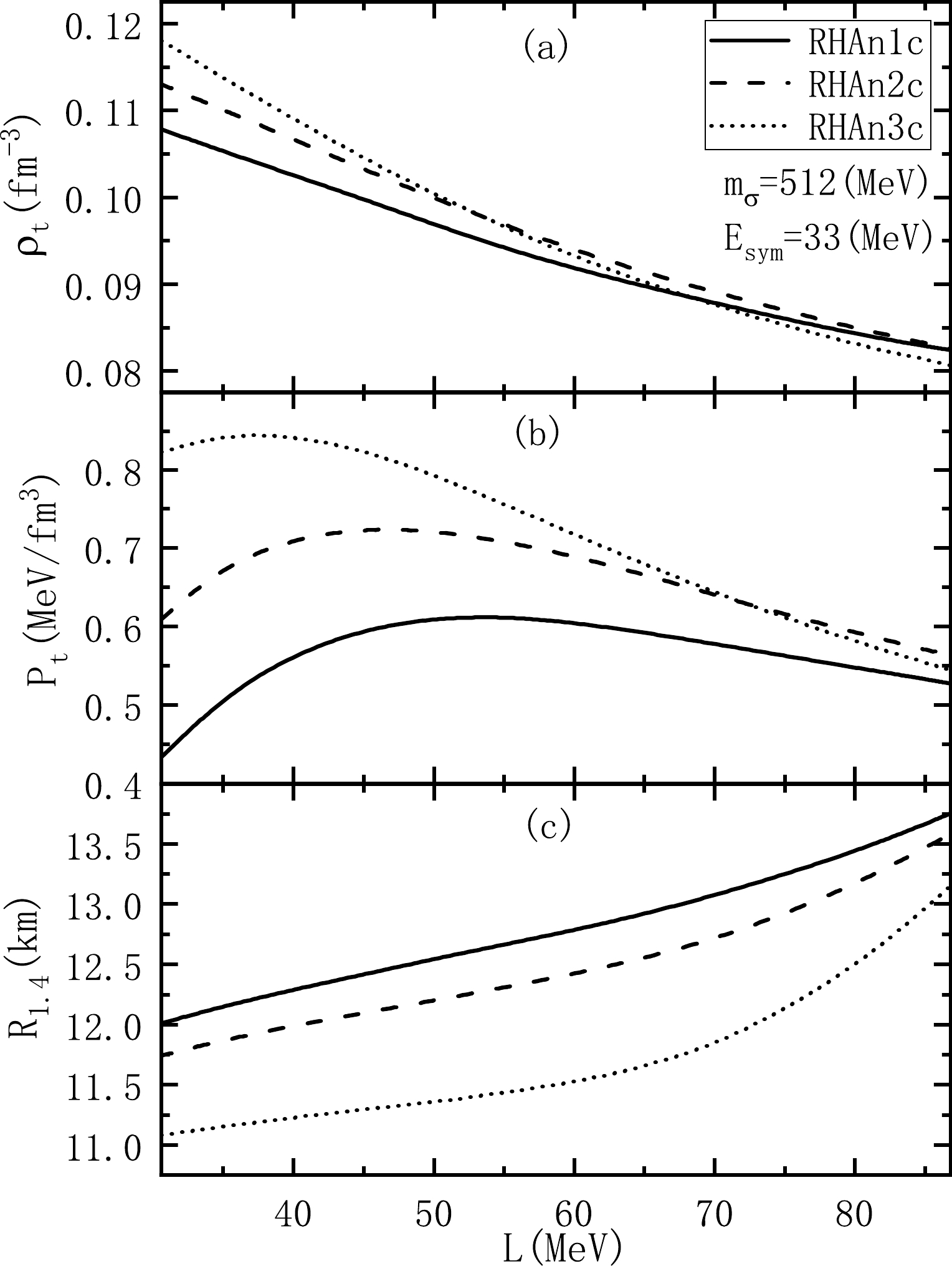
Figure 4.
$ P_{t} $ ,$ R_{1.4} $ , and$ \rho_{t} $ as a function of the slope of the symmetry energy L with the RHAn1c, RHAn2c, and RHAn3c.Now, we can calculate the ratio of the crustal moment of inertia
$ \Delta I/I $ , as it relies on three physical quantities:$ \rho_{t} $ , transition pressure$ P_{t} $ , and neutron star radius R, as seen from the approximate formula in Eq. (22); given the nuclear EOS,$ P_{t} $ and R can be obtained after$ \rho_t $ is determined. We can simply decompose Eq. (22) into three parts:$ P_{t} $ ,$ R^{3} $ , and the remaining part containing$ \rho_{t} $ . By comparing these components and analyzing the results in Fig. 5, we find that the effects of$ P_{t} $ ,$ R^{3} $ , and$ \rho_{t} $ are of the same magnitude and should be given equal consideration since the difference in the slope L can well specify the variation of the neutron star radius [4−8] and the correlation with$ \rho_t $ and$ P_t $ [42−47].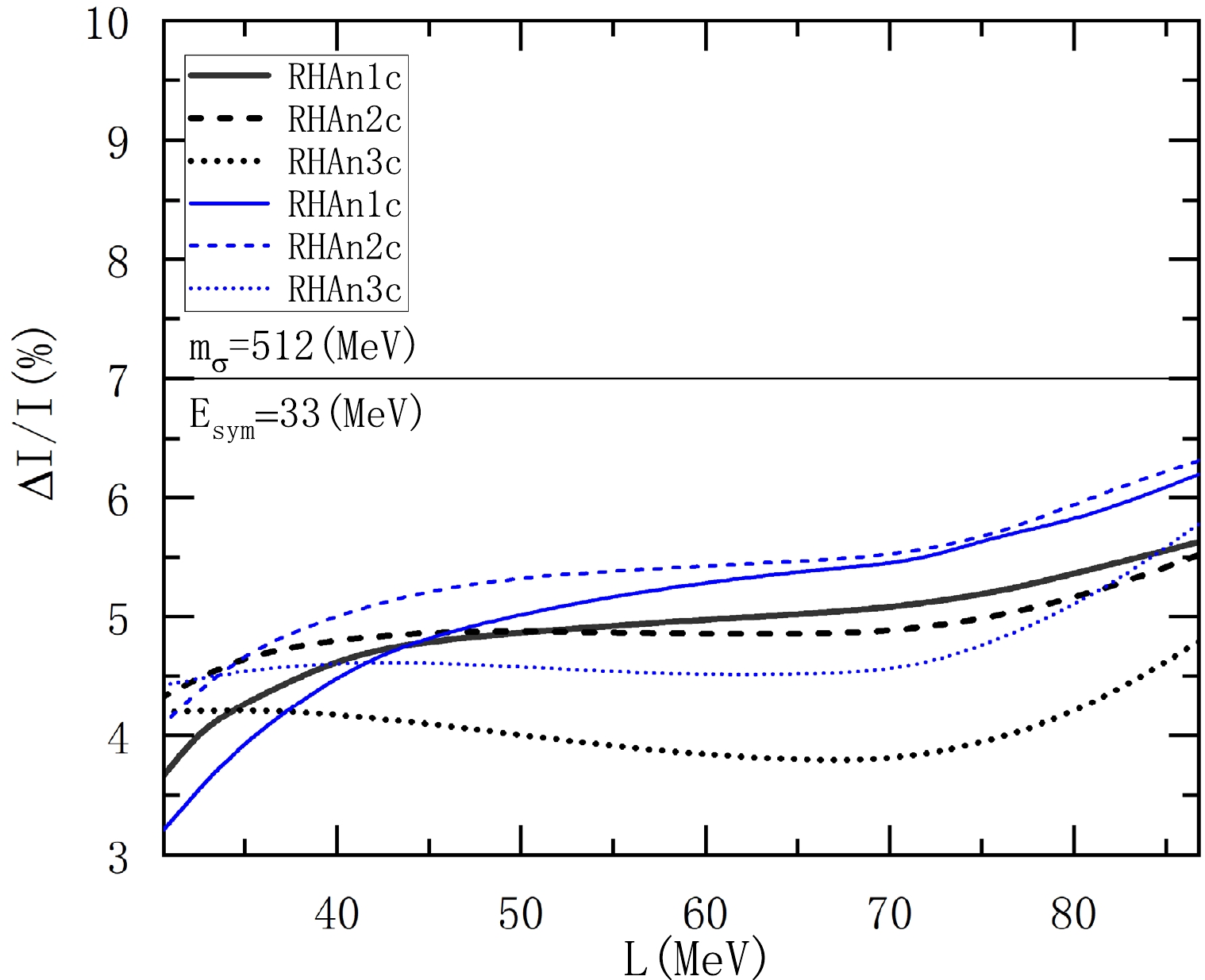
Figure 5. Fraction of crustal moment of inertia
$ \Delta I/I $ in the$ 1.4M_{\odot} $ neutron star as a function of the slope of symmetry energy L with three nonlinear RHA models. The thin blue and thick black curves are the results obtained from Eq. (21) and Eq. (22), respectively.The RHAn1c model results in Fig. 5 can be divided into three domains. In the small L domain, increasing radius
$ R_{1.4} $ and$ P_{t} $ have a positive impact on$ \Delta I/I $ , which exceeds the negative impact of decreasing$ \rho_{t} $ . Therefore,$ \Delta I/I $ significantly increases with the increase in L. In the intermediate L domain, the increase of$ P_{t} $ starts to slow down, and it gradually decreases, resulting in a balance between the counteracting roles of R and$ \rho_t $ in$ \Delta I/I $ . At this domain, the increase in$ \Delta I/I $ becomes very small, or the value even decreases with the increase of L. Finally, as L exceeds around 70 MeV, the rate of increase in$ R_{1.4} $ shows a slight acceleration, while the rate of decrease in$ \rho_{t} $ decelerates, resulting in a gradual rise in$ \Delta I/I $ . The situation is generally similar to the results with HAn2c and RHAn3c in Fig. 5, though in the small L domain,$ \Delta I/I $ is rather flat for the parametrization RHAn3c, which has a smaller incompressibility. The complete values of$ \Delta I/I $ with the formula in Eq. (21) are also shown in Fig. 5 and the figures below. We can see that the results from Eq. (21) tend to be generally higher than those obtained from Eq. (22) in Fig. 5. Based on these results and analyses, achieving the goal of$ \Delta I/I\geq7 $ % by simply increasing the slope of symmetry energy within a valid range is generally difficult in the RHAn models, although the required crustal moment of inertia can be satisfied in some RMF models [43, 55].As a significant positive
$ \rho_{t}-m_{\sigma} $ correlation, shown in Fig. 3, exists for the inclusion of the vacuum polarization, we intend to investigate whether altering the mass of σ meson within a reasonable region can lead to$ \Delta I/I\geq7 $ %. In the nonlinear RHA models, the increase in the σ meson mass decreases the ratio$ g^{2}_{\sigma}/m^{2}_{\sigma} $ to preserve the saturation property. Consequently, the increase of$ m_\sigma $ and the corresponding change in parameters lead to an increase in the$ P_{t} $ and radius$ R_{1.4} $ . Hence, increasing$ m_\sigma $ makes it easier to achieve$ \Delta I/I\geq7 $ %, as shown in Figs. 6 and 7, thus reproducing the pulsar glitch. By comparing the results in Figs. 6 and 7, it is clear that the approximate$ \Delta I/I $ in Eq. (22) are generally smaller than the complete results in Eq. (21). Notably, for larger L, e.g.,$ L=86.8 $ MeV, the difference between the two cases increases rapidly as$ m_{\sigma} $ increases. This large difference occurs because increasing$ m_{\sigma} $ under a larger L will lead to a more rapid increase in$ \rho_{t} $ up to saturation density. When the$ \rho_{t} $ approaches or exceeds saturation density, the conditions$ P_{t}\ll \varepsilon_{t} $ and$ M (r)\simeq M $ , necessary for the formula in Eq. (22), gradually fail owing to an increase in$ P_{t}/\varepsilon_{t} $ and a decrease in$ M(r)/M $ , widening the separation between the results obtained from Eqs. (21) and (22). Interestingly, the$ m_{\sigma} $ required to reach the limit of$ \Delta I/I\geq7 $ % with the complete formula in Eq. (21) is smaller than that with the approximate formula in Eq. (22), see the results in Figs. 6 and 7.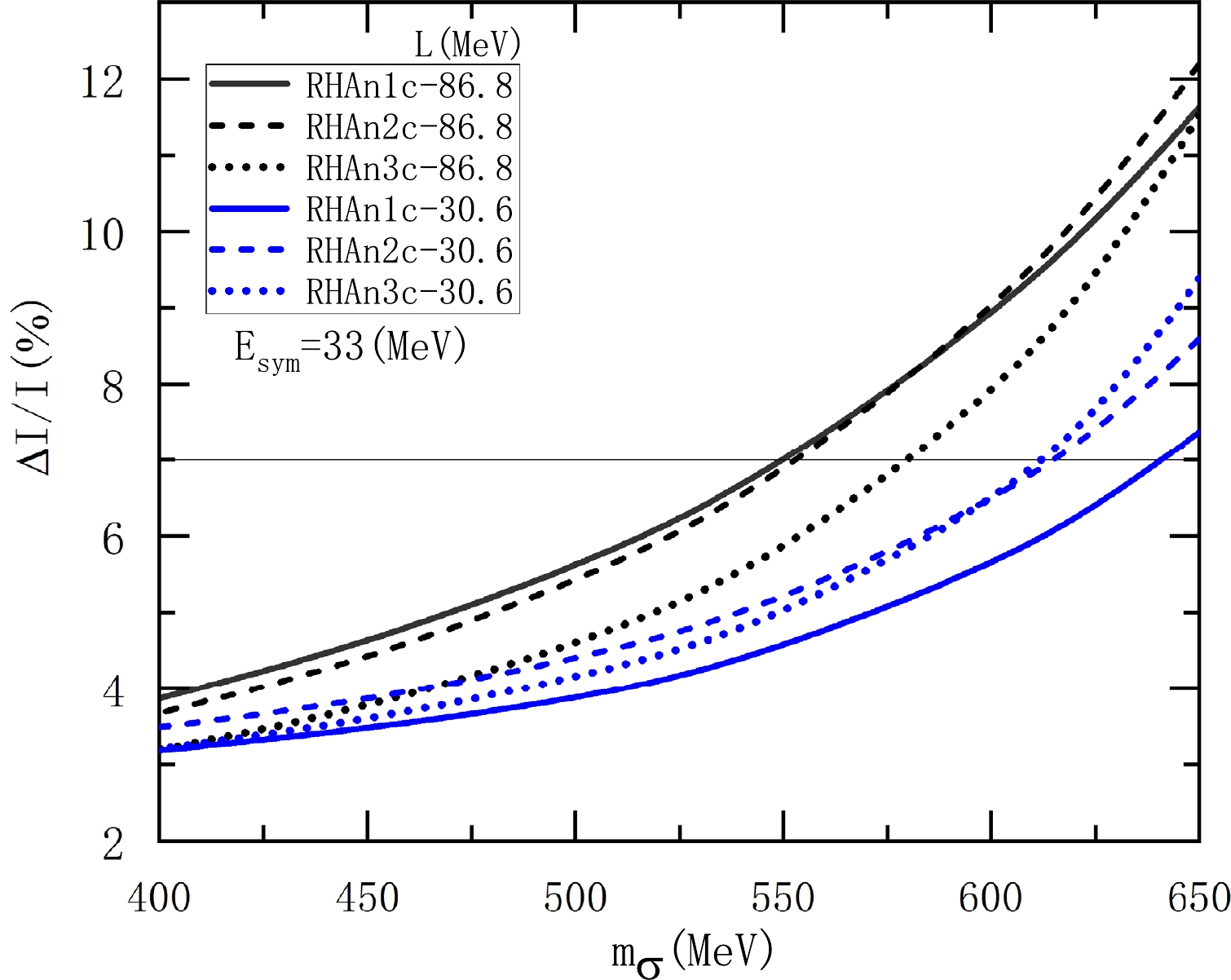
Figure 6. (color online) Fraction of crustal moment of inertia
$ \Delta I/I $ in the$ 1.4M_{\odot} $ neutron star as a function of the mass of σ meson. The results are obtained using the approximate formula in Eq. (22).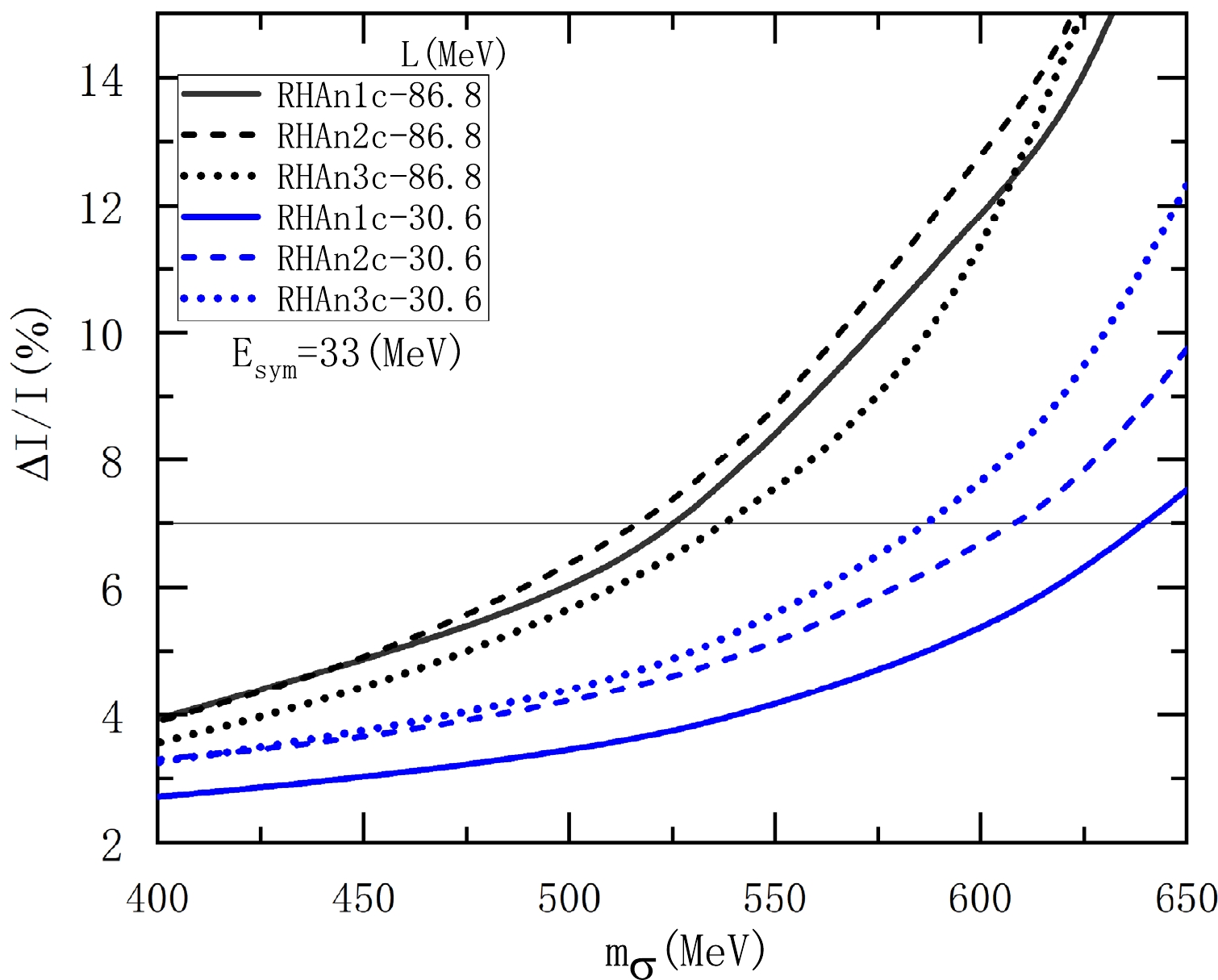
Figure 7. (color online) Fraction of crustal moment of inertia
$ \Delta I/I $ in the$ 1.4M_{\odot} $ neutron star as a function of the mass of σ meson. The results are obtained using the complete formula in Eq. (21).Accordingly, the occurrence of pulsar glitches is largely attributed to the significant effect of the vacuum, in which the scalar vacuum polarization plays a vital and indispensable role. We stress that incorporating the vacuum effect is crucial for the crustal moment of inertia and the glitch phenomena of pulsars. Recognizing that the traditional RMF models do neglect the vacuum effect and many RMF models are renormalizable according to the apparent dimension analysis, one can provide a more reasonable description of the glitch phenomena by renormalizing the vacuum contribution in many RMF models.
Here, it is worth mentioning that
$ \rho_t $ is almost independent of$ m_\sigma $ in the usual RMF models [48]. Currently, various extractions limit the σ meson mass to a range of 400 to near 650 MeV [71]. Though the finite nuclei properties limit the value of$ m_\sigma $ to some extent in some many-body approximations, the value of$ m_\sigma $ cannot be even determined solely but is dependent on the σ meson self-interactions ($ g_{2} $ ,$ g_{3} $ terms) in the RMF approximation. In the fit to properties of finite nuclei, the value of$ m_\sigma $ scatters in a large range, approximately from 450 to 600 MeV, relying on various considerations of the in-medium correlation effects. A special case to release the constraint on the meson masses is the point coupling model [72]. Without much consideration of the correlation effect on finite systems in this work, we took$ m_\sigma $ as an adjustable parameter in a reasonably acceptable range in the nonlinear RHA models that are constrained by the properties of bulk matters. In addition, these correlations would be tested with the self-consistent models that give a proper account of the finite nuclei properties once the σ-meson mass can be measured accurately or specified to be an unadjustable parameter. -
In this study, we use the nonlinear RHA models to investigate the neutron star properties, including the mass-radius trajectories, core-crust transition density
$ \rho_t $ , pressure$ P_t $ , and ratio of the crustal moment of inertia,$ \Delta I/I $ , necessary for the pulsar glitch. The models are extended to include the scalar-vector and ω-meson self-interacting terms and isoscalar-isovector coupling term to increase the maximum mass of neutron stars and adjust the slope of the symmetry energy, respectively. Emphasis is placed on analyzing the key factors affecting the transition density obtained in the relativistic RPA with the inclusion of the renormalized vacuum contribution. The vacuum and the slope of the symmetry energy are found to have a comparable role in the variation of$ \rho_t $ . The predictions of the nonlinear RHA models are found to align with astrophysical observations on the maximum mass of neutron stars and canonical radius$ R_{1.4} $ . Our study analyzes the impact of$ m_\sigma $ and slope of symmetry energy on the crustal moment of inertia$ \Delta I/I $ in neutron stars using the nonlinear RHA model, with the inclusion of vacuum polarization. Though the slope of symmetry energy affects$ \rho_{t} $ ,$ P_{t} $ , and R, which all contribute to determining$ \Delta I/I $ , our research indicates that merely adjusting the slope of symmetry energy within a reasonable region is inadequate to achieve$ \Delta I/I\geq7 $ %, which is necessary to account for the Vela pulsar's significant glitches. With the inclusion of the finite contribution of the scalar vacuum polarization, the$ \rho_{t} $ exhibits a direct increase with the rise of$ m_\sigma $ , whereas the$ P_{t} $ and radius R experience an indirect increase with the rise of$ m_\sigma $ . Therefore, together with the density dependence of the symmetry energy constrained by various experiments, adjusting$ m_\sigma $ proves to be an effective method to attain$ \Delta I/I\geq7 $ %. -
We thank the Big Data Computing Center of Southeast University for providing the facility support for the numerical calculations in this study.
Neutron star core-crust transition and the crustal moment of inertia in the nonlinear relativistic Hartree approximation
- Received Date: 2023-08-11
- Available Online: 2024-03-15
Abstract: We investigate the effects of the σ meson mass (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: