-
The wobbling motion seen in a triaxially deformed nucleus represents a distinctive rotational mode. This motion can be analogized to the movement of an asymmetric gyroscope in classical mechanics. The collective wobbling motion of the nucleus, as proposed by Bohr and Mottelson [1], is direct evidence of the presence of triaxiality. The nucleus favors rotating around the axis with the largest moment of inertia, as this corresponds to the state of lowest energy within the system. When it is excited with a slightly higher excitation energy, its rotational axis will deviate from the principal axis associated with the largest moment of inertia. Consequently, precession oscillations occur around the angular momentum vector fixed in space, leading to what is referred to as wobbling motion. The excitation energy associated with wobbling motion is characterized by the wobbling frequency or wobbling energy. In the originally predicted wobbler [1], the wobbling frequency escalates with increasing spin.
For a triaxial rotor coupled with a high-j quasiparticle, two types of wobbling motions, longitudinal wobbler (LW) and transverse wobbler (TW), were proposed by Frauendorf and Dönau [2]. The existence condition for the TW is that the quasiparticle is bottom (particle) or top (hole) occupied in a j-shell, whereas for the LW, it is mid-shell occupied. In the LW, the quasiparticle angular momentum and the principal axis with the largest moment of inertia are parallel, while in the TW, they are perpendicular. Both TW and LW exhibit enhanced
$ I \to I-1 \;\; E2 $ transitions between adjacent wobbling bands, characterized by a series of rotational$ E2 $ bands corresponding to the different oscillation quanta (n). However, the wobbling frequency of the LW increases with spin as the originally predicted wobbler, while that of a TW decreases with spin. In Ref. [3], Chen and Frauendorf further introduced a more comprehensive classification for the wobbling motion based on the topology of the classical orbits visualized by the corresponding spin coherent state (SCS) maps (also known as the azimuthal plot in Refs. [4−6]). These maps present the probability distribution for the angular momentum orientation on the unit sphere projected on the polar angle (θ) and azimuthal angle (φ) plane. According to this classification, the LW corresponds to a revolution of total angular momentum$ {\boldsymbol{I}} $ around the axis with the largest moment of inertia, while the TW corresponds to a revolution of$ {\boldsymbol{I}} $ around an axis perpendicular to the axis with the largest moment of inertia. By adopting these scientific classifications and models, we have gained a deeper understanding of the wobbling motions exhibited by triaxial rotors coupled with high-j quasiparticles. This has enriched our knowledge of the dynamics and behavior of these complex systems.The study of wobbling motion has attracted considerable attention in the nuclear structure community. Experimental and theoretical research have both played important roles in understanding this unique phenomenon. In terms of experimental studies, significant progress has been made in exploring wobbling motion. The first experimental signal of wobbling motion was reported in 2001 in a triaxial, strongly deformed band in the nucleus
$^{163}$ Lu [7], which was later interpreted as TW [2]. Subsequently, the first wobbling motion in a normally deformed nucleus was reported in$^{135}$ Pr as TW [8]. Moreover, the evidence for LW was found in$ ^{187} $ Au, where the expected signature partner band was successfully identified [9]. To date, wobbling candidate bands have been experimentally observed in more than 15 nuclei across different mass regions:$ A\approx 100 $ [10], 130 [8, 11−17], 160 [7, 18−23], and 190 [9, 24]. Notably, experimental evidence for wobbling motion based on a hole-configuration has not been observed thus far. This highlights an area that urges further investigation to gain a complete understanding of wobbling motion.In theoretical research, the presence of wobbling motion was initially predicted using the triaxial rotor model [1]. After the wobbling motion was confirmed in the odd-A nuclei [7], the triaxial particle-rotor model (PRM) became the primary means of describing physical quantities related to the wobbling motion, such as energy spectrum and electromagnetic transition properties [2, 3, 6, 14, 25−28]. Additionally, some approximate methods for solving the PRM have also been utilized to study wobbling motion [29−33], and different explanations for transverse wobbling motion were given [29, 31]. Furthermore, the cranking model plus random phase approximation (RPA) [34−37], the cranking model plus collective Hamiltonian [38, 39], and the triaxial projected shell model [11, 37, 40, 41] have been applied to investigate wobbling motion. By constructing bases with total angular momentum as a good quantum number, the PRM restores rotational symmetry in the system and allows for a fully quantized treatment of energy spectra and electromagnetic transitions. Relative to other models, the PRM is simpler and requires less computation, making it more suitable for the systematic study of wobbling motion. Consequently, this work will employ the PRM.
Based on the provided information, it is important to note that the wobbling motion based on a hole-configuration has not yet been observed experimentally. Additionally, there is a lack of thorough theoretical studies on this particular type of wobbling. However, it has been suggested that the type of wobbling mode is determined by the characteristics of the coupled quasiparticle, assuming that the quasiparticle remains frozen in alignment with one of the rotor axes [2]. A qualitative claim has been made about the development of TW-LW-TW through a high-j shell with an increasing Fermi surface. Nonetheless, further investigation into the specific characteristics of the wobbling motion is needed.
In this work, we willl investigate the phenomenon of wobbling motion in a system comprising a triaxial rotor and a single quasiparticle using the PRM framework. Specifically, our analysis will focus on analyzing the changes in energy spectra, wobbling frequencies, electromagnetic transition probabilities, g-factors, angular momentum geometries, and static quadrupole moments (SQM) in relation to the characteristics of the coupled quasiparticle. Furthermore, we will conduct a detailed quantitative examination of the qualitative assertion of TW-LW-TW in a j-shell, as mentioned in Ref. [2]. By approaching these investigations from a scientific standpoint, we hope to provide valuable insights and contribute to the existing knowledge in this field.
-
In the following, we use the PRM and thus treat angular momentum as a good quantum number. In the PRM, the total nucleus is separated into two parts. One is the triaxial rotor, and the other is the valence quasiparticle. The total Hamiltonian of the PRM takes the form [1]
$ \hat{H}_ {\rm{PRM}}=\hat{H}_{\rm coll}+\hat{H}_{\rm intr}\, , $

(1) with
$ \hat{H}_{ \rm{coll}} $ representing the collective rotor Hamiltonian$ \hat{H}_{\rm coll} =\sum\limits_{k=1}^3 \frac{\hat{R}_k^2}{2\mathcal{J}_k} =\sum\limits_{k=1}^3 \frac{(\hat{I}_k-\hat{j}_k)^2}{2\mathcal{J}_k}, $

(2) where the index
$ k=1 $ , 2, 3 denotes the three principal axes of the body-fixed frame. Here,$ \hat{R}_k $ and$ \hat{I}_k $ are the angular momentum operators of the collective rotor and the total nucleus, respectively, and$ \hat{j}_k $ is the angular momentum operator of a valence nucleon. Moreover, the parameters$ \mathcal{J}_k $ are the three principal axis moments of inertia.For the intrinsic Hamiltonian of valence nucleons, we apply a simple single-j shell model, which is a good approximation for high-j intruder orbitals and suitable for the present model study. The single-j shell Hamiltonian is taken as
$ \hat{h}_p=\frac{1}{2}C\bigg\{\cos \gamma\bigg(\hat{j}_3^2-\frac{j(j+1)}{3}\bigg) +\frac{\sin \gamma}{2\sqrt{3}}\big(\hat{j}_+^2+\hat{j}_-^2\big)\bigg\}. $

(3) The angle γ serves as the triaxial deformation parameter, and the coefficient C is proportional to the quadrupole deformation parameter β. In addition, pairing is taken into account by means of the BCS-quasiparticle energy
$ \varepsilon_{\rm intr}^{(\nu)}=\sqrt{(e_\nu-\lambda)^2+\Delta^2}. $

(4) Here, the single-particle energy
$ e_\nu $ is obtained from the solution of the single-j shell Hamiltonian$ \hat{h}_p $ . The parameters λ and Δ are the Fermi surface and pairing gap, respectively. When λ increases gradually from the bottom to the top of a j-shell, the valence quasiparticle changes its characteristics from particle-like to hole-like.We diagonalize the PRM Hamiltonian by using the BCS one-quasiparticle states for the particle wave functions. Therefore, we cannot go to very high spin states, but the calculation is sufficient for drawing conclusions about the problems treated in the present paper. Accordingly, the Hamiltonian
$ \hat{H}_{\mathrm{PRM}}$ of the total nuclear is solved by diagonalizing in a strong-coupled basis$ |I M K j k\rangle= \sqrt{\frac{2 I+1}{16 \pi^2}} D_{M K}^I({\boldsymbol{\omega}})|j k\rangle, $

(5) in which
$ D_{MK}^I({\boldsymbol{\omega}}) $ are the usual Wigner-functions, depending on the three Euler angles$ {\boldsymbol{\omega}}=(\psi^\prime, \theta^\prime,\varphi^\prime) $ . Here, I denotes the total angular momentum quantum number of the odd-mass nuclear system (rotor plus particle), and K (M) is the projection onto the three-axis of the intrinsic (laboratory) frame. Furthermore, k is the three-axis component of the particle angular momentum$ {\boldsymbol{j}} $ in the intrinsic frame.The corresponding PRM eigenstates
$ |IM\nu\rangle $ are hence expanded as$ |IM\nu\rangle=\sum\limits_{K,k} C_{IKk}^{(\nu)} |I M K j k\rangle. $

(6) Under the requirement of the
$ {D}_2 $ symmetry of a triaxial nucleus, when K and k in the sum run from$ -I $ to I and from$ -j $ to j, respectively, their difference$ K-k $ must be even, and the following symmetry relation fixes one half of all coefficients:$ C_{I-K-k}^{(\nu)}=(-1)^{I-j}C_{IKk}^{(\nu)}. $

(7) One further notes that to construct the matrix of the PRM Hamiltonian, in comparison with the case excluding pairing, each single-particle matrix element needs to be multiplied by a pairing factor
$ u_\mu u_\nu + v_\mu v_\nu $ , with v being the conventional occupation factor and$ u^2+v^2=1 $ . -
The probability of the electromagnetic transitions
$ B(E2) $ and$ B(M1) $ can be obtained from the PRM wave function with the$ E2 $ and$ M1 $ operators [42−44].For the
$ E2 $ transitions, the corresponding operator is taken as$ \mathcal{M}(E2,\mu)=\sqrt{\frac{5}{16 \pi}}\hat{Q}_{2\mu}, $

(8) $ \hat{Q}_{2\mu} =D_{\mu 0}^{2} Q_{20}^{\prime} +\left(D_{\mu 2}^{2}+D_{\mu-2}^{2}\right) Q_{22}^{\prime}, $

(9) with the intrinsic quadrupole moments
$ Q_{20}^{\prime}=Q_0 \cos \gamma, \quad Q_{22}^{\prime}=\frac{1}{\sqrt{2}} Q_0 \sin \gamma, $

(10) where
$ Q_0 $ is the intrinsic charge quadrupole moment.For the
$ M1 $ transitions, the corresponding operator is$ \mathcal{M}(M1,\mu)=\sqrt{\frac{3}{4 \pi}} \frac{e \hbar}{2 M c} \left(g_p-g_R\right) \hat{j}_{\mu}, $

(11) with
$ \hat{j}_\mu $ denoting the spherical tensor of quasiparticle angular momentum in the laboratory frame$ \hat{j}_\mu=\left(\hat{j}_0=\hat{j}_3, \quad \hat{j}_{ \pm 1} =\frac{\mp\left(\hat{j}_1 \pm i \hat{j}_2\right)}{\sqrt{2}}\right), $

(12) and
$ g_p $ and$ g_R $ being the gyromagnetic factors of the quasiparticle and rotor. -
In the following, we outline the methods employed to calculate the g-factor. For an odd-mass nuclear system, the angular momentum of the rotor, denoted as
$ {\boldsymbol{R}} $ , and the angular momentum of the particle (proton), denoted as$ {\boldsymbol{j}} $ , are coupled to form the total spin$ {\boldsymbol{I}} $ . This coupling occurs according to the relation$ {\boldsymbol{R}}+{\boldsymbol{j}}={\boldsymbol{I}}. $

(13) The magnetic moment μ of this system is determined from the wave function
$ |I,M=I\rangle $ , which represents the rotational motion. Here, M corresponds to the quantum number associated with the projection of$ {\boldsymbol{I}} $ onto the z-axis in the laboratory frame. The calculation of μ involves the evaluation of the expectation value of the z-component of the total spin operator,$ \hat{I}_z $ , using the expression$ \mu=gI=\langle II|g\hat{I}_z|II\rangle=\langle II|g_p\hat{j}_{z}+g_R \hat{R}_{z}|II\rangle, $

(14) where
$ \hat{I}_{z} $ ,$ \hat{j}_{z} $ , and$ \hat{R}_z $ represent the z-components of the respective angular momentum operators. Additionally,$ g_p $ and$ g_R $ correspond to the gyromagnetic ratios of the proton-particle and the core, respectively. It is important to note that the output quantity g pertains to the entire nuclear system. In our current investigation, we adopt the values$ g_R=Z/A=0.41 $ for the rotor and$ g_p=1.21 $ for the$ h_{11/2} $ valence-proton. Here, the spin g-factor, denoted as$ g_s=3.35 $ , has been scaled down to 0.6 times that of a free proton.We utilize the generalized Landé formula to express the matrix element in Eq. (14) in terms of the scalar products of angular momentum operators. As a result, we obtain the following expression for the magnetic moment μ
$ \mu=\frac{\langle II|g_p {\boldsymbol{j}}\cdot{\boldsymbol{I}} + g_R {\boldsymbol{R}}\cdot{\boldsymbol{I}}|II\rangle}{I(I+1)} \langle II|\hat{I}_z|II\rangle. $

(15) Through some rearrangement of terms, we derive the g-factor of the entire nuclear system as follows:
$ \begin{aligned}[b] g&=\frac{\langle g_p {\boldsymbol{j}}\cdot{\boldsymbol{I}} + g_R {\boldsymbol{R}}\cdot{\boldsymbol{I}} \rangle}{I(I+1)} \\ &=g_R+(g_p-g_R)\frac{\langle {\boldsymbol{j}}\cdot{\boldsymbol{I}} \rangle}{I(I+1)} \\ &=\frac{1}{2}\left[(g_p+g_R)+(g_p-g_R)\frac{j(j+1)-\langle {\boldsymbol{R}}^2\rangle}{I(I+1)}\right]. \end{aligned} $

(16) Notably, the g-factor reflects the relative orientations between the expectation values of
$ {\boldsymbol{j}} $ and$ {\boldsymbol{I}} $ . Specifically, in the case where$ {\boldsymbol{j}}\perp {\boldsymbol{I}} $ , we have$ g=g_R $ . In contrast, if$ {\boldsymbol{j}} \parallel {\boldsymbol{I}} $ , we obtain$ g=g_R+(g_p-g_R)\sqrt{\frac{j(j+1)}{I(I+1)}}. $

(17) -
From the PRM wave functions, one can study the underlying angular momentum geometry for the considered system to justify the existence of the wobbling motion. The first quantities studied in the present work are the root mean square expectation values of the projections on the principal axes of the total nucleus for the total angular momentum
$ {\boldsymbol{I}} $ , the proton angular momentum$ {\boldsymbol{j}} $ , and the collective rotor angular momentum$ {\boldsymbol{R}} $ . They are calculated by [3]$ I_i=\sqrt{\langle \hat I^2_i\rangle}=\sqrt{\sum\limits_{KK'} \rho_{KK'}^{(\nu)}\hat I^2_{i;K'K}}, $

(18) $ j_i=\sqrt{\langle \hat j^2_i\rangle}=\sqrt{\sum\limits_{kk'} \rho_{kk'}^{(\nu)}\hat j^2_{i;k'k}}, $

(19) $ \begin{aligned}[b] R_i&=\sqrt{\langle \hat R^2_i\rangle}\\ &=\sqrt{\sum\limits_{KK'kk'} C_{IKk}^{(\nu)*}\big(\hat I_i -\hat j_i\big)^2_{KK'kk'}C_{IK'k'}^{(\nu)}}\ , \end{aligned} $

(20) where
$ \rho_{kk'}^{(\nu)} $ and$ \rho_{KK'}^{(\nu)} $ are the reduced density matrices$ \rho_{kk'}^{(\nu)} =\sum\limits_K C_{IKk}^{(\nu)}C_{IKk'}^{(\nu)*}, $

(21) $ \rho_{KK'}^{(\nu)} =\sum\limits_k C_{IKk}^{(\nu)}C_{IK'k}^{(\nu)*}, $

(22) constructed from the expanding coefficients
$ C_{IKk}^{(\nu)} $ of the PRM wave functions (6).The second quantity investigated in this study is the so-called azimuthal plot [4−6] (also known as SCS map [3]). It is calculated by [3]
$ \begin{aligned}[b] \mathcal{P}(\theta,\, \varphi)_{I\nu} =&\frac{2I+1}{4\pi}\sin\theta\\ & \times \sum\limits_{K,K'=-I}^I D^{I*}_{IK}(0,\,\theta,\,\phi) \rho^{(\nu)}_{KK'}D^{I}_{K'I}(0,\,\theta,\,\phi), \end{aligned} $

(23) which satisfies the normalization condition
$ \begin{array}{*{20}{l}} \displaystyle\int_0^\pi {\rm d} \theta & \displaystyle\int_0^{2\pi} {\rm d} \phi\; \mathcal{P}(\theta, \,\varphi)_{I\nu}=1. \end{array} $

(24) One notes that the relation between the tilted angles
$(\theta,\,\varphi)$ and the Euler angles${\boldsymbol{\omega}}=(\psi^\prime, \,\theta^\prime,\,\varphi^\prime)$ is$ \theta=\theta^\prime, \quad \varphi=\pi-\varphi^\prime, $

(25) where the z axis in the laboratory frame is chosen along the angular momentum.
-
In order to gain insights into the orientation of angular momenta, we investigate the static quadrupole moment (SQM) as another measurable quantity in this study. The SQM serves as an indicator of the nuclear charge distribution and can be calculated using the expression
$ \begin{array}{*{20}{l}} Q(I)=\langle II|\hat{Q}_{20}|II\rangle, \end{array} $

(26) where
$ \hat{Q}_{20} $ represents the quadrupole moment operator in the laboratory frame, as given in Eq. (9). By investigating the SQM, we can acquire valuable information regarding the spatial arrangement of angular momenta in the nucleus under study.One approach to calculating the SQM involves utilizing the expectation value of the squared total angular momentum components along the principal axes, denoted as
$ \langle \hat{I}_k^2 \rangle $ [27, 28]. By employing this method, the SQM can be expressed as the sum of two components$ Q(I) =Q_0(I)+Q_2(I), $

(27) $ Q_0(I) = \frac{3\langle\hat{I}_3^2 \rangle - I(I+1)}{(I+1)(2I+3)} Q_0'\cos{\gamma}, $

(28) $ Q_2(I) = \frac{\sqrt{3} (\langle\hat{I}_1^2 \rangle - \langle\hat{I}_2^2 \rangle)}{(I+1)(2I+3)} Q_0'\sin{\gamma}. $

(29) This formulation offers the advantage of directly obtaining information about the spin orientation from the SQM. However, it is important to note that this information may not always be unambiguous, as
$ Q(I) $ depends on all three expectation values$ \langle \hat{I}_k^2 \rangle $ , which are generally unknown. By incorporating these expressions, we can extract valuable insights into the angular momentum orientation as well as the interplay between the nuclear charge distribution and intrinsic properties of the system. -
In the following calculations, the system consisting of a triaxial rotor and a single quasiparticle located at the
$ h_{11/2} $ shell will be considered. The coefficient C in Eq. (3) for the single-particle Hamiltonian is taken as$ 0.25 $ MeV. The triaxial deformation parameter is taken as$ \gamma=30^\circ $ and$ 20^\circ $ for comparison. The pairing correlation of the particle is neglected for simplicity, i.e.,$ \Delta=0 $ is fixed. The Fermi surface is taken as$ \lambda=e_1 $ ,$ e_2 $ ,$ e_3 $ ,$ e_4 $ ,$ e_5 $ , and$ e_6 $ to simulate multiple valence particles coupled with the triaxial rotor. The$ e_1 $ -$ e_6 $ are the single-particle energies$ e_\nu $ obtained from the solution of the single-j shell Hamiltonian$ \hat{h}_p $ in Eq. (3). The moment of inertia for the triaxial rotor is taken as irrotational flow type$\mathcal{J}_k= \mathcal{J}_0\sin^2(\gamma- 2k\pi/3)$ with$ \mathcal{J}_0 = 20\; \hbar^2/ \rm{MeV} $ . One notes that the ratios between the three moments of inertia for the intermediate (m), short (s), and long (l) axes are$ \mathcal{J}_m/\mathcal{J}_s/\mathcal{J}_l = $ 1.00/ 0.25/0.25 for$ \gamma=30^\circ $ and$\mathcal{J}_m/\mathcal{J}_s/\mathcal{J}_l \approx $ 1.00/0.43/0.12 for$ \gamma=20^\circ $ . For the electromagnetic transition probabilities, the intrinsic charge quadrupole momentum$ Q_0 $ takes a value of$ 3.5\; e \rm{b} $ , and the g factor$ g_p-g_R = 0.7 $ with$ g_p=1.21 $ and$ g_R=0.41 $ . -
The calculated energy spectra of the yrast band (labeled as B1 for signature
$ \alpha=-1/2 $ and B2 for$\alpha= +1/2$ ) with the Fermi surface$ \lambda=e_1 $ ,$ e_2 $ ,$ e_3 $ ,$ e_4 $ ,$ e_5 $ , and$ e_6 $ are plotted relative to a rigid-rotor reference in Fig. 1 for the triaxial deformation parameters$ \gamma= 30^\circ $ and$ \gamma = 20^\circ $ . The energy difference between the bands B2 and B1 is calculated as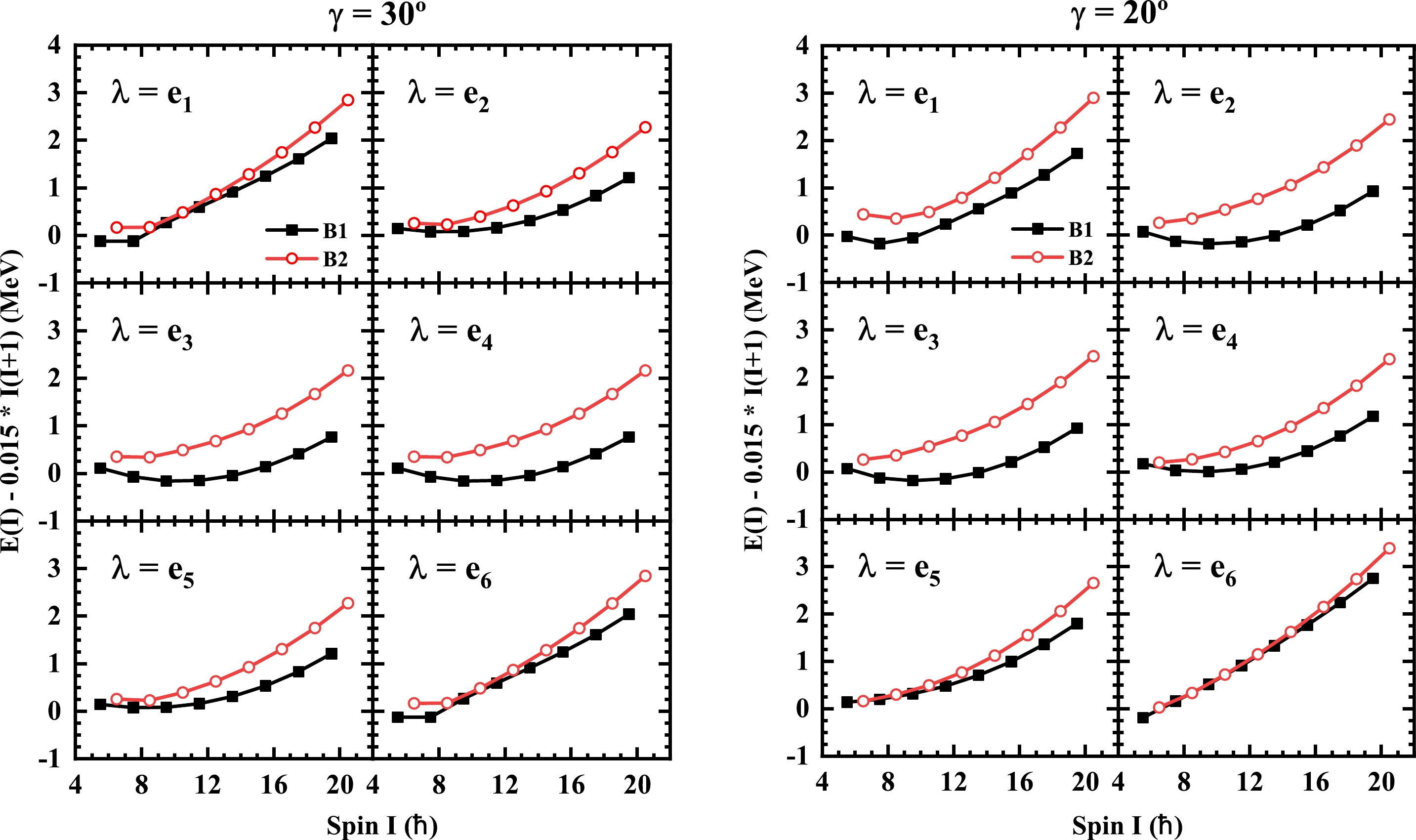
Figure 1. (color online) Energies relative to a rigid rotor reference of yrast and wobbling bands with the Fermi surface
$\lambda=e_1$ ,$e_2$ ,$e_3$ ,$e_4$ ,$e_5$ , and$e_6$ for the triaxial deformation parameters$\gamma= 30^\circ$ and$\gamma = 20^\circ$ .$ \begin{array}{*{20}{l}} \Delta E(I) =E_{ \rm{B2}}(I)-[E_{ \rm{B1}}(I+1)+E_{ \rm{B1}}(I-1)]/2, \end{array} $

(30) and the results are shown in Figs. 2(a)−(b). One notes that the total Hamiltonian considered in the present study is invariant under the transformation
$ \gamma \to 60^\circ-\gamma $ and$ \lambda=e_\nu \to \lambda=e_{7-\nu} $ . Therefore, for$ \gamma=30^\circ $ , the obtained energy spectra and their energy difference are identical for the Fermi surfaces$ e_\nu $ and$ e_{7-\nu} $ (c.f. Figs. 1 and 2(a)).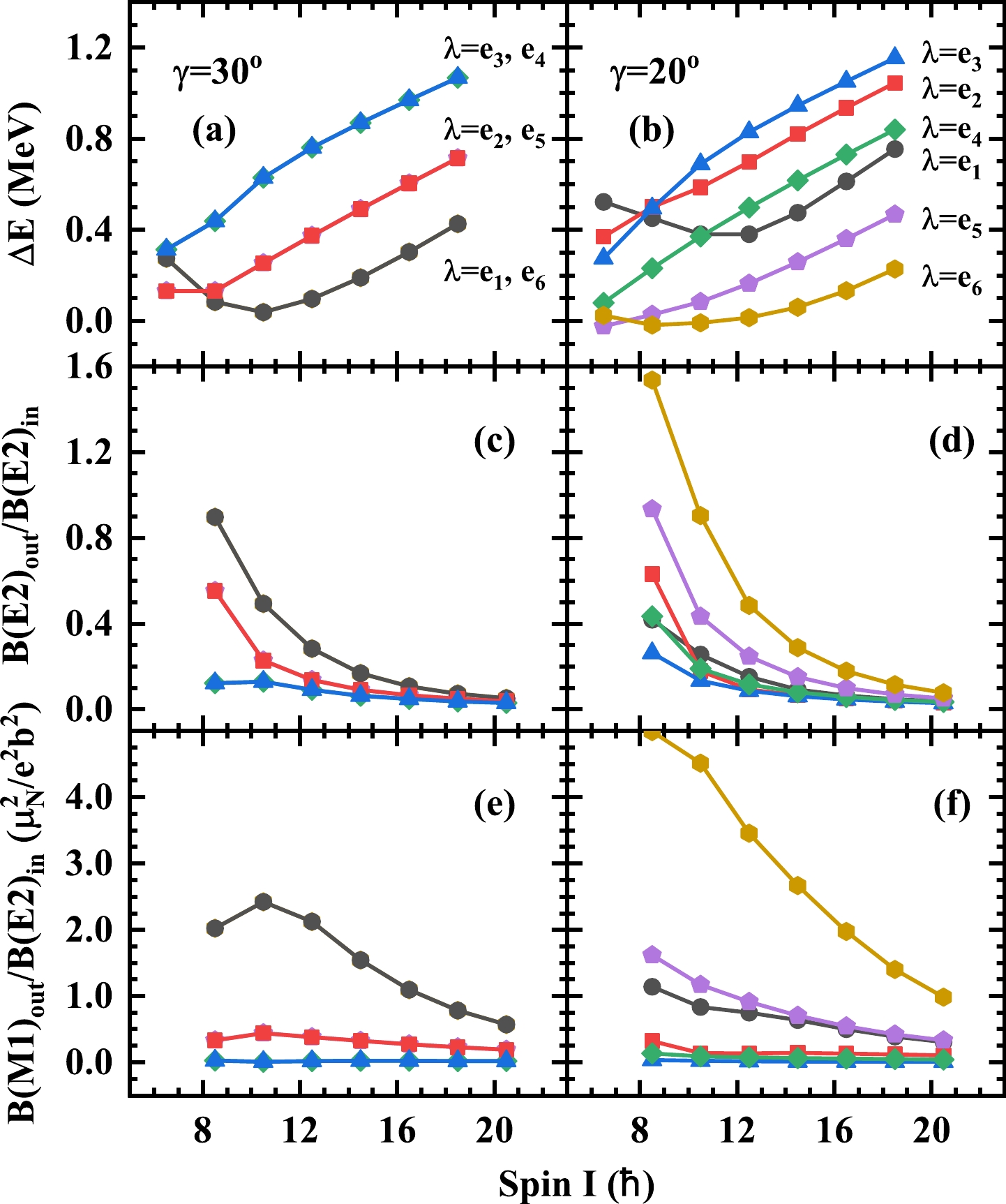
Figure 2. (color online) Energy difference between the bands B2 and B1
$ \Delta E $ as well as the ratios of$ B(E2)_{ \rm{out}}/B(E2)_{ \rm{in}} $ and$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ calculated by the PRM with the Fermi surface$ \lambda=e_1 $ ,$ e_2 $ ,$ e_3 $ ,$ e_4 $ ,$ e_5 $ , and$ e_6 $ for$ \gamma= 30^\circ $ and$ \gamma = 20^\circ $ . Here, the subscript "out" indicates the$ \Delta I=1 $ connecting transitions from band B2 to B1, while "in" indicates the$ \Delta I=2 $ transitions that connect band B2.When the Fermi surface λ changes from
$ e_1 $ to$ e_6 $ , the coupled valence particle changes from the bottom to the top of the$ h_{11/2} $ shell. Namely, the valence particle changes its characteristics from particle-like to hole-like. When$ \lambda=e_1 $ , namely a particle configuration, bands B2 and B1 come closer and separate with the increasing spin for both$ \gamma=30^\circ $ and$ 20^\circ $ . Correspondingly, the energy difference$ \Delta E $ between them decreases first and then increases. The critical spin values are$ I=21/2\hbar $ and$ 25/2\hbar $ for$ \gamma=30^\circ $ and$ 20^\circ $ , respectively. The larger critical spin value for$ \gamma=20^\circ $ is caused by the larger ratio of moments of inertia between s and m axes,$ \mathcal{J}_s/\mathcal{J}_m $ . For a wobbler, the$ \Delta E $ is treated as the wobbling energy. As pointed out in Ref. [2], the decreased$ \Delta E $ is the hallmark of TW, while the increased one corresponds to the LW. Thus, the calculated results imply a wobbling mode that changes from the transverse to the longitudinal one with the spin. Indeed, such a wobbling system has been observed experimentally, e.g., in$ ^{135} $ Pr [8].When
$ \lambda=e_6 $ , namely a hole configuration, bands B2 and B1 also come closer and separate with the increasing spin for both$ \gamma=30^\circ $ and$ 20^\circ $ . As aforementioned, the corresponding energy spectra are identical with$ \lambda=e_1 $ for$ \gamma=30^\circ $ , i.e., the critical spin is$ I=21/2\hbar $ as well. However, for$ \gamma=20^\circ $ , the critical spin is only up to$ I=17/2\hbar $ . The reduced critical spin is attributed to the reduced ratio of$ \mathcal{J}_l/\mathcal{J}_m $ from$ 0.25 $ at$ \gamma=30^\circ $ to$ \approx 0.12 $ at$ \gamma=30^\circ $ . One notes that in Ref. [2], the TW was predicted to exist in a hole configuration as well. However, the corresponding experimental evidence has not yet been reported. According to this study, the existence of TW in a hole configuration has been confirmed. Thus, further experimental efforts in this direction are suggested.When
$ \lambda=e_2 $ -$ e_5 $ , namely deviating from a particle or hole configuration, bands B2 and B1 are separated from the beginning of the rotation for both$ \gamma=30^\circ $ and$ 20^\circ $ . Correspondingly, the$ \Delta E $ increases with spin in all of the cases. As shown in Figs. 2(a)−(b), when$ \lambda=e_3 $ , the$ \Delta E $ is the largest. The increased behavior of the$ \Delta E $ is the characteristic of a LW, as suggested in Ref. [2]. Compared with the case of$ \lambda=e_1 $ , where the LW appears in the high spin region, in this case, the LW appears in the low spin region. Such kind of LW has also been observed, e.g., in$ ^{187} $ Au [9], where the wobbling band is built on a$ h_{9/2} $ configuration with the Fermi surface located close to the second energy level of the$ h_{9/2} $ shell. -
The experimental wobbling signatures on the electromagnetic transition probabilities, which are the
$ B(E2) $ values for transitions$ n \to n-1 $ between the adjacent wobbling excitations, are collectively enhanced. The wobbling motion of the entire charged body generates this phenomenon. This is in contrast with the case of signature partner bands, where the linking transitions are primarily$ M1 $ . In Figs. 2(c)-(f), we present the ratios of$ B(E2)_{ \rm{out}}/B(E2)_{ \rm{in}} $ and$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ for the$ \Delta I=1 $ connecting transitions from band B2 to B1 calculated with the Fermi surface$ \lambda=e_1 $ ,$ e_2 $ ,$ e_3 $ ,$ e_4 $ ,$ e_5 $ , and$ e_6 $ for$ \gamma= 30^\circ $ and$ \gamma = 20^\circ $ . Here, the subscript "out" indicates the$ \Delta I=1 $ connecting transitions from band B2 to B1, while "in" indicates the$ \Delta I=2 $ transitions that connect band B2. In general, the$ B(E2)_{ \rm{out}}/B(E2)_{ \rm{in}} $ and$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ values decrease with spin because the amplitude of the wobbling motion$ \propto 1/\sqrt{I} $ .For
$ \gamma=30^\circ $ ,$ B(E2)_{ \rm{out}}/B(E2)_{ \rm{in}} $ is collectively enhanced when$ \lambda=e_1 $ . In this case,$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ , which is of the order of$1\,\mu_N^2/e^2 \rm{b}^2$ , is relatively large. However, this is not expected for an ideal wobbling motion. The reason is that the wobbling motion is coupled to the vibrations of the proton and neutron currents against each other, i.e., the scissor mode, which can drop the$ M1 $ strength [35] but is not considered in the present PRM calculations. With the increase in the location of the Fermi surface, the$ B(E2)_{ \rm{out}}/B(E2)_{ \rm{in}} $ value decreases. Correspondingly, the$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ value also decreases. In particular, when λ increases to the middle shell ($ \lambda=e_3 $ or$ e_4 $ ), the transition probabilities of the magnetic dipole moment are almost zero and independent of the total spin. When λ continues to increase, both$ B(E2)_{ \rm{out}}/B(E2)_{ \rm{in}} $ and$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ increase. This is expected as the total PRM Hamiltonian considered is invariant under the transformation$ \lambda=e_\nu \to e_{7-\nu} $ for the considered triaxial deformation$ \gamma=30^\circ $ .The behaviors of the ratios
$ B(E2)_{ \rm{out}}/B(E2)_{ \rm{in}} $ and$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ at$ \gamma=30^\circ $ can be observed at$ \gamma=20^\circ $ as well. Namely, the magnitudes of both$ B(E2)_{ \rm{out}}/B(E2)_{ \rm{in}} $ and$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ decrease when the Fermi surface λ increases up to$ e_3 $ and then increase when the λ continues to increase. The decrease in the two ratios with increasing I becomes the most rapid when$ \lambda=e_6 $ , i.e., for a hole configuration. -
The upper panels of Fig. 3 present the results of calculations for the g-factor as a function of spin I, using the PRM for states in bands B1 and B2 with the Fermi surface
$ \lambda=e_1 $ ,$ e_2 $ ,$ e_3 $ ,$ e_4 $ ,$ e_5 $ , and$ e_6 $ for two different values of the triaxial deformation parameter$ \gamma=30^\circ $ and$ \gamma=20^\circ $ . Our calculations show that the calculated g-factors decrease with increasing spin I, which is mainly due to the denominator$ I(I+1) $ in Eq. (16), since$g_p -g_R=0.7$ is positive. Furthermore, we observe that, for the entire spin range, the g-factors for states in band B1 are larger than those for states in band B2. This suggests, according to Eq. (16), that the expectation value of the rotor angular momentum$ \langle {\boldsymbol{R}}^2\rangle $ is smaller in band B1 compared with that in band B2, which is induced by a wobbling motion (as shown in Figs. 4 and 5). We further note that the g-factor values are not highly sensitive to the Fermi surface or the triaxial deformation parameters used in our calculations. This indicates that the relative orientations between the expectation values of$ {\boldsymbol{j}} $ and$ {\boldsymbol{I}} $ , as well as the$ \langle {\boldsymbol{R}}^2\rangle $ , are not greatly affected by these factors. This phenomenon is illustrated by the variation of the rotor angular momentum R with spin I for different Fermi surfaces for the triaxial deformation parameters$ \gamma=20^\circ $ and$ 30^\circ $ in the lower panels of Fig. 3. The rotor angular momentum is calculated by$R=\sqrt{\langle {\boldsymbol{R}}^2\rangle} = \sqrt{\langle \hat{R}_s^2\rangle+\langle \hat{R}_m^2\rangle+\langle \hat{R}_l^2\rangle}$ . From the lower panels of Fig. 3, it can be observed that variations in the parameters of the Fermi surface and triaxial deformation have little impact on the angular momentum R of the rotor. This suggests that, while the orientation of quasiparticle angular momentum is influenced by the Fermi surface (c.f. Figs. 4 and 5) and the rotor is assumed to be associated with triaxial deformation, the magnitude of the angular momentum vector R is not significantly affected by changes in the Fermi surface and triaxial deformation. This behavior can be attributed to conserving the total angular momentum$ {\boldsymbol{I}}={\boldsymbol{R}}+{\boldsymbol{j}} $ , where the particle angular momentum$ {\boldsymbol{j}} $ remains a good quantum number in the PRM.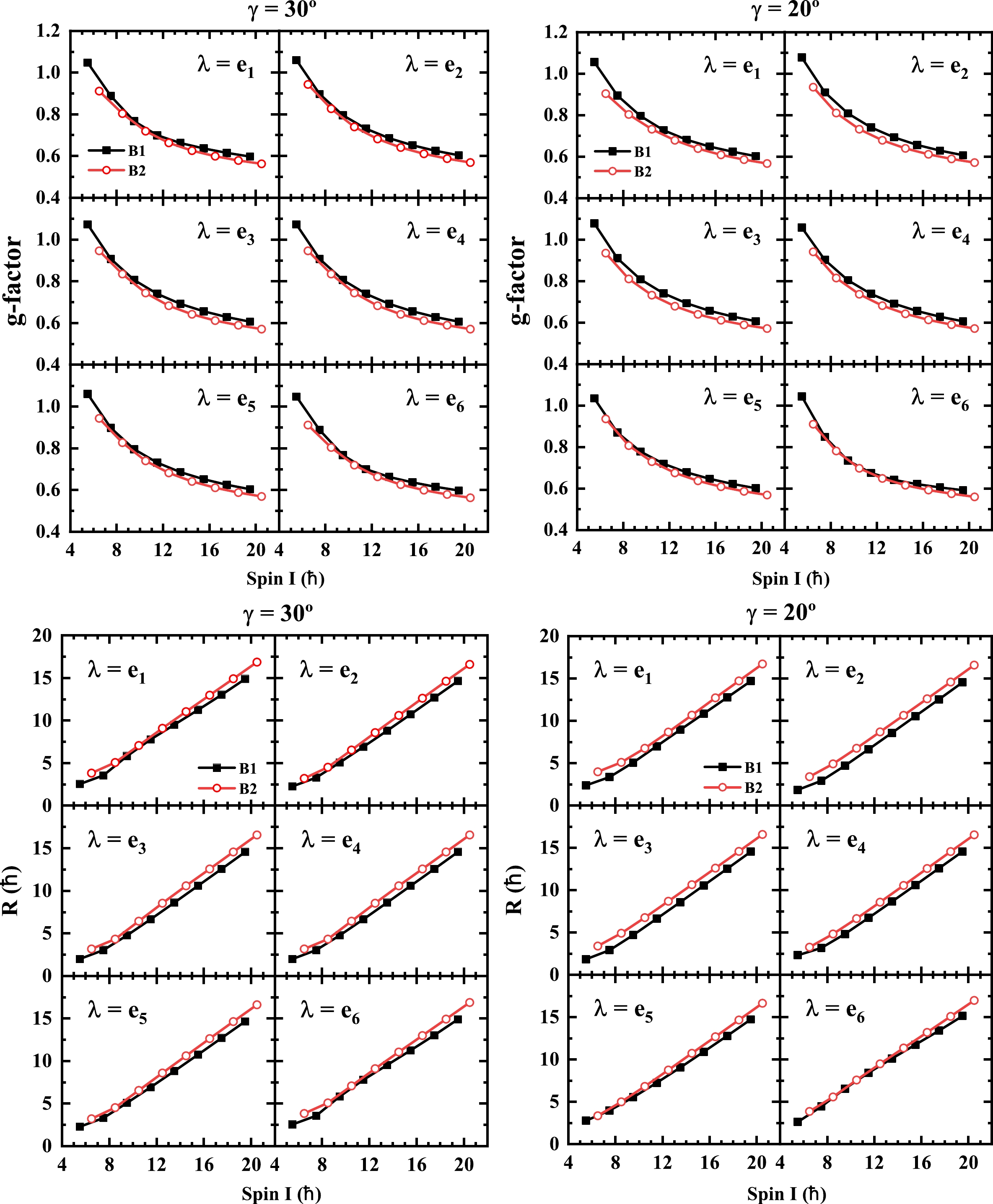
Figure 3. (color online) Calculated g-factors (upper panels) and rotor angular momentum
$R=|{\boldsymbol{R}}|=\sqrt{\langle \hat{R}_s^2\rangle +\langle \hat{R}_m^2\rangle+\langle \hat{R}_l^2\rangle}$ (lower panels) of yrast and wobbling bands with the Fermi surface$\lambda=e_1$ ,$e_2$ ,$e_3$ ,$e_4$ ,$e_5$ , and$e_6$ for the triaxial deformation parameters$\gamma= 30^\circ$ and$\gamma = 20^\circ$ .
Figure 4. (color online) Components along the intermediate (m, squares), short (s, circles), and long (l, triangles) axes of the angular momenta of the core
$ R_k=\langle \hat{R}_k^2\rangle^{1/2} $ , valence particle$ j_k=\langle \hat{j}_k^2\rangle $ , and total nucleus$ I_k=\langle \hat{I}_k\rangle^{1/2} $ for bands B1 and B2 calculated by the PRM with the Fermi surface$ \lambda=e_1 $ ,$ e_2 $ , and$ e_3 $ for$ \gamma= 30^\circ $ .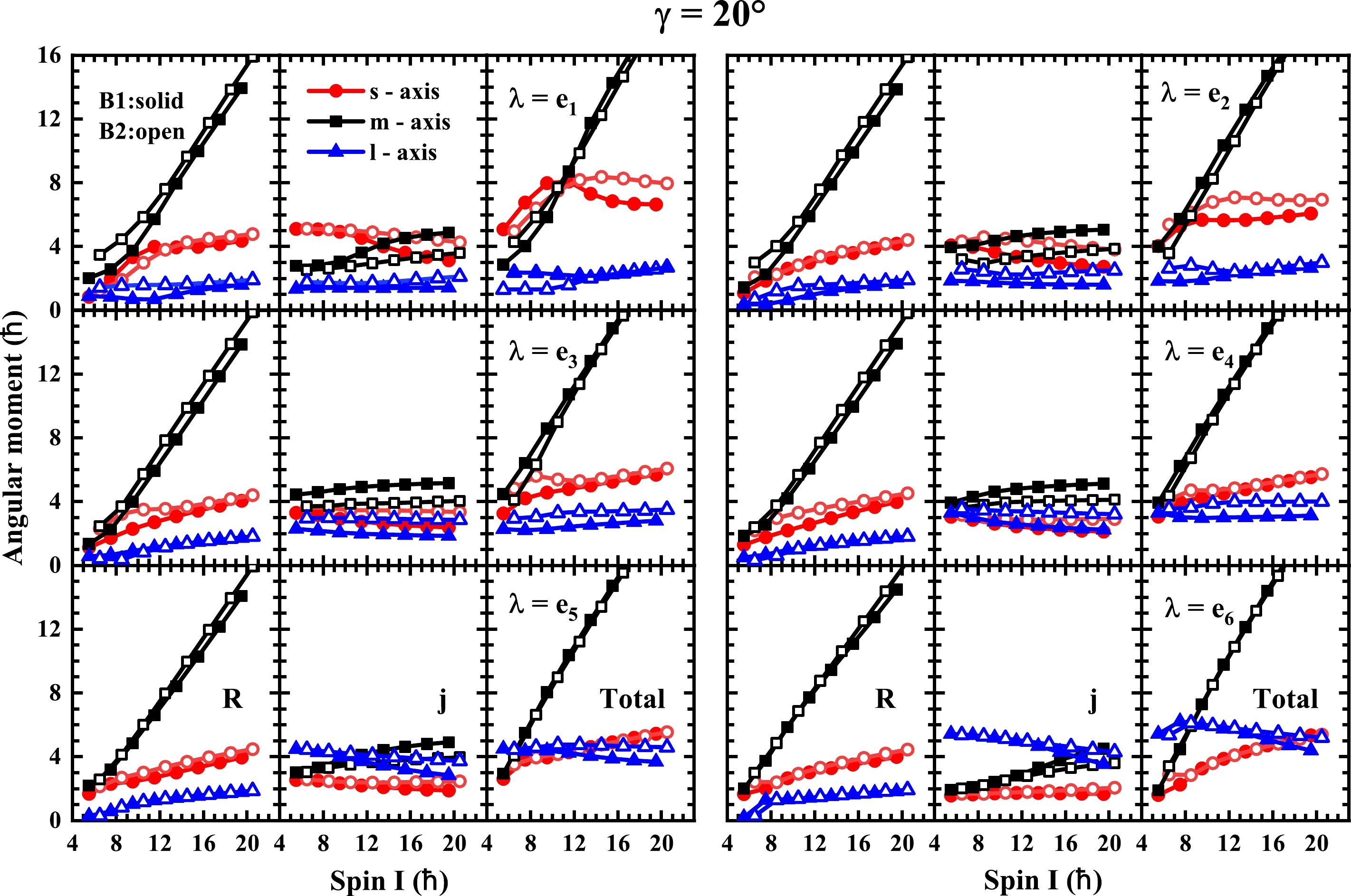
Figure 5. (color online) Same as Fig. 4, but with the Fermi surface
$\lambda=e_1$ ,$e_2$ ,$e_3$ ,$e_4$ ,$e_5$ , and$e_6$ for$\gamma= 20^\circ$ . -
Figures 4 and 5 illustrate how the root mean square angular momentum components along the intermediate (m), short (s), and long (l) axes of the rotor
$ {\boldsymbol{R}} $ , the particle$ {\boldsymbol{j}} $ , and the total nucleus$ {\boldsymbol{I}} $ change with spin I for the bands B1 and B2 for$ \gamma= 30^\circ $ and for$ \gamma= 20^\circ $ , respectively. For$ \gamma=30^\circ $ , the invariance of the Hamiltonian under the transformation$ \lambda=e_\nu \to e_{7-\nu} $ is reflected in the fact that the s and l components of the angular momentum are interchanged when$ \lambda=e_\nu \to e_{7-\nu} $ . Hence, only the results with$ \lambda=e_1 $ ,$ e_2 $ , and$ e_3 $ are shown in Fig. 4.According to Fig. 4, for
$ \gamma= 30^\circ $ , the variation of the rotor angular momentum components on the three principal axes with the total spin has little relationship with the choice of Fermi surface. The$ {\boldsymbol{R}} $ of the rotor mainly aligns with the m axis, while its l and s components stay small because the moment of inertia for rotation around the m axis is much larger than that of the l and s axes.For the angular momentum of the particle with
$ \lambda=e_1 $ , it is mainly aligned along the s axis ($ j_s \approx 5\hbar $ ) in the region$ I \leq 21/2\hbar $ because it maximizes the overlap of the particle orbit with the triaxial core, such that$ {\boldsymbol{j}} $ is approximately perpendicular to the m axis, presenting a TW angular momentum geometry. From$ I=23/2\hbar $ upward, the particle angular momentum shows a clear trend to align towards the m axis, driven by the Coriolis interaction between the particle and the collective core. As a result, the wobbling mode changes from the TW to LW mode, and$ \Delta E $ changes its behavior from decreasing to increasing. When the Fermi surface rises, the s component of$ {\boldsymbol{j}} $ becomes increasingly smaller while the m component becomes increasingly larger. When$ \lambda=e_3 $ , the particle aligns its angular momentum along the m axis, which presents the LW angular momentum geometry.In Ref. [45], for the axial limits
$ \gamma=0^\circ $ , a particle at the bottom of a shell was called a RAL (rotational aligned) particle, as it is very easily rotationally aligned. A hole at the top of a shell was called a DAL (deformation aligned) hole, as it is aligned with the symmetry axis of the deformed field. A mid-shell quasiparticle was called a FAL (Fermi aligned) quasiparticle, which corresponds to a coupling that prefers an angle of about$ 45^\circ $ with respect to the l axis. The RAL-DAL classification was introduced for axial nuclei to indicate whether the Coriolis force or deformed potential wins. In Ref. [46], the RAL-DAL classification was further extended to the triaxial case, where one has two axes (s and l) to which the quasiparticle aligns for DAL. It was pointed out that as the quasiparticle$ \lambda=e_1 $ and$ e_6 $ are aligned with s and l axes, both of them are DAL, namely DALs and DALl, respectively. Adopting the same classification terminology for the quasiparticle in a single-j shell, one concludes that the DALs particle or DALl hole configuration can establish a TW mode. Hence, we distinguish the two kinds of TW as DALs-TW and DALl-TW, respectively. In addition, the FAL quasiparticle configuration can form a LW mode.The coupling of
$ {\boldsymbol{R}} $ and$ {\boldsymbol{j}} $ gives the behavior of the total angular momentum$ {\boldsymbol{I}} $ . One clearly sees from Fig. 4 that, for the TW regime,$ {\boldsymbol{I}} $ revolves around the s axis if the quasiparticle is a DALs particle or a DALl hole. For the LW regime,$ {\boldsymbol{J}} $ revolves around the m axis. The picture is consistent with the generalized wobbling mode classification in Ref. [3]. Notably, the growth of the total angular momentum$ {\boldsymbol{I}} $ is essentially generated by an increase in the core angular momentum component along the wobbling axis. For example,$ R_s $ increases if it is a DALs-TW, and$ R_l $ increases if it is a DAL-TW. On the other hand,$ R_m $ increases in the LW region . However, the corresponding particle angular momentum$ {\boldsymbol{j}} $ stays almost constant.The behaviors of the angular momentum components of the rotor, particle, and the total nucleus appearing at
$ \gamma= 30^\circ $ can be observed at$ \gamma= 20^\circ $ , as shown in Fig. 5, which displays the angular momentum components as functions of spin I calculated with the Fermi surface$ \lambda=e_1 $ ,$ e_2 $ ,$ e_3 $ ,$ e_4 $ ,$ e_5 $ , and$ e_6 $ . The rotor angular momentum$ {\boldsymbol{R}} $ mainly aligns with the m axis, regardless of the choice of Fermi surface. In addition, the DALs particle aligns with the s axis, and the DALl hole aligns with the l axis, both of which give the TW mode. The FAL quasiparticle aligns with the m axis and gives a LW mode. Moreover, the total angular momentum$ {\boldsymbol{I}} $ revolves around the s axis if it is DALs-TW, or the l axis if it is DALl-TW. For the LW regime, it revolves around the m axis. The DALl-TW does not persist as stably as the DALs-TW. This is because the moment of inertia for rotation around the l axis$ \mathcal{J}_l $ is much smaller than that of the m axis$ \mathcal{J}_m $ ,$ \mathcal{J}_l/\mathcal{J}_m\approx 0.12 $ . Consequently, the m component of the rotor angular momentum$ R_m $ increases rapidly when the rotation begins so that$ I_m $ quickly takes the place of$ I_l $ and presents an LW characteristic. As shown in Fig. 2(b), this results in increased wobbling energy$ \Delta E $ from a small spin value.The angular momentum geometry can also be visualized clearly by the orientation profiles of the angular momentum on the
$(\theta,\, \varphi)$ plane$\mathcal{P}(\theta,\,\varphi)$ , i.e., the azimuthal plots [4−6] (also known as the spin coherent state (SCS) maps [3]). Here,$(\theta,\, \varphi)$ are the tilted angles of the total angular momentum with respect to the intrinsic reference frame. In the calculations, 1, 2, and 3 axes are chosen as the s, m, and l axes of the triaxially deformed body, respectively.Figure 6 shows how the
$\mathcal{P}(\theta,\,\varphi)$ develops with the spin in bands B1 and B2 for$ \gamma= 30^\circ $ with$ \lambda=e_1 $ ,$ e_2 $ ,$ e_3 $ ,$ e_4 $ ,$ e_5 $ , and$ e_6 $ . The distributions$\mathcal{P}(\theta,\,\varphi)$ are centered on the$ \theta=90^\circ $ plane, corresponding to the very small l component of$ {\boldsymbol{I}} $ shown in Fig. 4. When$ \lambda=e_1 $ , the profile for band B1 exhibits the features of a zero-phonon state. It is symmetric with respect to$ \varphi=0^\circ $ and has a maximum at$ \varphi=0^\circ $ at$ I=11/2\hbar $ , corresponding to the maximal alignment of$ {\boldsymbol{I}} $ with the s axis. With increased spin, the orientation of the total angular momentum$ {\boldsymbol{I}} $ is driven by the increasing m component of the rotor angular momentum$ {\boldsymbol{R}} $ and gradually deviates from the s axis starting from$ I=19/2\hbar $ . The planar rotation mode in the$ sm $ plane appears due to the competition between the particle$ {\boldsymbol{j}} $ and rotor$ {\boldsymbol{R}} $ . The total angular momentum$ {\boldsymbol{I}} $ finally moves to the m axis at$ I=35/2\hbar $ . For band B2, the profile shows that it is the one-phonon wobbling excitation, which is φ-antisymmetric with a minimum at$ \varphi=0^\circ $ at$ I=13/2\hbar $ . The maximal probabilities lie on a rim revolving around the s axis, which reflects the wobbling motion (precession) of$ {\boldsymbol{I}} $ around the s axis. This is the picture of the DALs-TW. At high spins ($ I \geq 29/2\hbar $ ), the excitation from the band B1 into the band B2 is LW about the m axis. This is in accordance with the fact that the φ coordinate of the maxima of$\mathcal{P}(\theta,\,\varphi)$ in the band B2 are smaller than those in band B1. In particular, the zero-phonon state at$ I=35/2\hbar $ peaks at$ \varphi=\pm 90^\circ $ (m axis), while the one-phonon state at$ I=37/2\hbar $ is at a minimum there. A similar LW scenario can be found in the$ \lambda=e_2 $ and$ e_3 $ cases for high spin states, as shown in Fig. 6. However, one notes that the LW is not formed immediately at the beginning of the rotation for$ \lambda=e_2 $ . Instead, the planar rotation modes in the$ sm $ plane that appear due to$ j_s $ and$ R_m+j_m $ are comparable, as shown in Fig. 4. Consequently, the increase in$ \Delta E $ is very slow at$ I\leq 17/2\hbar $ , as shown in Fig. 2(a). When$ \lambda=e_4 $ ,$\mathcal{P}(\theta,\,\varphi)$ for band B1 shows a principal axis rotation around the m axis in the entire spin region, similar to that for$ \lambda=e_3 $ . For band B2, the precession of$ {\boldsymbol{I}} $ around the m axis is clearly visualized in$ I\geq 21/2\hbar $ , as expected for a LW mode. When$ \lambda=e_5 $ , band B1 exhibits a planar rotation in the$ lm $ plane at$ I=11/2\hbar $ , followed by a rotation around the m axis at higher spins. Similarly, band B2 also demonstrates a planar rotation at$ I=13/2\hbar $ , followed by an LW mode at higher spin regions. For$ \lambda=e_6 $ , the maximal$\mathcal{P}(\theta,\,\varphi)$ of$ I=11/2\hbar $ in band B1 is located around$ (\theta\approx 20^\circ, \varphi=\pm 90^\circ) $ and$(\theta\approx 160^\circ, \;\varphi=\pm 90^\circ)$ , indicating a principal axis rotation around the l axis. This behavior is attributed to the increased l component of the particle angular momentum$ j_l $ . The DALl-TW is observed at$ I=13/2\hbar $ , with nodes present at$ \varphi=0^\circ $ and$ 180^\circ $ . Above the DALl-TW region, the LW mode appears. The energy difference$ \Delta E $ between the two bands increases slowly, as shown in Fig. 2(b). Therefore, for a DALl configuration, the rotational mode changes from the DALl-TW mode to planar rotation mode and eventually to the LW mode.
Figure 6. (color online) Density profiles for the orientation of the angular momentum on the
$(\theta, \,\varphi)$ plane, calculated at$I=11/2$ ,$19/2$ ,$27/2$ , and$35/2\hbar$ for band B1 and$I=13/2$ ,$21/2$ ,$29/2$ , and$37/2\hbar$ for band B2, with$\gamma= 30^\circ$ and$\lambda=e_1$ ,$e_2$ ,$e_3$ ,$e_4$ ,$e_5$ , and$e_6$ . Here, θ is the angle between the total spin${\boldsymbol{I}}$ and the l axis, and φ is the angle between the projection of${\boldsymbol{I}}$ onto the$sm$ plane and the s axis.The probability density distributions
$\mathcal{P}(\theta,\,\varphi)$ for the orientation of the total angular momenta$ {\boldsymbol{I}} $ calculated for$ \gamma= 20^\circ $ with$ \lambda=e_1 $ ,$ e_2 $ ,$ e_3 $ ,$ e_4 $ ,$ e_5 $ , and$ e_6 $ are shown in Fig. 7. The results of$ \lambda=e_1 $ ,$ e_2 $ , and$ e_3 $ are quite similar to those for$ \gamma= 30^\circ $ . The differences manifested include that the distribution$\mathcal{P}(\theta,\,\varphi)$ along the θ direction is more compressed, and at$ I=19/2\hbar $ , it still exhibits a rotation around the s axis due to the larger ratio of$ \mathcal{J}_s/\mathcal{J}_m \approx 0.43 $ and smaller ratio of$ \mathcal{J}_l/\mathcal{J}_m \approx 0.12 $ at$ \gamma= 20^\circ $ . In comparison,$ \mathcal{J}_s/\mathcal{J}_m=\mathcal{J}_l/\mathcal{J}_m=0.25 $ at$ \gamma= 30^\circ $ . When$ \lambda=e_4 $ , the$\mathcal{P}(\theta,\,\varphi)$ for band B1 shows a planar rotation in the$ lm $ plane at$ I=11/2\hbar $ and a rotation around the m axis in the higher spin region. For band B2, the precession of$ {\boldsymbol{I}} $ around the m axis is clearly visualized in$ I\geq 21/2\hbar $ , as expected for the LW mode. When$ \lambda=e_5 $ and$ e_6 $ , the LW mode appears in the higher spin states. As shown in Fig. 5, this is due to the increased l component of the particle angular momentum$ j_l $ . Below the LW region, the planar rotation mode in the$ lm $ plane appears. In Ref. [3], such a mode is named the flipping mode. Correspondingly,$ \Delta E $ between the two bands increases slowly, as shown in Fig. 2(b). In the lower spin region, the DALl-TW is observed at$ I=13/2\hbar $ when$ \lambda=e_6 $ . Hence, for a DALl configuration, the rotational mode changes from the DALl-TW mode to planar rotation mode and finally to the LW mode.
Figure 7. (color online) Same as Fig. 6, but for
$\gamma= 20^\circ$ .Therefore, our study demonstrates the development of TW-LW-TW through the j-shell as the Fermi surface increases. Furthermore, we provide a quantitative assessment of the qualitative claim made in Ref. [2].
-
The SQM serves as an experimental observable that effectively reflects the geometries of angular momentum. In Fig. 8, we present our computational results for the SQMs as a function of the spin I for bands B1 and B2, with Fermi surface
$ \lambda=e_1 $ ,$ e_2 $ ,$ e_3 $ ,$ e_4 $ ,$ e_5 $ , and$ e_6 $ , using the PRM. The calculations are performed for two distinct values of the triaxial deformation parameter$ \gamma=30^\circ $ and$ \gamma=20^\circ $ . To ensure consistency, we adopt a modification by replacing the triaxial deformation parameter γ with$ \gamma+240^\circ $ , which results in an equivalent shape. Consequently, the first contribution$ Q_0 $ nearly vanishes due to the smallness of$ \cos(\gamma+240^\circ) = -0.173 $ for$ \gamma=20^\circ $ ; this value is zero for$ \gamma=30^\circ $ . The modification enhances the potential to obtain valuable information about the angular momentum components from the second contribution$ Q_2(I) $ . Importantly, with this specific choice, the assignment of principal axes is defined as follows:$ 1 \to s $ ,$ 2 \to l $ , and$ 3 \to m $ .
Figure 8. (color online) Calculated static quadrupole moments of yrast and wobbling bands with the Fermi surface
$ \lambda=e_1 $ ,$ e_2 $ ,$ e_3 $ ,$ e_4 $ ,$ e_5 $ , and$ e_6 $ for triaxial deformation parameter values$ \gamma= 30^\circ $ and$ \gamma = 20^\circ $ .When
$ \gamma=30^\circ $ , the s and l components of the angular momentum experience an interchange when$\lambda=e_\nu \to e_{7-\nu}$ . Consequently, the corresponding values of SQM exhibit an opposite behavior to each other. Specifically, when$ \lambda=e_1 $ , the SQM of band B1 is greater than that of band B2 in the low spin region. This observation aligns with the concept of the DALs-TW, in which the total angular momentum precesses around the s axis, and the s axis component of band B2 becomes smaller than that of band B1. In the high spin region, however, a transition occurs wherein the SQM of band B1 becomes smaller than that of band B2. This behavior suggests the collapse of the TW and the gradual emergence of the LW mode. Similar patterns can be observed for cases with a higher Fermi surface or for the scenario of$ \gamma=20^\circ $ . Therefore, based on these findings, it can be concluded that the SQM serves as a valuable experimental observable for effectively capturing the transition of the wobbling mode from the TW to the LW. By utilizing the SQM as an analytical tool, a deeper understanding of the dynamics and evolution of the wobbling motion can be achieved, enabling further insights into the underlying nuclear properties and their interplay. -
The phenomenon of wobbling motion in a system comprising a triaxial rotor and a single quasiparticle is investigated using the PRM. Our analysis focuses on exploring the variations in energy spectra, wobbling frequencies, electromagnetic transition probabilities, g-factors, angular momentum geometries, and static quadrupole moments based on the characteristics of a coupled quasiparticle. Specifically, we examine the
$ h_{11/2} $ configuration with triaxial deformation parameters$ \gamma=30^\circ $ and$ 20^\circ $ .By extending the work of Ref. [2], our study demonstrates the development of TW-LW-TW through the j-shell as the Fermi surface increases. Furthermore, we provide a quantitative assessment of the qualitative claim made in the reference. Our findings reveal that the location of the Fermi surface and the characteristic of the valence quasiparticle decisively influence the behavior of
$ \Delta E $ with respect to spin, electromagnetic transition probabilities, g-factors, and angular momentum geometries as follows:(i) A DALs particle or DALl hole has been found to exhibit a parabolic wobbling energy
$ \Delta E $ . On the other hand, a FAL quasiparticle has been observed to only show a monotonic increase in$ \Delta E $ .(ii) A DALs particle or DALl hole significantly enhances inter-band transition probabilities. Conversely, observations suggest that inter-band transition probabilities are suppressed in the case of a FAL quasiparticle.
(iii) The variations in the ratios
$ B(E2)_{ \rm{out}}/B(E2)_{ \rm{in}} $ and$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ exhibit distinct patterns compared to the changes observed in the energy difference$ \Delta E $ between two bands as the Fermi surface increases. Higher values of$ \Delta E $ are associated with lower ratios of$ B(E2)_{ \rm{out}}/ B(E2)_{ \rm{in}} $ and$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ , whereas lower$ \Delta E $ values correspond to higher ratios of$ B(E2)_{ \rm{out}}/B(E2)_{ \rm{in}} $ and$ B(M1)_{ \rm{out}}/B(E2)_{ \rm{in}} $ .(iv) The g-factors for states in band B1 are larger than those for states in band B2, induced by a wobbling motion. The g-factor values are not very sensitive to the Fermi surface and the triaxial deformation parameters.
(v) The DALs particle exhibits alignment along the s axis, while the DALl hole demonstrates alignment along the l axis. This alignment of the particle and hole enables the generation of the TW mode. Additionally, the FAL quasiparticle aligns itself with the m axis, resulting in the emergence of the LW.
(vi) The total angular momentum
$ {\boldsymbol{I}} $ in a DALs-TW system revolves around the s axis, whereas in a DALl-TW system, it revolves around the l axis. In addition, it revolves around the m axis in a LW system.(vii) The DALl-TW mode exhibits lower stability compared to the DALs-TW one at
$ \gamma=20^\circ $ . The rotational mode undergoes rapid transitions, shifting from the DALl-TW mode to the planar rotation mode and, ultimately, to the LW mode.(viii) The SQM serves as a valuable experimental observable for effectively capturing the transition of the wobbling mode from the TW to LW mode.
The DALs-TW and LW phenomena have been extensively documented. However, the existence of DALl-TW remains unconfirmed. Consequently, it is highly recommended that future experimental efforts focus on investigating the occurrence of DALl-TW to attain a comprehensive comprehension of the wobbling motion. Considering this, theoretical calculations for specific nuclides for which the wobbling motion is built on a hole configuration will be carried out in the future. Moreover, it should be noted that very high spin energy levels cannot be solely explained by assuming a rigid triaxial core and one quasiparticle. Several other effects, such as multi-particle modes, can significantly influence the energy spectra and will be considered in future research.
-
We thank Professor Stefan Frauendorf for helpful suggestions.
Wobbling motion for a triaxial rotor plus a single quasiparticle
- Received Date: 2023-12-02
- Available Online: 2024-03-15
Abstract: Wobbling motion in a system comprising a triaxial rotor and a single quasiparticle is studied employing the particle-rotor model. The energy spectra, wobbling frequencies, electromagnetic transition probabilities, g-factors, angular momentum components, spin coherent state maps, and static quadrupole moments are investigated. These investigations were conducted with regard to the Fermi surface transitioning from the lowest





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: