Further monopole effects in neutron-rich Sb isotopes

The study of neutron-rich nuclei near $ ^{132} $Sn is an interesting topic not only for nuclear physics but also for nuclear astrophysics [1, 2]. The magic nature of $ ^{132} $Sn is explored extensively in both experiments and shell model theories [3−5]. The shell model describes well the magic numbers of protons (neutrons) 2, 8, 28, 50, and 82, as well as the neutron number 126 [6]. Its application range is expanded by some works published recently [7−10]. The evolution of single-particle states are essential to modify theoretical models and predict properties of unknown nuclei. In addition, unstable nuclei need a suitable interaction to predict their structural inputs for nuclear astrophysics. The rapid neutron-capture process (r-process) is responsible for approximately half of the elements heavier than Fe in our solar system [11]. Properties of neutron-rich nuclei near the N = 82 shell are important to understand the formation of the second r-process peak $ A \approx 130 $ [12, 13]. The calculations in N = 82 isotones have obtained strong evidence for the persistence of the N = 82 closed shell [14]. The observed ground-state inversions from $ ^{130} $In ($ ^{129} $Cd) to $ ^{128} $In ($ ^{127} $Cd) are explained well by a regular correlation between the neutron orbits $ h_{11/2} $ and $ d_{3/2} $ in the hole nuclei region of $ ^{132} $Sn [15].

With one proton above the Z = 50 shell, the Sb isotopes can be used to study the single-particle evolution in the proton major shell Z = (50, 82) by adding more neutrons. Different effects of tensor forces are discussed in the monopole-driven shell evolutions [16−20]. The monopole correction terms are necessary to modify the interactions that are derived from realistic two-body potentials (without three-body contributions) [21−23]. The monopole effects will be enhanced when the proton(neutron) number is close to the shell closure. For example, the ground state inversion in $ ^{129}_{48} $Cd$ _{81} $ is predicted to be driven by an attractive monopole effect between proton orbit $ g_{9/2} $ and neutron orbit $ h_{11/2} $ [24]. In this case, the first excited state (11/2$ ^- $) in $ ^{131} $Sn will be reversed into ground state when adding two proton holes in $ ^{129} $Cd. This prediction was confirmed recently [25].

In experiments, the ground state of $ ^{136} $Sb is confirmed as $ J^{\pi} = 1^- $ coupled by configuration $ \pi g_{7/2} \nu f^3_{7/2} $ [26]. This assignment is also supported by comparison with$ ^{212} $Bi, in which the ground state is 1$ ^- $ level coupled by configuration $ \pi h_{9/2} \nu g^3_{9/2} $. In $ ^{135} $Sb, the excited states populated in spontaneous fission of $ ^{248} $Cm are studied by means of prompt γ spectroscopy [27]. The information of the excited state in Sb isotopes is available in the neutron range N = [54, 84], and the ground state is 5/2$ ^+ $ up to N = 70 [28]. The excited state 7/2$ ^+ $ changes to the ground state of odd-A Sb isotopes when the neutron number reaches $ N \geq 72 $, and the first excited level 5/2$ ^+ $ continues growing to 962 keV when N = 82. This 5/2$ ^+ $ state drops to 282 keV in $ ^{135} $Sb when N = 84 [29, 30]. Shell-model calculations reproduce the energy drop by employing a realistic effective interaction [31, 32]. The drastic shrinking of the first excited state 5/2$ ^+ $ provides an evidence for proton single-particle evolution as the neutron number increases above the N = 82 shell.

Recently, the first experimental information of excited states was obtained in $ ^{137} $Sb [30]. The datum (5/2$ ^+ $) of this nucleus is reported at 84 keV, which confirms the shrinking tendency of the first excited state 5/2$ ^+ $ at N = 86. Whether this shrinking tendency continues at N = 88 will determine the unknown ground state of $ ^{139} $Sb. This motivates us to investigate the level spectra of neutron-rich Sb isotopes using the Hamiltonian in Ref. [33]. The model space includes proton shell $ Z = 50\sim82 $ and neutron shell $ N = 82\sim 126 $. The proton orbit $ 0g_{9/2} $ under $ Z = 50 $ and neutron orbits $ 1d_{3/2} $ and $ 0h_{11/2} $ under $ N = 82 $ are added for cross-shell excitations. The shell-model code NUSHELLX@MSU is used for the calculations [34].

The present configuration space includes six proton orbits ($ 0g_{9/2}, 0g_{7/2}, 1d_{5/2}, 1d_{3/2}, 2s_{1/2}, 0h_{11/2} $) and eight neutron orbits ($ 1d_{3/2}, 0h_{11/2}, 1f_{7/2}, 2p_{3/2}, 2p_{1/2}, 0h_{9/2}, 1f_{5/2}, 0i_{13/2} $). Among them, $ 1d_{3/2} $ and $ 0h_{11/2} $ ($ 0g_{9/2}) $ are neutron (proton) cross-shell excitations. This interaction provides a pathway to study monopole effects by employing monopole correction (Mc) terms:

Here, $ A^\dagger_{JM}(ia,i'c) $ and $ A_{JM} $ are the pair operators, and $ k_{\rm mc} $ is the monopole force strength. The $ i(i^\prime) $ means protons (neutrons), and a(c) represents different orbits in monopole correction terms. The monopole interaction reflects the bulk properties of nuclear binding, which can be described as the weighted average of interaction elements. In our previous work [33], five monopole terms were employed, as follows (MeV):

Here, the force strengths are determined by monopole effects in the data of $ ^{133} $Sb,$ ^{134} $Sb, $ ^{134} $Te, $ ^{135} $Te, and $ ^{135} $I. Mc1 and Mc2 modify the energy gap of the N = 82 shell. Mc3 is considered for configurations including both proton orbit $ 0g_{7/2} $ and neutron orbit $ 0h_{9/2} $. Mc4 is added for levels coupled with intruder orbit $ 0i_{13/2} $. Mc5 is considered for configurations including both proton orbit $ 0h_{11/2} $ and neutron orbit $ 1f_{7/2} $.

In this work, further monopole effects implied in the data of neutron-rich Sb isotopes enable the Hamiltonian to suit nuclei a little far from the doubly magic nucleus $ ^{132} $Sn. According to the data of high-spin levels (27/2$ ^- $) and (29/2$ ^- $) in $ ^{135} $Sb, the monopole corrections of ${\rm Mc}6 (\nu f_{7/2}, \nu i_{13/2}) = -0.52$ MeV and ${\rm Mc}7 (\nu h_{9/2}, \nu i_{13/2}) = -0.35$ MeV are added to modify the high calculation results. The attractive monopole interaction between proton orbit $ \pi d_{5/2} $ and neutron orbit $ \nu f_{7/2} $ can be used to explain the drastic shrinking of the first excited state 5/2$ ^+ $ in $ ^{135} $Sb, namely, ${\rm Mc}8 (\pi d_{5/2}, \nu f_{7/2}) = -0.70$ MeV. For the odd-odd nucleus $ ^{136} $Sb, the ground state (1$ ^- $) and excited levels (2$ ^- $), (4$ ^- $), and (6$ ^- $) are nicely reproduced by considering the monopole term ${\rm Mc}9 (\nu f_{7/2}, \nu h_{9/2}) = -0.19$ MeV.

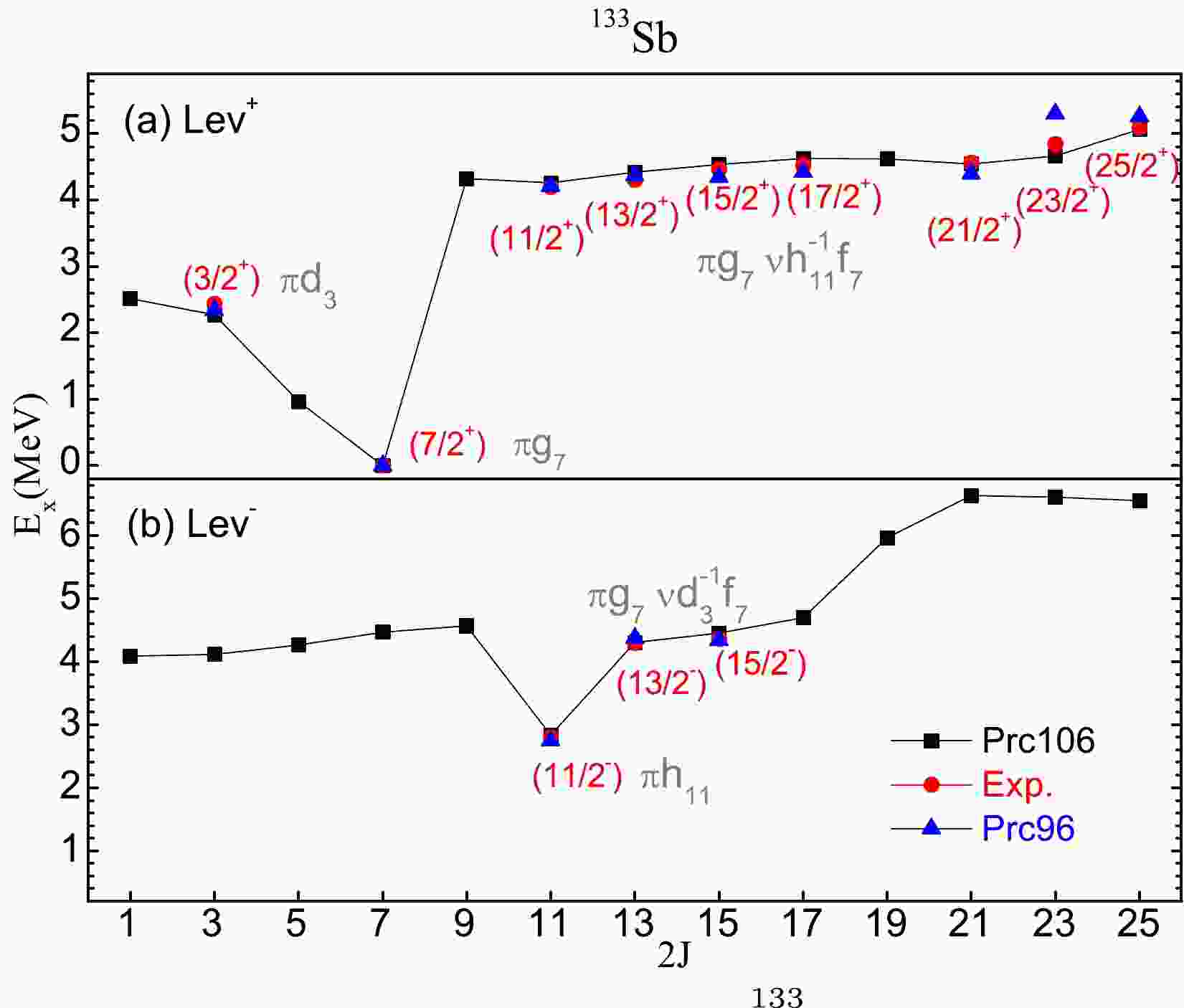
The single proton nucleus $ ^{133} $Sb was investigated in the particle-hole nuclei region in Ref. [35]. As shown in Fig. 1, its excited states are well reproduced by comparison with the corresponding data. In this work, we calculate these levels using the Hamiltonian in the particle nuclei region [33]. Note that the 23/2$ ^+ $ level at 5.3 MeV marked with Prc96 is 0.456 MeV higher, whereas the one marked with Prc106 at 4.624 MeV is much closer to the corresponding datum 4.844 MeV. For the 25/2$ ^+ $ level, the difference is only 24 keV in Prc106, whereas the difference in Prc96 is 167 keV. The two high-spin levels are coupled by the configuration $ \pi g_{7/2} \nu h^{-1}_{11/2} f_{7/2} $.

Figure 1.  (color online) Level spectra of $^{133}$Sb. Prc96 (Prc106) calculations provided by the Hamiltonian in Ref. [35] ([33]). The corresponding data are taken from Ref. [28].

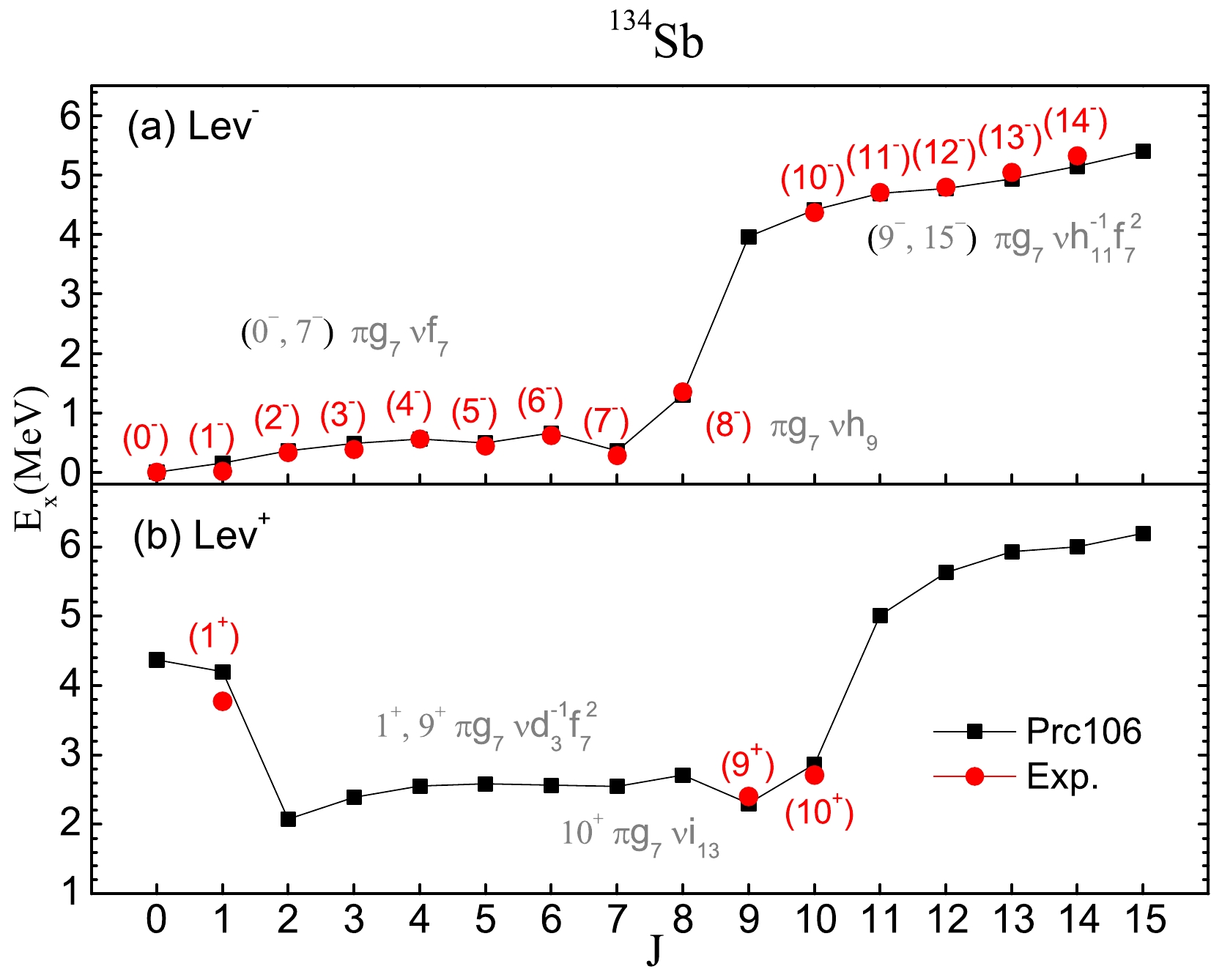
The $ ^{134} $Sb odd-odd nucleus is suitable to test the new Hamiltonian in the particle-particle nuclei region. The ground state of $ ^{134} $Sb is level 0$ ^- $ with a main configuration $ \pi g_{7/2} \nu f_{7/2} $ (Fig. 2). The excited levels from 1$ ^- $ to 7$ ^- $ also belong to this configuration. All members of this configuration are observed experimentally, and they are reproduced very well using the Hamiltonian in Ref. [33]. The level 8$ ^- $ at 1.296 MeV is coupled by the configuration $ \pi g_{7/2} \nu h_{9/2} $. With a difference factor of 0.959, the corresponding datum is 1.352 MeV. The higher spin levels from 9$ ^- $ to 15$ ^- $ are core excitations coupled by configuration $ \pi g_{7/2} \nu h^{-1}_{11/2} f^2_{7/2} $.

Figure 2.  (color online) Level spectra of $^{134}$Sb. Prc106 calculations provided by the Hamiltonian in Ref. [33]. The corresponding data are taken from Ref. [28].

For positive parity levels, the 0$ ^+ $, 1$ ^+ $, and 11$ ^+ $ are coupled by the cross-shell configuration $ \pi g_{7/2} \nu d^{-1}_{3/2} f^2_{7/2} $. The levels from 2$ ^+ $ to 9$ ^+ $ have a main configuration $ \pi i_{13/2} \nu f_{7/2} $. The level 10$ ^+ $ at 2.869 MeV is coupled by the configuration $ \pi g_{7/2} \nu i_{13/2} $. The difference is a factor 1.058 determined by comparing the value with the corresponding datum 2.713 MeV. The levels 12$ ^+ $ and 13$ ^+ $ are coupled by the cross-shell configuration $ \pi g_{7/2} \nu d^{-1}_{3/2} f_{7/2} h_{9/2} $. The levels 14$ ^+ $ and 15$ ^+ $ are coupled by the cross-shell configuration $ \pi h_{11/2} \nu h^{-1}_{11/2} f^2_{7/2} $.

It seems that the present Hamiltonian works well in nuclei close to the doubly magic $ ^{132} $Sn by considering the results of $ ^{133,134} $Sb, as well as those in Sn and Te isotopes. What about the nuclei further from $ ^{132} $Sn with more valence nucleons? Further monopole effects turn up while the neutron number increases. In $ ^{135} $Sb, monopole effects are implied in high-spin states with negative parity. As shown in Fig. 3, the ground state 7/2$ ^+ $ with a main configuration $ \pi g_{7/2} \nu f^2_{7/2} $is suggested by the consistency of the experimental and shell-model calculated level spectrum, which are the first five states up to approximately 0.90 MeV [28]. This configuration $ \pi g_{7/2} \nu f^2_{7/2} $ is also a large part of states 1/2$ ^+ $, and 7/2$ ^+ $ to 19/2$ ^+ $. The state 3/2$ ^+ $ is coupled by $ \pi g_{7/2} \nu f_{7/2} p_{3/2} $. The state 5/2$ ^+ $ is higher than the datum (5/2$ ^+ $) at 0.282 MeV. The states 21/2$ ^+ $ and 23/2$ ^+ $ are almost all coupled by the configuration $ \pi g_{7/2} \nu f_{7/2} h_{9/2} $. The states from 25/2$ ^+ $ to 29/2$ ^+ $ have a main configuration $ \pi h_{11/2} \nu f_{7/2} i_{13/2} $.

Figure 3.  (color online) Level spectra of $^{135}$Sb. Prc106 calculations provided by the Hamiltonian in Ref. [33]. The label "+Mc6,7" means adding monopole terms Mc6 and Mc7 to the Hamiltonian. The corresponding data are taken from Ref. [28].

For negative parity levels, the states 1/2$ ^- $, 3/2$ ^- $, 25/2$ ^- $, and 27/2$ ^- $ are coupled by the configuration $ \pi g_{7/2} \nu f_{7/2} i_{13/2} $. The states from 5/2$ ^- $ to 23/2$ ^- $ have a main configuration $ \pi h_{11/2} \nu f^2_{7/2} $. In comparison with high-spin data (27/2$ ^- $) and (29/2$ ^- $), the calculations marked Prc106 reproduce high values with difference factors of 1.167 and 1.102, respectively. This difference can not be reduced by considering cross-shell excitations. Including core excitations, the high spin levels from 25/2$ ^{\pm} $ to 29/2$ ^{\pm} $ have been obviously affected, while those with $ J^{\pi} \leq 23/2^{\pm} $ are almost the same.

Owing to the constrain from shell model calculations, only one nucleon in cross-shell orbit $ h_{11/2} $ ($ d_{3/2} $) is allowed, which is marked as $ \nu d^0_{3/2} h^1_{11/2} $ ($ \nu d^1_{3/2} h^0_{11/2} $). Here, index "0" means no cross-shell excitation, and "1" means allowing one nucleon as cross-shell excitation. The configuration of the level (27/2$ ^- $) at 3.249 MeV is suggested as $ \pi g_{7/2} \nu f_{7/2} i_{13/2} $ [28], which can be affected by further monopole effects when the valence nucleus occupies both the $ \nu f_{7/2} $ and higher $ i_{13/2} $ orbits. The configuration of the level (29/2$ ^- $) at 3.688 MeV is suggested as $ \pi g_{7/2} \nu h_{9/2} i_{13/2} $ [28]. After considering monopole corrections of ${\rm Mc}6 (\nu f_{7/2}, \nu i_{13/2}) = -0.52$ MeV and ${\rm Mc}7 (\nu h_{9/2}, \nu i_{13/2}) = -0.35$ MeV, the difference factors of level 27/2$ ^- $ and 29/2$ ^- $ become 1.007 and 1.008, respectively.

With a single proton above the Z = 50 shell, Sb isotopes can be used to study single particle evolutions in the proton major shell Z = (50, 82). Note that the 7/2$ ^+ $ level is the ground state of odd-A Sb isotopes after $ N \geq 72 $, and the first excited state 5/2$ ^+ $ continues growing until N = 82. This situation is described well with a strongly attractive monopole interaction between the $ 0g_{9/2} $ and $ 0h_{11/2} $ orbits. As shown in Fig. 1, the datum (5/2$ ^+ $) of $ ^{133} $Sb at 0.962 MeV is suggested with configuration $ \pi d_{5/2} $. The present Hamiltonian reproduces this state at 0.967 MeV. However, the level 5/2$ ^+ $ of $ ^{135} $Sb is calculated at 0.77 MeV, whereas the experimental value drops to 0.282 MeV. This shows that the evolution of the 5/2$ ^+ $ state in odd-A Sb isotopes changes largely when N = 84. To describe the shrinking tendency in the first excited state 5/2$ ^+ $ in $ ^{135} $Sb, the monopole correction term of ${\rm Mc}8 (\pi d_{5/2}, \nu f_{7/2}) = -0.70$ MeV is considered.

As shown in Fig. 4, this monopole term is quantified as the function of monopole force strength in the range [0.0,-1.0]. The level 5/2$ ^+ $ shrinks obviously when considering attractive monopole corrections between $ \pi d_{5/2} $ and $ \nu f_{7/2} $. By comparing Fig. 4 (a) and Fig. 4 (b), we find that this monopole effects become much stronger when the neutron number rises to N = 86 in $ ^{137} $Sb. The ground state of $ ^{137} $Sb will reverse after $\kappa_{\rm mc} = -0.6$ MeV, whereas the datum (5/2$ ^+ $) at 84 keV is very close to the ground state 7/2$ ^+ $. This $\kappa_{\rm mc}$ value is finally selected as −0.7 when considering the monopole effects of Mc6, Mc7, and Mc9. Following this dropping tendency, the ground state of odd-A Sb isotopes should be reversed into state (5/2$ ^+ $) in $ ^{139} $Sb.

Figure 4.  (color online) Monopole effects of Mc8($\pi d_{5/2},\nu f_{7/2}$) in state 5/2$^+$ of $^{135,137,139}$Sb.

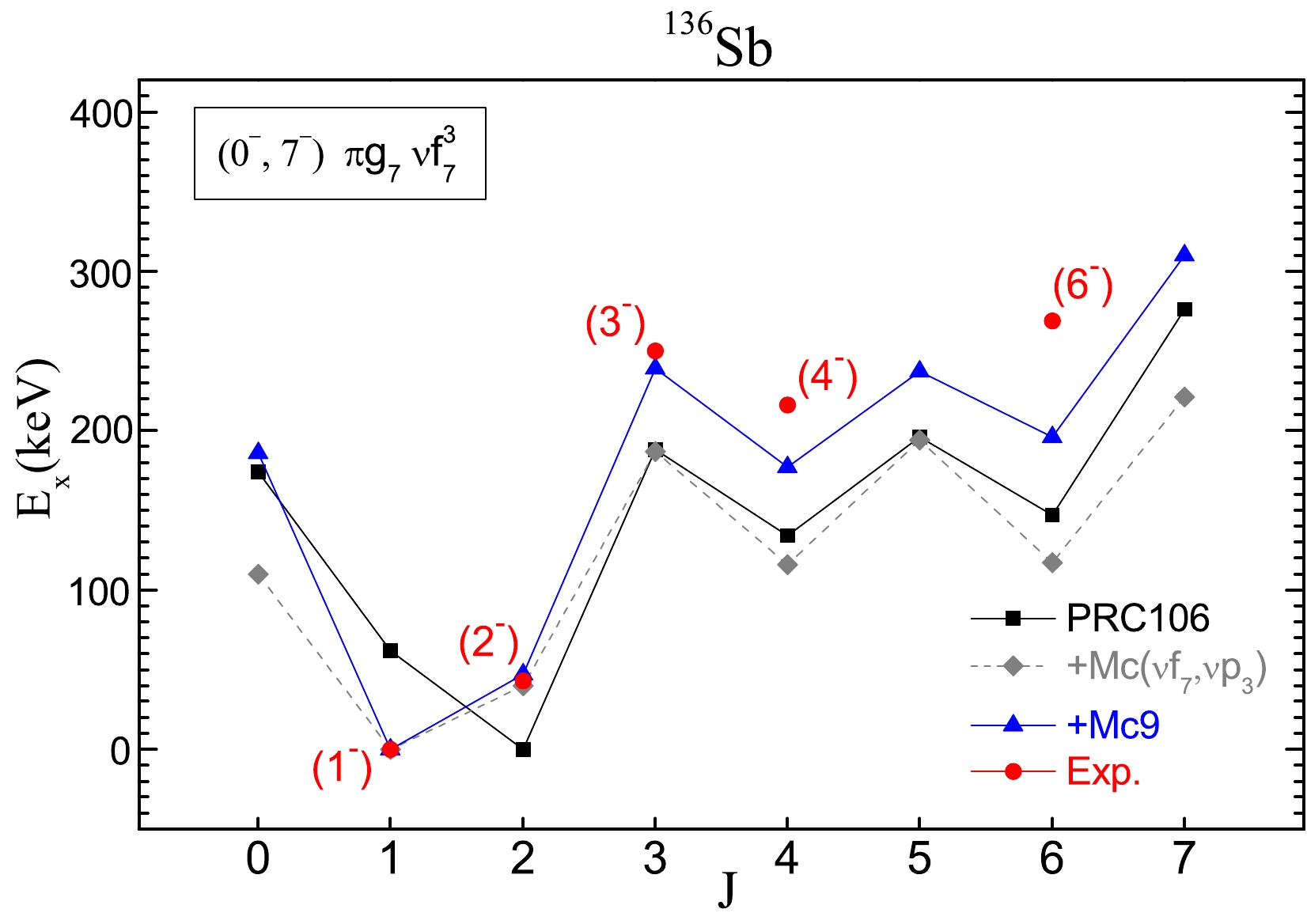
As shown in Fig. 5, the ground state of $ ^{136} $Sb is calculated as 2$ ^- $ in PRC106 calculations, whereas the 1$ ^- $ state is an excited state at 0.062 MeV. For the odd-odd nucleus $ ^{136} $Sb, its ground state is experimentally reported as $ J^{\pi} = 1^- $. The state 1$ ^- $ has a main configuration $ \pi g_{7/2} \nu f^3_{7/2} $, and two small configurations $ \pi g_{7/2} \nu f_{7/2} p^2_{3/2} $ and $ \pi g_{7/2} \nu f_{7/2} h^2_{9/2} $. Two monopole terms can solve the reversed ground state and reproduce the first excited state (2$ ^- $) very well, namely, Mc($ \nu f_{7/2}, \nu p_{3/2} $) and Mc($ \nu f_{7/2}, \nu h_{9/2} $).

Figure 5.  (color online) Level spectra of $^{136}$Sb. Prc106 calculations provided by the Hamiltonian in Ref. [33]. The label "+Mc9" means adding monopole terms Mc9 to the Hamiltonian. The corresponding data are taken from Ref. [30].

These two monopole terms affect the two small configurations, and then reverse their state orders. In addition to solve the ground state inversion, the monopole term $ {\rm Mc}9(\nu f_{7/2}, \nu h_{9/2})= - 0.19 $ MeV is also better to reproduce the (3$ ^- $), (4$ ^- $), and (6$ ^- $) data. The level (3$ ^- $) at 250 keV is reproduced well as 239 keV, the level 4$ ^- $ at 198 keV has a difference of 18 keV by comparing it with datum (4$ ^- $) at 216 keV, and the level 6$ ^- $ at 218 keV is also very close to the corresponding datum (6$ ^- $) at 269 keV. These levels are all coupled by $ \pi g_{7/2} \nu f^3_{7/2} $ ($ \geq 50{\text{%}} $).

The excited states of $ ^{137} $sb are the key to discover the evolution of the proton single-particle structure above N = 82. Recently, the first experimental information on the excited states of $ ^{137} $Sb was obtained by the β-decay of the semimagic Sn isotope $ ^{137} $Sn. The first excited state in this nucleus is suggested as level (5/2$ ^+ $) at 84 keV, which is much lower than the one in $ ^{133} $Sb or $ ^{135} $Sb. Such shrinking in the first excited state of odd-A Sb isotopes can be explained as the increasing attractive monopole effects when adding more neutrons in the orbit $ f_{7/2} $ above the N = 82 shell (Fig. 4). As shown in Fig. 6, these monopole effects drop down the state 5/2$ ^+ $ from 819 to 107 keV, which reproduces the datum (5/2$ ^+ $) very well.

Figure 6.  (color online) Level spectra of $^{137}$Sb. Prc106 calculations provided by the Hamiltonian in Ref. [33]. The labels "+Mc6,7","+Mc8", and "+Mc9" mean adding these monopole terms to the Hamiltonian one by one. The corresponding data are taken from Ref. [30].

By comparing them with the calculations marked Prc106, the monopole corrections of adding Mc6, 7 only affect the high-spin levels 25/2$ ^- $, 27/2$ ^- $, and 29/2$ ^- $. The state 29/2$ ^- $ is reduced from 3.478 to 2.309 MeV. The Mc8 monopole effect makes a large shrinking to levels 5/2$ ^+ $ and 13/2$ ^+ $. These two levels have the same main configuration $ \pi d_{5/2} \nu f^4_{7/2} $. When including the monopole term Mc9, the positive parity levels from 17/2$ ^+ $ to 29/2$ ^+ $ drop approximately 0.3 MeV, whereas the negative parity levels slightly increase, except 29/2$ ^- $. The 11/2$ ^- $ level at 0.638 MeV is predicted as a good isomer coupled by the configuration $ \pi d_{5/2} \nu f^4_{7/2} $.

The neutron-rich Sb isotopes are investigated by the shell-model space including both cross-shell orbits and intruder orbit $ \nu i_{13/2} $. Further monopole effects are found in the observed data of neutron-rich nuclei $ ^{135} $Sb, $ ^{136} $Sb, and $ ^{137} $Sb. After considering these monopole effects, the Hamiltonian becomes more suitable for nuclei further away from $ ^{132} $Sn. Our main conclusions are as follows:

(1) The level spectra of $ ^{133,134} $Sb can be well described with this Hamiltonian in comparison with known data.

(2) In $ ^{135} $Sb, two new monopole corrections connecting the intruder orbit $ \nu i_{13/2} $ are found in high-spin levels (27/2$ ^- $) and (29/2$ ^- $). The drastic dropping of level 5/2$ ^+ $ at 282 keV in the experiment shows an increasing attractive monopole shift between orbits $ \pi d_{5/2} $ and $ \nu f_{7/2} $ by adding more neutrons in orbit $ \nu f_{7/2} $ above the N = 82 shell.

(3) In $ ^{137} $Sb, the datum (5/2$ ^+ $) at 84 keV confirms the shrinking tendency, and ground state inversion will turn up when the neutron number reaches N = 88.

(4) In $ ^{136} $Sb, the attractive monopole correction is found between neutron orbits $ \nu f_{7/2} $ and $ \nu h_{9/2} $. This monopole effect reproduces the ground state (1$ ^- $) and the excited states (2$ ^- $), (3$ ^- $), (4$ ^- $), and (6$ ^- $) very well.

(5) In $ ^{139} $Sb, the ground state is predicted as 5/2$ ^+ $ according to the increasing attractive monopole effects after adding more neutrons in orbit $ \nu f_{7/2} $ above the N = 82 shell.