Thermal analysis and Joule-Thomson expansion of black hole exhibiting metric-affine gravity

The geometrical structure of black holes (BHs) in general relativity (GR) and modified theories of gravity is an attractive and challenging research subject [1]. The thermal characteristics of BHs and their behavior are analyzed by the well-known four laws of BH mechanics [2, 3]. After the study by Bekenstein, for the first time, Stephen Hawking presented the existence of BH radiations and formalized the tunneling process significantly close to the BH horizon owing to the vacuum fluctuations. It was observed that a small quantity of heat led to the eccentricity of quantum mechanics [4, 5]. In [6], it was noted that BHs contain thermodynamic features such as temperature and entropy. At the BH horizon, the Hawking temperature is proportional to its surface gravity because a BH behaves like a thermodynamical system. It was confirmed that the results of [7] are useful for all classical BHs at thermodynamic equilibrium.

The Hawking temperature phase transition occurs after the justification of an isomorphic phase structure associated with the van der Waals liquid-gas system in a Kerr RN-AdS BH [8] and an RN-AdS BH [8, 9]. In all previous BH thermodynamic studies, mass, volume, and pressure, the crucial thermodynamic variables, were missing. The contribution of pressure to this field was completed through the cosmological constant, which also had other basic implications such as the consistency of Smarr's relation with the first law [10]. The cosmological constant (Λ) was taken as the thermodynamic pressure, and the respective first law of thermodynamics was simultaneously modified by the expansion of the phase space with a $ PdV $ term, leading to novel understanding of the BH mass [11]. The new perspective on mass with the cosmological constant in BH thermodynamics generated phenomenal consequences in classical thermodynamics. Kubiznak et al. [12, 13] presented the AdS BH as a van der Waals system and investigated the critical behavior of the BH through the $ P-v $ isotherm, Gibbs free energy, critical exponents, and coincidence curves, which are all presented as similar to the van der Waals case. Moreover, these similar features were obtained on various AdS BHs in [14−19]. The similarities to classical thermodynamics, such as holographic heat engines [20], Joule Thomson expansion, phase transitions, and Clausius-Clapeyron equation, were also studied in [21, 22]. Javed et al. [23] investigated the thermodynamics of charged and uncharged BHs in symmetric teleparallel gravity. They also studied the thermal fluctuations and phase transition of the considered BHs. The dynamical configurations of thin-shell developed from BHs in metric- affine gravity composed with scalar field were studied in [24]. Some interesting physical characteristics of various BH solutions were dicussed in [25−26].

In addition, the Joule-Thomson expansion was investigated in AdS BHs by Ökcü and Aydiner [27], further proceeding to the isenthalpic process by which gas expands through a porous plug from a high-pressure section to a low-pressure section. The researchers also analyzed the Joule-Thomson expansion phenomenon in Kerr-AdS BHs within the extended phase space [28]. They examined both the isenthalpic and numerical inversion curves in the temperature-pressure plane, illustrating regions of cooling and heating for Kerr-AdS BHs. Additionally, they computed the ratio between the minimum inversion temperature and critical temperature for Kerr-AdS BHs [28]. This pioneering work was generalized to quintessence holographic superfluids of RN BHs in $ f(R) $ gravity [29−31]. More recently, we studied, in detail, the consequence of the dimensionality on the Joule-Thomson expansion in [31]. As stated in [31, 32], the ratio between the critical temperature and minimum inversion temperature decreases with the dimensionality d, while it retrieves the results when $ d=4 $. In this work, we investigated whether the existence of metric-affine gravity should influence the Joule-Thomson expansion, which is also motivated by the progress in our understanding of metric-affine gravity. Here, we propose that the adopted strategy is contextualized not only for BHs in metric-affine gravity but also for those in other alternative theories of gravity where new gravitational modes are well developed.

This paper is devoted to explore the effects of metric-affine gravity on the phase transition of BH geometry and also to study the Joule-Thomson expansion. The remaining of this paper is arranged as follows. In Sec. II, we present a brief review of our new class of BHs in metric-affine gravity. In Sec. III, we formulate the thermodynamic quantities, such as temperature, pressure, Gibbs free energy, and heat engine. Next, in Sec. IV, we introduce the Joule-Thomson expansion for a classical physical quantity. Finally, we present a few closing remarks.

GR is the most successful and physically acceptable theory of gravity, which precisely describes the gravitational interaction in the space-time geometry and the characteristics of matter via the energy-momentum tensor. From a geometrical perspective, the Lorentzian metric tensor $ g_{\mu \nu} $ is considered to study the smooth manifold that is used to develop the Levi-Civita affine connection $ \Gamma^\lambda _{\mu \nu} $. To establish a model where the largest family of BH solutions with dynamical torsion and nonmetricity in metric-affine gravity can be found, a propagating traceless nonmetricity tensor must be taken into account in the gravitational action of metric-affine gravity. As a geometrical correction to GR, a quadratic parity-preserving action presenting a dynamical traceless nonmetricity tensor in this situation is given as follows [33−37]:

where $ \tilde{R}^{(\lambda \rho) \mu \nu} $ and $ \tilde{R}_{(\mu\nu)} $ are the affine-connected form of Riemann and Ricci tensors. Here, R denotes the Ricci scalar, g is the determinant of the metric tensor, $\mathcal{L}_{m}$ depicts the matter Lagrangian, and $ f_1 $, $ f_2 $ are Lagrangian coefficients. This solution can also be easily generalized to take into account the cosmological constant and Coulomb electromagnetic fields with electric charge ($ q_e $) and magnetic charge ($ q_m $), which are decoupled from torsion [38, 39]. This assumes the minimal coupling principle.

These variations represent the third Bianchi of GR. By executing changes of the above equations with respect to the co-frame field and the anholonomic interrelation, the following field equations are established: $ Y 1_\mu^\nu =8 \pi \theta_\mu^\nu $ and $ Y 2^{\lambda \mu \nu} =4 \pi \Delta^{\lambda \mu \nu} $, where $ Y 1_\mu{ }^\nu $ and $ Y 2^{\lambda \mu \nu} $ are tensor quantities. $ \Delta^{\lambda \mu \nu} $ and $ \theta_\mu{ }^\nu $ are utilized to study the hyper momentum density and canonical energy-momentum tensors of matter, which are expressed as

Therefore, both matter representations act as sources of the extended gravitational field. In this scenario, metric-affine geometries utilize the Lie algebra of the general linear group GL(4, R) in anholonomic interrelation. This hypermomentum presents its proper decomposition into shear, spin, and dilation currents [36, 37]. Furthermore, the effective gravitational action of the model is provided in terms of these properties. The parameterizations of the spherically symmetric static spacetime are as follows: [39−43]

Compared with the standard case of GR, in the emission process, a matter current coupled to torsion and nonmetricity in a general splitting of the energy levels will potentially affect this spectrum and the efficiency. Interestingly, the performance of a perturbative interpretation on the energy-momentum tensor in vacuum fluctuations of the quantum field coupled to the torsion, as well as nonmetricity tensors of the solution, is used to study the rate of dissipation obtained on its event horizon, which would also cover the further corrections with respect to the system of GR [44, 45]. The metric function (Reissner-Nordström-de Sitter-like) is defined as [37]

which represents the broadest family-charged BH models obtained in metric-affine gravity with real constants $ e_1 $ and $ d_1 $. Here, $ \kappa_{\mathrm{sh}} $, $\kappa_{s}$, and $\kappa_{d}$ represent the shear, spin, and dilation charges, respectively.

A cosmological constant is treated as a thermodynamic variable. After the thermodynamic pressure of the BH is put into the laws of thermodynamics, the cosmological constant is considered as the pressure. From the equation of horizon $ \Psi(r)=0 $ and pressure $ P=-\dfrac{\Lambda}{8\pi} $ [29, 30], we can deduce the relation between the BH mass m and its event horizon radius, $ r_h $, which is expressed as follows

The Hawking temperature of the BH related to surface gravity can be obtained as

It has a peak as shown in Figs. 1 and 2 and shifts to right (positive) and increases with increasing $ P_c $ and $ \kappa_{s} $. The temperature becomes the absence of the electric charge $ (q= 0) $. As we increase the values of $ P_c $ and $ \kappa_{s} $, the local maximum of the Hawking temperature increases, as exhibited in Figs. 1 and 2. Further, the temperature converges when the horizon radius shrinks to zero for the considered BH manifold. The general form of the first law of BH thermodynamics can be written as [29−32, 46, 47]

Figure 1.  (color online) Plot of temperature T with fixed $ q_{e}= $ 0.28; $ q_m=0.08 $; $ d_1=0.004 $; $ f_1=0.313 $; $ \kappa _d =0.02 $; $ \kappa_s =0.8 $; and $ e_{1}=0.4 $.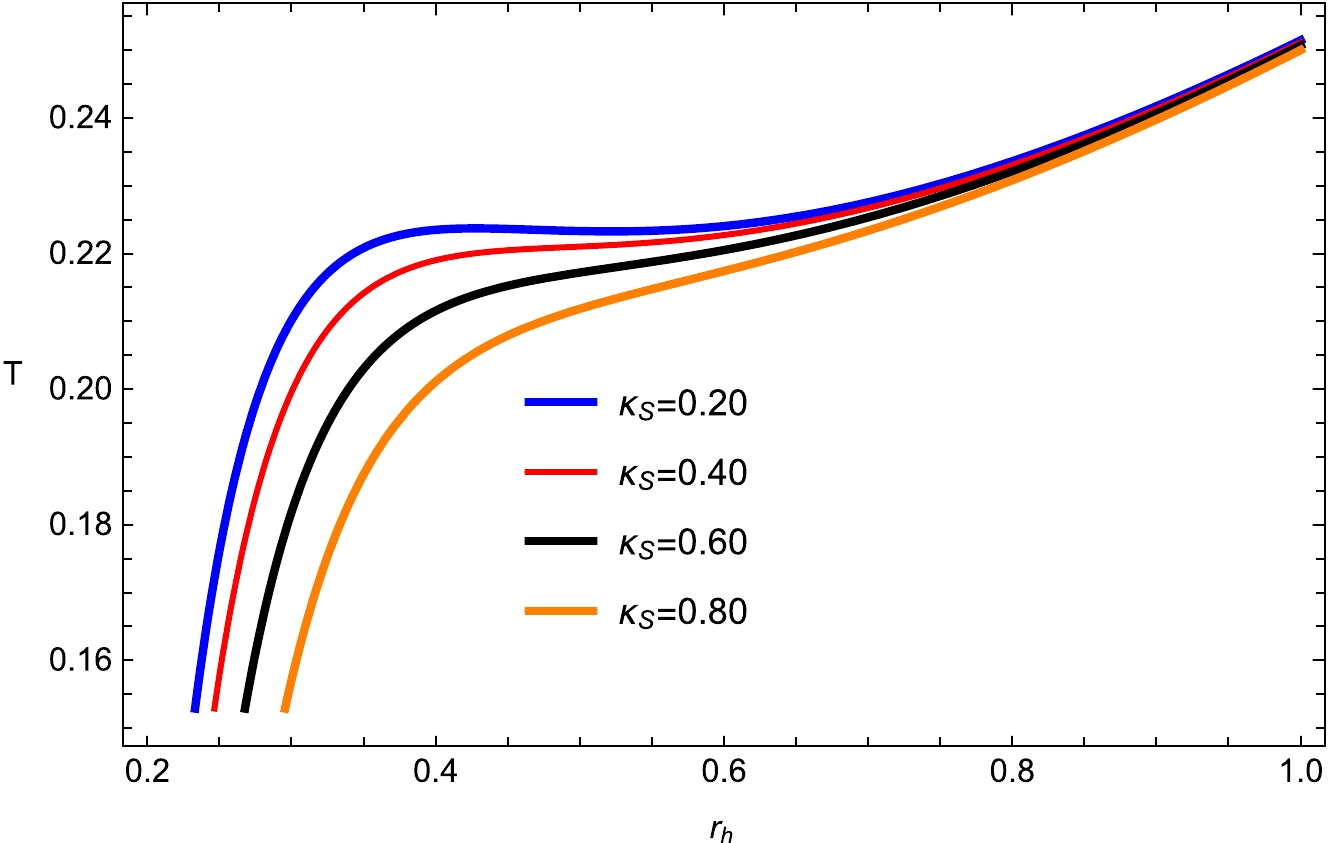

Figure 2.  (color online) Plot of temperature T with fixed $ q_{e }= $ 0.28; $ q_m=0.08 $; $ d_1=0.004 $; $ f_1=0.313 $; $ \kappa_d =0.02 $; and $ e_1=0.4 $.

where M, S, V, P, Q, Φ, and φ are the mass, entropy, volume, pressure, magnetic charge, and chemical potential of BH, respectively. They have been treated as thethermodynamic variables corresponding to the conjugating variables $ \Bbbk_{\rm sh} $, $ \Bbbk_{s} $, $ \Bbbk_{d} $, $ E1 $, and $ d_1 $, respectively. The volume and chemical potential of the BH are defined as

respectively. The BH entropy with the help of area is defined as [48−50]

From Eqs. (6) and (7), the equation of state for the BH can easily be expressed as

The red, blue, orange, and black colors indicate the divergence at pressures below the critical pressure. The oscillations of the isotherms at critical temperatures in the $ P - v_h $ diagram are equivalent to the unstable BHs that are presented by negative heat capacity in this section (Figs. 3 and 4). These divergences are the characteristics of the first-order phase transition that occurs between smaller and larger BHs that are stable and have a positive heat capacity. In response to changes in the value of the parameter $ T_c $, there is a corresponding shift in the horizontal axis; an increase in this parameter results in a reduction in the critical radius.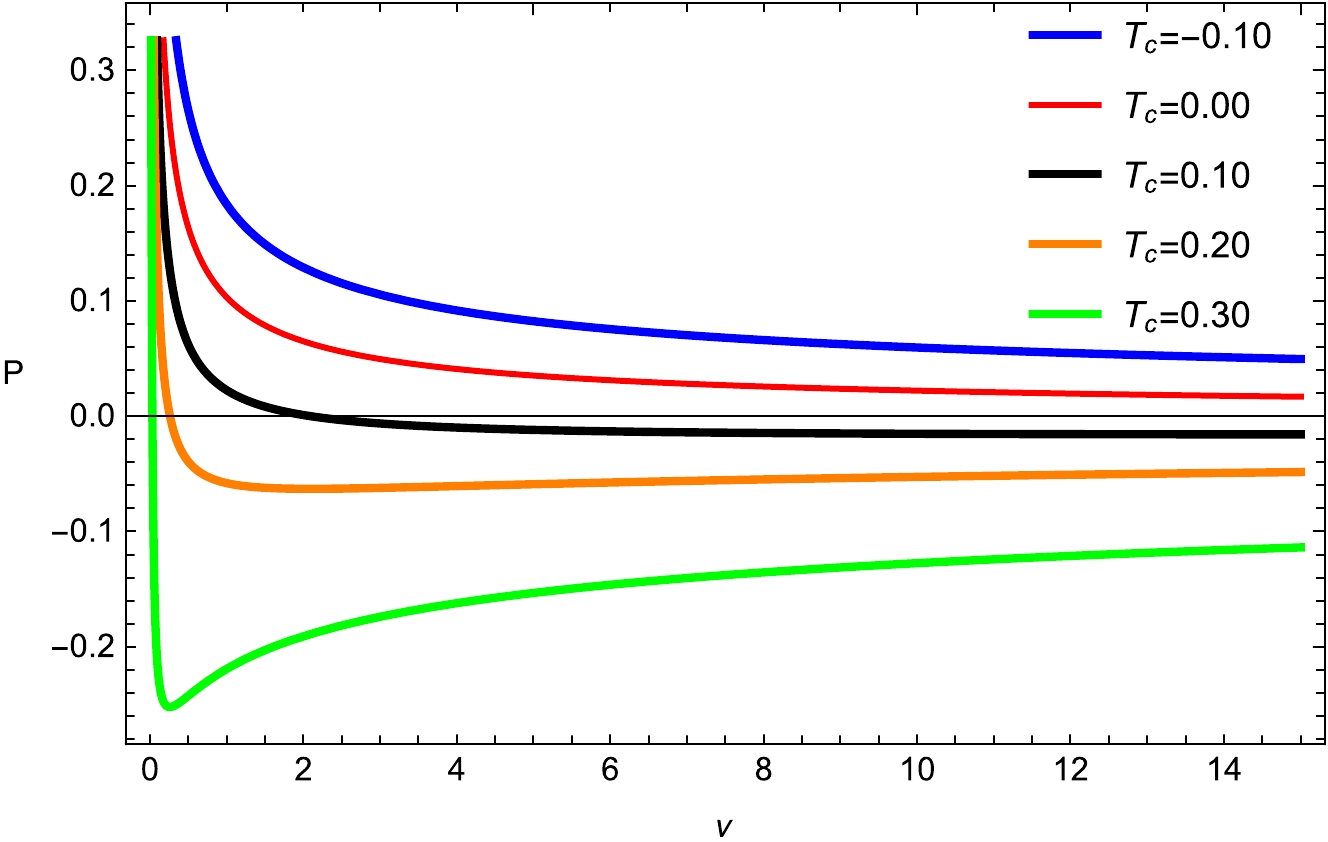

Figure 3.  (color online) Plot of temperature P with fixed $ q_m= $ 0.0002; $ d_1=0.004 $; $ f_1=0.003 $; $ \kappa _d =0.01 $; $ \kappa _s =0.03 $; and $ e _1=0.4 $.

Figure 4.  (color online) Plot of temperature P with fixed $ q_m= $ 0.0002; $ d_1=0.004 $; $ f_1=0.003 $; $ \kappa _d =0.01 $; $ \kappa _s =0.03 $; and $ e _1=0.4 $.

The thermodynamic variables V, Φ, φ and the conjugating quantities $\Bbbk_{\rm sh}$, $ \Bbbk_{s} $, $ \Bbbk_{d} $, $ E1 $, and $ d_1 $ are obtained from the first law as

The most important and basic thermodynamic quantity is the Gibbs free energy of a BH, which can be utilized to explore the small/larger BH phase transition by studying the $ G-r_h $ and $ G - T $ diagrams. In addition, the Gibbs free energy also helps us to investigate the global stability of a BH. It can be evaluated as [51, 52]

Using Eqs. (6) and (7) in (13), we obtain

We observe the graphical behavior of the phase transitions in the $ G-r_{h} $ plane as shown in Figs. 5 and 6. It is noted that the Gibbs free energy decreases as the critical radius increases. To calculate the critical thermodynamic properties of a BH, one can use the following condition:

Figure 5.  (color online) Plot of Gibbs free energy G with fixed $ q_m=0.003 $; $ d_1=0.200 $; $ f_1=0.050 $; $ \kappa _d =0.010 $; and $ e _1=0.050 $.

Figure 6.  (color online) Plot of Gibbs free energy G with fixed $ q_m=0.003 $; $ d_1=0.200 $; $ f_1=0.050 $; $ \kappa _d =0.010 $; and $ e _1=0.050 $.

Using Eq. (15), the critical temperature can be expressed as

From Eq. (15), the critical radius of BH is as follows:

The critical pressure in terms of other parameters takes the following form:

However, we applied a numerical analysis because calculating the critical numbers analytically is not a simple operation.

To find more data about a phase transition, we studied a thermodynamic quantity such as heat capacity. By applying the standard definition of heat capacity as follows: [46, 53]

with a few numerical calculations, one can obtain a dimensionless important relation for the amounts $ P_c $, $ T_c $, and $ v_c $. If the expression $ (d_1 \kappa_{s}^2-2 f_1 \kappa_{\text{sh}}^2+q_e^2+q_m^2-4 \kappa_d ^2 e_{1})\rightarrow 1.327765310 $ is provided, then our solution satisfies the well-known condition as

and similar results are studied in the context of the van der Waals equation and in an RN-AdS BH . Therefore, the negative heat capacity that gives the temperamental (unstable) BH is also related to the critical temperature in the $ P-\upsilon_{h} $ plane. The expressions of volume and entropy of a BH are presented in Eqs. (7) and (10). From Eq. (19), we obtain

It has been discovered that the critical amounts classify the behavior of thermodynamic quantities close to the critical point. In Figs. 7 and 8, for thermodynamically stable BHs, we separate the two cases in which the heat capacity is positive ($ r _h <r_ c $) and the case in which it is negative ($ r_ h> r_ c $). The second-order phase transition is implied by the instability areas of BHs, where the heat capacity is discontinuous at the critical temperature $ r _h=r _c $ [54, 55]. It is noted that the heat capacity diverges at $ r_h = 0.50 $, when $ T_h $ reaches its maximum value as $ T_h=0.24 $ for $ r_h = 1.00 $, $ q_m=0.08 $, $ d_1=0.004 $, $ f_1=0.313 $, $ \kappa _d =0.02 $, and $ e _1=0.4 $. The critical points in the alternate phase space are obtained by utilizing the standard definition, and we reduced the thermodynamic variables as follows:

Figure 7.  (color online) Plot of heat capacity with fixed $ q_m=0.08 $; $ d_1=0.004 $; $ f_1=0.313 $; $ \kappa _d =0.02 $; and $ e _1=0.4 $.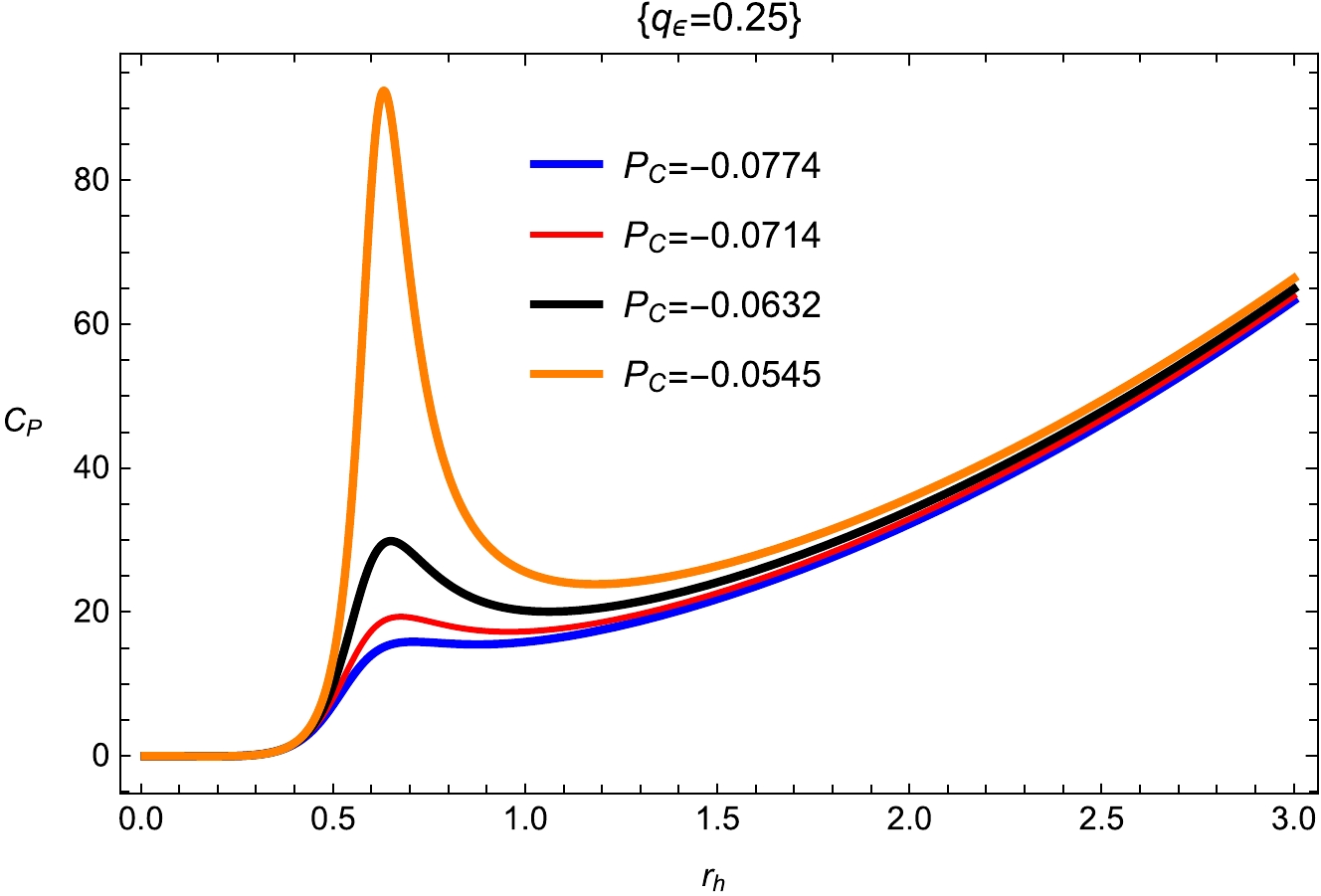

Figure 8.  (color online) Plot of heat capacity with fixed $ q_m=0.08 $; $ d_1=0.004 $; $ f_1=0.313 $; $ \kappa _d =0.02 $; and $ e _1=0.4 $.

The reduced variables can be written as

volume can be obtained as

and pressure is as follows:

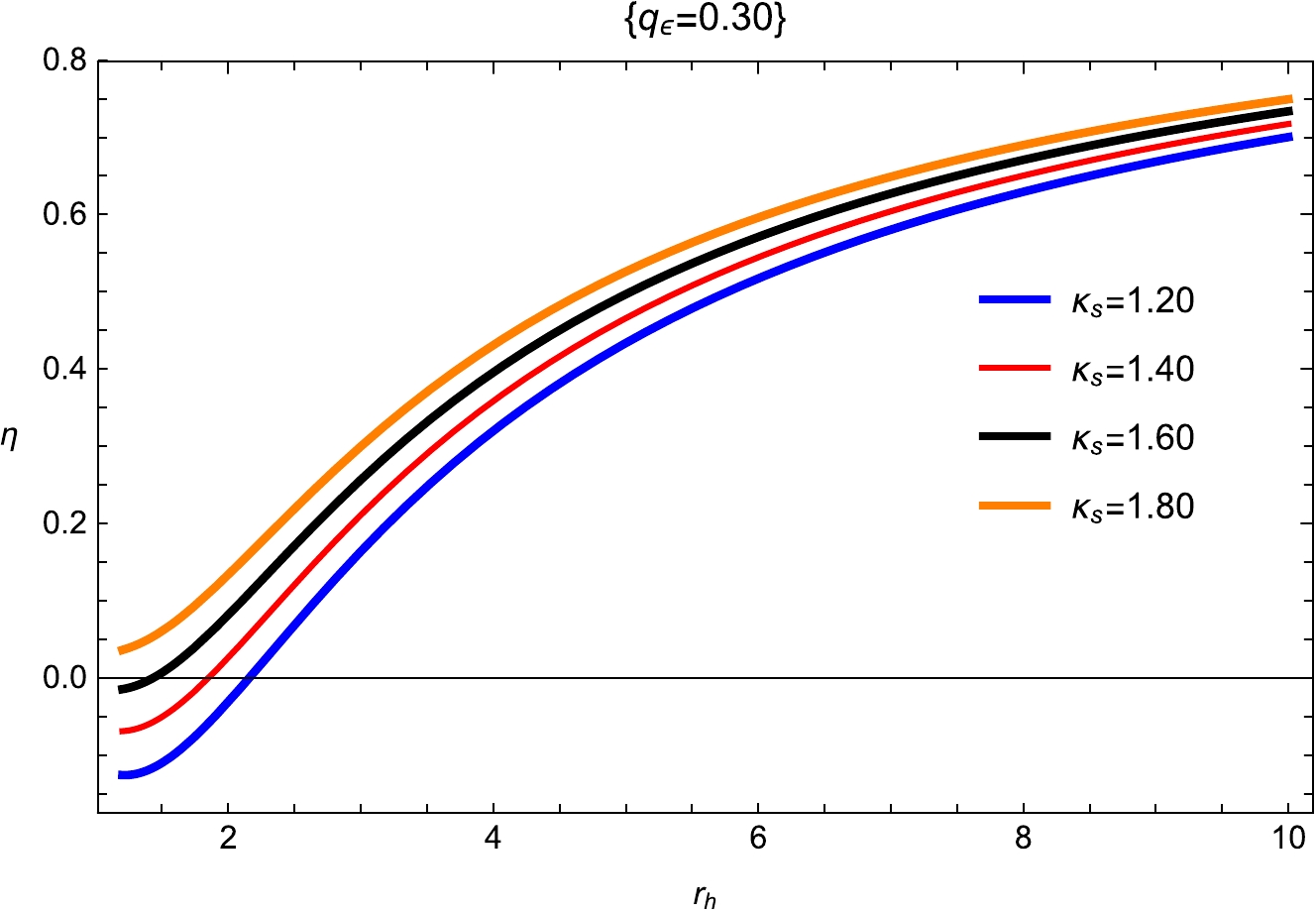
Two adiabatic and two isothermal processes combined to form the Carnot cycle are the hallmark of the most effective heat engine. The single most fundamental and critical feature of the Carnot cycle is that the heat engine efficiency is a function of reservoir temperatures:

and as a reservoir can never be at zero temperature, the efficiency cannot be one because $ T_c $ and $ T_h $ denote cold and hot reservoirs, respectively. Hence, we obtain

Now, we study the behavior of the heat engine efficiency η as a function of the the pressure P and entropy S matching to the heat cycle provided in Figs. 9 and 10, for the different values of metric-affine gravity parameters. From these figures, we can observe that the nature of the heat engine efficiency is essentially relying on the metric-affine gravity parameters. In addition, for a given set of input values, the efficiency of the heat engine increases monotonically as the horizon's radius grows. Because of this, larger BHs should expect higher heat-engine efficiency. In other words, they allow for a maximum efficiency curve to be provided for a heat engine by varying only a few fixed parameters (the BH works at the highest efficiency). Here, the local stability is related to the system, but it can be large with small changes in the values of thermodynamic parameters. Thus, the term heat capacity gives information on local stability. In [36], it is stated how the cosmological constant Λ can be studied by treating it as a scale parameter.

Figure 9.  (color online) Plot of efficiency η with fixed $ q_m=0.08 $; $ d_1=0.004 $; $ f_1=0.313 $; $ \kappa _d =0.02 $; and $ e _1=0.4 $.

Figure 10.  (color online) Plot of efficiency η with fixed $ q_m=0.08 $; $ d_1=0.004 $; $ f_1=0.313 $; $ \kappa _d =0.02 $; and $ e _1=0.4 $.

One of the best-known and classical physical processes to explain the change in temperature of a gas flowing from a high-pressure to a reduced pressure section through a porous plug is called the Joule-Thomson expansion. The main focus is on the gas expansion process, which expresses the cooling effect (when the temperature drops) and the heating effect (when the temperature increases), with the enthalpy remaining constant throughout the process. This change depends upon the Joule-Thomson coefficient: [28, 56]

Using Eqs. (7), (9), (21), and (28), the coefficient is calculated as follows:

The study of the Joule-Thomson coefficient versus the horizon $ r_h $ is shown in Figs. 11, 12, 13, and 14. We set $ d_1=0.004 $, $ f_1=0.313 $, $\kappa _{\rm sh} =0.05$, $ \kappa _d =0.02 $, $ \kappa _s =0.8 $, and $ e _1=0.4 $ in that order. There exist both divergence points and zero points for different variations of $ \kappa _d $, $ \kappa _s $, and $\kappa _{\rm sh}$ respectively. It is clear from a comparison of these figures that the zero point of the Hawking temperature and the divergence point of the Joule-Thomson coefficient is the same. This point of divergence gives information on the Hawking temperature and corresponds to the most extreme BHs. From Eq. (29) and utilizing the well-known condition $ \mu_{JT}=0 $, the temperature inversion occurs as

Figure 11.  (color online) Joule-Thomson coefficient $ \mu_{JT} $ plane with fixed $ d_1=0.03 $; $ f_1=0.01 $; $ \kappa _{d} =0.02 $; $ \kappa _s =0.10 $; and $ e _1=0.04 $.

Figure 12.  (color online) Joule-Thomson coefficient $ \mu_{JT} $ with fixed $ d_1=0.03 $; $ f_1=0.01 $; $ \kappa _{d} =0.02 $; $ \kappa _s =0.10 $; and $ e _1=0.04 $.

Figure 13.  (color online) Joule-Thomson coefficient $ \mu_{JT} $ with fixed $ d_1=0.03 $; $ f_1=0.01 $; $\kappa _{\rm sh} =0.10$; $ \kappa _d =0.02 $; and $ e _1=0.04 $.

Figure 14.  (color online) Joule-Thomson coefficient $ \mu_{JT} $ with fixed $ d_1=0.03 $; $ f_1=0.01 $; $\kappa _{\rm sh} =0.10$; $ \kappa _s =0.10 $; and $ e _1=0.04 $.

Because the Joule-Thomson expansion is an isenthalpic process, it is important to analyze the isenthalpic curves of BHs under metric-affine gravity, which are depicted in Figs. 15−18. Thus, we study the isenthalpic curves ($ T_i -P_i $ plane) by assuming different values of BH mass, which are investigated in Eq. (29) with a larger root of $ r_h $. We show the isenthalpic and inversion curves of BHs in metric-affine gravity and the result is consistent [57−60]. The heating and cooling zones are characterized by the inversion curve, and the isenthalpic curves possess positive slopes above the inversion curve. In contrast, the pressure always falls in a Joule-Thomson expansion and the slope changes sign when heating occurs below the inversion curve. The heating process appears at higher temperatures, as indicated by the negative slope of the constant mass curves in the Joule-Thomson expansion. When temperatures drop, cooling begins, which is linked to the positive slope of the constant mass curves. From above equation, one can deduce the inversion pressure as

Figure 15.  (color online) Isenthalpic curves $ (T-P) $ plane with fixed $ d_1=0.004 $; $ f_1=0.313 $; $\kappa _{\rm sh} =0.05$; $ \kappa _d =0.02 $; and $ e _1=0.4 $.

Figure 16.  (color online) Isenthalpic curves $ (T-P) $ plane with fixed $ d_1=0.004 $; $ f_1=0.313 $; $ \kappa _d =0.02 $; $ \kappa _s =0.8 $, and $ e _1=0.4 $.

Figure 17.  (color online) Isenthalpic curves $ (T-P) $ plane with fixed $ d_1=0.004 $; $ f_1=0.313 $; $\kappa _{\rm sh} =0.05$; $ \kappa _d =0.02 $; $ \kappa _s =0.8 $, and $ e _1=0.4 $.

Figure 18.  (color online) Isenthalpic curves $ {T-P} $ plane with fixed $ d_1=0.004 $; $ f_1=0.313 $; $\kappa _{\rm sh} =0.05$; $ \kappa _d =0.02 $; $ \kappa _s =0.8 $; and $ e _1=0.4 $.

The inversion curves for different values, $ d_1=0.004 $, $ f_1=0.313 $, $\kappa _{\rm sh} =0.05$, and $ \kappa _d =0.02 $, are shown in Figs. 19, 20, 21, and 22. The inversion temperature increases with variations of the important parameters m, $ q_e $, $\kappa _{\rm sh}$, and $ \kappa _s $, respectively. We can go back to the case of the BH in metric-affine gravity. Compared with the van der Waals fluids, we can observe from Figs. 19−22 that the inversion curve is not closed. From the above results, in the $ Ti-Pi $ plane at low pressure, the inversion temperature $ T_i $ decreases with the increase in charge $ q_e $ and mass m, and it shows the opposite behavior for higher pressure. It is also clear that, unlike the case with van der Waals fluids, the inversion temperature continues to rise monotonically with increasing inversion pressure, and hence, the inversion curves are not closed [59, 60].

Figure 19.  (color online) Inversion curves $ (Ti-Pi) $ with fixed $ d_1=0.004 $; $ f_1=0.313 $; $\kappa _{\rm sh} =0.05$; $ \kappa _d =0.02 $; $ \kappa _s =0.8 $; and $ e _1=0.4 $.

Figure 20.  (color online) Inversion curves $ (Ti-Pi) $ with fixed $ d_1=0.004 $; $ f_1=0.313 $; $\kappa _{\rm sh} =0.05$; $ \kappa _d =0.02 $; $ \kappa _s =0.8 $; and $ e _1=0.4 $.

Figure 21.  (color online) Inversion curves $ (Ti-Pi) $ plane with fixed $ d_1=0.004 $; $ f_1=0.313 $; $ \kappa _d =0.02 $; $ \kappa _s =0.8 $; and $ e _1=0.4 $.

Figure 22.  (color online) Inversion curves $ (Ti-Pi) $ plane with fixed $ d_1=0.004 $; $ f_1=0.313 $; $\kappa _{\rm sh} =0.05$; $ \kappa _d =0.02 $; and $ e _1=0.4 $.

In this work, we considered a BH in metric-affine gravity, studied the thermodynamics in the presence of Bekinstien entropy, and examined the standard thermodynamics relations. In detail, we thoroughly investigated the thermodynamics to analytically obtain thermodynamical properties such as the Hawking temperature, entropy, specific heat, and free energy associated with BHs in metric-affine gravity with a focus on the stability of the system. The heat capacity blows at$ r_c $, which is a double horizon, and local maxima of the Hawking temperature also occur at $ r_c $. It is shown that the heat capacity is positive for $ r_h < r_c $, providing stability to small BHs close to perturbations in the region, and at a critical radius a phase transition exists. The BH is unstable for $ r_h > r_c $ with negative heat capacity. The global analysis of the stability of BHs is also discussed by calculating the free energy $ G_h $. For negative free energy $ G_h < 0 $ and positive heat capacity $ C_p > 0 $, it is noted that smaller BHs are globally stable, and these results are also used in [14−19]. We calculated the inverse temperature, inverse pressure, and mass parameter, and investigated the Joule-Thomson process of the system. The negative cosmological constant in metric-affine gravity was investigated for phase transitions of BHs. Above the inversion curves, we examined the cooling region, whereas below the inversion curve there is a heating one. The corresponding results can be summarized as follows: both the inversion temperature and pressure become greater with an increasing BH in metric-affine gravity while they decrease with the charge $ q_e $. The physical consequences are analogous to those in holography; a BH would be a system as well as dual to conformal field theories. The BH in metric-affine gravity is studied and its thermodynamics is identical to that of usual systems; the thermodynamical analysis becomes more complete. Our results show that the Joule-Thomson coefficient is independent of the shear, spin, and dilation charges, which indicates that the Joule-Thomson expansion considered here is universal. In particular, we find novel isenthalpic curves in which the inversion temperature of the Joule-Thomson expansion, rather than the extreme one reported by previous works, separates heating and cooling phases [61−63]. Therefore, our inversion curves separate the allowable and forbidden regions for the Joule-Thomson effect to be observed, where the Joule-Thomson coefficient is the essential quantity to discriminate between the cooling and heating regimes of the system. It is worth noting that when a thermal system is amplified with a temperature, the pressure always decreases yielding a negative sign to $ \partial P $.

Our analysis of inversion curves in the plane revealed that the influence of the parameters on a BH may be more evident in space-time. We analyzed the BH in metric-affine gravity and the characteristics of the inversion curve; these included the shear, spin, and dilation charges. In these figures, we observed that the inversion curves are compatible with the extreme point of a specific isenthalpic curve, and the cooling as well as heating regions are identified. In other words, the boundary between the heating-cooling regions of the BH in metric-affine gravity influences the inversion curves. We also discovered the maximum expansion points of the cooling-heating regimes, as in [64−66]. For the BH heat engine, we investigated the analytical expression for efficiency in terms of horizon radius, pressures, and temperatures in various limits. We also studied the Joule-Thomson expansion, isenthalpic curves, and inversion curves of the considered BH in metric affine gravity, as follows:

● We examined the Joule-Thomson expansion for a BH in metric-affine gravity, where the cosmological constant is taken as a pressure. We mainly focused on the BH mass considered enthalpy, which is the mass that does not change during the expansion. The Joule-Thomson coefficient $ \mu_{JT} $ in terms of horizon $ r_h $ is shown in Figs. 11−14. There exist both divergence points and zero points with $ d_1=0.004 $, $ f_1=0.313 $, $\kappa _{\rm sh} =0.05$, $ \kappa _d =0.02 $, $ \kappa _s =0.8 $, and $ e _1=0.4 $. The zero point of the Hawking temperature, which is related to the most distant BHs, agrees with the divergence point of the Joule-Thomson coefficient, which is depicted in a consistent manner [59, 60].

● We also presented the isenthalpic curves, and the results are presented in higher dimensions as can be observed in Figs. 15−18. It is very interesting to explain that the positive slopes of the inversion curve are found as mentioned in the literature [28, 56]. This indicates that with the expansion of a metric-affine universe, a BH always cools above the inversion curve.

● To determine the temperature gradients between the cooling and heating zones for various values of $ d_1 $, $ f_1 $, $\kappa _{\rm sh}$, and $ \kappa _d $, we analyzed the inversion curve (Figs. 19−22).

It is concluded that the considered BH in metric affine gravity agrees with the results in the literature. This work is beneficial for future research.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This manuscript has no associated data, or the data will not be deposited. (There is no observational data related to this article. The necessary calculations and graphic discussion can be made available on request.)

G. Mustafa is very thankful to Prof. Gao Xianlong from the Department of Physics, Zhejiang Normal University, for his kind support and help during this research.