-
Nuclei, self-bound systems composed of protons and neutrons, are held together by the attractive nuclear force [1]. The proton and neutron can be viewed as two different states of the same particle, distinguished solely in terms of the isospin projection (
$ t_z $ ) [2, 3]. Furthermore, the nuclear force exhibits approximate charge symmetry, leading to remarkable symmetries in nuclear physics [4]. Owing to this symmetry, mirror nuclei, with the same number of nucleons but exchange in their proportion of protons and neutrons, should have identical properties, such as the excitation energy and transition probability [5].However, mirror symmetry (isospin symmetry) is broken between mirror nuclei, which is known as the isospin symmetry breaking (ISB) [6−11]. ISB studies allow for rigorous testing of nuclear models and offer profound insights into fundamental forces inside the nucleus [6−11]. One of the key quantities in the ISB studies is the mirror energy difference (MED) [6, 12], which is defined as the difference between the excitation energies of analogue states, written as
$ {\rm{MED}}(A, T, J^{\pi})=E_{ex}\left(A, T, J^{\pi}, T_{z_>}\right)-E_{ex}\left(A, T, J^{\pi}, T_{z_<}\right), $

(1) in which the
$ E_{ex} $ is the excitation energy and$ T_{z>} $ ($ T_{z<} $ ) refers to the isospin of the proton-rich nucleus (neutron-rich nucleus) in mirror nuclei considered in the MED calculations. It is noteworthy that the MED values of$ sd $ -shell nuclei have been of significant interest in nuclear physics for several decades [13−17]. These nuclei provide fascinating platforms for exploring exotic structural phenomena [4, 18], such as shell closures, shape coexistence, clustering, halo, and deformation. Moreover, ISB also manifests in$ sd $ -shell nuclei [14, 15].The MED serves as a sensitive probe of ISB, arising from the isospin-non-conserved Coulomb force and charge-dependent component of the nuclear force [6, 12, 13]. Furthermore, in mirror nuclei pairs, when the proton-rich nucleus is near the proton drip-line area, it behaves as a weakly-bound or unbound system, in contrast to the deeply-bound behavior of its neutron-rich counterpart. In such cases, the states of these mirror nuclei exhibit large MED values, with significant ISB, which is known as the Thomas-Ehrman (TE) shift [19, 20]. The
$ sd $ -shell nuclei, situated at the boundary between light and heavy nuclei, exhibit a wide range of nuclear structure phenomena that remain somewhat mysterious [21]. Recently, these nuclei have been explored using various experimental techniques [22−24]. These studies have not only permitted a more detailed exploration of their unique nuclear structures but also resulted in more accurate and precise measurements of MED values, thereby shedding light on ISB [24].On the other hand, several theoretical models have been developed to probe the MED values of
$ sd $ -shell nuclei, such as the standard shell model [4, 6, 10, 25], mean-field calculations [26, 27], and ab initio approaches [16, 28−30]. The standard shell model has been particularly successful in describing the structure and properties of$ sd $ -shell nuclei, and it has been used to calculate the MED values of many mirror nuclei pairs within this region. Mean-field calculations, such as the Skyrme-Hartree-Fock and relativistic mean-field models, have also been extensively employed in the MED studies, successfully reproducing experimental data for mirror nuclei. However, these models contain data-constrained parameters [4, 26, 31]. Recently, ab initio approaches have also been used in the MED studies, contributing significantly to our understanding of exotic structures and ISB [16, 28−30]. In the present work, we employ the ab initio valence-space in-medium similarity renormalization group (VS-IMSRG) method [32−34] to study MED in$ sd $ -shell nuclei. In our ab initio calculations, the Coulomb force and charge-dependent component of the nuclear force [35] are both taken into account in the adopted many-body Hamiltonian, in which no parameters are introduced into the ab initio calculations of nuclear properties.In this article, we provide a comprehensive overview of the current status of the MED studies of
$ sd $ -shell nuclei. We focus on the large MED mechanism using ab initio VS-IMSRG calculations, particularly the TE shift. Furthermore, we compare our ab initio results with those obtained using shell model calculations. These studies are helpful for our understanding of the Coulomb and nuclear forces, the weakly-bound effect, and the properties of exotic nuclei. Overall, we hope this article provides a comprehensive and insightful study of the isospin-symmetry breaking in$ sd $ -shell mirror nuclei. -
The intrinsic A-nucleon Hamiltonian can be written as
$ H_{\rm int}=\sum\limits_{i=1}^{A}\left(1-\frac{1}{A}\right) \frac{{\boldsymbol{p}}_{i}^{2}}{2 m}+\sum\limits_{i<j}^{A}\left(v_{i j}^{{\rm{NN}}}-\frac{{\boldsymbol{p}}_{i} \cdot {\boldsymbol{p}}_{j}}{m A}\right)+\sum\limits_{i<j<k}^{A} v_{i j k}^{3 {\rm{N}}}, $

(2) where
$ {\boldsymbol{p_i}} $ represents the nucleon momentum in the laboratory frame, while m refers to the nucleon mass. The quantities$ v^{\rm{NN}} $ and$ v^{\rm{3N}} $ correspond to the nucleon-nucleon (NN) and three-nucleon (3N) interactions, crucial for determining the behavior of a nuclear system. Recently, the chiral effective field theory (EFT) force has been shown to accurately describe nuclear interactions.In our present work, contributions up to next-to-next-to-next-to-leading order (N3LO) and next-to-next-to-leading order (N2LO) [36] are included to construct the NN and 3N interactions within the chiral EFT framework. Specifically, we utilize the well-established NN + 3N interaction provided by the 1.8/2.0 (EM) potential in our ab initio calculations. The 1.8/2.0 (EM) potential uses a softened N3LO NN force via a similarity renormalization group (SRG) evolution [37] using
$ \lambda_{\rm{SRG}} = 1.8 $ fm−1 and a cutoff of$ \Lambda = 2.0 $ fm−1 for the softened N2LO 3N interaction. To reproduce the triton binding energy and 4He radius, the short-range low-energy constants$ c_D $ and$ c_E $ are optimized [38]. The potential well reproduces ground-state energies up to 132Sn [39−44]. The charge-dependent components of the nuclear force, including the charge-symmetry breaking (CSB) and charge-independence breaking (CIB) effects, are accounted for in the chiral EFT framework via mass splitting in the pion exchange, pion-nucleon coupling constant, nucleon-mass splitting, electromagnetic corrections, and low-energy constants of contact terms, among others (details in Refs. [35, 45]). In addition, the Coulomb force between protons is also included in the many-body Hamiltonian of Eq. (2). In practical calculations, the harmonic oscillator (HO) basis is used for defining the model space. We consider$ \hbar \omega =16 $ MeV and 15 HO major shells (i.e.$ e=2n+l \leq e_{{\rm{max}}}=14 $ ), and the HO energies in the three-nucleon sector are limited as well to$ e_{3\max} = 2n_a+2n_b+2n_c+l_a+l_b+l_c\leq 14 $ .The intrinsic Hamiltonian in Eq. (2) can be rewritten as normal-ordered Hamiltonian in Eq. (3) by normal ordering with respect to the single determinant or ensemble reference state
$ |\Phi\rangle $ [32], such as the Hartree-Fock (HF) reference state, which has proven to be a useful strategy for calculating and analyzing nuclear many-body problems [32]. The normal ordered A-nucleon Hamiltonian can be expressed as follows:$ \begin{aligned}[b] H_{\rm{NO}}= & E+\sum_{ij} f_{ij}: a_{i}^{\dagger} a_{j}:+\frac{1}{4} \sum_{ijkl} \Gamma_{ijkl}: a_{i}^{\dagger} a_{j}^{\dagger} a_l a_k :\\ &+\frac{1}{36} \sum_{i j k l m n} W_{i j k l m n}: a_{i}^{\dagger} a_{j}^{\dagger} a_{k}^{\dagger} a_{n} a_{m} a_{l}:, \end{aligned}$

(3) Here, the strings of creation and annihilation operators obey
$ \langle\Phi|: a_{i}^{\dagger} \cdots a_{j}:| \Phi\rangle=0 $ . The individual normal-ordered contributions in Eq. (3) are then given by$ \begin{aligned}[b] E=&\left(1-\frac{1}{A}\right) \sum_{a} \sum_{i=1}^{A} \langle a| \frac{{\boldsymbol{p}}_{i}^{2}}{2 m} | a\rangle n_{a} \\ &+\frac{1}{2} \sum_{a b} \sum_{i<j}^{A} \langle a b\left| \left(v_{i j}^{{\rm{NN}}}-\frac{{\boldsymbol{p}}_{i} \cdot {\boldsymbol{p}}_{j}}{m A}\right)\right| a b\rangle n_{a} n_{b} \end{aligned} $

$ \begin{aligned}[b] &+\frac{1}{6} \sum_{a b c} \sum_{i<j<k}^{A} \langle a b c\left| v_{i j k}^{3 {\rm{N}}}\right| a b c\rangle n_{a} n_{b} n_{c}, \\ f_{12}=&\left(1-\frac{1}{A}\right) \sum_{i=1}^{A} \langle 1| \frac{{\boldsymbol{p}}_{i}^{2}}{2 m} | 2\rangle\\ &+\sum_{a} \sum_{i<j}^{A} \langle 1 a\left|\left(v_{i j}^{{\rm{NN}}}-\frac{{\boldsymbol{p}}_{i} \cdot {\boldsymbol{p}}_{j}}{m A}\right)\right| 2 a\rangle n_{a} \\ &+\frac{1}{2} \sum_{a b} \sum_{i<j<k}^{A} \langle 1 a b\left| v_{i j k}^{3 {\rm{N}}}\right| 2 a b\rangle n_{a} n_{b}, \\ \Gamma_{1234}=& \sum_{i<j}^{A} \langle 12\left|\left(v_{i j}^{{\rm{NN}}}-\frac{{\boldsymbol{p}}_{i} \cdot {\boldsymbol{p}}_{j}}{m A}\right)\right| 34\rangle\\ &+\sum_{a} \sum_{i<j<k}^{A} \langle 12 a\left| v_{i j k}^{3 {\rm{N}}}\right| 34 a\rangle n_{a}, \\ W_{123456}=& \sum_{i<j<k}^{A} \langle 123\left| v_{i j k}^{3 {\rm{N}}}\right| 456\rangle. \end{aligned} $

(4) The normal-ordered zero-, one-, and two-body parts of the normal ordered Hamiltonian (E,
$ f_{ij} $ and$ \Gamma_{ijkl} $ ) encompass the main contributions of$ v^{3N} $ . In addition, the contributions of the normal-ordered three-body terms are small and can be neglected in practical calculations. Consequently, it is feasible to exclude the numerically demanding normal-ordered three-body part$ W_{ijklmn} $ [46, 47]. The treatment enhances the computational efficiency and reduces the computational cost, as normal-ordered three-nucleon calculations are often expensive and time-consuming.The ab initio VS-IMSRG method was employed to solve the many-body Schrödinger equation for open-shell nuclear systems. Within the VS-IMSRG approach, the single-particle Hilbert space, i.e., the single-particle state of the HF basis, was divided into core, valence, and excluded spaces. For example, for
$ sd $ -shell isotopes, we selected the 16O as the inner core, the full$ sd $ shell above the 16O was chosen as the valence space for both valence protons and valence neutrons, and the remaining higher-energy single-particle states were considered as excluded spaces. By using a sequence of similarity unitary transformations [33, 37, 46–52], the low-energy degrees of freedom from high-energy excitations in many-body systems were decoupled. After that, the VS-IMSRG calculation yielded an effective Hamiltonian within the valence space, which was written as [32, 33]$ H_{\rm{eff}}(s) = U^{\dagger}(s) H_{\rm{NO}}(0) U(s), $

(5) where
$ U(s) $ is the unitary transformation operator and$ H_{\rm NO}(s=0) $ is the starting Hamiltonian, starting from the initial components of the normal-ordered Hamiltonian in Eq. (3). The decoupling was achieved by solving the flow equation$ \frac{{\rm d} H_{\rm{eff}}(s)}{{\rm d} s}=[\eta(s),H_{\rm{eff}}(s)], $

(6) with an anti-Hermitian generator
$ \eta(s)\equiv\frac{{\rm d}U(s)}{{\rm d}s}U^{\dagger}(s)=-\eta^{\dagger}(s). $

(7) Based on the fundamental commutators from Appendix A of Ref. [46] and with all operators truncated at the two-body level, Eq. (6) became
$\begin{aligned}[b] \frac{{\rm d} E}{{\rm d} s}=&\sum_{a b}\left(n_{a}-n_{b}\right) \eta_{a b} f_{b a}+\frac{1}{2} \sum_{a b c d} \eta_{a b c d} \Gamma_{c d a b} n_{a} n_{b} \bar{n}_{c} \bar{n}_{d}, \\ \frac{{\rm d} f_{12}}{{\rm d} s}=&\sum_{a}\left(1+P_{12}\right) \eta_{1 a} f_{a 2} \\ &+\sum_{a b}\left(n_{a}-n_{b}\right)\left(\eta_{a b} \Gamma_{b 1 a 2}-f_{a b} \eta_{b 1 a 2}\right) \\ &+\frac{1}{2} \sum_{a b c}\left(n_{a} n_{b} \bar{n}_{c}+\bar{n}_{a} \bar{n}_{b} n_{c}\right)\left(1+P_{12}\right) \eta_{c 1 a b} \Gamma_{a b c 2} \text {, } \\ \frac{{\rm d} \Gamma_{1234}}{{\rm d} s}=&\sum_{a} \left(1-P_{12}\right)\left(\eta_{1 a} \Gamma_{a 234}-f_{1 a} \eta_{a 234}\right) \\ & -\sum_{a}\left(1-P_{34}\right)\left(\eta_{a 3} \Gamma_{12 a 4}-f_{a 3} \eta_{12 a 4}\right) \\ &+\frac{1}{2} \sum_{a b}\left(1-n_{a}-n_{b}\right)\left(\eta_{12 a b} \Gamma_{a b 34}-\Gamma_{12 a b} \eta_{a b 34}\right) \\ &-\sum_{a b}\left(n_{a}-n_{b}\right)\left(1-P_{12}\right)\left(1-P_{34}\right) \eta_{b 2 a 4} \Gamma_{a 1 b 3}, \end{aligned} $

(8) Eq. (8) was solved iteratively using a self-consistent procedure until convergence. Nuclear observables were calculated by diagonalizing the effective Hamiltonian within the chosen valence space. Overall, the combination of chiral interactions and accurate ab initio many-body methods offered a powerful tool to study the nuclear structure of light and medium-mass nuclei.
In this work, we utilized the VS-IMSRG code of Ref. [53] with ensemble normal-ordering (ENO) [32, 53] to generate the valence-space Hamiltonian. The obtained effective Hamiltonian was exactly diagonalized with the shell model Kshell code [54]. In the present work, the
$ sd $ -shell isotopes were calculated within the full$ sd $ -shell valence spaces for both valence protons and valence neutrons, above the 16O inner core. The MED values of the mirror nuclei within$ sd $ -shell were calculated systematically. We discuss the mechanisms behind the MED values, focusing on the TE shift. -
We performed systematic calculations for the low-lying spectra of the
$ sd $ -shell nuclei to gain a comprehensive understanding of the MED. Our ab initio VS-IMSRG calculations were performed by accounting for both NN and NN+3N interactions. The calculated spectra, along with available experimental data, are presented in Fig. 1 and the appendix. In section A, we analyze the influence of the 3N force on the calculated low-lying spectra, taking examples, such as 21Al/21O, 22Al/22F, 23Al/23Ne, 24Al/24Na, 19Na/19O, and 20Mg/20O mirror partners. After that, we explore the evolution of the MED for proton-rich Al isotopes and$ N=8 $ isotones by combining the MED values and average occupations. The relationship between the MED and occupation of valence nucleons is investigated. Finally, we compare the results of our ab initio calculations with the shell model results and discuss the TE shift in the ground state.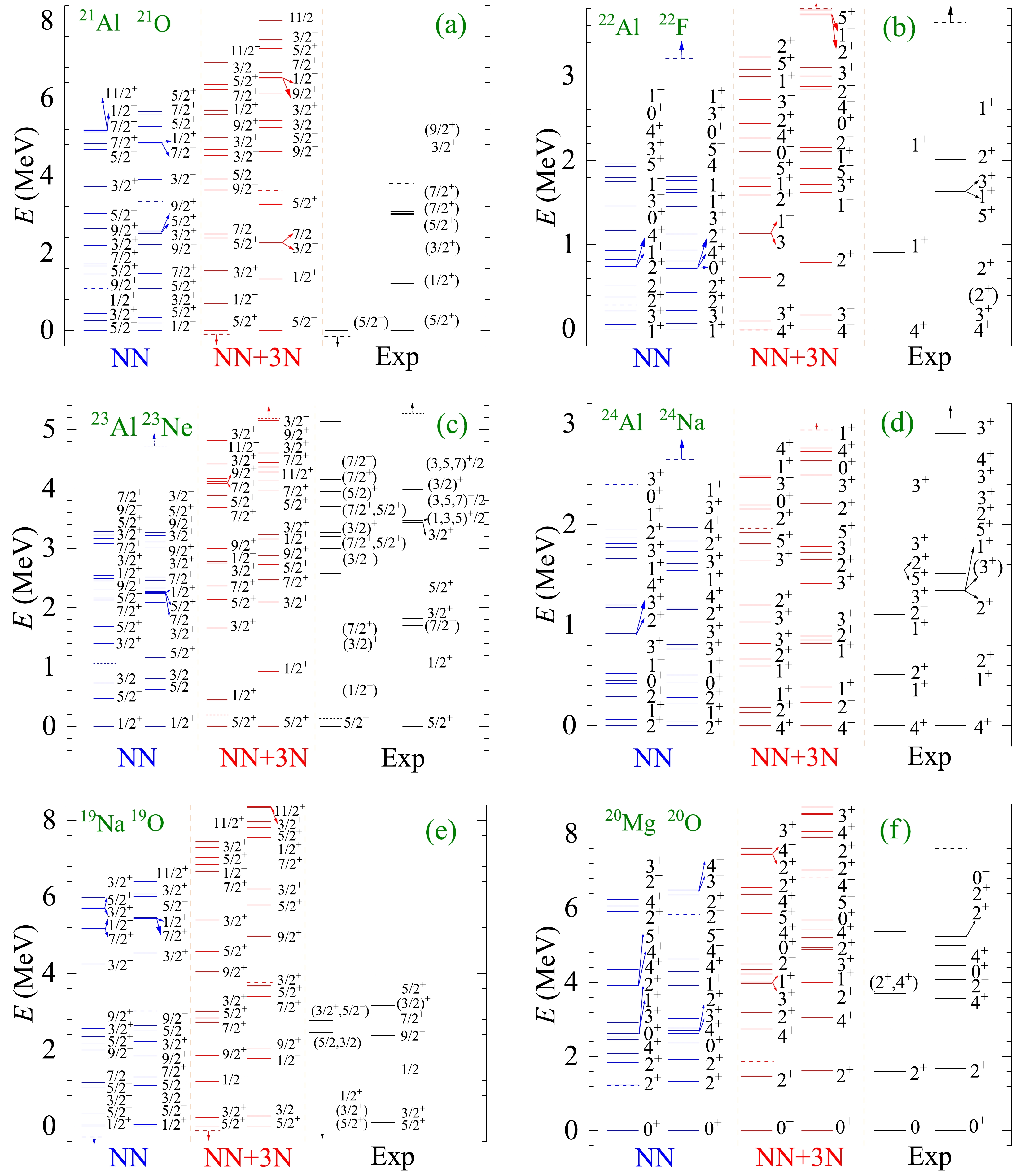
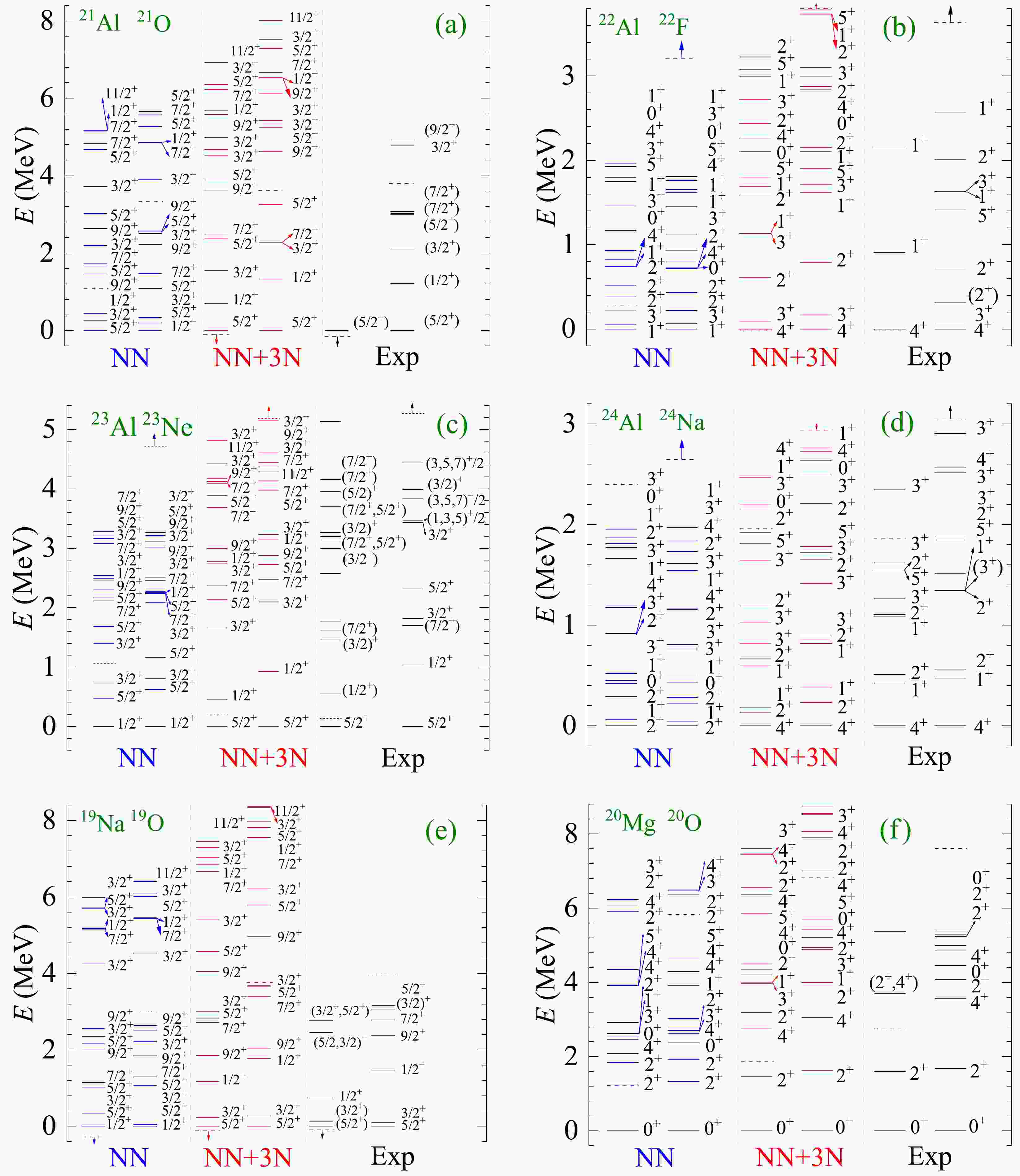
Figure 1. (color online) Spectral results for mirror nuclei, 21Al/21O, 22Al/22F, 23Al/23Ne, 24Al/24Na, 19Na/19O, and 20Mg/20O, using the ab initio VS-IMSRG method. The calculations with 1.8/2.0 (EM) nucleon-nucleon and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively. Experimental data are from Ref. [55]. The one-proton and -neutron separation energies are both denoted by the dashed lines or the dashed lines with arrows.
-
Firstly, we calculate the spectra of Al isotopes 21−24Al,
$ N=8 $ isotones 19Na and 20Mg, as well as their corresponding mirror nuclei. The results of the ab initio VS-IMSRG calculations with NN and NN+3N interaction are presented in Fig. 1, compared with available experimental data [55]. From Fig. 1, it is evident that the low-lying states obtained in calculations without including 3N forces, particularly the ground state, disagree with the experimental data. After incorporating the NN + 3N force into the VS-IMSRG calculations, a good agreement with the experimental data was obtained. The results demonstrate the significance of including 3N forces in the calculations of low-lying spectra. Overall, the deviation of the excited states obtained using our ab initio VS-IMSRG (NN+3N) calculations from the experimental data is within a few hundred keV. Therefore, we proceed with the NN + 3N calculation for further discussion.In this study, the effect of the 3N force was accounted for using the normal order approach (Eq. (3)). The techniques have also been utilized in the open-shell many-body perturbation theory [56] and ab initio Gamow shell model with core [16] to account for the 3N force. These calculations [16, 56] yielded similar results, demonstrating that including the 3N force improved the spectra calculations. A different approach, considering the 3N force used in Ref. [57], accounts for the 3N force effect by multiplying the A-dependent one- and two-body factors to the adopted Gamow shell model Hamiltonian. With respect to the spectra of 21Al, not known experimentally, our VS-IMSRG calculations overall agreed with the results reported in Refs. [56, 57].
-
Before discussing the energy differences between the excited states of mirror nuclei, we briefly analyze Coulomb displacement energies (CDE), which describe the differences between binding energies. The CDE for mirror nuclei is defined as
${\rm{CDE}}(A, T)=BE\left(T, T_{z_<}\right)-BE\left(T, T_{z_>}\right), $

(9) where
$ T_z = (N-Z)/2 $ is the z projection of isospin, and$ BE\left(T, T_{z_<}\right) $ as well as$ BE\left(T, T_{z_>}\right) $ are binding energies of the isospin multiplets with the smallest and largest number of protons, respectively. The CDE has been investigated using the shell model calculations in Refs. [58, 59].The CDEs calculated using the ab initio VS-IMSRG method for mirror pairs 21Al/21O, 22Al/22F, 23Al/23Ne, 24Al/24Na, 19Na/19O, and 20Mg/20O are presented in Table 1, along with available experimental data [55]. In our previous work [52], we systematically calculated the b coefficient of the isobaric multiple mass equation, a term representative of the CDE. The agreement with experimental data was quite satisfactory for the CDE, further substantiating that VS-IMSRG could be suitably employed to investigate the MED values of
$ sd $ -shell nuclei.$J^{\pi}$ (g.s.)

CDE/MeV VS-IMSRG Exp 21Al/21O $5/2^+$ 

21.998 22Al/22F $4^+$ 

18.520 18.530(408) 23Al/23Ne $5/2^+$ 

14.325 14.249 24Al/24Na $4^+$ 

10.028 9.934 19Na/19O $5/2^+$ 

12.050 11.943 20Mg/20O $0^+$ 

17.009 16.810 Table 1. The Coulomb displacement energies (CDE) for binding energies in mirror partners 21Al/21O, 22Al/22F, 23Al/23Ne, 24Al/24Na, 19Na/19O, and 20Mg/20O with ab initio VS-IMSRG calculations. The calculated CDE values are compared with available experimental data [55].
Based on the calculated spectra of mirror nuclei pairs, we observe that excited energies in proton-rich nuclei are consistently lower than their corresponding mirror analogue states in neutron-rich nuclei. This asymmetry in excited energies, known as MED and discussed in Eq. (1), is the focus of our investigation. To further analyze and understand the MED mechanisms, we calculated the MED values using VS-IMSRG(NN+3N), along with average occupations of single-particle valence orbits. The results are presented in Figs. 2 and 3, together with available experimental MED data.
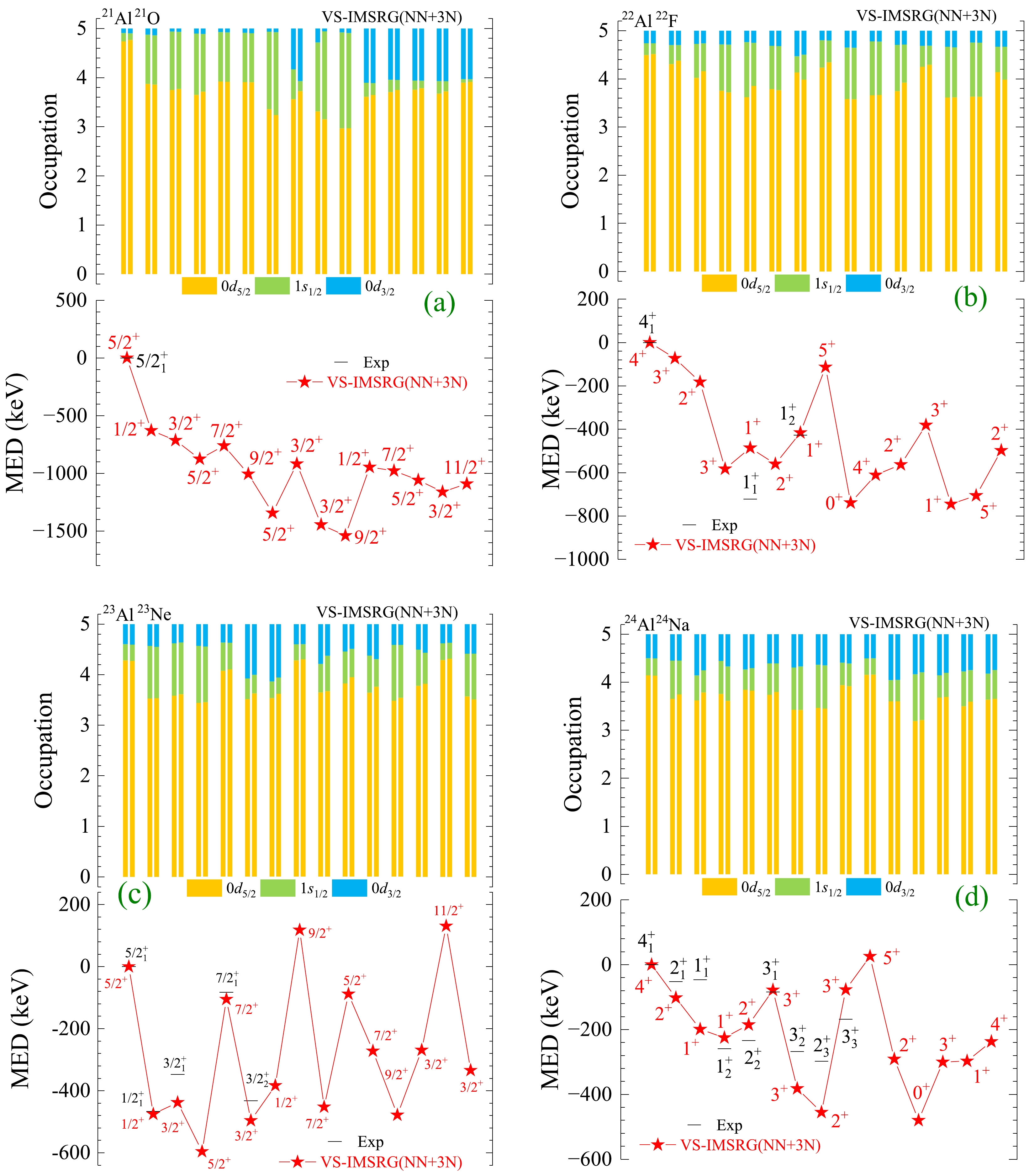
Figure 2. (color online) Calculated average occupations of single-particle valence orbits and mirror energy differences for low-lying states of mirror nuclei 21Al/21O, 22Al/22F, 23Al/23Ne, and 24Al/24Na, using VS-IMSRG based on the 1.8/2.0 (EM) NN + 3N interaction. The displayed average occupations correspond to the valence protons and neutrons in the respective mirror nuclei. Experimental data are from Ref. [55].

Figure 3. (color online) Similar to Fig. 2, but for mirror nuclei 19Na/19O and 20Mg/20O.
The calculated average occupations for the valence protons and neutrons of proton- and neutron-rich mirror nuclei, respectively, are nearly identical. The MED values obtained using the ab initio VS-IMSRG method for mirror nuclei 21Al/21O, 22Al/22F, 23Al/23Ne, 24Al/24Na, 19Na/19O, and 20Mg/20O all lead to the same conclusion. Specifically, we find that the large proton average occupations in the 1
$ s_{1/2} $ orbit correspond to large MED values, as observed for the$ 1/2^+_1 $ state of 19Na. In addition, we emphasize that the 0$ d_{3/2} $ orbital occupations also play a vital role in determining the MED values, as evident from the high excited states of 19Na in Fig. 3(a). In a brief explanation, the centrifugal barrier is proportional to the angular momentum quantum number$ l (l +1) $ . The absence of a centrifugal barrier for the s-wave ($ 1s_{1/2} $ ) in weakly-bound or unbound proton-rich nuclei results in an extended radial wave function for valence protons, whereas it is deeply bound for valence neutrons in the mirror neutron-rich nuclei. A thorough analysis can be found in our previous study [52].This article mainly focuses on the evolutions of MED values for proton-rich Al isotopes and
$ N=8 $ isotones. In a pair of mirror nuclei, owing to the repulsive Coulomb force between protons, the proton separation energy ($ S_p $ ) of the proton-rich nucleus is significantly lower than the neutron separation energy ($ S_n $ ) of the neutron-rich nucleus, as shown in Fig. 1. Notably, negative$ S_p $ values are observed for 21Al and 19Na. Consequently, proton-rich nuclei become weakly bound or even unbound as they approach the proton drip line, while neutron-rich nuclei remain deeply bound. In conjunction with Fig. 2, the weakly-bound or unbound effect of proton-rich nuclei near the proton drip line leads to a remarkable decline in their excitation energy, causing large MED values.A simplified and visual analysis reveals that as the proton-rich nucleus gradually approaches and crosses the drip line, ranging from 24Al/24Na to 21Al/21O, the MED values of low-lying states increase. This implies that we can expect to observe larger MED values in the vicinity of the proton drip-line nuclei. For instance, when comparing the mirror partners 21Al/21O and 23Al/23Ne, 23Al is weakly-bound and is located inside the proton drip line, while 21Al is unbound and is located beyond the proton drip line, as shown for
$ S_p $ in Fig. 2. The results show that the calculated MED values of low-lying states of 21Al/21O are larger than those of 23Al/23Ne.Furthermore, the calculated average occupations of the
$ 7/2^+_1 $ and$ 9/2^+_1 $ states of 21Al/21O are similar. However, the calculated MED values show a discrepancy of approximately 250 keV for these two states. This discrepancy mainly arises from the fact the$ 9/2_1^+ $ state is higher in terms of the excitation energy and exhibits stronger weakly-bound or unbound effects compared with the$ 7/2_1^+ $ state. A similar situation occurs between the ground state and the first excited state of 20Mg. As a result, we can also expect to observe large MED values in the high-excited states of the proton drip line nuclei.The mirror partners of
$ N=8 $ isotones and isotopes (19Na/19O, 20Mg/20O, and 21Al/21O) are also calculated, and the results are presented in Figs. 2 and 3. The ground states of$ N=8 $ isotones mainly occupy the$ 0d_{5/2} $ orbital. The excited state with valence protons excited to the$ 1s_{1/2} $ orbital exhibits large MED values, such as the$ 1/2^+_1 $ state of 19Na,$ 2^+_2 $ state of 20Mg, and$ 1/2^+_1 $ state of 21Al.In addition, 21Al is the lightest nucleus among experimentally observed Al isotopes so far. Our ab initio VS-IMSRG calculations with NN+3N suggest that the ground state of 21Al is
$ 5/2^+ $ states, which is aligned with the ground state of 21O. The valence protons (neutrons) of the ground states 21Al (21O) mainly occupy the π(ν)$ 0d_{5/2} $ orbital, as shown in the upper panel of Fig. 2(a). Moreover, the MED value of the$ 1/2_1^+ $ state is not sufficient for changing the ordering between the$ 1/2^+_1 $ and$ 5/2^+_1 $ ground states, as shown in the lower panel of Fig. 2(a). The obtained result agrees with the shell model calculations presented in Ref. [59], where the weakly-bound effect is taken into account by adjusting two-body interaction elements associated with the proton 1$ s_{1/2} $ orbit based on the USD and modified USD family interaction.Moreover, a recent experiment [17] investigated the low-lying states of 22Al and obtained large MED values for the
$ 1^+_1 $ and$ 1^+_2 $ states of 22Al by combining the available experimental data on 22F. The evidence suggests that the$ 1_1^+ $ state of 22Al is a candidate state with a halo structure [17]. The results of our ab initio VS-IMSRG (NN+3N) calculations suggest that the proton average occupations in the$ 1^+_1 $ state of 22Al are 3.605, 1.156, and 0.230 for the$ 0d_{5/2} $ ,$ 1s_{1/2} $ , and$ 0d_{3/2} $ orbits, respectively. The proton average occupations in the$ 1^+_2 $ state of 22Al are 4.089, 0.525, and 0.386 for the$ 0d_{5/2} $ ,$ 1s_{1/2} $ , and$ 0d_{3/2} $ orbits, respectively. The results indicate that the$ 1^+_1 $ state of 22Al has a larger 1$ s_{1/2} $ occupation but a smaller$ d_{3/2} $ occupation compared with the$ 1^+_2 $ state. These results are consistent with shell model calculations, including isospin-nonconserving forces in Ref. [17], both supporting the notion that the$ 1^+_1 $ state of 22Al exhibits a halo structure. The calculations suggest that the states with a large occupation of weakly-bound or unbound$ 1s_{1/2} $ orbital in the proton drip-line nuclei exhibit large MED values and may possess halo properties. -
The TE shift has also been investigated in shell model calculations using the calculated spectroscopic factors (details in Refs. [60, 61]). In this section, we compare the MED values obtained using our ab initio VS-IMSRG with those obtained using shell model calculations in Ref. [60, 61]. The comparison helps us gain insights into the mechanisms of MED.
In Table 2, we list the MED values calculated using the shell model and our ab initio VS-IMSRG for mirror partners 23Al/23Ne, 24Si/24Ne, 26P/26Na, 27P/27Mg, 28P/28Al, 28S/28Mg, and 29S/29Al, along with available experimental data [55]. The shell model results are taken from Refs. [60, 61]. The MED values obtained using the shell model calculations and ab initio VS-IMSRG are consistent with each other, and are also consistent with the available experimental data [55]. Notably, the MED values obtained using our ab initio VS-IMSRG calculations are closer to the experimental data compared with the shell model calculations, which is particularly evident for the MED values of the low-lying states of 27−28P and 28−29S. Furthermore, it is worth noting that the MED values of the states in 26−28P and 28S are positive.
$J^{\pi}$ 

TE shift MED shell model VS-IMSRG Exp 23Al $5/2^+$ 

−1 0 0 0 $1/2^+$ 

−427 −426 −475 −467 24Si $0^+$ 

−57 0 0 0 $2^+$ 

−84 −27 −165 −108 $2^+$ 

−253 −196 −434 −419 $4^+$ 

−17 40 86 $0^+$ 

−534 −477 −1145 −1001 26P $3^+$ 

−254 0 0 0 $1^+$ 

−171 83 60 82 $2^+$ 

−203 51 49 11 $2^+$ 

−259 −5 −22 27P $1/2^+$ 

−169 0 0 0 $3/2^+$ 

−42 127 60 138 $5/2^+$ 

−177 −8 −221 −174 $5/2^+$ 

−201 −32 6 28P $3^+$ 

−129 0 0 0 $2^+$ 

−85 44 26 75 $0^+$ 

−150 −21 −82 −95 $3^+$ 

−15 114 −9 120 $1^+$ 

−98 31 −12 −60 $1^+$ 

−96 33 −98 −53 $2^+$ 

−107 22 −114 −107 28S $0^+$ 

−187 0 0 0 $2^+$ 

−207 −20 −1 33 29S $5/2^+$ 

−166 0 0 0 $1/2^+$ 

−190 −24 −127 −176 $7/2^+$ 

−165 1 −118 −27 $5/2^+$ 

−225 −59 −168 −175 Table 2. The TE shifts for low-lying states in 23Al, 24Si, 26P, 27P, 28P, 28S, and 29S, obtained using shell model calculations. The inferred MED values for the shell model are compared with the results of our ab initio VS-IMSRG calculations and available experimental data [55]. The results of the shell model calculations are taken from Refs. [60, 61].
To further investigate the positive MED values of 26−28P and 28S and to further explore the mechanism behind the MED, we consider 27P/27Mg as an example for detailed comparison of the shell model with our ab initio VS-IMSRG calculation results. Our ab initio VS-IMSRG calculation results of the low-lying spectra, average occupations, and MED values for 27P/27Mg are presented in Figs. 4 and 5. In the shell model calculations, the TE shift for a state is given by the following expression:

Figure 4. (color online) Similar to Fig. 1, but for mirror nuclei 27P/27Mg.
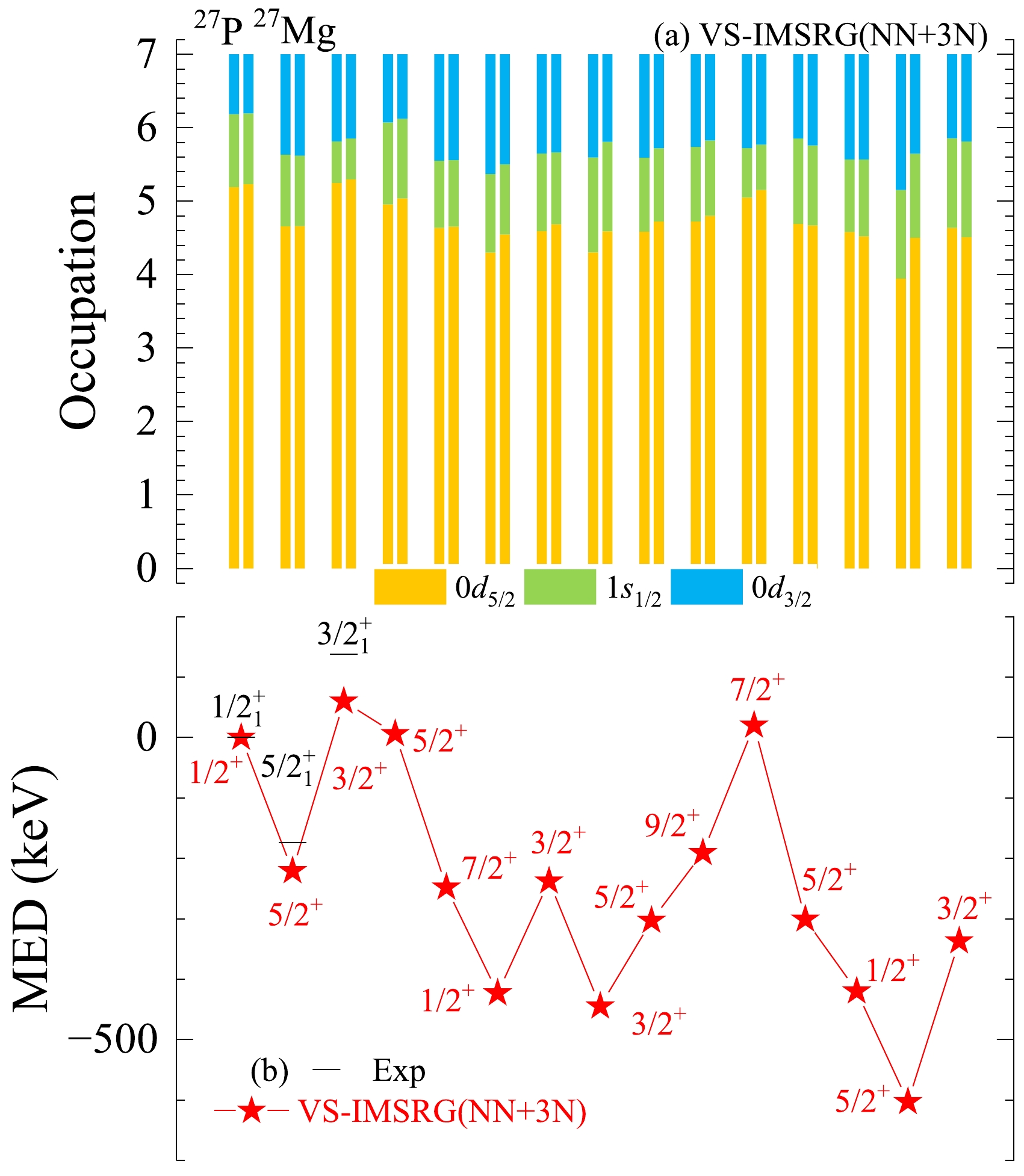
Figure 5. (color online) Similar to Fig. 2, but for mirror nuclei 27P/27Mg.
$\begin{aligned}[b] {\rm{TE}}\left[E_x\left({ }^{27} {\rm{P}}\right)\right] =& \left(\frac{27}{26}\right) \sum_{\left.E_x({ }^{26} {\rm{Si}}\right)}^{4{\rm{MeV}}} C^2 S\left({ }^{27} {\rm{P}} \rightarrow { }^{26} {\rm{Si}}\right)\\& \times {\rm{TE}}_{{\rm{WS}}}\left[S_p\left({ }^{27} {\rm{P}}\right)+E_x\left({ }^{26} {\rm{Si}}\right)-E_x\left({ }^{27} {\rm{P}}\right)\right], \end{aligned} $

(10) where the factor of (27/26) accounts for the center-of-mass correction,
$ C^2S $ is the spectroscopic factor,$ S_p $ denotes the single-proton separation energy,$ E_x $ is the excitation energy, and TEWS is the single-particle TE shift calculated using a Woods-Saxon potential [62]. Moreover, the TE shift is considered for the ground state of proton-rich nuclei, as shown in the third column of Table 2. In the shell model calculations, a negative TE shift of approximately –169 keV is obtained for the ground state of 27P. However, the$ 3/2^+ $ state exhibits a small TE shift of approximately$ -42 $ keV, resulting in a positive MED. The result is consistent with our ab initio VS-IMSRG calculations, which suggest that the average occupations of valence protons in the$ 1s_{1/2} $ orbitals are larger in the ground state of 27P compared with the$ 3/2^+ $ excited state. Moreover, the MED values of the low-lying states in 26,27,28P and 28,29S are either positive or weakly negative. This can be attributed to the strong TE shift effects in the ground states of these nuclei.As discussed above, the state with a large MED value, known as the TE shift, is characterized as a drop in the energy of a state with valence protons in the weakly-bound or unbound
$ s_{1/2} $ orbital at or near the particle threshold. VS-IMSRG calculations compute the MED values of dripline nuclei in a self-consistent manner, with results that are in excellent alignment with experimental data. Nevertheless, in the shell model calculations, approximations are formulated, anchored in the main concept of the TE shift, which is induced by the weakly bound or unbound$ s_{1/2} $ orbital [60−62]. The good agreements between the MED values calculated using the VS-IMSRG framework and shell model reveal that the approximations of the shell model MED calculations are valid, and support the notion that the large MED values observed in$ sd $ -shell dripline nuclei are predominantly caused by the occupations of weakly bound or unbound$ s_{1/2} $ orbital by valence protons. -
The mirror energy difference of
$ sd $ -shell nuclei has been investigated using the ab initio valence-space in-medium similarity renormalization group approach based on chiral interactions. The calculations took into account charge-symmetry breaking and charge-independent breaking effects in the adopted nuclear force, as well as the isospin-non-conserved Coulomb force.In this work, we systematically calculated the mirror spectra of
$ sd $ -shell nuclei using the ab initio VS-IMSRG method with both the nucleon-nucleon and three-nucleon interactions, and compared the results with experimental data. Specifically, we focused on pairs of mirror nuclei such as 21Al/21O, 22Al/22F, 23Al/23Ne, 24Al/24Na, 19Na/19O, and 20Mg/20O. Considering the low-lying states of these pairs of mirror nuclei, we demonstrated that the inclusion of three-nucleon forces is crucial for accurately reproducing available experimental spectra. Furthermore, we investigated the evolutions of the MED values for the Al isotopes, from 24Al to 21Al, and$ N=8 $ isotones, from 19Na to 21Al. In the regions of proton drip-line nuclei, the weakly-bound effects and large average occupations of the 1$ s_{1/2} $ orbit were the primary factors contributing to large MED values. The results revealed that the MED value of the low-lying state increased as the proton-rich nucleus approached or went beyond the proton drip line. Lastly, we compared the results of our ab initio VS-IMSRG method with those obtained using the shell model. The results demonstrated excellent concordance between the two approaches, unveiling significant relationships and connections between these two models. Furthermore, we analyzed the underlying reason for the occurrence of positive MED values. We hope that our calculations will contribute valuable predictions and analyses that will serve as a foundation for future experimental research. -
We acknowledge the Gansu Advanced Computing Center for providing computational resources.
-
The calculated spectra, along with available experimental data, are presented in the appendix.

Figure A1. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 19Na/19O using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A2. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 20Mg/20O using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A3. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 21Mg/21F using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A4. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 22Mg/22Ne using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A5. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 21Al/21O using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.
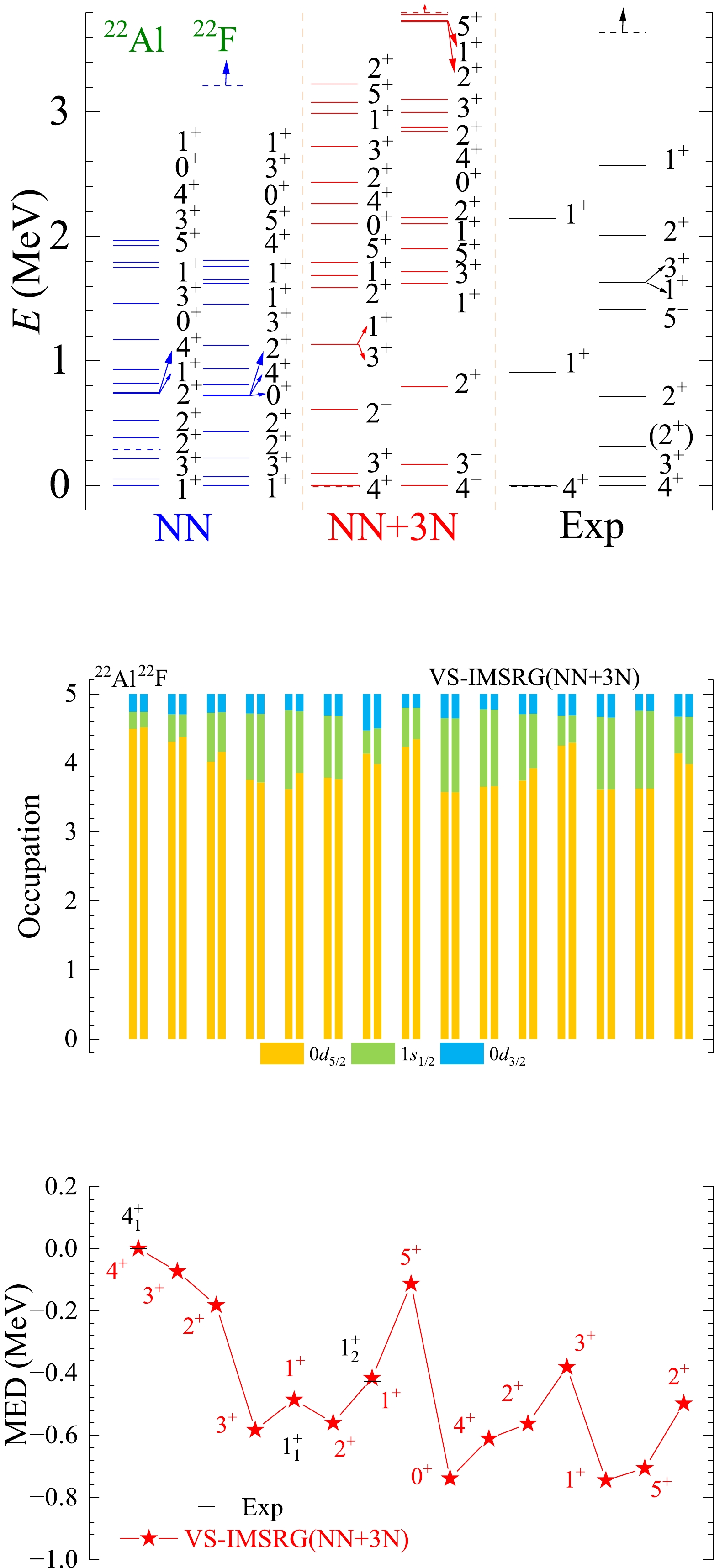
Figure A6. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 22Al/22F using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.
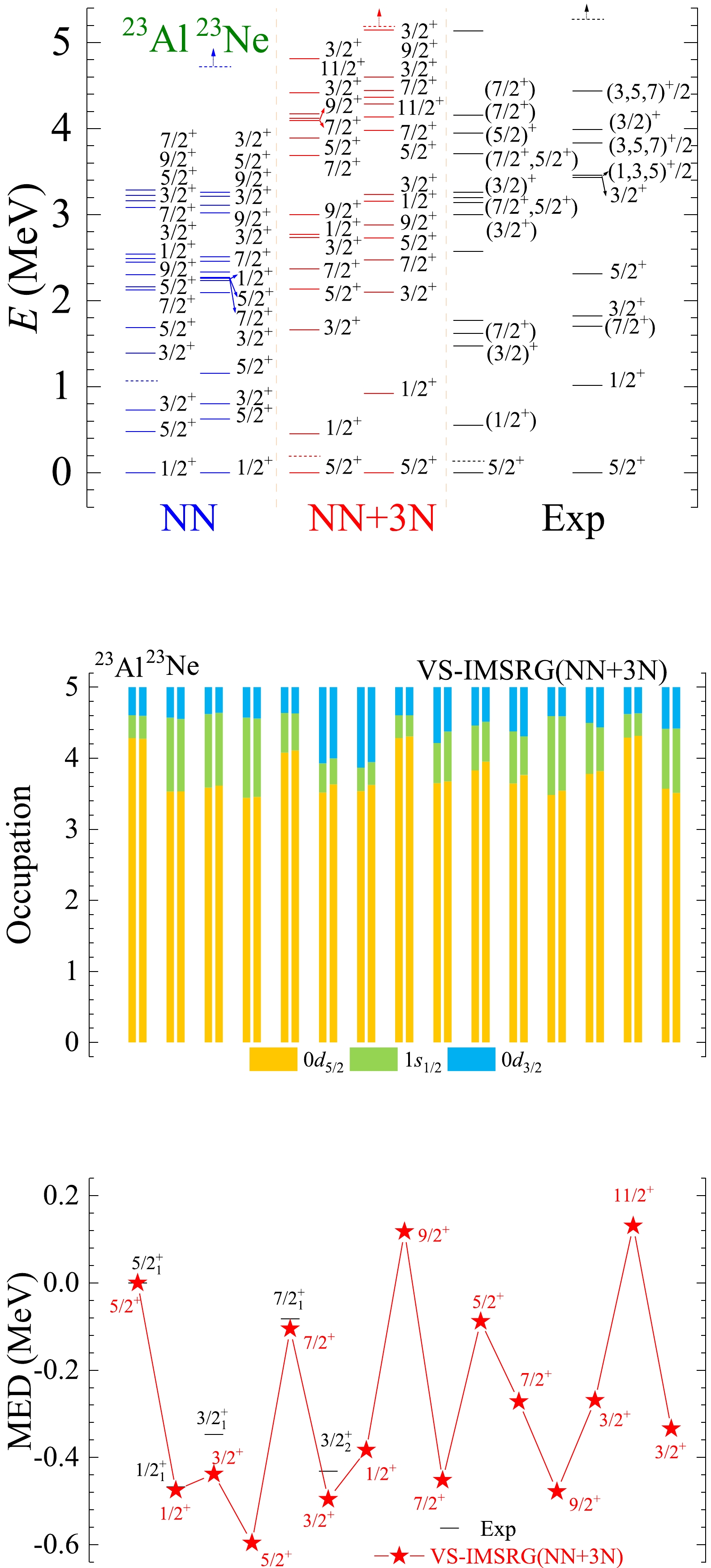
Figure A7. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 23Al/23Ne using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A8. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 24Al/24Na using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A9. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 22Si/22O using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.
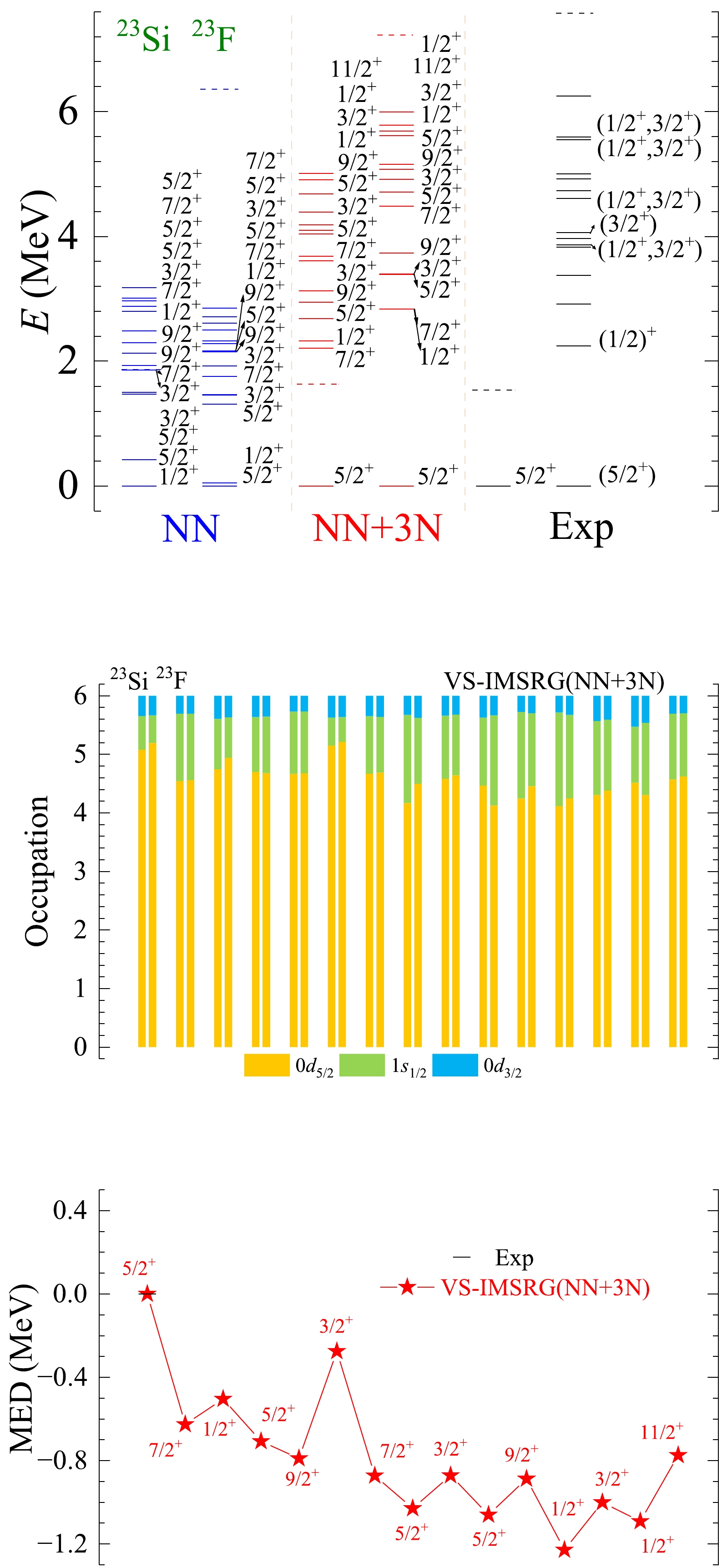
Figure A10. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 23Si/23F using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A11. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 24Si/24Ne using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A12. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 25Si/25Na using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A13. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 26Si/26Mg using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.
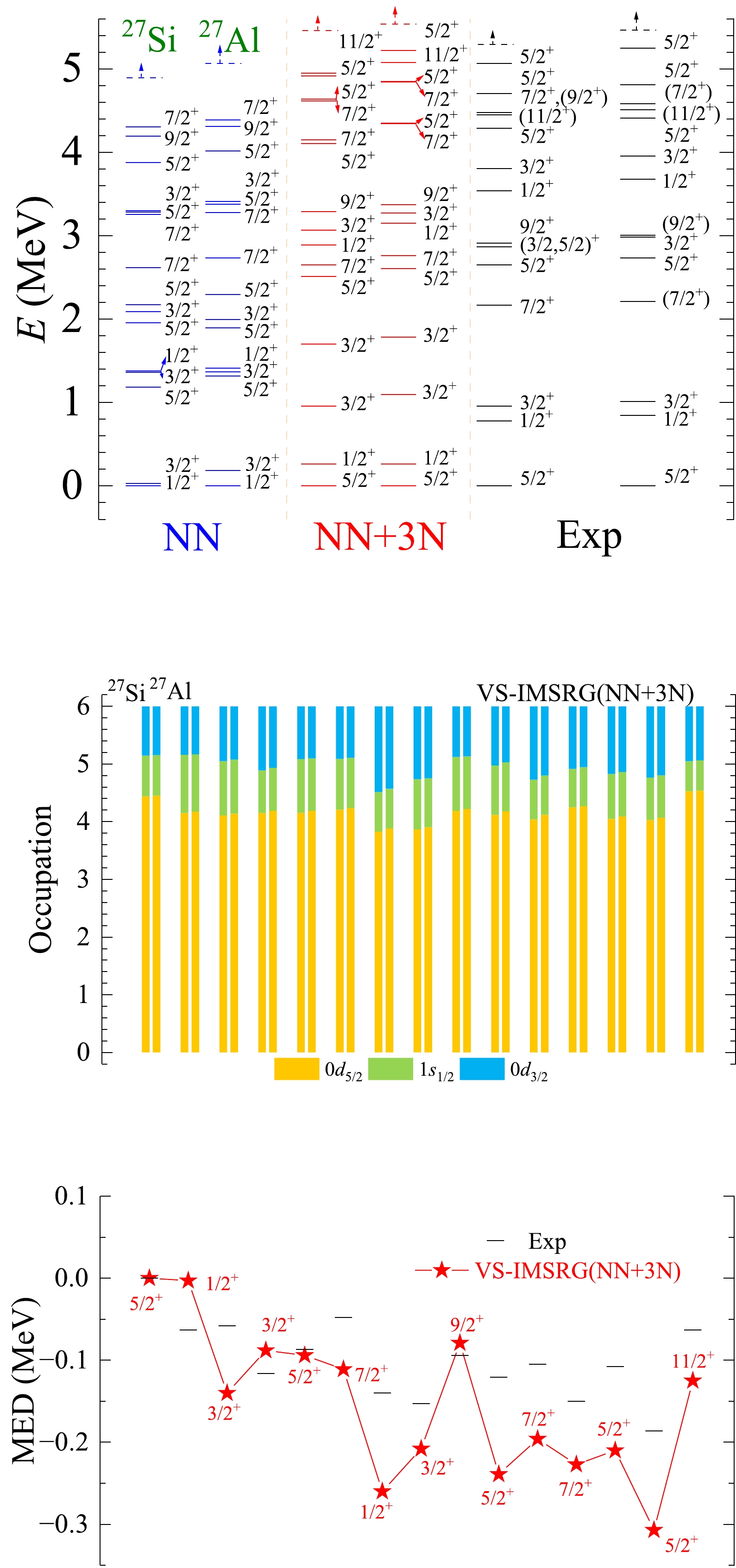
Figure A14. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 27Si/27Al using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A15. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 25P/25Ne using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.
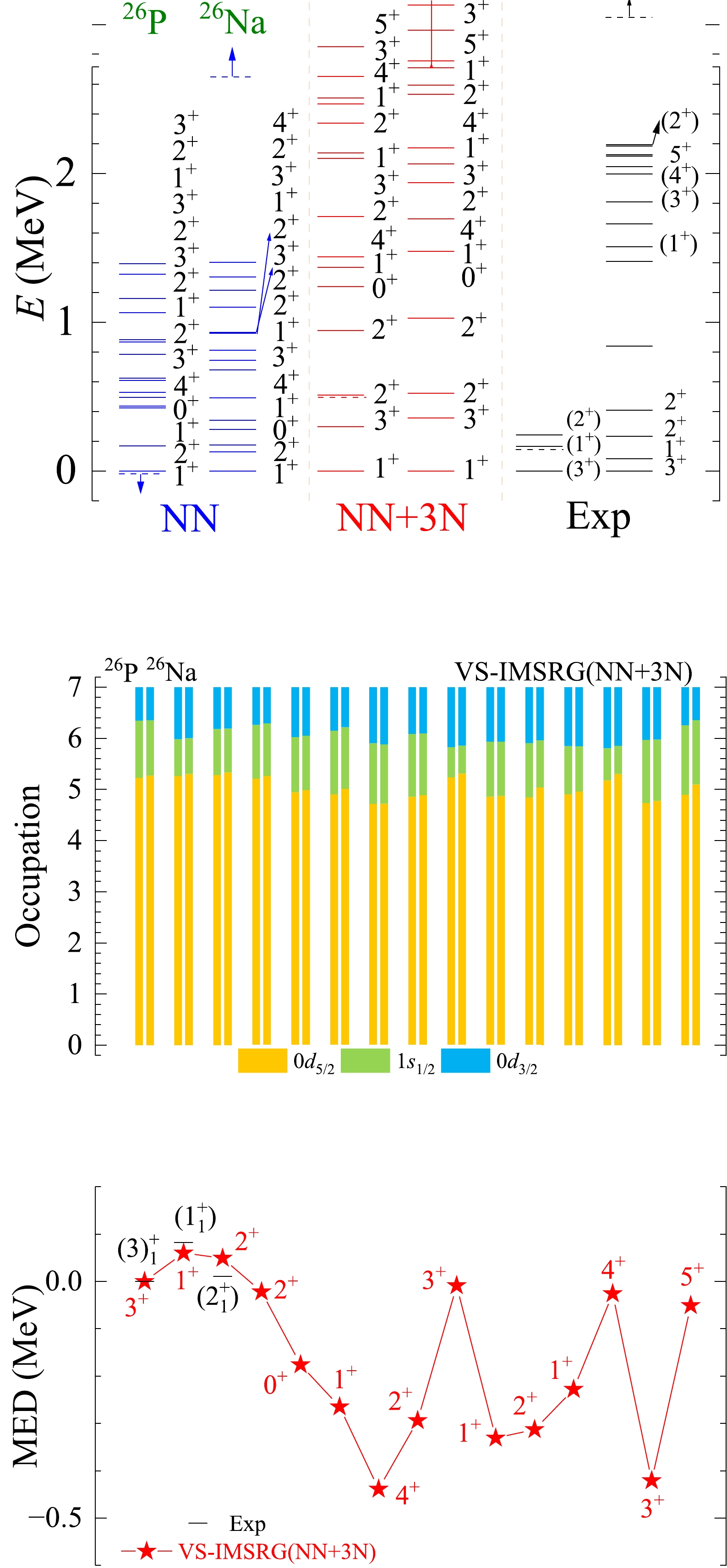
Figure A16. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 26P/26Na using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A17. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 27P/27Mg using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.
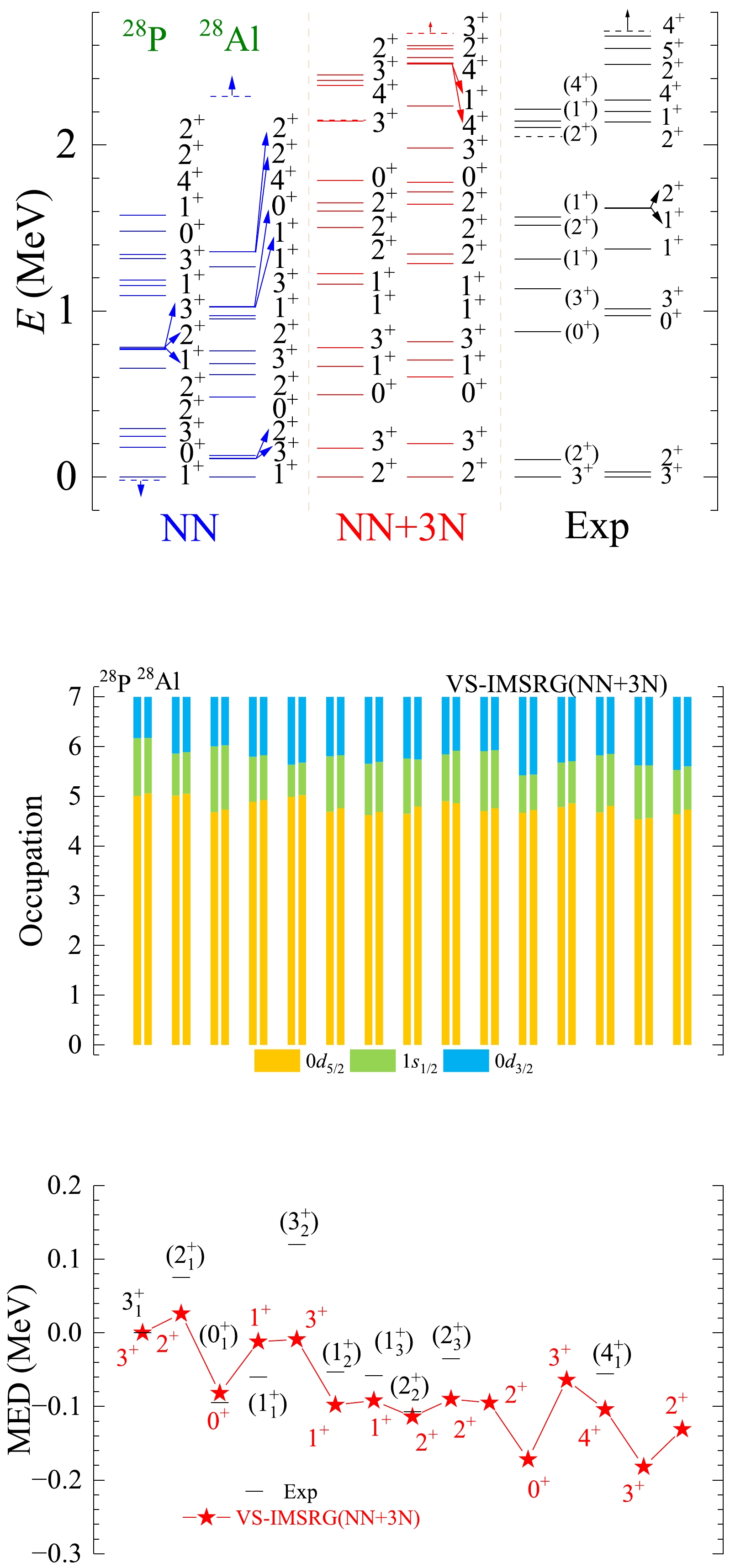
Figure A18. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 28P/28Al using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A19. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 27S/27Na using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A20. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 28S/28Mg using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A21. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 29S/29Al using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A22. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 30S/30Si using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A23. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 29Cl/29Mg using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.
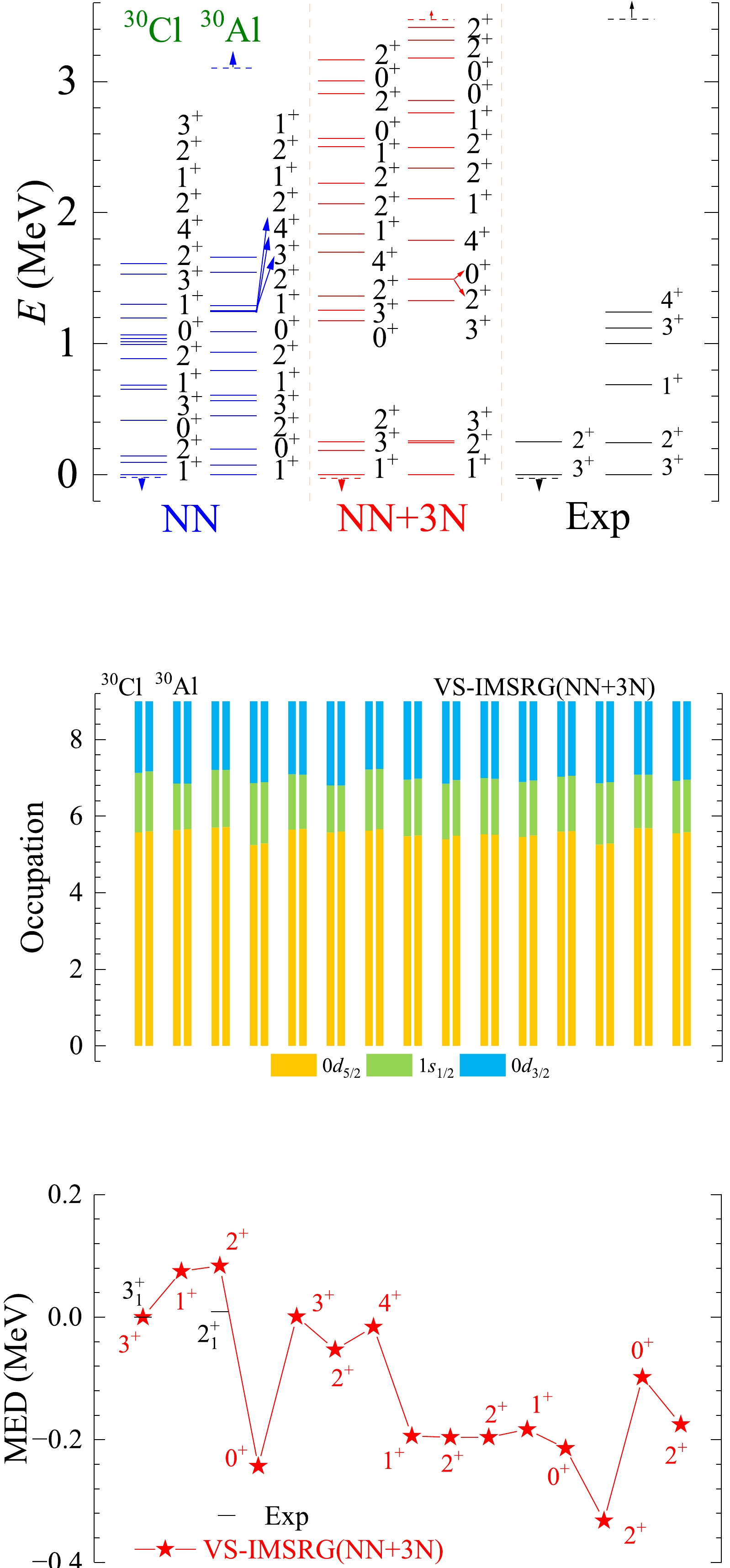
Figure A24. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 30Cl/30Al using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A25. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 31Cl/31Si using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.

Figure A26. (color online) The results of spectra, average occupations, and MED values for mirror nuclei 32Cl/32S using the ab initio VS-IMSRG method, along with available experimental data [55]. The calculations with 1.8/2.0 (EM) two- and three-nucleon potential and only bare N3LO NN potential are labeled by NN + 3N and NN, respectively.
Ab initio calculations of mirror energy difference in sd-shell nuclei
- Received Date: 2023-06-09
- Available Online: 2023-12-15
Abstract: Mirror energy difference is a key observable in isospin symmetry breaking, containing rich information about nuclear structure. Understanding the mechanisms underlying mirror energy difference is important in nuclear physics. In the present work, we extensively investigated mirror energy difference using ab initio valence-space in-medium similarity renormalization group approach, focusing specifically on





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: