-
The fusion of heavy-ion reactions is sensitive to the size and shape of interacting atomic nuclei [1]. The role of the deformation parameters is of particular interest. The fusion reaction 16O+16O with a spherical projectile and spherical target [2] results in a larger cross-section when compared to the fusion of the spherical and deformed nuclei of the reaction 12C+20Ne. Experimentally, it has been observed that the evaporation residue cross section for the fusion reaction 16O+34S is larger than the evaporation residue cross sections produced for the deformed and spherical nuclei 18O+32S [3]. It is also evident that the shape of the nuclei during a fusion reaction affects the barrier height [4]. A number of studies have been conducted on the role of deformation in sub-barrier fusion using the quantum diffusion technique [5−7]. Moreover, it is evident that heavy ion collisions near the Coulomb barrier have a significant influence on the internal structure of the colliding nuclei [8].
Using quantum mechanical fragmentation theory (QMFT) [9], studies have been performed on fusion reactions such as 248Cm+26Mg, 238U+36S, and 226Ra+48Ca for the synthesis of the compound nucleus 274Hs. Among the studied fusion reactions, 226Ra+48Ca enhances the evaporation residue cross sections owing to the presence of 48Ca. Many experiments have been conducted to synthesize superheavy element using actinide targets from U to Cf with the fusion of the projectile nucleus 48Ca [10−12]. The stability of superheavy elements with Z = 114 and N = 184 was predicted using macroscopic-microscopic models [13]. The concept of cold fusion using 208Pb as a target results in a large production cross section and an enhancement in the evaporation residue cross section, particularly for the 2n or 3n channel [14].
The synthesis of superheavy nuclei can be divided into two categories. The first uses "cold fusion reactions," with lead or bismuth as the target. With both being almost spherical, the production cross sections are found to be larger. The second involves "hot fusion reactions," in which 48Ca is used as the projectile. The superheavy elements Z = 116 and 118 were synthesized using curium and californium as the targets [15]. The role of entrance channel effects was studied in the superheavy region [16−18]. Theoretical studies have been proposed to synthesize the superheavy elements Z = 120−124 using Ti, Cr, and Fe as projectiles with actinide targets [19]. Chauhan et al. [20] investigated the fusion cross section and barrier distribution for the fusion reactions 16O+120Sn and 16O+208Pb. Using the three-stage classical dynamical model, the fusion cross sections of 16O+40Ca and 32S+40Ca [21] were studied. The nucleus-nucleus potential in the case of spherical-spherical fusion reactions, such as 40Ca+48Ca, 16O+208Pb, and 48Ca+48Ca, were studied using the Monte Carlo method [22].
Considerable experimental evidence proves that the fusion of spherical-spherical nuclei produces larger evaporation residue cross-sections compared to the fusion of spherical-deformed nuclei/deformed-deformed nuclei. The fusion reaction of spherical-spherical nuclei (4He+ 208Pb [23]) during the synthesis of the nucleus 212Po produces a larger evaporation residue cross section than the fusion of deformed-deformed (6He+206Pb) nuclei. The element radium (Ra) can be synthesized using many fusion reactions such as B+Bi, C+Pb, Ne+Pt, Ar+Yb, and Ti+Dy. Among these fusion reactions, the fusion of C+Pb produces a larger cross-section when compared to other projectile-target combinations.
Many theoretical models, such as the Fokker–Planck equation [24], GRAZING model [25], improved quantum molecular dynamics (ImQMD) model [26], DNS model [27, 28], complex WKB (CWKB) model [29], Langevin equations [30], time-dependent Hartree–Fock model [31], and quantum molecular dynamics model [32], predict the fusion and evaporation residue cross sections during the synthesis of superheavy elements. Multinucleon transfer reactions have been studied in fusion reactions of 40Ca+208Pb by bombarding energies close to the Coulomb barrier [29]. In addition, many researchers have theoretically predicted the evaporation residue cross sections in the superheavy region [17, 33–41] and investigated the role of the magic number of protons and neutrons in the superheavy region [42–44]. Litnevsky et al. [45] studied the capture, fusion, fission, and evaporation residue formation cross sections of superheavy nuclei within the previously proposed two-stage dynamical model. Siddiqui et al. [46] investigated spherical neutron magic numbers with N = 168, 174, and 178. Detailed investigations of experimental fusion reactions and production cross-sections have led to selection rules for projectile-target combinations according to Manjunatha et al. [47]. Such detailed investigations have led to the conclusion that the fusion of two spherical nuclei yields larger cross-sections. The effect of the deformation parameter was also considered in the evaluation of survival probability and quasifission barriers [48, 49].
After the synthesis of the superheavy element Z = 118, many attempts were carried out to synthesize the superheavy elements Z = 119 and 120 [50, 51]. Even though there are a number of predictions for the projectile-target combinations required to synthesize the superheavy elements, these predictions do not offer sufficient evidence to obtain a potential reason. From the detailed literature survey, we find that the fusion of spherical nuclei yields larger production cross-sections. Hence, in this study, we investigate fusion reactions to synthesize the nuclei polonium (Po), thorium (Th), and nobelium (No). In the first part, we investigate the fusion and evaporation residue cross-sections of the above nuclei. Second, we predict the evaporation residue cross-sections of the fusion reaction of 90Zr(208Pb, xn)298-x122.
This paper is organized as follows. Sec. II introduces the theory corresponding to theoretical models such as the dinuclear system (DNS) and advanced statistical model (ASM). The results and discussions are presented in Sec. III. The conclusions drawn from this study are presented in Sec. IV
-
According to the dinuclear system (DNS) model, the fusion between heavy ions is a complete transfer of nucleons from light to heavy nuclei and the formation of the compound nucleus. Fusion reactions take place in two stages. The first involves the capture process of the projectile-target by overcoming the Coulomb barrier, resulting in the formation of the DNS, and the second is the formation of stable nuclei via multi-nucleon transfer. Hence, the evaporation residue cross-sections [18] during multi-nucleon transfer are evaluated as follows:
$ \begin{align} \sigma_{\rm ER}^{Z,A}=\sum_{\ell=0}^{\infty} (2\ell+1)\sigma_{\ell}^{\rm fus}(E_{\rm cm},\ell)W_{\rm sur}^{Z,A}(E_{\rm cm},\ell) . \end{align} $

(1) Here,
$\sigma_{\ell}^{\rm fus}$ is the partial capture cross section, which represents the transition of the colliding nuclei over the Coulomb barrier and the formation of the initial DNS. The probability of the production of the residual nucleus (Z, A) from the excited entrance channel (DNS) into a distinct decay channel is described by the survival probability$W_{\rm sur}^{Z,A}(E_{\rm cm}, \ell)$ . The fusion cross section$\sigma_{\ell}^{\rm fus}(E_{\rm cm},\ell)$ is defined as$ \begin{align} \sigma_{\ell}^{\rm fus}(E_{\rm cm},\ell)=\sigma_{\ell}^{\rm cap}(E_{\rm cm},\ell)P_{\rm CN}(E_{\rm cm},\ell), \end{align} $

(2) where
$\sigma_{\ell}^{\rm cap}(E_{\rm cm},\ell)$ is evaluated as follows [52]:$ \begin{align} \sigma_{\ell}^{\rm cap}=\frac{\pi\hbar^{2}}{2\mu E_{\rm cm}}\sum_{\ell}(2\ell+1)T(E_{\rm cm},\ell). \end{align} $

(3) Here, the transmission probability is expressed as
$\begin{aligned}[b] & T\left(E_{\rm cm}, \ell\right)\\ =&\int f(B) \dfrac{1}{1+\exp \left\{-\dfrac{2 \pi}{\hbar \omega_{\ell}}\left[E_{\rm cm}-B-\dfrac{\hbar^2}{2 \mu R_B^2(\ell)} \ell(\ell+1)\right]\right\}} {\rm d} B, \end{aligned} $

(4) where
$ \hbar\omega(\ell) $ is the width of the parabolic form at the position of the barrier$ R_{B}(\ell) $ . The barrier distribution function$ \begin{align} f(B)=\frac{1}{N}{\rm exp}\left[-\left(\frac{B-B_{m}}{\Delta_{1}}\right)^2\right] (B<B_{m}) \end{align} $

and
$ \begin{align} f(B)=\frac{1}{N}{\rm exp}\left[-\left(\frac{B-B_{m}}{\Delta_{2}}\right)^2\right] (B>B_{m}) \end{align} $

with
$ \begin{align} B_{m}=(B_{o}+B_{s})/2, \end{align} $

$ B_{o} $ and$ B_{s} $ are the height of the Coulomb barrier in the waist-to-waist orientation and the height of the minimum barrier, respectively.The total potential is evaluated using a set of equations available in literature. The nucleus-nucleus potential
$V(R,Z_{1}, Z_{\rm CN}-Z_{1},\ell,\beta_{i})$ for a given mass and charge asymmetry includes the Coulomb ($ V_{C} $ ), nuclear ($ V_{N} $ ), and rotational ($V_{\rm rot}^{\rm DNS}$ ) potentials and is calculated as follows:$ \begin{aligned}[b] V(R,Z_{1}, Z_{\rm CN}-Z_{1},\ell,\beta_{i})=V_C(R,Z_{1}, Z_{\rm CN}-Z_{1},\ell,\beta_{i})+ V_N(R,Z_{1}, Z_{\rm CN}-Z_{1},\ell,\beta_{i})+V_{\rm rot.}^{\rm DNS}(R,\ell, \beta_{i}). \end{aligned} $ 
(5) The Coulomb potential is evaluated using the following equation:
$ V_C(R,Z_1,Z_2,\beta_{2i})=\frac{Z_1Z_2}{R}{\rm e}^2+\frac{Z_1Z_2}{R^3}{\rm e}^2\times \left[\left(\frac{9}{20\pi}\right)^{1/2}\sum_{i=1}^2R_i^2\beta_{2i}P_2(\cos\alpha_i)+\frac{3}{7\pi}\sum_{i=1}^2R_i^2[\beta_{2i}P_2(\cos\alpha_i)]^2\right]. $

(6) The nuclear potential (
$ V_N(R,Z_1,Z_2,\beta_{2i}) $ ) [53] is evaluated as follows:$ \begin{aligned}[b] V_N(R,Z_1,Z_2,\beta_{2i})=&V_o\Bigg\{\exp\left[\frac{-2(R-R_{12})\alpha}{R_{12}}\right] \\ &-2\exp\left[\frac{-(R-R_{12})\alpha}{R_{12}}\right]\Bigg\}, \end{aligned} $

(7) where the term
$ V_{0} $ is the strength of the potential,$ R_{12} $ is the separation distance between the two nuclei, and α is a function of the surface diffuseness parameter [53, 54]. The rotational energy$V_{\rm rot}$ is defined as$ \begin{align} V_{\rm rot}(R,l,\beta_{2i})=\frac{\hbar^2\ell(\ell+1)}{2\Im_{\rm DNS}(R,A,\beta_{2i})}, \end{align} $

(8) where
$\Im_{\rm DNS}$ [53] is the moment of inertia of the formed DNS. The compound nucleus probability in Eq. (2) is expressed as$ \begin{align} P_{\rm CN}=\frac{\rho\left(E^{*}_{\rm DNS}-B^{*}_{\rm fus}\right)}{\rho\left(E^{*}_{\rm DNS}-B^{*}_{\rm fus}\right)+\rho\left(E^{*}_{\rm DNS}-B_{qf}\right)}, \end{align} $

(9) where
$B^{*}_{\rm fus}$ [55] is the intrinsic fusion barrier on the potential energy surface, which is along the direction of the mass/charge asymmetry axis. The local excitation energy$E^{*}_{\rm DNS}$ is factorized as follows:$ \begin{align} E^{*}_{\rm DNS}=E^{*}_{\rm CN}(\ell)-U(R_{m}, Z,A,\ell), \end{align} $

(10) where
$E^{*}_{\rm CN}(\ell)=E_{\rm cm}+Q-V^{\rm CN}_{\rm rot}(\ell)$ , and$ U(R_{m}, Z,A,\ell) $ is the internuclear potential energy surface (PES) [53], defined as$ \begin{align} U(A,Z,R_m,\ell)=Q-V_{\rm rot}^{\rm CN}(\ell)+V(R,Z_{1},Z_{\rm CN}-Z_{1},\ell,\beta_{i} . \end{align} $

(11) The term
$ \rho\left(E^{*}_{\rm DNS}-B^{*}_{k}\right) $ in Eq. (9) is the level density and is evaluated as explained in Ref. [55]. The survival probability under the evaporation of x neutrons is expressed as$ \begin{align} W_{\rm sur}^{Z,A}(E_{\rm cm},\ell)=P_{xn}(E^{*}_{\rm CN})\prod_{i=1}^{i_{\rm max}=x}\left(\frac{\Gamma_{n}}{\Gamma_{n}+\Gamma_{f}}\right)_{i,E^{*}}, \end{align} $

(12) where i is the number of neutrons emitted,
${\Gamma_{n}}/{\Gamma_{f}}$ is the ratio of the decay width of the neutron to the fission width, and$ P_{xn} $ [56] is the probability of realization of the evaporation sequence, given by$ \begin{aligned}[b] P_{xn}= &\int_0^{E_0^*-B_n(1)}\frac{\Gamma_n}{\Gamma_{\rm tot}}(E_0^*,I_0).W_n(E_0^*,e_1)de_1\\ &\times \int_0^{E_1^*-B_n(2)}\frac{\Gamma_n}{\Gamma_{\rm tot}}(E_1^*,I_1).W_n(E_1^*,e_2)de_2......\\&\times \int_0^{E_{x-1}^*-B_n(x)}\frac{\Gamma_b}{\Gamma_{\rm tot}}(E_{x-1}^*,I_{x-1}).W_n(E_{x-1}^*,e_x)\\ &\times\prod_{i=1}^N\frac{\Gamma_\gamma}{\Gamma_{\rm tot}}(E_i^*,I_i)de_x \, . \end{aligned} $

(13) The decay width of neutron/fission is evaluated using the following equation:
$ \begin{align} \Gamma_{i}=\frac{R_{{\rm CN}_{i}}}{2\pi\rho(E^{*}_{\rm CN})} , \end{align} $

(14) where i=n for neutron emission, and i=f for the fission of compound nuclei.
$R_{{\rm CN}_{n}}$ is the probability of evaporation of neutrons,$ \begin{aligned}[b] R_{{\rm CN}_n}(E^*_{\rm CN})=&\sum_{J_d}\int_0^{E_{CN}^*-B_n-E_c}{\rm d}\epsilon\rho_{\rm d}(E_{\rm CN}^*-B_n-\epsilon,J_d)\\&\times\sum_{|J_d-s|}^{J_d+s}T_{lj}(\epsilon), \end{aligned} $

(15) $ B_{n} $ is the neutron separation energy,$\rho_d(E_{\rm CN}^*-B_n-\epsilon,J_d)$ is the level of the daughter nucleus, and$ T_{lj} $ is the probability of penetration of the Coulomb and centrifugal barriers by the emission of light particles from the compound nuclei. The fission probability is defined as$ \begin{align} R_{{\rm CN}_f}(E^*_{\rm CN})=\int_0^{E^*_{\rm CN}-B_f-E_C}\frac{\rho_f(E^*_{\rm CN}-B_f-\epsilon,J){\rm d}\epsilon}{1+\exp{[2\pi(\epsilon+B_f-E^*_{\rm CN})/(\hbar\omega)]}}, \end{align} $

(16) where
$\rho_f(E^*_{\rm CN}-B_f-\epsilon,J)$ is the level density at the saddle point, and$ \hbar\omega $ = 2.2 MeV.$ B_{f} $ is the fission barrier [57]. The level density [58] is defined as$ \begin{aligned}[b] \rho(E^*,J)=&K_{\rm vib}(E^*)K_{\rm rot}(E^*)\\&\times\frac{2J+1}{24\sqrt{2}\sigma_{\rm eff}^3[a(A,E^*-E_c)(E^*-E_c)^5]^{1/4}}\\&\times\exp{\left[2\sqrt{a(A,E^*-E_c)(E^*-E_c)}-\frac{(J+1/2)^2}{2\sigma_{\rm eff}^2}\right]}, \end{aligned} $

(17) where
$ E_{c} $ is the condensation energy [58], and$\sigma_{\rm eff}$ ,$K_{\rm rot}$ , and$K_{\rm vib}$ are evaluated using the set of equations from (7) to (9) in Ref. [58]. The level density parameter considering shell effects can be expressed as$ a(A,{E^*}-{E_c})=\tilde{a}(A)\left[1+\frac{1-{\exp}{[-({E^*}-{E_c})/{E_D^{'}}]}}{{E^*}-{E_c}} {\delta W}\right],$

(18) where we take the values
$ E_D^{'}=\alpha_{0}A^{4/3}/\tilde{a} $ [58] and$ \tilde{a}(A)=0.114A+0.162A^{2/3} $ . The terms$ E^{*} $ and$ \delta W $ are the excitation energy and shell correction, respectively.$ P_{xn} $ in Eq. (12) is the probability of evaporation of x neutrons from the compound nucleus and is evaluated as explained in literature [59].Quasi-fission is an important obstacle in the formation of a compound nucleus. The quasifission cross section is given by
$ \begin{aligned}[b] \sigma_{qf}(E_{\rm cm}, \beta_{p}, \alpha_{2})=&\sum^{\ell_{d}}_{\ell=\ell_{f}}(2\ell+1)\sigma^{\rm cap}_{\ell}\\&\times(1-P_{\rm CN}(E_{\rm cm}, \ell,\beta_{p}, \alpha_{2})), \end{aligned} $

(19) where
$\sigma^{\rm cap}_{\ell}$ and$P_{\rm CN}$ are evaluated as defined in Eqs. (23) and (9). -
The total potential required to evaluate the fusion barrier height and position is evaluated using the potentials defined in the below equations.
$ \begin{align} V(R)=V_N(R)+V_C(R). \end{align} $

(20) The Coulomb interaction potential (
$ V_C(R) $ ) is expressed as$ \begin{aligned}[b] V_{C}=& \left[\frac{Z_1Z_2{\rm e}^2}{r}\right][(1+n_1(R_{0,1}^2\beta_1+R_{0,2}^2\beta_2))\\&+ n_2(R_{0,1}^2\beta_1+R_{0,2}^2\beta_2)+n_3(R_{0,1}^4\beta_1+R_{0,2}^4\beta_2)+n_4\beta_1\beta_2], \end{aligned} $

(21) $ n_1=\dfrac{3}{2\sqrt{5}\pi r^2} $ ,$ n_2=\dfrac{3}{7\pi r^2} $ ,$ n_3=\dfrac{9}{14\pi r^4} $ , and$ n_4=\dfrac{27R_1^2R_2^2}{10\pi r^4} $ . Here,$ R_{i} $ is the radius of fission fragments and is evaluated using$ \begin{align} R_i(\theta)=R_{0,i}(1+\beta_iY_{20}(\theta)), \end{align} $

(22) where
$ Y_{20} $ is the spherical harmonic function. The nuclear interaction potential ($ V_N(R) $ ) is evaluated as follows:$ \begin{align} V_N(R)=\frac{V_0}{1+\exp[(R-R_0)/a]} . \end{align} $

(23) In the above equations,
$ Z_{1} $ and$ Z_{2} $ are the atomic number of the projectile and target, respectively,${e}^{2}\approx1.44$ , a is the diffuseness parameter, and$ R_0 $ is the minimum nuclear potential distance.$ R_{0} $ and$ V_{0} $ are evaluated as defined in Ref. [60]. The fusion barrier height ($ V_{B} $ ) and barrier position ($ R_{B} $ ) are evaluated using the following boundary conditions:$ \begin{align} \frac{{\rm d}V(r)}{{\rm d}r}\bigg|_{r=R_{B}}=0 \;\;\ {\rm and} \;\;\ \frac{{\rm d}^{2}V(r)}{{\rm d}r^{2}}\bigg|_{r=R_{B}}\le 0 , \end{align} $

(24) where V(r) is the total potential. The evaporation residue cross-section of superheavy elements [61] with subsequent emission of light particles is expressed as
$ \begin{align} \sigma_{{\rm EVR}}^{xn}=\frac{\pi}{k^2}\sum_{\ell=0}^\infty(2\ell+1)T_{\ell}(E_{\rm cm}) P_{\rm CN}(E^*,\ell)W_{\rm sur}^{xn}(E^*,\ell). \end{align} $

(25) Here, k is the wave number, l is the average angular momentum, and
$T_{\ell}(E_{\rm cm})$ is the energy-dependent barrier penetration factor, which is given by$ \begin{align} T_{\ell}(E_{\rm cm})=\left[1+{\rm exp}\left(\frac{2\pi}{\hbar\omega_{\ell}}(V_{B}-E_{\rm cm})\right)\right]^{-1} , \end{align} $

(26) where
$ \hbar\omega_{\ell} $ is the inverted parabola.$P_{\rm CN}$ is the compound nucleus probability and is given by$ \begin{align} P_{\rm CN}(E^*,\ell)=\frac{{\rm exp}[-c(\chi_{\rm eff}-\chi_{\rm thr})]}{1+{\rm exp}\left(\dfrac{E^{*}_{B}-E^*}{\Delta}\right)} , \end{align} $

(27) where
$ E^* $ is the compound nucleus excitation energy,$ E^{*}_{B} $ is the excitation energy of the compound nuclei when$E_{\rm cm}$ (center of mass energy) is equal to the Coulomb and proximity barrier, Δ,$\chi_{\rm thr}$ , and c are the adjustable parameters, and$\chi_{\rm eff}$ is the effective fissility, as defined in Ref. [40]. The survival probability of the fused system emits x number of neutrons followed by a sequence of α decay from the residue, which is given by$ \begin{align} W_{\rm sur}^{xn}=P_{xn}(E^*)\prod_{i=1}^{i_{\rm max}=x}\left(\frac{\Gamma_n}{\Gamma_n+\Gamma_f}\right)_{i,E^*} ,\end{align} $

(28) where
$ P_{xn} $ is the probability of x neutrons emitted from the compound nucleus, which is evaluated as follows:$ \begin{align} P_{xn}(E^*)=P[x]-P[x+1] \end{align} $

(29) and
$ \begin{align} P[x]=1-{\rm exp}(-\Delta_{x}/T)\left[1+\sum_{i=1}^{2x-3}\frac{(\Delta_{x}/T)^i}{i!}\right] ,\end{align} $

(30) where
$ \Delta_{x}=E^*-\sum_{k=1}^{x}B_{k} $ . Here,$T=\sqrt{E^*_{\rm CN}/2a}$ , and$ B_{k} $ is the separation energy of the evaporated neutron k. The level density parameter a is taken as$(A/10)~{\rm MeV}^{-1}$ .$ \Gamma_{n} $ and$ \Gamma_{f} $ are the decay width of the neutron and decay width of fission, respectively, where i is the number of neutrons emitted.${\Gamma_{n}}/{\Gamma_{f}}$ is the ratio of the decay width of the neutron to the fission width and is expressed as$ \begin{aligned}[b] \frac{\Gamma_{n}}{\Gamma_{f}}= &\frac{4A^{2/3}a_f[E^*-B_n]}{k_0a_n\{2\sqrt{a_f}[E^*-B_f]-1\}}\\&\times\exp{\left\{2\sqrt{a_n[E^*-B_n]}-2\sqrt{a_f[E^*-B_f]}\right\}}, \end{aligned} $

(31) where
$k_{0}=9.8~ {\rm MeV}$ ,$ B_{f} $ and$ B_{n} $ are the fission barrier and neutron separation energy, respectively [62], and$a_{n}=A/10~ {\rm MeV}^{-1}$ . -
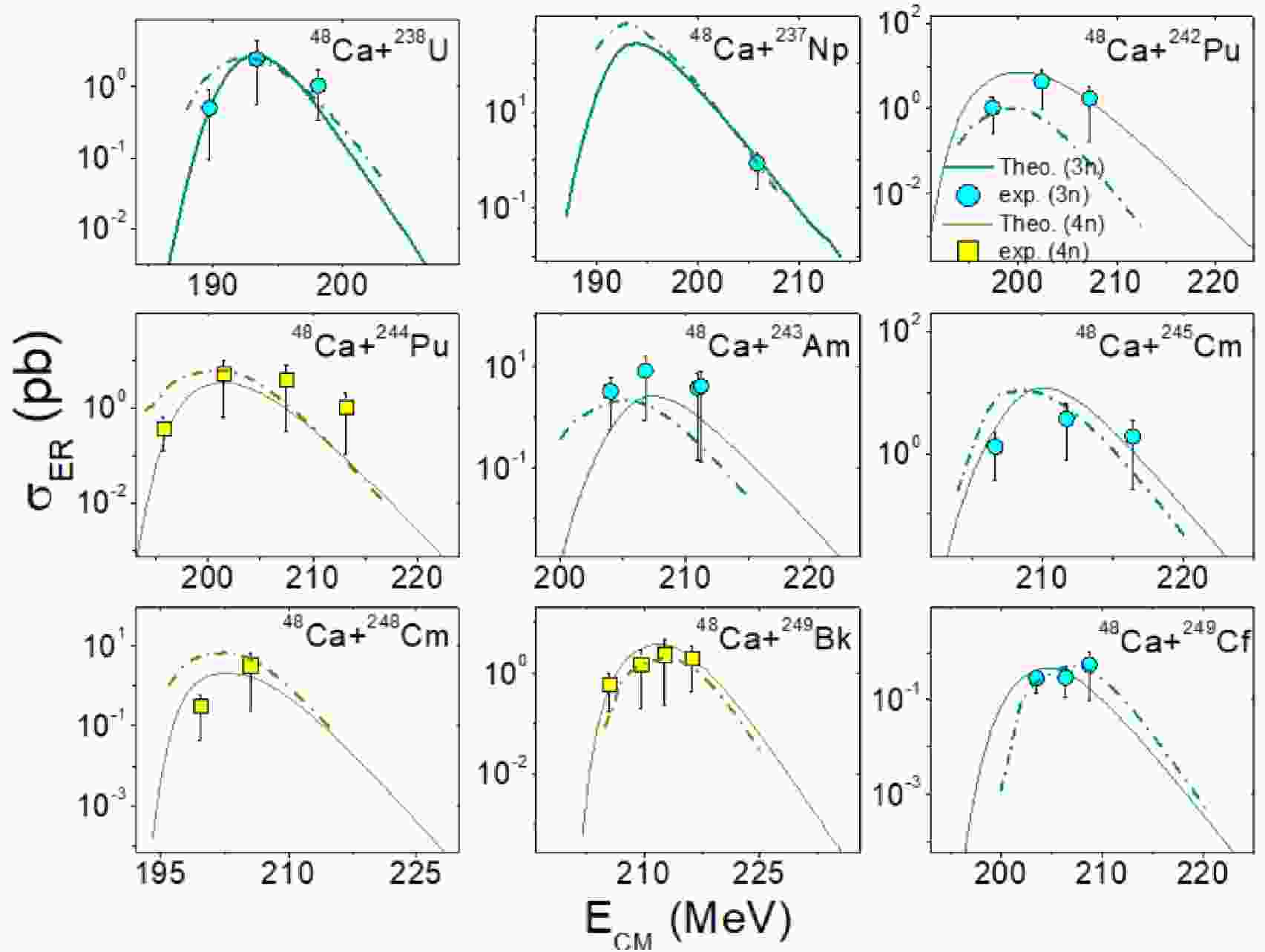
The applicability of the ASM and DNS is demonstrated by comparing the evaporation residue cross-sections with those of available experiments. Figure 1 shows a comparison of the evaporation residue cross-sections of 48Ca-induced reactions on actinide targets with those of experiments [15, 63–66, 68]. In the figure, the continuous lines correspond to evaporation residue cross-sections obtained using the ASM, whereas the dash-dot lines represent data obtained using the DNS model. In both cases, it is noticed that the evaporation residue cross-sections using the ASM and DNS agree with those of experiments.

Figure 1. (color online) Comparison of the evaporation residue cross-sections obtained from the ASM (continuous lines) and DNS (dashed dot lines) with those of available experiments for 48Ca projectiles on targets such as 238U [63], 237Np [64], 242,244Pu [65, 66], 243,245Am [67], 248Cm [65], 249Bk [68], and 249Cf [15].
With the confidence of reproducing experimental values, we consider three compound nuclei, polonium (Po), thorium (Th), and nobelium (No), which are synthesized through various projectile target combinations. The Po nuclei are synthesized using nine fusion experiments of different projectile target combinations, including 4,6He+208Pb [23, 69–71], 12C+194Pt [72], 40Ar+164Dy [73], 44Ca+158Gd [69], and 48Ca+154Gd [69]. Among them, the projectile-target combination 4He+208Pb is observed to be the fusion of spherical nuclei. Furthermore, thorium (Th) nuclei are synthesized using seventeen fusion experiments of different projectile-target combinations, including 16O+208Pb [74] 124Sn+90,92,94,96Zr [75, 76], 32S+182W [77] 40Ar+176-180Hf [78, 79], 48Ca+ 172-173,176Yb and 54Cr+162Dy [80]. Among these, 16O+208Pb is the fusion of spherical nuclei. Similarly, eleven fusion experiments are attempted to synthesize the heavy element nobelium (No), including 48Ca+208Pb [81–83], 12C+244,248Cm [84], 13C+244,246Cm [84], 44Ca+ 208Pb [82], 48Ca+204,206,207Pb [85]. Among these fusion reactions, the reaction 48Ca+208Pb possesses the largest evaporation residue cross sections. We reproduce the experimental evaporation residue cross sections using the well-accepted theoretical models ASM and DNS, which are shown in Table 1. The corresponding deformation parameters, fusion barrier, and fusion and quasifission cross sections are also presented in Table 1. The quasifission cross sections presented in Table 1 are evaluated using the DNS model. The quasifission cross sections corresponding to experimental energies during the synthesis of Po, Th, and No using different projectile-target combinations are shown in Fig. 2. Figure 2(a) depicts the quasifission cross sections during the synthesis of the heavy element Po using different projectile-target combinations. The quadruple deformation parameter (
$ \beta_{2} $ ) corresponding to different projectile-target combinations is also presented in the figure. Among the studied projectile-target combinations, 4He+208Pb produces the smallest value of quasifission cross-section. This may be due to the shape of the projectile and target nuclei. With both being spherical ($ \beta_{2P}. \beta_{2T} $ ), the chance of quasifission is observed to be smaller. From the figure, it is observed that spherical projectile-target combinations result in a smaller value of quasifission cross-section.Reaction Chann. $\beta_{2}$ 

$V_B$ /MeV

$E_{\rm cm}$ /MeV

$\sigma_{\rm fu}^{\rm max}$ /mb

$\sigma_{qf}$ 

$\sigma_{\rm ER}$ 

TOR Proj. Targ. Expt. ASM DNS $^{4}{\rm{He}}+^{208}{\rm{Pb}}\rightarrow^{212}{\rm{Po}}$ 

2n 0 0 19.1 30.8 1390[69] 1.07 μb 1260 mb[23] 1389 mb 1550 mb S-S $\rm ^{12}C+^{194}Pt\rightarrow^{206}Po$ 

4n 0 −0.15 54.5 63.1 450.2[69] 3.18 μb 386.6±7.5 mb[72] 418 mb 328.1mb S-D $\rm ^{6}He+^{206}Pb\rightarrow^{212}Po$ 

2n 0 −0.008 18.4 19.7 428.1[69] 42 μb 71.4±15 mb[85] 32.25 mb 69.4 mb S-D $\rm ^{40}Ar+^{164}Dy\rightarrow^{204}Po$ 

5n 0 0.29 138.3 146.3 700 11.4 μb 68±17 mb[73] 19.5 mb 48.2 mb S-D $\rm ^{6}He+^{206}Pb\rightarrow^{212}Po$ 

2n 0 −0.008 18.4 21.9 428.1[69] 4.06 μb 67.2 mb[23] 8.5 mb 3.6 mb S-D $\rm ^{6}He+^{206}Pb\rightarrow^{212}Po$ 

2n 0 −0.008 18.4 18.1 428.1[69] 2.17 mb 45.9±8.7 mb[70] 5.3 mb 7.2 mb S-D $\rm ^{6}He+^{206}Pb\rightarrow^{212}Po$ 

2n 0 −0.008 18.4 17.0 428.1[69] 2.20 mb 36±5.1 mb[71] 3.2 mb 9.4 mb S-D $\rm ^{48}Ca+^{154}Gd\rightarrow^{202}Po$ 

4n 0 0.24 148.7 150.1 207.7[69] 108 mb 4±0.6 mb [86] 8.2 mb 2.8 mb S-D $\rm ^{44}Ca+^{158}Gd\rightarrow^{202}Po$ 

3n 0 0.27 149.4 138.9 207.7[69] 0.3 mb 2.3±0.6 mb[87] 5.2 mb 6.3 mb S-D $\rm ^{16}O+^{208}Pb\rightarrow^{224}Th$ 

1n 0 0 74.9[88] 78.8 479.4[74] 1.750 nb 26.6±4.4 mb[89] 19 mb 25.9 mb S-S $\rm ^{48}Ca+^{176}Yb\rightarrow^{224}Th$ 

4n 0 0.28 155.4 158.8 160.4[69] 1.7 μb 0.9±0.1 mb 1.38 mb 1.25 μb S-D $\rm ^{40}Ar+^{180}Hf\rightarrow^{220}Th$ 

5n 0 0.28 149.2 164.0 574[79] 5.1 μb 133±11 μb[78] 74 μb 58.7 μb S-D $\rm ^{48}Ca+^{173}Yb\rightarrow^{221}Th$ 

4n 0 0.3 155.8 164.5 298.6 [69] 0.3 μb 117.4±10 μb 138.8 μb 122.5 μb S-D $\rm ^{48}Ca+^{172}Yb\rightarrow^{220}Th$ 

4n 0 0.3 155.9 164.3 287.4[69] 7.1 μb 86.8±6.1 μb 97.2 μb 101.4 μb S-D $\rm ^{40}Ar+^{179}Hf\rightarrow^{219}Th$ 

4n 0 0.28 149.3 152.4 579[79] 0.12 μb 77±10 μb[78] 88.2 μb 92 μb S-D $\rm ^{40}Ar+^{178}Hf\rightarrow^{218}Th$ 

5n 0 0.28 149.5 158.7 569[69] 0.032 μb 61±12 μb[78] 58.5 μb 76.4 μb S-D $\rm ^{40}Ar+^{177}Hf\rightarrow^{217}Th$ 

4n 0 0.28 149.6 158.3 531[69] 0.13 μb 33±5.6 μb[78] 4.8 μb 34.6 μb S-D $\rm ^{40}Ar+^{176}Hf\rightarrow^{216}Th$ 

3n 0 0.28 149.7 153.3 560[79] 0.16 μb 24±2.8 μb[78] 28.4 μb 30.5 μb S-D $\rm ^{124}Sn+^{96}Zr\rightarrow^{220}Th$ 

5n 0 0.22 213.6 247.3 60.6 [69] 1.74 μb 8.8±1.2 μb[75] 5.5 μb 0.2 μb S-D $\rm ^{124}Sn+^{96}Zr\rightarrow^{220}Th$ 

4n 0 0.22 213.6 234.1 60.6[69] 0.5 μb 6.2±1.7 μb[90] 4.85 μb 6.5 μb S-D $\rm ^{54}Cr+^{162}Dy\rightarrow^{216}Th$ 

5n 0.18 0.3 173.2 182.3 184.4[69] 2.9 μb 5±0.5 μb[80] 8.6 μb 9.5 μb D-D $\rm ^{124}Sn+^{94}Zr\rightarrow^{218}Th$ 

3n 0 0.062 224.8 234.2 363.8[69] 136 μb 3.7±0.4 μb[75] 3.8 μb 4.68 μb S-D $\rm ^{124}Sn+^{94}Zr\rightarrow^{218}Th$ 

3n 0 0.062 214.2 223.5 363.8[69] 69 μb 2.3±0.6 μb[76] 3.58 μb 4.68 μb S-D $\rm ^{124}Sn+^{92}Zr\rightarrow^{216}Th$ 

3n 0 0.053 214.8 236.6 387.9[69] 3.61 μb 1.1±0.5 μb[75] 0.98 μb 0.86 μb S-D $\rm ^{32}S+^{182}W\rightarrow^{214}Th$ 

3n 0 0.26 138.8 161.7 81[91] 2.5 μb 0.5±0.1 μb[77] 0.75 μb 0.58 μb S-D $\rm ^{124}Sn+^{90}Zr\rightarrow^{214}Th$ 

3n 0 0.035 215.5 233.1 305.6[69] 1.25 μb 0.3±0.1 μb[75] 0.15 μb 0.25 μb S-D $\rm ^{48}Ca+^{208}Pb\rightarrow^{256}No$ 

2n 0 0 173.4[92] 175.5 17.1[69] 1.1 μb 3.4±0.3 μb[83] 38 μb 48 μb S-S $\rm ^{12}C+^{246}Cm\rightarrow^{258}No$ 

4n 0 0.23 63.8 70.1 223.6 [69] 1.7nb 1.5±0.1 μb[84] 1.2 μb 2.5 μb S-D $\rm ^{48}Ca+^{207}Pb\rightarrow^{255}No$ 

2n 0 −0.008 173.5 175.9 7.8[69] 0.62 μb 1.3±0.4 μb 1.55 μb 1.32 μb S-D $\rm ^{13}C+^{248}Cm\rightarrow^{261}No$ 

4n 0 0.23 63.2 66.4 55.8[69] 0.1 μb 1.1±0.1 μb[84] 1.9 μb 1.25 μb S-D $\rm ^{12}C+^{248}Cm\rightarrow^{260}No$ 

4n 0 0.23 63.7 69.7 213.6[69] 40 nb 1±0.1 μb[84] 1.5 μb 0.8 μb S-D $\rm ^{48}Ca+^{206}Pb\rightarrow^{254}No$ 

2n 0 −0.008 173.5 176.1 7.2[69] 7.1 μb 0.5±0.1 μb 1.2 μb 2.3 μb S-D $\rm ^{48}Ca+^{206}Pb\rightarrow^{254}No$ 

2n 0 −0.008 173.5 176.1 7.2[69] 7.1 μb 0.4±0.1 μb 2.1 μb 0.3 μb S-D $\rm ^{12}C+^{244}Cm\rightarrow^{256}No$ 

4n 0 0.23 63.7 68.0 93.3[69] 5.2 μb 0.3±0.03 μb[84] 1.9 μb 2.3 μb S-D $\rm ^{13}C+^{244}Cm\rightarrow^{257}No$ 

4n 0 0.23 63.5 69.8 243.9[69] 20 nb 0.3±0.1 μb[84] 0.89 μb 1.2 μb S-D $\rm ^{48}Ca+^{204}Pb\rightarrow^{252}No$ 

2n 0 −0.008 173.9 175.4 0.6[69] 0.5 μb 13.2±10.1 nb 58 nb 39 nb S-D $\rm ^{48}Ca+^{204}Pb\rightarrow^{252}No$ 

2n 0 −0.008 173.9 175.7 0.6[69] 0.2 μb 7.1±1.5 nb 2.5 nb 1.85 nb S-D Table 1. Experimental and theoretical (DNS and ASM) evaporation residue cross section along with the deformation parameters, fusion barrier
$ (V_B) $ , and fusion and evaluated quasi-fission cross sections.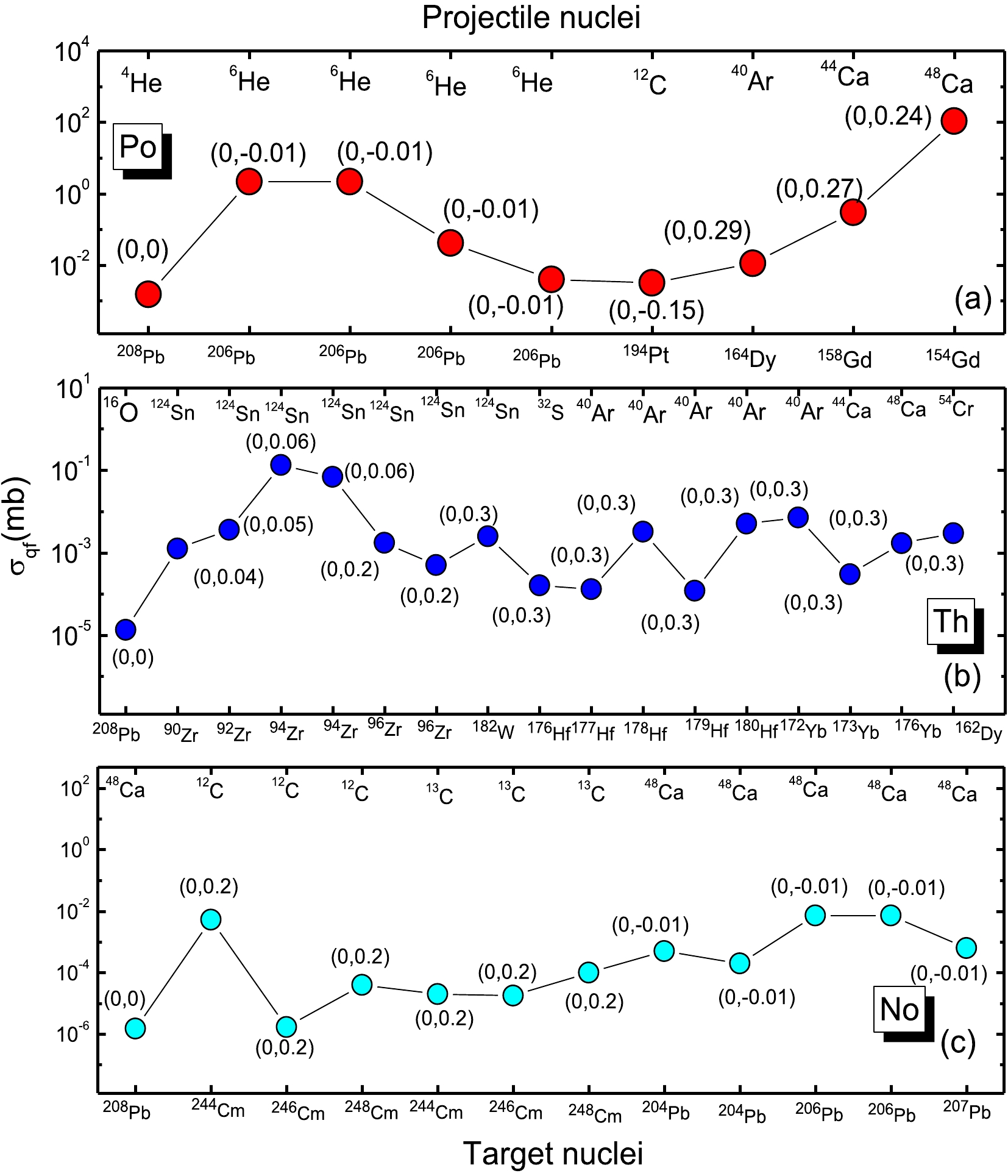
Figure 2. (color online) Evaluated quasifission cross section during the synthesis of (a) Po, (b) Th, and (c) No using different projectile-target combinations. Projectiles are represented along the top x-axis, and targets are shown along the bottom x-axis. The quadruple deformation of the projectile and target is presented within the brackets.
Similarly, Figs. 2(b) and 2(c) show the quasifission cross sections for different projectile-target combinations to synthesize the heavy elements Th and No, respectively. We find that the fusion of spherical nuclei 16O+208Pb and 48Ca+208Pb produces smaller quasifission cross sections than those of other projectile-target combinations for the synthesis of Th and No, respectively. To study the effect of deformation, the evaporation residue cross-sections are plotted as functions of the deformation parameter of the target nucleus. Figure 3 shows the evaporation residue cross-sections for the synthesis of Po, Th, and No nuclei using various projectile-target combinations of different deformation parameters. The geometric shapes of projectile nuclei are shown in red, and those of the target nuclei are shown in blue. The first layer of this figure shows the evaporation residue cross-sections for various projectile-target combinations of different geometric shapes used in the synthesis of the Po nucleus. From this figure, we find that the fusion of spherical-spherical nuclei, i.e, 4He+208Pb, yields the largest evaporation residue cross sections. The quantity
$\dfrac{\sigma_{\rm ER}}{\sigma_{\rm fus}}$ represents the survival probability of fusion reactions. The ratio of experimental evaporation residue cross-sections to the fusion cross-sections during the synthesis of Po, Th, and No using different projectile-target combinations are shown in Fig. 4. We also find that the ratio of${\sigma_{\rm ER}}$ to${\sigma_{\rm fus}}$ is larger for the projectile-target combinations 4He+208Pb, 16O+208Pb, and 48Ca+208Pb for the synthesis of Po, Th, and No, respectively.
Figure 3. (color online) Experimental evaporation residue cross section during the synthesis of (a) Po, (b) Th, and (c) No using different projectile-target combinations. Projectile nucleus shapes are shown in red, and target nucleus shapes are shown in blue.

Figure 4. (color online) Ratio of experimental evaporation residue cross section to the fusion cross section during the synthesis of (a) Po, (b) Th, and (c) No using different projectile-target combinations. Projectiles are represented along the top x-axis, and targets are shown along the bottom x-axis.
We study the neutron as well as charge particle evaporation emission cross sections of compound nuclei for the reactions and find that near the Coulomb barrier, the neutron evaporation cross section is larger than the charge particle evaporation cross-section. For instance, we compare the neutron evaporation cross-section with that of charge particle emission measured in two experiments for the compound nucleus
$ ^{220}{\rm Th} $ at 238 MeV and find that the neutron evaporation cross-section (1100 nb) is larger than the charge particle emission cross section (119.4 nb) of the nuclei [76], as shown in Table 2. Therefore, in this study, we focus on the neutron evaporation residue cross-sections.Reaction $E_{\rm CM}/{\rm MeV}$ 

$\sigma_{\rm ER}$ 

5n 5n+1p 124Sn+96Zr $ \rightarrow ^{220} $ Th

238 1100 119.4 Table 2. Comparison of neutron and charge particle evaporation residue cross sections.
From the literature, it is also well known that fusion reactions with shell closure [93] lead to larger cross sections. Cold fusion reactions using lead as the target and up to Strontium (Sr) as the projectile have been predicted to synthesize the superheavy element Z = 120 [58]. Hence, we extend our study to synthesize the superheavy element Z = 122 via the fusion of spherical nuclei. We also predict hot fusion reactions to synthesize the superheavy element Z = 122. Table 3 compares both cold and hot fusion reactions along with the evaporation cross-sections predicted by earlier researchers [94, 95] with those of the ASM and DNS model. The comparison clearly shows that the predicted cross-sections using the ASM and DNS model are in close agreement with the predicted cross-sections by earlier researchers. However, a small deviation of one order of magnitude is observed for the fusion reactions when synthesizing the superheavy element Z = 122. The fusion reaction 90Zr+208Pb produces evaporation residue cross sections of 50 fb and 39.41 fb at excitation energies of 25.06 MeV and 26.54 MeV using the DNS and ASM, respectively, for the 2n channel. A plot of evaporation residue cross-sections from the ASM and DNS model is shown in Fig. 5.
Reaction chann. $ E^* $ /MeV

$E_{\rm CM}$ /MeV

$ Z_1Z_2 $ 

$\sigma_{\rm ER}$ /pb

Th ASM DNS 90Zr+208Pb 2n 26.54(25.06) 350.7 3280 − 0.039 0.05 58Fe+248Cm [89] 4n 45 274.6 2496 1.69E-05 1.26E-4 1.69E-4 64Ni+242Pu [89] 4n 45 291.93 2632 1.59E-05 1.5E-4 1.08E-4 54Cr+249Cf [90] 4n 57.8 275.95 2352 1.34E-3 5.81E-3 1.91E-3 54Cr+249Cf[90] 3n 50.5 268.64 2352 3.79E-3 8.86E-4 1.1E-3 Table 3. Comparison of evaporation residue cross sections predicted using theoretical values (Th) with those of the ASM and DNS model.

Figure 5. (color online) Plot of evaporation residue cross sections as functions of excitation energy for the fusion reaction 90Zr+208Pb in the 1n and 2n channels using the DNS (continuous line) and ASM (dash-dot line).
As shown in Table 1, the fusion of spherical nuclei yields a larger cross-section, which may be due to the influence of the shell structure. Therefore, we attempt the fusion reaction
$^{90}{\rm Zr}+^{208}{\rm Pb}$ , which is also an example of the fusion of spherical nuclei and yields a larger cross-section. The evaporation residue cross section of$^{90}{\rm Zr}+^{208}{\rm Pb}$ is compared with those of$^{58}{\rm Fe}+^{248}{\rm Cm}$ ,$^{64}{\rm Ni}+^{242}{\rm Pu}$ , and$^{54}{\rm Cr}+^{249}{\rm Cf}$ , and we find that$^{90}{\rm Zr}+^{208}{\rm Pb}$ yields the largest cross-section presented in Table 3. We also evaluate the evaporation residue cross sections for cold fusion reactions from Z = 107 to 113 and compare them with experimental data, extending the process for Z = 122, as shown in Table 4. In addition, we study cold and hot fusion reactions, and Fig. 6 shows the experimental production cross-sections as functions of atomic number. The significant result shows a gradual decrease in the cross-sections with an increase in atomic number. However, the case of hot fusion reactions with$ ^{48} $ Ca as the projectile shows an increasing trend, reaches a maximum at Z = 115, and again gradually decreases with an increase in atomic number. Similarly, in the case of cold fusion reactions, the experimental cross sections are approximately fb in the case of Z = 113. Further investigations [96, 97] reveal an increasing trend for Z = 118($ ^{86} $ Kr+$ ^{208} $ Pb), 119($ ^{90} $ Rb+$ ^{208} $ Pb), and 120 ($ ^{88} $ Sr+$ ^{208} $ Pb) in the order of pb. In addition, we include the cross-section obtained using$ ^{70} $ Zr+$ ^{208} $ Pb, which is in the order of fb. The projectile-target combination$ ^{90} $ Zr+$ ^{208} $ Pb as the combination of the spherical-spherical nucleus will yield the largest evaporation residue cross sections. Hence, fusion with a spherical projectile and spherical target yields the largest cross-section in the order of fb.Reaction E $_{\rm cm}$ /MeV

Chann. $\sigma_{\rm ER}^{\rm exp.}$ 

$\sigma_{\rm ASM}$ 

$\sigma_{\rm DNS}$ 

$^{54}_{24}$ Cr+

$^{209}_{209}$ Bi

$\rightarrow^{262}_{107}$ Bh

209.3 1n $163^{+34}_{-34}\;{\rm{pb}}$ 

135 pb 161 pb $^{58}_{26}$ Fe+

$^{208}_{82}$ Pb

$\rightarrow^{265}_{108}$ Hs

221.9 1n $60^{+14}_{-14}\;{\rm{pb}}$ 

38 pb 58.9 pb $^{58}_{26}$ Fe+

$^{209}_{83}$ Bi

$\rightarrow^{266}_{109}$ Mt

225.6 1n $7.4^{+4.8}_{-3.3}\;{\rm{pb}}$ 

8 pb 7.3 pb $^{62}_{28}$ Ni+

$^{208}_{82}$ Pb

$\rightarrow^{269}_{110}$ Ds

239.6 1n $3.3^{+6.2}_{-2.7}\;{\rm{pb}}$ 

2.4 pb 3.3 pb $^{64}_{28}$ Ni+

$^{209}_{83}$ Bi

$\rightarrow^{272}_{111}$ Rg

245.6 1n $3.5^{+4.6}_{-2.3}\;{\rm{pb}}$ 

3.7 pb 3.6 pb $^{70}_{30}$ Zn+

$^{208}_{82}$ Pb

$\rightarrow^{277}_{112}$ Cn

257.4 1n $1^{+1.8}_{-0.4}\;{\rm{pb}}$ 

1.1 pb 0.9 pb $^{70}_{30}$ Zn+

$^{209}_{83}$ Bi

$\rightarrow^{278}_{113}$ Nh

261.7 1n $55^{+150}_{-45}\;{\rm{fb}}$ 

70.3 fb 54.9 fb $^{90}_{40}$ Zr+

$^{208}_{82}$ Pb

$\rightarrow^{298}$ 122

350.7 2n - 0.039 pb 0.05 pb Table 4. Comparison of
$\sigma_{\rm ER}$ for successful experiments of SHE synthesis with the ASM and DNS model.
Figure 6. (color online) Comparison of the evaporation residue cross sections of hot and cold fusion reactions. The last data point of the cold fusion reaction corresponds to the 2n channel of a larger cross-section obtained using the DNS model.
In addition to shell effects, the deformation of the compound nucleus plays an important role in the survival of the compound nucleus. Detailed analysis of the deformations of the compound nucleus reveals that larger values of the cross-section are obtained when the compound nucleus has
$ \beta_2 $ negative and$ \beta_4 $ positive values. For instance,$ ^{292}114 $ ($ \beta_2=-0.01 $ ,$ \beta_4=0 $ ) and$ ^{291}115 $ ($ \beta_2=-0.06 $ ,$ \beta_4=0 $ ) [98] with$ \beta_2 $ negative and$ \beta_4 $ is equal to 0. Eventually, peaks are observed at Z = 114 and 115. Furthermore, in a cold fusion reaction, either the projectile or target is said to be spherical and excitations are comparably smaller than those of a hot fusion reaction. In the case of cold fusion reactions, peaks are observed at$ ^{298}119 $ , at which$ \beta_2 $ is also said to be negative (–0.04) and$ \beta_4 $ is almost 0 [98].We study nine different reactions of different deformation configuration to synthesize the nucleus Po. Among the nine different projectile target combinations, the spherical-spherical projectile target combination yields the largest cross section. Furthermore, 17 fusion reactions of Th with different projectile target combinations of different deformation parameters also reveal that the fusion of spherical-spherical nuclei yields larger cross sections. This is also true in the case of the 11 reactions involved in the synthesis of No, as shown in Table 1. The cold fusion reaction involved in the synthesis of the superheavy element 113(
$ ^{70}_{30} $ Zn+$ ^{209}_{83} $ Bi$ \rightarrow ^{278}_{113} $ Nh) is the fusion of oblet and spherical nuclei; however, the predicted fusion reaction to synthesize the superheavy element 122 is the fusion of spherical-spherical nuclei. Hence, this may be the reason why the cross section is obtained as approximately 55 fb, which is smaller than the predicted cross section in the synthesis of the superheavy element 122($ ^{90}_{40} $ Zr+$ ^{208}_{82} $ Pb$ \rightarrow ^{298} $ 122). -
Quasifission and evaporation residue cross sections are studied using the ASM and DNS model with different projectile target combinations for the synthesis of the nuclei Po, Th, and No and compared with those of experiments. The production cross-section is larger in the case of the projectile-target combination in which the geometric shape is spherical. We also suggest the fusion reaction 90Zr+208Pb, which yields the largest cross-section in the order of fb. Thus, the fusion reaction of 90Zr(208Pb,2n)296122 may extend the periodic table up to Z = 122.
Heavy ion fusion of spherical nuclei
- Received Date: 2023-04-14
- Available Online: 2023-10-15
Abstract: We study the experimental and theoretical fusion reactions of compound nuclei synthesized using different projectile-target systems, among which at least one projectile/target nucleus is spherical. The first part of this study analyses the fusion cross sections obtained using different projectile-target combinations in the synthesis of polonium (Po), thorium (Th), and nobelium (No). In the second part of this study, we suggest the fusion reaction to synthesize the superheavy element Z = 122. We select three nuclei, polonium (Po), thorium (Th), and nobelium (No), which are synthesized using various projectile-target combinations. We also investigate fusion reactions such as





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: