-
At the Large Hadron Collider (LHC),
$ {\rm{Pb}}+{\rm{Pb}} $ and$ p+{\rm{Pb}} $ collision experiments have provided various data for exploring the properties of hot and cold nuclear matter [1−15]. In high-energy$ {\rm{Pb}}+{\rm{Pb}} $ collisions, the experimental findings on the suppression of hadron yields at large transverse momentum ($ p_{T} $ ) [16−20], collective flow phenomena [21–24], and strangeness enhancement [25, 26] give a hint of the generation of hot-dense matter, which is also known as quark-gluon plasma (QGP). Meanwhile, the initial-state nuclear effects, such as the shadowing and anti-shadowing,$ k_{T} $ broadening, and gluon saturations, are explored in$ p+{\rm{Pb}} $ collisions [3, 6, 12, 27−36]. In recent years, other observables have been measured in$ p+{\rm{Pb}} $ and$ {\rm{Pb}}+{\rm{Pb}} $ collisions, such as long-range correlations among final-state particles [37−40] and baryon-to-meson yield ratio enhancement at intermediate$ p_{T} $ , to see QGP from different viewpoints [41, 42].Interestingly, collective flow phenomena [21−24] have been found in
$ p+{\rm{Pb}} $ collisions. The existence of collective phenomena seems to imply that QGP is also produced in a small system. Meanwhile, one of the golden probes of QGP, i.e., the suppression of high$ p_{T} $ hadron production, has not been observed in$ p+{\rm{Pb}} $ collisions. Therefore, it is difficult to explain the collective behavior observed in$ p+{\rm{Pb}} $ collisions in terms of final state effects alone.To solve the puzzle, many mechanisms, such as color-reconnection among strings during the hadronization [43], hydrodynamics evolution driven by partonic cascade and escape [44], and a hybrid description including soft–hard interplay [45], were proposed to describe the experimental measurements in
$ p+{\rm{Pb}} $ collisions mentioned above. Moreover, it has been found that the initial-state effect is important for understanding the final-state particle production. However, the observed modifications of high-$ p_{T} $ inclusive particles and jet yields (the jet quenching effects) are not significant within experimental precision [3, 10−15]; it is possible that there are jet quenching effects in$ p+{\rm{Pb}} $ compensated by initial state effects. In this context, systematic study of the initial-state nuclear effects on the final-state particle production will help to reveal whether there is a QGP droplet in$ p+{\rm{Pb}} $ collisions at LHC energies [35, 36]. If the measured modifications of high-$ p_{T} $ hadron and jet yields in data are larger than the theoretical predictions, the initial-state cold nuclear matter (CNM) effects are considered by the latter. In addition, the upcoming$\rm O+O $ collisions at the LHC will fill the gap between$ p+{\rm{Pb}} $ and$ {\rm{Pb}}+{\rm{Pb}} $ collisions in terms of event multiplicity and complement the picture for understanding how particle production mechanisms evolve from small to large system collisions [46, 47]. The demonstration of CNM effects in$\rm O+O $ collisions will provide a guide to the experimental measurements. Moreover, once the experimental measurements are completed, better constraints will be given to the CNM effects.For more than three decades, it has been known that nuclear-modified parton distribution functions (nPDF) are different from their free-nucleon counterparts [48]. The ratio of nPDFs to their free-nucleon counterparts is the cold nuclear modification factor, which can isolate the physical mechanisms of shadowing, anti-shadowing, EMC effects, and Fermi motions [29−36]. At small Bjorken-x,
$x_{1,2}=p_{T}({\rm e}^{\pm \eta_1}+{\rm e}^{\pm \eta_2})/\sqrt{s_{{NN}}}$ , it is known that the shadowing takes effect if the cold nuclear modification factor is below unity. However, at middle-x, there is an anti-shadowing effect if the cold nuclear modification factor is above unity. The EMC effect and Fermi motion occur at large-x. Deep inelastic$ l+A $ scattering and Drell-Yan dilepton production in$ p+A $ collisions are two main kinds of experiment data for constraining the nPDFs. The abundant and high-precision data provided by the LHC with wide rapidities and colliding energies place new constraints on the CNM effects [1−15]. There are several types of nPDF parametrizations, which can render different values of observables owing to different uncertainty estimation approaches used in the modeling process of nPDF, especially the distributions of gluon and sea quarks in the small longitudinal momentum fraction x region. Such deviations have a significant influence on the predictions for the final-state observables [34]. Thus, we plan to study the CNM effect by using five sets of nPDFs (EPPS16, EPPS21, nCTEQ15, nCTEQ15WZSIH, and nNNPDF3.0) to unveil the role of the initial-state in the high energy heavy ion collisions.The development of nPDFs has seen great progress in recent years. In
$ 2009 $ , by taking into account the inclusive$ \pi^{0} $ production measured in d$ + $ Au and$ p+p $ collisions at RHIC, the EPS$ 09 $ group carried out a NLO analysis for the first time to estimate the nPDFs. The study provided important evidence of the shadowing and EMC effects on the nuclear-modified gluon distributions [29]. New experimental data, especially from LHC$ p+{\rm{Pb}} $ collisions, have been used to constrain the parton distribution in a wider kinematic range. The results from the new data provided more strict constraints for the gluon distribution and were released as EPPS16 and EPPS21 nPDFs [30, 31]. The nCTEQ15 nPDFs adopted different parametrization forms and extended the CTEQ proton PDFs to include the nuclear dependence [32]. The nCTEQ15WZ group added the$ W^{\pm}/Z $ production at the LHC to the analyses, which increases the strange and gluon distribution at small and intermediate x [33]. In 2021, the nCTEQ15WZSIH group added the single inclusive hadron in$ p+{\rm{Pb}} $ collisions to the analyses, which had a noticeable impact on the gluon distribution at low to medium x [34]. The nNNPDF1.0 group followed the free-proton PDFs to determine the nuclear PDFs and implemented stochastic gradient descent to optimize the model parameters for the first time [35]. The nNNPDF3.0 group used a machine learning framework with automated hyperparameter optimization to fit the free proton PDF and nuclear nPDFs [36]. From the above discussions, one can see that each nPDF has a specific feature. In this work, we aimed to study the differences among these nPDF parameterizations by using the direct photon and hadron production in small and large systems; in particular, the cold nuclear modification factor of photon production can effectively show the peculiarity of these nPDF sets.The ongoing LHC upgrade programs will provide higher collision energies, a wider rapidity region, and more precise data. They provide the unique opportunity to constrain the nPDFs at low Bjorken-x. Because photons do not participate in strong interactions owing to their color-neutral properties [49, 50], prompt photons are the purest electromagnetism probe. Thus, the modifications of their production can directly reflect the initial-state CNM effects. Moreover, they serve as the probe sensor for the gluon density through the
$ qg\rightarrow q \gamma $ process [51, 52]. Thus, studying the prompt photon production at LHC energies with the five widely used nPDF sets above can help us understand the initial-state effects, such as the shadowing and anti-shadowing [2, 53, 54]. Furthermore, as we know that hadrons are created in more diverse processes than prompt photons, their production can provide additional nPDF constraints on different parton species [3, 6, 10−13, 18, 27−28, 55−57].Therefore, the hadron production is also studied using the same framework as the prompt photon production to investigate the CNM effects from another viewpoint.In this paper, we investigate the impacts of different nPDF implementations (CNM effects) in the MC-based event generator on the final state observables. The outcomes will reveal a fundamental part of nature and how the strong-interacting nuclear environment impacts the partons’ behavior in a nucleus. We systematically study the colliding energy,
$ p_{T} $ , and rapidity dependence of the initial-state shadowing and anti-shadowing effects through the prompt photon and charged hadron production. The photon and hadron production cross sections are calculated by the NLO pQCD Monte Carlo event generator JETPHOX with five (EPPS16, EPPS21, nCTEQ15, nCTEQ15WZSIH, and nNNPDF3.0) nPDF sets [30−32, 34, 36]. The results can consistently describe the measured photon, hadron, and photon-jet production under certain uncertainties at LHC energies [58−60]. The remainder of this paper is organized as follows. Section II briefly introduces the pQCD-based parton model JETPHOX and the quantification of the nuclear modifications. The$ p_{T} $ -differential cross-section of photons and charged hadron production in$ p+p $ ,$ p+A $ , and$ A+A $ collisions and the corresponding nuclear modification factors in$ p+A $ and$ A+A $ collisions from JETPHOX predictions are presented in Sec. III. Finally, a summary is given in Sec. IV. -
In this work, we study the cold nuclear matter effect on the prompt photon and charged hadron production, which are calculated within a NLO pQCD Monte Carlo program JETPHOX [58−60].
-
To obtain high-precision and robust results, including high-order corrections, a phenomenology study is necessary. In this work, we use NLO cross-sections to carry out the photon and charged hadron production calculations, where the NLO corrections include the NLO PDFs, the NLO FFs, the NLO hard factor [58−61], and the NLO running coupling.
It is known that the prompt photons are produced via two mechanisms. First, a photon with large
$ p_{T} $ can be directly produced in the hard scattering process, which is usually called a "direct" photon. Second, a photon may come from the collinear fragmentation of a high$ p_{T} $ parton, which is often referred to as a "fragmentation" photon. Taking the NLO corrections into account, the inclusive cross section for the prompt photon production with transverse momentum$ p_{T}^{\gamma} $ can be expressed as the sum of the direct and fragmentation photons [58, 61]:$ \begin{aligned}[b] \frac{{\rm d}\sigma_{pp \rightarrow \gamma+X}}{{\rm d}y{\rm d}^2p_{T}^{\gamma}} =& \frac{{\rm d}\sigma^{D}}{{\rm d}y{\rm d}^2p_{T}^{\gamma}} + \frac{{\rm d}\sigma^{F}} {{\rm d}y{\rm d}^2p_{T}^{\gamma}} \\ =& \frac{{\rm d}\sigma^{D}}{{\rm d}y{\rm d}^2p_{T}^{\gamma}}+\sum\limits_{k=q,\bar{q},g}\frac{{\rm d}\sigma^{k}}{{\rm d}y{\rm d}^2p_{T}^{k}}\otimes D_{\gamma/k}. \end{aligned} $

(1) The first term on the right side is the contribution of direct photon production, which includes the Born term (
$ q\bar{q}\rightarrow \gamma g $ and$ qg \rightarrow q\gamma $ ) and a contribution from the NLO corrections. The second term on the right side denotes the contribution of the fragmentation photon.In
$ p+p $ collisions, the cross sections of direct and fragmentation photons at the NLO accuracy can be expressed as follows:$ \begin{aligned}[b] \frac{{\rm d}\sigma^{D}}{{\rm d}y{\rm d}^2p_{T}^{\gamma}}=&\sum\limits_{i,j=q,\bar{q},g}\int {\rm d}x_1 {\rm d}x_2 f_{i/p}(x_1,M) f_{j/p}(x_2,M)\frac{\alpha_s(\mu_R)}{2 \pi} \\ & \times \Bigg(\frac{{\rm d}\hat{\sigma}_{ij}}{{\rm d}y{\rm d}^2p_{T}^{\gamma}}+\frac{\alpha_s(\mu_R)}{2 \pi}K_{ij}^D(\mu_R,M,M_F)\Bigg), \end{aligned} $

(2) and
$ \begin{aligned}[b] \frac{{\rm d}\sigma^{F}}{{\rm d}y{\rm d}^2p_{T}^{\gamma}}=&\sum\limits_{i,j=q,\bar{q},g}\int {\rm d}x_1 {\rm d}x_2 \frac{{\rm d}z}{z^2}f_{i/p}(x_1,M) f_{j/p}(x_2,M) \\ & \times D_{\gamma/k}(z, M_F)(\frac{\alpha_s(\mu_R)}{2 \pi})^2 \\ &\times \Bigg(\frac{{\rm d}\hat{\sigma}_{ij}^k}{{\rm d}y{\rm d}^2p_{T}^{k}}+\frac{\alpha_s(\mu_R)}{2 \pi}K_{ij,k}^F(\mu_R,M,M_F)\Bigg), \end{aligned} $

(3) where
$ \mu_R $ , M, and$ M_F $ are the renormalization, initial-state factorization, and fragmentation scales, respectively. The factorization and fragmentation scales are chosen to be on the order of the transverse momentum of the final state particle in most studies. In Eqs. (2) and (3),$ f_{i/p}(x,M) $ denotes the parton distribution function for a parton i carrying momentum fraction x from a free nucleon.$ D_{\gamma/k}(z, M_F) $ is the fragmentation function of the partons (quarks or gluons) fragmenting into a photon. In this study, we used the Bourhis-Fontannaz-Guillet (BFG) II parametrizations, which include the contributions beyond the leading-logarithms approximation [62]. z is the momentum fraction carried by a photon decayed from a parton.$ K_{ij}^D $ [63−65] and$ K_{ij,k}^F $ [66−68] are the corresponding NLO correction terms of hard factors to the direct and fragmentation photons, respectively. To simplify the calculations, we neglect the terms from the fragmentation photons, as it has been found that the fragmentation photons make less than a 10% contribution to the photon production, and the contribution decreases as the photon energy increases. Thus, in this study, we focus on the cross-sections of direct photons.It is easy to attain the expression of the cross-section of hadron production by replacing the photon fragmentation function with the hadron fragmentation function
$ D_{h/k}(z, M_F) $ as follows:$ \begin{aligned}[b] \frac{{\rm d}\sigma^{h}}{{\rm d}y{\rm d}^2p_{T}^{h}}=&\sum\limits_{i,j=q,\bar{q},g}\int {\rm d}x_1 {\rm d}x_2 \frac{{\rm d}z}{z^2}f_{i/p}(x_1,M) f_{j/p}(x_2,M) \\ &\times D_{h/k}(z, M_F)(\frac{\alpha_s(\mu_R)}{2 \pi})^2 \\ & \times \Bigg(\frac{{\rm d}\hat{\sigma}_{ij}^k}{{\rm d}y{\rm d}^2p_{T}^{k}}+\frac{\alpha_s(\mu_R)}{2 \pi}K_{ij,k}^h(\mu_R,M,M_F)\Bigg), \end{aligned} $

(4) where the Kniehl-Kramer-Potter fragmentation functions are used in our calculations [69].
-
In
$ A+A $ collisions, we only replace the nucleon parton distribution function with the nuclear-modified parton distribution function to present the cold nuclear matter effect in our calculations with JETPHOX. This simplified calculation ignores the impact of iso-spin and Cronin effects, and the dependence of CNM effects on the impact parameter is weaker. Moreover, this simplification can reduce the calculation time and demonstrate the CNM effect more effectively. As the hot nuclear matter effect is not included in our calculations, the nuclear modification factor$ R_{AA}(p_{T}) $ defined in this work only reflects the role of the cold nuclear matter effect. When the nuclear geometry is ignored, the nuclear modification factor can be simply defined as follows [70]:$ R_{AA}(p_{T})=\frac{{\rm d}\sigma_{AA\rightarrow \gamma/h+X}/{\rm d}y{\rm d}^2p_{T}}{A^2 \; {\rm d}{\sigma}_{pp\rightarrow \gamma/h+X}/{\rm d}y{\rm d}^2p_{T}}. $

(5) In
$ p+A $ collisions, the nuclear modification factor$ R_{pA}(p_{T}) $ can be expressed as$R_{pA}(p_{T})=\frac{{\rm d}\sigma_{pA\rightarrow \gamma/h+X}/{\rm d}y{\rm d}^2p_{T}}{A \; {\rm d}{\sigma}_{pp\rightarrow \gamma/h+X}/{\rm d}y{\rm d}^2p_{T}}. $

(6) It is worth mentioning that we do not consider the hot nuclear matter effect in
$ p+A $ or$ A+A $ collisions. Thus, the nuclear modification factors ($ R_{AA}(p_{T}) $ and$ R_{pA}(p_{T}) $ ) only represent cold nuclear matter effects. -
In this section, the inclusive direct photon and hadron production cross-sections are calculated with the NLO pQCD JETPHOX program. The numerical results are compared with the experimental data for pp collisions at
$ \sqrt{s_{{NN}}} = 2.76 $ , 5.02, 7, and 8.16 TeV, respectively. Such calculations are further extended to$ p+{\rm{Pb}} $ , and$ {\rm{Pb}}+{\rm{Pb}} $ collisions at the LHC energies by using the EPPS16 [30], EPPS21 [31], nCTEQ15 [32], nCTEQ15-WZSIH [34], and nNNPDF$ 3.0 $ [36] nuclear-modified parton distribution function sets. Subsequently, the nuclear modification factors$R_{{pA}}$ and$R_{{AA}}$ in$ p+{\rm{Pb}} $ and$ {\rm{Pb}}+{\rm{Pb}} $ collisions are computed without considering the hot nuclear matter effects. Thus, the results illustrate the CNM effects on particle production in$ p+{\rm{Pb}} $ and$ {\rm{Pb}}+{\rm{Pb}} $ collision systems. To provide constraints in a wider Bjorken-x region, the nuclear modification factors in forward and backward rapidities are also explored. Finally, the predictions for the upcoming$ \rm O+O $ collisions at$\sqrt{s_{{NN}}} = 7$ TeV are studied. -
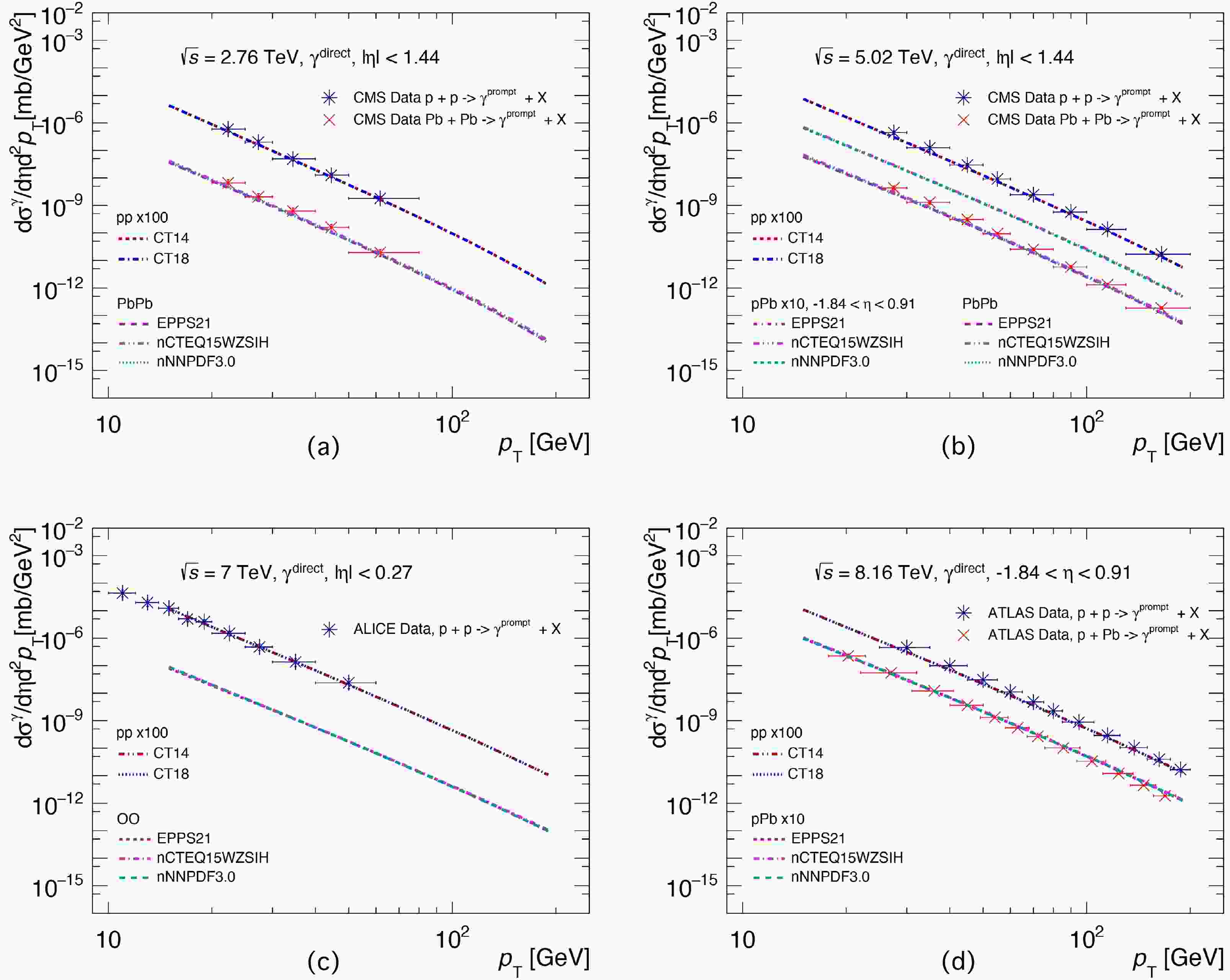
The
$ p_{T} $ -differential cross-sections of direct photon productions from JETPHOX calculations are shown in Fig. 1, where the factorization scale$ \mu = p_{T} $ is used in our calculations. The photon production spectra of$ p+A $ and$ A+A $ collisions are calculated with the pp program by replacing the PDF with nPDFs. In Fig. 1, panel (a) presents the results of prompt photon production in$ p+p $ and minimum-bias (MB)$ {\rm{Pb}}+{\rm{Pb}} $ collisions at midrapidity ($ |\eta| < 1.44 $ ) at$\sqrt{s_{{NN}}} = 2.76$ TeV. The solid circles and squares denote the prompt photon production experimental data in$ p+p $ and$ {\rm{Pb}}+{\rm{Pb}} $ collisions from the CMS collaboration [53, 54]. For$ p+p $ collisions, two PDF sets, i.e., CT14 (red dotted line) and CT18 (blue dot-dashed line), are employed in the calculations. The results are rescaled by multiplying by$ 100 $ to effectively separate them from the ones coming from the$ {\rm{Pb}}+{\rm{Pb}} $ collisions. One can see that our theoretical results are consistent with the CMS measurements within uncertainties. For$ {\rm{Pb}}+{\rm{Pb}} $ collisions, the initial-state nuclear effects are considered by employing the latest versions of the EPPS21, nCTEQ15WZSIH, and nNNPDF3.0 nPDF sets. The resulting direct photon production cross-sections are scaled by$ A^2 $ . Similar to what is observed in$ p+p $ collisions, the results with different nPDF choices are consistent with the corresponding CMS measurements under certain uncertainties. Fig. 1 (b) is similar to Fig. 1 (a) except for the collision energy of$\sqrt{s_{{NN}}} = 5.02$ TeV; these experimental data also come from the CMS collaboration [53]. Meanwhile, the predictions for$ p+{\rm{Pb}} $ collisions are also presented in Fig. 1 (b), and the corresponding predictions are rescaled by a factor of$ 10 $ to separate them from those from$ p+p $ and$ {\rm{Pb}}+{\rm{Pb}} $ collisions. From Fig. 1 (b), one can see that our theoretical results are in agreement with the CMS data points. The predictions of direct photon production cross-sections in$ |\eta|<0.27 $ in$ p+p $ collisions at$ \sqrt{s} = 7 $ TeV are given in Fig. 1 (c). The results are consistent with the corresponding ALICE measurements [71] within uncertainties. The predictions in$\rm O+O $ collisions are also shown, and a harder$ p_{T} $ spectrum related to$ p+p $ collisions is demonstrated. In Fig. 1 (d), we give the predictions in$ p+p $ and$ p+{\rm{Pb}} $ collisions at$\sqrt{s_{{NN}}} = 8.16$ TeV. The results are presented at backward rapidity in$ -1.84 < \eta <0.91 $ , which are consistent with the corresponding measurements using ATLAS [2, 72]. It is worth noting that in backward (and forward) rapidities, the production of direct photons in$ p+{\rm{Pb}} $ collisions is more sensitive to the nPDF of gluons at smaller Bjorken-x compared with the midrapidity. To conclude, all comparisons between the predictions and data measurements show that the pQCD-based JETPHOX model is robust for describing both the$ p_{T} $ - and rapidity-dependent spectra of the direct photon productions at the LHC energies.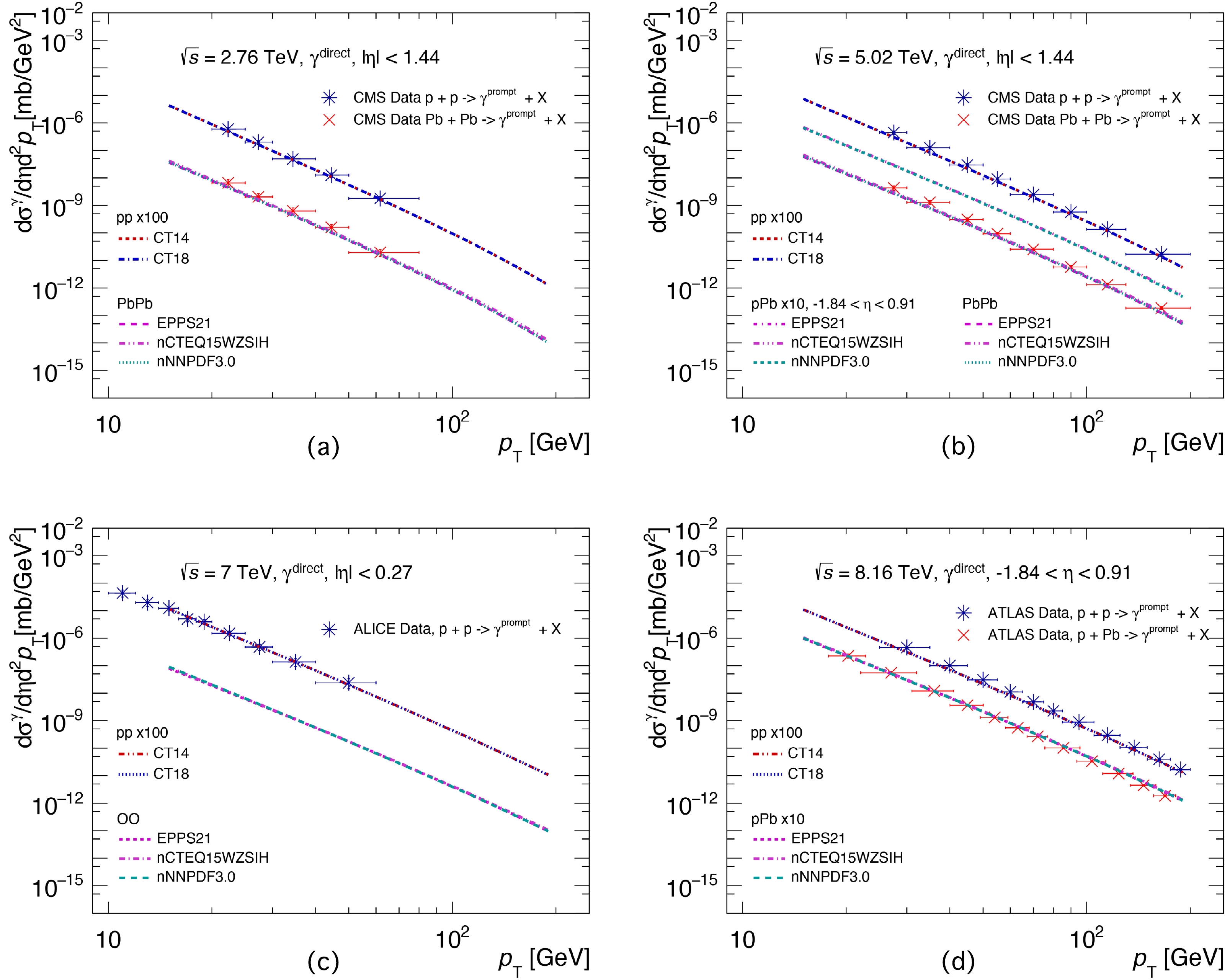
Figure 1. (color online) Inclusive photon production spectra based on the NLO pQCD JETPHOX program [58−60] as a function of
$ p_{T} $ at the LHC energies, compared with the experimental data [2, 53, 54, 71]. The spectra in$ p+p $ collisions are with CT14 [73] and CT18 PDFs [74]. The spectra for$ {\rm{Pb}}+{\rm{Pb}} $ collisions at$\sqrt{s_{{NN}}}=2.76$ TeV (a), for$ p+{\rm{Pb}} $ and$ {\rm{Pb}}+{\rm{Pb}} $ collisions at 5.02 TeV (b), for$\rm O+O $ collisions at 7 TeV (c), and for$ p+{\rm{Pb}} $ and${\rm{ Pb}}+{\rm{Pb}} $ collisions at 8.16 TeV (d) are with EPPS21 [31], nCTEQ15WZSIH [34], and nNNPDF3.0 [36] nPDFs. All of the spectra for$ p+A $ and$ A+A $ collisions are calculated with the pp program by replacing the PDF with nPDFs.In addition, the
$ p_{T} $ -differential cross-sections of charged hadron productions from the JETPHOX calculations are shown in Fig. 2. Because the inclusive hadron production process is different from the photon production process, a different factorization scale$ \mu = 1.2 ~p_{T} $ is used in the charged hadron production. The hadron production spectra of$ p+A $ and$ A+A $ collisions are calculated with the pp program by replacing the PDF with nPDFs. Similar to Fig. 1, panels (a) to (d) in Fig. 2 show the hadron cross-sections for colliding energies of 2.76, 5.02, 7, and 8.16 TeV, respectively. The experimental data in Fig. 2 come from the CMS [27, 75, 76], ATLAS [2, 56, 77], and ALICE [57] collaborations. From Fig. 2, one can see that our predictions reproduce the data points rather well, which indicates that our model can describe not only direct photon production but also charged hadron production. The results suggest that our model is robust.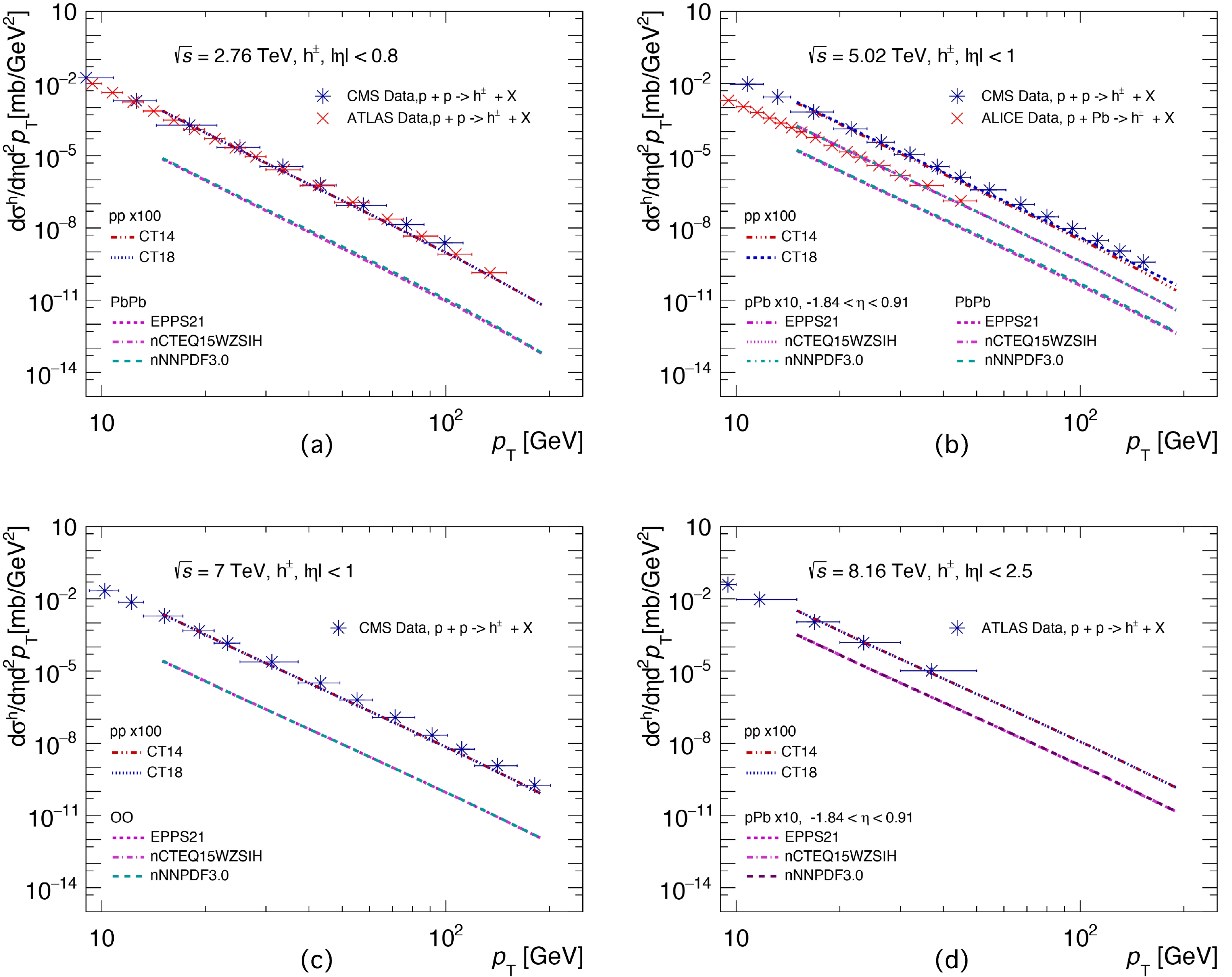
Figure 2. (color online) Charged hadron production spectra based on the NLO pQCD JETPHOX program [58−60] as a function of
$ p_{{T}} $ at the LHC energies, compared with the experimental data [2, 27, 56, 57, 75−77]. The spectra in$ p+p $ collisions are with CT14 [73] and CT18 PDFs [74]. The spectra for$ {\rm{Pb}}+{\rm{Pb}} $ collisions at$\sqrt{s_{{NN}}}=2.76$ TeV (a), for$ p+{\rm{Pb}} $ and${\rm{ Pb}}+{\rm{Pb}} $ collisions at 5.02 TeV (b), for$\rm O+O $ collisions at 7 TeV (c), and for$ p+{\rm{Pb}} $ and$ {\rm{Pb}}+{\rm{Pb}} $ collisions at 8.16 TeV (d) are with EPPS21 [31], nCTEQ15WZSIH [34], and nNNPDF3.0 [36] nPDFs. All the spectra for$ p+A $ and$ A+A $ collisions are calculated with the pp program by replacing the PDF with nPDFs. -
In this subsection, we systematically investigate the nuclear modification factor
$ R^{\gamma} $ for direct photons and$ R^{h} $ for charged hadron productions at the LHC energies, because the nuclear modification factor can effectively show the amount of shadowing and anti-shadowing encoded in the EPPS16, EPPS21, nCTEQ15, nCTEQ15WZSIH, and nNNPDF3.0 nPDF sets [30−32, 34, 36].In Fig. 3, we show the nuclear modification factor as a function of
$ p_{T} $ with five nPDFs (EPPS16 [30], EPPS21 [31], nCTEQ15 [32], nCTEQ15WZSIH [34], and nNNPDF3.0 [36]) in minimum-bias (MB)$ {\rm{Pb}}+{\rm{Pb}} $ collisions at$ \sqrt{s_{{NN}}}=2.76 $ TeV. Figure 3 panel (a) gives$ R_{{\rm{Pb}}{\rm{Pb}}}^{\gamma} $ for photon productions; the experimental data come from the CMS collaboration [54]. One can see that the values of$ R_{{\rm{Pb}}{\rm{Pb}}}^{\gamma} $ calculated by EPPS16, EPPS21, and nNNPDF3.0 are slightly smaller than unity in the entire$ p_{T} $ range. Meanwhile, the$ R_{{\rm{Pb}}{\rm{Pb}}}^{\gamma} $ values calculated with the nCTEQ15 and nCTEQ15WZSIH nPDFs are smaller than unity in the low$ p_{T} $ ($ p_{T}< $ 25 GeV) region and larger than unity in the high$ p_{T} $ ($ 25<p_{T}< $ 150 GeV) region, which means there is a shadowing effect in the low$ p_{T} $ region and an anti-shadowing effect in the high$ p_{T} $ region, respectively. Although there are differences among the five sets of nPDFs, our theoretical results can reproduce the CMS data within certain uncertainties. For comparison with charged hadron production, we also calculate the$ R_{{\rm{Pb}}{\rm{Pb}}}^{h} $ , as shown in Fig. 3 (b). Almost all the$ R_{{\rm{Pb}}{\rm{Pb}}}^{h} $ values are larger than unity, especially the results computed with the nNNPDF3.0 nPDFs. This is because for hadron production, the quark channel is dominant over other channels as$ p_{T} $ increases. The nNNPDF3.0 has the largest quark modification factor among the nPDFs. Our result seems to imply that there is more anti-shadowing in charged hadron production than in the direct photon production process.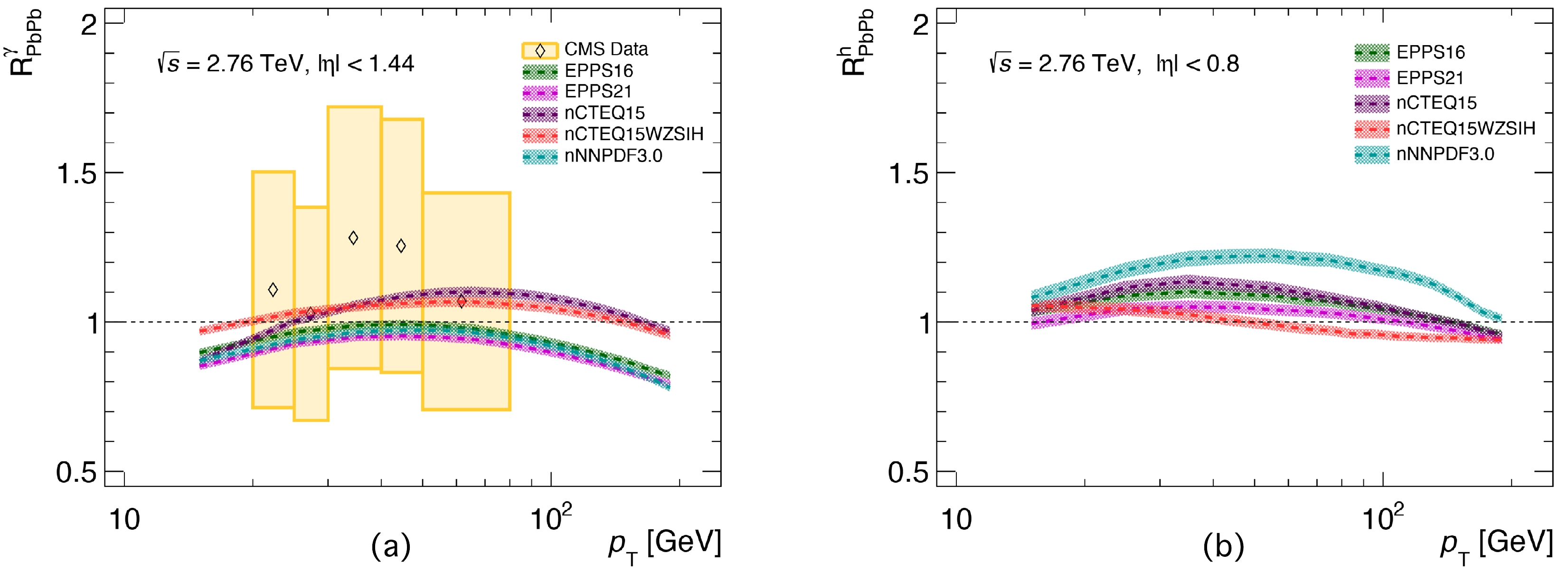
Figure 3. (color online) Nuclear modification factor
$ R_{\rm{PbPb}}^{\gamma} $ for the direct photon as a function of$ p_{{T}} $ based on the EPPS16 [30], EPPS21 [31], nCTEQ15 [32], nCTEQ15WZSIH [34], and nNNPDF3.0 [36] nPDFs in min-bias$\rm{ Pb+Pb} $ collisions at$\sqrt{s_{{NN}}}=2.76$ TeV, compared with experimental data [54] (a). The$ R_{\rm{PbPb}}^{h^\pm} $ of charged hadrons only considering the CNM effect (b).To further dip into the small-x kinematical region, we also calculate nuclear modification factors (
$ R_{{\rm{Pb}}{\rm{Pb}}}^{\gamma} $ and$ R_{{\rm{Pb}}{\rm{Pb}}}^h $ ) by only considering the CNM effects in MB$ {\rm{Pb}}+{\rm{Pb}} $ collisions at 5.02 TeV, as shown in Fig. 4. The experimental data come from the CMS collaboration [53]. First, we can see from Fig. 4 (a) that the$ R_{{\rm{Pb}}{\rm{Pb}}}^{\gamma} $ calculated by JETPHOX with five sets of nPDFs can describe the data point rather well. Second, the$ p_{T} $ region for$ R_{{\rm{Pb}}{\rm{Pb}}}^{\gamma}<1.0 $ is enlarged from$ p_{T}< $ 25 GeV in 2.76 TeV to$ p_{T}< $ 45 GeV in 5.02 TeV. The$ R_{{\rm{Pb}}{\rm{Pb}}}^h $ of charged hadron production is shown in Fig. 4 (b). The x in this figure corresponds to the range$ 0.013<x<0.18 $ , where the quark and gluon PDFs have received fine constraints, which leads to smaller differences among the five sets of nPDFs compared with the cases of 2.76 TeV in Fig. 3.
Figure 4. (color online) Nuclear modification factor
$ R_{\rm{PbPb}}^{\gamma} $ for the direct photon as a function of$ p_{{T}} $ based on the EPPS16 [30], EPPS21 [31], nCTEQ15 [32], nCTEQ15WZSIH [34], and nNNPDF3.0 [36] nPDFs in min-bias$\rm{ Pb+Pb} $ collisions at$\sqrt{s_{{NN}}}=5.02$ TeV, compared with experimental data [54] (a). The$ R_{\rm{PbPb}}^{h^\pm} $ of charged hadrons only considering the CNM effect (b).In order to obtain more detailed information about the CNM effects, we study the nuclear modification factors (
$ R_{p{\rm{Pb}}}^{\gamma} $ and$ R_{p{\rm{Pb}}}^h $ ) of direct photon and charged hadron productions in three different rapidity regions, i.e.,$ 1.09< \eta<1.90 $ (forward),$ -1.84<\eta<0.91 $ (middle), and$ -2.83< \eta<-2.02 $ (backward), in$ p+{\rm{Pb}} $ collisions at 5.02 and 8.16 TeV, as shown in Figs. 5 and 6, respectively. The experimental data come from CMS [13], ATLAS [2], and ALICE [6] collaborations. The heavy ion collisions at these two center-of-mass energies can provide a wider x region ($ 0.01<x<0.9 $ ) to investigate the initial state physics. We would like to point out that the rapidity regions are taken in terms of the photon production measurements in the ATLAS experiments [2]. The left panels of the plots in Figs. 5 and 6 present the results of photon productions, while the right panels denote the predictions of charged hadron productions. As shown in Fig. 5 (a), in the forward rapidity region, there is a flip between the shadowing and anti-shadowing as$ p_{T} $ increases, while$ R_{p{\rm{Pb}}}^{\gamma} $ approaches unity in the mid-rapidity regions without showing CNM effects, as shown in Fig. 5 (b). Surprisingly, there is an obvious difference for the$ R_{p{\rm{Pb}}}^{\gamma} $ calculated by the five sets of nPDFs in the backward rapidity region, as shown in Fig. 5 (c), which may be due to the loose constraints of the quark and gluon nPDFs in this region. Fig. 5 (c) shows that the values of$ R_{p{\rm{Pb}}}^{\gamma} $ from the nCTEQ15 and nCTEQ15WZSIH nPDF sets are larger than those from the other three sets. This is because of the nCTEQ15 and nCTEQ15WZSIH sets including large amounts of quark and anti-quark contributions. Figure 5 (d) shows similar results to panel (a). We compare our theoretical calculations with CMS and ALICE measurements in Fig. 5 (e). One can see that our results are in agreement with the data points in the mid-$ p_{T} $ region, while they deviate from the measurements in the high$ p_{T} $ region because large dynamical fluctuations at high$ p_{T} $ occur during the experimental measurements, leading to significant uncertainties of the$ R_{p{\rm{Pb}}}^{\gamma} $ .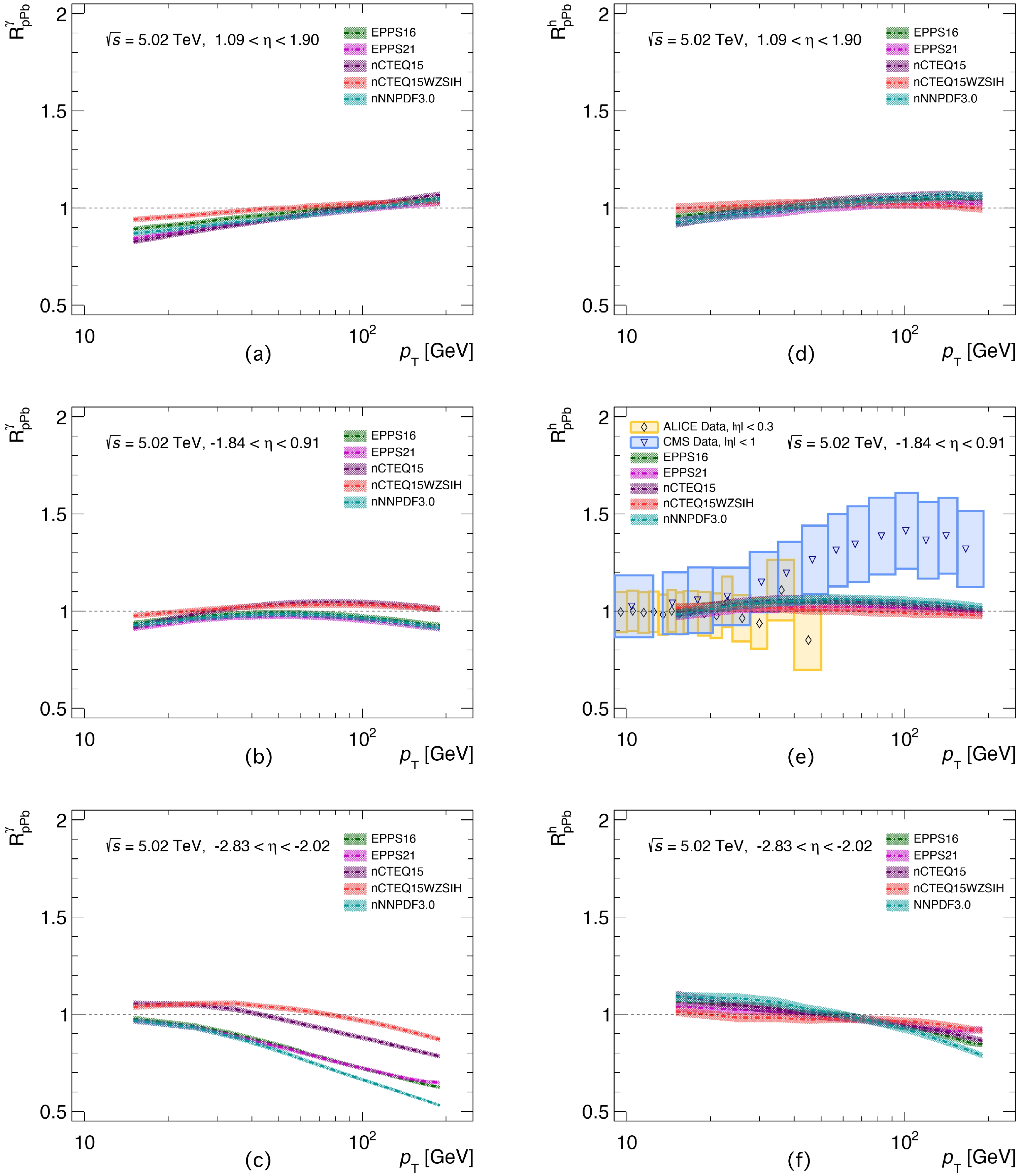
Figure 5. (color online) Nuclear modification factors
$ R_{p{\rm{Pb}}}^{\gamma} $ (a-c) and$ R_{p{\rm{Pb}}}^{h^{\pm}} $ (d-f) as a function of$ p_{{T}} $ based on the EPPS16, EPPS21, nCTEQ15, nCTEQ15WZSIH, and nNNPDF3.0 nPDFs in min-bias$ p+{\rm{Pb}} $ collisions at$\sqrt{s_{{NN}}}=$ 5.02 TeV for$ 1.09<\eta<1.90 $ ,$ -1.84<\eta<0.91 $ , and$ -2.83<\eta<-2.02 $ , respectively. The charged hadron results in central rapidity are compared with the experimental data [10, 13].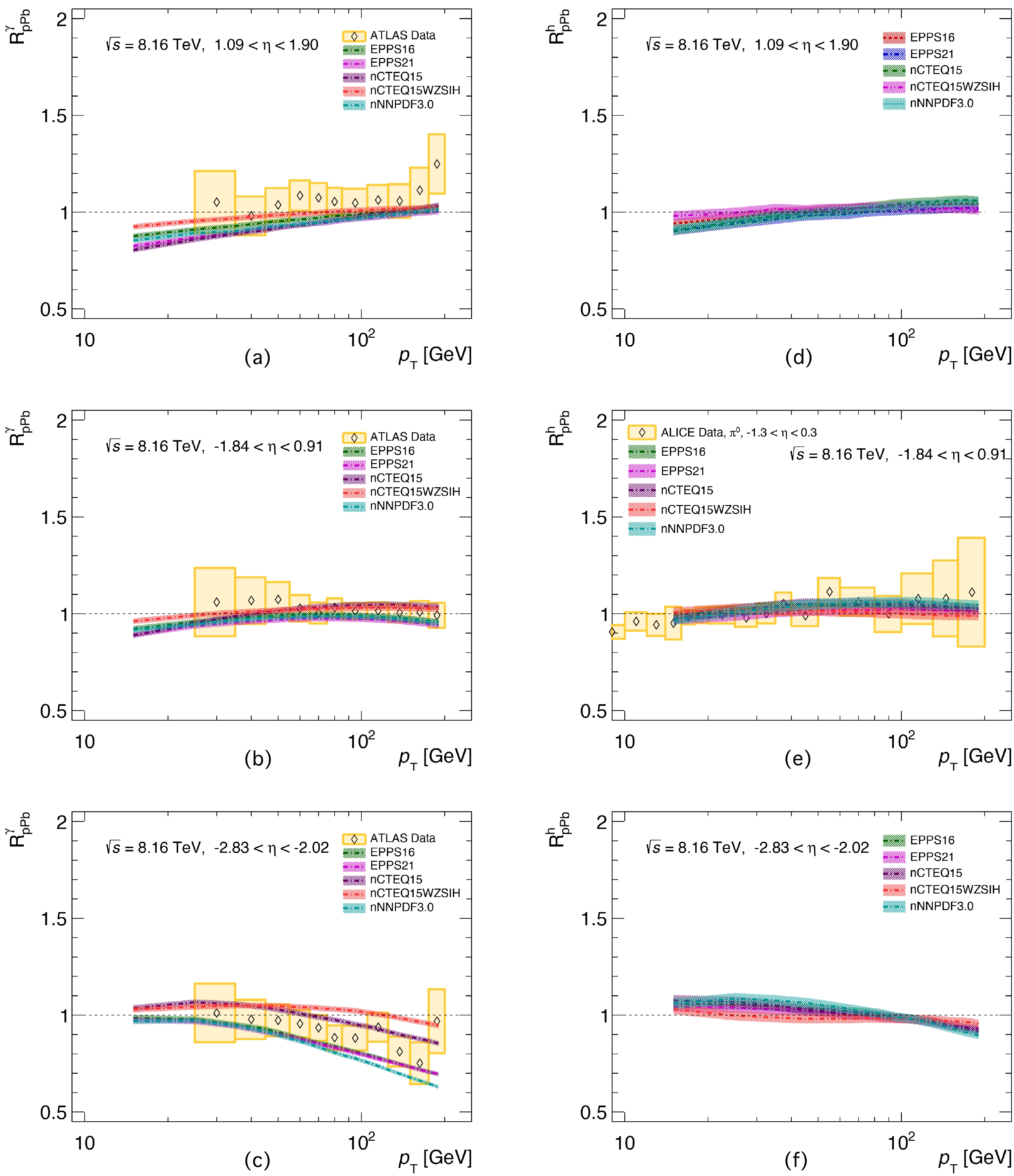
Figure 6. (color online) Nuclear modification factors
$ R_{p{\rm{Pb}}}^{\gamma} $ (a-c) and$ R_{p{\rm{Pb}}}^{h^{\pm}} $ (d-f) as a function of$ p_{{T}} $ based on the EPPS16, EPPS21, nCTEQ15, nCTEQ15WZSIH, and nNNPDF3.0 nPDFs in min-bias$ p+{\rm{Pb}} $ collisions at$\sqrt{s_{{NN}}}=$ 8.16 TeV for$ 1.09<\eta<1.90 $ ,$ -1.84<\eta<0.91 $ , and$ -2.83<\eta<-2.02 $ , respectively. The photon results are compared with ATLAS data [2], and the charged hadron results are compared with ALICE data for$ \pi^0 $ [6].Now, let us turn to Fig. 6. As the collision energy increased from 5.02 to 8.16 TeV, the precision of the experimental data increases. Thus, the ALICE data in panel (e) do not show a large deviation from unity in the high
$ p_{T} $ region. One can see from panels (a), (b), (c), and (e) that our calculations reproduce the data points rather well. By comparing the photons'$ R_{p{\rm{Pb}}}^{\gamma} $ with charged hadrons'$ R_{p{\rm{Pb}}}^h $ , one can find that in the backward rapidity region, the$ R_{p{\rm{Pb}}}^h $ is far more sensitive to nPDF sets owing to the invisible difference observed in Fig. 5 (c) and Fig. 6 (c). Thus, one can use this channel to improve the capacity of the nPDFs. Moreover, the photon has a relatively simple production channel and clean background, which can provide high-precision data for refining the nPDFs.As we know, the small system is an excellent candidate for studying the initial state effect, such as the CNM effect, because the final state effect (hot nuclear effect) is not supposed to exist in the small system. It was reported that the light quark jet quenching and suppression of heavy quark production were not observed in
$ p+{\rm{Pb}} $ collisions at LHC energies [57]. Meanwhile, some other QGP signals, e.g., strangeness enhancement, heavy quark elliptical flow, and increases in the baryon-to-meson ratios, were found in the small system, which led to the small system being widely studied in recent years. Thus, the$\rm O+O $ collisions at LHC energies are studied, as this collision system is large enough as compared to the$ p+{\rm{Pb}} $ collision system but small enough as respect to the$ {\rm{Pb}}+{\rm{Pb}} $ collisions. Thus, it can fill the gap between$ p+{\rm{Pb}} $ and$ {\rm{Pb}}+{\rm{Pb}} $ collisions. As one shall see, the CNM effect in$\rm O+O $ collisions becomes mild compared with that in$ {\rm{Pb}}+{\rm{Pb}} $ collisions.In Fig. 7, we present the nuclear modification factors, i.e.,
$ R_{p{\rm{Pb}}}^{\gamma} $ (right panel) and$ R_{p{\rm{Pb}}}^h $ (left panel), of direct photon and charged hadron productions in$\rm O+O $ collisions at 7 TeV. One can see that the CNM becomes smaller as the colliding nucleus becomes smaller, compared with$ {\rm{Pb}}+{\rm{Pb}} $ collisions. Fortunately, one still can see the difference coming from five sets of nPDFs in the$ R_{p{\rm{Pb}}}^{\gamma} $ , indicating that the photon production is more sensitive to the parton distributions. One can use this feature to refine the nPDFs. The right-hand panel of Fig. 7 shows that our theoretical values of the$ R_{p{\rm{Pb}}}^h $ are always close to unity, which implies that the CNM effect can be ignored in the charged hadron production process in$\rm O+O $ collisions. Our outcomes show that if the upcoming measurements at LHC indicate the suppression of charged hadron production in$\rm O+O $ collisions, the suppression can be attributed to the final state effect, e.g., jet quenching. Then, it indicates that QGP can exist in the small system.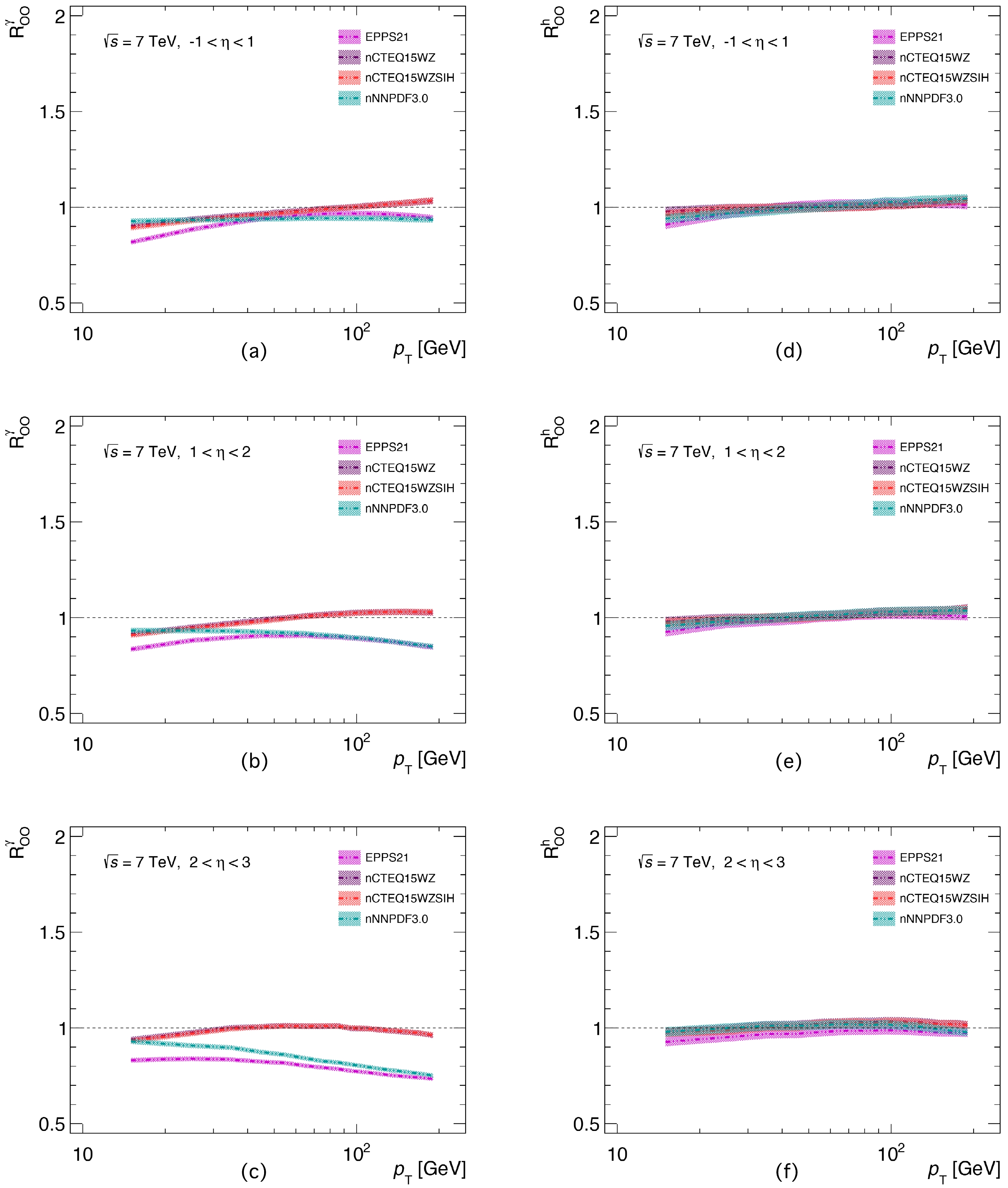
Figure 7. (color online) Nuclear modification factors
$ R_{OO}^{\gamma} $ (a-c) and$ R_{OO}^{h^{\pm}} $ (d-f) as a function of$ p_{{T}} $ based on the EPPS16, EPPS21, nCTEQ15, nCTEQ15WZSIH, and nNNPDF3.0 nPDFs in min-bias$\rm O+O $ collisions at$\sqrt{s_{{NN}}}=$ 7 TeV for$ -1<\eta<1 $ ,$ 1<\eta<2 $ and$ 2<\eta<3 $ , respectively. -
We perform a systematic study on the colliding energies, transverse momentum, and rapidity dependence of the CNM effects with the widely-used EPPS16, EPPS21, nCTEQ15, nCTEQ15WZSIH, and nNNPDF3.0 nPDFs through the direct photon and hadron productions at the LHC energies. The photon and hadron cross-sections are calculated using a NLO pQCD Monte Carlo program JETPHOX. The nuclear modification factors of direct photon and charged hadron with consideration of only the CNM effects in
$ p+{\rm{Pb}} $ and$ {\rm{Pb}}+{\rm{Pb}} $ collisions at$\sqrt{s_{{NN}}}=$ 2.76, 5.02, and 8.16 TeV are shown. Our calculations indicate that the photon production is more sensitive to the parton distribution functions (PDFs) than the hadron production process because the nuclear modification factors at backward rapidity exhibit clearly visible differences among the five sets of nPDFs. This indicates that the$ R_{p{\rm{Pb}}}^{\gamma} $ can be used to refine the nPDFs. Meanwhile, our numerical results show that the nCETQ15 and nCTEQ15WZSIH have larger quark PDFs than other sets.To see the CNM effects in the small system, we also study the nuclear modification factors for the upcoming
$\rm O+O $ collisions at LHC energies. As we know, the$\rm O+O $ collision system is located between$ p+{\rm{Pb}} $ and$ {\rm{Pb}}+{\rm{Pb}} $ in terms of multiplicity and is located between$ p+p $ and$ p+{\rm{Pb}} $ in terms of system size. Thus, it is a good candidate for fixing the CNM effects in heavy ion collisions. Our results indicate that there is no CNM effect in charged hadron production in$\rm O+O $ collisions. Hence, if there is a suppression of charged hadron yields, it can be caused by the final state effect. In other words, our study of the$\rm O+O $ collisions can provide an essential baseline for searching for QGP.
Systematic studies on the nuclear parton distribution with photon and hadron productions in nuclear collisions at the LHC
- Received Date: 2023-01-27
- Available Online: 2023-07-15
Abstract: A systematic study on the impact of widely-used nuclear-modified parton distribution function (nPDF) parameterizations on the production of direct photons and charged hadrons is performed by employing a next-to-leading order Monte Carlo event generator JETPHOX in hadronic collisions at LHC energies. The nuclear modification factors of photon and charged hadron productions are studied in three types of collision systems, i.e., small (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: