Entropies of the various components of the universe

Hao Yu; Yu-Xiao Liu; Jin Li

doi:10.1088/1674-1137/acc2ad

Chinese Physics C> 2023, Vol. 47> Issue(5) : 055105 DOI: 10.1088/1674-1137/acc2ad

Entropies of the various components of the universe

Hao Yu ^1, ,
Yu-Xiao Liu ^2,3, ,
Jin Li ^{1,,

,}

1.
College of Physics, Chongqing University, Chongqing 401331, China
2.
Institute of Theoretical Physics & Research Center of Gravitation, Lanzhou University, Lanzhou 730000, China
3.
Lanzhou Center for Theoretical Physics, Key Laboratory of Theoretical Physics of Gansu Province, School of Physical Science and Technology, Lanzhou University, Lanzhou 730000, China

Abstract
HTML
Reference
Related

PDF

Abstract：
In this study, we investigate the entropies of photons, ideal gas-like dust (baryonic matter), and a special kind of dark energy in the context of cosmology. When these components expand freely with the universe, we calculate the entropy and specific entropy of each component from the perspective of statistics. Under specific assumptions and conditions, the entropies of these components can satisfy the second law of thermodynamics independently. Our calculations show that the specific entropy of matter cannot be a constant during the expansion of the universe, except for photons. When these components interact with the space-time background, particle production (annihilation) can occur. We study the influence of the interaction on the entropies of these components and obtain the conditions guaranteeing that the entropy of each component satisfies the second law of thermodynamics.
- entropy of universe ,
- dark enengy ,
- dust ,
- photon ,
- the second law of thermodynamics

I. INTRODUCTION

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

Since it was found that the universe is expanding, the entropy problem and heat death of the universe have been intriguing topics about the past, present, and future entropies of the universe [1, 2]. The entropy problem includes two aspects involving the past and present entropies of the universe. Although physicists have predicted that the entropy production mechanism in the early universe may be associated with vacuum energy, Higgs particles, and the shear and bulk viscosities of the cosmological fluid [3–6], they have not explained satisfactorily why the initial state of the universe possesses low entropy. This question about the past entropy of the universe is also known as the Boltzmann-Penrose question (see [7] and references therein). For the present entropy of the universe, the problem boils down to why the value of the entropy is enormous, which is closely related to the horizon problem [8]. In 2008, Frampton et al. calculated the total entropy of the supermassive black holes inside the observable universe and found that it is the largest contributor to the entropy of the universe [9–11]. On the basis of the work of Frampton et al., the following year, Egan and Lineweaver took into account the latest measurements of the supermassive black hole mass function at the time and found that the total entropy of the supermassive black holes inside the observable universe is approximately $3.1^{+3.0}_{-1.7}\times10^{104}\,k$ [12], which is an unimaginably enormous number. As for cosmic heat death, it presents a gloomy prediction of the future entropy and the fate of the universe [13–15]. Research on the cosmic entropy shows that the entropy of an expanding universe generally satisfies the second law of thermodynamics [16–18]. Therefore, with the expansion of the universe, all life will eventually disappear, and the universe will be in a state of chaos and disorder. In order to avoid cosmic heat death, researchers proposed the cyclic model of the universe, in which the law of entropy increase may be inapplicable [19–21].

Thus far, the cosmic entropy has been generalized widely on the basis of classical thermodynamics, which contains horizon entropy [22, 23], information entropy [24, 25], entanglement entropy [26–28], etc. Moreover, there are studies focusing on the entropy of the universe in the presence of particle production (annihilation) and interaction (i.e., energy conversion). In general, particle production necessarily comes with interaction, but interaction does not necessarily lead to the phenomenon of particle production. The common feature of these two kinds of processes is that they can influence the thermodynamic properties of the universe. Therefore, it is important to study the entropy changes of these processes in cosmology.

The early pioneering works of Parker on particle production provided a microscopic mechanism of particle production in the context of cosmology [29–31], which laid the theoretical foundation for subsequent research on the entropy of the universe in the presence of particle production. From the perspective of quantum cosmology, particle production could be related to the origin of the universe [32–35]; thus, it may influence the low-entropy state of the early universe. On this issue, the Big Bang theory [36–39] and Big Bounce theory [40–44] already have multiple mechanisms to create the particles and entropy of the early universe. On the other hand, cosmological particle production can affect the entropy evolution of each component of the universe [22, 45–49]. In Refs. [50–52], the authors proposed using the second law of thermodynamics to constrain particle production in cosmology. In recent years, research on the entropy evolution in cosmology has shown that by using the thermodynamic constraints on the entropy, one can effectively restrain the gravitational theories in which there exists particle production. For example, considering scalar particle production in Horndeski's theory [53], the coupling coefficients between the scalar field and geometric quantities can be constrained with the second law of thermodynamics and thermodynamic equilibrium [54]. Similarly, if there exists particle production in running vacuum models [55, 56], the change rate of the running vacuum can be constrained by studying the entropy evolution of matter [57].

For most gravitational theories (such as non-minimal coupling theories [58–61]), if a matter field interacts with other fields (i.e., there is a non-minimal coupling between them), the energy-momentum tensor of the matter field is usually not conserved, unless one redefines the form of the energy-momentum tensor. The non-conservation of the energy-momentum tensor of the matter field, by analogy with the non-conservation of the particle number in an open thermodynamic system, can be explained as irreversible particle production [54, 62–65]. In this case, for these gravitational theories, the research on the entropy evolution of matter in cosmology is similar to the research on the entropy evolution of cosmological particle production [54, 57]. However, when the matter field interacts with other fields without particle production, how can we study the entropy evolution of matter in cosmology? We discuss this issue in the present work.

In addition, by investigating the statistical entropy of matter in a freely expanding universe, we will prove that the specific entropy of matter (except for photons) indeed evolves with the expansion of the universe [48, 66], whereas it is assumed to be a constant in some literature [52, 54, 63]. It is worth mentioning that it is an extremely special case that the specific entropy of matter in the universe remains unchanged. In classical thermodynamics, if the specific entropy of an isolated system (with a strictly conserved particle number) is a constant, it must be in thermal equilibrium (i.e., the total entropy is a constant). However, for an evolving isolated system (such as our expanding universe), the total entropy is increasing owing to the second law of thermodynamics. Thus, if the specific entropy of our expanding universe is a constant, there must exist particle production, and it needs to meet some extremely special conditions. In view of this, it is more reasonable to consider that the specific entropy of matter in the universe can evolve over time. Taking ideal gas-like dust (baryonic matter) as the main object of study, we will analyze the difference between the entropy changes in the cases with and without particle production.

The remainder of this paper is organized as follows. Sec. II is devoted to the review of some basic thermodynamic formulas related to cosmological particle production (annihilation). In Sec. III, we discuss the entropy and specific entropy of each component of the universe when they expand freely. We focus on photons, ideal gas-like dust (baryonic matter), and a special kind of dark energy. In Sec. IV, we describe the entropies and specific entropies of these components when they interact with the space-time background. The last part, Sec. V, is a summary of our research.

II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

We consider a homogeneous and isotropic universe, and the FLRW metric is given as

$\begin{eqnarray} \text{d}s^2=-c^2\text{d}t^2+a^2(t)\left(\dfrac{\text{d}r^2}{1-\tilde k\,r^2}+r^2\text{d}\theta^2+r^2\text{sin}^2\theta \,\text{d}\phi^2\right), \end{eqnarray}$

(1)

where $a(t)$ is the scale factor, c represents the speed of light, and $\tilde k$ represents the curvature of the space. For simplicity, we assume that the universe is spatially flat, i.e., $\tilde k=0$ .

Let us review some basic thermodynamic formulas of cosmological particle production (annihilation). Because we focus on the entropy of matter in the universe, it is appropriate to choose the co-moving volume as the thermodynamic system in this work. For a given species of matter, we label the particle number density as n, which, combined with the four velocity $U^\alpha$ of the co-moving observer, can be used to define the particle flow as $n^\alpha=n\, U^\alpha$ . If there exists a particle production (annihilation) process, the particle flow satisfies $\nabla_\alpha n^\alpha=\psi$ , where $\psi>0$ and $\psi<0$ represent a source and sink of particles, respectively. As the difference between particle production and annihilation only depends on the sign of ψ, hereinafter, they are collectively called particle production for convenience unless otherwise indicated. Then, one can define the particle production rate as follows:

$\begin{eqnarray} \Gamma=\dfrac{\nabla_\alpha n^\alpha}{n}=\dfrac{\psi}{n}. \end{eqnarray}$

(2)

For the co-moving observer, the entropy flow vector can be given as

$\begin{eqnarray} s^\alpha=n\,\sigma\, U^\alpha. \end{eqnarray}$

(3)

Note that σ represents the specific entropy of particles, which denotes the entropy per particle but not per unit mass. To calculate the specific entropy, we review the definition of the Gibbs free energy, which is given by

$\begin{eqnarray} G(p,T)=U+p\,V-T\,S=\tilde H-T\,S, \end{eqnarray}$

(4)

where U represents the internal energy of the system, p represents the pressure, V represents the volume, T represents the temperature, S represents the entropy, and $\tilde H$ represents the enthalpy. Because the statistics for the system with long-range interaction has not been constructed yet and the internal energy is in principle not additional for a general gravitational system, the integrated Gibbs free energy of a gravitational system cannot be directly equal to the sum of all components. However, if the energy density of the gravitational system is small enough, we can ignore the impact of gravity on the internal energy (and thus the Gibbs free energy) of each component. In this work, the universe we study does not involve the early stage; thus, the integrated Gibbs free energy can be approximately equal to the sum of all components:

$\begin{eqnarray} G_{t}(\tilde p,T)=\sum_{i}U_i+{\tilde p}\,V-T\sum_{i}S_i=\sum_{i}\tilde H_i-T\sum_{i}S_i. \end{eqnarray}$

(5)

Here, the evolution of the system is seen as a quasi-equilibrium process. The temperatures of all components are the same, and the parameter $\tilde p$ represents the total pressure of the system. For such an ideal system, it can be simplified as follows:

$\begin{eqnarray} G_{t}(\tilde p,T)=\sum_{i}u_iN_i, \end{eqnarray}$

(6)

where we have used $\displaystyle\sum\limits_{i}U_i=T\displaystyle\sum\limits_{i}S_i-\tilde p\,V+\displaystyle\sum\limits_{i}u_iN_i$ (Euler equation). The parameter $u_i$ represents the chemical potential of the i-th component, and $N_i$ represents the corresponding particle number. The total internal energy is equal to $V\displaystyle\sum\limits_{i}\rho_i$ , where $\rho_i$ represents the energy density of the i-th component. According to $\displaystyle\sum\limits_{i}U_i=V\displaystyle\sum\limits_{i}\rho_i$ and the Euler equation, the chemical potential of each component satisfies the following relationship:

$\begin{eqnarray} \sum_{i}u_iN_i=V\sum_{i}\rho_i+\tilde p\,V-T\sum_{i}S_i. \end{eqnarray}$

(7)

If there is only one kind of matter in the system, we can set i to 1. Then, the specific entropy of the matter is given by [48]

$\begin{eqnarray} \sigma =\dfrac{\rho+p}{T\,n}-\dfrac{u}{T}. \end{eqnarray}$

(8)

With Eq. (8) and the Gibbs-Duhem equation ( $\sum\limits_{i}S_i\text{d}T- V\,\text{d}\tilde p+ \sum\limits_{i}N_i\text{d}u_i=0$ ), for the system containing only one kind of matter, the differential form of Eq. (5) can be expressed as

$\begin{eqnarray} n\,T\, \text{d}\sigma=\text{d}\rho-\dfrac{\rho+p}{n} \text{d} n. \end{eqnarray}$

(9)

With this equation and the definition of the entropy flow (3), the authors in Ref. [48], for the first time, obtained the following formula for the thermodynamics of cosmological particle production:

$\begin{eqnarray} \nabla_\alpha s^\alpha=\nabla_\alpha (n\,\sigma\, U^\alpha)=\psi\, \sigma +n\, \dot{\sigma}=\dfrac{\theta}{T}\left(p+\rho+\dfrac{\dot \rho}{\theta}\right)-\dfrac{u\, \psi}{T}, \end{eqnarray}$

(10)

where $\theta=\nabla_\alpha U^\alpha$ . For the FLRW metric, $\theta=3H$ , where H is the Hubble parameter.

Note that the above pressure p includes only the pressure of the fluid itself. In cosmology, however, we usually treat the extraneous term caused by particle production in the equation of motion as an extra pressure, which is called production pressure. We label the production pressure as $p_c$ ; then, the equation corresponding to the divergence of the energy-momentum tensor of the (ideal) fluid can be written as

$\begin{eqnarray} \dot\rho+3H(p+\rho+p_c)=0. \end{eqnarray}$

(11)

Suppose that the production pressure satisfies $p_c= -\beta\, \psi/3H$ , where β is a positive parameter. For an expanding universe with a particle production (not annihilation) process, we have $3H>0$ and $\psi>0$ . Then, the production pressure should be $p_c<0$ , which is in line with the conclusion of most literature [49, 52, 67–72]. Substituting Eq. (11) into Eq. (10) yields

$\nabla_\alpha s^\alpha=\dfrac{\psi}{T}(\beta-u)=\psi\,\sigma+\left(\beta-\dfrac{\rho+p}{n}\right)\dfrac{\psi}{T},$

(12)

where we have used Eq. (8) to obtain the second equality. For $\psi>0$ and $\beta>u$ , the entropy of particles is increasing. If $\beta<u$ , we require $\psi<0$ (because of the second law of thermodynamics), which means that particles can be only annihilated. It is worth mentioning that β and u are not independent. Therefore, the condition $\beta<u$ is not easy to implement, which relies on the specific model of the universe and the species of matter. By comparing Eq. (12) with Eq. (10), one can obtain

$\begin{eqnarray} \dot{\sigma}=\dfrac{\psi}{n\,T}\left(\beta-\dfrac{\rho+p}{n}\right). \end{eqnarray}$

(13)

If the specific entropy σ is a constant, we need $\beta=(\rho+ p)/n$ or $\psi=0$ . $\psi=0$ implies that the particle number is conserved and the system has always been in a state of thermodynamic equilibrium. If $\beta=(\rho+p)/n$ , the production pressure is given as

$\begin{eqnarray} p_c=-\dfrac{\rho+p}{3H\,n}\psi. \end{eqnarray}$

(14)

According to Eq. (9), $\dot\sigma=0$ yields

$\begin{eqnarray} \dot\rho=\dfrac{\dot n}{n}(\rho+p). \end{eqnarray}$

(15)

With Eqs. (11), (14) and (15), we finally obtain $\dfrac{\dot n}{n}=-3H+ \Gamma$ , where Γ represents the particle production rate defined by Eq. (2). Here, it seems that $\dfrac{\dot n}{n}=-3H+\Gamma$ is based on σ being a constant, but it is easy to prove that the result also holds true for the universal σ with Eqs. (9), (11), and (13). This result actually can be obtained directly from the definition of the particle number inside the co-moving volume, which is given as $N\sim n\, a^3$ . Therefore, the intuitive definition of the particle production rate is

$\begin{eqnarray} \Gamma=\dfrac{\dot N}{N}=\dfrac{\dot n\, a^3+3n\,\dot a\, a^2}{n\,a^3} =\dfrac{\dot n }{n}+3H. \end{eqnarray}$

(16)

According to the definition of the specific entropy, the entropy of a given species of matter can be denoted as $S=\sigma\, n\, V=\sigma\, N$ . Therefore, the growth rate of the entropy in the thermodynamics of cosmological particle production is given by

$\begin{eqnarray} \dfrac{\dot S}{S}=\dfrac{\dot N}{N}+\dfrac{\dot\sigma}{\sigma} =\Gamma+\dfrac{\dot\sigma}{\sigma}=\dfrac{\dot n }{n}+3H+\dfrac{\dot\sigma}{\sigma}. \end{eqnarray}$

(17)

It is convenient to rewrite the change rate of the entropy of the system in the following form:

$\begin{eqnarray} \dfrac{\text{d}S}{\text{d}t}=S\left(\dfrac{\dot\sigma}{\sigma} +\Gamma\right). \end{eqnarray}$

(18)

If $\dot\sigma\neq0$ , the term $\dfrac{\dot\sigma}{\sigma}$ complicates the entropy evolution. For example, it can be seen that even though $\Gamma<0$ , $\dfrac{\text{d}S}{\text{d}t}>0$ can be still true with some special choices of the parameter σ [48], which means that particle annihilation can occur under the constraint of the second law of thermodynamics.

III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

It is known that for an expanding system in classical thermodynamics, the entropy evolution depends on the way the system expands and the properties of internal matter. Because the expansion of the universe is an intrinsic property of space-time, we can suppose that the boundary of the co-moving volume does not work on its surroundings. On the other hand, owing to the uniformity of the universe, the co-moving volume can be regarded as an adiabatic system. Therefore, there is no interaction between the matter in the co-moving volume and the outside, which means that the expansion of the universe is similar to the free expansion of a classical thermodynamic system. The non-conservation of the energy of the matter in the co-moving volume does not conflict with the free expansion, because there may exist interaction between the matter and the space-time background. For matter with unknown properties, we can assume that its specific entropy is a constant, so that the entropy of the system is only related to the particle number [52, 54, 63]. However, such an assumption is obviously rough, and the specific entropy evolving over time is more in line with the real situation of the universe [48, 66]. In this section, we assume that there is no interaction between any components of the universe, and we study the entropy and specific entropy of matter in the context of general relativity (that is, the coupling between matter and gravity is minimal). In this case, we can study different substances individually. Note that the substances we study here are the particles inside the co-moving volume. It is currently unclear whether the boundary of the co-moving volume has an area entropy similar to the horizon entropy. Even if it has an area entropy, we do not know whether the definition of the area entropy is consistent with the horizon entropy. Moreover, we do not know if the area entropy of the co-moving volume and the particle entropy inside the co-moving volume can convert to each other. If so, they should satisfy the general second law of thermodynamics, i.e., the particle entropy inside the co-moving volume plus the area entropy is always increasing. However, if they are independent, then when we study the evolution of the particle entropy, we can ignore the area entropy. In this work, we consider that they are independent and only focus on the particle entropy inside the co-moving volume; thus, we ignore the area entropy of the co-moving volume.

A Photons

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

We first consider the cosmic microwave background (CMB) radiation, which can be regarded as black-body radiation. Therefore, the entropy of photons inside the co-moving volume ( $V\sim a^3$ ) is given by [73–75]

$\begin{eqnarray} S=\dfrac{4\pi^2 k^4}{45c^3\hbar^3}V\,T^3=\text{Const.}, \end{eqnarray}$

(19)

where k is the Boltzmann constant and $T\sim a^{-1}$ represents the temperature of photons. Because the entropy of photons is a constant, we can think of photons as being in special thermodynamic equilibrium, which is in accordance with the second law of thermodynamics. The particle number of photons is given as

$\begin{eqnarray} N=\dfrac{2 k^3 \zeta(3)}{\pi^2 c^3\hbar^3}V\,T^3=\text{Const.}, \end{eqnarray}$

(20)

where $\zeta(n)$ is the Riemann zeta function. Therefore, the specific entropy of photons is

$\begin{eqnarray} \sigma(a)=\dfrac{S}{N}=\dfrac{2 \pi^4 k}{45\zeta(3)}, \end{eqnarray}$

(21)

which is also a constant. The result that the specific entropy of photons is a constant can also be obtained via Eq. (8), because the chemical potential of photons is zero [73–75] and the pressure of photons satisfies $p=\dfrac{1}{3}\rho$ . According to Eq. (8), the specific entropy of photons can be given as

$\begin{eqnarray} \sigma(a) =\dfrac{\rho+p}{T\,n}=\dfrac{4}{3}\dfrac{U}{N\,T}=\dfrac{2 \pi^4 k}{45\zeta(3)}, \end{eqnarray}$

(22)

where $U=\dfrac{\pi^2 k^4}{15c^3\hbar^3}V\, T^4$ represents the internal energy of photons. For matter whose chemical potential and equation of state are unclear, it is not feasible to calculate its specific entropy using Eq. (8).

B Ideal gas-like dust (baryonic matter)

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

Next, we consider ideal gas-like dust (baryonic matter). The so-called ideal gas-like dust refers to special dust with weak pressure, which can be regarded as an ideal gas. This consideration is based on two aspects. On the one hand, it is known that the substance with vanishing pressure (absolute zero temperature) actually does not exist; thus, the baryonic matter in the universe should also have kinetic energy. In cosmology, the kinetic energy of the baryonic matter is assumed as zero ( $p=0$ ), which is an appropriate approximation because the kinetic energy of the baryonic matter is so weak that it does not affect the results of most research. However, in studying the thermodynamic property of the universe, the vanishing kinetic energy of the baryonic matter is inadvisable owing to the third law of thermodynamics. Therefore, we assume that the baryonic matter has a weak pressure. On the other hand, the properties of the baryonic matter are similar to those of the ideal gas. The definition of the ideal gas can be reduced to two aspects: (a) the volume of a single particle can be ignored; (b) there is no potential energy between particles, and the collision is completely elastic. Because the average number density and kinetic energy of the baryonic matter are low after the early stage of the universe, they naturally satisfy condition (a). As for condition (b), because the gravitational potential energy between baryonic particles is negligible in practice, it can also be satisfied. Thus, we regard the baryonic matter as an ideal gas. It is worth mentioning that researchers generally agree that the pressure of dark matter is also weak [76], but the equation of state of dark matter is currently unclear (which even can be $p=-\dfrac13\rho$ [77]). In light of this, we do not regard dark matter as ideal gas-like dust in this work.

The equation of state of ideal gas-like dust is given as

$\begin{eqnarray} p=\dfrac{\tilde{n}\, \tilde{R}\, T}{V}, \end{eqnarray}$

(23)

where p and T represent the pressure and temperature of ideal gas-like dust, respectively. $V\sim a^3$ is still the co-moving volume. The parameter $\tilde{n}=N/N_A$ represents the amount of substance, where N represents the total number of ideal gas-like dust particles inside the co-moving volume and $N_A=6.022\times 10^{23}$ is the Avogadro constant. $\tilde{R}$ is the universal gas constant, whose value is the product of the Boltzmann constant k and Avogadro constant $N_A$ . It is convenient to rewrite Eq. (23) as

$\begin{eqnarray} p\, V=N\, k\, T. \end{eqnarray}$

(24)

If ideal gas-like dust expands freely from the co-moving volume $V_0$ to $V_1$ , by using the macro definition of entropy or letting the process be equivalent to a reversible isothermal expansion, the entropy change of ideal gas-like dust is expressed as

$\begin{eqnarray} \Delta S=S_1-S_0=\int_0^1\dfrac{\text{d}\hat Q}{T}=\int_0^1\dfrac{p\,\text{d}V}{T} =N\, k(\ln V_1-\ln V_0), \end{eqnarray}$

(25)

where $\text{d}\hat Q=\text{d}U+p\,\text{d}V$ . Because ideal gas-like dust expands freely, $\text{d}U=0$ and T is a constant throughout the process. The above formula indicates that the entropy of ideal gas-like dust satisfies the second law of thermodynamics in an expanding universe.

From the definition $S=\sigma\, n\, V=\sigma\, N$ , $\Delta S$ is also derived as

$\begin{eqnarray} \Delta S=\sigma_1N-\sigma_0N, \end{eqnarray}$

(26)

where $\sigma_1$ and $\sigma_0$ represent the specific entropies of ideal gas-like dust particles at the beginning and end of the process, respectively. By comparing Eqs. (25) and (26), we obtain

$\begin{eqnarray} \sigma_1-\sigma_0=k(\ln V_1-\ln V_0). \end{eqnarray}$

(27)

Because $V_1\neq V_0$ , σ is not a constant. According to Eq. (27), the specific entropy of ideal gas-like dust can be defined as

$\begin{eqnarray} \sigma(a)=k\,\ln V+\sigma_x=k\,\ln \left(a^3\right)+\sigma_x, \end{eqnarray}$

(28)

whose evolution is only related to the scale factor. The parameter $\sigma_x$ depends on the temperature, the particle number, and the mass of a single ideal gas-like dust particle. Here, the calculation of the entropy of ideal gas-like dust is concise according to classical thermodynamics. If the entropy of ideal gas-like dust is calculated according to statistics, the specific expression of $\sigma_x$ can be determined^①.

If there exists energy conversion between ideal gas-like dust and the space-time background, the expansion of the universe is not an isothermal process for ideal gas-like dust. To calculate the entropy change of ideal gas-like dust, one needs to determine the initial and final states of the system. Regardless of how the universe expands, the number of ideal gas-like dust particles inside the co-moving volume is always conserved in the absence of particle production. If we require $\dot\sigma=0$ (which means that $\Delta S=0$ ), the expansion of the universe obeys $\text{d}\hat Q=\text{d}U+ p\,\text{d}V=0$ . Therefore, in the absence of particle production, the specific entropy of ideal gas-like dust can remain constant only when the expansion of the universe is reversible and adiabatic.

C Dark energy

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

In this section, we discuss the entropy and specific entropy of a special kind of dark energy. Regarding the thermodynamic properties of dark energy, it has been determined that its pressure is negative, which makes it difficult to calculate its entropy using classical thermodynamics. Owing to the lack of exploratory data on dark energy, we have to make some assumptions in advance to study the entropy evolution of dark energy. In this work, we regard it as a special kind of substance that obeys classical statistical laws and has a non-conserved particle number. Then, we can calculate the entropy of dark energy with classical statistical mechanics. The main purpose of assuming that it satisfies classical statistical mechanics is to facilitate subsequent calculations. If we assume that dark energy particles obey quantum statistics, the calculations may be more complicated, but this does not mean that it is more significant. Definitely, it is a topic worth considering, but in this section, our main research target is a special kind of dark energy with a non-conserved particle number. As for what statistical laws it actually obeys, we are unable to judge this according to the current observation and experiment. In fact, dark energy (the accelerating expansion of the universe) is probably nothing but a macro phenomenon caused by particle production, although many physicists believe that dark energy may be vacuum energy or unknown particles with long-range interaction. The process of particle production in the universe can contribute a negative pressure to the Friedmann equations, which is a possible explanation for the accelerating expansion of the universe [49, 52, 67–72]. Because the particle number of the dark energy we study is non-conserved, even if "the dark energy particles" are some kind of known particles (without long-range interaction but evenly distributed throughout the universe), they can also result in the accelerating expansion of the universe. Therefore, the statistical law that dark energy particles satisfy does not have to be the statistics for the system with long-range interaction. We will not delve into the details of the issue here but try to provide a basis for the assumption that it is possible to regard dark energy (which can be the presently known matter with a non-conserved particle number) as a special ideal gas.

In order to study such dark energy, we assume that the number of free (decoupled) dark energy particles inside the co-moving volume can evolve with the expansion of the universe, and the corresponding particle production rate is Γ. Note that the decoupled dust and photons have no such special property, and this property is similar to the spontaneous decay of radioactive materials. The dark energy particles with such a property may have a complex entropy evolution. If dark energy particles expand freely from the co-moving volume $V_a$ to $V_b$ , the particle number is expressed as

$\begin{eqnarray} N_b=N_a\exp\left(\int_a^b\Gamma \text{d}t\right). \end{eqnarray}$

(29)

Because entropy is a quantity determined by the state of the system, to calculate the entropy change of dark energy in the process, we only need to determine the initial and final states of the system. For the given $N_b$ and $N_a$ , there could be different Γ's (see Fig. 1). For all lines, the thermodynamic arguments of dark energy in the initial (final) state are the same; thus, we can calculate the entropy change of dark energy with any of the lines shown in the figure. We choose the blue solid line to calculate the entropy change of dark energy from the co-moving volume $V_a$ to $V_b$ . From point a to point c, the particle number inside the co-moving volume does not change. For convenience, we can further assume that the statistical properties of dark energy particles are similar to those of an ideal monatomic gas. Because the statistical law that dark energy particles satisfy is not clear at present, in order to obtain intuitive results, we have to make such an unwarranted assumption. For different statistical laws, the particle number always has a significant effect on the entropy of the system. Therefore, the assumption on the statistical law of dark energy particles is a far less important effect on the entropy evolution of dark energy particles than the non-conserved particle number, and hence, the latter is the focus of our research.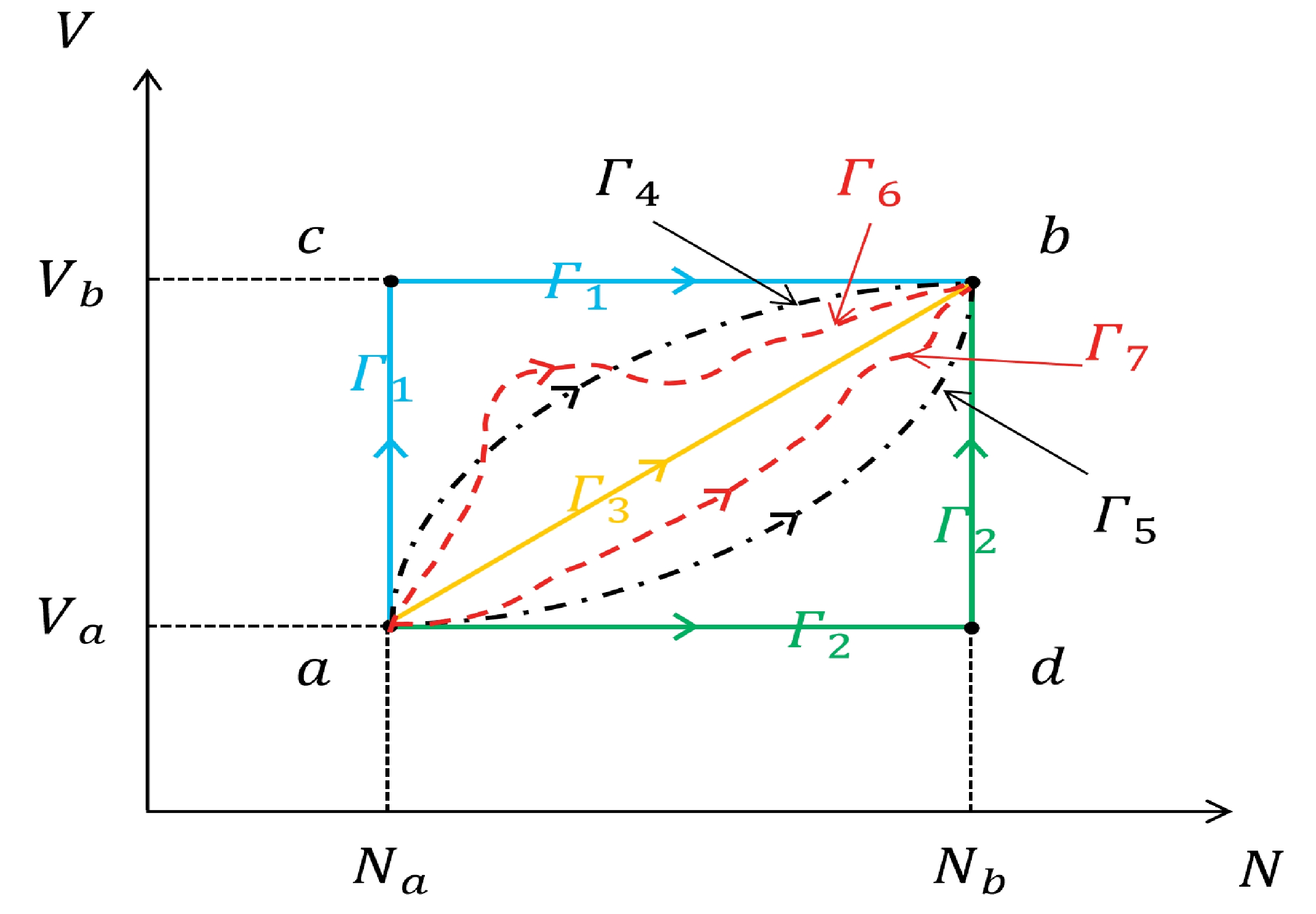

Figure 1

Figure 1. (color online) Plot of the relationship between the particle production rate (Γ) of dark energy and the volume of the system. For any

$\Gamma_i$ , we have

$N_b-N_a=\int_a^b\Gamma_i\,\text{d}t$ . Because the states of the system are definite at the points

$a (V_a, N_a)$ and

$b (V_b, N_b)$ , for all curves, the entropy changes of the system between the points a and b are the same. The blue solid line (

$\Gamma_1$ ) indicates that the system first expands from

$V_a$ to

$V_b$ with a conserved particle number, and then the particle number increases from

$N_a$ to

$N_b$ in the constant volume

$V_b$ . The processes of the green solid line (

$\Gamma_2$ ) are exactly the opposite of

$\Gamma_1$ . The solid yellow line (

$\Gamma_3$ ) indicates that the increase in the particle number is proportional to the increase in the volume. The two black dash-dotted lines indicate that the particle production rate changes with respect to the volume slowly first and fast afterwards for

$\Gamma_4$ and fast first and slowly afterwards for

$\Gamma_5$ . The two red dashed lines (

$\Gamma_6$ and

$\Gamma_7$ ) indicate the situation where the relationship between the particle production rate and the volume is complicated. It should be noted that we actually cannot judge which particle production rate is consistent with reality, because of a lack of observations. In other words, from a macro perspective, there is no physical motivation for these particle production rates, but we can determine which one is reasonable according to the (future) observation. We mentioned earlier that particle production can accelerate the expansion of the universe [49, 52, 67–72]. If we know all the details of the expansion of the universe, the particle production rate of dark energy can be theoretically determined.

DownLoad: Full-Size Img PowerPoint

Assume that the number of microscopic states of dark energy particles with energy between E and $E+\Delta E$ is given as

$\begin{eqnarray} \Omega(E)= \dfrac{3N}{2}\dfrac{\Delta E}{E}\left(\dfrac{V}{h_0^3}\right)\dfrac{(2\pi m\, E)^{3N/2}}{N!\left(\dfrac{3N}{2}\right)!}. \end{eqnarray}$

(30)

Here, m represents the mass of a single dark energy particle, and N represents the number of dark energy particles. It is worth noting that $h_0$ is a small quantity, whose dimension is the same as that of the Planck constant. In general, the smaller the value of $h_0$ , the higher the precision of our description of the classical thermodynamic system. For quantum statistics, $h_0$ is exactly the Planck constant. Because there is no concept of absolute entropy in classical thermodynamics, the value of $h_0$ can be arbitrarily small. However, the values of entropy corresponding to different $h_0$ 's differ only by a constant; thus, $h_0$ does not affect the evolution of entropy. According to the definition of Boltzmann entropy ( $S=k\ln \Omega$ ), the entropy of dark energy can be given as

$\begin{eqnarray} S= N\,k\ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\,m\, T}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N\,k. \end{eqnarray}$

(31)

Therefore, the entropy increase of dark energy in the process from point a to point c is

$\begin{eqnarray} \Delta S_{a\rightarrow c}=N_a k\left\{\ln \left[V_b(m_cT_c)^{3/2}\right]-\ln \left[V_a(m_aT_a)^{3/2}\right]\right\}. \end{eqnarray}$

(32)

If energy conservation holds for dark energy^②, the temperature of dark energy particles will remain unchanged. Because the particle number is conserved in the process, we have $m_cT_c=m_aT_a$ , which leads to Eq. (32) being equal to Eq. (25).

Then, from point c to point b, it is an isochoric process, and the particle number increases from $N_a$ to $N_b$ . According to Eq. (31), the entropy increase of dark energy in the process can be given by

$\begin{aligned}[b] \Delta S_{c\rightarrow b}=&N_a\exp\left(\int_a^b\Gamma \text{d}t\right) k\ln\left[\dfrac{V_b}{N_a\exp\left(\int_a^b\Gamma \text{d}t\right)}\left(\dfrac{2\pi k\, m_b T_b}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a\exp\left(\int_a^b\Gamma \text{d}t\right) k\\ &-\left\{N_a k\ln\left[\dfrac{V_b}{N_a}\left(\dfrac{2\pi k\, m_c T_c}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a k\right\}. \end{aligned}$

(33)

Then, the entropy increase of dark energy from point a to point b is

$\begin{aligned}[b] \Delta S_{a\rightarrow b}=&\Delta S_{a\rightarrow c}+\Delta S_{c\rightarrow b}=N_a\exp\left(\int_a^b\Gamma \text{d}t\right) k\ln\left[\dfrac{V_b}{N_a\exp\left(\int_a^b\Gamma \text{d}t\right)}\left(\dfrac{2\pi k\, m_b T_b}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a\exp\left(\int_a^b\Gamma \text{d}t\right) k\\ &-\left\{N_a k\ln\left[\dfrac{V_a}{N_a}\left(\dfrac{2\pi k\, m_a T_a}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a k\right\}. \end{aligned}$

(34)

There are many factors that affect the value of $\Delta S_{a\rightarrow b}$ ; thus, it is not easy to determine the conditions guaranteeing $\Delta S_{a\rightarrow b}>0$ . However, if we have

$\begin{aligned}[b]& \exp\left(\int_a^b\Gamma \text{d}t\right)>1,\,\,\,\,\,\, \text{and}\\& \dfrac{V_b}{N_a\exp\left(\int_a^b\Gamma \text{d}t\right)}\left(\dfrac{2\pi k\, m_b T_b}{h_0^2}\right)^{3/2}>\dfrac{V_a}{N_a}\left(\dfrac{2\pi k\, m_a T_a}{h_0^2}\right)^{3/2}, \end{aligned}$

(35)

$\Delta S_{a\rightarrow b}>0$ is tenable; thus, the second law of thermodynamics is satisfied. On account of energy conservation, $\exp\left(\int_a^b\Gamma \text{d}t\right) > 1$ means that $m_b T_b<m_a T_a$ . With Eq. (26), the specific entropy of dark energy particles can be defined as

$\begin{eqnarray} \sigma(V,N,m,T)= k\ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\, m\, T}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2} k, \end{eqnarray}$

(36)

which evolves with four parameters of the system composed of dark energy particles. If we can determine the particle production rate of dark energy during the expansion of the universe and the evolution of other variables over the scale factor, the specific entropy of dark energy particles will only evolve with the scale factor:

$\begin{eqnarray} \sigma(a)= k\ln\left[\dfrac{\dfrac{4\pi}{3}a^3}{N_0\exp\left(\int_0^a\Gamma(a) \text{d}t\right)}\left(\dfrac{2\pi k \, m(a) T(a)} {h_0^2}\right)^{3/2}\right]+\dfrac{5}{2} k, \end{eqnarray}$

(37)

where $N_0$ represents the number of dark energy particles in the initial state.

According to the above calculations, it is found that for a freely expanding component of the universe, the specific entropy generally evolves over time, except for photons. For the co-moving volume, the entropy of photons (which are considered as black-body radiation) is a constant (see Eq. (19)). Regarding dust as a classical ideal gas with weak pressure, its entropy inside the co-moving volume increases with the expansion of the universe (see Eq. (25)). As for dark energy (whose statistical law is assumed to be the same as that of a classical ideal monatomic gas but with a non-conserved particle number), the entropy inside the co-moving volume can satisfy the second law of thermodynamics under certain constraints (see Eq. (35)). In the next section, we discuss the entropy changes of these components in the presence of interaction.

IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

When matter interacts with an unknown substance (or the space-time background), there must be energy conversion between them. If we do not delve into the microscopic process of the interaction, the energy conversion may result in two extreme macro phenomena for the matter: A) the particle number is conserved but the energy of a single particle changes; B) the particle number is non-conserved but the energy of a single particle remains unchanged. Both of these situations lead to a change in the entropy of the matter. In this section, we analyze how these two different processes affect the entropy of the matter. For convenience, we ignore the entropy of the unknown substance (or the space-time background), which is the common practice employed in similar research, such as that on particle production induced by non-minimal coupling between matter and geometry [54, 62–65] or particle production induced by running vacuum [57]. We can consider the quantum field theory in curved space-time to calculate the particle production rate caused by the interaction between matter and the unknown substance (or the space-time background) in the context of cosmology, as in the research of Parker [29–31]. However, it is beyond the scope of this study and can be pursued as an independent study in the future. Here, we focus only on the possible effect of such interaction on the entropies of the components of the universe.

A Photons

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

In order to reasonably ignore the entropy of the substance coupled to the CMB radiation, we can assume that the CMB radiation is non-minimally coupled to the space-time background [78]. The thermodynamic state functions for a black-body photon gas indicate that one can completely describe photons inside the co-moving volume with an independent argument: temperature. Here, we need to emphasize two properties of photons. First, the particle number of photons must be non-conserved when they are coupled to the space-time background. For photons inside the co-moving volume, the particle number is proportional to the cube of temperature. In the standard ΛCDM model, the temperature of photons is inversely proportional to the scale factor; thus, the particle number of photons inside the co-moving volume is conserved. If photons are coupled to the space-time background, the temperature is no longer inversely proportional to the scale factor, which means that the particle number is no longer conserved. Because the particle number of photons inside the co-moving volume is only a function of the temperature, when photons are coupled to the space-time background, the two extreme cases mentioned above are completely equivalent on the macro level. Second, the energy of photons is not conserved in the universe. Even if photons are not coupled to any matter (as in the standard ΛCDM model), the energy ( $U=\dfrac{\pi^2 k^4}{15c^3\hbar^3 }V\, T^4$ ) of photons inside the co-moving volume always decreases with the expansion of the universe.

We suppose that the temperature of the CMB radiation is $T_0$ and the co-moving volume is $V_0$ at some point. After a period of time, the co-moving volume of the universe becomes $V_1$ . The temperature of photons becomes $T_1$ owing to the expansion of the universe and the interaction. The total energy transformed from the space-time background to photons is labeled as $\bar E$ .

When $\bar E<0$ (the energy of photons is absorbed by the space-time background), we have

$\begin{aligned}[b] U_1=&\dfrac{\pi^2 k^4}{15c^3\hbar^3}V_1\, T_1^4<U_x=\dfrac{\pi^2 k^4}{15c^3\hbar^3}V_1\, T_x^4\\& <U_0=\dfrac{\pi^2 k^4}{15c^3\hbar^3}V_0\, T_0^4. \end{aligned}$

(38)

Note that $U_x$ represents the energy of photons when the co-moving volume is equal to $V_1$ and $\bar E=0$ . In other words, $U_x$ represents the energy of the decoupled photons inside the co-moving volume $V_1$ . According to Eq. (19), for the decoupled photons inside the co-moving volume, the entropy is a constant; thus, we have $S_x=S_0$ The introduction of $U_x$ helps us judge the sizes of $T_1$ and $T_0$ . Because $V_1>V_0$ , it is obvious that $T_1<T_x<T_0$ . The entropy values for the three cases are denoted as $S_1 = \dfrac{4\pi^2 k^4}{45c^3\hbar^3}V_1T_1^3$ , $S_x = \dfrac{4\pi^2 k^4}{45c^3\hbar^3}V_1T_x^3$ , and $S_0 = \dfrac{4\pi^2 k^4}{45c^3\hbar^3}V_0T_0^3$ , respectively. Because $T_1<T_x<T_0$ and $S_x=S_0$ , the entropy change of photons can be calculated as

$\begin{eqnarray} S_1-S_0=S_1-S_x=\dfrac{4\pi^2 k^4}{45c^3\hbar^3}(V_1T_1^3-V_1T_x^3)<0, \end{eqnarray}$

(39)

which violates the second law of thermodynamics. It is worth emphasizing again that there are two reasons why we do not consider the area entropy of the co-moving volume or the entropy of the space-time background. First, their definitions need to be further confirmed, especially the entropy of the space-time background, which is completely unclear. Second, we do not know whether the entropy of photons and the entropy of the space-time background (or the area entropy of the co-moving volume) are independent. If we treat these entropies as a whole, it is usually difficult to determine the evolution of the total entropy, because some parameters in the total entropy are uncertain [57]. In order to avoid such a scenario, we treat them as independent entropies, and each satisfies the second law of thermodynamics.

We can compare the entropy of photons in this scheme with the result in Sec. III.A. Because the interaction causes the entropy of photons to decrease in this scheme, it must be lower than the entropy of the decoupled photons in Sec. III.A. The temperature evolution of photons in this scheme is determined by the interaction. If the temperature of photons satisfies $T\sim a^{-1-\delta}$ owing to the interaction, where $\delta>0$ is a constant, the ratio of the entropies of the photons in the two schemes is

$\begin{eqnarray} \dfrac{S_{\text{II}}}{S_{\text{I}}}\sim a^{-3\delta}. \end{eqnarray}$

(40)

As the scale factor or δ increases, the entropy ( $S_{\text{II}}$ ) of photons with the interaction will be far smaller than the entropy ( $S_{\text{I}}$ ) of the decoupled photons in Sec. III.A.

When $\bar E>0$ (photons absorb energy from the space-time background), we have

$\begin{eqnarray} U_1=\dfrac{\pi^2 k^4}{15c^3\hbar^3}V_1\, T_1^4>U_x=\dfrac{\pi^2 k^4}{15c^3\hbar^3}V_1\, T_x^4, \end{eqnarray}$

(41)

which implies $T_1>T_x$ . Note that we cannot judge the sizes of $U_1$ and $U_0$ , but this does not affect our determination of the entropy evolution. Because $T_1>T_x$ and $S_x=S_0$ , the entropy change of photons satisfies the second law of thermodynamics:

$\begin{eqnarray} S_1-S_0=S_1-S_x=\dfrac{4\pi^2 k^4}{45c^3\hbar^3}(V_1T_1^3-V_1T_x^3)>0. \end{eqnarray}$

(42)

Comparing the entropy of photons in this scheme with the result in Sec. III.A reveals that the entropy of photons in this scheme is higher than the entropy of the decoupled photons in Sec. III.A. Similarly, if the temperature of photons satisfies $T\sim a^{-1-\delta}$ owing to the interaction, where $\delta<0$ is a constant, the ratio of the entropies of the photons in the two schemes is still given by Eq. (40). As the scale factor increases or δ decreases, the entropy ( $S_{\text{II}}$ ) of photons with the interaction will be far larger than the entropy ( $S_{\text{I}}$ ) of the decoupled photons in Sec. III.A.

In summary, as long as photons absorb energy during the interaction process, the entropy of photons inside the co-moving volume will increase and vice versa. On the other hand, according to Eqs. (19) and (20), the specific entropy of photons is still a constant. The above study on the interaction between the CMB radiation and the space-time background can also be interpreted as the cosmic adiabatic photon production [78]. The black-body photon gas is a special ideal gas, whose particle number is always non-conserved in the presence of interaction. Therefore, we mainly focus on ideal gas-like dust (baryonic matter) and dark energy.

B Ideal gas-like dust (baryonic matter)

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

In this section, we still treat dust (baryonic matter) as an ideal monatomic gas, and we study its entropy and specific entropy in the presence of interaction. Similarly, we assume that ideal gas-like dust is non-minimally coupled to the space-time background. Because the universe is homogeneous and isotropic, the interaction can be regarded as occurring everywhere in the universe with equal probability. Thus, we can suppose that ideal gas-like dust is always in quasi-equilibrium. In this case, both the extremes (with and without particle production) can occur from a macro perspective.

1 In the presence of particle production

We first study the entropy change of ideal gas-like dust in the presence of particle production. In the initial state, we assume that the rest mass of an ideal gas-like dust particle is $m_0$ , the temperature of ideal gas-like dust is $T_0$ , and the co-moving volume is $V_0$ . The entropy of ideal gas-like dust can be given as

$\begin{eqnarray} S_0= N_0k\ln\left[\dfrac{V_0}{N_0}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_0k, \end{eqnarray}$

(43)

where $N_0$ represents the particle number. If the total energy transformed from the space-time background to ideal gas-like dust is $\bar E$ when the co-moving volume expands from $V_0$ to $V_1$ , according to special relativity, the change in the number of ideal gas-like dust particles is

$\begin{eqnarray} \Delta N=\dfrac{\bar E}{m_0\,c^2}. \end{eqnarray}$

(44)

Note that the temperature of ideal gas-like dust and the rest mass of an ideal gas-like dust particle have been assumed to remain constant in the presence of particle production. Therefore, when the co-moving volume is equal to $V_1$ , the entropy of ideal gas-like dust is given as

$\begin{aligned}[b] S_1=& (N_0+\Delta N)k\ln\left[\dfrac{V_1}{N_0+\Delta N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]\\&+\dfrac{5}{2}(N_0+\Delta N)k. \end{aligned}$

(45)

Thus, the entropy change of ideal gas-like dust is equal to

$\begin{aligned}[b] \Delta S_p=&S_1-S_0= \Delta N\, k\ln\left[\dfrac{V_1}{N_0+\Delta N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]\\&+ N_0 k\ln\left[\dfrac{V_1}{N_0+\Delta N}\dfrac{N_0}{V_0}\right]+\dfrac{5}{2}\Delta N\, k. \end{aligned}$

(46)

Let us compare Eq. (46) with Eq. (25). Note that $N_0$ in Eq. (46) is the parameter N in Eq. (25). Then, we obtain

$\begin{aligned}[b] \Delta S_p-\Delta S=& \Delta N\, k\ln\left[\dfrac{V_1}{N_0+\Delta N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]\\&+ N_0 k\ln\left(\dfrac{N_0}{N_0+\Delta N}\right)+\dfrac{5}{2}\Delta N\, k. \end{aligned}$

(47)

When $\Delta N=0$ , we have $\Delta S_p=\Delta S$ . It can be seen that the difference between the entropy of ideal gas-like dust with the interaction and the entropy of ideal gas-like dust without the interaction is determined by $\Delta N$ . If the change in the number of ideal gas-like dust particles is very small ( $|\Delta N| \ll N_0$ ) in the presence of the interaction, we have

$\begin{eqnarray} \Delta S_p-\Delta S\sim \Delta N\, k\ln\left[\dfrac{V_1}{N_0}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]+\dfrac{3}{2}\Delta N\, k. \end{eqnarray}$

(48)

Therefore, the difference is proportional to the change in the number of particles, which may not be of great significance, because $|\Delta N|\ll N_0$ . However, if the change in the number of particles does not satisfy $|\Delta N| \ll N_0$ , one cannot easily determine the sign of Eq. (47). Next, we analyze the entropy evolution of the ideal gas-like dust in the presence of particle production in detail.

When $\bar E<0$ (the energy of ideal gas-like dust is absorbed by the space-time background), the total number of ideal gas-like dust particles inside the co-moving volume decreases, i.e., $\Delta N<0$ . Let us check whether the specific entropy of ideal gas-like dust decreases as well. From Eqs. (43) and (45), it can be found that the difference in specific entropy between the initial and final states satisfies

$\begin{eqnarray} \sigma_1-\sigma_0= k\ln\left(\dfrac{V_1}{N_0+\Delta N}\dfrac{N_0}{V_0}\right)=k\ln\left(\dfrac{n_0}{n_1}\right), \end{eqnarray}$

(49)

where $n_0$ and $n_1$ represent the particle number densities of ideal gas-like dust in the initial and final states, respectively. Because the co-moving volume is increasing and the particle number is decreasing, we have $\dfrac{n_0}{n_1}>1$ , which implies $\sigma_1>\sigma_0$ . Therefore, the specific entropy of ideal gas-like dust increases as the particle number decreases. Accordingly, to determine the entropy change of ideal gas-like dust, we need to further discuss the parameters in Eq. (46). Note that there are five independent parameters ( $V_1$ , $V_0$ , $N_0$ , $\Delta N$ , and $m_0T_0$ ) that can influence the sign of Eq. (46). Taking no account of the constraints of observations, the values of the parameters at least need to satisfy the following fundamental constraints:

I) $S_0>0$ (entropy is positive);

II) $S_1>0$ (entropy is positive);

III) $V_1>V_0>0$ (the universe is expanding);

IV) $-N_0<\Delta N<0$ (the particle number in the final state cannot be negative);

V) $m_0T_0>0$ (the temperature of matter cannot be absolute zero).

Despite the above constraints, it is still difficult to determine whether Eq. (46) satisfies the second law of thermodynamics. To determine the entropy evolution of ideal gas-like dust, we can calculate the time derivative of the entropy of ideal gas-like dust. According to Eq. (43), it is given as

$\begin{aligned}[b] \dfrac{\text{d}S}{\text{d}t}=& N'k\ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right] +N\,k\left(\dfrac{V'}{V}-\dfrac{N'}{N}\right) +\dfrac{5}{2}N'k\\ =& N\,k\left\{\dfrac{N'}{N}\ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right] +\dfrac{3}{2}\dfrac{N'}{N} +\dfrac{V'}{V}\right\}, \end{aligned}$

(50)

where the prime indicates the derivative with respect to time. When N tends to 0, ideal gas-like dust particles are completely annihilated, and the entropy of the system must be 0. In this case, the system cannot always satisfy the second law of thermodynamics. To avoid the violation of the second law of thermodynamics, we assume that there is a critical particle number density $n_c$ for ideal gas-like dust at which the interaction will be terminated. We call this the truncation of the interaction between ideal gas-like dust and the space-time background. After the particle number density of ideal gas-like dust reaches the critical value, they will expand freely. From previous research, we know that the entropy of ideal gas-like dust always increases if it expands freely. Therefore, as long as the entropy of ideal gas-like dust keeps increasing before reaching the critical condition, the interaction between ideal gas-like dust and the space-time background does not violate the second law of thermodynamics. Next, we analyze the entropy evolution of ideal gas-like dust in three cases.

Case I: If the annihilation rate of ideal gas-like dust particles is far lower than the expansion rate of the universe ( $0<-\dfrac{N'}{N}\lll \dfrac{V'}{V}$ ), in order to determine the sign of Eq. (50), we need to estimate the value of $\ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]$ . Let $m_0$ be the average mass of a baryon, which is approximated as $m_0\sim1.6\times10^{-27}$ kg. We assume that the temperature of ideal gas-like dust in the universe is $\sim 1$ K. It is found in the following discussion that the temperature of ideal gas-like dust has little effect on the final result. If the particle number density of ideal gas-like dust is equal to the particle number density of baryons (which is about $0.2$ m $^{-3}$ at present), we can take $\dfrac{V}{N}\sim 5$ m $^3$ . By plugging the Boltzmann constant and Planck constant into $\ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]$ , we finally obtain

$\begin{aligned}[b]& \ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]\\&\sim \ln\left[5\left(\dfrac{2\pi \times 1.6\times10^{-27}\times 1.38\times10^{-23} }{(6.6\times10^{-34})^2}\right)^{3/2}\right]\sim62. \end{aligned}$

(51)

Note that with the annihilation of ideal gas-like dust and the expansion of the universe, $\dfrac{V}{N}$ will increase; thus, the value of the above expression will be larger. However, because of the logarithm to $\dfrac{V}{N}$ , the increase rate of Eq. (51) is extremely low. For example, even though $\dfrac{V}{N}=5\times10^{26}$ m $^3$ , Eq. (51) gives a value of only approximately 122. For the same reason, the temperature of ideal gas-like dust has little effect on the value of Eq. (51). When the temperature changes from $10^{-10}$ to $10^{10}$ K, it only increases from 28 to 97. Therefore, if $0<-\dfrac{N'}{N}\lll\dfrac{V'}{V}$ , we can deduce from Eq. (50) that $\dfrac{\text{d}S}{\text{d}t}>0$ for the general case (such as $5\,\text{m}^3<\dfrac{V}{N}<5\times10^{26}\,\text{m}^3$ , $m_0\sim1.6\times10^{-27}$ kg, and $10^{-10}\,\text{K}<T_0< 10^{10}\,\text{K}$ ). It is predictable that, for general $m_0$ and $T_0$ values, only when $\dfrac{V}{N}$ becomes extremely large can $\dfrac{\text{d}S}{\text{d}t}<0$ occur. Therefore, as long as the critical particle number density $n_c$ is not extremely small, the entropy of ideal gas-like dust can satisfy the second law of thermodynamics throughout the evolution of the universe.

Case II: If the annihilation rate of ideal gas-like dust particles is far higher than the expansion rate of the universe ( $-\dfrac{N'}{N}\ggg\dfrac{V'}{V}>0$ ), it is not difficult to obtain $\dfrac{\text{d}S}{\text{d}t}<0$ for the general case. Only when $\ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right] < -\dfrac{3}{2}$ can the entropy of ideal gas-like dust satisfy $\dfrac{\text{d}S}{\text{d}t}>0$ . Because the entropy of ideal gas-like dust is always positive definite:

$\begin{eqnarray} S= N\,k\ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2 }\right]+\dfrac{5}{2}N\,k>0, \end{eqnarray}$

(52)

we finally obtain that $\dfrac{\text{d}S}{\text{d}t}>0$ requires

$\begin{eqnarray} -\dfrac{5}{2}<\ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0 ^2}\right)^{3/2}\right]<-\dfrac{3}{2}. \end{eqnarray}$

(53)

In the subsequent study, we will see that this condition is unlikely to occur in the realistic universe. Therefore, in this case, the entropy of ideal gas-like dust usually violates the second law of thermodynamics.

Case III: If the annihilation rate of ideal gas-like dust particles is not significantly different from the expansion rate of the universe, we can set $\dfrac{V'}{V}=-b\dfrac{N'}{N}$ . Then, Eq. (50) can be rewritten as

$\begin{eqnarray} \dfrac{V}{V'}\dfrac{1}{N\,k}\dfrac{\text{d}S}{\text{d}t}=\left\{ -\dfrac{1}{b}\ln\left[V^{1+\frac{1}{b}}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]-\dfrac{3}{2b}+1\right\}, \end{eqnarray}$

(54)

where we have $\dfrac{V}{V'}\dfrac{1}{N\,k}>0$ . For convenience, we assume that the range of the parameter b is $0.01 \leq b\leq100$ , and we choose specific values of b to examine the entropy evolution of ideal gas-like dust. As shown in Fig. 2, for any value of b, the entropy increase rate of ideal gas-like dust decreases monotonically with volume V. When V is large enough, the entropy increase rate is negative, which violates the second law of thermodynamics. Moreover, when V tends to 0, the entropy increase rate of ideal gas-like dust is always positive. Therefore, if the truncation of the interaction occurs early enough, the entropy of ideal gas-like dust will not violate the second law of thermodynamics for any value of b. We assume that the critical particle number density $n_c$ for ideal gas-like dust corresponds to the volume $V_c=1\,\text{m}^3$ . Then, it can be seen that only when $61.955<b<100$ can the derivative of the entropy be larger than 0 at $V_c=1\,\text{m}^3$ . In other cases ( $0.01<b<61.955$ ), the derivative of the entropy will be less than 0 at $V_c=1\,\text{m}^3$ . Note that the critical value 61.955 is based on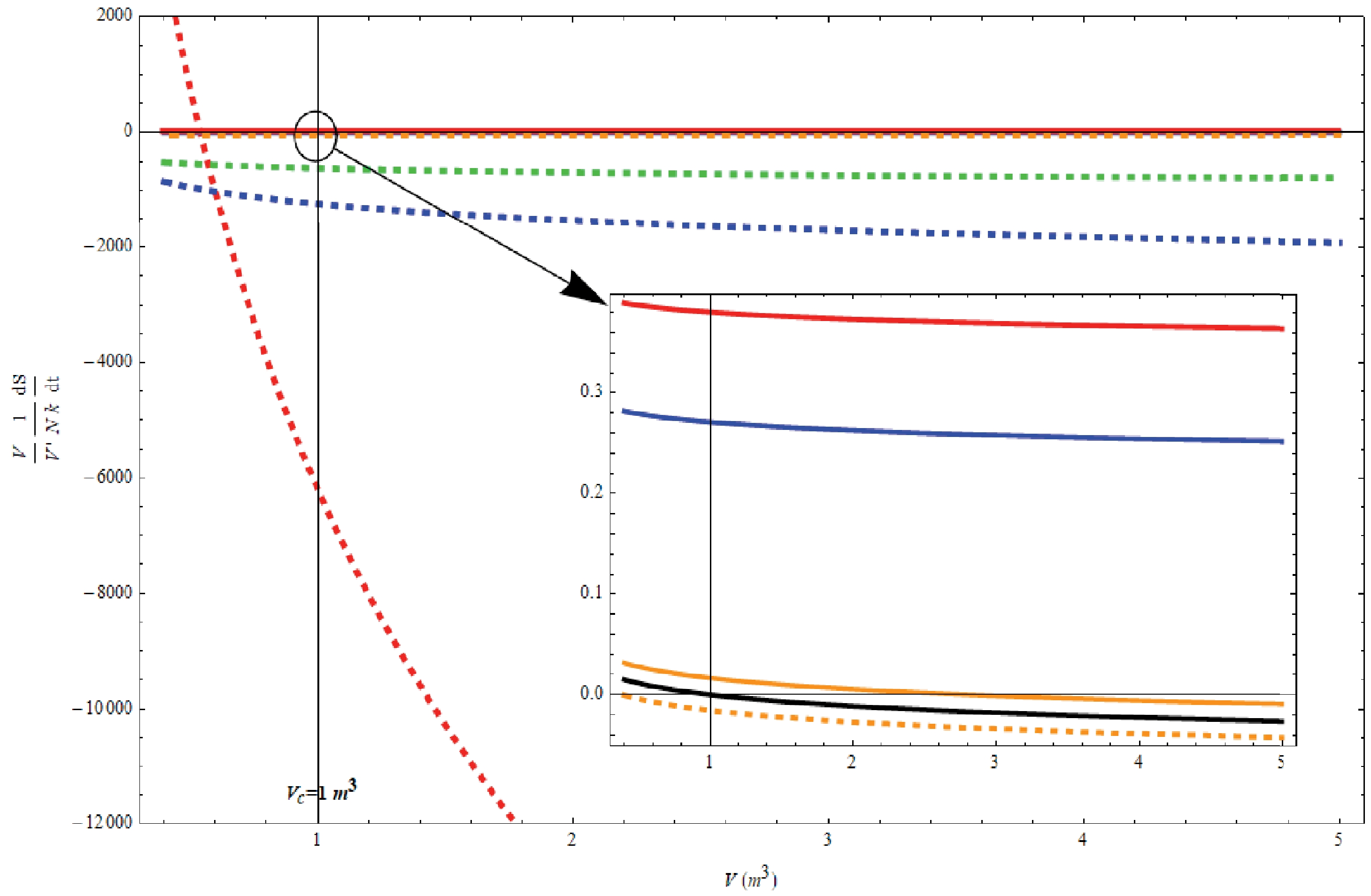

Figure 2

Figure 2. (color online) Plot of the entropy increase rate of ideal gas-like dust with the co-moving volume in the case of particle annihilation. There are eight values of the parameter b:

$b=0.01$ (red dashed line),

$b=0.05$ (blue dashed line),

$b=0.1$ (green dashed line),

$b=61$ (orange dashed line),

$b=61.955$ (black solid line),

$b=63$ (orange solid line),

$b=85$ (blue solid line), and

$b=100$ (red solid line). The entropy increase rates of all the dashed lines are negative at

$V_c=1\,\text{m}^3$ . The entropy increase rate of the black solid line (

$b=61.955$ ) is exactly 0 at

$V_c=1\,\text{m}^3$ . The entropy increase rates of all other solid lines are positive at

$V_c=1\,\text{m}^3$ .

DownLoad: Full-Size Img PowerPoint

$\begin{aligned}[b] \left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}=&\left[\dfrac{2\pi \times 1.6\times 10^{-27}\times 1.38\times10^{-23} }{(6.6\times10^{-34})^2}\right]^{3/2}\,\text{m}^{-3}\\&\sim 1.80\times10^{26}\,\text{m}^{-3}. \end{aligned}$

(55)

From the analysis of the three cases, we can conclude that if the interaction between ideal gas-like dust and the space-time background reduces the number of ideal gas-like dust particles, there is an upper limit to the annihilation rate of ideal gas-like dust particles, which is determined by the critical particle number density $n_c$ (or the corresponding $V_c$ ) and the expansion rate of the universe. Beyond the upper limit, the entropy evolution of ideal gas-like dust violates the second law of thermodynamics.

When $\bar E>0$ (ideal gas-like dust absorbs energy from the space-time background), the total number of ideal gas-like dust particles inside the co-moving volume increases, i.e., $\Delta N>0$ . The difference in the specific entropy of ideal gas-like dust between the initial and final states is also given by Eq. (49) but with $\Delta N>0$ . To judge whether the specific entropy is increasing, we need more details about the particle production rate of ideal gas-like dust and the expansion rate of the universe. Similarly, in light of Eq. (49), if the particle number density of ideal gas-like dust increases, the specific entropy decreases and vice versa.

The entropy evolution of ideal gas-like dust can be analyzed on the basis of the previous discussion. Review Eq. (50) and note that $\dfrac{N'}{N}>0$ . According to the positive definiteness of entropy (see Eq. (52)) and the first equality in Eq. (50), if $\dfrac{V'}{V}\geq\dfrac{N'}{N}>0$ , then $\dfrac{\text{d}S}{\text{d}t}>0$ is always true.

If $0<\dfrac{V'}{V}<\dfrac{N'}{N}$ , we can set $\dfrac{V'}{V}=b\dfrac{N'}{N}$ ( $V\sim N^b$ ) with $0< b< 1$ . Because $\dfrac{V}{N}=N^{b-1}$ ( $0<b<1$ ) decreases monotonically with particle number N, with the help of the second equality in Eq. (50), it is predictable that only when $\ln\left[\dfrac{V}{N}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]<0$ can we have $\dfrac{\text{d}S}{\text{d}t}<0$ . However, as stated earlier, this condition is uncommon in the realistic universe; thus, in this case, the entropy of ideal gas-like dust usually also satisfies the second law of thermodynamics. Let us briefly analyze why this condition and Eq. (53) are uncommon. We rewrite Eq. (50) as

$\begin{eqnarray} \dfrac{V}{V'}\dfrac{1}{N\,k}\dfrac{\text{d}S}{\text{d}t}=\left\{ \dfrac{1}{b}\ln\left[V^{1-\dfrac{1}{b}}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]+\dfrac{3}{2b}+1\right\}. \end{eqnarray}$

(56)

For any value of b ( $0< b< 1$ ), the entropy of ideal gas-like dust will decrease at some point as V increases. Owing to the existence of the truncation, if the entropy of ideal gas-like dust keeps increasing before the interaction is truncated, the second law of thermodynamics can be guaranteed. It can be seen from Fig. 3 that the larger b is, the larger $V_c$ can be. When b tends to 1 (i.e., $\dfrac{V'}{V}$ tends to $\dfrac{N'}{N}$ ), with the help of Eqs. (52) and (50), one finds that $V_c$ can be infinite. For example, when $b=0.9$ , $\dfrac{\text{d}S}{\text{d}t}=0$ corresponds the volume $V\sim 4.7\times10^{245}\,\text{m}^3$ , which means that the second law of thermodynamics is always satisfied as long as $V_c< 4.7\times10^{245}\,\text{m}^3$ . When b is very small (i.e., $\dfrac{V'}{V}$ is far smaller than $\dfrac{N'}{N}$ ), to guarantee that the entropy of ideal gas-like dust satisfies the second law of thermodynamics, $V_c$ must be small enough. If $V_c\leq1\,\text{m}^3$ , for any value of b ( $0< b< 1$ ), the second law of thermodynamics is always satisfied. For a given $V_c>1\,\text{m}^3$ , the second law of thermodynamics will give a lower bound on b. For example, if $V_c=2\,\text{m}^3$ , b needs to be larger than 0.011 (see Fig. 3). These results do not seem to suggest anything extreme. However, if one calculates the number of ideal gas-like dust particles inside the co-moving volume, one can find that the particle number density of ideal gas-like dust is unacceptable. According to $\dfrac{V}{N}=N^{b-1}$ , when $b=0.9$ and $V_c= 4.7\times10^{245}\,\text{m}^3$ , we have $N=9.3\times10^{272}$ . When $b=0.011$ and $V_c=2\,\text{m}^3$ , we have $N=2.3\times10^{27}$ . In both cases, the particle number densities of ideal gas-like dust are unrealistic. Therefore, if $0<\dfrac{V'}{V}<\dfrac{N'}{N}$ , the entropy of ideal gas-like dust under normal circumstances will not violate the second law of thermodynamics.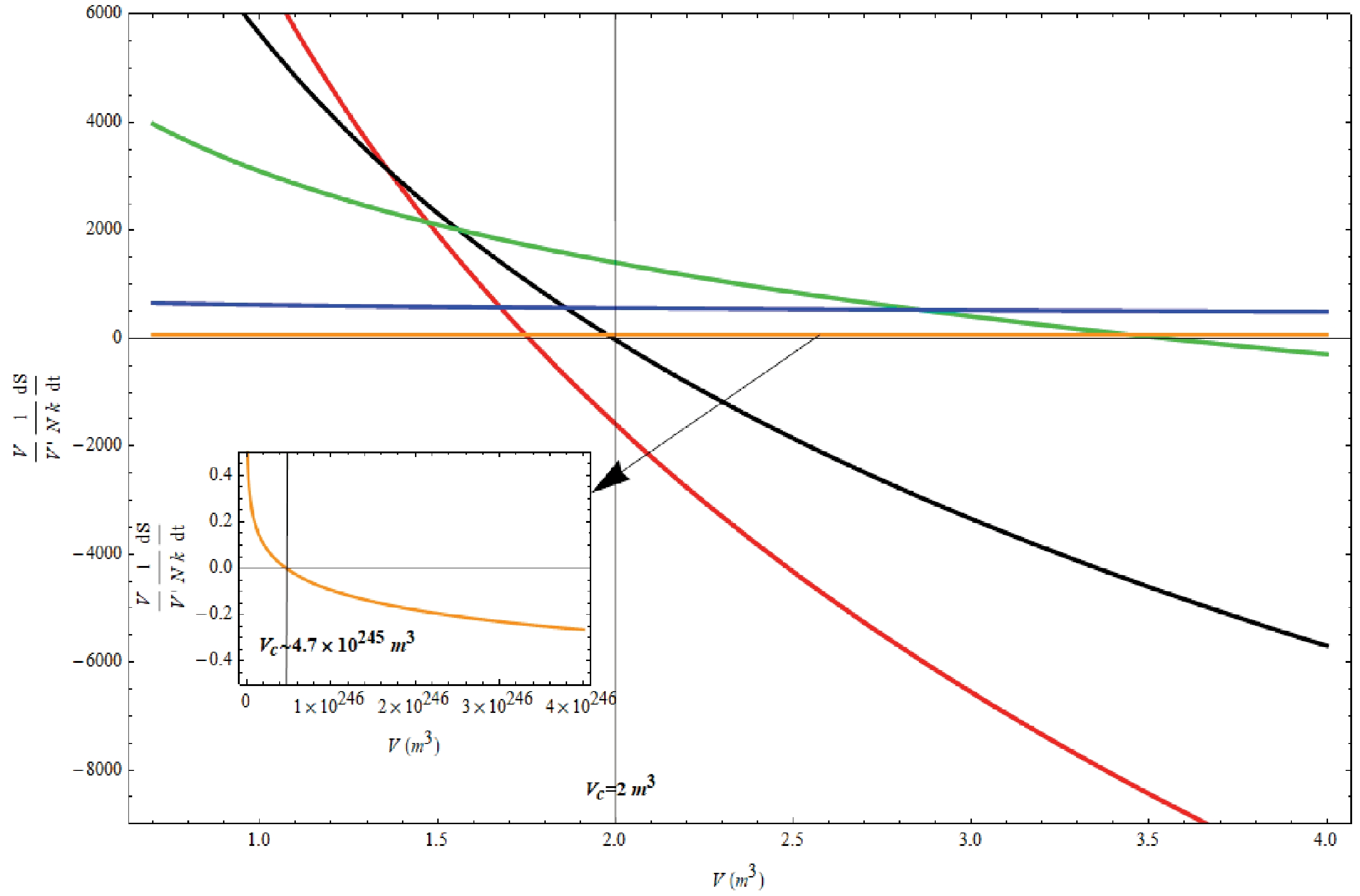

Figure 3

Figure 3. (color online) Plot of the entropy increase rate of ideal gas-like dust with respect to the co-moving volume in the case of particle production. There are five values of the parameter b:

$b=0.009$ (red line),

$b=0.011$ (black line),

$b=0.02$ (green line),

$b=0.1$ (blue line), and

$b=0.9$ (orange line). The entropy increase rate indicated by the red line is negative at

$V_c=2\,\text{m}^3$ . The entropy increase rate indicated by the black line (

$b=0.011$ ) is exactly 0 at

$V_c=2\,\text{m}^3$ . The entropy increase rates of all other lines are positive at

$V_c=2\,\text{m}^3$ .

DownLoad: Full-Size Img PowerPoint

According to the above discussion, we can conclude that, if the interaction between ideal gas-like dust and the space-time background increases the number of ideal gas-like dust particles, the entropy of ideal gas-like dust satisfies the second law of thermodynamics in general.

2 In the absence of particle production

Now, we study the entropy change of ideal gas-like dust in the absence of particle production. We assume that the initial state of the system is the same as that in the case of particle production: the rest mass of an ideal gas-like dust particle is $m_0$ , the temperature of ideal gas-like dust is $T_0$ , and the co-moving volume is $V_0$ . Therefore, the entropy of ideal gas-like dust in the initial state is given by Eq. (43). When the energy conversion between ideal gas-like dust and the space-time background is equal to $\bar E$ , the co-moving volume is still $V_1$ . In this case, both the temperature and the rest mass can change over time. For convenience, we can treat these two parameters as a whole. Although the energy of ideal gas-like dust is conserved as the universe expands, we cannot give the relationship between $\bar E$ and $m\,T$ (which depends on the specific microscopic process). Thus, we simply denote $m_1\,T_1$ as a function of $\bar E$ . Then, the entropy of ideal gas-like dust at the end of the process can be written as

$\begin{eqnarray} \hat S_1= N_0k\ln\left[\dfrac{V_1}{N_0}\left(\dfrac{2\pi k\, m_1 T_1} {h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_0k. \end{eqnarray}$

(57)

The entropy change of ideal gas-like dust is equal to

$\begin{eqnarray} \Delta \hat S_p=\hat S_1-S_0= N_0 k\ln\left[\dfrac{V_1}{V_0}\left(\dfrac{m_1 T_1}{m_0 T_0}\right)^{3/2}\right]. \end{eqnarray}$

(58)

We can compare Eq. (58) with Eq. (25), and $N_0$ in Eq. (58) is the parameter N in Eq. (25). Then, we can obtain

$\begin{eqnarray} \Delta \hat S_p-\Delta S=\dfrac32 N_0 k\ln \left(\dfrac{m_1 T_1}{m_0 T_0}\right). \end{eqnarray}$

(59)

When $m_1 T_1=m_0 T_0$ , we have $\Delta \hat S_p=\Delta S$ . The difference between the entropy of ideal gas-like dust with the interaction and the entropy of ideal gas-like dust without the interaction depends on $m_1 T_1$ . If the change in the temperature of ideal gas-like dust is slow in the presence of the interaction, in a relatively short period of time, we have $\Delta \hat S_p\sim\Delta S$ . However, if the change in the temperature of ideal gas-like dust is fast, $\Delta \hat S_p$ will soon deviate from $\Delta S$ . Regardless of whether $m_1 T_1$ is monotonically increasing or decreasing owing to the interaction, the gap between $\Delta \hat S_p$ and $\Delta S$ will increase over time.

When $\bar E<0$ , the total energy of ideal gas-like dust particles inside the co-moving volume will decrease. Because the energy of ideal gas-like dust particles expanding freely is conserved (i.e., $m\, T$ is a constant for ideal gas-like dust particles expanding freely), $\bar E<0$ means that $m_1 T_1<m_0 T_0$ . Because $m_1 T_1<m_0 T_0$ and $V_1>V_0$ , we cannot judge whether the value of Eq. (58) is larger than 0. However, if the expansion of the universe and the energy decay of ideal gas-like dust particles satisfy $\dfrac{V_1}{V_0} \left(\dfrac{m_1 T_1}{m_0 T_0}\right)^{3/2}=1$ , the entropy of ideal gas-like dust will remain unchanged. If $\dfrac{V_1}{V_0} \left(\dfrac{m_1 T_1}{m_0 T_0}\right)^{3/2}>1$ , $\hat S_1-S_0>0$ satisfies the second law of thermodynamics and vice versa. Moreover, the number of ideal gas-like dust particles is conserved; thus, the evolution of the specific entropy is consistent with the behavior of the entropy.

When $\bar E>0$ , the total energy of ideal gas-like dust particles inside the co-moving volume will increase, and we have $m_1 T_1>m_0 T_0$ . In this case, because $V_1>V_0$ , one can obtain $\dfrac{V_1}{V_0} \left(\dfrac{m_1 T_1}{m_0 T_0}\right)^{3/2}>1$ ; thus, $\hat S_1-S_0>0$ , which means that the second law of thermodynamics is always satisfied. Therefore, the specific entropy of ideal gas-like dust will keep increasing.

3 Comparison

In this section, we compare the entropy changes of ideal gas-like dust obtained in the above two cases and analyze the difference between these two kinds of entropy changes. Note that we do not know the specific relationship between $\bar E$ and $m\,T$ in the absence of particle production. Therefore, the relationship between $\bar E$ and $m\,T$ is the most critical factor in the comparison of the two kinds of entropy changes.

First, we discuss a special case in which the relationship between $\bar E$ and $m\,T$ can guarantee that the two kinds of entropy changes are equal. Comparing Eq. (46) with Eq. (58) reveals that the equivalence between the two kinds of entropy changes ( $S_1-S_0=\hat S_1-S_0$ ) requires that $m_1 T_1$ , $m_0 T_0$ , and $\bar E$ satisfy

$\begin{aligned}[b] \dfrac{\bar E}{m_0\,c^2} \ln\left[\dfrac{V_1}{N_0+\dfrac{\bar E}{m_0\,c^2}}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{{3}/{2}}\right]+\dfrac{5}{2}\dfrac{\bar E}{m_0\,c^2} = N_0 \ln\left[\dfrac{N_0+\dfrac{\bar E}{m_0\,c^2}}{N_0}\left(\dfrac{m_1 T_1}{m_0 T_0}\right)^{{3}/{2}}\right], \end{aligned}$

(60)

where we have substituted the expression of Eq. (44) for $\Delta N$ . Equation (60) indicates that $m_1\,T_1$ is related to the volume ( $V_1$ ) of the system, which contradicts the fact that the energy of ideal gas-like dust particles expanding freely is conserved. This contradiction can be comprehended in the following way. For ideal gas-like dust with a conserved particle number, if it absorbs the energy $\bar E$ , the temperature and the rest mass should be completely determined. These two parameters are entirely unrelated to the volume of the system, because the free expansion of the system does not change the temperature; thus, it does not change the rest mass. However, $m_1 T_1$ in Eq. (60) depends on the volume ( $V_1$ ) of the system. Therefore, Eq. (60) contradicts the fact that the energy of ideal gas-like dust particles expanding freely is conserved. The contradiction means that the two kinds of entropy changes cannot be consistent.

Next, we qualitatively analyze the difference between these two kinds of entropy changes under different circumstances. Because the initial states of the two cases are the same, we only need to consider the difference in the entropy in the final state between the two cases. Subtracting the entropy corresponding to particle conservation (see Eq. (45)) from the entropy corresponding to particle production (see Eq. (57)) yields

$\begin{aligned}[b] S_1-\hat S_1=&\dfrac{\bar E}{m_0\,c^2}k\ln\left[\dfrac{V_1}{N_0+\dfrac{\bar E}{m_0\,c^2}}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2} \right] + \dfrac{5}{2}\dfrac{\bar E}{m_0\,c^2}k\\ &+\,N_0k\ln\left[\dfrac{N_0}{N_0+\dfrac{\bar E}{m_0\,c^2}}\left(\dfrac{ m_0 T_0} {m_1 T_1}\right)^{3/2}\right].\\[-10pt] \end{aligned}$

(61)

It can be verified that the above formula gives a value of 0 when $\bar E=0$ . For a given $\bar E$ , because we do not know the specific expression of $m_1 T_1$ with respect to $\bar E$ , we can only qualitatively analyze the sign of Eq. (61). We assume that $\bar E$ is an infinitesimal quantity, i.e., the interaction is extremely weak, which is evidently in line with the current observations of the universe. Letting $m_1 T_1$ be an arbitrary function of $\bar E$ ; when $\bar E=0$ , we have $m_1 T_1(\bar E=0)=m_0 T_0$ . By expanding $S_1-\hat S_1$ in Eq. (61) with respect to the parameter $\dfrac{\bar E}{m_0\,c^2}$ and retaining the first-order term, we obtain

$\begin{aligned}[b]& S_1-\hat S_1\sim\dfrac{\bar E}{m_0\,c^2}k\left\{\ln\left[\dfrac{V_1}{N_0}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]\right.\\&\quad\left.+\dfrac{3}{2}-\dfrac{3}{2}N_0 \dfrac{(m_1T_1)'|_{\bar E=0}}{m_0T_0}\right\}, \end{aligned}$

(62)

where $(m_1T_1)'|_{\bar E=0}$ is the derivative of $m_1T_1$ with respect to $\dfrac{\bar E}{m_0\,c^2}$ evaluated at $\bar E=0$ . The value of $(m_1T_1)'|_{\bar E=0}$ reflects the change rate of $m\,T$ with respect to the energy $\bar E$ at the point $m_0T_0$ . The key to judging whether the right hand side of Eq. (62) is larger than 0 is to determine $\ln\left[\dfrac{V_1}{N_0}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]$ and $N_0\dfrac{(m_1T_1)'|_{\bar E=0}}{m_0T_0}$ . It is known from previous research that $\ln\left[\dfrac{V_1}{N_0}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]$ is insensitive to $\dfrac{V_1}{N_0}$ and $m_0 T_0$ . For example, even if $\dfrac{V_1}{N_0}$ takes values from 5 m $^3$ to $5\times10^{26}$ m $^3$ , the value of $\ln\left[\dfrac{V_1}{N_0}\left(\dfrac{2\pi k\, m_0 T_0}{h_0^2}\right)^{3/2}\right]$ (with $m_0\sim1.6\times10^{-27}$ kg and $T_0\sim 1$ K) only increases from 62 to 122. Therefore, whether the right hand side of Eq. (62) is larger than 0 mainly depends on $N_0\dfrac{(m_1T_1)'|_{\bar E=0}}{m_0T_0}$ . For the general case, we still cannot judge the sign of Eq. (62). Nevertheless, we can analyze the following two extreme cases.

When $m\,T$ changes rapidly with respect to the energy $\bar E$ at the point $m_0T_0$ (i.e., $|N_0\dfrac{(m_1T_1)'|_{\bar E=0}}{m_0T_0}|\gg1$ ), if $\bar E>0$ , then $N_0\dfrac{(m_1T_1)'|_{\bar E=0}}{m_0T_0}\gg1$ , and so $S_1<\hat S_1$ . Moreover, if $\bar E <0$ , then $N_0\dfrac{(m_1T_1)'|_{\bar E=0}}{m_0T_0}\ll-1$ , and one can also obtain $S_1<\hat S_1$ . Therefore, in this case, $S_1$ is always less than $\hat S_1$ .

When $m\,T$ changes slowly with respect to the energy $\bar E$ at the point $m_0T_0$ (i.e., $|N_0\dfrac{(m_1T_1)'|_{\bar E=0}}{m_0T_0}|\ll1$ ), if $\bar E>0$ , then $0<N_0\dfrac{(m_1T_1)'|_{\bar E=0}}{m_0T_0}\ll1$ , and so $S_1>\hat S_1$ . However, if $\bar E<0$ , then $0<-N_0\dfrac{(m_1T_1)'|_{\bar E=0}}{m_0T_0}\ll1$ , and we have $S_1<\hat S_1$ . Therefore, in this case, the sizes of $S_1$ and $\hat S_1$ depend on the sign of $\bar E$ .

In summary, when there exists energy conversion between ideal gas-like dust and the space-time background, it is unrealistic to keep the two kinds of entropy changes of ideal gas-like dust consistent. For $m\,T$ changing rapidly with respect to the energy, the entropy change of ideal gas-like dust corresponding to particle production is always smaller than that corresponding to no particle production, regardless of whether ideal gas-like dust absorbs energy from the space-time background. For $m\,T$ changing slowly with respect to the energy, when ideal gas-like dust absorbs energy, the entropy change of ideal gas-like dust corresponding to particle production is larger than that corresponding to no particle production. However, when the energy of ideal gas-like dust is absorbed, the conclusion is opposite. For the general case, we cannot decide which process has the larger entropy change.

C Dark energy

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

In this section, we discuss the entropy of dark energy when there exists interaction between dark energy and the space-time background. Because we have assumed that the number of dark energy particles may be a function of the temperature, if dark energy interacts with the space-time background, both the particle number and temperature (or rest mass) will change over time and be affected by the interaction. Therefore, there are not two kinds of entropy changes for dark energy. As it is difficult to quantitatively calculate the entropy change of dark energy in such a complicated situation, we qualitatively analyze the entropy change of dark energy in special cases.

Recalling Eq. (34), when $m_b T_b=m_a T_a$ , it degenerates into Eq. (46) (ideal gas-like dust with particle production), and when $\Gamma=0$ , it degenerates into Eq. (58) (ideal gas-like dust without particle production). Assuming that the energy conversion between dark energy and the space-time background is $\bar E$ during the expansion of the co-moving volume from $V_a$ to $V_b$ , the entropy change of dark energy is similar to that given by Eq. (34):

$\begin{aligned}[b]\\[-5pt] \Delta \bar S_{a\rightarrow b}=&N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right) k\ln\left[\dfrac{V_b}{N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right)}\left(\dfrac{2\pi k\, \bar m_b \bar T_b}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right) k\\ &-\left\{N_a k\ln\left[\dfrac{V_a}{N_a}\left(\dfrac{2\pi k\, m_a T_a}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a k\right\},\\ \end{aligned}$

(63)

where $\bar\Gamma$ represents the particle production rate of dark energy due to the expansion of the system and the interaction. The parameter $\bar m_b \bar T_b$ is a function of the energy $\bar E$ and the co-moving volume $V_b$ . Here, the specific entropy of dark energy can still be given by Eq. (36), but the parameters N, m, and T are affected by the energy $\bar E$ . For dark energy particles expanding freely, we know that, under the constraints of Eq. (35), the entropy of the system will increase. For dark energy particles interacting with the space-time background, the entropy of the system can satisfy the second law of thermodynamics under certain conditions.

Comparing Eq. (63) with Eq. (34) yields

$\begin{aligned}[b] \Delta \bar S_{a\rightarrow b}-\Delta S_{a\rightarrow b}= & N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right) k\ln\left[\dfrac{V_b}{N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right)}\left(\dfrac{2\pi k\, \bar m_b \bar T_b}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right) k\\& -\left\{N_a\exp\left(\int_a^b\Gamma \text{d}t\right) k\ln\left[\dfrac{V_b}{N_a\exp\left(\int_a^b\Gamma \text{d}t\right)}\left(\dfrac{2\pi k\, m_b T_b}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a\exp\left(\int_a^b\Gamma \text{d}t\right) k\right\}. \end{aligned}$

(64)

When $\bar m_b \bar T_b=m_b T_b$ and $\bar\Gamma=\Gamma$ , we have $\Delta \bar S_{a\rightarrow b}=\Delta S_{a\rightarrow b}$ . The difference between the entropy of dark energy with the interaction and the entropy of dark energy without the interaction actually only depends on the difference between $\bar\Gamma$ and Γ. In general, it is difficult to determine the sign of Eq. (64) without more information on the parameters. Therefore, here, we cannot judge the difference between the entropy of dark energy with the interaction and the entropy of dark energy without the interaction.

Now, we return to Eq. (63). When $\bar E>0$ , the number of dark energy particles at the end of the process satisfies

$\begin{eqnarray} \bar N_b=N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right)>N_b=N_a\exp\left(\int_a^b\Gamma \text{d}t\right)>N_a, \end{eqnarray}$

(65)

where Γ represents the particle production rate of dark energy in the absence of interaction (see Eq. (29)). Moreover, the energy of a single particle should be higher than that in the case without interaction, i.e., $\bar m_b \bar T_b> m_b T_b$ . With Eq. (65), $\bar m_b \bar T_b> m_b T_b$ , and the constraints on dark energy particles expanding freely (see Eq. (35)), we can prove that $\Delta \bar S_{a\rightarrow b}>0$ is generally tenable.

Because $\bar m_b \bar T_b> m_b T_b$ , it is obvious that

$\begin{aligned}\\[-4pt] \Delta \bar S_{a\rightarrow b}>N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right) k\ln\left[\dfrac{V_b}{N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right)}\left(\dfrac{2\pi k\, m_b T_b}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right) k-\left\{N_a k\ln\left[\dfrac{V_a}{N_a}\left(\dfrac{2\pi k\, m_a T_a}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a k\right\}. \end{aligned}$

(66)

Next, we investigate the properties of the following function:

$\begin{eqnarray} F(X)= X k\ln\left[\dfrac{V_b}{X}\left(\dfrac{2\pi k\, m_b T_b}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}X k, \end{eqnarray}$

(67)

where $X=N_a\exp\left[\int_a^b\bar\Gamma \text{d}t\right]$ . The derivative of $F(X)$ with respect to X is given as

$\begin{eqnarray} \dfrac{\text{d}F(X)}{\text{d}X}=k\ln\left[\dfrac{V_b}{X}\left(\dfrac{2\pi k\, m_b T_b}{h_0^2}\right)^{3/2}\right]+\dfrac{3}{2} k. \end{eqnarray}$

(68)

As we analyzed earlier, $\ln\left[\dfrac{V_b}{X}\left(\dfrac{2\pi k\, m_b T_b}{h_0^2}\right)^{3/2}\right]$ is generally positive, except if the particle number density of dark energy is extremely large. Therefore, $\dfrac{\text{d}F(X)}{\text{d}X}>0$ , and $F(X)$ increases with the variable X. With Eq. (65), we can finally obtain

$\begin{aligned}[b]\\[-4pt] \Delta \bar S_{a\rightarrow b}>N_a\exp\left(\int_a^b\Gamma \text{d}t\right) k\ln\left[\dfrac{V_b}{N_a\exp\left(\int_a^b\Gamma \text{d}t\right)}\left(\dfrac{2\pi k\, m_b T_b}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a\exp\left(\int_a^b\Gamma \text{d}t\right) k \end{aligned}$

$\begin{aligned}[b] \quad\quad -\left\{N_a k\ln\left[\dfrac{V_a}{N_a}\left(\dfrac{2\pi k\, m_a T_a}{h_0^2}\right)^{3/2}\right]+\dfrac{5}{2}N_a k\right\}=\Delta S_{a\rightarrow b}>0, \end{aligned}$

(69)

where $\Delta S_{a\rightarrow b}$ is given by Eq. (34).

When $\bar E<0$ , the number of dark energy particles at the end of the process satisfies

$\begin{eqnarray} \bar N_b=N_a\exp\left(\int_a^b\bar\Gamma \text{d}t\right)<N_b=N_a\exp\left(\int_a^b\Gamma \text{d}t\right). \end{eqnarray}$

(70)

where Γ is still the particle production rate of dark energy in the absence of interaction (see Eq. (29)). The energy of a single particle is lower than that in the case without interaction, i.e., $\bar m_b \bar T_b< m_b T_b<m_a T_a$ . In this case, it is not easy to judge the sign of $\Delta \bar S_{a\rightarrow b}$ . According to the previous analysis, if the energy of a single particle changes slowly in the process (i.e., $\bar m_b \bar T_b\sim m_b T_b\sim m_a T_a$ ) and the number of dark energy particles satisfies $\bar N_b=N_a\exp\left[\int_a^b\bar\Gamma \text{d}t\right]>N_a$ (the increase in the particle number caused by the expansion of the system is larger than the decrease in the particle number caused by the energy loss), the entropy of dark energy can keep increasing.

V. CONCLUSIONS

I. INTRODUCTION
II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)
III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION
     A Photons
     B Ideal gas-like dust (baryonic matter)
     C Dark energy
V. CONCLUSIONS

We reviewed the thermodynamics of cosmological particle production (annihilation). Combining classical statistics and cosmology, we studied the entropies of photons, ideal gas-like dust (baryonic matter), and dark energy in the context of the universe.

When these components of the universe are regarded as ideal fluids expanding freely, we can calculate their entropies and specific entropies separately. For photons, the entropy and specific entropy inside the co-moving volume are both constants (see Eqs. (19) and (21)). For dust (baryonic matter), we supposed that its thermodynamic properties are similar to those of an ideal gas; thus, it is called ideal gas-like dust (baryonic matter). It was found that both the entropy and the specific entropy of ideal gas-like dust increase with the expansion of the universe (see Eqs. (25) and (27)). Therefore, the entropy of ideal gas-like dust satisfies the second law of thermodynamics. For dark energy, because we do not know whether the number of dark energy particles is conserved, we assumed that the number of dark energy particles inside the co-moving volume evolves with the expansion of the universe (i.e., particle production occurs even if dark energy expands freely). Supposing that they possess the statistical law of an ideal monatomic gas, we found that if the free expansion of such special dark energy satisfies Eq. (35), the entropy of dark energy obeys the second law of thermodynamics.

It is worth noting that the assumption that dust is similar to an ideal gas is based on the properties and distribution of dust in the universe. Generally, the ideal gas has two characteristics: the volume of a single particle can be approximated to 0, and there is no interaction between particles (i.e., potential energy). Because the number density of dust particles in the universe is small enough, we can ignore the volume of a single dust particle. Moreover, the interaction between dust particles cannot be ignored only in the early universe. Therefore, it is feasible to treat dust as an ideal gas in this work. On the other hand, we assume that dark energy particles satisfy the classical statistical mechanics, which is mainly based on two aspects. First, dark energy may be a macro effect resulting from the known particles that satisfy the classical statistical mechanics, rather than the real vacuum energy. As long as such particles are generated continually in the universe, there will be a negative pressure in the Friedmann equations, which can be used to explain the accelerating expansion of the universe [49, 52, 67–72]. In this work, we focus on such special "dark energy particles"; thus, the property of the non-conserved particle number is necessary for dark energy. Second, if dark energy is composed of unknown particles and we do not know what statistical mechanics it satisfies, it is convenient to assume that it satisfies classical statistical mechanics, to simplify calculations. Dark energy satisfying quantum statistics is worthy of future detailed study.

When these components of the universe interact with the space-time background, their entropies and specific entropies are influenced by the interaction. For photons, if they absorb (lose) energy, the entropy inside the co-moving volume will increase (decrease) with the expansion of the universe. However, the specific entropy of photons is still a constant, which is independent of the interaction. For ideal gas-like dust, if it absorbs (loses) energy, there are two possible extreme outcomes. One is that the particle number inside the co-moving volume increases (decreases) and the energy per particle remains unchanged. The other is that the energy per particle increases (decreases) and the particle number inside the co-moving volume is conserved. We calculated the entropy and specific entropy of ideal gas-like dust in the two cases, respectively. By analyzing the relationship between the entropy and the parameters, we obtained the conditions for the entropy satisfying the second law of thermodynamics in different situations. When there exists particle production, the evolution of the specific entropy of ideal gas-like dust depends on the change in the particle number density. When there exists no particle production, the evolution of the specific entropy of ideal gas-like dust is consistent with the entropy. By comparing the entropy changes of ideal gas-like dust in the two cases, we found that the two kinds of entropy changes cannot be identical. The difference between the two kinds of entropy changes mainly depends on two aspects: the sign of the energy conversion and the change rate of $m\,T$ with the energy conversion. Finally, we analyzed the conditions for the entropy of dark energy continuously increasing in different situations when there exists interaction between dark energy and the space-time background.

The entropy of each component of the universe is closely related to the evolution of the universe. Studying the entropy of the universe is important for understanding the fate of the universe. For the realistic universe, both particle production and interaction between different substances are common phenomena. In this study, when we investigated the interaction between matter and the space-time background, we did not consider the microscopic process or the entropy of the space-time background, which is the practice followed in most literature [54, 57, 62–65]. Evidently, if the entropies of two interacting substances can be taken into account simultaneously, more convincing results can be obtained, which is a topic that we can study in the future.

According to classical statistical mechanics, for an ideal gas, the number of microscopic states satisfies $\begin{document}$ \Omega(N,E,V)\propto V^N $\end{document}$ . The entropy of the system is given as $\begin{document}$ S=k \ln\Omega(N,E,V) $\end{document}$ . To calculate $\begin{document}$ \sigma_x $\end{document}$ , we need to figure out the specific form of $\begin{document}$ \Omega(N,E,V) $\end{document}$ . For example, if the ideal gas consists of monatomic molecules, $\begin{document}$ S=k \ln\Omega(N,E,V)=N\, k\ln\left[\frac{V}{N}(\frac{2\pi k\,m\,T}{h_0^2})^{3/2}\right]+\frac{5}{2}N\, k $\end{document}$ , where m is the mass of a molecule. Note that $\begin{document}$ h_0 $\end{document}$ is an undetermined constant, because the concept of absolute entropy does not exist in classical statistics. Then, $\begin{document}$ \sigma_x $\end{document}$ is given as $\begin{document}$ \sigma_x=k\ln\left[\frac{1}{N}(\frac{2\pi k\,m\,T}{h_0^2})^{3/2}\right]+\frac{5}{2} k $\end{document}$ , where N, m, and T are all constants for the ideal gas that expands freely. In this work, we assume that the particle number densities of all substances (except photons) are low enough to render quantum effects negligible and thus they satisfy Maxwell-Boltzmann statistics. The statistical entropy obtained in this way is sufficient to reflect whether the thermodynamic evolution of the system is reasonable, without employing ensemble theory.

It is generally believed that only photons and ultra-relativistic particles have the characteristic of energy non-conservation in the expanding universe.

References

[1]	R. C. Tolman, Phys. Rev. 37, 1639 (1931) doi: 10.1103/PhysRev.37.1639
[2]	R. C. Tolman, Relativity, Thermodynamics and Cosmology, (Oxford University Press, 1934) [reprinted by Dover, New York (1987)]
[3]	S. Weinberg, Astrophys. J. 168, 175 (1971) doi: 10.1086/151073
[4]	Y. B. Zeldovich, Mon. Not. Roy. Astron. Soc. 160, 1P (1972) doi: 10.1093/mnras/160.1.1P
[5]	N. Caderni and R. Fabbri, Phys. Lett. B 69, 508 (1977) doi: 10.1016/0370-2693(77)90856-5
[6]	M. Morikawa and M. Sasaki, Prog. Theor. Phys. 72, 782 (1984) doi: 10.1143/PTP.72.782
[7]	T. Banks, arXiv: hep-th/0701146
[8]	E. W. Kolb and M. S. Turner, Front. Phys. 69, 1 (1990)
[9]	P. H. Frampton and T. W. Kephart, JCAP 06, 008 (2008) doi: 10.1088/1475-7516/2008/06/008
[10]	P. H. Frampton, S. D. H. Hsu, D. Reeb et al., Class. Quant. Grav. 26, 145005 (2009) doi: 10.1088/0264-9381/26/14/145005
[11]	P. H. Frampton, JCAP 10, 016 (2009) doi: 10.1088/1475-7516/2009/10/016
[12]	C. A. Egan and C. H. Lineweaver, Astrophys. J. 710, 1825 (2010) doi: 10.1088/0004-637X/710/2/1825
[13]	W. Thomson, Proceedings of the Royal Society of Edinburgh 3, 139 (1857) doi: 10.1017/S0370164600027541
[14]	F. J. Dyson, Rev. Mod. Phys. 51, 447 (1979) doi: 10.1103/RevModPhys.51.447
[15]	F. C. Adams and G. Laughlin, Rev. Mod. Phys. 69, 337 (1997) doi: 10.1103/RevModPhys.69.337
[16]	D. Pavón and N. Radicella, Gen. Rel. Grav. 45, 63 (2013) doi: 10.1007/s10714-012-1457-x
[17]	M. Morikawa and M. Sasaki, Phys. Lett. B 165, 59 (1985) doi: 10.1016/0370-2693(85)90690-2
[18]	J. P. Mimoso and D. Pavón, Phys. Rev. D 87, 047302 (2013) doi: 10.1103/PhysRevD.87.047302
[19]	D. N. Page, Phys. Rev. D 32, 2496 (1985) doi: 10.1103/PhysRevD.32.2496
[20]	L. Baum and P. H. Frampton, Phys. Rev. Lett. 98, 071301 (2007) doi: 10.1103/PhysRevLett.98.071301
[21]	L. Baum and P. H. Frampton, Mod. Phys. Lett. A 23, 33 (2008) doi: 10.1142/S0217732308026170
[22]	G. W. Gibbons and S. W. Hawking, Phys. Rev. D 15, 2738 (1977) doi: 10.1103/PhysRevD.15.2738
[23]	P. C. W. Davies, Class. Quant. Grav. 4, L225 (1987) doi: 10.1088/0264-9381/4/6/006
[24]	A. Hosoya, T. Buchert, and M. Morita, Phys. Rev. Lett. 92, 141302 (2004) doi: 10.1103/PhysRevLett.92.141302
[25]	N. Li, T. Buchert, A. Hosoya et al., Phys. Rev. D 86, 083539 (2012) doi: 10.1103/PhysRevD.86.083539
[26]	D. Bak, Phys. Lett. B 721, 323 (2013) doi: 10.1016/j.physletb.2013.03.023
[27]	P. F. Gonzalez-Diaz, C. L. Siguenza, and J. Martin-Carrion, Phys. Rev. D 86, 027501 (2012) doi: 10.1103/PhysRevD.86.027501
[28]	Y. Nakai, N. Shiba, and M. Yamada, Phys. Rev. D 96, 123518 (2017) doi: 10.1103/PhysRevD.96.123518
[29]	L. Parker, Phys. Rev. Lett. 21, 562 (1968) doi: 10.1103/PhysRevLett.21.562
[30]	L. Parker, Phys. Rev. 183, 1057 (1969) doi: 10.1103/PhysRev.183.1057
[31]	L. Parker, Phys. Rev. Lett. 28, 705 (1972) doi: 10.1103/PhysRevLett.28.705
[32]	L. H. Ford and L. Parker, Phys. Rev. D 17, 1485 (1978) doi: 10.1103/PhysRevD.17.1485
[33]	A. Vilenkin, Phys. Lett. B 117, 25 (1982) doi: 10.1016/0370-2693(82)90866-8
[34]	A. A. Grib, Gen. Rel. Grav. 32, 621 (2000) doi: 10.1023/A:1001963001501
[35]	A. Zecca, Eur. Phys. J. Plus 127, 18 (2012) doi: 10.1140/epjp/i2012-12018-x
[36]	M. Kawasaki and T. Moroi, Prog. Theor. Phys. 93, 879 (1995) doi: 10.1143/ptp/93.5.879
[37]	R. Durrer, K. E. Kunze, and M. Sakellariadou, New Astron. Rev. 46, 659 (2002) doi: 10.1016/S1387-6473(02)00235-X
[38]	M. Kawasaki, K. Kohri, and T. Moroi, Phys. Rev. D 71, 083502 (2005) doi: 10.1103/PhysRevD.71.083502
[39]	J. de Haro and S. Pan, Class. Quant. Grav. 33, 165007 (2016) doi: 10.1088/0264-9381/33/16/165007
[40]	M. Novello and S. E. P. Bergliaffa, Phys. Rept. 463, 127 (2008) doi: 10.1016/j.physrep.2008.04.006
[41]	J. Quintin, Y. F. Cai, and R. H. Brandenberger, Phys. Rev. D 90, 063507 (2014) doi: 10.1103/PhysRevD.90.063507
[42]	J. Haro and E. Elizalde, JCAP 10, 028 (2015) doi: 10.1088/1475-7516/2015/10/028
[43]	R. Brandenberger and P. Peter, Found. Phys. 47, 797 (2017) doi: 10.1007/s10701-016-0057-0
[44]	D. C. F. Celani, N. Pinto-Neto, and S. D. P. Vitenti, Phys. Rev. D 95, 023523 (2017) doi: 10.1103/PhysRevD.95.023523
[45]	H. Kodama, Prog. Theor. Phys. 67, 1415 (1982) doi: 10.1143/PTP.67.1415
[46]	B. L. Hu and H. E. Kandrup, Phys. Rev. D 35, 1776 (1987) doi: 10.1103/PhysRevD.35.1776
[47]	H. E. Kandrup, Phys. Rev. D 37, 3505 (1988) doi: 10.1103/PhysRevD.37.3505
[48]	M. O. Calvão, J. A. S. Lima, and I. Waga, Phys. Lett. A 162, 223 (1992) doi: 10.1016/0375-9601(92)90437-Q
[49]	W. Zimdahl, Phys. Rev. D 61, 083511 (2000) doi: 10.1103/PhysRevD.61.083511
[50]	I. Prigogine and J. Geheniau, Proc. Nati. Acad. Sci. USA. 83, 6245 (1986) doi: 10.1073/pnas.83.17.6245
[51]	I. Prigogine, J. Geheniau, E. Gunzig, and P. Nardone, Proc. Nati. Acad. Sci. USA. 85, 7428 (1988) doi: 10.1073/pnas.85.20.7428
[52]	I. Prigogine, J. Geheniau, E. Gunzig, and P. Nardone, Gen. Rel. Grav. 21, 767 (1989) doi: 10.1007/BF00758981
[53]	G. W. Horndeski, Int. J. Theor. Phys. 10, 363 (1974) doi: 10.1007/BF01807638
[54]	H. Yu, W. D. Guo, K. Yang et al., Phys. Rev. D 97, 083524 (2018) doi: 10.1103/PhysRevD.97.083524
[55]	J. Solà, J. Phys. Conf. Ser. 453, 012015 (2013) doi: 10.1088/1742-6596/453/1/012015
[56]	J. Solà, AIP Conf. Proc. 1606, 19 (2014) doi: 10.1063/1.4891113
[57]	J. Solà and H. Yu, Gen. Rel. Grav. 52, 17 (2020) doi: 10.1007/s10714-020-2657-4
[58]	A. B. Balakin and J. P. S. Lemos, Class. Quant. Grav. 22, 1867 (2005) doi: 10.1088/0264-9381/22/9/024
[59]	T. Harko, Phys. Lett. B 669, 376 (2008) doi: 10.1016/j.physletb.2008.10.007
[60]	T. Harko and F. S. N. Lobo, Eur. Phys. J. C 70, 373 (2010) doi: 10.1140/epjc/s10052-010-1467-3
[61]	T. Harko, F. S. N. Lobo, S. Nojiri et al., Phys. Rev. D 84, 024020 (2011) doi: 10.1103/PhysRevD.84.024020
[62]	T. Harko, Phys. Rev. D 90, 044067 (2014) doi: 10.1103/PhysRevD.90.044067
[63]	T. Harko, F. S. N. Lobo, J. P. Mimoso et al., Eur. Phys. J. C 75, 386 (2015) doi: 10.1140/epjc/s10052-015-3620-5
[64]	R. C. Nunes, Gen. Rel. Grav. 48, 107 (2016) doi: 10.1007/s10714-016-2104-8
[65]	M. P. L. P. Ramos and J. Páramos, Phys. Rev. D 96, 104024 (2017) doi: 10.1103/PhysRevD.96.104024
[66]	R. I. Ivanov and E. M. Prodanov, Eur. Phys. J. C 79, 973 (2019) doi: 10.1140/epjc/s10052-019-7475-z
[67]	L. H. Ford, Phys. Rev. D 35, 2955 (1987) doi: 10.1103/PhysRevD.35.2955
[68]	J. H. Traschen and R. H. Brandenberger, Phys. Rev. D 42, 2491 (1990) doi: 10.1103/PhysRevD.42.2491
[69]	R. C. Nunes and D. Pavón, Phys. Rev. D 91, 063526 (2015) doi: 10.1103/PhysRevD.91.063526
[70]	S. Pan, B. K. Pal, and S. Pramanik, Int. J. Geom. Meth. Mod. Phys. 15(3), 1850042 (2018) doi: 10.1142/S0219887818500421
[71]	R. C. Nunes and S. Pan, Mon. Not. Roy. Astron. Soc. 459, 673 (2016) doi: 10.1093/mnras/stw566
[72]	L. R. W. Abramo and J. A. S. Lima, Class. Quant. Grav. 13, 2953 (1996) doi: 10.1088/0264-9381/13/11/011
[73]	R. Baierlein, American Journal of Physics. 69, 423 (2001) doi: 10.1119/1.1336839
[74]	F. Herrmann and P. Würfel, American Journal of Physics. 73, 717 (2005) doi: 10.1119/1.1904623
[75]	H. S. Leff, American Journal of Physics. 70, 792 (2002) doi: 10.1119/1.1479743
[76]	G. Bertone, D. Hooper, and J. Silk, Phys. Rept. 405, 279 (2005) doi: 10.1016/j.physrep.2004.08.031
[77]	F. Rahaman, K. K. Nandi, A. Bhadra et al., Phys. Lett. B 694, 10 (2010) doi: 10.1016/j.physletb.2010.09.038
[78]	J. A. S. Lima, S. R. G. Trevisani, and R. C. Santos, Phys. Lett. B 820, 136575 (2021) doi: 10.1016/j.physletb.2021.136575

References

[1]	R. C. Tolman, Phys. Rev. 37, 1639 (1931) doi: 10.1103/PhysRev.37.1639
[2]	R. C. Tolman, Relativity, Thermodynamics and Cosmology, (Oxford University Press, 1934) [reprinted by Dover, New York (1987)]
[3]	S. Weinberg, Astrophys. J. 168, 175 (1971) doi: 10.1086/151073
[4]	Y. B. Zeldovich, Mon. Not. Roy. Astron. Soc. 160, 1P (1972) doi: 10.1093/mnras/160.1.1P
[5]	N. Caderni and R. Fabbri, Phys. Lett. B 69, 508 (1977) doi: 10.1016/0370-2693(77)90856-5
[6]	M. Morikawa and M. Sasaki, Prog. Theor. Phys. 72, 782 (1984) doi: 10.1143/PTP.72.782
[7]	T. Banks, arXiv: hep-th/0701146
[8]	E. W. Kolb and M. S. Turner, Front. Phys. 69, 1 (1990)
[9]	P. H. Frampton and T. W. Kephart, JCAP 06, 008 (2008) doi: 10.1088/1475-7516/2008/06/008
[10]	P. H. Frampton, S. D. H. Hsu, D. Reeb et al., Class. Quant. Grav. 26, 145005 (2009) doi: 10.1088/0264-9381/26/14/145005
[11]	P. H. Frampton, JCAP 10, 016 (2009) doi: 10.1088/1475-7516/2009/10/016
[12]	C. A. Egan and C. H. Lineweaver, Astrophys. J. 710, 1825 (2010) doi: 10.1088/0004-637X/710/2/1825
[13]	W. Thomson, Proceedings of the Royal Society of Edinburgh 3, 139 (1857) doi: 10.1017/S0370164600027541
[14]	F. J. Dyson, Rev. Mod. Phys. 51, 447 (1979) doi: 10.1103/RevModPhys.51.447
[15]	F. C. Adams and G. Laughlin, Rev. Mod. Phys. 69, 337 (1997) doi: 10.1103/RevModPhys.69.337
[16]	D. Pavón and N. Radicella, Gen. Rel. Grav. 45, 63 (2013) doi: 10.1007/s10714-012-1457-x
[17]	M. Morikawa and M. Sasaki, Phys. Lett. B 165, 59 (1985) doi: 10.1016/0370-2693(85)90690-2
[18]	J. P. Mimoso and D. Pavón, Phys. Rev. D 87, 047302 (2013) doi: 10.1103/PhysRevD.87.047302
[19]	D. N. Page, Phys. Rev. D 32, 2496 (1985) doi: 10.1103/PhysRevD.32.2496
[20]	L. Baum and P. H. Frampton, Phys. Rev. Lett. 98, 071301 (2007) doi: 10.1103/PhysRevLett.98.071301
[21]	L. Baum and P. H. Frampton, Mod. Phys. Lett. A 23, 33 (2008) doi: 10.1142/S0217732308026170
[22]	G. W. Gibbons and S. W. Hawking, Phys. Rev. D 15, 2738 (1977) doi: 10.1103/PhysRevD.15.2738
[23]	P. C. W. Davies, Class. Quant. Grav. 4, L225 (1987) doi: 10.1088/0264-9381/4/6/006
[24]	A. Hosoya, T. Buchert, and M. Morita, Phys. Rev. Lett. 92, 141302 (2004) doi: 10.1103/PhysRevLett.92.141302
[25]	N. Li, T. Buchert, A. Hosoya et al., Phys. Rev. D 86, 083539 (2012) doi: 10.1103/PhysRevD.86.083539
[26]	D. Bak, Phys. Lett. B 721, 323 (2013) doi: 10.1016/j.physletb.2013.03.023
[27]	P. F. Gonzalez-Diaz, C. L. Siguenza, and J. Martin-Carrion, Phys. Rev. D 86, 027501 (2012) doi: 10.1103/PhysRevD.86.027501
[28]	Y. Nakai, N. Shiba, and M. Yamada, Phys. Rev. D 96, 123518 (2017) doi: 10.1103/PhysRevD.96.123518
[29]	L. Parker, Phys. Rev. Lett. 21, 562 (1968) doi: 10.1103/PhysRevLett.21.562
[30]	L. Parker, Phys. Rev. 183, 1057 (1969) doi: 10.1103/PhysRev.183.1057
[31]	L. Parker, Phys. Rev. Lett. 28, 705 (1972) doi: 10.1103/PhysRevLett.28.705
[32]	L. H. Ford and L. Parker, Phys. Rev. D 17, 1485 (1978) doi: 10.1103/PhysRevD.17.1485
[33]	A. Vilenkin, Phys. Lett. B 117, 25 (1982) doi: 10.1016/0370-2693(82)90866-8
[34]	A. A. Grib, Gen. Rel. Grav. 32, 621 (2000) doi: 10.1023/A:1001963001501
[35]	A. Zecca, Eur. Phys. J. Plus 127, 18 (2012) doi: 10.1140/epjp/i2012-12018-x
[36]	M. Kawasaki and T. Moroi, Prog. Theor. Phys. 93, 879 (1995) doi: 10.1143/ptp/93.5.879
[37]	R. Durrer, K. E. Kunze, and M. Sakellariadou, New Astron. Rev. 46, 659 (2002) doi: 10.1016/S1387-6473(02)00235-X
[38]	M. Kawasaki, K. Kohri, and T. Moroi, Phys. Rev. D 71, 083502 (2005) doi: 10.1103/PhysRevD.71.083502
[39]	J. de Haro and S. Pan, Class. Quant. Grav. 33, 165007 (2016) doi: 10.1088/0264-9381/33/16/165007
[40]	M. Novello and S. E. P. Bergliaffa, Phys. Rept. 463, 127 (2008) doi: 10.1016/j.physrep.2008.04.006
[41]	J. Quintin, Y. F. Cai, and R. H. Brandenberger, Phys. Rev. D 90, 063507 (2014) doi: 10.1103/PhysRevD.90.063507
[42]	J. Haro and E. Elizalde, JCAP 10, 028 (2015) doi: 10.1088/1475-7516/2015/10/028
[43]	R. Brandenberger and P. Peter, Found. Phys. 47, 797 (2017) doi: 10.1007/s10701-016-0057-0
[44]	D. C. F. Celani, N. Pinto-Neto, and S. D. P. Vitenti, Phys. Rev. D 95, 023523 (2017) doi: 10.1103/PhysRevD.95.023523
[45]	H. Kodama, Prog. Theor. Phys. 67, 1415 (1982) doi: 10.1143/PTP.67.1415
[46]	B. L. Hu and H. E. Kandrup, Phys. Rev. D 35, 1776 (1987) doi: 10.1103/PhysRevD.35.1776
[47]	H. E. Kandrup, Phys. Rev. D 37, 3505 (1988) doi: 10.1103/PhysRevD.37.3505
[48]	M. O. Calvão, J. A. S. Lima, and I. Waga, Phys. Lett. A 162, 223 (1992) doi: 10.1016/0375-9601(92)90437-Q
[49]	W. Zimdahl, Phys. Rev. D 61, 083511 (2000) doi: 10.1103/PhysRevD.61.083511
[50]	I. Prigogine and J. Geheniau, Proc. Nati. Acad. Sci. USA. 83, 6245 (1986) doi: 10.1073/pnas.83.17.6245
[51]	I. Prigogine, J. Geheniau, E. Gunzig, and P. Nardone, Proc. Nati. Acad. Sci. USA. 85, 7428 (1988) doi: 10.1073/pnas.85.20.7428
[52]	I. Prigogine, J. Geheniau, E. Gunzig, and P. Nardone, Gen. Rel. Grav. 21, 767 (1989) doi: 10.1007/BF00758981
[53]	G. W. Horndeski, Int. J. Theor. Phys. 10, 363 (1974) doi: 10.1007/BF01807638
[54]	H. Yu, W. D. Guo, K. Yang et al., Phys. Rev. D 97, 083524 (2018) doi: 10.1103/PhysRevD.97.083524
[55]	J. Solà, J. Phys. Conf. Ser. 453, 012015 (2013) doi: 10.1088/1742-6596/453/1/012015
[56]	J. Solà, AIP Conf. Proc. 1606, 19 (2014) doi: 10.1063/1.4891113
[57]	J. Solà and H. Yu, Gen. Rel. Grav. 52, 17 (2020) doi: 10.1007/s10714-020-2657-4
[58]	A. B. Balakin and J. P. S. Lemos, Class. Quant. Grav. 22, 1867 (2005) doi: 10.1088/0264-9381/22/9/024
[59]	T. Harko, Phys. Lett. B 669, 376 (2008) doi: 10.1016/j.physletb.2008.10.007
[60]	T. Harko and F. S. N. Lobo, Eur. Phys. J. C 70, 373 (2010) doi: 10.1140/epjc/s10052-010-1467-3
[61]	T. Harko, F. S. N. Lobo, S. Nojiri et al., Phys. Rev. D 84, 024020 (2011) doi: 10.1103/PhysRevD.84.024020
[62]	T. Harko, Phys. Rev. D 90, 044067 (2014) doi: 10.1103/PhysRevD.90.044067
[63]	T. Harko, F. S. N. Lobo, J. P. Mimoso et al., Eur. Phys. J. C 75, 386 (2015) doi: 10.1140/epjc/s10052-015-3620-5
[64]	R. C. Nunes, Gen. Rel. Grav. 48, 107 (2016) doi: 10.1007/s10714-016-2104-8
[65]	M. P. L. P. Ramos and J. Páramos, Phys. Rev. D 96, 104024 (2017) doi: 10.1103/PhysRevD.96.104024
[66]	R. I. Ivanov and E. M. Prodanov, Eur. Phys. J. C 79, 973 (2019) doi: 10.1140/epjc/s10052-019-7475-z
[67]	L. H. Ford, Phys. Rev. D 35, 2955 (1987) doi: 10.1103/PhysRevD.35.2955
[68]	J. H. Traschen and R. H. Brandenberger, Phys. Rev. D 42, 2491 (1990) doi: 10.1103/PhysRevD.42.2491
[69]	R. C. Nunes and D. Pavón, Phys. Rev. D 91, 063526 (2015) doi: 10.1103/PhysRevD.91.063526
[70]	S. Pan, B. K. Pal, and S. Pramanik, Int. J. Geom. Meth. Mod. Phys. 15(3), 1850042 (2018) doi: 10.1142/S0219887818500421
[71]	R. C. Nunes and S. Pan, Mon. Not. Roy. Astron. Soc. 459, 673 (2016) doi: 10.1093/mnras/stw566
[72]	L. R. W. Abramo and J. A. S. Lima, Class. Quant. Grav. 13, 2953 (1996) doi: 10.1088/0264-9381/13/11/011
[73]	R. Baierlein, American Journal of Physics. 69, 423 (2001) doi: 10.1119/1.1336839
[74]	F. Herrmann and P. Würfel, American Journal of Physics. 73, 717 (2005) doi: 10.1119/1.1904623
[75]	H. S. Leff, American Journal of Physics. 70, 792 (2002) doi: 10.1119/1.1479743
[76]	G. Bertone, D. Hooper, and J. Silk, Phys. Rept. 405, 279 (2005) doi: 10.1016/j.physrep.2004.08.031
[77]	F. Rahaman, K. K. Nandi, A. Bhadra et al., Phys. Lett. B 694, 10 (2010) doi: 10.1016/j.physletb.2010.09.038
[78]	J. A. S. Lima, S. R. G. Trevisani, and R. C. Santos, Phys. Lett. B 820, 136575 (2021) doi: 10.1016/j.physletb.2021.136575

[1]	Sergei P. Maydanyuk , Ju-Jun Xie , Kostiantyn A. Shaulskyi . Bremsstrahlung emission from nucleon-nucleus reactions in dense medium of compact stars. Chinese Physics C, 2025, 49(4): 044105. doi: 10.1088/1674-1137/ada377
[2]	Shi-Qian Hu , Bo Liu , Xiao-Mei Kuang , Rui-Hong Yue . Revisiting black hole thermodynamics in massive gravity: charged particle absorption and infalling shell of dust. Chinese Physics C, 2020, 44(10): 105107. doi: 10.1088/1674-1137/abab8a
[3]	Hai-Nan Lin , Xin Li , Yu Sang . Local probes strongly favor ∧CDM against power-law and R_h=ct universe. Chinese Physics C, 2018, 42(9): 095101. doi: 10.1088/1674-1137/42/9/095101
[4]	Xin Wang , Jun-Li Li , Zhen Wu , Rui Qiu , Chun-Yan Li , Man-Chun Liang , Hui Zhang , Zhi Gang , Hong Xu . Improved algorithms and coupled neutron-photon transport for auto-importance sampling method. Chinese Physics C, 2017, 41(1): 014103. doi: 10.1088/1674-1137/41/1/014103
[5]	Gang Xu , Yi Jiao , Yue-Mei Peng . ESRF-type lattice design and optimization for the High Energy Photon Source. Chinese Physics C, 2016, 40(2): 027001. doi: 10.1088/1674-1137/40/2/027001
[6]	Ming Chen , Yong-Chang Huang . Thermodynamic surface system of static black holes and area law. Chinese Physics C, 2016, 40(11): 113101. doi: 10.1088/1674-1137/40/11/113101
[7]	Zaki Dizaji . Energy response improvement for photon dosimetry using pulse analysis. Chinese Physics C, 2016, 40(2): 026203. doi: 10.1088/1674-1137/40/2/026203
[8]	ZHANG Xu-Ning . Hyperbolic Cardassian universe. Chinese Physics C, 2014, 38(7): 075102. doi: 10.1088/1674-1137/38/7/075102
[9]	XU Gang , JIAO Yi . Towards the ultimate storage ring: The lattice design forBeijing Advanced Photon Source. Chinese Physics C, 2013, 37(5): 057003. doi: 10.1088/1674-1137/37/5/057003
[10]	YAN Qiu-Rong , ZHAO Bao-Sheng , LIU Yong-An , YANG Hao , SHENG Li-Zhi , WEI Yong-Lin . Two-dimensional photon counting imaging detector based on a Vernier position sensitive anode readout. Chinese Physics C, 2011, 35(4): 368-373. doi: 10.1088/1674-1137/35/4/009
[11]	FU Yong-Ping , LI Yun-De . Large transverse momentum dilepton production in heavy ion collisions with two-photon processes. Chinese Physics C, 2011, 35(2): 109-112. doi: 10.1088/1674-1137/35/2/001
[12]	SU Nan , Jens O , Michael Strickland . Hard-thermal-loop QED thermodynamics. Chinese Physics C, 2010, 34(9): 1527-1529. doi: 10.1088/1674-1137/34/9/091
[13]	MAO Ya-Xian , Yves Schutz , ZHOU Dai-Cui , Christophe Furget , Gustavo Conesa Balbastre . QGP tomography with photon tagged jets in ALICE. Chinese Physics C, 2010, 34(9): 1491-1493. doi: 10.1088/1674-1137/34/9/081
[14]	BIAN Jian-Ming , HE Kang-Lin , LI Wei-Guo , HU Tao , FU Cheng-Dong , HUANG Bin , LIU Ying , NING Fei-Peng , SONG Wen-Bo , SUN Sheng-Sen , XU Min , YAN Jie , YAN Liang , . Absolute photon energy calibration for the BESⅢ EMC. Chinese Physics C, 2010, 34(1): 72-77. doi: 10.1088/1674-1137/34/1/013
[15]	H. Nakazawa . Two-photon processes at Belle. Chinese Physics C, 2010, 34(6): 801-806. doi: 10.1088/1674-1137/34/6/031
[16]	ZHOU Jing , LIU Zhi-Yi , MENG Qiu-Ying , ZHOU Shu-Hua . Photon discrimination simulation with the PCA method. Chinese Physics C, 2010, 34(10): 1632-1635. doi: 10.1088/1674-1137/34/10/015
[17]	ZHOU Li-Juan , ZHANG Ben-Wei , ZHANG Han-Zhong , WANG En-Ke . Jet-photon conversion with energy loss in heavy ion collisions. Chinese Physics C, 2009, 33(3): 201-204. doi: 10.1088/1674-1137/33/3/008
[18]	Andreas Thomas , for the , oa MAMI , and A . Recent result from the A2 real photon facility at MAMI. Chinese Physics C, 2009, 33(12): 1120-1126. doi: 10.1088/1674-1137/33/12/012
[19]	MAO Ya-Xian , ZHOU Dai-Cui , XU Chun-Cheng , YIN Zhong-Bao . Study of the photon identification efficiency with ALICE photon spectrometer. Chinese Physics C, 2008, 32(7): 543-547. doi: 10.1088/1674-1137/32/7/006
[20]	Han Jiaxiang , Xu Zizong , Chen Hongfang , Li Cheng , Zeng Hui . Single Photon Time Spectra in Gas Avalanches. Chinese Physics C, 1996, 20(S4): 319-323.

Access

Figures(3)

Get Citation

Hao Yu, Yu-Xiao Liu and Jin Li. Entropies of the various components of the universe[J]. Chinese Physics C. doi: 10.1088/1674-1137/acc2ad

Hao Yu, Yu-Xiao Liu and Jin Li. Entropies of the various components of the universe[J]. Chinese Physics C. doi: 10.1088/1674-1137/acc2ad shu

RIS(for EndNote,Reference Manager,ProCite)

BibTex

Txt

Milestone

Received: 2022-12-23

Article Metric

Article Views(1569)
PDF Downloads(17)
Cited by(0)

Policy on re-use

To reuse of subscription content published by CPC, the users need to request permission from CPC, unless the content was published under an Open Access license which automatically permits that type of reuse.

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

HTML

I. INTRODUCTION

Since it was found that the universe is expanding, the entropy problem and heat death of the universe have been intriguing topics about the past, present, and future entropies of the universe [1, 2]. The entropy problem includes two aspects involving the past and present entropies of the universe. Although physicists have predicted that the entropy production mechanism in the early universe may be associated with vacuum energy, Higgs particles, and the shear and bulk viscosities of the cosmological fluid [3–6], they have not explained satisfactorily why the initial state of the universe possesses low entropy. This question about the past entropy of the universe is also known as the Boltzmann-Penrose question (see [7] and references therein). For the present entropy of the universe, the problem boils down to why the value of the entropy is enormous, which is closely related to the horizon problem [8]. In 2008, Frampton et al. calculated the total entropy of the supermassive black holes inside the observable universe and found that it is the largest contributor to the entropy of the universe [9–11]. On the basis of the work of Frampton et al., the following year, Egan and Lineweaver took into account the latest measurements of the supermassive black hole mass function at the time and found that the total entropy of the supermassive black holes inside the observable universe is approximately $3.1^{+3.0}_{-1.7}\times10^{104}\,k$ [12], which is an unimaginably enormous number. As for cosmic heat death, it presents a gloomy prediction of the future entropy and the fate of the universe [13–15]. Research on the cosmic entropy shows that the entropy of an expanding universe generally satisfies the second law of thermodynamics [16–18]. Therefore, with the expansion of the universe, all life will eventually disappear, and the universe will be in a state of chaos and disorder. In order to avoid cosmic heat death, researchers proposed the cyclic model of the universe, in which the law of entropy increase may be inapplicable [19–21].

Thus far, the cosmic entropy has been generalized widely on the basis of classical thermodynamics, which contains horizon entropy [22, 23], information entropy [24, 25], entanglement entropy [26–28], etc. Moreover, there are studies focusing on the entropy of the universe in the presence of particle production (annihilation) and interaction (i.e., energy conversion). In general, particle production necessarily comes with interaction, but interaction does not necessarily lead to the phenomenon of particle production. The common feature of these two kinds of processes is that they can influence the thermodynamic properties of the universe. Therefore, it is important to study the entropy changes of these processes in cosmology.

The early pioneering works of Parker on particle production provided a microscopic mechanism of particle production in the context of cosmology [29–31], which laid the theoretical foundation for subsequent research on the entropy of the universe in the presence of particle production. From the perspective of quantum cosmology, particle production could be related to the origin of the universe [32–35]; thus, it may influence the low-entropy state of the early universe. On this issue, the Big Bang theory [36–39] and Big Bounce theory [40–44] already have multiple mechanisms to create the particles and entropy of the early universe. On the other hand, cosmological particle production can affect the entropy evolution of each component of the universe [22, 45–49]. In Refs. [50–52], the authors proposed using the second law of thermodynamics to constrain particle production in cosmology. In recent years, research on the entropy evolution in cosmology has shown that by using the thermodynamic constraints on the entropy, one can effectively restrain the gravitational theories in which there exists particle production. For example, considering scalar particle production in Horndeski's theory [53], the coupling coefficients between the scalar field and geometric quantities can be constrained with the second law of thermodynamics and thermodynamic equilibrium [54]. Similarly, if there exists particle production in running vacuum models [55, 56], the change rate of the running vacuum can be constrained by studying the entropy evolution of matter [57].

For most gravitational theories (such as non-minimal coupling theories [58–61]), if a matter field interacts with other fields (i.e., there is a non-minimal coupling between them), the energy-momentum tensor of the matter field is usually not conserved, unless one redefines the form of the energy-momentum tensor. The non-conservation of the energy-momentum tensor of the matter field, by analogy with the non-conservation of the particle number in an open thermodynamic system, can be explained as irreversible particle production [54, 62–65]. In this case, for these gravitational theories, the research on the entropy evolution of matter in cosmology is similar to the research on the entropy evolution of cosmological particle production [54, 57]. However, when the matter field interacts with other fields without particle production, how can we study the entropy evolution of matter in cosmology? We discuss this issue in the present work.

In addition, by investigating the statistical entropy of matter in a freely expanding universe, we will prove that the specific entropy of matter (except for photons) indeed evolves with the expansion of the universe [48, 66], whereas it is assumed to be a constant in some literature [52, 54, 63]. It is worth mentioning that it is an extremely special case that the specific entropy of matter in the universe remains unchanged. In classical thermodynamics, if the specific entropy of an isolated system (with a strictly conserved particle number) is a constant, it must be in thermal equilibrium (i.e., the total entropy is a constant). However, for an evolving isolated system (such as our expanding universe), the total entropy is increasing owing to the second law of thermodynamics. Thus, if the specific entropy of our expanding universe is a constant, there must exist particle production, and it needs to meet some extremely special conditions. In view of this, it is more reasonable to consider that the specific entropy of matter in the universe can evolve over time. Taking ideal gas-like dust (baryonic matter) as the main object of study, we will analyze the difference between the entropy changes in the cases with and without particle production.

The remainder of this paper is organized as follows. Sec. II is devoted to the review of some basic thermodynamic formulas related to cosmological particle production (annihilation). In Sec. III, we discuss the entropy and specific entropy of each component of the universe when they expand freely. We focus on photons, ideal gas-like dust (baryonic matter), and a special kind of dark energy. In Sec. IV, we describe the entropies and specific entropies of these components when they interact with the space-time background. The last part, Sec. V, is a summary of our research.

II. THERMODYNAMICS OF COSMOLOGICAL PARTICLE PRODUCTION (ANNIHILATION)

III. (SPECIFIC) ENTROPY OF MATTER IN ABSENCE OF INTERACTION

IV. (SPECIFIC) ENTROPY OF MATTER IN PRESENCE OF INTERACTION

V. CONCLUSIONS

We reviewed the thermodynamics of cosmological particle production (annihilation). Combining classical statistics and cosmology, we studied the entropies of photons, ideal gas-like dust (baryonic matter), and dark energy in the context of the universe.

When these components of the universe are regarded as ideal fluids expanding freely, we can calculate their entropies and specific entropies separately. For photons, the entropy and specific entropy inside the co-moving volume are both constants (see Eqs. (19) and (21)). For dust (baryonic matter), we supposed that its thermodynamic properties are similar to those of an ideal gas; thus, it is called ideal gas-like dust (baryonic matter). It was found that both the entropy and the specific entropy of ideal gas-like dust increase with the expansion of the universe (see Eqs. (25) and (27)). Therefore, the entropy of ideal gas-like dust satisfies the second law of thermodynamics. For dark energy, because we do not know whether the number of dark energy particles is conserved, we assumed that the number of dark energy particles inside the co-moving volume evolves with the expansion of the universe (i.e., particle production occurs even if dark energy expands freely). Supposing that they possess the statistical law of an ideal monatomic gas, we found that if the free expansion of such special dark energy satisfies Eq. (35), the entropy of dark energy obeys the second law of thermodynamics.

It is worth noting that the assumption that dust is similar to an ideal gas is based on the properties and distribution of dust in the universe. Generally, the ideal gas has two characteristics: the volume of a single particle can be approximated to 0, and there is no interaction between particles (i.e., potential energy). Because the number density of dust particles in the universe is small enough, we can ignore the volume of a single dust particle. Moreover, the interaction between dust particles cannot be ignored only in the early universe. Therefore, it is feasible to treat dust as an ideal gas in this work. On the other hand, we assume that dark energy particles satisfy the classical statistical mechanics, which is mainly based on two aspects. First, dark energy may be a macro effect resulting from the known particles that satisfy the classical statistical mechanics, rather than the real vacuum energy. As long as such particles are generated continually in the universe, there will be a negative pressure in the Friedmann equations, which can be used to explain the accelerating expansion of the universe [49, 52, 67–72]. In this work, we focus on such special "dark energy particles"; thus, the property of the non-conserved particle number is necessary for dark energy. Second, if dark energy is composed of unknown particles and we do not know what statistical mechanics it satisfies, it is convenient to assume that it satisfies classical statistical mechanics, to simplify calculations. Dark energy satisfying quantum statistics is worthy of future detailed study.

When these components of the universe interact with the space-time background, their entropies and specific entropies are influenced by the interaction. For photons, if they absorb (lose) energy, the entropy inside the co-moving volume will increase (decrease) with the expansion of the universe. However, the specific entropy of photons is still a constant, which is independent of the interaction. For ideal gas-like dust, if it absorbs (loses) energy, there are two possible extreme outcomes. One is that the particle number inside the co-moving volume increases (decreases) and the energy per particle remains unchanged. The other is that the energy per particle increases (decreases) and the particle number inside the co-moving volume is conserved. We calculated the entropy and specific entropy of ideal gas-like dust in the two cases, respectively. By analyzing the relationship between the entropy and the parameters, we obtained the conditions for the entropy satisfying the second law of thermodynamics in different situations. When there exists particle production, the evolution of the specific entropy of ideal gas-like dust depends on the change in the particle number density. When there exists no particle production, the evolution of the specific entropy of ideal gas-like dust is consistent with the entropy. By comparing the entropy changes of ideal gas-like dust in the two cases, we found that the two kinds of entropy changes cannot be identical. The difference between the two kinds of entropy changes mainly depends on two aspects: the sign of the energy conversion and the change rate of $m\,T$ with the energy conversion. Finally, we analyzed the conditions for the entropy of dark energy continuously increasing in different situations when there exists interaction between dark energy and the space-time background.

The entropy of each component of the universe is closely related to the evolution of the universe. Studying the entropy of the universe is important for understanding the fate of the universe. For the realistic universe, both particle production and interaction between different substances are common phenomena. In this study, when we investigated the interaction between matter and the space-time background, we did not consider the microscopic process or the entropy of the space-time background, which is the practice followed in most literature [54, 57, 62–65]. Evidently, if the entropies of two interacting substances can be taken into account simultaneously, more convincing results can be obtained, which is a topic that we can study in the future.

Reference (78)

Entropies of the various components of the universe

Abstract：

Figure 1

1 In the presence of particle production

Figure 2

Figure 3

2 In the absence of particle production

3 Comparison

References

References

Access

Article Metrics

Metrics

通讯作者: 陈斌, bchen63@163.com

Email This Article

Entropies of the various components of the universe

Corresponding author: Jin Li, cqujinli1983@cqu.edu.cn

HTML

A. Photons

B. Ideal gas-like dust (baryonic matter)

C. Dark energy

A. Photons

B. Ideal gas-like dust (baryonic matter)

1. In the presence of particle production

2. In the absence of particle production

3. Comparison

C. Dark energy

目录