-
Since 2012, semileptonic decay
$ B\to D\ell\bar{\nu}_\ell $ has been considered as one of the processes most likely to prove the existence of new physics beyond the standard model (SM). The reason is well known, that is, the significant difference between the experimental measurements of the ratio$ {\cal{R}}(D) $ and the theoretical predictions of the SM. The latest statistics published on the Heavy Flavor Average Group website [1] indicate that the experimental average value of$ {\cal{R}}(D) $ is$ {\cal{R}}^{\rm exp.}(D) = 0.339 \pm 0.026 \pm 0.014 $ , whereas the average value of SM predictions is${\cal{R}}^{\rm the.}(D) = 0.300 \pm 0.008$ [2]. The former comes from the experimental measurements for semileptonic decay$ B\to D\ell\bar{\nu}_\ell $ performed by BaBar Collaboration in 2012 [3] and 2013 [4] and by Belle Collaboration in 2015 [5] and 2019 [6]. The latter was obtained by combining two lattice calculations performed by MILC Collaboration [7] and HPQCD Collaboration [8]. The authors of Ref. [9] fit experimental and lattice results for$ B\to D\ell\bar{\nu}_\ell $ to obtain${\cal{R}}(D) = 0.299 \pm 0.003$ . Within the framework of the Heavy-Quark Expansion, Ref. [10] obtained${\cal{R}}(D) = 0.297 \pm 0.003$ . By fitting the experimental data, lattice QCD, and QCD sum rule (SR) results for$ \bar{B}\to D\ell\bar{\nu}_\ell $ , Ref. [11] predicted$ {\cal{R}}(D) = 0.299 \pm 0.003 $ . Along with the experimental data, Ref. [12] used the lattice predictions [7, 8] for the form factors of$ B\to D\ell\bar{\nu}_\ell $ as inputs, the prediction for$ {\cal{R}}(D) $ with the Caprini-Lellouch-Neubert parameterization [13] of the form factors is given by${\cal{R}}(D) = 0.302 \pm 0.003$ , while using Boyd-Grinstein-Lebed parameterization [14], the authors obtain${\cal{R}}(D) = 0.299 \pm 0.004$ . Earlier, according to the heavy quark effective theory (HQET), Refs. [15, 16] predicted$ {\cal{R}}(D) = 0.302 \pm 0.015 $ . By using a light-cone sum rule (LCSR) approach with B-meson distribution amplitudes (DAs) in HQET, Ref. [17] obtained${\cal{R}}(D) = 0.305^{+0.022}_{-0.025}$ in 2017. According to the D-meson DAs [18, 19] obtained by QCD SRs in the framework of background field theory (BFT) [20, 21], our previous work indicated that$ {\cal{R}}(D) = 0.320^{+0.018}_{-0.021} $ [19] with LCSRs.In
$ B\to D $ semileptonic decay and other D-meson-related processes, the D-meson twist-2 DA$ \phi_{2;D}(x,\mu) $ and twist-3 DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ are usually the key input parameters and the main error sources. Among them, there are more studies on leading-twist DA$ \phi_{2;D}(x,\mu) $ ; e.g., the Kurimoto-Li-Sanda (KLS) model [22] based on the expansion of the Gegenbauer polynomials, the Li-Lü-Zou (LLZ) model [23] considering a sample harmonic-like$ k_\perp $ -dependence on the basis of the KLS model, the Gaussian-type Li-Melic (LM) model [24] employing the solution of a relativistic scalar harmonic oscillator potential for the orbital part of the wavefunction (WF), and the light-cone harmonic oscillator (LCHO) model [25, 26] based on the Brodsky-Huang-Lepage (BHL) prescription [27] have been developed. Recently, in 2019, Ref. [28] studied D-meson twist-2 DA$ \phi_{2;D}(x,\mu) $ with the light-front quark model (LFQM) by adopting the Coulomb plus exponential-type confining potential, and the values of the first six ξ-moments were obtained. We researched the D-meson twist-2 DA$ \phi_{2;D}(x,\mu) $ in 2018 [18]. We studied$ \phi_{2;D}(x,\mu) $ by combining the phenomenological LCHO model and non-perturbative QCD SRs approach. By introducing the longitudinal WF$ \varphi_{2;D}(x) $ , we improved the LCHO model of$ \phi_{2;D}(x,\mu) $ proposed in Refs. [25, 26]. The behavior of our DA is determined by the first four Gegenbauer moments. Those Gegenbauer moments were calculated with QCD SRs in the framework of BFT. Subsequently, in the same year, we used the same method to study D-meson twist-3 DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ and further studied the$ B\to D $ transition form factors (TFFs) with LCSRs and calculated$ {\cal{R}}(D) $ [19].Last year, we proposed a new scheme to study the pionic leading-twist DA
$ \phi_{2;\pi}(x,\mu) $ reported in Ref. [29]. First, we suggested a new sum rule formula for the ξ-moment of$ \phi_{2;\pi}(x,\mu) $ based on the fact that the sum rule of zeroth moment can not be normalized in entire Borel parameter region. Second, we adopted the least squares method to fit the values of the first 10 ξ-moments to determine the behavior of$ \phi_{2;\pi}(x,\mu) $ . In fact, several other approaches, such as traditional QCD sum rules [30], the Dyson-Schwinger equation [31], and lattice calculation [32, 33], can be adopted in the study of the DAs of mesons, particularly light mesons. In comparison, the scheme suggested in Ref. [29] has its own unique advantages. In this scheme, the new sum rule formula of the ξ-moment can reduce the system uncertainties caused① by the truncation of the high-dimensional condensates as well as the simple parametrization of quark-hadron daulity for continuum states, which increases the prediction accuracy of QCD SRs and the prediction ability for higher moments. The least squares method is used to fit the ξ-moments to determine the DA, which avoids the extremely unreliable high-order Gegenbauer moments and can absorb as much information about the DA carried by high-order ξ-moments as possible to clarify the behavior of the DA [34]. Recently, this scheme was used to study the kaon leading-twist DA$ \phi_{2;K}(x,\mu) $ by considering the$S U_f(3)$ symmetry breaking effect [35], the axial-vector$ a_1(1260) $ -meson longitudinal twist-2 DA [36], the scalar$ K_0^\ast(1430) $ , and$ a_0(980) $ -meson leading-twist DAs [37, 38]. Inspired by Refs. [29, 35], we revisit the D-meson twist-2, 3 DAs$ \phi_{2;D}(x,\mu) $ ,$ \phi_{3;D}^p(x,\mu) $ , and$ \phi_{3;D}^\sigma(x,\mu) $ in this study.The remainder of this paper is organized as follows. In Sec. II, we present new sum rule formulae for the ξ-moments of
$ \phi_{2;D}(x,\mu) $ ,$ \phi_{3;D}^p(x,\mu) $ , and$ \phi_{3;D}^\sigma(x,\mu) $ , and briefly describe and improve the LCHO models of these DAs. In Sec. III, we analyze the behavior of these DAs according to the new values of the ξ-moments in detail. Section IV summarizes the paper. -
As discussed in Ref. [29], the new sum rule formula for the ξ-moments is based on the fact that the sum rule of the zeroth moment cannot be normalized in entire Borel parameter region. Therefore, our discussion begins with the sum rule formulae for the ξ-moments of the D-meson twist-2 DA
$ \phi_{2;D}(x,\mu) $ obtained in Ref. [18] and the twist-3 DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ obtained in Ref. [19].By giving up the priori setting for zeroth ξ-moment normalization, Eq. (28) in Ref. [18] can be modified as
$ \begin{aligned}[b]&\left<\xi^n\right>_{2;D}\left<\xi^0\right>_{2;D} \\=& \frac{M^2 {\rm e}^{m_D^2/M^2}}{f_D^2} \left\{ \frac{1}{\pi} \frac{1}{M^2} \int^{s_D}_{m_c^2} {\rm d} s {\rm e}^{-s/M^2} {\rm Im} I_{\rm pert}(s) \right. \\&+ \hat{L}_M I_{\left<\bar{q}q\right>}(-q^2) + \hat{L}_M I_{\left<G^2\right>}(-q^2) + \hat{L}_M I_{\left<\bar{q}Gq\right>}(-q^2) \\&+ \left. \hat{L}_M I_{\left<\bar{q}q\right>^2}(-q^2) + \hat{L}_M I_{\left<G^3\right>}(-q^2) \right\}, \end{aligned} $

(1) for the nth ξ-moment
$ \left<\xi^n\right>_{2;D} $ of$ \phi_{2;D}(x,\mu) $ . Eq. (27) in Ref. [19] should be modified as$ \begin{aligned}[b]&\left<\xi^n_p\right>_{3;D}\left<\xi^0_p\right>_{3;D} \\=& \frac{M^2 {\rm e}^{m_D^2/M^2}}{(\mu_D^p)^2 f_D^2} \left\{ \frac{1}{\pi} \frac{1}{M^2} \int^{s_D}_{m_c^2} {\rm d} s {\rm e}^{-s/M^2} {\rm Im} I^p_{\rm pert}(s) \right. \\&+ \hat{L}_M I^p_{\left<\bar{q}q\right>}(-q^2) + \hat{L}_M I^p_{\left<G^2\right>}(-q^2) + \hat{L}_M I^p_{\left<\bar{q}Gq\right>}(-q^2) \\&+ \left. \hat{L}_M I^p_{\left<\bar{q}q\right>^2}(-q^2) + \hat{L}_M I^p_{\left<G^3\right>}(-q^2) \right\}, \end{aligned} $

(2) for the nth ξ-moment
$ \left<\xi^n_p\right>_{3;D} $ of$ \phi_{3;D}^p(x,\mu) $ . Eq. (28) in Ref. [19] should be modified as$ \begin{aligned}[b]&\left<\xi^n_\sigma\right>_{3;D}\left<\xi^0_p\right>_{3;D} \\=& \frac{3M^2 {\rm e}^{m_D^2/M^2}}{(n+1)\mu_D^p \mu_D^\sigma f_D^2} \frac{m_D^2}{m_D^2-m_c^2} \\&\times \left\{ \frac{1}{\pi} \frac{1}{M^2} \int^{s_D}_{m_c^2} {\rm d} s {\rm e}^{-s/M^2} {\rm Im} I^\sigma_{\rm pert}(s) + \hat{L}_M I^\sigma_{\left<\bar{q}q\right>}(-q^2) \right. \\&+ \hat{L}_M I^\sigma_{\left<G^2\right>}(-q^2) + \hat{L}_M I^\sigma_{\left<\bar{q}Gq\right>}(-q^2) + \hat{L}_M I^\sigma_{\left<\bar{q}q\right>^2}(-q^2) \\&+ \left. \hat{L}_M I^\sigma_{\left<G^3\right>}(-q^2) \right\}, \end{aligned} $

(3) for the nth ξ-moment
$ \left<\xi^n_\sigma\right>_{3;D} $ of$ \phi_{3;D}^\sigma(x,\mu) $ . In Eqs. (1), (2), and (3),$ m_D $ represents the D-meson mass,$ m_c $ represents the current charm-quark mass,$ f_D $ is the decay constant of the D-meson,$ s_D $ represents the continuum threshold, and$ \hat{L}_M $ denotes the Borel transformation operator with the Borel parameter M.$ \mu_D^p $ and$ \mu_D^\sigma $ are the normalization constants of DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ respectively. Usually,$ \mu_D^p = \mu_D^\sigma = \mu_D = m_D^2/m_c $ in the literature, in accordance with the equations of motion of on-shell quarks in the meson. However, as discussed in Refs. [39, 40], the quarks inside the bound state are not exactly on-shell. Thus,$ \mu_D^p $ and$ \mu_D^\sigma $ are taken as undetermined parameters in this study and are determined via the sum rules of the zeroth ξ-moments of DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ following the idea of Refs. [19, 39, 40]. In addition, in sum rules (1), (2), and (3), the subscript "pert" indicates the terms coming from the contribution of perturbative part in operator product expansion, and the subscripts$ \left<\bar{q}q\right> $ ,$ \left<G^2\right> $ ,$ \left<\bar{q}Gq\right> $ ,$ \left<\bar{q}q\right>^2 $ , and$ \left<G^3\right> $ indicate the terms proportional to the double-quark condensate, double-gluon condensate, quark-gluon mixing condensate, four-quark condensate, and triple-gluon condensate, respectively. For the expressions of these terms in Eqs. (1), (2) and (3), one can refer to the appendices in Refs. [18, 19]. By setting$ n = 0 $ in Eqs. (1) and (2), one can obtain the sum rules for the zeroth ξ-moments$ \left<\xi^0\right>_{2;D} $ and$ \left<\xi^0_p\right>_{3;D} $ . As the functions of the Borel parameter, the zeroth ξ-moments$ \left<\xi^0\right>_{2;D} $ in Eq. (1) and$ \left<\xi^0_p\right>_{3;D} $ in Eqs. (2) and (3) obviously cannot be normalized in entire$ M^2 $ region. Therefore, more reasonable and accurate sum rules are$\left<\xi^n\right>_{2;D} = \frac{\left<\xi^n\right>_{2;D}\left<\xi^0\right>_{2;D} \big|_{\rm From\ Eq.\; (1)}}{\sqrt{\left<\xi^0\right>^2_{2;D}} \big|_{\rm By\ taking\ {\it n}=0\ in\ Eq.\; (1)}}, $

(4) $ \left<\xi^n_p\right>_{3;D} = \frac{\left<\xi^n_p\right>_{3;D}\left<\xi^0_p\right>_{3;D} \big|_{\rm From\ Eq.\; (2)}}{\sqrt{\left<\xi^0_p\right>^2_{3;D}} \big|_{\rm By\ taking\ {\it n}=0\ in\ Eq.\; (2)}}, $

(5) and
$ \left<\xi^n_\sigma\right>_{3;D} = \frac{\left<\xi^n_\sigma\right>_{3;D}\left<\xi^0_p\right>_{3;D} \big|_{\rm From\ Eq.\; (3)}}{\sqrt{\left<\xi^0_p\right>^2_{3;D}} \big|_{\rm By\ taking\ {\it n}=0\ in\ Eq.\; (2)}}, $

(6) for
$ \left<\xi^n\right>_{2;D} $ ,$ \left<\xi^n_p\right>_{3;D} $ , and$ \left<\xi^n_\sigma\right>_{3;D} $ , respectively. -
In Refs. [18, 19], we suggested LCHO models for D-meson twist-2, 3 DAs. In this subsection, we briefly review these models and then improve them by reconstructing their longitudinal distribution functions.
The D-meson leading-twist DA
$ \phi_{2;D}(x,\mu) $ can be obtained by integrating out the transverse momentum$ {k}_\perp $ component in its WF$ \Psi_{2;D}(x, {k}_\perp) $ , i.e.,$\phi_{2;D}(x,\mu_0) = \frac{2\sqrt{6}}{f_D} \int_{\left| {k}_\perp\right|^2 \leq \mu_0^2} \frac{{\rm d}^2 {k}_\perp}{16\pi^3} \Psi_{2;D}(x, {k}_\perp).$

(7) According to the BHL description [27], the LCHO model for the D-meson leading-twist WF consists of the spin-space WF
$ \chi_{2;D}(x, {k}_\perp) $ and spatial WF$ \psi_{2;D}^R(x, {k}_\perp) $ , i.e.,$ \Psi_{2;D}(x, {k}_\perp) = \chi_{2;D}(x, {k}_\perp) \psi_{2;D}^R(x, {k}_\perp) $ . The spin-space WF is$ \chi_{2;D}(x, {k}_\perp) = \widetilde{m}/\sqrt{ {k}_\perp^2 + \widetilde{m}} $ . Here,$ \widetilde{m} = \hat{m}_c x + \hat{m}_q \bar{x} $ with the constituent charm-quark mass$ \hat{m}_c $ and light-quark mass$ \hat{m}_q $ . In this study, we set$\hat{m}_c = 1.5 ~{\rm GeV}$ and$\hat{m}_q = 0.25 ~{\rm GeV}$ [35]. As discussed in Ref. [18], we set$ \chi_{2;D} \to 1 $ approximately because$ \hat{m}_c \gg \Lambda_{\rm QCD} $ . Then, the D-meson leading-twist WF is expressed as$ \begin{aligned}[b] \Psi_{2;D}(x, {k}_\perp) =& A_{2;D} \varphi_{2;D}(x) \\ & \times \exp \left[ -\frac{1}{\beta_{2;D}^2} \left( \frac{ {k}_\perp^2 + \hat{m}_c^2}{\bar{x}} + \frac{ {k}_\perp^2 + \hat{m}_q^2}{x} \right) \right], \end{aligned} $

(8) where
$ \bar{x} = 1-x $ ,$ A_{2;D} $ is the normalization constant,$ \beta_{2;D} $ is a harmonious parameter that dominates the WF's transverse distribution, and$ \varphi_{2;D}(x,\mu) $ dominates the WF's longitudinal distribution.By substituting Eq. (8) into Eq. (7), the expression of the D-meson leading-twist DA
$ \phi_{2;D}(x,\mu_0) $ can be obtained:$ \begin{aligned}[b] \phi_{2;D}(x,\mu) =& \frac{\sqrt{6}A_{2;D}\beta_{2;D}^2}{\pi^2 f_D} x\bar{x} \varphi_{2;D}(x) \\ & \times \exp \left[ - \frac{\hat{m}_c^2x + \hat{m}_q^2\bar{x}}{8\beta_{2;D}^2 x\bar{x}} \right] \\& \times \left\{ 1 - \exp \left[ - \frac{\mu^2}{8\beta_{2;D}^2 x\bar{x}} \right] \right\}.\end{aligned} $

(9) Following the method for constructing the D-meson leading-twist DA, the LCHO models for the D-meson twist-3 DAs
$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ are expressed as follows:$ \begin{aligned}[b] \phi_{3;D}^p(x,\mu) =& \frac{\sqrt{6}A_{3;D}^p (\beta_{3;D}^p)^2}{\pi^2 f_D} x\bar{x} \varphi_{3;D}^p(x) \\ & \times \exp \left[ - \frac{\hat{m}_c^2x + \hat{m}_q^2\bar{x}}{8(\beta_{3;D}^p)^2 x\bar{x}} \right] \\ &\times \left\{ 1 - \exp \left[ - \frac{\mu^2}{8(\beta_{3;D}^p)^2 x\bar{x}} \right] \right\}, \end{aligned} $

(10) and
$ \begin{aligned}[b] \phi_{3;D}^\sigma(x,\mu) =& \frac{\sqrt{6}A_{3;D}^\sigma (\beta_{3;D}^\sigma)^2}{\pi^2 f_D} x\bar{x} \varphi_{3;D}^\sigma(x) \\ &\times \exp \left[ - \frac{\hat{m}_c^2x + \hat{m}_q^2\bar{x}}{8(\beta_{3;D}^\sigma)^2 x\bar{x}} \right] \\ &\times \left\{ 1 - \exp \left[ - \frac{\mu^2}{8(\beta_{3;D}^\sigma)^2 x\bar{x}} \right] \right\}, \end{aligned} $

(11) respectively.
For the longitudinal distribution functions
$ \varphi_{2;D}(x) $ ,$ \varphi_{3;D}^p(x) $ , and$ \varphi_{3;D}^\sigma(x) $ , we used to take the first five terms of Gegenbauer expansions for the corresponding DAs in Refs. [18, 19]. As discussed in Ref. [29, 35], higher order Gegenbauer polynomials introduce spurious oscillations [31], while the corresponding coefficients obtained by directly solving the constraints of Gegenbauer moments or ξ-moments are not reliable. We improve these three longitudinal distribution functions as follows:$\varphi_{2;D}(x) = \left[ x(1-x) \right]^{\alpha_{2;D}} \left[ 1 + \hat{B}_1^{2;D} C_1^{3/2}(2x-1) \right],$

(12) $ \varphi_{3;D}^p(x) = \left[ x(1-x) \right]^{\alpha_{3;D}^p} \left[ 1 + \hat{B}_{1,p}^{3;D} C_1^{1/2}(2x-1) \right],$

(13) $\varphi_{3;D}^\sigma(x) = \left[ x(1-x) \right]^{\alpha_{3;D}^\sigma} \left[ 1 + \hat{B}_{1,\sigma}^{3;D} C_1^{3/2}(2x-1) \right].$

(14) Considering the normalization conditions for the D-meson twist-2, 3 DAs
$ \phi_{2;D}(x,\mu) $ ,$ \phi_{3;D}^p(x,\mu) $ , and$ \phi_{3;D}^p(x,\mu) $ , that is,$ \begin{aligned}[b] \int^1_0 {\rm d} x \phi_{2;D}(x,\mu) = \int^1_0 {\rm d} x \phi_{3;D}^p(x,\mu) \end{aligned} $

$ \begin{aligned}[b] = \int^1_0 {\rm d} x \phi_{3;D}^\sigma(x,\mu) = 1, \end{aligned} $

(15) there are three undetermined parameters in the LCHO models for DAs
$ \phi_{2;D}(x,\mu) $ ,$ \phi_{3;D}^p(x,\mu) $ , and$ \phi_{3;D}^p(x,\mu) $ , respectively, which are taken as the fitting parameters to fit the first 10 ξ-moments② of corresponding DAs by adopting the least squares method in next section.It should be noted that the D-meson twist-2, 3 DAs are the universal non-perturbative parameters in essence, and non-perturbative QCD should be used to study them in principle. However, owing to the difficulty of non-perturbative QCD, in the present study, these DAs are examined by combining the phenomenological model, that is, the LCHO model, and the non-perturbative QCD SRs in the framework of BFT. Otherwise, the improvement of the LCHO model of DAs
$ \phi_{2;D}(x,\mu) $ ,$ \phi_{3;D}^p(x,\mu) $ , and$ \phi_{3;D}^p(x,\mu) $ , that is, to reconstruct their longitudinal distribution functions, is only based on mathematical considerations. The rationality of this improvement can be judged by the goodness of fit. -
To perform the numerical calculation for the ξ-moments of the D-meson twist-2, 3 DAs, we take the scale
$ \mu = M $ as usual and take$ \Lambda_{\rm QCD}^{(n_f)} \simeq $ 324, 286, 207 MeV for the numbers of quark flavors$ n_f = $ 3, 4, 5, respectively [29, 35]. For other inputs, we take [41]$ \begin{array}[b] m_{D^-} =1869.66 \pm 0.05 ~{\rm MeV}, \\ f_D = 203.7 \pm 4.7 \pm 0.6 ~{\rm MeV}, \\ \bar{m}_c(\bar{m}_c) = 1.27 \pm 0.02 ~{\rm GeV}, \\ m_d(2~{\rm GeV}) = 4.67^{+0.48}_{-0.17} ~{\rm MeV}, \end{array} $

(16) $ \begin{aligned}[b] &\left<\bar{q}q\right>(2{\rm GeV}) = \left( -2.417^{+0.227}_{-0.114} \right) \times 10^{-2} {\rm GeV}^3, \\ &\left<g_s\bar{q}\sigma TGq\right>(2{\rm GeV}) = \left( -1.934^{+0.188}_{-0.103} \right) \times 10^{-2} {\rm GeV}^5, \\ & \left<g_s\bar{q}q\right>^2(2{\rm GeV}) = \left( 2.082^{+0.734}_{-0.697} \right) \times 10^{-3} {\rm GeV}^6, \\ & \left<\alpha_sG^2\right> = 0.038 \pm 0.011 {\rm GeV}^4, \\ & \left<g_s^3fG^3\right> = 0.045 {\rm GeV}^6.\end{aligned} $

(17) The renormalization group equations of these inputs are [29]
$ \begin{aligned}[b] & m_d (\mu) = m_d (\mu_0) \left[ \frac{\alpha_s(\mu_0)}{\alpha_s(\mu)} \right]^{-4/\beta_0}, \\ &\bar{m}_c (\mu) = \bar{m}_c (\bar{m}_c) \left[ \frac{\alpha_s(\bar{m}_c)}{\alpha_s(\mu)} \right]^{-4/\beta_0}, \\ &\langle \bar{q}q\rangle (\mu) = \langle \bar{q}q\rangle (\mu_0) \left[ \frac{\alpha_s(\mu_0)}{\alpha_s(\mu)} \right]^{4/\beta_0}, \\ &\langle g_s\bar{q}\sigma TGq\rangle (\mu) = \langle g_s\bar{q}\sigma TGq\rangle (\mu_0) \left[ \frac{\alpha_s(\mu_0)}{\alpha_s(\mu)} \right]^{-2/(3\beta_0)}, \\ & \langle g_s\bar{q}q\rangle^2 (\mu) = \langle g_s\bar{q}q\rangle^2 (\mu_0) \left[ \frac{\alpha_s(\mu_0)}{\alpha_s(\mu)} \right]^{4/\beta_0}, \\ & \langle \alpha_s G^2\rangle (\mu) = \langle \alpha_s G^2\rangle (\mu_0), \\ & \langle g_s^3fG^3\rangle (\mu) = \langle g_s^3fG^3\rangle (\mu_0), \end{aligned} $

(18) with
$ \beta_0 = (33-2n_f)/3 $ . For the continuum threshold, we used to take$ s_D \simeq 6.5 {\rm GeV}^2 $ in Ref. [18, 19]. This value comes from the square of the mass of the D-meson's first exciting state, i.e.,$ D^0(2550) $ , as suggested by Refs. [43, 44]. In Refs. [29, 35], we took the continuum threshold parameters$ s_\pi $ and$ s_K $ by requiring that there are reasonable Borel windows to normalize the zeroth ξ-moments of the pion and kaon leading-twist DAs. In this study, we follow the suggestion in Refs. [29, 35] and obtain$s_D \simeq 6.0 ~{\rm GeV}^2$ . -
Thus, we can calculate the values of the ξ-moments of the D-meson twist-2, 3 DAs with the sum rules (4), (5), and (6). First, we need to determine the appropriate Borel windows for these ξ-moments by following usual criteria, such as the minimum contributions of the continuum state and dimension-six condensate and stable values of these ξ-moments in corresponding Borel windows. Table 1 presents the limits to the continuum state's contributions and the dimension-six condensate's contributions for the first 10 ξ-moments of the D-meson twist-2, 3 DAs. Here, the symbol "
$ - $ " indicates that the corresponding continuum state's contribution is smaller than 10% or the dimension-six condensate's contribution is far smaller than 5% over a wide Borel parameter region. This is reasonable because both the continuum state's contribution and the dimension-six condensate's contribution are depressed by the sum rules of the zeroth ξ-moments in the denominator of the new sum rule formulae (4), (5), and (6). Compared with the criteria presented in Tables 1 and 4 in Ref. [19], the criteria listed in Table 1 are far stricter, which reflects one of the advantages of the new sum rule formulae (4), (5), and (6); that is, they reduce the system uncertainty of the sum rule. Thus, for these ξ-moments, only the upper or lower limits of the corresponding Borel windows are clearly determined. To obtain complete Borel windows, we directly take their lengths as$ 1\; {\rm GeV}^2 $ . Figure 1 shows the D-meson twist-2, 3 DA ξ-moments$ \langle \xi^n\rangle _{2;D} $ ,$ \langle \xi^n_p\rangle _{3;D} $ , and$ \langle \xi^n_\sigma\rangle _{3;D} $ with$(n=1,2,\cdots,10)$ versus the Borel parameter$ M^2 $ . Here, the uncertainties caused by the errors of input parameters are not drawn, to clearly show the curves of different ξ-moments. Meanwhile, the Borel windows are shown with the shaded bands. By taking all error sources, such as the D-meson mass and decay constant, u- and c-quark masses, vacuum condensates, etc., shown in Eqs. (16) and (17), into consideration and adding the uncertainties in quadrature, the values of the first 10 ξ-moments of the D-meson twist-2, 3 DAs are obtained, as shown in Table 2. Here, we give the first two Gegenbauer moments of the D-meson twist-2, 3 DAs for reference, that is,Continue Contribution
(%)Dimension-six Contribution
(%)Continue Contribution
(%)Dimension-six Contribution
(%)$ \left <\xi^1\right>_{2;D} $ 

$<15 $ 

$<10 $ 

$ \left<\xi^2\right>_{2;D} $ 

$<20 $ 

$<10 $ 

$ \left<\xi^3\right>_{2;D} $ 

$ - $ 

$<15 $ 

$ \left<\xi^4\right>_{2;D} $ 

$<20 $ 

$<15 $ 

$ \left<\xi^5\right>_{2;D} $ 

$ - $ 

$<20 $ 

$ \left<\xi^6\right>_{2;D} $ 

$<20 $ 

$<20 $ 

$ \left<\xi^7\right>_{2;D} $ 

$ - $ 

$<25 $ 

$ \left<\xi^8\right>_{2;D} $ 

$<20 $ 

$<20 $ 

$ \left<\xi^9\right>_{2;D} $ 

$ - $ 

$<25 $ 

$ \left<\xi^{10}\right>_{2;D} $ 

$<20 $ 

$<20 $ 

$ \left<\xi^1_p\right>_{3;D} $ 

$ - $ 

$<5 $ 

$ \left<\xi^2_p\right>_{3;D} $ 

$<15 $ 

$<10 $ 

$ \left<\xi^3_p\right>_{3;D} $ 

$ - $ 

$<10 $ 

$ \left<\xi^4_p\right>_{3;D} $ 

$<15 $ 

$<10 $ 

$ \left<\xi^5_p\right>_{3;D} $ 

$ - $ 

$<15 $ 

$ \left<\xi^6_p\right>_{3;D} $ 

$<15 $ 

$<10 $ 

$ \left<\xi^7_p\right>_{3;D} $ 

$ - $ 

$<15 $ 

$ \left<\xi^8_p\right>_{3;D} $ 

$<15 $ 

$<10 $ 

$ \left<\xi^9_p\right>_{3;D} $ 

$ - $ 

$<15 $ 

$ \left<\xi^{10}_p\right>_{3;D} $ 

$<15 $ 

$<10 $ 

$ \left<\xi^1_\sigma\right>_{3;D} $ 

$<20 $ 

$ - $ 

$ \left<\xi^2_\sigma\right>_{3;D} $ 

$<45 $ 

$ - $ 

$ \left<\xi^3_\sigma\right>_{3;D} $ 

$<20 $ 

$<5 $ 

$ \left<\xi^4_\sigma\right>_{3;D} $ 

$<45 $ 

$ - $ 

$ \left<\xi^5_\sigma\right>_{3;D} $ 

$<25 $ 

$<5 $ 

$ \left<\xi^6_\sigma\right>_{3;D} $ 

$<45 $ 

$ - $ 

$ \left<\xi^7_\sigma\right>_{3;D} $ 

$<25 $ 

$<5 $ 

$ \left<\xi^8_\sigma\right>_{3;D} $ 

$<45 $ 

$ - $ 

$ \left<\xi^9_\sigma\right>_{3;D} $ 

$<25 $ 

$<5 $ 

$ \left<\xi^{10}_\sigma\right>_{3;D} $ 

$<45 $ 

$ - $ 

Table 1. Criteria for determining the Borel windows of the first 10 ξ-moments of the D-meson twist-2, 3 DAs.
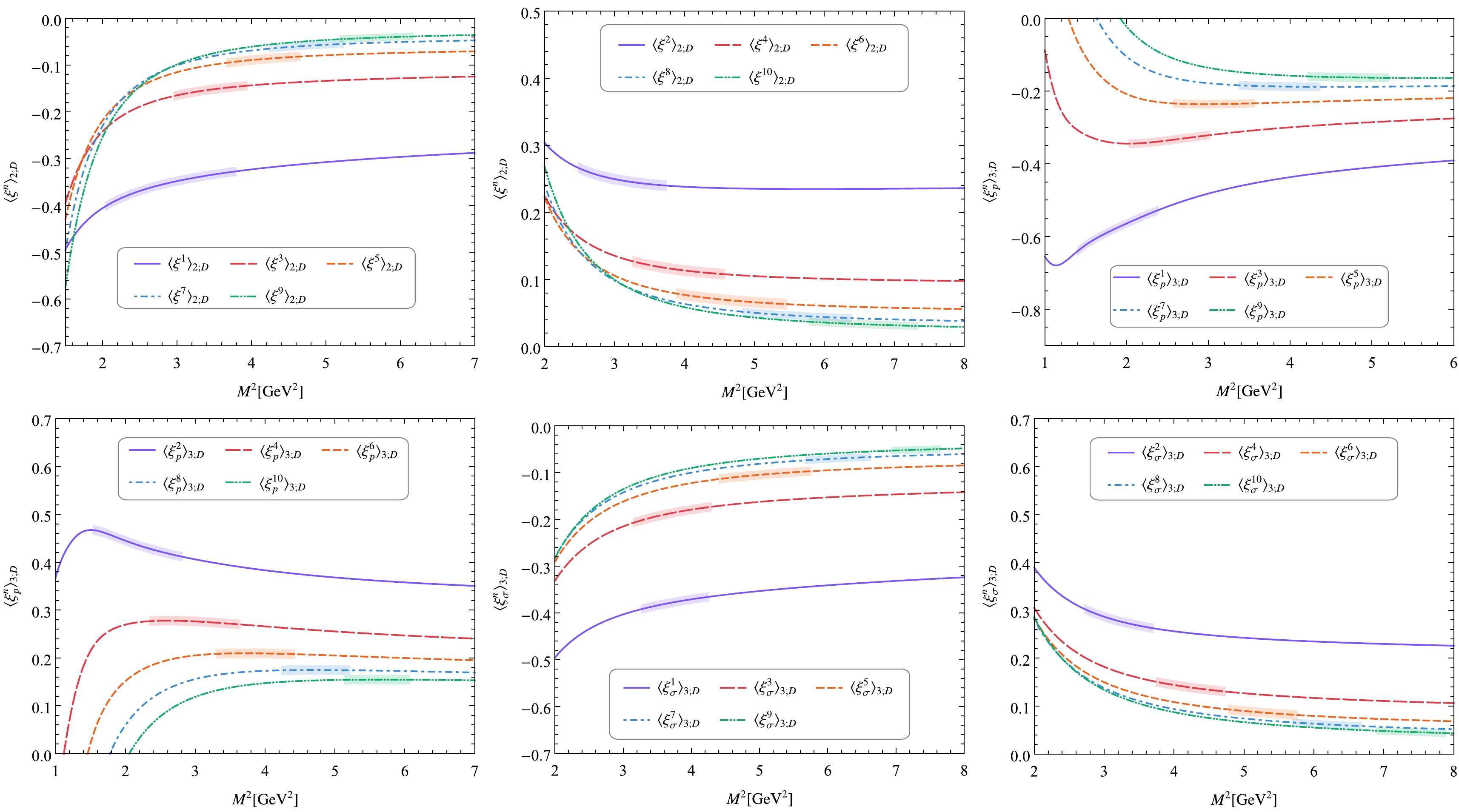
Figure 1. (color online) D-meson twist-2, 3 DA ξ-moments
$ \langle \xi^n\rangle _{2;D} $ ,$ \langle \xi^n_p\rangle _{3;D} $ , and$ \langle \xi^n_\sigma\rangle _{3;D} $ with$(n=1,2,\cdots,10)$ versus the Borel parameter$ M^2 $ . To clearly show the curves of different ξ-moments, only the central values of ξ-moments are given, which are obtained by taking the central values of the input parameters shown in Eqs. (16) and (17).$ \left<\xi^1\right>_{2;D} $ 

$ -0.349^{+0.037}_{-0.037} $ 

$ \left<\xi^2\right>_{2;D} $ 

$ 0.251^{+0.014}_{-0.014} $ 

$ \left<\xi^3\right>_{2;D} $ 

$ -0.152^{+0.012}_{-0.012} $ 

$ \left<\xi^4\right>_{2;D} $ 

$ 0.117^{+0.010}_{-0.010} $ 

$ \left<\xi^5\right>_{2;D} $ 

$ -0.0883^{+0.0072}_{-0.0072} $ 

$ \left<\xi^6\right>_{2;D} $ 

$ 0.0715^{+0.0084}_{-0.0084} $ 

$ \left<\xi^7\right>_{2;D} $ 

$ -0.0606^{+0.0054}_{-0.0054} $ 

$ \left<\xi^8\right>_{2;D} $ 

$ 0.0479^{+0.0052}_{-0.0052} $ 

$ \left<\xi^9\right>_{2;D} $ 

$ -0.0429^{+0.0034}_{-0.0034} $ 

$ \left<\xi^{10}\right>_{2;D} $ 

$ 0.0348^{+0.0035}_{-0.0035} $ 

$ \left<\xi^1_p\right>_{3;D} $ 

$ -0.555^{+0.063}_{-0.061} $ 

$ \left<\xi^2_p\right>_{3;D} $ 

$ 0.430^{+0.034}_{-0.036} $ 

$ \left<\xi^3_p\right>_{3;D} $ 

$ -0.325^{+0.026}_{-0.023} $ 

$ \left<\xi^4_p\right>_{3;D} $ 

$ 0.272^{+0.017}_{-0.020} $ 

$ \left<\xi^5_p\right>_{3;D} $ 

$ -0.232^{+0.019}_{-0.017} $ 

$ \left<\xi^6_p\right>_{3;D} $ 

$ 0.209^{+0.014}_{-0.017} $ 

$ \left<\xi^7_p\right>_{3;D} $ 

$ -0.185^{+0.019}_{-0.017} $ 

$ \left<\xi^8_p\right>_{3;D} $ 

$ 0.175^{+0.016}_{-0.017} $ 

$ \left<\xi^9_p\right>_{3;D} $ 

$ -0.163^{+0.017}_{-0.016} $ 

$ \left<\xi^{10}_p\right>_{3;D} $ 

$ 0.157^{+0.015}_{-0.016} $ 

$ \left<\xi^1_\sigma\right>_{3;D} $ 

$ -0.376^{+0.021}_{-0.021} $ 

$ \left<\xi^2_\sigma\right>_{3;D} $ 

$ 0.280^{+0.023}_{-0.023} $ 

$ \left<\xi^3_\sigma\right>_{3;D} $ 

$ -0.188^{+0.020}_{-0.019} $ 

$ \left<\xi^4_\sigma\right>_{3;D} $ 

$ 0.141^{+0.012}_{-0.013} $ 

$ \left<\xi^5_\sigma\right>_{3;D} $ 

$ -0.1078^{+0.0104}_{-0.0103} $ 

$ \left<\xi^6_\sigma\right>_{3;D} $ 

$ 0.0890^{+0.0077}_{-0.0079} $ 

$ \left<\xi^7_\sigma\right>_{3;D} $ 

$ -0.0735^{+0.0055}_{-0.0054} $ 

$ \left<\xi^8_\sigma\right>_{3;D} $ 

$ 0.0635^{+0.0054}_{-0.0055} $ 

$ \left<\xi^9_\sigma\right>_{3;D} $ 

$ -0.0550^{+0.0037}_{-0.0036} $ 

$ \left<\xi^{10}_\sigma\right>_{3;D} $ 

$ 0.0489^{+0.0041}_{-0.0042} $ 

Table 2. First 10 ξ-moments of the D-meson twist-2, 3 DAs
$ \phi_{2;D}(x,\mu) $ ,$ \phi_{3;D}^p(x,\mu) $ , and$ \phi_{3;D}^\sigma(x,\mu) $ at scale$ \mu = 2\; {\rm GeV} $ .$ \begin{array}{l} a_1^{2;D} = -0.582^{+0.062}_{-0.062}, \quad\quad a_2^{2;D} = 0.148^{+0.042}_{-0.042}, \\ a_{1,p}^{3;D} = -1.665^{+0.188}_{-0.182}, \quad\quad a_{2,p}^{3;D} = 0.726^{+0.252}_{-0.273}, \\ a_{1,\sigma}^{3;D} = -0.626^{+0.036}_{-0.035}, \quad\quad a_{2,\sigma}^{3;D} = 0.232^{+0.067}_{-0.068}, \end{array} $

(19) at scale
$\mu = 2~{\rm GeV}$ .In the above work, to calculate the ξ-moments of D-meson twist-3 DAs
$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ , one should calculate the normalization constants$ \mu_D^p $ and$ \mu_D^\sigma $ first. Under the assumption that the sum rules of zeroth ξ-moments$ \left<\xi^0_p\right>_{3;D} $ and$ \left<\xi^0_\sigma\right>_{3;D} $ can be normalized in appropriate Borel windows, the sum rules of$ \mu_D^p $ and$ \mu_D^\sigma $ can be obtained by taking$ n=0 $ in Eqs. (5) and (6) and substituting$ \left<\xi^0_p\right>_{3;D} = \left<\xi^0_\sigma\right>_{3;D} = 1 $ into these two sum rules. We require the continuum state's contributions to be less than 30% and the dimension-six condensate's contributions to be no more than 5% and 0.5% to determine the Borel windows for$ \mu_D^p $ and$ \mu_D^\sigma $ , respectively. By adding the uncertainties derived from all the error sources in quadrature, we obtain$ \mu_D^p = 2.717^{+0.087}_{-0.087}, \quad\quad \mu_D^\sigma = 2.231^{+0.073}_{-0.068}, $

(20) at scale
$ \mu = 2{\rm GeV} $ . Compared with the values in Ref. [19],$ \mu_D^p $ in (20) is increased by approximately 7.2%, and$ \mu_D^\sigma $ is reduced by approximately 12.0%. The former is caused by the update of input parameters, and the latter is caused by the new sum rule formula, i.e., Eq. (6), in addition to the update of input parameters.Then, we can determine the model parameters of our LCHO models for the D-meson twist-2 DA
$ \phi_{2;D}(x,\mu) $ and twist-3 DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ by using the ξ-moments presented in Table 2 via the least squares method following the method suggested in Refs. [29, 35]. Taking the D-meson leading-twist DA$ \phi_{2;D}(x,\mu) $ as an example, we first take the fitting parameters θ as the undetermined LCHO model parameters$ \alpha_{2;D} $ ,$ B_1^{2;D} $ and$ \beta_{2;D} $ , i.e.,$\theta = (\alpha_{2;D}, B_1^{2;D}, \beta_{2;D})$ , as discussed in Sec. II.B. By minimizing the likelihood function$ \chi^2(\theta) = \sum\limits_{i=1}^{10} \frac{(y_i - \mu(i,\theta))^2}{\sigma_i^2}, $

(21) the optimal values of the fitting parameters θ that we are looking for can be obtained. In Eq. (21), i represents the order of the ξ-moments of
$ \phi_{2;D}(x,\mu) $ ; the central values of ξ-moments$\langle\xi^n\rangle_{2;D} (n = 1,2,\cdots,10)$ , whose errors are presented in Table 2, are regarded as the independent measurements$ y_i $ and the corresponding variance$ \sigma_i $ . One can intuitively judge the goodness of fit according to the magnitude of probability$P_{\chi^2_{\rm min}} = \int^\infty_{\chi^2_{\rm min}} f(y;n_d) {\rm d} y$ with the probability density function of$ \chi^2(\theta) $ , i.e.,$f(y; n_d) = \dfrac{1}{\Gamma(n_d/2) 2^{n_d/2}}\times y^{n_d/2 - 1} {\rm e}^{-y/2}$ , where$ n_d $ represents the number of degrees of freedom. The obtained optimal values of the model parameters$ \alpha_{2;D} $ ,$ B_1^{2;D} $ , and$ \beta_{2;D} $ at scale$ \mu = 2\; {\rm GeV} $ and the corresponding goodness of fit are presented in Table 3. Following the same procedure, the LCHO model parameters for the D-meson twist-3 DAs$ \phi^p_{3;D}(x,\mu) $ and$ \phi^\sigma_{3;D}(x,\mu) $ at scale$ \mu = 2\; {\rm GeV} $ and the corresponding goodness of fits are obtained, as shown in Table 3. Then, the corresponding behaviors of DAs$ \phi_{2;D}(x,\mu) $ ,$ \phi^p_{3;D}(x,\mu) $ , and$ \phi^\sigma_{3;D}(x,\mu) $ are determined. To intuitively show the behaviors of these three DAs, we present their curves in Fig. 2. For comparison, the results of models reported in the literature for the D-meson leading-twist DA$ \phi_{2;D}(x,\mu) $ , i.e., the KLS model [22], LLZ model [23], LM model [24], and the form with LFQM [28], and our previous research results [18, 19] for$ \phi_{2;D}(x,\mu) $ ,$ \phi^p_{3;D}(x,\mu) $ , and$ \phi^\sigma_{3;D}(x,\mu) $ based on the LCHO model are also shown. In Fig. 2, we observe that our prediction for$ \phi_{2;D}(x,\mu) $ is closest to that of the LM model. Compared with the KLS and LLZ models, our$ \phi_{2;D}(x,\mu) $ is narrower and supports a large momentum distribution of the valence quark in$ x \sim $ [0.05, 0.5]. Compared with our previous work reported in Refs. [18, 19], our new predictions for$ \phi_{2;D}(x,\mu) $ ,$ \phi^p_{3;D}(x,\mu) $ , and$ \phi^\sigma_{3;D}(x,\mu) $ presented in this paper are smoother, and the spurious oscillations introduced by the high-order Gegenbauer moments in the old LCHO model are eliminated.$A_{2;D}/{\rm GeV}^{-1}$ 

$ \alpha_{2;D} $ 

$ B_1^{2;D} $ 

$\beta_{2;D}/{\rm GeV}$ 

$ \chi^2_{\rm min} $ 

$ P_{\chi^2_{\rm min}} $ 

$ 34.4712 $ 

$ -0.861 $ 

$ 0.107 $ 

$ 0.535 $ 

$ 0.873219 $ 

$ 0.996623 $ 

$A_{3;D}^p/{\rm GeV}^{-1}$ 

$ \alpha_{3;D}^p $ 

$ B_{1,p}^{3;D} $ 

$\beta_{3;D}^p/{\rm GeV}$ 

$ \chi^2_{\rm min} $ 

$ P_{\chi^2_{\rm min}} $ 

$ 0.536764 $ 

$ -1.360 $ 

$ -0.922 $ 

$ 1.135 $ 

$ 2.39892 $ 

$ 0.934514 $ 

$A_{3;D}^\sigma/{\rm GeV}^{-1}$ 

$ \alpha_{3;D}^\sigma $ 

$ B_{1,\sigma}^{3;D} $ 

$\beta_{3;D}^\sigma/{\rm GeV}$ 

$ \chi^2_{\rm min} $ 

$ P_{\chi^2_{\rm min}} $ 

$ 28.9986 $ 

$ -1.403 $ 

$ 0.228 $ 

$ 0.484 $ 

$ 0.594628 $ 

$ 0.999021 $ 

Table 3. Goodness of fit and the values of the LCHO model parameters for the D-meson twist-2 DA
$ \phi_{2;D}(x,\mu) $ and twist-3 DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ at scale$ \mu = 2\; {\rm GeV} $ .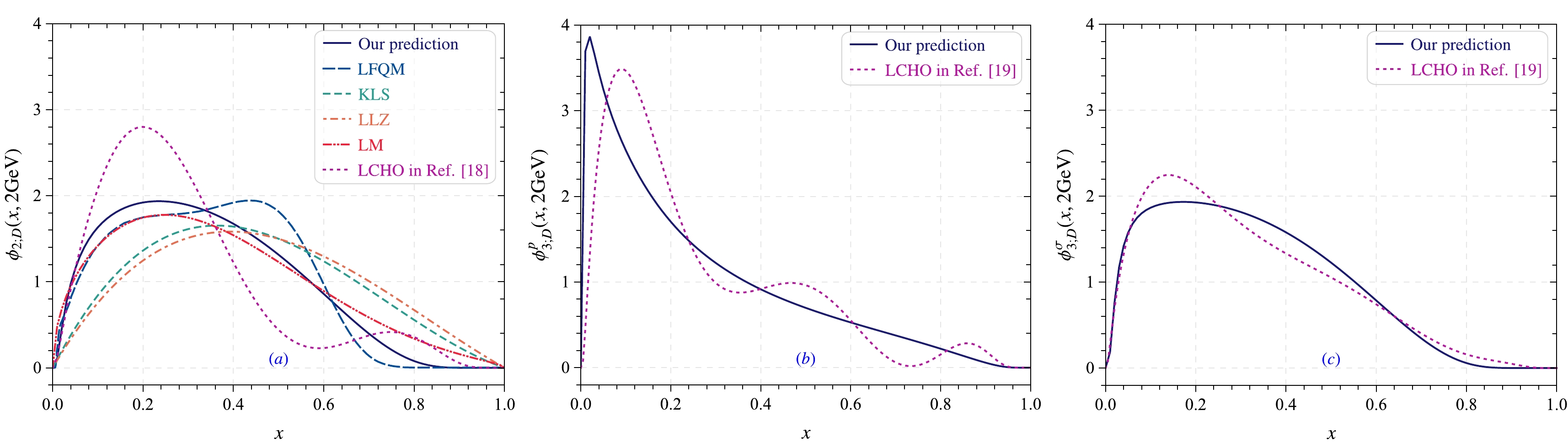
Figure 2. (color online) Curves of the D-meson twist-2 DA
$ \phi_{2;D}(x,\mu) $ and twist-3 DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ at scale$ \mu = 2\; {\rm GeV} $ . The results of models reported in the literature, i.e., the KLS model [22], LLZ model [23], LM model [24], and the form with LFQM [28], and our previous research results [18, 19] based on the LCHO model are shown for comparison. -
We revisited the D-meson leading-twist DA
$ \phi_{2;D}(x,\mu) $ and twist-3 DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ with QCD SRs in the framework of BFT by adopting a new scheme suggested in our previous work [29]. New sum rule formulae for the ξ-moments$ \langle\xi^n\rangle_{2;D} $ ,$ \langle\xi^n_p\rangle_{3;D} $ , and$ \langle\xi^n_\sigma\rangle_{3;D} $ , i.e., Eqs. (4), (5), and (6), respectively, were proposed and used to calculate their values, as shown in Table 2. The LCHO models for the DAs$ \phi_{2;D}(x,\mu) $ ,$ \phi_{3;D}^p(x,\mu) $ , and$ \phi_{3;D}^\sigma(x,\mu) $ were improved. By fitting the values of the ξ-moments$ \langle\xi^n\rangle_{2;D} $ ,$ \langle\xi^n_p\rangle_{3;D} $ , and$ \langle\xi^n_\sigma\rangle_{3;D} $ shown in Table 2 via the least squares method, the model parameters were determined, as shown in Table 3. Then, the predicted curves for the D-meson leading-twist DA$ \phi_{2;D}(x,\mu) $ and twist-3 DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ were obtained, as shown in Fig. 2.The criteria adopted to determine the Borel windows for the ξ-moments of the D-meson leading-twist DA
$ \phi_{2;D}(x,\mu) $ and twist-3 DAs$ \phi_{3;D}^p(x,\mu) $ and$ \phi_{3;D}^\sigma(x,\mu) $ shown in Table 1 imply that the new sum rule formulae (4), (5), and (6) can reduce the system uncertainties and yield more accurate predictions for the ξ-moments$ \langle\xi^n\rangle_{2;D} $ ,$ \langle\xi^n_p\rangle_{3;D} $ , and$ \langle\xi^n_\sigma\rangle_{3;D} $ , respectively. The goodness of fit values for$ \phi_{2;D}(x,\mu) $ ,$ \phi_{3;D}^p(x,\mu) $ , and$ \phi_{3;D}^\sigma(x,\mu) $ were$ P_{\chi^2_{\rm min}} = $ 0.996623,$ 0.934514 $ , and$ 0.999021 $ , respectively, indicating that our improved LCHO models presented in Sec. IIB with the model parameters in Table 3 can well prescribe the behaviors of these three DAs. The predicted DAs' curves shown in Fig. 2 indicate that the improved LCHO models presented in this work can eliminate the spurious oscillations introduced by the high-order Gegenbauer moments in old LCHO models obtained in Refs. [18, 19]. Otherwise, to simply investigate the influence of the new D meson twist-2, 3 DAs presented in this work on the relevant physical quantities, the TFFs$ f_{+,0}^{B\to D}(q^2) $ and$ {\cal{R}}(D) $ are calculated. For the relevant formulae, one can refer to Ref. [19]. We find that the new DAs can change$ f_{+,0}^{B\to D}(0) $ and$ {\cal{R}}(D) $ by approximately 10% and 6%, respectively. To obtain more accurate TFFs and a more accurate$ {\cal{R}}(D) $ , it is necessary to consider the next-to-leading order corrections for the contributions of D meson twist-3 DAs, which will be our next step.
Revisiting D-meson twist-2, 3 distribution amplitudes
- Received Date: 2022-12-13
- Available Online: 2023-05-15
Abstract: Owing to the significant difference between the experimental measurements and the theoretical predictions of the standard model (SM) for the value of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: