-
A deconfined matter consisting of quarks and gluons called "Quark-Gluon Plasma" (QGP) is believed to be produced in relativistic heavy-ion collisions [1]. Heavy quarks are produced in the initial parton hard scatterings in nuclear collisions. The thermal production in the medium is negligible owing to the large thresh-hold of heavy quark mass [2–4]. Therefore, heavy quarks and quarkonium have been proposed to be clean probes for the early stage of the hot deconfined medium in heavy-ion collisions [5–14]. Heavy quarks suffer significant energy losses in the medium [15–17] via both elastic collisions [18] and medium-induced parton radiation [19–21]. The coupling strength between heavy quarks and the QGP is believed to be strong, as suggested by studies about the production of open and hidden heavy flavor hadrons in nucleus-nucleus collisions [22–26]. Assuming a small momentum transfer in each collision, heavy quark evolution in the QGP can be treated as a Brownian motion. The energy loss of heavy quarks has been studied with classical models such as the Langevin equation [27, 28] and transport equation [29].
Heavy quarks and quarkonium subjected to the quantum environment can also be described with an open quantum system approach [30–34], such as the stochastic Schrödinger equation model, which treats medium interactions as stochastic potentials in the Hamiltonian [35, 36]. In analogy with Brownian particles diffusing in the classical phase space along classical stochastic trajectories, quantum states of the system (heavy quark) diffuse in the Hilbert space with stochastic modifications of the wave function. In classical models, the interaction between a heavy quark and the medium is encoded in the diffusion coefficient of the Langevin equation [37, 38]. While in quantum models, the interaction potential can be included directly in the Hamiltonian of the heavy quark.
In this study, we treat a heavy quark as an open quantum system and the QGP as the quantum environment. We start with the full Schrödinger equation including two wave functions of the system and the environment. Tracing out the degree of freedom of the environment, we obtain a reduced Schrödinger equation with an external time-dependent stochastic potential describing the random interactions with the medium. In the Markovian case where the time-correlation in the stochastic potential becomes a delta function, SSE has been proved to be equivalent to the Lindblad equation, after the ensemble average over a set of stochastically-evolved wave functions [39]. The computing cost in the framework of evolving wave functions directly is, however, much smaller than that of the Lindblad equation evolving the density matrix. In this study, we obtain SSE and apply it to the thermalization of a heavy quark in the static medium.
The study is organized as follows. In Sec. II, we derive the SSE for a heavy quark in the Markovian limit. In Sec. III, we present the evolutions of heavy quark momentum distribution in the static medium. A summary and discussion about further applications of SSE in heavy-ion collisions are given in Sec. IV.
-
To treat a heavy quark as an open quantum system in a medium, we follow Ref. [39] and note the full Schrödinger equation for both the system and the environment (with natural units
$ \hbar=c=1 $ ),$ {\rm i} {{\rm d}\left|\Phi(t) \right\rangle \over {\rm d}t} = (\hat{H}_{S} + \hat{H}_{B} + \lambda \hat{W}(t))\left|\Phi(t) \right\rangle, $

(1) where
$ \hat{H}_S $ and$ \hat{H}_B $ are the Hamiltonian of the system and the thermal bath (environment), respectively.$ \hat{W}(t) $ is the interaction between the system and the environment. λ is the coupling constant.$ \left|\Phi(t) \right\rangle $ is the full wave function of the system and the environment. In the interaction picture, the Schrodinger equation becomes,$ {\rm i} {{\rm d}\left|\Phi_I(t) \right\rangle \over {\rm d}t} = \lambda \hat{W}_I(t)\left|\Phi_I(t) \right\rangle , $

(2) where the full wave function in the interaction picture consists of two parts: the wave functions of the system (
$ \left|\varphi_I \right\rangle $ ) and the environment ($ \left|n \right\rangle $ ),$ \left|\Phi_I(t)\right\rangle=\sum_n\left|\varphi_I^n(t)\right\rangle \otimes \left|n \right\rangle $ . To solve Eq. (2), we introduce the projection operators$ \hat{P}={1}_S\otimes \left|l \right\rangle \left\langle l \right| $ and$ \hat{Q}=1_S\otimes\sum_{n\neq l} \left|n \right\rangle \left\langle n \right| $ , which separate one specific state of the environment$ \left|l \right\rangle $ from other states$ \sum_{n\neq l}\left|n \right\rangle $ [39–41] and satisfy the relation$ \hat{P}+\hat{Q}={1} $ . Applying$ \hat{P} $ and$ \hat{Q} $ projection operators on the Schrödinger equation Eq. (2), respectively, one can separate the full Schrödinger equation into two equations,$ \begin{aligned}[b] {\rm i} {\rm d} P\left|\Phi_I (t) \right\rangle =& \lambda\hat{P}\hat{W}_I(t)\hat{P}\left|\Phi_I (t) \right\rangle {\rm d}t \\&+ \lambda\hat{P}\hat{W}_I(t)\hat{Q}\left|\Phi_I (t) \right\rangle {\rm d}t, \end{aligned} $

(3) $ \begin{aligned}[b] {\rm i} {\rm d}\hat{Q}\left|\Phi_I (t) \right\rangle =& \lambda\hat{Q}\hat{W}_I(t)\hat{P}\left|\Phi_I (t) \right\rangle {\rm d}t \\&+ \lambda\hat{Q}\hat{W}_I(t)\hat{Q}\left|\Phi_I (t) \right\rangle {\rm d}t, \end{aligned} $

(4) From Eq. (4) one can deduce the time evolution of the selected state
$ \hat{Q}\left|\Phi_I(\Delta t) \right\rangle $ to be,$ \begin{aligned}[b] \hat{Q}\left|\Phi_I (\Delta t) \right\rangle =& (1-{\rm i} \lambda\hat{Q}\hat{W_I}(0) \hat{Q})\left|\Phi_I (0) \right\rangle )\Delta t \\ & - {\rm i}\lambda\hat{Q}\hat{W_I}(0)\hat{P}\left|\Phi_I (0) \right\rangle \Delta t, \end{aligned} $

(5) where
$ \Delta t $ is the time step of the evolution. Substituting Eq. (5) back into the Schrödinger equation Eq. (3), one can get the equation for the projected state$ \hat{P}\left|\Phi_I(t) \right\rangle $ . The Schrödinger equation can be written in a form including different orders in the coupling strength [42, 43]. To get a simplified formula, we assume that the coupling strength λ is small and only keep the first-order interaction term temporarily in the following calculations,$ \begin{aligned}[b] {\rm i} {\rm d}\hat{P}\left|\Phi_I (t) \right\rangle =& \lambda \hat{P}\hat{W_I}(t)\hat{P}\left|\Phi_I (t) \right\rangle {\rm d}t, \\ &+ \lambda \hat{P}\hat{W_I}(t)\hat{U}(t)\hat{Q}\left|\Phi_I (0) \right\rangle {\rm d}t +\mathcal{O}(\lambda^2), \end{aligned} $

(6) where the evolution operator satisfies the relation
${\rm d}\hat{U}(t)= -{\rm i}\lambda \hat{Q}\hat{W}_I(t)\hat{Q}\hat{U}(t){\rm d}t$ . Introducing the commutation relation$ [\hat{U}(t),\hat{Q}]=0 $ and considering the expansion of$ \hat{U}(t) $ over λ in the weak coupling limit, we obtain the following equation for the selected state$ \hat{P}\left|\Phi_I(t) \right\rangle $ ,$ \begin{aligned}[b] {\rm i} {\rm d}{P}\left|\Phi_I (t) \right\rangle =& \lambda {P}{W_I}(t)P\left|\Phi_I (t) \right\rangle {\rm d}t +\lambda P W_I(t) Q\left|\Phi_I(0) \right\rangle \\ &+\mathcal{O}(\lambda^2), \end{aligned} $

(7) which describes the evolutions of the system wave function with the environment located in one specific state selected by the operator
$ \hat{P} $ . Now we consider a linear form of the interaction term$ \hat{W}_I(t)=\sum_\alpha \hat{V}_\alpha \otimes \hat{B}_\alpha $ in the SSE. After multiplying$ \left\langle l \right| $ in Eq. (7), the first term on the R.H.S becomes zero when we redefine the operator$ \hat{B}_\alpha $ to obtain the relation$ \left\langle l \right|\hat{B}_\alpha\left|l \right\rangle =0 $ . The dynamical equation for l-th mode wave function$ \varphi_I^l(t) $ becomes,$ \begin{aligned}[b] \left\langle l \right|{\rm i} d\hat{P}\left|\Phi_I (t) \right\rangle =& {\rm i} {\rm d}\varphi^l_I(t) \\ =& \lambda \sum\limits_{\alpha,n\neq l} \left\langle l \right| \hat{B_\alpha}\left|n \right\rangle \hat{V_\alpha}\left|\varphi_I^n (0) \right\rangle {\rm d}t +\mathcal{O}(\lambda^2) \\ =&\lambda \sum\limits_{\alpha,n\neq l} \left\langle l \right| \hat{B_\alpha}\left|n \right\rangle \hat{V_\alpha} {\rm e}^{-{\beta\over 2} (\epsilon_n-\epsilon_l)}{\rm e}^{{\rm i} (\theta_n-\theta_l)}\left|\varphi_I^l (0) \right\rangle {\rm d}t \\&+\mathcal{O}(\lambda^2), \end{aligned} $

(8) where the λ-terms describe the influence of different environment modes (
$ n\neq l $ ) on the wave function$ \left|\varphi_I^{l}(0) \right\rangle $ . Obtaining the last line of Eq. (8), we consider a system in an equilibrated medium, and the initial wave function of the system is considered a pure state$ \phi(0) $ . The initial full wave function of the system and the environment can then be written as$\left|\Phi_I(0) \right\rangle =\sum_n \left|\phi_I(0) \right\rangle \otimes \sqrt{{{\rm e}^{-\beta\epsilon_n}\over Z_B}} {\rm e}^{{\rm i} \theta_n}\left|n \right\rangle$ with$ \beta\equiv1/T $ , where T is the temperature. The thermal particles consisting of the medium are assumed to satisfy the Boltzmann distribution.$ \epsilon_n $ is the energy of the medium (which are thermal massless particles) located at n-th eigenstate.$ Z_B=\rm{Tr_B} e^{-\beta T} $ is the partition function.$ \theta_n $ is the phase factor in the wave function of the environment. With these setups, the initial conditions of Eq. (8) becomes$\left|\varphi_I^n(0) \right\rangle = \left|\phi_I(0) \right\rangle \sqrt{{{\rm e}^{-\beta\epsilon_n}\over Z_B}} {\rm e}^{{\rm i}\theta_n}$ . From the definition of the wave function$ \left|\varphi_I^{n (t)} \right\rangle $ , we can see that it includes both the system wave function$ \left|\phi_I(t) \right\rangle $ and the information of the environment states, which enters into the evolution of the system wave function. Considering that Eq. (7) describes the evolution of a specific wave function$ \left|\varphi_I^l \right\rangle $ , we perform an average over the different medium eigenstates to obtain the evolution of the state$ \left|\phi_I(t) \right\rangle $ , which is considered as the wave function of the system. In the Schrödinger picture, the reduced Schrödinger equation with the interactions between the system and the environment is,$ {\rm i} {{\rm d}\left|\phi(t) \right\rangle \over {\rm d}t}=\hat{H}_s\left|\phi(t) \right\rangle +\lambda \sum\limits_\alpha \gamma_\alpha(t) \hat{V}_\alpha\left|\phi(t) \right\rangle, $

(9) where
$ \gamma_\alpha $ is a stochastic noise term,$ \gamma_\alpha(t)= \sum\limits_{l,n\neq l} {1\over \sqrt{Z_B}} \left\langle l \right| \hat{B}_\alpha\left|n \right\rangle {\rm e}^{-{\beta\over 2} \epsilon_n}{\rm e}^{{\rm i}(\theta_n-\theta_l)} $

(10) and
$ \hat{H}_s $ is the Hamiltonian of the system without interactions.$ \theta_n $ is the phase factor transferred from the medium wave function to the system wave function. In the Markovian limit, the stochastic interaction is treated as white noise in the Hamiltonian. the time correlation of the random phase factors satisfies a delta function,$ \begin{array}{*{20}{l}} \langle \theta_i(t)\theta_j(t^\prime)\rangle = \Theta\delta_{ij}\delta(t-t^\prime), \end{array} $

(11) where i and j are the indices of different medium eigenstates. The random phase factor is uniformly distributed in
$ [-\pi,\pi] $ , which gives$ \Theta={\pi^2\over 3} $ . The term random phase makes the system evolve towards a uniform distribution over all the states. The other damping term${\rm e}^{-{\beta\over 2}\epsilon_n}$ makes the system evolve towards the low energy states [36]. The competition between the two factors draws the system towards the thermal distribution of the medium.Here, quark-gluon plasma as an environment is assumed to be an ideal massless gas, in which thermal particles are located in N kinds of discrete eigenstates. The wave function of the medium is expressed as
$ \left|n_1, n_2,..., n_N \right\rangle $ .$n_\xi (\xi=1,2,...,N)$ represents the number of thermal particles located at the ξ-th eigenstate with the momentum$ \xi\cdot \Delta p_{\rm en} $ , where$ \Delta p_{\rm en} $ is the momentum gap between the eigenstates. In the one-dimensional situation, the system wave function can also be expressed with a series of discrete eigenstates$ \left|\phi(t) \right\rangle =\sum_{i=0}^M c_i(t) \left|i \right\rangle $ , with the momentum step between those eigenstates to be$ \Delta p_{\rm sys} $ , and M being the total number of the system eigenstates in the numerical calculations. From its interaction, heavy quark can obtain the momentum$ \xi\cdot \Delta p_{\rm en} $ from the medium by absorbing a thermal particle at the state$ \left|n_\xi \right\rangle $ or dump energy to the medium by emitting a corresponding particle. For the latter, the medium wave function is changed from the$ \left|n_\xi \right\rangle $ to the$ \left|n_\xi +1 \right\rangle $ state, correspondingly. There is also a transition between the i-th and j-th eigenstate in heavy quark wave function under the rule$|j-i|\cdot \Delta p_{\rm sys}= \xi\cdot \Delta p_{\rm en}$ . The interaction term between the heavy quark and the medium can thus be written as,$ \hat{W} =\sum\limits_{i=1}^{M-1}\sum\limits_{j=i+1}^{M} \hat{a}_{\xi}\left|j \right\rangle \left\langle i \right| + \hat{a}^\dagger_{\xi}\left|i \right\rangle \left\langle j \right| , $

(12) where the annihilation operator
$ \hat{a}_{\xi} $ and the creation operator$ \hat{a}_{\xi}^\dagger $ change the medium state$ \left|n_1,n_2,...n_\xi... \right\rangle $ as$ \hat{a}_{\xi}\left|n_\xi \right\rangle =\sqrt{n_\xi}\left|n_\xi-1 \right\rangle $ and$ \hat{a}^{\dagger}_{\xi}\left|n_\xi \right\rangle =\sqrt{n_\xi+1}\left|n_\xi+1 \right\rangle $ . The heavy quark wave function is changed from the i-th to the j-th state according to the rule$ \xi\cdot \Delta p_{\rm en}=|j-i|\cdot \Delta p_{\rm sys} $ . To label all the variables in SSE with the index of the system eigenstates, we perform the replacement$ \epsilon_\xi=\epsilon_{ij} $ and$ \left|n_\xi \right\rangle =\left|n_{ij} \right\rangle $ according to the transition rule$ \xi\Delta p_{\rm en}= |j-i|\Delta p_{\rm sys} $ . The lowering operator$ \hat{a}_{ij} $ reduces the number of thermal particles located at the medium eigenstate$ \left|n_{\xi} \right\rangle $ , and heavy quark is shifted from the i-th to the j-th state ($ j>i $ ). The term with the raising operator$ \hat{a}^\dagger_{ij} $ represents the process of a heavy quark dumping energy into the environment by emitting a thermal particle. The SSE for heavy quark evolution as an open quantum system is then written as$\begin{aligned}[b] {\rm i} \frac{{\rm d}|\phi(t)\rangle}{{\rm d} t}=&\hat{H}_s|\phi(t)\rangle \\ & +\frac{\lambda}{\sqrt{Z_B}} \sum\limits_{i=1}^{M-1} \sum\limits_{j=i+1}^M\left[\left\langle n_{i j}-1\left|\hat{a}_{i j}\right| n_{i j}\right\rangle {\rm e}^{-\frac{\beta}{2} \epsilon_{n_{i j}}} {\rm e}^{i \theta_{i j}^{\prime}} c_i|j\rangle\right. \\ & \left.\quad+\left\langle n_{i j}+1\left|\hat{a}_{i j}^{\dagger}\right| n_{i j}\right\rangle {\rm e}^{-\frac{\beta}{2} \epsilon_{n_{i j}}} {\rm e}^{i \theta_{i j}^{\prime \prime}} c_j|i\rangle\right],\\[-13pt] \end{aligned} $

(13) where
$ \hat{H_s} $ is the Hamiltonian of a heavy quark without interactions. The heavy quark mass is considered to be 1.5 GeV. In Eq. (13),$ \theta_{ij}^\prime=\theta_{n_{ij}} - \theta_{n_{ij}-1} $ and$ \theta_{ij}^{\prime\prime}=\theta_{n_{ij}} - \theta_{n_{ij}+1} $ are the random phase factors transferred from the medium wave function to the heavy quark wave function in each interaction. We note that the i on the L.H.S of the equation represents the imaginary number, while$ i,j $ in the summation and subscript are the indexes of the heavy quark state.$ \epsilon_{n_{ij}} $ is the energy of the$ n_{ij} $ thermal particles located at the medium ξ-th eigenstate with$ \xi\Delta p_{\rm en}= |j-i|\Delta p_{\rm sys} $ . λ is the coupling constant. -
As a preliminary study, we study the heavy quark kinetic thermalization in a static uniformly-distributed medium. The medium state is represented by discrete eigenstates with the momentum gap
$ \Delta p_{\rm en}=0.2 $ GeV/c. Assuming the medium to be an ideal gas, we can obtain the number of thermal particles located at each eigenstate. We initialize the total number of thermal particles at different states to be$ \sum_i n_i=100 $ , where$ n_i $ satisfies the Boltzmann distribution with the temperature$ T=1 $ GeV. For the heavy quark wave function, it is written as a quantum superposition of eigenstates, with the momentum gap$ \Delta p_{\rm sys}=0.12 $ GeV/c. The total number of system eigenstates is chosen to be$ M=30 $ . The time step for the numerical evolution of Eq. (13) is considered to be$ dt=0.001 $ fm/c. We have verified that using different steps for the time and momentum does not affect the results appreciably. We consider different cases of the coupling strength between a heavy quark and the environment. Inspired by the heavy quark potential at finite temperature [44, 45], we consider the coupling strength to be$ \lambda=0.3 $ and$ 0.5 $ to perform the preliminary calculations. An accurate determination of the λ will be performed in future work. At each time step, the heavy quark exchanges the momentum and phase factor with the medium by emitting or absorbing a massless thermal particle. As an open quantum system, the wave function of the heavy quark, which is not normalized owing to the stochastic interactions, is normalized by hand. With a large set of stochastic wave functions, we obtain a mean wave function$ \overline{\phi(t)} $ after the ensemble average.$ |\left\langle i \right|\left|\overline{\phi(t)} \right\rangle |^2 $ can be interpreted as the probability for the heavy quark to be located at the state with the momentum$ i\cdot \Delta p_{\rm sys} $ .In Fig. 1, we initialize the wave function of the heavy quark with a uniform distribution. The momentum distributions of a heavy quark at different times are plotted with different colors. The effect of the damping factor
$ e^{-{\beta\over 2}\epsilon_{n_{ij}}} $ , which comes from the part of the medium wave function, reduces the density of heavy quark at high momentum states while increasing its density at low momentum eigenstates. The term with random phase factor makes a heavy quark uniformly distributed over all the momentum eigenstates. The combined effect of the two effects makes the system evolve towards the thermal distribution of the medium.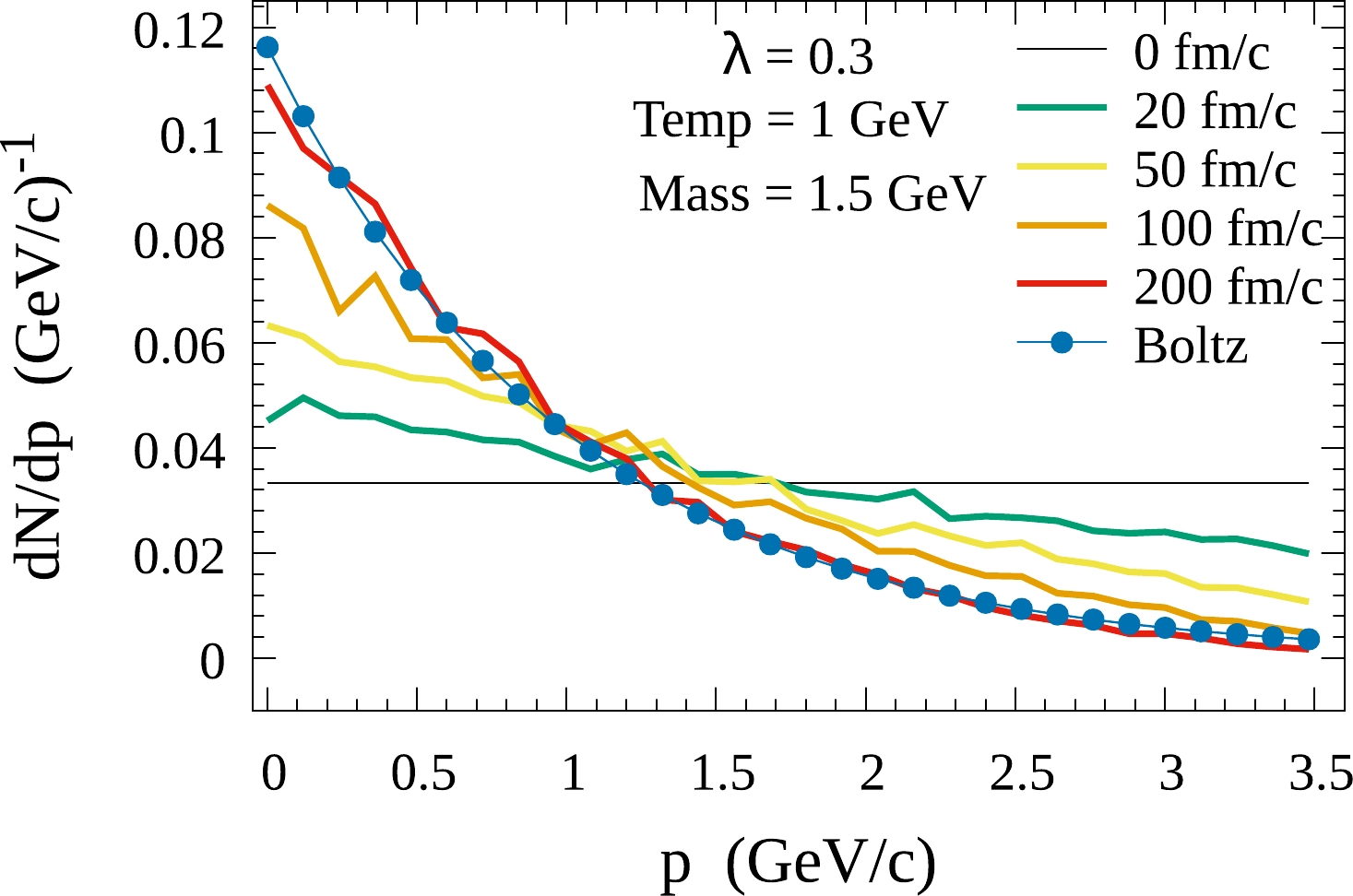
Figure 1. (color online) Time evolution of heavy quark momentum distribution at different times. The normalized distribution
${\rm d}N/{\rm d}p$ represents the probability of a heavy quark located at the momentum p. Results are obtained for the heavy quark mass$ m=1.5 $ GeV, the temperature$ T=1 $ GeV, and the coupling strength$ \lambda=0.3 $ . The initial momentum distribution of heavy quark is considered to be a uniform distribution. The blue-marked line is the Boltzmann distribution corresponding to the thermal limit.To study the effects of the coupling strength on the thermalization process, we consider
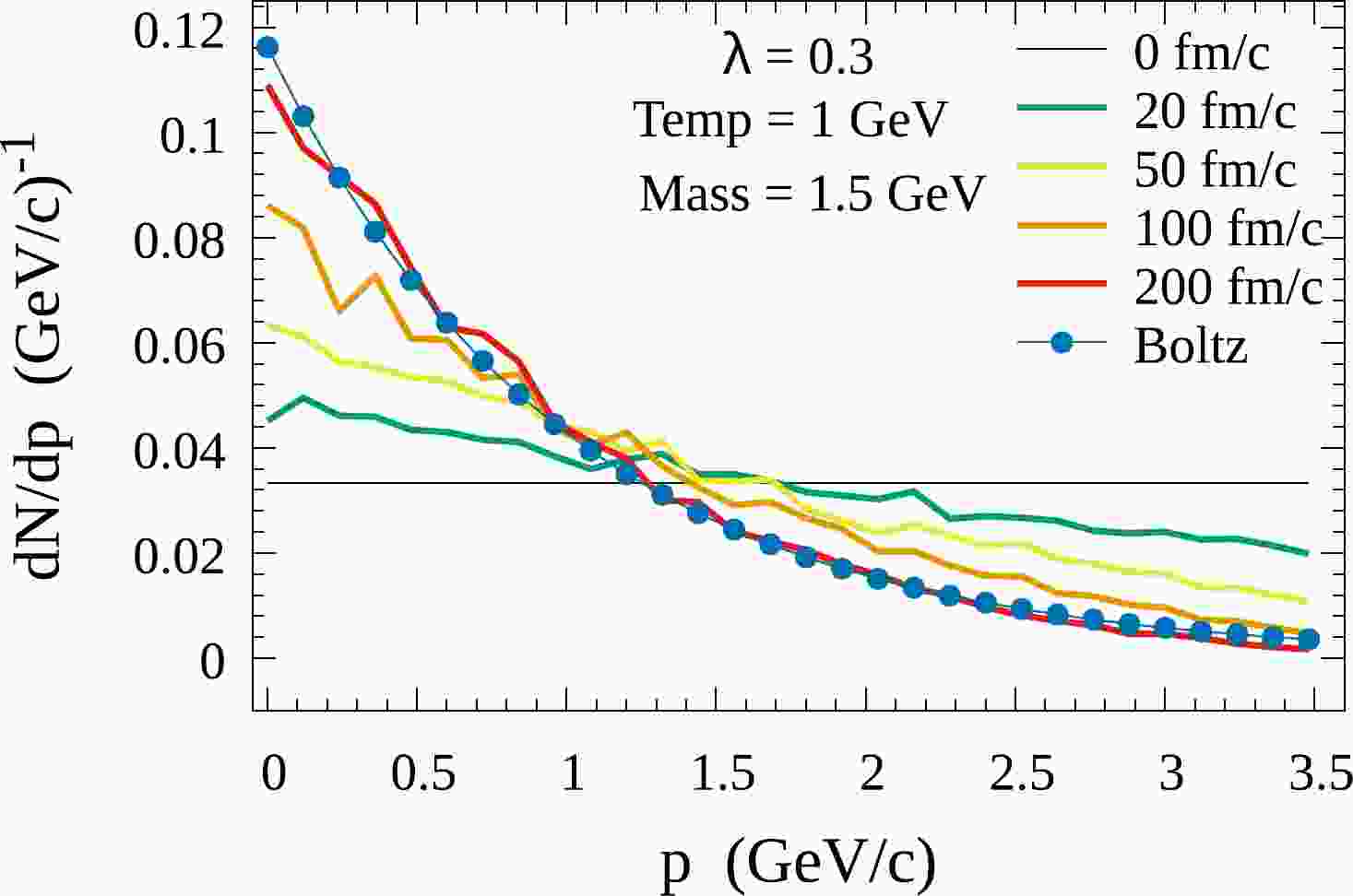
$ \lambda=0.5 $ , and the results are shown in Fig. 2. The thermalization time with the stronger coupling strength becomes much shorter than that in Fig. 1 [46, 47]. The thermalization process also depends on the density of thermal particles in the environment. In the case of heavy-ion collisions, the realistic initial momentum distribution of heavy quarks and the density of the medium should be considered. By employing a realistic momentum distribution instead of a uniform distribution, the thermalization time is much shorter than that in Figs. 1 and 2. The motivation of this work is not comparision with experimental data about heavy quark thermalization but building the SSE model to treat a heavy quark as an open quantum system. In future work, we will apply this open quantum system approach to the realistic evolutions of a heavy quark and to the case of heavy quarkonium in heavy-ion collisions.
Figure 2. (color online) Time evolution of heavy quark momentum distribution
${\rm d}N/{\rm d}p$ at different times. The coupling strength is considered to be$ \lambda=0.5 $ . Other parameters are the same as in Fig. 1. -
In this study, we treat a heavy quark as an open quantum system in a medium and obtain the SSE for a heavy quark from the full Schrödinger equation. The random interactions between heavy quark (system) and the medium (environment) are included via the stochastic potential, which exchange the momentum and phase factor between wave functions of a heavy quark and the medium. As a preliminary study, we initialize the momentum distribution of a heavy quark with a uniform distribution, while the static medium consisting of massless particles satisfies a Boltzmann distribution. A large set of stochastic wave functions of a heavy quark are obtained by solving the SSE along different quantum trajectories. After the ensemble average, the mean wave function and momentum distribution of a heavy quark at different times are presented, which is seen to evolve toward the thermal distribution of the medium. Thermalization processes with different coupling strengths between the system and environment are also studied. In future studies, we will apply this SSE model to the realistic evolutions of a heavy quark in heavy-ion collisions and extend the model to the quarkonium case.
Open quantum system approach for heavy quark thermalization
- Received Date: 2022-12-28
- Available Online: 2023-05-15
Abstract: We treat heavy quark as an open quantum system in a hot medium and rederive the stochastic Schrödinger equation (SSE) from the full Schrödinger equation for both heavy quarks and the medium. We apply the SSE to the dynamical evolutions of a heavy quark (as a system) in the static hot medium (as an environment). Heavy quarks interact with the medium via random scatterings, which exchange the momentum and phase factor randomly between two wave functions of the system and the environment. The exchange of momentum and phase factor results in the transition between different eigenstates of the system. These are included via an external stochastic potential in the Hamiltonian of SSE. Stochastic wave functions of a heavy quark are evolved with the stochastic external potential. The mean wave functions and corresponding momentum distributions of heavy quarks are obtained after the ensemble average over a large set of stochastic wave functions. We present the thermalization of heavy quarks in the static medium with different coupling strengths.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: