Search for heavy Majorana neutrinos at future lepton colliders

Peng-Cheng Lu; Zong-Guo Si; Zhe Wang; Xing-Hua Yang; Xin-Yi Zhang

doi:10.1088/1674-1137/acb997

Chinese Physics C> 2023, Vol. 47> Issue(4) : 043107 DOI: 10.1088/1674-1137/acb997

Search for heavy Majorana neutrinos at future lepton colliders

Peng-Cheng Lu ^{1,
,} ,
Zong-Guo Si ^{1,
,} ,
Zhe Wang ^1, ,
Xing-Hua Yang ^2, ,
Xin-Yi Zhang ^1,

1.
School of Physics, Shandong University, Jinan 250100, China
2.
School of Physics and Optoelectronic Engineering, Shandong University of Technology, Zibo 255000, China

Abstract
HTML
Reference
Related

PDF

Abstract：
A nonzero neutrino mass may be a sign of new physics beyond the standard model (SM). To explain the small neutrino mass, we can extend the SM using right-handed Majorana neutrinos in a low-scale seesaw mechanism, and the CP violation effect can be induced due to the CP phase in the interference of heavy Majorana neutrinos. The existence of heavy Majorana neutrinos may lead to lepton number violation processes, which can be used to search for the signals of heavy Majorana neutrinos. In this paper, we focus on the CP violation effect related to two generations of heavy Majorana neutrinos at $15$ GeV $<m_{N_1}< 70$ GeV in the pair production of W bosons and rare decays. It is valuable to investigate Majorana neutrino production signals and the related CP violation effects in rare W boson decays at future lepton colliders.
- Majorana ,
- CP violation ,
- future lepton colliders ,
- lepton number violation

I. INTRODUCTION

I. INTRODUCTION
II. BRIEF REVIEW OF THEORETICAL MODEL
III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS
IV. SUMMARY
ACKNOWLEDGEMENTS
APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

Neutrinos in the standard model (SM) are strictly massless owing to the absence of right-handed chiral states and the requirement of $S U(2)_L$ gauge invariance and renormalizability. However, neutrino oscillation experiments show that neutrinos have minor non-zero masses, which insinuates the existence of new physics (NP) beyond the SM. To explain the tiny neutrino mass, we must extend the SM, and the mechanism with respect to neutrino mass generation is attracting increasing attention. An interesting mechanism to generate the neutrino mass which introduces heavy right-handed Majorana neutrinos ( $\overline{N^c_R}$ ) is known as the type-I seesaw mechanism [1–5]. In this mechanism, the Dirac neutrino mass terms are generated after spontaneous gauge symmetry breaking. In addition, the Majorana neutrinos can also form Majorana mass terms, $\overline{N^c_R}M_RN_R$ . The introduction of heavy Majorana neutrinos may lead to CP violation, which gives a reasonable explanation for the asymmetry of matter and antimatter. The asymmetry of baryon number in our Universe can be measured by the baryon-to-photon density ratio $\eta=n_B/n_\gamma$ . According to an analysis of a recent Planck measurement of the cosmic microwave background, the value of η is approximately $\eta\simeq (6.12\pm 0.03)\times10^{-10}$ [6]. This result is too large compared to the result expected by the SM. In a famous mechanism called leptogenesis, this asymmetry of baryon number can be produced by the lepton number asymmetry caused by the decay of Majorana neutrinos in the early Universe; the latter may turn into baryon number asymmetry through sphaleron processes [7, 8] in this situation. The existence of heavy Majorana neutrinos also leads to the violation of lepton number by two units, $\Delta L=2$ , such as the neutrinoless double-beta decay $(0\nu\beta\beta)$ [9, 10]. In our study, we consider rare W decay through Majorana neutrino exchange, which produces a same-sign dilepton in the final state. Generally, both light and heavy Majorana neutrinos can contribute to the W decay amplitude. However, the contribution of light Majorana neutrinos is strongly suppressed and can be safely neglected owing to the small mass, such as $\mathcal{O}(eV)$ . The process of the rare W decay $W^-\rightarrow \ell_1^-N\rightarrow \ell_1^-\ell_2^-(q\bar{q}^\prime)^+$ has been studied in literature (for examples of a review, see Refs. [11–15]). In the mass range $M_N<M_W$ , the $\Delta L=2$ same-sign dilepton production signal has been studied in rare meson decays [16–20], tau lepton decays [21–23], and even top quark decays [24–27]. There is a nonzero CP asymmetry induced by the difference between the rates of $W^+\rightarrow \ell_1^+\ell_2^+(\bar{q}q^\prime)^-$ and its CP-conjugate process $W^-\rightarrow \ell_1^-\ell_2^-(q\bar{q}^\prime)^+$ . This difference arises from the significant interference of different heavy Majorana neutrinos. We can use the lepton number violation (LNV) process as a probe to study heavy Majorana neutrinos. Theorists have conducted numerous studies on the prospect of observing CP asymmetry via LNV processes in which CP asymmetry can be observed in the decays of mesons [28–32] and tau leptons [33, 34]. Recently, the authors of Refs. [35, 36] studied CP asymmetry in rare W decays at the LHC; however, the CP violation effect produced in the situation they considered is influenced by the initial parton distribution functions in protons. In this study, we investigate the prospect of searching for heavy Majorana neutrinos in future lepton colliders such as the Compact Linear Collider (CLIC) [37], International Linear Collider (ILC) [38], and Muon Collider (MuC) [39], which provide a significantly cleaner environment. We analyze the process of $W^\pm$ pair production in $e^+e^-$ collisons with the ILC running at 190 GeV and the $\mu^+\mu^-$ collison with the MuC running at 190 GeV, where $W^+$ and $W^-$ arise from $e^+e^-$ and $\mu^+\mu^-$ collisions, and the influence of the parton distribution functions in protons on CP violation can be canceled. In principle, the number n of right-handed heavy Majorana neutrinos introduced in the type-I seesaw mechanism is a free parameter. We take $n\geq 2$ as two neutrino mass-squared differences between observed light neutrinos. Another reason is that CP violation requires the interference of at least two different Majorana neutrinos. For convenience, we take only two heavy Majorana neutrinos, $N_1$ and $N_2$ , into consideration, and the general case with more Majorana neutrinos can be analyzed in a similar way.

This paper is organized as follows. The model including heavy Majorana neutrinos is briefly reviewed in Section II. Then, we investigate W pair production and their rare decays via Majorana neutrinos at future lepton colliders in Section III. Finally, a short summary is given in Section IV.

II. BRIEF REVIEW OF THEORETICAL MODEL

I. INTRODUCTION
II. BRIEF REVIEW OF THEORETICAL MODEL
III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS
IV. SUMMARY
ACKNOWLEDGEMENTS
APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

An effective extension of the SM introduces three right-handed neutrinos, which are singlets under the SM gauge group. CP violation stems from different Majorana neutrinos, and for convenience, we only consider two generations of Majorana heavy neutrinos, denoted as $N_1$ and $N_2$ . We can write the Lagrangian of the model as [40]

$\begin{array}{*{20}{l}} \mathcal{L}=\mathcal{L}_{\rm SM}+\mathcal{L}_{N}+\mathcal{L}_{WN\ell}+\mathcal{L}_{ZN\nu}+\mathcal{L}_{HN\nu}, \end{array}$

(1)

where $\mathcal{L}_N$ is the sum of the kinetic and mass terms for heavy neutrinos,

$\begin{array}{*{20}{l}} \mathcal{L}_N=\xi_\nu \left(\bar{N_k} {\rm i} \not \partial N_k-m_{N_k}\bar{N_k}N_k\right), \end{array}$

(2)

where $k=1,2$ , and the overall factor $\xi_\nu=1$ for the Dirac neutrinos and $\xi_\nu=\dfrac{1}{2}$ for Majorana neutrinos. In our case, $\xi_\nu=\dfrac{1}{2}$ . $\mathcal{L}_{WN\ell}$ corresponds to heavy neutrino interactions with a W boson,

$\mathcal{L}_{WNl}=-\frac{g}{\sqrt{2}}W_\mu^+\sum\limits_{k=1}^{2}\sum\limits_{l=e}^{\tau}\bar{N_k}R_{l k}^\ast\gamma^\mu P_L\ell^- + {\rm h.c.},$

(3)

$\mathcal{L}_{ZN\nu}$ corresponds to interactions with a Z boson,

$\mathcal{L}_{ZN\nu}=-\frac{g}{2\text{cos}\theta_{W}}Z_{\mu}\sum\limits_{k=1}^{2}\sum\limits_{l=e}^{\tau}\bar{N_k}R_{lk}^\ast\gamma^{\mu}P_L\nu_{l} + {\rm h.c.},$

(4)

and $\mathcal{L}_{HN\nu}$ corresponds to interactions with a Higgs boson,

$\mathcal{L}_{HN\nu}=-\frac{gm_N}{2M_W}h\sum\limits_{k=1}^{2}\sum\limits_{l=e}^{\tau}\bar{N_k}R_{lk}^\ast P_L\nu_l + {\rm h.c.}.$

(5)

In our process, we only use $\mathcal{L}_{WNl}$ . We can then write the weak charged-current interaction Lagrangian as

$\begin{aligned}[b] \mathcal{L}_{\rm cc} =& -\frac{g}{\sqrt{2}} W^+_{\mu} \sum\limits_{\ell=e}^{\tau} \sum\limits_{m=1}^{3} V_{\ell m}^{\ast} \overline{\nu_{m}} \gamma^{\mu} P_{L} \ell \\& - \frac{g}{\sqrt{2}} W^+_{\mu} \sum\limits_{\ell=e}^{\tau} \sum\limits_{k=1}^{2} R_{\ell k}^{\ast} \overline{N^{c}_{k}} \gamma^{\mu} P_{L} \ell + {\rm h.c.}. \; \end{aligned}$

(6)

Here, $V_{\ell m}$ is the neutrino mixing matrix, and we can measure its parameters from neutrino oscillation experiments. We neglect the contributions of light Majorana neutrinos to LNV processes because of their small masses. $R_{\ell k}$ are the mixing elements between heavy Majorana neutrinos and charged-leptons, which can be parameterized as [41]

$\begin{array}{*{20}{l}} R_{\ell k}=\left|R_{\ell k}\right| {\rm e}^{{\rm i}\phi_{\ell k}} , \; \; \; \ell= e, \mu, \tau, \; \; \; k=1, 2 . \end{array}$

(7)

Now, we give the mixing relations between neutrino flavor eigenstates and mass eigenstates as follows [42]:

$\nu_{\ell L} = \sum\limits_{m=1}^{3} V_{\ell m} \nu_{m L} + \sum\limits_{k=1}^{2} R_{\ell k} N^{c}_{kL} \; .$

(8)

Complex phases, $\phi_{\ell k}$ , contribute to CP violation when there is interference from two different heavy Majorana neutrinos and can be determined in possible collider experiments. The constraints on the mixing parameters between heavy Majorana neutrinos and leptons have been investigated in previous studies [43, 44]. According to the constraints on the mixing parameters, in the range $15$ GeV $<m_{N_1}<70$ GeV, the parameters in the following range all satisfy the constraints:

$\begin{aligned}[b] & \left|R_{e i}\right|^2 \leq8\times10^{-6} \; ,\quad\; \; \left|R_{\mu i}\right|^2 \leq1\times10^{-5},\; \; \\& \left|R_{\tau i}\right|^2 \leq1\times10^{-5} \; , \quad\; {\rm for} \; \; i = 1, 2 \; . \end{aligned}$

(9)

For convenience, we set these parameters as $\left|R_{e i}\right|^2 = 8\times 10^{-6}, ~ \left|R_{\mu i}\right|^2 =1\times10^{-5}, ~ \left|R_{\tau i}\right|^2 =1\times10^{-5}$ and take the case in which two generations of heavy Majorana neutrinos are nearly degenerate, where $\Delta m=m_{N_2}-m_{N_1}$ . We also consider the result when $\Delta m=m_{N_2}-m_{N_1}=20$ GeV to observe the effects of $\Delta m$ in our study.

III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS

I. INTRODUCTION
II. BRIEF REVIEW OF THEORETICAL MODEL
III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS
IV. SUMMARY
ACKNOWLEDGEMENTS
APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

As mentioned before, many processes generating heavy Majorana neutrinos have been investigated; however, their generation processes have backgrounds that are not negligible, some of which influence CP violation. Therefore, we choose an approach that is clean enough to generate heavy Majorana neutrinos at future lepton colliders. We find that the processes $e^+e^-(\mu^+\mu^-)\rightarrow W^+W^-,W^\pm\rightarrow N\ell^\pm$ are clean in that no obvious backgrounds and no CP violation is observed in W pair production. For convenience, we take $\ell^\pm=\mu^\pm$ in our calculation. First, we want to see if it is possible to search for heavy Majorana neutrinos in the processes of $W^+W^-$ pair production. W pair production can be expressed as $e^+(\mu^+)(l_2)+e^-(\mu^-)(l_1)\rightarrow W^+(k_p)+ W^-(k_m)$ , where $l_1$ , $l_2$ , $k_p$ , and $k_m$ are the four-momentum of the corresponding particles, and its cross section can be written as

$\sigma=\frac{1}{2s}\int {\rm d}{\cal L}_{ips2}\overline{\left|{\cal M}\right|^2}.$

(10)

Here, s denotes the center-of-mass energy squared, and ${\rm d}{\cal L}_{ips2}$ represents the two-body Lorentz invariant phase space of the final particles. $\overline{\left|{\cal M}\right|^2}$ is the squared scattering amplitude averaged (summed) over the initial (final) particles, which can be expressed as

$\begin{align} \overline{\left|{\cal M}\right|^2} = \; & \frac{1}{4} \left(\overline{\left|{\cal M}_{\rm SM}\right|^2}+\overline{\left|{\cal M}_{\rm NP}\right|^2}+2{\rm Re}\overline{\left[{\cal M}_{\rm SM} {\cal M}_{\rm NP}^\ast\right]}\right) , \end{align}$

(11)

$\begin{aligned}[b] \overline{\left|{\cal M}_{\rm SM}\right|^2} =\; & g^4\biggl\{\text{sin}^4\theta_w\left|D_\gamma(q)\right|^2{\cal T}_\gamma+\left|D_Z(q)\right|^2{\cal T}_Z\\&+\frac{1}{4}\left|D_\nu(p_n)\right|^2{} -\text{sin}^2\theta_w{\cal F}_{12}\\&+\frac{1}{2}\text{sin}^2\theta_w{\cal F}_{13}-\frac{1}{2}{\cal F}_{23} \}\; , \end{aligned}$

(12)

$\begin{align} \overline{\left|{\cal M}_{\rm NP}\right|^2} =\; & \frac{g^4\left|R_{eN}\right|^4}{4}\biggl\{{\cal T}_n\left(\left|D_{N_1}(p_n)\right|^2+\left|D_{N_2}(p_n)\right|^2\right)+{\cal F}_{45}\}\; , \end{align}$

(13)

$\begin{aligned}[b] 2{\rm Re}\overline{\left[{\cal M}_{\rm SM} {\cal M}_{\rm NP}^\ast\right] }=\; & g^4\biggl\{\frac{\text{sin}^2\theta_w\left|R_{eN}\right|^2}{2}\left({\cal F}_{14}+{\cal F}_{15}\right)\\&-\frac{\left|R_{eN}\right|^2}{2}\left({\cal F}_{24}+{\cal F}_{25}\right){} \\ &+\frac{\left|R_{eN}\right|^2}{4}{\cal T}_n\left({\cal F}_{34}+{\cal F}_{35}\right) \}\; , \end{aligned}$

(14)

where $q=l_1+l_2$ , $p_n=l_1-k_m$ , $\overline{\left|{\cal M_{\rm SM}}\right|^2}$ is the contribution from the SM part, $\overline{\left|{\cal M_{\rm NP}}\right|^2}$ is the contribution from the NP part, and $2{\rm Re}\overline{\left[{\cal M}_{\rm SM} {\cal M}_{\rm NP}^\ast\right]}$ is from the interference between the contributions of the SM and NP parts. The explicit expressions of $D_\gamma$ , $D_Z$ , $D_\nu$ , $D_{N_1}$ , $D_{N_2}$ , ${\cal T}_\gamma$ , ${\cal T}_Z$ , ${\cal T}_n$ , ${\cal F}_{12}$ , ${\cal F}_{13}$ , ${\cal F}_{23}$ , ${\cal F}_{45}$ , ${\cal F}_{14}$ , ${\cal F}_{15}$ , ${\cal F}_{24}$ , ${\cal F}_{25}$ , ${\cal F}_{34}$ , and ${\cal F}_{35}$ in the amplitude are shown in Appendix A. To observe obvious CP violation, we take two heavy Majorana neutrinos in the nearly degenerate case most of the time, except when we study the influence of $\Delta m$ on CP violation and the cross section of $e^+e^-(\mu^+\mu^-)\rightarrow W^+ W^-$ in the NP part. $W^\pm$ pairs are produced directly from this type of lepton-antilepton collision. In the SM view of lepton collisions, there are no heavy Majorana neutrinos in the decay channels. To consider the contribution of physics beyond the SM, we take two right-handed Majorana neutrinos into account as propagators of the t channel in lepton-antilepton collisions. We calculate the cross section of W pair production, and the result of $\Delta\sigma/\sigma_{\rm SM}$ is shown in Fig. 1, where $\Delta\sigma=\sigma_{\rm total}-\sigma_{\rm SM}$ , $m_{N_1}=15$ GeV, and $\left|R_{e i}\right|^2 =8\times10^{-6}$ . The black lines show that the two neutrinos are nearly degenerate, and the spot lines correspond to $\Delta m=m_{N_2}- m_{N_1}=20$ GeV, where they are not nearly degenerate. (a) and (b) show the difference between cross sections in $e^+e^-\rightarrow W^+W^-$ and $\mu^+\mu^-\rightarrow W^+W^-$ . We can see that $\Delta\sigma$ represents the contribution of the NP part, which is too small when compared to the cross section of the SM part; hence, it is difficult to study Majorana neutrinos in the $W^+W^-$ pair production sector, and we should search for them in rare W decay.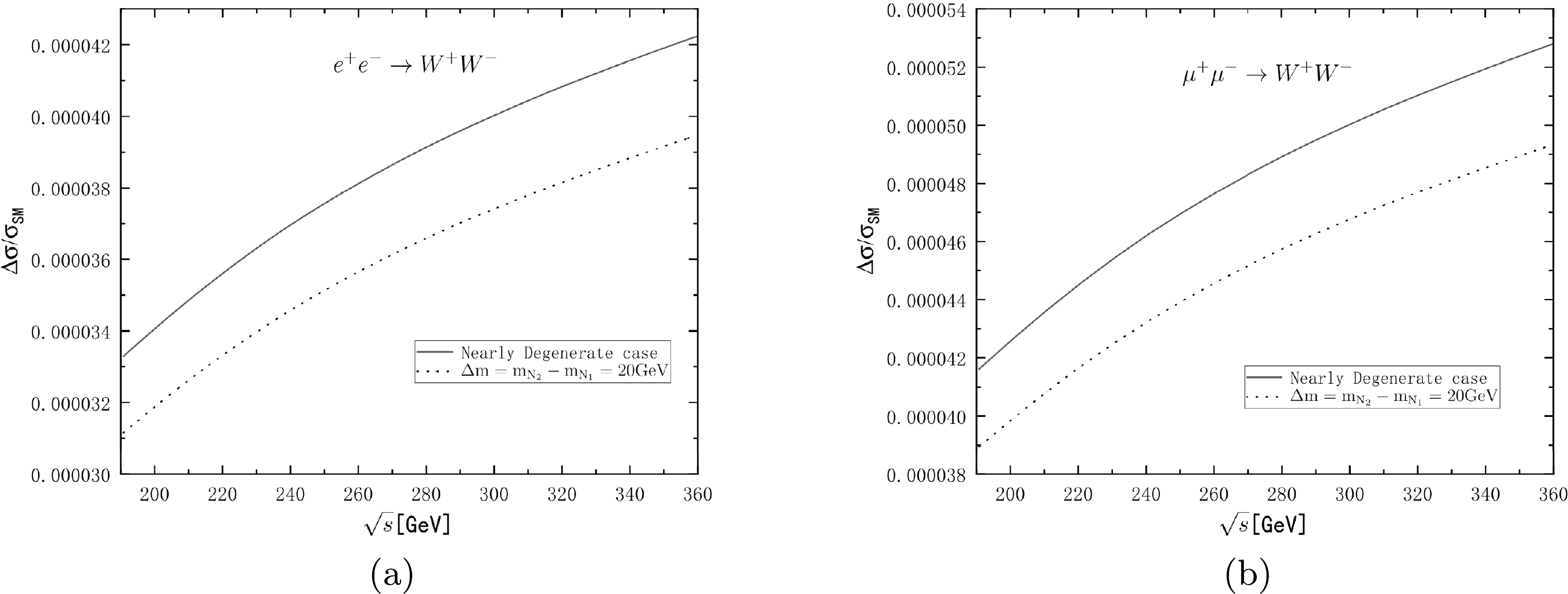

Figure 1

Figure 1. Cross section

$\Delta\sigma=\sigma_{\rm total}-\sigma_{\rm SM}$ of (a)

$e^+e^-\rightarrow W^+W^-$ and (b)

$\mu^+\mu^-\rightarrow W^+W^-$ compared with the cross section of the SM part

$\Delta\sigma/\sigma_{\rm SM}$ as a function of centre-of-mass energy

$\sqrt{s}$ . The black curves represent the case in which two heavy Majorana neutrinos are nearly degenerate, and the dotted curves correspond to the case in which

$\Delta m=m_{N_2}-m_{N_1}=20$ GeV, where

$m_{N_1}=15$ GeV.

DownLoad: Full-Size Img PowerPoint

We calculate the total cross section of the process $e^+e^-(\mu^+\mu^-)\rightarrow W^\pm W^\mp\rightarrow \ell^\pm\ell^\pm+4j$ . In this study, we take $\ell = \mu$ , and the case of $\ell = e$ can be analyzed using the same method. According to Eq. (7), there are phases in the mixing parameters $R_{\ell k}$ . When there is interference between different heavy Majorana neutrinos, one term appears, which we refer to as the CP phase $\Delta\phi= \phi_{\ell N_2}-\phi_{\ell N_1}$ . This phase also influences the total cross section and causes the difference between the cross sections of $e^+e^-\rightarrow \ell^+\ell^+4j$ and $e^+e^-(\mu^+\mu^-)\rightarrow \ell^-\ell^-4j$ , which leads to CP violation. The results of the total cross section of $e^+e^-\rightarrow \ell^\pm\ell^\pm 4j$ and $\mu^+\mu^-\rightarrow \ell^\pm\ell^\pm 4j$ are shown in Fig. 2, where the total cross sections are functions of $\sqrt{s}$ . To observe the difference between $e^+e^- (\mu^+\mu^-) \rightarrow \ell^+\ell^++4j$ and $e^+e^-(\mu^+\mu^-)\rightarrow \ell^-\ell^-+4j$ clearly, the CP phase is set to $\Delta\phi=-3\pi/5$ , where CP violation is close to the maximum value [14]. The cross sections reach the maximum at approximately $\sqrt{s}=190$ GeV. To observe the influence of the CP phase $\Delta\phi$ on cross section, we present the result of the cross sections as a function of $\Delta\phi$ in Fig. 3. The total cross sections of $e^+e^-(\mu^+\mu^-)\rightarrow W^+W^-\rightarrow \mu^+\mu^+4j$ and $e^+e^-(\mu^+\mu^-)\rightarrow W^+W^- \rightarrow \mu^-\mu^-4j$ reach the maximum at approximately $\Delta\phi=-0.1\pi$ and $\Delta\phi=0.1\pi$ , respectively. We also calculate the events and total cross sections at future lepton colliders for $e^+e^-(\mu^+\mu^-)\rightarrow \ell^+\ell^+4j$ and $e^+e^-(\mu^+\mu^-) \rightarrow \ell^-\ell^-4j$ with $\Delta\phi=-\pi/10$ and $\Delta\phi= \pi/10$ separately at $\sqrt{s}=$ 190 GeV and $m_{N_1}=15$ GeV. The events for $e^+e^-\rightarrow \ell^\pm\ell^\pm 4j$ with a luminosity of ${\cal L}= 3000~\rm fb^{-1}$ can reach 13 with $\sigma_{\rm total}=4.6\times 10^{-3}~\rm fb$ , whereas for $\mu^+\mu^-\rightarrow \ell^\pm\ell^\pm 4j$ with a luminosity of ${\cal L}=1000~\rm fb^{-1}$ , they can reach 4 with $\sigma_{\rm total}=4.6\times 10^{-3}~\rm fb$ . Therefore, it is possible to find heavy Majorana neutrinos at future lepton colliders at a luminosity of ${\cal L}=1000~\rm fb^{-1}$ or higher. We then analyze the CP violation in the process $\ell^+\ell^-\rightarrow \mu^+\mu^+4j$ , where $\ell^+\ell^-=e^+e^-$ or $\mu^+\mu^-$ , and we define the CP violation as

Figure 2

Figure 2. Total cross section of (a)

$e^+e^-\rightarrow \mu^\pm\mu^\pm 4j$ and (b)

$\mu^+\mu^-\rightarrow \mu^\pm\mu^\pm 4j$ as functions of

$\sqrt{s}$ . The CP phase is set to

$\Delta\phi=\phi_{\ell N_2}-\phi_{\ell N_1}=-3\pi/5$ , and

$m_{N_1}=15$ GeV, where two heavy Majorana neutrinos are nearly degenerate.

DownLoad: Full-Size Img PowerPoint

Figure 3

Figure 3. Total cross section of (a)

$e^+e^-\rightarrow \mu^\pm\mu^\pm 4j$ and (b)

$\mu^+\mu^-\rightarrow \mu^\pm\mu^\pm 4j$ as functions of the CP phase

$\Delta\phi$ .

$\sqrt{s}=190$ GeV and

$m_{N_1}=$ 15 GeV, where two heavy Majorana neutrinos are nearly degenerate.

DownLoad: Full-Size Img PowerPoint

$\begin{eqnarray} {\cal A}_{CP}=\frac{{\rm Br}(\ell^+\ell^-\rightarrow \mu^+\mu^+4j)-{\rm Br}(\ell^+\ell^-\rightarrow \mu^-\mu^-4j)}{{\rm Br}(\ell^+\ell^-\rightarrow \mu^+\mu^+4j)+{\rm Br}(\ell^+\ell^-\rightarrow \mu^-\mu^-4j)}\;, \end{eqnarray}$

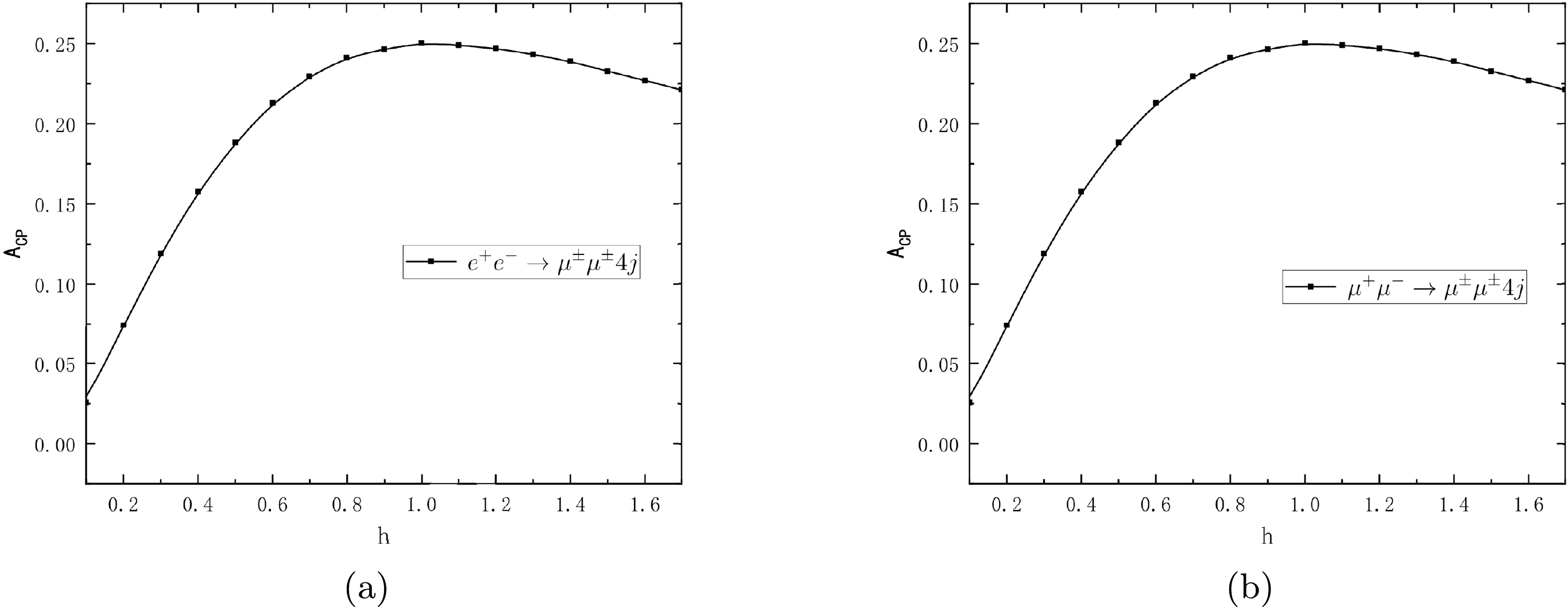
(15)

and then we define $h=\Delta m/\Gamma_{N_1}$ , where $\Gamma_{N_1}$ is the total decay width of a heavy Majorana neutrino $N_1$ , and its influence on CP violation is presented in Fig. 4. We can see that CP violation of $e^+e^-\rightarrow \mu^\pm\mu^\pm 4j$ reaches the maximum value at approximately $h=1$ , the same as in $\mu^+\mu^-\rightarrow \mu^\pm\mu^\pm 4j$ .

Figure 4

Figure 4.

${A}_{CP}$ of (a)

$e^+e^-\rightarrow \mu^\pm\mu^\pm 4j$ and (b)

$\mu^+\mu^-\rightarrow \mu^\pm\mu^\pm 4j$ as a function of

$\Delta m=m_{N_2}-m_{N_1}$ ,

$\Delta\phi=-\pi/2$ ,

$m_{N_1}=15$ GeV,

$\sqrt{s}=190$ GeV.

DownLoad: Full-Size Img PowerPoint

IV. SUMMARY

I. INTRODUCTION
II. BRIEF REVIEW OF THEORETICAL MODEL
III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS
IV. SUMMARY
ACKNOWLEDGEMENTS
APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

Neutrino oscillation experiments show that neutrinos have minor non-zero masses, which insinuates the existence of NP beyond the SM. If we extend the SM by introducing heavy Majorana neutrinos and allowing for LNV, we can explain the tiny neutrino masses via seesaw mechanisms and the baryon asymmetry of the Universe. In this paper, we investigate the prospect of searching for heavy Majorana neutrinos in rare W decays at future lepton colliders, such as the CLIC, ILC, and MuC. The LNV process can be used as a probe to find NP. CP violation exists in this type of rare decay of W pairs. The significant interference of contributions from two different Majorana neutrinos produces CP violation between $W^+\rightarrow \ell^+_\alpha\ell^+_\beta(\bar{q}q^\prime)^-$ and $W^-\rightarrow \ell^-_\alpha\ell^-_\beta(q\bar{q}^\prime)^+$ . In this study, we analyze the process of W pair production via $e^+e^-$ and $\mu^+\mu^-$ collisions at the CLIC and MuC, where we add two heavy Majorana neutrinos as the contributions of the NP part. The cross section of the NP part is too small in W pair production, and it is not possible to search for heavy Majorana neutrinos here. Instead, we must find them in rare W decays. We find that for the case in which $\Delta m$ is considerable, the cross section contributed by the NP part is significantly smaller when the neutrinos are nearly degenerate. We find that the total cross section of the process reaches the maxium value at approximately $\sqrt{s}=$ 190 GeV. At $\sqrt{s}=190$ GeV, there are 13 events with a luminosity of ${\cal L}=3000~\rm fb^{-1}$ for $e^+e^-\rightarrow \ell^+\ell^+4j$ and four events with a luminosity of ${\cal L}=1000~ \rm fb^{-1}$ for $\mu^+\mu^-\rightarrow \ell^+\ell^+4j$ . The investigation in this paper may help search for NP signals with respect to the LNV process via heavy Majorana neutrinos at future high energy lepton colliders.

ACKNOWLEDGEMENTS

I. INTRODUCTION
II. BRIEF REVIEW OF THEORETICAL MODEL
III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS
IV. SUMMARY
ACKNOWLEDGEMENTS
APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

The authors thank the members of the Institute of Theoretical Physics of Shandong University for their helpful discussions.

APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

I. INTRODUCTION
II. BRIEF REVIEW OF THEORETICAL MODEL
III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS
IV. SUMMARY
ACKNOWLEDGEMENTS
APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

In this appendix, we explicitly show the squared scattering amplitude given in Eqs. (11)–(14).The functions ${\cal F}_{12}$ , ${\cal F}_{13}$ , ${\cal F}_{23}$ , ${\cal F}_{45}$ , ${\cal F}_{14}$ , ${\cal F}_{15}$ , ${\cal F}_{24}$ , ${\cal F}_{25}$ , ${\cal F}_{34}$ , and ${\cal F}_{35}$ can be expressed as

${\cal F}_{12}={\cal T}_{\gamma Z}\left(D_\gamma D_Z^\ast+D_ZD_\gamma^\ast\right)\; ,\tag{A1}$

${\cal F}_{13}={\cal T}_{\gamma n}\left(D_\gamma D_\nu^\ast+D_\nu D_\gamma^\ast\right)\; ,\tag{A2}$

${\cal F}_{14}={\cal T}_{\gamma n}\left(D_\gamma D_{N_1}^\ast+D_{N_2}D_\gamma^\ast \right)\; , \tag{A3}$

${\cal F}_{15}={\cal T}_{\gamma n}\left(D_\gamma D_{N_2}^\ast+D_{N_2}D_\gamma^\ast \right)\; , \tag{A4}$

${\cal F}_{23}={\cal T}_{Zn}\left(D_Z D_{\nu}^\ast+D_{\nu}D_Z^\ast \right)\; , \tag{A5}$

${\cal F}_{24}={\cal T}_{Zn}\left(D_Z D_{N_1}^\ast+D_{N_1}D_Z^\ast \right)\; , \tag{A6}$

${\cal F}_{25}={\cal T}_{Zn}\left(D_Z D_{N_2}^\ast+D_{N_2}D_Z^\ast \right)\; , \tag{A7}$

${\cal F}_{34}={\cal T}_{n}\left(D_\nu D_{N_1}^\ast+D_{N_1}D_\nu^\ast \right)\; , \tag{A8}$

${\cal F}_{35}={\cal T}_{n}\left(D_\nu D_{N_2}^\ast+D_{N_2}D_\nu^\ast \right)\; , \tag{A9}$

${\cal F}_{45}={\cal T}_{n}\left(D_{N_1} D_{N_2}^\ast+D_{N_2}D_{N_1}^\ast \right)\; , \tag{A10}$

respectively, where $D_X(p^2)$ is the Breit-Wigner propagator, which can be defined as

$D_X(p^2)=\frac{1}{p^2-m^2_X+{\rm i} m_X\Gamma_X}\; , \tag{A11}$

with $m_X$ and $\Gamma_X$ as the mass and total decay width of the corresponding particles.

The explicit expressions of ${\cal T}_\gamma$ , ${\cal T}_Z$ , ${\cal T}_n$ , ${\cal T}_{\gamma Z}$ , ${\cal T}_{\gamma n}$ , and ${\cal T}_{Z n}$ can be given by

$\begin{aligned}[b] {\cal T}_{\gamma}= & -24m_W^2s-\frac{2s^2t(s+t)}{m_W^4}-24(s^2+st+t^2)\\&+\frac{2s(3s^2+4st+t^2)}{m_W^2}\;, \end{aligned} \tag{A12}$

$\begin{aligned}[b] {\cal T}_{Z}=& \frac{(4\sin^2\theta_w-8\sin^4\theta_w-1)}{4m_W^4}\biggl\{12m_W^6s+s^2t(s+t)\\&+12m_W^4(s^2+st+t^2)-{} m_W^2s(3s^2+4st+4t^2)\}\;, \end{aligned}\tag{A13}$

${\cal T}_{n}=-m_W^2+(s-5t)t+\frac{(s-2t)t^2}{m_W^2}-\frac{t^3(s+t)}{m_W^4}\;, \tag{A14}$

$\begin{aligned}[b] {\cal T}_{\gamma Z}= & \frac{(1-4\sin^2\theta_w)}{2m_W^4}\biggl\{12m_W^6s+s^2t(s+t)\\&+12m_W^4(s^2+st+t^2)-m_W^2s(3s^2+4st+4t^2)\}\;, \end{aligned} \tag{A15}$

$\begin{aligned}[b] {\cal T}_{\gamma n}= & -6m_W^2s+\frac{st^2(s+t)}{m_W^4}-3(s^2+2t^2)\\&-\frac{t(2s^2+st+2t^2)}{m_W^2} \;, \end{aligned}\tag{A16}$

$\begin{aligned}[b] {\cal T}_{Zn}= & \frac{1-2\sin^2\theta_w}{2m_W^4}\biggl\{6m_W^6s-st^2(s+t)\\&+3m_W^4(s^2+2t^2)+m_W^2t(2s^2+st+2t^2)\}\;, \end{aligned}\tag{A17}$

where $s=2(l_1\cdot l_2)$ , and $t=-2(l_2\cdot k_p)$ .

References

[1]	P. Minkowski, Phys. Lett. B 67, 421-428 (1977) doi: 10.1016/0370-2693(77)90435-X
[2]	T. Yanagida, In Proceedings of the Workshop on Unified Theory and the Baryon Number of the Universe, edited by O. Sawada and A. Sugamoto, (KEK, Tsukuba, 1979), p. 95
[3]	M. Gell-Mann, P. Ramond, and R. Slansky, In Supergravity, edited by P. van Nieuwenhuizen and D. Z. Freeman, (North-Holland, Amsterdam, 1979), p. 315
[4]	S. L. Glashow, In Quarks and Leptons, edited by M. Levy et al., (Plenum, New York, 1980), p. 707
[5]	R. N. Mohapatra and G. Senjanovic, Phys. Rev. Lett. 44, 912 (1980) doi: 10.1103/PhysRevLett.44.912
[6]	N. Aghanim et al. (Planck), Astron. Astrophys. 641, A6 (2020) [Erratum: Astron. Astrophys. 652, C4 (2021)]
[7]	N. S. Manton, Phys. Rev. D 28, 2019 (1983) doi: 10.1103/PhysRevD.28.2019
[8]	F. R. Klinkhamer and N. S. Manton, Phys. Rev. D 30, 2212 (1984) doi: 10.1103/PhysRevD.30.2212
[9]	W. H. Furry, Phys. Rev. 56, 1184-1193 (1939) doi: 10.1103/PhysRev.56.1184
[10]	S. R. Elliott and J. Engel, J. Phys. G 30, R183-R215 (2004) doi: 10.1088/0954-3899/30/9/R01
[11]	S. Antusch, E. Cazzato, and O. Fischer, Int. J. Mod. Phys. A 32(14), 1750078 (2017) doi: 10.1142/S0217751X17500786
[12]	Y. Cai, T. Han, T. Li et al., Front. in Phys. 6, 40 (2018) doi: 10.3389/fphy.2018.00040
[13]	F. F. Deppisch, P. S. Bhupal Dev, and A. Pilaftsis, New J. Phys. 17(7), 075019 (2015) doi: 10.1088/1367-2630/17/7/075019
[14]	P. C. Lu, Z. G. Si, Z. Wang et al., Chin. Phys. C 46(10), 103108 (2022) doi: 10.1088/1674-1137/ac7eb2
[15]	P. C. Lu, Z. G. Si, Z. Wang et al., Phys. Rev. D 104(11), 115003 (2021) doi: 10.1103/PhysRevD.104.115003
[16]	A. Atre, V. Barger, and T. Han, Phys. Rev. D 71, 113014 (2005) doi: 10.1103/PhysRevD.71.113014
[17]	G. Cvetic, C. Dib, S. K. Kang et al., Phys. Rev. D 82, 053010 (2010) doi: 10.1103/PhysRevD.82.053010
[18]	Y. Wang, S. S. Bao, Z. H. Li et al., Phys. Lett. B 736, 428-432 (2014) doi: 10.1016/j.physletb.2014.08.006
[19]	H. R. Dong, F. Feng, and H. B. Li, Chin. Phys. C 39(1), 013101 (2015) doi: 10.1088/1674-1137/39/1/013101
[20]	G. Cvetic and C. S. Kim, Phys. Rev. D 94(5), 053001 (2016) [Erratum: Phys. Rev. D 95(3), 039901 (2017)]
[21]	V. Gribanov, S. Kovalenko, and I. Schmidt, Nucl. Phys. B 607, 355-368 (2001) doi: 10.1016/S0550-3213(01)00169-9
[22]	A. Kobach and S. Dobbs, Phys. Rev. D 91(5), 053006 (2015) doi: 10.1103/PhysRevD.91.053006
[23]	H. Yuan, Y. Jiang, T. h. Wang et al., J. Phys. G 44(11), 115002 (2017) doi: 10.1088/1361-6471/aa8a1e
[24]	S. Bar-Shalom, N. G. Deshpande, G. Eilam et al., Phys. Lett. B 643, 342-347 (2006) doi: 10.1016/j.physletb.2006.10.060
[25]	Z. Si and K. Wang, Phys. Rev. D 79, 014034 (2009) doi: 10.1103/PhysRevD.79.014034
[26]	D. Delepine, G. Lopez Castro, and N. Quintero, Heavy Majorana Neutrinos and Delta L=2 B and top decays in B factories, PoS DSU2012, 025 (2012)
[27]	N. Liu, Z. G. Si, L. Wu et al., Phys. Rev. D 101(7), 071701 (2020) doi: 10.1103/PhysRevD.101.071701
[28]	G. Cvetic, C. Dib, C. S. Kim et al., Symmetry 7, 726-773 (2015) doi: 10.3390/sym7020726
[29]	G. Cvetic, C. S. Kim, S. Mendizabal et al., Eur. Phys. J. C 80(11), 1052 (2020) doi: 10.1140/epjc/s10052-020-08625-0
[30]	R. M. Godbole, S. P. Maharathy, S. Mandal et al., Phys. Rev. D 104, 095009 (2021) doi: 10.1103/PhysRevD.104.095009
[31]	J. Zhang, T. Wang, G. Li et al., Phys. Rev. D 103(3), 035015 (2021) doi: 10.1103/PhysRevD.103.035015
[32]	A. Abada, C. Hati, X. Marcano et al., JHEP 09, 017 (2019) doi: 10.1007/JHEP09(2019)017
[33]	J. Zamora-Saa, JHEP 05, 110 (2017) doi: 10.1007/JHEP05(2017)110
[34]	S. Tapia and J. Zamora-Saá, Nucl. Phys. B 952, 114936 (2020) doi: 10.1016/j.nuclphysb.2020.114936
[35]	F. Najafi, J. Kumar, and D. London, JHEP 04, 021 (2021) doi: 10.1007/JHEP04(2021)021
[36]	A. Abada, P. Escribano, X. Marcano et al., Eur. Phys. J. C 82(11), 1030 (2022) doi: 10.1140/epjc/s10052-022-11011-7
[37]	L. Linssen, A. Miyamoto, M. Stanitzki et al., Physics and Detectors at CLIC: CLIC Conceptual Design Report, doi: 10.5170/CERN-2012-003, arXiv: 1202.5940[physics.ins-det]
[38]	T. Behnke, J. E. Brau, B. Foster et al., The International Linear Collider Technical Design Report - Volume 1: Executive Summary, arXiv: 1306.6327[physics.acc-ph]
[39]	D. Stratakis et al. (Muon Collider), A Muon Collider Facility for Physics Discovery, arXiv: 2203.08033 [physics.acc-ph]
[40]	K. Mekała, J. Reuter, and A. F.Zarnecki, JHEP 06, 010 (2022) doi: 10.1007/JHEP06(2022)010
[41]	Z. z. Xing, Phys. Lett. B 660, 515-521 (2008) doi: 10.1016/j.physletb.2008.01.038
[42]	A. Atre, T. Han, S. Pascoli et al., JHEP 05, 030 (2009) doi: 10.1088/1126-6708/2009/05/030
[43]	A. M. Sirunyan et al. (CMS), Phys. Rev. Lett. 120(22), 221801 (2018) doi: 10.1103/PhysRevLett.120.221801
[44]	J. L. Tastet, O. Ruchayskiy, and I. Timiryasov, JHEP 12, 182 (2021) doi: 10.1007/JHEP12(2021)182

References

[1]	P. Minkowski, Phys. Lett. B 67, 421-428 (1977) doi: 10.1016/0370-2693(77)90435-X
[2]	T. Yanagida, In Proceedings of the Workshop on Unified Theory and the Baryon Number of the Universe, edited by O. Sawada and A. Sugamoto, (KEK, Tsukuba, 1979), p. 95
[3]	M. Gell-Mann, P. Ramond, and R. Slansky, In Supergravity, edited by P. van Nieuwenhuizen and D. Z. Freeman, (North-Holland, Amsterdam, 1979), p. 315
[4]	S. L. Glashow, In Quarks and Leptons, edited by M. Levy et al., (Plenum, New York, 1980), p. 707
[5]	R. N. Mohapatra and G. Senjanovic, Phys. Rev. Lett. 44, 912 (1980) doi: 10.1103/PhysRevLett.44.912
[6]	N. Aghanim et al. (Planck), Astron. Astrophys. 641, A6 (2020) [Erratum: Astron. Astrophys. 652, C4 (2021)]
[7]	N. S. Manton, Phys. Rev. D 28, 2019 (1983) doi: 10.1103/PhysRevD.28.2019
[8]	F. R. Klinkhamer and N. S. Manton, Phys. Rev. D 30, 2212 (1984) doi: 10.1103/PhysRevD.30.2212
[9]	W. H. Furry, Phys. Rev. 56, 1184-1193 (1939) doi: 10.1103/PhysRev.56.1184
[10]	S. R. Elliott and J. Engel, J. Phys. G 30, R183-R215 (2004) doi: 10.1088/0954-3899/30/9/R01
[11]	S. Antusch, E. Cazzato, and O. Fischer, Int. J. Mod. Phys. A 32(14), 1750078 (2017) doi: 10.1142/S0217751X17500786
[12]	Y. Cai, T. Han, T. Li et al., Front. in Phys. 6, 40 (2018) doi: 10.3389/fphy.2018.00040
[13]	F. F. Deppisch, P. S. Bhupal Dev, and A. Pilaftsis, New J. Phys. 17(7), 075019 (2015) doi: 10.1088/1367-2630/17/7/075019
[14]	P. C. Lu, Z. G. Si, Z. Wang et al., Chin. Phys. C 46(10), 103108 (2022) doi: 10.1088/1674-1137/ac7eb2
[15]	P. C. Lu, Z. G. Si, Z. Wang et al., Phys. Rev. D 104(11), 115003 (2021) doi: 10.1103/PhysRevD.104.115003
[16]	A. Atre, V. Barger, and T. Han, Phys. Rev. D 71, 113014 (2005) doi: 10.1103/PhysRevD.71.113014
[17]	G. Cvetic, C. Dib, S. K. Kang et al., Phys. Rev. D 82, 053010 (2010) doi: 10.1103/PhysRevD.82.053010
[18]	Y. Wang, S. S. Bao, Z. H. Li et al., Phys. Lett. B 736, 428-432 (2014) doi: 10.1016/j.physletb.2014.08.006
[19]	H. R. Dong, F. Feng, and H. B. Li, Chin. Phys. C 39(1), 013101 (2015) doi: 10.1088/1674-1137/39/1/013101
[20]	G. Cvetic and C. S. Kim, Phys. Rev. D 94(5), 053001 (2016) [Erratum: Phys. Rev. D 95(3), 039901 (2017)]
[21]	V. Gribanov, S. Kovalenko, and I. Schmidt, Nucl. Phys. B 607, 355-368 (2001) doi: 10.1016/S0550-3213(01)00169-9
[22]	A. Kobach and S. Dobbs, Phys. Rev. D 91(5), 053006 (2015) doi: 10.1103/PhysRevD.91.053006
[23]	H. Yuan, Y. Jiang, T. h. Wang et al., J. Phys. G 44(11), 115002 (2017) doi: 10.1088/1361-6471/aa8a1e
[24]	S. Bar-Shalom, N. G. Deshpande, G. Eilam et al., Phys. Lett. B 643, 342-347 (2006) doi: 10.1016/j.physletb.2006.10.060
[25]	Z. Si and K. Wang, Phys. Rev. D 79, 014034 (2009) doi: 10.1103/PhysRevD.79.014034
[26]	D. Delepine, G. Lopez Castro, and N. Quintero, Heavy Majorana Neutrinos and Delta L=2 B and top decays in B factories, PoS DSU2012, 025 (2012)
[27]	N. Liu, Z. G. Si, L. Wu et al., Phys. Rev. D 101(7), 071701 (2020) doi: 10.1103/PhysRevD.101.071701
[28]	G. Cvetic, C. Dib, C. S. Kim et al., Symmetry 7, 726-773 (2015) doi: 10.3390/sym7020726
[29]	G. Cvetic, C. S. Kim, S. Mendizabal et al., Eur. Phys. J. C 80(11), 1052 (2020) doi: 10.1140/epjc/s10052-020-08625-0
[30]	R. M. Godbole, S. P. Maharathy, S. Mandal et al., Phys. Rev. D 104, 095009 (2021) doi: 10.1103/PhysRevD.104.095009
[31]	J. Zhang, T. Wang, G. Li et al., Phys. Rev. D 103(3), 035015 (2021) doi: 10.1103/PhysRevD.103.035015
[32]	A. Abada, C. Hati, X. Marcano et al., JHEP 09, 017 (2019) doi: 10.1007/JHEP09(2019)017
[33]	J. Zamora-Saa, JHEP 05, 110 (2017) doi: 10.1007/JHEP05(2017)110
[34]	S. Tapia and J. Zamora-Saá, Nucl. Phys. B 952, 114936 (2020) doi: 10.1016/j.nuclphysb.2020.114936
[35]	F. Najafi, J. Kumar, and D. London, JHEP 04, 021 (2021) doi: 10.1007/JHEP04(2021)021
[36]	A. Abada, P. Escribano, X. Marcano et al., Eur. Phys. J. C 82(11), 1030 (2022) doi: 10.1140/epjc/s10052-022-11011-7
[37]	L. Linssen, A. Miyamoto, M. Stanitzki et al., Physics and Detectors at CLIC: CLIC Conceptual Design Report, doi: 10.5170/CERN-2012-003, arXiv: 1202.5940[physics.ins-det]
[38]	T. Behnke, J. E. Brau, B. Foster et al., The International Linear Collider Technical Design Report - Volume 1: Executive Summary, arXiv: 1306.6327[physics.acc-ph]
[39]	D. Stratakis et al. (Muon Collider), A Muon Collider Facility for Physics Discovery, arXiv: 2203.08033 [physics.acc-ph]
[40]	K. Mekała, J. Reuter, and A. F.Zarnecki, JHEP 06, 010 (2022) doi: 10.1007/JHEP06(2022)010
[41]	Z. z. Xing, Phys. Lett. B 660, 515-521 (2008) doi: 10.1016/j.physletb.2008.01.038
[42]	A. Atre, T. Han, S. Pascoli et al., JHEP 05, 030 (2009) doi: 10.1088/1126-6708/2009/05/030
[43]	A. M. Sirunyan et al. (CMS), Phys. Rev. Lett. 120(22), 221801 (2018) doi: 10.1103/PhysRevLett.120.221801
[44]	J. L. Tastet, O. Ruchayskiy, and I. Timiryasov, JHEP 12, 182 (2021) doi: 10.1007/JHEP12(2021)182

[1]	M. Ablikim , M. N. Achasov , P. Adlarson , O. Afedulidis , X. C. Ai , R. Aliberti , A. Amoroso , M. R. An , Q. An , Y. Bai , O. Bakina , I. Balossino , Y. Ban , H.-R. Bao , V. Batozskaya , K. Begzsuren , N. Berger , M. Berlowski , M. Bertani , D. Bettoni , F. Bianchi , E. Bianco , A. Bortone , I. Boyko , R. A. Briere , A. Brueggemann , H. Cai , X. Cai , A. Calcaterra , G. F. Cao , N. Cao , S. A. Cetin , J. F. Chang , G. R. Che , Y. Z. Che , G. Chelkov , C. Chen , Chao Chen , G. Chen , H. S. Chen , M. L. Chen , S. J. Chen , S. L. Chen , S. M. Chen , T. Chen , X. R. Chen , X. T. Chen , Y. B. Chen , Y. Q. Chen , Z. J. Chen , Z. Y. Chen , S. K. Choi , G. Cibinetto , S. C. Coen , F. Cossio , J. J. Cui , H. L. Dai , J. P. Dai , A. Dbeyssi , R. E. de Boer , D. Dedovich , Z. Y. Deng , A. Denig , I. Denysenko , M. Destefanis , F. De Mori , B. Ding , X. X. Ding , Y. Ding , Y. Ding , J. Dong , L. Y. Dong , M. Y. Dong , X. Dong , M. C. Du , S. X. Du , Z. H. Duan , P. Egorov , Y. H. Fan , J. Fang , S. S. Fang , W. X. Fang , Y. Fang , Y. Q. Fang , R. Farinelli , L. Fava , F. Feldbauer , G. Felici , C. Q. Feng , J. H. Feng , K. Fischer , M. Fritsch , C. D. Fu , J. L. Fu , Y. W. Fu , H. Gao , Y. N. Gao , Yang Gao , S. Garbolino , I. Garzia , L. Ge , P. T. Ge , Z. W. Ge , C. Geng , E. M. Gersabeck , A. Gilman , K. Goetzen , L. Gong , W. X. Gong , W. Gradl , S. Gramigna , M. Greco , M. H. Gu , Y. T. Gu , C. Y. Guan , A. Q. Guo , L. B. Guo , M. J. Guo , R. P. Guo , Y. P. Guo , A. Guskov , J. Gutierrez , T. T. Han , W. Y. Han , X. Q. Hao , F. A. Harris , K. K. He , K. L. He , F. H. Heinsius , C. H. Heinz , Y. K. Heng , C. Herold , T. Holtmann , P. C. Hong , G. Y. Hou , X. T. Hou , Y. R. Hou , Z. L. Hou , B. Y. Hu , H. M. Hu , J. F. Hu , T. Hu , Y. Hu , G. S. Huang , K. X. Huang , L. Q. Huang , X. T. Huang , Y. P. Huang , T. Hussain , F. Hölzken , N. Hüsken , N. in der Wiesche , J. Jackson , S. Jaeger , S. Janchiv , Q. Ji , Q. P. Ji , X. B. Ji , X. L. Ji , Y. Y. Ji , X. Q. Jia , Z. K. Jia , H. B. Jiang , P. C. Jiang , S. S. Jiang , T. J. Jiang , X. S. Jiang , Y. Jiang , J. B. Jiao , Z. Jiao , S. Jin , Y. Jin , M. Q. Jing , X. M. Jing , T. Johansson , S. Kabana , N. Kalantar-Nayestanaki , X. L. Kang , X. S. Kang , M. Kavatsyuk , B. C. Ke , V. Khachatryan , A. Khoukaz , R. Kiuchi , R. Kliemt , O. B. Kolcu , B. Kopf , M. Kuessner , X. Kui , N. Kumar , A. Kupsc , W. Kühn , J. J. Lane , P. Larin , A. Lavania , L. Lavezzi , T. T. Lei , Z. H. Lei , M. Lellmann , T. Lenz , C. Li , C. Li , C. H. Li , Cheng Li , D. M. Li , F. Li , G. Li , H. B. Li , H. J. Li , H. N. Li , Hui Li , J. R. Li , J. S. Li , J. W. Li , K. Li , K. L. Li , L. J. Li , L. K. Li , Lei Li , M. H. Li , P. R. Li , Q. X. Li , S. X. Li , T. Li , W. D. Li , W. G. Li , X. H. Li , X. L. Li , X. Y. Li , Y. G. Li , Z. J. Li , Z. X. Li , C. Liang , H. Liang , H. Liang , Y. F. Liang , Y. T. Liang , G. R. Liao , L. Z. Liao , Y. P. Liao , J. Libby , A. Limphirat , D. X. Lin , T. Lin , B. J. Liu , B. X. Liu , C. Liu , C. X. Liu , F. Liu , F. H. Liu , Feng Liu , G. M. Liu , H. Liu , H. B. Liu , H. H. Liu , H. M. Liu , Huihui Liu , J. B. Liu , J. Y. Liu , K. Liu , K. Y. Liu , Ke Liu , L. Liu , L. C. Liu , Lu Liu , M. H. Liu , P. L. Liu , Q. Liu , S. B. Liu , T. Liu , W. K. Liu , W. M. Liu , X. Liu , Y. Liu , Y. Liu , Y. B. Liu , Z. A. Liu , Z. Q. Liu , X. C. Lou , F. X. Lu , H. J. Lu , J. G. Lu , X. L. Lu , Y. Lu , Y. P. Lu , Z. H. Lu , C. L. Luo , M. X. Luo , T. Luo , X. L. Luo , X. R. Lyu , Y. F. Lyu , F. C. Ma , H. Ma , H. L. Ma , J. L. Ma , L. L. Ma , M. M. Ma , Q. M. Ma , R. Q. Ma , X. Y. Ma , Y. M. Ma , F. E. Maas , M. Maggiora , S. Malde , A. Mangoni , Y. J. Mao , Z. P. Mao , S. Marcello , Z. X. Meng , J. G. Messchendorp , G. Mezzadri , H. Miao , T. J. Min , R. E. Mitchell , X. H. Mo , B. Moses , N. Yu. Muchnoi , J. Muskalla , Y. Nefedov , F. Nerling , I. B. Nikolaev , Z. Ning , S. Nisar , Q. L. Niu , W. D. Niu , Y. Niu , S. L. Olsen , Q. Ouyang , S. Pacetti , X. Pan , Y. Pan , P. Patteri , Y. P. Pei , M. Pelizaeus , H. P. Peng , Y. Y. Peng , K. Peters , J. L. Ping , R. G. Ping , S. Plura , V. Prasad , F. Z. Qi , H. Qi , H. R. Qi , M. Qi , T. Y. Qi , S. Qian , W. B. Qian , C. F. Qiao , X. K. Qiao , J. J. Qin , L. Q. Qin , L. Y. Qin , X. P. Qin , X. S. Qin , Z. H. Qin , J. F. Qiu , S. Q. Qu , C. F. Redmer , K. J. Ren , A. Rivetti , M. Rolo , G. Rong , Ch. Rosner , M. Q. Ruan , S. N. Ruan , N. Salone , A. Sarantsev , Y. Schelhaas , K. Schoenning , M. Scodeggio , K. Y. Shan , W. Shan , X. Y. Shan , J. F. Shangguan , L. G. Shao , M. Shao , C. P. Shen , H. F. Shen , W. H. Shen , X. Y. Shen , B. A. Shi , H. Shi , H. C. Shi , J. L. Shi , J. Y. Shi , Q. Q. Shi , X. Shi , J. J. Song , T. Z. Song , W. M. Song , Y. J. Song , Y. X. Song , S. Sosio , S. Spataro , F. Stieler , Y. J. Su , G. B. Sun , G. X. Sun , H. Sun , H. K. Sun , J. F. Sun , K. Sun , L. Sun , S. S. Sun , T. Sun , W. Y. Sun , Y. Sun , Y. J. Sun , Y. Z. Sun , Z. T. Sun , C. J. Tang , G. Y. Tang , J. Tang , Y. A. Tang , L. Y. Tao , Q. T. Tao , M. Tat , J. X. Teng , V. Thoren , W. H. Tian , W. H. Tian , Y. Tian , Z. F. Tian , I. Uman , Y. Wan , S. J. Wang , B. Wang , B. L. Wang , Bo Wang , C. W. Wang , D. Y. Wang , F. Wang , H. J. Wang , J. P. Wang , K. Wang , L. L. Wang , L. W. Wang , M. Wang , N. Y. Wang , S. Wang , S. Wang , T. Wang , T. J. Wang , W. Wang , W. Wang , W. P. Wang , X. Wang , X. F. Wang , X. J. Wang , X. L. Wang , Y. Wang , Y. D. Wang , Y. F. Wang , Y. L. Wang , Y. N. Wang , Y. Q. Wang , Yaqian Wang , Yi Wang , Z. Wang , Z. L. Wang , Z. Y. Wang , Ziyi Wang , D. H. Wei , F. Weidner , S. P. Wen , C. Wenzel , U. Wiedner , G. Wilkinson , M. Wolke , L. Wollenberg , C. Wu , J. F. Wu , L. H. Wu , L. J. Wu , X. Wu , X. H. Wu , Y. Wu , Y. H. Wu , Y. J. Wu , Z. Wu , L. Xia , X. M. Xian , T. Xiang , D. Xiao , G. Y. Xiao , S. Y. Xiao , Y. L. Xiao , Z. J. Xiao , C. Xie , X. H. Xie , Y. Xie , Y. G. Xie , Y. H. Xie , Z. P. Xie , T. Y. Xing , C. F. Xu , C. J. Xu , G. F. Xu , H. Y. Xu , M. Xu , Q. J. Xu , Q. N. Xu , W. Xu , W. L. Xu , X. P. Xu , Y. Xu , Y. C. Xu , Z. P. Xu , Z. S. Xu , F. Yan , L. Yan , W. B. Yan , W. C. Yan , X. Q. Yan , H. J. Yang , H. L. Yang , H. X. Yang , T. Yang , Y. Yang , Y. F. Yang , Y. F. Yang , Y. X. Yang , Z. W. Yang , Z. P. Yao , M. Ye , M. H. Ye , J. H. Yin , Z. Y. You , B. X. Yu , C. X. Yu , G. Yu , J. S. Yu , T. Yu , X. D. Yu , Y. C. Yu , C. Z. Yuan , L. Yuan , S. C. Yuan , Y. Yuan , Z. Y. Yuan , C. X. Yue , A. A. Zafar , F. R. Zeng , S. H. Zeng , X. Zeng , Y. Zeng , X. Y. Zhai , Y. C. Zhai , Y. H. Zhan , A. Q. Zhang , B. L. Zhang , B. X. Zhang , D. H. Zhang , G. Y. Zhang , H. Zhang , H. C. Zhang , H. H. Zhang , H. H. Zhang , H. Q. Zhang , H. Y. Zhang , J. Zhang , J. Zhang , J. J. Zhang , J. L. Zhang , J. Q. Zhang , J. W. Zhang , J. X. Zhang , J. Y. Zhang , J. Z. Zhang , Jianyu Zhang , L. M. Zhang , Lei Zhang , P. Zhang , Q. Y. Zhang , S. H. Zhang , Shulei Zhang , X. D. Zhang , X. M. Zhang , X. Y. Zhang , Y. Zhang , Y. Zhang , Y. T. Zhang , Y. H. Zhang , Y. X. Zhang , Yan Zhang , Z. D. Zhang , Z. H. Zhang , Z. L. Zhang , Z. Y. Zhang , Z. Y. Zhang , G. Zhao , J. Y. Zhao , J. Z. Zhao , L. Zhao , Lei Zhao , M. G. Zhao , R. P. Zhao , S. J. Zhao , Y. B. Zhao , Y. X. Zhao , Z. G. Zhao , A. Zhemchugov , B. Zheng , J. P. Zheng , W. J. Zheng , Y. H. Zheng , B. Zhong , X. Zhong , L. P. Zhou , S. Zhou , X. Zhou , X. K. Zhou , X. R. Zhou , X. Y. Zhou , Y. Z. Zhou , J. Zhu , K. Zhu , K. J. Zhu , L. Zhu , L. X. Zhu , S. H. Zhu , S. Q. Zhu , T. J. Zhu , Y. C. Zhu , Z. A. Zhu , J. H. Zou , J. Zu , (BESIII Collaboration) . Search for the lepton number violation decay ϕ → π⁺π⁺e⁻e⁻ via J/ψ → ϕη. Chinese Physics C, 2025, 49(4): 043001. doi: 10.1088/1674-1137/ada350
[2]	Ke-Yao Feng , Xia Wan , You-Kai Wang , Chao Wu . Exploring HVV amplitudes with CP violation using decomposition and the on-shell scattering amplitude method. Chinese Physics C, 2023, 47(3): 033106. doi: 10.1088/1674-1137/aca8f5
[3]	Sheng Zeng , Yue Xu , Xiao-Rong Zhou , Jia-Jia Qin , Bo Zheng . Prospects of CP violation in Λ decay with a polarized electron beam at the STCF. Chinese Physics C, 2023, 47(11): 113001. doi: 10.1088/1674-1137/ace9c5
[4]	Gang Lü , Yan-Lin Zhao , Liang-Chen Liu , Xin-Heng Guo . Direct CP violation of three body decay processes from the resonance effect. Chinese Physics C, 2022, 46(11): 113101. doi: 10.1088/1674-1137/ac80ef
[5]	Peng-Cheng Lu , Zong-Guo Si , Zhe Wang , Xing-Hua Yang . Measuring CP violation in rare W decays at the LHC. Chinese Physics C, 2022, 46(10): 103108. doi: 10.1088/1674-1137/ac7eb2
[6]	Jing-Juan Qi , Zhen-Yang Wang , Jing Xu , Xin-Heng Guo . Studying the localized CP violation and the branching fraction of the ${\bar{B}^0\rightarrow K^-\pi^+\pi^+\pi^-}$ decay. Chinese Physics C, 2020, 44(10): 103104. doi: 10.1088/1674-1137/abac00
[7]	Hong-Lei Li , Peng-Cheng Lu , Cong-Feng Qiao , Zong-Guo Si , Ying Wang . Study of the Standard Model and Majorana neutrino contributions to ${ B}^{{ +}} { \to} { K}^{{ (*){ \pm}}}{ \mu}^{ +}{ \mu}^{{ \mp}}$ . Chinese Physics C, 2019, 43(2): 023101. doi: 10.1088/1674-1137/43/2/023101
[8]	DING Gui-Jun , ZHOU Ye-Ling . Predicting lepton flavor mixing from Δ(48) and generalized CP symmetries. Chinese Physics C, 2015, 39(2): 021001. doi: 10.1088/1674-1137/39/2/021001
[9]	XING Zhi-Zhong . Implications of the Daya Bay observation of θ₁₃ on the leptonic avor mixing structure and CP violation. Chinese Physics C, 2012, 36(4): 281-297. doi: 10.1088/1674-1137/36/4/L01
[10]	LIU Hao , GUO Xin-Heng , . Direct CP violation in B_(s)→J/ψP(V). Chinese Physics C, 2012, 36(7): 585-591. doi: 10.1088/1674-1137/36/7/003
[11]	WANG Dian-Fu , SUN Xiao-Yu , LIANG Chao . Dynamical CP violation at finite temperature. Chinese Physics C, 2012, 36(9): 805-809. doi: 10.1088/1674-1137/36/9/002
[12]	WANG Dian-Fu , SUN Xiao-Yu , CHANG Xiao-Jing . Dynamical CP violation of the generalized Yang-Mills model. Chinese Physics C, 2011, 35(2): 130-134. doi: 10.1088/1674-1137/35/2/004
[13]	XING Zhi-Zhong . An overview of D⁰-D⁰ mixing and CP violation. Chinese Physics C, 2008, 32(6): 483-487. doi: 10.1088/1674-1137/32/6/015
[14]	LI Hai-Bo . D⁰-D⁰ mixing and CP violation at BES-Ⅲ. Chinese Physics C, 2008, 32(6): 470-476. doi: 10.1088/1674-1137/32/6/013
[15]	XING Zhi-Zhong . Possible Implications of Small or Large CP Violation in Bd0 vs Bd0→J/ψKS Decays. Chinese Physics C, 2002, 26(3): 197-200.
[16]	YUE ChongXing , YANG ZhengTao , LU GongRu , LI WeiBin , SUN JunFeng . ETC Interactions and CP Violation in Top Quark Pair Production at the Next Linear Collider. Chinese Physics C, 2000, 24(12): 1088-1093.
[17]	Liu Yaoyang , Jiang Xiangdong , Zhou Jiange . A Quark Model Including Lepton Structure. Chinese Physics C, 1996, 20(S4): 339-351.
[18]	Xing Zhizhong . Quark Mass Matrices and CP Violation. Chinese Physics C, 1995, 19(7): 667-671.
[19]	LI Chong-Sheng , HU Shi-Ke . ONE LOOP CORRECTIONS OF THE FERMION MASSES AND THE CP-VIOLATION CALCULATIONS OF THE STRONG AND WEAK INTERACTIONS. Chinese Physics C, 1983, 7(3): 333-341.
[20]	CHEN FENG-ZHI , HAO CHUN . THE CP VIOLATION OF SU(7) MODEL. Chinese Physics C, 1982, 6(1): 30-35.

Access

Figures(4)

Get Citation

Peng-Cheng Lu, Zong-Guo Si, Zhe Wang, Xing-Hua Yang and Xin-Yi Zhang. Search for heavy Majorana neutrinos at future lepton colliders[J]. Chinese Physics C. doi: 10.1088/1674-1137/acb997

Peng-Cheng Lu, Zong-Guo Si, Zhe Wang, Xing-Hua Yang and Xin-Yi Zhang. Search for heavy Majorana neutrinos at future lepton colliders[J]. Chinese Physics C. doi: 10.1088/1674-1137/acb997 shu

RIS(for EndNote,Reference Manager,ProCite)

BibTex

Txt

Milestone

Received: 2022-12-20

Article Metric

Article Views(1646)
PDF Downloads(24)
Cited by(0)

Policy on re-use

To reuse of Open Access content published by CPC, for content published under the terms of the Creative Commons Attribution 3.0 license (“CC CY”), the users don’t need to request permission to copy, distribute and display the final published version of the article and to create derivative works, subject to appropriate attribution.

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

HTML

I. INTRODUCTION

Neutrinos in the standard model (SM) are strictly massless owing to the absence of right-handed chiral states and the requirement of $S U(2)_L$ gauge invariance and renormalizability. However, neutrino oscillation experiments show that neutrinos have minor non-zero masses, which insinuates the existence of new physics (NP) beyond the SM. To explain the tiny neutrino mass, we must extend the SM, and the mechanism with respect to neutrino mass generation is attracting increasing attention. An interesting mechanism to generate the neutrino mass which introduces heavy right-handed Majorana neutrinos ( $\overline{N^c_R}$ ) is known as the type-I seesaw mechanism [1–5]. In this mechanism, the Dirac neutrino mass terms are generated after spontaneous gauge symmetry breaking. In addition, the Majorana neutrinos can also form Majorana mass terms, $\overline{N^c_R}M_RN_R$ . The introduction of heavy Majorana neutrinos may lead to CP violation, which gives a reasonable explanation for the asymmetry of matter and antimatter. The asymmetry of baryon number in our Universe can be measured by the baryon-to-photon density ratio $\eta=n_B/n_\gamma$ . According to an analysis of a recent Planck measurement of the cosmic microwave background, the value of η is approximately $\eta\simeq (6.12\pm 0.03)\times10^{-10}$ [6]. This result is too large compared to the result expected by the SM. In a famous mechanism called leptogenesis, this asymmetry of baryon number can be produced by the lepton number asymmetry caused by the decay of Majorana neutrinos in the early Universe; the latter may turn into baryon number asymmetry through sphaleron processes [7, 8] in this situation. The existence of heavy Majorana neutrinos also leads to the violation of lepton number by two units, $\Delta L=2$ , such as the neutrinoless double-beta decay $(0\nu\beta\beta)$ [9, 10]. In our study, we consider rare W decay through Majorana neutrino exchange, which produces a same-sign dilepton in the final state. Generally, both light and heavy Majorana neutrinos can contribute to the W decay amplitude. However, the contribution of light Majorana neutrinos is strongly suppressed and can be safely neglected owing to the small mass, such as $\mathcal{O}(eV)$ . The process of the rare W decay $W^-\rightarrow \ell_1^-N\rightarrow \ell_1^-\ell_2^-(q\bar{q}^\prime)^+$ has been studied in literature (for examples of a review, see Refs. [11–15]). In the mass range $M_N<M_W$ , the $\Delta L=2$ same-sign dilepton production signal has been studied in rare meson decays [16–20], tau lepton decays [21–23], and even top quark decays [24–27]. There is a nonzero CP asymmetry induced by the difference between the rates of $W^+\rightarrow \ell_1^+\ell_2^+(\bar{q}q^\prime)^-$ and its CP-conjugate process $W^-\rightarrow \ell_1^-\ell_2^-(q\bar{q}^\prime)^+$ . This difference arises from the significant interference of different heavy Majorana neutrinos. We can use the lepton number violation (LNV) process as a probe to study heavy Majorana neutrinos. Theorists have conducted numerous studies on the prospect of observing CP asymmetry via LNV processes in which CP asymmetry can be observed in the decays of mesons [28–32] and tau leptons [33, 34]. Recently, the authors of Refs. [35, 36] studied CP asymmetry in rare W decays at the LHC; however, the CP violation effect produced in the situation they considered is influenced by the initial parton distribution functions in protons. In this study, we investigate the prospect of searching for heavy Majorana neutrinos in future lepton colliders such as the Compact Linear Collider (CLIC) [37], International Linear Collider (ILC) [38], and Muon Collider (MuC) [39], which provide a significantly cleaner environment. We analyze the process of $W^\pm$ pair production in $e^+e^-$ collisons with the ILC running at 190 GeV and the $\mu^+\mu^-$ collison with the MuC running at 190 GeV, where $W^+$ and $W^-$ arise from $e^+e^-$ and $\mu^+\mu^-$ collisions, and the influence of the parton distribution functions in protons on CP violation can be canceled. In principle, the number n of right-handed heavy Majorana neutrinos introduced in the type-I seesaw mechanism is a free parameter. We take $n\geq 2$ as two neutrino mass-squared differences between observed light neutrinos. Another reason is that CP violation requires the interference of at least two different Majorana neutrinos. For convenience, we take only two heavy Majorana neutrinos, $N_1$ and $N_2$ , into consideration, and the general case with more Majorana neutrinos can be analyzed in a similar way.

This paper is organized as follows. The model including heavy Majorana neutrinos is briefly reviewed in Section II. Then, we investigate W pair production and their rare decays via Majorana neutrinos at future lepton colliders in Section III. Finally, a short summary is given in Section IV.

III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS

IV. SUMMARY

Neutrino oscillation experiments show that neutrinos have minor non-zero masses, which insinuates the existence of NP beyond the SM. If we extend the SM by introducing heavy Majorana neutrinos and allowing for LNV, we can explain the tiny neutrino masses via seesaw mechanisms and the baryon asymmetry of the Universe. In this paper, we investigate the prospect of searching for heavy Majorana neutrinos in rare W decays at future lepton colliders, such as the CLIC, ILC, and MuC. The LNV process can be used as a probe to find NP. CP violation exists in this type of rare decay of W pairs. The significant interference of contributions from two different Majorana neutrinos produces CP violation between $W^+\rightarrow \ell^+_\alpha\ell^+_\beta(\bar{q}q^\prime)^-$ and $W^-\rightarrow \ell^-_\alpha\ell^-_\beta(q\bar{q}^\prime)^+$ . In this study, we analyze the process of W pair production via $e^+e^-$ and $\mu^+\mu^-$ collisions at the CLIC and MuC, where we add two heavy Majorana neutrinos as the contributions of the NP part. The cross section of the NP part is too small in W pair production, and it is not possible to search for heavy Majorana neutrinos here. Instead, we must find them in rare W decays. We find that for the case in which $\Delta m$ is considerable, the cross section contributed by the NP part is significantly smaller when the neutrinos are nearly degenerate. We find that the total cross section of the process reaches the maxium value at approximately $\sqrt{s}=$ 190 GeV. At $\sqrt{s}=190$ GeV, there are 13 events with a luminosity of ${\cal L}=3000~\rm fb^{-1}$ for $e^+e^-\rightarrow \ell^+\ell^+4j$ and four events with a luminosity of ${\cal L}=1000~ \rm fb^{-1}$ for $\mu^+\mu^-\rightarrow \ell^+\ell^+4j$ . The investigation in this paper may help search for NP signals with respect to the LNV process via heavy Majorana neutrinos at future high energy lepton colliders.

ACKNOWLEDGEMENTS

The authors thank the members of the Institute of Theoretical Physics of Shandong University for their helpful discussions.

APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

Reference (44)

Search for heavy Majorana neutrinos at future lepton colliders

Abstract：

I. INTRODUCTION

I. INTRODUCTION
II. BRIEF REVIEW OF THEORETICAL MODEL
III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS
IV. SUMMARY
ACKNOWLEDGEMENTS
APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

II. BRIEF REVIEW OF THEORETICAL MODEL

I. INTRODUCTION
II. BRIEF REVIEW OF THEORETICAL MODEL
III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS
IV. SUMMARY
ACKNOWLEDGEMENTS
APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

Figure 1

Figure 2

Figure 3

Figure 4

IV. SUMMARY

I. INTRODUCTION
II. BRIEF REVIEW OF THEORETICAL MODEL
III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS
IV. SUMMARY
ACKNOWLEDGEMENTS
APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

ACKNOWLEDGEMENTS

I. INTRODUCTION
II. BRIEF REVIEW OF THEORETICAL MODEL
III. $\boldsymbol{W^+W^-}$ PAIR PRODUCTION AND THE SEARCH FOR HEAVY MAJORANA NEUTRINOS AT FUTURE LEPTON COLLIDERS
IV. SUMMARY
ACKNOWLEDGEMENTS
APPENDIX A: CALCULATION OF THE SQUARED SCATTERING AMPLITUDE

References

References

Access

Article Metrics

Metrics

通讯作者: 陈斌, bchen63@163.com

Email This Article